A Guide to Simple and Informative Binding Assays

Abstract

The aim of binding assays is to measure interactions between two molecules, such as a protein binding another protein, a small molecule, or a nucleic acid. Hard work is required to prepare reagents, but flaws in the design of many binding experiments limit the information obtained. In particular many experiments fail to measure the affinity of the reactants for each other. This essay describes simple methods to get the most out of valuable reagents in binding experiments.

INTRODUCTION

One of the most common experiments in biochemistry and cellular and molecular biology is testing whether two molecules interact with each other. This includes two proteins binding to each other, a small molecule binding to a protein, or a protein binding to a nucleic acid. In spite of apparent simplicity, many binding experiments reported in this and other journals are poorly designed and fall short of extracting all of the useful information available from the valuable reagents that were collected to do the experiment. In particular many experiments fail to measure the affinity of the reactants for each other. This is a loss, because binding reactions are not digital, with black/white, yes/no answers. Rather, the answer to whether two molecules interact with each other should always be quantitative, with a number that describes the affinity, or if binding is weak, a limit on the possible affinity.

Many attempts to measure affinities fail to meet one or both criteria for a successful binding experiment: the reactions must be at equilibrium at the time of measurement, and the concentration of one reactant must be varied. For example, after much labor an investigator prepares the reactants and mixes them to allow binding; so far, so good. But then the investigator makes the fatal mistake of disturbing the equilibrium by separating the reactants and products before measuring the extent of the reaction. For example, think of typical “GST pull down” or “immunoprecipitation” assays where pelleted material is washed free of the reactants. Even if the extent of the reaction is measured at equilibrium, many forget to vary the concentration of one of the reactants and thus miss the opportunity to measure the affinity. Journals should insist (where practical) that all binding reactions be carried out at equilibrium and that reagents be used to measure (where practical) the equilibrium constant. Otherwise precious reagents and hard work go to waste.

This essay explains proven experimental strategies to maximize the information obtained from reagents painstakingly acquired by biologists for binding studies. The tools for powerful binding assays are available in most laboratories. The essay also points out features of well-designed assays, which greatly simplify analysis of binding data.

THE BASIC BINDING REACTION

Let's begin with a basic, reversible, bimolecular binding reaction: molecule A binds to molecule B forming a complex AB:

Conceptually such reactions are straightforward. In the forward reaction (indicated by the right facing arrow) one molecule of A and one molecule of B collide and bind together. In this case the stoichiometry is 1:1, which is true for most biological binding reactions. Where the final product consists of more than two molecules, the process usually involves a series of reactions each with 1:1 stoichiometry. In the reverse reaction (indicated by the left facing arrow) one AB complex dissociates into A and B.

The association reaction A + B → AB involves two reactants, so it is by definition a second order reaction. The rate of such a second order reaction is

The parameter k₊ is a second order “association rate constant” (lower case k) with units of M⁻¹s⁻¹ (pronounced per molar per second). (A) and (B) are the free concentrations of the molecules available for reacting at the given moment in time. A useful rule of thumb is that association rate constants for molecules the sizes of typical proteins are often in the range of 10⁶ to 10⁷ M⁻¹s⁻¹. These reactions are typically limited by the rates of collisions between molecules, which are determined by both the rates of diffusion of the molecules and the sizes of their interaction surfaces. Small molecules diffuse faster than large molecules, but this is offset by smaller interaction surfaces, restricting most protein association constants to this relatively small range. For more detail see Chapter 4 in Pollard and Earnshaw (2007).

When a complex of two molecules, AB, dissociates, AB → A + B, AB is the only reactant, so by definition this is a first-order reaction. The rate such a first-order dissociation reaction is

The parameter k₋ is a first-order rate constant called a “dissociation rate constant” with units of s⁻¹ (pronounced per second) and (AB) is the concentration of AB. The dissociation rate constant is simply the probability that the complex will fall apart in a unit of time.

EQUILIBRIUM CONSTANTS

A number called the equilibrium constant characterizes the affinity of molecules for each other. A few simple relationships define equilibrium constants and form the basis for determining their values experimentally. By definition at equilibrium the forward and reverse rates of a reaction are equal, so at equilibrium the forward and reverse rates of our binding reaction are equal:

By definition the equilibrium constant (capital K) is equal to the ratio of the forward and reverse rate constants or the ratio of the concentration of products to the concentrations of free reactants at equilibrium.

Defined in this way the equilibrium constant K_eq for the binding reaction has the units of M⁻¹. This definition has the advantage that the value of K_eq is proportional to the affinity. Thus the larger the value of K_eq, the stronger the reaction and the more completely the reactants A and B are converted into the product AB.

The reciprocal of this expression for a binding reaction describes the “dissociation equilibrium constant” or K_d

This form of the equilibrium constant has the units of M, moles per liter. Biologists favor this definition owing to the familiar units. Defined thus, the lower the value of K_d, the stronger the reaction, and the more completely reactants A and B are converted into the product AB.

Given the small range of association rate constants, the value of the dissociation rate constant often determines the affinity. Low affinity interactions with K_ds in the micromolar range have dissociation rate constants around 1 s⁻¹. For a first-order reaction this corresponds to a halftime for dissociation of 0.7 s (t_1/2 = ln 2/k = 0.693/k). On the other hand, high-affinity interactions with K_ds in the nanomolar range have dissociation rate constants around 0.001 s⁻¹ and half lives >10 min.

The equilibrium constant is a thermodynamic parameter directly related to the free energy change (ΔG) for the reaction under a particular set of conditions.

where R is the gas constant and T is the absolute temperature. Favorable reactions have a large K_eq and a large negative free energy change, which drives the reaction toward products.

TWO STRATEGIES TO MEASURE EQUILIBRIUM CONSTANTS

Two general options are available to measure affinities. 1) In an equilibrium experiment, one determines the extent of the reaction as a function of the concentration of one of the reactants. Analysis of these data gives the equilibrium constant. 2) In a kinetic experiment, one determines the rates of the forward and reverse reactions as a function of the concentration of one of the reactants. Analysis of these data gives the rate constants for the forward and reverse reactions. The ratio of these rate constants gives the equilibrium constant.

The kinetic approach is more revealing, because it gives not only the thermodynamic parameter, the equilibrium constant, but also the rate constants, which characterize the dynamics of the system. Note that the street is one way from rate constants to equilibrium constants. Knowing only the affinity from an equilibrium experiment reveals nothing about the rates of the forward or reverse reactions. Although generally stronger than equilibrium experiments, kinetic experiments often require more reagents and more sophisticated assays.

EQUILIBRIUM BINDING EXPERIMENTS

This section outlines the strategy to measure affinity with an equilibrium binding experiment. The following sections provide practical advice about each step.

The reaction in question is simple reversible binding of molecules A and B:

where

(Equations 4 and 5)

We will assume that the stoichiometry is 1:1. Other more complicated outcomes are possible, but this is a reasonable starting assumption.

The task is to measure the equilibrium concentrations of A, B, and AB over a range of concentrations of one of the reactants, A or B. With good design, this experiment is simple compared with the effort required to make the reagents. With a powerful assay the whole experiment may take only a few minutes. Five steps yield the affinity.

Step 1: Develop a sensitive assay to measure the concentration of A_eq, B_eq, or AB. Note that (A_eq) and (B_eq) are the concentrations of free A and free B. To reinforce this essential point, this essay will use (A_free) and (B_free). Measuring one of these concentrations usually suffices for this simple type of reaction, because one generally knows the total concentrations of A and B and therefore can calculate the unknown concentrations by difference from the total concentrations and measurements of (A_free), (B_free), or (AB).

Step 2: Design an experiment with the lowest concentration of A_free, B_free, or AB that can be measured accurately. Put some thought into which reactant to fix and which to vary. Make the decision based on the abundance of the reactants available and the ease of the measurements The following examples use a low concentration of A. This key decision greatly simplifies the experiment and its analysis.

Step 3: Set up a series of reactions, each with a fixed, low concentration of total A and a wide range of concentrations of B. The concentrations of B_free should span a range from less than the K_d to high enough to convert essentially all of A into AB. Pilot experiments will reveal the appropriate concentrations.

Step 4: Let the reactions equilibrate. The time required is often much less (seconds) than often assumed. Then measure either (A_free), (B_free), or (AB) without disturbing the equilibrium.

Step 5: Plot the concentration of AB versus the concentration of B_free and calculate the K_d from the shape of the curve (as explained below) or from the concentration of B_free required for half of A_total to be converted to AB.

ADVICE ON ASSAYS TO MEASURE BINDING REACTIONS

The assay for A_free, B_free, or AB should be sensitive and as simple as possible. Note again that A_free and B_free are the concentrations of free A and free B, not the total concentrations. The assay can be an optical measurement, a chemical measurement, the density of the band on a gel or an immunoblot or anything else, but the signal must be directly proportional to the concentration. The following paragraphs explain how to use chemical and optical assays for binding reactions.

Chemical Assays

When properly calibrated, chemical assays including gel electrophoresis, ELISA, and immunoblots are excellent ways to measure concentrations with materials available in most labs, but these assays must be done without altering the equilibrium. Making chemical measurements at equilibrium is generally possible but rarely achieved.

Faults with Nonequilibrium Chemical Assays

Typical assays prepare an equilibrium mixture of reactants and products but then separate products from reactants, at which point the products start to dissociate to achieve a new equilibrium. Examples of this mistake are assays where products are pelleted, the supernatant containing the free reactants is removed, and the pellet is washed one or more times with buffer without reactants. Because the solution containing the resuspended pellet has no reactants, the forward reaction rate is zero and the products will dissociate. If the affinity is low, the dissociation reaction is typically fast, for example >1 s⁻¹ for a K_d of 1 μM. Therefore the products will dissociate with a half-time of <1 s, making it impossible to measure the equilibrium concentration of products.

Equilibrium Chemical Assays

One way to use a chemical assay at equilibrium is to separate products from reactants without disturbing the equilibrium (Figure 1). If the products differ in sedimentation coefficient from one of the reactants, the products can be pelleted leaving an equilibrium mixture of reactants in the supernatant. For example, reactant B can be attached to a bead (through a GST tag, for example) and equilibrated with a solution of a low concentration of reactant A. Simply pelleting the beads does not change the equilibrium but separates all of the B attached to the beads along with any A bound to B from the free A in the supernatant. Rather than examining the pellet, simply measure the concentration of free A in the supernatant and calculate by difference the concentration of AB in the pellet.

Figure 1.

A quantitative GST pull down assay. Supernatant depletion assay for GST-2/3/A (part of the tail of Acanthamoeba myosin-I) binding amoeba Arp2/3 complex. Conditions: 0.3 mM amoeba Arp2/3 complex in 65 mM NaCl, 10 mM Tris (pH 7), 1 mM DTT was titrated with (•) GST-2/3/A immobilized on glutathione beads or (○) the same volumes of glutathione beads without GST-2/3/A. Beads were pelleted at 16,000 × g, and supernatant proteins were separated by SDS-PAGE, stained with Coomassie, and scanned to measure the fraction bound. The binding isotherm gives a K_d of ∼3 μM. (Inset) Coomassie-stained gel of the supernatants showing Arp2/3 complex depletion. Numbers above each lane indicate total GST-2/3/A μM concentration on the beads (Lee et al., 2000).

To measure affinity carry out this assay with a low, fixed concentration of A and a range of concentrations of B attached to beads (by varying the concentration of beads). The equilibrium concentration of AB as a function of B_free (∼total B) is the data required to calculate the affinity. Figure 1 shows an example of such a quantitative pull down assay, where gel electrophoresis and Coomassie blue staining were used to measure the concentration of a purified Arp2/3 complex in the supernatant after equilibration with a range of concentrations of a GST-ligand bound to beads. In this case the ligand was a region from the tail of myosin-I.

Note that this strategy can be applied to a crude system, if an assay such as a quantitative immunoblot or ELISA is available to measure free A. For example one can titrate a crude cellular extract, diluted to contain a low concentration of A, with a range of concentrations of B bound to beads and measure free A remaining in the supernatant.

If one finds it necessary to measure the complex of AB in the pellet, this can be done with minimal washing using a cushion of glycerol or sucrose in the bottom of the tube. By keeping the washing time brief (seconds) the equilibrium will not drift too far. Washing through a cushion is done by 1) equilibrating the reaction, 2) pelleting the beads through a small volume of buffer with 5–10% glycerol or sucrose, 3) removing the supernatant including most of the cushion, and 4) measuring bound B in the pellet.

The Advantages of Optical Assays

The rewards for developing an optical assay outweigh the effort, because optical measurements have the advantages of speed and simplicity. Speed allows for both equilibrium and kinetic measurements. Good optical assays measure the concentration of one component in equilibrium with the other components of the reaction.

Fluorescence Intensity

The simplest optical assay is a difference in the fluorescence intensity of the product compared with the reactants. In a few favorable cases the intrinsic tryptophan fluorescence of a protein changes when a ligand binds. For example, poly-L-proline binding increases the intrinsic tryptophan fluorescence of profilin (Figure 2). Unfortunately, few reactions give an intrinsic fluorescence signal, but do not fail to check whether your system gives such a signal, because it will save much time and effort. A variant of this approach is a change in the fluorescence intensity of a dye bound to one of the reactants when the product forms, but again such changes are not common. One example is the decrease in fluorescence of pyrene-labeled actin filaments when cofilin binds. This assay was used to collect the binding data for Figure 3.

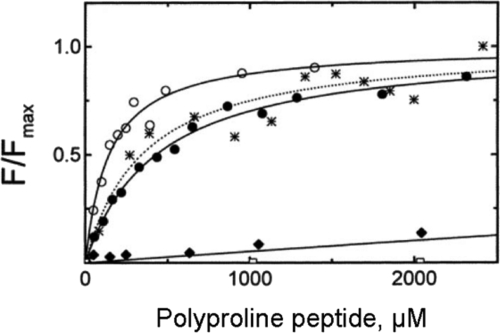
Figure 2.

Equilibrium binding of poly-L-proline oligomers to profilin measured by the increase in intrinsic fluorescence. These experiments tested the effects of peptide size and ionic strength on this simple bimolecular binding reaction. Conditions: 5 μM Acanthamoeba profilin I in 10 mM Tris (pH 7.5), 75 mM KCl, and 3.1 mM NaN₃, 22°C. Excitation 295 nm, emission intensity 318 nm. All data sets are normalized (F/Fmax) to their maximum fluorescence change. Equilibrium dissociation constants (K_d) were obtained by fitting data directly using nonlinear least squares analysis. (•) L-proline₁₀, K_d = 433 μM proline; (*) L-proline₁₅, K_d = 344 μM proline; (O) L-proline₈₂, K_d = 120 μM proline; and (♦) L-(proline-proline-glycine)₅, K_d = 34.1 mM proline; and (□) L-(proline-hydroxyproline-glycine)₅ (Petrella et al., 1996).

Figure 3.

Equilibrium binding of fission yeast cofilin to pyrene-labeled ADP-actin filaments measure by titrating 2 μM pyrenyl actin filaments with 50 nM to 10 μM S. pombe cofilin. Cofilin binding quenches the fluorescence and was used to measure the extent of the reaction. This plot of binding density (fraction of actin bound determined from the extent of quenching of fluorescence) versus free cofilin concentration is sigmoidal owing to positive cooperativity. The apparent K_d = 1/w K_a, where w is the cooperativity factor (8.5 in this case) and K_a = k₊/k₋ measured in kinetics experiments to be 0.12 μM⁻¹, so the apparent K_d is 1.0 μM (Andrianantoandro and Pollard, 2006).

Fluorescence Anisotropy

A universally useful approach is to measure the fluorescence anisotropy of one reactant tagged with a fluorescent dye. Fluorescence anisotropy measures the rotational diffusion of a molecule, so when the reactant binds its partner, the larger product has a lower rotational diffusion coefficient and a higher fluorescence anisotropy. One example is the increase in fluorescence anisotropy when a rhodamine-labeled fragment of the Wiskott Aldrich syndrome protein (the VCA region of WASp) binds Arp2/3 complex (Figure 4). One typically uses a very low concentration of the tagged molecule and titrates in a range of concentrations of the untagged partner molecule. This gives the affinity of the tagged molecule for its partner. The fluorescent dye may influence the binding reaction, so an essential control with any tagged molecule is a competition experiment with the untagged molecule. Fixed concentrations of the tagged molecule and its partner are titrated with a range of concentrations of the untagged molecule to measure the affinity of the untagged molecule for the partner.

Figure 4.

Fluorescence anisotropy assay of equilibrium binding of a rhodamine-labeled ligand to Arp2/3 complex. Rhodamine-WASp-VCA (0.025 μM) was titrated with the Arp2/3 complex in the presence (•; K_d ∼ 0.05 μM) or absence (□; K_d = 0.25 μM) of 5 μM actin filaments (Marchand et al., 2001).

Other Optical Assays

Fluorescence energy transfer is also useful to measure binding but requires fluorescent tags on both reactants, doubling the work in reagent preparation and doubling the chances of artifacts due to the labels. Some products scatter more light than the reactants, so light scattering can be used to measure these products. However, the signal is usually noisy compared with fluorescence assays. Keep in mind that light scattering scales with the inverse fourth power of the wavelength, so using short wavelengths gives much higher signals.

ADVICE ON EXPERIMENTAL DESIGN

An ideal binding experiment has a fixed total concentration of one of the two reactants, let's choose A, that is lower than the K_d. Ten-fold lower than the K_d is fine. Using a low concentration of total A simplifies the execution of the experiment and interpretation of the data, because essentially all of the other reactant B is free under all conditions. The practical limitation is that the assay must be able to measure the concentration of free or bound A.

If one chooses a low concentration of total A, then the experiment is to determine the extent of the reaction over a wide range of concentrations of B. When the concentration of B is below the K_d, most of B is free, because, given the low concentrations of both reactants, little binding will occur. At higher concentrations of B more AB forms, but the concentration of A is so low that virtually all of B is free. Because most of B is free both below and above the K_d, B_free ∼ B_total one does not have to compensate for any B bound to A when analyzing the data.

If the assay lacks the sensitivity to do the experiment with a concentration of A below the K_d, then use the lowest practical concentration of A. Later, when analyzing the data (see below), compensate for the finite amount of B bound to A at each concentration of total B in the sample.

ANALYSIS OF EQUILIBRIUM BINDING DATA

One plots the concentration of AB as a function of the concentration of B_free. This plot will reveal the extent of the reaction. Providing that the experiment included high concentrations of B, B will saturate A and the concentration of AB will reach a plateau. Without reaching this plateau, one does not know the amplitude of the reaction and, unfortunately, without the amplitude, one cannot calculate the equilibrium constant. Many binding experiments reported in reputable journals fail to saturate the reaction and reach a plateau of AB, compromising the value of the hard work. A Scatchard plot is an alternative method to plot the data as (bound)/(free) versus (bound). This formulation was useful in the days before computers, because such plots of the data for a simple bimolecular reaction are linear. However, Scatchard plots are now discouraged, because they can easily hide the fact that a binding curve did not reach a plateau.

Let's take a closer look at a binding curve such as Figure 1. In a successful binding reaction, when B_free is zero, all A is free and (AB) = 0. At the other extreme, when the concentration of B_free is high, all active A is bound to B. The binding curve can reveal whether some A is inactive, because at very high concentrations of B some A is still free. It is important to document in this way the amount of inactive A, which can be ignored in the analysis. Some A may be inactive, because it is denatured, but the existence of inactive A may be interesting and important from a biological perspective. For example, some A may be inactive because a posttranslational modification compromises binding to B.

Two methods are available to determine the equilibrium constant from the binding curve. For a simple bimolecular binding reaction a plot of the fraction of total molecule A that is bound (the fractional saturation) versus B_free is a hyperbola:

The shape of the hyperbola depends on the equilibrium constant. Readily available software can be used to fit the equation to the data and calculate the equilibrium constant. Inspection of the equation reveals that the concentration of B_free required to convert half of A to AB (fractional saturation = 0.5) is equal to the K_d, which can be read directly from a binding curve (Figure 1).

Practically speaking, experiments are set up with concentrations of A_total either below the K_d or higher. If A_total is well below the K_d, essentially all B is free at every concentration of B used in the experiment, so B_free ∼ B_total. Under these circumstances a plot of (AB) versus B_total is a hyperbola with a shape dependent on the equilibrium constant and a half saturating value of B_total is equal to K_d. No math, software, or even much thinking is required with good experimental design.

On the other hand, if the assay requires that the experiment be set up with a concentration of A_total in the range of the K_d, a considerable fraction of total B will be bound to A. Therefore an additional calculation is required to determine B_free. Under these circumstances a quadratic equation can used to fit the binding data and calculate the K_d.

where [LR] is the concentration ligand bound to the receptor, [R] is the total concentration of receptor (B_total in our example, which is varied), [L] is the total concentration of ligand (A_total in our example), and [LR]/[L] is the fraction of ligand bound to receptor. This equation can be fit to the data to obtain the K_d. Using a low concentration of A_total avoids having to deal with this equation.

If the concentrations of both A and B are far above the K_d, then essentially all of the added B will bind to A up to the point where A is saturated. Little or nothing is learned about the affinity in such an experiment, except that the K_d is less than the concentrations of A and B.

COOPERATIVE BINDING REACTIONS

Sometimes the plot of (AB) versus (B_free) is not a hyperbola. This indicates something more complicated than a simple bimolecular binding reaction. For example, when the protein cofilin binds to actin filaments, the binding curve is sigmoidal, evidence for cooperativity in the reaction (Figure 3). Cooperativity means that binding of one ligand molecule to a receptor influences the affinity of subsequent ligand molecules to the same receptor. Binding of oxygen to the four sites on hemoglobin is the classic example (Morgan and Chichester, 1935), where each successive bound oxygen increases the affinity for subsequent oxygens. Both of these examples exhibit positive cooperativity.

Analysis of cooperativity requires models based on physical interactions, an interesting subject beyond the scope of this essay. Figuring out mechanisms in cooperative systems can be complicated. Investigators have been working on cooperative binding of oxygen to hemoglobin for more than 50 years and cooperative binding of cofilin to actin filaments for nearly two decades. For the purposes of this essay, the important point is that a binding curve from a well-designed assay will distinguish a simple bimolecular reaction from a cooperative reaction.

KINETIC BINDING EXPERIMENTS

As noted above kinetic experiments yield more information about binding reactions than equilibrium experiments, but kinetic experiments are much less common. One reason is that more materials, better assays, and specialized equipment are sometimes required. Another reason is that many investigators have no classroom or practical experience with the type of kinetic assays used to evaluate binding reactions. Most biochemistry courses cover only steady state enzyme kinetics. Although useful in some circumstances, neither the experiments nor the methods of analysis are appropriate for binding experiments. To make matters worse, most students find analysis of steady state enzyme kinetics by Michaelis–Menton equations baffling or irrelevant to their work.

Analysis of binding reactions requires a different type of kinetic experiments called presteady state or transient state kinetic experiments. Fortunately, the concepts behind and the execution of presteady experiments are not complicated. One simply changes conditions and observes the time course of the reequilibration of the system. For example, mixing A and B changes the conditions. Then one watches what happens over time. Pretty simple.

A detailed explanation of the methods used in presteady state kinetics is beyond the scope of this essay, but a few general points are useful for any biologist. Let's consider our binding reaction from a kinetics perspective. The reaction is A + B ⇆ AB. The goal is to measure the rate constants, k₊ and k₋, for the two reactions. Some reactions can be measured manually by using low concentrations of reactants to slow the reactions. For fast reactions that take place on a subsecond time scale mechanical mixing in stopped flow or quenched flow devices is required.

Forward Binding Reaction

The second order reaction is A + B → AB, with rate = k₊(A)(B). One can measure the rate constant by observing the time course of the formation of AB after mixing A and B. To simplify the experiment one usually uses “pseudofirst-order conditions” with a low concentration of one reactant, let's say A, and a range of higher concentrations of the other reactant, let's say B. As in the equilibrium binding experiments, the low concentration of A means that most of B is free and its concentration does not change as A is converted to AB. For the purpose of this argument, we will assume that binding is irreversible. With B in excess, the time course of the formation of AB (= the time course of the depletion of A) is an exponential with an observed rate constant k_obs = k₊ (B). By varying (B) one can evaluate k₊.

Dissociation Reaction

The rate of a first-order dissociation reaction AB → A + B is equal to k₋(AB). One can observe this reaction in several ways. Simplest, one can dilute an equilibrium mixture of A, B, and AB and observe the time course of the dissociation of AB to establish new equilibrium concentrations of A and B. Another strategy useful with optical assay is to compete a fluorescent ligand from its receptor with a large excess of unlabeled ligand. The fluorescent ligand dissociates at a rate determined by k₋ and does not rebind, because the unlabeled ligand takes its place.

Because many association reactions have rate constants in the range of 10⁶ to 10⁷ M⁻¹s⁻¹, the rate constant for dissociation of the products is usually the main determinant of the affinity. For example, dissociation rate constants will be on the order of 1 s⁻¹ for a low affinity reaction with a K_d of 1 μM and 0.001 s⁻¹ for a high-affinity reaction with a K_d of 1 nM.

Dealing with Reversible Reactions

These examples ignore the reality that the binding reaction is reversible, which is legitimate for pseudofirst-order conditions or the competition dissociation experiment. On the other hand, many kinetics experiments need to take both reactions into account—a more advanced topic. An important but surprising feature of a reversible binding reaction is that k_obs for the formation of AB is equal to the sum of the rate constants for the two reactions, so for our reaction under pseudofirst-order conditions k_obs = k₊ (B) + k₋. One way to reconcile this in your mind is that the time required for equilibration after mixing A and B is less, because the reverse reaction limits the extent of the reaction.

Note that if one knows K_d from an equilibrium experiment and measures k₋ or k₊, one can calculate the missing rate constant, because K_d = k₋/k₊.

LINKED REACTIONS

Many binding reactions actually occur in two steps:

where the conformation of AB* differs from AB and the second reaction is a pair of reversible first-order reactions. Often such a conformational change is favorable and will pull the overall reaction to the right. Most chemical assays will not distinguish AB and AB*, but the signals from AB and AB* differ in some optical assays, so kinetics can be used to characterize the second reaction.

Everyone trying to understand molecular mechanisms, even experts on kinetics and thermodynamics, is tempted to violate fundamental principles by proposing mechanisms that sound nice but are impossible thermodynamically. One can avoid this trouble by paying attention to something called detailed balance or “microreversibility,” which outlaws perpetual motion machines. The concept of detailed balance is that the free energy change around any cycle of reactions must be zero. Thus the product of the equilibrium constants around the cycle must be one. An “energy square” with the linked binding reactions among molecules A, B, and C illustrates the concept.

Note that direction of each reaction is defined in one direction around this square, so reactions 1 and 2 are given as association reactions with K_eq = k₊/k₋ while reactions 3 and 4 are given as dissociation reactions with K_d = k₋/k₊. If K₁ × K₂ × K₃ × K₄ does not equal 1, something is wrong.

One can use energy squares to calculate unknown equilibrium constants. For example, if one knows that A binds to B with K_eq = 10 μM⁻¹ (association reaction), B binds to C with K_d = 10 μM (dissociation reaction), and AB binds to C with K_eq = 1 μM⁻¹ (association reaction), one can calculate the affinity of BC for A.

MAIN POINTS TO CONSIDER WHEN PLANNING A BINDING EXPERIMENT

• Create a good assay to measure reactants or products.

• Consider the advantages of optical assays.

• Use a low concentration of one of the reactants.

• Vary the concentration of the other reactant, including concentrations that saturate the first reactant.

• Do not disturb the equilibrium when measuring concentrations of reactant or products.

• Calculate the equilibrium constant from the dependence of complex formation on the concentration of the varied reactant.

• Consider measuring rate constants to learn more about the reaction.

• Check detailed balance to avoid pitfalls in linked reactions.