Advection and Diffusion of Substances in Biological Tissues With Complex Vascular Networks

Abstract

For highly diffusive solutes the kinetics of blood–tissue exchange is only poorly represented by a model consisting of sets of independent parallel capillary–tissue units. We constructed a more realistic multicapillary network model conforming statistically to morphometric data. Flows through the tortuous paths in the network were calculated based on constant resistance per unit length throughout the network and the resulting advective intracapillary velocity field was used as a framework for describing the extravascular diffusion of a substance for which there is no barrier or permeability limitation. Simulated impulse responses from the system, analogous to tracer water outflow dilution curves, showed flow-limited behavior over a range of flows from about 2 to 5 ml min⁻¹ g⁻¹, as is observed for water in the heart in vivo. The present model serves as a reference standard against which to evaluate computationally simpler, less physically realistic models. The simulated outflow curves from the network model, like experimental water curves, were matched to outflow curves from the commonly used axially distributed models only by setting the capillary wall permeability–surface area (PS) to a value so artifactually low that it is incompatible with the experimental observations that transport is flow limited. However, simple axially distributed models with appropriately high PSs will fit water outflow dilution curves if axial diffusion coefficients are set at high enough values to account for enhanced dispersion due to the complex geometry of the capillary network. Without incorporating this enhanced dispersion, when applied to experimental curves over a range of flows, the simpler models give a false inference that there is recruitment of capillary surface area with increasing flow. Thus distributed models must account for diffusional as well as permeation processes to provide physiologically appropriate parameter estimates.

INTRODUCTION

When considering a transport process that is distributed in space (governed by partial differential equations) it is important to realize that the geometry of the system plays an important role in influencing its behavior. Therefore, when modeling mass transport in the microvasculature it is important that the structuring of the microvasculature be represented as accurately as possible. The difficulties associated with representing a complex, non-tree-like, three-dimensional network of vessels are often avoided by using models that are distributed in only one dimension (for examples, see Refs. ^{4, 7, 22}, and ⁴⁰). In contrast, we have produced a three-dimensional network model to serve as a foundation upon which to solve associated problems of mass transport. In order to do this we have developed a model based on sets of parallel capillaries between muscle fiber bundles using the basic geometric arrangement shown in the heart by Bassingthwaighte et al.³ and modified by the more extensive data on the types and spacings of capillary-to-capillary connections from Refs. ¹² and ²⁵.

We developed an idealized hexagonal arrangement of parallel capillaries (axial vessels) with numerous cross-connecting capillaries (Figs. 1 and 3). The flow distribution throughout the network is found by posing a linear network problem associated with the topology of the network model. Tracer transport is then simulated based on the advection–diffusion equation.

FIGURE 1.

Hexagonal distribution of axially aligned segments. The network is modeled as a periodic arrangement of 16 axial segment positions in the x–y plane.

FIGURE 3.

Topology of a network generated by randomly placing 160 cross-connecting segments between nearest-neighbor axial vessels. This is a two-dimensional representation of the three-dimensional model. The axial vessel number (see Fig. 1) is plotted vs the axial position. Nodes are indicated as small circles; the large filled circle indicates the arteriolar source; the large open circles indicate venular sinks. The minimum distance along a capillary between cross connections d_min is 15 μm.

The modeling of the transport of diffusible substances plays a role in a variety of physiological studies. For example, understanding the transport of tracer water and tracer oxygen is important in interpreting the results of positron emission tomography (PET) experiments used to discover information related to local perfusion and metabolism in the myocardium.^18,29 Modeling change in flow and its effect on local bulk oxygen concentration is important in interpreting the physiological meaning of blood-oxygenation-level-dependent (BOLD) contrast magnetic resonance imaging (MRI) (Refs. ²⁰ and ³¹) and ¹⁷O nuclear magnetic resonance (NMR) imaging³⁴ of the working brain. The multiple indicator dilution (MID) technique is a tool used to probe the in vivo metabolism of various organs based on injecting tracers and analyzing the outflow concentration curves. (See, for examples, Refs. ^{30, 43}, and ⁴⁷.) The majority of the above-mentioned methods consider compartmental or (at best) one-dimensionally distributed multiregional models for the transport of physiological substances.

The first mass conservative distributed model for tracer kinetics mentioned in the literature is the axially distributed, two-region linear model of Sangren and Sheppard.⁴⁰ This model developed from the distributed model for loss across a capillary barrier developed by Bohr,¹³ from which evolved the calculation for the permeability–surface area product (PS) for the membrane across which the solute is lost, PS=−F log(1 −E), where F is the flow and E is the maximum instantaneous extraction of a permeating solute in the outflow relative to an intravascular reference outflow dilution curve.^17,37 The Sangren–Sheppard model has been extended by many workers to include multiple regions, multiple pathways, and to account for large-vessel dispersion, chemical reaction, nonlinear binding, and axial diffusion. For a review of the simpler models, see Ref. 7. While these models have proven valuable for simulating the transport of a number of substances, their reliability has not been proven for highly diffusible substances such as water.

In the absence of a membrane barrier, an apparent PS due to limitation to extravascular diffusion of the solute can be estimated by Eq. (1), which is derived in Appendix A,

$$\text{PS}=\frac{2D}{\left(\frac{R_o^2}{R_o^2-R_i^2}log(R_o/R_i)-\frac{1}{2}\right)\rho R_o^2}.$$ (1)

Here, D is the extravascular intratissue radial molecular diffusion coefficient, R_o is the outer radius of the effective extravascular Krogh cylinder, R_i is the inner radius, L is the length of the tissue cylinder, and ρ is the density of the tissue in g ml⁻¹. Using D = 1 × 10⁻⁵ cm² s⁻¹, ρ = 1.0 g ml⁻¹, R_i = 3.5 μm, and R_o = 15 μm, one obtains an estimate of PS=500 ml min⁻¹ g⁻¹.

Yet many workers consistently estimate a much lower PS for water from analyzing outflow dilution curves using one-dimensionally distributed models. Model-free analysis based on the similarity of outflow curves for water and antipyrine⁴⁹ and of iodoantipyrine residue curves⁵ over a wide range of flows convincingly demonstrates the insignificance of any radial barrier limitation, which is exactly what is predicted for the heart, from the PS of 500 ml min⁻¹ g⁻¹ calculated in Eq. (1). In striking contrast, Rose et al.³⁹ attribute their low estimates for water permeability, PS values, to significant barriers to water transport across the capillary wall and the cardiac muscle cell membrane. Bassingthwaighte et al.⁶ attribute low PS estimates such as those of Rose et al.³⁹ to diffusional shunting that is not represented at all by the axially distributed models of Ref. 39 (even though the models did account for flow heterogeneity). An alternative model that approximates diffusional shunting is one that accounts for exchange between neighboring capillary–tissue regions by using axial, not radial, diffusion or Gaussian dispersion coefficients with values considerably higher than for molecular diffusion⁹ to approximate the observed curve shapes while incorporating appropriately high values of membrane PSs.⁵⁰

Another inadequately understood phenomenon associated with tracer transport is the apparent increase in PS with increasing flow. This has, perhaps partially erroneously, been attributed to capillary recruitment. A number of studies report that PS appears to increase as the flow in a particular organ is increased. Goresky and co-workers^23,24 found that while lung blood volume increases with cardiac output, carbon monoxide uptake increases with flow even after maximum recruitment has been achieved, indicating an increase in capillary permeability concurrent with increasing flow. Examples have been reported for a variety of tracers in the heart,^16,32 pancreas,⁴⁵ skeletal muscle,³³ brain,¹⁵ and other organs. Of these investigators, most used small hydrophilic solutes whose exchange was clearly barrier limited. Those authors who did not account for the heterogeneity of regional flows²⁶ underestimated PS, we believe. The error is greater at low flows than at high flows, so estimates of PS overestimate the degree of recruitment. Those using highly diffusible tracers that can exhibit flow-limited behavior or diffusional shunting have really no measure of PS or of recruitment of capillary surface area: when PS is so high that it does not impede escape of tracer from blood to tissue, the standard axially distributed Krogh-cylinder-type models grossly underestimate PS. We will use the present multicapillary–tissue model to demonstrate that the apparent recruitment, when there is actually none in the model system, is due to analyzing dilution curves with less complete models that fail to account for exchange between neighboring capillaries.

We are not the first investigators to recommend caution when interpreting the effects of flow on parameter estimates. For example, Audi et al.^1,2 have noted that the Crone–Renkin model and other axially distributed descriptions of tracer transport may lead to variations in estimates of parameters (such as permeability) with flow. A comparison of the behavior of an alternative model (our three-dimensional network model) to that of axial-distributed models, provides new insight into this issue. By simulating a tracer transport experiment performed on our network model and analyzing the washout curves using axial distributed models, we are able to reproduce the artifactually increase in PS predicted by standard models and design an improved axial model in which the unphysical behavior is eliminated.

In this paper we follow standard nomenclature conventions⁸ wherever possible (see the nomenclature at the end of the paper).

METHODS

Structure of the Model

The network geometry is illustrated in Figs. 1 and 3. Parallel to the z axis, 16 vessels are arranged hexagonally in the x–y plane, where the positions are numbered 1–16. This structure is assumed to be periodic in the x and y directions, as indicated in Fig. 1. The structure is also assumed to be periodic in the z direction, with a spatial period of 1000 μm, as illustrated in Fig. 2. The arteriolar and venular zones indicated in Fig. 2 are concepts used by Batra and Rakusan¹² and by Kassab and Fung;²⁵ arteriolar sources are located in arteriolar zones and venular sinks are located in venular zones, and their separation defines the minimum capillary length. The distance between the centers of mass of adjacent arteriolar and venular zones, called the functional capillary length (L_f), was measured in pig hearts²⁵ to be 501 ± 12.9 and 512 ± 11.7 μm in the right ventricle and the left ventricle, respectively. In this study we set L_f = 500 μm (see Table 1). Distances obtained¹² in rat hearts were somewhat longer, which we could also have used as a model parameter.

FIGURE 2.

The network model is arranged periodically in the z (axial) direction. An arteriolar source occurs at a z position chosen from a Gaussian distribution with mean of 500 μm and standard deviation of 50 μm. Venular sinks occur at 125±25 and 875±25 μm.

TABLE 1.

Comparison of model to coronary capillary morphometry.

Tissue	Distance between cross connections (μm)	Functional mean length (μm)	Reference
Dog left ventricle	80	500–1000	Bassingthwaighte et al. (1974) (Ref. 3)
Rat myocardium arterial capillaries	93	598	Batra and Rakusan (1990) (Ref. 12)
Rat myocardium venular capillaries	76	598	Batra and Rakusan (1990) (Ref. 12)
Pig right ventricle	57.8 ± 40.4	501 ± 178	Kassab and Fung (1994) (Ref. 25)
Pig left ventricle	52.7±39.6	512±163	Kassab and Fung (1994) (Ref. 25)
Model	50±37.16	500

Arteriole and Venule Locations

An arteriolar source axial position is chosen from a Gaussian distribution with mean of 500 μm and standard deviation of 50 μm. Two axial positions of venular sinks are chosen from Gaussian distributions of 125 ±25 and 875±25μm. The source and sinks each have an equal probability of occurring in any of the 16 axial segment positions in the x–y plane (see Fig. 1). For example, in the network illustrated in Fig. 3, the source occurs at z=545 μm at position 6. The venular sinks occur at z= 120 μm, position 12, and at z = 890μm, position 10.

Cross-Connecting Segments

The geometry is made realistic by adding cross-connecting segments between axial vessels. Cross-connecting segments are assumed to be parallel to the x–y plane and connect a given axial vessel to any of its six nearest-neighboring axial vessels. By placing 160 cross-connecting segments in the network, an average distance between cross connections of 50 μm is achieved. By randomly choosing the positions of the cross connections from a uniform distribution (with the restriction that no two cross connections on the same axial vessel be separated by less than a given minimum distance d_min) the standard deviation of distance between cross connections was found to be 37.16 μm (see Table 1). An example of a topology created by this algorithm with d_min=15μm is shown in Fig. 3. Notice that the periodic boundary conditions allow nearest-neighbor connections across the boundary sketched in Fig. 1, for example, between axial vessel numbers 2 and 14.

It is interesting to note that such a naive approach to generating a network structure produces a standard deviation of lengths between cross connections that agrees with the anatomic data.²⁵

Modeling Advection and Diffusion in Three Dimensions

This anatomical model of a microvascular structure can be used as a framework for modeling mass transport in a biological system. The advection and diffusion of a nonmetabolizing substance is modeled by Eq. (2):

$$\frac{\partial C}{\partial t}+\mathbf{v}·\nabla C=D{\nabla }^{2}C,$$ (2)

where C is the concentration of the substance, v is the advective velocity vector field describing the motion of blood in the vascular network, and D is the molecular diffusion coefficient in the tissue. Here diffusion is isotropic and occurs homogeneously throughout intravascular as well as extravascular regions. The velocity distribution v(x), is a function of position x and can be generated by solving a hydrodynamic problem related to the network geometry. The velocity vector is nonzero only for positions which correspond to the interior of the vascular network. Permeation into stagnant (nonvascular) regions occurs through passive diffusion. For extravascular tracers we impose periodic boundary conditions on the simulated tissue region.

The transport of an intravascular tracer can be modeled by imposing the no-flux boundary condition on the vessel walls. This condition can be expressed as n · ∇C = 0, where n denotes the unit vector normal to the surface of the vessel wall.

Finding the Flow Distribution

A simple linear model is used to generate a flow distribution for the network shown in Fig. 3. If we denote the hydrostatic pressure at the ith node in the network by p_i and the pressure at neighboring nodes by p_j, then following the usual rules of a resistor network we can write the following flow conservation equation at each node:

$$\sum _j\frac{1}{L_{ij}}(p_i-p_j)=0,$$ (3)

where we assume that the conductivity of the vessel connecting the ith and jth node is inversely proportional to the length of the vessel L_ij. Summation in Eq. (3) implies summation over all nodes that are neighbors of node i. This formulation is based on the assumptions: (1) that all capillary resistances per unit length are the same, (2) that there is no variation in diameter, and (3) that there is no variation in hematocrit or viscosity. The conservation law takes on a slightly different form at the arterial input node:

$$\sum _j\frac{1}{L_{\text{in}-j}}(p_{\text{in}}-p_j)=F_{\text{in}},$$ (4)

where p_in is the input pressure, L_in-j is the length of the segment connecting the input node to the jth node, and F_in is the input flow. We fix the output nodes at a common (arbitrary) ground pressure, force the system by specifying F_in, and solve for the pressures (or equivalently, the flows) throughout the network.

Since the system is linear, the calculated flows can be scaled by any constant factor and still represent a solution to Eq. (3). In practice, the network problem is solved for only one specific value of F_in. Then a solution for any other flow is obtained by scaling.

Simulating Diffusive Tracer Transport

A numerical procedure is applied on a finite grid to solve Eq. (2). The mesh points are hexagonally distributed in the x–y plane as illustrated in Fig. 4, and regularly spaced in the z direction. We have engineered the computational grid so that a vessel cross section corresponds to one grid point. Thus plug–flow velocity profiles are implicitly assumed in our simulations.

FIGURE 4.

Hexagonal grid in the x–y plane used for numerical computation. The positions of axial vessels are indicated by closed circles.

A Strang splitting scheme⁴⁴ is used to simplify the problem into two numerical procedures during each time step: the two numerical procedures are, first, a procedure to calculate the diffusive process, and then a procedure to calculate the advective process. In order to achieve second-order accuracy one half of the normal time step is used in the first call to the diffusion procedure and the last call to the advective procedure.

An explicit finite-volume technique which is second-order accurate in time and fourth-order accurate in space for smooth solutions to the diffusion equation can be derived based on a Taylor series expansion in time:

$$\begin{array}{l}C(\mathbf{x},t+k)\approx C(\mathbf{x},t)+k\frac{\partial C}{\partial t}+\frac{k^2}{2}\frac{{\partial }^{2}C}{\partial t^2}\\ \approx C(\mathbf{x},t)+kD{\nabla }^{2}C+\frac{k^2{D}^2}{2}{\nabla }^{4}C,\end{array}$$ (5)

where k is the duration of the time step.

Notation used for the numerical method is illustrated in Fig. 5. Consider a node in the tissue to have concentration C_i. The six surrounding nodes in the x–y plane are denoted by $C_i^1-C_i^6$. Nodes are separated by the spatial step size g. We denote the neighboring concentration in the positive z direction by $C_i^7$ and the neighboring concentration in the negative z direction by $C_i^8$. A numerical approximation to the Laplacian operator on the mesh is given below and denoted by L₂{C_i}:

$$L_2\{C_i\}=\frac{2}{3g^2}\left(\sum _{j=1}^6{C}_i^j-6C_i\right)+\frac{1}{g^2}(C_i^7+C_i^8-2C_i).$$ (6)

FIGURE 5.

Concentration at grid point is denoted by C_i. Concentrations in the six surrounding points in the x–y plane are denoted by $C_i^1$ through $C_i^6$.

If we denote the estimated concentration after the diffusion step by Ĉ_i, then it follows from Eqs. (5) and (6) that

$${\widehat{C}}_i(t+k)=C_i(t)+{\mathit{kDL}}_2\{C_i(t)\}+\frac{k^2{D}^2}{2}{L}_2\{L_2\{C_i(t)\}\}.$$ (7)

Then the advection step proceeds by the standard upwind method:²⁸

$$C_i={\widehat{C}}_i,$$ (8)

for C_i corresponding to a stagnant (nonvascular) tissue region, and

$$C_i={\widehat{C}}_i+k\sum _{j=1}^8{\mathrm{\Delta }}_{ij}\frac{F_{ij}}{V_g}({\widehat{C}}_i^j-{\widehat{C}}_i),$$ (9)

for C_i corresponding to a vascular grid point. Here, F_ij is the flow from the jth neighbor (see Fig. 5), and V_g is the finite volume associated with each grid point. The parameter Δ_ij is set to either 0 or 1, depending on the direction of the flow between the i and j grid point. If the jth grid point corresponds to stagnant tissue, or if blood flows from point i to j, then Δ_ij = 0. If blood flows from point j to i, then Δ_ij = 1. Numerical inaccuracy associated with the use of the upwind method is studied in Appendix B.

To simulate the transport of an intravascular tracer, it is necessary to simulate advection and diffusion within the intravascular region while not allowing the tracer to permeate into the stagnant tissue. This is done using the above equation, but in this case the Laplacian operator is modified so that the no-flux boundary condition is enforced on the vessel wall:

$$L_2\{C_i\}=\frac{2}{3g^2}\left(\sum _{j=1}^6{\alpha }_j[C_i^j-C_i]\right)+\frac{{\alpha }_7}{g^2}(C_i^7-C_i)+\frac{{\alpha }_8}{g^2}(C_i^8-C_i).$$ (10)

Here α_j = 1 When j corresponds to a grid point in the vascular network, and α_j = otherwise.

Modeling Advection and Diffusion in One Dimension

The three-region axially distributed blood–tissue exchange model described by Bassingthwaighte et al.¹⁰ is reduced to two regions, the same as the two-region axially distributed model of Bassingthwaighte⁴ which accounts for advected plasma and stagnant tissue. We use it to analyze the outflow data generated from the three-dimensional network model. The governing equations for this two-region model in the absence of consumption are:

$$\frac{\partial C_p}{\partial t}=-\frac{FL}{V_p}\frac{\partial C_p}{\partial z}-\frac{{\text{PS}}_e}{V_p}(C_p-C_t)+D_p\frac{{\partial }^2{C}_p}{\partial z^2},$$ (11)

$$\frac{\partial C_t}{\partial t}=-\frac{{\text{PS}}_e}{V_t}(C_t-C_p)+D_t\frac{{\partial }^2{C}_t}{\partial z^2},$$ (12)

where C_p is the concentration of tracer in the plasma, C_t is the concentration in the tissue, F is the blood flow in ml min⁻¹ g⁻¹, L is the length of the capillary in mm, V_p is the volume of the plasma space in ml g⁻¹, and V_t, is the volume to the tissue space in ml g⁻¹. PS_e is the effective permeability–surface area product for which the axially distributed model best matches the behavior of the three-dimensional network model. D_p and D_t are the axial diffusion coefficients in plasma and tissue; when these are zero the equations represent the Sangren–Sheppard model,⁴⁰ and the two-region form of the capillary–tissue exchange unit of the model of Rose et al.³⁹

RESULTS

Tracer Washout From the System

To find the tracer washout following an impulse input into the three-dimensional system, Eq. (2) is solved with the initial condition:

$$C(\mathbf{x},0)=\delta (\mathbf{x}-{\mathbf{x}}_a),$$ (13)

where x_a is the position of the arteriolar source. The outflow concentration is then given by:

$$C_o(t)=\frac{F_{v1}C({\mathbf{x}}_{v1},t)+F_{v2}C({\mathbf{x}}_{v2},t)}{F_{\text{in}}},$$ (14)

where C(x_vi, t) is the concentration at the ith venular sink, and F_vi is the flow into the ith venular sink, and F_in is the input flow from the arteriolar source. The impulse response or frequency function of transit times h(t) is given by:

$$h(t)=\frac{C_o(t)}{{\int }_0^{\infty }{C}_o(t)dt}.$$ (15)

Intravascular tracer washout curves for flows of 0.25, 1.0, and 10 ml min⁻¹g⁻¹ are plotted in Fig. 6. The non-dimensional quantity t̄ · (t/t̄) is plotted vs t/t̄, where t̄ is the mean-transit time of the system, which may be calculated as the volume of the system divided by the flow, or may be computed via the integral $\overline{t}={\int }_0^{\infty }th(t)dt$. The curves have a similar overall shape. As flow decreases, the outflow curve becomes more smooth due to intravascular diffusion.

FIGURE 6.

Intravascular tracer washout simulation from the network model for various flows. The shapes of the curves are similar. But as flow increases, the effects of diffusion are diminished. At low flows the outflow curve is relatively smooth, while at the highest flow shown (10 ml min⁻¹ g⁻¹), the outflow curve is not unim odal.

In Fig. 7 we show concentration profiles of a diffusible (extravascular) tracer in a slice through the x–z plane following injection of an impulse bolus at the arterial inflow (indicated by the yellow arrow in the t = 0 slice). The total flow in the system is 2 ml min⁻¹ g⁻¹ and D = 1 × 10⁻⁵ cm²s⁻¹. Each profile corresponds to a different time in the simulation, as indicated to the left of Fig. 7. The tracer spreads through the tissue as a traveling wave: a plane wave of concentration moves in the z direction. But this is not the traveling wave described by Goresky in 1963.²² Here, a nearly uniform concentration in the transverse (x-y) plane extends over regions supplied by vessels with variable flow. In addition, the concentration wave disperses in the z direction as it moves through the tissue.

FIGURE 7.

Simulated concentration profiles in a slice through the x-z plane are shown following injection of an impulse bolus at the arterial inflow. Each profile corresponds to a different time in the simulation. The injection point is indicated in the top slice (t=0) by an arrow. The color bar to the right indicates concentration in arbitrary units. Tracer spreads from the injection point into the venular zones with concentration remaining relatively constant in the x (and y) direction. This simulation was performed using a flow of 2 ml min⁻¹ g⁻¹.

Tracer washout curves from the system for various flows are shown in Figs. 8 and 9 for D = 1 × 10⁻⁵ cm² s⁻¹. For a flow-limited tracer in an axially distributed system, as defined by Goresky,²² one would expect the curves plotted in Fig. 8 to superimpose with one another, and with the intravascular washout curves plotted in Fig. 6. In fact, the impulse response in the flow-limited case reduces to a delayed impulse for each pathway. This corresponds to Goresky’s²² traveling wave description. But the curves in Fig. 8 are dispersed and do not superimpose due to the effects of diffusional and advective exchange between neighboring capillaries. As flow decreases, the peak in the outflow curve occurs relatively earlier. This demonstrates that the Sangren–Sheppard type of axially distributed model is not appropriate for highly diffusible tracers.

FIGURE 8.

Tracer washout simulation from the network model for various flows. Lower flow washouts show an earlier peak due to diffusional shunting. The diffusion coefficient D is 10⁻⁵cm²s⁻¹.

FIGURE 9.

Tracer washout simulation from the network model for various flows. A flow-limited regime exists for flows between 2 and 5 ml min⁻¹ g⁻¹ in which the normalized outflow curves appear similar. At higher flow (10 ml min⁻¹ g⁻¹) an early peak occurs due to a bolus of tracer that remains intravascular during its passage through the network. The diffusion coefficient D is 10⁻⁵cm²s⁻¹.

Normalized outflow curves for higher flows are plotted in Fig. 9. These data are quite similar over a range of flow of 2–5 ml min⁻¹g⁻¹. At a much higher flow (10 ml min⁻¹g⁻¹) the outflow concentration is no longer similar to the curves in the flow-limited regime. Notice that an early peak occurs that is due to a bolus of about 0.05% of the total tracer which is the nonescaping throughput fraction that remains intravascular during its passage through the network. The ratio of intravascular to extravascular volume is about 0.04 (perhaps a little low for heart, but quite suitable for skeletal muscle), and the intravascular tracer first appears at about one quarter of the mean-transit time in Fig. 6. Thus the intravascular bolus appears at about 1% of the mean-transit time for the case of an extravascular tracer.

Permeability–Surface Area Product as a Curve-Shaping Factor

To compare the behavior of the three-dimensional network simulation described above to the behavior of an axially distributed model [Eqs. (11) and (12)], the output predicted by the model of Bassingthwaighte et al.¹⁰ was fitted to the simulated outflow concentration “data” obtained from the three-dimensional model using the SENSOP optimization routine.¹⁴ The estimated permeability-surface area product PS_e was optimized to obtain a best fit to the data obtained from the three-dimensional network simulation with the diffusion coefficients D_p and D_t set to the molecular diffusion coefficient value used in the network simulation: 1 × 10⁻⁵ cm²s⁻¹. Model fits were obtained using both a single pathway and a heterogeneous flow (20-pathway) implementation. For the 20-pathway model, a Gaussian distribution of flows with relative dispersion of 40% was used in order to approximate the intravascular washout curves over the range of mean flows studied. In fitting the outflow curves using the single-pathway model, it was necessary to vary the ratio of plasma volume to extravascular tissue volume V_p/V_t to obtain good fits (see below). This ratio was constrained to not exceed the value 0.1, and achieved this maximum allowed value for each data set. The heterogeneous flow model was less sensitive to the choice of V_p/V_t, and the ratio was fixed at 0.04 for all of the model fits.

The estimated PS_e is plotted as a function of flow in Fig. 10. Estimated PS_e, based on the single-pathway model is plotted as circles; and estimates based on the parallel-pathway model are plotted as diamonds. The estimates of PS_e are one to two orders of magnitude lower than the Krogh cylinder approximation of 500 ml min⁻¹ g⁻¹ calculated from Eq. (1). The values range from 0.82 ml min⁻¹ g⁻¹ at a flow of 0.25 ml min⁻¹ g⁻¹ to 38.2 ml min⁻¹ g⁻¹ at a flow of 10 ml min⁻¹ g⁻¹ for the single-pathway model fits, and monotonically increase with flow even though there was no change in the expected PS in the data generated from the network model. For the parallel-pathway model estimates, the range is slightly greater, and the behavior is analogous. This increase with flow is akin to those observations of PS for highly diffusible solutes versus F that have been interpreted to imply recruitment of capillary surface area.

FIGURE 10.

Estimated permeability–surface area product PS_e obtained from fitting simulated outflow data to the axially distributed two-region model described in Bassingthwaighte et al. (Ref. ¹⁰). Diamonds correspond to model fits using a heterogeneous flow model (20 parallel units) with a relative dispersion of flows equal to 40%. The circles correspond to model fits obtained from a single-tube axial distributed model.

Using an Axial Dispersion Coefficient to Fit Data

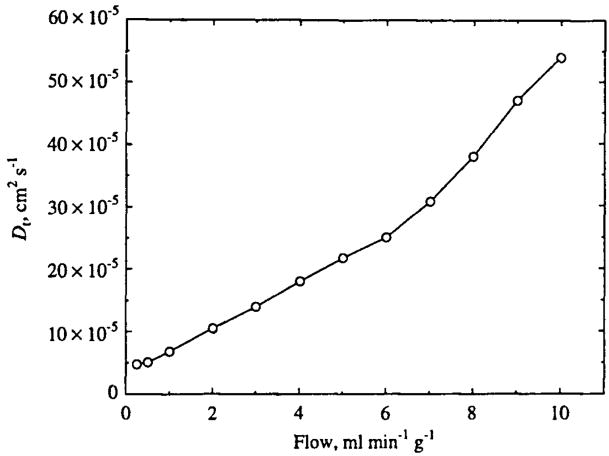
To fit the outflow data from the three-dimensional model using the axially distributed model with the more physically appropriate value of PS_e = 500ml min⁻¹ g⁻¹ while approximating the enhanced mixing associated with the three-dimensional advection and diffusion in our network model (see Fig. 7) and in real tissue, we use a high value of the extravascular diffusion or dispersion coefficient D_t for the axial model solutions [Eqs. (11) and (12)]. In allowing D_t to be greater than the molecular diffusion coefficient we are using the diffusive term in Eq. (12) to phenomenologically describe the enhanced dispersive effects associated with the three-dimensional model. With the intravascular diffusion coefficient kept at D_p = 1 × 10⁻⁵cm²s⁻¹ and PS_e, set at 500 ml min⁻¹ g⁻¹, D_t was estimated by again fitting the data predicted by the three-dimensional model, using a single-pathway axial model. The estimates are plotted in Fig. 11 and range from 4.8 × 10⁻⁵cm²s⁻¹ at a flow of 0.25 ml min⁻¹ g⁻¹ to 54 × 10⁻⁵ cm²s⁻¹ at a flow of 10 ml min⁻¹ g⁻¹ and increase almost linearly with flow. In using axial dispersion to fit the outflow data, the ratio V_p/V_t=0.04 was used for all of the data sets. Using the physically reasonable value for PS_e, the network data could not be fit by the parallel flow model, regardless of the value of the axial dispersion coefficient.

FIGURE 11.

Estimated extravascular dispersion coefficient D_t obtained from fitting simulated outflow data to an axially distributed two-region single-capillary model (see Refs. ⁴ and ¹⁰) with the capillary PS_e set to the value of 500 ml g⁻¹ min⁻¹, corresponding to the expected effective PS based on Eq. (1). Plasma diffusion D_p is 10⁻⁵cm²s⁻¹.

Examples of model fits to the data obtained at a flow of 5 ml min⁻¹ g⁻¹ are shown in Fig. 12. The output from the network model is plotted as a solid line. The axially distributed model, with physically realistic parameters, PS=500 ml min⁻¹ g⁻¹ and D_t = 1 × 10⁻⁵cm²s⁻¹ predicts an outflow curve that is much less dispersed than that predicted by the three-dimensional (3D) network model. The peak is shifted to the right and occurs near the mean-transit time of 12 s. The curves obtained by varying PS_e and D_t do a much better job of approximating the shape of the outflow curve and the location of its peak. After the addition of a reasonable amount of experimental noise and increased dispersion due to transport in arteries and veins, these outflow curves would not be distinguishable from that of the network model.

FIGURE 12.

Various axially distributed model fits are shown for the simulated outflow curve from the 3D network model. The solid line indicates output from the network model calculated at a flow of 5 ml min⁻¹ g⁻¹. The axial model approximates the network model behavior only for unrealistically low PS or high D_t.

Microvascular Unit Network Behavior Best Approximated by a Single Pathway

We note that when a multiple-tube (parallel) model is used to mimic the behavior of the three-dimensional network, the estimates of PS_e are similar to those obtained based on the single-tube model. More importantly, the trend in the estimates as a function of flow are identical. So our conclusions are supported equally well by data fitting using either implementation of the axial model (single tube or parallel tube). Yet we believe that the more appropriate axially distributed model for comparison is the single-pathway model, because our network model is anatomically based on a single arteriole input into the capillary network. The single-pathway model is supported by the tracer profiles shown in Fig. 7. Here, the tracer moves through the system with a relatively constant concentration in the x–y plane. The increase in dispersion, when compared to a single-pathway axially distributed flow-limited model, is not due to a number of parallel pathways delivering the tracer to the output at different mean times, as could be described by a heterogeneous-flow axially distributed model.

In contrast to the parallel-flow description, in Fig. 7 the bulk of the tracer tends to move through the system with the mean-axial flow. Variations in axial flow in both the axial and longitudinal directions, and the presence of cross-connecting flows contribute to an “advective–diffusive” shunting which brings the appearance time and peak of the outflow concentration-time curves closer together and earlier than would occur in an axially distributed model (see Fig. 12). The shapes are a little closer to monoexponential shapes than those from the axially distributed model. Furthermore, the dependence of the transport kinetics upon the precise geometry of the microvascular network is rather weak, so long as the topology is tortuous enough to result in enhanced dispersion in the axial direction and nearly uniform concentration in the transverse plane. Hence, it is not surprising that, for physically reasonable values of PS, the axial model fits the data better when a single pathway is used and when D_t is allowed higher values than the molecular diffusion coefficient.

DISCUSSION

While the advection and molecular diffusion of substances in tissues containing three-dimensional vascular networks is important in physiological studies of mass transport and metabolism, and for describing the behavior of any diffusible substance that is carried in the blood, mathematical models typically do not consider the complex three-dimensional structure of the vascular network. Progress has been made by other workers toward modeling the steady-state oxygen distribution in complex geometries.^41,42,48 But until now little information on kinetic modeling of advection and diffusion in complex physiological geometries has appeared in the literature. We have found that a model of mass transport that does consider the tissue and the network to be three-dimensional predicts behavior that is strikingly different from that of one-dimensional models. In fact, PS estimated by fitting the one-dimensional model to the outflow generated from the three-dimensional model are two orders of magnitude lower than one expects based on direct calculation using a radially symmetric Krogh cylinder. Therefore, the three-dimensional transport problem cannot be accurately reduced to a one-dimensional problem or a three-dimensional problem based on a radially symmetric tissue cylinder.

The normalized nondimensional outflow concentration curves plotted in Fig. 8 are much more dispersed than are predicted by the model of Sangren and Sheppard.⁴⁰ Since the Sangren and Sheppard model reduces to the one-dimensional advection equation as the ratio of PS to flow approaches infinity,²² the impulse response becomes a delayed impulse. Bassingthwaighte and Goresky⁷ refer to this case as flow-limited transport. According to their formulation, the normalized outflow concentration curves t·h(t/t̄) from a flow-limited system should be similar for a range of flows as long as the fraction of flow in each pathway remains constant. If the model of Sangren and Sheppard⁴⁰ is modified to include axial diffusion the output curves become more dispersed. Yet estimated PS values based on fitting a one-dimensional model to the outflow curves from the three-dimensional model are much too low to be consistent with flow-limited behavior in a one-dimensional system. This model fits the data only when unrealistically low values of PS are used to shape the model solutions, resulting in PSs ranging from 0.86 ml min⁻¹ g⁻¹ at a flow of 0.25 ml min⁻¹ g⁻¹ to 43 ml min⁻¹ g⁻¹ at a flow of 10 ml min⁻¹ g⁻¹.

An approximately flow-limited regime exists for our model for flows between 2 and 5 ml min⁻¹ g⁻¹ (Fig. 9). Though the real PS is high, PS values estimated from one-dimensional models for these same curves are quite low. Outside of this range the shape of the outflow curve changes significantly. For the highest flow case (10 ml min⁻¹ g⁻¹) an early peak occurs that corresponds to tracer that remains intravascular during its passage through the network. The flow-limited behavior is consistent with the results reported by Yipintsoi and Bassingthwaighte.⁴⁹ Likewise the earlier peaks at low flows are consistent with the tracer water dilution curves in their study. One observes flow-limited behavior with intravascular markers where radial permeation and diffusion play no role.²⁷ Yipintsoi and Bassingthwaighte⁴⁹ found that the transport of tracer water in isolated dog hearts is flow limited for flows up to three times the normal, but did not achieve high enough flow to demonstrate any barrier limitation. For low flows they detected an early appearance of tracer that was attributed to diffusional shunting which is in agreement with the three-dimensional model, but not the one-dimensional model. Similar behavior has been reported for thermodilution curves obtained in the heart by Bassingthwaighte et al.,⁶ in correspondence with the generally expected behavior in organs where diffusional shunting can occur.⁵

The behavior of the network model at medium flows is in agreement with the theory of Goresky.²² Note that Goresky’s strategy was quite different: he recorded out flow curves for five tracers injected simultaneously and found they were superimposed on each other by the same scaling that we have used here, which indicated that there were no apparent diffusional hindrances to the transport of any of the solutes and that convection dominated. This is excellent strategy and is even better if repeated over a wide range of flows. As flow is increased in a system the ratio of PS to flow decreases, and the behavior may no longer fall into the flow-limited regime. As flow decreases the ratio of PS to flow increases and the outflow curves produced by the Sangren–Sheppard⁴⁰ and Goresky model²² remain in the flow-limited regime. But the normalized outflow curves generated from the network model at low flow (Fig. 8) show earlier peaks as flow is decreased. This is due to the effects of diffusional shunting which becomes more apparent at low flow. The three-dimensional model captures this shunting behavior because the complex topology of the network produces a variety of functional capillary lengths. Also, advection occurs in directions in three space other than along the straight line between arteriole and venule, enhancing the mixing of tracer in the tissue.

For highly diffusible solutes, particularly small solutes with high solubility in lipids, blood–tissue exchanges take place not only in the capillary but also in arterioles and venules. Duling and Berne¹⁹ showed oxygen loss from arterioles of nearly 100 μm diam; water, a smaller molecule, can be expected to exchange across arterioles and veins of similar size. So the functional exchange region is much longer for such solutes,^21,35 as Renkin³⁸ has pointed out with respect to osmotic water fluxes. This is not accounted for in our multicapillary–tissue model because it did not include the exchanges with arterioles and venules but in principal this is a simple extension of the present model and does not change the concept.

Although the washout from the network model is approximately flow limited over a range of flows, this does not discount the existence of diffusional shunting in the system. There is a common misconception that shunting does not occur if it can be shown that tracer transport is approximately flow limited over a range of flows. This is clearly not the case. We have demonstrated that the outflow curves for flows in the flow-limited regime have an early peak which is not consistent with washout from axially distributed models with high PS. Furthermore, when flow is lowered sufficiently there is overt precession of tracer compared to the flow-limited expectation. In other words, simply because the normalized outflow concentration curves appear similar over a range of flows, one should not conclude that the microvascular transport can be adequately modeled by an axially distributed model reduced to the flow-limited case.

Based on analysis of bulk oxygen concentration changes following a step increase in flow, van der Ploeg et al.⁴⁶ concluded that cardiac oxygen transport was better represented by a single-compartment model than by a Krogh cylinder model. This conclusion is related to the inconsistencies between the behavior of axially distributed models and that of a three-dimensional vascular system (the coronary microvasculature). We also demonstrate inconsistencies between an axially distributed model and a three-dimensional system. In a sense, the increased mixing of tracer observed in our network model causes its behavior to fall somewhere between the extremes of a well-mixed compartment and an axially distributed system. However, we do not advocate the use of compartmental models to describe the transport of highly diffusible substances such as oxygen or water. We emphasize that blood–tissue exchange is a distributed process that is best modeled by spatially distributed partial differential equations. The approach we have taken herein is to describe the geometry of the microvasculature as realistically as possible and to solve an advection–diffusion equation distributed in three dimensions. It may be possible to reduce the number of spatial dimensions to two without losing any relevant information.

Another approach that we have introduced is to modify axially distributed models to include a mechanism for enhanced mixing in the extravascular region. In this case, a nonphysical parameter (namely, the low PS product) is eliminated and replaced by a realistically high (or infinite for practical purposes) value. This method is appealing because the model complexity is reduced to one dimension. In addition, this approach seems reasonable in a phenomenological sense, because increased axially dispersion is the most striking feature of the tracer concentration profiles obtained from the network model (Fig. 7).

With the D in Eqs. (11) and (12) set to a suitable value for the molecular diffusion coefficient, the axially distributed model that we used to fit the outflow concentration predicted by the network model includes no such mechanism for enhanced mixing in the tissue region. In this case PS_e is the only parameter available as a curve-shaping factor to fit data obtained from the three-dimensional model. Unrealistically low values of PS_e are obtained due to the early peaks in the outflow data. Since the peaks occur earlier as flow decreases, PS_e estimates also decrease as flow decreases (see Fig. 10).

When PS_e is set to the physically realistic value predicted by Eq. (1), we have been able to fit the data predicted by the three-dimensional model using extravascular diffusion coefficients almost two orders of magnitude higher than the molecular diffusion coefficient (Fig. 11). Thus increased dispersion in the extravascular space provides a reasonable description of the enhanced mixing of tracer that is associated with a complex three-dimensional vascular network, but it is not sufficient to obliterate axial concentration gradients to the level where van der Ploeg’s mixing chamber could be applied (see Fig. 7). However, increasing D_t does of course tend to reduce the axial gradients and may be of practical utility. While the present advection–diffusion multicapillary model is computationally demanding, the standard blood–tissue exchange (BTEX) models represented by Eqs. (11) and (12) and computed using the highly efficient Lagrangian step method are not. Because they can fit both real data and the simulated “data” as shown here by increasing D_t, one could simplify the analysis by using D_t as a constant ratio to F. From Fig. 11 one can say empirically that D_t ≅ 5×10⁻⁵cm²s⁻¹+40 × 10⁻⁵F(cm²s⁻¹)/(ml g⁻¹ min⁻¹) for the tissue model geometry used here. This factor relating D_t to F will have to be determined for real tissues as it must be dependent on the actual tissue geometry.

This analysis suggests that reports of PS increasing with flow are due at least partially to an artifact of the use of oversimplified axially distributed single-capillary models to fit data obtained from complex three-dimensional capillary–tissue network systems. However, this study focuses on the analysis of model tracer dilution curves for solutes with very high membrane permeabilities. Substances like sucrose or EDTA which do not enter cells truly have low capillary PS products since they traverse the capillary wall only via the interendothelial clefts. Thus analyses for these solutes based on axially distributed models³² are more likely to provide accurate estimates of PS increases due to recruitment. It will be important to study this effect carefully and to determine its dependence on network geometry, on capillary PS, and on the diffusion coefficient of the tracer in the tissue.

NOMENCLATURE

C

concentration of tracer

C_i

concentration of tracer at the ith grid point on the computational grid

$C_i^j$

concentration of tracer at jth neighbor of ith grid point on the computational grid (see Fig. 4)

C_p

concentration of tracer in the advecting (or plasma) region of the two-region axially distributed model

C_t

concentration of tracer in the stagnant (or tissue) region of the two-region axially distributed model

D

molecular diffusion coefficient used in the three-dimensional network model

D_p

diffusion coefficient in the advecting (plasma) region of the two-region axially distributed model

D_t

diffusion coefficient in the stagnant (tissue) region of the two-region axially distributed model

d_min

minimum distance between cross-connecting segments in the microvascular network model

I₁

first-order modified Bessel function

F

flow in the two-region axially distributed model

F_in

arterial inflow into the network model

g

finite grid spacing for numerical computation

h(t)

transit time distribution function

k

finite-time step for numerical computation

L

length of the axially distributed model capillary–tissue unit

L₂{·}

finite-difference approximation of Laplacian operator

L_ij

length of vessel connecting the ith and jth nodes in the three-dimensional microvascular network model

n

unit vector normal to the surface of a vessel wall

PS

permeability–surface area product

PS_e

effective permeability–surface area product obtained from fitting the output of the axially distributed model to the output of the three-dimensional model

P_i

pressure at the ith node in the microvascular network

q

mass flow out of the vessel (and into the tissue cylinder). Used in deriving an expression for the effective PS of a stagnant tissue cylinder

r

independent variable denoting distance from the center

R_i

inner radius of the tissue cylinder used in deriving an expression for the effective PS of a stagnant tissue cylinder

R₀

outer radius of the tissue cylinder used in deriving an expression for the effective PS of a stagnant tissue cylinder

t

independent variable denoting time

t̄

mean-transit time

V_g

volume associated with one grid point of the computational grid

V_t

volume of stagnant tissue region in the two-region axially distributed model

V_p

volume of advecting plasma region in the two-region axially distributed model

x

vector denoting position

ν(x)

velocity vector

x,y,z

three-space variables denoting Cartesian coordinates

α_i

computational device used to differentiate between vascular and stagnant tissue regions on the numerical grid

Δ_ij

computational device specifies the direction of flow between the ith and jth grid points on the numerical grid

ρ

mass density of the tissue

APPENDIX A: ESTIMATING THE PS OF A TISSUE CYLINDER

Imagine a radially symmetric blood–tissue exchange unit composed of an advecting capillary surrounded by stagnant tissue. The time-dependent advection–diffusion equation can be written as:

$$\frac{\partial }{\partial t}C(r,z,t)=-\nu (r)\frac{\partial C}{\partial z}+D\left[\frac{1}{r}\frac{\partial }{\partial r}r\frac{\partial }{\partial r}+\frac{{\partial }^2}{\partial z^2}\right]C,$$ (A1)

where ν(r), the fluid velocity, is zero in the stagnant tissue. This system describes advection in a capillary surrounded by a stagnant tissue cylinder.

When the extravascular radial diffusion is rapid compared to the axial diffusion, as is the case when the radius of the tissue cylinder is much smaller than its length, we can remove the explicit dependence on r from Eq. (A1) and reduce the system to a standard two-region axially distributed model. Here, we describe how to compute the effective PS of such a model.

Assuming that radial concentration profiles relax to a quasiequilibrium, then the dependence of concentration on radius is approximately a solution to Laplace’s equation at any axial position z:

$$\frac{1}{r}\frac{\partial }{\partial r}\left[r\frac{\partial }{\partial r}C(r,z,t)\right]=0.$$ (A2)

The following two conditions can be imposed on the solution to Eq. (A2). First, the concentration at the vessel wall, C(r=R_i), is equal to the concentration in the plasma (which is assumed to not depend on r):

$$C(R_i,z,t)=C_p(z,t).$$ (A3)

Second, we introduce the average concentration in the tissue, which is defined to be:

$$C_t(z,t)=\frac{2}{R_o^2-R_i^2}{\int }_{R_i}^{R_o}r·C(r,z,t)dr,$$ (A4)

where R_o is the outer radius of the effective extravascular Krogh cylinder. Solving Eq. (A2) with these conditions gives the concentration in a tissue cylinder at any position z:

$$C(r,z,t)=\left[\frac{C_t(z,t)-C_p(z,t)}{\frac{R_o^2}{R_o^2-R_i^2}{log}_e(R_o/R_i)-\frac{1}{2}}\right]log\left(\frac{r}{R_i}\right)+C_p(z,t).$$ (A5)

The mass flow out of the vessel (and into the tissue cylinder) dq/dt can then be written in terms of an approximate PS times the concentration difference:

$${\frac{dq}{dt}=-2\pi R_{i}LD\frac{d}{dr}C(r)|}_{r=R_i}=PS·(C_p-C_t)(\rho \pi L{R}_o^2),$$ (A6)

where P is the permeability, S is the surface area of capillaries per unit mass of tissue, L is the length of the tissue cylinder, and ρ is the tissue specific gravity. Evaluating Eq. (A6) and solving for PS gives:

$$\text{PS}=\frac{2D}{\left(\frac{R_o^2}{R_o^2-R_i^2}log(R_o/R_i)-\frac{1}{2}\right)[\rho R_o^2]}.$$ (A7)

APPENDIX B: ACCURACY OF THE UPWIND METHOD

Inaccuracies associated with the use of the upwind method [Eq. (9)] are manifested as a “numerical diffusion” which causes concentration profiles to artificially disperse in space.²⁸,³⁶ This principle is illustrated in Fig. 13 where outflow concentration-time curves following an impulse input into a single-capillary model with no permeation are plotted. In this case the model equation is the one-dimensional advection equation:

$$\frac{\partial C_p}{\partial t}=-\frac{FL}{V_p}\frac{\partial C_p}{\partial z},$$ (B1)

where C_p is the concentration in the capillary, F = 3.0 ml min⁻¹ g⁻¹ is the capillary flow per unit mass, L= 1.0 mm is the length of the capillary, and V_p = 0.05 ml g⁻¹ is the capillary volume per unit mass of tissue. The output predicted by the upwind model is compared to the output predicted by the minmod method,²⁸ a second-order flux-limiter method, for a grid size of h = 5 μm and a time step of k = 0.0025 s. Each method predicts an outflow curve that is substantially dispersed compared to the theoretical delayed impulse output curve. But the minmod method behaves substantially better and introduces less artificial dispersion. When there is no exchange between capillary and tissue, then the Lagrangian sliding fluid element algorithm⁴,¹¹ gives an undispersed output.

FIGURE 13.

Comparison of upwind method to minmod flux-limiter method. Outflow concentration curves following an impulse injection are plotted for the axial-distributed model with one advecting region and no permeation. Theoretical output curve (solid arrow) is a delayed impulse. The upwind method introduces substantially more dispersion than the minmod method. Grid size g=5 μm and a time step k = 0.0025 s.

Unfortunately flux-limiter methods such as the minmod limiter can be computationally costly and complicated to apply in a complex geometry like the three-dimensional network described above (see “structure of the model” in the methods section). But if the tracer dispersion due to permeation and extravascular diffusion dominates the numerical diffusion associated with the upwind method, then it is reasonable to use the simple upwind method for the advection step.

The artificial diffusion introduced by the upwind method for a permanent tracer can be studied using the model equations of Sangren and Sheppard:⁴⁰

$$\frac{\partial C_p}{\partial t}=-\frac{FL}{V_p}\frac{\partial C_p}{\partial z}-\frac{{PS}_e}{V_p}(C_p-C_t),$$ (B2)

$$\frac{\partial C_t}{\partial t}=-\frac{{PS}_e}{V_t}(C_t-C_p),$$ (B3)

which are similar to Eqs. (9) and (11) but contain no molecular diffusion terms. The analytic solution for the output concentration following an impulse input into this system is given by:

$$h(t)=e^{-PS(1/F+(t-V_c/F/V_t))}\times \frac{PS}{\sqrt{V_{t}F(t-V_c/F)}}{I}_1\left(2PS\sqrt{\frac{t-V_c/F}{{FV}_t}}\right),$$ (B4)

where I₁ is the modified Bessel function of first order.

The solution predicted by Eq. (B4) for F = 3.0 ml min⁻¹g⁻¹, V_p = 0.05ml g⁻¹, V_t = 0.95 ml g⁻¹, and PS=30 ml min⁻¹ g⁻¹ is plotted as a solid line in Fig. 14. A numerical solution is constructed using a split scheme which uses the upwind method for the advection step, again using a grid size of g = 5 μm and a time step of k = 0.0025 s. In this case the numerical solution is virtually identical to the theoretical result. This is because permeation between the stagnant and advecting regions is responsible for the majority of the tracer dispersion and the error introduced by the upwind method is relatively small.

FIGURE 14.

Numerical and analytic solutions to Eqs. (B2) and (B3) are compared. The numerical solution (dashed line) is virtually indistinguishable from the analytic solution (solid line). The numerical method is a splitting scheme which uses the upwind method for the advection step. Grid size g=5 μm and a time step k= 0.0025 s.

The numerical diffusion associated with the upwind method disappears when the time step is matched to the grid size according to k=V_pg/FL. This is equivalent to the Lagrangian method described in detail by Bassingth-waighte et al.¹⁰ For a time step of k= 0.0025 s, the Lagrangian approach requires a grid size of g = 2.5 μm and results in a numerical solution within 1% of the theoretical curve. It is impossible to consider using the Lagrangian method for the network model because the flow magnitude varies throughout the network.