Adrenal Gland Abnormality Detection Using Random Forest Classification

Abstract

Adrenal abnormalities are commonly identified on computed tomography (CT) and are seen in at least 5 % of CT examinations of the thorax and abdomen. Previous studies have suggested that evaluation of Hounsfield units within a region of interest or a histogram analysis of a region of interest can be used to determine the likelihood that an adrenal gland is abnormal. However, the selection of a region of interest can be arbitrary and operator dependent. We hypothesize that segmenting the entire adrenal gland automatically without any human intervention and then performing a histogram analysis can accurately detect adrenal abnormality. We use the random forest classification framework to automatically perform a pixel-wise classification of an entire CT volume (abdomen and pelvis) into three classes namely right adrenal, left adrenal, and background. Once we obtain this classification, we perform histogram analysis to detect adrenal abnormality. The combination of these methods resulted in a sensitivity and specificity of 80 and 90 %, respectively, when analyzing 20 adrenal glands seen on volumetric CT datasets for abnormality.

Introduction

Abnormalities of the adrenal glands range from benign adenomas to more worrisome primary adrenal malignancies and metastatic disease. A significant body of imaging literature dedicates itself to differentiating between these entities [1–3]. The overwhelming majority of the methods described in the literature require increasingly busy radiologists to analyze the imaging characteristics of adrenal lesions, often with manually drawn regions of interest (ROIs). While this is the standard of care, it is no small task. Up to 5 % of thoracoabdominal computed tomography (CT) scans are estimated to demonstrate some adrenal abnormality [4]. Identification and differentiation of adrenal “incidentalomas” as benign or malignant, is critical to proper patient workup, follow-up, and overall medical care. The sheer number of adrenal abnormalities makes them a good potential candidate for automated detection and analysis.

Common image processing techniques used for organ segmentation include atlas-based techniques and other supervised, semi-automatic methods [5–8]. While these could be applied to the automated image analysis of adrenal glands, drawbacks include the availability of accurate deformable registration techniques, issues associated with the registration algorithms, and their inability to provide a completely automated solution. The random forest approach has gained much popularity for image classification tasks. In [9], it is shown that using random forests, the training and testing costs can be reduced compared to a multi-way Support Vector Machine (SVM) classifier. The “Extremely Randomized Clustering Forests” [10] have shown to be resistant to background clutter and reports efficiencies in training and testing. The final classification task, however, is handled by a SVM trained separately. In [11], a unary classification is performed by integrating topological information into the random forest framework. A few other papers which have utilized random forests to perform classification tasks are [12–15].

A random forest classification framework is a classification technique whose strength lies in its ability to capture visual patterns as discriminating features. While random forests have been leveraged for identification of other organs from volumetric CT acquisitions before [16], [17], a pixel-wise classification of the adrenal glands on CT using random forests has not been used in combination with histogram analysis to determine abnormality. Our approach can be used to create a fully automated decision support tool for routine image processing and analysis of the adrenal glands. We are not aware of any such implementations of coupling the random forest and histogram analysis techniques for abnormality detection of the adrenal glands.

The purpose of this study was to determine if a random forest classification framework in combination with statistical image processing tools can be leveraged together to identify the adrenal glands from a volumetric CT acquisition and determine whether they are normal or abnormal. Achieving this would require classification of an entire CT volume (abdomen and pelvis) into three classes: right adrenal, left adrenal, and background. Subsequently, a Kullback–Leibler (KL) distance measure is utilized to categorize the identified adrenal pixels as normal or abnormal. The resulting tool would be a completely automatic tool which detects adrenal abnormality without human intervention. Such a tool can provide economies of efficiency, technology, and personnel by alerting radiologists or other physicians that an adrenal abnormality requires their closer scrutiny.

Materials and Methods

The study involved human subjects and/or clinical information and was approved by a local Institutional Review Board.

Data

Fifteen anonymized volumetric computed tomography scans were retrospectively obtained for evaluation of the system. This dataset yielded 30 individual adrenal glands for analysis, 10 of them were used for training and the other 20 were used for testing. There were 13 males and 2 females with a mean age of 70.

Reference Standard

A board-certified radiologist with 30 years of experience manually segmented each adrenal gland. This manual segmentation served as the reference standard for evaluation of the random forest classification where each pixel in the dataset represented a right adrenal, left adrenal, or background pixel. In addition, two board-certified radiologists reached a consensus regarding whether each adrenal gland was normal or abnormal. The manual segmentation and consensus interpretation served as the reference standard.

Training

Random Forest Classification

Our training data for the random forest classification consisted of five CT volumes with both normal and abnormal adrenal glands. Each pixel from each of these volumes was manually labeled for the three classes: right adrenal (RA), left adrenal (LA), and background (BG).

Next, the adrenal glands from this dataset were utilized to train the random forest according to the following method. For simplicity let’s consider a single CT training volume “V” and define a few terms:

The position of a pixel in the volume “V” is defined by:

The index into set of classes is given by:

Now let us consider a single tree as shown in Fig. 1, and let us consider a single node where a set of pixels “S” is being split into “S₁” and “S₂.” The objective of the split is to decrease the entropy in the set “S” and at the same time try to achieve the best split controlled by certain conditions. In other words, we mean to achieve purer distributions as we go down the tree as shown on the left hand side of Fig. 1. When we reach the leaf node, we expect to achieve a distribution, which is pure enough to distinguish the three classes when we plot the posterior probability distributions of the three classes.

Fig. 1.

Single classification tree

The node split function at each node is given by:

where,

a_j

upper threshold

δ_j

feature, coupling between the boxes and a reference pixel “X” (Fig. 2)

b_j

lower threshold

and the feature response,

Fig. 2.

Feature, δ_j: fixed coupling between subvolumes F₁ and F₂ with respect to pixel “X”

In the equation above, C₁ and C₂ are the channels, and in our case, we use “C₁ = C₂ = intensity” or “gradient.” F₁ and F₂ are the subvolumes as shown in Fig. 2, and in our case, we use λ = 1.

The size of “F” can vary anywhere from a cuboid of (1 × 1 × 1 mm) to (100 × 100 × 100 mm) and is not necessarily a cube, and the size is determined by a random feature selection approach.

At each node, the node optimization is given by:

where,

H(S)

Entropy of set “S” with respect to its class labels

The above term is actually a measure of distribution purity. As shown in Fig. 1, the distribution gets purer and purer as we proceed towards the leaf node. Thus, a binary test is chosen to minimize the uncertainty of the class labels in the subsets. The feature and threshold pair used to split the pixel set “S” into “S₁” and “S₂” which gives the maximum gain (I) is selected to be the node feature/threshold. In our case, we use 500 randomly selected features at each node, and the best feature/threshold pair is selected to be the node feature/threshold. Once the split is done, the two children nodes are created with the two subsets, and the recursive step continues till the leaf node is reached. In our case, we fix the tree depth (depth = 10). So each tree has 1,024 leaf nodes. For each leaf node, we then record the average class label of the labeled pixels that have reached that node. This average class label can be interpreted as the posterior probability of the pixel being RA, LA, or BG given the fact that this pixel falls into that leaf. The posterior distribution is given by:

Where

l

leaf number

t

tree number

c

class label

Once we obtain the posterior probability at each leaf node for all the trees in the forest (three in our case), the training is said to be complete.

Histogram Analysis

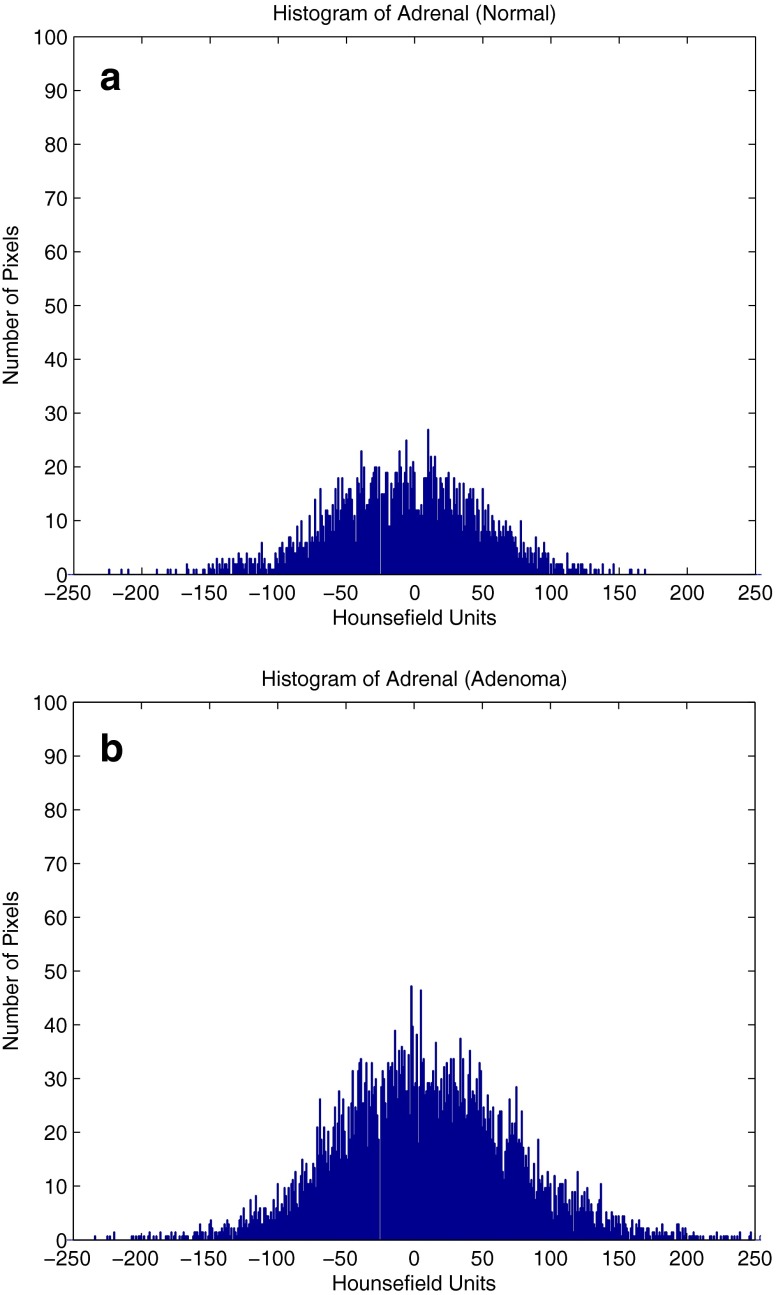
The training for this portion of our system consisted of manually tracing the adrenal glands of our training data which consisted of five normal adrenals and five abnormal adrenals. For each patient, the complete adrenal gland was traced manually and the respective histogram was plotted. Fig. 3a displays the histogram plot for a normal adrenal and Fig. 3b for an abnormal adrenal. Using a probabilistic mixture model, the histograms for the normal patients were combined to generate a “normal histogram,” and the histograms of the abnormal patients were combined to generate an “abnormal histogram.” The mixture model is given by:

Fig. 3.

Histogram of a normal adrenal and b abnormal adrenal

Where

f_x(n)

the combined histogram

a

scaling factor

f_y(n)

individual histograms from each adrenal

These histograms were fit to a Gaussian curve thus giving us a “normal curve” and an “abnormal curve.” The training was said to be complete with the generation of these curves.

Testing

Random Forest Classification

With three trees and at each node fixing a node feature and node threshold (found in training), a test volume can be processed from the root of the tree till all the pixels from the test volume reach the leaf nodes. Figure 4 shows the three trees with the posterior distribution for the leaf nodes.

Fig. 4.

Random forest with three trees

Since each pixel reaches a certain leaf node for each of the tree, we arrive at three posterior distributions. The final ensemble posterior for each pixel (the combination of the posteriors) is given by:

where,

T = 3

(Number of trees)

Thus at the end of testing, each pixel is associated with a distribution, and this distribution predicts the probability of the pixel belonging to each of the three classes. We use the hard decision approach and classify a pixel into that class which has the highest posterior probability among the three classes. Thus at the end of the testing stage, each pixel will be labeled as belonging to one of the three classes. In our case, we tested our random forest to classify 20 adrenal glands from the CT volumes, and the results are discussed later.

Histogram Analysis of the Adrenal Glands

In the testing stage, pixels identified as adrenal were obtained from our random forest framework, and the corresponding histogram was plotted. A Gaussian curve was then fit to this histogram, and the KL distance was measured for this curve with respect to the “normal curve” and “abnormal curve.” If the test curve was closer to the “normal curve,’ then the adrenal gland was classified to be normal and vice versa. Figure 5 shows the test histogram to be closer to the abnormal curve; thus, it was classified to be an abnormal adrenal. The test case was an abnormal adrenal.

Fig. 5.

Histogram of test adrenal classified to be abnormal

Statistical Analysis

For evaluation of the random forest, results of the pixel-wise classification of the CT volumes into right adrenal, left adrenal, and background were compared with the manual segmentation, which served as a reference standard. For each pixel, a determination was made as to whether it was accurately classified or not. This resulted in an overall calculation of sensitivity and specificity.

For evaluation of the ability of the use of histogram—KL distance analysis to determine whether the segmented adrenal glands are normal or abnormal, a comparison was made with the reference standard established by the consensus of two board-certified radiologists. Again, sensitivity and specificity were determined.

Hardware

The current system has been implemented on a Dell Precision workstation with 12 GB RAM and a quad-core processor.

Results

As we have discussed above, our technique performs classification of the entire CT volume (abdomen and pelvis) to obtain three classes namely RA, LA, and BG. Once this classification task is done, the pixels belonging to RA and LA are analyzed to detect abnormality. Thus in this section, we will show two different sets of results. The first set of results is with respect to the classification accuracy of the random forest classification algorithm, and the second set of results will show the accuracy of the overall system in automatically detecting adrenal abnormality.

The output of our random forest classification framework is displayed in Fig. 6 (3D view) for two of our patients in which the classified adrenal pixels can be seen. The kidney is also displayed just for reference. As we can see, the adrenal glands are classified accurately which sit on top of the kidneys. Our system was tested for 20 individual adrenal glands, and the results of the classification are as shown in Table 1.

Fig. 6.

3D view of segmentation results of the adrenal glands for two cases

Table 1.

Results of random forest classification

Sl. No	Class	Sensitivity
1	RA	76
2	LA	87
3	RA	85
4	LA	72
5	RA	80
6	LA	77
7	RA	86
8	LA	89
9	RA	75
10	LA	70
11	RA	78
12	LA	82
13	RA	85
14	LA	80
15	RA	79
16	LA	83
17	RA	70
18	LA	74
19	RA	78
20	LA	88

The mean specificity across all the cases was approximately 99 %. Mean sensitivity was 79.7 %. The final step of our technique is histogram analysis of these classified adrenal pixels to detect abnormality. Table 2 shows the results of abnormality detection. From the table above, the final results we have achieved in the detection of adrenal abnormalities are a sensitivity of 80 % and specificity of 90 %.

Table 2.

Results of abnormality

Case no.	Ground truth	Detection
1	Norm	Norm
2	Abn	Abn
3	Norm	Norm
4	Norm	Abn
5	Norm	Norm
6	Norm	Norm
7	Abn	Abn
8	Abn	Norm
9	Abn	Abn
10	Abn	Abn
11	Norm	Norm
12	Abn	Abn
13	Abn	Abn
14	Norm	Norm
15	Norm	Norm
16	Abn	Abn
17	Abn	Norm
18	Abn	Abn
19	Norm	Norm
20	Norm	Norm

Detection (Norm normal, Abn abnormal)

Discussion

The main results of the study are that a random forest classification framework in combination with histogram analysis was able to achieve 79.7 % sensitivity and 99 % specificity in classifying adrenal glands and a sensitivity of 80 % and specificity of 90 % in detecting abnormalities of adrenal glands. The high specificity for the classification task is in part because the count of the adrenal pixels was very low compared to the whole volume or in other words the percentage of BG pixels in the CT volume was very high compared to the percentage of pixels belonging to the adrenal glands.

While random forests have been used for labeling of organs in the past [16], to our knowledge, they have not been used on a pixel-wise classification basis for identification of the adrenal glands combined with histogram analysis to detect abnormality. A random forest is a collection of classification trees. While widely used in the recent past, to perform deterministic classification tasks, individual classification trees may suffer issues like overfitting. The random forest approach seems to have resolved this issue [16]. The technique now achieves higher generalization and better classification accuracy.

Previously, some studies suggest that evaluation of Hounsfield units within a ROI or a histogram analysis of a ROI can be used to determine the likelihood that an adrenal gland is abnormal [18–27]. This however has the inherent drawback that the selection of ROI can be arbitrary and operator dependent. This subjective ROI selection can lead to contradicting diagnosis. Also, previous studies have utilized thick sections (2.5–10 mm), and this becomes a problem when there is localized fat which can be averaged out with a thick section. We took three steps to overcome these issues

1. To segment the entire adrenal gland

2. To create a histogram of the entire adrenal gland

3. To perform histogram analysis to detect abnormality

There are several limitations of this study. Currently, the classification forest algorithm has been trained on 10 adrenal glands and tested on 20 previously unseen adrenal glands. To make the system more robust, bigger data sets could be used. One of the inherent problems with the random forest approach is the lengthy training time. Further parallelization of code could be utilized to further reduce this time.

As described, histogram analysis of the entire adrenal gland is used to classify it as normal or abnormal. Histogram analysis alone may not be the most efficient way to detect abnormality. As a future step, other statistical analysis techniques need to be tested to detect abnormality.

Conclusions

Our technique of automatically detecting adrenal abnormality first by classifying the adrenal pixels automatically from the entire CT volume using the random forest classification framework and then using histogram analysis to detect abnormality was tested on 20 adrenal glands and achieved a sensitivity of 80 % and a specificity of 90 %. With future work involving training and testing on larger datasets, accuracy is likely to improve. This combination of techniques is promising for evaluation of abdominal pathology.