MEGA6: Molecular Evolutionary Genetics Analysis Version 6.0

Abstract

We announce the release of an advanced version of the Molecular Evolutionary Genetics Analysis (MEGA) software, which currently contains facilities for building sequence alignments, inferring phylogenetic histories, and conducting molecular evolutionary analysis. In version 6.0, MEGA now enables the inference of timetrees, as it implements the RelTime method for estimating divergence times for all branching points in a phylogeny. A new Timetree Wizard in MEGA6 facilitates this timetree inference by providing a graphical user interface (GUI) to specify the phylogeny and calibration constraints step-by-step. This version also contains enhanced algorithms to search for the optimal trees under evolutionary criteria and implements a more advanced memory management that can double the size of sequence data sets to which MEGA can be applied. Both GUI and command-line versions of MEGA6 can be downloaded from www.megasoftware.net free of charge.

The Molecular Evolutionary Genetics Analysis (MEGA) software is developed for comparative analyses of DNA and protein sequences that are aimed at inferring the molecular evolutionary patterns of genes, genomes, and species over time (Kumar et al. 1994; Tamura et al. 2011). MEGA is currently distributed in two editions: a graphical user interface (GUI) edition with visual tools for exploration of data and analysis results (Tamura et al. 2011) and a command line edition (MEGA-CC), which is optimized for iterative and integrated pipeline analyses (Kumar et al. 2012).

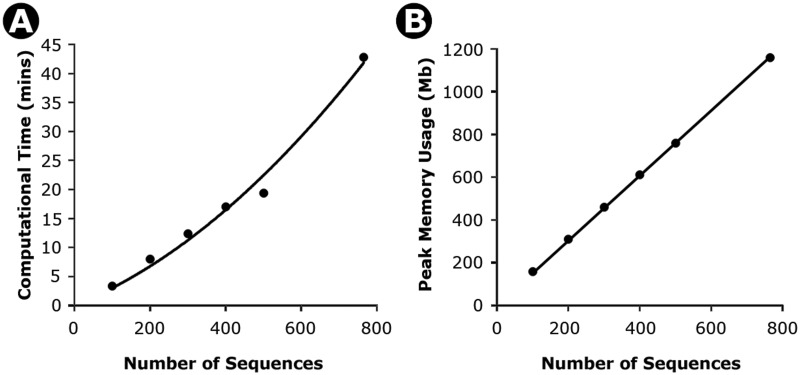
In version 6.0, we have now added facilities for building molecular evolutionary trees scaled to time (timetrees), which are clearly needed by scientists as an increasing number of studies are reporting divergence times for species, strains, and duplicated genes (e.g., Kumar and Hedges 2011; Ward et al. 2013). For this purpose, we have implemented the RelTime method, which can be used for large numbers of sequences comprising contemporary data sets, is the fastest method among its peers, and is shown to perform well in computer simulations (Tamura et al. 2012). RelTime produces estimates of relative times of divergence for all branching points (nodes) in any phylogenetic tree without requiring knowledge of the distribution of the lineage rate variation and without using clock calibrations and associated distributions. Relative time estimates produced by MEGA will be useful for determining the ordering and spacing of sequence divergence events in species and gene family trees. The (relative) branch rates produced by RelTime will also enable users to determine the statistical distribution of evolutionary rates among lineages and detect rate differences between species and duplicated gene clades. In addition, relative times obtained using molecular data can be directly compared with the times from nonmolecular data (e.g., fossil record) to test independent biological hypotheses. The RelTime computation in MEGA6 is highly efficient in terms of both performance and memory required. For a nucleotide alignment of 765 sequences and 2,000 bp (data from Tamura et al. [2011]), MEGA6 required just 43 min and 1 GB memory (including the calculation steps mentioned below). Both time and memory requirements increase linearly with the number of sequences in MEGA6 (fig. 1). Figure 2 shows a timetree produced by MEGA6 and displayed in the Tree Explorer, which has been upgraded from previous versions of MEGA to display confidence intervals and to export relative divergence times and evolutionary rates for branches, along with absolute divergence times and confidence intervals (see below). The Tree Explorer also allows customization of the timetree display in many ways for producing publication quality images.

Fig. 1.

Time (A) and memory (B) needed for increasingly larger data sets for timetree calculations in MEGA6. Results shown are from an analysis of a nucleotide sequence alignment of 765 sequences and 2,000 bp. An increasingly larger number of sequences were sampled from this alignment to obtain the computational time (minutes) and computer memory (Megabytes, Mb). The time taken increases polynomially with the number of sequences (4 × 10⁻⁰⁵x² + 2.64 ×10⁻²x; R² = 0.99), where x is the number of sequences. However, a linear regression also fits well (0.048x; R² = 0.93). Similarly, the memory required increases linearly with the number of sequences (1.52x, R² = 0.99). All calculations were performed on the same computer with an Intel Xeon E5-2665 CPU, 128 GB RAM, and running Windows Server 2012 64-bit edition.

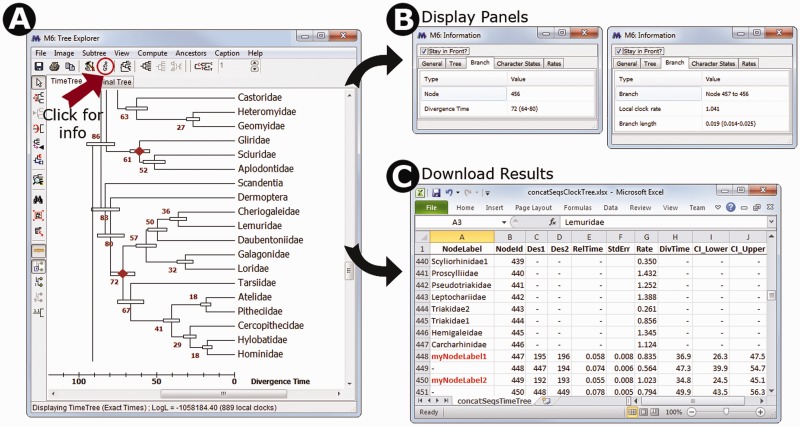
Fig. 2.

(A) Timetree inferred in MEGA6 and shown in the Tree Explorer, where it is displayed with divergence times and their respective 95% confidence intervals. A scale bar for absolute divergence times is shown. (B) An information panel that can be made visible by pressing the icon marked with an “i”. When focused on a tree node (left side), it shows the internal node identifier, and absolute or relative divergence time as appropriate; when focused on a branch (right side), it displays the local clock rate as well as the relative branch length. (C) A timetable exported using the displayed timetree, which shows the ancestor–descendant relationship along with relative node times, relative branch rates, absolute divergence times, and confidence intervals. Users can display internal node identifiers in the Tree Explorer as well as internal node names, which can be provided in the input topology file. On pressing the “Caption” in the Tree Explorer menu bar, MEGA produces the following text to inform the user about the methods, choices, and data used. Caption: The timetree shown was generated using the RelTime method. Divergence times for all branching points in the user-supplied topology were calculated using the Maximum Likelihood method based on the General Time Reversible model. Relative times were optimized and converted to absolute divergence times (shown next to branching points) based on user-supplied calibration constraints. Bars around each node represent 95% confidence intervals which were computed using the method described in Tamura et al. (2013). The estimated log likelihood value of the topology shown is −247671.60. A discrete Gamma distribution was used to model evolutionary rate differences among sites (4 categories, +G, parameter = 38.07). The tree is drawn to scale, with branch lengths measured in the relative number of substitutions per site. The analysis involved 446 nucleotide sequences. All positions with less than 95% site coverage were eliminated. That is, fewer than 5% alignment gaps, missing data, and ambiguous bases were allowed at any position. There were a total of 1,048 positions in the final data set. Evolutionary analyses were conducted in MEGA6 (Tamura et al. 2013).

Using calibrations to translate relative times to absolute times: The relative times produced by the RelTime method can be directly converted into absolute times when a single known divergence time (calibration point) based on fossil or other information is available. This facility is incorporated in MEGA6 where a global time factor (f), which is computed from the given calibration point, converts all estimates of relative times (NTs) to absolute times (ATs) where AT_x = f × NT_x for the internal node x. This approach is taken because NTs are already shown to be linearly related with the true time (Tamura et al. 2012). However, researchers often use multiple calibration points along with information on upper and/or lower bounds on one or more calibration points. In order to consider those constraints when estimating f, we have extended the RelTime implementation such that the estimate of f produces estimates of AT that satisfy the calibration constraints. In this case, if there are a range of values for f that do not violate the calibration constraints, then the midpoint of that range becomes the estimate of f. If one or more of the ATs fall outside the calibration constraints, then f is set so that their deviation from the constraints is minimized. In this case, NTs for the nodes with estimated ATs are adjusted to satisfy the calibration constraints, such that the estimated ATs for the offending nodes will lie between the minimum and maximum constraint times specified by the user. These adjustments to NTs are followed by re-optimizing all other NTs in the tree recursively using the standard RelTime algorithm. Figure 2 shows a timetree display with absolute times in the Tree Explorer, where 95% confidence intervals are shown for each node time (see below).

Confidence intervals for time estimates: MEGA6 also provides confidence intervals for relative and absolute divergence times, which are necessary to assess the uncertainty in the estimated time and test biological hypotheses. In this formulation, variance contributed by the presence of rate variation among lineages (V_R,i) is combined with the estimated variance of relative node time (V_NT,i). We compute V_R,i using the mean of the coefficient of variation of lineage rates over all internal nodes (C_R). It is obtained by first computing the mean (µ) and standard deviation (σ) of the node-to-tip distance for each internal node in the original tree with branch lengths. Then, C_R = ∑[σ_i/µ_i]²/(n-3), where n is the number of sequences. For node i, V_R,i = (NT_i × √C_R)². The variance of node height (V_H,i) is estimated by the curvature method obtained during the maximum likelihood estimation of branch lengths, and thus relative NTs, for each node. Then, the variance of NT is V(NT_i) = V_NT,i + V_R,i, which is used to generate a 95% confidence interval. The bounds of this interval in terms of relative time are then multiplied by the factor f to provide confidence intervals on absolute times when calibrations are provided. It is important to note that this variance does not incorporate the uncertainty specified in the calibration times by the user through the specifications of minimum and maximum bounds, because the statistical distribution of the calibration uncertainty is rarely known. Therefore, we only use the range of calibration bounds during the estimation of f that converts relative times into absolute times, as described above, but this range does not affect the size of the confidence interval in any other way. In the future, we plan to enhance the estimation of f when users provide statistical distributions specifying the calibration uncertainty (see also, Hedges and Kumar 2004).

Timetree Wizard: In practice, the estimation of timetrees can be cumbersome, as one must provide a phylogeny, a sequence data set, and calibration points with constraints. To simplify this process, we have programmed a Timetree Wizard to enable users to provide all of these inputs through an intuitive step-by-step graphical interface. Figure 3A shows a flowchart of the Timetree Wizard, where the user first provides a sequence alignment and a tree topology for use in building a timetree. MEGA6 validates these inputs by mapping (sequence) names in the topology to the names in the alignment data. If the topology contains a subset of sequences present in the alignment, MEGA automatically subsets the sequence data. Additional automatic subsetting of data is provided in the Analysis Preferences Dialog box (see fig. 3E). In the next step, the user has the option to provide calibration constraints by using a new Calibration Editor in MEGA6 where calibration points are specified by 1) point-and-click on individual nodes in the tree display (fig. 3B), 2) selecting name-pairs from dropdown lists such that their most recent common ancestor on the topology refers to the desired node (fig. 3C), and/or 3) uploading a text file containing calibration constraints in a simple format (fig. 3D). If no calibration constraints are provided, then only relative times and related statistical measurements will be produced by MEGA6, but users still have an option to specify them in the Tree Explorer where the timetree containing relative times is displayed.

Fig. 3.

(A) The flowchart of the Timetree Wizard. When launching the timetree analysis, a user first provides a data file containing a sequence alignment and another file containing a phylogeny (topology). (B) The Calibration Editor is invoked when the user needs to specify calibration constraints, which contains facilities to mark calibrations on top of the user-specified topology. (C) Users may also specify calibrations selecting two sequence names whose most recent common ancestor (MRCA) points to the node to use for calibration. (D) The user may also upload constraints via formatted text files for which two types of formats are supported. In one, the calibration time constraints and the names of two taxa whose MRCA is the node to calibrate are given (panel C style). In the second, a node name in addition to the time constraints is given and this node name matches an internal node label that is included in the Newick tree file that contains the topology that is used for the timetree analysis. (E) Analysis Preferences Dialog enables the user to select methods, models, and data subset options.

The next step in Timetree Wizard is for the user to select various analysis options in the Analysis Preferences Dialog, including the types of substitutions to consider (e.g., nucleotide, codon, or amino acid), evolutionary model describing the substitution pattern, distribution of substitution rates among sites (e.g., uniform or gamma-distributed rates and the presence of invariant sites), options for excluding certain alignment positions, and stringency for merging evolutionary clock rates during timetree analysis. These options are available in a context-dependent manner based on the type of sequence data being used in the analysis (e.g., nucleotide, coding vs. non-coding, or proteins). For coding nucleotide data, the users may subset the data based on the desired codon positions or ask MEGA to automatically translate codons into amino acids and conduct analysis at the protein sequence level. The data subset options also allow for handling of gaps and missing data, where one can choose to use all the data or exclude positions that contain a few or more gaps or missing data (e.g., Partial Deletion option). The stringency for merging clock rates option indicates the statistical significance to use for deciding conditions in which the ancestor and descendant rates will be the same (rate merging), which is important to reduce the number of rate parameters estimated and to avoid statistical over-fitting. Once these and other options are set, the RelTime computation begins.

Other enhancements in MEGA: In addition to the new timetree system in MEGA6, we have made several other useful enhancements. First, we have added the subtree-pruning-and-regrafting (SPR) algorithm to search for the optimal tree under the maximum likelihood (ML) and maximum parsimony (MP) criteria (Swofford 1998; Nei and Kumar 2000). In addition, the tree-bisection-and-regrafting (TBR) algorithm is now included to search for the MP trees. These algorithms replace the close-neighbor-interchange (CNI) approach and allow for a more exhaustive search of the tree space (Swofford 1998; Nei and Kumar 2000). These algorithms were tested on simulated data sets that were analyzed in Tamura et al. (2011). The final trees produced by SPR heuristic search were, on average, more optimal than the true tree, a phenomenon explained by Nei et al. (1998). Therefore, MEGA6 heuristic searches are expected to perform well in practical data analysis.

We have also upgraded MEGA source code to increase the amount of memory that MEGA can address in 64-bit computers, where it can now use up to 4 GB memory, which is twice its previous limit. The source code upgrade has also increased the canvas size in Tree Explorer, which can now render trees with as many as 4,000 taxa. Finally, we have implemented a usage analytics system to assess options and analyses that are the most used. At the time of installation, users have a choice to participate in this effort, where we wish to generate a better understanding of the needs of the user community for prioritizing future developments. For the future, we have already planned the release of a full 64-bit version of MEGA as well as support for partitioned ML phylogenetic analyses. An outcome of this effort is a 64-bit command-line version of MEGA6 that supports the timetree analysis, which can be downloaded from www.megasoftware.net/reltime (last accessed October 19, 2013) and used for very large sequence data sets.