Evaluation of Electronic Effects in the Solvolyses of p-Methylphenyl and p-Chlorophenyl Chlorothionoformate Esters

Abstract

The solvolyses of p-tolyl chlorothionoformate and p-chlorophenyl chlorothionoformate are studied in a variety of organic mixtures of widely varying nucleophilicity and ionizing power values. This solvolytic data is accumulated at 25.0 °C using the titration method. An analysis of the rate data using the extended (two-term) Grunwald-Winstein equation, and the concept of similarity of substrates based on their l/m ratios, shows the occurrence of simultaneous side-by-side addition-elimination and unimolecular S_N1 mechanisms.

1. Introduction

Chlorothionofomate esters are useful as derivatizing agents [1] and common organic building blocks in the synthesis of commercial thiocarbonate esters, nitriles, and isonitriles [2,3]. High fungicidal activity was demonstrated [4] for the p-substituted aryl thiocarbamate analogs which are also cytotoxic [5].

Queen and McKinnon [6] affirmed that phenyl chlorothionoformate (PhOCSCl, 1) and alkyl chlorothionoformates (ROCSCl) in general hydrolyze rapidly to yield hydrochloric acid, carbonyl sulfide and the corresponding alcohol. In water at 4.96 °C, they obtained rates of 0.374 × 10^-4 s^-1, 1.73 × 10^-4 s^-1, and 25.4 × 10^-4 s^-1, for PhOCSCl, methyl chlorothionoformate (MeOCSCl), and ethyl chlorothionoformate (EtOCSCl) respectively. The increase in reactivity observed with the increase in the electron-donating ability of the alkyl group, coupled with the positive entropy of activation, and a solvent deuterium isotope effect, k(D₂O)/k(H₂O) of 0.78 for the hydrolysis of MeOCSCl, made them conclude [6] that such aryl and alkyl chlorothionoformate esters hydrolyze by unimolecular S_N1 mechanisms.

Lee at al. [7-9] expanded on Queen’s MeOCSCl and PhOCSCl mechanistic work to include in their study the substrates ethanolyses, methanolyses, and solvolyses in water, aqueous ethanol, and aqueous acetone. They then proposed that MeSCOCl [7,8] had S_N1 character in the water-rich solvents and a greater S_N2 character in the more organic mixtures. For PhOCSCl, Lee, Koo, and others [9] also suggested a general base catalyzed S_N2 mechanism in the aqueous binary mixtures of ethanol (EtOH), methanol (MeOH), and acetone.

On the basis of large negative cross-interaction coefficients obtained for the aminolysis of substituted aryl chlorothionoformates with substituted anilines in acetonitrile, Lee et al. [10] proposed a concerted mechanism with a four-membered hydrogen bonded cyclic transition state. On the other hand, Castro, Santos and coworkers [11-16] proposed that the aminolysis of chlorothionoformates using pyridine, alicyclic and bicyclic amines, is a stepwise process with the formation of a zwitterionic tetrahedral intermediate while their phenolysis [17] is concerted.

In a recently summarized [18] and ongoing solvolytic mechanistic study of nucleophilic substitution in chloroformate (ROCOCl), chlorothioformate (RSCOCl), chlorothionoformate (ROCSCl), and chlorodithioformate (RSCSCl) esters, we have successfully correlated their solvolytic rate coefficients in a series of binary aqueous organic mixtures of varying solvent nucleophilicity (N_T) [19,20] and ionizing power (Y_Cl) [21-23] values using the extended (two-term) Grunwald-Winstein (G-W) equation (equation 1) [24].

$$\log (k/k_o)=\mathit{lN}+\mathit{mY}+c$$ (1)

In equation 1, k and k_o are the specific rates of solvolysis of a substrate in a given solvent and the standard solvent (80% ethanol) respectively, l is the sensitivity to changes in solvent nucleophilicity (N), m represents the sensitivity that controls the importance of the solvent ionizing power value (Y), and c is a constant (residual) term.

A thorough Grunwald-Winstein analysis in 49 solvents yielded an l value of 1.66, and an m value of 0.56 for phenyl chloroformate (PhOCOCl, 2) [25,26]. The l/m ratio of 2.96 obtained was advanced as being characteristic for a stepwise addition-elimination (A-E) process that is associated with the formation of a rate-determining tetrahedral intermediate [26]. For phenyl chlorodithionformate (PhSCSCl, 3), we obtained l = 0.69, m = 0.95, and l/m = 0.73, and proposed a unimolecular S_N1 ionization with strong rear-side nucleophilic solvation of the developing dithioacylium cation [26,27]. We further recommended [18] that the l and m values for 2 and 3 can be taken as typical values for bimolecular addition-elimination (A-E) and unimolecular ionization (S_N1) mechanisms occurring in alkyl and aryl ROCOCl substrates, including those where sulfur is substituted for one or both oxygens.

The substitution of one sulfur for the ether oxygen in PhOCOCl yields phenyl chlorothioformate (PhSCOCl, 4). For 4 in the more nucleophilic solvents we obtained [28] l = 1.74, m = 0.48, l/m = 3.63, and, l =0.62, m = 0.92, and l/m = 0.67 in the highly ionizing fluoroalcohol mixtures. On the other hand, for PhOCSCl (1), an l value of 1.88, an m value of 0.56, and an l/m ratio of 3.36 was obtained [26,27] in nucleophilic solvents favoring the stepwise addition-elimination pathway (Scheme 1), and an l value of 0.34, an m value of 0.93 and an l/m ratio of 0.37 was obtained in the highly ionizing solvents suggesting a dissociative S_N1 mechanism (Scheme 2) with moderate rear-side nucleophilic solvation of the developing carbocation. These results and others recently obtained [18,25-43] clearly demonstrate that the introduction of one sulfur in ROCOCl substrates does induce a variety of superimposed mechanisms and the ranges of dominance is dependent on the R group, the presence of one or two sulfurs, and the types of solvent studied (i.e. on the N_T and Y_Cl values).

Scheme 1.

Stepwise addition-elimination mechanism through a tetrahedral intermediate for chlorothionoformate esters.

Scheme 2.

Unimolecular step-wise solvolysis of chlorothionoformate esters.

Drawing upon extensive literature data and using equation 1 for benzoyl chloride (PhCOCl), we obtained [44] l = 1.27, m = 0.46, and l/m = 2.76 in the less ionizing solvents, and l = 0.47, m = 0.79, and l/m = 0.59 in the highly ionizing aqueous-organic mixtures. Recently, Bentley et al. [45,46] provided convincing evidence that concurrent interchange mechanisms involving one dissociative and one an associative pathway do indeed occur in the solvolyses of p-substituted benzoyl chlorides.

Bentley [47] also calculated the Gaussian 03 (G3) values at 298K for the heterolytic bond dissociation energies (HBDEs) differences and arrived at values of PhOCOCl = +4.7 kcal/mol, PhSCSCl = -18.4 kcal/mol, PhOCSCl = -13.1 kcal/mol, PhSCOCl = -8.5 kcal/mol, and PhCOCl = -11.7 kcal/mol. The calculations involve comparisons with acetyl chloride and the acetyl cation [47] and support the possible operation of a heterolytic fission of the covalent carbon chlorine bond in PhSCSCl, PhOCSCl, PhSCOCl, and PhCOCl, to generate a positively charged acylium (or thioacylium) ion.

Like many other ROCOCl substrates, benzyl chloroformate (PhCH₂OCOCl) proceeds through a stepwise A-E process in all of the typical aqueous organic solvents except in the aqueous fluoroalcohols where a solvolysis-decomposition type mechanism with loss carbon dioxide is dominant [48].

Kyong, Kevill et al. [49] showed that phenyl fluorothionoformate (5) solvolyzes by a bimolecular pathway in all solvents (including the fluoroalcohols) studied with the addition step of the addition-elimination reaction being rate-determining. They obtained an l value of 1.32, an m value of 0.39, an l/m ratio of 3.38, a solvent deuterium isotope effect value for methanolysis (k_MeOH/k_MeOD) of 2.11, and entropies of activation in the range of -26.2 to -21.0 cal mol^-1K^-1.

An analysis of the solvolytic data for p-fluorophenyl chlorothionoformate (8) using equation 1 recently confirmed dual mechanistic channels (Scheme 1 and 2) occurring in the fifteen binary aqueous organic solvents studied at 35.0 °C and these pathways were shown to be highly dependent on the solvents ionizing ability [40].

We now present the first-order specific rate constants at 25.0°C for the solvolyses of p-tolyl (p-methylphenyl) chlorothionoformate (6) and p-chlorophenyl chlorothionoformate (7) in ethanol and methanol and binary mixtures of aqueous ethanol (EtOH), aqueous methanol (MeOH), aqueous acetone, aqueous 2,2,2-trifluoroethanol (TFE), and aqueous 1,1,1,3,3,3-hexafluoro-2-propanol (HFIP). We compare the experimental rate data of 6 and 7 and their correlation results obtained using the two-term Grunwald-Winstein equation (equation 1) to those previously published [9, 25-28, 40, 49-51] for compounds 1-5 and 8.

2. Results and Discussion

The first-order specific rates of solvolysis of 6 and 7 at 25.0 °C in pure and aqueous organic mixtures of widely varying nucleophilicity (N_T) and ionizing power values (Y_Cl) are reported in Table 1. In 6 and 7, there is a gradual rate increase that coincides with the increase of water content in the aqueous-organic mixtures (with increasing Y_Cl values). On the other hand in the strongly hydrogen-bonding aqueous-HFIP mixtures, the first-order specific rates for 6 and 7 decrease with increasing water content (and increasing N_T and decreasing Y_Cl values). One can also observe that 7 is approximately 10-fold faster than 6 in the aqueous ethanol solvents and 2 to 3-fold faster in the aqueous methanol and acetone mixtures, but this situation is reversed with 6 being the faster in the aqueous fluoroalcohol (TFE and HFIP) mixtures.

Table 1.

Specific rates of solvolysis (k) of 6, and 7, in several binary solvents at 25.0 °C and literature values for N_T and Y_Cl.

Solvent (%)a	6 @ 25.0 °C; 105k, s-1b	7 @ 25.0 °C; 105k, s-1b	NTc	YCld
100% MeOH	11.3 ± 0.9	29.9 ± 2.2	0.17	-1.2
90% MeOH	22.5 ± 1.5	47.9 ± 1.6	-0.01	-0.20
80% MeOH	30.1 ± 1.6	64.5 ± 1.1	-0.06	0.67
100% EtOH	1.51 ± 0.17	15.9 ± 1.0	0.37	-2.50
90% EtOH	3.02 ± 0.24	26.4 ± 1.1	0.16	-0.90
80% EtOH	4.30 ± 0.12	39.6 ± 0.8	0.00	0.00
70% EtOH	6.64 ± 0.19		-0.20	0.80
90% Acetone	0.327 ± 0.018	0.870 ± 0.015	-0.35	-2.39
80% Acetone	0.577 ± 0.029	1.85 ± 0.25	-0.37	-0.80
70% Acetone	0.980 ± 0.026	2.78 ± 0.16	-0.42	0.17
97% TFE (w/w)	1.07 ± 0.07	0.0456 ± 0.0012	-3.30	2.83
90% TFE (w/w)	1.49 ± 0.17	0.354 ± 0.024	-2.55	2.85
80% TFE (w/w)	2.12 ± 0.12		-2.22	2.90
50% TFE (w/w)		1.88 ± 0.17	-1.73	3.16
80T-20E	0.399 ± 0.012	0.332 ± 0.015	-1.76	1.89
60T-40E	0.626 ± 0.009	1.03 ± 0.04	-0.94	0.63
40T-60E	1.16 ± 0.05	3.26 ± 0.15	-0.34	0.48
20T-40E	2.34 ± 0.12	10.6 ± 0.4	0.08	-1.42
97%HFIP (w/w)	24.3 ± 1.2	1.92 ± 0.06	-5.26	5.17
90%HFIP (w/w)	23.0 ± 0.9	1.39 ± 0.13	-3.84	4.31
70%HFIP (w/w)	18.2 ± 1.3		-2.94	3.83
50% HFIP (w/w)		0.888 ± 0.015	-2.49	3.80

^aSubstrate concentration of ca. 0.0052 M; binary solvents on a volume-volume basis at 25.0 °C, except for TFE-H₂O and HFIP-H₂O solvents which are on a weight-weight basis. T-E are TFE-ethanol mixtures.

^bWith associated standard deviation.

^cRefs. 19,20.

^dRefs. 21-23.

In 100% EtOH at 25.0 °C, the rates of solvolysis for substrates 1-8 are 3.15 ± 0.04 × 10^-5 s^-1 [27], 260 ± 3 × 10^-5 s^-1 [25], 1.00 ± 0.02 × 10^-5 s^-1 [27], 6.73 ± 0.15 × 10^-5 s^-1 [28], 1740 × 10^-5 s^-1 (estimated from specific rates at lower temperature) [49], 1.51 ± 0.17 × 10^-5 s^-1, 15.9 ± 1.0 × 10^-5 s^-1, and 11.9 ± 1.1 × 10^-5 s^-1 [40], respectively. For compounds 1-5 and 8, a tetrahedral A-E transition state is proposed for their ethanolyses [25,27,28,40,49]. The rate order in pure ethanol of k₅ ≫ k₂ ≫ k₇ > k₈ > k₄ > k₁ > k₆ > k₃ reveals that the rate of the dithio ester is the slowest. This suggests that the inductive capacity of the thiophenoxy group in 3 is very inefficient.

A comparison of just the p-substituted aryl chlorothionoformate ethanolysis rate exhibits a rate order of k₇ > k₈ > k₁ > k₆. These observations are consistent with the Hammett σ_p values of + 0.23, + 0.06, and -0.17 [52] for para-Cl, para-F, and para-CH₃ respectively, with increased electron-withdrawing ability for the substituent favoring the rate-determining addition of a solvent molecule at the carbonyl carbon.

An addition-elimination mechanism with the addition step rate-determining is favored for phenyl fluorothionoformate (5) in all of the solvents studied at 10.0 °C [49]. Using the similarity model concept [29,53], we first compared the log (k/k_o) values for p-tolyl chlorothionoformate (6) to those obtained for 5. This plot is shown in Figure 2 for the seventeen common binary solvents studied. This xy-graph results in an abominable correlation coefficient (R) of 0.169, slope of 0.10 ± 0.16, intercept (c) of -0.08 ± 0.21, and F-test of 0.4. A review of the plot shows significant deviation for the 90 HFIP, 70HFIP, and 90 TFE values and a noticeable divergence from the line-of-best fit for the four TFE-EtOH mixtures, especially for the 80T-20E point. Removal of these seven data points does indeed improve the correlation significantly resulting in a R value of 0.973, slope of 1.32 ± 0.11, and c = 0.22 ± 0.06. This illustrates that like 5, the A-E mechanism is the dominant pathway for 6 in the ten remaining ethanol, methanol, and binary mixtures of aqueous ethanol, methanol, and acetone. The slope of 1.32 + 0.11 indicates that in these ten solvents there is a much later transition state for addition to 6 when compared to that seen for the solvolyses of 5.

Figure 2.

The plot of log (k/k_o) for 4-tolyl chlorothionoformate (6) at 25.0 °C against log (k/k_o) for phenyl fluorothionoformate (5) at 10.0 °C in the seventeen common pure and binary solvents studied.

Using the extended Grunwald-Winstein equation (equation 1) for all of the twenty specific rates of solvolysis of 6 listed in Table 1 leads to a very inferior correlation coefficient (R) of 0.505, l =0.33 ± 0.22, m = 0.34 ± 0.16, c = -0.03 ± 0.20, and a very low F-test value of 2.9. For the two-term G-W analyses these are unacceptable correlation and F-test values and this could reflect the presence of concurrent mechanisms.

In Table 2, we report the relevant G-W analyses for substrates 1-8. Figure 2 clearly shows that the highly ionizing common solvents (90 HFIP, 70HFIP, 90 TFE, and 80T-20E) deviate the most in the plot that is presented for log (k/k_o)₆ versus log (k/k_o)₅. Removal of the three HFIP (97, 90, and 70) values, the three TFE (97, 90, and 80) values, and the 80T-20E rate value, in the G-W analyses of 6 results in a marginal R = 0.881, l = 1.63 ± 0.31, m = 0.46 ± 0.10, c = 0.30 ± 0.12, and a F-test of 17. However, deletion of any additional TFE-EtOH points does not improve the correlation coefficient but the P-value (probability value indicating that the results are statistically insignificant) for the l term rises and the F-test value decreases substantially. The resulting l/m ratio of 3.54 observed is in line with values observed in the aryl chlorothionoformate substrates 1 (l/m = 3.36) and 8 (l/m = 3.26) for solvents governed by a dissociative A-E mechanism shown in Scheme 1.

Table 2.

Correlations of the specific rates of solvolysis of 1-8 using the extended Grunwald-Winstein equation (equation 1).

Substrate	na	lb	mb	cb	Rc	Fd	l/m	Mechanism
1e	9	1.88 ± 0.28	0.56 ± 0.15	0.38 ± 0.15	0.950	28	3.36	A-E
	18	0.34 ± 0.05	0.93 ± 0.09	-2.54 ± 0.34	0.955	77	0.37	SN1
2f	49	1.66 ± 0.05	0.56 ± 0.03	0.15 ± 0.07	0.980	568	2.96	A-E
3e	31	0.69 ± 0.05	0.95 ± 0.03	0.18 ± 0.05	0.987	521	0.72	SN1
4g	16	1.74 ± 0.17	0.48 ± 0.07	0.19 ± 0.23	0.946	55	3.62	A-E
	6	0.62 ± 0.08	0.92 ± 0.11	-2.29 ± 0.13	0.983	44	0.67	SN1
5h	22	1.32 ± 0.13	0.39 ± 0.08	-0.02 ± 0.10	0.952	95	3.38	A-E
6	13i	1.63 ± 0.31	0.46 ± 0.10	0.30 ± 0.12	0.881	17	3.54	A-E
	7j	0.45 ± 0.13	1.07 ± 0.14	-2.25 ± 0.20	0.986	69	0.42	SN1
7	13i	1.79 ± 0.16	0.45 ± 0.07	-0.05 ± 0.09	0.966	69	3.98	A-E
8k	10	1.76 ± 0.28	0.54 ± 0.15	0.34 ± 0.15	0.943	28	3.26	A-E
	5	0.53 ± 0.18	0.89 ± 0.18	-2.66 ± 0.35	0.967	15	0.60	SN1

^an is the number of solvents.

^bWith associated standard error.

^cCorrelation coefficient.

^dF-test value.

^eValues taken from ref. 26, 27.

^fValues taken from ref. 25, 26.

^gValues taken from ref. 28.

^hValues taken from ref. 49.

ⁱExcluding the data points in aqueous HFIP, aqueous TFE, and 80T-20E in regression calculations.

^jUsing only the data points in aqueous HFIP, aqueous TFE, and 80T-20E in regression calculations.

^kValues taken from ref. 40.

For 6, in the seven strongly hydrogen bonding solvents of 80T-20E, aqueous TFE, and aqueous HFIP, we get an l value of 0.45 ± 0.13, an m value of 1.07 ± 0.14, a c value of -2.25 ± 0.20, an R value of 0.986, and a F-test value of 69, all derived from a G-W analyses using equation 1 (and listed in Table 2). The l value has an associated P-value of 0.03, indicating that the result is statistically significant [54]. A large negative c value is observed because the experimental k_o value is the one applying to the other reaction channel. For 6 in the ionizing fluoroalchohol mixtures, the l and the m values and the l/m ratio of 0.42 are in the range previously observed for ionization reactions (Scheme 2) for 1 (l/m = 0.37) and 8 (l/m = 0.60).

A plot of log (k/k_o)₆ against 1.63 N_T + 0.46 Y_Cl in the twenty pure and binary solvents studied is shown in Figure 3. The seven fluoroalcohol-containing mixtures (80T-20E; 97, 90, 70, HFIP; and 97, 90, 80 TFE) were excluded in the correlation analysis but are added on the plot to show their extent of deviation from the correlation line. In Figure 3 if one carefully scrutinizes the positioning of the 80T-20E data point, one can discern that there may well be some contribution from the A-E pathway in this solvent mixture. Using the equation log (k/k_o)₆ = 1.63 N_T + 0.46 Y_Cl + 0.30, one can estimate the addition-elimination pathway specific rate for 6 in 80T-20E to be 8.6 × 10^-7 s^-1. This would suggest that in 80T-20E there is a 22% contribution from the addition-elimination pathway.

Figure 3.

The plot of log (k/k_o) for 4-tolylphenyl chlorothionoformate (6) against 1.63 N_T + 0.46 Y_Cl in the twenty pure and binary solvents studied. The points for TFE-H₂O and HFIP-H₂O are not included in the correlation. They are added to show the extent of their deviation from the correlation.

In Figure 4, we show a plot of log (k/k_o) for 4-chlorophenyl chlorothionoformate (7) against log (k/k_o) for phenyl fluorothionoformate (5) in the seventeen common pure and binary solvents studied. This linear regression results in an inadequate correlation coefficient on 0.812, slope of 0.61 ± 0.11, intercept of -0.38 ± 0.16, and an F-test value of 29. It is apparent from Figure 4 that the 90 HFIP and 90 TFE values digress considerably from the correlation line. Excluding these two values leads to a significantly improved R = 0.962, slope of 1.13 ± 0.09, intercept of -0.12 ± 0.08, and an F-test value of 160. This analysis promotes the possibility that for 7, in the remaining fifteen solvents a similar bimolecular addition-elimination pathway is operative.

Figure 4.

The plot of log (k/k_o) for 4-chlorophenyl chlorothionoformate (7) against log (k/k_o) for phenyl fluorothionoformate (5) in the seventeen common pure and binary solvents studied.

For 7 using equation 1 for all of the nineteen solvents listed in Table 1 results in a low correlation coefficient of 0.679, to values with high standard errors associated of l = 0.58 ± 0.24, m = 0.18 ± 0.17, c = -0.54 ± 0.23, and a dismal F-test value of 7. Observing that the 90 HFIP and 90 TFE values deviated significantly in Figure 4, it would be expected that if specific rates for solvolysis of 5 had been available the deviations for 97 HFIP and 97 TFE would have been even greater.

Excluding the 97, and 90 HFIP, and 97 and 90 TFE data points in the G-W analyses using equation 1, we obtain improved values of R = 0.934, l = 1.58 ± 0.19, m = 0.49 ± 0.09, c = -0.06 ± 0.12, and an F-test value of 41. Further omission of the three aqueous HFIP (97, 90, and 50) and the three aqueous TFE (97, 90, and 50) values leads to a much improved R = 0.966, l = 1.79 ± 0.16, m = 0.45 ± 0.07, c = -0.05 ± 0.09, and F-test value = 69 (reported in Table 2). The sensitivities l and m obtained are typical for substrates undergoing overall nucleophilic substitution (A-E mechanism) involving rate-determining formation of a tetrahedral intermediate (shown in Scheme 1). The l/m ratio of 3.98 observed is a little higher than those observed for solvolyses of aryl chlorothionoformate esters 1 (l/m = 3.36), 6 (l/m = 3.54), and 8 (l/m = 3.26).

We have used the l/m ratio to suggest earlier and later transition states within otherwise very similar mechanisms and as a useful indicator for the presence of general base catalysis [55,56] in solvolytic reactions of this type [29]. The l/m ratios for p-chlorobenzoyl chloride, p-nitrobenzoyl chloride, p-nitrophenyl chloroformate, and p-nitrobenzyl chloroformate of 3.19, 3.29, 3.67, and 3.50 [29, 44] are of similar values to those obtained for the aryl chlorothionoformate 1 and 6-8 when they are reacting by the addition-elimination channel.

A plot of log (k/k_o) for 4-chlorophenyl chlorothionoformate (7) against 1.79 N_T + 0.45 Y_Cl in the nineteen pure and binary solvents studied is shown in Figure 5. The six data points for 97, 90, and 50 HFIP and 97, 90, and 50 TFE were excluded from the G-W analyses using equation 1, but were added to the plot to show their positive deviations from the correlation line.

Figure 5.

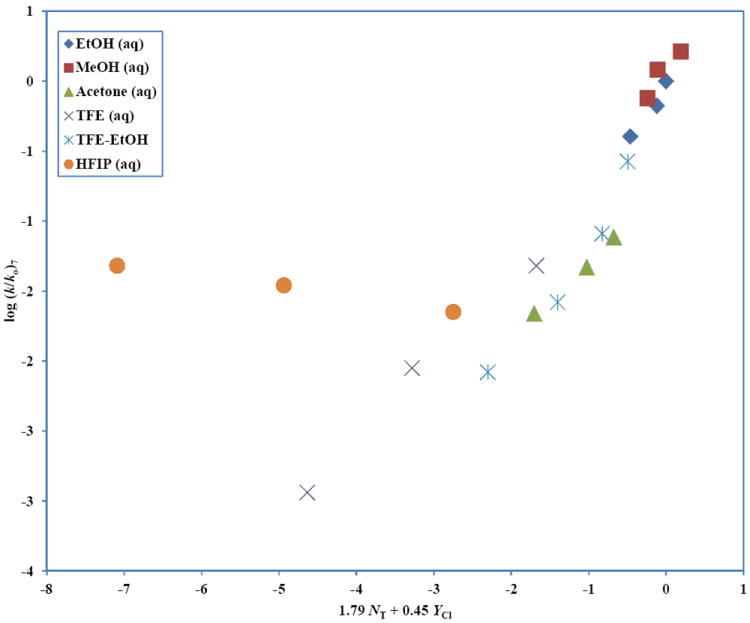
The plot of log (k/k_o) for 4-chlorophenyl chlorothionoformate (7) against 1.79 N_T + 0.45 Y_Cl in the nineteen pure and binary solvents studied. The points for TFE-H₂O and HFIP-H₂O are not included in the correlation. They are added to show the extent of their deviation from the correlation.

Examination of Figure 5 indicates that the 50 TFE point is quite adjacent to the correlation line. Hence for this solvent there is the possibility of having a concurrent contribution from the A-E pathway. Using the equation log (k/k_o)₇ = 1.79 N_T + 0.45 Y_Cl − 0.05, we have estimated A-E rates of 8.22 × 10^-9 s^-1, 1.85 × 10^-7 s^-1, 7.47 × 10^-6 s^-1, 1.77 × 10^-6 s^-1 and 6.32 × 10^-7 s^-1, for 97 TFE, 90 TFE, 50 TFE, 80T-20E, and 50 HFIP respectively. These calculations correspond to 2%, 5%, 40%, 53%, and 7% contributions from the A-E pathway for the solvolyses in these solvents.

After subtracting out the A-E component in the rates of reaction of 7 that were indicated to be occurring in the seven fluoroalcohol mixtures (97-50 HFIP, 97-50 TFE, and 80T-20E), we can then carry out a correlation of the estimated specific rates remaining to get R = 0.913, l = 0.43 ± 0.17, m = 0.82 ± 0.20, c = -3.45 ± 0.40 (large negative value because k_o is for the A-E pathway), and a F-test value of 10. The l/m ratio of 0.52 is typical for S_N1 mechanisms seen in acyl halides and of the type shown in Scheme 2.

For the aryl chlorothionoformate esters 1, 6, 7, and 8, the evidence for a change in mechanism from a bimolecular A-E pathway to an ionization (S_N1) mechanism in the highly ionizing fluoroalcohol mixtures is compelling and occurs even in substrates (7 and 8) that contain electron-withdrawing halogen substituents in the para position. These observations are consistent with Bentley’s G3 calculations that a C=S bond strongly stabilizes the developing carbocation [47]. This formation of a cationic transition-state, favored in the highly ionizing solvent mixtures, is in all probability due to sulfur’s ability to modify its electron cloud and therefore to be highly polarizable.

3. Conclusions

The p-tolyl chlorothionoformate (6) and the p-chlorophenyl chlorothionoformate (7) are shown to solvolyze by the generation of concurrent bimolecular stepwise addition-elimination and unimolecular ionization (S_N1) mechanisms. The exact delineation of the change in mechanism is identified utilizing the concept of substrate similarity based on l/m ratios, and statistical results obtained through the application of the two-term extended Grunwald-Winstein equation (equation 1).

For 6 in the more nucleophilic solvents we obtain an l value of 1.63, an m value of 0.46, and an l/m ratio of 3.54. For 7 in a similar set of solvents, we obtain an l value of 1.79, an m value of 0.45, and an l/m ratio of 3.98. It is now proposed that in such nucleophilic solvents 6 and 7 undergo an addition-elimination (association-dissociation) process with the addition-step being rate determining.

In the strongly hydrogen-bonding aqueous HFIP, aqueous TFE, and 80T-20E mixtures, we obtain an l value of 0.45, an m value of 1.07, and an l/m ratio of 0.42 for 6, and an l value of 0.43, an m value of 0.82, and an l/m ratio of 0.52 for 7. The sensitivities for l and m obtained (for 6 and 7) are befitting the proposal of an ionization component with an appreciable nucleophilic solvation of the developing cationic transition state.

We also found that for solvolyses of 6 there is evidence for a superimposed addition-elimination component of 22% in 80T-20E, and for 7 there are contributions from the A-E pathway of 2%, 5%, 40%, 53%, and 7% in 97 TFE, 90 TFE, 50 TFE, 80T-20E, and 50 HFIP respectively.

4. Experimental Section

The p-tolyl chlorothionoformate (97%, Sigma-Aldrich) and the p-chlorophenyl chlorothionoformate (98%, Sigma-Aldrich) was used as received. Solvents were purified and the kinetic runs carried out as described previously [19]. A substrate concentration of approximately 0.005 M in a variety of solvents was employed. For some of the runs, calculation of the specific rates of solvolysis (first-order rate coefficients) was carried out by a process [57] in which the conventional Guggenheim treatment was modified so as to give an estimate of the infinity titer, which was then used to calculate for each run a series of integrated rate coefficients. The specific rates and associated standard deviations, as presented in Table 1, were obtained by averaging all of the values from, at least, duplicate runs.

Multiple regression analyses were carried out using the Excel 2010 package from the Microsoft Corporation, and the SigmaPlot 9.0 software version from Systat Software, Inc., San Jose, CA, was used for the Guggenheim treatments.

Figure 1.

Molecular structures of phenyl chlorothionoformate (1), phenyl chloroformate (2), phenyl chlorodithioformate (3), phenyl chlorothioformate (4), phenyl fluorothionoformate (5), p-tolyl chlorothionoformate (6), p-chlorophenyl chlorothionoformate (7), and p-fluorophenyl chlorothionoformate (8).