Summary
Contemporary research suggests that the mammalian brain is a complex system, implying that damage to even a single functional area could have widespread consequences across the system. To test this hypothesis, we pharmacogenetically inactivated the rhesus monkey amygdala, a subcortical region with distributed and well-defined cortical connectivity. We then examined the impact of that perturbation on global network organization using resting-state functional connectivity MRI. Amygdala inactivation disrupted amygdalocortical communication and distributed corticocortical coupling across multiple functional brain systems. Altered coupling was explained using a graph-based analysis of experimentally established structural connectivity to simulate disconnection of the amygdala. Communication capacity via monosynaptic and polysynaptic pathways, in aggregate, largely accounted for the correlational structure of endogenous brain activity and many of the non-local changes that resulted from amygdala inactivation. These results highlight the structural basis of distributed neural activity and suggest a strategy for linking focal neuropathology to remote neurophysiological changes.
Introduction
Modern neuroscience continues to shift its focus from an emphasis on the function of individual brain regions towards understanding brain function in terms of complex network dynamics. Functional connectivity (FC) neuroimaging methods, which measure the temporally correlated nature of activity in different brain regions, are now being exploited to understand how large-scale network-level activity associated with healthy cognition is impacted by brain injury (Fornito et al., 2015) and neurodegeneration (Seeley et al., 2009). Lesion-induced functional pathology frequently manifests in a distributed and complex manner (Gratton et al., 2012; He et al., 2007), and the precise relationship between function and structure at the network level is incompletely understood. Consequently, establishing a framework to relate disorders of brain communication to specific neuroanatomical underpinnings remains a critical and unresolved challenge.
The analysis of how anatomical connectivity supports functional interactions between distinct brain areas has emerged as a fertile area of research (Honey et al., 2009; Miranda-Dominguez et al., 2014). It is now evident that correlations in spontaneous activity measured via resting-state functional connectivity MRI (rs-fcMRI) can be reasonably well predicted in the healthy brain with knowledge of the mono- and poly-synaptic pathways between regions and the manner in which those pathways are topologically embedded within the whole-brain network (Goni et al., 2014). Multiple related approaches at modeling FC from whole-brain structural connectivity (SC) have recently been validated in healthy human brains (Hansen et al., 2015; Messe et al., 2014). These advances raise the possibility that complex, global disturbances in function might quantitatively predict focal brain pathology underlying neurological and psychiatric disorders. Despite theoretical support for this view (Alstott et al., 2009; Honey and Sporns, 2008), structurally based models of FC have not yet been validated through experimental perturbations.
The advent of Designer Receptors Exclusively Activated by Designer Drugs (DREADDs) provides a new, minimally invasive means to manipulate brain activity in vivo (Armbruster et al., 2007; Eldridge et al., 2016; Michaelides et al., 2013). DREADDs provide systemic pharmacological modulation of specific neuroanatomical circuits, allowing the influence of local circuit activity on global functional network organization to be revealed. Furthermore, DREADDs provide an avenue to empirically reexamine the relationship between structural and functional connectivity. As part of a long-term research program investigating the structure and function of the nonhuman primate amygdala, this study was carried out to examine functional imaging consequences of transiently inhibiting the amygdala. We used the inhibitory DREADD hM4Di (Armbruster et al., 2007) in a cohort of rhesus macaque monkeys and assessed changes in distributed region-to-region communication using rs-fcMRI.
We hypothesized that DREADD-induced transient deactivation of the amygdala would degrade FC between the amygdala and areas that anatomically connect strongly and reciprocally with the amygdala, particularly the medial and orbital prefrontal cortices, the cingulate cortex, and the temporal lobe (Amaral and Price, 1984; Stefanacci and Amaral, 2002). Given that there might be variable expression of the hM4Di receptor across animals, we hypothesized that the magnitude of FC disruption in each animal would correlate with the number of amygdala neurons that demonstrated DREADD expression. Due to the dependence of FC on polysynaptic communication, it was also hypothesized that FC would change within the distributed systems in which these cortical regions participate. We report on a previously established graph analytic measure, communicability (Crofts and Higham, 2009; Estrada and Hatano, 2008), as a means for approximating FC in the primate brain. We apply this measure to a previously published SC dataset representing a collation of experimental literature of tract-tracing studies (Bezgin et al., 2012), in order to assess whether simulated structural lesions of the amygdala could explain empirical FC changes across the connectome.
Results
An overview of experimental procedures is provided in Figure 1.
Figure 1. Overview of experimental procedures and network analyses.
A–C) Procedures for experimentally inactivating the amygdala and assessing functional changes across the brain. A) First, the amygdala (labeled in red) was transfected with a viral vector construct containing the inhibitory DREADD gene hM4Di. The DREADD ligand, CNO, selectively deactivates DREADD-transfected cells when administered peripherally. B) Second, rs-fcMRI scans were acquired on each animal six to twelve months later. One scan was acquired using CNO injection i.v. and the other with saline i.v. Scans are divided into 5 consecutive 12-minute blocks with injections performed between the first and second block. C) Third, functional connectomes are built for each block using the RM parcellation scheme. Connectomes comprise pairwise Pearson correlations (z-transformed) between timeseries of all region pairs, illustrated as a whole-brain network. This allows assessment of baseline functional connectivity (FC) or FC change due to CNO injection relative to saline (ΔFC).
D–E) Procedures for predicting ΔFC across the brain. D) SC connectome is obtained from the CoCoMac database of tract-tracer data. Communicability across all node pairs of the SC connectome is used as a predictor for baseline FC. E) Simulated lesion (disconnection) of the amygdala generates changes in communicability across all node pairs of the connectome. Change in communicability is used as a predictor of ΔFC.
Distribution of DREADD expression
The amygdala was transfected bilaterally with the inhibitory G-protein coupled hM4Di receptor containing a pan-neuronal synapsin promoter. Immunoreactivity of the mCherry reporter protein was carried out to identify the locations of transfected neurons (Figures 2 and S1). Stereological analyses confirmed substantial populations of transfected cell bodies within the amygdala bilaterally in all cases, although there was considerable variability in the number of labeled neurons and in their distribution across amygdala subnuclei from case to case (see Tables S1 and S2 and Supplemental Experimental Procedures). We also observed substantial labeling of monosynaptic anterograde projections and almost no retrograde labeling (with the exception of the rostral entorhinal cortex), indicating little or no transynaptic spread of mCherry (see Figure S1 and Supplemental Experimental Procedures).
Figure 2. Histological evaluation of DREADD expression.
Photomicrographs of representative coronal sections through the amygdala in cases M2 (A–E) which had the lowest level of neuronal transfection within the amygdala and M1 (F–J) which had the highest level of transfection in the amygdala illustrating the overall distribution of hM4Di-mCherry immunoreactivity. Sections are ordered from most rostral (A and F) to most caudal (E and J). Each immunohistochemically stained section (A–J) is displayed next to an adjacent section stained by the Nissl method (A’-J’). The location of the amygdala (A), caudate nucleus (Cd) enothrinal cortex (EC), claustrum (Cl) and anterior commissure (ac) are indicated in some of the sections. The syringe needle track is indicated for case M2 by arrows. Slight leakage and cellular labeling is indicated in the caudate nucleus of both cases (asterisks). In panel J, the entorhinal cortex is indicated (--> *). Anterograde labeling was observed in the superficial layers and retrograde labeling was observed in layer V. This is consistent with the known monosynaptic connections between the amygdala and the entorhinal cortex. Scale bar = 5mm. See also Figure S1 and Tables S1–S2.
MRI analysis of amygdala functional connectivity
Four rhesus macaques were lightly anesthetized and scanned using a 60-minute, iron contrast-enhanced functional sequence divided into 5 blocks lasting 11.7 minutes. The synthetic DREADD-activating ligand Clozapine-N-Oxide (CNO, 10mg/kg) or saline was administered after the first block (the baseline). At baseline, the amygdala demonstrated significant FC (z-transformed correlations of temporal activity) with numerous cortical and subcortical areas (Figure 3A). The cortical and subcortical FC patterns are in general agreement with the known patterns of neuroanatomical connectivity in the macaque monkey amygdala (Amaral and Price, 1984). The strongest cortical FC appeared in the ventral and medial prefrontal cortices (vmPFC), anterior cingulate cortices, and throughout the temporal cortices. Strong FC also appeared in the frontal polar cortex, dorsomedial prefrontal cortex, and ventral portions of the insula. Weaker, but significant connectivity, was observed in the posterior cingulate cortex, retrosplenial cortex, and medial parietal cortex. In subcortical areas, strong FC appeared in the nucleus accumbens (NAcc), head of the caudate nucleus, midline thalamus, hypothalamus, and midbrain. Overall, FC was substantially bilateral for both left and right amygdala and strongly homotopic.
Figure 3. Changes in amygdala FC following DREADD activation, across time.
A) Significant baseline FC is shown using the amygdala as the seed ROI. Images show Z-scores. Widespread positive FC, and no significantly negative FC, was found. Images oriented using radiological convention. B) CNO-induced transient inactivation in the first 12-minute, post-injection block (i.e. block 2) results in widespread reduction of amygdala FC. The effect of CNO was computed relative to the effect of saline and converted to Z-scores. Warm and cool colors show significant FC reductions and increases, respectively. C–E) Same as B, for blocks 3–5, respectively.
Given the lack of background parametric data on DREADD alterations of brain activity in the primate brain, we first evaluated the time course and spatial extent of FC changes resulting from DREADD inactivation of the amygdala. Administration of CNO versus saline significantly reduced amygdala FC in all post-injection blocks (Z>2.3, cluster-corrected p<0.05; Figure 3B–E). No consistent increases occurred. Reduced FC appeared in most cortical areas showing positive baseline connectivity, but was seen most consistently in the vmPFC, subgenual cingulate cortex (CCs), inferior temporal cortex (TCi), superior temporal sulcus (TCc), and in the NAcc. Reduced subcortical FC was also apparent in the caudate nucleus and thalamus. Across all blocks, changes were noticeably stronger for the left amygdala than the right. This was likely a consequence of the generally higher number of transfected neurons in the left amygdala compared to the right side (see Figure 4B–C and Table S1).
Figure 4. Changes in amygdala FC are correlated with DREADD transfection.
A) Amygdalocortical SC, as catalogued in the TTu connectome. B) Scatterplots showing amygdala ΔFC as a function of stereologically estimated populations of DREADD-transfected cells in the amygdala. Left and right amygdala are included separately for each case. Amygdala ΔFC was averaged across regions with known amygdala SC. Trend lines are shown for CNO (dark line) and saline (lighter line) conditions. C) Same as B, averaging ΔFC across regions without amygdala SC.
Figure 4 shows the association between FC changes in the amygdala and postmortem DREADD immunoreactivity. For reference, the known anatomical connectivity of the amygdala (collated in (Bezgin et al., 2012)) is shown in 4A. To reduce statistical noise, post-injection blocks were averaged across blocks and then compared against baseline. For each subject, and within each hemisphere separately, changes in amygdala FC due to CNO or saline injection (ΔFC-amyg) were averaged across regions-of-interest (ROIs) with known amygdala SC. Averaged ΔFC-amyg correlated negatively with the estimated population of DREADD-transfected cells after CNO (r=−0.87, p=0.005), but not after saline (r=−0.32, p=0.44). A weaker, but significant negative association was also detected using ΔFC-amyg averaged over ROIs without amygdala SC (CNO: r=−0.77, p=0.025; saline: r=−0.23, p=0.58). In summary, greater numbers of DREADD-transfected cells in the amygdala was associated with more substantial degradation of FC between the amygdala and regions with which it is monosynaptically connected and unconnected.
Network connectivity changes
We next assessed the effects of amygdala inactivation across the brain, within the context of the brain’s modular organization (Figure 5). Modules are defined as partitions of the whole-brain network that maximize the within-module connectivity, providing a view of the brain’s intrinsic functional organization. At baseline, 7 modules were identified (see Experimental Procedures), including the limbic (orange), default mode (red), visual (blue), dorsal attention (green), insular/opercular (pink), auditory (yellow), and somatomotor (cyan) (Figure 5A). The limbic module included the amygdala, PFCoi, PFCol, TCpol, and TCi. As community detection is non-deterministic, we replicated all modularity-based results using an alternative modularity algorithm (see Experimental Procedures). The alternative partition is highly similar (Variation of Information = 0.174) and implies a strong functional relationship between the limbic and default mode modules, and between the somatomotor and dorsal attention modules (see Figure S2).
Figure 5. Corticocortical networks are negatively and positively altered by amygdala inactivation.
A) Seven color-coded functional brain modules, i.e. subsets of regions with high intra-modular FC, identified at baseline. B) Average amygdala FC of nodes within each module, sorted high to low. Limbic and default mode nodes have the highest amygdala FC; somatomotor nodes have the lowest. C) FC changes due to amygdala inactivation between limbic and default mode nodes. Red lines indicate reduced FC (Z < 2.6 per edge, corrected p=0.031, edge width denotes Z score magnitude, node size denotes sum of edges incident to node). D) FC changes due to amygdala inactivation between somatomotor nodes. Blue lines indicate increased FC (Z > 2.6 per edge, corrected p=0.011). See also Figures S2 and S3.
In order to distinguish between network effects that were topologically near vs distant from the amygdala, analyses were stratified according to modules with high vs low baseline amygdalar FC. The amygdala was functionally connected most strongly to other nodes in the limbic module and in the default mode module, while it was most weakly connected with somatomotor nodes (Figures 5B and S2B). In the limbic and default mode modules, FC decreased between regions such as the medial prefrontal cortices (PFCm, PFCdm) and orbitofrontal cortices (PFCom, PFCol, PFCoi), CCs, CCr, TCi, TCc, and TCpol (Z<-2.6 for each edge, FDR-corrected p=0.031; see also Figure S2). No significant increase in FC (Z>2.6) was found in these modules. On the other hand, FC increased between somatomotor nodes, particularly S1 and M1 (Z>2.6 for each edge, FDR-corrected p=0.011; see also Figure S2), while no decreased FC (Z<-2.6) was found.
For additional validation, all FC changes |Z|>2.6 (p<0.01 uncorrected) are shown in Figure S3 unrestricted by modules and uncorrected for multiple comparisons across edges. The network of reduced FC was almost entirely contiguous and highlighted the left amygdala as the crucial hub. The nodes in this network overlapped significantly with the known anatomical connections of the amygdala (χ²(1)=8.14, p=0.0043), while somatomotor nodes showed the largest increase in FC. Without statistical thresholding, the left amygdala exhibited the most substantial change in correlation values pre-inactivation vs post-inactivation relative to all other nodes (see Supplemental Information).
Brain-wide visualizations
Qualitative observations in the graph visualizations seen in Figure 6 are reflective of statistical effects and provide additional context. Examining the block graphs in Figure 6A–B, reduced FC was most extreme within the limbic module, though it was also apparent between the limbic and default mode modules and within the default mode. Increased FC was most apparent within the somatomotor module.
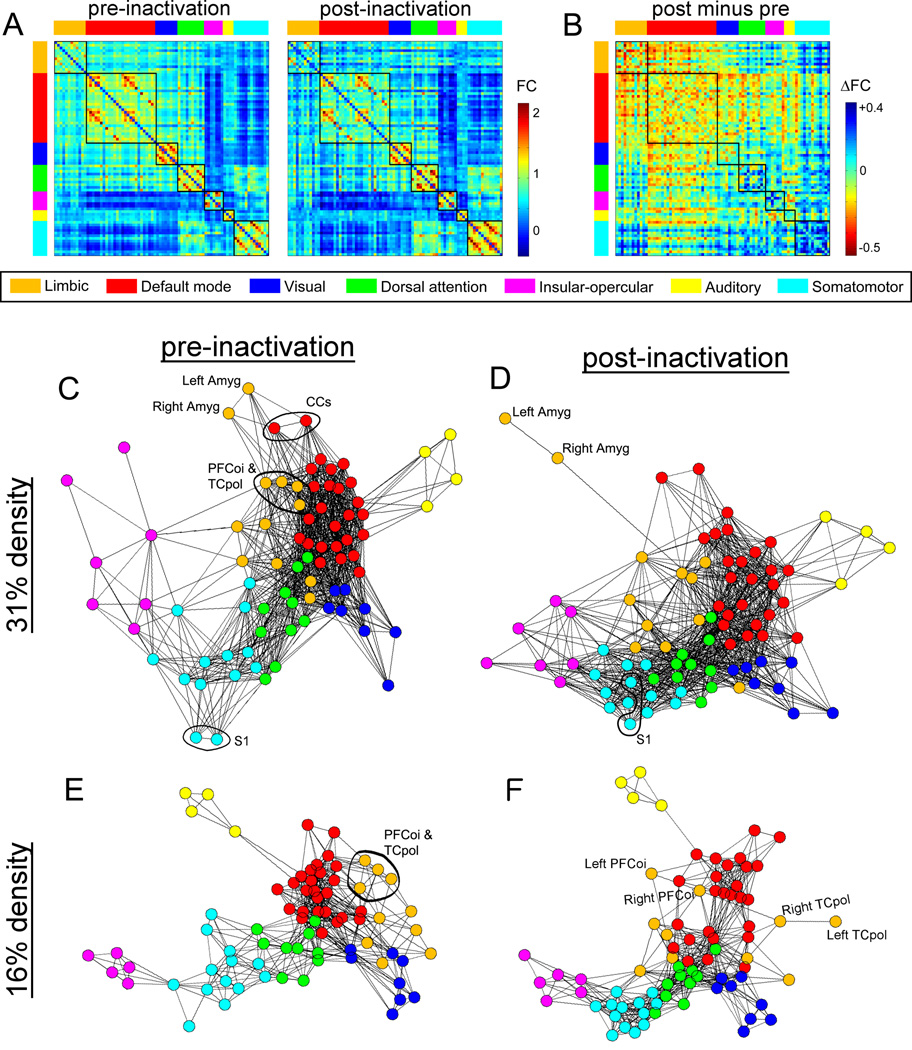
Figure 6. Whole-brain network visualizations highlight changes to nodes that are topologically near vs distant from the amygdala.
A) Baseline FC matrix and post-inactivation matrix; nodes ordered by module assignments shown in vertical and horizontal colored bars. Square areas inside the matrix indicate within-module connectivity. Connectivity of the limbic module (top left; orange bar) is strongest with itself and the default mode (red bar) modules, and weakest with the somatomotor module (cyan bar). B) CNO-induced FC changes. Reduced FC (warmer colors) is most apparent within the limbic module, within the default mode module, and between the limbic and default mode modules. Increased FC (cooler colors) is most apparent within the somatomotor module. C) Force-directed graph layout of the baseline FC network at 31% density. The left and right amygdala are attached to both the default mode and limbic modules. CCs, PFCoi, and TCpol are functionally closest to the amygdala, whereas the somatomotor module is most distant. D) Graph layout of the post-inactivation network at 31% density. The left and right amygdala are decoupled from the rest of the network, attached only via the right TCpol. E) Baseline FC network at 16% density, excluding the left and right amygdala. F) Post-inactivation network at 16% density. Disruption of connectivity within the limbic and default mode modules and increased connection density in the somatomotor module are visible. See also Figure S2.
Force-directed graph layouts (Figure 6C–F) highlight more regionally specific effects. At baseline (Figure 6C), the amygdala is attached to the CCs (default mode), TCpol (limbic), and PFCoi (limbic). The TCpol and PFCoi have the strongest baseline amygdala FC (0.821 and 0.788, respectively). After amygdala inactivation, the amygdala decouples from the network (Figure 6D), highlighting that the bilateral amygdala (and particularly the left) are central to the changes observed. The TCpol and PFCoi also noticeably decouple (Figure 6E–F; see statistical effects in Figures 5, S2, and S3).
The weak FC between the limbic and somatomotor modules (Figure 6A), particularly between the amygdala and somatomotor nodes (Figure 5B), is reflected in their topological distance in the baseline graph layout (Figure 6C). Increased somatomotor FC post-inactivation (statistical effects in Figures 5, S2, and S3) is seen as denser clustering of somatomotor nodes post-inactivation vs pre-inactivation (Figure 6D vs 6C, and 6F vs 6E). S1 has the weakest amygdala FC of all nodes (0.053) and shows the largest increase in FC (Figure S3), which mirrors effects seen in Figure 6C–D.
Structure-function relationships
Overview
We investigated the relationship between structural and functional brain connectivity using graph-based metrics of mutual communication. The initial goal was to establish whether FC between a given pair of regions in the baseline functional network was associated with their topological position within a corresponding structural connection (SC) matrix. After this initial validation, we tested whether FC changes due to amygdala inactivation could be explained by simulated structural lesion of the amygdala. We use an “unenhanced” tract-tracer (TTu) matrix for SC, representing a collation of experimentally established neuroanatomical connections from the CoCoMac database (see (Stephan et al., 2001) and (Bezgin et al., 2012)), between the 80 ROIs used in the current study. Connection weights in the TTu take values of 0 (non-existent), 1 (weak), 2 (moderate), or 3 (strong). We also use an “enhanced” version of this matrix (denoted TTx), produced in a recent study that optimized the simulation of BOLD FC by iteratively reweighting the TTu links to be more continuous and exponentially distributed (for details, see (Deco et al., 2014)).
Baseline FC
In order to establish a biologically plausible link between structural and functional connectivity, we consider the communicability metric (Estrada and Hatano, 2008) as a proxy for FC. Communicability (denoted G) is a graph theoretic measure that describes the ‘ease of communication’ between two regions across the combination of direct (i.e. monosynaptic) and all indirect (i.e. polysynaptic) structural pathways. G takes the weighted sum of these pathways where shorter paths with stronger connections are weighted more heavily (see Supplemental Information for calculations). It was hypothesized that G would strongly correlate with FC, implying a structural basis for endogenously coupled activity.
Figure S4 shows the relationship between within-hemisphere G and baseline FC. G and FC were strongly correlated across amygdalocortical ROI pairs (r=0.737, p<10−6, 95% CI [0.55, 0.854] for TTx; r=0.613, p<10−4, 95% CI [0.369, 0.778] for TTu; p-values estimated at 10−6 max precision) and across all corticocortical ROI pairs (r=0.6, p<10−6, 95% CI [0.552, 0.645] for TTx; r=0.523, p<10−6, 95% CI [0.469, 0.574] for TTu). Correlations were driven by the inclusion of walk lengths between 1 and 3 in the communicability metric (Figures S4 and S5A–B). Other predictors (e.g. shortest path length, Euclidean distance between ROI centroids) were tested and described in Table S3. A multiple linear regression model predicting FC using 1) TTx communicability, 2) TTu communicability, and 3) Euclidean distance, as joint predictors, demonstrated that TTx contributed most to model performance while Euclidean distance contributed minimally (see Supplemental Information).
FC changes
We next sought to explain empirical FC changes (ΔFC) due to DREADD inactivation of the amygdala through simulated disconnection of the amygdala in the SC networks. Specifically, we tested whether simulated changes in G would correlate with the distributed functional changes observed after DEADD inactivation. In concrete terms, this hypothesis assumes that loss of signal spread through monosynaptic and polysynaptic amygdalocortical pathways can account for the primary changes observed (i.e. amygdalocortical ΔFC). It is assumed that loss of signal spread through the polysynaptic cortico-amygdalo-cortical links can account for the secondary changes observed (i.e. corticocortical ΔFC).
Simulated lesion of the amygdala produced ΔSC-communicability (ΔG) values that correlated strongly with ΔFC across within-hemisphere amygdalocortical ROI pairs (r=0.696, p<10−6, 95% CI [0.488, 0.829] for TTx; r=0.647, p<10−5, 95% CI [0.416, 0.799] for TTu) and moderately strongly across within-hemisphere corticocortical ROI pairs (r=0.456, p<10−6, 95% CI [0.397, 0.512] for TTx; r=0.427, p<10−6, 95% CI [0.367, 0.484] for TTu). Scatterplots of ΔG and ΔFC are shown for the TTx in Figure 7A–B and for the TTu in Figure S6A–B. Correlations resulted from the inclusion of walk lengths up to, but not greater than, 4 or 5 in the communicability metric (Figures 7C–D, S5C–D, and S6C–D). Correlations across both hemispheres and within individual hemispheres are listed in Table S4. Qualitatively, simulated ΔG and empirical ΔFC show notable similarities with regard to the topological alterations to functional modules. For instance, amygdalocortical G and FC are both disrupted most prominently within the limbic and default mode modules (Figure 7E), while amygdala-somatomotor interaction is least impacted. The strongest negative changes to corticocortical G and FC both occur within the limbic and default mode modules (Figure 7F). Corticocortical G appears to be least affected among the somatomotor nodes, coinciding with increased FC.
Figure 7. Correspondence of amygdala inactivation and simulated structural lesions.
Scatterplots show ΔFC due to CNO versus ΔSC-communicability (ΔG, log-transformed) due to simulated disconnection lesion of the amygdala in the TTx connectome. Results are for within-hemisphere amygdalocortical ROI pairs (A) and all within-hemisphere corticocortical ROI pairs (B). Each dot represents mean ΔFC across subjects. C) Line graphs show the dependence of amygdalocortical ΔG-ΔFC correlations and D) corticocortical ΔG-ΔFC correlations upon different walk lengths. Different colored lines represent different subsets of region pairs, such as those with at least a disynaptic connection that traverses the amygdala, or those with either a disynaptic or trisynaptic connection that traverses the amygdala. All corticocortical pairs have at least a tetrasynaptic connection via the amygdala. E) ΔFC of amygdalocortical ROI pairs. ROIs are ordered by functional modules (see Figure 5) shown in color bars on top. E’) ΔG using the same ordering of regions. F) ΔFC matrix of corticocortical ROI pairs. ROIs are ordered by functional modules. F’) ΔG matrix, showing correspondence with ΔFC (note that due to the exponential distribution of SC weights in the TTx connectome, ΔG of the TCpol scales differently from other regions, resulting in the appearance of the dark red line in the matrix). G) Correlations between ΔFC and ΔG using simulated lesions of each ROI. Results are shown for primary region pairs (those including the lesioned region). Color blocks next to ROI names illustrate the strength of amygdala SC as defined in the TTx (for display purposes, SC values were log-transformed, inverted, and normalized to a max value of 1). The top 3 strongest predictors were the amygdala, TCpol, and superior temporal sulcus (TCc). H) Uses the same simulated lesions as in G, showing correlations for secondary region pairs (non-incident to the lesioned region). Top 3 predictors were the CCs, amygdala, and TCpol. See also Figure S6 and Table S4.
Lesions were then simulated for each cortical ROI separately in order to examine the specificity of ΔG-ΔFC correlations. Results are shown for the TTx in Figure 7G–H and for the TTu in Figure S6E–F. Across primary region pairs (i.e. those including the lesioned region), lesion of the amygdala in the TTx produced stronger correlations than did lesions to any other region. Lesioning the TCpol, to which the amygdala has substantially more SC than any other region, produced the next strongest correlation (r=0.637, p<10−4). Overall, regions with the most amygdala SC tended to show the strongest positive correlations and regions with the least amygdala SC produced the most negative correlations. ΔG-ΔFC correlations across secondary region pairs (i.e. those excluding the lesioned region) were slightly less specific, but still show the amygdala and TCpol (r=0.446, p<10−6) as the second and third best predictors in the TTx, respectively. The subgenual cingulate (CCs), which is topologically quite close to the amygdala (Figure 6D), had the strongest correlation (r=0.522, p<10−6). The overall trend relating each region’s amygdala SC to the strength of ΔFC prediction was maintained as well. Simulated lesions in the TTu connectome also gave similar top rankings (Figure S6E–F). Overall these results demonstrate that simulated disconnection of the amygdala, and its topologically closest neighbors, are substantially associated with FC changes.
Changes in nodal signal variance and pairwise covariance are additional ways to examine the impacts of inactivation, by taking into account changes in the amplitude of signal fluctuations. To relate changes in variance to simulated amygdala lesions, we compute the total change in each region’s input G (ΔGinput), which can be calculated separately from output G since SC weights are directed. Figures 8A–C and S6G–H show that alterations in variance were both positive and negative, but significantly correlated with ΔGinput (using raw Δvariance: r=0.461, p<0.005 for TTx and r=0.443, p<0.01 for TTu; using %Δvariance: r=0.757, p<10−6 for TTx and r=0.627, p<10−4 for TTu). Next, we examined covariance as an alternative measure of coupling. Figures 8D–E and S6I–J show that changes in covariance networks had even higher correlations with ΔG than did correlation-only (i.e. FC) networks. For amygdalocortical pairs, ΔG-Acovariance correlations were r=0.719, 95% CI [0.522, 0.843] for TTx, and r=0.695, 95% CI [0.486, 0.829] for TTu (both p<10−6). For corticocortical pairs, correlations were r=0.547, 95% CI [0.495, 0.596] for TTx, and r=0.517, 95% CI [0.462, 0.568] for TTu (both p<10−6). ΔG-Δcovariance correlations were also specific to the amygdala and TCpol lesions (Figures 8F–G for TTx and S6K–L for TTu). In the TTx, the TCpol and amygdala lesions were the top 2 predictors of primary effects; the TCpol, TCi, and amygdala were the top 3 predictors of secondary effects (all p<10−6). In the TTu, the amygdala was the top predictor of both primary and secondary effects, followed by the TCpol and TCv (all p<10−6). These results emphasize that changes in signal amplitude are also associated with simulated lesions and are concomitant with positive and negative changes in coupling.
Figure 8. Changes in regional signal variance and pairwise covariance are explained by simulated lesion.
A) Raw changes in the variance of regional timecourses (Δvariance) as a function of changes in input (ΔGinput) due to simulated amygdala lesion in the TTx connectome. Left and right hemisphere Δvariances were averaged. Each dot represents mean across subjects. The magenta line shows the amygdala. B) Same as A, except Δvariances were normalized against the baseline variance to yield %Δvariance. C) %Δvariances plotted on the brain. Changes in pairwise covariance (Δcovariance) as a function of ΔG, for within-hemisphere amygdalocortical ROI pairs (D) and all within-hemisphere corticocortical ROI pairs (E). D, E, F, and G are analogous to graphs shown in Figure 7, using covariance here as the empirical measure of coupling instead of FC. F and G) Δcovariance-ΔG correlations using simulated lesions of each ROI, assessed across primary region pairs (F) and secondary region pairs (G). See also Figure S6.
Discussion
The present study has achieved two fundamental and novel goals. First, we combined a focal DREADD manipulation with rs-fcMRI to identify changes in local and global network organization in vivo. The integration of these experimental tools carries significant potential for basic comparative neuroscience and translational research. Rs-fcMRI has been widely applied to study large-scale distributed networks in humans and homologous networks in the macaque (Grayson et al., 2014; Hutchison and Everling, 2012; Miranda-Dominguez et al., 2014). DREADDs offer the ability to measure the influence of specific circuits on network organization, and on behavior, without the restriction of chronic implants or the complications arising from lesion-induced compensatory changes.
Second, a novel application of graph theory was used to link structure and function in order to explain baseline FC patterns and distributed FC disruptions. These findings provide a proof-of-principle regarding the potential to reverse-engineer pathological features of neuroanatomical circuitry from resting-state functional networks.
Amygdala functional connectivity
We have first delineated an amygdalocentric FC map with detailed spatial specificity, which agrees strongly with the primate amygdala’s known pattern of extrinsic anatomical connectivity to cortical (Aggleton et al., 1980; Amaral and Price, 1984; Stefanacci and Amaral, 2002) and subcortical (Mehler, 1980; Russchen et al., 1985) regions. Anatomically, the primate amygdala connects extensively throughout the temporal cortex in a high-to-low gradient along the rostral-to-caudal direction. The amygdala also connects with medial and ventral prefrontal cortices, with anterior cingulate cortices, and with anterior and ventral insular cortices (Aggleton et al., 1980; Amaral and Price, 1984; Stefanacci and Amaral, 2002). These observations are all reflected in the distribution of FC in this study. On the other hand, the posterior cingulate, medial parietal, and retrosplenial cortex were also functionally connected to the amygdala despite evidence against the existence of direct anatomical linkage (Aggleton et al., 2012; Amaral and Price, 1984; Stefanacci and Amaral, 2002). These FC patterns may reflect the presence of indirect structural pathways between the amygdala and these areas. The fact that amygdala FC was correlated much more strongly with communicability (which represents monosynaptic and polysynaptic links) than with monosynaptic SC lends strong support for this view.
DREADD activation causes primary and secondary loss of FC
As expected, activation of the inhibitory DREADD robustly decreased amygdala FC. In order to understand the effects of focal disruption, it is necessary to consider not only the primary loss of neuronal function, but also the physiological changes to regions remote from the damage. For instance, loss of FC between regions anatomically distinct from the lesion is a frequent and clinically significant consequence of a variety of stroke and injury disorders (Carrera and Tononi, 2014; Gratton et al., 2012), in some cases correlating with behavioral deficits much more strongly than functional changes in the damaged region itself (He et al., 2007). In parallel, structural connectivity studies demonstrate that communicability helps to identify network alterations subsequent to stroke (Crofts and Higham, 2009; Crofts et al., 2011), emphasizing the importance of lesion-induced changes in interaction across indirect paths. Existing simulation studies predict that focal insult should directly cause changes in function to remote regions which depend sensitively on the lesion site (Alstott et al., 2009; Honey and Sporns, 2008). The current study lends empirical support for these predictions by demonstrating extensive degradation of links between the medial prefrontal, orbitofrontal, anterior cingulate, and anterior temporal cortices. Critically, functional network changes were correlated with the effects of simulated amygdala lesion within the structural connectome, suggesting that losses in corticocortical coupling are linked to losses in indirect communication mediated via the amygdala. These results corroborate the notion that focal lesions inhibit the spread of oscillatory activity between topologically neighboring nodes (Joyce et al., 2013) and offer a plausible structural basis.
Effects of DREADD activation on non-local network topology
The primate amygdala has been characterized previously as having low centrality in the context of the brain’s structural connectome (for instance, a relatively small number of the brain’s shortest paths run through it) (Goulas et al., 2014). These conclusions are supported by our functional graph layouts. While previous studies have ascertained that certain topological features of global brain organization are more resilient to damage inflicted upon nodes that are less central (Gratton et al., 2012; Joyce et al., 2013), it is nonetheless clear that amygdala inactivation led to large and differential changes in network dynamics. The organization of the limbic and default mode modules fragmented, while FC increased between nodes that were structurally and functionally distant from the amygdala (i.e. the somatomotor complex). These data support the long-standing theory that distributed increases in FC should accompany patterns of degradation due to focal lesions (Alstott et al., 2009). In the present study, effects can be interpreted in the light of recent applications of control theory to large-scale brain networks. Alterations to low-centrality nodes, also known as modal controllers, are theoretically capable of steering the brain into difficult-to-reach functional states (Gu et al., 2015). Transient damage to the amygdala (low-centrality) causes differential effects to distant systems, potentially corroborating such predictions. More speculatively, given that S1 (also low-centrality (Goulas et al., 2014); see also our graph layouts) showed the largest positive change in FC, it could be that distant low-centrality nodes exert competing attractive forces on network dynamics.
Structure-function relationships
Our method of relating structure to function corroborates a similar report that FC in the human brain is analytically predicted by a linear combination of communication metrics (Goni et al., 2014). In Goni et al., however, FC predictions relied on identification of the shortest communication path between node pairs. The notion that signal flow occurs preferentially along the shortest path is potentially a tenuous assumption within biological networks, since regions cannot ‘know’ where to distribute information. Communicability, by contrast, makes no assumptions about the primacy of the shortest path by allowing contributions from all walks of reasonably short length. In addition, the directionality of these walks meaningfully influence the metric. Our observations show a stronger correspondence between communicability and FC when the directionality of SC is incorporated, in line with previous structure-function studies (Shen et al., 2012). Interestingly, FC may also be modulated by common efferent vs afferent pathways in ways that are potentially inconsistent with serial relay patterns (Adachi et al., 2012), which form the basis of the communicability measure. Thus, there is clearly room for further exploration regarding complex network-level effects that give rise to correlated activity.
One of the most novel aspects of this study was the application of communicability towards identifying the loci of inactivation that best explain functional effects (i.e. the amygdala and TCpol). Current trends in translational research emphasize the goal to exploit network FC data in neurological patients with focal damage in order to predict outcomes (Gratton et al., 2012; Warren et al., 2014) or pinpoint potential pathways for targeted intervention (Carrera and Tononi, 2014; Fornito et al., 2015; He et al., 2007). Demonstrating that accurate deduction of neuroanatomical connectopathy is achievable opens the door for continued application and development of this approach in multiple contexts of atypical brain function.
Limitations and future directions
The present study bridges the gap between functional disturbance and circuit-level pathology by simulating lesions at the level of individual nodes. Several limitations can be stated about this approach. First, while DREADD injections were fairly circumscribed to the amygdala, variability of nuclei-specific transfection could have led to a more heterogeneous pattern of amygdalocortical disruption than accounted for by node-lesion simulation. Second, the lack of subcortical SC data, aside from the amygdala, might also limit the model. Current literature suggests that the best performing predictions of corticocortical FC, which have generally been based on corticocortical SC alone, are limited to roughly the strength observed here (0.6<r<0.7) (Goni et al., 2014; Hansen et al., 2015; Honey et al., 2009; Messe et al., 2014), highlighting the need to evaluate the influence of subcortical pathways as additional mediators of cortical coupling. Third, the model used here is not generative in the sense that brain activity is explicitly simulated. Rather, communicability is a static measure that appears to provide reasonable association with FC. In principle, generative models could be applied to the present data and combined with simulated lesions to gain more detailed mechanistic insights via parameter exploration.
Other limitations concern the construction of the FC networks themselves. Averaging individual subject matrices together is an important limitation, since group-averaged matrices can theoretically be non-representative of the individual constituents (Simpson et al., 2012). In addition, the use of anesthesia is known to alter resting-state FC networks by limiting their ability to dynamically reconfigure between different states over time (Barttfeld et al., 2015). Here we have only attempted to describe static FC patterns, but future experimental research in awake animals could explore how circuit-level function influences global temporal dynamics.
Experimental Procedures
Procedures were approved by the Institutional Animal Care and Use Committee at the University of California, Davis and carried out at the California National Primate Research Center (CNPRC).
Subjects
Subjects were four adult male rhesus macaques (Macaca mulatta) averaging 5.25 years of age (SD=0.49) and weighing, on average, 9.51 kg (SD=0.94) at time of surgery. Prior to surgeries, each subject’s serum was assayed in the Immunology Core at the University of Pennsylvania and confirmed negative (below the detectable limit) for the presence of AAV5 neutralizing antibodies.
Transfection procedures
The Vector Core at the University of North Carolina at Chapel Hill provided the rAAV5/hSyn-hM4D-mCherry vector. Lot AV5373B was used for subjects M1 and M2 at a concentration of 1.3×10^13 virus molecules per ml. Lot AV5373 was used for M3 and M4, at a concentration of 2.4×10^12 virus molecules per ml. Each animal underwent a 3D T1 weighted MRI to determine stereotactic coordinates of the amygdala. Craniotomies were made over the left and right amygdala and the vector was injected bilaterally in a cubic matrix of 8 injection sites per hemisphere. Each site received 5µl of the vector, administered using 10µl Hamilton syringes (26 gauge beveled needles) at a rate of 0.2µl per minute.
Histological evaluation of transfection
Animals were sacrificed and perfused on average 356.5 days following surgery (SD=28.36). Procedures for perfusions, sectioning, and NissL staining followed our standard laboratory protocol (see Supplemental Information). Briefly, coronal sections were cut in seven series at 30µm. Nissl-staining was performed with thionin. Sections adjacent to the Nissl stained section were immunostained using antibodies against mCherry. Avidin-Biotin Block (Vector Laboratories SP-2001, Burlingame, CA) was used to reduce non-specific background. Sections were then placed into Primary antiserum containing 1:1000 anti-mCherry (Abcam #ab167453; RRID:AB_2571870) and amplified through diaminobenzidine peroxidase reaction.
The basic description of the morphological characteristics of the amygdala nuclei have been described in detail previously by (Pitkanen and Amaral, 1998) for the cynomolgus monkey (Macaca fascicularis). We used these descriptions to determine the boundaries of four main nuclei (lateral, basal, accessory basal, and central) and of the amygdala in the Macaca mulatta. Boundaries were determined in the Nissl-stained sections and applied to the adjacent immunostained sections for stereological sampling. The total number of transfected neurons in each nucleus was estimated using the optical fractionator method (West et al., 1991).
Imaging procedures
MR imaging was performed an average of 258 days after transfection (see Table S1) on a 3T Siemens Skyra scanner with a custom built 8-channel head coil optimized for monkey brain scanning. Animals were sedated with an initial dose of ketamine (5 mg/kg), intubated, placed in an MR-compatible stereotaxic apparatus, and maintained under 1.3–1.7% isoflurane. Scanning included acquisition of a 3D T1-weighted image followed by a 60-minute functional scan sequence.
The functional scan was divided into five consecutive analysis blocks, each lasting 305 frames (11 min, 42 sec). Between the first and second block, CNO (10mg/kg in a 5mg/ml solution) was delivered and allowed one minute to equilibrate. CNO promotes selective inhibition of hM4Di expressing cells in the rodent and rhesus monkey brain (Armbruster et al., 2007; Eldridge et al., 2016; Michaelides et al., 2013). Each of the final three blocks began immediately after the previous. To control for time-dependent changes in signal across blocks, each animal was scanned again within 2–3 weeks using a saline injection of equal volume to the prior CNO injection. All other scanning and anesthetic protocols were maintained.
The raw fMRI data was preprocessed to reduce artifacts and spatially transform ROIs into native fMRI space (see Supplemental Experimental Procedures for full details). While we have used global signal regression (GSR) in previous rs-fcMRI investigations to remove global artifact (Grayson et al., 2014; Miranda-Dominguez et al., 2014) such as motion effects, the current report represents a special case. Movement was minimized by the anesthesia and stereotactic head restraint, and exogenous contrast was utilized in order to boost sensitivity relative to BOLD (see Figure S7). We found that GSR had distinct effects depending on data acquisition procedures, such that GSR improved structure-function relationships in standard BOLD acquisitions, but weakened them in the current dataset (see Figure S8). Thus, GSR was not used in the current report, although it is likely recommended in more conventional scenarios (see Supplemental Information for a full and detailed analysis).
Functional connectivity (FC) analyses
Amygdala seed-based FC
Time series were computed for each scanning block for the left and right amygdala separately by averaging the time series across all voxels within the ROI. Pearson correlations (r-values) were computed between the ROI and all other voxels in the brain. The r-value at each voxel was Fisher’s z-transformed to yield z-values (denoted z) that are theoretically normally distributed across conditions and across subjects. Statistical significance was computed using fixed effects (FFX) analyses. For each subject, individual z-values were converted to Z scores by dividing by the square root of the expected variance (EV; see Supplemental Experimental Procedures regarding calculation of the EVs). Z scores were combined across subjects using FFX (summed and divided by the square root of the sample size).
To generate significance maps of baseline amygdala FC, the pre-injection period (i.e. block 1) of both CNO and Saline conditions were collapsed across subjects and thresholded at |Z-score|>6, providing sufficient correction for multiple comparisons across voxels using a stringent Bonferroni correction (P<0.001). To test for changes in connectivity due to CNO, the FC maps (i.e. z-values) computed for each post-injection block (2, 3, 4, or 5) were compared to block 1, and the difference was compared across CNO and saline conditions. Specifically, the contrast [z(post-CNO) − z(pre-CNO)] − [z(post-Saline) − z(pre-Saline)] was converted to Z-scores using FFX. Analysis was restricted to areas of significantly positive baseline FC, then thresholded at |Z-score|>2.3 and corrected for cluster size (122 contiguous voxels, P<0.05; 10,000 Monte Carlo simulations using Gaussian Random Field theory).
Network connectivity
All cortical ROIs (see Table S5) were predefined with a parcellation of the rhesus macaque brain known as the Regional Map (RM) (Bezgin et al., 2012). The RM consists of 82 regions covering the entire cortical mantle and the amygdala. In this study, the hippocampus was excluded and the amygdala was redrawn manually. The RM parcellation is paired with a matching anatomical connectivity matrix collated from the Cocomac database of tract-tracer (TT) studies (Bezgin et al., 2012).
To assess changes in connectivity across the network, z-transformed correlations were first computed between all ROI pairs, yielding a unique 80×80 symmetric matrix (78 cortical ROIs plus the left and right amygdala) for each block in each subject. The pre-injection block here was compared against all post-injection blocks. Specifically, we computed the contrast C = [z(block2) + z(block3) + z(block4) + z(block5)]/4 − z(block1), for CNO and Saline conditions separately. The final contrast was taken as CCNO − CSaline, denoted hereafter as ΔFC. The same contrast was also used to assess changes in the variance of regional timecourses and their pairwise covariances, averaged across subjects (denoted Δvariance and Δcovariance). ΔFC was combined across subjects and tested for significance using FFX analysis.
Community detection and graph layouts
The baseline FC network was obtained by averaging z-transformed correlations across subjects and across block 1 of CNO and saline runs. Modular partitions of the network were obtained using the community detection algorithm for undirected, weighted matrices adapted from Newman (2006) and improved upon with the additional “final-tuning” algorithm described in (Sun et al., 2009). This algorithm recursively bisects a given adjacency matrix into non-overlapping groups of nodes (communities, or modules) in a way that maximizes the modularity index, or the fraction of edge weights within module partitions relative to the expected fraction of such weights in an equivalent randomized network. Modularity was computed after thresholding the baseline FC matrix at the minimum connection density that preserved full connectedness (the ability to traverse from one node to any other node in the network; 28%). However, due to the increased interest in studying fully weighted networks we also repeated all modularity-based analyses on the unthresholded network using a community detection algorithm for weighted, signed matrices (Rubinov and Sporns, 2011) (Figure S2). This weighted approach offered fewer modules at the default resolution, therefore it should be interesting for future studies to study finer scale structure by tuning the resolution parameter of the algorithm, as per (Bassett et al., 2013; Lohse et al., 2014).
Force-directed graph layouts also provide an intuitive way to visualize networks. In these layouts, connections serve as attractive forces between nodes such that well connected groups of nodes are pulled closer together. The algorithm by (Fruchterman and Reingold, 1991) was used to visualize the baseline FC matrix and the FC matrix accounting for the effect of DREADD activation (computed by adding ΔFC to the baseline network). Visualizations are provided at two thresholds: 1) using the minimum density that preserved full connectedness across both matrices, including the amygdala (31%) and excluding the amygdala (16%).
Relating structural to functional connectivity
Baseline FC
The general approach taken to predict baseline FC from SC networks is described in the main Results section. In summary, theoretic communication between each ROI pair in the structural connectomes (the TTu and TTx matrices) was quantified using the communicability metric (denoted G), which is used as a proxy for FC. G is computed for weighted networks via the matrix exponential of Wn, where Wn is the connectivity matrix after normalizing each connection weight by the geometric mean of the two node strengths (Crofts and Higham, 2009). See Supplemental Information, Figures S4 and S5, and Table S3 for further details.
FC changes
Changes in FC due to DREADD activation were compared against predictions derived from the TTu/x connectomes using the general framework of matrix communicability. Simulated disconnection lesions of the amygdala were carried out as follows. Given Wn, as described above, the matrix exponential (eWn) computes the pre-lesion G values. Separately, all links incident to the amygdala in Wn were removed to simulate disconnection. The matrix exponential was computed on this separate matrix to generate post-lesion G values. The difference post vs pre (ΔSC-communicability, or ΔG) was calculated and log-transformed.
Correlations were assessed between ΔFC and ΔG across the connectome (i.e. across node pairs). Because G incorporates all possible paths between two regions, simulated lesion of any one region generated ΔG values for all ROI pairs. Lesions were first carried out on the amygdala and ΔFC-ΔG correlations were examined across primary (amygdalocortical) and secondary (all corticocortical) ROI pairs. To examine the specificity of these correlations, this process was then repeated across all ROIs, simulating disconnection of the region and examining ΔFC-ΔG correlations across primary ROI pairs (those including the lesioned region) and secondary ROI pairs (all others). Correlations are reported separately for primary and secondary effects on each simulated region. This entire process was then repeated using Δcovariance as the empirical measure of coupling (rather than ΔFC), in order to examine the influence of potential alterations in signal variance.
In order to simulate effects that relate to regional changes in signal variance, the total change in input (ΔGinput) was calculated on each ROI, by summing all pairwise ΔGinput values incident to the ROI. Since TTx and TTu are both asymmetric matrices, the ΔG matrix is also asymmetric, allowing input and output effects to be summed separately.
Supplementary Material
Acknowledgments
This research was supported by NIH grants R21 MH098585 (DGA), R01 MH096773 (DAF), UL1TR000128 (DAF), AA109431 (KG), AA13510 (KG), and K99 MH10138 (EBM), and was conducted, in part, at the California National Primate Research Center (OD011107). We thank Joe Mandeville and Bruce Jenkins for imaging consultation, Bryan Roth for advice on DREADD experiments, and Gustavo Deco, Gleb Bezgin, and Anthony McIntosh for contributing analytic resources.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Author Contributions
DGA and DSG designed the research and wrote the paper; DSG, EBM, CJM, BJ, and DGA performed the experiments; DSG conducted data analysis; KS, DAF, and KG contributed data and analytic resources.
References
- Adachi Y, Osada T, Sporns O, Watanabe T, Matsui T, Miyamoto K, Miyashita Y. Functional connectivity between anatomically unconnected areas is shaped by collective network-level effects in the macaque cortex. Cereb Cortex. 2012;22:1586–1592. doi: 10.1093/cercor/bhr234. [DOI] [PubMed] [Google Scholar]
- Aggleton JP, Burton MJ, Passingham RE. Cortical and subcortical afferents to the amygdala of the rhesus monkey (Macaca mulatta) Brain Res. 1980;190:347–368. doi: 10.1016/0006-8993(80)90279-6. [DOI] [PubMed] [Google Scholar]
- Aggleton JP, Wright NF, Vann SD, Saunders RC. Medial temporal lobe projections to the retrosplenial cortex of the macaque monkey. Hippocampus. 2012;22:1883–1900. doi: 10.1002/hipo.22024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alstott J, Breakspear M, Hagmann P, Cammoun L, Sporns O. Modeling the impact of lesions in the human brain. PLoS Comput Biol. 2009;5:e1000408. doi: 10.1371/journal.pcbi.1000408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amaral DG, Price JL. Amygdalo-cortical projections in the monkey (Macaca fascicularis) J Comp Neurol. 1984;230:465–496. doi: 10.1002/cne.902300402. [DOI] [PubMed] [Google Scholar]
- Armbruster BN, Li X, Pausch MH, Herlitze S, Roth BL. Evolving the lock to fit the key to create a family of G protein-coupled receptors potently activated by an inert ligand. Proc Natl Acad Sci U S A. 2007;104:5163–5168. doi: 10.1073/pnas.0700293104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barttfeld P, Uhrig L, Sitt JD, Sigman M, Jarraya B, Dehaene S. Signature of consciousness in the dynamics of resting-state brain activity. Proc Natl Acad Sci U S A. 2015;112:887–892. doi: 10.1073/pnas.1418031112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bassett DS, Porter MA, Wymbs NF, Grafton ST, Carlson JM, Mucha PJ. Robust detection of dynamic community structure in networks. Chaos. 2013;23:013142. doi: 10.1063/1.4790830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bezgin G, Vakorin VA, van Opstal AJ, McIntosh AR, Bakker R. Hundreds of brain maps in one atlas: registering coordinate-independent primate neuro-anatomical data to a standard brain. NeuroImage. 2012;62:67–76. doi: 10.1016/j.neuroimage.2012.04.013. [DOI] [PubMed] [Google Scholar]
- Carrera E, Tononi G. Diaschisis: past, present, future. Brain. 2014;137:2408–2422. doi: 10.1093/brain/awu101. [DOI] [PubMed] [Google Scholar]
- Crofts JJ, Higham DJ. A weighted communicability measure applied to complex brain networks. J R Soc Interface. 2009;6:411–414. doi: 10.1098/rsif.2008.0484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crofts JJ, Higham DJ, Bosnell R, Jbabdi S, Matthews PM, Behrens TE, Johansen-Berg H. Network analysis detects changes in the contralesional hemisphere following stroke. NeuroImage. 2011;54:161–169. doi: 10.1016/j.neuroimage.2010.08.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deco G, McIntosh AR, Shen K, Hutchison RM, Menon RS, Everling S, Hagmann P, Jirsa VK. Identification of optimal structural connectivity using functional connectivity and neural modeling. J Neurosci. 2014;34:7910–7916. doi: 10.1523/JNEUROSCI.4423-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eldridge MA, Lerchner W, Saunders RC, Kaneko H, Krausz KW, Gonzalez FJ, Ji B, Higuchi M, Minamimoto T, Richmond BJ. Chemogenetic disconnection of monkey orbitofrontal and rhinal cortex reversibly disrupts reward value. Nat Neurosci. 2016;19:37–39. doi: 10.1038/nn.4192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Estrada E, Hatano N. Communicability in complex networks. Phys Rev E Stat Nonlin Soft Matter Phys. 2008;77:036111. doi: 10.1103/PhysRevE.77.036111. [DOI] [PubMed] [Google Scholar]
- Fornito A, Zalesky A, Breakspear M. The connectomics of brain disorders. Nat Rev Neurosci. 2015;16:159–172. doi: 10.1038/nrn3901. [DOI] [PubMed] [Google Scholar]
- Fruchterman TMJ, Reingold EM. Graph Drawing by Force-Directed Placement. Software-Practice & Experience. 1991;21:1129–1164. [Google Scholar]
- Goni J, van den Heuvel MP, Avena-Koenigsberger A, Velez de Mendizabal N, Betzel RF, Griffa A, Hagmann P, Corominas-Murtra B, Thiran JP, Sporns O. Resting-brain functional connectivity predicted by analytic measures of network communication. Proc Natl Acad Sci U S A. 2014;111:833–838. doi: 10.1073/pnas.1315529111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goulas A, Bastiani M, Bezgin G, Uylings HBM, Roebroeck A, Stiers P. Comparative Analysis of the Macroscale Structural Connectivity in the Macaque and Human Brain. PLoS Comp Biol. 2014;10:e1003529. doi: 10.1371/journal.pcbi.1003529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gratton C, Nomura EM, Perez F, D'Esposito M. Focal brain lesions to critical locations cause widespread disruption of the modular organization of the brain. J Cogn Neurosci. 2012;24:1275–1285. doi: 10.1162/jocn_a_00222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grayson DS, Kroenke CD, Neuringer M, Fair Da. Dietary omega-3 Fatty acids modulate large-scale systems organization in the rhesus macaque brain. The Journal of neuroscience : the official journal of the Society for Neuroscience. 2014;34:2065–2074. doi: 10.1523/JNEUROSCI.3038-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gu S, Pasqualetti F, Cieslak M, Telesford QK, Yu AB, Kahn AE, Medaglia JD, Vettel JM, Miller MB, Grafton ST, et al. Controllability of structural brain networks. Nat Commun. 2015;6:8414. doi: 10.1038/ncomms9414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansen EC, Battaglia D, Spiegler A, Deco G, Jirsa VK. Functional connectivity dynamics: modeling the switching behavior of the resting state. NeuroImage. 2015;105:525–535. doi: 10.1016/j.neuroimage.2014.11.001. [DOI] [PubMed] [Google Scholar]
- He BJ, Snyder AZ, Vincent JL, Epstein A, Shulman GL, Corbetta M. Breakdown of functional connectivity in frontoparietal networks underlies behavioral deficits in spatial neglect. Neuron. 2007;53:905–918. doi: 10.1016/j.neuron.2007.02.013. [DOI] [PubMed] [Google Scholar]
- Honey CJ, Sporns O. Dynamical consequences of lesions in cortical networks. Hum Brain Mapp. 2008;29:802–809. doi: 10.1002/hbm.20579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Honey CJ, Sporns O, Cammoun L, Gigandet X, Thiran JP, Meuli R, Hagmann P. Predicting human resting-state functional connectivity from structural connectivity. Proceedings of the National Academy of Sciences of the United States of America. 2009;106:2035–2040. doi: 10.1073/pnas.0811168106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutchison RM, Everling S. Monkey in the middle: why non-human primates are needed to bridge the gap in resting-state investigations. In Frontiers in Neuroanatomy. 2012 doi: 10.3389/fnana.2012.00029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joyce KE, Hayasaka S, Laurienti PJ. The human functional brain network demonstrates structural and dynamical resilience to targeted attack. PLoS Comput Biol. 2013;9:e1002885. doi: 10.1371/journal.pcbi.1002885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lohse C, Bassett DS, Lim KO, Carlson JM. Resolving anatomical and functional structure in human brain organization: identifying mesoscale organization in weighted network representations. PLoS Comput Biol. 2014;10:e1003712. doi: 10.1371/journal.pcbi.1003712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mehler WR. Subcortical afferent connections of the amygdala in the monkey. J Comp Neurol. 1980;190:733–762. doi: 10.1002/cne.901900407. [DOI] [PubMed] [Google Scholar]
- Messe A, Rudrauf D, Benali H, Marrelec G. Relating structure and function in the human brain: relative contributions of anatomy, stationary dynamics, and non-stationarities. PLoS Comput Biol. 2014;10:e1003530. doi: 10.1371/journal.pcbi.1003530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michaelides M, Anderson SAR, Ananth M, Smirnov D, Thanos PK, Neumaier JF, Wang G-J, Volkow ND, Hurd YL. Whole-brain circuit dissection in free-moving animals reveals cell-specific mesocorticolimbic networks. The Journal of clinical investigation. 2013;123:5342–5350. doi: 10.1172/JCI72117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miranda-Dominguez O, Mills BD, Grayson D, Woodall a, Grant Ka, Kroenke CD, Fair Da. Bridging the Gap between the Human and Macaque Connectome: A Quantitative Comparison of Global Interspecies Structure-Function Relationships and Network Topology. J Neurosci. 2014;34:5552–5563. doi: 10.1523/JNEUROSCI.4229-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newman MEJ. Modularity and community structure in networks. Proceedings of the National Academy of Sciences of the United States of America. 1998;103:8577–8582. doi: 10.1073/pnas.0601602103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pitkanen A, Amaral DG. Organization of the intrinsic connections of the monkey amygdaloid complex: projections originating in the lateral nucleus. J Comp Neurol. 1998;398:431–458. doi: 10.1002/(sici)1096-9861(19980831)398:3<431::aid-cne9>3.0.co;2-0. [DOI] [PubMed] [Google Scholar]
- Rubinov M, Sporns O. Weight-conserving characterization of complex functional brain networks. NeuroImage. 2011;56:2068–2079. doi: 10.1016/j.neuroimage.2011.03.069. [DOI] [PubMed] [Google Scholar]
- Russchen FT, Bakst I, Amaral DG, Price JL. The amygdalostriatal projections in the monkey. An anterograde tracing study. Brain Res. 1985;329:241–257. doi: 10.1016/0006-8993(85)90530-x. [DOI] [PubMed] [Google Scholar]
- Seeley WW, Crawford RK, Zhou J, Miller BL, Greicius MD. Neurodegenerative diseases target large-scale human brain networks. Neuron. 2009;62:42–52. doi: 10.1016/j.neuron.2009.03.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen K, Bezgin G, Hutchison RM, Gati JS, Menon RS, Everling S, McIntosh AR. Information processing architecture of functionally defined clusters in the macaque cortex. The Journal of neuroscience : the official journal of the Society for Neuroscience. 2012;32:17465–17476. doi: 10.1523/JNEUROSCI.2709-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simpson SL, Moussa MN, Laurienti PJ. An exponential random graph modeling approach to creating group-based representative whole-brain connectivity networks. NeuroImage. 2012;60:1117–1126. doi: 10.1016/j.neuroimage.2012.01.071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stefanacci L, Amaral DG. Some observations on cortical inputs to the macaque monkey amygdala: an anterograde tracing study. J Comp Neurol. 2002;451:301–323. doi: 10.1002/cne.10339. [DOI] [PubMed] [Google Scholar]
- Stephan KE, Kamper L, Bozkurt A, Burns GA, Young MP, Kotter R. Advanced database methodology for the Collation of Connectivity data on the Macaque brain (CoCoMac) Philos Trans R Soc Lond B Biol Sci. 2001;356:1159–1186. doi: 10.1098/rstb.2001.0908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun Y, Danila B, Josic K, Bassler KE. Improved community structure detection using a modified fine-tuning strategy. Epl. 2009;86 [Google Scholar]
- Warren DE, Power JD, Bruss J, Denburg NL, Waldron EJ, Sun H, Petersen SE, Tranel D. Network measures predict neuropsychological outcome after brain injury. Proc Natl Acad Sci U S A. 2014;111:14247–14252. doi: 10.1073/pnas.1322173111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- West MJ, Slomianka L, Gundersen HJ. Unbiased stereological estimation of the total number of neurons in thesubdivisions of the rat hippocampus using the optical fractionator. Anat Rec. 1991;231:482–497. doi: 10.1002/ar.1092310411. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.