Continuous immunotypes describe human immune variation and predict diverse responses

Significance

The human immune system consists of many different white blood cells that coordinate their actions to fight infections. The balance between these cell populations is determined by direct interactions and soluble factors such as cytokines, which serve as messengers between cells. Understanding how the interactions between cell populations influence the function of the immune system as a whole will allow us to better distinguish patients most at risk for specific infections or immune-mediated diseases and inform vaccination strategies. Here, we determine key collective interactions between white blood cells present in blood samples taken from healthy individuals. This perspective allows us to predict functional responses and describe previously unappreciated differences between age groups and in individuals carrying cytomegalovirus.

Abstract

The immune system consists of many specialized cell populations that communicate with each other to achieve systemic immune responses. Our analyses of various measured immune cell population frequencies in healthy humans and their responses to diverse stimuli show that human immune variation is continuous in nature, rather than characterized by discrete groups of similar individuals. We show that the same three key combinations of immune cell population frequencies can define an individual’s immunotype and predict a diverse set of functional responses to cytokine stimulation. We find that, even though interindividual variations in specific cell population frequencies can be large, unrelated individuals of younger age have more homogeneous immunotypes than older individuals. Across age groups, cytomegalovirus seropositive individuals displayed immunotypes characteristic of older individuals. The conceptual framework for defining immunotypes suggested by our results could guide the development of better therapies that appropriately modulate collective immunotypes, rather than individual immune components.

In the peripheral blood of humans over 100 different immune cell populations can be distinguished based on the expression of cell surface and intracellular markers. These cell populations span various activation and differentiation states within broader classes of principal immune cell lineages in the adaptive and innate immune systems (1). With recent advances in single-cell measurement technologies such as high-dimensional flow cytometry and mass cytometry (2), these different immune cell populations can be simultaneously quantified in an individual sample. Leveraging these developments, recent population studies have profiled the global immune cell composition in healthy adult humans (3–5) and found these to be highly stable within an individual over the course of weeks to months, but highly variable between individuals (3, 6). Although variations in a few immune cell populations are heritable, the majority of immune cell population frequencies and functional responses are largely determined by nonheritable influences in healthy individuals (4). For example, cohabitation has been shown to be a strong influence, emphasizing the importance of shared environmental factors within a household (6). Most of the specific environmental factors that shape human immune systems have yet to be determined, but monozygotic (MZ) twin pairs discordant for human cytomegalovirus (HCMV) seropositivity were more different in the majority of immune measurements compared with seronegative twins (4).

Many studies have focused on individual immune cell populations, their functional properties, regulatory roles, and clinical significance. However, a prototypical immune response involves the coordinated action of multiple cell populations (7, 8), providing both inhibitory and stimulatory feedback, leading to a balanced response that fulfills its protective function while preventing immunopathology. The rules for immune cell interdependence are understood in only a few cases, but there may be many that are unknown. Many current therapies target individual cell populations and sometimes give rise to unexpected side effects, involving completely different cell populations from the ones directly targeted. For example, a subgroup of patients treated with the B-cell–depleting antibody Rituximab, which targets the CD20 antigen expressed on B cells, developed delayed neutropenia despite the fact that neutrophils do not express CD20 (9). An understanding of why such complications occur in selected patients requires a more complete knowledge of how specific immune cell populations depend on each other, regulate each other, and affect systemic responses.

The immune system is a complex adaptive system, without any apparent master regulator. Therefore, all systemic behaviors are emergent properties dependent upon the collective actions of all system components. As such, immune responses will be unpredictable until these emergent properties are understood. Furthermore, specific immune cell populations are dependent upon each other for stimulation and inhibition, and different cell population frequencies vary widely across healthy individuals. Therefore, we hypothesized that differences in immune responses between individuals are influenced by differences in some collective measures of their frequencies of various immune cell populations; i.e., certain combinations of immune cell populations are determinants of response. In this paper, we test this hypothesis by analyzing responses to stimuli in cohorts of healthy humans.

We first analyzed immune cell composition data from a total of 1,575 healthy individuals across multiple cohorts, both published (6, 10) and previously unpublished (149 individuals) in addition to our previously published data (4), combined in Dataset S1. We also took advantage of a set of diverse functional responses measured in 329 individuals from a number of Stanford cohorts (refs. 4 and 11 and previously unpublished data, combined in Datasets S2 and S3). Our goal was to define a small number of collective variables, or specific combinations of cell populations, variations in which could predict functional responses. Thus, our results depend on the specific cell populations and functional responses measured in this study. As such, future studies across additional independent cohorts from different geographical locations measuring the same or different cell populations and functional responses are needed to further validate the concept that a few properly chosen collective variables can predict a person’s immune response to stimulation. Nonetheless, our current analysis is a proof of concept that immunology can benefit from a more collective view of the immune system as a whole.

We identified three key combinations of immune cell frequencies (not individual cell frequencies) that robustly predict diverse functional responses in healthy individuals. Viewed from the perspective of how individual humans are different in terms of key combinations of cell populations, we find that, rather than separate clusters of individuals sharing immunological traits, there is a continuum of human immune variation. This variation is influenced, but not dictated, by age, sex and HCMV seropositivity. Even though young individuals vary greatly in their frequencies of individual cell populations, they are highly similar to each other in terms of these three key combinations of immune cell frequencies. With age, unrelated individuals become more heterogeneous when viewed from this perspective, likely reflecting the diversity of environmental exposures with time. Our results show that HCMV seropositivity is associated with a shift in immune phenotype along an age axis, leading to a phenotype characteristic of older populations, irrespective of the actual age of the individual. This conceptual framework of defining immunotypes using the collective states of many immune system components provides a sensitive way of describing immune variation and could guide the development of better immune modulatory therapies in the future.

Results

Human Cohorts and Measurements.

We analyzed human immune cell frequency data from multiple cohorts, described in further detail in Materials and Methods. These are referred to as the Stanford cohorts of 398 individuals, 226 MZ and dizygotic (DZ) twins from a published twin study (4), 23 individuals from a published longitudinal study (11), and 149 previously unpublished subjects (combined in Dataset S1); the Roederer et al. (10) cohort, consisting of 669 female twins sampled in the United Kingdom; and the Carr et al. (6) cohort, consisting of 670 nontwin subjects, both men and women, sampled in Belgium.

All three cohorts measured the frequencies of various immune cell populations in samples of peripheral blood mononuclear cells (PBMCs). In addition, for the Stanford cohort, a diverse set of functional responses was measured, including 168 signaling responses to cytokine stimulation in vitro (Dataset S2), as well as response to vaccination to five influenza strains (Dataset S3), listed in Materials and Methods. The cell signaling and antibody responses are referred to as functional responses.

Variation of Immune Cell Composition Across Healthy Individuals Is Continuous Rather than Discrete.

There has been much interest recently in characterizing immune variation across healthy individuals over a variety of ages (3–6, 10, 12–15). It is also well established that healthy individuals respond differently to the same immunological stimulation. A puzzling example of this is that although most patients receiving certain influenza vaccines mount robust antibody responses, some otherwise healthy patients fail to produce a protective response. The reasons for such disparities are only partially understood (16). Along the same lines, novel immune-modulatory drugs used for cancer therapy yield variable and unpredictable responses in different patients (17, 18).

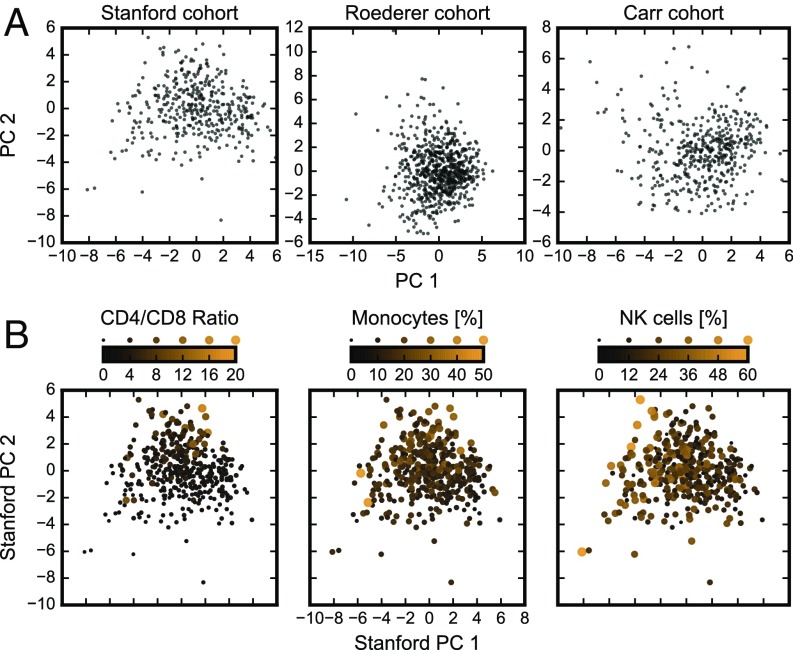
To understand such similarities and differences in immune responsiveness, a conceptual framework for assessing and studying interindividual differences in immune cell composition will be helpful. Using data from the three cohorts, we asked whether a healthy population formed well-separated clusters of individuals with similar immune cell composition traits. We analyzed each dataset separately as differences in the measurement panels prevented us from combining them (Table S1). Principal component analysis (PCA) (19) was used to project high-dimensional immune cell compositions onto the two principal components (PCs) that account for most of the underlying variance in each dataset (Fig. 1A). In each of the three datasets, individuals were spread across a continuous “cloud” and did not segregate into separate clusters.

Table S1.

Immune cell populations measured in each of the Stanford, Roederer, and Carr cohorts, related to Fig. 2

Cell population	Stanford	Roederer	Carr
Lymphocytes	✓	✓	✓
B cells	✓	✓	✓
Naïve B cells	✓	✓	✓
Memory B cells	✓	✓	✓
T cells	✓	✓	✓
CD4+ T cells	✓	✓	✓
CD8+ T cells	✓	✓	✓
Naïve CD4+ T cells	✓	✓	✓
Naïve CD8+ T cells	✓	✓	✓
Effector memory CD4+ T cells	✓	✓	✓
Effector memory CD8+ T cells	✓	✓	✓
Central memory CD4+ T cells	✓	✓	✓
Central memory CD8+ T cells	✓	✓	✓
NK cells	✓	✓	✓
NKT cells	✓	✓	✓
IgD–CD27– B cells	✓	✓
IgD–CD27+ B cells	✓	✓
IgD+CD27– B cells	✓	✓
IgD+CD27+ B cells	✓	✓
CD161+CD4+ T cells	✓	✓
CD161+CD8+ T cells	✓	✓
CD28+CD8+ T cells	✓	✓
CD4+CD28+ T cells	✓	✓
Effector CD4+ T cells	✓	✓
Effector CD8+ T cells	✓	✓
Tregs	✓		✓
γδ T cells	✓		✓
Populations unique to cohort	Monocytes, viable/singlets, CD20–CD3– lymphocytes, transitional B cells, CD161–CD45RA– Tregs, CD161–CD45RA+ Tregs, CD85j+CD8+ T cells	HLADR–CD38–CD4+ T cells, HLADR–CD38–CD8+ T cells, HLADR–CD38+CD4+ T cells, HLADR–CD38+CD8+ T cells, HLADR+CD38–CD4+ T cells, HLADR+CD38–CD8+ T cells, HLADR+CD38+CD4+ T cells	Bswitch, CD4+ EMRA, CD4+IL2+, CD4+ RTE, CD8+ EMRA, CD8+IL2+, CD8+ RTE, DCs, iNKT, mDCs, pDCs, Tc1, Th1, Th17, Th2

A ✓ in a given column indicates that the indicated immune cell population was measured in the cohort corresponding to that column. The last row lists all immune cell populations that are unique to each cohort. As described in the text, some cell populations are removed based on missing data; this table contains only those populations that were retained for the clustering analysis.

Fig. 1.

Immune cell composition varies continuously across the healthy human population. (A) Projection of immune cell compositions of the Stanford, Roederer, and Carr cohorts onto the top two of their respective PCs (Fig. S1). (B) Overlay of individuals from the Stanford cohorts with extreme values of individual immune cell populations (or two, in the case of CD4/CD8 ratio) on the top two PCs of immune cell composition data. Solid circles scale linearly in both area and color (Fig. S2).

We quantified this by performing k-means clustering on the top PCs for each dataset (Fig. S1). The extent of clustering, when quantified (by average silhouette coefficient and between-cluster variance, Fig. S1 B and C), is no higher for the cohorts in this study compared with randomized “null” datasets (Materials and Methods, Clustering Methods). Although Fig. 1A shows only the top two PCs, the analyses in Fig. S1 B and C show lack of clustering using up to the top 10 PCs (which explain around 70% of total variance; Fig. S1A). Finally, t-distributed stochastic neighbor embedding (20–22), a nonlinear dimensionality reduction technique that overcomes the limitation of linearity in PCA, also reveals a similarly continuous distribution of individuals with respect to their immune cell composition (Fig. S1D). Thus, we concluded that there is no evidence of clustering of individuals based on their immune cell composition in any of these datasets. We acknowledge the possibility that discrete clusters were not found simply because the particular cell populations measured in these studies represent a limited panel. However, this possibility is unlikely given the number and diversity of cell populations analyzed, and instead our results suggest that human immune cell composition variation is continuous rather than discrete among healthy individuals.

Fig. S1.

Additional clustering analysis for the Stanford, Roederer, and Carr cohorts reveals no clustering, related to Fig. 1A. (A) Cumulative explained variance of PCs from PCA. Datasets dominated by top PCs often show a kink (or “shoulder”) in the graph, indicating that most of the variability can be explained by only a few PCs. This feature is notably absent from our analyses. (B and C) Clustering using the k-means algorithm was performed on the immune cell compositions, using up to the top 10 PCs (line colors range from black to orange, indicating 1, 2, 3, 4, 5, and 10 PCs used in clustering; analysis using 6–9 PCs showed a similar trend, but these lines were removed for visual clarity) and specifying up to 10 clusters (x axis). The quality of clustering was evaluated using one of two metrics: (B) average silhouette coefficient or (C) between-cluster explained variance. Both metrics are compared with a suitable null distribution (Materials and Methods, Clustering Methods), in dashed, semitransparent lines. Larger values indicate a greater degree of clustering for either metric. Thus, because neither metric is significantly larger than the corresponding null distribution, we conclude that these datasets do not cluster any more readily than randomly generated datasets. (D) Dimensionality reduction using two-component t-SNE also reveals no visual clustering.

Healthy Individuals with Extreme Values of Specific Cell Types Are Not Outliers in the Context of Their Collective Immune Cell Composition.

Within these continuously distributed immune cell compositions, we sought to understand whether individuals with extreme outlier values of specific immune cell population frequencies are also outliers when taking the full set of measurements into account. As three key examples involving both innate and adaptive cells, we analyzed CD4/CD8 ratios (i.e., the ratio between CD4⁺ and CD8⁺ T-cell population frequencies) and monocyte and NK cell frequencies. The CD4/CD8 ratios are commonly studied and have been related to diverse immunological conditions (23–25), most notably as a prime indicator of AIDS before the identification of the virus (26). Normal ratios are believed to be ∼2 and our results show that CD4/CD8 ratios among healthy individuals varied broadly, from 0.34 to 16 (Fig. 1B). To our surprise, the outlier individuals with very high or very low CD4/CD8 ratios were distributed throughout the cloud of points representing healthy individuals when viewed in the context of their collective cell composition (Fig. 1B). In other words, the CD4/CD8 ratio, although exhibiting a large range, did not significantly contribute to the underlying correlated variation captured by PC1 and PC2. A similar pattern was found for other well-defined cell populations such as monocytes, which varied broadly from 0% to 49% of non–T- and non–B-cell PBMCs, and NK cells, which varied from 0% to 59% of non–T- and non–B-cell PBMCs (Fig. 1B). Despite such extreme individual values of specific cell population frequencies, these individuals were not outliers with respect to their global immune cell composition (Fig. 1B). Fig. S2 corroborates this finding by overlaying the bottom and top 5% of these three individual immune cell frequencies onto the distribution of the top four PCs individually. We conclude from these findings that individual immune cell measurements alone cannot identify individuals with outlier phenotypes and only by taking the collective state of their immune cell composition can such individuals be defined. This has important implications for the definition of immunological health and disease risk.

Fig. S2.

Individuals considered outliers in individual immune cell populations are not outliers using a collective description via PCs, related to Fig. 1B. Shown are distributions of PC scores across the Stanford cohort population (PCs 1–4 in A–D, respectively). For each of CD4/CD8 ratio, monocytes, and NK cells, outlier individuals (defined as being in the top (red) or bottom (blue) 5% of the respective individual population distribution) are indicated by open circles on the x axis. Because these outlier individuals are distributed throughout the ranges of PCs 1–4, we find that outliers in individual populations do not necessarily constitute outliers in the collective description of immune cell composition.

Diverse Functional Responses Can Be Predicted Based on an Individual’s Immune Cell Composition.

Given that the immune cell compositions are continuously distributed among healthy individuals and that the possible combinations of immune cell frequencies in any individual are large, we explored whether the extent to which an individual’s immune system responds to stimuli can be adequately predicted by a smaller set of specific combinations of individual immune cell frequencies; each such combination is a collective variable. In other words, we sought to choose a small set of collective variables in a way such that individuals with similar coordinates in the space defined by these collective variables respond similarly to a particular stimulation. Toward this end, we used partial least-squares (PLS) regression (27) to correlate the immune cell compositions of individuals in the Stanford cohort with a large set of measured functional responses, thereby defining a particular choice of collective variables [termed the PLS “latent variables” (LVs)]; note that response measurements were not available for the Roederer and Carr cohorts so this analysis applies only to the Stanford cohort. The functional responses analyzed involved three JAK-STAT signaling pathways. These pathways are prototypic membrane to nucleus pathways stimulated by a range of cytokines and growth factors and regulate growth, survival, differentiation, and pathogen resistance in the immune system (28). We analyzed the phosphorylation of STAT1(pY701), STAT3(pY705), and STAT5(pY694) in response to one of seven different cytokines (IL-2, Il-6, IL-7, IL-10, IL-21, IFN-α, or IFN-γ) in PBMCs in vitro (4, 11). The three responses were analyzed by intracellular antibody staining and flow cytometry, allowing for the responses of eight different immune cell populations [monocytes, B cells, total CD4⁺, naive CD4⁺ (CD45RA⁺), memory CD4⁺ (CD45RA^–), total CD8⁺, naive CD8⁺ (CD45RA⁺), and memory CD8⁺ (CD45RA^–) T cells] to be analyzed separately. Also, antibody responses 28 d after a seasonal flu vaccination were included as a different form of functional responses (4). Interindividual differences in such responses have previously been shown to distinguish differentially regulated immune systems (29–31).

For each of the 168 responses above, PLS (Materials and Methods and Dataset S4) was used to find the LVs or the set of linear combinations of immune cell frequencies that have the highest covariance with the functional response. Our measurements span a high-dimensional space defined by axes, wherein each axis represents the frequency of a particular cell population. The LV signatures for the $k$-th functional response make up the columns of the LV matrix, ${\mathbf{R}}^{\left(k\right)},$ where the $j$-th column represents the direction in this high-dimensional space most correlated with the portion of the functional response unexplained by the previous $j-1$ LVs. This front loading (ordering of LVs in the order of explanatory power) means that potentially only a small number of such directions would have predictive value. Each direction corresponding to a LV can be viewed as an axis representing a specific combination of individual cell frequencies. A particular person’s coordinates in the low-dimensional space defined by a small number of combinations of cell populations (or axes) defines how he or she will respond to the stimulus—i.e., location of an individual’s cell composition in this lower-dimensional space defines what we term the individual’s immunotype.

We compared the performance of PLS with principal component regression (PCR), another widely used technique in which the few important axes are chosen to be the PCs, ordered to explain the most to least variance within the multidimensional immune cell compositions across patients. Model performance was measured using cross-validation to estimate an out-of-sample negative Spearman correlation between measured and predicted response (Materials and Methods). Both PLS and PCR models perform significantly better than a null model in which response measurements are permuted across individuals to destroy any relationship between immune cell composition and response (Fig. 2 A and B). This indicates that the correlations between immune cell composition and these functional responses are unlikely to occur by chance. Although this is true for all but six signaling responses (Materials and Methods, PLS Regression), only one of the five flu-vaccine responses (antibodies to influenza B/Brisbane/60/2008 strain) could be predicted by PLS/PCR better than by a null model. The 10 responses with poor PLS fit were removed from further analysis because the results are not statistically significant. Compared with PCR, the PLS models achieve lower cross-validation error with fewer LVs, a result of the “front-loaded” explanatory power in the first LVs. For a typical functional response, the first LV of PLS accounts for 50% of the possible explanatory power, whereas the first PC of PCR accounts for only 20%, requiring approximately nine PCs to reach the same model performance (Fig. 2A).

Fig. 2.

A few key combinations of immune cell frequencies predict functional responses: regression model analysis. (A and B) Learning curves for PLS and PCR models, which plot model error as a function of number of variables (LVs or PCs for PLS and PCR, respectively) included in the model. The curves are either normalized (A) or raw (B), calculated across all responses [median ± interquartile range (IQR)]. Raw error is defined as 10-fold cross-validated negative Spearman correlation between measured and predicted responses to estimate out-of-sample error. Normalized error is defined as the remaining fraction of total possible reduction in raw error $\left(\frac{e-e_{min}}{0.0-e_{min}}\right).$ (C–E) Raw latent variable signatures (gray) with mean ± SD (orange) across all responses, for the top three LVs (C, D, and E, respectively) (Fig. S3).

Remarkably, the top three most predictive LV signatures were highly concordant across different functional responses (Fig. 2 C–E). To quantify this, we calculated the similarities of predictive signatures as absolute dot products between their respective LV signatures. According to this metric, more than 64% of response pairs showed similar LV1–3 signatures (P values < 0.05 compared with a null distribution of randomly chosen vector pairs on a 34-dimensional hypersphere, Fig. S3). This result suggests that similar combinations of immune cell population frequencies are predictive of functional responses to diverse stimuli, such as IL-2–induced STAT5 phosphorylation and IFN-α–induced STAT1 phosphorylation. The fact that functional responses to many different stimuli can be predicted from immune cell population frequencies only suggests a previously unappreciated relationship between immune cell composition and functional competence in a given individual. Furthermore, the similarities between predictive signatures suggest that particular collective dependencies between immune cell populations are especially important in determining even diverse functional responses spanning multiple pathways and stimuli. However, not all responses are explained by the same three LVs, and we decided to study more carefully the responses not explained by these key combinations of immune cell frequencies.

Fig. S3.

Distribution of similarity metric (the dot product between the LVs of two responses) across all response pairs, related to Fig. 2. The similarities of the top three LVs across responses are quantified using distributions of absolute dot product between two LVs (SI Materials and Methods, Latent Variable Similarities). For example, Top Left distribution compares LV1 with LV1 across all response pairs; the labeled arrow indicates that 70% of response pairs have similarities with P < 0.05, corresponding to a dot product greater than 0.335 (SI Materials and Methods, Latent Variable Similarities).

The Response to Influenza Vaccination Is Predicted by Different Combinations of Immune Cell Populations Compared with Those That Predict Responses to Cytokines.

In contrast to in vitro stimulation with one given cytokine, in vivo responses are complex and involve multiple pathways within several cell populations. One powerful way of querying such complex responses in humans is offered by studying immune responses to vaccination. Such responses involve multiple stimuli and signaling pathways acting in concert in vivo and synergies between these components that could result in predictive LVs different from those found to predict responses to cytokines above. However, responses to vaccination were measured only in one case for a sufficient number of individuals to enable statistically meaningful analysis using PLS. This vaccine response involved the antibody responses to the influenza B/Brisbane/60/2008 strain contained in a commercial vaccine (Fluzone; Sanofi-Pasteur), measured using the hemagglutination inhibition (HAI) assay (4).

There was no measurable response to this vaccine in 31% of individuals and the PLS method had much improved explanatory power when these nonresponders were removed (Fig. S4A). Hence, our LV description of immune cell composition is predictive of the degree of response in the event that one does occur, but not of which patients do not mount an immune response at all. Importantly, the first three LVs that predict the response to vaccination are distinct from those that are predictive of the responses to in vitro stimulation by individual cytokines, in line with our hypothesis that vaccination elicits a more complex set of stimuli. This may be why different synergies between immune cell populations (different LVs) determine vaccine responsiveness compared with stimulation with a single cytokine. Some of these synergies are well known in the field, such as the requirement for T-cell “help” to enable most antibody responses, but there may be many other dependencies revealed here that have been less well characterized previously.

Fig. S4.

Analysis of LV1 heterogeneity across functional responses, related to Fig. 3. (A) Learning curves for Brisbane strain vaccination HAI response, when individuals exhibiting no fold increase in HAI titers (“nonresponders”) are either included or removed. (B) Similarity matrix of response pairs (measured by absolute value of the dot product between LV1 for two functional responses), sorted into two clusters by spectral clustering (SI Materials and Methods, Spectral Clustering). The larger cluster in the lower left is referred to as “group 1,” whereas the smaller cluster in the upper right is referred to as “group 2” (Dataset S5). (C) Distribution of log-modulus–transformed response values across signaling responses in groups 1 and 2.

To further explore why 30% of the cytokine-signaling responses were not predicted by the LVs that predicted the responses to all other responses to cytokine stimulation (Fig. 2), we clustered the similarity matrix (SI Materials and Methods, Spectral Clustering) within the first LV for all of the cytokine responses (Fig. S4B). This analysis revealed two clusters of responses (Dataset S5), the larger of which (“group 1”) contained 123 responses and the smaller of which (“group 2”) contained 43 responses. The response magnitudes in these groups were very different (Fig. S4C); specifically, the 43 responses in group 2 involved signaling responses of very low dynamic ranges, i.e., weak to no induction of phospho-STAT1, -3, or -5 in response to stimulation. In contrast, the 123 responses in group 1 showed stronger amplitudes and variation across these responses was predicted quantitatively by the same LVs. We again conclude from this observation that immune cell composition is predictive of the relative strength of a functional response upon stimulation.

Our findings are summarized in Fig. 3, which compares the LVs of the vaccination response to a selection of representative signaling responses from group 1. This representation highlights shared cell populations across predictive signatures, suggesting that these populations have larger weight in the specific combinations of immune cell populations that define the LVs for response to cytokine stimulation or vaccination. For cytokine stimulation, 12 subtypes tend to have the largest weights, most of which have the same sign across responses—a positive (negative) sign indicates that a high (low) frequency of that cell population is associated with strong functional responses. This is in contrast with the signature for the vaccination responses, in which a different immune cell signature was found with a different combination of immune cell populations being predictive of strong vaccine responsiveness.

Fig. 3.

Predictive signatures for diverse signaling responses are uniform across responses but distinct from that for vaccination by a single strain of influenza. Signatures show the top LV from group 1 responses (see text), averaged over responding cell type (top 10 rows), contrasted with that for the single flu-vaccination response (antibodies to influenza B/Brisbane/60/2008 strain; bottom row). Each solid circle represents the contribution of a particular immune cell population in the top LV that is predictive of functional response. Circle area is proportional to magnitude of the average LV1 signature coefficient, with positive or negative sign indicated by orange or purple, respectively (Fig. S4 and Dataset S5).

Spectral Clustering.

Spectral clustering of the LV1 signature similarity matrix (across responses) was performed using the sklearn.cluster.SpectralClustering() class in scikit-learn v0.17 (40). The affinity matrix was precomputed as the similarity matrix of the absolute value of the dot product described in the previous section. All other parameters used their default values. The average silhouette coefficient (41) was calculated as a function of number of clusters specified; the final execution of the spectral clustering algorithm specified two clusters, as it gave the largest average silhouette coefficient.

Immunotypes Become More Heterogeneous with Age.

The immunotypes of individuals can be visualized by projecting individuals onto the space defined by the top three LVs. Analyzing the distribution of individuals within this space can help us better understand human immune variation. The individuals studied correspond to a cloud of points distributed in a roughly conical shape. Younger individuals concentrate near the vertex of the cone and older individuals are distributed toward the base of the cone (Fig. 4A). Thus, older populations exhibit greater heterogeneity in their immunotypes than younger individuals.

Fig. 4.

Heterogeneity in immunotypes increases with age. This is defined by the top three LVs, averaged over group 1 responses (Dataset S5). (A) Individuals plotted in the immunospace defined by the first three PLS LVs. Individuals are colored in gradient from youngest (black) to oldest (orange) by rank order. The dashed red line indicates an “immunological age axis,” the direction of gradient in age (found by logistic regression of age on the top three LVs). The plots contain grayscale “shadows” projected onto the LV1–LV2 plane to aid 3D visualization, as well as a transparent cone to highlight shape of point cloud. (B) Probability distributions of interpatient Euclidean distances defined on top three LVs for different age groups (youngest 10%, 20%, and 60% corresponding to ages <15.6 y, 20 y, and 44 y, respectively, and the oldest 10% corresponding to ages >75 y). Twin pairs are excluded from all three distributions. (C) Regression coefficients (normalized to unit vector) of immune cell populations that define the immunological age axis of A, where populations are ordered by size of coefficient.

The conical shape of the point cloud, and differences in immunotypes across populations of differing ages, can be quantified by graphing distributions of interpatient distances (defined as Euclidean distance on the top three LVs) in different age groups (Fig. 4B), revealing that the youngest 10% of individuals have a much narrower distribution than the older patients. Thus, an older person’s immune response is not predicted very well by age, but rather by the individual’s immunotype. Young people are similar enough in their immunotypes for their immune responses to be better predicted by age alone. Furthermore, the diversification appears to be quite rapid, where distributions of interprofile distance for the youngest 20% and 60% (age <21 y and <43 y, respectively) quickly approach the overall distribution (Fig. 4B). One interpretation of this is that fewer significant new environmental exposures with an influence on immune variation are encountered after the mid-40s.

This result is consistent with a previous study in which immune cell frequencies were found to be more similar between younger (<20 y) than older (>60 y) monozygotic twins, presumably as a consequence of cumulative environmental influences occurring during the decades in between 20–60 y of age (4). However, it is important to emphasize that the distributions shown in Fig. 4B were calculated after excluding MZ or DZ twin pairs, as such pairs are expected to share many determinants of their immunotypes. Our findings thus show that all young individuals, and not just MZ twins, are more similar to one another than older individuals are, presumably as a consequence of the diverse cumulative influences shaping an individual’s immune system over time.

The contributions of individual immune cell populations to the age-related changes (Fig. 4C) reveal an expected shift from naive to memory cells within adaptive lymphocyte populations, but also a lesser-known increase in CD161⁺ CD4⁺ T cells and NKT cells with age. In contrast, monocyte frequencies are stable throughout life (Fig. 4C). Finally, because the heterogeneity is observed specifically in the top LVs predictive of diverse immune system responses, it indicates that the diversification of immune cell composition with age in response to environmental influences has important effects on the functional responses elicited by an aging human immune system.

Collective Predictors of Immune Responses Are Shaped by Heritable and Nonheritable Influences.

Brodin et al. (4) found that the majority of immune cell frequencies were determined by nonheritable influences. However, in defining a small set of combinations of immune cell measurements that predict functional responses, one confounds potentially heritable and nonheritable influences that shape these immunological parameters. Together with the assumption that twin pairs share many of the same environmental influences, at least early in life, we expect twin pairs to have more similar immunotypes than randomly selected pairs of individuals. Indeed, both MZ and DZ twin pairs have lower interindividual distances (Euclidean distance between immunotypes) compared with randomly chosen pairs of individuals in our cohort (Fig. 5); the random pairs of individuals were chosen with an age distribution comparable to the twin pair age distribution. The interindividual distances were lower in MZ twins than in DZ twins, illustrating the influence of both heritable and nonheritable factors for determining immunotypes (Fig. 5). This result confirms previous results and, importantly, also illustrates that the immunotypes we have defined on the basis of immune cell composition and functional responses provide an accurate representation of interindividual immune variation.

Fig. 5.

Twin pairs have similar immunotypes. Shown are interindividual distances (Euclidean distance on the top three LVs from PLS) between MZ twin pairs and DZ twin pairs, along with appropriate null models. The null models are constructed from randomly chosen pairs of individuals in the cohort restricted to a similar age distribution as exhibited by the MZ twin pairs or DZ twin pairs, respectively, as described in SI Materials and Methods, Twin Pair Immunotype Similarities Null Model.

HCMV Seropositivity Is Associated with a Shift Toward an Older Immunotype Across All Age Groups.

Given the dominance of nonheritable factors in shaping human immune systems, investigating the specific factors of importance and how they influence immunotypes is important. HCMV is known to affect the majority of immune system components (4). To this end, we reasoned that it would be interesting to compare the immunotypes of HCMV-seropositive and HCMV-seronegative individuals. Graphs analogous to Fig. 4A for HCMV serostatus (Fig. S5B) do not reveal any clear separation of individuals based on immune cell composition alone. In fact, if the LVs are used to correlate HCMV serostatus (using cross-validated logistic regression), many more LVs are required than those needed to describe the effects of aging (using cross-validated ridge regression), as shown in Fig. S5C. Fig. S5D indicates that the metadata alone (age, gender, HCMV serostatus) are insufficient to accurately predict these functional responses, and adding them to the immune cell composition data does not improve model performance, suggesting that the information provided by the metadata is less predictive than the immunotypes we have defined. This is best exemplified by the great heterogeneity seen in older individuals (Fig. 4A), whose responses can be predicted by a person’s immunotype, but not by age.

Fig. S5.

Analysis of Stanford cohort metadata, related to Fig. 6. (A and B) Immunotypes of Individuals plotted (the first three LVs from PLS), with individuals colored black or orange to indicate (A) gender or (B) CMV serology. The plots contain grayscale “shadows” projected onto the LV1–LV2 plane to aid 3D visualization. (C) Spearman correlation between predicted and observed metadata using ridge (age) or logistic (gender/CMV) regression models trained using PLS LVs (median ± IQR). (D) PLS learning curves using immune cell composition alone, metadata alone, and both (median ± IQR).

Several studies have suggested that HCMV may promote accelerated immunological aging, and it has been implicated as a driver of the immunosenescence in the elderly that is associated with an increase in all-cause mortality (32). HCMV serostatus has not been found to influence influenza vaccine responses in the elderly (32–36), but in young adults and mice, HCMV and mouse CMV (MCMV), respectively, enhance influenza immunity (33). To test whether HCMV seropositivity was reflected by a change in immunotype, we projected each individual’s cell composition onto the line within the space defined by the top three LVs that best correlates with age (Fig. 4A). This line represents an “age axis” in this space. The distributions of individual cell compositions along this line are graphed in Fig. 6A (grouped by actual age and HCMV serostatus). Fig. 6A shows that across all age groups, the distribution of HCMV seropositive individuals is shifted upward along the age axis. Because this association is true for individuals with the same actual age, we conclude that HCMV seropositivity does induce a shift in immunotypes toward one associated with older individuals. The study of individuals of similar age eliminated the confounding effect of older individuals having a greater chance of exposure to the virus and more rounds of viral reactivation. This finding is important in relation to the ongoing discussion about the role of HCMV during immunosenescence (36) and suggestive of a much broader role for HCMV, visible also in individuals as young as adolescents when viewed from the perspective of their immunotypes.

Fig. 6.

HCMV seropositive individuals have immunotypes shifted toward that characteristic of older populations. (A) Individuals in the cohort are projected onto the immunological age axis (predicting age from the top three LVs) from Fig. 4A. The distributions of positions on this line are compared between HCMV seronegative and seropositive (circles and triangles, respectively) individuals for young and old (y and o, respectively) age groups defined at various age thresholds along the x axis (mean ± SD). Age thresholds were chosen as percentiles 10–90 in increments of 10 based on the ages of individuals in the Stanford cohort. Asterisks indicate statistical significance (P < 0.05 according to a two-tailed t test) between HCMV seropositive or seronegative individuals for the young (black) and old (orange) groups. (B) Schematic illustrating immunotypes, represented as a continuously distributed point cloud. An additional small cluster in purple indicates a hypothetical (as-yet undiscovered) disease-associated region of immunospace. Grayscale shadows are projected into the CV1–CV2 plane to aid 3D visualization. Arrows corresponding to age and HCMV serostatus emphasize that external factors exist that influence individuals’ immunotypes throughout their lifetime. The arrow from the disease-associated to the “healthy” region of immunospace represents the potential for the proposed immunotype framework to guide the development of novel therapies that modulate immunotypes in a desired direction (Fig. S5).

Discussion

Here we present a conceptual framework for analyzing human immune systems in terms of “immunotypes” within a space defined by axes that represent key combinations of immune cell frequencies. First, we find that individuals’ immunotypes are distributed continuously across several healthy populations and are predictive of diverse functional immune responses as shown by in vitro cell signaling results, and these responses cannot be predicted from individual immune cell frequency measurements alone. Next, we show that specific factors, most notably age and HCMV serostatus, are associated with reproducible shifts in immunotype across unrelated, healthy individuals (shown schematically in Fig. 6B). Furthermore, by analyzing the distribution of individuals’ immunotypes, we show that the immune systems of unrelated young individuals are more similar to each other, whereas older individuals are characterized by heterogeneous immunotypes. Our results suggest that an individual’s immune cell composition may be globally modifiable by interventions to transform it from a less responsive to a more responsive immunotype.

Our findings are in accordance with recent data on the dominant influence of nonheritable factors in shaping human immune systems (4–6, 10). They further support previous findings suggesting that environmental influences exert a cumulative influence over time, leading to the divergence of immune phenotypes between MZ twins (4). The finding that collective sets of immune cell frequency measurements predict diverse functional responses is interesting and suggests that the composition of an individual’s circulating immune system reflects a functional network of cell populations and that the balance between these cell populations determines the overall responsiveness of the system. It also suggests that modulating this balance and perturbing the network, for example by depleting one specific cell type, can have broad implications for the functional responsiveness of all remaining cells. This is an important observation given that such depleting strategies are routine practice in current medical practice. An example of a manifestation of this hypothesis is the clinical observation of delayed loss of neutrophils upon depletion of CD20-expressing B cells by an anti-CD20 antibody (Rituximab) (37). Another important implication of this is that the infusion of specific cell populations, such as tumor-specific lymphocytes or populations of stem cells infused for a range of clinical conditions, could impact the global network of immune cell populations with unpredictable consequences for the immune competence of the individual patient.

The relationship between immune cell measurements and metadata—age, gender, and HCMV serostatus—also adds to our understanding of human immune system variation. The fact that these metadata alone cannot accurately predict functional responses shows the need for collective indicators of immune health (immunotypes) such as those defined in Fig. 2 C–E. Second, a description of an aging immune system requires far fewer LVs than does gender or HCMV serostatus, suggesting that these characteristics of an individual play a more complex role in regulating the immune system. The fact that older individuals are increasingly heterogeneous with respect to their immunotypes also makes age insufficient as a predictor of immune responsiveness.

Despite the potential our conceptual framework has to pose and answer important questions in immunology, it is necessary to address possible improvements in our results and methods that can be addressed in future work. First, we emphasize that PLS regression is only one method for choosing the collective variables with which to define immunotypes. Extending this method using kernels to account for nonlinear interactions between immune parameters, in addition to introducing regularization into the LV decomposition (with a sufficiently large cohort size to allow unbiased fitting and evaluation of the regularization parameter), would likely lead to more robust definitions of immunotypes. Next, we acknowledge that predictions of our functional immune responses from immunotype, although statistically significant, are moderate correlations. This is likely due to a number of reasons, the most prominent being that the 34 immune cell populations (which are restricted to peripheral blood subsets) do not afford a complete definition of immunotypes, and thus we cannot expect perfect predictions. However, more extensive immune system measurements (serum cytokines, chemokines and growth factors, antibodies, including information from additional tissue compartments, etc.), as well as taking other factors, such as the symbiotic microbiota into account, may lead to even more reliable definitions of an individual’s immunotype. Related to this, an expansion of immune measurements would also increase the potential for front loading of explanatory power into the top three LVs, covering a comparatively larger fraction of the global immune system variation in humans.

It is also important to note that our finding of a continuous distribution of immunotypes may also be sensitive to the specific immune cell populations measured in this study. An expansion of the immune measurements, as described above, could potentially reveal discrete clustering of individuals, especially if the additional immune parameters themselves exhibit discrete distributions. In addition, it is always the case that in clustering analysis, finding no evidence of discrete clusters does not prove their absence, although we are confident given our thorough analysis that discrete clusters are not present in these datasets. However, we also predict that this result could change if our cohorts were expanded to include, in addition to the healthy individuals studied here, individuals with perturbed immunotypes—e.g., patients treated with immunosuppressive drugs or individuals suffering from primary and secondary immunodeficiency syndromes with severe infectious diseases susceptibility and autoinflammatory symptoms may form a distinct cluster. We predict that these individuals may be qualitatively much different from the healthy individuals in the cohorts we studied, the discovery of which would be a next step for development of immune-modulatory therapies.

A possible criticism of the results we present here is that responses to cytokine stimulation in vitro may not be reflective of actual immune system competence that determines an individual’s risk of immune-mediated disease or severe infectious diseases. However, several lines of evidence suggest that the broadly different signaling responses, mediated via different signaling pathways, are reliable correlates of global immune competence. For example, in a recent study, Shen-Orr et al. (11) found that defective responsiveness in the JAK-STAT pathway to the same type of in vitro stimuli was strongly predictive of cardiovascular disease in a cohort of elderly individuals.

It will be important to test the concepts revealed by studying the cohorts considered in this paper by carrying out similar analyses in additional cohorts for which both immune cell compositions (or other markers) and responses to stimuli have been measured. We anticipate that the concept of continuous immunotypes predictive of immune responses will be further validated. The precise definitions of the key combinations of cell types (LVs) that define immunotypes may be cohort dependent. Indeed, it will be interesting to study how the precise definition of the LVs depends upon diet, infection history, etc., by studying cohorts of different geographical and environmental contexts whose experiences in this regard are expected to be distinct from those of the Stanford cohorts described here. Finally, the conceptual framework we have described should be augmented by a mechanistic understanding of why and how a few specific combinations of immune cell populations define an individual’s immunotype.

By addressing the above limitations in our method, we believe that our findings and the framework presented here could guide future developments of better immunomodulatory therapies designed to induce perturbations of an individual’s immunotype rather than individual immune components (Fig. 6B). This framework could also be of particular importance for the development of improved vaccines in the future, taking immunotypes into account, perhaps personalizing adjuvants and vaccine formulations as well as optimizing the time for vaccination to improve responsiveness. Also within the field of cancer immunotherapy, the induction of antitumor immune responses could be improved by stimulating immunotypes rather than individual cells to improve responsiveness. As more data become available and immunotype definitions become more robust, modeling of necessary perturbations to elicit a desired response would become possible. We envision that such a framework would make the responsiveness of individual patients to such therapies more predictable because compensatory relationships between individual cell populations are taken into account in a way in which more traditional analyses, focusing on individual cell populations only, do not. Thus, the conceptual framework we have described may have important implications for predicting immunological health and the risk of disease.

Materials and Methods

Cohorts.

In this work, we analyzed human immune cell frequency data from three cohorts. The Stanford cohort consisted of 398 individuals, both men and women, between ages 8 y and 89 y of age, sampled at the Stanford University clinical trials unit. The study protocol was approved by the Stanford University Administrative Panels on Human Subjects in Medical Research, and written informed consent was obtained from all participants. A total of 226 of these individuals were twin subjects from both MZ and DZ pairs from the Twin Research Registry at SRI International as previously described (4). A total of 23 additional subjects were included from a longitudinal study of aging in the immune system (11) and 149 previously unpublished subjects were included as well (combined in Datasets S1–S3). All demographic information of the subjects in the Stanford cohort is available in Dataset S1. The Stanford cohort comprises individuals from the following ClinicalTrials.gov study IDs: NCT01827462, NCT03020498, NCT03022396, NCT03022422, and NCT03022435. The Roederer et al. (10) cohort consists of 669 female twins sampled in the United Kingdom. The Carr et al. (6) cohort consists of 670 nontwin subjects, both men and women sampled in Belgium.

Immune Cell Population Frequency Measurements.

All three cohorts analyzed PBMCs, using either flow cytometry or mass cytometry. The immune cell composition data for the Stanford cohort were generated by the Human Immune Monitoring Center, using mass cytometry and antibody panels (4, 11). All cells were classified by manual gating, using the FlowJo Software (ThreeStar Inc.), and gating schemes are presented in the original publications. The PBMCs from the Roederer et al. (10) and Carr et al. (6) cohorts were analyzed by a combination of consecutive flow cytometry panels and manual gating.

Functional Response Measurements.

Frozen PBMCs were thawed and stimulated, with one of seven different cytokines (IL-2, IL-6, IL-7, IL-10, IL-21, IFN-α, or IFN-γ) for 30 min; fixed; and stained with antibodies to surface antigens (identifying eight responding cell populations: monocytes, B cells, CD4⁺, CD4⁺CD45RA⁺, CD4⁺CD45RA^–, CD8⁺, CD8⁺CD45RA⁺, and CD8⁺CD45RA^– T cells) as well as intracellular phosphor-STAT1, -3, and -5, respectively, as described in detail previously (4). The 90th percentile fluorescence intensity of stimulated samples was compared with the 90th percentile in PBS-treated cells (unstimulated) as a fold-change ratio used for downstream analyses (Dataset S2). In addition to the cell-signaling responses, we also include an analysis of antibody responses to seasonal flu vaccines (years 2010–2012) (Dataset S3). The vaccine administered was the Fluzone quadrivalent vaccine (Sanofi-Pasteur Inc.) and the vaccine-induced antibody responses were measured in a strain-specific manner, using HAI assays, and fold changes day 28/day 0 were used for analyses as described in detail in ref. 4. The flu-vaccine data included eight strains: A/Texas/50/2012, B/Massachusetts/2/2012, B/Brisbane/60/2008, A/California/07/2009(H1N1), A/Perth/16/2009(H3N2), A/South Dakota/06/2007(H1N1), A/Uruguay/716/2007(H3N2), and Wisconsin. The A/Texas/50/2012, B/Massachusetts/2/2012, and Wisconsin strains were removed due to small sample size (Data Preprocessing).

Data Preprocessing.

Of the 136 cell population frequencies measured in the Stanford cohort, 34 were considered in this study. We removed 89 cell populations because they were measured in only 10.3%, 29.1%, 39.4%, or 70.8% of the 398 patients. We also removed the following 13 subtypes because they either are rare or are the complement in a set of rare cell populations: plasmablasts, HLADR⁺ NK cells, CD161⁺CD45RA⁺ Tregs, CD161⁺CD45RA⁻ Tregs, CD85j⁺CD4⁺ T cells, HLADR⁺CD38⁺CD4⁺ T cells, HLADR⁺CD38⁺CD8⁺ T cells, HLADR⁺CD38⁻CD4⁺ T cells, HLADR⁺CD38⁻CD8⁺ T cells, HLADR⁻CD38⁺CD4⁺ T cells, HLADR⁻CD38⁺CD8⁺ T cells, HLADR⁻CD38⁻CD4⁺ T cells, and HLADR⁻CD38⁻CD8⁺ T cells. To remove measurement dependence on measurement year (2009–2012), we applied the ComBat algorithm (38), an empirical Bayes method for removing nonbiological experimental variation that has been found to outperform other batch effect correction methods according to many metrics (39). Patient 398 was removed due to missing batch information, leaving a total of 397 patients studied from the Stanford cohort. A summary of the immune cell population frequencies and demographics data for the Stanford cohort is available in Dataset S1.

Functional responses having fewer than 34 patients (equal to the number of retained cell populations) were removed from consideration: three influenza strains (A/Texas/50/2012, B/Massachusetts/2/2012, and Wisconsin), as well as all 21 cytokine stimulation responses measured in the “Non-BT” cell subtype.

Clustering Methods.

The Stanford, Roederer et al. (10), and Carr et al. (6) cohorts included composition measurements of nonidentical immune cell populations (Table S1 for a list of cell subtypes in each cohort), thus precluding a combined clustering analysis of the full dataset. The “monocytes” cell population was removed from the Roederer et al. (10) cohort as it was missing in 7.6% of the 729 patients. Of the remaining 32 populations, 11 had missing data in at most 1.6% of patients. For the Carr et al. (6) cohort, patients containing >20% missing measurements were removed, leaving a total of 449 patients. Cell populations with >10% missing values across patients were removed from consideration. Of the remaining 32 populations, 5 had missing data in at most 4% of patients. Missing values in both cohorts were imputed to the average across all patients.

Clustering analysis was performed on the PC scores (projections of immune cell composition data onto the eigenvectors of the correlation matrix—this places all immune cell population frequencies on the same scale). Clustering of individuals was performed on the top PCs with a k-means clustering algorithm implemented using the sklearn.cluster.KMeans() class in scikit-learn v0.17 (40), using interpoint Euclidean distance in PC space. The quality of clusters from this algorithm was quantified using two metrics:

• i)The silhouette coefficient (41) is defined for each data point, $i$, as $\left(b_i-a_i\right)/\max \left\{a_i,b_i\right\}$ in which $a_i$ is the average pairwise Euclidean distance between data point $i$ and all other points within the same cluster as $i,$ whereas $b_i$ is the lowest average pairwise Euclidean distance between data point $i$ and all data points in any other cluster. The silhouette coefficient ranges from −1 to 1, with a high value indicating good clustering.
• ii)The between-cluster fractional explained variance is defined as the variance in the data where each point is replaced by the average of the points in the same cluster, divided by the total variance, $V^{tot},$ in the data (equal to the sum of between-cluster and within-cluster variance, $V^{b/w}$ and $V^{w/i},$ respectively). More formally, let ${\mathbf{x}}_i={\left(\begin{array}{cccc}{x}_i^{\left(1\right)}& x_i^{\left(2\right)}& \dots & x_i^{\left(d\right)}\end{array}\right)}^{\text{T}}$ be a vector of PC scores (PCs $1-d$) for patient $i$ and $\mu ={\displaystyle \sum _{i=1}^N}{\mathbf{x}}_i/N$ be the mean over all $N$ patients. Now, let the clustering algorithm assign each patient to one of $C$ clusters, $c_i\in \left\{1,\dots ,C\right\},$ and let ${\mathbf{X}}_c$ be a matrix composed of the subset of rows of $X$ corresponding to patients assigned to cluster $c;$ i.e., the rows of ${\mathbf{X}}_c$ are the set $\left\{{\mathbf{x}}_i\mathrm{:}{c}_i=c\right\}.$ Finally, let ${\mu }_{\text{c}}=\frac{1^{\text{T}}\mathbf{X}}{\#\left\{i\mathrm{:}{c}_i=c\right\}}$ be the cluster average, where $1$ is a vector of ones. Then, the between-cluster fractional explained variance, $V^{b/w,\hspace{0.17em}frac},$ is calculated as follows:

$$V^{tot}=\text{tr}\left[{\left(\mathbf{X}-\mu \right)}^{\text{T}}\left(\mathbf{X}-\mu \right)\right]$$

$$V^{w/i}={\displaystyle \sum _{c=1}^C}\text{tr}\left[{\left({\mathbf{X}}_{\text{c}}-{\mu }_{\text{c}}\right)}^{\text{T}}\left({\mathbf{X}}_{\text{c}}-{\mu }_{\text{c}}\right)\right]$$

$$V^{b/w,\hspace{0.17em}frac}=\frac{V^{Tot}-V^{w/i}}{V^{tot}}=\frac{V^{b/w}}{V^{tot}}.$$

Because these measures of cluster performance are difficult to interpret alone, they are compared with a null model formed by the following: (i) For each PC, $i,$ in the original data, calculate the difference, $a_i,$ between the 97.5th and 2.5th percentiles of the scores of that PC. This gives a robust-to-outliers measure of the spread in each PC. (ii) Choose a number of PCs, $d,$ to include in the clustering. (iii) Generate a uniform random sample of profiles within the PC space contained within a $d$-dimensional ellipsoid with principal axes equal to the respective differences calculated in i. If $x_i$ represents the randomly generated value for the PC $i$ score, the null model satisfies

$${\displaystyle \sum _{i=1}^d}\frac{x_i^2}{{\left(a_i/2\right)}^2}<1.$$

This null model was chosen because the PC projections appear ellipsoid with apparent uniform density of points except at the outskirts (although with a fatter tail than a multivariate Gaussian). Thus, using a uniform density for the null model is conservative (i.e., it will tend to give a larger number of clusters than the real data).

These analyses are presented in Fig. S1, along with corresponding t-distributed stochastic neighbor embedding (t-SNE) plots, implemented using the sklearn.manifold.TSNE() class in scikit-learn v0.17 (40) with two components, perplexity of 30.0, and learning rate of 1,000.0. The t-SNE method for visualizing high-dimensional data overcomes some of the limitations of the linear PCA method (20).

PLS Regression.

Formally, we sought to develop a set of regression models that separately predict the values of each functional response, ${\mathbf{y}}^{\left(k\right)},$ given the immune cell compositions, $\mathbf{X},$ of a group of individuals. Here, element $y_i^{\left(k\right)}$ of vector ${\mathbf{y}}^{\left(k\right)}$ represents the value of response $k$ for individual $i$, whereas element $X_{ij}$ refers to the immune cell population frequency $j$ in individual $i.$ Linear models assume that the responses and predictors are related through the functional form ${\widehat{\mathbf{y}}}^{\left(k\right)}=\mathbf{X}{\mathbf{\beta }}^{\left(\mathit{k}\right)},$ where the “hat” distinguishes the predicted responses from the experimentally measured ones, and ${\mathbf{\beta }}^{\left(\mathit{k}\right)}$ is the regression vector for functional response $k.$ The elements of the regression vector are the weights of each cell population that define a linear combination that best predicts the functional response.

For the regression models, the functional responses were first transformed using the log-modulus transformation (42) to preserve rank ordering of responses while minimizing the effect of large outliers. For each functional response, PLS (Dataset S4) is used to find a set of linear combinations (termed the LVs) of cell populations that have the highest covariance with the functional response. These LV signatures, ${\mathbf{r}}_j^{\left(k\right)},$ are the directions in the space of possible immune cell compositions that explain a particular functional response, ordered from best to least, as columns of the LV matrix ${\mathbf{R}}^{\left(k\right)}.$ In this way it is possible that only a small number of such directions need to be identified to predict functional responses well. The advantages of using PLS are its simplicity, the avoidance of multicollinearity issues resulting from highly correlated immune cell populations (SI Materials and Methods, Regression Methods), and the conceptual advantage afforded by grouping cell populations together into latent variables that collectively explain a response of interest. We compared the performance of PLS with PCR, in which directions in the space of possible immune cell compositions are chosen to explain the greatest variance in immune cell composition across patients.

The regression models are evaluated using learning curves of 10-fold cross-validated (CV) negative Spearman correlation coefficients between observed and predicted response measurements for both PLS and PCR regression models. As described in ref. 43, cross-validation estimates out-of-sample model performance for smaller datasets by fitting a model on only a fraction of the available data and testing predictions on the remaining data left out. We used a 10-fold cross-validation scheme based on recommendations by Hastie et al. (43). The dataset is randomly partitioned into 10 groups and a PLS model separately fitted on each possible combination of 9/10 of those groups. The predictions on the left-out groups are compared with their experimental values, using a negative Spearman correlation coefficient. Learning curves are made by calculating CV error as a function of the number of LVs included in the model. The default error (when no LVs are used) is a correlation coefficient of zero. Error bars on learning curves are generally reported as SEs (44). However, because our measure of error combines errors over the entire dataset, we report error bars as SD of error calculated over 100 random instantiations of the CV learning curve (corresponding to different random 10-fold partitioning of the dataset).

We wish to verify that the PLS model is fitting meaningful correlations between both the immune markers and response functions and that improved model performance is not an artifact of the model-fitting procedure. To address these concerns, we evaluate the performance of a “null model,” created by random reassignment of responses across patients. This randomization eliminates the relationship between a patient’s immune cell composition and the value of the corresponding response, and the model-fitting procedure should correctly detect that there is no underlying structure to be learned from the data. We calculate 95% confidence intervals of the null model learning curve, using 100 instantiations of the null model to summarize how variable the estimates from the null model are. Responses for which the minimum error plus error bar come within 0.05% of the 95% confidence interval of the null model learning curve are removed from further consideration. Six signaling responses (IL-6/Mono/STAT5, IL-7/CD4⁺CD45RA⁺/STAT1, IL-7/CD4⁺CD45RA^–/STAT1, IL-7/CD4⁺/STAT1, IFN-γ/CD8⁺CD45RA^–/pSTAT3, and IFN-γ/CD4⁺CD45RA⁺/pSTAT3) and four of the five flu-vaccine responses [A/California/07/2009(H1N1), A/Perth/16/2009(H3N2), A/South Dakota/06/2007(H1N1), and A/Uruguay/716/2007(H3N2)] were so removed.

Finally, to indicate the amount of front loading of explanatory power into the top LVs, we also report a normalized error defined as follows: If the minimum observed error for a given functional response in either PLS or PCR is denoted $e_{min},$ and the raw model error is denoted $e,$ the normalized error is defined as $e_{norm}=\left(e-e_{min}\right)/\left(0.0-e_{min}\right),$ where an error of 0.0 indicates a degenerate model in which the mean of the response measurements is predicted regardless of an individual’s immune cell composition.

As discussed in the main text, the PLS model for the HAI response to the influenza B/Brisbane/60/2008 strain was fitted on only the subset of individuals who had a measurement increase in HAI titer upon vaccination (31% of patients with a post- to prevaccination HAI titer ratio of 1 were not included in the fit). Furthermore, the fit benefits from further outlier moderation; seven patients with log-modulus HAI titer ratios greater than 4.0 (corresponding to HAI titer ratios >53.6) were adjusted to this 4.0 threshold for further outlier moderation. These seven individuals had HAI titer ratios equal to 64, 80 (for three individuals), 160, 320, and 640. The average HAI titer ratio for the remaining individuals was 11.3.

Regression Methods.

We highlight three linear regression methods in this section. The main regression method used in this study is PLS regression. However, ordinary least squares (OLS) and PCR are discussed first to illustrate the shortcomings that the PLS method addresses. Furthermore, the OLS results are used repeatedly in the development of the PCR and PLS methods.

SI Materials and Methods

OLS.

OLS (43) is the simplest linear regression method and forms the conceptual basis for more complex methods like PCR and PLS regression. The OLS model assumes that within error $\epsilon ,$ the response variable, $\mathbf{y},$ is a linear combination of covariates, represented by a set of regression coefficients $\mathbf{\beta }.$ Here the covariates are the individual features in the observed data (columns in $\mathbf{X}$), which are treated as fixed and known.

The model, least-squares estimate of the regression coefficients, $\widehat{\mathbf{\beta }},$ and its variance are given by

$$\mathbf{y}=\mathbf{X}\mathbf{\beta }+\epsilon$$

$${\widehat{\mathbf{\beta }}}^{OLS}={\left({\mathbf{X}}^{\text{T}}\mathbf{X}\right)}^{-1}{\mathbf{X}}^{\text{T}}\mathbf{y}$$

$$\mathbb{V}\left[{\widehat{\mathbf{\beta }}}^{OLS}\right]={\left({\mathbf{X}}^{\text{T}}\mathbf{X}\right)}^{-1}{\sigma }^2,$$

where ${\sigma }^2$ characterizes the error term, assuming spherical normal errors:

$$\mathbb{V}\left[\epsilon \hspace{0.17em}|\hspace{0.17em}\mathbf{X}\right]={\sigma }^2{\mathbf{I}}_{\text{n}}.$$

PCR.

Rather than using the original features as covariates as in OLS, PCR performs linear regression by using as features the PC scores, $\mathbf{Z},$ instead of $\mathbf{X}$ directly (see above). The regression coefficients in PCR are thus exactly the OLS result using transformed covariates, $\mathbf{Z}:$ ${\widehat{\mathbf{\beta }}}^{PCR}={\left({\mathbf{Z}}^{\text{T}}\mathbf{Z}\right)}^{-1}{\mathbf{Z}}^{\text{T}}\mathbf{y}.$ The variance of the PCR regression vector has a simplified (diagonal) form owing to the linear transformation to uncorrelated covariates (i.e., the PC scores): $\mathbb{V}\left[{\widehat{\mathbf{\beta }}}^{PCR}\right]={\mathbf{\Lambda }}^{-1}{\sigma }^2.$ The dependence of the variance of the PCR regression coefficients on the inverse of the eigenvalue matrix illustrates that low-eigenvalue PCs (potentially as a result of multicollinearity) lead to high variance in the corresponding coefficients of the estimates. The effect of these low-eigenvalue modes on the OLS regression coefficients is more complicated because the original, nontransformed covariates are correlated linear combinations of the uncorrelated PCs. The effect of this can be seen by expressing the variance of the OLS regression estimator in terms of the PCs, ${\left(\mathbb{V}\left[{\widehat{\mathbf{\beta }}}^{OLS}\right]\right)}_{ii}=\left({\displaystyle \sum }_k{\lambda }_k^{-1}{\text{V}}_{ik}^2\right){\sigma }^2,$ which is proportional to the sum over all PCs, $k,$ of the reciprocal eigenvalue times the square of the loading of that covariate in PC $k.$ Here, matrix $\mathbf{V}$ is the eigenvector matrix. Intuitively, this says that covariates with high loadings in the low-eigenvalue PCs tend to have inflated variance that leads to difficulties in interpretation. PCR avoids the issue of multicollinearity by regressing on a reduced subset of $r<k,$ PCs with corresponding eigenvalues sufficiently large; i.e., ${\widehat{\mathbf{\beta }}}_r^{PCR}={\left({\mathbf{Z}}_r^{\text{T}}{\mathbf{Z}}_r\right)}^{-1}{\mathbf{Z}}_r^{\text{T}}\mathbf{y},$ where ${\mathbf{Z}}_r=\mathbf{X}{\mathbf{V}}_r$ and subscript $r$ indicates that the matrix comprises only the first $r$ columns.

PLS.

PCR suffers from an important limitation: The PCs, although capturing the maximum variability in $\mathbf{X},$ may or may not be relevant for the task of predicting the response $\mathbf{Y}$ (single-response vector $\mathbf{y}$ is expanded to multiple-response matrix $\mathbf{Y},$ indicating that these methods can be applied to multiple responses simultaneously), because no information regarding $\mathbf{Y}$ is incorporated in computing the PCs. This is addressed by PLS, which computes a simultaneous decomposition of $\mathbf{X}$ and $\mathbf{Y}$ such that these components explain as much as possible of the covariance between $\mathbf{X}$ and $\mathbf{Y}.$ The PLS method works by decomposing both the covariate, $\mathbf{X},$ and the response, $\mathbf{Y},$ matrices into sums of $h$ rank-1 matrices. These decompositions are termed the “outer relations” for $\mathbf{X}$ and $\mathbf{Y}:$

$$\mathbf{X}={\displaystyle \sum _{i=1}^h}{\mathbf{t}}_i{\mathbf{p}}_i^{\text{T}}+{\mathbf{E}}_h={\mathbf{T}}_h{\mathbf{P}}_h^{\text{T}}+{\mathbf{E}}_h$$

$$\mathbf{Y}={\displaystyle \sum _{i=1}^h}{\mathbf{u}}_i{\mathbf{q}}_i^{\text{T}}+{\mathbf{F}}_h^{\ast }={\mathbf{U}}_h{\mathbf{Q}}_h^{\text{T}}+{\mathbf{F}}_h^{\ast }.$$

Here, ${\mathbf{E}}_h$ and ${\mathbf{F}}_h^{\ast }$ refer to error terms from (potentially) incomplete decomposition. An example of such a decomposition is PCA, in which individual PCs and corresponding scores give these rank-1 approximations; i.e., $\mathbf{X}=\mathbf{Z}{\mathbf{V}}^{\text{T}}.$ Matrices ${\mathbf{T}}_h$ and ${\mathbf{U}}_h$ are referred to as score matrices, whereas matrices ${\mathbf{P}}_h$ and ${\mathbf{Q}}_h$ are referred to as loading matrices, in analogy with PCA. Unlike the PCA loading matrix, $\mathbf{V},$ however, ${\mathbf{P}}_h$ and ${\mathbf{Q}}_h$ are not necessarily orthogonal. The score matrices are modeled to be related by the linear “inner relation”:

$${\mathbf{U}}_h={\mathbf{T}}_h{\mathbf{D}}_h+{\mathbf{G}}_h.$$

Here, ${\mathbf{D}}_h$ is an $h$ × $h$ matrix of OLS regression coefficients relating the respective scores of $\mathbf{X}$ and $\mathbf{Y},$ whereas ${\mathbf{G}}_h$ is the inner relation error. Note that substituting this inner relation into the outer relation for $\mathbf{Y}$ results in a linear relationship between responses $\mathbf{Y}$ and the scores of $\mathbf{X}:$

$$\begin{array}{c}\mathbf{Y}={\mathbf{U}}_h{\mathbf{Q}}_h^{\text{T}}+{\mathbf{F}}_h^{\ast }\\ =\left({\mathbf{T}}_h{\mathbf{D}}_h+{\mathbf{G}}_h\right){\mathbf{Q}}_h^{\text{T}}+{\mathbf{F}}_h^{\ast }\\ ={\mathbf{T}}_h{\mathbf{D}}_h{\mathbf{Q}}_h^{\text{T}}+{\mathbf{G}}_h{\mathbf{Q}}_h^{\text{T}}+{\mathbf{F}}_h^{\ast }\\ ={\mathbf{T}}_h{\mathbf{M}}_h^{\text{T}}+\mathbf{H},\hspace{0.17em}\text{where}\hspace{0.17em}{\mathbf{M}}_h^{\text{T}}\equiv {\mathbf{D}}_h{\mathbf{Q}}_h^{\text{T}}\hspace{0.17em}\text{and}\hspace{0.17em}\mathbf{H}\equiv {\mathbf{G}}_h{\mathbf{Q}}_h^{\text{T}}+{\mathbf{F}}_h^{\ast }.\end{array}$$

Thus, unlike PCA, which determines the score matrix for $\mathbf{X}$ without considering $\mathbf{Y},$ PLS incorporates information about $\mathbf{Y}$ for the decomposition; the first set of PLS scores, ${\mathbf{t}}_1$ and ${\mathbf{u}}_1,$ is chosen to maximize their covariance:

$${\mathbf{w}}_1,{\mathbf{c}}_1=\underset{\Vert \mathbf{w}\Vert ,\Vert \mathbf{c}\Vert =1}{\arg \hspace{0.17em}\max }{\left[\mathrm{Cov}\left(\mathbf{X}\mathbf{w},\mathbf{Y}\mathbf{c}\right)\right]}^2$$

$${\mathbf{t}}_1=\mathbf{X}{\mathbf{w}}_1$$

$${\mathit{u}}_1=\mathbf{Y}{\mathbf{c}}_1.$$

Here, vectors ${\mathbf{w}}_1$ and ${\mathbf{c}}_1$ are unit vectors that weight covariates (columns in $\mathbf{X}$) and responses (columns in $\mathbf{Y}$) to generate the linearly transformed scores, ${\mathbf{t}}_1$ and ${\mathbf{u}}_1,$ respectively. In this study, ${\mathbf{w}}_1$ is referred to as “latent variable 1” (“LV1”) (note that there is ambiguity in naming subsequent latent variables due to deflation, discussed below), whereas ${\mathbf{t}}_1$ is termed the “LV1 scores.” Note that the optimal ${\mathbf{w}}_1$ and ${\mathbf{c}}_1$ are equal to the first left- and right-singular vectors from the singular value decomposition of the cross-product matrix ${\mathbf{X}}^{\text{T}}\mathbf{Y},$ with covariance equal to the corresponding singular value.

PLS employs a “deflation” scheme to ensure that latent variable scores are statistically uncorrelated and that later latent variables attempt to model only the portion of the responses that are not already well captured by earlier latent variables. After each latent variable, LV $i,$ is chosen, $\mathbf{X}$ and $\mathbf{Y}$ are deflated as follows:

$$\begin{array}{c}{\mathbf{p}}_i={\mathbf{X}}^{\text{T}}{\mathbf{t}}_i/\left({\mathbf{t}}_i^{\text{T}}{\mathbf{t}}_i\right)\\ \mathbf{X}\leftarrow \mathbf{X}-{\mathbf{t}}_i{\mathbf{p}}_i^{\text{T}}\\ {\mathbf{m}}_i={\mathbf{Y}}^{\text{T}}{\mathbf{t}}_i/\left({\mathbf{t}}_i^{\text{T}}{\mathbf{t}}_i\right)\\ \mathbf{Y}\leftarrow \mathbf{Y}-{\mathbf{t}}_i{\mathbf{m}}_i^{\text{T}}.\end{array}$$

The rank-1 approximations, ${\mathbf{t}}_i{\mathbf{p}}_i^{\text{T}}$ and ${\mathbf{t}}_i{\mathbf{m}}_i^{\text{T}},$ are obtained by OLS regression of (deflated versions of) $\mathbf{X}$ and $\mathbf{Y},$ respectively, on score ${\mathbf{t}}_i.$ As a consequence of this asymmetric deflation scheme, the process of selecting latent variables in PLS can be continued until the number of latent variables equal to the number of covariates in $\mathbf{X}$ has been obtained, using the same objective function, with now $\mathbf{X}$ and $\mathbf{Y}$ deflated:

$${\mathbf{w}}_i,{\mathbf{c}}_i=\underset{\Vert \mathbf{w}\Vert ,\Vert \mathbf{c}\Vert =1}{\arg \hspace{0.17em}\max }{\left[\mathrm{Cov}\left(\mathbf{X}\mathbf{w},\mathbf{Y}\mathbf{c}\right)\right]}^2$$

$${\mathbf{t}}_i=\mathbf{X}{\mathbf{w}}_i$$

$${\mathbf{u}}_i=\mathbf{Y}{\mathbf{c}}_i.$$

Because the approximation to $\mathbf{Y}$ is imperfect (i.e., it is obtained by regressing on LV scores for $\mathbf{X}$ rather than for Y itself), PLS still works if the number of latent variables used is greater than the number of responses in Y, and even a full model may not result in a residual matrix of $0.$

A final consideration in the PLS model is that interpretation of the weight vectors $\mathbf{W}$ is complicated by the fact that they are calculated on an iteratively deflated $\mathbf{X}$ matrix. In other words, $\mathbf{T}\ne \mathbf{X}\mathbf{W}.$ Thus, we define a matrix $\mathbf{R},$ such that columns of $\mathbf{R}$ describe linear combinations of the original $\mathbf{X}$ covariates that give rise to the score matrix $\mathbf{T};$ i.e., $\mathbf{T}=\mathbf{X}\mathbf{R}.$ In this study, column $j$ of $\mathbf{R}$ is referred to as the “latent variable $j$” even though latent variable often refers to columns of matrix $\mathbf{W}$ in other studies. This allows the PLS results to be expressed in terms of an estimated regression matrix ${\widehat{{\rm B}}}_h^{PLS},$ based on $h$ latent variables, in analogy with OLS and PCR:

$$\begin{array}{c}\mathbf{Y}={\mathbf{T}}_h{\mathbf{M}}_h^{\text{T}}+\mathbf{H}\\ =\left(\mathbf{X}{\mathbf{R}}_h\right){\mathbf{M}}_h^{\text{T}}+\mathbf{H}\\ =\mathbf{X}{\widehat{{\rm B}}}_h^{PLS}+\mathbf{H}\\ {\widehat{{\rm B}}}_h^{PLS}={\mathbf{R}}_h{\mathbf{M}}_h^{\text{T}}.\end{array}$$

In the case of a single response variable, this reduces to

$$\begin{array}{c}\mathbf{y}={\mathbf{T}}_h{\mathbf{m}}_h^{\text{T}}+\mathbf{h}\\ =\left(\mathbf{X}{\mathbf{R}}_h\right){\mathbf{m}}_h^{\text{T}}+\mathbf{h}\\ =\mathbf{X}{\widehat{\mathbf{\beta }}}_h^{PLS}+\mathbf{h}\\ {\widehat{\mathbf{\beta }}}_h^{PLS}={\mathbf{R}}_h{\mathbf{m}}_h^{\text{T}}.\end{array}$$

Whereas ${\mathbf{M}}_h$ previously had a number of rows equal to the number of responses, ${\mathbf{m}}_h$ is now an $h$-dimensional row vector. Pseudocode for a modified PLS algorithm, which makes use of the NIPALS algorithm described in ref. 45, is provided in Dataset S4.

Latent Variable Similarities.

We calculated the similarities between LVs $i$ and $j$ of functional responses $k_1$ and $k_2$ as the absolute dot product between them: $\left|{\mathbf{r}}_i^{\left(k_1\right)}\cdot {\mathbf{r}}_j^{\left(k_2\right)}\right|=\left|{\displaystyle {\sum }_l{\text{r}}_{i,l}^{\left(k_1\right)}{\text{r}}_{j,l}^{\left(k_2\right)}}\right|,$ with the absolute value indicating that the LVs extend in both positive and negative directions. The distributions for these dot products across all pairs of responses are shown in Fig. S3. The extent of similarity is found as the fraction of response pairs with P value <0.05 (corresponding to absolute dot product >0.335) compared with a null distribution of randomly chosen pairs of vectors on a 34-dimensional unit hypersphere (Fig. S3). This null distribution was approximated by simulating 1 million random pairs of vectors according to the null model. To assess whether the number of statistically similar pairs, $n,$ is significantly greater than expected given the null distribution, we sum the corresponding binomial distribution to find the P value,

$$p={\displaystyle \sum _{i=n}^N}\left(\begin{array}{c}N\\ n\end{array}\right){0.05}^n{0.95}^{N-n},$$

where $\left(\begin{array}{c}\cdot \\ \cdot \end{array}\right)$ is the binomial coefficient, and $N$ is the total number of response pairs. Note that this assumes response LVs are independent; however, the extent to which responses are correlated (due to sharing of cytokine stimulant, responding cell type, and/or STAT measurement) is unknown.

Immunological Aging Axis.

The immunological aging axis from Fig. 4 was calculated using logistic regression of age on the top three LV scores. All ages below the median were binarized to zero whereas the remaining ages greater than or equal to the median were binarized to unity. Logistic regression was favored over ridge regression to diminish the effect of outliers, especially near the base of the cone. Logistic regression was implemented using the sklearn.linear_model.LogisticRegressionCV() class in scikit-learn v0.17 (40), with a 10-fold randomized cross-validation scheme. The dashed red line in Fig. 5A is plotted as $\mathbf{a}={\mathbf{a}}_0+\mathbf{\beta }t,$ where $\mathbf{\beta }$ is the regression vector from logistic regression, $t$ parameterizes the equation, and ${\mathbf{a}}_0$ is chosen to minimize the sum of perpendicular distances (2-norm) from each point to the dashed line,

$${\mathbf{a}}_0=\arg \underset{{\text{a}\prime }_0}{\min }{{\displaystyle \sum _{i=1}^N}\Vert \left({\mathbf{a}\prime }_0-{\mathbf{x}}_i\right)-\left(\left({\mathbf{a}\prime }_0-{\mathbf{x}}_i\right)\cdot \mathbf{\beta }\right)\mathbf{\beta }\Vert }_2,$$

where ${\mathbf{x}}_i$ is a vector specifying the top three LV scores for individual $i.$

The coefficients of the age axis from Fig. 4C are obtained by the product of the first three columns of the LV matrix, ${\mathbf{R}}_3,$ with the logistic regression vector, $\mathbf{\beta },$ from above; i.e., the coefficients of the age axis are the elements of ${\mathbf{R}}_3\mathbf{\beta }.$

Twin Pair Immunotype Similarities Null Model.

To determine the effect of twin status on immunotype similarities, we compared the interindividual distances between twin pairs (MZ or DZ) to those between randomly chosen individuals in the cohort. However, we wanted to ensure that the null distribution had the same distribution of ages as that in the twin distributions (note that this age distribution may be different for MZ vs. DZ twins, so a separate null model is constructed for both). Using the MZ null as an example, for each age, $a,$ represented in the MZ distribution, we randomly select two nontwin individuals from the full dataset where the age of each individual is within the $k$ nearest individuals by age to $a$—note that as ages in the dataset are discrete by year, the set of individuals may be larger than $k$ itself if there are many individuals in the age group farthest away from $a.$ Using this as a null distribution, with $k$ chosen to be 10 nearest neighbors, we find that the means of both the MZ and DZ distributions are significantly lower than the means of their respective null distributions (P < 0.0001), indicating twin status is correlated with similarity in immunotype. Although this result is theoretically dependent on $k,$ where low values of $k$ indicate more strict enforcement of age correction in the null model at the expense of greater sampling noise, we found the conclusion robust to choice of $k$ up to 10.