Skip to main content
NCBI home page
Journal of Orthopaedics logoLink to Journal of Orthopaedics
. 2018 Aug 16;15(3):820–825. doi: 10.1016/j.jor.2018.08.002

Flatfoot and normal foot a comparative analysis of the stress shielding

V Filardi 1
PMCID: PMC6104143  PMID: 30140126

Abstract

Objective

this study aims to develop a comprehensive 3D FE model of the foot to investigate the effect of soft tissue stiffness on the plantar pressure distributions and the internal load transfer between bony structures.

Methods

the stress shielding occurring on the plantar surface of a flatfoot was investigated and compared with the mechanical behavior of a healthy foot, trough baropodometric analyses and the FE models.

Results

the flatfoot evidences a more intensive stress-shielding map with significant values of pressure acting on the medial plantar fascia.

Conclusion

Clinically and radiographically, symptomatic adult flatfoot is a complex abnormality involving all three dimensions and multiple joints within the foot.

Keywords: Foot model, CAD, FE analysis

1. Introduction

The foot is definitely one of the most important sensory organs of our body, even more important than the hand. One can speak of the foot as a postural receptor organ that offers the brain information about the body itself as its position in space, its balance and its oscillations. This is why not infrequently the pathologies involving the foot can find an explanation in the individual's posture or in other cases may be the direct cause of an altered posture. The flat foot or pronator syndrome is perhaps the most common deformity of the foot. The foot consists of about 28 bones, numerous muscles and joints, but in particular there are 3 structures that are involved when it comes to flatfoot: the astragalus, the calcaneus and the posterior tibial tendon. From an exquisitely medical and orthopedic point of view, the flat foot sees a “collapseˮ of the astragalus which tends to become vertical and a tendency of the calcaneus to value itself. The tendon that most of all suffers for this alteration of the form is the posterior tibial that is found stretched and stretched in an attempt to support the plantar vault. Using a simpler and less technical terminology, the flat foot presents itself with the tendency of the medial vault to flatten and give inward, while the heel is pushed to compensate the outside. The foot provides the base of support to the whole body allowing to unload the weight on the ground and plays a fundamental role in maintaining the balance. Under normal conditions, the supporting surface of the foot is not constituted by the entire plantar surface, but is located electrically at three points:

  • •

    head of the first metatarsal

  • •

    heads of the fourth and fifth metatarsals

  • •

    calcaneal tuberosity.

The conjunction of these three points constitutes the so-called arches on arches: a transverse (anterior), two longitudinal (medial and lateral). The medial plantar vault is formed by the calcaneus, the astragalus, the scaphoid, the three cuneiforms and the first three metatarsals. The curvature of the medial plantar vault is supported by the plantar fascia and by the plantar ligaments, with the dynamic support of the posterior tibialis tendons and the long peroneal, which are called caving muscles of the foot for their function. The flattening of this medial longitudinal vault may be due to the failure of one or more of the mentioned structures and causes an anomaly in weight distribution, with consequent alteration of the relationships between the various bone components and the development of degenerative and painful phenomena, see Fig. 1. The foot can be divided into two major parts, the medial column and the lateral column. The talus, navicular, cuneiforms, and the first three rays comprise the medial column and the calcaneus, cuboid, and lateral 2 rays comprise the lateral column.1,2 The lateral column is inherently stable. The medial column has an adaptive function during the weight-bearing stage and acts as a stabilizer during the propulsive phase. Although the etiology of symptomatic adult flatfoot is still debated, most agree that it is produced by abnormal repetitive loading on the medial column, which leads to attenuation or dysfunction of the ligamentous and tendinous stabilizers of the medial column, resulting in the bony deformities seen both clinically and radiographically. Thus, although the inciting factor leading to the development of flatfoot is not well understood, it is clear that injury to both dynamic and static structures in the foot are responsible for the deformity we call flatfoot. The severity of flatfoot deformity on radiographs does not correlate well with symptoms, i.e.; some cases with extensive radiographic deformities may be asymptomatic whereas other cases of mild deformity may be significantly symptomatic. In addition, the onset of flatfoot deformity is often insidious. Thus, it is important to be able to recognize early radiographic signs. This variability in presentation underscores the need to take into account all available information, both clinical and radiographic, when evaluating foot alignment abnormalities. Patients with flatfoot may develop lower extremity pain, swelling, abnormal gait, and difficulty walking. There are various causes of flatfoot, deriving from posterior tibial tendon (PTT) dysfunction (e.g., rupture, attenuation, or laceration), midfoot laxity, external rotation of the hindfoot, trauma (e.g., lisfranc, talonavicular joint, or calcaneus injuries), and neuromuscular imbalance.3 Although flatfoot is a very common foot deformity, it remains one of the least understood, and optimal treatment is not widely accepted.4 Experimental and computational models have been investigated in the literature in order to study the biomechanics of flatfoot. Because of the limitation of donors, experimental studies have been carried out by adapting cadaver healthy human feet, rather than pathological flatfeet. Thus, flatfoot models were obtained modifying specific ligaments and tendons.5, 6, 7 A limitation of these experimental models is due to the bone shapes and configuration, which is different in healthy foot and flatfoot. For these reasons, computational models could offer a feasible solution in order to better characterize to peculiar bony structure.8, 9, 10, 11 FE models are also determinant in development of all those surgical prosthesis adopted to heal bony fracture,12, 13, 14 and can represent a valid instrument to investigate flatfoot deformity. However, very few FE models of flatfoot have been published to date. Lewis4 realized a flatfoot FE model consisting of 14 bone segments, 65 ligaments, and part of the plantar soft tissue, toes and dorsal soft tissue were not included. Spratley et al.15 developed a rigid-body flatfoot model to investigate the kinematic behavior of the flatfoot skeleton. Other FE models, were proposed for studying the entire bony chain of leg taking into acoount stress and strain occurring in healthy feet, examining various applications.16, 17, 18 Filardi presented an FE foot model based on MR images investigating the stress map distribution on the different bony part of the foot.

Fig. 1.

Fig. 1

Open in a new tab

Supporting surface of the foot “aeches on arches”.

Cheung et al.20 developed a model of the foot to study the effects of soft tissue stiffening on the stress distribution of the plantar surface during balanced standing. The same model was also used to study the biomechanical effects of different types of foot orthosis for improving design principles.21 In this paper two detailed FE models of the healthy human foot and a flatfoot were realized and tested by loading them with a vertical force of 350 N balanced by the reaction force of 175 N offered by the Achilles's tendon applied on the calcaneus.

The isostatic configuration was realized by imposing the contact of the feet with a rigid wall. All the bony and soft parts were modelled as solid tetrahedrons, while for ligaments monodimensional truss elements were used. Linear elastic laws were selected to characterize bones while a hyperplastic law was used for skin. Finally results were compared with baropodometric analyses conducted on two patients one healthy and the second with the flatfoot, already involved on the project to obtain the CT geometry of the feet. The objective of this study was to develop a comprehensive 3D FE model of the foot to investigate the effect of soft tissue stiffness on the plantar pressure distributions and the internal load transfer between bony structures.

2. Materials and methods

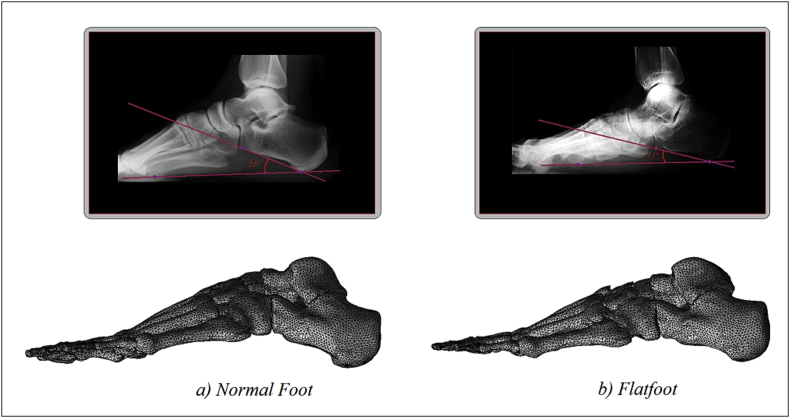
Postural evaluation and biomechanical analyses were carried out by a Maxi Platforms FreeMed® on a normal adult patient (70 [kg] BM), and another adult patient suffering by a flatfoot (68 [kg] BM). Successively two numerical models of the foot ware obtained by matching nuclear magnetic resonance (MRI) for soft tissues, and a computerized tomography (CT) for bones, carried on the two patients. In particular, as reported in Fig. 2 a red line is drawn from the plantar-most surface of the calcaneus to the inferior border of the distal articular surface. The angle made between this line and the transverse plane (or the line from the plantar surface of the calcaneus to the inferior surface of the 5th metatarsal head) is the calcaneal pitch (Fig 2(a)). A decreased calcaneal pitch is consistent with pes planus, (Fig 2(b)). Unfortunately, there have been differing opinions between authors concerning the normal range of calcaneal pitch 18–32° is generally considered normal, although measurements reporting a calcaneal pitch with angle minor than 18° represent a flatfoot syndrome. Obtained data were imported into the commercial Hypermesh code by Altair®, where the final finite element model of the foot was reconstructed. In Fig. 2 and Table 1 are reported the FE bony segments, skin, and rigid wall including numbers of nodes and elements.

Fig. 2.

Fig. 2

Open in a new tab

2a)Normal Calcaneal pitch. 2b) Calcaneal pitch with flatfoot.

Table 1.

FE bony segments including numbers of nodes and elements.

 Image 1
 Image 2
Bony component nodes elements nodes elements
Talus 4701 14095 4694 13989
Calcaneus 3236 9926 3248 9948
Navicular 1595 5013 1603 5123
Cuboid 1286 3941 1296 4005
1st Cuneiform 1246 3808 1259 3812
2nd Cuneiform 694 2096 712 2158
3th Cuneiform 5395 16191 5377 16096
1st to 5th Metatarsal 7675 23741 7645 23842
1st to 5th Toe 6464 20896 6485 21002
Skin 10687 66853 10520 66714
Rigid wall 142 612 142 612
Open in a new tab

Ligaments, other connective tissues, and the plantar fascia were defined, by 98 truss mono dimensional elements, connecting the corresponding attachment points on the bones. All the bony and ligamentous structures were embedded in a volume of soft tissues. To simulate the frictionless contact between the joint surfaces, ABAQUS automated surface-to-surface contact option was used. According to the model developed by Gefen et al.22 adopting the linear elastic material law, the Young's modulus and Poisson's ratio for the bony structures were assigned as 7300 MPa and 0.3, respectively. The mechanical properties of ligaments23 were selected from the literature, see Table 2.

Table 2.

Mechanical and geometrical properties of the FE model.

Component Element type Young modulus Poisson's ratio Cij and Di material parameters
Bony parts 3d Tetrahedrons 7.300 [MPa] 0.3 C10 = 0.08556 C02 = 0.00851
Soft tissue 3d Tetrahedrons hyperelastic / C01 = −0.05841 D1 = 3.65273
ligaments 1d Truss 350 [MPa] / C20 = 0.03900 D2 = 0.00000
Rigid wall 3d Tetrahedrons 210.000 [MPa] 0.3 C11 = −0.02319
Open in a new tab

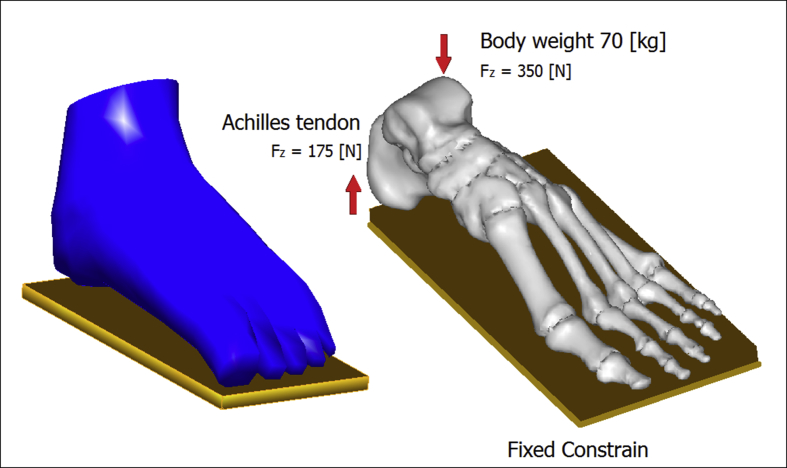
The rigid wall was simulated reproducing mechanical properties of steel. The encapsulated soft tissue was defined as nonlinearly elastic material. The stress–strain data on the plantar heel pad from the in vivo ultrasonic measurements24 were used to represent the normal soft tissue stiffness. The hyperelastic material model was used to represent the nonlinear and nearly incompressible nature of the encapsulated soft tissue, while the second-order polynomial strain energy potential was adopted to evaluate the Cij and Di material parameters, see Table 2. A rigid wall of steel was used as ground support using surface-to-surface contact elements in combination with the penalty algorithm with a normal contact stiffness of 600 N/mm and a friction coefficient of 0.4. A vertical force of approximately 350 N is applied on the top of the talus corresponding to a BW of 70 kg. The vertical upward force of the Achilles tendon, with magnitude of 175 N, was applied at the posterior extreme of the calcaneus, see Fig. 3.

Fig. 3.

Fig. 3

Open in a new tab

Numerical model and loading and constrain setup.

3. Results

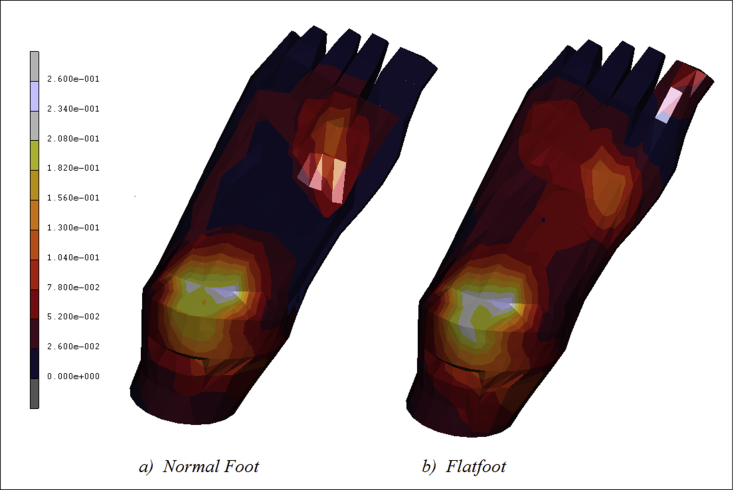
Baropodometric analyses were carried out in order to validate 3D FE model of the human foot and compare the stresses/strains distribution in a normal foot and in a flatfoot. In Fig. 4 are reported the plantar pressure contour maps evaluated in the normal patient 4(a) and the second one with the flatfoot 4(b). As it is possible to notice in Fig. 4(a) pressure is mostly concentered on the calcaneus, reaching values acting around 0.26 MPa, the same as on the lateral plantar fascia, and from the first to the fifth metatarsal head regions. The medial plantar fascia appears less stressed with values of pressure aging around 0.05 MPa. On the contrary, the flatfeet depicted in Fig. 4(b) evidence a more intensive stress-shielding map with significant values of pressure, around 0.13 MPa, acting on the medial plantar fascia.

Fig. 4.

Fig. 4

Open in a new tab

Contour maps of plantar pressure evaluated in normal feet and flatfoot.

In addition, the region from the first to the fifth metatarsal head presents higher values of stress acting around 0.17 MPa.

In Fig. 5 are depicted the Equivalent Von Mises contour maps of the two feet analyzed. As it is possible to notice Fig. 5(a) confirms a stress concentration on the calcaneus, reaching values acting around 0.24 MPa. The lateral plantar fascia reaches values of 0.07 while from the first to the fifth metatarsal head regions the trend of stress is decreasing with a peak of 0.19 MPa reached on the first metatarsal. The medial plantar fascia appears almost unstressed. The numerical flatfoot depicted in Fig. 5(b) evidences values of stress of around 0.08 MPa acting also on the medial plantar fascia. In addition, the region from the first to the fifth metatarsal head presents higher values of stress acting around 0.20 MPa.

Fig. 5.

Fig. 5

Open in a new tab

Contour maps of Eq. V. Mises stress[MPa] evaluated on the plantar surface of the feet.

In Fig. 6a) is reported the equivalent von mises contour map evaluated on the bony parts constituting the foot. As it is possible to notice the stress reaches its peak on the calcaneus, about 8.23 MPa, spreading on the lateral plantar fascia with values of 2.74 MPa. In the metatarsal area, the maximum stress is evidenced by the first metatarsal, about 3.65 MPa, while the other four metatarsal evidence an equivalent stress of 1.82 MPa. A peak of stress is registered on the first proximal phalange equal to 7.31 MPa, gradually decreasing on the remaining others since a value of 1.82 MPa.

Fig. 6.

Fig. 6

Open in a new tab

Contour maps of Eq. V. Mises stress[MPa] evaluated on the bony parts of the feet.

Fig. 6b) reports the stress contour map of the flat foot evidencing concentrations of local stress on the medial plantar fascia of about 3.70 MPa. On the calcaneus the stress remains on level of 8.23 MPa, while the metatarsal area, appears more stressed than in the case of normal foot. The peak of stress is registered also in this case on the first proximal phalange equal to 7.31 MPa.

4. Discussion

In this paper, the stress shielding occurring on the plantar surface of a flatfoot was investigated and compared with the mechanical behavior of a healthy foot. The FE model was validated trough baropodometric analyses carried on two, one healthy and the second with flatfeet, patients. The two patients were successively examined by MRI and CT in order to obtain the FE models of their feet.

There are 3 components that are involved in producing the alignment abnormalities of symptomatic adult flatfoot:

  • 1.

    Collapse of the longitudinal arch. The most useful measurements are in bold: 1st metatarsal talar angle, Lateral: Calcaneal pitch

  • 2.

    Hind foot valgus. The most useful measurements are in bold: Lateral: Talo-calcaneal angle, AP: Talo-calcaneal angle

  • 3.

    Forefoot abduction. The most useful measurements are in bold: AP: Talonavicular coverage angle, AP: 1st metatarsal talar angle

A measurement that is quite useful for evaluating pes planus on AP views is lateral subluxation of the navicular on the talus, or talonavicular uncoverage.22 This is an indication of forefoot abduction, one of the three components of flatfoot. This measurement is taken off a weight-bearing AP (dorsolateral view). This angle represents the degree of shift of the navicular on the talus. Two lines are drawn, one connecting the edges of the articular surface of the talus, and one connecting the edges of the articular surface of the navicular. The angle formed by these two lines is the talonavicular coverage angle. An angle of greater than 7° indicates lateral talar subluxation. Probably the most familiar line to radiologists, and a more direct measurement of pes planus, or collapse of the longitudinal arch, is the talar-1st metatarsal angle. This is an angle formed between the long axis of the talus and first metatarsal on a weight-bearing lateral view. This line is used as a measurement of collapse of the longitudinal arch. Collapse may occur at the talo-navicular joint, naviculo-cuneiform, or cuneiform-metatarsal joints. In the normal weight-bearing foot, the midline axis of the talus is in line with the midline axis of the first metatarsal. An angle that is greater than 4° convex downward is considered pes planus with an angle of 15°–30° considered moderate, and greater than 30° severe. An angle greater than 4° convex upward is considered a pes cavus. A line drawn through the mid-axis of the talus should be in line with the first metatarsal shaft, if it is angled medial to the first metatarsal it indicates pes planus. The lateral talocalcaneal angle is the angle formed by the intersection of the line bisecting the talus with the line along the axis of the calcaneus on lateral weight-bearing views. A line is drawn at the plantar border of the calcaneus (or a line can be drawn bisecting the long axis of the calcaneus). The other line is drawn through two midpoints in the talus, one at the body and one at the neck. The angle is formed by the intersection of these axes. The normal range is 25–45°, an angle over 45° indicates hind foot valgus, a component of pes planus. AP talocalcaneal angle (Kite's angle) tends to be unreliable and difficult to measure because many AP radiographs not well exposed in this region. This is the angle formed by the intersection of a line bisecting the head and neck of the talus and a line running parallel with the lateral surface of the calcaneus. The range of normal for adults is 15–30°. An angle greater than 30° would indicate hind foot valgus, seen with pes planus.

Cheung et al.20 found that the predicted plantar pressures were higher than the measured values. As the FE analysis provided solutions of nodal contact pressure rather than an average pressure calculated from nodal force per element's surface area, the F-scan measured peak plantar pressure was therefore expected to be smaller than the predicted values. With increased plantar soft tissue stiffness, the pressure tended to concentrate beneath the heel and the medial metatarsal heads especially for the second and third metatarsals. In all calculated cases, the peak plantar pressure was located at the center of the heel and beneath the second and third metatarsal heads. From the FE prediction, the rate of increase in peak plantar pressure was found to be lower than the corresponding increase of soft tissue stiffness. From the FE predictions, the rate of peak pressure increase tended to decrease with stiffening of soft tissue.

5. Conclusions

Clinically and radiographically, symptomatic adult flatfoot is a complex abnormality involving all three dimensions and multiple joints within the foot. Each measurement used to assess flatfoot is a two dimensional representation of this three-dimensional abnormality. Therefore, one must take into account all information available on both views in making an overall assessment of alignment.

The load-bearing characteristic of the ankle–foot structures under different stance phases requires the incorporation of detailed muscular loading, which will be the future development of the FE model. In the real cases, the tissue stiffening may occur in discrete area of foot especially on the plantar foot and may exhibit different degrees of stiffening. Simulations of various physiological loading conditions in addition to experimental validations are needed before a conclusion can be made. To simplify the analysis in this study, homogeneous and linearly elastic material properties were assigned to the bony and ligamentous structures and the ligaments within the toes and other connective tissue such as the joint capsules were not considered.

Footnotes

Appendix A

Supplementary data related to this article can be found at https://doi.org/10.1016/j.jor.2018.08.002.

Appendix A. Supplementary data

The following is the supplementary data related to this article:

Data Profile
mmc1.xml (267B, xml)

References

  • 1.Di Giovanni J.E., Smith S.D. Normal biomechanics of the adult rearfoot: a radiographic analysis. J Am Podiatry Assoc. 1976;66(11):812–824. doi: 10.7547/87507315-66-11-812. [DOI] [PubMed] [Google Scholar]
  • 2.Figura M.A., Smith S.D. Frontal plane deformity of the subtalar joint in flexible flat foot: a preliminary study. J Am Podiatry Assoc. 1976;66(11):867–872. doi: 10.7547/87507315-66-11-867. [DOI] [PubMed] [Google Scholar]
  • 3.McCormack A.P., Ching R.P., Sangeorzan B.J. Biomechanics of procedures used in adult flatfoot deformity. Foot Ankle Clin. 2001;6(1):15–23. doi: 10.1016/s1083-7515(03)00072-x. [DOI] [PubMed] [Google Scholar]
  • 4.Lewis G.S. The Pennsylvania State University; State College, PA: 2008. Computational Modeling of the Mechanics of Flatfoot Deformity and its Surgical Corrections. Ph.D. dissertation. [Google Scholar]
  • 5.Kitaoka H.B., Luo Z., An K. Three-dimensional analysis of flatfoot deformity: cadaver study. Foot Ankle Int. 1998;19(7):447–451. doi: 10.1177/107110079801900705. [DOI] [PubMed] [Google Scholar]
  • 6.Niu W., Yang Y., Fan Y., Ding Z., Yu G. vol. 19. 2008. Experimental modeling and biomechanical measurement of flatfoot deformity; pp. 133–138. (Proc. 7th Asian-Pacific Conference on Medical and Biol. Eng. (IFMBE)). [Google Scholar]
  • 7.Blackman A.J., Blevins J.J., Sangeorzan B.J., Ledoux W.R. vol. 27. 2009. pp. 1547–1554. (Cadaveric Flatfoot Model: Ligament Attenuation and Achilles Tendon Overpull). (12) [DOI] [PubMed] [Google Scholar]
  • 8.Filardi V. Finite element analysis of sagittal balance in different morphotype: forces and resulting strain in pelvis and spine. J Orthop. 2017;14(2):268–275. doi: 10.1016/j.jor.2017.03.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Filardi V. Healing of femoral fractures by the meaning of an innovative intramedullary nail. J Orthop. 2018;15(1):73–77. doi: 10.1016/j.jor.2018.01.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Montanini R., Filardi V. In vitro biomechanical evaluation of antegrade femoral nailing at early and late postoperative stages. Med Eng Phys. 2010;32(8):889–897. doi: 10.1016/j.medengphy.2010.06.005. [DOI] [PubMed] [Google Scholar]
  • 11.Filardi V., Montanini R. Measurement of local strains induced into the femur by trochanteric Gamma nail implants with one or two distal screws. Med Eng Phys. 2007;29(1):38–47. doi: 10.1016/j.medengphy.2006.01.010. [DOI] [PubMed] [Google Scholar]
  • 12.Filardi V. Numerical comparison of two different tibial nails: expert tibial nail and innovative nail. Int J Interact Des Manuf. 2018:1–11. [Google Scholar]
  • 13.Filardi V. Characterization of an innovative intramedullary nail for diaphyseal fractures of long bones. Med Eng Phys. 2017;49:94–102. doi: 10.1016/j.medengphy.2017.08.002. [DOI] [PubMed] [Google Scholar]
  • 14.Filardi V. The healing stages of an intramedullary implanted tibia: a stress strain comparative analysis of the calcification process. J Orthop. 2015;12:S51–S61. doi: 10.1016/j.jor.2015.01.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Spratley E.M., Matheis E.A., Hayes C.W., Adelaar R.S., Wayne J.S. Validation of a population of patient-specific adult acquired flatfoot deformity models. J Orthop Res. 2013;31(12):1861–1868. doi: 10.1002/jor.22471. [DOI] [PubMed] [Google Scholar]
  • 16.Filardi V., Milardi D. Experimental strain analysis on the entire bony leg compared with FE analysis. J Orthop. 2017;14(1):115–122. doi: 10.1016/j.jor.2016.10.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Filardi V. FE analysis of stress and displacements occurring in the bony chain of leg. J Orthop. 2014;11(4):157–165. doi: 10.1016/j.jor.2014.08.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Filardi V. Stress shielding in the bony chain of leg in presence of varus or valgus knee. J Orthop. 2015;12(2):102–110. doi: 10.1016/j.jor.2014.06.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Cheung J.T.M., Zhang M., Leung A.K.L., Fan Y. Three- dimensional finite element analysis of the foot during standing–a material sensitivity study. J Biomech. 2006;38(5):1045–1054. doi: 10.1016/j.jbiomech.2004.05.035. [DOI] [PubMed] [Google Scholar]
  • 21.Cheung J.T.M., Zhang M. ABAQUS Users' Conference. 2006. Finite element modeling of the human foot and footwear; pp. 145–159. [Google Scholar]
  • 22.Gefen A., Megido-Ravid M., Itzchak Y., Arcan M. Biomechanical analysis of the three-dimensional foot structure duringg ait: a basic tool for clinical applications. J Biomech Eng. 2000;122:630–639. doi: 10.1115/1.1318904. [DOI] [PubMed] [Google Scholar]
  • 23.Siegler S., Block J., Schneck C.D. The mechanical characteristics of the collateral ligaments of the human ankle joint. Foot Ankle. 1988;8:234–242. doi: 10.1177/107110078800800502. [DOI] [PubMed] [Google Scholar]
  • 24.Lemmon D., Shiang T.Y., Hashmi A., Ulbrecht J.S., Cavanagh P.R. The effect of insoles in therapeutic footwear: a finite element approach. J Biomech. 1997;30:615–620. doi: 10.1016/s0021-9290(97)00006-7. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Data Profile
mmc1.xml (267B, xml)

Articles from Journal of Orthopaedics are provided here courtesy of Elsevier

RESOURCES