Contributions of the glycocalyx, endothelium, and extravascular compartment to the blood–brain barrier

Significance

The vascular endothelium constitutes the main barrier that restricts the transport of molecules from blood to brain. However, the barrier properties of structures adjacent to the vascular endothelium are understudied. Based on two-photon microscopy imaging of single cortical capillaries, we found that the blood–brain barrier (BBB) consisted of at least three elements: the endothelial glycocalyx, which forms a barrier on the blood side to large but not small molecules; the endothelium; and the basement membrane and astrocyte endfeet—the final line of defense on the brain side. All three elements restricted permeation of large molecules and should be taken into account when studying drug delivery and disease states.

Abstract

The endothelial cells that form the blood–brain barrier (BBB) are coated with glycocalyx, on the luminal side, and with the basement membrane and astrocyte endfeet, on the abluminal side. However, it is unclear how exactly the glycocalyx and extravascular structures contribute to BBB properties. We used two-photon microscopy in anesthetized mice to record passive transport of four different-sized molecules—sodium fluorescein (376 Da), Alexa Fluor (643 Da), 40-kDa dextran, and 150-kDa dextran—from blood to brain, at the level of single cortical capillaries. Both fluorescein and Alexa penetrated nearly the entire glycocalyx volume, but the dextrans penetrated less than 60% of the volume. This suggested that the glycocalyx was a barrier for large but not small molecules. The estimated permeability of the endothelium was the same for fluorescein and Alexa but several-fold lower for the larger dextrans. In the extravascular compartment, co-localized with astrocyte endfeet, diffusion coefficients of the dyes were an order of magnitude lower than in the brain parenchyma. This suggested that the astrocyte endfeet and basement membrane also contributed to BBB properties. In conclusion, the passive transport of small and large hydrophilic molecules through the BBB was determined by three separate barriers: the glycocalyx, the endothelium, and the extravascular compartment. All three barriers must be taken into account in drug delivery studies and when considering BBB dysfunction in disease states.

The blood–brain barrier (BBB) is a unique defense system that protects the brain from harmful agents and pathogens. Unfortunately, the BBB also restricts entry of a wide range of drugs developed to treat brain diseases. Tracer kinetic analysis was developed to quantify whole-brain uptake of compounds, but that technique has provided little information about the microstructure of the BBB (1–4). Advances in confocal and two-photon fluorescence imaging have allowed researchers to study the BBB at the microscopic level, on scales that range from an entire brain region down to a single vessel (5–8).

The majority of two-photon microscopy studies of BBB permeability have focused on imaging a brain region (typically spanning several hundred microns) and recording fluorescence intensities from extra- and intravascular compartments. Those data allowed calculations of BBB permeability based on theoretical models (7, 9, 10). In those models, BBB permeability was described as an average property of all vessels in the imaged region.

Those experiments could not resolve the contributions of individual vessels and even less the composition of the barrier. Several studies have, however, suggested that, in addition to the vascular endothelium, structures associated with the endothelium might also act as barriers (11–16). These structures include the endothelial glycocalyx, basement membrane, and astrocyte endfeet.

Here, we hypothesized that the BBB consists of a sequence of barriers, each limiting blood-to-brain transport of small and large molecules. To test this hypothesis, we performed high-resolution two-photon imaging of single capillaries and introduced fluorescent dyes into the bloodstream. We also used different fluorescent dyes to label the glycocalyx and astrocyte endfeet, which enabled us to associate fluorescent tracers that crossed the BBB with each anatomical component. Our data suggested that the BBB consisted of at least three different barriers that individually affected BBB permeability. The properties of this “tripartite” BBB should be considered when designing the delivery of large drug molecules and when studying disease states.

Results

Imaging Setup.

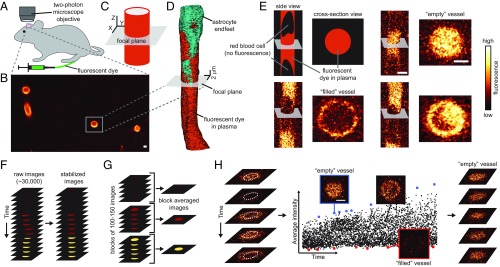
We used fast-scanning two-photon microscopy to record real-time images of single brain blood vessels oriented perpendicular to the focal plane. During these recordings, we continuously injected fluorescent dyes into the blood (Fig. 1 A and B). We evaluated changes in the distribution of fluorescence intensity outside the vessel, caused by the dye traversing the BBB. We performed this evaluation with a theoretical model (see Theory), based on the cylinder concept developed by Krogh. This model was designed to analyze the blood-to-brain transfer of an inert, diffusible solute that could permeate blood vessel walls (17). A blood vessel was modeled as an infinite cylinder inside a medium that was rotationally symmetric about the vessel (Fig. 1C). Therefore, we only analyzed data from blood vessels that were oriented perpendicular to the focal plane (Fig. 1D). To assist in the interpretation of the recorded images, we estimated the resolution of our microscope inside the brain with quantum dots that bind to the endothelial glycocalyx (see Estimating the Resolution of a Two-Photon Microscope Inside the Brain).

Fig. 1.

The imaging setup and pipeline of data analysis. (A) Images of brain vessels were collected from anesthetized mice through a cranial window with a two-photon microscope. Fluorescent dyes were continuously injected into a femoral vein with a pump. (B) An image of a brain region, showing blood vessels filled with Dex150. Only blood vessels oriented perpendicular to the focal plane were recorded and analyzed. (C) We modeled the selected blood vessels as cylinders, oriented perpendicular to the focal plane (gray area) and surrounded by a medium that was rotationally symmetric about the vessel. (D) Reconstruction of capillary geometry from images taken at different depths. The vessel is perpendicular to the focal plane, and it is approximately a cylinder for 10 $\mathrm{\mu }$m above and below the focal plane. (E) Comparison between fast-scanned images of two blood vessels, one viewed from the side, another viewed in cross-section. When blood cells are imaged, they replace the plasma and, hence, the fluorescent dye is absent (“filled” vessel). Consequently, filled vessels have dark shadows of various shapes inside them. (F) Before analysis, all recorded images were stabilized to correct for tissue movement (see SI Appendix, Image Registration). (G) To estimate the diffusion coefficient of the dye, $\mathrm{D}*$, in the extravascular compartment, stabilized images were block-averaged in time. (H) The average fluorescence intensity in the central part of the vessel (dotted white circles) was calculated for each recorded image and plotted as a function of time (Right). The points of highest intensity (blue) represent the fluorescence intensity in plasma. Images without blood cells (“empty” vessels) that corresponded to these points were extracted (SI Appendix, Fig. S6) and used to calculate the coefficient, ${\alpha }_g$, of dye partitioning between the plasma and the glycocalyx. The points of lowest intensity (red) correspond to most of the vessel volume being occupied by a blood cell (“filled” vessel). (Scale bar, 2 $\mathrm{\mu }$m.)

High acquisition rates (1–2 ms per image) allowed us to capture some images of vessels, when they contained only plasma without blood cells (called empty vessels; Fig. 1 E and H). Blood cells perturbed the structure of the endothelial glycocalyx (11) and reduced intravascular fluorescence by replacing the dye-containing plasma. Only images of the empty vessel showed the unperturbed distribution of the fluorescent dye in the vessel lumen. Therefore, we identified images of empty vessels (Fig. 1H) and used them to estimate the distribution of fluorescence intensity inside the vessel. In particular, we analyzed the partitioning of the fluorescent dye between the center of the vessel and the glycocalyx.

A Tripartite BBB.

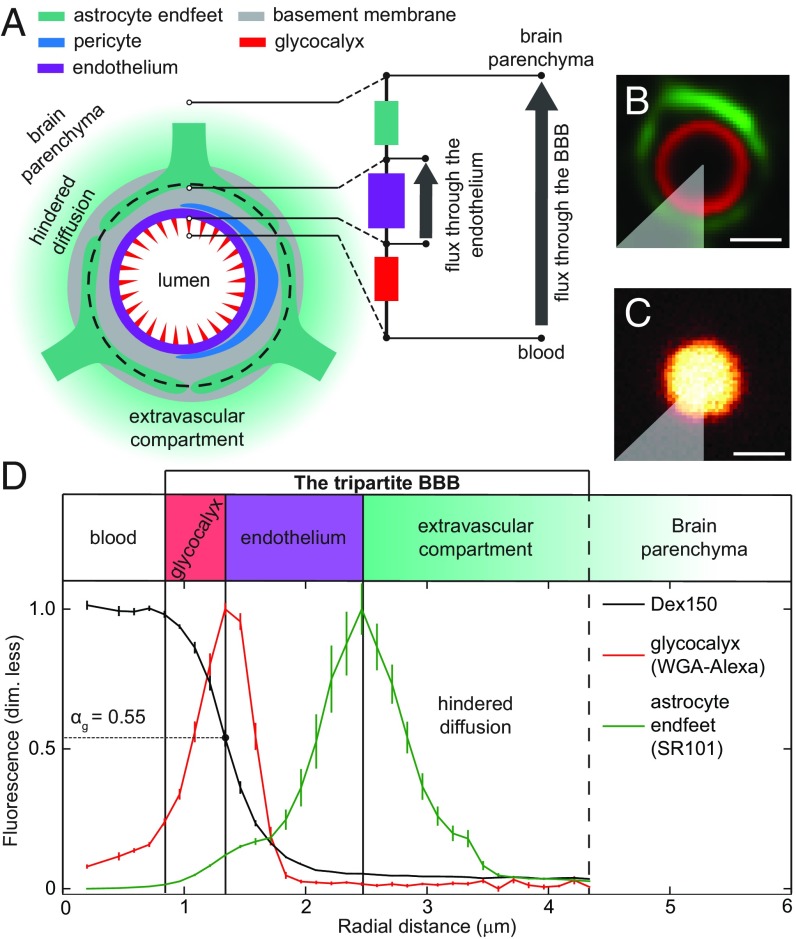
We hypothesized that the entire region that separates the vessel lumen from the brain parenchyma contributes to the BBB (Fig. 2A). Thus, the glycocalyx on the luminal side of the endothelium, the endothelium itself, and the extravascular compartment all contribute to the BBB. We found experimental support for this hypothesis as follows.

Fig. 2.

Components of the tripartite BBB. Glycocalyx and astrocyte endfeet were labeled and used as landmarks to locate the components of the tripartite BBB on recorded images. (A) Simplified diagram showing the main components of the BBB. We partitioned the BBB into three compartments—glycocalyx (red), endothelium (purple), and extravascular compartment (green)—based on their functional transport properties (glycocalyx partition coefficient, permeability, and diffusion coefficients) revealed by our data. The transport properties of these three compartments are analogous to three Ohmic resistors connected in series (schematic on the right side in A; see Discussion for more explanation). Thus, for a given concentration difference across the BBB, the glycocalyx and the extravascular compartment reduce the drop in concentration across the endothelium, and hence reduce the flux through it, in a manner that depends on the type of molecules in question. (B) Glycocalyx (red) and astrocyte endfeet (green) were labeled with WGA-Alexa and SR101, respectively. (C) Distribution of Dex150 fluorescence in the vessel lumen. The intensity is normalized by its maximum value. (D) Radial intensity profiles were obtained by selecting a sector (gray area, in B and C) and averaging the pixel values located at the same distances from the center of the vessel (SI Appendix, Fig. S1). The maxima of WGA-Alexa and SR101 fluorescence intensities defined the inner and outer boundaries, respectively, of the endothelium. The partition coefficient, ${\alpha }_g$, is the ratio between the fluorescence intensities of the dye at the peak of the WGA-Alexa distribution (red in B) and in the plasma (C). Error bars were estimated, as described in SI Appendix, Statistics. (Scale bar, 2 $\mathrm{\mu }$m.)

We located these three compartments in images by locating the endothelial glycocalyx and the astrocyte endfeet. To this end, the glycocalyx was labeled with Alexa Fluor (AF) 594-conjugated wheat germ agglutinin (WGA-Alexa; red in Fig. 2B), and the endfeet were labeled with sulforhodamine 101 (SR101; green in Fig. 2B). Then we analyzed the distribution across the three compartments independently for each of four diffusing dyes. Fig. 2C shows the distribution of one of the dyes, the 150-kDa fluorescein isothiocyanate-dextran (Dex150).

We based our definition of the extravascular compartment on the values we found for the diffusion coefficients in this region and the large difference between these values and the values found in the brain parenchyma. Starting at the peak of the fluorescence emitted by astrocyte endfeet (dashed circle in Fig. 2A), our extravascular compartment spanned the region, in which the experimental distribution of fluorescence agreed with the fitted solution to Eq. 1. Note that this fitted solution assigns a given dye a diffusion coefficient that is constant in time and space throughout the compartment. This simple but demanding property defines the compartment.

This extravascular compartment did not include the space closest to the vascular endothelium, because there, the distributions of fluorescence were not typically rotationally symmetric. Moreover, we could not determine an exact boundary between the extravascular compartment and the brain parenchyma from our data. We believe that a continuous transition between the two spaces was more likely.

We treated the space between the glycocalyx and the extravascular compartment as a single compartment, called “the endothelium” (see Fig. 2D). Based on the anatomy of the neurovascular unit (18, 19), this space, in addition to the vascular endothelium, may contain fragments of basement membrane, perivascular space, and pericytes, which we did not identify on our fluorescence images.

Our definitions of the endothelium and the extravascular compartment were based not on their anatomy but on their functional transport properties (permeability and diffusion coefficients) revealed by our data. The third compartment that we studied was the glycocalyx, located between the vessel lumen and the endothelium (see Fig. 2D).

Estimation of the Glycocalyx Partition Coefficient.

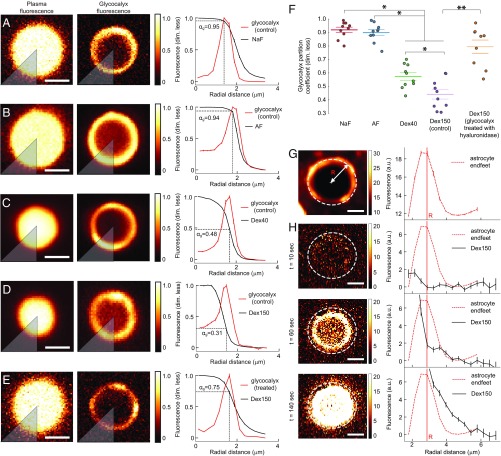
We defined the partition coefficient, ${\alpha }_g$, as the ratio of two fluorescence intensities. The first intensity was the Dex150 fluorescence at the point that it coincided with the peak of the WGA-Alexa fluorescence, which labeled the glycocalyx (Fig. 2D); the second intensity was the Dex150 fluorescence in the plasma, at the middle of the vessel. Thus, the ${\alpha }_g$ could be interpreted as the fraction of glycocalyx volume that was accessible to the dye-containing plasma (20). Fig. 2D shows that the fluorescence intensity of Dex150 was uniform in the center of the vessel, but it dropped by almost 50% in the glycocalyx. Fig. 3 A–F summarizes the values obtained for ${\alpha }_g$ with all four dyes, and SI Appendix, Fig. S8 discusses potential sources of bias in these estimates. We found no difference in ${\alpha }_g$ between sodium fluorescein (NaF; mean $\pm$ SEM: 0.93 $\pm$ 0.02) and AF (mean $\pm$ SEM: 0.91 $\pm$ 0.02). For both NaF and AF, ${\alpha }_g$ values were roughly twice as large as the ${\alpha }_g$ value of 40-kDa fluorescein isothiocyanate-dextran (Dex40; mean $\pm$ SEM: 0.56 $\pm$ 0.03) and Dex150 (mean $\pm$ SEM: 0.44 $\pm$ 0.03). Dex40, which was smaller than Dex150, penetrated the glycocalyx more efficiently than Dex150 (Fig. 3F). When we treated the glycocalyx with the enzyme hyaluronidase, ${\alpha }_g$ of Dex150 increased from 0.44 $\pm$0.03 (mean $\pm$ SEM) to 0.80 $\pm$ 0.05 (mean $\pm$ SEM; Fig. 3F), which was consistent with the findings reported by Henry and Duling (21).

Fig. 3.

Analysis of the glycocalyx partition coefficient of the dye and its diffusion in the extravascular compartment. Glycocalyx partition coefficients (${\alpha }_g$) were determined for (A) NaF, (B) AF, (C) Dex40, (D) Dex150, and (E) Dex150 (after enzymatically treating the glycocalyx). All extracted images of empty vessels (Fig. 1H) were normalized to the fluorescence intensity measured at the center of the vessel, and then, the normalized images were averaged. The resulting images of plasma fluorescence (Left) and glycocalyx fluorescence (Middle) were split into eight sectors (a single sector is shown in gray); for each sector, the ${\alpha }_g$ was estimated from the radial intensity distributions (Right). The mean value of all eight sectors was used as the total estimated partition coefficient, ${\alpha }_g$. For the dyes that effectively permeated the glycocalyx (NaF and AF), the intensity of plasma fluorescence (left column) in the center of the vessel was almost the same as the intensity in the glycocalyx. For the dyes that permeated the glycocalyx less effectively (Dex40 and Dex150), the plasma fluorescence distribution was narrower (left column), and the plasma fluorescence intensity in the glycocalyx was reduced. The relative reduction in fluorescence was quantified as ${\alpha }_g$. (F) Partition coefficients show that NaF and AF were distributed nearly throughout the entire glycocalyx volume, whereas Dex40 and Dex150 occupied less than 60% of the glycocalyx. Enzymatic treatment of the glycocalyx significantly increased the partition coefficient for Dex150. (G) Astrocyte endfeet fluorescence (Left) and its radial intensity profile (Right), obtained by azimuthal averaging of pixel intensities. (H) Time sequence of Dex150 fluorescence images (Left) and corresponding radial intensity profiles (Right) show the dye distribution as it penetrates the endothelium and travels into the extravascular compartment (outside the white circle). Before analysis, all images were stabilized and block-averaged (see Fig. 1 F and G). Pixels in the center of the vessel were oversaturated to enhance the weaker fluorescence in the extravascular compartment. Only data with rotationally symmetric fluorescence distributions were used for the analysis, which allowed us to model these data with Eq. 1. For a discussion on factors that can affect the extravascular fluorescence intensity, see SI Appendix, Fig. S9. Error bars were estimated as described in SI Appendix, Statistics. (Scale bar, 2 $\mathrm{\mu }$m.) $*$P < 0.05, one-way ANOVA with Tukey’s post hoc test. $**$P < 0.001, Wilcoxon rank-sum test.

Diffusion Explains the Observed Transport of Fluorescent Dyes in the Extravascular Compartment.

For the quantitative analysis of dye diffusion, we applied polar coordinates with origin in the center of the vessel (SI Appendix, Fig. S1). We found that the instantaneous distributions of fluorescence did not depend on the polar angle. This rotational symmetry of the data simplified the ensuing analysis by making the radial dimension the only spatial dimension of relevance. By allowing us to average data values over the polar angle, the rotational symmetry also improved the statistics of data. This made it more challenging to fit a model to data and hence more significant that we achieved to do so.

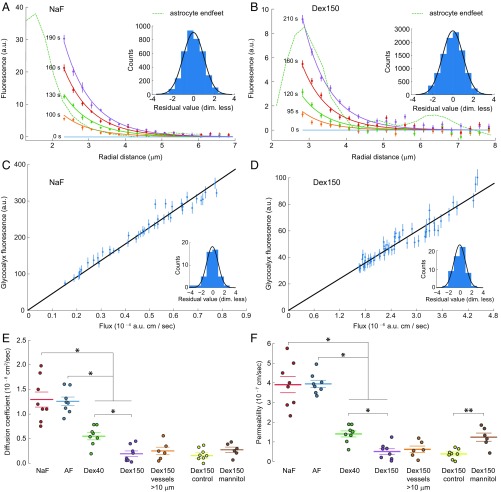
Fig. 3 G and H shows how Dex150 traverses the brain endothelium and travels beyond the astrocyte endfeet when a sufficiently large concentration gradient is created across the BBB. We collected and analyzed data from vessels loaded with NaF, AF, Dex40, or Dex150. We found that the changes in fluorescence intensity, $I_{ev}$, for dyes in the extravascular compartment of either small capillaries (3–5 $\mathrm{\mu }$m diameter) or larger vessels ($>$10 $\mathrm{\mu }$m) could be described with the radial reaction–diffusion equation:

$$\frac{\partial I_{ev}}{\partial t}=D^{*}\left(\frac{{\partial }^2{I}_{ev}}{\partial r^2}+\frac{1}{r}\frac{\partial I_{ev}}{\partial r}\right)-k_r\hspace{0.17em}{I}_{ev},$$ [1]

where $D^{*}$ is the diffusion coefficient of the dye in the extravascular compartment, $r$ is the radial distance from the center of the vessel, and $k_r\hspace{0.17em}{I}_{ev}$ is a reaction term that accounts for photobleaching and other first-order kinetic reactions. The value of $k_r$ depends on the incident laser intensity, which we were not able to measure. We did not analyze the values we obtained for $k_r$, apart from noting that the four $k_r$ values for Dex150 given in Table 1 were consistent with a single value. Fig. 4 A and B shows examples of fits of the model to experimental data for NaF (${\chi }^2=2.2$) and Dex150 (${\chi }^2=2.5$). An example of the diffusion of Dex150 into the extravascular compartment of a penetrating arteriole is shown in SI Appendix, Fig. S7. Diffusion coefficients for Dex150 suggested that the values were identical for small capillaries and large vessels (Fig. 4E). Table 1 summarizes the values of diffusion coefficients and reaction constants. The values of $D^{*}$ for all fluorescent dyes studied (Table 1) were approximately one order of magnitude lower than those reported for molecules of similar size in the brain parenchyma (22–25).

Table 1.

Diffusion coefficients ($\mathbf{D}\mathit{*}$), endothelial permeabilities ($\mathbf{P}$), and reaction constants (${\mathbf{k}}_{\mathbf{r}}$) for NaF, AF, Dex40, and Dex150

Molecule	$D*$, $10^{-8}\hspace{0.17em}{\mathrm{c}\mathrm{m}}^2$/s	$P$, $10^{-7}$ cm/s	$k_r$, $10^{-2}$ s${-}^1$
NaF†	1.30±0.16 (8)	3.91±0.41 (8)	6.3±1.4 (8)
AF†	1.25±0.09 (8)	3.95±0.18 (8)	0.8±0.6 (8)
Dex40†	0.55±0.07 (8)	1.40±0.15 (8)	2.6±0.5 (8)
Dex150†	0.19±0.06 (8)	0.51±0.14 (8)	1.7±0.5 (8)
Dex150‡	0.25±0.07 (6)	0.62±0.17 (6)	2.3±0.6 (6)
Dex150†,§	0.18±0.06 (8)	0.38±0.09 (8)	3.1±0.8 (8)
Dex150†,¶	0.27±0.05 (6)	1.24±0.20 (6)	1.5±0.7 (6)

Data represent the mean ± SEM of n independent measurements.

^†Diameter ≈3–5 μm.

^‡Diameter > 10 μm.

^§Intracarotid injection of saline (control).

^¶Intracarotid injection of mannitol.

Fig. 4.

Diffusion coefficients of the extravascular compartment and permeabilities of the vascular endothelium. (A and B) Experimentally measured radial distributions of fluorescence intensity of NaF and Dex150 (points with error bars) and the space-time distribution of fluorescence according to simple diffusion with bleaching, as described by Eq. 1 (lines), which was fitted to the experimental fluorescence data. Different colors indicate different times of measurement and solutions to Eq. 1 at corresponding times. The dashed line indicates the fluorescence of the astrocyte endfeet. (Insets) Histograms of the standardized residuals of the fits shown. A standard Gaussian distribution of standardized residuals indicates a perfect fit. For comparison, a standard Gaussian distribution is plotted (black line) on each histogram. (C and D) Fluorescence intensity in the glycocalyx plotted against the flux across the endothelium. The fluorescence intensities in the glycocalyx are experimental results from inside the blood vessel, and the fluxes across the endothelium are derived from the dependence of the extravascular fluorescence intensity on radial distance. The slope of the straight line through the origin was fitted to the data shown. The permeability of the vascular endothelium was estimated as the reciprocal of that slope (SI Appendix, Eq. 6). (Insets) Same as in A and B. (E and F) Vessel size and BBB integrity effects on (E) diffusion coefficients of fluorescent dyes in the extravascular compartment and (F) endothelial permeability. Mannitol was used to compromise the integrity of the BBB. Individual points represent measurements in different mice; horizontal lines represent the mean, and error bars are the $\pm$SEM. Error bars were estimated as described in SI Appendix, Statistics. $*$P < 0.05, one-way ANOVA with Tukey’s post hoc test. $**$P < 0.01, Wilcoxon rank-sum test.

Permeability of the Vascular Endothelium.

We estimated the permeability, $P$, of the vascular endothelium, as described in Fig. 4 C and D (see also Theory). The quality of the one-parameter fits shown in Fig. 4 C and D demonstrated that

• i)our interpretation of the space-time distribution of fluorescence outside the blood vessel showed that the flux away from the vessel was simply proportional to the independently observed fluorescence inside the vessel;
• ii)since the vessel was the only source of fluorophores in the experiment, the fluorophores were transported across the vascular endothelium; and
• iii)this transport was proportional to the difference in concentration across the endothelium—in effect the concentration inside, in the glycocalyx, because the concentration outside was negligible in comparison. Consequently, the transport across the endothelium could be described by a single parameter, its permeability.

Although these results were not surprising, they lent strong experimental support to our data analysis, both its logic and its execution.

The permeabilities of vessels to dyes are given in Table 1 and Fig. 4F. We found no difference between the permeabilities of NaF and AF but lower permeabilities for the dextrans, Moreover, the permeability was lower for Dex150 than for Dex40, which suggested a size-dependent mechanism of permeation. We did not find a significant difference in permeabilities between small capillaries (3–5 $\mathrm{\mu }$m diameter) and larger vessels.

This approach was tested on vessels after the BBB was compromised by injecting mannitol. Mannitol has been used routinely to increase the BBB permeability (26, 27). We found that an intracarotid injection of mannitol caused a $>2$-fold increase in BBB permeability to Dex150 and did not change the diffusion coefficient of Dex150 in the extravascular compartment (Fig. 4 E and F); thus, mannitol did not affect the permeability of the extravascular compartment, even when it strongly affected the vascular endothelium. In 6 out of 22 selected vessels, the initial circular symmetry of the fluorescence distribution was preserved. The data from these six vessels were used for our analysis. In 16 out of 22 vessels, the circular symmetry was disrupted by the treatment. Data from those vessels were excluded from our analysis.

Discussion

The Tripartite BBB Acts as Three Sequential Resistors.

The BBB that emerged from this analysis can be thought of as three Ohmic resistors connected in series: the glycocalyx, the endothelium, and the extravascular compartment (Fig. 2A). A concentration difference across the BBB corresponds to a voltage difference across the three resistors. The flux of molecules across the BBB corresponds to the electrical current through the three resistors. This analogy is deep, because permeability and conductance are simply different names for parameters that quantify a linear relationship between cause (difference in voltage/concentration) and effect (current/flux). Thus, because the glycocalyx and extravascular compartments function as barriers in comparison with the vessel lumen and the brain parenchyma, respectively, for a given concentration difference between the vessel lumen and the parenchyma, they reduce the concentration difference across the endothelium, and hence, they reduce the flux through it. This effect is greater for larger molecules, because they encounter greater resistance in the glycocalyx. Moreover, as the resistance in the extravascular compartment slows diffusive transport away from the blood vessel, potential pathogens may be exposed to immune cells near the blood vessel for a longer time.

In Vivo Estimates of Fluorophore Partitioning into the Glycocalyx Provide a Better Description than Glycocalyx Thickness.

We reported glycocalyx partition coefficients for fluorescent dyes entering into the glycocalyx in single vessels in vivo. In our opinion, this coefficient is more descriptive than the glycocalyx thickness or related quantities reported elsewhere (13, 21, 28–30). The partition coefficient is specific to individual molecules, and it can be interpreted as the fraction of the glycocalyx volume that is accessible to the specific molecule. In contrast, the glycocalyx thickness does not contain molecule-specific information. We propose that the partition coefficient can be interpreted in terms of the glycocalyx microstructure. Electron microscopy images have demonstrated that the glycocalyx is a collection of dense, bush-like structures, which cover the surface of an endothelial cell (31, 32).

We showed that NaF and AF distributed nearly throughout the entire glycocalyx volume, which indicated that the glycocalyx did not serve as a barrier to small molecules, like NaF and AFs; instead, the glycocalyx was essentially equivalent to blood plasma. However, based on our results with Dex40 and Dex150, larger molecules were less able to penetrate the dense glycocalyx structures. An integration of the fluorescence signals over low- and high-density regions showed that Dex150 fluorescence in the glycocalyx was 44% of its intensity in the blood plasma (Fig. 3F).

When a molecule has a low glycocalyx partition coefficient, it may only reach a fraction of the endothelial surface, which reduces its flux through the BBB and, consequently, its total brain uptake. Our results were supported by the findings of Vink and Duling, who demonstrated that small dyes and low-molecular weight dextrans could penetrate the glycocalyx of cremaster muscle capillaries, but 70 kDa anionic and neutral dextrans were confined to the central part of the capillary (11, 33).

Knowledge of the glycocalyx partition coefficient might increase the accuracy of measurements of the glycocalyx thickness. Previously, these measurements typically relied on the assumption that high-molecular weight anionic dextrans (like 70-kDa dextran) could not permeate the glycocalyx (30). Nieuwdorp et al. (34) developed a quantitative approach for measuring the glycocalyx volume in human patients. They assumed that a reference fluorescent dye could distribute throughout the entire glycocalyx volume. In a review of that approach, Michel and Curry (20) questioned that assumption and suggested that a method for measuring the glycocalyx partition coefficient was required. In the present study, we have provided that method.

The Extravascular Compartment Is also a Diffusion Barrier.

After a molecule in the blood has traversed the glycocalyx and the endothelium, it encounters the extravascular compartment. With the simplest possible reaction–diffusion model, we showed that, for the four fluorescent dyes we studied, the diffusion coefficients in the extravascular compartment were approximately one order of magnitude lower than the diffusion coefficients of similar-sized compounds in the brain parenchyma (22, 25).

Once a molecule has crossed the endothelium, we expect a significant increase in the geometric path length of its radial diffusion: Instead of diffusing radially, the molecule is forced to travel along the astrocyte endfeet (and possibly the pericyte membrane) to find the exit points between the neighboring endfeet (Fig. 2A). Moreover, astrocyte endfeet are connected to each other through gap-junctions, and they are connected to endothelial cells through complex interactions with the basal lamina and extracellular matrix (figure 3 in ref. 18). This tight complex may serve as an additional barrier to compounds that cross the vascular endothelium (18, 19, 35, 36). Indeed, Nuriya et al. (15) demonstrated that astrocyte endfeet formed a barrier for compounds moving from the brain parenchyma to the blood vessel. Several studies have also shown that compounds in the perivascular spaces (19) were hindered in a size-dependent manner (16, 37), consistent with the size dependence of the diffusion coefficients we observed (Table 1).

Convective transport occurs in the perivascular spaces of large brain vessels and inside the brain ventricles (37–41), but it is debatable whether convection is important for the transport of compounds within the brain parenchyma (18, 42). Here, we demonstrated that the local fluorescence intensity in the extravascular compartment changed over time and space in a manner consistent with simple diffusion. The radial diffusion coefficient was constant in space and time. Consequently, we could exclude convection as a mechanism of transport.

Diffusion coefficients in the brain parenchyma are typically estimated by injecting a fluorescent dye through a pipette and modeling the spatiotemporal changes in local fluorescence. That approach assumes that the medium is homogeneous and isotropic across hundreds of microns around the injection site (22, 43). On the other hand, to simplify our calculations for the extravascular compartment, we only needed to assume that the medium was rotationally invariant with respect to rotations around the center of the vessel; thus, we only studied vessels that exhibited this property. Because the radial span of the vessel was only a few microns, we assumed, and we could confirm, that the vessel was the only source of fluorescent dye in a given extravascular compartment. However, on a larger spatial scale, all blood vessels are sources of fluorescence in the brain, which makes modeling prohibitively complex. This complexity prevented us from analyzing diffusion in the brain parenchyma based on fluorescence.

Shi et al. estimated the diffusion coefficients of fluorescent dyes in the space surrounding cerebral blood vessels. They reported values that agreed well with diffusion coefficients previously reported for the brain parenchyma. However, although they used a radial diffusion model that assumed rotational symmetry with respect to the vessel, their image data (figure 4a in ref. 8) showed an absence of the symmetry, which challenges the accuracy of their estimates. Our results suggested two different diffusion coefficients for each dye. One coefficient described diffusion in the extravascular compartment, and the other described diffusion in the brain parenchyma. Single-molecule tracking might be a suitable method for measuring both diffusion coefficients for a single dye molecule (44). That approach would have high reliability because it would not require switching methods between measurements (45).

Vascular Endothelium Permeability from Two-Photon Images.

Early quantitative methods showed that the permeability of blood vessels in the brain was much smaller than in other tissues (46, 47). Currently, microscopic imaging methods are routinely used to estimate BBB permeability both in vitro (48, 49) and in vivo (7–9, 50). In the present work, we injected fluorescent dyes intravenously (i.v.), which resulted in minimal interference with cerebral blood flow compared with other in vivo methods (8, 50). We developed a method for measuring the resulting plasma fluorescence intensity directly from images without red blood cells. For diffusion in the vessel periphery, we measured only the fluorescence close to the vessel (3–5 $\mathrm{\mu }$m), and the experiments were brief (1–2 min). Thus, we effectively eliminated any potential contributions to the observed fluorescence from vessels other than the one on which we focused. Finally, we identified some anatomical components of the BBB and separated the glycocalyx and extravascular components from the measurement of vascular endothelium permeability.

The permeabilities presented here were within an order of magnitude of permeabilities reported previously for fluorescent dyes of similar size, both in vivo (8, 50–52) and in vitro (48, 49, 53, 54). In particular, our estimation of Dex40 permeability ($1.40\pm 0.15\times 10^{-7}$ cm/s) agreed well with other in vivo estimates of $1.15\pm 0.23\times 10^{-7}$ cm/s (table 1 in ref. 8) and $1.7\pm 0.9\times 10^{-7}$ (table 1 in ref. 50). Our permeability for Dex150 ($0.51\pm 0.14\times 10^{-7}$ cm/s) was, as expected, lower than that for Dex70 and higher than that of IgG (table 1 in ref. 8). Yuan et al. and Shi et al. (8, 50) reported a higher BBB permeability for NaF than our value. However, they studied postcapillary venules, which were shown to exhibit loose BBB architecture compared with capillaries (55); hence, venules are expected to have higher BBB permeability than capillaries.

Our finding that estimated permeabilities declined with increasing dye size (Table 1) was consistent with a paracellular transport mechanism. It was not surprising that high-molecular weight polymers, particularly dextrans, could move through narrow spaces that are smaller than their size, estimated by the hydrodynamic radius or the radius of gyration, because the properties of linear polymers differ from those of rigid particles of similar size (see SI Appendix, Using Fluorescently Labeled Dextrans as Probes to Study Transport in Brain Tissue). The polymer coil can thread through tight and narrow spaces, by starting at one of its ends or by starting with a “hernia.” For example, one can directly visualize how a single 48.5-kbp DNA diffuses through pores that are approximately seven times smaller than its radius of gyration (figure 5 in ref. 56). Indeed, experimental data from glomerular capillaries showed higher permeability for dextrans than for proteins of similar size (57–60). However, the probability of dextran passage through the narrow BBB spaces is much smaller than that of a compact molecule with a diameter similar to a dextran monomer. This low probability results in very small, but experimentally measurable, BBB permeabilities to large dextrans.

Another way to cross the BBB is through an endothelial cell. Particularly, fluid-phase endocytosis has been used to explain how some proteins and dextrans can penetrate the BBB (61, 62). If this transport is not limited by the number of vesicles available for endocytosis, one may expect the flux of dextran through the BBB to be proportional to the concentration of dextran in the blood. Consequently, this contribution to the flux of dextran across the BBB is inseparably included in the permeability we measure (Fig. 4 C and D).

For hydrophobic compounds that can diffuse through the endothelial plasma membrane, a threshold exists in the 400–600 Da range, which could supposedly distinguish BBB-permeable from BBB-nonpermeable molecules (63). We found no evidence for such a threshold for hydrophilic NaF (376 Da) and AF (643 Da) (Table 1). Our data indicate that the endothelium permeability for hydrophilic compounds depends more smoothly on molecular weight and that the differences in the total flux of a compound through the BBB depends also on its glycocalyx partition coefficient and on its diffusion coefficient in the extravascular compartment.

Finally, we showed that mannitol did not change the diffusion coefficient in the extravascular compartment but produced a more than twofold increase in endothelium permeability. Our results supported the hypothesis that mannitol induced endothelial cell shrinkage, which then increased the paracellular permeability (64).

Limitations of the Model.

The method of analysis developed here applies only to vessels that are oriented perpendicular to the focal plane. These vessels were not expected to differ from vessels with different orientations. Larger vessels are scarcer than small capillaries; thus, it might be challenging, and hence time-consuming, to find a large vessel with a cylindrical shape and a perpendicular orientation. Our method also demanded rotational invariance in the distribution of fluorescence around the vessel. In the case of the mannitol-disrupted BBB, this demand was not satisfied for a large fraction of the vessels; consequently, those vessels were not studied. For a more detailed discussion of factors that affect estimates of the measured extravascular fluorescence intensity and the partition coefficients of the glycocalyx, see SI Appendix, Figs. S8 and S9.

Summary.

We have developed and applied a theoretical framework for a quantitative analysis of the BBB in single capillaries. We isolated the glycocalyx, endothelium, and extravascular compartment adjacent to the brain parenchyma. Together, these three structures form a sequence of diffusional constraints that may be termed the tripartite BBB. We quantified the transport properties of the three structures in the tripartite BBB separately, as independent units, by tracking the transfer of fluorescent molecules from the glycocalyx, through the endothelium, to the extravascular compartment. The next step in understanding the BBB might be to study the processes that regulate the properties of the glycocalyx, endothelium, and extravascular compartment in health and disease.

Materials and Methods

Animal Handling.

All procedures involving animals were approved by the Danish National Committee, according to the guidelines of the European Council’s Convention for the Protection of Vertebrate Animals Used for Experimental and Other Scientific Purposes (https://www.coe.int/en/web/conventions/full-list/-/conventions/rms/090000168007a67b). In addition, all procedures were in compliance with Animal Research: Reporting of in Vivo Experiments (ARRIVE) guidelines. We used male $C57BL/6J$, 8–12-wk-old mice and followed surgical procedures described elsewhere (65). Internal carotid artery catheterization was based on a previously described method (66). Anesthesia was induced with intraperitoneal bolus injections of xylazine (10 mg/kg) and ketamine (60 mg/kg). Ketamine (30 mg/kg) was used to maintain anesthesia during the experiments. A 2–3-mm cranial window was drilled over the somatosensory barrel cortex region (Fig. 1A). After the dura was removed, we applied 0.75% agarose gel to the brain surface and covered the craniotomy with a glass coverslip.

Materials.

We used NaF (Sigma-Aldrich; 1% solution in saline), AF 488 (AF; Sigma-Aldrich; 0.2% solution in saline), 40 kDa fluorescein isothiocyanate–dextran (Dex40; Sigma-Aldrich; 2.5% solution in saline), and 150 kDa fluorescein isothiocyanate–dextran (Dex150; Sigma-Aldrich; 2.5% solution in saline) as fluorescent dyes, which were injected i.v. using a syringe pump at a rate of 0.15–0.3 mL/h. Resolution of the two-photon microscope in the brain was estimated (see section below) using quantum dots conjugated with WGA (Qdot655-WGA, Thermo Fisher Scientific; 1 $\mathrm{\mu }$M stock solution diluted 200 times in saline). Astrocytes were labeled with SR101 (Sigma-Aldrich; 50 $\mathrm{\mu }$M in saline) applied to a brain surface. Glycocalyx was labeled with AF 594-conjugated WGA (WGA-Alexa; Thermo Fisher Scientific; 100 $\mathrm{\mu }$L of 1 mg/mL solution in saline) injected i.v. 45 min before imaging. To enzymatically degrade the glycocalyx, we used hyaluronidase (Sigma-Aldrich type IV-S; 750–3,000 units per milligram; 5 mg in 150 $\mathrm{\mu }$L saline) injected into the internal carotid artery 1 h before imaging. Control animals received the same amount of denatured hyaluronidase heated for 10 min at ${\mathrm{95}}^{○}$. Mannitol (Sigma-Aldrich; 100 $\mathrm{\mu }$L of 20% solution in saline) was injected into the internal carotid artery; controls received the same amount of saline.

Two-Photon Imaging Parameters.

Data were recorded with a FluoView FVMPE-RS two-photon microscope (Olympus) equipped with a MaiTai DeepSee laser (Millenia Pro, Spectra Physics) and a fast resonant-scanning system. Imaging was performed with a 25$\times$ (N.A. = 1.05) water immersion objective (Olympus). Samples were illuminated with 800-nm laser light, and emitted fluorescence was split and recorded into channels equipped with high-sensitivity GaAsP detectors. Images were sampled at $\sim$80 Hz; individual images were recorded for 1–2 ms (depending on the size) at 0.07 $\mathrm{\mu }$s per pixel and 0.124 $\mathrm{\mu }$m per pixel resolution. Recorded data were stored on the servers of the Department of Neuroscience at the University of Copenhagen, and they are available upon request.

Estimating the Resolution of a Two-Photon Microscope Inside the Brain.

We used quantum dots conjugated with WGA (referred to as quantum dots below) to estimate our microscope’s lateral and axial resolutions, ${\mathrm{\Delta }}_{XY}$ and ${\mathrm{\Delta }}_Z$, respectively, both outside and inside the brain. To assess the performance of our imaging setup, we collected images of quantum dots immobilized on a glass coverslip. This specimen was created by placing several drops of 1,000-fold diluted stock solution of quantum dots (1 $\mathrm{\mu }$M) on a microscope coverslip and drying the solution. Then, the coverslip was placed on a microscope slide. The space between the coverslip and the slide was filled with 1% agarose gel to facilitate immobilization of the quantum dots. From a time series of images of a quantum dot, one can see a characteristic “blinking” of fluorescence (67), which can be used to identify single quantum dots.

SI Appendix, Fig. S2 A and B shows images of quantum dots on a glass slide recorded in 3D, from which we extracted radial (SI Appendix, Fig. S2C) and axial (SI Appendix, Fig. S2D) distributions of fluorescence intensity emitted by a selected quantum dot. These distributions agreed well with the fitted theoretical point-spread function (PSF) of a two-photon microscope, which is known from the literature (equations 6 and 16 in ref. 68). The theoretical PSF was fitted to data based on the following fitting parameters: location, amplitude, a constant background, and the refractive index of the immersion medium.

The refractive index, $n$, defines the width of the fitted PSF, because the wavelength of the excitation laser, $\lambda$, and the collection angle of the objective, $\alpha$, are fixed, known values (equation 3 in ref. 69). With the fitted values of $n$, we estimated the N.A. of the objective as $n\cdot \sin \alpha$. For the fits shown in SI Appendix, Fig. S2 C and D, the estimated N.A. values were $1.04\pm 0.01$ and $0.97\pm 0.07$, respectively. These values are consistent with the known $\mathrm{N}\mathrm{A}=1.05$ of our water-immersion objective. From our collected data, we concluded that our imaging system performed adequately, to its theoretical limit.

The fact that the simplest paraxial theory of image formation agrees well with the data obtained with a relatively high-N.A. objective (N.A. = 1.05) has been explained theoretically and shown experimentally (70, 71). Consequently, we estimated the resolution of the microscope with theoretical values for the full-width-at-half-maximum (FWHM) of the microscope’s theoretical PSFs (table 1 and equation 3 in ref. 69). The estimated resolutions, measured from quantum dots on a glass slide, were ${\mathrm{\Delta }}_{XY}=0.28\hspace{0.17em}\mathrm{\mu }$m and ${\mathrm{\Delta }}_Z=1.06\hspace{0.17em}\mathrm{\mu }$m.

As in other turbid media, imaging in the brain deteriorates with increasing depth, in both lateral and axial resolutions. We collected fluorescence intensities at the interface between blood and brain tissues. There, one may expect a further reduction in resolution, due to a mismatch of refractive indices. To estimate the two-photon microscope’s resolution there, we used quantum dots conjugated with WGA lectin, which binds to the endothelial glycocalyx. After a bolus injection of quantum dots (100 $\mathrm{\mu }$L of a 5-nM solution), we could identify quantum dots in clusters or in isolation, sparsely covering the inner surfaces of vessels. SI Appendix, Fig. S3 A and B shows images of quantum dots inside the brain. We analyzed these images in the same way that we analyzed the images of quantum dots on a glass slide. Based on the fits shown in SI Appendix, Fig. S3 C and D, the estimated values of N.A. were $0.61\pm 0.02$ and $0.38\pm 0.07$, respectively. The effect of the brain, therefore, can be thought of as a reduction in the “effective” N.A. of the objective, a reduction that differs for the lateral and axial dimensions. We found that, in the brain, at depths from 50 to 100 $\mathrm{\mu }$m, ${\mathrm{\Delta }}_{XY}=0.49\pm 0.05\hspace{0.17em}\mathrm{\mu }$m (mean $\pm$ SEM; n = 10 beads from three different mice) and ${\mathrm{\Delta }}_Z=3.20\pm 0.18\hspace{0.17em}\mathrm{\mu }$m (mean $\pm$ SEM; n = 10 beads from three different mice).

Our method for in situ estimation of the resolution of a two-photon microscope may be useful for other studies that use high-resolution imaging in the brain. In comparison with the injection of quantum dots or fluorescent beads into the brain with a pipette, our method is less invasive and technically simple (it requires only single i.v. injection), and it can be used for routine checks of resolution.

Theory.

Our model was based on the following assumptions, which are similar to those of Krogh’s cylinder model (17, 72):

• i)The vessel has a cylindrical shape and is oriented perpendicular to the focal plane.
• ii)The distribution of fluorescence intensity in the extravascular compartment has cylinder symmetry.
• iii)Diffusion is the only mechanism of transport in the extravascular compartment.
• iv)The studied vessel is the only source of diffusing compound in the imaging region.
• v)The vessel’s diameter does not change during the experiment.
• vi)Loss of fluorescence by photobleaching or otherwise can be described with a first order reaction.

The flux, $J\left(t\right)$, of a fluorescent dye through a unit surface of the BBB is proportional to its permeability, $P$:

$$J\left(t\right)=P\left(C_g\left(t\right)-C_{\mathrm{e}\mathrm{v}}\left(t\right)\right)\hspace{0.17em},$$ [2]

where $C_g\left(t\right)$ and $C_{\mathrm{e}\mathrm{v}}\left(t\right)$ are the concentrations of the fluorescent dye in the glycocalyx and at the inner surface of the extravascular compartment, respectively (Fig. 2D). We assumed that the measured fluorescence intensity $I\left(t,r\right)$ was proportional to the dye concentration, $I\left(t,r\right)=K^{-1}\hspace{0.17em}C\left(r,t\right)$, where $K$ was the proportionality constant.

When the dye was distributed only in the extracellular spaces, not in cells, the coefficient $\alpha$ could be introduced to estimate the volume fraction of the extracellular spaces, relative to the total volume of the tissue (43). Then, the relationship between the fluorescence intensity measured in the extravascular compartment of a vessel, $I_{\mathrm{e}\mathrm{v}}$, and the concentration of the dye, $C_{\mathrm{e}\mathrm{v}}$, could be calculated as $C_{\mathrm{e}\mathrm{v}}\left(t\right)=K\cdot I_{\mathrm{e}\mathrm{v}}\left(t\right)/\alpha$, where $0<\alpha <1$.

We assumed that only a fraction of the glycocalyx volume, ${\alpha }_g$, was accessible to the fluorescent dye and that an equilibrium existed between the dye in the plasma and that in the glycocalyx at all times. Accordingly, the dye’s concentration in the glycocalyx was $C_g\left(t\right)={\alpha }_g\hspace{0.17em}K\hspace{0.17em}{I}_i\left(t\right)$, where $I_i\left(t\right)$ was the fluorescence intensity in blood plasma. Thus, $J\left(t\right)$, from Eq. 2, could be expressed in terms of the measured fluorescence intensities as follows:

$$J\left(t\right)=P\left({\alpha }_g\hspace{0.17em}K\hspace{0.17em}{I}_i\left(t\right)\hspace{0.17em}-\hspace{0.17em}\frac{1}{\alpha }\hspace{0.17em}K\hspace{0.17em}{I}_{\mathrm{e}\mathrm{v}}\left(t\right)\right)\approx {\alpha }_{g}P\hspace{0.17em}K\hspace{0.17em}{I}_i\left(t\right).$$ [3]

The approximate expression was valid for the majority of datasets when $I_i\left(t\right)\gg I_{\mathrm{e}\mathrm{v}}\left(t\right)$.

We used NaF, AF, Dex40, and Dex150 as fluorescent dyes. We assumed that the dyes moved freely within the vessel and had no interactions with any blood components (73, 74). We also assumed that the dyes, as hydrophilic molecules, could not permeate cell membranes but instead distributed in the extracellular spaces (22, 75).

We showed that the spread of fluorescence of the studied dyes in the extravascular compartment agreed well with the reaction–diffusion equation (Eq. 1). The effective diffusion coefficient, $D*$, was related to the diffusion constant in free medium (agarose gel), $D$, and the tortuosity of the tissue, $\lambda$, through ${\lambda }^2=D/D*$ (43).

We placed the surface of our model cylinder at the location of the peak of the SR101 (astrocyte) fluorescence (Fig. 2D). There, we set a time-dependent boundary condition. SI Appendix, Fig. S5A shows an example of experimentally measured fluorescence intensity at the boundary, $I_{\mathrm{e}\mathrm{v}}\left(t,R\right)$, and its smoothed version, calculated with a locally weighted scatterplot smoothing regression.

The second boundary condition was defined by assuming a zero flux far ($R_{\infty }$) from the cylinder surface. This assumption holds when no molecule reaches $R_{\infty }$ from the studied vessel or any other vessel during the experiment. In the numerical model, we placed $R_{\infty }$ approximately 30 $\mathrm{\mu }$m away from the cylinder surface; thus, $R_{\infty }\gg R$.

A straightforward way to implement an initial condition for Eq. 1 is to use the measured fluorescence distribution at the initial time, $I_{\mathrm{e}\mathrm{v}}\left(t_0,r\right)$, but this approach has several disadvantages. First, like any experimentally measured intensity profile, the $I_{\mathrm{e}\mathrm{v}}\left(t_0,r\right)$ contained noise, which would influence the fitting, particularly at early times, before the irregularities of $I_{\mathrm{e}\mathrm{v}}\left(t_0,r\right)$ were smoothed by diffusion. Second, the reaction term $k_r\hspace{0.17em}{I}_{\mathrm{e}\mathrm{v}}\left(r,t\right)$ in Eq. 1 depended on the absolute value of fluorescence intensity, which could contain dye-independent autofluorescence. In general, measurements of fluorescence intensity contain both the dye fluorescence and nonspecific autofluorescence. See SI Appendix for more theory.

Statistics and Software.

Standard statistical tests and open source software were used for the data analysis. See SI Appendix, Statistics and Software Libraries.