Abstract
Thousands of maize landraces are stored in seed banks worldwide. Doubled-haploid libraries (DHL) produced from landraces harness their rich genetic diversity for future breeding. We investigated the prospects of genomic prediction (GP) for line per se performance in DHL from six European landraces and 53 elite flint (EF) lines by comparing four scenarios: GP within a single library (sL); GP between pairs of libraries (LwL); and GP among combined libraries, either including (cLi) or excluding (cLe) lines from the training set (TS) that belong to the same DHL as the prediction set. For scenario sL, with N = 50 lines in the TS, the prediction accuracy (ρ) among seven agronomic traits varied from −0.53 to 0.57 for the DHL and reached up to 0.74 for the EF lines. For LwL, ρ was close to zero for all DHL and traits. Whereas scenario cLi showed improved ρ values compared to sL, ρ for cLe remained at the low level observed for LwL. Forecasting ρ with deterministic equations yielded inflated values compared to empirical estimates of ρ for the DHL, but conserved the ranking. In conclusion, GP is promising within DHL, but large TS sizes (N > 100) are needed to achieve decent prediction accuracy because LD between QTL and markers is the primary source of information that can be exploited by GP. Since production of DHL from landraces is expensive, we recommend GP only for very large DHL produced from a few highly preselected landraces.
Keywords: Genomic Prediction, doubled-haploid, maize landraces, GenPred, shared data resources
Genetic diversity is fundamental for selection progress. In plant breeding, high selection pressure and the usage of few key ancestors in the development of new germplasm contributed to a strong decline of the genetic diversity present in elite germplasm (Messmer et al. 1992; Reif et al. 2005a; Technow et al. 2013). Recourse to the rich cultural heritage of landraces stored in seed banks worldwide is considered a promising strategy to broaden genetic diversity (Salhuana and Pollak 2006; Warburton et al. 2008; Strigens et al. 2013). Landraces represent an attractive source of diversity because they are the predecessors of modern cultivars and have been cultivated by farmers for centuries. During the last century, modern varieties have replaced nearly all landraces, many of which have been conserved in seed banks. However, a major obstacle for using landraces in breeding is the performance gap to modern hybrid cultivars, which continuously widens due to ongoing selection progress. Therefore, novel approaches are urgently needed to “turbocharge” the use of landraces as genetic resources in breeding (Yu et al. 2016).
In allogamous crops, mining the genetic diversity of seed bank accessions entails two challenges. First, one must identify the most promising accessions, commonly based on passport data provided by seed banks and results from field trials, in which the landraces are evaluated for their per se performance and/or testcross performance with suitable testers (Salhuana and Pollak 2006; Böhm et al. 2014). Selection among accessions is not sufficient because both molecular and phenotypic data from various crops suggest that more genetic variation lies within than between landraces (Greene et al. 2014; Monteiro et al. 2016; Böhm et al. 2017; Mayer et al. 2017). Therefore, the second challenge is mining the genetic diversity within landraces, preferably in the form of inbred lines. Unlike the stored landraces, which represent populations of heterozygous individuals, inbred lines produced from landraces can be identically multiplied ad libitum and, hence, can be phenotyped with any degree of precision desired to characterize the source germplasm used as the donor of new genetic variation.
Line development has traditionally been accomplished by recurrent selfing or full-sib matings (Poehlman 1987). When applied to landraces of allogamous species, success rates are generally extremely low, because the high genetic load revealed in advanced selfing generations is manifested in poor vigor (inbreeding depression), and a loss of inbred lines due to the fixation of detrimental or (sub)lethal alleles (Böhm et al. 2017). Recently, Melchinger et al. (2017) showed that large-scale production of doubled-haploid (DH) lines from landraces in maize is possible, albeit at much higher expenditures compared with elite materials. They also showed that DH libraries (DHL, see Supplemental Material, Table S1 for list of abbreviations) capture the allelic diversity of landraces in an unbiased way, and recommended the use of DHL for conservation purposes in seed banks and as source materials for prebreeding programs.
As DHL become available, the breeding potential of the DH lines must be assessed prior to their use in breeding programs. A first priority is evaluating their line per se performance, because many of the DH lines from landraces display severe weaknesses such as lodging, tillering, susceptibility to diseases, and low pollen production. Phenotyping in multilocation trials entails high costs and requires large seed quantities, yet seed multiplication is generally a problem due to the poor seed set and reduced vigor of these materials (Strigens et al. 2013; Böhm et al. 2017). Subsequent evaluation for testcross performance should be restricted to lines showing acceptable per se performance (Wilde et al. 2010).
For elite germplasm, genomic prediction (GP) has emerged as a powerful tool to complement the expensive phenotyping of test candidates in breeding programs (Crossa et al. 2017). GP consists of training a statistical model in a set of individuals containing both phenotypic and genotypic information to predict the breeding values of individuals with only genotypic information. For the autogamous species sorghum (Sorghum bicolor L.), Yu et al. (2016) recently demonstrated the use of GP with a model trained across landraces to choose promising accessions from the vast amount of germplasm archived in seeds banks and expedite the germplasm evaluation process. However, the use of GP for mining genetic diversity within landraces of allogamous species was not investigated by this study and, hence, requires further research.
In animal and plant breeding, statistical models have been developed to perform GP between populations (Lehermeier et al. 2015; Wientjes et al. 2015). Using models trained with data from cattle breeds with large sample sizes yielded low accuracies for estimating the breeding value of individuals from a different breed with smaller size (Hayes et al. 2009), whereas combining several cattle breeds with small sample sizes into a larger set resulted in similar or higher accuracies than prediction within breeds (Pryce et al. 2011; Chen et al. 2014; Iheshiulor et al. 2016). A similar situation exists for DHL, because the number of lines is generally low due to limited success rates in the production of DH lines from landraces (Melchinger et al. 2017). However, GP from one landrace to another, and particularly pooling different landraces in a combined training set (TS), has not been investigated hitherto.
Here, we use maize (Zea mays L.) as a model to demonstrate how a combination of modern techniques could support mining of the genetic diversity present in landraces of allogamous crops. Our example is from the flint heterotic pool that represents one pillar in the dent × flint heterotic pattern employed for hybrid maize breeding in Central Europe. Our objectives were to investigate for various agronomic traits the accuracy of GP with DHL in four scenarios: (i) GP within a single library (sL); (ii) GP between pairs of libraries (LwL); (iii) GP among libraries with a combined TS composed of several DHL, including lines from the DHL to be predicted (cLi); and (iv) GP among libraries with a TS composed of several DHL, excluding lines from the DHL to be predicted (cLe). Further, we examined the influence of the sample size, linkage disequilibrium (LD) within DHL, and linkage phase similarity (LPS) between pairs of DHL on the prediction accuracy. For all scenarios, we compared the empirical prediction accuracies with forecasts obtained from deterministic equations developed by Daetwyler et al. (2008, 2010) and Wientjes et al. (2015).
Materials and Methods
Plant materials
We used a set of 351 DH lines derived from six flint landraces and 53 elite flint (EF) lines from the maize breeding program of the University of Hohenheim. The landraces from which the six DHL were derived, their respective abbreviation, their country of origin, and the number () of DH lines in each DHL were: Campan Galade (CG, France, = 19), Gelber Badischer (GB, Germany, = 50), Strenzfelder (SF, Germany, = 54), Rheintaler (RT, Switzerland, = 34), Satu Mare (SM, Romania, = 101), and Walliser (WA, Switzerland, = 93). The EF and DH lines used in this study represent a subset of the full panel described in a companion paper (Böhm et al. 2017), encompassing in total 460 lines, including the above-mentioned lines plus 56 further lines not considered in this study from five landraces with less than eight DH lines per landrace, as well as a set of Iodent and flint founder lines.
Field trials and recorded traits
Field trials were carried out in 2013 across four agro-ecologically diverse locations in Germany, always using a 46 × 10 α lattice design with two replications, as detailed by Böhm et al. (2017). Briefly, they recorded 16 traits for per se performance, of which we chose for this study seven agronomically important traits reflecting vegetative plant development, disease resistance, and product quality, as well as yield. The traits were: early vigor, scored in ratings from 1 (no shoot viable) to 9 (excellent shoot vigor); female flowering, measured as the number of days from sowing until silk emergence; Fusarium ear rot resistance, scored from 1 (all ears infested) to 9 (all ears healthy); plant height, measured in centimeters from the ground to the lowest tassel branch; oil content in %, measured with nuclear magnetic resonance; protein content of seeds in %, measured with near-infrared spectroscopy; and grain yield, measured in grams per plant. Boxplots with the range of values for each trait and each landrace are shown in Figure S1.
Genotypic data
The 404 lines (351 DH lines from the six DHL plus 53 EF lines) were genotyped with the Illumina MaizeSNP50 Beadchip, which contained 56,110 SNPs (Ganal et al. 2011). A quality check was performed by removing SNPs with call frequency < 0.9, minor allele frequency < 0.025, and heterozygosity > 1%, following Riedelsheimer et al. (2012). Missing SNPs were imputed with software BEAGLE version 3.3.2 (Browning and Browning 2007), which resulted in 32,492 high-quality SNPs.
Statistical analysis
Best linear unbiased estimates (BLUEs) of all DH and EF lines were computed in two steps. First, an ordinary lattice analysis with all 460 entries from Böhm et al. (2017) was performed with the data from each location to obtain adjusted entry means and effective error mean squares (Cochran and Cox 1957). Second, a combined analysis of variance across locations was performed using the subset of 404 lines, comprising the six DHL and the EF lines. BLUEs for each genotype were calculated in the second stage using the following model:
| (1) |
where is the overall mean; is the fixed effect for population (i.e., the six DHL and the EF lines); is the fixed effect of genotype nested in population ; and are the random effects for location and the interaction of location with population , respectively; and refers to the genotype × location interaction confounded with the error of the adjusted entry means from the first stage, and was modeled to account for heterogeneity of corresponding variances across the different DHL and the EF lines. All calculations were performed with the ASReml-R package (Butler et al. 2009) using the R statistical language (R Core Team 2017).
Genetic distances, LD, and LPS
Genetic distances between genotypes were calculated using the modified Rogers’ distance (Reif et al. 2005b). Further, a neighbor-joining tree was computed with the R package “ape” (Paradis et al. 2004) and the unrooted tree was plotted with the R package “phyclust” (Chen 2011). LD was calculated as the squared correlation () between pairs of markers (Hill and Robertson 1968). The decay of LD as a function of the distance between markers was calculated separately for each DHL and EF line using a sliding window approach over a distance of 5 Mb, divided into 30 bins, following Technow et al. (2013). The width of each bin was 170 kb, and the average between all pairs of markers within this range was calculated for each bin and then averaged over the bins on all chromosomes. The LPS was calculated between pairs of populations (DHL and EF lines) using the cosine similarity measure for each marker pair (Schopp et al. 2017a), which takes a value of 1.0 if the linkage phase is identical in both populations and a value of 0.0 if the linkage phases coincide as expected at random. The same sliding window approach as for the LD was applied for the LPS.
Prediction model
We performed Genomic Best Linear Unbiased Prediction (GBLUP) by using the model
| (2) |
where is an -dimensional vector of the BLUEs obtained from the second step of the statistical analysis of the genotypes described above; is the overall mean and is a vector with 1’s; is an -dimensional vector assumed to follow , where is a variance–covariance matrix, which is described below; and is an -dimensional vector of residuals assumed to follow , where is a dimensional block diagonal matrix with each block referring to the genotypes in population (DHL or EF lines), with , and being an identity matrix (with referring to the number of genotypes from population ) and the variance of effects in population . The design matrix () assigns genotypes to the random genotype effects .
Matrix has a block structure related to pairwise combinations of populations and , with , where is the dimensional genomic relationship matrix constructed using the method of Chen et al. (2014) with the modification suggested by Schopp et al. (2017b), and and are the corresponding genotypic SD. The off-diagonal blocks () of the matrix were calculated as, where is a matrix of genotypes and their SNP markers, which is centered by the allele frequencies of the -th population, and is the frequency of the major allele at the -th locus in population , where the major allele is defined across all populations. This simplifies for the diagonal blocks () to the genomic relationship matrix obtained by method 1 of VanRaden (2008). In addition, for the EF, we performed predictions replacing by the numerator relationship matrix calculated as described by Westhues et al. (2017), using pedigree information at least up to the grandparents. The variance components and were computed from the combined analysis of adjusted entry means across all locations using Equation 1, but with the term used as a random effect and as the genomic relationship matrix. Trait heritabilities () for each population were calculated with the formula , where is the number of locations. The variance components were estimated using the ASReml-R package (Butler et al. 2009) within the R environment (R Core Team 2017). All predictions for each scenario were computed using mixed model equations implemented within R (R Core Team 2017).
Prediction scenarios
We used four different prediction scenarios using the DHL or EF lines, as well as combinations of these populations, which are summarized in Table S2. (i) The sL scenario in combination with leave-one-out cross-validation (LOOCV) was performed with each of the four largest DHL (GB, SF, SM, and WA) and the EF lines. In each population , = 50 genotypes were randomly sampled and the prediction was carried out with LOOCV. Using the two largest DHL (SM and WA), we additionally evaluated for this scenario how an increase of influences the predictions. We increased from 20 to 90 genotypes in increments of five. (ii) In the LwL scenario, we randomly sampled = 90 genotypes from one of the two largest DHL (SM and WA), which served as TS, and used all lines from one of the other five DHL or from the EF lines as the prediction set (PS) for simple validation (SV). In addition, we evaluated this scenario using one of the four libraries (GB, SF, SM, and WA) with random samples of = 50 genotypes as TS to predict each of the other three libraries. (iii) In the cLi scenario, = 50 genotypes from each of the four largest DHL (GB, SF, SM, and WA) were randomly sampled and combined in one data set to perform LOOCV. The prediction accuracy was calculated separately for the 50 genotypes of each library. (iv) In the cLe scenario, = 50 genotypes from each of the four largest DHL (GB, SF, SM, and WA) were randomly sampled and three DHL were combined to construct the TS, comprising a total of 150 genotypes. All genotypes of the fourth DHL not included in the TS were used as PS for SV, and each DHL was used once as the PS. We additionally evaluated for this scenario another combination of TS, consisting of random samples of = 19 genotypes (corresponding to the sample size of the smallest DHL, CG) from each of five of the six DHL (GB, SF, SM, WA, CG, and RT), to predict the remaining DHL or the EF lines.
In each scenario described above, we calculated the prediction accuracy (ρ) as the correlation between the BLUEs obtained from the second step of the statistical analysis and the genomic estimated breeding values obtained from Equation 2 divided by the square root of in the PS (Dekkers 2007). The sampling of the genotypes used in the various scenarios from the entire number (n) of genotypes available from each DHL was repeated 100 times and ρ averaged over all repetitions was reported. In addition, for every repetition, we estimated the SE of ρ with 500 bootstrap samples with replacement (Kadam et al. 2016) and averaged these values over the 100 repetitions.
Forecast of the prediction accuracy
The prediction accuracies for the scenarios sL and LwL were forecasted with deterministic equations originally devised by Daetwyler et al. (2008, 2010), denoted as , and Wientjes et al. (2013, 2015), denoted as . However, we used a modified version of these equations proposed by Schopp et al. (2017b) accounting for (i) inbreeding of the genotypes, because all our genotypes were pure-breeding lines, and (ii) the different proportion of polymorphic markers in the TS and PS. A further modification (multiplication by ) proposed by Lian et al. (2014) was implemented, which accounts for incomplete linkage between quantitative trait loci (QTL) and markers by assuming that the QTL position is located close to the midpoint between markers. The deterministic equation is based on population parameters and was calculated as:
| (3) |
where is the mean of the square root of the between pairs of adjacent markers; is the number of individuals in the TS; is the heritability in the PS; and is the effective number of chromosome segments calculated as (Wientjes et al. 2015), where refers for to the variance of the elements in matrix and for to the variance of the off-diagonal elements in matrix , and , where is the number of loci polymorphic in population and is the number of loci polymorphic in both and , which equals 1 in scenario sL. To calculate , the reliability of the GBLUP value for genotype within population , serving as the PS, was computed as:
| (4) |
where is a vector of genomic relationship values for this genotype with all genotypes in population , serving as the TS. The forecasted prediction accuracy was calculated as the average over genotype in population as
| . | (5) |
Data availability
All statistical analyses were carried out in the R environment (R Core Team 2017). Data for agronomic traits of the DH lines and the EF lines are available in supplemental file “FileS1.txt.” For the same genotypes, the genomic data are available in the supplemental file “FileS2.txt.” Supplemental material available at Figshare: https://doi.org/10.25386/genetics.6667481.
Results
Heritability () was generally high, with moderate variation among traits and populations (Table 1). The mean for each trait across the six DHL ranged from 0.59 for Fusarium ear rot to 0.85 for female flowering. The range in for Fusarium ear rot was larger than for the other traits, with a maximum of 0.76 for SF and a minimum of 0.22 for the EF lines. The latter were highly selected for this trait and, consequently, displayed a small genetic variance. High values were found in all DHL for female flowering and oil content except for SF and SM.
Table 1. Heritability () of seven agronomic traits for the EF lines and DHL from landraces GB, SF, SM, WA, CG, and RT.
| Landrace | ||||||||
|---|---|---|---|---|---|---|---|---|
| Trait | EF | GB | SF | SM | WA | CG | RT | Mean |
| Early vigor | 0.91 | 0.79 | 0.54 | 0.67 | 0.67 | 0.69 | 0.81 | 0.70 |
| Female flowering | 0.94 | 0.90 | 0.79 | 0.72 | 0.90 | 0.90 | 0.90 | 0.85 |
| Fusarium ear rot | 0.22 | 0.57 | 0.76 | 0.65 | 0.74 | 0.36 | 0.45 | 0.59 |
| Plant height | 0.73 | 0.72 | 0.53 | 0.85 | 0.80 | 0.73 | 0.65 | 0.71 |
| Grain yield | 0.74 | 0.75 | 0.63 | 0.75 | 0.84 | 0.87 | 0.75 | 0.76 |
| Oil content | 0.94 | 0.90 | 0.75 | 0.79 | 0.91 | 0.89 | 0.78 | 0.84 |
| Protein content | 0.79 | 0.78 | 0.70 | 0.78 | 0.78 | 0.93 | 0.80 | 0.79 |
EF, elite flint; GB, Gelber Badischer; SF, Strenzfelder; SM, Satu Mare; WA, Walliser; CG, Campan Galade; RT, Rheintaler.
For the sL scenario, the highest ρ values were observed for the EF lines, which generally exceeded ρ of the DHL, except female flowering in SF, SM, and WA, and plant height in SF (Table 2). Among the DHL, ρ was higher in WA and SM than in GB and SF for most traits, except Fusarium ear rot and plant height. Averaged across DHL, ρ showed the highest value for female flowering (0.29) and the lowest for grain yield (−0.18). The forecasted prediction accuracies and were averaged for each population because we observed only small differences across values (Table S3). In addition, the mean values for were similar to , with differences ranging between 0.01 and 0.05. The forecasted prediction accuracies were generally close to ρ for EF and SM, but exceeded ρ for GB, SF, and WA.
Table 2. Prediction accuracy (ρ ± SE) of seven agronomic traits from GP for scenario sL, obtained with GBLUP by LOOCV using = 50 sampled from the EF lines or DH lines from the landraces GB, SF, SM, and WA, as well as the means of the forecasted prediction accuracies and across traits.
| Landrace | |||||||
|---|---|---|---|---|---|---|---|
| Trait | EF (P) | EF | GB | SF | SM | WA | Mean |
| Early vigor | 0.48 ± 0.11 | 0.42 ± 0.13 | 0.15 ± 0.22 | −0.26 ± 0.12 | 0.37 ± 0.12 | 0.38 ± 0.12 | 0.16 |
| Female flowering | 0.21 ± 0.13 | 0.33 ± 0.11 | 0.01 ± 0.18 | 0.40 ± 0.12 | 0.34 ± 0.11 | 0.41 ± 0.12 | 0.29 |
| Fusarium ear rot | −0.11 ± 0.10 | 0.47 ± 0.10 | 0.26 ± 0.13 | 0.14 ± 0.15 | 0.10 ± 0.13 | −0.01 ± 0.11 | 0.12 |
| Plant height | 0.68 ± 0.09 | 0.56 ± 0.11 | −0.03 ± 0.16 | 0.57 ± 0.11 | 0.36 ± 0.11 | 0.14 ± 0.12 | 0.26 |
| Grain yield | 0.40 ± 0.14 | 0.53 ± 0.12 | −0.27 ± 0.14 | −0.53 ± 0.10 | −0.06 ± 0.14 | 0.14 ± 0.12 | −0.18 |
| Oil content | 0.54 ± 0.12 | 0.71 ± 0.07 | −0.24 ± 0.14 | 0.03 ± 0.15 | 0.48 ± 0.11 | 0.31 ± 0.12 | 0.14 |
| Protein content | 0.56 ± 0.11 | 0.74 ± 0.07 | −0.24 ± 0.12 | 0.05 ± 0.13 | 0.30 ± 0.12 | 0.52 ± 0.11 | 0.16 |
| 0.50 | 0.16 | 0.28 | 0.35 | 0.46 | |||
| 0.47 | 0.21 | 0.33 | 0.36 | 0.41 | |||
The results obtained for the EF with pedigree-Best Linear Unbiased Prediction (P) are also given. EF, elite flint; GB, Gelber Badischer; SF, Strenzfelder; SM, Satu Mare; WA, Walliser.
Increasing in scenario sL resulted in a convex curve of ρ for all traits in the two largest DHL (SM and WA) analyzed (Figure 1). As expected, the increments were biggest from = 20 to = 50, but increasing to 90 still raised ρ by around 0.11 on average for both DHL when compared to = 50. Although the trend was similar across traits, ρ differed for each trait and for each DHL. For example, the prediction of protein content using individuals from SM had the fifth highest ρ (0.41 with = 90), whereas the same trait predicted with individuals from WA had the highest ρ (0.59 with = 90). The only trait that had similar ρ between the two DHL was grain yield, which was poor in both cases.
Figure 1.
Prediction accuracy (ρ) of seven agronomic traits from genomic prediction for the scenario sL obtained with Genomic Best Linear Unbiased Prediction by leave-one-out cross-validation using increasing sample size () from doubled-haploid lines sampled from the landraces Satu Mare or Walliser.
For scenario LwL using WA and SM as the TS ( = 90), predictions showed poor results with high variation (Table 3). Among the different TS/PS combinations, SM/CG and SM/GB showed higher ρ values in the majority of traits. Averaged across DHL, when SM served as the TS, ρ ranged between 0.25 for Fusarium ear rot and −0.19 for female flowering, whereas ρ ranged between 0.13 for oil content and −0.08 for plant height when WA served as the TS. Estimates of ρ varied strongly across traits for specific combinations of TS and PS, with the highest and lowest ρ estimate observed for combinations SM/CG (0.81) and WA/EF (−0.66), respectively, for Fusarium ear rot. Forecasting by and yielded values between 0.05 and 0.10. The LwL scenario with the four largest DHL (GB, SF, SM, and WA) and = 50 also showed ρ values close to zero for all cases (Figure S2). For combinations including SM or WA as the TS, the values hardly differed from those in Table 3.
Table 3. Prediction accuracy (ρ ± SE) of seven agronomic traits from GP for scenario LwL obtained with GBLUP by SV, using the DH lines sampled from the landraces SM or WA as the TS ( = 90), and the EF lines or DH lines from other landraces as the PS, as well as the means of the forecasted prediction accuracies and across traits.
| Trait | EF | Landrace | ||||||
|---|---|---|---|---|---|---|---|---|
| GB | SF | SM | WA | CG | RT | Mean | ||
| SM | ||||||||
| Early vigor | 0.00 ± 0.12 | 0.15 ± 0.16 | −0.02 ± 0.13 | — | 0.01 ± 0.10 | −0.30 ± 0.19 | −0.04 ± 0.18 | −0.04 |
| Female flowering | 0.24 ± 0.14 | −0.14 ± 0.13 | −0.36 ± 0.11 | — | −0.08 ± 0.11 | −0.28 ± 0.19 | −0.09 ± 0.18 | −0.19 |
| Fusarium ear rot | 0.00 ± 0.12 | 0.16 ± 0.19 | −0.14 ± 0.15 | — | 0.15 ± 0.11 | 0.81 ± 0.24 | 0.25 ± 0.11 | 0.25 |
| Plant height | −0.16 ± 0.17 | 0.27 ± 0.12 | 0.33 ± 0.13 | — | 0.06 ± 0.10 | 0.22 ± 0.22 | 0.21 ± 0.25 | 0.22 |
| Grain yield | −0.26 ± 0.13 | 0.08 ± 0.17 | 0.16 ± 0.12 | — | −0.09 ± 0.10 | 0.23 ± 0.18 | −0.50 ± 0.14 | −0.03 |
| Oil content | −0.05 ± 0.11 | 0.13 ± 0.14 | 0.10 ± 0.14 | — | 0.12 ± 0.10 | 0.48 ± 0.26 | −0.44 ± 0.15 | 0.08 |
| Protein content | 0.08 ± 0.13 | −0.25 ± 0.15 | 0.21 ± 0.13 | — | −0.27 ± 0.10 | −0.18 ± 0.22 | −0.05 ± 0.19 | −0.11 |
| 0.09 | 0.07 | 0.06 | — | 0.06 | 0.06 | 0.04 | ||
| 0.09 | 0.06 | 0.05 | — | 0.06 | 0.06 | 0.05 | ||
| WA | ||||||||
| Early vigor | 0.41 ± 0.10 | −0.13 ± 0.14 | 0.24 ± 0.12 | −0.06 ± 0.09 | — | 0.10 ± 0.24 | −0.24 ± 0.17 | −0.02 |
| Female flowering | −0.16 ± 0.13 | 0.03 ± 0.16 | 0.12 ± 0.15 | −0.03 ± 0.09 | — | 0.18 ± 0.25 | 0.23 ± 0.15 | 0.11 |
| Fusarium ear rot | −0.67 ± 0.09 | 0.19 ± 0.10 | −0.14 ± 0.13 | 0.11 ± 0.08 | — | −0.11 ± 0.20 | 0.01 ± 0.14 | 0.01 |
| Plant height | 0.04 ± 0.15 | 0.03 ± 0.15 | −0.07 ± 0.11 | −0.14 ± 0.11 | — | −0.05 ± 0.35 | −0.14 ± 0.16 | −0.08 |
| Grain yield | 0.02 ± 0.13 | 0.11 ± 0.14 | 0.01 ± 0.12 | −0.17 ± 0.11 | — | 0.02 ± 0.25 | 0.11 ± 0.14 | 0.02 |
| Oil content | −0.10 ± 0.16 | −0.07 ± 0.15 | 0.29 ± 0.14 | 0.26 ± 0.10 | — | 0.06 ± 0.22 | 0.09 ± 0.21 | 0.13 |
| Protein content | 0.19 ± 0.14 | 0.08 ± 0.14 | 0.03 ± 0.15 | −0.16 ± 0.09 | — | −0.18 ± 0.27 | 0.31 ± 0.17 | 0.02 |
| 0.05 | 0.07 | 0.07 | 0.10 | — | 0.06 | 0.06 | ||
| 0.06 | 0.07 | 0.07 | 0.06 | — | 0.05 | 0.07 | ||
EF, elite flint; GB, Gelber Badischer; SF, Strenzfelder; SM, Satu Mare; WA, Walliser; CG, Campan Galade; RT, Rheintaler.
By combining genotypes into a larger TS in the cLi scenario, ρ was higher than sL for all combinations of traits and DHL, except protein content for WA (Table 4). Scenario cLe, where three of the four largest DHL (GB, SF, SM, and WA) were combined with equal numbers (Ni = 50) to form the TS, yielded generally low ρ values with smaller variation than observed for scenario LwL. Likewise, no improvement in ρ values was attained by combining five of the six DHL (GB, SF, SM, WA, CG, and RT each with = 19; Table S4), indicating that scenario cLe has similarly low ρ compared to LwL.
Table 4. Prediction accuracy (ρ ± SE) of seven agronomic traits from GP for scenarios cLi and cLe obtained with GBLUP by LOOCV and by SV, respectively.
| Landrace | |||||
|---|---|---|---|---|---|
| Trait | GB | SF | SM | WA | Mean |
| cLi | |||||
| Early vigor | 0.39 ± 0.18 | 0.10 ± 0.13 | 0.45 ± 0.12 | 0.56 ± 0.11 | 0.38 |
| Female flowering | 0.13 ± 0.17 | 0.40 ± 0.12 | 0.39 ± 0.12 | 0.48 ± 0.11 | 0.35 |
| Fusarium ear rot | 0.79 ± 0.11 | 0.28 ± 0.13 | 0.24 ± 0.12 | 0.08 ± 0.12 | 0.35 |
| Plant height | 0.32 ± 0.14 | 0.86 ± 0.11 | 0.49 ± 0.10 | 0.26 ± 0.12 | 0.48 |
| Grain yield | −0.01 ± 0.15 | −0.45 ± 0.11 | 0.10 ± 0.14 | 0.26 ± 0.12 | −0.02 |
| Oil content | 0.06 ± 0.15 | 0.27 ± 0.15 | 0.59 ± 0.11 | 0.36 ± 0.12 | 0.32 |
| Protein content | 0.06 ± 0.13 | 0.21 ± 0.13 | 0.36 ± 0.13 | 0.47 ± 0.12 | 0.27 |
| cLe | |||||
| Early vigor | 0.04 ± 0.14 | 0.29 ± 0.13 | 0.09 ± 0.10 | −0.08 ± 0.11 | 0.08 |
| Female flowering | −0.24 ± 0.15 | −0.27 ± 0.12 | −0.29 ± 0.08 | −0.17 ± 0.09 | −0.24 |
| Fusarium ear rot | 0.27 ± 0.16 | 0.00 ± 0.15 | 0.14 ± 0.07 | 0.08 ± 0.11 | 0.12 |
| Plant height | 0.20 ± 0.13 | 0.23 ± 0.12 | 0.23 ± 0.10 | −0.04 ± 0.10 | 0.15 |
| Grain yield | 0.05 ± 0.15 | 0.05 ± 0.12 | 0.04 ± 0.11 | 0.15 ± 0.10 | 0.07 |
| Oil content | 0.04 ± 0.15 | 0.24 ± 0.13 | 0.27 ± 0.10 | 0.22 ± 0.10 | 0.19 |
| Protein content | 0.03 ± 0.13 | 0.13 ± 0.13 | −0.15 ± 0.09 | −0.01 ± 0.11 | 0.00 |
The combined libraries comprised = 50 doubled-haploid lines from each of four landraces (cLi) or three landraces (cLe); ρ was calculated separately for each doubled-haploid library. GB, Gelber Badischer; SF, Strenzfelder; SM, Satu Mare; WA, Walliser.
Discussion
GP with DHL from landraces of allogamous crops
The fundamental idea behind GBLUP, namely replacement of the relationship matrix in the Best Linear Unbiased Prediction (BLUP) approach of Henderson (1985) by a marker-based relationship matrix, was initially put forward by Bernardo (1994) for the prediction of hybrid performance. GP in the present form was originally proposed for cattle breeding (Meuwissen et al. 2001) and was rapidly adopted by plant breeders (Jannink et al. 2010; Albrecht et al. 2011; de los Campos et al. 2013; Crossa et al. 2017). However, constraints in TS size and specific population structure often pose difficulties for GP in plant breeding compared to animal breeding (Hickey et al. 2017). Apart from and , the LD and actual relationships between genotypes in the TS and PS have a profound influence on the magnitude and variation of the prediction accuracy (Habier et al. 2007; Schopp et al. 2017a).
GP in plant breeding has been found to be most promising within biparental families because all genotypes are related, and GP can exploit the Mendelian sampling variance by cosegregation of markers and linked QTL (Habier et al. 2007, 2013; Riedelsheimer et al. 2013; Crossa et al. 2014; Schopp et al. 2017a,b). For the same values of and , estimates of ρ for the DHL in our study were considerably lower than ρ reported in the literature for biparental families (Riedelsheimer et al. 2013; Lehermeier et al. 2014; Lian et al. 2014). This discrepancy is attributable to the fact that DHL of landraces of allogamous crops differ fundamentally from these types of populations in two ways. First, landraces are expected to display a much lower level of LD due to the hundreds of panmictic generations during their evolution (Mayer et al. 2017). Random mating is expected to reduce LD in each generation (Falconer and Mackay 1996), provided the population size is sufficiently large (Hill and Robertson 1968). Second, the genotypes in a DHL have a very shallow pedigree relationship if a sufficiently large effective population size was employed in the collection and afterward in the maintenance of the accessions. Thus, the probability that two genotypes have a common ancestor in recent generations is extremely small unless two DH lines originated from the same S0 plant used for in vivo haploid induction. With the low success rate of DH production from landraces (Melchinger et al. 2017), this is expected to occur rarely. We found no evidence for such an event in all six landraces based on the boxplots of modified Rogers’ distances between pairs of DH lines (Figure S3), because all observations exceeded half of the mean value.
There is also a fundamental difference between GP in landraces of allogamous and autogamous species due to their population structure. Accessions of autogamous crops generally consist of a single line, or a bulk of closely related lines with little genetic variation within and much variation among landraces (Dreisigacker et al. 2005); for this reason, prediction accuracy across landraces is of primary interest. In addition, autogamous species show high LD due to limited recombination during selfing generations and moderately high relatedness between landraces (Cavanagh et al. 2013; Daetwyler et al. 2014). This explains the high prediction accuracy observed for GP across landraces in wheat (Crossa et al. 2016) and sorghum (Yu et al. 2016). In contrast, most of the genetic variation of allogamous crops is within and not among accessions, as applies to the six DHL in our study (Böhm et al. 2017; Melchinger et al. 2017). For this reason, GP is mainly concerned with prediction within landraces.
Prediction accuracy within DHL from landraces and EF lines
Among the DHL, ρ values obtained for scenario sL with = 50 were moderate for SM and WA, and generally low for GB and SF, with both positive and negative estimates of ρ for individual traits (Table 2). This corresponds to the ranking of the four DHL for LD, showing a high level in WA and SM, and a rapid decay of LD in GB and SF (Figure 2A). A low-level and steep decay of LD goes along with a high effective number of chromosome segments, which reduces ρ based on theoretical expectations (Daetwyler et al. 2008, 2010). This suggests that LD is a major factor influencing the prediction accuracy within landraces besides , the genetic architecture of the trait, and the size of the TS.
Figure 2.
(A) Linkage disequilibrium (LD) and (B) cluster analysis based on modified Rogers’ distance for each doubled-haploid line from landraces GB (Gelber Badischer), SF (Strenzfelder), SM (Satu Mare), WA (Walliser), CG (Campan Galade), and RT (Rheintaler), as well as the elite flint (EF) lines.
The prediction accuracy for most traits was higher in the EF than in the DHL GB, SF, SM, and WA (Table 2). Although EF and WA display similar levels of LD and LD decay (Figure 2A), prediction within EF yielded larger ρ than within WA. This difference is likely due to closer pedigree relationship between some EF lines (Figure S3 and Figure S5). This hypothesis is supported by only slightly higher ρ values for GBLUP than for pedigree-BLUP obtained in EF (Table 2). Thus, in addition to LD, additive genetic relationships contributed to GP for EF.
The results for GB and SF suggest that GP is not promising for DHL with low levels of LD and a sample size of = 50 genotypes (Table 2). However, even with higher LD in WA and SM, the ρ values for = 50 were close to zero for several traits. Increasing in these two DHL from 50 to 90 improved the ρ values by 51% on average (Figure 1), but for grain yield and Fusarium ear rot, ρ was still far too low to be of practical benefit. Further research is required to assess the ρ values with larger sample sizes, because with = 90 we did not observe a plateau of the prediction accuracy curve with increasing TS size.
The population structure of landraces closely resembles that of synthetics produced by intermating a large number of parental components, especially if several generations of recombination were applied prior to selection. In an empirical study with synthetic populations of alfalfa (Medicago sativa L.), ρ values were ∼0.30 for = 125 (Annicchiarico et al. 2015). In a simulation study by Müller et al. (2017), with synthetics from 16 parental lines and five cycles of recombination prior to construction of the TS, ρ values ranged between 0.20 and 0.40, depending on the ancestral LD. Moreover, the contribution of pedigree relationships to ρ was drastically reduced with additional recombination cycles, whereas the contribution of LD remained constant. Altogether, these results further corroborate that LD is the driving force for GP in DHL from landraces.
Variation in the prediction accuracy among traits
Averaged across the four DHL, there was considerable variation in ρ among traits (Table 2). Such variation was also observed among segregating biparental populations in experiments with maize (Lehermeier et al. 2014; Lian et al. 2014) and in simulations (Schopp et al. 2017b). A possible explanation is that each trait has a different genetic architecture, so that covariances among individuals estimated by genome-wide markers may not equally well reflect the conditions at the underlying QTL. We also observed a large SE of ρ under small sample size ( = 50) for scenario sL (Table 2). This seems to be a shortcoming of LOOCV in comparison with ordinary K-fold cross-validation, as demonstrated for the DHL SM (Figure S6).
The large number of low, and sometimes even negative, ρ values for grain yield and other traits in GB and SF could also be attributed to the high genetic load in these DHL, as suggested by the low success rate of DH production in these landraces compared with SM and WA. While the DH production has a positive effect on purging landraces from their genetic load (Strigens et al. 2013; Melchinger et al. 2017), it seems likely that many detrimental alleles still escaped complete elimination, as reflected by the poor seed set in these materials (Böhm et al. 2017). Such alleles are largely missed by GBLUP because they occur at low frequency and are not likely to be tagged by SNP arrays designed for elite material. Detrimental alleles can also negatively interact with the genetic background and the GBLUP model is not efficient in accounting for epistatic effects (Jiang and Reif 2015; Martini et al. 2017).
GP between DHL from landraces
GP between populations was first investigated in animal breeding, where it showed much lower accuracy compared to GP within populations (Hayes et al. 2009; Toosi et al. 2010; Kachman et al. 2013). As shown by simulations (Schopp et al. 2017a) and empirical results in maize (Riedelsheimer et al. 2013), ρ values for GP between biparental families were ∼60% lower for unrelated families compared with the estimates of ρ for GP within full-sib families. Although GBLUP benefits mainly from the relatedness among genotypes, the LD between QTL and markers can also contribute to prediction accuracy for scenario LwL (Habier et al. 2013; Schopp et al. 2017a). However, similar to the studies in animal breeding, we obtained ρ values close to zero in this scenario, either using SM or WA with = 90 (Table 3), or GB, SF, SM, or WA with = 50 (Figure S2) as the TS and a different DHL as the PS.
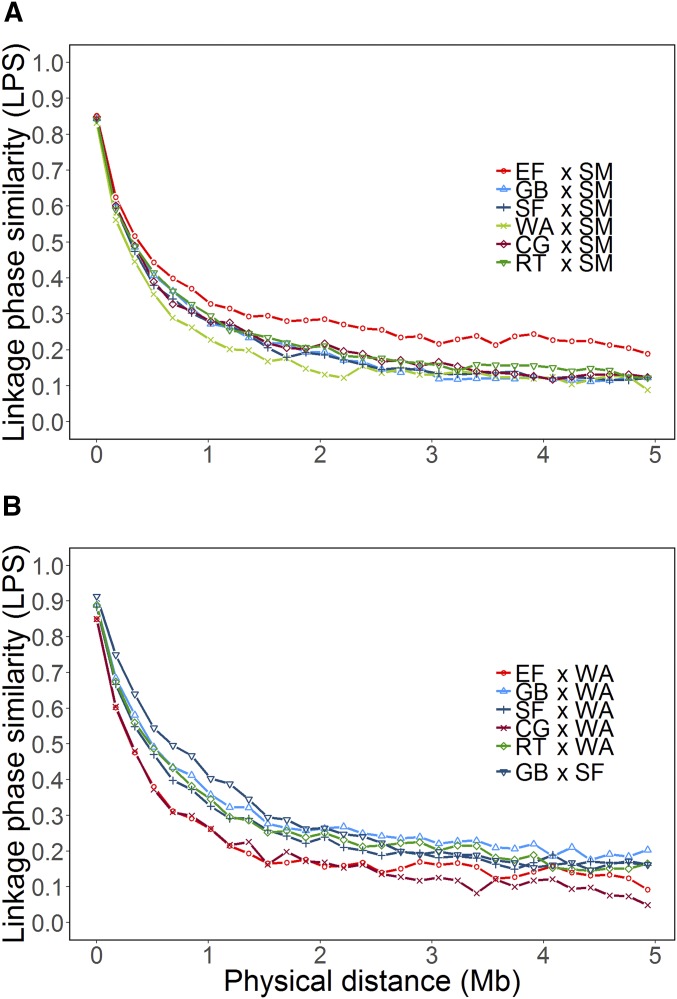
A possible explanation for the low ρ values in scenario LwL is that many QTL, which segregate in the PS, do not segregate in the DHL serving as the TS. Thus, the effects of those genomic regions of the PS cannot be properly predicted from the TS, which gives poor ρ, as demonstrated for biparental families by Schopp et al. (2017b). A further reason is the difference in allele substitution effects of markers between two DHL (Lehermeier et al. 2015; Han et al. 2018). The low persistency of LD pattern between landraces, as reflected by the low level of LPS (Figure 3, A and B), particularly outside the centromeric regions (data not shown), is an indication of such differences in estimated marker effects. However, no pattern could be recognized between the LPS of pairwise combinations of DHL and the observed ρ because means of ρ were quite low, and there was a large variation of ρ for different combinations of TS/PS and traits (Table 3). In predictions across unrelated biparental families (Schopp et al. 2017b), the LPS was only loosely correlated with the prediction accuracy, whereas the parameter , referring to the proportion of polymorphic markers between two DHL, was much more important. However, in our study, we observed no association between (Figure S4) and ρ.
Figure 3.
Linkage phase similarity (LPS) of pairwise combinations of doubled-haploid (DH) lines (A) from SM (Satu Mare) with the elite flint (EF) lines, as well as all other DH lines from landraces GB (Gelber Badischer), SF (Strenzfelder), SM, WA (Walliser), CG (Campan Galade), and RT (Rheintaler); (B) from WA with the EF lines as well as DH lines from landraces CG, GB, RT, and SF, and from GB with DH lines from landrace SF.
GP combining DHL of landraces
By combining multiple landraces in scenario cLi, ρ was on average 0.17 higher than for scenario sL (Table 4). This is in agreement with the literature, in which the combination of multiple populations yielded higher accuracies (Hayes et al. 2009; Schulz-Streeck et al. 2012; Chen et al. 2014; Iheshiulor et al. 2016). Therefore, predictions in scenario cLi benefited from the larger TS compared to scenario sL. Interestingly, accounting for population structure (cf. Figure 2B) by including fixed effects for the different DHL in Equation 2 had a negative impact on ρ for scenario cLi (data not shown), as also reported in other studies with multiple populations (Daetwyler et al. 2012; Crossa et al. 2016). Hence, differences between populations, which may lead to false positives in genome-wide association studies, can be exploited beneficially in GP.
Scenario cLe ( = 150), where the DHL in the TS did not include the DHL serving as the PS, showed similarly low ρ values as scenario LwL (Table 4). This result is similar to GP when combining unrelated biparental families, which yielded ρ values close to zero or even negative values although the TS size was increased (Riedelsheimer et al. 2013; Würschum et al. 2017). Further research is warranted to investigate under which circumstances inclusion of DH lines from another landrace will improve the prediction accuracy in a combined TS.
Forecasting prediction accuracy with deterministic formulas
Forecasting ρ by modifications of the methods of Daetwyler et al. (2008) and Wientjes et al. (2015) yielded for scenario sL a similar ranking of the four DHL for the and values as for the empirical ρ values averaged over traits (Table 1). However, the forecasted values were much higher than the empirical ones, particularly for GB and SF. This most likely reflects a violation of the assumptions used in the derivation of the formulas, such as (i) high LD between QTL and markers (Wientjes et al. 2015) and (ii) additive gene action at the QTL. Assumption (i) was relaxed by multiplication with (Lian et al. 2014), which accounts for incomplete linkage between QTL and markers. Assumption (ii) would not hold true if detrimental alleles have negative epistatic effects in the DHL, as discussed above. Further, if allele frequencies of SNPs and QTL are different, this can lead to a substantial bias in and (Schopp et al. 2017b). The latter problem most likely applies to our study, because we used a SNP array optimized for temperate and tropical dent germplasm (Ganal et al. 2011) that is prone to ascertainment bias in flint materials (Frascaroli et al. 2013). Obviously, the consequences are more severe if GP relies predominantly on exploiting LD, but are only weak if additive genetic relationships are the driving force of GP, as was the case in the EF. Calculating and as well as LD might also provide clues about the minimum TS size required to achieve the desired size of ρ.
Use of landraces in breeding programs
With DHL, the genetic diversity among gametes within landraces can be conserved in the form of “immortalized” genotypes. Nevertheless, DH production from landraces is still laborious and expensive, and the success rate is unpredictable (Melchinger et al. 2017). Therefore, it is crucial to screen a large number of accessions for their agronomic performance in line per se and testcross trials (Böhm et al. 2014, 2017), and test their suitability for DH production before embarking on the production of DHL from landraces and the application of GP.
To balance the expenditures for GP in DHL with the gains expected for genomic selection, a large enough DHL must be constructed, which is justified only in combination with an equally large PS to compensate for the high investments (Riedelsheimer and Melchinger 2013). Thus, a high selection intensity on the line per se performance of the DH lines would be possible, while retaining a sufficient number of genotypes for subsequent evaluation of their testcross performance, before channeling the most promising lines into prebreeding programs. Alternatively, a few (∼10) of the highest-performing DH lines could be selected and intercrossed to conduct a genomic recurrent selection program. However, choosing a small number of lines is expected to generate new sample LD (Schopp et al. 2017a), which may invalidate the prediction model established with the DHL.
In contrast to the development of DHL, harboring the genome of gametes from a landrace in pure form, one might apply “gamete selection” (Stadler 1944). In this method, the landrace serves as pollinator of an elite line, and selection is carried out in selfing or backcross generations derived from the cross. GP could benefit this method, as shown in simulations (Gorjanc et al. 2016). In particular, it might be of interest to evaluate application of the prediction model established by our approach to crosses of the original landrace with an elite inbred.
Conclusions
DH lines from landraces of allogamous crops are highly diverse and virtually unrelated by pedigree. Consequently, LD is the main source of quantitative genetic information exploitable for prediction. Owing to the rapid decay of LD, high-density genome-wide markers and large TS sizes are required for the successful implementation of GP in such populations. Based on the trends for ρ in the two largest DHL (SM and WA), we speculate that a minimum TS size of > 100 DH lines per landrace is required to reach a decent prediction accuracy, but this warrants further research. GP across DHL failed, if the DHL to be predicted was not represented in the TS (scenarios LwL and cLe). However, if several smaller DHL plus genotypes from the DHL to be predicted were included in the TS (scenario cLi), this yield improved and more stable results were obtained than for GP within the DHL alone (scenario sL). Altogether, the DH technology combined with GP offers a powerful approach to exploit the idle genetic diversity within landraces, but substantial investments are needed to mine this “gold reserve” for future breeding.
Acknowledgments
We thank Willem Molenaar and Tobias Schrag for valuable suggestions to improve the manuscript; the technical staff from the University of Hohenheim for excellence in conducting the field experiments; and KWS SAAT SE in Einbeck for the additional field experiment, as well as T. Presterl and T. Bolduan for conducting it. This research was funded by the German Federal Ministry of Education and Research (Bundesministerium für Bildung und Forschung) within the scope of the funding initiatives AgroClustEr “Synbreed-Synergistic plant and animal breeding” (project number: 0315528D) and MAZE “Plant Breeding Research for the Bioeconomy” (funding identifier: 031B0195).
Footnotes
Supplemental material available at Figshare: https://doi.org/10.25386/genetics.6667481.
Communicating editor: F. van Eeuwijk
Literature Cited
- Albrecht T., Wimmer V., Auinger H. J., Erbe M., Knaak C., et al. , 2011. Genome-based prediction of testcross values in maize. Theor. Appl. Genet. 123: 339–350. 10.1007/s00122-011-1587-7 [DOI] [PubMed] [Google Scholar]
- Annicchiarico P., Nazzicari N., Li X., Wei Y., Pecetti L., et al. , 2015. Accuracy of genomic selection for alfalfa biomass yield in different reference populations. BMC Genomics 16: 1020 10.1186/s12864-015-2212-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernardo R., 1994. Prediction of maize single-cross performance using RFLPs and information from related hybrids. Crop Sci. 34: 20–25. 10.2135/cropsci1994.0011183X003400010003x [DOI] [Google Scholar]
- Böhm J., Schipprack W., Mirdita V., Utz H. F., Melchinger A. E., 2014. Breeding potential of European flint maize landraces evaluated by their testcross performance. Crop Sci. 54: 1665 10.2135/cropsci2013.12.0837 [DOI] [Google Scholar]
- Böhm J., Schipprack W., Utz H. F., Melchinger A. E., 2017. Tapping the genetic diversity of landraces in allogamous crops with doubled haploid lines: a case study from European flint maize. Theor. Appl. Genet. 130: 861–873. 10.1007/s00122-017-2856-x [DOI] [PubMed] [Google Scholar]
- Browning S. R., Browning B. L., 2007. Rapid and accurate haplotype phasing and missing-data inference for whole-genome association studies by use of localized haplotype clustering. Am. J. Hum. Genet. 81: 1084–1097. 10.1086/521987 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butler D. G., Cullis B. R., Gilmour A. R., Gogel B. J., 2009. Mixed models for S language environments. ASReml-R reference manual: release 3.0. technical report. ASReml estimates variance components under a general linear mixed model by residual maximum likelihood (REML).
- Cavanagh C. R., Chao S., Wang S., Huang B. E., Stephen S., et al. , 2013. Genome-wide comparative diversity uncovers multiple targets of selection for improvement in hexaploid wheat landraces and cultivars. Proc. Natl. Acad. Sci. USA 110: 8057–8062. 10.1073/pnas.1217133110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen L., Vinsky M., Li C., 2014. Accuracy of predicting genomic breeding values for carcass merit traits in Angus and Charolais beef cattle. Anim. Genet. 46: 55–59. 10.1111/age.12238 [DOI] [PubMed] [Google Scholar]
- Chen, W.-C., 2011 Overlapping codon model, phylogenetic clustering, and alternative partial expectation conditional maximization algorithm, Ph.D. Thesis, Iowa State University, Ames, IA. [Google Scholar]
- Cochran W. G., Cox G. M., 1957. Experimental Designs, Ed. 2 Wiley, London. [Google Scholar]
- Crossa J., Pérez P., Hickey J., Burgueño J., Ornella L., et al. , 2014. Genomic prediction in CIMMYT maize and wheat breeding programs. Heredity (Edinb) 112: 48–60. 10.1038/hdy.2013.16 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crossa J., Jarquín D., Franco J., Pérez-Rodríguez P., Burgueño J., et al. , 2016. Genomic prediction of gene bank wheat landraces. G3 (Bethesda) 6: 1819–1834. 10.1534/g3.116.029637 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crossa J., Pérez-Rodríguez P., Cuevas J., Montesinos-López O., Jarquín D., et al. , 2017. Genomic selection in plant breeding: methods, models, and perspectives. Trends Plant Sci. 22: 961–975. 10.1016/j.tplants.2017.08.011 [DOI] [PubMed] [Google Scholar]
- Daetwyler H. D., Villanueva B., Woolliams J. A., 2008. Accuracy of predicting the genetic risk of disease using a genome-wide approach. PLoS One 3: e3395 10.1371/journal.pone.0003395 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daetwyler H. D., Pong-Wong R., Villanueva B., Woolliams J. A., 2010. The impact of genetic architecture on genome-wide evaluation methods. Genetics 185: 1021–1031. 10.1534/genetics.110.116855 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daetwyler H. D., Kemper K. E., van der Werf J. H. J., Hayes B. J., 2012. Components of the accuracy of genomic prediction in a multi-breed sheep population1. J. Anim. Sci. 90: 3375–3384. 10.2527/jas.2011-4557 [DOI] [PubMed] [Google Scholar]
- Daetwyler H. D., Bansal U. K., Bariana H. S., Hayden M. J., Hayes B. J., 2014. Genomic prediction for rust resistance in diverse wheat landraces. Theor. Appl. Genet. 127: 1795–1803. 10.1007/s00122-014-2341-8 [DOI] [PubMed] [Google Scholar]
- de los Campos G., Vazquez A. I., Fernando R., Klimentidis Y. C., Sorensen D., 2013. Prediction of complex human traits using the genomic best linear unbiased predictor. PLoS Genet. 9: e1003608 10.1371/journal.pgen.1003608 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dekkers J. C. M., 2007. Marker-assisted selection for commercial crossbred performance. J. Anim. Sci. 85: 2104–2114. 10.2527/jas.2006-683 [DOI] [PubMed] [Google Scholar]
- Dreisigacker S., Zhang P., Warburton M. L., Skovmand B., Hoisington D., et al. , 2005. Genetic diversity among and within CIMMYT wheat landrace accessions investigated with SSRs and implications for plant genetic resources management. Crop Sci. 45: 653–661. 10.2135/cropsci2005.0653 [DOI] [Google Scholar]
- Falconer D. S., Mackay T. F. C., 1996. Introduction to Quantitative Genetics, Ed. 4 Pearson, London. [Google Scholar]
- Frascaroli E., Schrag T. A., Melchinger A. E., 2013. Genetic diversity analysis of elite European maize (Zea mays L.) inbred lines using AFLP, SSR, and SNP markers reveals ascertainment bias for a subset of SNPs. Theor. Appl. Genet. 126: 133–141. 10.1007/s00122-012-1968-6 [DOI] [PubMed] [Google Scholar]
- Ganal M. W., Durstewitz G., Polley A., Bérard A., Buckler E. S., et al. , 2011. A large maize (Zea mays L.) SNP genotyping array: development and germplasm genotyping, and genetic mapping to compare with the B73 reference genome. PLoS One 6: e28334 10.1371/journal.pone.0028334 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gorjanc G., Jenko J., Hearne S. J., Hickey J. M., 2016. Initiating maize pre-breeding programs using genomic selection to harness polygenic variation from landrace populations. BMC Genomics 17: 30 10.1186/s12864-015-2345-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greene S. L., Kisha T. J., Yu L.-X., Parra-Quijano M., 2014. Conserving plants in gene banks and nature: investigating complementarity with Trifolium thompsonii Morton. PLoS One 9: e105145 10.1371/journal.pone.0105145 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Habier D., Fernando R. L., Dekkers J. C. M., 2007. The impact of genetic relationship information on genome-assisted breeding values. Genetics 177: 2389–2397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Habier D., Fernando R. L., Garrick D. J., 2013. Genomic BLUP decoded: a look into the black box of genomic prediction. Genetics 194: 597–607. 10.1534/genetics.113.152207 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han S., Miedaner T., Utz H. F., Schipprack W., Schrag T. A., et al. , 2018. Genomic prediction and GWAS of Gibberella ear rot resistance traits in dent and flint lines of a public maize breeding program. Euphytica 214: 6 10.1007/s10681-017-2090-2 [DOI] [Google Scholar]
- Hayes B. J., Bowman P. J., Chamberlain A. C., Verbyla K., Goddard M. E., 2009. Accuracy of genomic breeding values in multi-breed dairy cattle populations. Genet. Sel. Evol. 41: 51 10.1186/1297-9686-41-51 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henderson C. R., 1985. Best linear unbiased prediction of nonadditive genetic merits in noninbred populations. J. Anim. Sci. 60: 111–117. 10.2527/jas1985.601111x [DOI] [Google Scholar]
- Hickey J. M., Chiurugwi T., Mackay I., Powell W., Hickey J. M., et al. , 2017. Genomic prediction unifies animal and plant breeding programs to form platforms for biological discovery. Nat. Genet. 49: 1297–1303. 10.1038/ng.3920 [DOI] [PubMed] [Google Scholar]
- Hill W. G., Robertson A., 1968. Linkage disequilibrium in finite populations. Theor. Appl. Genet. 38: 226–231. 10.1007/BF01245622 [DOI] [PubMed] [Google Scholar]
- Iheshiulor O. O. M., Woolliams J. A., Yu X., Wellmann R., Meuwissen T. H. E., 2016. Within- and across-breed genomic prediction using whole-genome sequence and single nucleotide polymorphism panels. Genet. Sel. Evol. 48: 15 10.1186/s12711-016-0193-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jannink J.-L., Lorenz A. J., Iwata H., 2010. Genomic selection in plant breeding: from theory to practice. Brief. Funct. Genomics 9: 166–177. 10.1093/bfgp/elq001 [DOI] [PubMed] [Google Scholar]
- Jiang Y., Reif J. C., 2015. Modeling epistasis in genomic selection. Genetics 201: 759–768. 10.1534/genetics.115.177907 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kachman S. D., Spangler M. L., Bennett G. L., Hanford K. J., Kuehn L. A., et al. , 2013. Comparison of molecular breeding values based on within- and across-breed training in beef cattle. Genet. Sel. Evol. 45: 30 10.1186/1297-9686-45-30 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kadam D. C., Potts S. M., Bohn M. O., Lipka A. E., Lorenz A. J., 2016. Genomic prediction of single crosses in the early stages of a maize hybrid breeding pipeline. G3(Bethesda) 6: 3443–3453 [corrigenda: G3 (Bethesda) 7: 3557–3558 (2017)]. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lehermeier C., Krämer N., Bauer E., Bauland C., Camisan C., et al. , 2014. Usefulness of multiparental populations of maize (Zea mays L.) for genome-based prediction. Genetics 198: 3–16. 10.1534/genetics.114.161943 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lehermeier C., Schon C.-C., de los Campos G., 2015. Assessment of genetic heterogeneity in structured plant populations using multivariate whole-genome regression models. Genetics 201: 323–337. 10.1534/genetics.115.177394 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lian L., Jacobson A., Zhong S., Bernardo R., 2014. Genomewide prediction accuracy within 969 maize biparental populations. Crop Sci. 54: 1514 10.2135/cropsci2013.12.0856 [DOI] [Google Scholar]
- Martini J. W. R., Gao N., Cardoso D. F., Wimmer V., Erbe M., et al. , 2017. Genomic prediction with epistasis models: on the marker-coding-dependent performance of the extended GBLUP and properties of the categorical epistasis model (CE). BMC Bioinformatics 18: 3 10.1186/s12859-016-1439-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mayer M., Unterseer S., Bauer E., de Leon N., Ordas B., et al. , 2017. Is there an optimum level of diversity in utilization of genetic resources? Theor. Appl. Genet. 130: 2283–2295. 10.1007/s00122-017-2959-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Melchinger A. E., Schopp P., Müller D., Schrag T. A., Bauer E., et al. , 2017. Safeguarding our genetic resources with libraries of doubled-haploid lines. Genetics 206: 1611–1619. 10.1534/genetics.115.186205 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Messmer M. M., Melchinger A. E., Boppenmaier J., Brunklaus-Jung E., Herrmann R. G., 1992. Relationships among early European maize inbreds: I. genetic diversity among flint and dent lines revealed by RFLPs. Crop Sci. 32: 1301 10.2135/cropsci1992.0011183X003200060001x [DOI] [PubMed] [Google Scholar]
- Meuwissen T. H. E., Hayes B. J., Goddard M. E., 2001. Prediction of total genetic value using genome-wide dense marker maps. Genetics 157: 1819–1829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monteiro F., Vidigal P., Barros A. B., Monteiro A., Oliveira H. R., et al. , 2016. Genetic distinctiveness of rye in situ accessions from Portugal unveils a new hotspot of unexplored genetic resources. Front. Plant Sci. 7: 1–17. 10.3389/fpls.2016.01334 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Müller D., Schopp P., Melchinger A. E., 2017. Persistency of prediction accuracy and genetic gain in synthetic populations under recurrent genomic selection. G3 (Bethesda) 7: 801–811. 10.1534/g3.116.036582 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paradis E., Claude J., Strimmer K., 2004. APE: analyses of phylogenetics and evolution in r language. Bioinformatics 20: 289–290. 10.1093/bioinformatics/btg412 [DOI] [PubMed] [Google Scholar]
- Poehlman J. M., 1987. Breeding Field Crops. AVI publishing Co., Westport, CT: 10.1007/978-94-015-7271-2 [DOI] [Google Scholar]
- Pryce J. E., Gredler B., Bolormaa S., Bowman P. J., Egger-Danner C., et al. , 2011. Short communication: genomic selection using a multi-breed, across-country reference population. J. Dairy Sci. 94: 2625–2630. 10.3168/jds.2010-3719 [DOI] [PubMed] [Google Scholar]
- R Core Team , 2017. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna. [Google Scholar]
- Reif J. C., Hamrit S., Heckenberger M., Schipprack W., Maurer H. P., et al. , 2005a. Genetic structure and diversity of European flint maize populations determined with SSR analyses of individuals and bulks. Theor. Appl. Genet. 111: 906–913. 10.1007/s00122-005-0016-1 [DOI] [PubMed] [Google Scholar]
- Reif J. C., Melchinger A. E., Frisch M., 2005b. Genetical and mathematical properties of similarity and dissimilarity coefficients applied in plant breeding and seed bank management. Crop Sci. 45: 1 10.2135/cropsci2005.0001 [DOI] [Google Scholar]
- Riedelsheimer C., Melchinger A. E., 2013. Optimizing the allocation of resources for genomic selection in one breeding cycle. Theor. Appl. Genet. 126: 2835–2848. 10.1007/s00122-013-2175-9 [DOI] [PubMed] [Google Scholar]
- Riedelsheimer C., Technow F., Melchinger A. E., 2012. Comparison of whole-genome prediction models for traits with contrasting genetic architecture in a diversity panel of maize inbred lines. BMC Genomics 13: 452 10.1186/1471-2164-13-452 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riedelsheimer C., Endelman J. B., Stange M., Sorrells M. E., Jannink J.-L., et al. , 2013. Genomic predictability of interconnected biparental maize populations. Genetics 194: 493–503. 10.1534/genetics.113.150227 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salhuana W., Pollak L., 2006. Latin American maize project (LAMP) and germplasm enhancement of maize (GEM) project: generating useful breeding germplasm. Maydica 51: 339–355. [Google Scholar]
- Schopp P., Müller D., Technow F., Melchinger A. E., 2017a. Accuracy of genomic prediction in synthetic populations depending on the number of parents, relatedness, and ancestral linkage disequilibrium. Genetics 205: 441–454. 10.1534/genetics.116.193243 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schopp P., Müller D., Wientjes Y. C. J., Melchinger A. E., 2017b. Genomic prediction within and across biparental families: means and variances of prediction accuracy and usefulness of deterministic equations. G3 (Bethesda) 7: 3571–3586. 10.1534/g3.117.300076 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schulz-Streeck T., Ogutu J. O., Karaman Z., Knaak C., Piepho H. P., 2012. Genomic selection using multiple populations. Crop Sci. 52: 2453–2461. 10.2135/cropsci2012.03.0160 [DOI] [Google Scholar]
- Stadler L. J., 1944. Gamete selection in corn breeding. J. Am. Soc. Agron. 36: 988–989. [Google Scholar]
- Strigens A., Schipprack W., Reif J. C., Melchinger A. E., 2013. Unlocking the genetic diversity of maize landraces with doubled haploids opens new avenues for breeding. PLoS One 8: e57234 10.1371/journal.pone.0057234 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Technow F., Bürger A., Melchinger A. E., 2013. Genomic prediction of northern corn leaf blight resistance in maize with combined or separated training sets for heterotic groups. G3 (Bethesda) 3: 197–203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Toosi A., Fernando R. L., Dekkers J. C. M., 2010. Genomic selection in admixed and crossbred populations. J. Anim. Sci. 88: 32–46. 10.2527/jas.2009-1975 [DOI] [PubMed] [Google Scholar]
- VanRaden P. M., 2008. Efficient methods to compute genomic predictions. J. Dairy Sci. 91: 4414–4423. 10.3168/jds.2007-0980 [DOI] [PubMed] [Google Scholar]
- Warburton M. L., Reif J. R., Frisch M., Bohn M., Bedoya C., et al. , 2008. Genetic diversity in CIMMYT nontemperate maize germplasm: landraces, open pollinated varieties, and inbred lines. Crop Sci. 48: 617 10.2135/cropsci2007.02.0103 [DOI] [Google Scholar]
- Westhues M., Schrag T. A., Heuer C., Thaller G., Utz H. F., et al. , 2017. Omics-based hybrid prediction in maize. Theor. Appl. Genet. 130: 1927–1939. 10.1007/s00122-017-2934-0 [DOI] [PubMed] [Google Scholar]
- Wientjes Y., Veerkamp R. F., Bijma P., Bovenhuis H., Schrooten C., et al. , 2015. Empirical and deterministic accuracies of across-population genomic prediction. Genet. Sel. Evol. 47: 5 10.1186/s12711-014-0086-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wientjes Y. C. J., Veerkamp R. F., Calus M. P. L., 2013. The effect of linkage disequilibrium and family relationships on the reliability of genomic prediction. Genetics 193: 621–631. 10.1534/genetics.112.146290 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilde K., Burger H., Prigge V., Presterl T., Schmidt W., et al. , 2010. Testcross performance of doubled-haploid lines developed from European flint maize landraces. Plant Breed. 129: 181–185. 10.1111/j.1439-0523.2009.01677.x [DOI] [Google Scholar]
- Würschum T., Maurer H. P., Weissmann S., Hahn V., Leiser W. L., 2017. Accuracy of within- and among-family genomic prediction in triticale. Plant Breed. 136: 230–236. 10.1111/pbr.12465 [DOI] [Google Scholar]
- Yu X., Li X., Guo T., Zhu C., Wu Y., et al. , 2016. Genomic prediction contributing to a promising global strategy to turbocharge gene banks. Nat. Plants 2: 16150 10.1038/nplants.2016.150 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All statistical analyses were carried out in the R environment (R Core Team 2017). Data for agronomic traits of the DH lines and the EF lines are available in supplemental file “FileS1.txt.” For the same genotypes, the genomic data are available in the supplemental file “FileS2.txt.” Supplemental material available at Figshare: https://doi.org/10.25386/genetics.6667481.