Dynamics of breast cancer relapse reveal late recurring ER-positive genomic subgroups

Introduction

The rates and routes of lethal systemic spread in breast cancer are poorly understood due to the lack of molecularly characterized cohorts with long-term, detailed follow-up. Long-term follow-up is especially essential for ER-positive (ER+) breast cancer, where tumors continue to recur up to two decades after initial diagnosis^1–6 and there is a critical need to identify high-risk patients prior to lethal recurrence^7–9. Here we present a statistical framework to model distinct disease stages (loco-regional recurrence (LR), distant recurrence (DR) and breast cancer-related death) and competing risks of breast cancer mortality, while yielding individual risk of recurrence predictions. Application of this model to 3240 breast cancer patients, including 1980 with molecular data, delineates the spatio-temporal patterns of relapse across the immunohistochemical (IHC), intrinsic (PAM50)^10,11, and integrative (IntClust)^12,13 subtypes. We identify four late-recurring integrative subtypes, comprising a quarter (26%) of ER+, human epidermal growth factor receptor 2-negative (HER2-) tumors, each with characteristic genomic copy number driver alterations and high (median 42–55%) risk of recurrence up to 20 years post-diagnosis. Additionally, we define a subgroup of triple-negative breast cancers (TNBC) that rarely recur after 5 years and a separate subgroup that remain at risk. The integrative subtypes improve prediction of late distant relapse beyond clinical covariates (nodal status, tumor size, grade and IHC subtype). These findings illuminate opportunities for improved patient stratification and biomarker-driven clinical trials.

Main

Breast cancer is a multistate disease with clinically relevant intermediate endpoints such as LR and DR¹⁴. Critically, a patient’s prognosis can differ dramatically depending on when and where a relapse occurs, time since surgery, and time since LR or DR^15,16 These events are associated, and individual survival analyses of disease-free survival (DFS) or overall survival (OS) alone cannot fully capture patterns of recurrence associated with differential prognosis. Additionally, most survival analyses employ disease-specific death (DSD) as the primary endpoint and censor natural deaths. However, when competing risks of mortality occur, this approach induces bias¹⁷. This is particularly problematic for breast cancer, where ER+ patients experience higher mortality from non-malignant causes due to their increased age at diagnosis relative to ER− patients. We evaluated the extent of such bias on breast cancer survival estimates by analysing 3240 patients diagnosed between 1977–2005 with median 14 years clinical follow-up (referred to as the Full Dataset FD; Extended Data Fig.1, Supplementary Table 1, Methods). We compared the naïve cumulative incidence for DSD (computed as 1 – the survival probability) stratified by ER status considering only cancer-related deaths (Extended Data Fig.2a) relative to the estimates with the proper cumulative incidence functions accounting for different causes of death (Extended Data Fig.2b). These comparisons indicate that the incidence of DSD is overestimated for ER+ tumors (0.46 vs 0.37 at 20 years) due to the increased age of diagnosis (median 63.9 vs 53.0 years; p-value <1E-6) (Extended Data Fig.2c) relative to ER− tumors. Moreover, because the baseline survival functions for these subgroups are distinct, their differences cannot be adequately summarized with a single parameter in a Cox proportional hazards model.

To overcome these limitations, we developed a non-homogenous (semi) Markov chain model that accounts for different disease states (LR, DR) and timescales (time since surgery, LR or DR), as well as competing risks of mortality and distinct baseline hazards across molecular subgroups, thereby enabling individual risk of relapse predictions (Fig.1a, Methods). The model also incorporates clinical variables known to influence breast cancer survival^18,19, including age, tumor grade, tumor size and number of positive lymph nodes (all measured at diagnosis). We refer to this as the base clinical model onto which molecular subtype information can be incorporated. We fit this multistate model to the FD and recorded the hazards of moving through distinct states and the number of transitions between each pair of states (Supplementary Table 2, Methods). As expected, the majority of cancer related deaths (83% in ER+ and 87% in ER− tumors) occurred after distant metastasis. The remainder of cases likely reflect undetected recurrences or death due to other malignancies. Age at diagnosis was associated with the transition to death by other causes (p-value < 1E-6). Examination of the log hazard ratios and 95% confidence intervals for all other variables indicated that their effect decreased with disease progression (Extended Data Fig.2d). That is, clinical variables related to the primary tumor were more prognostic for earlier transitions than for later transitions. However, several tumor characteristics informed the risk of progression from LR to DR and from DR to death. In ER+ disease, higher tumor grade, number of positive lymph nodes and tumor size all increased the risk of progression to a later state. A longer time between surgery and LR or DR decreased the risk of transition to a later state and was more pronounced in ER− disease. We confirmed that our models were well calibrated, concordant with the established tool PREDICT¹⁸ and that they performed comparably in external datasets (Extended Data Fig.1, Extended Data Fig.3, Methods, Supplementary Information).

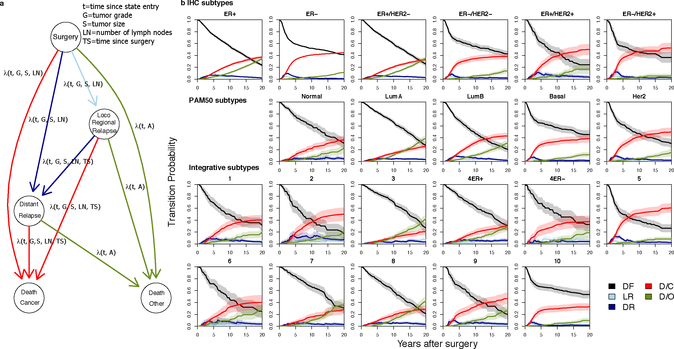
Figure 1. A multistate model of breast cancer relapse enables individual risk of relapse predictions throughout disease progression.

a. Graphical representation of the model. Nodes represent possible states and arcs possible transitions between states, where parameters that have an effect on the hazard are indicated. b. Subtype-specific risk of relapse at diagnosis. Transition probabilities from surgery to other states (DF=Disease-free, LR=Loco-regional relapse, DR=Distant relapse, D/C=Cancer specific death, D/O=Death by other causes) are shown for individual average patients across the breast cancer subtypes. Subtypes were defined based on ER status using the FD and for IHC, PAM50 and integrative (IntClust) subtypes using the MD. 95% confidence bands (shaded areas) were computed using the bootstrap (see Methods).

A powerful feature of our multistate model is that hazard rates can be transformed into transition probabilities representing the probability of moving from one state into another after a given time. To evaluate the patterns of recurrence across the established breast cancer molecular subgroups, we turned to the METABRIC molecular dataset (MD) composed of 1980 patients (Extended Data Fig.1), which includes assignments to the IHC subtypes (ER+/HER2+, ER+/HER2−, ER−/HER2+, ER−/HER2−), PAM50¹¹ expression subtypes and the genomic driver based IntClust subtypes^12,13 (Supplementary Table 3). We computed the baseline transition probabilities from surgery, LR or DR at various time intervals (2, 5, 10, 15 and 20 years) and the corresponding standard errors (SE) for average individuals in each subgroup (using the FD for comparisons by ER status and the MD for all others, Supplementary Table 4). After surgery, state transitions differed substantially across the various subtypes (Fig.1b). For example, the transition probabilities post surgery reveal different change points for ER+ versus ER− disease where ER− patients had a higher risk of DR and cancer death (D/C) in the first five years, after which their risk decreased considerably. In contrast, ER+ patients had a smaller, but longer risk period during the first ten years and this increased at a lower rate. Among ER− patients, the PAM50 Basal-like subgroup was nearly indistinguishable from the ER−/HER2− subgroup with the majority of cancer deaths in the first 5 years, similar to HER2+ patients (prior to the widespread use of trastuzumab). In contrast, the three predominantly ER− IntClust subgroups (IntClust4ER−, IntClust5 and IntClust10) exhibited substantial differences in their recurrence trajectories. As expected, IntClust5 (HER2+ enriched) generally had poor prognosis at 5 years (0.48, SE=0.04) with risk increasing to 0.65 (SE=0.04) at 20 years. For IntClust10 (Basal-like enriched), the first 5 years from surgery largely defined patient outcomes: the probability of relapse at 5 years was 0.33 (SE=0.03) and after 20 years rose to only 0.37 (SE=0.04) for an average patient. This pattern was distinct from IntClust4ER− patients who exhibited a persistent and increasing risk of relapse with a probability of 0.30 (0.05) at 5 years and 0.49 (0.05) after 20 years.

The distinction between IntClust4ER− and IntClust10 is further apparent when examining the average probabilities of relapse among all patients across the IntClust subtypes after surgery or after being disease-free for 5 and 10 years (Fig.2a). Indeed, through the course of the disease, the risk of relapse changed considerably across the integrative subtypes and to a lesser extent the IHC and PAM50 subtypes (Fig.2a, Extended Data Fig.4). Moreover, the probabilities of DR or cancer death amongst ER−/Her2− patients who were disease free at 5 years post diagnosis revealed low (IntClust10) and high (IntClust4ER-) risk of late relapse TNBC subgroups, whereas IHC (and PAM50) subtypes homogenized this risk (Extended Data Fig.5).

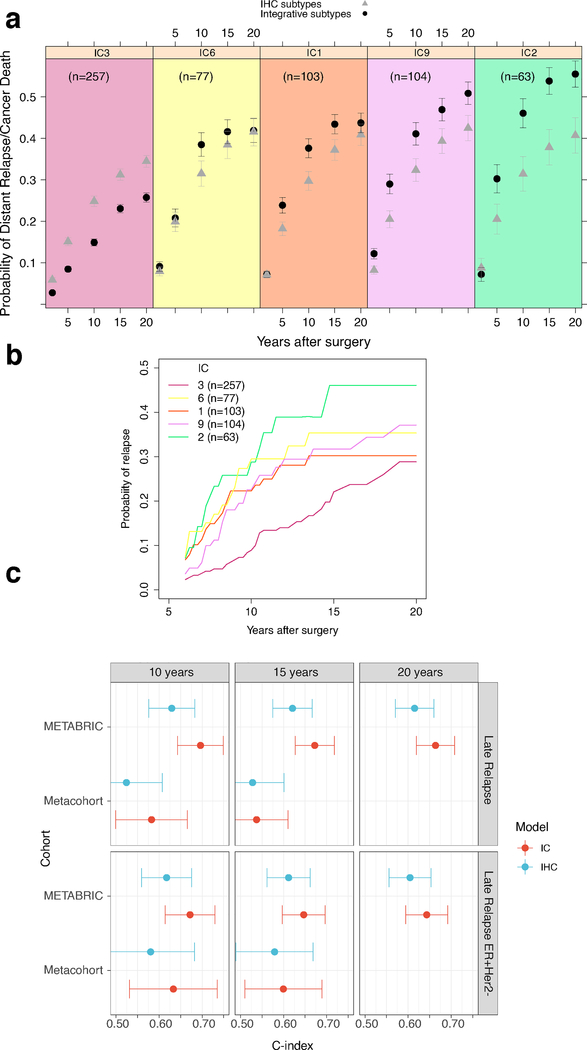
Figure 2. The integrative breast cancer subtypes exhibit distinct patterns of relapse.

a. Mean probabilities of having a relapse after surgery and after being 5 and 10 years disease-free for the patients in each of the 11 integrative (IntClust/IC) subtypes, ordered by increasing risk of relapse. IC3, IC7, IC8 and IC4ER+ represent lower risk ER+ subtypes; IC10 and IC4ER− TNBC subtypes with variable relapse patterns; IC1, IC6, IC9 and IC2 late relapsing ER+ subtypes; and IC5 HER2+ tumors prior to trastuzumab. Error bars represent 95% confidence intervals. The lower colored bar shows the prevalence of each integrative subtype in the breast cancer population. b. Frequencies of copy number amplifications in specific IntClust subtypes (IC1, IC6, IC9 and IC2). Putative driver genes indicated by an asterisk. c. Proportion of ER+ tumors that belong to the four late-relapsing IntClust subtypes. This analysis was done with the MD.

Dramatic differences were also apparent amongst ER+ patients with IntClust3, IntClust7, IntClust8 and IntClust4ER+ exhibiting better prognosis while IntClust1, IntClust2, IntClust6 and IntClust9 corresponded to late-recurring poor prognosis patients (Fig.2a). These four subgroups had exceedingly high-risk of relapse with mean probabilities ranging from 0.42 to 0.56 up to 20 years post surgery. IntClust2 exhibited the worst prognosis with a probability of relapse (0.56, SE: 0.02) second only to IntClust5. Collectively, these subgroups comprise 26% of ER+ cases (Fig.2bc) and thus define the minority of patients who may benefit from extended monitoring and treatment given the chronic nature of their disease^5,6.

Importantly, the four high-risk of relapse subgroups were enriched for characteristic genomic copy number alterations, which represent the likely drivers of each subgroup (Fig.2b). For example, IntClust2 tumors were defined by amplification and concomitant over-expression of multiple oncogenes on chromosome 11q13, including CCND1, FGF3, EMSY, PAK1 and RSF1^20–22. IntClust2 accounts for 4.5% of ER+ cases, 96% of which have RSF1 amplification, compared to 0–22% of other subgroups. IntClust6 (5.5% of ER+ tumors) are characterized by focal amplification of ZNF703²³ and FGFR1²⁴ on chromosome 8p12 (100% of IntClust6 cases vs. 2–21% of others). IntClust1 (8% of ER+ tumors) exhibited amplification of chromosome 17q23 spanning the mTOR effector, RPS6KB1 (S6K1)²⁵, which was gained or amplified in 96% and 70% of cases, respectively (vs. amplification in 0–25% of others). IntClust9 accounted for another 8% of ER+ cases and was characterized by amplification of the MYC oncogene at 8q24 with amplification in 89% of IntClust9 tumors (vs 3–42% of other groups). Thus the late-recurring ER+ subgroups are defined by genomic drivers, several of which are viable therapeutic targets ^25–27.

Similar differences in the probability of late distant relapse were seen in the subset of patients whose tumors were ER+/HER2− (Fig.3ab, Extended Data Fig.4a–f), a group in which late relapse and strategies to target this, such as extended endocrine therapy, represent critical clinical challenges. In particular, the probabilities of DR or cancer death amongst patients who were disease free 5 years post diagnosis reveals significant risk for IntClust 1,2,6,9 (relative to IntClust3) that varied over time. Moreover, the risk was not fully captured by a model that included IHC subtype with clinical variables (age, tumor size, grade, number of positive lymph nodes, time since surgery) that have been shown to dictate distant relapse outcomes even after a long disease-free interval⁵ (Fig.3a). We therefore assessed whether the integrative subtypes provided information about a patient’s risk of late distant relapse above and beyond what could be inferred optimally from standard clinical information. We found that the model including clinical variables combined with IHC subtype provided substantial information about the probability of distant relapse in ER+/HER2− patients who were relapse-free at 5 years: C-index of 0.63 (CI 0.58–0.68) at 10 years, 0.62 (CI 0.58–0.67) at 15 years, and 0.61 (CI 0.57–0.66) at 20 years (Fig.3c). However, including the IntClust subtypes significantly improved its predictive value: C-index of 0.70 (CI 0.64–0.75; improvement over the clinical model P = 0.00011) at 10 years, 0.67 (CI 0.63–0.72, P = 0.0016) at 15 years, and 0.66 (CI 0.62–0.71, P = 0.0017) at 20 years. These trends were recapitulated in an external validation cohort despite the smaller sample size and shorter follow-up times (prohibiting analyses at 20 years). Thus, information about the dynamics of late relapse provided by integrative subtype could not be inferred from standard clinical variables, including IHC subtype.

Figure 3. The integrative subtypes improve prediction of late distant recurrence in ER+/HER2− breast cancer beyond clinical covariates.

a. Probabilities of distant relapse (DR) or disease-specific death (DSD) amongst ER+/HER2− patients who were disease free at 5 years post diagnosis reveals significant risk for IntClust (IC) 1,2,6,9 relative to IC3, which varies over time and is not captured by the standard clinical model. Dots represent average probabilities and error bars 95% confidence intervals. b. Average probabilities of DR or DSD for ER+/HER2− patients in the four late-relapsing subgroups relative to IC3 for patients who were relapse free five years post diagnosis. c. Evaluation of the utility of the IHC model relative to the IntClust model for predicting late DR in ER+/HER2− patients who were relapse-free at 5 years. C-indices are shown for both models at different time intervals in the METABRIC cohort (n=1337, ER+/HER2− n=1013) and the external validation cohort (n=1080, ER+/HER2− n=739). Error bars represent 95% confidence intervals. This analysis was done with the MD.

We subsequently turned to the subset of patients who experienced a LR. LR is commonly treated with curative intent and is thought to be a high-risk event associated with increased rates (45 to 80%) of DR²⁸. The transition probabilities after LR varied substantially according to pathological features of the primary tumor at diagnosis and molecular subtype, highlighting opportunities for intervention (Extended Data Fig.6, Extended Data Fig.7, Supplementary Tables 2–3). In contrast, following the initial DR all subgroups exhibited a high probability of cancer death, although the median times differed (Extended Data Fig.8, Supplementary Tables 2–3).

Unique to our cohort is a subset of 618 patients (out of 1079 from the FD who relapsed) with a complete description of all recurrences (recurrent event dataset, RD), thereby enabling the detailed analysis of the rates and routes of distant metastasis and their lethality. These data revealed the varied time course over which metastases occurred and indicated that no sites of metastasis are exclusive to ER+ or ER− disease (Extended Data Fig.9a). Moreover, multiple distant metastases were common, even among favorable prognosis subgroups (Extended Data Fig.9b). We next examined the cumulative incidence and number of metastases at different organ sites stratified by ER status (Fig.4a). ER− cases harbored significantly more visceral disease (e.g. brain/meningeal: 27% vs. 11%, pulmonary: 50% vs. 41%) relative to ER+ cases. As previously reported^29,30, bone metastases were more common in ER+ versus ER− cases (71% vs. 43%), but the cumulative incidence was similar. Thus, the higher proportions observed in ER+ disease appear not to reflect site-specific tropism: rather, bone metastases take a long time to develop, and ER− patients tend to die of other metastases first. ER+ tumors also more commonly present with the first metastasis in the bone (76% vs 61%). Similar comparisons stratified by IHC, PAM50, and IntClust subtypes revealed additional variability (Extended Data Fig.10). Striking differences in the rates of distant metastasis were also evident: ER− disease was characterised by a rapid series of relapses early after diagnosis, while most ER+ patients suffered just one early relapse (commonly bone) and if a second relapse occurred, the probability of additional relapses increased (Fig.4b, Methods). Thus after distant recurrence, subtype continues to dictate the rate of subsequent metastases, underscoring the importance of tumor biology. Both the number and site of relapses influenced the risk of death after recurrence with brain metastasis being most predictive. Risk estimates (Fig.4c) were comparable between ER+ and ER− tumors, suggesting that the impact of the site of metastasis on progression to death is similar.

Figure 4. Organ-specific patterns and timing of distant relapse in ER+ and ER− patients.

a. Percentages of patients and cumulative incidence (1-Kaplan-Meier estimates) for each site of metastasis in ER+ and ER− cases. Upright triangles indicate significant positive differences and inverted triangles indicate significant negative differences in that group with respect to the overall mean (see Methods). b. Relapse-free survival curves for sequential recurrences in ER− (n=186) and ER+ (n=419) patients computed using a conditional PWP model. Each curve shows the probability of not having any other relapse for individuals that had a previous relapse. The top bar shows the median time until the n-th relapse. c. Log Hazard ratios of disease-specific death (DSD) with 95% confidence intervals of the time-dependent Cox model for distant relapse (DR) in ER− (n=179) and ER+ (n=410) patients. This analysis was done with the RD.

In summary, by leveraging a cohort of 3240 patients, including 1980 from METABRIC with detailed molecular characterization, LR and DR information, we have delineated the spatio-temporal dynamics of breast cancer relapse at unprecedented resolution. Our analyses are based on a powerful multi-state statistical model that yields individual risk of relapse estimates based on tumor features, clinical, pathological and molecular covariates, as well as disease chronology, and is available via a web application (see ^URL below). Unlike existing models used to calculate the benefits of adjuvant therapy at diagnosis such as PREDICT¹⁸, this research tool can be used to assess how a patient’s risk of recurrence changes throughout follow-up. Learning whether specific treatments change the outcomes of different integrative subtypes is important and will require analysis of randomized clinical trial cohorts.

By classifying breast tumors into the 11 integrative subtypes, important differences in recurrence rates that were obscured in the IHC and PAM50 subtypes became apparent. Amongst TNBC patients, IntClust10 largely remains relapse-free after 5 years, whereas IntClust4ER− patients continue to be at significant risk of recurrence. Amongst ER+/HER2-patients, IntClust 1, 2, 6, and 9 have markedly increased risk of DR up to 20 years post-diagnosis and together account for one quarter of all ER+ tumors and the vast majority of late recurrences. Moreover, the integrative subtypes significantly improved the prediction of distant recurrence after 5 years in ER+/HER2− patients. Our findings thus address one of the contemporary challenges in breast oncology, namely identification of the subset of ER+ patients with high-risk of recurrence and tumor biomarkers that are more predictive of recurrence than standard clinical covariates^7,8. Integrative subtyping may help determine whether women who are relapse-free 5 years after diagnosis might benefit from extended endocrine therapy or other interventions to improve late outcomes. Critically, the four late-recurring ER+ subgroups are enriched for genomic copy number driver alterations that can be therapeutically targeted^24–27, thus paving the way for new treatment strategies for these high-risk patient populations.

Methods

Clinical cohort

We employed data from 3240 patients (with a median follow-up of 9.77 years overall, and 14 years amongst patients who remain alive) derived from five tumor banks in the UK and Canada diagnosed between 1977–2005. Primary breast tumors and linked pseudo-anonymized clinical data were obtained with ethical approval from the relevant institutional review boards. The METABRIC study protocol was approved by the ethics committees at the University of Cambridge and British Columbia Cancer Research Centre. Manual curation and basic quality control was performed on the data. Observations that had relapse times equal to zero or relapse times equal to the last observed time were shifted 0.1 days. Local relapses that occurred after distant relapses were omitted. In total, 11 cases with stage 4 were also removed from all analyses. Benign and phylloid tumors were also discarded. Last follow-up time or time of death was the final endpoint for all patients. Special care was taken to remove second primary tumors from the dataset. Clinical parameters, such as tumor grade, were not centrally reviewed, which can lead to variability in the estimation of their effects. Samples were allocated to three datasets depending on the information available. The Full Dataset (FD) Clinical and pathological variables are available for this cohort (15394 transitions from 3147 patients). For a subset of 1980 patients we previously described an integrated genomic analysis based on gene expression and copy number data¹² and refer to this as the molecular dataset or METABRIC MD (9512 transitions from 1962 patients). For this cohort, tumors were stratified based on the IHC subtypes (ER+/HER2+, ER+/HER2−, ER−/HER2+, ER−/HER2−), the intrinsic subtypes (PAM50)^10,11 and the integrative (IntClust) subtypes^12,13. Finally, for a subset of patients who experienced distant metastasis (618 out of the 1079 who relapsed from the FD), the date of each recurrence is available, enabling analysis of their spatio-temporal dynamics. We refer to this as the recurrent events dataset RD. The three datasets are summarized in Extended Data Fig.1a with clinical details and basic parameters describing the intermediate endpoints of LR and DR across distinct subgroups in Supplementary Table 1. We also established an independent metacohort composed of 1380 breast cancer patients from eight cohorts enabling external validation of our findings, despite their shorter median follow-up (8 years) (Extended Data Fig.1b). We sought to use the maximum information available to fit the models, keeping all the transitions with complete observations needed to estimate the hazard of that specific transition. Therefore, the total number of cases used in each model differs due to different missing values in clinical variables, molecular classification, etc that can affect different transitions.

Model description

The general model we fitted to our datasets is a multistate model that reflects the different risks of loco-regional relapse, distant relapse or disease-specific death conditioned on the current status of the patient. Although multistate survival models for breast cancer were proposed more than 60 years ago³¹, there are few such analyses in the literature^14,32,33. Specifically, we employed a non-homogenous semi-Markov Chain with two absorbent states (Death/Cancer and Death/Other) as shown schematically in Fig.1. The model was stratified by molecular subtype and used a clock-reset time scale, in which the clock stops (clock-reset) when the patient enters a new state. Although there were a small number of transitions from distant to local relapse (15 ER+ cases and 7 ER−), we omitted the local relapse in these instances as we considered it redundant and only allowed transitions from local to distant relapse in our model. We also included the possibility of cancer death without a recurrence to account for cases where metastasis was not detected. R packages survival³⁴ and mstate³⁵ were used to fit the data.

Several covariates were included in the model: age at state entry (diagnosis or relapse), tumor grade, tumor size and the number of positive lymph nodes, all of them as continuous variables (although in the case of lymph nodes, all values larger than 10 lymph nodes were coded as 10, to avoid excessive influence in the slope from extreme cases). The time from diagnosis was also included as continuous. Note that these formulations are a simplification from the modelling in our previous work¹², where age, size and lymph nodes were modelled non-linearly through splines. We have simplified these effects to reduce the number of parameters in the model, but also, in the case of age, because its non-linearity is only relevant when overall survival is the endpoint.

For dataset FD, a Cox model was fitted stratified on ER status. The effect of age on death/other causes was modelled with a different coefficient for each transition into non-malignant death (in each ER status), to account for differences in the age at relapse or diagnosis. Grade, Size and Lymph Nodes were allowed to have different coefficients from the starting state to states of recurrence/cancer death for each ER status. Time since diagnosis had different coefficients from the starting state of relapse to states of recurrence/ cancer death for each ER status and time since LR had different coefficients from distant relapse state to cancer related death for each ER status. The time since LR was not predictive of the time to DR and therefore was not included in further analyses.

For dataset MD, and because of the large number of molecular subtypes, we reduced the number of parameters constraining their values to be the same for the different molecular subtypes. Based on different fits and the results of likelihood ratio tests we observed some effects to be markedly different between transitions: age had a coefficient for transitions from surgery or loco-regional relapse into death/other causes for all molecular subtypes and another for transitions from distant relapse into death/other causes. Grade and lymph nodes had a value for transitions from diagnosis and another for transitions from relapse to states of recurrence/death, identical for each molecular subtype. Size had a value for transitions from diagnosis and another for transitions from loco-regional relapse to states of recurrence/death, identical for each molecular subtype. Time since diagnosis had the same coefficient from the starting state of relapse to states of recurrence/death, identical for all molecular subtype. This model was fit three times, one for each molecular classification, based on ER/HER2 status (FourGroupsM), PAM50 (Pam50M) and the Integrative Clusters (ICM); each of them stratified by the respective molecular subgroups. We used a robust variance estimate in all models (option cluster(id) in coxph() function) and performed likelihood ratio tests in order to reduce the number of parameters in each model. Since the number of samples in the MD is smaller than the FD, we retained only the most important covariates and assumed the same effect in each subgroup.

Transition probabilities for each molecular subtype

Using the model fit, we obtained the hazards for each transition for a given individual. We used these hazards to compute the corresponding transition probabilities as follows. We employ a clock-reset model and define all probabilities starting at the time of entry to the last state. All times s, t are also defined starting from the time of entry. Let the set of states be {S=disease-free/after surgery, L=loco-regional relapse D=distant relapse, C=cancer death, O=other cause of death}. We condition on the vector of clinical covariates x, which includes the time from surgery (in the case of relapse this variable has an effect on the hazards).

Transitions from distant relapse

Following^14,36, we define the conditional probability of having no further event between times t and s for a patient with distant relapse at time t as

$${\mathrm{S}}_{\mathrm{D}}(\mathrm{s},\mathrm{t}|\mathrm{x})=\exp \left\{-{\int }_{\mathrm{t}}^{\mathrm{s}}\left({\mathrm{\lambda }}_{\mathrm{D},\mathrm{C}}(\mathrm{u}|\mathrm{x})+{\mathrm{\lambda }}_{\mathrm{D},\mathrm{O}}(\mathrm{u}|\mathrm{x})\right)\mathrm{d}\mathrm{u}\right\}$$

where λ_i,j (t|x) is the hazard of moving from state i to state j at time t with the vector of covariates x (including the time from surgery or age, that must be updated after a relapse).

Then, the prediction probabilities for each path are:

$${\mathrm{\pi }}_{\mathrm{D}}^{\mathrm{C}}(\mathrm{u},\mathrm{t}|\mathrm{x})={\int }_{\mathrm{t}}^{\mathrm{u}}{\mathrm{\lambda }}_{\mathrm{D},\mathrm{C}}(\mathrm{s}|\mathrm{x}){\mathrm{S}}_{\mathrm{D}}(\mathrm{s},\mathrm{t})\mathrm{d}\mathrm{s}$$

$${\mathrm{\pi }}_{\mathrm{D}}^{\mathrm{O}}(\mathrm{u},\mathrm{t}|\mathrm{x})={\int }_{\mathrm{t}}^{\mathrm{u}}{\mathrm{\lambda }}_{\mathrm{D},\mathrm{O}}(\mathrm{s}|\mathrm{x}){\mathrm{S}}_{\mathrm{D}}(\mathrm{s},\mathrm{t})\mathrm{d}\mathrm{s}$$

$${\mathrm{\pi }}_{\mathrm{D}}(\mathrm{u},\mathrm{t}|\mathrm{x})=1-({\mathrm{\pi }}_{\mathrm{D}}^{\mathrm{C}}(\mathrm{u},\mathrm{t}|\mathrm{x})+{\mathrm{\pi }}_{\mathrm{D}}^{\mathrm{O}}(\mathrm{u},\mathrm{t}|\mathrm{x}))$$

Transitions from loco-regional relapse

Similarly, we obtain:

$${\mathrm{S}}_{\mathrm{L}}(\mathrm{s},\mathrm{t}|\mathrm{x})=\exp \left\{-{\int }_{\mathrm{t}}^{\mathrm{s}}\left({\mathrm{\lambda }}_{\mathrm{L},\mathrm{D}}(\mathrm{u}|\mathrm{x})+{\mathrm{\lambda }}_{\mathrm{L},\mathrm{C}}(\mathrm{u}|\mathrm{x})+{\mathrm{\lambda }}_{\mathrm{L},\mathrm{O}}(\mathrm{u}|\mathrm{x})\right)\mathrm{d}\mathrm{u}\right\}$$

$${\mathrm{\pi }}_{\mathrm{L}}^{\mathrm{D},\mathrm{C}}(\mathrm{u},\mathrm{t}|\mathrm{x})={\int }_{\mathrm{t}}^{\mathrm{u}}{\mathrm{\lambda }}_{\mathrm{L},\mathrm{D}}(\mathrm{s}|\mathrm{x}){{\mathrm{\pi }}_{\mathrm{D}}^{\mathrm{C}}(\mathrm{u}-\mathrm{s},0|\mathrm{x})\mathrm{S}}_{\mathrm{L}}(\mathrm{s},\mathrm{t}|\mathrm{x})\mathrm{d}\mathrm{s}$$

$${\mathrm{\pi }}_{\mathrm{L}}^{\mathrm{D},\mathrm{O}}(\mathrm{u},\mathrm{t}|\mathrm{x})={\int }_{\mathrm{t}}^{\mathrm{u}}{\mathrm{\lambda }}_{\mathrm{L},\mathrm{D}}(\mathrm{s}|\mathrm{x}){{\mathrm{\pi }}_{\mathrm{D}}^{\mathrm{O}}(\mathrm{u}-\mathrm{s},0|\mathrm{x})\mathrm{S}}_{\mathrm{L}}(\mathrm{s},\mathrm{t}|\mathrm{x})\mathrm{d}\mathrm{s}$$

$${\mathrm{\pi }}_{\mathrm{L}}^{\mathrm{D}}(\mathrm{u},\mathrm{t}|\mathrm{x})={\int }_{\mathrm{t}}^{\mathrm{u}}{\mathrm{\lambda }}_{\mathrm{L},\mathrm{D}}(\mathrm{s}|\mathrm{x}){{\mathrm{\pi }}_{\mathrm{D}}^{}(\mathrm{u}-\mathrm{s},0|\mathrm{x})\mathrm{S}}_{\mathrm{L}}(\mathrm{s},\mathrm{t}|\mathrm{x})\mathrm{d}\mathrm{s}$$

$${\mathrm{\pi }}_{\mathrm{L}}^{\mathrm{C}}(\mathrm{u},\mathrm{t}|\mathrm{x})={\int }_{\mathrm{t}}^{\mathrm{u}}{\mathrm{\lambda }}_{\mathrm{L},\mathrm{C}}(\mathrm{s}|\mathrm{x}){\mathrm{S}}_{\mathrm{L}}(\mathrm{s},\mathrm{t}|\mathrm{x})\mathrm{d}\mathrm{s}$$

$${\mathrm{\pi }}_{\mathrm{L}}^{\mathrm{O}}(\mathrm{u},\mathrm{t}|\mathrm{x})={\int }_{\mathrm{t}}^{\mathrm{u}}{\mathrm{\lambda }}_{\mathrm{L},\mathrm{O}}(\mathrm{s}|\mathrm{x}){\mathrm{S}}_{\mathrm{L}}(\mathrm{s},\mathrm{t}|\mathrm{x})\mathrm{d}\mathrm{s}$$

$${\mathrm{\pi }}_{\mathrm{L}}(\mathrm{u},\mathrm{t}|\mathrm{x})=1-({\mathrm{\pi }}_{\mathrm{L}}^{\mathrm{D},\mathrm{C}}(\mathrm{u},\mathrm{t}|\mathrm{x})+{\mathrm{\pi }}_{\mathrm{L}}^{\mathrm{D},\mathrm{O}}(\mathrm{u},\mathrm{t}|\mathrm{x})+{\mathrm{\pi }}_{\mathrm{L}}^{\mathrm{D}}(\mathrm{u},\mathrm{t}|\mathrm{x})+{\mathrm{\pi }}_{\mathrm{L}}^{\mathrm{C}}(\mathrm{u},\mathrm{t}|\mathrm{x})+{\mathrm{\pi }}_{\mathrm{L}}^{\mathrm{O}}(\mathrm{u},\mathrm{t}|\mathrm{x}))$$

Transitions after surgery

$${\mathrm{S}}_{\mathrm{S}}(\mathrm{s},\mathrm{t}|\mathrm{x})=\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\int }_{\mathrm{t}}^{\mathrm{s}}\left({\mathrm{\lambda }}_{\mathrm{S},\mathrm{L}}(\mathrm{u}|\mathrm{x})+{\mathrm{\lambda }}_{\mathrm{S},\mathrm{D}}(\mathrm{u}|\mathrm{x})+{\mathrm{\lambda }}_{\mathrm{S},\mathrm{C}}(\mathrm{u}|\mathrm{x})+{\mathrm{\lambda }}_{\mathrm{S},\mathrm{O}}(\mathrm{u}|\mathrm{x})\right)\mathrm{d}\mathrm{u}\right]$$

$${\mathrm{\pi }}_{\mathrm{S}}^{\mathrm{L},\mathrm{D},\mathrm{C}}(\mathrm{u},\mathrm{t}|\mathrm{x})={\int }_{\mathrm{t}}^{\mathrm{u}}{\mathrm{\lambda }}_{\mathrm{S},\mathrm{L}}(\mathrm{s}|\mathrm{x}){\mathrm{\pi }}_{\mathrm{L}}^{\mathrm{D},\mathrm{C}}(\mathrm{u}-\mathrm{s},0){\mathrm{S}}_{\mathrm{S}}(\mathrm{s},\mathrm{t}|\mathrm{x})\mathrm{d}\mathrm{s}$$

$${\mathrm{\pi }}_{\mathrm{S}}^{\mathrm{L},\mathrm{D},\mathrm{O}}(\mathrm{u},\mathrm{t}|\mathrm{x})={\int }_{\mathrm{t}}^{\mathrm{u}}{\mathrm{\lambda }}_{\mathrm{S},\mathrm{L}}(\mathrm{s}|\mathrm{x}){\mathrm{\pi }}_{\mathrm{L}}^{\mathrm{D},\mathrm{O}}(\mathrm{u}-\mathrm{s},0){\mathrm{S}}_{\mathrm{S}}(\mathrm{s},\mathrm{t}|\mathrm{x})\mathrm{d}\mathrm{s}$$

$${\mathrm{\pi }}_{\mathrm{S}}^{\mathrm{L},\mathrm{C}}(\mathrm{u},\mathrm{t}|\mathrm{x})={\int }_{\mathrm{t}}^{\mathrm{u}}{\mathrm{\lambda }}_{\mathrm{S},\mathrm{L}}(\mathrm{s}|\mathrm{x}){\mathrm{\pi }}_{\mathrm{L}}^{\mathrm{C}}(\mathrm{u}-\mathrm{s},0){\mathrm{S}}_{\mathrm{S}}(\mathrm{s},\mathrm{t}|\mathrm{x})\mathrm{d}\mathrm{s}$$

$${\mathrm{\pi }}_{\mathrm{S}}^{\mathrm{L},\mathrm{O}}(\mathrm{u},\mathrm{t}|\mathrm{x})={\int }_{\mathrm{t}}^{\mathrm{u}}{\mathrm{\lambda }}_{\mathrm{S},\mathrm{L}}(\mathrm{s}|\mathrm{x}){\mathrm{\pi }}_{\mathrm{L}}^{\mathrm{O}}(\mathrm{u}-\mathrm{s},0){\mathrm{S}}_{\mathrm{S}}(\mathrm{s},\mathrm{t}|\mathrm{x})\mathrm{d}\mathrm{s}$$

$${\mathrm{\pi }}_{\mathrm{S}}^{\mathrm{L},\mathrm{D}}(\mathrm{u},\mathrm{t}|\mathrm{x})={\int }_{\mathrm{t}}^{\mathrm{u}}{\mathrm{\lambda }}_{\mathrm{S},\mathrm{L}}(\mathrm{s}|\mathrm{x}){\mathrm{\pi }}_{\mathrm{L}}^{\mathrm{D}}(\mathrm{u}-\mathrm{s},0){\mathrm{S}}_{\mathrm{S}}(\mathrm{s},\mathrm{t}|\mathrm{x})\mathrm{d}\mathrm{s}$$

$${\mathrm{\pi }}_{\mathrm{S}}^{\mathrm{D},\mathrm{C}}(\mathrm{u},\mathrm{t}|\mathrm{x})={\int }_{\mathrm{t}}^{\mathrm{u}}{\mathrm{\lambda }}_{\mathrm{S},\mathrm{D}}(\mathrm{s}|\mathrm{x}){\mathrm{\pi }}_{\mathrm{D}}^{\mathrm{C}}(\mathrm{u}-\mathrm{s},0){\mathrm{S}}_{\mathrm{S}}(\mathrm{s},\mathrm{t}|\mathrm{x})\mathrm{d}\mathrm{s}$$

$${\mathrm{\pi }}_{\mathrm{S}}^{\mathrm{D},\mathrm{O}}(\mathrm{u},\mathrm{t}|\mathrm{x})={\int }_{\mathrm{t}}^{\mathrm{u}}{\mathrm{\lambda }}_{\mathrm{S},\mathrm{D}}(\mathrm{s}|\mathrm{x}){\mathrm{\pi }}_{\mathrm{D}}^{\mathrm{O}}(\mathrm{u}-\mathrm{s},0){\mathrm{S}}_{\mathrm{S}}(\mathrm{s},\mathrm{t}|\mathrm{x})\mathrm{d}\mathrm{s}$$

$${\mathrm{\pi }}_{\mathrm{S}}^{\mathrm{L}}(\mathrm{u},\mathrm{t}|\mathrm{x})={\int }_{\mathrm{t}}^{\mathrm{u}}{\mathrm{\lambda }}_{\mathrm{S},\mathrm{L}}(\mathrm{s}|\mathrm{x}){\mathrm{\pi }}_{\mathrm{L}}^{}(\mathrm{u}-\mathrm{s},0){\mathrm{S}}_{\mathrm{S}}(\mathrm{s},\mathrm{t}|\mathrm{x})\mathrm{d}\mathrm{s}$$

$${\mathrm{\pi }}_{\mathrm{S}}^{\mathrm{D}}(\mathrm{u},\mathrm{t}|\mathrm{x})={\int }_{\mathrm{t}}^{\mathrm{u}}{\mathrm{\lambda }}_{\mathrm{S},\mathrm{D}}(\mathrm{s}|\mathrm{x}){\mathrm{\pi }}_{\mathrm{D}}^{}(\mathrm{u}-\mathrm{s},0){\mathrm{S}}_{\mathrm{S}}(\mathrm{s},\mathrm{t}|\mathrm{x})\mathrm{d}\mathrm{s}$$

$${\mathrm{\pi }}_{\mathrm{S}}^{\mathrm{C}}(\mathrm{u},\mathrm{t}|\mathrm{x})={\int }_{\mathrm{t}}^{\mathrm{u}}{\mathrm{\lambda }}_{\mathrm{S},\mathrm{C}}(\mathrm{s}|\mathrm{x}){\mathrm{S}}_{\mathrm{S}}(\mathrm{s},\mathrm{t}|\mathrm{x})\mathrm{d}\mathrm{s}$$

$${\mathrm{\pi }}_{\mathrm{S}}^{\mathrm{O}}(\mathrm{u},\mathrm{t}|\mathrm{x})={\int }_{\mathrm{t}}^{\mathrm{u}}{\mathrm{\lambda }}_{\mathrm{S},\mathrm{O}}(\mathrm{s}|\mathrm{x}){\mathrm{S}}_{\mathrm{S}}(\mathrm{s},\mathrm{t}|\mathrm{x})\mathrm{d}\mathrm{s}$$

${\mathrm{\pi }}_{\mathrm{S}}^{}(\mathrm{u},\mathrm{t}|\mathrm{x})$ can be computed as 1 minus the sum of the others.

Prediction probabilities for being in a particular state at a certain time can also be computed summing the appropriate paths. Note that the main difficulty in computing these probabilities is updating the corresponding hazards every time a transition occurs, as they may depend on variables that change over time or after a transition to a different state. In our implementation we tried to follow the style in the mstate package³⁵.

Standard Errors for the transition probabilities in our model

If our model was Markovian (as the clock-forward model), the transition probabilities could be easily computed through the product-integral representation³⁷ and it would also be straightforward to obtain estimates of their standard errors. However, for our clock-reset model the estimation of standard errors is complicated, so we used a semi-parametric bootstrap approach to obtain such estimates³⁸. Briefly, for every bootstrap replicate (B=100), we sampled trajectories for each observation in our original dataset based on our fitted model. These trajectories were fitted to the original model and bootstrap hazards for the original average individuals were computed. Then, the formulas described earlier were used to obtain bootstrap transition probabilities. Because these bootstrap estimates are not likely to converge to the theoretical estimates in transitions with a small number of observed instances, we computed the standard deviation of the bootstrap estimates as an indication of the variability of these predictions for a given patient.

Transition probabilities for specific events

The transition probabilities obtained for each patient can be aggregated to obtain probabilities of visiting specific states (LR, DR) or specific endpoints. We used these probabilities in two ways: as an example of individual predictions for an average patient for each molecular subtype (based on typical or average values of each covariate), as in Supplementary Table 4B, Fig.1b, Extended Data Fig.6 and Extended Data Fig.8 together with a confidence interval computed using the obtained probabilities +/− 1.96 times the standard deviation of the bootstrap estimates described above, that represent variability around individual predictions. We also computed probabilities for all patients to show their distribution in each molecular subtype, as in Supplementary Table 4A and Fig.2a, Fig.3a, Extended Data Fig.4 and Extended Data Fig.5. Confidence intervals computed using the mean of the probabilities +/− 1.96 times the standard error of the mean represent variability around the mean in each subtype.

Sites of relapse

For the RD datasets, each patient can have several relapses. Instead of adding the site to our multistate models, we selected only patients who had distant relapse. First, in Fig.4a and Extended Data Fig.10, we tested if the proportions of relapses in each organ differed by molecular subtype. We fitted a logistic regression model with relapse as a binary variable and the sites of metastases as dependent variables. We computed simultaneous tests using the R package multcomp³⁹ using the Dunnet method⁴⁰. Only those proportions with a p-value smaller than 0.05 were considered significant. In the same figures, cumulative incidence distributions for each organ were computed independently, that is, no competing risk model was fitted.

We modelled recurrent distant metastases (Fig.4b) using the Prentice, Williams and Peterson⁴¹ (PWP) conditional model. This model allows for different baseline hazards for each consecutive recurrence while keeping at risk for recurrence i only those individuals that have experimented the recurrence i-1.

Finally, in Fig.4c we fitted a Cox model with time dependent variables to estimate the hazard of having metastasis in each organ. We also included in this model the clinical variables from the primary tumor (tumor grade, tumor size and number of positive lymph nodes).

Goodness of fit testing

Goodness of fit testing was performed for all models. Proportional hazards assumption was tested using the Schoenfeld Residuals vs. time using the survival function cox.zph()³⁴. None of the models showed covariates that violated the assumption, except the model for sites of metastasis (ER+), where the number of metastases and “other metastasis” were significant and the model for sites of metastasis (ER-) where grade and the number of metastases were significant. Visual inspection of the plots showed that the trend was roughly flat and thus the violation was not critical. In the model that includes ER, as previously shown ER violates the proportional hazard assumption. However, this model was only used to test differences in the hazard ratios of the other covariates according to ER.

Model Validation and Calibration

We validated each of the models using several approaches, as outlined below.

Internal validation

We validated the global predictions of the model on all transitions using the bootstrap approach described in detail in⁴² using the rms R package. We used the following measures of predictive ability:

• Somers’ Dxy rank correlation (Dxy). This is 2(c-0.5), where c is the c-index

• Nagelkerke’s R2, which is the square root of the proportion of log likelihood explained by the model from the log likelihood that could be explained by a “perfect” model, with a penalty for model complexity

• Slope shrinkage (slope), a measure of how much the estimates are affected by extreme observations

• Discrimination index D, derived from the log-likelihood at the shrunken linear predictor

• Unreliability index U, a measure of the difference between the model maximum log likelihood is from a model with frozen coefficients

• Overall quality index Q, a normalized and penalized for unreliability log likelihood

• g-index (g) on the log relative hazard (linear predictor) scale (Gini’s mean difference)

Each measure was computed on the training set and on 200 bootstrap test sets, estimating the optimism and the corrected indexes for predictions at 5, 10 and 15 years (see Extended Data Fig.3a).

Internal calibration

We also employed the following procedure for model calibration as described in⁴²:

• Interpolation of the hazard function using splines (hare method) among all the cases as a general function of the predictor variables and time

• Computation of the predicted values for a given time point (5, 10 or 15 years)

• Computation of the differences between observed and predicted

• Using 200 bootstrap datasets, computation of the optimism in those differences

Extended Data Fig.3b shows a boxplot of the mean absolute error of all predictions.

External calibration

As an external comparison of the predicted probabilities of our models, we used predict v2.1¹⁸, a tool that has been validated extensively. PREDICT uses a model with several variables (including the effect of treatment) and produces estimates of the probability of cancer-specific death (C/D) and non-malignant death (O/D), as well as estimates of the effect of treatment. We compared the probabilities for these events with PREDICT using Pearson correlation (see Extended Data Fig.3cd).

External validation

We used two sets of external samples to validate the predictions of our models:

1. A set of METABRIC samples that were not used in the original study including 121 patients with copy number data and 57 patients with expression data. We already had survival data from these patients (in fact they are part of the full dataset FD, but because they have not been used to fit the IntClust Model, they could be employed to test the validity of the c-index on an external dataset). We classified these tumours into IntClust groups using the iC10¹³ package.

2. An external dataset of 1380 patients from 8 different cohorts and different survival information. We validated predictions of disease-specific survival (DSS), overall survival (OS), relapse-free survival (RFS) and distant-relapse free survival (DRFS). We compiled a metacohort by merging early breast cancer cohorts where expression data (Affymetrix array), outcome and covariates are available, including GSE19615 (DFHCC⁴³), GSE42568 (Dublin⁴⁴), GSE9195 (Guyt2⁴⁵), GSE45255 (IRB/JNR/NUH⁴⁶), GSE11121 (Maintz⁴⁷), GSE6532 (TAM⁴⁵), GSE7390 (Transbig⁴⁸) and GSE3494 (Upp⁴⁹). Original data (raw CEL files) were downloaded and pre-processed using the rma function from the affy⁵⁰ package. The intensities were then quantile normalized and corrected for batch effects with the COMBAT function from the sva⁵¹ package. PAM50 was called using the genefu⁵² package. ER, PR and Her2 status were extracted from the expression using probes 205225_at, 208305_at and 216836_s_t using a Gaussian mixture model. IC10 subgroups was called using iC10 package. C-indices and summary c-indices were calculated using survcomp⁵³ package. For the combined metacohort scores, we calculated c-scores for each individual cohort and then combined them using the function combine.est from survcomp⁵³ package. Confidence intervals and p-values for comparing c-indexes were computed with the same package. Extended Data Fig.3e shows the c-indices and confidence intervals for these comparisons.

General Statistical considerations

All tests were performed two-sided (except where indicated). Adjustment for multiple comparisons was done as described in the sections “Comparison of probabilities of relapse in ER+ high risk Integrative Subtypes” (see Supplementary Methods) and the comparison of proportions of metastases in each organ from Fig.4a and Extended Data Fig.10. All analyses were conducted in R 3.5.1⁵⁴

Extended Data

Extended Data Fig.1 |. Description of the cohorts used in this study.

a. Description of the METABRIC discovery cohort, clinical characteristics and flow chart of sample inclusion for analysis. b. Description of the validation cohort, clinical characteristics and flow chart of sample inclusion for analysis.

Extended Data Fig.2 |. Effect of censoring non-malignant deaths in the estimation of disease-specific survival and prognostic value of clinical covariates at different disease states.

a. Cumulative incidence computed as 1-Kaplan-Meier estimator using only disease-specific death as endpoint and censoring other types of death. b. Cumulative incidence computed using a competing-risk model that takes into account different causes of death. The bias of the 1-Kaplan-Meier estimator is visible. c. Distribution of age at the time of diagnosis for ER− and ER+ patients. The number of patients in each group is indicated in all Panels. This analysis was done with the FD. d. Log Hazard Ratios (HR) calculated using the multistate model stratified by ER status (n=3147) for different covariates, namely grade, lymph node (LN) status, tumor size (size), time from local relapse, time from surgery. Log HR are shown from different states, including post surgery (PS; HR of progressing to relapse or DSD), loco-regional recurrence (LR; HR of progressing to DR or DSD) and distant recurrence (DR; HR of cancer-specific death). 95% confidence intervals are shown. This analysis was done with the FD.

Extended Data Fig.3 |. Model calibration and validation in an external dataset.

a. Internal validation of the global predictions of the models on all transitions using bootstrap (n=200). Boxplots are computed using the median of the observations, the first and third quartiles as hinges and the +/−1.58 Interquartile range divided by the square root of the sample size as notches. The optimism (difference between the training predictive ability and the test predictive ability of several discriminant measures (see Methods). b. Internal calibration of the global predictions of the models on all transitions using bootstrap (n=200). The distribution of the mean absolute error between observed and predicted is plotted. Boxplot defined as above (see Methods). c. External calibration of disease-specific death (DSD) risk and non-malignant death risk using PREDICT 2.1 (n=1841). The distribution of the mean absolute error between the predictions of PREDICT and our model based on ER status only is plotted. Boxplots defined as above. d. Scatterplot of the predictions of DSD risk computed by PREDICT and our model based on the IntClust subtypes only at 10 years (n=1841) (see Methods). Pearson correlation is shown. e. Concordance index (c-index) of prediction of risk of distant relapse (distant relapse free survival, DRFS), disease-specific death (disease specific survival, DSS), death (overall survival, OS) and relapse (relapse free survival, RFS) in the 178 withheld METABRIC samples and in a metacohort composed of 8 published studies amongst ER−/HER2− patients in the high-risk IntClust subtypes, where results are shown for individual cohorts and the combined metacohort (see Methods, Supplementary Information). Error bars correspond to 95% confidence intervals for the c-index. The number of patients in each group is indicated.

Extended Data Fig.4 |. Different subtypes have distinct probabilities of recurrence.

a. Average probability of experiencing a distant relapse (DR, defined as the probability of having a distant relapse at any point followed by any other transition) for the high risk ER+ IntClust (IC) subtypes (IC1; n=134, IC6; n=81, IC9; n=134, IC2; n=69) relative to IC3 (n=269), the best prognosis ER+ subgroup. This analysis was restricted to ER+/HER2− cases, which represent the vast majority for each of these subtypes. Error bars represent 95% confidence intervals for the mean. b. As in Panel (a), but showing the average probability of experiencing DR or cancer related death after a LR (IC1; n=21, IC6; n=10, IC9; n=21, IC2; n=13, IC3; n=30). c. Average probability of recurrence (distant relapse or cancer-specific death) after loco-regional relapse for all patients in each of the 11 IntClust subtypes. d. Median time until an additional relapse (DR or cancer specific death) after LR for all patients in each the 11 IntClust subtypes (n=270). This has been computed using a Kaplan-Meier approach with competing risks of progression and non-malignant death. Error bars represent 95% confidence intervals for the median time. Asterisks denote situations where the median time cannot be computed because less than 50% of the patients relapsed. This analysis was done with the MD. e. Average probability of cancer related death after DR for all patients by subtype. f. As in Panel (d), except that the median time until cancer specific death after DR is shown (n=596). g. Mean probabilities of having relapse after surgery and after being 5 and 10 years disease-free (see Methods and Supplementary Table 3) for the patients in each of the four clinical subtypes. Error bars represent 95% confidence intervals. The number of patients in each group is indicated. h, i, j, k. Same as Panels (b, c, d, e) for the IHC subtypes (same sample sizes). l. As in Panel (g) but for the PAM50 subtypes. The number of patients in each group is indicated. m, n, o, p. Same as Panels (b, c, d, e) for the PAM50 subtypes (same sample sizes except for Panel (p); n=593).

Extended Data Fig.5 |. The ER−/HER2− integrative subtypes exhibit distinct risks of relapse.

Probabilities of distant relapse (DR) or cancer related death (C/D) amongst ER−/Her2− patients who were disease free at 5 years post diagnosis reveals dramatic differences in the risk of relapse for TNBC IntClust (IC) subtypes IC4ER− versus the IC10 (Basal-like enriched) subtype. Here the base clinical model with IHC subtypes is compared with the base clinical model plus IntClust subtype information. Error bars represent 95% confidence intervals. The number of patients in each group is indicated.

Extended Data Fig.6 |. Subtype specific risks of relapse after loco-regional relapse.

Transition probabilities from LR to other states (LR=Loco-regional relapse, DR=Distant relapse, D/C=Cancer/disease specific death, D/O=Death by other causes) for individual average patients stratified based on ER status, IHC, PAM50, or IntClust subtypes. 95% confidence bands were computed using bootstrap. This analysis was done with the FD for ER+/ER− comparisons and the MD for the remainder.

Extended Data Fig.7 |. Associations between probabilities of distant relapse 10 years after loco-regional relapse with clinico-pathological and molecular features of the primary tumor.

For each patient that had a loco-regional recurrence (LR), the 10-year probability of having distant relapse (DR) or cancer-related death (D/C) is plotted against different variables. A loess fit is overlaid in order to highlight the relationship between the probability and tumor size or time of relapse. Boxplots are computed using the median of the observations, the first and third quartiles as hinges and the +/−1.58 interquartile range divided by the square root of the sample size as notches. This analysis was done with the MD and the model was stratified by IntClust subtype (n=257).

Extended Data Fig.8 |. Subtype specific risks of relapse after a distant relapse.

Transition probabilities from DR to other states (LR=Loco-regional relapse, DR=Distant relapse, D/C=Cancer related death, D/O=Death by other causes) for individual average patients stratified based on ER status, IHC, PAM50 or IntClust subtypes. 95% confidence bands were computed using bootstrap. This analysis was done with the FD for ER+/ER− comparisons and the MD for the remainder.

Extended Data Fig.9 |. Distribution of the number of relapses by molecular subtype.

a. Times of distant recurrence (DR) for ER− and ER+ patients (n=605). Each dot represents a distant recurrence, coded by color for different sites. b. Distribution of the number of distant relapses for different subtypes (n=611), based on ER/HER2 status (ER+/HER2+ n=36, ER+/HER2− n=263, ER−/HER2+ n=41, ER−/HER2− n=82), PAM50 (Basal n=79, Her2 n=69, Luminal A n=101, Luminal B n=138, Normal n=33) and IntClust subtypes (IC1 n=40, IC2 n=25, IC3 n=32, IC4ER+ n=46, IC4ER− n=16, IC5 n=72, IC6 n=23, IC7 n=24, IC8 n=54, IC9 n=38, IC10 n=52). ER status was imputed based on expression in 6 samples. These analyses were done with RD cohort.

Extended Data Fig.10 |. Site specific patterns of relapse in the IHC, PAM50 and IntClust subtypes.

a. Left Panel: Percentages of patients with a given site of metastasis in the IHC subtypes (barplots, total numbers also indicated). Upright triangles indicate significant positive differences in that group with respect to the overall mean and inverted triangles indicate significant positive differences in that group with respect to the overall mean using simultaneous testing of all sites (see Methods). Location of metastatic sites is not anatomically accurate. Right Panel: Cumulative incidence functions (as 1-Kaplan-Meier estimates) for each site of metastasis in the IHC subtypes. The same patient can have multiple sites of metastasis. b. Same as in Panel (a) but for the PAM50 subtypes. c. Same as in Panel (a) but for the IntClust subtypes. These analyses were done with RD cohort.