A practical framework and online tool for mutational signature analyses show inter-tissue variation and driver dependencies

Abstract

Mutational signatures are patterns of mutations that arise during tumorigenesis. We present an enhanced, practical framework for mutational signature analyses. Applying these methods on 3,107 whole genome sequenced (WGS) primary cancers of 21 organs reveals known signatures and nine previously undescribed rearrangement signatures. We highlight inter-organ variability of signatures and present a way of visualizing that diversity, reinforcing our findings in an independent analysis of 3,096 WGS metastatic cancers. Signatures with a high level of genomic instability are dependent on TP53 dysregulation. We illustrate how uncertainty in mutational signature identification and assignment to samples affects tumor classification, reinforcing that using multiple orthogonal mutational signature data is not only beneficial, it is essential for accurate tumor stratification. Finally, we present a reference web-based tool for cancer and experimentally-generated mutational signatures, called Signal (https://signal.mutationalsignatures.com), that also supports performing mutational signature analyses.

As a cell transforms from normality towards malignancy, a number of mutational processes occur that leave characteristic DNA imprints. These mutational signatures^1,2 provide insights into etiologies of each tumor. They report environmental exposures and may be informative of intrinsic biological abnormalities that are therapeutically targetable³. Thus, the ability to correctly identify mutational signatures and to quantify them in a given sample is crucial.

Since the first description of how to extract mutational signatures using Non-negative Matrix Factorization (NMF)^2,4, various mathematical methodologies have been proposed for mutational signature extraction from catalogues of cancer somatic mutations^5,6. An unresolved issue in the field relates to best practice. In this work, we highlight several methodological issues and present a practical framework for performing mutational signature analyses. We acknowledge uncertainties and limitations associated with this field, such as multiple potential solutions of signature extraction, and suggest how to overcome them. Our results are compared to those that are used widely by the community. In so doing, we reveal that there may be organ-specific variation between signatures. We identify previously undescribed rearrangement signatures. Through association analyses with driver mutations, we emphasize interesting dependencies including multiple mutational signatures of genomic instability that are contingent on TP53 dysregulation. Finally, we demonstrate that using a single read-out such as a substitution signature causes high false positive calls for Homologous Recombination Deficient (HRD) tumor stratification. Instead, uncertainties in signature identification and assignment to samples can be circumvented using algorithms that rely on multiple signatures.

Results

Optimal mutational signature extraction framework

To evaluate competing methodologies, we performed in silico analyses simulating a dataset of 30 catalogues using ten known mutational signatures of single base substitutions. We investigated how the accuracy of signature extraction was affected by three factors. First, the NMF optimization algorithm: we compared three optimization algorithms using Lee and Seung KL divergence (Lee-KLD) and Frobenius norm (Lee-Frobenius) algorithms^7,8 and non-smooth NMF (nsNMF)⁹. Second, the clustering algorithm: we evaluated hierarchical clustering (HC), partitioning around the medoids (PAM) and clustering with matching (CM), whereby the lattermost approach enforces a critical additional constraint that signatures from the same NMF run should not belong to the same cluster (Methods). Third, discarding of poor local minima or solutions: we defined a metric using a relative tolerance (RTOL) from the best NMF run (i.e. the run with the lowest minimum, Methods and Extended Data Fig. 1), which we used to remove poor solutions from the analysis. We recovered all ten signatures with robust cosine similarities above 0.9, identifying the correct number of signatures only when using Lee-KLD and CM-clustering in combination with filtering for the best NMF runs (RTOL-filtering) (Fig. 1a-c and Methods).

Figure 1. Optimization of signature extraction framework.

A total of 30 mutational catalogues were simulated using 10 COSMIC signatures (n=5 replicate simulated datasets). Mutational signatures were extracted using different combinations of optimization, clustering and filtering algorithms: filter = only the best NMF runs are considered; no filter = all NMF runs are used; Lee KLD = Lee and Seung 2001 multiplicative algorithm with Kullback-Leibler Divergence (KLD); Lee Frobenius = Lee and Seung 2001 with Frobenius norm; nsNMF = non-smooth NMF with KLD; HC=hierarchical clustering with average linkage; CM = clustering with matching; PAM = partitioning around the medoids. (a) cosine similarity between the 10 COSMIC signatures and the signatures identified by each combination when the correct number of signatures k=10 is used, for each of the 5 simulated dataset replicates. (b) Average silhouette width (ASW) obtained after clustering using different numbers of signatures (range 8-12) and different combinations. Lines and error bars are mean and standard error of n=5 replicate simulated datasets. (c) Average normalized error using different numbers of signatures. Lines and error bars are mean and standard error of n=5 replicate simulated datasets. Note inflection point that indicates the number of signatures (10) in the cohort (d) Workflow of signature extraction and analysis using 3107 whole cancer genomes in this study. Source data for the analyses shown in this figure can be found in Source Data File 1.

Revisiting mutational signatures and identifying uncharacterized rearrangement signatures

The extraction framework of Lee-KLD, CM-clustering and RTOL-filtering identified above was applied to 3,107 whole genome sequenced (WGS) samples of 21 organs from the International Cancer Genome Consortium (ICGC) ^10–12 (Fig. 1d). A single global extraction was also performed on all samples in aggregate and deficiencies relating to this approach are provided (Supplementary Notes and Extended Data Fig. 2).

Organ-wise independent extractions yielded 192 substitution signatures (range of 3 to 15 signatures per tumor-type, named with a lettering system, e.g. Uterus_A, Uterus_B) and 116 rearrangement signatures (range of 2 to 10 per tumor-type) (Extended Data Fig. 3-6). Hierarchical clustering was performed on all organ-wise signatures (Extended Data Fig. 7a and 8a). The mean of each cluster group was defined as a Reference Signature (Extended Data Fig. 7b and 8b). Substitution reference signatures were numbered in accordance with the most similar COSMIC substitution signature ¹³ when possible without ambiguity, e.g. RefSig 1 was akin to COSMIC 1 (Extended Data Fig. 7b and 9). However, there were discrepancies. Two mismatch repair (MMR) reference signatures were obtained and did not map perfectly to COSMIC signatures: RefSig MMR1, bore similarities to COSMIC 6, 20 and 44; while RefSig MMR2, closely resembled both COSMIC 12 and 26. Notice that this does not necessarily mean that two MMR signatures exist. Rather, it implies that it was possible to cluster organ-specific MMR signatures into two groups. One reference signature resembled the profile induced by platinum-based compounds and was termed RefSig PLATINUM. Three reference signatures (RefSig MIXED1, MIXED2 and MIXED3) were likely recurrent combinations of other reference signatures. Unexplained and/or artefactual signatures were prefixed with letter N, from N1 to N12.

Rearrangement reference signatures were numbered as an extension of breast cancer rearrangement signatures reported previously ¹², with an R prefix to distinguish them from substitution signatures, e.g. RefSig R1 is equivalent to formerly identified rearrangement signature 1. Multiple rearrangement signatures were revealed. We previously presented two tandem duplication signatures: RefSig R1, characterized by tandem duplications of 100kb-1Mb and RefSig R3, comprising mainly short tandem duplications (<10kb) and associated with BRCA1-deficiency. Our analyses reveal a third tandem duplication signature: RefSig R14, distinct from RefSig R1, comprising very long tandem duplications (>1Mb) and seen specifically in ovarian cancers. Three distinct deletion signatures were also apparent: RefSig R5, characterized mainly by short deletions (<10kb) and sizeable contributions of deletions of 10-100kb and 100kb-1Mb, and previously reported to be associated with BRCA2 mutations; RefSig R7, characterized by longer deletions of 100kb-1Mb; and RefSig R9, defined specifically by extremely short deletions (<10kb).

There were three distinct signatures associated with clustered rearrangements: R6a (known), R6b and R12 (uncharacterized). One signature was associated with clustered (R4) and unclustered translocations (R2) each, both reported previously. R10 is associated with non-clustered rearrangements of most classes with shorter lengths, and R11 is characterized by non-clustered rearrangements of longer lengths. R13 is dominated by inversions. R15-R20 are only found in single tumors, are not pronounced, do not demonstrate hypermutator phenotypes, and could represent artefactual signatures, and therefore require further validation. In all, we identify nine previously uncharacterized rearrangement phenotypes and dissect distinct driver associations below.

Visualizing similarities and differences between organ-wise signature extractions

Although informative for seeking commonalities across tissues, reference signatures are simply mathematical norms. Exploring cosine similarities between signatures within each cluster and their reference signature, we find some organ-derived mutational signatures were very similar to their reference signatures while others showed greater variability (Fig. 2a-h). For example, cosine similarities for RefSig 2 show a very tight distribution, while cosine similarities for RefSig 17 show a broad distribution (Extended Data Fig. 7c and 8c). Consequently, we considered that sources of variation could be due to mathematical limitations or possibly due to inter-tissue differences.

Figure 2. Relationships between organ-specific mutational signatures.

(a,b,c) signatures similar to COSMIC13 and that belong to the RefSig 13 cluster, extracted independently from Breast, Uterus and Cervix cancer datasets. Organ-specific signature names are given as letters and numbers, where numbers represent the reference signatures that are present in each signature according to the conversion matrix. (d) RefSig 13, obtained as the average of 8 signatures (n=8) extracted from different organs, error bars are standard error. (e,f,g) signatures similar to COSMIC3 and that belong to the RefSig 3 cluster, extracted independently from Breast, Ovary and Uterus cancer datasets. (h) RefSig 3, obtained as the average of 8 signatures (n=8) extracted from different organs, error bars are standard error. (i) Signature Uterus_F (Uterus_3_8) can be reconstructed as a linear combination of two Breast signatures (0.95 cosine similarity). (j) Signature Biliary_C (Biliary_2_13) can be reconstructed as a linear combination of two Breast signatures (0.98 cosine similarity). (k) Network connecting highly similar signatures across different organs. Each circle represents a signature and is colored according to the closest COSMIC signature (C1-C30) based on cosine similarity. An arrow is drawn from signature A to B (with A and B from different organs) if A has at least 0.89 cosine similarity with B, or if a linear combination of A and C (with A and C from the same organ) has at least 0.89 cosine similarity with B. To focus only on high contributions of the linear combination, only the arrows that represent a contribution of at least 65% are shown (e.g. if a combination of 65% of A and 35% of C is used, then only the arrow from A to B is shown, but not the arrow from C to B). Because of this restriction, only 157 of the 192 signatures and 861 of the 1925 edges are shown. To explore these parameters in more depth, an interactive version of these plots can be found here: https://signal.mutationalsignatures.com/explore/cancer/network. Detailed data for the analyses shown in this figure can be found in Extended Data Figs 3-4 and Supplementary Table S2 (organ-specific substitution signatures), Extended Data Fig 7 and Supplementary Table S4 (Reference signatures), and Supplementary Table S11 (substitution signatures network).

To explore this systematically, we asked whether signatures derived from every organ could be matched by combinations of signatures from other organs (Methods). For example, Uterus_F appears to be a mix of homology-directed recombination repair deficiency (HRD) patterns and is very similar to a linear combination of Breast_E (analogous to COSMIC 8) and Breast_K (analogous to COSMIC 3) (0.95 cosine similarity, Fig. 2i). Likewise, Biliary_C is a mix of APOBEC-related signatures Breast_B (COSMIC 2) and Breast_C (COSMIC 13) (0.98 cosine similarity, Fig. 2j).

Signature relationships obtained in this analysis can be visualized as a network, whereby nodes are signatures and directed edges indicate the direction of the matches (Fig. 2k). It provides a representation of how similar (or diverse) extracted signatures are between organs, and which signatures can be independently extracted or tend to mix (browsable map: https://signal.mutationalsignatures.com/explore/cancer/network).

Some interesting insights were uncovered. Signatures that are recurrently extracted from many tissues and are relatively alike between organs form highly-connected, dense subnetworks, for example the subnetworks associated with deamination of methyl-cytosine, COSMIC 1 (C1), and a signature of unknown aetiology (C17). Subnetworks of APOBEC-related damage (associated with C2 and C13) are connected. While some tissues exhibited distinct separation between C2 (mainly transitions of C>T at a TpCpN context) and C13 (mainly transversions of C>G at TpCpN context) (e.g. breast), others (e.g. cervix) consistently produced a mixed phenotype in spite of high numbers of mutations and adequate power in these tissues. Signatures due to mutations in POLE (C10) and associated with exposure to aristolochic acid (C22) are only found in two tissues but are virtually identical in independent extractions, and form small, isolated subnetworks. By contrast, signatures that are associated with redox damage (C18) are frequently found across organs but less similar between them and have a loosely-connected subnetwork. Signatures associated with mismatch repair deficiency (MMR) are found recurrently across organs, and are dissimilar to each other forming lowly-connected subnetworks. The subnetwork of signatures associated with deficiency of HR (C3) are notably connected to other subnetworks (C8 and C5), while the C5 subnetwork is not dense and connected to subnetworks of C30 and C16. These data provide an awareness of the complexity of mutational signature extraction and the variation in behaviors of different signatures. More critically, it suggests that taking a one-size-fits-all method of using a mathematical average such as a reference signature or COSMIC signature to perform the fitting step, i.e. quantifying the amount of each signature (or exposures) in each sample, may not perhaps be the most appropriate approach. Indeed, enforcing a COSMIC/reference signature that is rather different to what is truly present in that tissue could propagate bias throughout the rest of the signature fitting process.

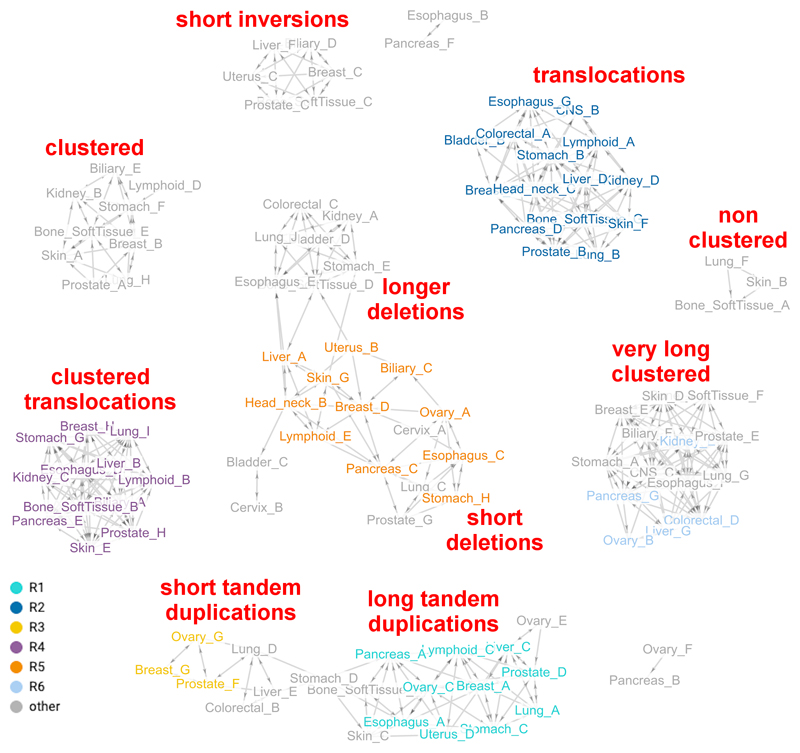
Interestingly, the rearrangement network (Fig. 3) presents ten subnetworks. Of these, eight are fully-discretized, including highly-recurrent signatures characterized by clustered rearrangements, short inversions and translocations, and infrequent signatures resulting in three small subnetworks. The long deletion subnetwork was connected to the short deletion subnetwork. Likewise, there was a connected set of tandem duplication subnetworks.

Figure 3. Relating rearrangement mutational signatures obtained from independent organ-wise extractions.

Network connecting highly similar rearrangement signatures across different organs. Each circle represents a signature and is colored according to the closest rearrangement signature derived in Nik-Zainal et al. 2016, based on cosine similarity. Principles of visualization are based on description in Figure 2. 106 of the 116 signatures and 676 of the 1146 edges are shown. Detailed data for the analyses in this figure can be found in Extended Data Figs 5-6 and Supplementary Table S3 (organ-specific rearrangement signatures), and Supplementary Table S12 (rearrangement signatures network).

Network visualization illustrates variation of signatures between organs and raises interesting points. Signature variability could reflect organ-specific biological variance where different tissues possess subtle differences in mutational outcomes even for the same gene defect. This could be because there is frequent biological co-occurrence of two mutational processes in some tissues more than others (e.g. APOBEC signatures 2 and 13). It is also possible that that the lack of power due to a low number of mutations caused by certain mutational processes and/or a low number of samples per organ may be confounding the extraction process. This is less likely because of the large number of samples available for relevant organs. Also, some signatures are consistently difficult to distinguish regardless of mutation burden or sample size, possibly due to the presence of multiple solutions to the NMF problem. Multiple solutions can be visualized by principal components analysis (PCA) as circular structures (Extended Data Fig. 1d,e). This involves selected signatures (e.g. COSMIC 3, 5 and 8 in Extended Data Fig. 1e) indicating that it is an intrinsic property of particular signatures only.

Analysis in another cohort reinforces mutational signature inter-tissue variation

To understand whether observed inter-tissue variation in mutational signatures are recurring and reproducible, we sought an independent cohort of WGS samples. 3,096 metastatic cancers derived from 15 tissue-types were available for analyses from the Hartwig consortium¹⁴. Organ-wise signature extractions were performed based on primary-tissue-of-origin (e.g. a lung metastasis of a breast cancer was grouped into “breast”). Comparing each set of signatures extracted from an individual organ in the metastatic cohort against all signatures extracted in the previously analyzed primary ICGC cohort (‘ICGC cohort’) revealed that signatures from the same organ are usually most similar to each other (Methods and Fig. 4). The highest similarities between organ-specific signatures across the two cohorts was evident for 14 of 15 organs compared, seen as enrichment along the diagonal in Fig. 4 (p-value lower than 0.01 in eight organs). Pancreatic cancers appeared to be an exception, possibly due to the large number of signatures present (15) and lower number of samples in the metastatic cohort (75 as opposed to 313 in the ICGC cohort). A recurring concern in the mutational signatures field is the uncertainty around the number of signatures that are present in a dataset. Thus, in our analysis, we show that even when the number of signatures picked for the metastatic cohort is not the optimal one, allowing the number of signatures extracted to be +1, +2 or -1 and -2 around the optimal solution, we find the resulting metastatic cohort signatures to remain most strongly associated with signatures extracted from the matching organ in the ICGC cohort. These results reinforce the notion that there are tissue-specificities in mutational signatures of diverse organs.

Figure 4. Comparison of organ-specific signatures in two cohorts.

Comparison across 15 organs present in both primary (ICGC, n=3107 samples) and metastatic (Hartwig, n=3096 samples) cohorts. We considered the probability of a set of m from h signatures extracted in each organ in Hartwig (x axis) to best match the K signatures extracted in each organ in ICGC (y axis), when performing a comparison with a total of N=150 signatures obtained across the 15 organs. Color intensity indicates the -log10 of the p-value obtained with a one-sided fisher-test, and p-value <0.01 are highlighted with an asterisk. For each organ, the optimal number of signatures for Hartwig is the middle number shown on the x axis. The results for the signatures obtained for the two preceding and subsequent ranks of extraction [h-2,h+2] are also shown respectively on the left and on the right of the optimal number. Detailed Data for the analyses shown in this figure can be found in Supplementary Table S2 (ICGC signatures) and S111 (Hartwig signatures).

Fitting mutational signatures into samples

Given the observed organ-specificity, we estimated sample exposures by fitting organ-specific signatures rather than reference signatures (Fig. 1d). Reference signatures are therefore used mainly for purposes of orientation, informing us regarding which general mutational processes may be present. If required, one can convert organ-specific signature exposures into exposures of reference signatures using a conversion matrix (Methods and Fig. 5i, Supplementary Tables 9 and 10). The conversion matrix also allows us to name the organ-specific signatures using reference signature numbers (Extended Data Fig. 3-6).

Figure 5. Fit of mutational signatures per sample.

(a) A simulated mutational catalogue composed of a combination of COSMIC signatures 1, 5, 12, 13 and 18 and added Poisson noise. (b) Mathematical model of the simulated sample in (a) as the linear combination of ten mutational signatures, where the number of mutations for each signature (i.e. point estimate exposures) is the median across n=100 bootstrapped runs of KLD optimization (shown in d), followed by removing exposures of signatures that are not statistically higher than the threshold of 5% of total mutations (p-value threshold 0.05, p-value estimated as the proportion of values less than or equal to 5% of total mutations – one sided test). (c) The mutations that are removed are considered unassigned. (d) The numbers of mutations for each signature across the 100 runs. Boxes show median, 1^st and 3^rd quartile, with whiskers extending at most 1.5∙IQR. The blue cross indicates the original number of mutations used to simulate the sample, and the red circle indicates the point estimate exposures as described in (b). The green line indicates the threshold of 5% of total mutations. (e) Correlation between exposures of signatures across the 100 runs (same data as in d). Examples of correlations of exposures (same data as in (d)) between (f) signatures 12 and 5 (g) signatures 5 and 3. (h) Normalized reconstruction error across the 30 samples in the simulated cohort. The sample with significantly higher error than the others is Sample_5, the same sample in (a). The p-value threshold for a one-sided test was 0.01, and the p-value was estimated for each sample as the probability of an error greater than or equal to the one obtained for the sample, considering a normal distribution with mean and standard deviation estimated from all the samples’ errors excluding the tested sample. (i) Conversion matrix Q used to map exposures of Biliary organ-specific signatures of a sample e into exposures of reference signatures e’. Each organ specific signature can map to one or more reference signatures. (j) Correlation between the number of signatures extracted in each organ and the average number of unassigned mutations in the samples of the same organ. Detailed data for the analyses shown in this figure can be found in Source Data file 1 (simulated datasets), Supplementary Table S9 (conversion matrix), and Supplementary Tables S2,S13-S33,S112 (substitution signatures, exposures and catalogues used in panel j).

We acknowledge the ambiguity associated with fitting mutational signatures to individual samples, which comes from having multiple similarly suitable solutions. To investigate this, we used a recently published bootstrap-based method ¹⁵ that produces a distribution of exposures. Point estimate exposures were obtained as the median of the distribution. To increase specificity, exposures were set to zero if they were not statistically higher than a given threshold (p-value of 0.05) (Methods, Fig. 5d and Extended Data Fig. 10). Mutations removed were considered unassigned (Fig. 5c). The higher the fraction of unassigned mutations, the more uncertain the overall signature fit.

To illustrate our method, we considered a simulated sample: Sample_5 of repeat 4 of our simulation study (Fig. 5a-g). The original simulated sample comprised five signatures (COSMIC 1, 5, 12, 13 and 18) (Fig. 5d). All signatures were assigned correctly with the exception of COSMIC 5, which presented high uncertainty in exposures across bootstrap runs, and was hence not assigned (Fig. 5d). To understand this uncertainty, we looked at correlations of exposures across bootstrap runs (Fig. 5e) and found that COSMIC 5 exposures negatively correlated with COSMIC 12, 3 and 8. In some bootstrap runs, it was possible to replace COSMIC 5 with a combination of COSMIC 12 and 3 (Fig. 5f,g). Thus, signatures that should not be present in a sample (here COSMIC 3) affected robustness of fitting of signatures. Often, samples that are particularly difficult to model can be spotted, as they present a higher normalized error than the rest of the samples in the dataset (Fig. 5h).

Lastly, when a higher number of mutational signatures were used for fitting, a higher number of unassigned mutations were observed implying greater uncertainty in signature fitting (Fig. 5j). Uncertainty could therefore be reduced by presenting fewer a priori mutational signatures for fitting. Moreover, it makes little sense to present a very wide a priori set of signatures for fitting into individual samples, especially when those signatures are not known to be present in a particular tissue. The risk of over-fitting and mis-assigning a signature to a sample when it is not there, is greater.

Thus, here we captured the uncertainty intrinsic to fitting mutational signatures. We are, however, able to report the degree of uncertainty and identify samples that are difficult to fit. We also suggest that reducing the number of signatures to be fitted to a dataset improves the fitting process. This is best achieved by making an informed choice of the closest tissue-of-origin of any interrogated dataset. As an example, seeking the presence of signatures for a set of biliary cancers could be restricted to known biliary signatures. This would not preclude the possibility of finding novel signatures which may be reported in remaining mutations that are unassigned to the known signatures (Fig. 5c). This functionality is available via the Signal analysis interface (https://signal.mutationalsignatures.com/analyse).

Associations between drivers and mutational signatures

We next explore relationships between substitution/rearrangement signatures and curated substitution/indel mutations that are predicted to be drivers and copy number aberrations including amplifications and homozygous deletions as characterized by the ICGC Pan-Cancer Analysis Working Group¹⁶. While we use organ-specific signatures in the statistical analysis, we convert the exposures of these signatures into reference signatures using the conversion matrix, in order to identify the most-likely related mutational processes across organs (Methods).

Driver-signature relationships are presented as target plots (Fig. 6). Strength of association (p-value) is reflected in depth of color of the central circle. The left-hand semi-circle reports the proportion of samples that carry the driver that also have the signature. The right-hand semi-circle reports the proportion of samples that carry the signature and also carry the driver. The outermost ring reports the organs of the samples that have the associated driver and signature. Some interesting insights are revealed.

Figure 6. Signature-Driver associations.

Sets of samples with specific drivers and reference signatures are compared using two-sided Fisher Exact test with Bonferroni multiple hypothesis testing correction, assuming a p-value threshold of 0.01 before correction. The amount of reference signature in each sample is obtained by converting exposures of organ-specific signatures using the conversion matrix (Methods). An explanation of the driver-signature association circle plot is shown on the top-right corner. The central number indicates how many samples have both the signature and the driver, with red shade background indicating the negative log10 p-value of the association. The two blue semicircles indicate the proportion of samples with the driver that also have the signatures (left) and the proportion of samples with the signature that also have the driver (right). The outermost circle indicates the originating organs of the samples in the intersection. (a) Substitution or rearrangement reference signatures are shown on the left and the corresponding signature-driver associations are shown on the right. Details about the reference signatures can be found in Extended Data Fig. 7. (b) All TP53 associations obtained from the analysis. Detailed data for the analyses of this figure, along with sample sizes and p-values for each driver-signature association can be found in Supplementary Tables S53-S110.

The association between Signature 10 with POLE mutations is well-known¹⁷. Here, the association is present across multiple tissues (colorectal and endometrial) and is highly specific (dark left and right semi-circles), i.e. samples with the driver always have the signature and vice versa. A similarly strong driver-signature relationship was found between CDK12 mutations and RefSig R14¹⁸ (characterized by dispersed tandem-duplications of 100Kb-10Mb), an ovarian-specific signature.

Other previously-described associations are RefSig 3 and RefSig 8 with BRCA1/BRCA2 mutations¹², RefSig R3 (unclustered tandem duplications 1-100Kb) with BRCA1 mutations¹⁹, and RefSig R5 (unclustered deletions up to 100kb) with BRCA2. Previously uncharacterized signature RefSig R9 (unclustered deletions up to 1-10Kb)—found in esophagus, lung, stomach, pancreas and prostate—is also significantly associated with BRCA2 in this analysis. For these relationships, target plots demonstrate a dark left semi-circle but relatively light right semi-circle. This is because samples that have these drivers almost always carry these respective mutational signatures. However, the reverse does not hold true: samples that have these individual mutational signatures do not always carry these drivers. This is important to recognize as it suggests a lack of specificity of the signature. Furthermore, for substitution signature RefSig 3 which has started to be used to define HR-deficiency for patient stratification²⁰, other driver mutations are also associated including MYC, NF1, ARID1A and LINC00290. While it is difficult to absolutely exclude confounding, these associations would suggest that RefSig 3 individually is not as specific to BRCA1/BRCA2 as has been previously assumed. Mechanistically, a source for RefSig 3 mutagenesis has not been definitively worked-out. It may reflect non-specific upregulation of error-prone translesion activity when a broad range of genes/pathways are compromised.

An association between RefSig R1 (long tandem duplications) and CCNE1 amplifications was previously described. Here, we reveal that the association is not limited to breast and ovarian cancer and is also found in esophagus, lung, pancreas and stomach. In individual samples (e.g. DO50452 in esophagus; DO25010 in lung; DO51485 and DO51476 in pancreas; DO218030 in stomach), RefSig R1 manifests as a marked, hypermutator phenotype. RefSig R1 has previously been linked to replication through its particular enrichment in early replicating domains²¹. It was reported to possibly create mini-drivers through minor copy number increases of breast cancer super-enhancer and breast cancer susceptibility loci at hotspots in the genome.²² This tandem duplicator phenotype is thus a highly malignant signature. Interestingly, CCNE1 mutations are also associated with RefSig 17, a signature that has been associated with metastatic disease and poor outcome²³. CCNE1 has a role in regulating cell cycle control. Driver mutations in this gene could result in replication stress which may be contributing to the observed signature phenotypes. We postulate that CCNE1 driver mutations predispose to genomic phenotypes of high genomic instability at substitution and structural variation levels, which promote evolvability and aggressive malignant disease.

By contrast, the association observed between RefSig 17 and enhancer region chr7:86865600-86866400 must be considered differently²⁴. Mutations at chr7:86865600-86866400 are often T>C transitions and T>G transversions, in-keeping with Signature 17 sequence-context specificity, indicating that these mutations developed as a consequence of the signature. A similar consequential relationship between signature and driver underpins the association between RefSig MMR1 and RPL22, where a polynucleotide tract in the gene is frequently mutated in MMR deficient samples²⁵. Likewise, PIK3CA mutations have also been previously described as a consequence of APOBEC-related RefSig 13²⁶.

Other associations of note include MDM2 mutations and CDK4 amplifications with RefSig R4, R6a and R6b. FAT1 mutations are also noted to be associated with Refsig 13. These observations are interesting because resistance to cyclin dependent kinase 4/6 (CDK4/6) inhibitors (CDK4/6i) in estrogen receptor-positive (ER⁺) breast cancers was recently shown to be attributed to loss-of-function mutations in FAT1²⁷, inducing resistance through the Hippo pathway. RefSig 13 may thus be a harbinger of aggressive biological phenotypes and is enriched in metastatic cancers.

Lastly, driver mutations in TP53 appear to be strongly associated with multiple signatures (Fig. 6b). Unlike other driver/signature relationships, target plots recurrently present a dark right-semicircle and light left semi-circle across multiple tissues. Thus, the vast majority of tumors carrying these signatures are TP53-mutated, but the reverse is not true—not all TP53-mutated tumors carry the individual signatures. Many of the associated signatures can create hypermutator phenotypes resulting in striking genomic instability (RefSig 17, 18, R1, R3 and R5). We therefore postulate that most mutational signatures with hypermutator phenotypes have a dependency on TP53 dysregulation. The considerable amount of genomic instability that is associated with these signatures is likely only tolerable in cells that are permissive, such as those that have compromised DNA-damage-response. Notable exceptions are the signatures associated with MMR deficiency and POLE mutations, which do not depend on TP53 mutations.

Estimation of a confidence interval for the HRDetect score

HRDetect is a classifier that uses multiple mutational signatures to estimate an HRD probability score^11,28 (Methods).

HRDetect’s classification performance remained robust (near 1 AUROC) despite changes in signature extraction and assignment procedures. This was confirmed in a variety of datasets, including a newly-sequenced dataset of triple negative breast cancers²⁹ (Fig. 7a).

Figure 7. Prediction of Homologous Recombination Deficiency (HRD) across 21 organs.

(a) Receiver operating curves (ROC) obtained by applying HRDetect to four independent datasets: breast (n=327 samples, of which 93 with BRCA1 or BRCA2 biallelic loss), ovary (n=68 samples, of which 27 with BRCA1 or BRCA2 biallelic loss) and pancreatic (n=89 samples, of which 5 with BRCA1 or BRCA2 biallelic loss) cancer data used in this and previous studies ¹¹, and SCANB data (n=235 samples, of which 95 with HRD), an independent breast cancer dataset²⁹. The mutational signature analysis in the four datasets was recalculated using the bootstrap signature fit framework presented in this article. (b) Empirical distributions of HRDetect score for four breast cancer samples. Boxes show median, 1^st and 3^rd quartile, with whiskers extending at most 1.5∙IQR. Yellow diamonds indicate the HRDetect single score. Red dots are the HRDetect samples that compose the empirical distribution (n=1000). (c) Estimation of HRD in 741 breast cancer samples. HRDetect single score is indicated in black; median and 5%-95% quantiles of the HRDetect score distribution are indicated in red and light grey respectively; BRCA1 or BRCA2 null samples are indicated in green at the bottom. (d) HRD across 21 organs as predicted by HRDetect or RefSig 3. The total number of samples in each organ is indicated in red at the top. Each bar indicates the percentage of samples classified as HRD. Cut-offs are as follows: HRDetect confidence interval (5-95^th percentile) entirely above 0.5 (white); HRDetect single score higher than 0.7 (grey); at least 1000 mutations attributed to RefSig 3 (blue); RefSig 3 present in the sample (orange). The amount of reference signature in each sample is obtained by converting exposures of organ-specific signatures using the conversion matrix (Methods). Detailed data for the analyses shown in this figure can be found in Supplementary Table S8.

We introduced confidence intervals by calculating an empirical distribution, repeatedly computing HRDetect scores while sampling from the distribution of input features, for each sample (Methods, Fig. 7b-c). The confidence interval was calculated as the 5-95^th percentile interval of the score distribution. Some samples presented clear HRD classification, with narrow distributions for both high or low HRDetect scores (e.g. PD11346a and PD22355a, Fig. 7b). Other samples had wider distributions (e.g. PD24186a and PD13622a, Fig. 7b), indicating that classification was less certain. HRDetect confidence intervals (Fig. 7c) therefore provide additional information that could aid decision-making.

Homologous recombination deficiency across 21 organs

Finally, uncertainty in estimating signature exposures could affect tumor stratification of therapeutically-targetable biological abnormalities like HRD. HRD was estimated in samples across 21 organs using four approaches: HRDetect with confidence interval above 0.5, HRDetect single score above 0.7, any exposure of substitution signature RefSig 3 (equivalent to COSMIC 3), and a conservative exposure of RefSig 3 (>1000 mutations) (Fig. 7d). Note that although we refer to the signature as “RefSig 3”, we use the organ-specific signatures and convert the samples’ exposures to reference signatures using the conversion matrix (Fig. 5i).

The two HRDetect-based approaches (Fig. 7d, white and grey bars) corresponded with each other in HRD estimation, with the highest HRD incidences observed in ovary, breast and uterine cancers. RefSig3-based prediction overestimated HRD (Fig. 7d, blue vs white bars) in esophagus, lung, head and neck, and uterine cancers. When RefSig 3 presence was used for classification, the number of samples miscalled as HRD increased (Fig. 7d, orange vs blue bars). Thus, the mere assignment of RefSig 3 to a sample does not imply HRD.

Of note, RefSig3-rich samples can be distinguished into two subsets: one enriched with BRCA1/BRCA2 mutations, high proportion of deletions with microhomology and high HRDetect scores, while the other not. Yet, both subsets were associated with other drivers such as RB1, NF1 and MYC (Fig. 8a). RefSig 3 is therefore likely not as specific as previously believed. The identification of HRD should rely on multiple orthogonal mutational signatures like that provided by HRDetect.

Figure 8. Analysis of samples with high mutational burden of RefSig 3 and overview of the signature analysis framework.

(a) Features that are known to correlate with homologous recombination deficiency (HRD) have been standardized (subtract mean and divide by standard deviation) and visualized as a heatmap. Only samples with high burden of RefSig 3 (at least 1000 mutations) are included in this analysis (n=489 samples). On the right of the heatmap, sample annotations are shown, including organ of origin, HRDetect classification and relevant driver mutations. The amount of reference signature in each sample is obtained by converting exposures of organ-specific signatures using the conversion matrix (Methods). (b) Signatures are extracted and fit to samples organ-wise. Extracted signatures are clustered to determine reference signatures, which represent common mutational patterns that are likely to be caused by the same mutational process. Organ-specific signature exposures are converted into reference signature exposures using a conversion matrix, obtained by mapping organ-specific signatures to one or more reference signatures. (c) If a new sample needs to be analyzed, organ-specific signatures corresponding to the organ of origin are fit to the sample to obtain organ-specific exposures, which are then converted into reference signature exposures, which in turn can be used in other analyses such as HRD prediction with HRDetect. Detailed data for the analyses shown in this figure can be found in Supplementary Table S8.

Signal: A website for mutational signatures

Finally, to crystallize these analyses into a browsable format, we present Signal, a comprehensive online reference database of mutational signatures (https://signal.mutationalsignatures.com). It is divided into two distinct sections: Explore, which allows users to explore cancer-derived mutational signatures across 21 tumor-types as described in this manuscript, as well as experimentally-generated mutational signatures³⁰ from previously published datasets; and Analyze, which serves as an analysis website permitting users to upload their own data and perform refitting of previously identified signatures (including prior versions of COSMIC signatures). It also reports residual mutations that may be new signatures in a given dataset. Further details of how to use the website can be found in supplementary information. The website will be updated as more datasets are sequenced, and as new knowledge emerges in due course.

Discussion

We offer a consolidated mutational signature analysis framework, apply it to a cohort of >3,000 WGS tumors and identify known and previously undescribed signatures. We highlight relationships with driver mutations including TP53-dependency in hypermutator-associated signatures. We reinforce the importance of accurately assigning signatures to individual samples, demonstrating the impact on a clinical application, HRDetect. We shed awareness into the complexity of mutational signatures and herewith make practical suggestions for using our analytical framework, with an accompanying web-based tool for ease of use.

An important principle that we present is that “reference” mutational signatures may not be elemental. Although it is possible that observed inter-organ variation is caused by mathematical idiosyncrasies, there may be biological variation of similar mutational processes in different tissues, which may result in variation in signatures between tissues. This is plausible: for any given gene, we already know that expression is variable from one tissue to another. Protein products may also behave differently, may have an assortment of interactors, and may be called upon at different times in diverse tissues. Our framework does not suppress that variation and permits it to be appreciated for further evaluation in due course.

Additionally, far from being simply of academic fascination, it may have important implications in the assignment of mutational signatures into individual samples: enforcing signature profiles that are not in fact present in a tissue will have downstream consequences on the rest of signature assignments, perpetuating bias.

On this score, it is important to appreciate that fitting of signatures into samples (given a set of a priori signatures) is purely mathematical. The critical factor is what a priori signatures are presented for fitting. Simply choosing all 40 known signatures does not make biological sense. Given those options, the mathematical fitting step will try to fit as many of those signatures as possible, unless arbitrary constraints, such as a maximum number of signatures, are introduced. Our pragmatic recommendation is to fit signatures as follows: when analyzing a naive sample (Fig. 8b,c), organ-specific signatures that correspond to the closest cell-of-origin of the sample should be used. If organ-specific exposures need to be converted into reference signatures exposures, such as for HRDetect analysis, a conversion matrix can be used to do so (Fig. 5i).

This work acknowledges the extensive complexity in extracting signatures and assigning them to samples. We suggest a framework of how to pragmatically deal with these issues. As experimental data begins to come through, we should remain critical of previous assumptions and revisit these frameworks, paying particular attention to rare, or highly mutagenic signatures and aiming to reduce false positive signature assignments to samples.

Methods

Datasets

We used two large pan-cancer datasets: one for the main analysis, the ICGC cohort; and the other for validation, the Hartwig cohort.

In the ICGC cohort we used somatic variants data of primary tumors from published whole genome datasets: i) a dataset of 560 breast cancers ¹² (EGAS00001001178); ii) a dataset of 80 breast cancers ¹¹ (EGAD00001002740); iii) a dataset with 2577 tumors from the Pan Cancer Analysis of Whole Genomes (PCAWG) ¹⁰ of the International Cancer Genome Consortium (ICGC) (EGAS00001001692). The PCAWG dataset is organized into 21 organs as follows: Biliary (34), Bladder (23), Bone_SoftTissue (89), Breast (211), Cervix (20), CNS (287), Colorectal (52), Esophagus (97), Head_neck (56), Kidney (186), Liver (314), Lung (84), Lymphoid (197), Myeloid (38), Ovary (110), Pancreas (313), Prostate (199), Skin (107), Stomach (68), Thyroid (48), Uterus (44). There are 110 samples that belong to both the 560 breast cancers and the Breast PCAWG dataset, thus the final size of the Breast cancer dataset used for extraction is 741 samples (450+80+211). Overall, the total number of samples used for signature extraction is 3107, for a total of 47,864,577 SNVs and 358,096 rearrangements.

The Hartwig cohort contains 3096 metastatic cancers across 15 organs (data access at www.hartwigmedicalfoundation.nl/en) organized as follows: Bone_SoftTissue (164), Breast (661), Nervous System (78), Colon-Rectum (493), Esophagus (138), Head_and_Neck (61), Kidney (100), Liver (48), Lung (368), Ovary (144), Pancreas (75), Prostate (368), Skin (293), Stomach (39), Uterus (66). The total number of SNVs in this cohort is 86,244,691.

Non-negative matrix factorization

Briefly, given an M-by-N positive matrix C that contains M mutational features, also called channels, for N samples, NMF seeks to find two positive matrices P (M-by-k) and E (k-by-N) such that C ≈ PE. The columns of P are then normalized to sum to unity, so that each column of P contains the probabilities of the mutational features in one of the k mutational signatures, while E, called exposure or activity matrix, contains the number of mutations that are attributed to each signature in each sample. Thus, in NMF, the mutational profile of each sample in C, called the catalogue, is modelled as a linear combination of mutational signatures. The number of signatures k is not known a priori and needs to be estimated. To do so, for each k, NMF is run multiple times on bootstrapped mutational catalogues, the solutions are clustered and goodness-of-clustering metrics such as average silhouette width (ASW) are computed. The ASW, along with the average error (the difference between reconstructed catalogues based on putative signatures and the original catalogue), is used to manually estimate the number of signatures k⁴. The estimation of k can be ambiguous, for example when the number of signatures present in a dataset is large. After clustering the solutions, we select as consensus mutational signatures the medoids of the clusters.

To compute the NMF optimization we used the R package NMF ³¹, which supports the Lee and Seung multiplicative algorithms ⁸, with the Kullback-Leibler divergence (Lee KLD) (method “brunet”) and Frobenius norm (Lee Frobenius) (method “lee”) objective functions, and the non-smooth NMF (nsNMF KLD) algorithm (method “nsNMF”) ⁹, with KLD objective function. In nsNMF KLD, a smoothing matrix S (k-by-k) is introduced and the optimisation problem becomes to find P′ and E′ such that C ≈ P′SE′. Matrix S = (1 − θ)I + (θ/k)11^T’, with the smoothing factor θ = 0.5. We then set the exposure matrix to E = E’ and the signatures matrix to P = P′S, so that C ≈ PE, inducing E to be sparse and P to be smooth. For all three algorithms, random initialization is used, while the convergence of the connectivity matrix is used as stop criterion.

For clustering, we considered hierarchical clustering with average linkage (HC), partitioning around the medoids (PAM) and clustering with matching (CM). The lattermost approach enforces an additional constraint that signatures from the same NMF run should not belong to the same cluster (Supplementary Notes).

To identify the best NMF solutions which should be used for clustering, and discard poor local minima, we defined a relative tolerance (RTOL) from the best NMF solution (i.e. the run with the lowest minimum). Examining multiple NMF runs applied to a dataset of 560 breast cancers (Extended Data Fig. 1a,c), we observed that an RTOL of 0.1% improves cluster separation (Extended Data Fig. 1d,f) and hence, the ASW. This was confirmed in other datasets (e.g. PCAWG, Extended Data Fig. 1g), and is robust for a minimum of 100 runs (Extended Data Fig. 1h). Thus, we used RTOL=0.1% in subsequent analyses.

Clustering with matching

Clustering with matching is an algorithm that clusters mutational signatures obtained from multiple runs of NMF, with the constraint that signatures from the same run cannot belong to the same cluster. We developed this algorithm to be more rapid (Supplementary Notes) than general-purpose constrained clustering algorithms, such as constrained k-means ³². The algorithm is composed of two parts. In the first part, signatures from n runs are matched pair-wise by solving the assignment problem ³³ (e.g. the k signatures from run 1 are matched against the k signatures from run 2, and so on for all combinations), minimizing the average cosine similarity between matched signatures. This results in n(n − 1/2) matches of signatures that can be ordered with respect to the average cosine similarity of the matches. In the second part, starting from the match with the highest average cosine similarity, the individual matches are merged until all runs are merged and thus all signatures assigned to a cluster. See Supplementary Notes for details.

Simulation study and signature extraction procedures

We consider ten of the most ubiquitous COSMIC mutational signatures, namely signatures 1, 2, 3, 5, 6, 8, 12, 13, 17 and 18. We simulate 30 samples using these signatures, so that each sample is a linear combination of five randomly selected signatures, with the addition of Poisson noise. Note that we do not simulate a very large number of samples because this does not reflect real-world user datasets, which are often smaller (tens). The number of mutations in each sample is randomly selected between 1000 and 50000 mutations, in log scale so that a lower number of mutations is more likely to be selected. The proportion of each signature in each sample is also random.

To obtain a bootstrapped catalogue we resample the same number of mutations in the original catalogue and we assign them to the channels using as probability for this assignment the proportion of the channels in the original catalogue.

In the “filter” approach, for each of 20 bootstrap catalogues, we perform 50 NMF runs and select only the runs that have optimal objective function value within a relative tolerance (RTOL) of 0.1% from the best. To limit the computation time of the clustering, we limit the number of signatures that need to be clustered by selecting at most 10 random best NMF runs for each bootstrap catalogue. In the “no filter” approach, we perform only one NMF run for each bootstrap catalogue and use 1000 bootstrap catalogues, so that the total number of NMF runs performed in the filter and no filter approaches is the same. Then, we cluster the mutational signatures obtained from all 1000 NMF runs.

According to our in-silico analysis, only while using Lee KLD in combination with filtering for the best NMF runs did we recover all ten signatures with a cosine similarity robustly above 0.9. (Fig. 1a).

The number of mutational signatures is estimated using ASW and the level of error. If too many signatures are selected for a solution, ASW decreases sharply and the error stops decreasing ⁴. In the simulated scenario, only when Lee KLD optimization algorithm was combined with RTOL-filtering of best NMF runs and CM clustering, were the correct number of signatures identified from a clear descent in ASW (Fig. 1b). Moreover, only when using Lee KLD did the error stop decreasing at the correct number of signatures (Fig. 1c).

Overall, our analyses indicated that Lee KLD for optimization combined with filtering of best NMF runs significantly improved identification of mutational signatures. The constraint preventing signatures from the same run clustering together was critical in improving the identification of the correct number of signatures based on ASW (Fig. 1b).

Signature extraction in 21 organs

We performed 23 extractions for substitutions and 19 for rearrangements, and assigned letters to the obtained signatures, prefixed with the organ name (e.g. Kidney_A, Lung_A and Lung_B). In the case of the Skin and Colorectal cancer substitutions datasets, two extractions for each organ were performed, one with hypermutated samples (with overwhelming presence of COSMIC signatures 7 and 10) and one with the remaining samples. This yielded 2 sets of signatures for these organs that were combined into one set for each organ. Samples with less than 20 rearrangements were excluded from the rearrangement extraction. Rearrangement extraction was not performed on Thyroid and Myeloid because of the low incidence of rearrangements in these organs. For each extraction, 20 bootstraps and at least 500 NMF runs per bootstrap were used. Best NMF runs were filtered using RTOL of 0.1%. Algorithms Lee KLD and clustering with matching were used. All 192 substitution signatures and 116 rearrangement signatures are presented in Supplementary Tables S2 and S3.

Signature Visualization Network

To produce Fig. 2k and Fig. 3, we used a simplified signature fit procedure to fit at most two signatures from one organ into signatures from other organs. A single optimization run with KLD objective function was used to perform each fit. Signature fits were considered valid only if the cosine similarity was at least 0.89. If both a fit with a single signature and a fit with a combination of two signatures were valid, the combination was preferred if it increased the cosine similarity by at least 0.02. Network directed edges visualize which signatures were fitted into other signatures. Edges have weights that describe the proportion of each signature used for fitting into the fitted signature (e.g. Fig. 2i,j). Parameters used in this procedure were manually tuned to achieve a reasonable trade-off between false positive and false negative edges. Both substitution and rearrangement networks are available in tabulated format (Supplementary Tables S11 and S12) can be interactively explored at the web link https://signal.mutationalsignatures.com/explore/cancer/network.

Reference Signatures

Organ-specific mutational signatures were clustered using hierarchical clustering with average linkage, using 1 – cosine similarity as a distance metric (Extended Data Fig. 7a and 8a). Signatures were partitioned into groups according to the hierarchical clustering dendrogram (Extended Data Fig. 7a and 8a). Reference signatures were computed as the mean of each group (Extended Data 7b and 8b). Three substitution reference signatures were likely a mix of other signatures and were excluded from further analysis (RefSig MIXED1, MIXED2 and MIXED3, Extended Data Fig. 7b). Reference signatures are available in Supplementary Tables S4 and S5.

Comparison of organ-specific signatures obtained from two large pan-cancer studies

We compared signatures extracted using the ICGC/PCAWG study with the signatures obtained in a pan-cancer metastatic cohort provided by Hartwig¹⁴. We considered 3096 samples across 15 organs (based on the tissue-of-origin rather than the biopsied metastatic site) that were also present in the ICGC cohort. For the comparison, we only considered organs with a minimum of 35 samples in both cohorts.

We applied the extraction procedure as proposed in this manuscript to obtain signatures for each organ individually. The extracted signatures can be found in Supplementary Table S111. We expect to find some differences in the total number of signatures identified because there are differences in cohort size (number of samples), and metastatic cancers may also carry additional signatures due to longer tumor evolution and therapeutic regimens. Thus, comparing total numbers of signatures would be of limited value and would not reveal whether the signatures were similar or otherwise.

Our comparison instead consisted of the following steps:

Given a set of h signatures extracted in an organ p in the metastatic cohort, and a set of K signatures extracted in an organ p’ in the PCAWG cohort:

1. Evaluate the cosine similarity between these h signatures and all N=150 signatures extracted in the 15 organs in PCAWG. For each signature extracted select the corresponding signature with greatest cosine similarity. Consider only correspondence when cosine similarity >0.85. This will produce a match of m signatures from p that are most similar to signatures in p’.

2. Calculate the probability that from the h signatures extracted in the metastatic cohort, m signatures have a match (most similar) in a specific organ p’ in PCAWG.

3. For each organ p in Hartwig this probability follows a hypergeometric distribution, thereafter we can apply fisher exact test to obtain the associated p-values. We considered p-values < 0.01 as significant.

The optimal number of signatures extracted in the metastatic cohort was based on the ASW and reconstruction error. To account for uncertainty in the precise number of signatures, we also explored neighboring solutions, i.e. given the number of signatures extracted h, we considered the rank interval [h-2,h+2]. Finding that this “organ match” systematically occurs for different ranks increases the confidence in the result. The results obtained by one-sided fisher test are presented in Figure 4.

A caveat in the comparison is that the Hartwig cohort is composed of metastatic samples, resulting in the presence of additional signatures due to treatment and/or as a result of mutations acquired posterior to the seeding from the primary site. Thus, there will be additional signatures in the metastatic cohort that are simply not present in the matching primary of the ICGC cohort e.g. the presence of signature 7 (UV-light) in metastatic cancers of primary breast origin, which does not show a similarity to ICGC breast signatures, but shows strong similarity to ICGC skin cancer primary signatures.

Signatures assignment to samples

Given a matrix C of mutational catalogues and a signature matrix P, the assignment of organ-specific signatures to samples is to find a matrix E such that C ≈ PE. This problem has a unique solution for both KLD and Frobenious norm objective functions and can be estimated efficiently. To estimate E, we use the R package NNLM, with KLD objective function. As explained in the text, we run n=100 optimisations on bootstrapped data and obtain a distribution of exposures for each sample, similarly to previously described ¹⁵. To obtain point estimates, we consider the median exposures and use a sparsity increase procedure to reduce false positives. In this procedure we set exposures of a signature to zero if more than 5% of the bootstrapped exposure values (empirical p-value 0.05) are below the threshold of 5% of total mutations in the sample. The 5% threshold was identified using our simulation study as a compromise of sensitivity and specificity of the signature assignment to samples (Extended Data Fig. 10). Point estimates of exposures for all organ-specific signatures in all organs can be found in Supplementary Tables S13-S52.

Conversion matrix to convert organ-wise signature exposures into reference signature exposures

In some datasets, it might be difficult to separate mutational signatures, either because of the small size of the cohort or because some processes often co-occur in the samples. A conversion matrix provides a way to identify individual processes, by expressing an organ-specific mutational signature as a linear combination of reference signatures. A conversion matrix is constructed using a semi-automatic procedure, where we fit each reference signature or any combination of two or three reference signatures to each organ-specific signature, and then manually select the most appropriate combination among the ones most similar. A single optimization run with KLD objective function was used to perform each fit. In practice (Fig. 5i), most organ-specific signatures simply map to exactly one reference signature (e.g. Biliary_B maps to RefSig 1/COSMIC 1), while in some cases they map to a combination of two reference signatures (e.g. Biliary_C maps to RefSig 2/COSMIC 2 and RefSig 13/COSMIC 13), in which case the conversion matrix will indicate in what proportion to split the number of mutations attributed to each reference signature (e.g. Biliary_C into 80% RefSig 2 and 20% RefSig 13). Conversion matrices for substitution and rearrangement signatures can be found in Supplementary Tables S9 and S10. Reference signature exposures obtained by applying the conversion matrices to the organ-specific signatures exposures can be found in Supplementary Tables S6 and S7. Using the conversion matrix, we renamed the organ specific signatures using the numbers of the reference signatures associated with them, e.g. Biliary_B is renamed to Biliary_1 and Biliary_C is renamed to Biliary_2_13.

Associations between signatures and drivers

We use the Fisher Exact test (two-sided) to compare the set of samples with a certain driver with the set of samples with a certain signature. Bonferroni multiple hypothesis testing correction is applied to a 0.01 p-value cut-off. In this analysis, we consider a sample to have a certain signature if its exposure is of at least 1000 and 50 mutations for substitutions and rearrangements respectively. The curated list of driver mutations for each sample was obtained from the ICGC Pan-Cancer Analysis Working Group (Sabarinathan et al ¹⁶, Suppl. Table S3). In this study, driver mutations where predicted using statistical methods that evaluated the likelihood of positive selection given many factors including predicted amino acid effect, recurrence, non-synonymous/synonymous ratios amongst others, as well as prior literature information.

To reduce false positive associations, for example due to confounding of organ-specific signatures and drivers, we perform each driver-signature association test considering only samples from the organs where both driver and signature are found. For example, POLE drivers and Ref.Sig. 10 were found only in Colorectal and Uterus, therefore we considered only samples from these two organs when testing the association (Supplementary Table S61).

HRDetect score in 21 organs

HRDetect is a logistic regression classifier that computes a probability score of HRD based on six input features: proportion of small deletions with microhomology at the breakpoint junction, number of mutations attributed to COSMIC signatures 3 and 8 and to rearrangement signatures 3 and 5 ¹², and HRD index ³⁴. Here, we used RefSig 3, 8, R3 and R5 in place of the COSMIC 3 and 8 and rearrangements signatures 3 and 5 respectively, as they represent the same mutational processes. We calculated the HRDetect score using the model coefficient and the procedure previously described ¹¹. In brief, for each sample, the proportion of deletions with microhomology, HRD index ³⁴, substitution RefSig 3, 8, R3 and R5 exposures were estimated using our methods of signature extraction and fit of tissue-specific signatures, followed by conversion of tissue specific signature exposures into reference signature exposure (Fig. 5i). Values of the above six features are normalized and used in the HRDetect logistic regression model as previously detailed ¹¹. A small number of samples were excluded from this analysis because either rearrangement or indel data were not available. To obtain confidence intervals for HRDetect scores, we computed an empirical distribution by repeatedly (n=1000) computing the HRDetect score after sampling from the distribution of input features, for each sample. A confidence interval was calculated as the 5-95% percentile interval of the score distribution. We used results from our signature fit procedure to approximate a distribution of signature exposures (Fig. 5d). The distribution of proportion of deletions at microhomology was obtained by bootstrapping the classified deletions, while the distribution of the HRD index was constructed as a Poisson distribution with the calculated HRD index as average. Overall, this framework accounts for the uncertainty of the six features used by HRDetect and produces a distribution of scores for each sample. HRDetect scores and input features values for all samples can be found in Supplementary Table S8.

Statistics & Reproducibility

The study analyzed large datasets of published data. All sample sizes and statistics used have been reported in the main text, methods and figure legends as necessary. Data access information and methods description along with software code was provided to allow reproducibility of the results. All methods have been described in detail in the Methods section and in the Supplementary Notes. No statistical method was used to predetermine sample size. No data were excluded from the analyses. The experiments were not randomized. The investigators were not blinded to allocation during experiments and outcome assessment. Further information on research design is available in the Nature Research Reporting Summary linked to this article.

Extended Data

Extended Data Fig. 1. Optimal relative tolerance for the selection of best NMF runs.

(a-f) Repeated NMF application to the Breast 560 dataset (560 patient samples and 1000 NMF runs) of SNV organized in 96 channels. (a) Distribution of the optimal Kullback-Leibler divergence (KLD) obtained from 1000 NMF runs (n=1000) and for different number of k mutational signatures extracted (k from 9 to 13). Red vertical lines indicate the best (lowest) KLD, the 0.1% relative tolerance (RTOL) from best and the 1% RTOL from best. (b) Convergence of global minimum for different k values. The 1000 values of optimal KLD in (a) are randomly ordered 50 times and the minimum KLD after each run is computed for each ordered sequence. Average (solid lines) and standard deviation (dotted lines) are then plotted. Red horizontal lines indicate the best KLD and 0.1% RTOL from best. (c) The same KLD values from the five plots in (a) are combined in one single plot. (d-f) PCA plots of mutational signatures obtained from the Breast 560 catalogue, with number of signatures k = 10. In each row, three plots show principal components (PC) 1 with 2, 1 with 3 and 2 with 3, using the same projection of the first row. Colors indicate clusters computed with the clustering with matching algorithm, triangles are the medoids of the clusters and on top of the triangles the most similar COSMIC signatures (or sum of signatures), according to cosine similarity, are indicated. A black line connects the two closest medoids according to cosine similarity. The cosine similarity of the two closest medoids (max cos sim of medoids) and the average silhouette width (ASW) are indicated for each row. (d) PCA plot obtained using 1000 NMF runs (n=1000). (e) PCA plot obtained using only the NMF runs within 1% RTOL from the best run. (f) PCA plot obtained using only the NMF runs within 0.1% RTOL from the best run. The 1000 NMF runs used in this plot are the same as in panel (a) (k = 10). (g-h) Repeated NMF application to the Breast 560 dataset and additional PCAWG datasets. ASW of clustering mutational signatures from best NMF runs for different values of relative tolerance (g) or different number of total NMF runs (h). (g) For each of the six datasets and for different number of mutational signatures (n sig), multiple NMF runs are performed (1000 for Breast 560 and 500 for the others). A relative tolerance (RTOL) with respect to the best (lowest) optimization function value obtained is used to select a subset of best NMF runs, i.e. all runs with optimization function value less or equal to best*(1+RTOL). For each selected set of best runs, the obtained signatures are clustered using clustering with matching, and the ASW is computed. The six plots show the value of the ASW for different values of RTOL and number of signatures extracted (n sig). (h) For each of the six datasets and for different number of mutational signatures (n sig), multiple NMF runs are performed (plot x axis). A relative tolerance (RTOL=0.1%) with respect to the best (lowest) optimization function value obtained is used to select a subset of best NMF runs, i.e. all runs with optimization function value less or equal to best*(1.001). For each selected set of best runs, the obtained signatures are clustered using clustering with matching, and the ASW is computed. The six plots show the average of n = 10 replicates of the ASW for different number of total NMF runs performed and number of signatures extracted (n sig). Detailed data for the analyses shown in this figure can be found in Supplementary Tables S1 and S112.

Extended Data Fig. 2. Global Signature Extraction.

24 substitution signatures obtained from a signature extraction pooling 2,486 tumours across 21 organs. Several artefactual signatures are present among these signatures (details of the analysis can be found in Supplementary Notes). Detailed data for the analyses shown in this figure can be found in Supplementary Table S112.

Extended Data Fig. 3. Substitution signatures extracted per organ from 3107 samples, part 1.

First part of 192 organ-specific substitution signatures, obtained across 21 organs (n=3107 samples). Signatures names have letters or numbers (between parentheses), where numbers indicate the associated reference signatures as defined by the conversion matrix (Methods and Suppl. Table S9). Detailed data for the analyses shown in this figure can be found in Supplementary Table S2 and S112.

Extended Data Fig. 4. Substitution signatures extracted per organ from 3107 samples, part 2.

Second part of 192 organ-specific substitution signatures, obtained across 21 organs (n=3107 samples). Signatures names have letters or numbers (between parentheses), where numbers indicate the associated reference signatures as defined by the conversion matrix (Methods and Suppl. Table S9). Detailed data for the analyses shown in this figure can be found in Supplementary Table S2 and S112.

Extended Data Fig. 5. Rearrangement signatures extracted per organ from 3107 samples, part 1.

First part of 116 organ-specific substitution signatures, obtained across 19 organs (n=3021 samples). Signatures names have letters or numbers (between parentheses), where numbers indicate the associated reference signatures as defined by the conversion matrix (Methods and Suppl. Table S10). Detailed data for the analyses shown in this figure can be found in Supplementary Table S3 and S113.

Extended Data Fig. 6. Rearrangement signatures extracted per organ from 3107 samples, part 2.

Second part of 116 organ-specific substitution signatures, obtained across 19 organs (n=3021 samples). Signatures names have letters or numbers (between parentheses), where numbers indicate the associated reference signatures as defined by the conversion matrix (Methods and Suppl. Table S10). Detailed data for the analyses shown in this figure can be found in Supplementary Table S3 and S113.

Extended Data Fig. 7. Hierarchical clustering of substitution mutational signatures obtained from organ-wise independent extraction.

(a) Clustering of organ-wise extracted substitution signatures, using hierarchical clustering with average linkage and 1 – cosine similarity as distance metric. Red boxes indicate the identified signature groups and the corresponding group reference signature is indicated at the bottom. (b) Reference signatures for each group in (a), given as the mean and standard error of the signatures in each group. Cosine similarity with the most similar COSMIC signature is indicated, along with the number of signatures in the group (n) and the reference signature name. (c) Cosine similarity between the reference signature of each group and the individual signatures that belong to each group. Group sizes are the same as in panel (b). Boxes show median, 1^st and 3^rd quartile, with whiskers extending at most 1.5∙IQR. Detailed data for the analyses shown in this figure can be found in Supplementary Table S2 and S4.

Extended Data Fig. 8. Hierarchical clustering of rearrangement mutational signatures obtained from organ-wise independent extraction.

(a) Clustering of organ-wise extracted rearrangement signatures, using hierarchical clustering with average linkage and 1 – cosine similarity as distance metric. Red boxes indicate the identified signature groups and the corresponding group reference signature is indicated at the bottom. (b) Reference signatures for each group in (a), given as the mean and standard error of the signatures in each group. Cosine similarity with the most similar rearrangement signature from Nik-Zainal et al. 2016 is indicated, along with the number of signatures in the group (n) and the reference signature name. (c) Cosine similarity between the reference signature of each group and the individual signatures that belong to each group. Group sizes are the same as in panel (b). Boxes show median, 1^st and 3^rd quartile, with whiskers extending at most 1.5∙IQR.

Detailed data for the analyses shown in this figure can be found in Supplementary Table S3 and S5.

Extended Data Fig. 9. Similarity between substitution reference signatures and single base substitution COSMIC signatures.

Cosine Similarity between the substitution reference signature (Extended Data Figure 7b) and the COSMIC single base substitution signatures (SBS) was computed. Red squares indicate a cosine similarity higher than 0.9; blue squares indicated a cosine similarity between 0.85 and 0.9; white squares indicate a cosine similarity lower than 0.85. Detailed data for the analyses shown in this figure can be found in Supplementary Table S4.

Extended Data Fig. 10. Simulated experiments, mutational signature assignment to samples.

A total of 30 mutational catalogues were simulated (n=5 replicate simulated datasets) using 10 COSMIC signatures. Mutational signatures were extracted using different approaches, and assigned to the 30 samples using a bootstrap signature fit approach. Each sample was bootstrapped 100 times and each time signature activity in the sample was estimated by optimizing the Kullback-Leibler Divergence (KLD). A consensus activity is then computed for each sample as the median of the results, and then the sparsity of the activity is increased by setting to zero activities that are not statistically higher than a given threshold (threshold=0, 1, 2, 5, 10 percent of total number of mutations and p-value 0.05, i.e. set to 0 if more than 5% of the runs is below the threshold). The correct number of signatures k=10 is used. Filter: only the best NMF runs are considered; no filter: all NMF runs are used; Lee KLD: Lee and Seung 2001 multiplicative algorithm with Kullback-Leibler Divergence (KLD); Lee Frobenius: Lee and Seung 2001 with Frobenius norm; nsNMF: non-smooth NMF with KLD; HC: hierarchical clustering with average linkage; CM: clustering with matching; PAM: partitioning around the medoids. (a) Root mean squared error (RMSE) between original mutation assignment matrix and the fitted model. (b) Sensitivity of signature assignment. (c) Specificity of signature assignment. Detailed data for the analyses shown in this figure can be found in Source Data File 1.