Improving the Assessment of Measurement Invariance: Using Regularization to Select Anchor Items and Identify Differential Item Functioning

Abstract

A common challenge in the behavioral sciences is evaluating measurement invariance, or whether the measurement properties of a scale are consistent for individuals from different groups. Measurement invariance fails when differential item functioning (DIF) exists, i.e., when item responses relate to the latent variable differently across groups. To identify DIF in a scale, many data-driven procedures iteratively test for DIF one item at a time while assuming other items have no DIF. The DIF-free items are used to anchor the scale of the latent variable across groups, identifying the model. A major drawback to these iterative testing procedures is that they can fail to select the correct anchor items and identify true DIF, particularly when DIF is present in many items. We propose an alternative method for selecting anchors and identifying DIF. Namely, we use regularization, a machine learning technique that imposes a penalty function during estimation to remove parameters that have little impact on the fit of the model. We focus specifically here on a lasso penalty for group differences in the item parameters within the two-parameter logistic item response theory model. We compare lasso regularization with the more commonly used likelihood ratio test method in a two-group DIF analysis. Simulation and empirical results show that when large amounts of DIF are present and sample sizes are large, lasso regularization has far better control of Type I error than the likelihood ratio test method with little decrement in power. This provides strong evidence that lasso regularization is a promising alternative for testing DIF and selecting anchors.

Translational Abstract

Measurement in the psychological sciences is difficult in large part because two individuals with identical values on a construct (e.g., depression) may appear unequal when measured. This can happen when an item (e.g., cries easily) is not only tapping into that construct but also into some other background characteristic of the individual – for instance, their sex. This is formally referred to as differential item functioning (DIF). If undetected and unaddressed, DIF can distort inferences about individual and group differences. There are many procedures for statistically detecting DIF, most of which are data-driven and use multiple statistical tests to determine where DIF occurs in a scale. Unfortunately, these procedures make assumptions about other untested items that are unlikely to be true. Specifically, when testing for DIF in one item, one or more other items must be assumed to have no DIF. This is paradoxical, in that the same item is assumed to have DIF in one test but assumed not to have DIF in all other tests. We propose a machine learning approach known as lasso regularization as an alternative. Lasso regularization considers DIF in all items simultaneously, rather than one item at a time, and uses a penalized estimation approach to identify items with and without DIF rather than inference tests with dubious assumptions. Computer simulations and a real data validation study show that lasso regularization performs increasingly better than a commonly used traditional method of DIF detection (the likelihood ratio test approach) as the number of items with DIF and sample size increase.

Measuring unobservable constructs presents unique challenges for scientists, one of which is ensuring an instrument’s measurement properties are consistent between groups of individuals. On a depression scale, for instance, the item “cries easily” is more frequently endorsed by females than males for the same underlying level of depression (Steinberg & Thissen, 2006). Treating this item as the same for both sexes when computing scale scores (e.g., by summing items) would be problematic because women would tend to receive higher scores than men even after accounting for any actual sex differences in depression. There may be other downstream consequences as well, such as identifying specious treatment differences between men and women, or women being selected for treatment more than men, potentially leading to over- and under-treatment, respectively. Items like “cries easily” that relate to the latent construct (depression) differently for different groups of people therefore pose a major threat to scientific validity.

Generally, differential item functioning (DIF) refers to the condition in which an item is endorsed more or less frequently (or more or less reliably) by individuals from one group than another even when these individuals have equal levels of the underlying latent construct. More formally, DIF occurs when the parameters linking the distribution of the item responses to the latent variable differ across groups. As noted above, when DIF is present but unaddressed, this can have deleterious effects on subsequent outcomes. Fortunately, these effects can be ameliorated by removing items with DIF from the scale (Zwick, 2012) or allowing item parameters for the subset of items with DIF to vary between groups (Byrne, Shavelsford, & Muthén, 1992). Those items without DIF are then referred to as anchor items because their presence permits the latent variable to be anchored to the same scale in each group. First, however, one must correctly separate the items with DIF from the anchor items.

A variety of approaches have been proposed for empirically testing DIF / selecting anchors. One challenge these approaches must contend with is the need to impose certain constraints on the model so that all parameters can be uniquely estimated (i.e., to identify the model). These constraints can be troublesome. For instance, one way to identify the model is to set the latent means and variances of the latent variable to fixed values in each group, such as assuming means of zero and variances of one in each group. Under these constraints it is possible to test across-group differences in all of the parameters linking the items to the latent variable. Often, however, there is no reason to suppose that the groups have equal means and variances and assuming this to be the case when it is not will bias all subsequent tests of DIF. Another way to identify the model is to pre-select at least one item to be an anchor item. This anchors the scale of the latent variable, allowing for estimation of mean and variance differences between groups. If, however, the anchor item selected is not actually equivalent for the two groups (and is instead really a DIF item), then tests of DIF in other items will be biased. In either case, we must assume information that we would prefer to evaluate empirically.

Fortunately, great strides have been made in the development of parameter selection methods within the statistical sciences which hold promise for addressing this problem. These methods include use of regularization techniques, which includes the lasso (least absolute shrinkage and selection operator; Tibshirani, 1996). In this article, we evaluate whether lasso regularization can accurately identify which items require group-varying parameters, reflecting DIF, versus those that do not (i.e., anchors). Although important initial research has evaluated regularization for testing DIF and factorial invariance (Huang, 2018; Magis, Tuerlinckx, & De Boeck, 2015; Tutz & Schauberger, 2015), no research to our knowledge has done so with the 2-parameter logistic (2PL) item response theory model, where item intercepts and slopes are allowed to vary (although see Bauer, Belzak, & Cole, in press). Furthermore, we are aware of no research comparing regularization to one of the most commonly implemented DIF detection procedures, namely the item response theory likelihood ratio DIF testing procedure (IRT-LR-DIF; Thissen, Steinberg, & Wainer, 1993). The goal of this article is to address these gaps in the literature by formulating the lasso estimator for the 2PL model and then examining the empirical performance of this approach relative to conventional IRT-LR-DIF. Our comparison of these procedures consists of two parts. First, we conduct a standard simulation study comparing DIF detection through regularization versus IRT-LR-DIF with artificial data generated under known conditions. Second, we compare the performance of these techniques in a real-world setting with primary data obtained using an experimental manipulation specifically intended to induce DIF for a subset of items. As context, we begin with a brief conceptual review of measurement invariance and DIF, an introduction to the 2PL model, and a description of conventional DIF testing procedures.

Measurement Invariance and Differential Item Functioning

Measurement invariance exists when the distribution of the item responses is unrelated to any background variables beyond the influence that those background variables may have on the latent variable itself (Mellenbergh, 1989; Millsap, 2011). For instance, the latent variable of depression may vary between men and women, but at any given level of depression the item responses have the same distribution for both sexes. This can be stated mathematically as

$$f\left(y_i|{\eta }_i,x_i\right)=f\left(y_i|{\eta }_i\right)$$ (1)

where f(·) is a probability (response) distribution, y_i is a p × 1 vector of observed item responses for person i, η_i is an r × 1 vector of latent variables, and x_i is a q × 1 vector of background variables (e.g., G – 1 coding variable to differentiate G groups). Equation 1 states that measurement invariance holds when the probability of endorsing items y_i depends solely on the target latent variables η_i and not on background variables x_i. In practice, Equation 1 often simplifies to a unidimensional measurement model with two groups differentiated by one coding variable: f(y_i|η_i, x_i) = f(y_i|η_i), where η_i and x_i are scalars. For simplicity, we focus on this two-group scenario here. In other work, however, we consider the possibility of multiple background variables (Bauer, Belzak, & Cole, in press).

Measurement invariance fails to hold when, for at least one item, the response distribution conditionally depends on a background variable. This can be written

$$f\left(y_i|{\eta }_i,x_i\right)\ne f\left(y_i|{\eta }_i\right).$$ (2)

Equation 2 states that the probability of endorsing one or more items in y_i does not solely depend on the latent variable but also on group membership defined by x_i, that is, differential item functioning is present. When this occurs for a subset of items, then the measure is said to be partially invariant.

It is important to note that DIF is fundamentally different than impact, which occurs when the distribution of η_i depends on x_i in some way. For instance, one group might have a higher mean level for the latent variable than the other, or one group might be more heterogeneous (have higher variance) than the other. The purpose of identifying and correcting for DIF is not to nullify any differences that may exist on the latent variable η_i over levels of the background variable x_i; rather, it is to ensure that these differences, if present, are not over- or understated due to artifacts of measurement.

In practice, testing DIF requires a statistical model in which groups differences in item responses can be evaluated while controlling for differences on the underlying latent variable. We describe a common model for doing so next.

Item Response Theory: Two-Parameter Logistic Model

Item response theory is a statistical framework for modeling multiple categorical items as indicators of one or more latent variables (Embretson & Reise, 2000). Most applications of IRT involve a unidimensional measurement model: a single latent variable affects all item responses on a scale. A common response type modeled in IRT is a dichotomous outcome; each item is coded 1 or 0 to indicate, for instance, whether a person answered an item correctly (e.g., achievement test), endorsed a belief (e.g., attitudinal measure), or experienced a symptom (e.g., clinical symptom inventory). Although we focus on models for dichotomous data here, we direct readers to de Ayala (2008) for a thorough treatment on other response types.

The two-parameter logistic model (2PL) is frequently used to model dichotomous item responses (e.g., wrong/right or absent/present), and is defined as

$$P\left(Y_{ij}=1|{\theta }_i\right)=\frac{1}{1+e^{-\left(c_j+a_j{\theta }_i\right)}}$$ (3)

where y_ij ~ Bernoulli(p_ij), with p_ij indicating the model-implied probability of person i endorsing item j; θ_i is the latent score for person i, typically assumed to be θ_i ~ Normal(0,1); and c_j and a_j are the intercept and slope parameters, respectively, for item j. The intercept-slope parameterization in Equation 3 expresses the 2PL-IRT model similarly to a typical logistic regression model, with θ_i as the sole predictor of the outcome y_ij.¹ In addition, this parameterization directly parallels binary factor analysis, with the exception that usually binary factor analysis is implemented with a probit rather than logistic item response function (see Kamata & Bauer, 2008, for further discussion on these relationships as well as other common parameterizations).

Within the 2PL-IRT model, DIF exists if groups differ in their values for the intercept and/or slope parameters. We may introduce an index g, denoting group membership, to the 2PL model as follows:

$$P\left(Y_{ijg}=1|{\theta }_i\right)=\frac{1}{1+e^{-\left(c_{jg}+a_{jg}{\theta }_i\right)}}$$ (4)

Equation 4 implies that a_j and c_j may differ by g. In addition, each group may be characterized by its own mean and variance for the latent trait, i.e., θ_j ~ Normal(${\mu }_g,{\sigma }_g^2$). Identification constraints are, however, required for the scale of the latent variable and must be chosen well to properly link the scale across groups (Millsap, 2011). In the case of two groups (also applicable to G > 2), one common way to identify a 2PL-IRT model is to: (1) fix the distribution of the latent variable in the reference group, G_R, with a mean of 0 (μ_R = 0) and variance of 1 (${\sigma }_R^2=1$), while allowing the latent distribution of the corresponding focal group, G_F, to be freely estimated as Normal(${\mu }_F,{\sigma }_F^2$); and (2) constrain the parameters of one or more anchor items to be equal between groups. This two-fold identification scheme has one strong advantage: it does not assume that the latent distributions between groups are identical. As noted before, the latent means and variances may vary across groups even when measurement invariance holds (i.e., impact); it is only the conditional distribution of the observed items given the latent variable that must be invariant for valid comparisons to be made.

Identifying a multiple-groups model in this way, however, comes with a crucial trade-off. In particular, this identification scheme implies that no differential functioning is present for the chosen anchor item(s). The problem is that there is seldom sufficient prior knowledge to confidently designate one or more anchor items. Thus, some kind of empirical search procedure is required. We now review some of the more common procedures that have been proposed for anchor item selection and DIF determination.

Methods for Testing Differential Item Functioning

Some common procedures for identifying the anchor item and testing for DIF include likelihood ratio tests (Thissen, Steinberg, & Wainer, 1988, 1993), Wald tests (Lord, 1977, 1980; Langer, 2008), and score tests (also known as modification indices or Lagrange multiplier tests; Oort, 1998; Steenkamp & Baumgartner, 1998).

One common approach for using likelihood ratio tests to locate DIF is the IRT-LR-DIF procedure proposed by Thissen (2001; although see Kim & Cohen, 1995, and Woods, 2009, for other variants). IRT-LR-DIF begins by fixing the reference group mean and variance to 0 and 1, respectively, and allows the focal group mean and variance to be freely estimated. Two models are then defined and fit to the data: a baseline model and DIF model. The baseline model, denoted M₀, designates all items as anchors (i.e., no DIF on any items). The hypothesized DIF model, M₁, specifies DIF by constraining parameters for all items, except the intercept and slope for a single item, to equality over groups. Both parameters for this single item are left unconstrained and thus are allowed to vary freely across the reference and focal groups. Because M₀ is nested in M₁, the likelihood values for both models may be statistically compared. The IRT-LR-DIF procedure tests for DIF in each item while constraining all others equality. Once all items have been tested for DIF, anchor items are chosen by identifying those DIF tests that were non-significant. Conversely, items with significant differences in the parameters are designated as having DIF and their parameters remain freely estimated between groups (unless these items are simply removed).

A variety of other DIF detection methods have been proposed that use Wald tests instead of likelihood ratio tests. First recommended by Lord (1978, 1980) for DIF analysis, the procedure begins by separately fitting measurement models to each group. Then, differences between groups on the difficulty and discrimination parameters are computed. For each item, a Wald test determines whether these differences are statistically significant. Those items for which the test is significant are designated as having DIF, and the others are taken to be anchors. One complication is that some form of scale linking needs to be performed because models are fit separately for each group. Recent improvements to Lord’s Wald statistic have been made that obviate the need to externally link the scales across groups (Cai, Thissen, & du Toit, 2011; Woods, Cai, Wang, 2013). This is accomplished by specifying one or more anchor items to link both groups to the same latent scale, similar to IRT-LR-DIF. Thus, no further linking or concurrent calibration is necessary to perform multiple-group DIF testing with Wald tests.

A third approach is to use score tests (i.e., modification indices or Lagrange multipliers) to identify DIF (Oort, 1998; Steenkamp & Baumgartner, 1998). Like the IRT-LR-DIF procedure discussed previously, this approach begins by fitting M₀, in which all items are assumed to be anchors. The score test indicates whether releasing across-group equality constraints on a given item parameter would significantly improve model fit. Items with significant score tests are declared to have DIF, whereas those without significant score tests are taken as anchor items. This approach is often done iteratively (Oort, 1998), refitting the model each time an equality constraint is released. That is, the largest significant score test at each iteration is released, with re-inspection of the updated score tests at each iteration. This procedure continues until there are no item parameters that would lead to better fit if allowed to be freely estimated between groups.

All of these approaches suffer from a common problem: they conduct many inference tests for which the p-values are often inaccurate even when attempts are made to correct for multiple comparisons (for instance, using the Benjamini-Hochberg false discovery rate correction; Thissen, Steinberg, & Kuang, 2002). The principal problem is that the inference tests conducted to evaluate DIF assume that the anchor item set in the hypothesized model to be correct when in fact it may be “contaminated” by items with as yet undetected DIF. For instance, in IRT-LR-DIF, the parameters for all but one item are assumed to be equal across groups in the M₁ model. If any other items have DIF, however, then the anchor item set is contaminated and the M₁ model is misspecified. Consequently, Type I error rates tend to be higher than the nominal rate, sometimes much higher (Finch, 2005; Stark, Chemyshenko, & Drasgow, 2006). Additionally, parameter estimates of group differences are biased (Wang, 2004) and latent mean differences are inaccurate (Wang, 2004; Wang & Yeh, 2003). Similarly inflated Type I error rates have been documented for the improved Wald test (Woods et al., 2013) and score test (Millsap & Kwok, 1993). Excessive Type I errors may not be problematic in settings where item pools are large and items identified to have DIF can be replaced at relatively low cost (e.g., educational testing). In psychological assessment, however, there is often a more limited item pool to draw from (e.g., only so many symptoms of depression), and it is more important to avoid false positives.

Regularization

Interestingly, many of the problems with testing DIF and identifying anchor items are akin to problems that have plagued stepwise procedures for predictor selection in regression models. In that context, regularization procedures have been developed as a superior alternative to stepwise regression (Lockhart, Taylor, Tibshirani, & Tibshirani, 2014). We argue that they hold similar advantages for anchor item detection.

Most generally, regularization is a family of statistical techniques that introduces new information or constraints to the loss function (e.g., sum of squared residuals in least squares estimation, the likelihood in maximum likelihood estimation) to enhance the stability of the model. Originally used as a solution to mitigate under-determined models (Tikhonov, Goncharsky, Stepanov, & Yagola, 2013), regularization more recently has been used for the purpose of selecting parameters (Hastie, Tibshirani, & Friedman, 2017; Tibshirani, 1996). The general idea is to add a penalty term to the loss function so that some model parameters may shrink toward or exactly to 0. The regularization procedure known as the lasso can be written generally as

$$L_{\mathit{\text{lasso}}}=L+\tau \Vert \cdot {\Vert }_1$$ (5)

where L_lasso is the lasso regularized loss function; L is a loss function defined by the researcher; τ is a tuning parameter that augments the strength of the new information; and ‖ · ‖₁ is the l₁ norm, which simply is the sum of the absolute values of the penalized parameters. We first describe how the lasso is applied within the classic linear regression model for predictor selection, and then extend the application of this approach to anchor item detection and DIF evaluation in IRT models.

Regularized Linear Regression

Lasso is commonly used in linear regression for the purpose of selecting a subset of possible predictors (McNeish, 2015). The lasso loss function in linear regression is

$$RSS{(\beta )}_{\mathit{\text{lasso}}}=\text{argmin}\left\{\sum _{i=1}^N{\left(y_i-{\beta }_0-\sum _{j=1}^p{\beta }_j{x}_{ij}\right)}^2+\tau \sum _{j=1}^p\left|{\beta }_j\right|\right\}$$ (6)

where RSS(β)_lasso is the lasso residual sum of squares loss function; argmin{·} is the function that minimizes RSS(β)_lasso with respect to β. The first summand within argmin{·} is the conventional OLS loss function, where y_i is the value of the outcome for individual i, x_ij is the value of predictor j for individual i, β₀ is the intercept, and β_j is the regression coefficient for predictor j. The second summand, $\tau {\sum }_{j=1}^p\left|{\beta }_j\right|$, is the lasso penalty function, wherein the absolute values of the βs are summed and multiplied by τ. Higher values of τ increase the penalty on the βs. When τ = 0, the penalty is removed, and we obtain the usual OLS estimates. As τ increases, however, more and more coefficients shrink to zero and their corresponding predictors are removed from the model until eventually all predictors are removed. The trick is to determine the optimal value of τ and thus which predictors to include/exclude. In practice, τ is incremented over a range of values, and the optimal value is chosen on the basis of fit index values (e.g., Bayes’ information criterion [BIC] or Akaike’s information criterion [AIC]) or cross-validation (e.g., see Ch. 7 in Hastie et al., 2017).

Regularized Differential Item Functioning

Similar to selecting coefficients in linear regression, lasso can also be used to select which item parameters to allow to differ across groups in a psychometric model like the 2PL IRT model. We refer to this approach as regularized DIF detection, or Reg-DIF. Implementing the lasso is made easier by re-expressing the two-group 2PL model as follows:

$$P\left(Y_{ij}=1|{\theta }_i,x_i\right)=\frac{1}{1+e^{-\left({\text{c}}_{oj}+c_{1j}{x}_i\right)-\left(a_{0j}+{\text{a}}_{1j}{x}_i\right){\theta }_i}}$$ (7)

where x is a coding variable with values of zero for members of the reference group and values of 1 for members of the contrast group. This expression differs from Equation 4 in that we do not estimate group-specific item intercepts and slopes but rather we estimate baseline intercepts and slopes for the reference group, c_0j and a_0j, and differences in the intercepts and slopes for the contrast group relative to the reference group, c_1j and a_1j. We continue to set the mean and variance of the latent variable to zero and one for the reference group and to estimate the mean and variance for the contrast group.

This re-parametrization allows us to specifically penalize the difference parameters during model estimation. If the difference parameters are removed, then the item is an anchor, otherwise the item expresses DIF. As detailed in the next section, the lasso penalty for Reg-DIF takes the form $\tau {\sum }_{j=1}^p\left[\left|c_{1j}\right|+\left|{\text{a}}_{1j}\right|\right]$. That is, the tuning parameter τ is multiplied by the sum of the absolute values of the difference parameters for all p items. This penalty function is simply applied to the likelihood (loss) function for the 2PL IRT model, and τ is augmented until an optimal value is identified via a fit index where some item parameters have been removed from the model. In the sections to follow, we provide more technical detail on the estimation, identification, anchor selection, and inference of Reg-DIF. Readers who are less interested in the technical details of implementing Reg-DIF may prefer to skip ahead to the Previous Research section, which highlights recent empirical work on using regularization to test for DIF.

Estimation.

To show specifically how Reg-DIF is implemented, we first describe the general likelihood function without the penalty. This is written as

$$l{(\gamma )}_{DIF}=\text{log}\left(\prod _{i=1}^N\int p\left(Y_i|{\theta }_i,x_i;\mathbf{\varpi }\right)\varphi \left({\theta }_i|x_i;\pi \right)d{\theta }_i\right)$$ (8)

where l(γ)_DIF is the marginal log-likelihood function of the two-group 2PL IRT model that is maximized with respect to γ, or the vector of model parameters; $p\left(Y_i|{\theta }_i,x_i;\mathit{\varpi }\right)$ represents the conditional response pattern distribution, where Y_i is the vector of p item responses for individual i, θ_i is individual i’s latent score, x_i is the coding variable that defines group membership, and $\mathbf{\varpi }$ is the vector of item parameters governing the conditional response pattern distribution for individual i (i.e., the intercept and slope parameters shown in Equation 7); ϕ(θ_i|x_i; π) represents the normal density function for the latent variable, where π is a vector of parameters governing the conditional latent variable distribution for individual i (i.e., the latent mean and variance difference between the reference and focal groups); finally, dθ_i refers to the fact that we are integrating over the latent variable on an individual-by-individual basis to identify the marginal likelihood of observing the response pattern for individual i. This likelihood function may be maximized using adaptive quadrature to approximate the integral (Rabe-Hesketh, Skrondal, & Pickles, 2004; Schilling & Bock, 2005). Taken together, Equation 8 states that we must choose unique values of the model parameters (γ, or $\mathit{\varpi }$ and π) that maximize the likelihood of observing the item responses given by the respondents.

Having defined the general likelihood function for testing DIF, we apply the lasso penalty to define the Reg-DIF likelihood function as

$$l{(\gamma )}_{Reg-DIF}=l{(\gamma )}_{DIF}-\tau \sum _{j=1}^p\left[\left|{\text{c}}_{1j}\right|+\left|{\text{a}}_{1j}\right|\right]$$ (9)

where τ is the tuning parameter for the penalty function, and ${\sum }_{j=1}^p\left[\left|c_{1j}\right|+\left|{\text{a}}_{1j}\right|\right]$ is the sum of the absolute values of the DIF parameters, c_1j and a_1j, for each item j. Larger values of τ effectively lead to greater shrinkage of DIF parameters in γ, with the goal being to remove these for anchor items that are free of DIF. Similar to regularization in linear regression, all DIF parameters are removed from the model when τ becomes large enough, and conversely, the usual maximum likelihood estimates are obtained when τ = 0, provided that the model is identified. Note that we subtract the penalty in Equation 9 because we are maximizing the log-likelihood function rather than minimizing the residual sum of squares as shown in Equation 6.

Identification.

Model identification is an interesting issue within the regularization literature, given that the penalty is sometimes motivated for the purpose of estimating otherwise undetermined models (Tikhonov et al., 2013). Likewise, with Reg-DIF, we have specified a model that would be under-identified in the absence of the penalty, that is, where there are no anchor items (i.e., DIF is present on all items) and impact is present. The addition of the lasso penalty, however, provides “extra” information that makes it possible to obtain unique estimates for the model (Tibshirani, 1996; Tutz & Schauberger, 2015). In this sense it functions similarly to the use of a prior distribution in Bayesian estimation to achieve “approximate identification.” Nevertheless, the model remains under-identified when the tuning parameter τ = 0 because there is no extra information in the likelihood function to use for estimation. Thus, when the penalty is zero, we must adopt another strategy. Here, we address this problem by using a ridging technique, known as the Moore-Penrose pseudoinverse (Barata & Hussein, 2012), which essentially identifies unique estimates in an under-identified model by finding the minimum Euclidean norm among all solutions, or those estimates that minimize the distance from the origin (i.e., from each other).² Thus, we use the Moore-Penrose pseudoinverse when τ = 0 to obtain estimates for the Reg-DIF model. Furthermore, in practice, even when τ > 0 and no anchor items have been identified, the amount of information provided by the penalty function may not be enough to provide unique estimates. As such, we use the Moore-Penrose pseudoinverse until either the penalty is large enough to obtain unique estimates or at least one anchor item has been identified (at which point the model is formally identified in the traditional sense).³

Anchor Selection.

Another issue in model estimation is how to remove DIF parameters and select anchor items for the model when the tuning parameter τ becomes large enough. The main problem with estimating parameters in regularization is that the penalized likelihood function is not differentiable because the lasso penalty includes an absolute value function. In particular, the derivative of an absolute valued parameter is undefined at zero. For this reason, a soft-thresholding operator (Tibshirani, 1996) is often used when estimating the model parameters. Given the limitations of existing software, however, our implementation relies on a different approach. Specifically, we define an arbitrarily small threshold value that, when a penalized DIF estimate falls below this threshold, a coding statement simply sets its value to zero. In effect, this alternative mechanism removes DIF effects from the measurement model as τ increases, thereby selecting which items are anchors.⁴

Final Model and Inference.

Finally, the penalty function in lasso regularization introduces bias to the parameter estimates in the service of less variance (Hastie et al., 2017), with the goal to obtain estimates with lower mean squared error (a combination of bias and variance) overall. After the regularization procedure is complete and we have selected the smallest BIC model, we may also consider ways to reduce estimator bias. In particular, research has shown that re-estimating the final model without the penalty reduces bias, albeit to the detriment of greater variance (Hastie et al., 2017). In this context, we can re-estimate the final model to reduce bias, including all DIF effects that were present in the smallest BIC model but without the penalty function shown in Equation 9. More specifically, Equation 8 shows the log-likelihood function that is maximized for the final re-estimated model, except that the anchors and DIF effects have already been chosen through the regularization procedure. Thus, in Equation 8, some item-specific parameter estimates in $\mathbf{\varpi }$ are fixed to zero (i.e., anchored across groups) in the final re-estimated model. In addition to re-estimation of the final model, recent empirical work by our research group has shown that using p-values in the final re-estimated model to determine significance of DIF effects leads to superior Type I error rates compared to simply counting those effects that remain in the final model but may or may not be significant (Bauer et al., in press). It is well known, however, that the sampling distributions used to compute these p-values are incorrect because they fail to incorporate the uncertainty that arises from using the available data to identify which effects are included in the model (Lockhart, Taylor, Tibshirani, & Tibshirani, 2014; also see Ch. 6 in Hastie, Tibshirani, & Wainwright, 2015). In other words, these p-values are computed assuming that each model fit (i.e., different values of τ) is done with independently drawn data. This is obviously not the case when using regularization to select anchor items. Based on recent post-hoc empirical evaluations, however, using these incorrect p-values to ultimately determine which items are anchors and which are DIF appears to yield smaller Type I errors with similar amounts of power for Reg-DIF (Bauer et al., in press). We describe this research, among other related work, in the following section.

Previous Research

Bauer et al. (in press) implemented Reg-DIF in a moderated nonlinear factor analysis model where more than one DIF covariate may affect item intercepts and slopes, as well as impact. Simulation findings indicated that Reg-DIF had smaller Type I errors compared to using likelihood ratio tests, although empirical power was smaller as well. In larger sample sizes, however, empirical power rates for Reg-DIF approached those for IRT-LR-DIF, despite still achieving fewer Type I error rates. This indicates that Reg-DIF may be most advantageous in large sample sizes. As mentioned above, these results also showed smaller Type I errors without much decrement in power when using p-values from univariate Wald tests of individual DIF parameters (after re-estimating the model without the penalty function). This suggests that p-values may provide useful information for identifying DIF.

Similar prior approaches to using regularization for DIF detection have also shown promising results. In particular, Magis et al. (2015) applied the lasso penalty to a 1-parameter logistic model (using sum scores as an observed proxy for the latent variable) and found that lasso had advantages at smaller sample sizes. Furthermore, Tutz and Shauberger (2015) applied lasso to a 1-parameter logistic IRT model (directly modeling the latent variable), focusing on testing DIF for multiple covariates (e.g., gender, age, etc.). They found that lasso achieved greater control of Type I error than conventional DIF detection techniques when the proportion and magnitude of DIF was large. Huang (2018) also used a variety of penalty functions within a two-group structural equation model, including on slope differences, finding that regularization performed better when sample size and the magnitude of DIF were both large.

The current work, although closely related to Bauer et al. (in press), provides a more thorough empirical investigation of Reg-DIF across a variety of conditions. In particular, we analyze smaller sample sizes, smaller amounts of DIF, and a greater number of items with a larger sample size. As recent work with DIF analysis (Tutz & Shauberger, 2015) and structural equation modeling in model selection (Jacobucci, Brandmaier, & Kievit, 2019) has shown that regularization outperforms other common methods in small sample sizes, it is important to evaluate Reg-DIF in small samples as well. We also focus on the simpler case of two groups, the most common scenario under which DIF analysis is conducted in practice and the scenario that has received the most attention in methodological evaluation of DIF detection procedures. In particular, it is critical to evaluate Reg-DIF against other commonly used procedures like IRT-LR-DIF in situations that are widely encountered in education, psychology, and health outcomes. Furthermore, given that regularization has also shown better performance when there are many predictors (Jacobucci et al., 2019), it is not entirely evident whether lasso regularization performs well when there is only one DIF covariate (i.e., group membership). Although Bauer et al. (in press) and Tutz and Shauberger (2015) showed regularization works well with multiple DIF covariates, it is possible that more conventional procedures outperform Reg-DIF in the most common two-group scenario. Finally, apart from Bauer et al., the current work is the first application of regularized DIF detection to consider both intercept and slope differences simultaneously.⁵

Simulation

As an initial evaluation of Reg-DIF, we conducted a Monte Carlo simulation study comparing its performance to the commonly used IRT-LR-DIF procedure. Below, we describe the study design, the population parameters, the data generation and modeling procedure, and finally the study outcomes.

Method

Design.

The study design includes four factors with varying levels of sample size (3 levels), number of items (2 levels), proportion of DIF (3 levels), and magnitude of DIF (2 levels). In addition, we specified different latent distributions for each group to allow for mean impact. This will be described in greater detail below. The factorial design resulted in 36 distinct cells. We ran 200 replications per cell per method (Reg-DIF vs. IRT-LR-DIF).

Sample Size.

We evaluated three levels of sample size: 250, 500, and 1000, reflecting the range common to behavioral science applications (Finch, 2005; Kim & Cohen, 1998; Meade & Bauer, 2007). We split each sample evenly between the two groups.

Number of Items.

We considered 6 and 12 item conditions, reflecting a range that applies to both IRT and factor analysis applications (Cheung & Rensvold, 2002; Smith & Reise, 1998). In Table 1, Items 1–6 correspond to the first condition, and Items 1–12 correspond to the second condition.

Table 1.

Simulated Item Parameters

				Intercept (cij)			Slope (aij)
Item	DIF 1-item	DIF $\frac{1}{3}$	DIF $\frac{1}{2}$	Baseline (c0j)	Δ DIF-S (c1j)	Δ DIF-L (c1j)	Baseline (a0j)	Δ DIF-S (a1j)	Δ DIF-L (a1j)
1				0.8			0.7
2	*	*	*	0.2	−0.4	−1.0	1.0	−0.2	−0.4
3			*	−0.4	0.4	1.1	1.3	0.2	0.5
4		*	*	−1.0	0.4	1.2	1.6	0.2	0.6
5				−1.6			1.9
6				−2.2			2.2
7				0.8			0.7
8		*	*	0.2	−0.4	−1.0	1.0	−0.2	−0.4
9			*	−0.4	0.4	1.1	1.3	0.2	0.5
10		*	*	−1.0	0.4	1.2	1.6	0.2	0.6
11				−1.6			1.9
12				−2.2			2.2

Note. Population values for intercepts and slopes varied across replications and were randomly sampled from uniform distributions with means equal to the tabled values and a range of ± .30 for intercepts and ± .15 for slopes. Asterisk operators * indicate DIF for the 1-item DIF condition, 1/3 proportion of DIF condition, or 1/2 proportion of DIF condition. Δ DIF-S and Δ DIF-L indicate the difference in the slope and intercept between the two groups for small and large DIF conditions, respectively.

Proportion of DIF.

We evaluated three conditions with varying proportions of DIF: 1 item with DIF, 1/3 of items with DIF, or 1/2 of items with DIF. These proportions are also common in studies of DIF procedures (Finch, 2005; Wang & Yeh, 2003; Woods, 2009). Table 1 shows which items had DIF in each condition. These items were chosen so that DIF occurred in items with moderate information about the latent trait (i.e., moderate magnitude of a_j).

Magnitude of DIF.

We evaluated two magnitudes of DIF: small and large. DIF was quantified using the weighted area between the curves index (wABC; Edelen, Stucky, & Chandra, 2015; Hansen et al., 2013) with wABC values of approximately .1 for small DIF and approximately .2 for large DIF (see Edelen et al., 2015, for cut-off recommendations). Table 1 shows the DIF effects.

Data Generation.

We used R software (R Core Team, 2017) to generate data consistent with a two-group 2PL-IRT measurement model (Equation 8). Shown in Table 1, we choose baseline intercepts and slopes to reflect a relatively broad range of values that are commonly seen in practice. We drew baseline intercept and slope values from a uniform distribution with means listed in Table 1 and ranges of ± .30 for intercepts and ± .15 for slopes. Varying the baseline intercepts and slopes across replications allowed for greater generalization of our results, while the restricted range maintained ecological validity for what we might expect in practice. In contrast, we held DIF effects (c_1j and a_1j) constant across replications within a given condition, to avoid mixing within- and between-condition variability in the magnitude of DIF.

Data generation then proceeded through four steps. First, we assigned half of the individuals into each group, with group membership scored as x_i = 0 or 1. Second, for each individual, we drew a latent trait score from a normal distribution. For the reference group, the mean and variance were zero and one. For the contrast group, the mean was .5 and the variance was one. Thus, the population model included mean impact but not variance impact (although both forms of impact were estimated in the fitted models). Third, we computed individual probabilities of endorsing each item from each person’s latent trait score and the slope and intercept population parameters given in Table 1. Finally, we generated item response values of 0 or 1 from these probabilities of endorsement.

Procedure.

We followed Bauer and Hussong (2009) in using a nonlinear mixed effects modeling procedure in SAS software (PROC NLMIXED; SAS Institute, 2016) to implement Reg-DIF (see Supplemental Material accompanying this article for a step-by-step guide for the procedure). Specifically, there is a one-to-one mapping of latent variable parameters to nonlinear mixed effects parameters (Bauer, 2003; Curran, 2003; Mehta & Neale, 2005; Rijmen, Tuerlinckx, de Boeck, & Kuppens, 2003), as item responses are considered nested in persons. That is, the random effect represents the latent variable, and the fixed effects represent the item parameters.⁶ This procedure offers the opportunity to specify a custom likelihood function, allowing for the inclusion of the lasso penalty function. We then called NLMIXED within a macro that iterated through more than 100 values of the tuning parameter, τ, in varying increments, with the value generating the best BIC taken as optimal (similar to Magis et al, 2015; Tutz & Shauberger, 2015). In pilot testing, we found that smaller increments in the lower end of the range of τ allowed for finer differentiation so that only one parameter would be removed from the model at a time. In addition, we found that larger increments of τ in the higher end of the range ensured a global minimum of BIC was identified before choosing the best fitting model. To select out an effect, a coding statement in the SAS macro fixed a parameter estimate to zero when it crossed an arbitrarily small threshold (i.e., < .00001) and remained at zero for all larger values of τ. The macro stopped when all DIF parameters were removed from the model (i.e., set to zero). Once all DIF parameters were removed from the model, we used BIC to identify the model with the best fit. This model was then re-estimated with the remaining DIF parameters but without the penalty, which aimed to remove bias from the parameter estimates that occurs due to shrinkage by the penalty (Hastie et al., 2017). More details about implementing Reg-DIF in the NLMIXED procedure can be found in the supplemental material accompanying this article.

For IRT-LR-DIF, we utilized the mirt package in R (Chalmers, 2012). mirt implements the IRT-LR-DIF routine as described in this article. That is, each item is tested for DIF while all others are constrained to equality. Impact is also present for each test of DIF.

Outcomes.

To evaluate the performance of Reg-DIF against IRT-LR-DIF, we tallied true positives and false positives. A true positive refers to correct identification of a DIF parameter that exists in the data-generating model (see Table 1). A false positive refers to incorrect identification of a DIF parameter that does not exist in the data-generating model. For Reg-DIF, we recorded true and false positives for (1) DIF effects that were simply present in the best-BIC model (i.e., denoted Reg-DIF), regardless of statistical significance, and (2) DIF effects that were statistically significant when the best-BIC model was re-estimated without the penalty (i.e., denoted Reg-DIF p < .05). For IRT-LR-DIF, we recorded true and false positives for items with significant likelihood ratio tests after implementing the Benjamini-Hochberg false discovery rate correction procedure (Thissen et al., 2002). In addition to true and false positives, we evaluated mean squared error (MSE) as a combination of squared bias and variance for both Reg-DIF and IRT-LR-DIF, in each case based upon a final model including all identified DIF effects. More fine-grained results, including impact estimates and true and false positives for intercept versus slope DIF (parameter-level results versus item-level results), may be found in the Appendix.

Results

The primary results comparing Reg-DIF with IRT-LR-DIF are given below. We first compare false positives (i.e., Type I errors) and then true positives (i.e., power) between Reg-DIF and IRT-LR-DIF. Subsequently we evaluate bias, variance, and MSE for the model estimates.

False Positives (Type I errors).

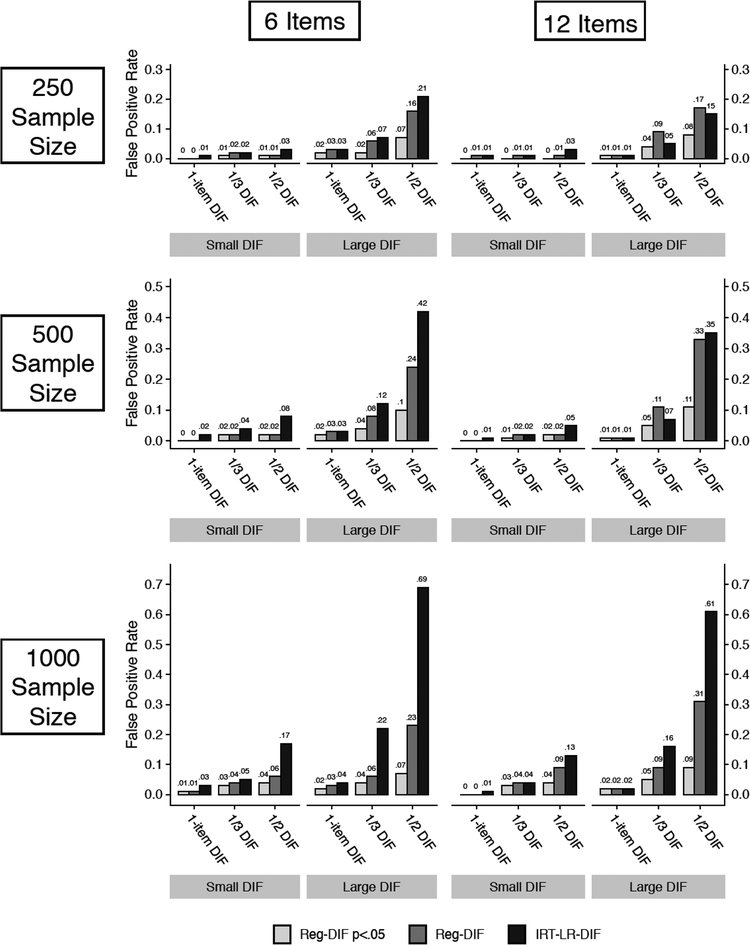
Figure 1 provides false positive (FP) rates for Reg-DIF p < .05, Reg-DIF (without considering statistical significance), and IRT-LR-DIF with the nominal alpha level set at .05. We found that IRT-LR-DIF exhibited severely inflated FP rates as the proportion of items with DIF and the magnitude of DIF increased, exacerbated by larger sample sizes. In the largest sample size of 1000, for instance, FPs increased to 69% when three of six (1/2) items had large DIF in the population model. Conversely, IRT-LR-DIF showed relatively few Type 1 errors when only 1 item had DIF. These outcomes are consistent with previous research showing that large amounts of DIF, that is, large model misspecification, leads to high Type I error rates for IRT-LR-DIF (Stark et al., 2006). In contrast, Reg-DIF p < .05 showed better control of Type I error, never increasing above 11% FPs for any study condition. Although false positives for Reg-DIF (without considering statistical significance) showed higher Type I error rates than Reg-DIF p < .05, they remained mostly lower than IRT-LR-DIF. Overall, these results suggest that Reg-DIF is more conservative than IRT-LR-DIF, particularly as sample sizes and DIF increase. Given our use of BIC as a selection criterion, this finding is consistent with previous research, which has shown BIC to be one of the most conservative selection criteria for regularization applications (Jacobucci, Grimm, & McArdle, 2016; Magis et al., 2015). Furthermore, Reg-DIF was more conservative when considering statistical significance despite the p-values being computed from incorrect sampling distributions. This is also in line with previous research (Bauer et al., in press). At small sample sizes and more scale items, however, Reg-DIF without significance showed slightly larger Type I errors compared to IRT-LR-DIF. In relation to prior work, these results support the notion that lasso can be too liberal (Hastie et al., 2017; Lindstrøm & Dahl, in press), although our use of BIC largely dampened this effect. Finally, a more granular analysis of Type I errors for intercept and slope DIF (separately) revealed results similar to those identified here. We present these results in the Appendix (see Figures 1A and 2A).

Figure 1. False positives for Reg-DIF and IRT-LR-DIF (empirical Type I error).

True Positives (Power).

Figure 2 presents true positives (TP) for Reg-DIF p < .05, Reg-DIF (without considering significance), and IRT-LR-DIF. Generally, we observed that IRT-LR-DIF exhibited greater power than both Reg-DIF p < .05 and Reg-DIF without significance across most study conditions. This was particularly the case when sample size was moderate and the amount of DIF was small. However, in light of the empirical Type I error rates, it appears that IRT-LR-DIF had greater power because it often indiscriminately identified too many effects as significant. This supports previous research showing that IRT-LR-DIF is a powerful method of detecting DIF when DIF is minimal, but when DIF becomes pervasive in a scale and large sample sizes lead to high power, IRT-LR-DIF tends to be far too liberal (Finch, 2005; Stark et al, 2006). Therefore, which procedure performed best on balance depends on sample size and the extent of DIF. For instance, Reg-DIF p < .05 provided a better balance of Type I errors and power in larger samples and when more DIF was present. In these same conditions, IRT-LR-DIF still had greater power but at the cost of unacceptably high Type I error rates. These results are consistent with prior research showing that regularization in multiple group SEM contexts has good parameter recovery in large sample sizes (Huang, 2018; Jacobucci et al., 2016).

Figure 2. True positives for Reg-DIF and IRT-LR-DIF (empirical power).

Interestingly, Reg-DIF without significance did not see large gains in power compared to Reg-DIF p < .05 despite having higher Type I error rates, which is consistent with parallel research (Bauer et al., in press). On the other hand, Reg-DIF without significance showed slightly greater power than IRT-LR-DIF (and Reg-DIF p < .05) in identifying DIF effects in small samples and with more items in the scale (12), but false positives were also slightly greater. Given that prior research has shown that Reg-DIF performs well in smaller samples (Jacobucci et al., 2019; Magis et al., 2015), our inconclusive small sample results are likely a function of using the conservative BIC criterion for model selection and introducing large degrees of model misspecification in the simulated data via more scale DIF (e.g., see Magis et al., 2015, for differences between selection criteria in DIF recovery). Lastly, we found that true positive results for intercept DIF were largely the same as found in the aggregated analysis here. In contrast, we found that slope DIF effects were recovered at higher rates for both Reg-DIF p < .05 and Reg-DIF without significance compared to IRT-LR-DIF, although power was generally lower for slope DIF compared to intercept DIF across the board. More detailed results on true positives for intercept versus slope DIF are also presented in the Appendix (see Figures 3A and 4A).

Mean Squared Error.

Figures 3 and 4 display mean squared error (MSE) as a combination of squared bias and variance for the largest sample size in the original simulation design (i.e., 1000). Figure 3 shows MSE for estimated DIF effects that were not present in the population model (i.e., population values of DIF effects = 0), and Figure 4 shows MSE for estimated DIF effects that were present in the population model (i.e., population values of DIF effects ≠ 0; see Table 1). Here, we compare estimates from Reg-DIF that was re-estimated without the penalty function with estimates from IRT-LR-DIF that was also re-estimated with all DIF detected.⁷

Figure 3. Mean squared error for DIF estimates that were not present in the population.

Note. MSE for sample sizes of 1000, collapsing across number of scale items (i.e., 6 and 12). DIF estimates were simulated to have DIF = 0 in the population.

Figure 4. Mean squared error for DIF estimates that were present in the population.

Note. MSE for sample sizes of 1000, collapsing across number of scale items (i.e., 6 and 12). DIF estimates were simulated to have DIF ≠ 0 in the population.

For DIF estimates that were not present in the population, Figure 3 shows that Reg-DIF had uniformly smaller MSE error than IRT-LR-DIF in all study conditions. This was primarily due to lower estimator variance for Reg-DIF as opposed to smaller bias, although Reg-DIF also had lower bias than IRT-LR-DIF as the proportion of DIF increased. For those DIF effects that were present in the population (Figure 4), Reg-DIF had larger MSE than IRT-LR-DIF for intercept DIF in nearly all study conditions. The main exception occurred in the largest magnitude and highest proportion of DIF condition, where both bias and variance increased greatly for IRT-LR-DIF but not Reg-DIF. In contrast to intercept DIF, Reg-DIF showed almost uniformly lower MSE for slope DIF compared to IRT-LR-DIF, with the largest proportion of DIF condition also showing considerably higher variance (but not bias) for IRT-LR-DIF. This finding parallels our more granular findings (Figure 4A in Appendix), showing that Reg-DIF had greater power than IRT-LR-DIF at recovering slope DIF.

Summary.

These results showed that both Reg-DIF p < .05 and Reg-DIF (without considering significance) had far better control of Type I error compared to IRT-LR-DIF, particularly when the magnitude and proportion of DIF and sample size were all large. IRT-LR-DIF showed greater power in identifying DIF when DIF was smaller in magnitude and sample sizes were moderate, although these advantages were often offset by markedly inflated Type I error rates. At smaller sample sizes, Reg-DIF (without significance) showed slightly greater power than IRT-LR-DIF in some conditions, but this was also at the cost of higher Type I errors compared to IRT-LR-DIF. Additionally, these results indicated that Reg-DIF had smaller MSE in the intercept and slope DIF effects that were not present in the population (when DIF = 0). Reg-DIF also had smaller slope MSE for slope DIF effects that were present in the population (when DIF ≠ 0). In contrast, for non-zero intercept DIF the opposite was found: IRT-LR-DIF had lower MSE than Reg-DIF. Finally, Reg-DIF was more sensitive for detecting slope DIF than IRT-LR-DIF.

Empirical Demonstration and Validation

In this section, we further compare Reg-DIF p < .05 to IRT-LR-DIF by applying these procedures to data from the REAL-U project, a study specifically designed to generate human-subjects data with which to empirically validate psychometric methodology.⁸ Participants in REAL-U were randomly assigned to different “studies” using similar but somewhat altered measures related to alcohol and substance use. In the conditions examined here, the wording of specific items was modified to reflect differences commonly observed across independently conducted studies. For instance, on an alcohol use problems scale, the item “Relatives avoided you” became “Family members rejected you because of your drinking.” Given the random assignment of participants to conditions, we would expect only these modified items (and perhaps only a subset) to evince DIF as a function of study.⁹

Given our knowledge of where DIF between study groups should and should not occur, this example affords a unique opportunity to compare Reg-DIF p < .05 against IRT-LR-DIF with greater ecological validity. In particular, we expect that IRT-LR-DIF to identify more DIF both within the perturbed item set (owing to greater power) and within the non-perturbed item set (reflecting the higher Type I error rate). In contrast, we expect Reg-DIF p < .05 to perform better at isolating DIF specifically to those items that were perturbed.

Methods

Sample and Procedure.

The sample included 854 participants (54% female) between the ages 18 to 23 who were enrolled at a large southeastern university and indicated alcohol use in the last year. Of these, 416 participants were randomly assigned the unperturbed items and 438 were randomly assigned the perturbed items. This study was approved by the university-affiliated institutional review board.

Measure.

We used a shortened form of the Rutgers Alcohol Problem Index (RAPI; White & Labouvie, 1989) with 17 of the original 23 items (Neal, Corbin, & Fromme, 2006).¹⁰ The RAPI measures cognitive, emotional, and behavioral consequences due to alcohol use by asking participants to “Indicate how many times each of the following things happen to you at some point in your life.” The item responses were ordinal, with a range 0–3: None (0), 1–2 times (1), 3–5 times (2), More than 5 times (3), or Refuse to answer (missing). Given that nearly 80% of the responses on average were in the None (0) category, we collapsed responses into Not Present (0) or Present (1). On the perturbed version, 9 of the 17 item stems were modified. Both the unaltered and perturbed item stems are shown in Table 2.

Table 2.

Unperturbed and perturbed versions of the Rutgers Alcohol Problems Index (RAPI)

Item	Unperturbed RAPI Items	Perturbed RAPI Items
1	Got into fights with other people (friends, relatives, strangers)
2	Went to work or school high or drunk	Gone to class or a job when drunk
3	Caused shame or embarrassment to someone	Made others ashamed by your drinking behavior or something you did when drinking
4	Neglected your responsibilities
5	Relatives avoided you	Family members rejected you because of your drinking
6	Felt that you needed more alcohol than you used to in order to get the same effect
7	Tried to control your drinking (tried to drink only at certain times of the day or in certain places, that is, tried to change your pattern of drinking)
8	Had withdrawal symptoms, that is, felt sick because you stopped or cut down on drinking
9	Noticed a change in your personality	Acted in a very different way or did things you normally would not do because of your drinking
10	Felt that you had a problem with alcohol
11	Wanted to stop drinking but couldn’t	Tried unsuccessfully to stop drinking
12	Suddenly found yourself in a place that you could not remember getting to	Awakened the morning after some drinking the night before and could not remember a part of the evening.
13	Passed out or fainted suddenly	Passed out after drinking
14	Kept drinking when you promised yourself not to
15	Felt you were going crazy	Your drinking made you feel out of control even when you were sober
16	Felt physically or psychologically dependent on alcohol
17	Was told by a friend, neighbor or relative to stop or cut down drinking	Near relative or close friend worried or complained about your drinking

Results

Table 3 provides results comparing Reg-DIF p < .05 with IRT-LR-DIF using the perturbed version of the RAPI. For the most part, both procedures identified DIF in the same items. Where the two procedures differed, however, was in line with our expectations given the simulation results. More specifically, Reg-DIF p < .05 identified one item (Item 1) with DIF that was not perturbed, whereas IRT-LR-DIF identified two items (Items 1 and 4) with DIF that were not perturbed. Under the assumption that non-perturbed items should not have DIF, the higher number of these items indicated as having DIF by IRT-LR-DIF compared to Reg-DIF p < .05 is consistent with our simulation results showing more Type I errors with IRT-LR-DIF. Conversely, IRT-LR-DIF identified DIF in five perturbed items (Items 2, 3, 9, 12, and 13) whereas Reg-DIF p < .05 identified DIF in four perturbed items (Items 2, 9, 12, and 13). The additional item for which DIF was detected by IRT-LR-DIF had the smallest likelihood ratio test statistic of the set of DIF items. That this was detected by IRT-LR-DIF and not Reg-DIF p < .05 is consistent with the greater power observed for IRT-LR-DIF in the simulation.

Table 3.

Reg-DIF vs. IRT-LR-DIF on Perturbed RAPI

Item	Reg-DIF p < .05	IRT-LR-DIF
1	*	*
2	*	*
3		*
4		*
5
6
7
8
9	*	*
10
11
12	*	*
13	*	*
14
15
16
17

Note. The asterisk operator * indicates significant effect. Shading indicates perturbed items.

Discussion

Identifying the optimal approach for testing DIF and selecting anchor items when assessing measurement invariance has been a vexing problem in psychometrics for many decades. Our main objective here was to advance regularization as a method for identifying DIF with potential advantages relative to conventional DIF testing procedures. In this paper, we demonstrated how lasso regularization could be applied to the commonly used 2PL-IRT model to evaluate across-group measurement invariance in both intercepts and slopes. We compared lasso regularization (Reg-DIF) with IRT-LR-DIF, the most conventional method for testing DIF, and found via a traditional Monte Carlo simulation and an empirical validation study that Reg-DIF had better Type I error control than IRT-LR-DIF, especially when the amount of DIF and sample size were both large. At smaller sample sizes, Reg-DIF also performed well in terms of both Type I error and power, sometimes achieving greater power than IRT-LR-DIF. Taken together, the primary advantage of Reg-DIF over IRT-LR-DIF is most clearly salient when DIF is more pervasive in a scale and large in magnitude, and as the power differential dissipates with larger sample sizes.

There are, however, contexts within which IRT-LR-DIF may be preferred. In particular, IRT-LR-DIF produced higher power and relatively low Type I error rates when sample sizes were moderate and there was less DIF (both in magnitude and proportion). This suggests that IRT-LR-DIF may be more advantageous in research contexts where these conditions are more likely. Additionally, an analyst might prefer IRT-LR-DIF if Type I errors are considered to be of low consequence (because items are easily replaced, even if erroneously identified as having DIF) and Type II errors are high cost (as in high stakes testing where bias due to unidentified DIF would be unacceptable). Such considerations seem more likely to apply in an educational research context. In psychological research, there are fewer opportunities for researchers to simply replace DIF items with new items because item pools are often limited and less studied.

These findings build upon previous work using lasso regularization to identify DIF. In particular, we identified similar patterns in our simulation results as other researchers (Huang, 2018; Magis et al., 2015; Tutz & Schauberger, 2015). Similar to Huang (2018), lasso regularization showed good parameter recovery at larger sample sizes when using BIC, as MSE was reliably smaller for Reg-DIF at sample sizes of 1000 in the current study. Similar to Tutz and Schauberger (2015), Reg-DIF showed the greatest advantage over IRT-LR-DIF when there were large amounts of DIF present, both in magnitude and proportion. Similar to Magis et al. (2015), Reg-DIF also showed good recovery of DIF at smaller sample sizes. However, these small sample results were less conclusive than Magis et al.’s findings and other research findings (Jacobucci et al., 2019). This discrepancy may be explained by our use of BIC as a model selection criterion and our focus on large amounts of DIF (i.e., model misspecification). For instance, Magis et al. reported that “BIC outperforms all methods…when group sizes and percentages of DIF and DIF sizes are large” (p. 130). With less amounts of DIF, BIC may be too conservative at smaller sample sizes, and other selection criterion may be more fruitful. Huang (2018) found that “under non-null cases [DIF is present] the AIC could outperform the BIC if either the effect size or the sample size was small”. Parallel research by our group, however, has shown that AIC is too liberal of a criterion, resulting in far too many Type I errors (Bauer et al., in press). Other research efforts found that a weighted combination of AIC and BIC (i.e., Weighted Information Criterion [WIC]) was a good balance for identifying DIF effects across a variety of scenarios (Magis et al., 2015).

In addition to this prior work, we also extended research on using lasso regularization as a method for DIF testing. Specifically, we have shown that regularization can be used to penalize both intercepts and slopes in a 2PL-IRT model (rather than just intercepts in a 1PL-IRT model or just slopes in a multiple-group SEM). We have also shown that using p-values after re-estimating the final model without the penalty leads to fewer false positives than simply counting those effects that remain in the final model, and that power was not considerably affected as a consequence. We also found that Reg-DIF may perform well with smaller numbers of scale items, a condition that was not examined in previous research. Lastly, we evaluated Reg-DIF within the most common context for DIF evaluation, comparing two groups, and against the most commonly applied DIF detection procedure, IRT-LR-DIF, finding that Reg-DIF outperforms IRT-LR-DIF when sample sizes and DIF are both large. These findings indicate that Reg-DIF is a promising technique for evaluating DIF in common testing situations.

Limitations and Future Directions

Some limitations of the study are worth noting and offer opportunities for exploration in future research. As is true for all simulation studies, we were unable to examine all possible conditions that might occur in applied settings. Additional simulations should consider other conditions, such as a larger number of scale items, varying levels of impact, and differences in group sizes. In particular, we did not consider conditions in which variance impact was different across groups, which may have affected the relatively good recovery of slope DIF for Reg-DIF. We also did not consider cases in which sample size differed between groups. However, previous research has shown that the effects of sample size on the recovery of DIF is largely influenced by the size of the smallest group rather than an imbalance between groups (Woods, 2009).

Software developments will also be important for future research. Our ability to consider additional simulation conditions was limited by the computational inefficiency of the NLMIXED procedure we used to fit the models. For instance, having more scale items (and thus more parameters) resulted in longer optimization times in NLMIXED, sometimes taking as long as a week or more to return estimates for a sequence of tuning parameter values. Therefore, our implementation is limited to 10–20 items at most, and even this requires much patience from the researcher. Another potential limitation is our method of selecting anchor items with a coding statement in SAS and an arbitrarily small threshold value. We did not use soft-thresholding within the optimization procedure as is commonly done with regularization but rather performed thresholding (setting parameter estimates to zero) after the model was estimated at each progressive value of τ_, and this may have led to sub-optimal results. However, given that our results are consistent with findings from Magis et al. (2015), Huang (2018), and Tutz & Schauberger (2015), our method of thresholding appears to have performed similarly to soft-thresholding. Nevertheless, more work is necessary to determine whether this alternative method of thresholding affects Reg-DIF performance relative to soft-thresholding. Important recent work on estimation using regularization in IRT and factor analysis provides a promising foundation to build more efficient, tractable, and principled estimation algorithms for Reg-DIF that will allow for more scale items and soft-thresholding (Huang, 2018; Jacobucci et al., 2016; Sun et al., 2016; Yang & Yuan, 2018). Some of these implementations of regularization include use of the Bock-Aitken (1981) EM algorithm, providing the opportunity to run Reg-DIF with many more items and possibly more factors. Providing software that is computationally efficient and more user friendly for applied researchers will also increase the likelihood that Reg-DIF will be used in practice. As such, our research group is currently working on an EM algorithm that runs Reg-DIF more flexibly and efficiently.

Another potential limitation of these results is the use of p-values in tallying true and false positives for Reg-DIF. As mentioned previously, these p-values are computed from incorrect sampling distributions because they assume that each fit of the model with a new tuning parameter value is based on independently drawn data. Given that this is not the case, as we use the same data for each model fit, statistical theory indicates that these p-values are incorrect. However, our empirical results here and in Bauer et al. (in press) suggest they may nevertheless be useful for distinguishing real DIF from sampling errors. This, of course, may be a function of the simulation conditions explored here and in Bauer et al., and thus may not generalize to other applications of testing DIF with regularization. Future research should therefore examine the use of p-values when using regularization to select anchor items. Until then, we caution applied researchers in using p-values when implementing Reg-DIF. One recommendation is to use both p-values (after re-estimating the model without the penalty) in conjunction with theory to determine whether an item parameter differs between groups. That is, if Reg-DIF p < .05 indicates DIF in a particular item and theory supports this finding (e.g., girls are more likely to endorse items about crying on a depression inventory), then one will have greater confidence that DIF is truly present.

Another fruitful direction for future research would be to compare Reg-DIF as implemented here to other variations of the procedure. For instance, we used BIC to select the optimal model, but it would be useful to contrast this with other criteria. In particular, other research groups have shown potential use for WIC, AIC, and k-fold cross-validation (Magis et al., 2015). The dilemma, however, is that we often do not know how much DIF is present in a scale. Although using AIC, for instance, may lead to greater power with small Type I error rates when there is less DIF present (Huang, 2018), larger amounts of DIF will invariably lead to more Type I error (see Bauer et al., in press). Thus, a better approach may be for scientists to decide which error to minimize – Type I or Type II – based on the goals of the research. Nevertheless, evaluating alternative fit criterion for different research objectives should be explored in future research. Additionally, we examined only one type of penalty function, the lasso or l₁ penalty. Other penalties exist, including the adaptive lasso (Zou, 2006), the Smoothly Clipped Absolute Deviation (SCAD; Fan & Li, 2001) penalty, and the Minimax Concave Penalty (MCP; Zhang, 2010), which may improve the performance of Reg-DIF. These alternative penalties generally serve to mitigate the bias from using the l₁ norm by lessening the strength of the penalty on estimates that are large in absolute value to begin with (Hastie et. al., 2017). Specifically, using different penalties such as these may result in better performance for distinguishing large DIF effects from small DIF effects. Notably, Haung (2018) implemented the MCP in a multiple-group structural equation modeling approach, although their results were largely similar to those found in the current study. Finally, we examined only one form of the lasso penalty function here, applying this identically to all DIF intercepts and slopes. Using a different penalty for the intercepts and slopes to reflect the different scales of these parameters might be advantageous. Another variation would be the hierarchical group-lasso (Lim & Hastie, 2014), which penalizes groups of parameters that are conceptually related and ensures that higher order effects (slope DIF) are not included in the model without the lower order terms (intercept DIF).¹¹

Despite these limitations, we believe the current findings provide strong initial evidence of the advantages of Reg-DIF relative to conventional procedures and a useful foundation for future research on this topic.