Forcing cells into shape: the mechanics of actomyosin contractility

Abstract

Actomyosin-mediated contractility is a highly conserved mechanism for generating mechanical stress in animal cells and underlies muscle contraction, cell migration, cell division and tissue morphogenesis. Whereas actomyosin-mediated contractility in striated muscle is well understood, the regulation of such contractility in non-muscle and smooth muscle cells is less certain. Our increased understanding of the mechanics of actomyosin arrays that lack sarcomeric organization has revealed novel modes of regulation and force transmission. This work also provides an example of how diverse mechanical behaviours at cellular scales can arise from common molecular components, underscoring the need for experiments and theories to bridge the molecular to cellular length scales.

Cells use contractile stresses to drive shape changes and movements at the organelle, cell and tissue-length scales to regulate diverse physiological processes, including intracellular transport, genome replication and cell migration, as well as the formation and maintenance of a structured, multicellular tissue^1–5. For example, platelets generate a uniform, isotropic contraction (FIG. 1a) to reduce their overall size and drive the compaction of clots. Fibroblasts, epithelial cells and endothelial cells establish a front–back polarity and generate anisotropic stresses (FIG. 1b) on the surrounding extracellular matrix (ECM) or neighbouring cells. Such anisotropic contraction is used in matrix remodelling and tissue morphogenesis. In cytokinesis, contractile stresses are localized at the cell equator to drive furrow ingression and locally contract the cell (FIG. 1c). In cell migration, spatially regulated contractility is utilized both in symmetry breaking and in tail retractions (FIG. 1d,e). These diverse morphogenic changes all require large shape changes over second-to-hour timescales.

Figure 1 |. Types of contractile deformations generated by cells and tissues.

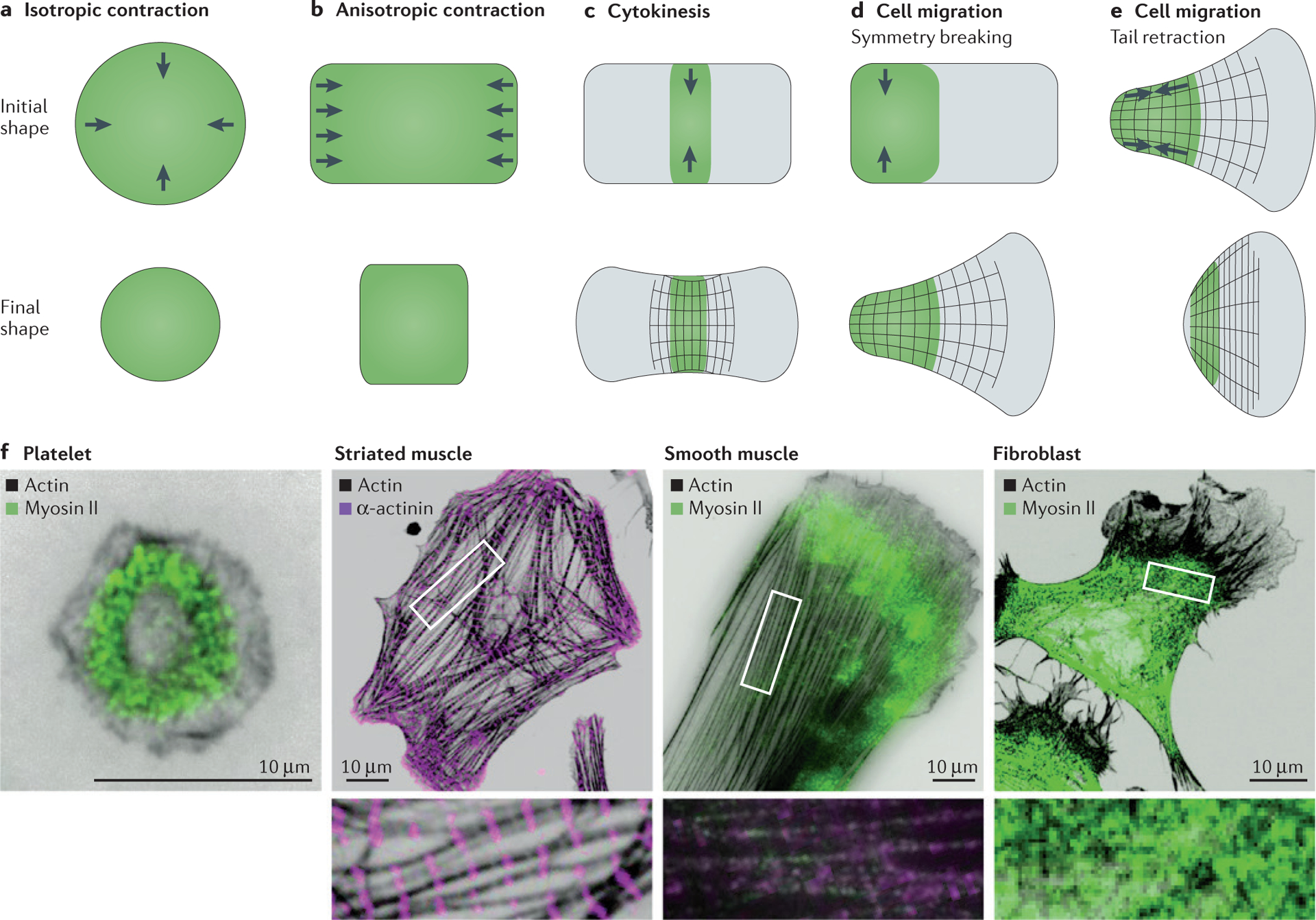
a | Isotropic contraction, which is performed by platelets, is uniform around the cell perimeter and induces a uniform change in shape and in the force generated. b | Anisotropic contraction, which is performed by striated and smooth muscle cells, induces contraction and force generation along one axis. c–e | In cytokinesis and cell migration, contractile stresses are spatially localized in a particular region of the cell to generate large deformations in cytokinesis (panel c), during symmetry breaking in migrating cells (panel d) and during tail retraction in migrating cells (panel e). f | Immunofluorescence images of several adherent cell types stained for actin, myosin II and α-actinin, including human platelets, striated muscle from a rat heart, smooth muscle from a human airway and mouse NIH 3T3 fibroblasts. Insets are a magnification of the corresponding boxed region and highlight the actomyosin organization within the cell. Myosin II was visualized using an antibody against phosphorylated myosin light chain, α-actinin was visualized via direct antibody staining and actin was visualized via phalloidin staining. Image of striated muscle cell courtesy of B. Hissa, University of Chicago, Illinois, USA, and image of smooth muscle cell courtesy of Y. Beckham, University of Chicago, Illinois, USA.

Force generation and transmission are controlled by a relatively well-conserved set of protein-based machines in the cytoskeleton. At the molecular level, force generation occurs by harnessing chemical energy into mechanical work. Cells have evolved myriad mechanoenzymes as molecular-scale force generators. For example, molecular motors, such as members of the myosin family, comprise a broad class of proteins that convert chemical energy into translational or rotational movement. Local stresses can also be generated by harnessing the energy that is used to construct polar and dynamic cytoskeletal filaments such as actin and microtubules. For instance, the polymerization of filamentous (F)-actin generates protrusive forces at the leading edge of migrating cells, whereas F-actin depolymerization can power cytokinesis in cell division⁶. Independent of the cytoskeleton, mechanical stresses can also be harnessed from adhesion energy⁷ as well as from osmotic pressure⁸. Thus, the molecular origins of mechanical forces in cell biology are diverse. Exactly how the mechanoenzymatic activities of the individual constituent proteins are transmitted through the cytoskeleton to determine the mechanical behaviour of cells is still not fully understood. Knowledge of cytoskeleton mechanics is essential for building quantitative and predictive models of physiologica l processes.

In this Review, we describe the progress that has been made in understanding the physics of the actomyosin cytoskeleton in non-muscle and smooth muscle cells (FIG. 1f). The molecular interactions between F-actin and non-muscle myosin II govern the generation of mechanical forces across diverse length scales, from the contraction of subcellular architectures in order to modulate cell shape⁵, division^4,5 and migration³, to the cooperative contraction of multicellular populations as occurs in smooth muscle and non-muscle tissue^9,10. Historically, contractility has been studied extensively in the context of striated muscle tissue, in which the actomyosin machinery is organized into sarcomeres^11,12. However, myosin II evolved millions of years before the sarcomere, which suggests that alternative modes of actomyosin contractility must exist¹³. The characterization of actomyosin arrays in smooth and non-muscle cells increasingly indicates that, although the molecular components are well conserved, the physics of contractile force transmission are fundamentally different from those in striated muscle.

The contractile cytoskeleton toolbox

The molecular composition of contractile actomyosin networks and bundles is highly conserved, despite large differences in their organization and dynamics across different cell types (FIG. 1f). Polymers of F-actin serve as the scaffold for myosin II motors and accessory proteins. Actin filaments are polarized: barbed ends and pointed ends correspond to their fast-growing and slow-growing ends, respectively (FIG. 2a). The minimal prerequisite for contraction is the coordinated activity of myosin II within the F-actin scaffold. All myosin II motors operate within larger bipolar ensembles known as myosin filaments, which vary in size from a few dozen heads for mini-filaments of non-muscle myosin II to hundreds of heads for the thick filaments of skeletal muscle myosin^14–18 (FIG. 2a). Myosin II filaments drive the translocation of F-actin filaments towards their barbed ends, which results in the contraction or extension of two bound actin filaments depending on the location of myosin II with respect to the middle of the filaments (FIG. 2b). In addition, a host of accessory actin-binding proteins modulate the architecture and mechanics of the F-actin network (for example, α-actinin, filamin and tropomyosin) as well as the filament length and lifetime (for example, ENA/VASP, formin and ADF/cofilin). Finally, actin-binding proteins also modify the coupling of actin filaments to the plasma membrane and membrane-associated organelles (for example, talin, vinculin, ezrin, radixin and spectrin).

Figure 2 |. Contractility in sarcomeres.

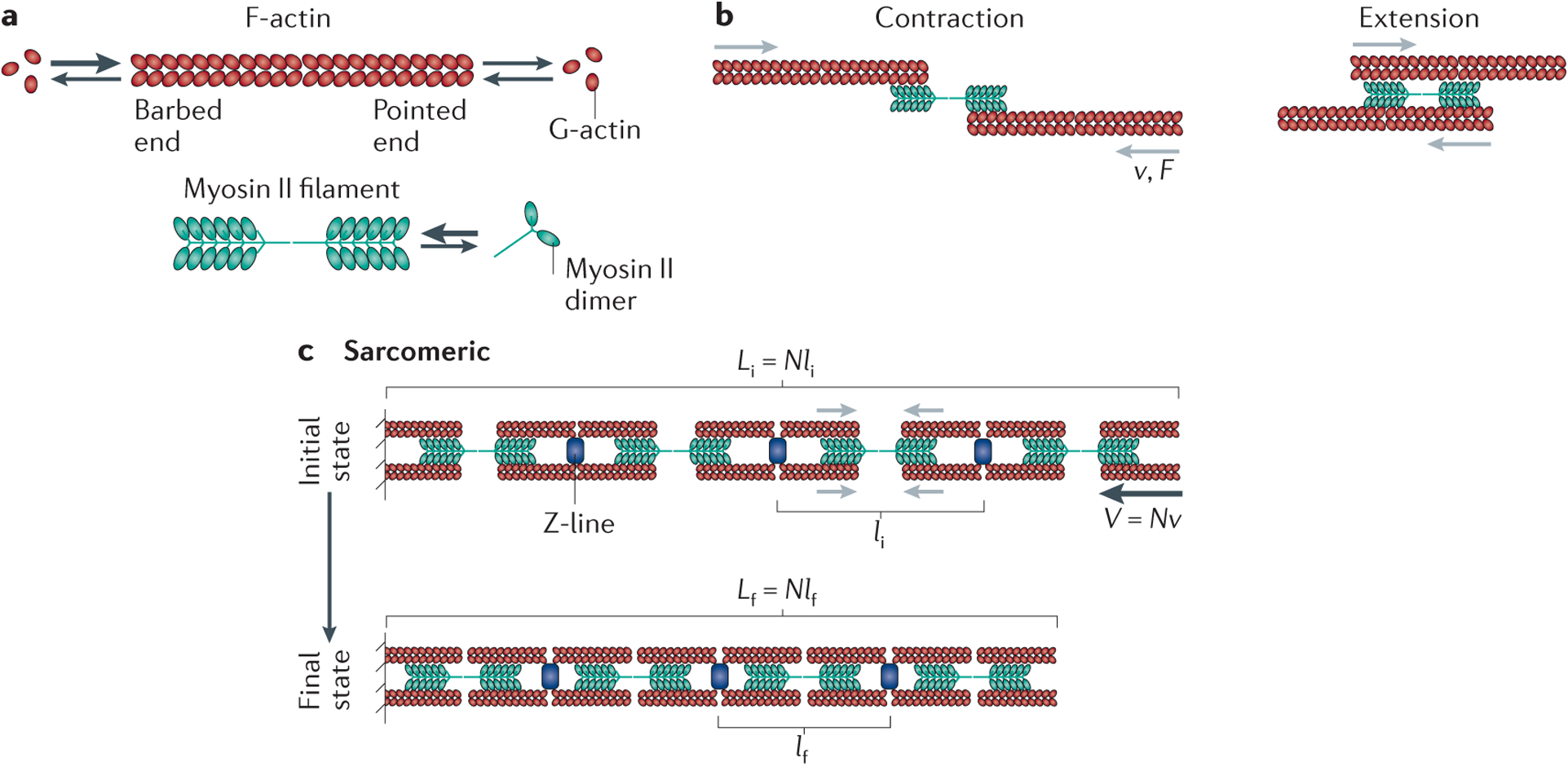
a | Filamentous (F)-actin has a barbed end and a pointed end (indicated by the ‘open’ and ‘closed’ direction, respectively, of the depicted actin chevrons that make up the polymer), and it can associate with globular (G)-actin from a pool of monomers or add G-actin back to this pool, as indicated by the arrows. Higher association rates of monomeric actin to the barbed end are indicated by a larger arrow. Bipolar myosin filaments with a central bare zone that lacks motor heads are assembled from myosin II dimers. b | Myosin II filaments drive the translocation of F-actin filaments towards their barbed ends with a characteristic force (F) and gliding velocity (v) relationship. This can result in the contraction (left) or extension (right) of two bound actin filaments, depending on the location of myosin II with respect to the middle of these filaments. c | Actomyosin organization within sarcomeres. Here myosin filaments are segregated towards the F-actin pointed ends, and F-actin barbed ends are localized at Z-bands, which contain numerous regulatory proteins, including α-actinin crosslinkers. The initial and final contractile unit length are indicated by l_i and l_f, respectively, in the initial (i) and final (f) states. Black arrows in the initial state indicate the direction of F-actin translocation. The contractile unit size is set by the sarcomere geometry, with the bundle shortening velocity (V) equal to the number of contractile units (N) times the myosin gliding velocity (v) such that V = Nv. The reduction in sarcomere length between the initial state and the final state arises from increased overlap between the F-actin and the myosin bare zone. The entire bundle length L is determined by the number N of contractile units multiplied by their length (l). Thus, the initial and final bundle lengths are given by L_i = Nl_i and L_f = Nl_f respectively.

Actomyosin contractility in sarcomeres

The best understood example of contractile force generation occurs in striated muscle. Here, actomyosin is organized in nearly crystalline arrays known as sarcomeres^19,20. Actin and myosin filaments assemble structures with the actin filament barbed ends localized to the Z-line, which contains crosslinking proteins (for example, α-actinin) and actin-binding proteins (CapZ), to form the ends of the sarcomeric unit (FIG. 2c). Myosin II thick filaments are segregated towards the pointed ends of actin filaments. As myosin pulls antiparallel actin filaments together, the increased overlap of the actin with the myosin reduces the sarcomere length²¹. The mechanochemistry of myosin II determines the force–velocit y curve characteristic of the sarcomeres. In turn, the maximal rate of myofibril shortening at zero force (that is, its unloaded velocity) is determined by the number of sarcomeres per unit length and the unloaded gliding speed of myosin II. Because there is little variation in sarcomeric spacing and myosin II speed, the contraction rate of striated muscle is largely constant¹¹. Likewise, the myofibril stall force is determined by the number of parallel motor heads within each sarcomere and, as skeletal muscle myosin filaments are a well-defined and constant size, the stall force of the myofibril is also largely constant.

The maximal extent of contraction in sarcomeres is limited by the maximal amount of increase in overlap between the thin (F-actin) and thick (myosin) filaments and determined by the length of the portion of the myosin filament that lacks motors, which is known as the ‘bare zone’ (FIG. 2a,c). This limits the extent of contraction to about 30% of the total sarcomere length. This process is cyclic, with actin returning to its original position after myosin detachment, leaving the architecture of the sarcomere unchanged²². Thus, the sarcomeric organization of actomyosin enables fast contraction, with small reductions in length and little regulation of the force–velocity characteristics. Although sarcomeric contractility can be understood in the absence of F-actin polymerization kinetics, recent data have shown that sarcomeric F-actin is surprisingly dynamic²³.

Non-sarcomeric actomyosin

The actomyosin cytoskeleton in non-muscle and smooth muscle cells is organized in various of ways that are not seen in sarcomeres to drive distinct physiological processes (FIG. 1f). Smooth muscle cells contain loosely organized actomyosin bundles that lack sarcomeric alignment and thus appear ‘smooth’ (REFS 24,25). The cell cortex contains a thin, membrane-bound and highly disordered actomyosin network that controls cell shape⁴, and during cell division a contractile actomyosin ring is generated to drive cytokinesis⁵. In the lamella of adherent non-muscle cells, actomyosin is organized into a contractile network^26,27 and a variety of bundles, including transverse arcs, radial stress fibres, peripheral bundles and ventral stress fibres^2,3. Although some of these bundles exhibit sarcomere-like banding patterns of α-actinin and myosin^28,29, they lack the regulation of actin filament length and periodic polarity that is found in striate d myofibrils³⁰.

Non-muscle and smooth muscle cell physiology requires spatial and temporal control of the contractile stresses underlying shape change and force transmission. In contrast to striated muscle, these cells exhibit high variability in the duration of contractile force generation (from seconds to hours), the contraction rate and the magnitude of shape changes. For example, the shape changes in cytokinesis and during tail retraction in migrating cells (FIG. 1f) far exceed the ~30% contractile strain of striated muscle. Contractile stresses can also support steady-state flow within the cytoskeleton. For example, the flow of actomyosin within the lamellum from the cell periphery to the centre in a retrograde manner is important in adhesion assembly³¹, intracellular transport and fibronectin remodelling³². During development, both steady-state and oscillatory contractile flows have important roles in morphogenic processes^33–36.

To sustain cytoplasmic flows and spatiotemporal regulation, contractile actomyosin arrays in non-muscle and smooth muscle cells are highly dynamic. Weak affinities (in the range of seconds) of crosslinkers and myosin for F-actin give rise to stress relaxation and structural remodelling in response to stress³⁷. The affinities are typically force dependent and will influence force transmission under varying levels of internal and external forces^38–40. Moreover, both actin and myosin filaments typically undergo turnover or cycles of disassembly–assembly that can be on similar timescales to contractility (~10–30 seconds)^4,41–43. Actin polymerization dynamics must be coordinated with myosin-generate d stresses to maintain a coherent actin cytoskeleton⁴⁴. In such situations, the contractile machinery cycles through periods of assembly, activity and disassembly. Thus, non-sarcomeric actomyosin machinery is highly dynamic and disordered, precluding standard models of sarcomeric contraction.

Generating self-organized contractility

In actomyosin bundles that lack sarcomeric organization, alternative mechanisms to generate local contractile forces are necessary. Myosin II motors translocate on actin filaments towards the barbed end, with no intrinsic preference for generating contractile or extensile forces. This implies that the overall organization of actin filaments with respect to myosin II within the bundle or network determines the net contractility. By way of example, consider the actions of myosin II filaments on a bundle containing actin filaments with random polarities (FIG. 3a). Here, motors drive the translocation of F-actin at a uniform rate, and thus a polarity sorting within the bundle tends to occur. These motions generate equivalent amounts of contractile and extensile force, and thus do not result in contraction⁴⁵. To break this symmetry and therefore promote contractility, a mechanism must exist to favour contractile motions over extensile ones.

Figure 3 |. Contractility in disordered actomyosin bundles.

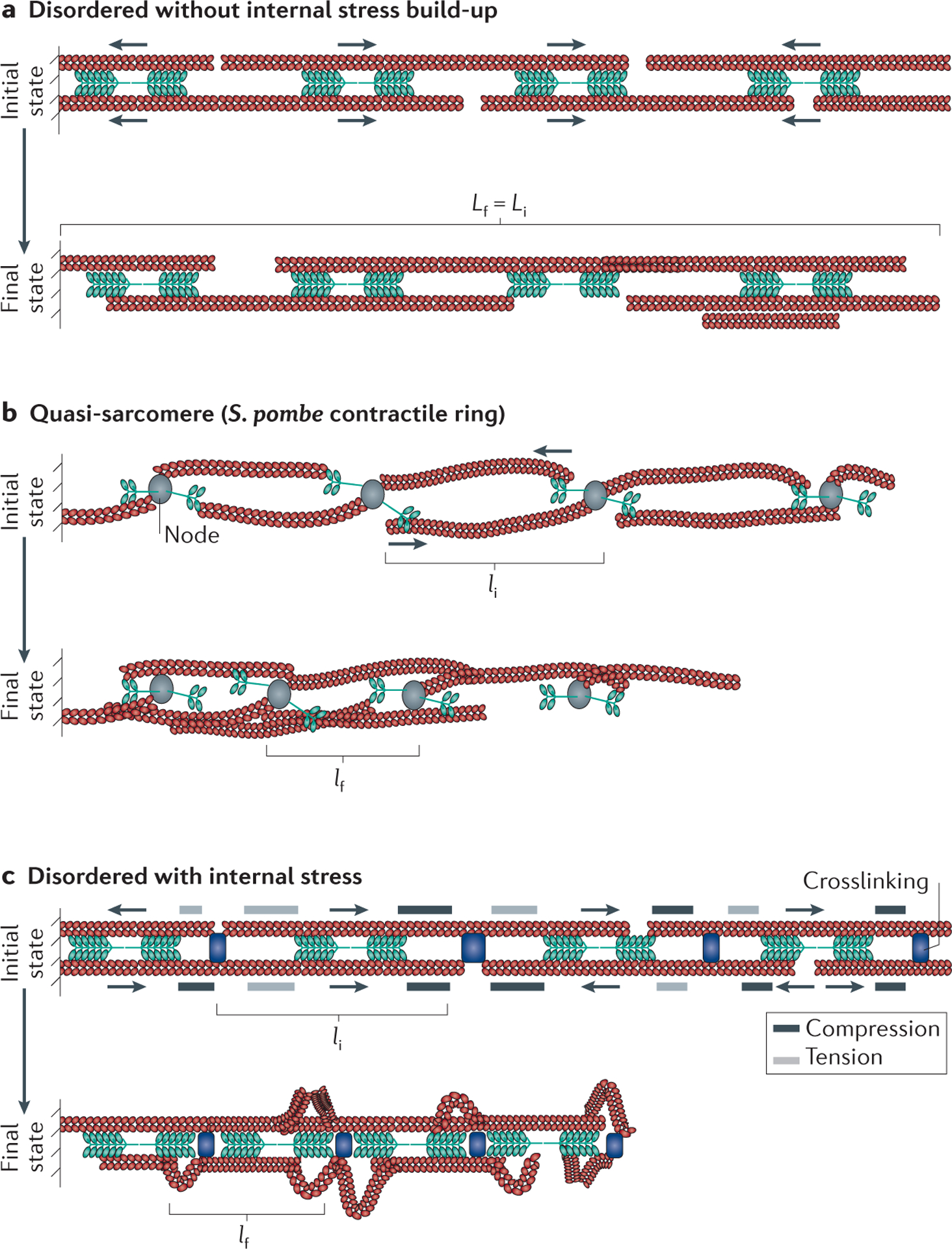
Throughout the figure the initial (i) and final (f) configurations are indicated, and the initial and final contractile unit length is indicated by l_i and l_f, respectively. Actin chevrons indicate the direction of the actin; the actin barbed end and actin pointed end are depicted by the ‘open’ and ‘closed’ direction of the chevrons, respectively. a | In a bundle with disordered actomyosin orientations, myosin II activity results in the internal sorting of F-actin polarity but does not lead to an overall reduction in the average bundle length (the initial and final bundle lengths are equal L_f = L_i). b | Quasi-sarcomeric organizations arise in some cytoskeletal assemblies, such as the Schizosaccharomyces pombe contractile ring, in which myosin II and formins are localized to nodes. Formins cluster F-actin barbed ends, thus localizing myosin II activity from neighbouring nodes towards F-actin pointed ends. This is effectively a sarcomere-like geometry and results in contractility over time. c | In a disordered actomyosin bundle similar to that shown in part a but with added crosslinking, myosin II activity generates internal compressive and tensile stresses, which cause the compression or extension of F-actin portions, respectively, depending on the relative position of motors and crosslinks with respect to F-actin barbed ends. If sufficiently large, these internal stresses deform and buckle portions of F-actin, which relieves compressive stress and enables bundle shortening. In this model, the average contractile unit size is the average distance between F-actin buckling events.

Putative mechanisms for breaking symmetry.

Breaking the symmetry caused by equivalent amounts of contractile and extensile force can be accomplished if a quasi-sarcomeric organization emerges from the local microscopic dynamics of the system. This occurs in the contractile ring of fission yeast where myosin motors and formins are localized to small nodes (FIG. 3b). Here formins promote the growth of F-actin, which localizes at the barbed ends of actin filaments so that they can interact with myosin from neighbouring nodes to generate a contractile force⁴⁶. Contractility is thus facilitated by the node composition, which enforces spatial segregation of myosin II to F-actin pointed ends. Another means to achieve the spatial segregation of motor behaviour at F-actin pointed ends is a potential change in motor velocity along the F-actin length, which has been explored theoretically^47,48. If motors stall at F-actin barbed ends, they then behave as crosslinkers, creating a possibly transient, quasi-sarcomeric structure. Thus, the dynamics and spatial organization of microscopic components can be a powerful symmetry-breaking mechanism.

A further method to break symmetry requires the presence of an inherent mechanical nonlinearity in the system. One natural mechanism to consider is the nonlinear response of F-actin to compressive stresses and tensile stresses. Whereas F-actin can withstand tensile stress of up to 300 pN (REF. 49), it buckles readily in response to compressive forces as low as 1 pN (REFS 50,51). Myosin II motors can generate internal stresses within actin bundles and networks. As shown in FIG. 3c, regions where a crosslinker is proximal to the barbed end of actin will experience a compressive stress; by contrast, if a crosslinker is proximal to the pointed end, a tensile stress will be generated. In a bundle comprising filaments with arbitrary polarity, these two geometries occur with a similar frequency. In a linear system, these stresses will balance out, and no overall net contraction or extension will occur. However, if F-actin buckles or ruptures under compression, compressed regions will collapse, whereas extended ones will remain essentially unaffected, resulting in overall buckle shortening (FIG. 3c). If motors buckle the filaments, compressive stresses are suppressed within the bundle and tensile stresses that drive contraction dominate. This asymmetric response of F-actin to compressive and tensile force is a means of breaking symmetry, allowing overall bundle contraction, and has been observed experimentally^52,53.

Other symmetry-breaking mechanisms that drive contractility are also likely to exist. For example, selective actin filament severing under compression either through mechanical⁵³ or biochemical⁵⁴ effects would similarly remove the ability of a bundle to resist internal compressive stresses, again yielding contraction. Interestingly, a nonlinear motor force–velocity relationship is not sufficient to break this symmetry, indicating the important role of nonlinearities in the actin filament mechanics⁴⁵.

Therefore, in actomyosin bundles that lack organization of filament polarity, the nonlinear response of actin filaments combined with random compressive and tensile stresses generates self-organized contractility. In vitro experiments^53,55 and theoretical estimates⁵⁶ further suggest that mechanisms similar to those described above for one-dimensional bundles also mediate contractility in disordered two- or three-dimensional actomyosin networks.

Contraction rate in disordered actomyosin.

Measurements of the relationship between the speed of contraction and the size of the system provide insight into the underlying force-generating processes that occur within the material. The rate of contraction is governed by the number of contractile units per length and the rate of contraction of each unit (BOX 1). In sarcomeres, these two parameters are determined by the sarcomere size and the force–velocity relationship of skeletal myosin II motors, whereas in disordered networks, the contractile unit lacks a straightforward structural signature. In the self-organized contractility framework (see above), however, the spatial frequency at which internal stresses generate F-actin buckling defines a contractile unit length scale⁵².

Box 1 |. Considering qualitative differences in model predictions.

The power of physical models is that they can predict how a system will evolve over time. In the case of contractility, sarcomere-based contraction and models of self-organized contraction predict qualitatively different behaviours for biochemically identical bundles. This can be considered using biochemically identical actomyosin bundles that contain a fixed number of myosin dimers and actin monomers (see the figure, step 1). Myosin is then assembled into differently sized filaments (see the figure, step 2). In scenario ‘A’, filaments are small so more myosin filaments (N) can be formed. In scenario ‘B’, the filament size is large, so fewer filaments can be formed. After constructing bundles that either have sarcomeric organization or are disorganized (see the figure, step 3), the bundle contraction rate (γ̇)— the speed at which the bundle shortens (V) per length (L) — is compared (see the figure, step 3). Thus, at the macroscopic level, γ̇ = V/L. At the microscopic level, γ̇ is the contraction speed of an individual contractile unit (v) divided by the contractile unit size l, such that γ̇ = v/l. In sarcomeric contraction, the contractile unit size is determined by the average spacing between myosin filaments, so the contractile unit in scenario ‘A’ is much smaller than that of ‘B’, and thus the bundle with numerous small myosin filaments will contract faster (γ̇_A > γ̇_B). In the case of the self-organized contraction of disorganized bundles, the smaller filaments generate less internal stress and contribute to increased internal crosslinking, which results in a larger distance between buckles and, thus, a large contractile unit size (‘A’) compared with the bundle constructed with larger filaments (‘B’). Thus, in this case, bundle ‘B’ will contract faster (γ̇_A < γ̇_B). This scenario was carried out in experiments on reconstituted actomyosin bundles, and results consistent with the model of self-organized contraction were found⁵⁷.

To illustrate the contrasting regulation of sarcomere-like contractility and self-organized contractility, consider two biochemically identical bundles consisting of the same number of myosin II motors and actin filaments with identical lengths and orientations (BOX 1). The only distinguishing feature between the two bundles is that the myosin II motors are constructed into filaments of different sizes. In the first bundle (bundle A), the myosin filaments are small but numerous, whereas bundle B has large but sparse myosin filaments. Which of these bundles contracts at a faster rate? In a sarcomeric organization, the spacing of myosin II filaments determines the sarcomere size and, as there are more contractile units per bundle length in bundle A, it will contract faster. However, in the model of self-organized contractility, internal stresses are needed to drive filament deformation, favouring the large motors and sparse crosslinking of bundle B. Moreover, motor-mediated dense crosslinking prevents filament deformation in bundle A. Thus, according to the model of self-organized contractility, the stronger internal forces but weaker crosslinking of bundle B promote contractile unit formation and thus faster contraction. Interestingly, when this model was performed on disordered actomyosin bundles in vitro, it yielded results consistent with the model of self-organized contractility⁵⁷. Although it is not meant to be inclusive of all biological circumstances, this reasoning demonstrates that the biophysics of contractile cytoskeletal assemblies can be highly dependent on the context. In sarcomeres, contractility is determined purely by the geometry, whereas in self-organized actomyosin the mechanical response to internal stresses determines contractility.

Regulating contractile strain in disordered actomyosin.

The extent of contraction in sarcomeres is determined by the extent of the increase in overlap between the thin and thick filaments — this overlap can reduce the overall length of sarcomeres by approximately 30% of the initial length. In non-muscle and smooth muscle cells, reductions of up to 100% in the length of actomyosin bundles can occur (see above), requiring the inclusion of additional mechanisms such as filament deformation or disassembly. F-actin disassembly occurs within contractile networks^41,58 and bundles⁵⁹, indicating that large-scale contraction could also occur through the removal of F-actin from within the network. F-actin bending is robustly observed in the contraction of disordered actomyosin networks and bundles formed in vitro. Moreover, the extent of end-to-end shortening of individual actin filaments that occurs through buckling corresponds exactly to the extent of network strain and is observed over a wide range of network conditions⁵³. The shortening of F-actin length via bending facilitates contractile strains of up to 80%. The bending of F-actin bundles has also been observed in vivo⁶⁰, but whether this has a causal role in the contractility of bundles and networks in vivo is unknown. Crosslinking proteins that prevent F-actin deformation could regulate the rate and extent of contraction. F-actin deformation might also create a mechanical feedback mechanism to regulate the dynamics of F-actin polymerization (see below). Although the mechanisms that operate to regulate the extent of contraction in disordered actomyosin in non-muscle and smooth muscle cells in vivo are still not clear, it is increasingly apparent that they are qualitatively different to those in sarcomeres.

Spatiotemporal regulation of contractility

Contractile stresses within non-muscle cells are spatially regulated at the subcellular, cellular and tissue length scales to mediate diverse physiological processes such as the establishment of polarity, cytokinesis, cell migration and tissue morphogenesis^5,9,10. This spatial regulation is dependent on the localization of contractile forces, the manner in which these forces are transmitted through the actin cytoskeleton and the ability of the actin cytoskeleton to reduce its size in response to stresses. Modifying any one of these parameters will influence the location, duration and extent of the ensuing shape change.

Localization of contractile force.

Spatial variations in contractile stresses in non-muscle cells in vivo are typically controlled through the phosphorylation of myosin II, which promotes its enzymatic activity and filament assembly⁶¹. Soluble growth factors, adhesion receptor signalling and environmental factors all influence myosin II phosphorylation through factors that signal upstream of it, including RHOA, RHO-kinase and myosin light chain kinase⁶². The spatiotemporal control of RHOA activation drives the anisotropic shape changes and guides the assembly of the contractile machinery in numerous processes illustrated in FIG. 1, including cytokinesis⁶³, cell migration⁶⁴ and polarity establishment⁶⁵.

Transmission of contractile force.

Force transmission through F-actin networks is determined by their architecture and mechanics. The ‘connectivity’ of F-actin networks is a measure of how well individual actin filaments are physically coupled to each other and is determined by actin filament length and density as well as by the type and quantity of crosslinking proteins. In vitro experiments in which the F-actin architecture can be systematically varied while maintaining a constant motor density provide a powerful means to test these parameters (BOX 2) and have demonstrated that a minimal amount of crosslinking is required to facilitate myosin-mediated network contractility at large (that is, >100 μm) length scales^66,67. Indeed, the extent of crosslinking strongly influences the transmission of contractile stresses⁵³. Although crosslinking can be carried out by crosslinking proteins such as filamin A, α-actinin, or fascin, myosin filaments themselves can also function as crosslinkers^53,57,68. In addition, the length of F-actin influences network crosslinking and entanglement, with longer filaments resulting in higher network connectivity, and thus itself has profound effects on contraction⁶⁶. Recent data have also suggested that feedback between contractility and stress-mediated F-actin breakage drives the system to a critically connected state that is just sufficient to support contraction⁶⁹.

Box 2 |. In vitro reconstitutions of actomyosin.

The reconstitution of F-actin networks from purified protein components is a powerful approach for understanding the physics of cytoskeletal networks. Such experiments enable the precise control and modulation of network composition and regulatory factors (for example, temperature and ATP concentration), which facilitates our understanding of how the architecture and mechanics of the actin cytoskeleton are regulated. Moreover, these studies are often more amenable to physical measurement and high-resolution imaging, as the length scales of materials constructed can span from microscopic to macroscopic. Here, we highlight three different types of actomyosin reconstitution experiments. During a macroscopic contraction of a reconstituted actomyosin network in a test tube (see the figure, part a), a homogeneous network (left panel) contracts via myosin activity, separates from the test tube walls (middle panels) and eventually forms a dense network that sits on top of the mixture (right panel). The first and last images in this sequence were taken 15 minutes apart. A two-dimensional actomyosin network formed adjacent to a lipid membrane as a model for the cell cortex (see the figure, part b, left panel). Myosin filaments are added at 0 s, and their activity drives the remodelling and compaction of the F-actin network (see the figure, part b, middle and right panels). A lipid vesicle encapsulating F-actin and myosin II to form a model cortex is depicted (see the figure, part c, left panel). The images show that the contracted actomyosin network remains on the interior side of the vesicle boundary. Each of these model systems has proven useful in isolating features of cellular contractility through in vitro reconstitution; the year each system was established is shown in brackets. Images in part a are reprinted with permission from REF. 66, The Rockefeller University Press.

Control of cytoskeletal deformation.

The mechanical response of F-actin networks that govern network contractility is determined by F-actin density and length, and crosslinker density and type. For instance, increased cross-link density and F-actin length results in networks that stiffen under strain^70,71. Some studies have reported that, at a constant myosin filament density, contractility is impeded as the network connectivity increases^66,67. This reduced contractility at a high crosslink density presumably arises when the network becomes too stiff, thus hampering myosin-mediated deformation. These results are consistent with the idea that the deformation of individual F-actin and F-actin bundles is necessary for contractility.

Although sufficient network connectivity is a prerequisite for network contraction, not all crosslinking proteins promote contraction equally. Crosslinking proteins vary in their size, affinity and compliance. Likewise, they can have differential effects on the organization of the F-actin network itself, forming networks or bundles that can affect the propensity to contract (TABLE 1). Recent studies have shown, for example, that crosslinking proteins such as fascin, which bind to polar, parallel F-actin, do not support contraction to the same extent as other crosslinking proteins, such as cortexillin and fimbrin, that bind to filaments in a polarity-independent fashion⁷². Increased levels of polar crosslinking proteins might even give rise to non-contractile, dynamic steady states of F-actin⁷². Finally, the spatial organization of F-actin polarity can also determine the extent to which contraction is observed⁷³. Thus, the architecture of the actin network qualitatively determine s the myosin-mediated behaviours of actomyosin.

Table 1 |.

Biophysical regulators of myosin II-mediated contractile force generation

Process (and factors involved)	Cellular location	Effect on actomyosin architecture	Effect on contractility	koff(dissociation rate constant in s−1)	Refs
F-actin crosslinking
Fascin	Filopodia	Unipolar bundling	Promotes dynamic non-contractile steady states, increased length scale*	9 s−1	69,72, 112–116
Filamin	Smooth muscle, stress fibres and cortex	Isotropic networks and apolar bundles	Increased length scale*	0.6 s−1 (F=0‡) 0.087 s−1 (F > 0§)	39,66,75, 117–122
03B1-actinin	Myofibrils, stress fibres, contractile ring and cortex	Isotropic networks and apolar bundles	Increased length scale*	0.4 s−1 (F=0) 0.066 s−1 (F > 0)	39,67,118, 122–126
Anillin	Cleavage furrow	Apolar bundles	Increased length scale*	Unknown	121, 127–129
Cortexillin	Cleavage furrow	Apolar bundles	Increased length scale*	Unknown	113, 130,131
Solution pH	Cytosol	Higher pH enhances F-actin crosslinking	Increased length scale	Unknown	121
F-actin length
Gelsolin capping protein	Cell cortex	Reduced F-actin length	Increased speed and reduced length scale	Unknown	66, 132
Membrane attachment
Ezrin, moesin and filamin	Cell cortex	Adds viscous drag to F-actin, resisting its mobility	Reduced length scale	Unknown	53, 133–135

^*Non-monotonic effect on contractility. Excessive crosslinker or capping protein inhibits contraction.

^‡F = 0 corresponds to unloaded (zero force) conditions.

^§F > 0 corresponds to loaded (non-zero force) conditions.

Effects of boundary conditions.

The architecture and dynamics of contractile actomyosin networks are also dependent on the environment to which they are attached, which is often referred to as ‘boundary conditions’. In cells, these include links to the extracellular environment, such as focal adhesions that connect the cytoskeleton to the ECM or adherens junctions that connect the cytoskeleton to other cells. These boundaries determine how much force is transmitted to the surrounding environment and provide resistance to internal dynamics. For instance, the actin retrograde flow rate is tenfold lower in the presence of adhesions than in their absence^28,74. In vitro, the physical coupling of F-actin to the plasma membrane reduces the length scale of contraction through enhanced entanglement of F-actin and an added stiffness that exceeds myosin- induced stresses (TABLE 1). Thus, the forces sustained at these cell boundaries determine the build-up of internal tension within the contractile networks. Consequently, this tension directly alters the velocity of motors by affecting their mechanochemistry. It is also likely to alter the network rigidity, as the stiffness of F-actin networks increases nonlinearly under applied load^75,76. Finally, more complex remodelling events can occur to stabilize certain structures under tension. For instance, the self-organization of stress fibres occurs at high tension within adherent cells²⁸.

Feedback in contractile systems

In order to support the dynamic steady states observed within the cytoskeleton, mechanical stresses must be coordinated with the biochemical regulation of actin polymerization dynamics. This is necessary, for example, to maintain a constant density of actin filaments, which, in the absence of regulated polymerization, would become heterogeneous. In principle, this feedback could arise from either biochemical⁵⁴ or mechanical mechanisms during actomyosin contraction. In vitro, F-actin buckling results in the mechanically induced severing of F-actin when filaments are bent below a critical radius of curvature of 300–400 nm (REFS 50,51). Actin filament severing increases the number of barbed ends and can thus promote F-actin assembly or disassembly via the activity of available actin-binding proteins. For example, in the presence of capping proteins, severing will result in F-actin disassembly. By contrast, barbed-end assembly factors such as DIA1 and ENA/VASP will promote F-actin assembly in locations with a high density of barbed ends. These resulting changes in F-actin density and length will alter local actomyosin contractility. Interestingly, F-actin disassembly occurs robustly in contractile networks, whereas F-actin assembly occurs locally in sites undergoing extension⁷⁷. Such interplay between mechanical and biochemical feedback loops is likely to be important in the regulation of actomyosin force transmission. Furthermore, these feedback loops could potentially act as force-sensing mechanisms for controlling transcriptional pathways that influence cell fate⁷⁸.

The architecture and dynamics of actomyosin networks can also influence the localization of actin-binding proteins that regulate other cellular functions. Exploiting the dynamic actomyosin cytoskeleton as a substrate for actin-binding partners is thought to be important in the dynamic regulation of the localization of partitioning defective (PAR) proteins during polarity establishment⁷⁹. The flow of actomyosin is also important for clustering adhesion receptors in epithelial and immune cells⁸⁰, whereas the high F-actin density within stress fibres is thought to provide a scaffold to stabilize proteins necessary for focal adhesion maturation³². Using the cytoskeleton as a dynamic scaffold is a natural way to spatially coordinate signals and cues across the cell to facilitate a rapid response to perturbations. This would serve as a natural mechanism of mechanochemical feedback to sustain dynamic steady states of contractile systems.

Contractile networks as mechanosensors

The stiffness of contractile actomyosin networks is highly sensitive to small changes in internal or external forces⁷⁵. F-actin networks formed in vitro at physiological protein concentrations with typical filament lengths and crosslinker types (for example, filamin) are very compliant when the network is deformed with low stress. The stiffness is in the order of 1 Pa, which is approximately 1,000-fold softer than is typical for adherent cells. When the magnitude of external forces is increased, however, the network stiffness increases considerably, up to several hundred-fold^{70,75,76,81–83}. This nonlinearity in the elastic response is robustly observed in F-actin networks and in networks consisting of other biopolymers.

When myosin II motors are incorporated into the actin network, they generate internal stresses within the system and also stiffen the network⁸⁴. The effect of such stiffening by internal stresses is equivalent to the stiffening induced by the application of external stresses⁷⁵. Thus, these in vitro assays recapitulate cellular pre-stress or the modulation of cellular stiffness by myosin II activity^85–89. This would imply that the actomyosin cytoskeleton is being driven into a highly nonlinear regime, whereby small changes in external or internal forces can have dramatic effects on the mechanical response of the system. These changes in stiffness of the actomyosin networks are likely to be important for responding to external forces. Further work is necessary to elucidate how cells interpret external mechanical cues to control signals that regulate cell proliferation, survival and differentiation. Although most attention has been on the mechanical signalling at focal adhesions, force sensing and an appropriate response is also likely to occur within the actomyosin cytoskeleton.

Contractility ‘stirs’ the cytoplasm

Myosin-generated stresses within actomyosin networks drive the local movement of proteins. These motions can result in deformation and flow of the actin cortex at subcellular or cellular length scales⁹. However, they can also create movements that seem to be random and resemble thermal diffusion, but that still require ATP-dependent mechanochemical activity of myosin motors within the cytoskeleton^84,90. These random internal stresses have consequences on the local movement of cytoskeletal filaments and the cytoplasm. For instance, the bending fluctuations of F-actin and microtubules increase as a result of this active, thermal-like stress^53,91. Moreover, these forces also increase the motion of organelles and proteins embedded within the network, resulting in an active diffusion or ‘stirring’ process that enhances transport over thermal diffusion within the cytoplasm⁹². Although myosin II activity is involved in this process, recent reports have shown this to be a more general ATP-dependent phenomenon that occurs in a wide range of eukaryotic and prokaryotic cell types^93,94. These processes provide a means by which internal mechanochemical activity within the cytoskeleton can enhance intracellular transport and homogenize intracellular signalling independentl y of directed motor-driven transport.

Control of tissue-scale contractility

As the mechanical behaviours of cells are determined by the cytoskeleton, the mechanics of multicellular tissue are determined by the mechanics of individual cells. Many of the same concepts described above for control of force generation and transmission at the subcellular length scales are also relevant for force transmission in multicellular tissue. Within tissue, spatiotemporal control of contractile tension within a small subset of cells generates local contractile force. How these forces are transmitted through the tissue to effect tissue shape change is determined by regulation of cell–cell adhesion and the mechanical response of surrounding cells. Recent evidence that adherens junctions undergo force-dependent assembly and mechanosensitivity⁹⁵ is one way in which the long-range transmission of force is ensured. Such spatial regulation of contractility at the tissue scale drives morphogenic changes in developmental processes^1,96 and facilitates wound healing, collective cell migration and tissue-scale mechanosensation^97,98.

Models of contractile cells and tissue

The complexity of cytoskeletal assemblies raises questions as to the level of detail that is necessary to determine how forces are distributed in cells and tissues. Microscopic models are enticing as they provide the flexibility to include details believed to be relevant to the biological process. However, this same flexibility also increases the complexity of the model and makes it difficult to pinpoint important physical parameters. For this reason, ‘coarse-grained’ models that include the molecular details of several key emergent physical parameters are useful. An example of such a coarse-grained model can be found in the Navier–Stokes equations that describe the motions of fluids. Instead of requiring knowledge of the molecular-scale detail of the fluid, only a few key parameters (for example, viscosity and average density) are needed to describe the motion of the system. The challenge, however, is to determine the key cellular scale parameters that are necessary to understand force transmission in cells and tissues.

One coarse-grained approach, active gel theory, models the actomyosin cortex as a homogeneous, compressible viscoelastic gel with an internal stress. This model has been used successfully to capture shape changes and internal actomyosin dynamics during cell division⁹⁹, during blebbing¹⁰⁰, in adherent cells^101–103 and during the establishment of polarity¹⁰⁴. Because lamellar actomyosin in adherent cells transmits myosin II-generated stresses to the underlying ECM, these stresses can be directly measured using techniques such as traction force microscopy and compared to the model predictions (FIG. 4a). Recent work has shown that a similar model that also incorporates a tension acting along the cell edge, or line tension, is sufficient to describe adherent cells of different sizes and shapes¹⁰⁵. In fact, these experiments demonstrated that spread area alone regulates the total contractile work done by the cell, independent of cell shape, adhesion morphology and ECM stiffness. In FIG. 4b, a fibroblast cell is shown for three distinct shapes with the same spread area. Although the geometry regulates the internal architecture and distribution of traction stresses, the total mechanical work done by these cells is similar. Thus, adherent cells can be characterized by an inherent contractility as the work done per spread area¹⁰⁵ (FIG. 4c). This quantity reflects the amount of energy a cell or cell colony can use to exert stress on the surrounding ECM or neighbouring cells. Comparing this quantity over a range of different cell types demonstrates that a large range of internal contractilities can exist, despite cells having similar machinery (FIG. 4d). Interestingly, platelets, which contain only disordered actomyosin and non-muscle myosin IIA, generate significantly more contractile energy per unit area than smooth and even striated muscle cells. These results serve to underscore the weak correlation that exists between internal actomyosin organization into sarcomeres and force output. These data suggest that, at least in certain cases, coarse-grained models with very few parameters can capture the essence of cell mechanical behaviours.

Figure 4 |. Inherent contractility of adherent cells.

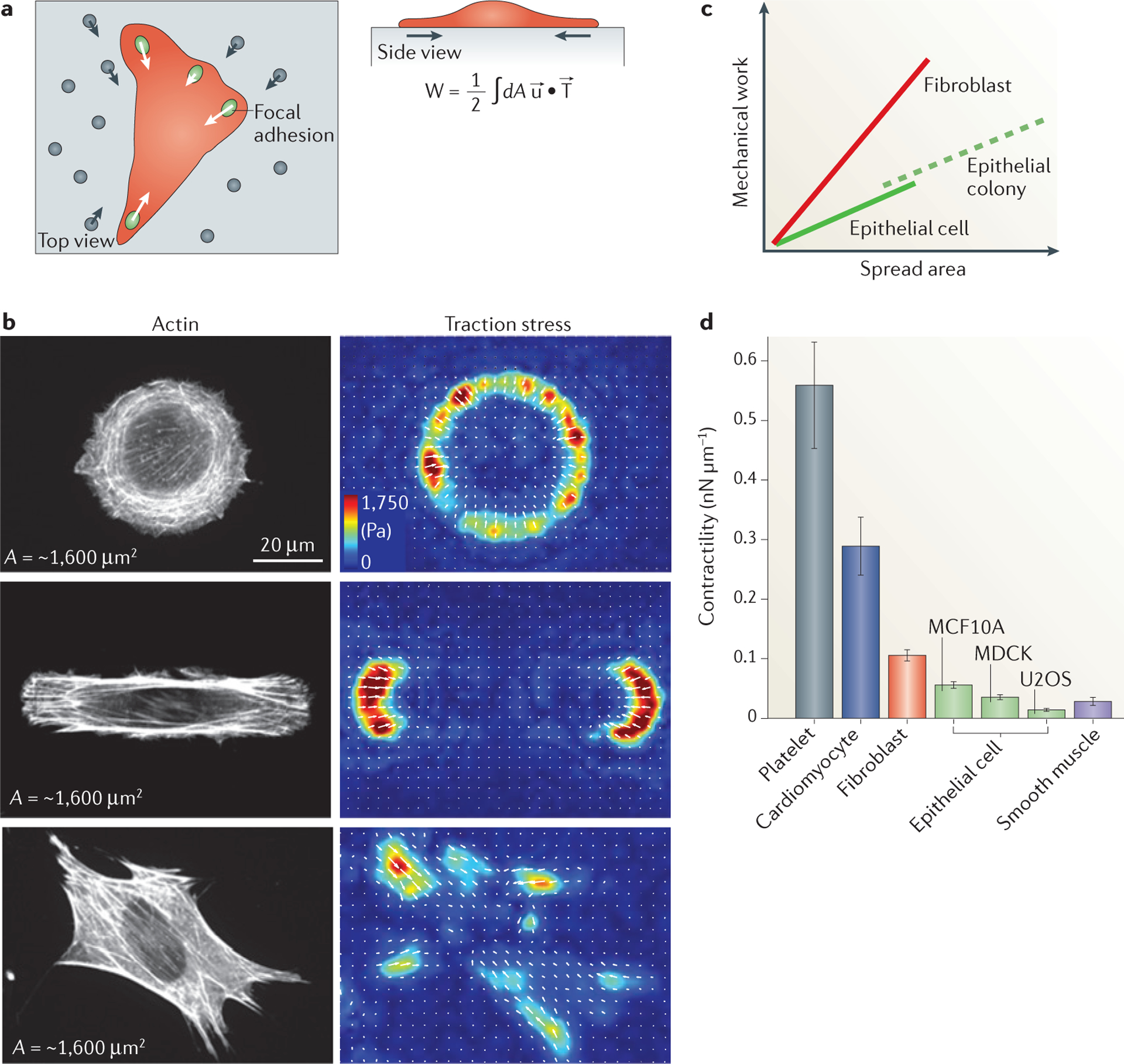
a | Traction force microscopy measures the distribution and magnitude of traction stresses of adherent cells (indicated in red) exerted through focal adhesions (green ovals) by probing the deformation of the underlying compliant matrix (grey) as measured by fiduciary markers (grey circles). Using this technique, we can calculate the strain in the substrate (u; grey arrows), the traction stresses applied by the cell (T; white arrows) and the amount of work performed to deform the substrate (W). The strain and stress are both vector fields, meaning that at each position these quantities have both a direction and magnitude. The total work is determined by integrating the dot product of the strain and stress vectors over the entire area (dA). b | The traction stress direction and magnitude for NIH 3T3 fibroblast cells of similar areas (~1,600 μm²) plated on a circular (top), oblong (middle) and unpatterned (bottom) surface are shown. The cell area is approximately constant in each of the three conditions, resulting in a similar amount of mechanical work performed on the environment by each of these three cells¹⁰⁶. Different cell geometries, however, result in different distributions of stresses (measured in Pa, as indicated) on the surface. c | Numerous experimental groups have found that the strain energy is proportional to the spread area for a wide range of cell types and for multicellular islands. The magnitude of this ratio (that is, slope of the line) is a measure of the characteristic contractility, and thus is cell type dependent. Multicellular islands of epithelial cells scale similarly to those for single cells when the area of the entire island is considered¹⁰⁴. d | The ratio of strain energy to spread area shows a characteristic contractility value for different muscle and non-muscle cells.

The limitation of these models is likely to arise when predicting the subcellular distribution of forces, shape and dynamics. For these questions, models that take into account the actomyosin architecture are needed¹⁰⁶. Future work will be required to identify the limits of such models and the length scales at which information about internal structures are needed.

Future endeavours

A wealth of studies have demonstrated the rich biophysical behaviours and regulation of cytoskeletal assemblies that are constructed from highly conserved constituent components of actin filaments and myosin II. Although the geometry of striated myofibrils facilitates our understanding of tissue-scale contractility from microscopic components, the mechanisms leading to self-organized and robust contractility in disordered and dynamic actomyosin assemblies probably rely on nonlinearities and asymmetries in the constituent macromolecules. Moreover, force influences the properties and activities of motors¹⁰⁷, filaments, actin assembly factors^38,40 and crosslinking proteins¹⁰⁸. How these force-dependent phenomena work in concert to support self-assembly of dynamic steady states in contractile matter is not well understood. The existing data underscore that a molecular-scale understanding of motor–filament interactions might not directly reflect the biophysical properties that emerge from subcellular and cellular length scales and ensembles. This body of work also provides a good case study to demonstrate how the mechanics of cytoskeletal assemblies at cellular length scales cannot be determined from the molecular composition alone.

Despite this complexity, we optimistically hope that these emergent behaviours can be understood by predictive physical theory, which will enable the identification of important regulatory parameters and reveal how properties can be tuned by molecular-scale activities. The ability to recapitulate contractility in cytoplasmic extracts¹⁰⁹ and with purified proteins strongly suggests this possibility. To achieve this, a solid feedback between theory and quantitative biophysical measurements is needed. Most importantly, there is an urgent need for experimentalists and theorists who are willing to challenge the predictions of prevailing models, as has proved successful in condensed matter physics.

We envision a class of physical models that can describe the behaviours of actomyosin arrays in a variety of physiological contexts and can predict relationships between architectures and physiological behaviours. Moreover, there is increasing evidence that contractility can arise independently of myosin II-generated motive forces but that it is instead dependent on myosin II crosslinking^6,110. Understanding how these alternative mechanisms of contractile force generation are regulated is an area of great promise. One exciting possibility is to identify models that can be generalized more broadly for other types of motor-filament arrays, such as microtubule-based machines, which would provide a greater understanding of the design principles underlying active cellular materials. These macromolecular assemblies are at the root of new classes of ‘living’ materials with internal mechanochemical activity, an exciting area for condensed matter physics and materials science¹¹¹. Understanding how such macromolecular assemblies facilitate the complex physiology of cells, tissues and organisms remains an exciting research area at the intersection of biology, physics and engineering.

Glossary

Isotropic contraction

Shortening that is uniform in all directions.

Anisotropic stresses

Shortening that is not uniform in all directions.

Z-line

A region at the boundaries of muscle sarcomeres in which the actin filaments are anchored. It appears as a dark transverse line in electron micrographs.

Force–velocity curve

The relationship between the force applied to a motor and the speed at which it moves relative to its substrate.

Myofibril

The structural unit of striated muscle fibres, which is formed from longitudinally joined sarcomeres. Several myofibrils form each fibre.

Unloaded velocity

The speed at which a motor moves under no applied load. Typical unloaded velocities for myosin II motors range from 50–1,000 nm s–1.

Stall force

The applied force that stops the motion of the motor. Typical stall forces for individual molecular motors are 1–10 pN.

Lamella

RHOA-dependent actomyosin organelles in adherent cells. Actomyosin is organized into a variety of contractile bundles and networks and tethered to the matrix by mature focal adhesions.

Transverse arcs

Actomyosin bundles in the lamella that are parallel to the cell periphery and undergo myosin II-dependent retrograde flow towards the cell centre.

Radial stress fibres

Actin bundles tethered at one end to focal adhesions and integrated into transverse arcs along their length and, thus, oriented in a radial fashion with respect to the cell centre on the dorsal surface. Radial stress fibres do not contain myosin II and assemble in a DIA1- and INF2-dependent manner. They are also known as dorsal stress fibres.

Peripheral bundles

Actomyosin bundles found at non-adherent edges of cells that are responsible for cell shape maintenance.

Ventral stress fibres

Actomyosin bundles formed at the ventral surface that are attached to focal adhesions at each end.

Contractile strain

Deformation of a structure that results in shortening of length, area or volume.

Steady-state flow

Movements that occur at a constant rate, or velocity, over time.

Stress relaxation

The decrease of force that occurs in structures owing to viscous, or fluid, effects.

Compressive forces

Force that results in pushing, or compression, on a structure.

Tensile force

Force that results in pulling, or tension, on a structure

Compliance

The tendency of a material to deform in response to an external force. A more compliant material will deform to a greater extent than a less compliant one.

Focal adhesions

Cellular structures that link the extracellular matrix on the outside of the cell, through integrin receptors, to the actin cytoskeleton inside the cell.

Adherens junctions

Protein complexes that contain cadherin and catenin proteins. They are formed between neighbouring cells in the tissue and serve not only to maintain cell–cell adhesion but also to regulate intracellular signalling and cytoskeletal organization.

Elastic response

The tendency of structures to store mechanical energy. The initial shape is preserved upon release of external forces.

Traction force microscopy

A technique to calculate stresses generated by cells by measuring the deformation of the matrix to which they are attached.