ABSTRACT
Dietary interventions often target foods that are underconsumed relative to dietary guidelines, such as vegetables, fruits, and whole grains. Because these foods are only consumed episodically for some participants, data from such a study often contains a disproportionally large number of zeros due to study participants who do not consume any of the target foods on the days that dietary intake is assessed, thus generating semicontinuous data. These zeros need to be properly accounted for when calculating sample sizes to ensure that the study is adequately powered to detect a meaningful intervention effect size. Nonetheless, this issue has not been well addressed in the literature. Instead, methods that are common for continuous outcomes are typically used to compute the sample sizes, resulting in a substantially under- or overpowered study. We propose proper approaches to calculating the sample size needed for dietary intervention studies that target episodically consumed foods. Sample size formulae are derived for detecting the mean difference in the amount of intake of an episodically consumed food between an intervention and a control group. Numerical studies are conducted to investigate the accuracy of the sample size formulae as compared with the ad hoc methods. The simulation results show that the proposed formulae are appropriate for estimating the sample sizes needed to achieve the desired power for the study. The proposed method for sample size is recommended for designing dietary intervention studies targeting episodically consumed foods.
Keywords: dietary intervention trials, episodic consumption, power, sample size, type I error
Introduction
Intake of whole plant foods is associated with reduced risk of numerous adverse health outcomes including obesity, cardiovascular disease, diabetes, and certain cancers (1–18). These foods are consistently underconsumed in the US diet, and as such, are often targeted in dietary intervention studies (19–25). Because these foods may only be episodically consumed by some participants, data from 24-h recalls may contain a sizable number of participants who do not consume any of a target food group during the recall period (26, 27). The resulting distribution, which contains a disproportionally large number of zeros yields a so-called semicontinuous data structure (28). For example, data for children aged 2–8 y from the NHANES, 2001–2004 showed nonconsumption of total fruit, whole fruit, whole grains, total vegetables, dark green or orange vegetables or legumes, and milk on any single day among 17%, 40%, 42%, 3%, 50%, and 12% of participants, respectively (26).
The excessive zeros influence both the design and analysis of the trial and they need to be dealt with appropriately; otherwise the trial may be poorly powered, and the study findings may be biased and misleading. In addition to the excessive zeros, a further complication which also needs to be considered is that the intervention can change the percent of zeros in the intervention arm compared with the control arm.
There is a considerable body of work in the statistical literature on modeling and analysis of semicontinuous data (29–34). However, limited attention has been paid to the design of an intervention study that involves such data, and appropriate statistical methods for estimating sample sizes and power are lacking for comparison concerning the overall mean of the semicontinuous data. An extensive review of relevant literature has found a sizable number of interventional trials targeting vegetables, fruits, and whole grains (35–40). To the best of our knowledge, however, few published studies have provided details on sample size determination and power analysis, let alone consideration of accounting for excessive zeros in the outcome. Among those that discussed sample size calculation and power analysis, ad hoc methods suitable for continuous outcomes are often cited for sample size calculation.
In this commentary, we confine our attention to a 2-arm trial investigating the efficacy of an intervention to increase the consumption of an episodically consumed food, such as whole fruits or vegetables. The dietary intake data are collected using an assessment tool such as The Automated Self-Administered 24-h dietary recall developed by the National Cancer Institute (41). We assume that the primary objective of the trial is to compare the average amount of intake between the intervention and the control. Because a dietary intervention targeting an episodically consumed food can increase (or decrease) not only the average amount of intake of the food if consumed, but also the rate of consumption of the food, the sample size calculation should take both aspects into account.
In what follows, we present the appropriate approaches to computing the sample sizes and evaluate their performance using Monte Carlo simulation as compared with the ad hoc methods for comparison of 2 means. The sample size formulae are also provided (Supplemental Technical Details) for 1-arm trials against a historical control and prepost trials comparing intervention results with that prior to intervention.
The Common (but Incorrect) Practice
It is common in 2-arm trials with continuous outcomes to use the 2 sample size formulae for comparing the means of 2 independent populations. One assumes equal SD and the other assumes unequal SDs for the control and intervention arms (42).
Consider a 2-arm trial with equal allocation. For a study participant in the kth arm (k = 1 if control and 2 if intervention), let  denote the amount of food consumed, taking values of either 0 if the food was not consumed or a positive numerical value if the food was consumed. The mean of
denote the amount of food consumed, taking values of either 0 if the food was not consumed or a positive numerical value if the food was consumed. The mean of  is denoted by
is denoted by  and the SD is denoted by
and the SD is denoted by  . The null hypothesis to be tested is
. The null hypothesis to be tested is 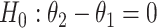 , that is, the mean amount of intake in the intervention arm is the same as in the control arm. We would like to test the null hypothesis at a significance level α, and to determine the sample size per arm n so that the trial is powered at (1−β) level to detect a prespecified meaningful difference of
, that is, the mean amount of intake in the intervention arm is the same as in the control arm. We would like to test the null hypothesis at a significance level α, and to determine the sample size per arm n so that the trial is powered at (1−β) level to detect a prespecified meaningful difference of 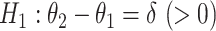 , that is, the intervention increases the mean amount of intake by
, that is, the intervention increases the mean amount of intake by  as compared with the control arm (alternative hypothesis). To calculate the sample size using the formula for 2 means, 1 specifies the values for the 2 SDs, say
as compared with the control arm (alternative hypothesis). To calculate the sample size using the formula for 2 means, 1 specifies the values for the 2 SDs, say  for control and
for control and 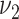 for intervention, and then compute the sample size per arm from the following formula:
for intervention, and then compute the sample size per arm from the following formula:
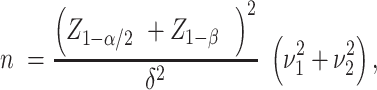 |
(1) |
where  is the 100γ% quantile of the standard normal distribution.
is the 100γ% quantile of the standard normal distribution.
If we assume the 2 SDs are equal, that is,  , then the sample size formula (1) becomes:
, then the sample size formula (1) becomes:
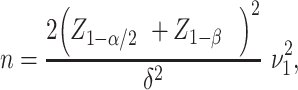 |
(2) |
which is also commonly used in practice when designing a clinical trial, particularly when empirical data are scarce, making it difficult to specify the SD for the intervention arm of the study.
With the prespecified values of the 2 SDs, the targeted mean difference (effect size), level of significance, and power to detect the effect size, the sample sizes needed for the trial are then conveniently obtained from statistical software such as R, SAS, and PASS (43–45). In practice, these 2 formulae are frequently used when the endpoints, such as the amount of intake of whole fruits, are semicontinuous. As we demonstrate below, specifying the SDs for a semicontinuous outcome is more complicated than for a continuous outcome, especially under the alternative hypothesis needed for power analysis. We numerically show that using these ad hoc formulae yield inadequate estimation of the sample sizes, resulting in a study either seriously underpowered (thus compromising the ability of the trial to detect meaningful intervention effects) or unnecessarily overpowered (thus increasing the financial and administrative burden to conduct the trial).
The Appropriate Approach: Accounting for Nonconsumption
The amount of intake of an episodically consumed food from an interventional trial is semicontinuous with observations characterized by many zeros due to nonconsumption of the food. In general, the trial data in each arm can be divided into 2 parts (26): nonconsumption during assessment (consisting of all the zeros) and any consumption during assessment (consisting of the reported amount of intake). To properly compute the sample sizes, we need to take the distributions of both parts into consideration.
Suppose that, for the kth arm, the probability that the food is consumed is  , and the mean and SD of the amount of intake given the food is consumed are respectively,
, and the mean and SD of the amount of intake given the food is consumed are respectively,  and
and  . The probability
. The probability  fully captures the distribution of the nonconsumption part of the data and
fully captures the distribution of the nonconsumption part of the data and  and
and  are 2 important parameters characterizing the distribution of the consumption part of the data.
are 2 important parameters characterizing the distribution of the consumption part of the data.
To link the above parameters with the mean 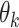 and SD
and SD 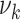 of the amount of intake
of the amount of intake  , we have
, we have 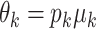 , and:
, and:
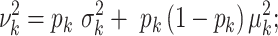 |
(3) |
see Supplementary Equation (S1) in the Supplemental Technical Details for more detail. Hence the SD of  depends on the mean
depends on the mean  and SD
and SD  of the amount of intake when the food is consumed, as well as the probability
of the amount of intake when the food is consumed, as well as the probability  that the food is consumed. The null hypothesis to be tested becomes
that the food is consumed. The null hypothesis to be tested becomes 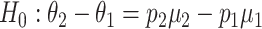 = 0 and the alternative hypothesis to be powered is
= 0 and the alternative hypothesis to be powered is  . Furthermore, we denote the SD of
. Furthermore, we denote the SD of  by
by 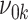 when the null hypothesis
when the null hypothesis  is true and by
is true and by  when the alternative hypothesis
when the alternative hypothesis 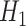 is true. Then, the sample size n needed for each arm is given by:
is true. Then, the sample size n needed for each arm is given by:
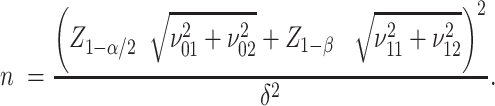 |
(4) |
See Supplementary Equation (S4) in the Supplemental Technical Details for more detail. To use formula (4) to compute the sample size, the key prerequisite is to specify the 4 SDs ( , each depending on the corresponding percent consuming and the means and SDs of the amount of intake when the food is consumed, as given by equation (3).
, each depending on the corresponding percent consuming and the means and SDs of the amount of intake when the food is consumed, as given by equation (3).
To compute the sample size appropriately, we recommend the following steps.
Step 1. Specify the level of significance α, usually set to be at 5% for a randomized trial; for a historical trial, it may be at 10%.
Step 2. Specify the desired power (1−β) for the study, usually set to be between 80 and 95%.
Step 3. Specify the intervention effect size δ to be detected at power 1−β. Note that the effect size is the difference between 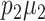 and
and  , not
, not 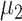 and
and  .
.
Step 4. For the control arm, specify the probability that the food is consumed, as well as the mean and SD of the amount of intake when the food is consumed, that is,  ,
,  , and
, and 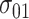 under
under  and
and 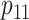 ,
,  , and
, and 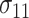 under
under 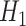 .
.
Step 5. Similarly for the intervention arm, specify the probability that the food is consumed, as well as the mean and SD of the amount of intake when the food is consumed, that is, 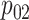 ,
, 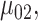 and
and 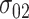 under
under  and
and 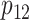 ,
, 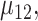 and
and  under
under 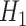 .
.
When specifying the values of the design parameters, the 2 constraints under the null and the alternative hypotheses,  and
and 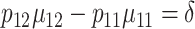 , must be satisfied. Values of the parameters in Steps 4 and 5 can be derived based on historical/existing data from subjects similar to those in the present study. Otherwise, some plausible educational guesses are required. With these prespecified values of the design parameters, the 4 SDs in (4) can then be derived using (3), and subsequently the sample size can be computed using formula (4).
, must be satisfied. Values of the parameters in Steps 4 and 5 can be derived based on historical/existing data from subjects similar to those in the present study. Otherwise, some plausible educational guesses are required. With these prespecified values of the design parameters, the 4 SDs in (4) can then be derived using (3), and subsequently the sample size can be computed using formula (4).
We next demonstrate that using the ad hoc sample size formulae (1–2) for comparing 2 means is problematic. Under the null hypothesis  of no intervention effect on the average amount of intake, it can be further assumed that (
of no intervention effect on the average amount of intake, it can be further assumed that ( , that is, the intervention has no effect on either the probability of consumption of the food or the mean amount of intake if the food is consumed. This implies that
, that is, the intervention has no effect on either the probability of consumption of the food or the mean amount of intake if the food is consumed. This implies that  , that is, the amount of intake
, that is, the amount of intake  has a common SD for both arms under the null hypothesis. Moreover, for the control group, the assumption that (
has a common SD for both arms under the null hypothesis. Moreover, for the control group, the assumption that ( , leading to
, leading to  , is also reasonable under the alternative hypothesis
, is also reasonable under the alternative hypothesis  . For this simple case, the sample size formula reduces to:
. For this simple case, the sample size formula reduces to:
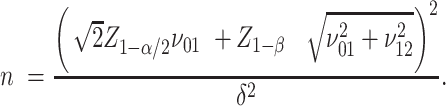 |
(5) |
Note that under the alternative hypothesis, the 2 rates 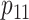 and
and 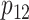 and the 2 means
and the 2 means  and
and 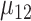 are subject to the constraint that
are subject to the constraint that  . Such constraint makes
. Such constraint makes 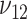 always different from the other 3 SDs; see Supplemental Figure 1. Therefore, the appropriate sample size formula (5) yields much different results from the ad hoc sample size formulae (1–2) for 2 means with either equal or unequal SDs.
always different from the other 3 SDs; see Supplemental Figure 1. Therefore, the appropriate sample size formula (5) yields much different results from the ad hoc sample size formulae (1–2) for 2 means with either equal or unequal SDs.
It is also worth noting that the mean 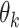 and SD
and SD 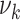 of the amount of intake
of the amount of intake  differ considerably from their counterpart
differ considerably from their counterpart  and deviation
and deviation  of the amount of intake given the food is consumed, especially in the presence of the relatively high likelihood that the food is not consumed. Hence the SDs
of the amount of intake given the food is consumed, especially in the presence of the relatively high likelihood that the food is not consumed. Hence the SDs 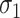 and
and  of the amount of consumption given the food is consumed cannot be used in lieu of
of the amount of consumption given the food is consumed cannot be used in lieu of  and
and 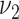 when computing the sample size.
when computing the sample size.
Numerical Results and Comparisons
Numerical studies via direct calculation or Monte Carlo simulation were conducted to investigate the performance of the sample size formula (4), as compared with that of the ad hoc formula (1) for comparing 2 means, which is obtained from (4) by replacing  by
by  and
and  by
by 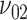 . In all settings, the 2-sided nominal significance level α is set to be 5%, and the power is set to be 90%. The 3 distributional parameters, the probability that the food is consumed, and the mean and SD of the amount of intake given the food is consumed, are set to be 0.6, 0.5, and 1 for both arms when the null hypothesis is true. We vary these parameters under the alternative hypotheses to compute the required sample sizes. For all alternative hypotheses under consideration, we assume that 1) the SD of the amount of intake given the food is consumed in the intervention arm is 0.1 larger than that in the control arm, that is,
. In all settings, the 2-sided nominal significance level α is set to be 5%, and the power is set to be 90%. The 3 distributional parameters, the probability that the food is consumed, and the mean and SD of the amount of intake given the food is consumed, are set to be 0.6, 0.5, and 1 for both arms when the null hypothesis is true. We vary these parameters under the alternative hypotheses to compute the required sample sizes. For all alternative hypotheses under consideration, we assume that 1) the SD of the amount of intake given the food is consumed in the intervention arm is 0.1 larger than that in the control arm, that is,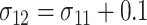 ; 2) the mean of the amount of intake given the food is consumed is 0.4 for the control arm, that is,
; 2) the mean of the amount of intake given the food is consumed is 0.4 for the control arm, that is,  ; and 3) the intervention increases the probability that the food is consumed by 5%, i.e.,
; and 3) the intervention increases the probability that the food is consumed by 5%, i.e., 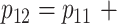 0.05. The intervention effect size is then derived from
0.05. The intervention effect size is then derived from  by plugging in the above alternative distributional parameters.
by plugging in the above alternative distributional parameters.
With each configuration of the design parameters, the sample sizes were calculated from equations (1) and (4) and are presented in Table 1, in the row labeled as “Ad hoc” and “Appropriate,” respectively. As demonstrated from Table 1, the sample sizes calculated using the ad hoc sample size formula differ substantially from that using the appropriate approach. Nevertheless, there is no clear pattern between them; in many cases the former is much larger and many others much smaller.
TABLE 1.
Sample sizes per arm from the proposed (“Appropriate”) and ad hoc approach
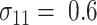
|
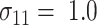
|

|
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
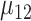
|
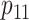
|
0.6 | 0.7 | 0.8 | 0.9 | 0.6 | 0.7 | 0.8 | 0.9 | 0.6 | 0.7 | 0.8 | 0.9 |
| 1.0 | δ | 0.41 | 0.47 | 0.53 | 0.59 | 0.41 | 0.47 | 0.53 | 0.59 | 0.41 | 0.47 | 0.53 | 0.59 |
| Appropriate | 69 | 53 | 42 | 34 | 90 | 72 | 59 | 49 | 117 | 95 | 78 | 66 | |
| Ad hoc | 83 | 63 | 49 | 40 | 83 | 63 | 49 | 40 | 83 | 63 | 49 | 40 | |
| 0.8 | δ | 0.28 | 0.32 | 0.36 | 0.40 | 0.28 | 0.32 | 0.36 | 0.40 | 0.28 | 0.32 | 0.36 | 0.40 |
| Appropriate | 142 | 111 | 90 | 73 | 190 | 153 | 126 | 105 | 247 | 202 | 169 | 144 | |
| Ad hoc | 177 | 135 | 107 | 87 | 177 | 135 | 107 | 87 | 177 | 135 | 107 | 87 | |
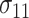 and
and  are the SDs in the control and intervention arm of the amount of intake, given the food is consumed, under the alternative hypothesis;
are the SDs in the control and intervention arm of the amount of intake, given the food is consumed, under the alternative hypothesis; 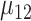 is the mean under the alternative hypothesis of the amount of intake given the food is consumed in the intervention arm;
is the mean under the alternative hypothesis of the amount of intake given the food is consumed in the intervention arm;  is the probability that the food is consumed in the control arm;
is the probability that the food is consumed in the control arm;  is the intervention effect size. The test statistic
is the intervention effect size. The test statistic  in the Supplemental Technical Details was used to obtain the results.
in the Supplemental Technical Details was used to obtain the results.
For each sample size n in Table 1, the power of the test was estimated based on 10,000 Monte Carlo replicates. For each replicate, the number of nonzeros (i.e., number of participants who consumed the food) in the control and intervention arm was generated from the Bernoulli distribution with success probability  and
and  , respectively. Subsequently, the corresponding amount of intake was generated from the normal distribution with mean
, respectively. Subsequently, the corresponding amount of intake was generated from the normal distribution with mean  (SD
(SD  and mean
and mean 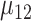 (SD
(SD  , respectively.
, respectively.
The empirical power results are presented in Figure 1. It is evident that the proposed formula yields sample sizes that satisfactorily achieve the 90% nominal power (blue line), whereas the ad hoc formula fails to do so. As shown in Figure 1, the sample sizes from the ad hoc formula (red line) can either seriously underpower the study (thus compromising the ability of the trial to detect meaningful intervention effects) or unnecessarily overpower the study (thus increasing the financial and administrative burden to conduct the trial). In addition, we also compared the type I error rates of the tests based on the 2 formulae; see Supplemental Table 1. The results show that the proposed approach adequately controls, whereas the ad hoc approach tends to inflate, the type I error rates when the probabilities that the food is consumed differ between the 2 arms.
FIGURE 1.
Empirical powers of the test for the sample sizes (annotated as text label) calculated using the proposed and ad hoc approach based on the nominal significance level of 0.05 and power of 90%. The blue lines are for the proposed approach and the red lines are for the ad hoc approach. The results are obtained based on the test statistic  in the Supplemental Technical Details.
in the Supplemental Technical Details.
Discussion
For 2-arm parallel dietary intervention trials targeting episodically consumed foods, we have demonstrated that sample sizes computed using ad hoc methods are not adequate and proposed an appropriate approach for sample size calculation. As the numerical results showed, the proposed approach adequately controls the type I error rates (see Supplemental Table 1) and achieves the desired power for the study. Hence, we recommend that investigators use our proposed method rather than the ad hoc methods for designing intervention studies targeting episodically consumed foods. It is worth pointing out that the difference between the proposed formula and the ad hoc formula will decrease as the probability that the food is consumed increases. When the probability is close to 1, the ad hoc formula can serve as a good approximation to the proposed one.
We have also considered 2 other types of trial designs, the 1-arm trial and prepost trial. The former evaluates the efficacy of an intervention scheme by comparing the dietary intake of the study participants under intervention with the available dietary records in a comparable general population. The latter does so by comparing dietary intake collected before and after the intervention; for such a prepost trial, the correlation between the dietary intake before and after intervention must be accounted for when computing the sample sizes, resulting in more complex formulae. In the Supplemental Technical Details, we have provided detailed derivation of the sample size formulae for the 2 types of trials.
Longitudinal dietary intake data collected from diet recalls at multiple time points across the study duration are common in dietary intervention studies. Sample size calculations technically become more complicated since the proportion of participants who consumed the food and the average amount of intake when the food is consumed could differ between treatment arms and between time points. Moreover, dietary data at any 2 time points from the same study participant are correlated. Other complex dietary intervention studies such as crossover trials and community-based trials also yield correlated data. The sample size calculations and power analysis need to properly incorporate all these aspects; thus, further research expanding upon these methods is needed.
In addition to the mean difference, the median difference of the amount of intake between the 2 arms can be used as a measure of intervention effect. In this case, nonparametric tests which are robust against distributional assumptions are preferred. However, for the food with a disproportionally large number of zeros, common nonparametric measures such as the Wilcoxon rank test would lead to many ties, which may result in substantial loss of power. To address this issue, Hallstrom (46) proposed a truncated Wilcoxon test by removing an equal (and maximal) number of zeros from each arm, but its performance depends on the respective difference direction of the proportion of consumption of the food and the average amount of intake of the food if consumed between the 2 arms. Further research is needed along this line.
The sample size required for a clinical trial depends on the null hypothesis and its corresponding test statistic. In the present article, the sample size calculations are based on testing the equality of the overall mean intake, i.e.,  . To the best of our knowledge, most dietary intervention studies published in the literature used the overall mean intake as the measure of intervention effect and success. Alternatively, success of the intervention can be defined as an increase in either the proportion of the food consumed or the mean intake when the food is consumed. Accordingly, the null hypothesis becomes
. To the best of our knowledge, most dietary intervention studies published in the literature used the overall mean intake as the measure of intervention effect and success. Alternatively, success of the intervention can be defined as an increase in either the proportion of the food consumed or the mean intake when the food is consumed. Accordingly, the null hypothesis becomes  and
and 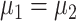 , and a global test such as the
, and a global test such as the 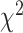 test (47) can be used. However, the global test is less informative upon rejection of the null hypothesis because it only tells that ≥1 equality is rejected, whereas in contrast, the proposed test provides additional information on whether the overall mean intake differs between the 2 arms. In practice, when designing a dietary intervention trial with episodically consumed foods, the choice of the null hypothesis to be tested should depend on the primary scientific interest which uniquely defines the measure of effect and success of the intervention.
test (47) can be used. However, the global test is less informative upon rejection of the null hypothesis because it only tells that ≥1 equality is rejected, whereas in contrast, the proposed test provides additional information on whether the overall mean intake differs between the 2 arms. In practice, when designing a dietary intervention trial with episodically consumed foods, the choice of the null hypothesis to be tested should depend on the primary scientific interest which uniquely defines the measure of effect and success of the intervention.
Semicontinuous data are frequently encountered in other research areas such as health expenditures, hospital length of stay, physical activities, and daily alcohol consumption (28). Our proposed methods for sample size calculation and power analysis are also recommended for designing an intervention study in these areas. It is worth noting that the power calculation formula is derived based on large sample theory. Studying the exact distribution for small samples of semicontinuous data is an important direction for future research.
Supplementary Material
Acknowledgments
We thank the editor, associate editor, and the referees for their insightful comments which led to an improved article.
The authors’ responsibilities were as follows—WZ and AL: prepared the first draft of the manuscript; and all authors: designed and implemented the methodology and read and approved the final manuscript. The authors report no conflicts of interest.
Notes
The authors reported no funding received for this commentary. Research of AL and TN was supported by the Intramural Research Program of the Eunice Kennedy Shriver National Institute of Child Health and Human Development (NICHD).
Supplemental Technical Details, Supplemental Table 1, and Supplemental Figure 1 are available from the “Supplementary data” link in the online posting of the article and from the same link in the online table of contents at https://academic.oup.com/ajcn/.
Contributor Information
Wei Zhang, Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing, China.
Aiyi Liu, Biostatistics and Bioinformatics Branch, Eunice Kennedy Shriver National Institute of Child Health and Human Development, NIH, Bethesda, MD, USA.
Zhiwei Zhang, Biostatistics Branch, Division of Cancer Treatment and Diagnostics, National Cancer Institute, NIH, Bethesda, MD, USA.
Tonja Nansel, Social and Behavioral Sciences Branch, Eunice Kennedy Shriver National Institute of Child Health and Human Development, NIH, Bethesda, MD, USA.
Susan Halabi, Department of Biostatistics and Bioinformatics, Duke University, Durham, NC, USA.
References
- 1. Ziegler RG. Vegetables, fruits, and carotenoids and the risk of cancer. Am J Clin Nutr. 1991;53(Suppl):251S–9S. [DOI] [PubMed] [Google Scholar]
- 2. Block G, Patterson B, Subar AF. Fruit, vegetables, and cancer prevention: a review of the epidemiological evidence. Nutr Cancer. 1992;18:1–29. [DOI] [PubMed] [Google Scholar]
- 3. Ziegler RG, Subar AF, Craft NE, Ursin G, Patterson BH, Graubard BI. Does β-carotene explain why reduced cancer risk is associated with fruit and vegetable intake? Can Res. 1992;52:2060S–6S. [PubMed] [Google Scholar]
- 4. Havas S, Heimendinger J, Damron D, Nicklas TA, Cowan A, Beresford SA, Sorensen G, Buller D, Bishop D, Baranowski T et al.. 5 a day for better health – nine community research projects to increase fruit and vegetable consumption. Public Health Rep. 1995;110:68–79. [PMC free article] [PubMed] [Google Scholar]
- 5. Ames BN, Gols LS, Willett WC. The causes and prevention of cancer. Proc Natl Acad Sci USA. 1995;92:5258–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Hung HC, Joshipura KJ, Jiang R, Hu FB, Hunter D, Smith-Warner SA, Colditz GA, Rosner B, Spiegelman D, Willett WC. Fruit and vegetable intake and risk of major chronic disease. J Natl Cancer Inst. 2004;21:1577–84. [DOI] [PubMed] [Google Scholar]
- 7. Key TJ. Fruit and vegetables and cancer risk. Br J Cancer. 2011;104:6–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Boeing H, Bechthold A, Bub A, Ellinger S, Haller D, Kroke A, Leschik-Bonnet E, Müller MJ, Oberritter H, Schulze M et al.. Critical review: vegetables and fruit in the prevention of chronic diseases. Eur J Nutr. 2012;51:637–63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Wang X, Ouyang Y, Liu J, Zhu M, Zhao G, Bao W, Hu FB. Fruit and vegetable consumption and mortality from all causes, cardiovascular disease, and cancer: systematic review and dose-response meta-analysis of prospective cohort studies. BMJ. 2014;349:g4490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. He FJ, Nowson CA, MacGregor GA. Fruit and vegetable consumption and stroke: meta-analysis of cohort studies. Lancet. 2006;367:320–6. [DOI] [PubMed] [Google Scholar]
- 11. Dauchet L, Amouyel P, Hercberg S, Dallongeville J. Fruit and vegetable consumption and risk of coronary heart disease: a meta-analysis of cohort studies. J Nutr. 2006;136(10):2588–93. [DOI] [PubMed] [Google Scholar]
- 12. Benetou V, Orfanos P, Lagiou P. Vegetables and fruits in relation to cancer risk: evidence from the Greek EPIC cohort study. Cancer Epidemiol Biomarkers Prev. 2008;17:387–92. [DOI] [PubMed] [Google Scholar]
- 13. Boffetta P, Couto E, Wichmann J, Ferrari P, Trichopoulos D, Bueno-de-Mesquita HB, van Duijnhoven FJB, Büchner FL, Key T, Boeing H et al.. Fruit and vegetable intake and overall cancer risk in the European Prospective Investigation into Cancer and Nutrition. J Natl Cancer Inst. 2010;102:529–37. [DOI] [PubMed] [Google Scholar]
- 14. George SM, Park Y, Leitzmann MF, Freedman ND, Dowling EC, Reedy J, Schatzkin A, Hollenbeck A, Subar AF. Fruit and vegetable intake and risk of cancer: a prospective cohort study. Am J Clin Nutr. 2009;89:347–53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. World Cancer Research Fund/American Institute for Cancer Research. Food, Nutrition, Physical Activity, and the Prevention of Cancer: a Global Perspective. Washington DC: AICR; 2007. [Google Scholar]
- 16. Emaus MJ, Peeters PH, Bakker MF, Overvad K, Tjønneland A, Olsen A, Romieu I, Ferrari P, Dossus L, Boutron-Ruault MC et al.. Vegetable and fruit consumption and the risk of hormone receptor-defined breast cancer in the EPIC cohort. Am J Clin Nutr. 2016;103(1):168–77. [DOI] [PubMed] [Google Scholar]
- 17. Perez-Cornago A, Travis RC, Appleby PN, Tsilidis KK, Tjønneland A, Olsen A, Overvad K, Katzke V, Kühn T, Trichopoulou C et al.. Fruit and vegetable intake and prostate cancer risk in the European Prospective Investigation into Cancer and Nutrition (EPIC). Int J Cancer. 2017;141(2):287–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Melina V, Craig W, Levin S. Position of the Academy of Nutrition and Dietetics: vegetarian diets. J Acad Nutr Diet. 2016;116:1970–80. [DOI] [PubMed] [Google Scholar]
- 19. Resnicow K, Jackson A, Wang T, De AK, McCarty F, Dudley WN, Baranowski T. A motivational interviewing intervention to increase fruit and vegetable intake through black churches: results of the eat for life trial. Am J Public Health. 2001;91:1686–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Alexander GL, McClure JB, Calvi JH, Divine GW, Stopponi MA, Rolnick SJ, Heimendinger J, Tolsma DD, Resnicow K, Campbell MK et al.. A randomized clinical trial evaluating online interventions to improve fruit and vegetable consumption. Am J Public Health. 2010;100:319–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Chlebowski RT, Aragaki AK, Anderson GL, Simon MS, Manson JE, Neuhouser ML, Pan K, Stefanic ML, Rohan TE, Lane D et al.. Association of low-fat dietary pattern with breast cancer overall survival: a secondary analysis of the Women's Health Initiative randomized clinical trial. JAMA Oncol. 2018;4:e181212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Ravasco P, Monteiro-Grillo I, Camilo M. Individualized nutrition intervention is of major benefit to colorectal cancer patients: long-term follow-up of a randomized controlled trial of nutritional therapy. Am J Clin Nutr. 2012;96:1346–53. [DOI] [PubMed] [Google Scholar]
- 23. Hummel S, Pflüger M, Hummel M, Bonifacio E, Ziegler AG. Primary dietary intervention study to reduce the risk of islet autoimmunity in children at increased risk for type 1 diabetes: the BABYDIET study. Diabetes Care. 2011;34:1301–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Wright N, Wilson L, Smith M, Duncan B, McHugh P. The BROAD study: a randomized controlled trial using a whole food plant-based diet in the community for obesity, ischaemic heart disease or diabetes. Nutr Diabetes. 2017;7(3):e256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Estruch R, Ros E, Salas-Salvadó J, Covas M, Corella D, Arós F, Gómez-Gracia E, Ruiz-Gutiérrez V, Fiol M, Lapetra J et al.. Primary prevention of cardiovascular disease with a Mediterranean diet. N Engl J Med. 2013;368:1279–90. [DOI] [PubMed] [Google Scholar]
- 26. Zhang S, Midthune D, Guenther PM, Krebs-Smith SM, Kipnis V, Dodd KW, Buckman DW, Tooze JA, Freedman L, Carroll RJ. A new multivariate measurement error model with zero-inflated dietary data, and its application to dietary assessment. Ann Appl Stat. 2011;5(2B):1456–87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Kassahun-Yimer W, Albert PS, Lipsky LM, Nansel TR, Liu A. A joint model for multivariate hierarchical semicontinuous data with replications. Stat Methods Med Res. 2019;28(3):858–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Neelon B, O'Malley AJ, Smith VA. Modeling zero-modified count and semicontinuous data in health services research part 1: background and overview. Stat Med. 2016;35:5070–93. [DOI] [PubMed] [Google Scholar]
- 29. Duan N, Manning WG Jr, Morris CN, Newhouse JP. A comparison of alternative models for the demand for medical care. J Bus Econ Stat. 1983;1(2):115–26. [Google Scholar]
- 30. Olsen MK, Schafer JL. A two-part random-effects model for semicontinuous longitudinal data. J Am Statist Assoc. 2001;96:730–45. [Google Scholar]
- 31. Tooze JA, Grunwald GK, Jones RH. Analysis of repeated measures data with clumping at zero. Stat Methods Med Res. 2002;11:341–55. [DOI] [PubMed] [Google Scholar]
- 32. Lu SE, Lin Y, Shih WC. Analyzing excessive no changes in clinical trials with clustered data. Biometrics. 2004;60:257–67. [DOI] [PubMed] [Google Scholar]
- 33. Chai HS, Bailey KR. Use of log-skew-normal distribution in analysis of continuous data with a discrete component at zero. Stat Med. 2008;27:3643–55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Burgette LF, Paddock SM. Bayesian models for semicontinuous outcomes in rolling admission therapy groups. Psychol Methods. 2017;22(4):725–42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Pomerleau J, Lock K, Knai C, McKee M. Interventions designed to increase adult fruit and vegetable intake can be effective: a systematic review of the literature. J Nutr. 2005;135(10):2486–95. [DOI] [PubMed] [Google Scholar]
- 36. Thomson CA, Ravia J. A systematic review of behavioral interventions to promote intake of fruit and vegetables. J Am Diet Assoc. 2011;111(10):1523–35. [DOI] [PubMed] [Google Scholar]
- 37. Evans CE, Christian MS, Cleghorn CL, Greenwood DC, Cade JE. Systematic review and meta-analysis of school-based interventions to improve daily fruit and vegetable intake in children aged 5 to 12 y. Am J Clin Nutr. 2012;96(4):889–901. [DOI] [PubMed] [Google Scholar]
- 38. Ganann R, Fitzpatrick-Lewis D, Ciliska D, Peirson L. Community-based interventions for enhancing access to or consumption of fruit and vegetables among five to 18-year olds: a scoping review. BMC Public Health. 2012;12:711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Deliens T, Van Crombruggen R, Verbruggen S, De Bourdeaudhuij I, Deforche B, Clarys P. Dietary interventions among university students: a systematic review. Appetite. 2016;105:14–26. [DOI] [PubMed] [Google Scholar]
- 40. Savoie-Roskos MR, Wengreen H, Durward C. Increasing fruit and vegetable intake among children and youth through gardening-based interventions: a systematic review. J Acad Nutr Diet. 2017;117(2):240–50. [DOI] [PubMed] [Google Scholar]
- 41. Subar AF, Kirkpatrick SI, Mittl B, Zimmerman TP, Thompson FE, Bingley C, Willis G, Islam NG, Baranowski T, McNutt S et al.. The Automated Self-Administered 24-hour dietary recall (ASA24): a resource for researchers, clinicians, and educators from the National Cancer Institute. J Acad Nutr Diet. 2012;112(8):1134–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Julious SA. Sample Sizes for Clinical Trials. Boca Raton, FL: Chapman and Hall/CRC Press, 2010. [Google Scholar]
- 43. Champely S, Ekstrom C, Dalgaard P, Gill J, Weibelzahl S, Anandkumar A, Ford C, Volcic R, Rosario HD. Package: pwr 2018; [Internet]. Available from: http://cran.r-project.org/package=pwr. [Google Scholar]
- 44. SAS/STAT User's 9.2 Guide. 2008. Cary, NC: SAS Institute Inc; 2008. [Google Scholar]
- 45. PASS 2019 Power Analysis and Sample Size Software. NCSS, LLC. Kaysville, UT; 2019; [Internet]. Available from: https://www.ncss.com/software/pass/. [Google Scholar]
- 46. Hallstrom AP. A modified Wilcoxon test for non-negative distributions with a clump of zeros. Stat Med. 2010;29:391–400. [DOI] [PubMed] [Google Scholar]
- 47. Lachenbruch PA. Power and sample size requirements for two‐part models. Stat Med. 2001;20:1235–8. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.



