Axon morphology is modulated by the local environment and impacts the noninvasive investigation of its structure–function relationship

Significance

Axons, the brain’s communication cables, have been described as cylinders since their discovery in 1860. Their structure is linked to how fast they conduct signals and is thus indicative of brain health and function. Here, we demonstrate an interplay between the micromorphology of axons and other extra-axonal structures, showing that axons are noncylindrical and exhibit environment-dependent diameter and trajectory variations. The nonspecificity in diameter, and thus conduction velocity, challenges the current knowledge of how axons communicate signals. Diffusion magnetic resonance imaging can be used to measure axon diameter in the living brain in order to explore the brain network and detect potential biomarkers of disease, but we show here that the observed complex morphologies of axons bias these measurements.

Abstract

Axonal conduction velocity, which ensures efficient function of the brain network, is related to axon diameter. Noninvasive, in vivo axon diameter estimates can be made with diffusion magnetic resonance imaging, but the technique requires three-dimensional (3D) validation. Here, high-resolution, 3D synchrotron X-ray nano-holotomography images of white matter samples from the corpus callosum of a monkey brain reveal that blood vessels, cells, and vacuoles affect axonal diameter and trajectory. Within single axons, we find that the variation in diameter and conduction velocity correlates with the mean diameter, contesting the value of precise diameter determination in larger axons. These complex 3D axon morphologies drive previously reported 2D trends in axon diameter and g-ratio. Furthermore, we find that these morphologies bias the estimates of axon diameter with diffusion magnetic resonance imaging and, ultimately, impact the investigation and formulation of the axon structure–function relationship.

Axons form the communication infrastructure of the brain network. Upon their initial discovery by Otto Friedrich Karl Deiters circa 1860, they were described as “cylinders”—a description still widely used today. The saltatory conduction velocity (CV) of action potentials along myelinated axons depends on their morphology, including axon diameter (AD) (1) and thickness of the CV-boosting, insulating myelin sheath (2). The ratio of AD to the outer fiber diameter, the g-ratio, is thought to be fixed to an optimal value that promotes high CVs and minimizes energy consumption (3). Simulation studies (4, 5) predict optimal g-ratios around 0.7 in the central nervous system (CNS), matching histological data (6, 7). The concept of a given g-ratio along straight, cylindrical axons enables an inference of the outer fiber diameter from the inner AD, allowing classical structure–function relations between outer fiber diameter and CV (8, 9) to be reformulated in terms of AD and a constant g-ratio (8, 9). This makes an investigation of brain network function accessible with techniques that can measure AD.

Histological tracer studies of axons between brain sites reveal that the diameter, and thus CV, of an axon depends on its origin (10) and target (7), corroborating the functional significance of AD. AD is potentially also a biomarker for neurodegenerative diseases like multiple sclerosis, which has been shown to preferentially attack smaller axons (11). To provide useful diagnostic information, the white matter (WM) microstructure and axon morphology must be characterized in vivo. Diffusion magnetic resonance imaging (MRI) uses the diffusion of water molecules to noninvasively probe the WM microstructure in the living brain. Although MRI voxels are typically on the scale of ∼1 mm, it is possible to estimate axonal dispersion (12), the axon diameter distribution (ADD) (13), and the mean of the ADD (14) by fitting three-dimensional (3D) biophysical models to the acquired diffusion signal (15). However, diffusion MRI-based AD estimates (14, 16, 17) are larger than those obtained by histology (15, 18). Potential causes include the following: limited gradient strength in the diffusion MRI acquisition (19), sequence parameters (15), tissue shrinkage in histology (17), and—as discussed here—inaccurate modeling of the WM compartments, including the century-old representation of myelinated axons as cylinders. A validation of the 3D WM anatomy could thus improve diffusion MRI-based AD estimations (17) and shed light on the validity of enforcing a cylindrical geometry and constant g-ratio in axonal structure–function relations. Recent 3D electron microscopy (EM) studies on axon morphology of the mouse reveal, in high resolution, nonuniform ADs and trajectories (20, 21). However, axons are only tracked for up to 20 µm, a fraction of their length in MRI voxels.

Here, we characterize the long-range micromorphologies of axons against the backdrop of the complex 3D WM environment consisting of blood vessels, cells, and vacuoles. With synchrotron X-ray nano-holotomography (XNH), we acquire MRI measurements of the WM from the same monkey brain as in Alexander et al. (14) and Dyrby et al. (19), in which the MRI-derived AD estimates were larger than those estimated by histology. The 3D WM environment is mapped at a voxel size of 75 nm and volume of ∼150 × 150 × 150 μm³. By combining adjacent XNH volumes, we extract axons >660 µm in length and show that AD, axon trajectory, and g-ratio depend on the local microstructural environment. The 3D measurements shed light on the interpretation of 2D measurements, highlighting the importance of the third dimension for a robust description of single-axon structure and function. Last, by performing Monte Carlo (MC) diffusion simulations on axonal substrates with morphological features deriving from the XNH-segmented axons, we show that geometrical deviations from cylinders cause an overestimation of AD with diffusion MRI.

Results

Volumetric Mesoscopic White Matter Features.

The mean AD indices in the corpus callosum (CC) were fitted on diffusion MRI volumes of the monkey brain and exhibited the expected trend in diameter from the splenium to the genu, but with overestimated diameters (19) (Fig. 1A). In the splenium, along the interhemispheric connection between visual cortices V1/V2, the mean AD index was 1.3 µm. The connection length was delineated by tractography to 49.7 mm (SD = 1.9 mm) as described in Materials and Methods, resulting in a conduction delay of 4.8 ms.

Fig. 1.

Observed anatomical microstructures within the white matter of the monkey brain. (A) Diffusion-MRI mean AD estimations with the ActiveAx method in the midsagittal plane of corpus callosum (CC) of the monkey brain spanning the splenium (S), midbody (M), and genu (G). The arrows show biopsy locations. The interhemispheric callosal connection between primary visual cortices (V1/V2) is delineated with tractography and is shown in green. (B) Three-dimensional XNH volume from the splenium with an isotropic voxel size of 75 nm, showing detectable anatomical features. The volume interior is exposed to reveal the vessels. (C) Close-up of a vacuole (asterisk). (D) Close-up of a cell cluster. (E) Nissl stain light microscopy image showing nuclei in the same splenium region as D in an age-matched monkey (BrainMaps: An Interactive Multiresolution Brain Atlas; brainmaps.org).

To further investigate the microstructure underlying the diffusion MRI estimates with XNH, we extracted and processed cylindrical tissue volumes of 1 mm in diameter. Tissue was taken from the CC and a crossing fiber region, located in the anterior centrum semiovale at a point where the diffusion MRI data indicated the existence of crossing axon bundles (SI Appendix, Fig. S2). Four tissue structures were examined, as shown in an XNH volume of the CC splenium in Fig. 1 B–D: 1) long-range myelinated axons, 2) blood vessels, 3) cells, and 4) vacuoles.

Myelinated axons were identifiable as bright, tubular shapes with dark contours. The contrast was given by the electron density of the sample, with bright regions corresponding to low-density structures, while the dark borders were due to the binding of electron-dense osmium tetroxide to myelin. Axons exhibited varying diameters throughout the volume. Like axons, blood vessels appeared as bright, tubular structures. Their larger diameters and ability to branch distinguished them from axons. Blood cells were rarely detected since they were flushed out during the perfusion process. Cell nuclei were distinguishable by their DNA inclusions (Fig. 1D). Due to its high electron density, DNA—seen with a Nissl stain in Fig. 1E—gave rise to round, dark structures, contained within a less dense nucleoplasm. Generally, the cells clustered and aligned with the axons/blood vessels in the CC samples. The majority are believed to be glial cells, but the existence of neuronal cell bodies cannot be ruled out, as shown in the macaque CC (22). Vacuoles appeared as hyperintense spheroids and could be located within axons (Fig. 1C).

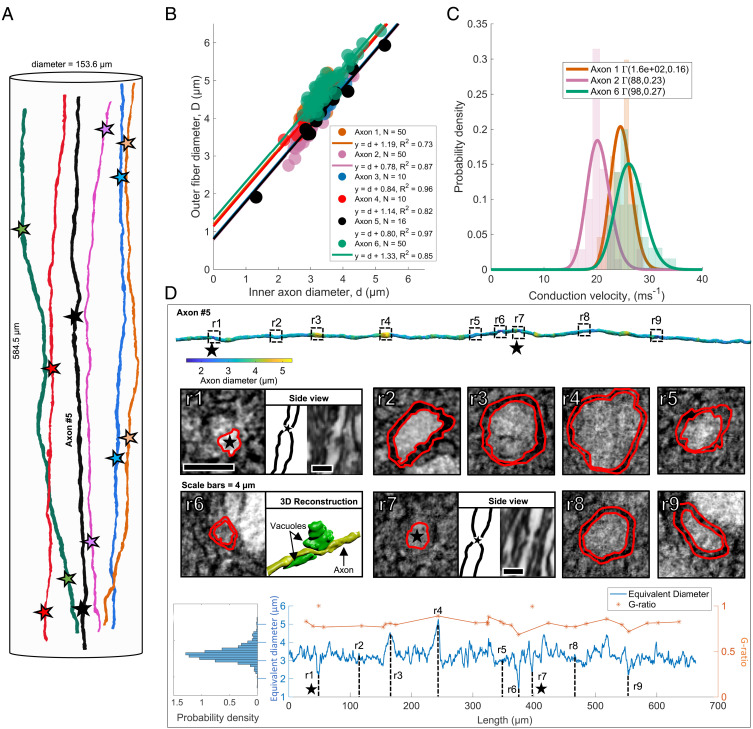
A volumetric quantification of the cell nuclei, vacuoles, and blood vessels was performed within an extended cylindrical volume, composed of four stitched XNH volumes having a combined diameter of 153.6 µm and length of 584.5 µm, as in Fig. 2A. The tissue compartments were segmented and are shown in Fig. 2.

Fig. 2.

Volumetric quantification of cell clusters, vessels, and vacuoles. (A) Two-dimensional slice through four overlapping XNH volumes (13.6-µm overlap) of the monkey brain splenium. Blue arrow, cell body. Green arrow, vacuole. Red arrow, blood vessel. (B) Three-dimensional reconstructions of the cell clusters (blue), blood vessels (red), and vacuoles (green) within the cylindrical volume of length 584.4 µm and diameter 153.6 µm. (C) λ₁, λ₂, and λ₃ denote the average first, second, and third principal-component lengths of tensors fitted to the cell cluster/vacuole structures. These are visualized by ellipsoids. In blue/green: examples of an individual cell cluster/vacuole. (D) Three-dimensional visualization of cell cluster, blood vessel, and vacuole segmentations. (E and F) Histograms showing the mean values and distributions of the following: inclination angle (compared to the axon population direction), principal axis length, mean volume, and FA across the cellular (blue) and vacuole (green) components, respectively.

Generally, the cell clusters, blood vessels, and vacuoles were evenly distributed throughout the volumes, as shown in Fig. 2B. The average volume fractions of the quantified structures in the splenium were 4.6%, 0.6%, and 1.5% for the cell clusters, blood vessels, and vacuoles, respectively. The extracellular space (ECS) could not be distinguished. Since the samples were dehydrated during tissue processing, it may have shrunk considerably, and the remaining volume fraction is thought to be occupied mostly by myelinated axons. The blood vessels were few but occupied the largest volume fraction after the axons with diameters between 4 and 10 µm.

Morphological characteristics of the cell clusters are shown in Fig. 2E. The cell nuclei had a mean diameter of 5.5 µm (SD = 0.73 µm; N = 38). Assuming spherical nuclei, the average cell cluster of volume 1,057 µm³ contained 12 cells. They could be represented by tensors whose principal axes often aligned with the axons or nearest blood vessels. The typical cell cluster tensor shape, produced by averaging the first, second, and third principal axis lengths of all clusters, is shown in Fig. 2C and has a fractional anisotropy (FA) of 0.57 and principal axis lengths between 6.5 and 21.2 µm. The morphological characteristics of the smaller vacuoles are shown in Fig. 2F. The typical vacuole tensor shape (Fig. 2C) had $\text{FA}=0.31$ and principal axis lengths ranging between 4.2 and 7.8 µm. The vacuoles were scattered throughout the XNH volume, with some situated within the axons (Fig. 1C).

Axonal Micromorphology in 3D: Diameters and Dispersion.

Axons differed from cylinders in terms of diameter and trajectory changes. Axons $\left(N=54\right)$ with mean diameters between 2.1 and 3.8 µm were segmented from the XNH volume in Fig. 1B as described in Materials and Methods. The 54-axon population, shown in Fig. 3A, had a mean diameter of 2.7 µm and a volume-weighted mean diameter of 2.9 µm, both significantly larger than the diffusion MRI estimate of 1.3 µm. This was expected, since the diffusion MRI estimate was based on modeling of the signal from all axons in the image voxels, small and large, while the XNH estimate was extracted solely from the geometries of larger axons. Smaller axons were observable, but the image resolution and signal-to-noise level of the XNH volumes challenged a robust segmentation. In general, large-diameter (>2 µm) axons were evenly distributed throughout the tissue at a density of 0.0123/µm² and were surrounded by smaller axons. The midbody CC and the crossing fiber region were similarly organized (SI Appendix, Fig. S3).

Fig. 3.

Distribution and morphology of large axons. (A) Distribution of 54 large axons (red) in a 2D slice of the monkey splenium. (B) Fifty-four segmented axons from the monkey splenium. The axon lengths range from 124 to 170 µm, with average ADs between 2.1 and 3.8 µm. (C) Combined 3D ADD consisting of diameter measurements every 150 nm along all 54 axons and associated gamma distribution fit (black). For comparison, the fits of the longitudinal ADDs of the thinnest (blue) and thickest axon (green) are shown. (D) The SD of the longitudinal AD correlates positively with average AD. (E) Histogram and gamma distribution fit (black striped line) of combined 3D ADD, along with gamma distribution fits of the 2D ADD, sampled every 200 slices of the image subvolume in which all 54 axons were present.

Longitudinal AD variations.

The trajectories of the 54 segmented axons, shown in Fig. 3B, ranged in length between 124 and 170 µm, with a combined length of 8.36 mm. Their diameters varied nonsystematically along their lengths. We define AD to be the equivalent diameter, the diameter of a circle with the same area as the axonal cross-section perpendicular to its local trajectory, as in Abdollahzadeh et al. (20). The combined 3D ADD, representing all diameters measured at 150-nm intervals along all 54 axons, had a mean diameter of 2.7 µm, and followed a gamma distribution with parameters $a=27$ and $b=0.2$ (Fig. 3C).

We use the terms “longitudinal” AD and ADD to describe the ADs and ADDs along single axons. Gamma distributions were fitted to the individual longitudinal ADDs of the largest and smallest mean diameter axons, respectively. The longitudinal ADD of the largest axon was similar in width to that of the combined 3D ADD, while that of smallest axon was significantly narrower (Fig. 3C). A weak linear relationship $\left(R^2=0.29\right)$ was found between the mean AD and the SD of the longitudinal AD (Fig. 3D), suggesting that larger axons exhibit larger diameter variations than small axons, but with significant variability. The maximum encountered SD of 0.5 µm (Fig. 3D) entails that the majority of diameter fluctuations occur within ±0.5 µm of the mean AD.

To compare with measurements from 2D techniques, we calculated the slice-wise ADs for the 1,139 slices in which all 54 axons were present. The conventional 2D ADDs from six of these slices are shown in Fig. 3E and overlap with the combined 3D ADD. The mean 2D diameter of the fiber population throughout their common volume was 2.9 µm; from slice to slice, this value varied at most ±150 nm.

Axonal dispersion.

Axonal dispersion is a measure of disorder of the axonal trajectories. On the bundle level, 54 axons, the orientation dispersion (OD) describes the angular spread of the axons around the main bundle direction. Although axons in the CC were expected to be aligned and straight, the mean OD was $7°$ (Fig. 4 A and B).

Fig. 4.

Trajectory variations of large axons. (A) Histogram of the OD—the axonal inclination with respect to the main bundle direction—within the axon population. (B) Fifty-four axons from the splenium of the monkey brain translated to a common origin to illustrate the mesoscopic dispersion within the volume. Axon color represents inclination angle compared to the z axis. The Inset shows the quantification of microdispersion along axons: The axon is aligned with the z axis and a window of length L slides along the axon centerline (blue) at intervals of L/4. A principal-component analysis is performed on points within the window to determine their directionality. The inclination angle to the z axis is calculated and averaged over all windows. (C) Variation of microdispersion relative to main axon direction with sampling length, L (data points every 1 µm).

On the single-axon level, we used microdispersion to quantify dispersion on different length scales as described in Materials and Methods. The microdispersion describes the angle between the main axon direction and axon segments of certain lengths. The microdispersion decayed smoothly with increasing sampling length (Fig. 4C). Between sampling lengths of 1 and 30 µm, the average microdispersion decreased from 14 to 7°.

The longitudinal ADD, and not the myelin thickness, dominates longitudinal g-ratio variations.

We investigated how the g-ratio, and consequently the CV, varied along axonal internodes—the axon segment between consecutive nodes of Ranvier—by mapping the long-range behavior of six axons (>580-µm length) in the monkey splenium, as shown in Fig. 5A. The equivalent inner AD and equivalent outer fiber diameter were evaluated by manual segmentation at N randomly generated locations along the axonal internodes (Fig. 5B). This revealed a linear correlation between the inner and outer longitudinal diameters, suggesting a constant myelin thickness. The distributions of CVs along the internodes of axons 1, 2, and 6 (Fig. 5C) were calculated using the classical relationship (8) CV = 5.5⋅D, where $D$ is the outer fiber diameter. Using the tract length of 49.7 mm from tractography, the mean conduction delays along the respective fibers were 2.0, 2.4, and 1.9 ms.

Fig. 5.

Long-range quantification of axon morphology and myelination. (A) Six long axons segmented from the extended cylindrical XNH volume of the monkey splenium shown in Fig. 2 A and D. The stars mark identified nodes of Ranvier. (B) Inner AD vs. outer fiber diameter (including myelin sheath) at N randomly sampled points along the internodes of the six axons. Straight lines represent linear fits to the six datasets. The high linear correlation suggests that the myelin thickness remains approximately constant along the internodes, and that the y intercept is representative of twice the myelin thickness. (C) Histograms and associated gamma distribution fits of CVs along the internodes of axons 1, 2, and 6. (D) Row 1: segmentation of long axon (number 5, black, in A and B), colored according to diameter. The dotted squares marked r1–r9 indicate nine ROIs. Black stars mark the positions of the nodes of Ranvier. Row 2: ROI intensity images. The red lines show a manual segmentation of the inner axonal boundary and the outer myelin boundary, respectively. At r1 and r7, nodes of Ranvier are shown in an orthogonal view. At r6, the axon (yellow) is squeezed by two vacuoles (green). Row 3: on Left: ADD along axon. Blue line: the longitudinal equivalent AD measured every 150 nm along the axonal trajectory. In orange, the g-ratio for the 9 marked ROIs and 20 additional randomly generated positions along the axon.

Fig. 5D depicts the morphological changes occurring over the 662-µm-long trajectory of axon 5. Its diameter varied between 1.5 and 5.3 µm, and averaged at 3.3 µm. Of nine selected regions of interest (ROIs) labeled r1 to r9, local diameter minima occurred at points r1, r6, r7, and r9. At r1 and r7, we identified nodes of Ranvier (black stars), separated by 348 µm. At r6, the reduced diameter was caused by two vacuoles. The g-ratio was evaluated at the nine ROIs shown in Fig. 5, and at 10 randomly chosen positions inside and outside the internode, respectively. As expected of a constant myelin thickness, the g-ratio followed the trend in diameter, with the exception of the nodes of Ranvier at points r1 and r7.

In contrast to the 54-axon population for which the mean diameter did not deviate more than ±150 nm in any slice of the volume, the mean AD in a single axon could not be reliably established from one measurement. As a measure of stability of the AD, we calculated the cumulative mean AD along axon 5 in Fig. 5D. The point at which the cumulative mean diameter became stable to within ±150 nm depended on the position along the axon at which measurements were commenced and was up to 200 µm for some positions.

Local obstacles such as vacuoles, blood vessels, cell clusters, and crossing axon bundles alter the morphology of axons.

The presence of certain extra-axonal obstacles gave rise to noticeable trajectory changes. For example, blood vessels visibly warped the surrounding microstructure and disrupted axon trajectories as illustrated in Fig. 6 A–C.

Fig. 6.

Blood vessels, vacuoles, and crossing axons cause axonal trajectory variations. (A) XNH image looking into a vessel, marked V. Cell nuclei, marked by an asterisk, cluster around the vessel. The vessel significantly impacted the nearby axonal trajectories, depicted by the red arrow. (B) Three-dimensional reconstruction of A. Fifteen segmented axons are colored according to the deviation from their expected linear trajectories (a linear interpolation of the axon centerline above and below the blood vessel). Yellow, strong deviation; dark blue, little/no deviation. (C) Deviation from expected linear trajectory as a function of distance along the axon, centered on the maximum deviation. (D and E) Three-dimensional reconstructions of select cell clusters (blue), vacuoles (green), and axons, whose diameters are given by the color bar, in the XNH volume of the monkey splenium shown in Fig. 3B. The axon trajectories are impacted by the presence of cell clusters, and their diameters and shapes are impacted by neighboring vacuoles. (F) Three-dimensional reconstruction of axons in an XNH volume of a crossing fiber region. Two different projection directions are marked by green and yellow. Two axons, colored red and blue, twist around each other.

A subvolume spanning 690 slices and containing a blood vessel of diameter ∼10 µm was isolated (Fig. 6 A and B). The expected linear trajectories of the axons, based on their positions in the first and last 75 slices of the volume, were calculated. The axon trajectories exhibited maximum deviations from their expected trajectories between 2 and 9 µm, with the most significant deviations occurring along axon segments within ±10 µm of the blood vessel (Fig. 6C). Axonal trajectory changes were also found in response to cell clusters (Fig. 6D) and other axons in a crossing fiber region (Fig. 6F), in which two axons were found to twist around each other three times within the available volume. Although vacuoles did not cause trajectory variations, they caused a reduction in AD as shown in Fig. 5D (point r6) where two vacuoles cause a local decrease in AD, and in Fig. 6E.

The influence of axon morphology on diffusion MRI measurements.

To assess how axon morphology influences noninvasive diffusion MRI estimates of mean AD, we performed MC simulations of the diffusion process in six different 54-axon substrates (see Materials and Methods for details). The substrates differed in morphological complexity, ranging from the simplest geometry, G1, parallel cylinders, to G6, the XNH segmentation (Fig. 7A). Each axon in each substrate inherited its morphological properties (OD, microdispersion, and mean diameter/longitudinal diameter) from the respective XNH-segmented axons.

Fig. 7.

Examining the diffusion properties of different axonal geometries. (A) The morphological features of the XNH-segmented axons in Figs. 3 and 4 are directly mapped to the six different axon classes generated for MC simulations. G1, straight cylinders of diameter corresponding to XNH axon mean diameters; G2, same as G1 plus segmented OD; G3, segmented OD and longitudinal ADD; G4, segmented OD and microdispersion; G5, segmented OD, microdispersion, and longitudinal ADD; and G6, the XNH segmentation. (B) The variation of estimated AD and (C) parallel intra-axonal ADC with diffusion time for geometries G1–G6. Error bars represent the SE, reflecting the spread in diameters/ADCs across the individual axons.

After an initial diffusion time of 6 ms, the mean AD in the parallel cylinders remained constant, as expected, at the true volume-weighted mean AD of 2.9 µm. For the other substrates, however, AD was overestimated. The degree of overestimation increased with diffusion time and substrate complexity (Fig. 7B). The simulations also demonstrated the effects of OD (G2) on AD and revealed that the overestimation of AD is more significant when there is microdispersion than diameter variations (G3 vs. G4).

The parallel apparent diffusion coefficient (ADC) describes the rate of diffusion along a cylinder, or axon, and is often assumed to be a fixed value in MRI-based AD estimation. Our results show parallel ADC in parallel cylinders (G1) was constant and equal to the chosen intrinsic diffusivity of 6 × 10⁻¹⁰ m²/s. However, for substrates that exhibited OD, microdispersion, and/or diameter variations, the parallel ADC decreased with diffusion time and substrate complexity. Substrates with longitudinal AD variations (G4, G5, G6) exhibited particularly steep decreases in the parallel ADC with diffusion time. The 3D effects of AD variation and dispersion (OD and microdispersion) could thus be distinguished from each other based on the time dependence of the parallel ADC.

Discussion

By performing high-resolution 3D XNH on intact white matter samples from a monkey brain, we demonstrate the interplay between extra-axonal structures (blood vessels, cells, vacuoles) and the micromorphology of axons. Contrary to Deiters’ century-old description of axons as cylinders, we find that AD and trajectory vary along the length of the axon, often due to obstacles in the local microstructural environment. These morphological changes entail that large axons are nonspecific in terms of diameter and CV. We thus question the value of precisely measuring their diameters and the validity of enforcing cylindrical geometries in axonal structure–function relationships. Furthermore, we show that the 3D morphologies of axons may drive previously reported trends in 2D AD distributions and g-ratio distributions. Our results have significant impact for AD determination with 2D techniques and—as we show here—diffusion MRI. We foresee that a thorough morphological characterization of axons and their structural context will guide the noninvasive investigation of axon morphology with diffusion MRI and, consequently, the investigation of brain network function.

The Nonspecificity of the Diameters and g-Ratios of Large Axons.

Single axons lack well-defined diameters, and this has implications for the interpretation of 2D ADDs. Our findings show that individual axons exhibit longitudinal ADDs whose widths correlate with AD. Controversially, single axons are not always well described by classical 2D histological measurements. For one 662-µm-long axon, we show that a robust characterization of its mean diameter demands that AD be sampled for up to 200 µm at intervals of 0.15 µm. However, we find the opposite for a quantification of population mean AD. In axon populations, the 2D slice-wise ADDs match the 3D ADD, indicating that the 3D longitudinal AD variations are represented in the 2D ADDs. This has two consequences. First, it entails that previously reported 2D ADDs from EM (23) and light microscopy (7) also reflect the 3D ADD of the axon population if quantified over a sufficiently large volume. Second, contrary to the conventional interpretation of the ADD, it implies that the 2D ADDs are not directly representative of individual ADs. Instead, the 2D ADD may be interpreted as the sampling of the longitudinal ADD of each axon. We thus propose that the characteristic tail of the 2D ADD may arise as a result of the broad longitudinal ADDs of large axons. Therefore, observations of “giant axons” (15, 23) may not indicate the presence of very large axons, but instead the local AD variations along large axons.

The morphological nonspecificity of large axons may indicate that they have different functions to smaller axons. Their wide and overlapping longitudinal ADDs entail that their mean diameters are less defined than those of smaller axons, which exhibit narrower longitudinal ADDs. Given these effects, we suggest a categorization of axons into “large” and “small.” Similar categorizations are made in the peripheral nervous system (PNS). The fast-conducting, larger Alpha/Beta axons of the sciatic nerve have a broad ADD that partially overlaps the narrower ADD of the smaller, slower C and Alpha/Delta fibers (24). Although the structure–function relationship of CNS axons is not as well described as that of the sciatic nerve, it has been shown that CNS AD correlates with neuron soma size (25). ADs may thus be cell type specific. The possibility that smaller and larger axons may encode different functional features (26) further supports a size-specific axon categorization. Hence, we suggest that it may be meaningful to pursue a size-specific axon categorization, although explicit definitions of the “large” and “small” categories are yet to be established—and may possibly overlap, similar to the PNS categorization.

The longitudinal ADDs drive variations in g-ratio, while myelin remains stable between nodes of Ranvier. Along single internodes, we found a linear relationship between the inner AD and outer fiber diameter, entailing a nonlinear relationship between g-ratio and AD. Interestingly, this trend is of similar shape to that observed in 2D EM measurements of g-ratios in populations of CNS axons (27). For such 2D measurements, Berthold et al. (28) formulated a log-linear relationship between the number of myelin lamellae (proportional to myelin thickness, assuming a constant lamellar spacing) and the inner AD. For single axons, however, we did not find that the myelin thickness varied as a function of local AD within internodes. Instead, the linear correlation between the longitudinal inner AD and outer fiber diameter indicated that the myelin thickness along internodes was constant. Deviations from the linear trend could be due to too few sampling points, the myelin wrapping mechanism (29), measurement uncertainty in the inner and outer ADs, or myelin-disturbing vacuoles or fixation effects. Histological studies suggest that the myelin thickness shows a stronger correlation to CV than the AD (2), while simulation studies report that myelin is energetically inefficient, and potentially time consuming, to remodel (30). A constant myelin thickness along internodes is thus motivated from a signal timing and energy perspective, entailing that the longitudinal g-ratio variation can be driven by the longitudinal ADD. We expect the 2D g-ratio distributions to represent a sampling of the 3D longitudinal g-ratio distribution, in the same way as the 2D ADDs reflect the longitudinal AD variations. Consequently, Berthold’s log-linear relationship relating the number of myelin lamellae to the AD may also be partially driven by longitudinal variations in AD. Furthermore, although large g-ratios can be detected in 2D images, these may be confined to local axonal segments. The g-ratio measurements of individual axons are therefore not meaningful on their own, since they capture only a snapshot of the 3D axon morphology. Indeed, our findings here apply only to large axons with diameters >2 µm, and smaller axons remain to be investigated.

Longitudinally varying axon morphologies suggest that individual myelinated axons exhibit varying CVs. The calculated mean conduction delays along three axons in the interhemispheric, callosal V1/V2 connection were between 1.9 and 2.4 ms, contrasting with our diffusion MRI-estimated conduction delay of 4.8 ms. The longer delay of 4.8 ms agrees with the calculated conduction delay within the same tract in the larger macaque brain, where the tract length was estimated with tracers to 63.4 mm, the average AD to be 0.95 µm, and the calculated conduction delay to be 4.6 ms (SD = 1.2 ms) (31). As expected from the literature (31), we conclude that the same tract can contain many different-sized axons, resulting in a range of conduction delays. Further demonstrating the nonspecificity of large axons, the range of CVs along single internodes is large, ranging, for example, between 22 and 35 m/s in axon 6 of Fig. 5. Additionally, we note that diffusion MRI and tracer-based histology calculations of CV reformulate Waxman’s classical relation to incorporate a constant g-ratio (9, 18), which we show is not the case. Other factors, such as the internodal spacing, also affect the saltatory CV along an entire axon (32). Nodes of Ranvier were identifiable and internodal distances could be measured in the long axons in Fig. 5, but such an analysis was beyond the scope of this study. Several studies have investigated the relationship between CV and axon morphology, e.g., AD (3), node of Ranvier length (30), internodal length (30), g-ratio (4, 5), and a longitudinally varying AD (33), but none have yet considered the effects of a longitudinal distribution of g-ratios.

Changes to Axonal Morphology May Be Caused by Extra-axonal Obstacles.

The longitudinal variations in AD and trajectory in the vicinity of extra-axonal structures could contribute to the high intracellular volume fraction of around 80% in the brain (34). In the extended volume of the monkey splenium, the blood vessels, cell clusters, and vacuoles accounted for 6.7% of the volume. Aside from the cells clustering parallel to the axons and blood vessels in the CC, the extra-axonal structures occupied space independently of the surrounding axons in the midbody CC, splenium, and the crossing fiber region. Morphological variations and spatial distributions of the extra-axonal compartments could not be linked to the presence of axons. On the other hand, the diameter and trajectory variations of axons could be linked to the presence of extra-axonal structures.

Local AD minima were at times associated with the presence of vacuoles. Vacuoles have been reported in EM studies of the healthy CC (20) and described in ref. 35, but it is possible that vacuolation occurs as a fixation or embedding artifact (36). Reduced ADs were also observed at nodes of Ranvier, as described in the literature. It has been described that AD is regulated by the axonal cytoskeleton (37), which maintains axon shape and consists of nanometer-thick neurofilaments. Decreases in AD have been shown to occur when axons are subjected to axial or circumferential tension, or microtubule disruption (38). Similarly, a reduction of tension through disruption of the axonal actin filaments or myosin II causes a diameter increase (38, 39). Adjacent structures such as vacuoles and neighboring axons may place local circumferential tension on the axons, affecting the organization of microtubules and possibly causing the diameter decreases we observe. This could not be confirmed in the XNH volumes as the microtubules and neurofilaments were too small to be resolved. Furthermore, in unmyelinated axons, local AD increases occur in conjunction with signal firing (40). Consequently, the signal conduction process itself may modulate AD in myelinated axons, meaning that the XNH volumes reveal only a structural snapshot of a truly complex and dynamic tissue environment.

Axonal trajectory changes were caused by blood vessels (Fig. 6 A–C), cells (Fig. 6D), and other crossing axons (Fig. 6F). The 54-axon population exhibited both low- and high-frequency trajectory changes. We quantified the dispersion effects across length scales from the microscopic (1 µm) to the mesoscopic (30 µm). Nonstraight trajectories are commonly observed in tracer-labeled axonal projections over long distances (9, 10, 18), and axonal growth has been shown to follow nonstraight trajectories in axons from the frog and chick (17, 41). Although axons may have predefined targets during axonal growth, we postulate that their trajectories are modified by the extra-axonal environment. In our data, the axons skirt around extra-axonal obstacles, i.e., cell clusters and blood vessels ranging in size from 4 to 10 μm, and this effect may be a major contributor to the meso-dispersion. The microdispersion could be a characteristic of axonal growth, or simply a consequence of the meso-dispersion, which, by definition, gives rise to microdispersion.

The quantification of axon OD is based on the trajectories of the 54 axons from the CC splenium and the results from their analysis are supported by inspection of XNH volumes of the CC midbody. Axons in crossing fiber regions exhibited similar nonstraight trajectories and also intertwining; such effects have previously been observed histologically in tracer-labeled axons (42). Previously, we have detected indications of local undulations in the CC [results presented in Dyrby et al. (43)] with histology, and other studies have derived the theoretical impact of sinusoidal undulation on the diffusion signal for AD estimation (44). The axon trajectories observed here, however, were irregular. Our 3D XNH data suggest that mesoscopic dispersion can occur due to axons projecting around large obstacles, e.g., blood vessels. If these obstacles are aligned and evenly distributed, they may result in the appearance of axonal “undulation.”

Impacts on AD Estimation with Diffusion MRI.

Our findings on the longitudinal ADD and g-ratio variations, as well as the relationship between axon morphology and extra-axonal obstacles, impact microstructural MRI techniques for noninvasive AD estimation. Our MC simulations show that any morphological variation from parallel cylinders incurs an overestimation of AD. This will be the case for all diffusion MRI models that assume a cylindrical axonal geometry and base the AD estimation on measurements perpendicular to the axon population, confirming the need to account for fiber dispersion effects (14, 16, 19, 45). Some studies implement biophysical models to account for axon dispersion or crossing axon effects (12, 46), but the intra-axonal MRI signal profile intermingles with that of the ECS, challenging a robust fitting (47). We could not extract the ECS from our XNH data due to insufficient resolution and shrinkage caused by the tissue processing. As such, we simulated only diffusion within the intra-axonal space. A recent study uses spherical averaging of the diffusion MRI signal to eliminate OD effects with sequence parameters that suppress the ECS signal (48). Although there exist methods to remove the bias caused by OD, none accounts for the effects of microdispersion that we see in Fig. 7. Further challenging accurate AD estimates with diffusion MRI, we found that the parallel ADC is time dependent for realistic axonal substrates. Consequently, measured values of the parallel ADC are likely lower than the true intrinsic diffusivity of the tissue. This potentially influences the ActiveAx-estimated mean AD of 1.3 µm that we present here, since the model assumes that the parallel ADC and intrinsic diffusivity of the tissue are equivalent (14). Simulated substrates with longitudinal AD variations (G3 and G5 in Fig. 7) exhibited stronger time dependence of the parallel ADC than substrates with constant ADs (G2, G4), suggesting that diameter variations could be a potential source of the axial time dependence observed in other studies (49), in line with the suggestions of Fieremans et al. (50).

To ensure robust fitting of the axon model to the diffusion MRI data in Alexander et al. (14) and Dyrby et al. (19), one had to account for a “dot” compartment that represented a small fraction of isotropically restricted water molecules. From the XNH volumes, possible dot compartments could potentially be the cell clusters (4.6% volume fraction) and, assuming their presence in hydrated tissue, the vacuoles (1.4% volume fraction).

Future Directions.

Synchrotron XNH of the monkey WM provides anatomical information within volumes approaching the size of MRI voxels, including the micromorphologies of axons and the volume fractions and morphologies of cells, vacuoles, and blood vessels. However, the ECS is not visible, perhaps due to tissue shrinkage, insufficient signal-to-noise ratio (SNR) and limited resolution at 75 nm. Although scaling factors can be employed to compensate for shrinkage, it is not known if shrinkage affects all WM compartments equally (17). To fully reconstruct the volume fractions of the respective WM compartments, including the ECS, cryo-techniques could be implemented to preserve the hydrated microstructure. Both cryo-EM (51) and cryo-XNH provide alternatives to do so.

The tissue analyzed here belongs to one female, 32-mo-old vervet monkey. Given that 3D EM studies of the mouse CC (20, 21) also demonstrate morphological variations in axons, we expect that the modulation of axonal morphology by extra-axonal structures is present in the WM regions of other individuals and species. However, the “fingerprints” of axonal diameter and trajectory variation (Figs. 3C and 4C) may differ with species, age, gender, and disease, and it is relevant to pursue further studies into this matter.

As with many imaging techniques, XNH is subject to a trade-off between the size of the image volume and the resolution. The image quality depends on the acquisition time and sample processing, including the sample size, staining, and smoothness of the embedding medium. We imaged at voxel sizes of 75 nm (splenium) and 100 nm (crossing fiber and midbody), but the SNR challenged the segmentation of axons with mean diameters smaller than ∼2 µm. The morphological behavior of smaller axons thus remains to be studied. This is possible with XNH, given that one prioritizes resolution and optimizes the sample preparation. However, EM provides superior resolution and there are ongoing efforts to develop large-scale 3D mapping of neural tissue by stacking 2D EM images (52). Still, EM is time demanding and there is a need to combine techniques that bridge different resolutions and volumes. Di-attenuation imaging has recently been demonstrated on sections of the vervet monkey brain at an effective resolution of 27 µm/pixel, and shows sensitivity to fiber orientation, diameter, and myelin sheath thickness (53). Further combination of XNH with EM and di-attenuation imaging would be valuable for mapping fiber microstructure, and the whole-brain network architecture.

Last, the axonal diameter variations and dispersion behavior presented here could act as an axonal “fingerprint” to guide the construction of anatomically informed axonal phantoms for MC simulations. Existing frameworks to model morphological features such as fiber undulation (44, 54) (although we do not observe periodic undulations in our data) and diameter variations (55, 56) exist. Others allow for the generation of a more complex WM environment with beaded axons and cells (57). None, however, has yet imposed anatomically realistic trajectory patterns or longitudinal ADDs.

Materials and Methods

Monkey Brain Tissue.

The tissue came from a 32-mo-old female perfusion fixated vervet (Chlorocebus aethiops) monkey brain, obtained from the Montreal Monkey Brain Bank. The monkey, cared for on the island of St. Kitts, had been treated in line with a protocol approved by The Caribbean Primate Center of St. Kitts. The brain had previously been stored and prepared according to Dyrby et al. (58) and ex vivo MRI scanned using the optimized ActiveAx framework for volume-weighted mean AD estimation from previous work (14, 19). Prior to synchrotron XNH, the tissue was prepared for whole-brain ex vivo MRI for the estimation of AD and the segmentation of interhemispheric callosal fibers with tractography, as described in the following.

MRI Scanning, AD Estimation, and Tractography.

MRI scanning.

The diffusion MRI dataset was collected on an experimental 4.7-tesla Agilent MRI scanner with a maximum gradient strength of 600 mT/m. An optimized three-shell ActiveAx MRI protocol based on a maximal gradient strength of 300 mT/m for ex vivo tissue as in Dyrby et al. (19) was used. The noncollinear diffusion weighting encoding directions were obtained from the Camino Toolbox (RRID: SCR_001638) (59). Further details of the protocol are included in SI Appendix. Prior to AD fitting and tractography, the diffusion MRI datasets were denoised (60) and processed to remove Gibbs ringing artifacts (61) in the MRTrix3 software toolbox (RRID: SCR_006971).

AD estimation.

AD estimation was performed using the ActiveAx framework, based on the four-compartment minimal model of white matter diffusion (MMWMD) as described in ref. 14.

The MMWMD model was fitted to the diffusion MRI data with the same parameter settings and multistage fitting method as in Dyrby et al. (19) using the ActiveAx implementation of the Camino Toolbox. Since MRI probes volumes, larger axons contribute more to the intra-axonal signal than smaller ones. Hence, the estimated mean AD using diffusion MRI is a volume-weighted index (14). A ROI was manually drawn to cover the midsagittal plane of the CC within which the volume-weighted mean AD was calculated voxelwise as the average of 100 repeated estimations.

Segmentation of interhemispheric brain connections with tractography-based MRI.

Streamline-based tractography was used to estimate the length of the interhemispheric connection that, via the splenium in the CC, connects the two primary visual cortical areas at the V1/V2 border that represents the vertical in meridian in most species including cats, monkeys, and humans (62). We used a constrained spherical deconvolution method (63) implemented in MRTrix3 to obtain voxelwise multifiber reconstructions of the whole brain. Probabilistic streamline tractography was then implemented with the SD-STREAM function in MRtrix3 using standard parameters to extract 2,000 streamlines (64). Further details are included in SI Appendix.

Tractography-based estimation of conduction velocity.

To estimate the end-to-end conduction delay of the interhemispheric connection between the V1/V2 border regions and passing through the splenium, the tract was assumed to have a g-ratio, g, of 0.7 as in other studies (10, 31). The CV was calculated according to the following (9): CV = 5.5/g⋅d, where d is the inner AD. The inner AD used was the AD index obtained by fitting ActiveAx to the diffusion MRI dataset of the monkey brain, as previously described. Together with the tract length from tractography, L, the conduction delay (t) was given by the following: $t=L/\mathrm{CV}$.

Synchrotron XNH Imaging and Segmentation.

Tissue preparation for XNH imaging.

After MRI acquisition, the whole monkey brain was agar-embedded for mechanical stability and cut into sagittal slices at thicknesses between 2 and 4 mm in a mold. Samples from the midsagittal CC and crossing fiber regions were extracted with a biopsy punch of diameter 1 mm and fixed in 2.5% glutaraldehyde before being stained with 0.5% osmium tetroxide (OsO₄) at room temperature for 2 h. The OsO₄ did not fully penetrate the tissue sample. However, the stained peripheries of the samples were large enough to cover the XNH field of view. The stained tissue was dehydrated with an alcohol series and embedded in EPON resin. Excess EPON was removed to produce blocks of approximately 1 × 1 × 4 mm.

Synchrotron XNH imaging.

XNH was performed at beamline ID16A of the European Synchrotron Research Facility (ESRF). Samples were imaged using a nano-focused cone beam (65, 66) of energy 17 keV. Holograms of the samples were recorded at different distances with respect to the focus and the detector to obtain phase maps (66, 67). In practice, sequential tomographic scans were acquired at four different propagation distances by rotating the samples over $180°$, and corresponding angular holographic projections were aligned and combined to generate phase maps of the sample. For each tomographic scan, 1,800 projections were acquired with exposure times of 0.22 s using a pixel size of 75 nm. The reconstructed image volumes were cylindrical, with dimensions 2,048 × 2,048 × 2,048 voxels. Acquiring one full scan took ∼4 h.

Segmentation of cell clusters, blood vessels, and vacuoles.

We implemented an in-house intensity- and morphology-based approach in MATLAB to segment the cell clusters, blood vessels, and vacuoles from the four consecutively acquired XNH volumes (Fig. 2A). This used classic low-level image analysis operations such as intensity thresholds, morphological operations, and connected components analysis. Further information can be found in SI Appendix.

Segmentation of axon diameters.

The XNH volumes were downsampled by a factor of 5 by extracting every fifth slice, and performing a slicewise cubic interpolation and Gaussian smoothing (kernel width of 5 pixels) in MATLAB (version 2019b) to achieve volumes of dimension 410 × 410 × 410 voxels with isotropic voxel size of 375 nm. A rough segmentation of the axons from these volumes was then performed using the adaptive paintbrush in ITK-Snap (RRID: SCR_002010). This allowed for the extraction of an approximate centerline by a simple slicewise estimate of the axon centroid. With the centerline as input, we employed a MATLAB-based, in-house segmentation method to extract the axons and update their centerlines from the high-resolution volumes of voxel size 75 nm. This is described in SI Appendix.

Quantification of Axonal Dispersion of Segmented Axons.

For each of the 54 axons, the point-to-point vectors within their centerlines were averaged to obtain a main axon direction. The average of all 54 main axon directions was defined as the main bundle direction. The OD of each axon was defined as the inclination angle between the main bundle direction and the main axon direction.

We introduced the concept of microdispersion at different length scales, L, to quantify the deviation of axons from their linear main directions. To calculate the microdispersion, we first aligned the axons with the z axis. Then, the cumulative distance along the centerline was calculated, and the centerline was divided into segments of length, L, corresponding to the sampling length. A principal-component analysis was performed on the set of points within each segment to determine the segment direction in MATLAB. Thereafter, the inclination angle between the segment direction and the main axon direction was calculated. The average inclination angle of all segments (weighted according to the number of points in each segment) was defined to be the mean inclination angle of the axon at a length scale L. For a robust quantification, the axon skeleton was queried four times for each length scale L by shifting the starting position of the quantification by L/4 as shown in Fig. 4B. We studied length scales, L, ranging between 1 and 30 µm.

MC Simulations of the Diffusion Process in Synthetic Axons.

Substrates G1–G5 in Fig. 7 were based on the 54 segmented axons (substrate G6). The 54 axons in geometries G1–G5 inherited one or more of the following from the segmented axons in G6: mean AD, longitudinal diameter variation, OD, microdispersion (trajectory). This was attained through modeling of the axons as deformed cylinders.

Prior to simulations, the XNH segmentations were meshed and postprocessed as described in SI Appendix.

Simulations were performed using the Monte Carlo Diffusion and Collision simulator from Rafael-Patino et al. (54). Each axon in each geometry was simulated separately, and the intra-axonal diffusivity was set to 6.0 × 10⁻¹⁰ m²⋅s⁻¹ as measured in ref. 19, as is conventional for ex vivo diffusion MRI. Particles were initialized uniformly within the central region of the axon meshes at a minimum distance of 20 µm from the axon ends. This confined initialization ensured that virtually no particle was able to diffuse outside the mesh. Perfectly elastic mesh boundaries were implemented, as in ref. 54. The number of particles and time-step duration were chosen using a bootstrap-based analysis of the convergence of the simulation as explained in ref. 54. In this investigation, we studied diffusion times, $D_t$, between 1 and 50 ms at intervals of 1 ms and used 2 × 10⁵ particles and 5 × 10⁵ time steps with a duration of 1 × 10⁻⁵ s. The simulator output the mean-squared displacement, $\langle {\left(\mathrm{\Delta }x\right)}^2\rangle$, of the particles in the directions parallel and perpendicular to the main bundle direction.

The reported ADCs were calculated from $\langle {\left(\mathrm{\Delta }x\right)}^2\rangle$ by the Einstein relationship (68):

$$\langle {\left(\mathrm{\Delta }x\right)}^2\rangle =2\cdot ADC\cdot D_t.$$

The AD estimations were based on the analytical expression for diffusion perpendicular to cylinders (69): ${\lambda }^2=R^2/2$, where ${\lambda }^2$ is the mean-squared displacement perpendicular to the cylinder and $R$ is its radius.

Data Availability.

The four XNH image volumes of the monkey brain splenium and the segmentation of cells, vacuoles and blood vessels are publicly available on the download center of the Danish Research Centre for Magnetic Resonance (https://www.drcmr.dk/axon-morphology-dataset). The diffusion MRI datasets of the same brain as the XNH image volumes are also available on the same link and include the raw diffusion MRI data covering the mid sagittal region of the corpus callosum, used for axon diameter fitting, and the whole-brain diffusion MRI data set used for tractography.