Free-breathing abdominal T₁ mapping using an optimized MR fingerprinting sequence

Abstract

In this work, we propose a free-breathing magnetic resonance fingerprinting (MRF) method that can be used to obtain B₁⁺-robust quantitative T₁ maps of the abdomen in a clinically acceptable time. A three-dimensional MRF sequence with a radial stack-of-stars trajectory was implemented, and its k-space acquisition ordering was adjusted to improve motion-robustness in the context of MRF. The flip angle pattern was optimized using the Cramér–Rao Lower Bound, and the encoding efficiency of sequences with 300, 600, 900 and 1800 flip angles was evaluated. To validate the sequence, a movable multicompartment phantom was developed. Reference multiparametric maps were acquired under stationary conditions using a previously validated MRF method. Periodic motion of the phantom was used to investigate the motion-robustness of the proposed sequence. The best performing sequence length (600 flip angles) was used to image the abdomen during a free-breathing volunteer scan. When using a series of 600 or more flip angles, the estimated T₁ values in the stationary phantom showed good agreement with the reference scan. Phantom experiments revealed that motion-related artifacts can appear in the quantitative maps and confirmed that a motion-robust k-space ordering is essential. The in vivo scan demonstrated that the proposed sequence can produce clean parameter maps while the subject breathes freely. Using this sequence, it is possible to generate B₁⁺-robust quantitative maps of T₁ and B₁⁺ next to M₀-weighted images under free-breathing conditions at a clinically usable resolution within 5 min.

1 ∣. INTRODUCTION

Most routine clinical magnetic resonance imaging (MRI) measurements depict a relative contrast between tissues. In addition to the tissue properties, the measured signal intensities depend on experimental factors, such as RF excitation and receive sensitivities.¹ Consequently, the obtained qualitative contrast depends on the specific sequence parameters and scanner hardware used to acquire the data. Quantitative MRI, on the other hand, strives to directly measure physical or chemical properties of tissues, most notably the longitudinal (T₁) and transverse (T₂) relaxation times. Compared with qualitative images, such quantitative maps enable more straightforward comparisons between scans from different patients, different time points, or using different hardware.^2,3

Quantification of MR parameters can be performed using several techniques. Historically, relaxometry measurements were performed by fitting exponentials to a series of inversion times or echo times to quantify T₁ or T₂ relaxation times, respectively.¹ However, such measurements are too slow for routine clinical usage. Over the years many techniques have been developed to provide a better balance between accuracy and acquisition speed, such as the Look-Locker method⁴ or DESPOT1 and DESPOT2,⁵ among others. Recently, MR fingerprinting (MRF) has been proposed for the fast and simultaneous quantification of multiple parameters.⁶ This method uses a variable flip angle train that produces unique signal evolutions, so-called “fingerprints”, for different tissue parameter combinations. By comparing the measured fingerprints with the entries in a precomputed dictionary, the underlying tissue parameters, such as T₁, T₂ and equilibrium magnetization (M₀), can be estimated.

Several challenges arise when attempting quantitative imaging of the abdomen. Intestinal gas in the abdomen can cause susceptibility artifacts, especially for field strengths of 3 T and higher.⁷ Furthermore, the relatively short wavelength of the RF can lead to interferences in the B₁⁺ field, resulting in an inhomogeneous excitation.^7,8 Moreover, respiratory, cardiac, gastrointestinal and voluntary motion can cause other image artifacts⁹ and can corrupt the MRF-based parameter maps.¹⁰ Although breathholds can be used to eliminate respiratory motion during an MRF experiment,¹¹ it places restrictive limits on scan time and thus on spatial resolution or volumetric coverage. Besides, not all patients can hold their breath (e.g. pediatric patients).^12,13 Therefore, it is preferable that the sequence is inherently robust against motion, such that the subject can breathe freely during the scan.¹⁴

In this work, we present a free-breathing 3D MRF sequence to generate quantitative T₁ and B₁⁺ maps, as well as M₀-weighted images. The k-space ordering was adjusted to improve robustness against motion, while B₁⁺-related artifacts were addressed by including B₁⁺ in the parameter estimation. The flip angles were optimized to improve the efficiency of the sequence and to decrease the scan time. The method was validated using a movable phantom and subsequently evaluated in vivo during free-breathing abdominal measurements.

2 ∣. METHODS

2.1 ∣. Sequence design

Building on prior work,¹⁵ an MRF sequence was designed to generate a distinct signal pattern for every combination of T₁ and B₁⁺. By including the B₁⁺ value in the parameter estimation, the effect of an inhomogeneous excitation field can be dealt with.^16,17 Since most B₀-robust T₂-encoding solutions are particularly motion sensitive,¹⁰ only fast low angle shot (FLASH) segments with a repetition time (TR) of 5 ms were used. These segments were gradient- and RF-spoiled to avoid T₂ dependence.

To reduce the sensitivity of the sequence to motion, a radial readout sampling pattern was chosen.¹⁴ This trajectory samples the center of k-space, which encodes the global image contrast with every readout. Consequently, the motion during acquisition is averaged out in the resulting image. Furthermore, undersampling artifacts are expressed as streaks in the image,¹⁸ instead of the less desirable ghosts that occur with a Cartesian sampling pattern. These streaks lead to incoherent, noise-like artifacts in the reconstructed images, which can be filtered out by the dictionary-matching process. The extension to 3D can be made by stacking multiple partitions on top of each other, where each partition consists of several radial readouts, to form a stack-of-stars trajectory.¹⁴

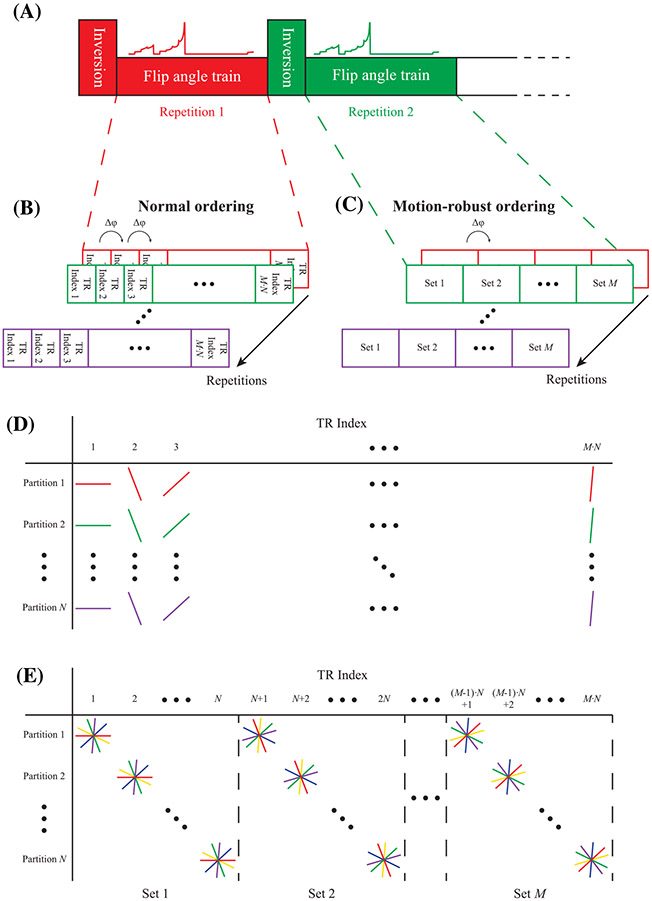
The simplest stack-of-stars implementation, hereafter referred to as normal ordering, keeps the partition index fixed during the flip angle sequence (Figure 1). The readout angle is changed by 111.25 degrees (the golden angle) every readout.¹⁹ The flip angle sequence is then repeated once for every partition, after which one shot has been acquired. To increase the sampling density, multiple shots can be acquired. Using this ordering, lines in adjacent partitions are acquired using the same flip angle, and thus have the same contrast weighting. However, this ordering scheme results in a time interval of several seconds between adjacent lines in the partition direction, and any motion during this time results in motion artifacts in the fingerprints.

FIGURE 1.

Proposed motion-robust 3D MRF sequence. (A), The data are acquired using a repeated flip angle sequence, each generating a fingerprint encoding T₁ and B₁⁺. Every repetition is preceded by a nonselective adiabatic inversion pulse. Each repetition is indicated with a separate color. (B), In the normal ordering, each fingerprint sequence consists of M·N TRs. Each TR index generates a separate k-space. (C), In the motion-robust ordering, each fingerprint sequence consists of M sets, containing N TRs each. All readouts acquired during the TR indices corresponding to one set are grouped together to form a single k-space. (D), Readout lines acquired for the normal ordering. Every TR, the readout angle is incremented with the golden angle (Δφ = 111.25 degrees), while the partition index stays the same. This results in a single undersampled k-space for every TR index. All lines of the same color are acquired sequentially during the same repetition. (E), Readout lines acquired for the motion-robust ordering. Every TR, the readout angle stays the same, but the partition index is increased. Note how readouts in adjacent partitions with the same angle are acquired successively in the motion-robust ordering, while in the normal ordering, the next partition is sampled during the next repetition of the sequence

To obtain motion robustness while using a stack-of-stars sampling pattern, all partitions are typically acquired in quick succession before changing the readout angle.¹⁴ However, during an MRF experiment, the MR signal is in a transient state because the flip angle changes for every TR index. Hence, it is not possible to sample all partitions with the same contrast weighting in quick succession. Therefore, to retain motion robustness, we propose to increase the TR index and the partition index simultaneously (hereafter referred to as motion-robust ordering; see Figure 1). For every readout, the next partition is sampled, until the last partition is reached, after which the first partition is sampled again. To remain consistent with the normal ordering, one shot is defined to be completed after the flip angle sequence has been repeated as many times as the number of partitions. For each repetition, the sequence of partition indices remains the same, but all readout angles are incremented with the golden angle.

To allow reconstruction of the data with the motion-robust ordering, the measured signals are divided into sets, with each set containing the data from as many consecutive TR indices as the number of partitions. Note that this will introduce some contrast mixing during the Fourier transform along the partition direction. When the flip angles change smoothly, it is our hypothesis that the differences in signal intensities along the partition direction will remain acceptable.

For both ordering schemes, data acquisition was started from the second repetition onwards to ensure that the initial magnetization at the start of each repetition was identical.²⁰

2.2 ∣. Dictionary construction

The Bloch equations²¹ were used to create a precomputed dictionary consisting of 17,600 simulated fingerprints, each with a unique combination of T₁ and B₁⁺ values. The T₁ values ranged from 50 to 3764 ms with relative increments of 2.5%, and B₁⁺ effects were implemented by multiplying the desired flip angle with a relative weighting factor ranging from 0.02 to 2.0 in steps of 0.02. The complete sequence consisted of gradient echoes with both gradient- and RF-spoiling, which prevented the formation of stimulated echoes and thus eliminated any T₂ contrast.¹⁶ In addition, the echo time (TE) was held fixed, resulting in a constant scaling of the fingerprints caused by T₂* effects. However, since this effect is indistinguishable from M₀ contrast, T₂* effects were not simulated in the dictionary.

For every combination of T₁ and B₁⁺ in the dictionary, the whole sequence was simulated for two repetitions. The first repetition was used to obtain the initial magnetization during a continuous scan, while the second repetition was used to obtain the fingerprint. Next, for the motion-robust ordering, the fingerprint signals from N_partitions consecutive readouts were grouped into sets (as in Figure 1), and the signals within each set were averaged. The dictionary was compressed by projecting the fingerprints onto the first five singular vectors of the dictionary.²² This rank-5 approximation retained more than 99.5% of the energy in all dictionaries, where the energy is defined as the sum of the squared singular values. Finally, all simulated and averaged fingerprints were normalized to have unit Euclidean norm.

2.3 ∣. Sequence optimization

Besides making the sequence motion robust, the flip angle pattern was optimized to bring the acquisition time down to under 5 min. Four different patterns were designed, corresponding to a sequence of 300, 600, 900 and 1800 flip angles. Consecutive flip angles were placed 5 ms apart, with a nonselective adiabatic inversion pulse²³ at the start of each sequence. Note, however, that the optimization algorithm can set the flip angle to 0 degrees, thus effectively creating a delay.

As a measure of optimality, the Cramér–Rao Lower Bound (CRLB)²⁴ was used. This measure expresses the minimum variance of a set of estimated parameters, in this case T₁ and B₁⁺, obtained using an unbiased estimator, here the MRF reconstruction. The CRLB has previously been used to find optimal parameters for an MRI experiment, as well as for MRF in particular.^25-28

The measurements are assumed to be subject to white Gaussian noise:

$$s_n(\theta ,\alpha )=M_n(\theta ,\alpha )+w_n,$$ (1)

where s_n is the measured signal intensity in the nth set, M_n is the normalized and averaged signal intensity of the nth set as calculated by the same simulator used for the dictionary, $\theta \in {\mathbb{R}}^p$ is the vector of all estimated parameters (T₁ and B₁⁺ in this case), $\alpha \in {\mathbb{R}}^q$ is the vector containing all flip angles in the sequence, and $w_n\sim \mathcal{N}(0,{\sigma }^2)$ is normally distributed noise with standard deviation σ. Since the fingerprints are normalized, the standard deviation of the measurement noise should be scaled identically to obtain the right σ. The Fisher information matrix (FIM), which can be used to obtain the CRLB,²⁴ can be written as:

$$I(\theta ,\alpha )=\frac{1}{{\sigma }^2}\sum _{n=1}^N{J}_n(\theta ,\alpha {)}^T\cdot J_n(\theta ,\alpha ),$$ (2)

with $I(\theta ,\alpha )\in {\mathbb{R}}^{p\times p}$ the FIM, σ the standard deviation scaled according to the normalization of the fingerprint, and $J_n=\partial M_n∕\partial \theta \in {\mathbb{R}}^{1\times p}$ the Jacobian of the signal M_n with respect to the estimated parameters θ. Taking the inverse of the FIM gives a matrix, whose diagonal elements indicate the CRLBs of the estimated parameters given the flip angle sequence²⁴:

$$\mathsf{Var}({\widehat{\theta }}_i\mid \alpha )\ge [I^{-1}(\theta ,\alpha ){]}_{i,i}.$$ (3)

These variances were normalized by the square of the true T₁ and B₁⁺ values, respectively, to give the coefficient of variation (COV) for both parameters. To make the MRF sequence sensitive to both T₁ and B₁⁺, the sum of these two relative CRLBs (the trace of the covariance matrix) was minimized.

The CRLB of a parameter gives an estimate of the sensitivity around a specific parameter value. Since we want the MRF experiment to be sensitive to a range of parameter values, the relative CRLBs for N_l different combinations of T₁ and B₁⁺ values were calculated and averaged. Furthermore, all flip angles were limited to 60 degrees, corresponding to the peak transmit voltage for an average subject when using an apodized sinc-shaped RF-pulse of 1.5 ms with a time-bandwidth factor of 8. The final optimization problem is given by Equation 4:

$$\begin{gathered} \underset{\alpha }{\mathsf{min}}\frac{1}{N_l}\sum _{l=1}^{N_l}\mathsf{tr}(W\cdot I^{-1}({\theta }_l,\alpha )) \\ s.t.{\mathsf{O}}^{{}_{°}}\le {\alpha }_n\le {60}^{{}_{°}},1\le n\le q. \end{gathered}$$ (4)

Here, ${\theta }_l\in {\mathbb{R}}^p$ is the lth parameter combination, $W\in {\mathbb{R}}^{p\times p}$ is a diagonal matrix with weighting factors for the parameters, tr(·) denotes the trace of a matrix, α_n is the nth flip angle in the sequence, and q is the total number of flip angles. We used $W=\text{diag}\left(\left[1∕(T_1{)}^2,1∕(B_1^{+}{)}^2\right]\right)$, which normalized the variances of both parameters.

During optimization, the number of flip angles was fixed. To investigate the influence of different sequence lengths, the sequence was optimized for 300, 600, 900 and 1800 flip angles, using T₁ values between 500 and 1500 ms in steps of 250 ms, and relative B₁⁺ values of 0.75, 1.0 and 1.25, giving N_l = 15. The sequences were initialized with smooth random flip angle patterns with values between 0 and 10 degrees. The optimization was repeated for 20 different initializations. The optimized sequence with the lowest objective value after optimization was selected. There was no explicit delay time between subsequent repetitions of the sequence. However, note that the optimization algorithm was able to set the flip angles to negligible low values, thus effectively creating a delay that allowed the magnetization to relax towards equilibrium.

The optimization problem given in Equation 4 was implemented in MATLAB (MathWorks, Natick, MA, USA). Automatic differentiation,^27,29 implemented using the CasADI toolbox,³⁰ was used to calculate the Jacobian in Equation 2, as well as the gradient and Hessian-times-vector product of the objective function in Equation 4. The minimization problem was solved with the MATLAB function fmincon. The code used to optimize the flip angles is available on our bitbucket: https://bitbucket.org/MaxvRiel/free-breathing-mr-fingerprinting/.

2.4 ∣. Imaging experiments

All experiments were performed on a clinical 3-T MRI scanner (Prisma, Siemens Healthineers, Erlangen, Germany). A phantom containing seven glass tubes with different T₁ values was placed on a cart made from LEGO bricks (The Lego Group, Billund, Denmark). This cart was placed on a slope of approximately 7 degrees and connected to a motor just outside the scanner room, which was controlled using the RWTH Mindstorms NXT Toolbox for MATLAB (RWTH Aachen University, Aachen, Germany). An 18-channel body coil (Siemens) was placed over the phantom and the cart (Figure 2). The phantom was scanned while stationary and while moving back and forth with frequencies of 0.22, 0.24 and 0.30 Hz, which are within the range of normal breathing frequencies in adults.³¹ The peak-to-peak amplitude of the motion was 32 mm. All scans were performed with both ordering schemes. A previously validated 2D MRF implementation with slice profile correction¹⁵ was used to obtain reference T₁ values in the absence of motion. In addition, to validate the quantitative B₁⁺ values, a gold standard B₁⁺ map was obtained using the saturation prepared turbo-FLASH method.³²

FIGURE 2.

Experimental setup. (A), The phantom placed on a movable cart. This cart is placed on a ramp. Under the influence of gravity, the cart moves to the right, while a rope connected to a motor can pull the cart to the left. (B), The 18-channel body coil that was used to acquire the data was placed over the movable phantom

In order to keep the same acquisition time of 4 min 30 s for the different flip angle trains, more shots were used for shorter sequences. This resulted in six, three, two and one shots for the sequences with 300, 600, 900 and 1800 TRs, respectively.

Abdominal scans were performed on six healthy volunteers after obtaining written informed consent. The study was approved by the institutional review board at the New York University School of Medicine. The same scanner and body coil were used as during the phantom scan. The volunteers were instructed to breathe normally, but to avoid taking deep breaths (by sighing or yawning). The parameters used for both experiments are summarized in Table 1. In addition, a DESPOT1 scan⁵ was performed for one volunteer to compare the resulting T₁ maps. Furthermore, for one volunteer we acquired data at a higher resolution of 1.0 mm × 1.0 mm × 3.0 mm and with five shots.

TABLE 1.

Image acquisition parameters used in the phantom and in vivo experiments

Parameter	Value (phantom)	Value (in vivo)
Repetition time (TR)	5.0 ms
Echo time (TE)	2.4 ms
Inversion time (TI)	10 ms
Number of partitions	30
Acquisition time	4 min 30 s
Resolution	1.0 mm × 1.0 mm × 6.0 mm	1.3 mm × 1.3 mm × 3.0 mm
Field of view	256 mm × 256 mm × 180 mm	420 mm × 420 mm × 90 mm

2.5 ∣. Image reconstruction

After acquiring all the data, the receive channels were compressed to five (phantom) or 10 (in vivo) virtual coils for every slice independently, retaining more than 98.5% of the energy in all datasets. A fast Fourier transform (FFT) was performed in the partition direction. A rank-5 approximation of the k-space data was made using the same five singular vectors computed for the dictionary compression.²² Next, every partition was reconstructed separately using nonuniform FFT (NUFFT),³³ and the virtual coil channels were combined using a matched-filter reconstruction.³⁴

For every voxel, the dot product between the fingerprint and the dictionary was maximized to identify the T₁ and B₁⁺ values associated with that voxel. The Euclidean norm corresponding to the (unnormalized) dictionary entry was used to estimate M₀. The image reconstruction, dictionary construction and dictionary matching were all implemented in MATLAB. The code used to reconstruct the parameter maps is available at https://bitbucket.org/MaxvRiel/free-breathing-mr-fingerprinting/.

2.6 ∣. Image analysis

In order to analyze the parameter maps of the moving phantom, a region of interest (ROI) was drawn in each of the seven tubes. The mean and standard deviation of all estimated parameters were calculated for each tube. The estimated T₁ values were validated against those from the reference scan.

Three ROIs were drawn in each in vivo dataset, where care was taken to avoid any vessels. The mean and standard deviation of T₁ values were determined from these ROIs, and these values were compared with values from the literature.

3 ∣. RESULTS

3.1 ∣. Flip angle patterns

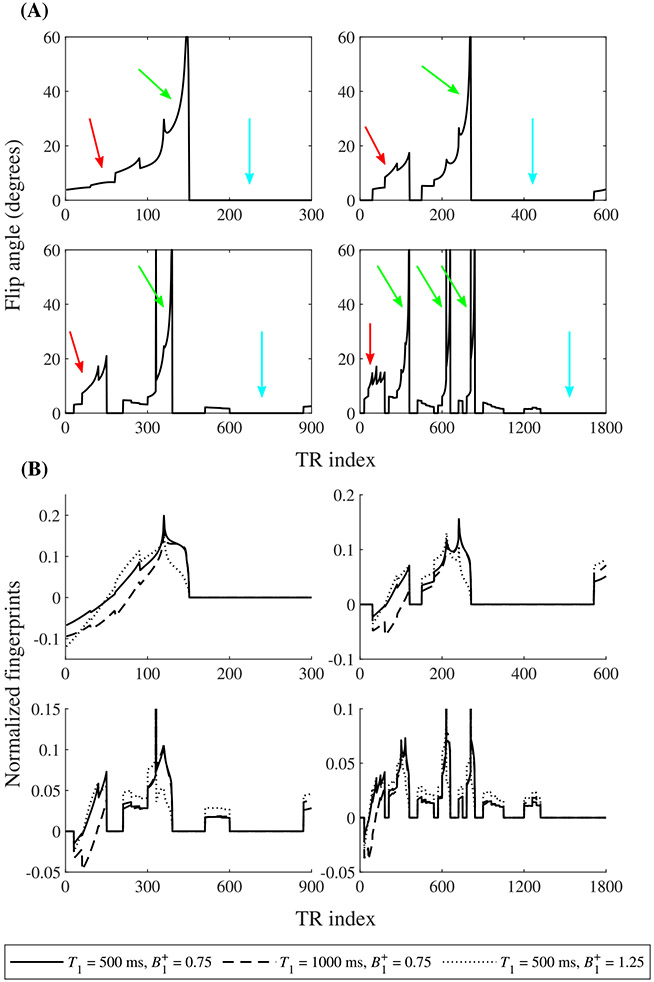
The flip angles optimized for different train lengths (Figure 3) showed similar patterns. Within each set of 30 consecutive TRs (the number of partitions), the flip angles generally increase smoothly, which results in smoothly varying signal intensities within each set. The flip angles show large jumps only between sets.

FIGURE 3.

Results of the flip angle optimization. (A), Optimized flip angle patterns for 300, 600, 900 and 1800 TRs (left to right, top to bottom). Note the smoothly varying flip angles within each set. Indicated are the main T₁-encoding part (red arrows), the main B₁⁺-encoding part (green arrows) and the delay (light blue arrows). (B), Normalized fingerprints for different combinations of T₁ and B₁⁺ values for the same four flip angle patterns

Furthermore, the flip angles of the first few sets in all sequences follow a similar pattern, which occurs around the zero-crossing of the inverted magnetization. Hence, it is mostly dependent on T₁ and mainly serves to encode T₁ in the fingerprint (solid and dashed lines in Figure 3B).

Next, there is a recurring pattern that consists of a single high flip angle, followed by a set of increasing flip angles. This pattern is particularly visible in the sequences with 900 and 1800 TRs but is also present in the sequences with 300 and 600 TRs. It mainly serves to provide B₁⁺-sensitive signals (solid and dotted lines in Figure 3B). The single high flip angle partly saturates the signal, with the amount of saturation depending on the B₁⁺ value. The succeeding excitations then provide the B₁⁺-dependent signal for the fingerprint. Note that this pattern is repeated several times in the sequence with 1800 TRs.

Since the magnetization is saturated after this B₁⁺-encoding pattern, any subsequent excitations would not generate much signal. The optimization resulted in multiple segments with very small flip angles. These segments do not provide much useful information. Instead, they decrease patient discomfort as the scanner produces more noise. Therefore, we decided to set all flip angles smaller than 1.5 degrees to zero. During these segments, the magnetization can recover before the next repetition of the sequence.

3.2 ∣. Phantom results

The T₁ maps from the phantom scan for all four optimized sequences can be seen in Figure 4. For M₀, T₁, and B₁⁺ maps, acquired using all tested motion speeds, see Figures S1-S8. The sequence with 300 flip angles and six shots slightly underestimated higher T₁ values, while the longest flip angle train (1800 flip angles, one shot) showed large variability in the T₁ estimates. This is also visible when looking at the correlation between the estimated and the reference T₁ values (Figures 5 and S9). The other two sequences showed a better compromise between the number of shots and encoding capability.

FIGURE 4.

T₁ maps of the phantom scan without (left) and with (right) motion, for both ordering schemes, and for all four sequence lengths for which the flip angles were optimized. For the maps with motion, the motion speeds with the most severe artifacts were selected for each sequence separately. Note the severe motion-related artifacts visible when using the normal ordering, which are greatly reduced by using the motion-robust ordering

FIGURE 5.

Correlation plots between the estimated T₁ values (vertical axis) and the corresponding T₁ values from the reference scan (horizontal axis) for each map in Figure 4. Each point indicates the mean T₁ values of both scans within one single tube, with the standard deviation depicted as error bars. The dashed line is the identity line. Note the increased deviation from the identity line for the normal ordering compared with the motion-robust ordering

The sequence with 600 flip angles was selected to be investigated further, as this sequence showed the highest accuracy for the T₁ estimation when using the motion-robust ordering. Phantom scans without motion also indicated that the obtained quantitative B₁⁺ values correlate well with the saturation prepared turbo-FLASH method (Figure S10).

In Figure 6, the estimated parameter maps for this sequence with both ordering schemes, and both with and without motion, are shown. Without motion, both ordering schemes showed good agreement with the reference scan. In the presence of motion, however, the normal ordering showed notable motion artifacts in all parameter maps, and a large deviation from the identity line in the T₁ correlation plots. The normalized root mean square error, comparing the estimated T₁ values of the tubes measured in the absence of motion with the measurements including motion, was also reduced from 0.17 for the normal ordering to 0.05 for the motion-robust ordering.

FIGURE 6.

M₀-weighted (top row), quantitative T₁ (middle row) and quantitative B₁⁺ (bottom row) maps of the phantom, both without (left) and with (right) motion, and with both ordering schemes, using the optimized sequence with 600 flip angles and three shots. Note the motion-related artifacts in the parameter maps acquired with the normal ordering

The severity of the observed motion artifacts depends on the frequency of the motion. Presented here are the results obtained with the speeds that caused the most severe artifacts when using the normal ordering. Nevertheless, it should be noted that the motion-robust ordering performed well independent of the speed of the motion (Figure S4).

3.3 ∣. In vivo results

Since the standard deviation of the T₁ values obtained using the sequence with 600 flip angles was the lowest, this sequence was evaluated in vivo (Figure 7). The estimated T₁ values inside the liver (Table 2) were comparable with values found in the literature.^11,35 Note the variations of the excitation field strength in the B₁⁺ maps, which are simultaneously quantified using our method.

FIGURE 7.

In vivo M₀-weighted (top row), quantitative T₁ (middle row) and quantitative B₁⁺ (bottom row) maps of all six volunteers for the normal ordering and the motion-robust ordering, using the optimized sequence with 600 flip angles and three shots. The motion-robust ordering reveals more details in the T₁ map and removes the motion-related artifacts visible in the maps of all three parameters. Areas with strong artifacts are highlighted with yellow ROIs

TABLE 2.

Distribution (mean ± standard deviation) of in vivo T₁ values in the liver

	T1 – Normal ordering	T1 – Motion-robust ordering
Volunteer 1	689 ± 58 ms	725 ± 65 ms
Volunteer 2	596 ± 64 ms	587 ± 53 ms
Volunteer 3	731 ± 58 ms	724 ± 60 ms
Volunteer 4	657 ± 67 ms	657 ± 67 ms
Volunteer 5	756 ± 58 ms	760 ± 66 ms
Volunteer 6	646 ± 69 ms	632 ± 59 ms
Literature	745 ± 65 ms11 767 ± 82 ms35

The motion-robust ordering resulted in a sharper T₁ map, where the vessels in the liver are much more visible, when compared with the normal ordering. Furthermore, there are severe motion artifacts visible in the maps acquired using the normal ordering, as highlighted by the yellow ROIs in Figure 7. These artifacts are no longer visible when using the motion-robust ordering.

To investigate the effect of including B₁⁺ in the dictionary, we reconstructed one dataset with the motion-robust ordering while constraining the relative B₁⁺ value to 1.0. The results can be seen in Figure 8. The estimated T₁ maps are very similar. This indicates that B₁⁺ can be estimated without decreasing the quality of the T₁ estimates. Moreover, the T₁ difference map resembles the pattern seen in the B₁⁺ map, indicating that omitting the estimation of B₁⁺ influences the estimation of the T₁ values. The estimated T₁ values as determined by DESPOT1 can be seen in Figure 8 as well. Here, some very clear B₁⁺-related artifacts are visible, which lead to reduced T₁ values.

FIGURE 8.

In vivo M₀-weighted, (top row) quantitative T₁ (middle row) and quantitative B₁⁺ (bottom row) maps of volunteer 4, as estimated by four different reconstruction methods. The first two columns correspond to the 3D MRF sequence with the normal ordering and the motion-robust ordering, respectively, as in Figure 7. For the third column, the motion-robust ordering was used, but the relative B₁⁺ value in the dictionary was fixed to 1. The top figure in the fourth column shows the estimated T₁ map from the DESPOT1 sequence. Notice the severe B₁⁺ artifacts when using this last method. The bottom figure in the fourth column shows the difference map between the T₁ maps when using the motion-robust ordering, with and without fixing B₁⁺ during matching. Notice that the difference map resembles the B₁⁺ pattern

Figure 9 shows the estimated parameter maps for volunteer 6 at a higher resolution. Since the number of shots was increased from three to five to keep the signal-to-noise ratio (SNR) sufficiently high, the acquisition time increased as well. However, the higher resolution reveals the differences between the two orderings schemes.

FIGURE 9.

In vivo quantitative M₀ (top row), T₁ (middle row) and B₁⁺ (bottom row) maps of volunteer 6, at a resolution of 1.3 mm × 1.3 mm × 3.0 mm (left two columns) and 1.0 mm × 1.0 mm × 3.0 mm (right two columns). Each image consists of an axial, a coronal and a sagittal view. Notice the motion artifacts when using the normal ordering at both resolutions

4 ∣. DISCUSSION

In this work, we have demonstrated a 3D MRF sequence for free-breathing abdominal T₁ mapping. In addition, small effects of excitation field inhomogeneities were accounted for by including B₁⁺ in the parameter estimation. Note that receive sensitivities and T₂* effects are included in the M₀ maps besides the proton density, as these quantities cannot be estimated separately using our method. Therefore, we refer to them as M₀-weighted images, instead of quantitative M₀ maps.

Both phantom and in vivo scans showed that motion artifacts are reduced when using the motion-robust ordering. Because the MR signal in an MRF experiment is not in steady state, the signal intensity within each set is not constant in the partition direction when using the motion-robust ordering scheme. An additional constraint could be added to the optimization problem to enforce signal smoothness. However, the absence of such a constraint did not result in significant artifacts in the parameter maps when using the motion-robust ordering.

All optimized flip angle trains included a segment without any data acquisition. Other MRF implementations used a delay time between flip angle segments^6,16 to allow the magnetization to recover. In this work, the delay time was not set explicitly. Instead, the total time of data acquisition was set by determining the number of TRs. The optimization algorithm could thus find the optimal compromise between delay time and data acquisition. In particular, when using more TRs, the optimization resulted in longer delays.

When optimizing the three shortest sequences (300, 600 and 900 TRs), the same optimal objective value was reached for the majority of the 20 different random initializations. By contrast, the longest sequence (1800 TRs) was more affected by local minima in the optimization. This might indicate that this sequence could be optimized even further by increasing the number of initializations. However, it is important to note that the goal of the sequence optimization was not to find the most optimal sequence, but instead to get more time-efficient sequences, which is achieved even when the optimization reaches a local minimum.

One important thing to note is that the phantom was moved at different speeds, but not all speeds showed the motion artifacts when using the normal ordering (Figures S1-S8). This was probably caused by interference between the motion pattern and the timing of the sequence, which repeats the flip angle train every few seconds (the exact duration depends on the number of flip angles in the sequence). In other words, if the phantom happens to be in the same place at the start of each flip angle train, the motion artifacts are minimal. However, human subjects have a wide range of breathing frequencies. Moreover, these breathing rhythms can be irregular. Consequently, as demonstrated in the in vivo scan, the proposed motion-robust ordering is important to prevent motion artifacts.

Different sequence lengths were compared using the moving phantom. Shorter sequences are less flexible in their encoding but are faster to acquire per repetition. To compare different sequence lengths, we used more shots (and thus more repetitions) for shorter sequences to keep the total acquisition time constant. For the shortest sequence, the parameter estimations were less accurate, especially for the tubes with longer T₁ values. Most likely, the duration of one repetition was too short to observe the slow dynamics of the long T₁ samples. By increasing the sequence length to 600 and 900 TRs, the estimated quantitative values were improved when using the motion-robust ordering. For the longest sequence with 1800 TRs, however, the accuracy decreased again, presumably because the undersampling artifacts were more pronounced in the reconstructed images due to the lower number of shots. We found an optimal compromise between encoding capability and acquisition speed around 600 TRs, corresponding to a 3000-ms interval between two inversion pulses. Note that our optimization routine sets some of these flip angles to zero to create delays.

Besides the change in acquisition ordering, there is an additional difference between the normal ordering and the motion-robust ordering. In order to be able to perform a Fourier transform in the partition direction, the data need to be grouped together into sets for the motion-robust ordering. To investigate what effect this has on the parameter maps, we reconstructed the normal-ordering dataset while also grouping together sets of 30 successive TR indices (Figure S11). The differences in the resulting parameter maps were only minor, suggesting that most of the differences between the two ordering schemes are caused by the change in k-space ordering, and not by taking together the data of several readouts during the Fourier transform. In addition, we performed a simulation experiment to investigate the difference in matching error for small T₁ values (Figure S12). This analysis showed that there is no noticeable difference in the resulting error, whether the fingerprints were averaged or not.

The volunteers in this study were instructed to breathe normally. We acquired one additional dataset for one volunteer, who we asked to breathe deeply (Figure S13). Although the quality of the resulting maps is still acceptable, we do expect that our method will break down when the subject has irregular breathing or has unexpected motion such as hiccups.

Although considerable effort went into optimizing the sequence, there is still room for further improvements. It is possible that the insertion of inversion or saturation pulses in the sequence could improve the encoding capability. Currently, the optimization algorithm is unable to do this, since the peak flip angle is limited to 60 degrees to account for the peak power the system can provide. Additionally, it could be investigated whether regularization could improve the optimization algorithm. For example, the signal differences within one set could be minimized by adding a term in Equation 4. These signal variations could act as a filter applied to the images,³⁶ and by making the fingerprint signals more smooth, the effect of this filter is reduced.^26,27 Furthermore, in this work only spoiled gradient echoes were used. The inclusion of fast imaging with steady-state precession (FISP) segments, as used before in MRF,^16,37 could add valuable clinical information. However, this would increase the complexity for both the dictionary construction and the optimization algorithm. Moreover, FISP segments are notoriously sensitive to motion.¹⁰ Finally, it is important to keep in mind that the CRLB assumes only white Gaussian noise on the data, while the data is also subject to radial undersampling artifacts. These artifacts are non-Gaussian and depend on both the parameter maps and the sequence parameters. Taking them into account during the sequence optimization could result in better sequences.^38,39

Besides the sequence itself, the reconstruction process could be improved as well. Low-rank methods⁴⁰ or parallel imaging techniques⁴¹ could be used to reduce the undersampling artifacts and improve the quantitative maps. These methods could also be used to increase the number of partitions, thereby increasing the field of view.

Changing the acquisition ordering is not the only method that can be used to reduce motion artifacts.⁴² The acquisition can be prospectively triggered to only acquire data at the same respiratory position. Alternatively, the data can be retrospectively binned into several respiratory phases. However, these methods will only address respiratory motion, and come at the cost of longer acquisition times or less available data, respectively. Another approach would be to actively correct the motion in the data, as has been done for rigid motion in brain MRF.^43-46 However, motion in the abdomen is nonrigid. Therefore, further studies will be needed to explore if such a motion-correction step is feasible in the abdomen.

The goal of this work was to introduce a new free-breathing MRF sequence. Additional studies will have to be performed to show the repeatability and reproducibility of our method, especially regarding the B₁⁺ maps, because it has not yet been compared quantitatively with other motion-robust mapping strategies.^47,48 Finally, to investigate the performance of the sequence with different pathologies, several clinical scans with patients will have to be performed as well.

5 ∣. CONCLUSION

A free-breathing MRF sequence was demonstrated for B₁⁺-robust quantitative abdominal T₁ mapping. Four different flip angle patterns were optimized. A movable phantom was used to validate the sequences. The flip angle train with 600 TRs provided the best trade-off between T₁-encoding power and sampling density. In vivo measurements confirmed the advantage of the motion-robust k-space ordering. With this free-breathing MRF implementation it is possible to collect crisp M₀-weighted images and clean T₁ maps of the abdomen at a clinically usable resolution within 5 min.

Abbreviations used:

B₁⁺

excitation field strength

COV

coefficient of variation

CRLB

Cramér–Rao Lower Bound

DESPOT1

driven equilibrium single pulse observation of T₁

DESPOT2

driven equilibrium single pulse observation of T₂

FFT

fast Fourier transform

FIM

Fisher information matrix

FISP

fast imaging with steady-state precession

FLASH

fast low angle shot

M₀

equilibrium magnetization

MRF

magnetic resonance fingerprinting

MRI

magnetic resonance imaging

NUFFT

nonuniform fast Fourier transform

ROI

region of interest

SNR

signal-to-noise ratio

T₁

longitudinal relaxation time

T₂

transverse relaxation time

TE

echo time

TR

repetition time