Spatiotemporal dynamics of EEG microstates in four- to eight-year-old children: Age- and sex-related effects

Abstract

The ultrafast spatiotemporal dynamics of large-scale neural networks can be examined using resting-state electroencephalography (EEG) microstates, representing transient periods of synchronized neural activity that evolve dynamically over time. In adults, four canonical microstates have been shown to explain most topographic variance in resting-state EEG. Their temporal structures are age-, sex- and state-dependent, and are susceptible to pathological brain states. However, no studies have assessed the spatial and temporal properties of EEG microstates exclusively during early childhood, a critical period of rapid brain development. Here we sought to investigate EEG microstates recorded with high-density EEG in a large sample of 103, 4–8-year-old children. Using data-driven k-means cluster analysis, we show that the four canonical microstates reported in adult populations already exist in early childhood. Using multiple linear regressions, we demonstrate that the temporal dynamics of two microstates are associated with age and sex. Source localization suggests that attention- and cognitive control-related networks govern the topographies of the age- and sex-dependent microstates. These novel findings provide unique insights into functional brain development in children captured with EEG microstates.

Highlights

• •Resting-state EEG microstates are stable periods of scalp potential topographies.
• •They reflect the activity of large-scale neural networks at the millisecond-level.
• •Age and sex relate to the temporal dynamics of two microstates during early childhood.
• •Their sources represent attention- and cognitive control-related networks.
• •Microstates provide unique insights into brain development during early childhood.

1. Introduction

Early childhood is a period of rapid brain development and behavioral change. Characterizing the developmental properties of network-based brain connectivity during early childhood is likely to critically inform our understanding of normative and atypical patterns of neurocognitive development. One electroencephalography (EEG) method that has emerged as highly useful for characterizing the spatiotemporal dynamics of large-scale brain networks is microstate analysis (for reviews, see Khanna et al., 2015; Michel and Koenig, 2018). EEG microstates (Lehmann et al., 1987) are patterns of scalp potential topographies that transition between each other every approximately 60–120 milliseconds (ms) and reflect transient periods of synchronized neural activity that evolve dynamically over time (Michel and Koenig, 2018). Importantly, recent research suggests that reliable estimates of microstates and their properties can be derived from just two minutes of EEG data (Liu et al., 2020); a critical advance when working with sensitive research groups that may find remaining still for prolonged periods of time very challenging, including young children and individuals with psychiatric conditions. Nevertheless, few studies to date have used this approach in children, and none have focused exclusively on children under the age of eight years. As a result, the potential to provide unique insights into brain development during the earliest years of life by combining the practical nature of EEG data collection with the analytical approach of microstate analysis remains largely unexplored.

Previous studies in older age groups using clustering methods have reported that four microstates – canonically labeled A–D – explain the majority of variance in the scalp potential topography of resting-state EEG (Michel and Koenig, 2018). Simultaneous EEG-functional magnetic resonance imaging (fMRI) studies as well as EEG source imaging have shown that the spatial patterns of these microstates resemble well-known resting-state networks (RSNs; e.g., microstate A representing auditory, B representing visual, C representing salience, and D representing attention networks) (Bréchet et al., 2019, Britz et al., 2010, Custo et al., 2017). Existing research indicates that rapid transitions between microstates reflect the dynamic reorganization of large-scale functional networks (Michel and Koenig, 2018, Ville et al., 2010). Importantly, the millisecond temporal resolution of EEG allows unique information about the temporal properties of each microstate to be quantified, including its global explained variance (GEV; i.e., percentage of total variance in the data explained by a given microstate), average duration, percentage of time for which it is present (i.e., coverage), and frequency of occurrence per second. As a result, prior studies support EEG microstate analysis as a novel method for measuring the spatiotemporal properties of network-based connectivity (Lehmann, 2010).

To date, only two studies have examined microstates in children (Koenig et al., 2002, Tomescu et al., 2018), neither of which included typically developing children under the age of six. In a cross-sectional study including participants 6–80 years old, Koenig et al. (2002) found no differences in the temporal parameters between the four canonical microstates in 6–12-year-olds, but comparatively shorter microstate A, B, and D and longer C durations in 12–16-year-olds. Microstates C and D occurred more frequently and had longer durations than microstates A and B in 12–16-year-olds (Koenig et al., 2002). In 16–21-year-olds, microstate C was the longest and occurred most frequently – an observation that remained in 21–80-year-olds – while D dropped in duration and occurrence (Koenig et al., 2002). Microstates A and B remained the shortest and least frequent in 21–80-year-olds but occurred more frequently than in 16–21-year-olds (Koenig et al., 2002). Tomescu et al. (2018) extended these findings by reporting sex effects in a cross-sectional sample of 6–87-year-olds. Males compared to females had shorter durations of microstate C. The duration of this microstate decreased from the 14–19-year-old period to the 20–30-year-old period in males only, during which males had shorter microstate C durations than females (Tomescu et al., 2018). Males compared to females had a higher occurrence of Microstate D, and this pattern was present in all age groups except during the 14–19-year-old period (Tomescu et al., 2018). However, Microstate D increased in frequency from the 14–19-year-old period to the 20–30-year-old period for both sexes (Tomescu et al., 2018). Together, these studies suggest age- and sex-related effects in the spatiotemporal dynamics of resting-state EEG across the lifespan, particularly in the duration and occurrence of microstates C and D. While supporting the developmental nature of microstates, neither study utilized source localization to determine the brain regions underlying each microstate. As a result, the significance of their findings on functional brain network organization and potential links with behavior in children remain unclear. Furthermore, both studies identified group-level microstates using all participants regardless of age. Thus, some important developmental variations in EEG microstate topographies and temporal dynamics that are specific to children may have been overlooked. Since the brain undergoes developmental changes in its functional organization, especially during early childhood (Brown and Jernigan, 2012; Johnson, 2011; Long et al., 2017), these variations may be particularly important.

The current study examined the spatiotemporal characteristics of EEG microstates and age and sex effects in a large group of 103, 4–8-year-old children using high-density EEG collected during eyes-closed rest. Given our use of a data-driven method for identifying microstates (Bréchet et al., 2019, Custo et al., 2017) and the absence of microstate research in young children, we did not make group-level predictions about the number of microstates that would be present, their topographies, or whether the temporal parameters would differ between microstates. However, we expected that the temporal parameters would change with increasing age and show sex differences (Tomescu et al., 2018), although we did not make specific hypotheses regarding the directionality of effects. We also localized the sources of the microstates and expected them to resemble well-established RSNs captured with fMRI or EEG given previous findings in older groups (Bréchet et al., 2019, Britz et al., 2010, Custo et al., 2017). Since the development of cognitive functions is prolonged in children, we expected larger age and sex effects for microstates resembling networks involved in higher-order cognitive functions and network integration compared to microstates resembling motor and sensory networks (Bie et al., 2012).

2. Methods

2.1. Participants

Participants were children 4–8 years of age recruited from a database maintained by the Department of Psychology and Neuroscience at Duke University and community events. Recruitment details, including inclusion/exclusion criteria, are provided in the Supplementary materials. After screening 323 children, 249 were eligible. Of these, 171 children completed their first study visit. Resting-state EEG was added to the study approximately halfway through data collection. The number of eligible children who participated at a time when EEG was part of the study protocol was 140. Thirty-two children did not complete EEG because they were noncompliant (e.g., refused to wear the EEG net). In sum, 108 participants completed an EEG session at either their first or second study visit and 103 of them provided adequate data for analyses (see below). Data collection for the final sample of 103 participants occurred between April 2019 and June 2021. All research was approved by Duke University’s Institutional Review Board and carried out in accordance with the Declaration of Helsinki. Caregivers provided informed consent and children provided verbal assent. Compensation was provided for study participation. Participant demographics are described in Table 1.

Table 1.

Participant demographics.

	Mean (SD)	Range
Age (years)	6.37 (1.07)	4.51–8.65
Income-to-Needs Ratio	3.04 (1.03)	0.15–4.69
	n	Percent (%)
Biological Sex
Females	58	56.31
Males	45	43.69
Race
White	77	74.76
Mixed	15	14.56
Black or African American	7	6.80
Asian	2	1.94
Other	2	1.94
Native Hawaiian or Other Pacific Islander	0	0
Ethnicity
Not Hispanic or Latino	91	88.35
Hispanic or Latino	12	11.65
Maternal Education
High School Diploma or GED	1	0.97
Some College	15	14.56
Graduated 2-Year College	10	9.71
Graduated 4-Year College	33	32.04
Part Graduate or Professional School	4	3.88
Graduated from Graduate or Professional School	40	38.83

Note. The Income-to-Needs Ratio was calculated by dividing total family income by a poverty threshold determined by the United States Census Bureau, which considered the year assessed and household family size.

2.2. EEG data acquisition and preprocessing

EEG was recorded using a 128-channel HydroCel Geodesic Sensor Net (Electrical Geodesics, Eugene, OR) at 1000 Hertz (Hz), referenced online to the vertex. Impedances were maintained below 50 kilohms throughout the paradigm, which consisted of eight one-minute blocks of alternating eyes-open and eyes-closed resting-state (i.e., four minutes of each condition). Verbal cues given by the experimenter and text displayed through E-Prime software (Psychological Software Tools, Pittsburgh, PA) instructed participants to relax with their eyes open or closed. Following previous research (e.g., Tomescu et al., 2018), only the eyes-closed condition was analyzed for the current study.

Offline preprocessing was performed with MATLAB (The MathWorks Inc, Natick, MA) and EEGLAB (Delorme and Makeig, 2004) using custom scripts available on https://github.com/DEEDLabEEG. Detailed steps are provided in the Supplementary materials. Briefly, channels located on the outer ring of the EEG net were removed. Data were downsampled to 250 Hz, low-pass filtered at 40 Hz, and high-pass filtered at 1 Hz. Remaining electrical line noise at 60 Hz was attenuated using the CleanLine plugin (Mullen, 2012). Bad channels were removed if they 1) were flat for more than five seconds, 2) contained more than four standard deviations of line noise relative to their signal, or 3) correlated at less than .8 to an estimate based on nearby channels. Artifact Subspace Reconstruction (ASR) removed portions of data containing artifacts (Mullen et al., 2015). Additional data periods were removed if more than 25% of channels’ power exceeded seven standard deviations. Independent component analysis (ICA; Lee et al., 1999) with principal component analysis (30 components) was performed, and the ICA matrix was copied over to the full-length data (i.e., before ASR removed artifacted portions). The ICLabel plugin (Pion-Tonachini et al., 2019) removed components with a probability greater than .7 of being eye or muscle artifacts. Data were segmented into nonoverlapping one-second epochs and removed using the TBT plugin (Ben-Shachar, 2018) if at least 10 channels had 1) amplitudes greater than 100 microvolts (μV) or less than − 100 μV, or 2) joint probabilities above three standard deviations for local/global thresholds. If less than 10 channels met rejection criteria, the epoch was not removed, but the channels were interpolated for that epoch only. Lastly, channels removed previously were interpolated using spherical splines, and all channels were re-referenced to the average.

After preprocessing and removing five participants whose data did not pass quality control (see Supplementary Table 1), the minimum amount of data across 103 participants was 145 seconds (s). To reduce potential effects of varying data lengths across participants on further analyses, data for all participants were trimmed to their first 145 s, exceeding the previously published two-minute mark for the reliability of microstate analysis (Liu et al., 2020).

2.3. Microstate analysis

Microstate analysis was performed with Cartool (Brunet et al., 2011), first at the individual-level and then at the group-level. At the individual-level, a spatial filter (Michel and Brunet, 2019) was applied to each participant’s EEG data to remove topographic outliers and smooth topographies. For each participant’s EEG data, topographies at global field power (GFP) peaks representing timepoints of the highest signal-to-noise ratio (Brunet et al., 2011) were extracted. Fifty epochs of 833 random subsamples of each participant’s previously extracted GFP peaks (covering 99.9% of each participant’s data) were submitted to a polarity-invariant modified k-means cluster analysis (Pascual-Marqui et al., 1995), which was set to repeat 50 times and identify 1–12 clusters of topographies for each epoch. A meta-criterion, an aggregate measure of seven independent criteria (Bréchet et al., 2019, Custo et al., 2017), then determined the optimal number of clusters for each epoch, resulting in 50 epochs each composed of k optimal clusters.

At the group-level, the 50 sets of optimal clusters from each participant identified in the individual-level analysis were combined resulting in 5150 sets (103 participants × 50 sets). Next, 100 epochs each composed of 1500 randomly sampled sets (covering 99.7% of the sets) were submitted to a polarity-invariant modified k-means cluster analysis, which was set to repeat 100 times and identify 1–15 clusters of topographies for each epoch. The meta-criterion determined the optimal number of clusters for each epoch, resulting in 100 epochs each composed of k optimal clusters. Lastly, these 100 sets were combined and submitted to a final polarity-invariant modified k-means cluster analysis, which was set to repeat 100 times and identify 1–15 clusters of topographies. The meta-criterion determined the optimal number of clusters, now referred to as the group-level microstates. The resampling approach is thought to improve the reliability of k-means clustering and has been used in recent work (Férat et al., 2022).

These microstates were backfitted to each participant’s original spatially filtered data, including all data points (not just at GFP peaks). The data was normalized by the median of GFP to account for individual differences in scalp potential due to varying skull conductivity. Backfitting involved calculating the spatial correlation between each microstate at the group-level and each individual data point for each participant, such that the microstate with the highest correlation was assigned to that data point. The polarity of maps was ignored when calculating the correlation. The minimum correlation for data points assigned to a microstate was 50%. After backfitting, temporal smoothing (window half-size of 32 ms, Besag factor of 10; Pascual-Marqui et al., 1995) was applied, and the removal of improbably small segments, such that segments smaller than 32 ms were divided in half with the first half added to the preceding segment and the second half added to the following segment. The backfitting procedure produced values of each microstate’s GEV, duration, coverage, and occurrence.

2.3.1. Source localization of microstates

Six thousand solution points were distributed equally in a grey matter-constrained head model of a child MRI brain volume template. The EEG net template was co-registered to the MRI head model. The Local Spherical Model with Anatomical Constraints (LSMAC; Brunet et al., 2011) calculated an adaptive local spherical model at each electrode by estimating the thicknesses of the scalp, skull, cerebrospinal fluid, and brain under each electrode. These thicknesses were then used in a 4-shell spherical model with local radiuses, allowing the real geometry between solution points and electrodes to be accounted for. A distributed linear inverse solution, LORETA (Low Resolution Brain Electromagnetic Tomography; Pascual-Marqui et al., 1994), was calculated. The results were optimized with regularization, which accounted for background EEG noise and enforced smoothness of the results, and were standardized to correct for the variability of EEG power across time (these procedures are automatically implemented in Cartool and described in Michel and Brunet, 2019). The amplitude of dipoles was saved as scalar, positive values at each solution point and averaged across timepoints for each microstate.

Each microstate’s source map was thresholded to the solution points above the 95th percentile of activations across participants (Bréchet et al., 2020, Bréchet et al., 2021). Source maps were converted to volumes and imported to the Analysis of Functional NeuroImages (AFNI; Cox, 1996) program. In AFNI, they were demeaned by subtracting the mean of all source maps from each source map to highlight microstate-specific sources (Custo et al., 2017). Additional information is provided in the Supplementary Materials.

2.4. Statistical analyses

Statistical analyses were conducted in R (R Core Team, 2021) and conceptualized as exploratory. Four one-way, repeated-measures, equal-n, Type II sum of squares, analysis of variance (ANOVA) models were computed to compare the mean of each temporal parameter (GEV, duration, coverage, occurrence) between microstates. Extreme outliers were determined using boxplots; values above Quartile 3 + 3 *IQR or below Quartile 1–3 *IQR (IQR = Interquartile Range) were identified and removed for each ANOVA. If the assumption of sphericity was violated according to Mauchly’s test, the Greenhouse-Geisser correction was applied. For each statistically significant ANOVA, post-hoc paired t-tests were performed between microstates, and p values were Benjamini-Hochberg-corrected for 24 comparisons (Benjamini and Hochberg, 1995). We also calculated estimation statistics-based effect sizes and confidence intervals (CIs) using the DABEST package (Bernard, 2019, Claridge-Chang and Assam, 2016, Ho et al., 2019). Effect sizes were calculated as the paired mean difference between comparisons. Bias-corrected, accelerated 95% CIs of the paired mean differences were calculated by performing nonparametric bootstrap resampling (5000 resamples).

Next, separate multiple linear regressions with each microstate’s temporal parameter as the dependent variable and mean-centered age, dummy coded sex (males = − 1, females = 1), and an age by sex interaction term as the independent variables were computed (Kraemer and Blasey, 2004). Multivariate outliers were determined by the Minimum Covariance Determinant for each regression separately and removed (Rousseeuw and Driessen, 1999). To minimize the rate of type I errors, p values for the omnibus F test of the overall significance of the complete set of predictors were Benjamini-Hochberg-corrected for 16 comparisons. Statistically significant interactions were explored by testing whether the slope of age predicting the microstate’s temporal parameter was significant for each sex, and the Johnson-Neyman procedure was used to determine at which age(s) the simple slope of sex significantly differed from zero at p < .05 (Johnson and Neyman, 1936).

3. Results

The meta-criterion for determining the optimal number of microstates revealed four microstates labeled 1–4 (Fig. 1). In previous literature, microstates 1–3 correspond to the canonical A–C, respectively (Michel and Koenig, 2018). The topography of microstate 4 is less consistent in the previous literature; some studies show a fronto-central maximum while others show a posterior-central maximum (Michel and Koenig, 2018). Three-dimensional views of each microstate and spatial correlations between their topographies are presented in Supplementary Fig. 1 and 2, respectively. A mean of 3.40 s of data (SD = 1.76 s) across participants did not meet the minimum spatial correlation threshold of 50% during backfitting to be assigned a microstate. Descriptive statistics of the temporal parameters of the microstates are provided in Table 2.

Fig. 1.

The four microstates. Note. Microstates were derived from a polarity-invariant clustering algorithm.

Table 2.

Descriptive statistics of the temporal parameters of the four microstates.

	Microstate 1	Microstate 2	Microstate 3	Microstate 4
GEV
Mean (SD)	.09 (.03)	.16 (.05)	.28 (.08)	.06 (.03)
Range	.02–.16	.06–.36	.11–.50	.004–.16
Duration (ms)
Mean (SD)	78.82 (4.59)	85.52 (6.97)	100.52 (10.95)	74.16 (5.91)
Range	67.82–94.81	74.23–111.86	77.83–136.40	58.22–87.46
Coverage (%)
Mean (SD)	19.78 (4.13)	27.00 (5.94)	38.97 (7.95)	14.26 (5.49)
Range	9.63–30.72	13.63–48.86	19.20–58.41	2.15–29.19
Occurrence (per s)
Mean (SD)	2.18 (0.33)	2.68 (0.36)	3.16 (0.31)	1.68 (0.53)
Range	1.14–2.82	1.63–3.45	2.14–3.71	0.35–2.99

3.1. Between-microstate differences in the means of their temporal parameters

Differences in the means of GEV, duration, coverage, and occurrence between the four microstates were examined using one-way repeated-measures ANOVAs with post-hoc contrasts Benjamini-Hochberg-corrected for 24 comparisons. The results of all models with outliers excluded are presented in Fig. 2 and reported below. Estimation statistics-based effects sizes and 95% CIs were also calculated and are provided in Fig. 2. Models with outliers included are shown in the Supplementary Materials.

Fig. 2.

Violin- and box-plots (left) and paired mean difference estimates plots (right) show differences in the means of the temporal parameters between microstates. Note. All post-hoc combinations of ANOVA comparisons were significant at p < .0001, Benjamini-Hochberg-corrected for 24 multiple comparisons. Vertical bars in the paired mean difference estimates plots represent the 95 % confidence interval of the paired mean difference estimates; numerical values are presented as the paired mean difference value [95 % confidence interval]. M1 = Microstate 1; M2 = Microstate 2; M3 = Microstate 3; M4 = Microstate 4.

3.1.1. GEV

There was a significant difference in the mean GEV between microstates, F(1.78, 182.03) = 295.16, p < .0001, η²_g = 0.74. Planned post-hoc contrasts revealed that microstate 1 GEV was lower than microstate 2 GEV, t(102) = − 11.24, p < .0001, and microstate 3 GEV, t(102) = − 21.13, p < .0001, but higher than microstate 4 GEV, t(102) = 7.34, p < .0001. Microstate 2 GEV was lower than microstate 3 GEV, t(102) = − 11.05, p < .0001, but higher than microstate 4 GEV, t(102) = 16.03, p < .0001. Microstate 3 GEV was higher than microstate 4 GEV, t(102) = 22.72, p < .0001.

3.1.2. Duration

There was a significant difference in the mean duration between microstates, F(1.99, 199.48) = 219.72, p < .0001, η²_g = 0.66. Planned post-hoc contrasts revealed that microstate 1 duration was lower than microstate 2 duration, t(100) = − 8.09, p < .0001, and microstate 3 duration, t(100) = − 17.71, p < .0001, but higher than microstate 4 duration, t(100) = 6.91, p < .0001. Microstate 2 duration was lower than microstate 3 duration, t(100) = − 10.56, p < .0001, but higher than microstate 4 duration, t(100) = 12.65, p < .0001. Microstate 3 duration was higher than microstate 4 duration, t(100) = 19.95, p < .0001.

3.1.3. Coverage

There was a significant difference in the mean coverage between microstates, F(2.26, 230.88) = 241.56, p < .0001, η²_g = 0.70. Planned post-hoc contrasts revealed that microstate 1 coverage was lower than microstate 2 coverage, t(102) = − 9.62, p < .0001, and microstate 3 coverage, t(102) = −18.85, p < .0001, but higher than microstate 4 coverage, t(102) = 7.98, p < .0001. Microstate 2 coverage was lower than microstate 3 coverage, t(102) = − 9.86, p < .0001, but higher than microstate 4 coverage, t(102) = 14.72, p < .0001. Microstate 3 coverage was higher than microstate 4 coverage, t(102) = 21.21, p < .0001.

3.1.4. Occurrence

There was a significant difference in the mean occurrence between microstates, F(2.48, 253.13) = 234.49, p < .0001, η²_g = 0.67. Planned post-hoc contrasts revealed that microstate 1 occurrence was lower than microstate 2 occurrence, t(102) = − 10.28, p < .0001, and microstate 3 occurrence, t(102) = − 20.99, p < .0001, but higher than microstate 4 occurrence, t(102) = 8.13, p < .0001. Microstate 2 occurrence was lower than microstate 3 occurrence, t(102) = − 9.12, p < .0001, but higher than microstate 4 occurrence, t(102) = 14.49, p < .0001. Microstate 3 occurrence was higher than microstate 4 occurrence, t(102) = 21.01, p < .0001.

3.2. Age and sex effects of each microstate’s temporal parameters

The extent to which each microstate’s four temporal parameters could be predicted by age, sex, and age by sex interaction was examined using multiple linear regression models, Benjamini-Hochberg-adjusted for 16 comparisons at the level of the overall model. For interpretability, age values for Johnson-Neyman intervals are reported in years and only within the range of observed values in the sample. The results of models with outliers excluded are summarized in Table 3 and described below. Models with outliers included are presented in Supplementary Table 2.

Table 3.

Regressions examining age and sex effects of each microstate’s temporal parameters.

	GEV				Duration				Coverage				Occurrence
Variable	B	SE B	β	p	B	SE B	β	p	B	SE B	β	p	B	SE B	β	p
Microstate 1	F(3, 99) = 2.13, R2 = .03, p = .18				F(3, 98) = 0.99, R2 = − .0002, p = .49				F(3, 99) = 1.92, R2 = .03, p = .21				F(3, 98) = 3.34, R2 = .06, p = .06
(Intercept)	0.09	0.003	–	< 0.001***	78.61	0.43	–	< 0.001***	19.66	0.41	–	< 0.001***	2.18	0.03	–	< 0.001***
Age	0.003	0.003	0.10	.30	0.48	0.41	0.12	.24	0.31	0.38	0.08	.42	0.02	0.03	0.07	.46
Sex	0.01	0.003	0.21	.03*	0.40	0.43	0.09	.36	0.90	0.41	0.22	.03*	0.09	0.03	0.30	.003**
Age * Sex	-0.002	0.003	-0.08	.40	0.26	0.41	0.06	.53	-0.20	0.38	-0.05	.60	-0.01	0.03	-0.03	.78
Microstate 2	F(3, 98) = 0.41, R2 = − .02, p = .80				F(3, 95) = 0.47, R2 = − .02, p = .80				F(3, 98) = 0.28, R2 = − .02, p = .84				F(3, 99) = 1.01, R2 = .0003, p = .49
(Intercept)	0.16	0.005	–	< 0.001***	84.71	0.60	–	< 0.001***	26.79	0.56	–	< 0.001***	2.68	0.04	–	< 0.001***
Age	-0.002	0.004	-0.04	.73	0.62	0.55	0.12	.26	0.02	0.53	0.004	.97	-0.03	0.03	-0.09	.37
Sex	0.002	0.005	0.05	.64	-0.19	0.58	-0.03	.74	0.05	0.56	0.01	.93	-0.01	0.04	-0.02	.83
Age * Sex	-0.004	0.004	-0.09	.38	0.002	0.55	0.0003	.998	-0.48	0.53	-0.09	.37	-0.04	0.03	-0.13	.20
Microstate 3	F(3, 98) = 1.82, R2 = .02, p = .22				F(3, 97) = 4.46, R2 = .09, p = .046*				F(3, 99) = 2.97, R2 = .05, p = .08				F(3, 92) = 2.18, R2 = .04, p = .18
(Intercept)	0.28	0.01	–	< 0.001***	100.27	0.97	–	< 0.001***	39.24	0.77	–	< 0.001***	3.22	0.02	–	< 0.001***
Age	0.01	0.01	0.08	.41	1.40	0.91	0.15	.13	0.61	0.72	0.08	.41	-0.03	0.02	-0.14	.17
Sex	-0.01	0.01	-0.21	.04*	-3.20	0.97	-0.32	.001**	-2.18	0.77	-0.27	.005**	-0.03	0.02	-0.16	.12
Age * Sex	-0.01	0.01	-0.07	.46	-0.19	0.91	-0.02	.83	-0.39	0.72	-0.05	.59	-0.02	0.02	-0.12	.23
Microstate 4	F(3, 97) = 3.77, R2 = .08, p = .046*				F(3, 99) = 3.70, R2 = .07, p = .046*				F(3, 99) = 3.95, R2 = .08, p = .046*				F(3, 99) = 3.84, R2 = .08, p = .046*
(Intercept)	0.06	0.003	–	< 0.001***	74.08	0.57	–	< 0.001***	14.13	0.52	–	< 0.001***	1.67	0.05	–	< 0.001***
Age	-0.004	0.003	-0.15	.14	-0.19	0.53	-0.03	.72	-0.69	0.49	-0.14	.17	-0.07	0.05	-0.15	.13
Sex	0.01	0.003	0.20	.04*	0.67	0.57	0.11	.24	1.04	0.52	0.19	.049*	0.11	0.05	0.20	.03*
Age * Sex	0.01	0.003	0.23	.02*	1.66	0.53	0.30	.002**	1.31	0.49	0.26	.009**	0.11	0.05	0.23	.02*

Note. The denominator or error degrees of freedom for each model varies because observations flagged as outliers were removed (i.e., the sample size for each model varies). R² values were adjusted for three predictors. Full model p values were Benjamini-Hochberg-corrected for 16 comparisons, but p values at the predictor-level were not corrected:

^*p < .05.

^**p < .01.

^***p < .001.

3.2.1. Microstates 1 and 2

The complete set of predictors did not explain a significant proportion of the observed variation in either microstate 1 or 2 GEV, duration, coverage, or occurrence.

3.2.2. Microstate 3

The complete set of predictors explained a significant proportion of the observed variation in microstate 3 duration, with an effect size of Cohen’s f² = .10. The main effect of sex was significant, with males having a higher microstate 3 duration than females, t(97) = −3.32, p = .001, 95 % CI [− 5.12, − 1.29]. Neither age, t(97) = 1.53, p = .13, 95 % CI [− 0.41, 3.21], nor the age by sex interaction, t(97) = − 0.21, p = .83, 95 % CI [− 2.01, 1.62], was significant. The complete set of predictors did not explain a significant proportion of the observed variation in microstate 3 GEV, coverage, or occurrence.

3.2.3. Microstate 4

The complete set of predictors explained a significant proportion of the observed variation in all temporal parameters of microstate 4:

For GEV, the effect size was Cohen’s f² = .09 (Fig. 3a). The main effect of sex was significant, t(97) = 2.13, p = .04, 95 % CI [0.0004, 0.01], but the main effect of age was not, t(97) = − 1.50, p = .14, 95 % CI [− 0.01, 0.001]. These main effects were qualified by the presence of a significant age by sex interaction, t(97) = 2.37, p = .02, 95 % CI [0.001, 0.01]. Post-hoc analyses revealed the slope of age predicting microstate 4 GEV was significant and negative for males, t(97) = − 2.52, p = .01, 95 % CI[− 0.02, − 0.002], but nonsignificant for females, t(97) = 0.68, p = .50, 95 % CI [− 0.004, 0.01]. The Johnson-Neyman procedure revealed that the simple slope of sex for the prediction of microstate 4 GEV was significantly different from zero at p < .05 when age was 6.32–8.65 years.

Fig. 3.

Statistically significant interactions between age and sex on the temporal parameters of microstate 4. Note. The shaded areas represent Johnson-Neyman regions of significance (i.e., the interval of ages for which the simple slope of sex significantly differed from zero at p < .05). Johnson-Neyman plots are provided in the Supplementary Materials.

For duration, the effect size was Cohen’s f² = .08 (Fig. 3b). Neither main effects of age, t(99) = − 0.35, p = .72, 95 % CI [− 1.25, 0.87], or sex, t(99) = 1.19, p = .24, 95 % CI [− 0.45, 1.79], were significant. These main effects were qualified by the presence of a significant age by sex interaction, t(99) = 3.11, p = .002, 95 % CI [0.60, 2.72]. Post-hoc analyses revealed the slope of age predicting microstate 4 duration was significant and negative for males, t(99) = −2.24, p = .03, 95 % CI[− 3.48, − 0.21], but significant and positive for females, t(99) = 2.16, p = .03, 95 % CI [0.12, 2.82]. The Johnson-Neyman procedure revealed that the simple slope of sex for the prediction of microstate 4 duration was significantly different from zero at p < .05 when age was either 4.51–4.70 years or 6.68–8.65 years.

For coverage, the effect size was Cohen’s f² = .09 (Fig. 3c). The main effect of sex was significant, t(99) = 1.99, p = .049, 95 % CI [0.003, 2.08], but the main effect of age was not, t(99) = − 1.40, p = .17, 95 % CI [− 1.67, 0.29]. These main effects were qualified by the presence of a significant age by sex interaction, t(99) = 2.66, p = .009, 95 % CI [0.33, 2.29]. Post-hoc analyses revealed the slope of age predicting microstate 4 coverage was significant and negative for males, t(99) = − 2.63, p = .01, 95 % CI[− 3.51, − 0.49], but nonsignificant for females, t(99) = 0.99, p = .33, 95 % CI [− 0.63, 1.87]. The Johnson-Neyman procedure revealed that the simple slope of sex for the prediction of microstate 4 coverage was significantly different from zero at p < .05 when age was 6.38–8.65 years.

For occurrence, the effect size was Cohen’s f² = .09 (Fig. 3d). The main effect of sex was significant, t(99) = 2.14, p = .03, 95 % CI [0.01, 0.21], but the main effect of age was not, t(99) = − 1.54, p = .13, 95 % CI [− 0.17, 0.02]. These main effects were qualified by the presence of a significant age by sex interaction, t(99) = 2.39, p = .02, 95 % CI [0.02, 0.21]. Post-hoc analyses revealed the slope of age predicting microstate 4 occurrence was significant and negative for males, t(99) = − 2.55, p = .01, 95 % CI[− 0.33, − 0.04], but nonsignificant for females, t(99) = 0.67, p = .51, 95 % CI [− 0.08, 0.16]. The Johnson-Neyman procedure revealed that the simple slope of sex for the prediction of microstate 4 occurrence was significantly different from zero at p < .05 when age was 6.31–8.65 years.

3.3. Sources of microstates

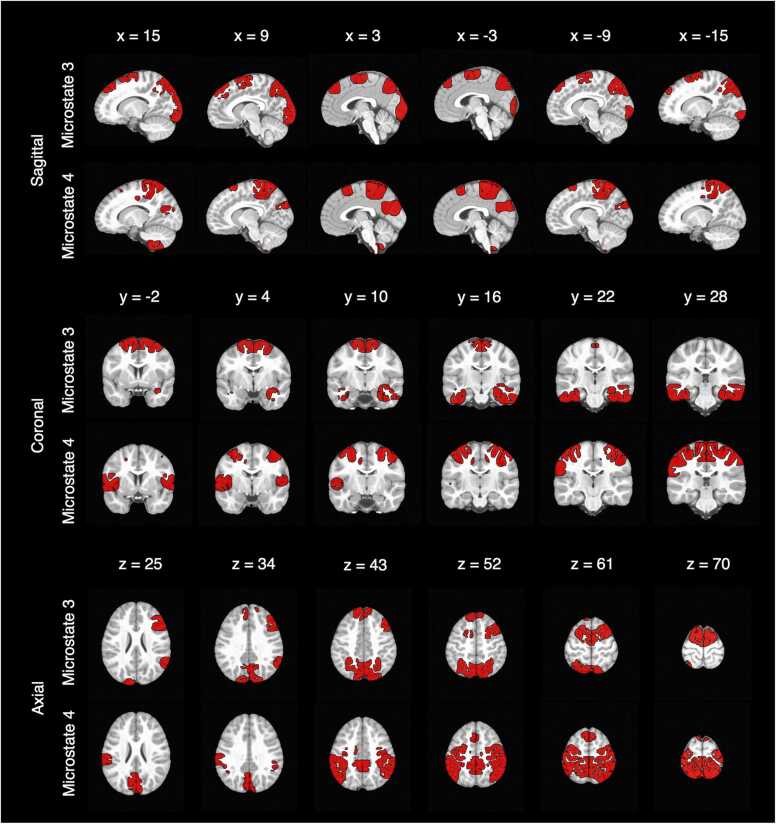
The sources of each of the four microstates were estimated and thresholded to the solution points above the 95th percentile of activations across participants. The mean of the four thresholded source maps (Supplementary Fig. 4) was subtracted from each of the source maps. The resulting cortical regions distinctly associated with each microstate are presented in Table 4. Given the observed relationships between age and sex on the temporal parameters of microstates 3 and 4, their sources are overlayed on an MRI in Fig. 4 (see Supplementary Figs. 5–8 for the sources of all the microstates).

Table 4.

Neural sources of the four microstates.

Microstate	Neural sources
Microstate 1	Left inferior temporal gyrus
	Bilateral middle temporal gyri
	Right superior temporal gyrus
	Right anterior & posterior cingulate cortex
	Right inferior & middle frontal gyri
	Bilateral superior & medial frontal gyri
	Bilateral inferior & middle occipital gyri
	Left superior occipital gyrus
	Bilateral fusiform gyri
	Bilateral rectal gyri
	Right orbital gyrus
	Right lingual gyrus
	Bilateral cuneus
	Right precuneus
	Right superior parietal lobule
	Bilateral precentral & postcentral gyri
	Bilateral paracentral lobules
Microstate 2	Bilateral superior & middle temporal gyri
	Right inferior temporal gyrus
	Left inferior frontal gyrus
	Bilateral middle frontal gyri
	Bilateral medial & superior frontal gyri
	Right superior & inferior occipital gyri
	Bilateral middle occipital gyri
	Bilateral inferior parietal lobules
	Left superior parietal lobule
	Bilateral fusiform gyri
	Left lingual gyrus
	Bilateral cuneus & precuneus
	Right anterior cingulate cortex
	Left supramarginal gyrus
	Right postcentral gyrus
Microstate 3	Bilateral inferior & middle temporal gyri
	Right superior temporal gyrus
	Bilateral parahippocampal gyri
	Bilateral fusiform gyri
	Bilateral lingual gyri
	Bilateral inferior & middle occipital gyri
	Bilateral supramarginal gyri
	Right inferior frontal gyrus
	Bilateral middle, medial, & superior frontal gyri
	Bilateral cuneus & precuneus
	Bilateral inferior and superior parietal lobules
Microstate 4	Bilateral superior temporal gyri
	Bilateral insula
	Bilateral inferior, middle, medial, & superior frontal gyri
	Bilateral cuneus & precuneus
	Bilateral posterior cingulate cortex
	Bilateral inferior & superior parietal lobules
	Bilateral supramarginal gyri
	Bilateral precentral & postcentral gyri
	Bilateral paracentral lobules

Note. Neural sources were determined visually with the assistance of the whereami? function and Talairach-Tournoux Atlas in AFNI (Cox, 1996). Sources in the cerebellum and deep brain (i.e., subcortical) structures were ignored due to the lack of established validity in measuring these sources with EEG.

Fig. 4.

Neural sources of Microstates 3 and 4. Note. Sagittal slices (x plane) are presented as left (positive coordinates) to right (negative coordinates) parts of the brain. Coronal slices (y plane) are presented as anterior (negative coordinates) to posterior (positive coordinates) parts of the brain. Axial slices (z plane) are presented as inferior to superior parts of the brain.

4. Discussion

The current study conducted a novel investigation of EEG microstates in a large sample of 4–8-year-old children using a data-driven method. As reported previously, four canonical microstates were replicated. Microstate 3 (canonical C) had the largest temporal parameters while microstate 4 (canonical D) had the smallest values relative to the other microstates (Koenig et al., 2002, Tomescu et al., 2018). In line with Tomescu et al. (2018), the temporal parameters of microstates 3 and 4 showed relationships with age and sex while those of microstates 1 (canonical A) and 2 (canonical B) did not. Microstate 3 duration was more prominent for males compared to females, and microstate 4 showed age by sex interactions for all its temporal parameters. The values of microstate 4 GEV, coverage, and occurrence decreased with increasing age for males but did not change with age for females. The values of microstate 4 duration decreased with age for males but increased with age for females. Post-hoc analyses revealed that the differences in the slopes of age between sexes changed from non-significant to significant at approximately 6.5 years across all microstate 4 models. Further, EEG source localization suggested observed effects potentially relate to attention- and cognitive control-related networks.

4.1. Four microstate topographies are present in young children

A four-microstate solution was the best fit for the EEG data in our sample of children, mirroring previous reports of four microstates in adults. These microstates each had a similar scalp potential topography as those previously reported in adults (see Fig. 3 in Michel and Koenig, 2018), suggesting that despite ongoing brain development in children, a similar global organization of scalp topographies exists between children and adults. This also suggests that, rather than large topographic changes in patterns of scalp potentials, it is their temporal parameters that change in children with development. This pattern of results parallels fMRI studies showing globally similar RSNs between children and adults, with differences largely seen in within- and between-network patterns of connectivity rather than network structure (Bie et al., 2012, Muetzel et al., 2016, Supekar et al., 2009).

4.2. Source localization of microstates suggests relationships with fMRI RSNs and provides insight into age and sex relationships with temporal parameters

Source localization indicated that the neural generators for microstate 3 partially overlap with regions of the dorsal frontoparietal network (D-FPN; Uddin et al., 2019). Commonly referred to as the “dorsal attention network,” the D-FPN is broadly involved in visuospatial attention and is thought to be responsible for goal-directed, top-down processing (Farrant and Uddin, 2015, Uddin et al., 2019, Yeo et al., 2011). Microstate 3 also revealed sources that partially overlap with regions of the lateral frontoparietal network (L-FPN), broadly involved in goal-directed control processes such as executive functions (Uddin et al., 2019). One subsystem within the L-FPN has been shown to preferentially connect to regions of the D-FPN and may be involved in the regulation of visuospatial attention and working memory performance (Dixon et al., 2018, Murphy et al., 2020). Portions of the D-FPN and L-FPN may underly the same microstate and support attentional orienting and control processes, which undergo a critical period of development during early childhood (Anderson, 2002, Rueda et al., 2005). As such, the observation that males had larger microstate 3 durations than females may signal a maturational difference in the development of attention and/or control systems between sexes. For example, at rest, males may spend more time in microstate 3 than females. However, the meaning of lower versus higher values of a particular microstate’s duration is not well understood; spending more or less time in certain states may be advantageous or disadvantageous. Taken together, more research is needed to better understand the underlying sources of microstate 3, whether these sources are different in children compared to adults, and the relationships between its temporal parameters and age and sex.

Source localization indicated that the neural generators for microstate 4 partially overlap with regions of the midcingulo-insular network (M-CIN), another control network broadly responsible for identifying salient information in line with current goals as well as for switching between the medial frontoparietal network (i.e., the default mode network or M-FPN) and the L-FPN (Goulden et al., 2014, Uddin et al., 2019). The M-CIN also includes the previously characterized “ventral attention” and “cingulo-opercular” networks, which are involved in directing attention to the spatial locations of salient stimuli and in set-maintenance activities, respectively (Corbetta and Shulman, 2002, Dosenbach et al., 2008, Uddin et al., 2019). The observation that the values of microstate 4 GEV, duration, coverage, and occurrence decreased with age for males but not females, except for duration, which increased with age for females, may indicate unique developmental trajectories in the activity of the M-CIN between 4–8-year-old males and females. In line with this hypothesis, the 4–8-year-old period is characterized by the rapid development of executive function and moderate-to-strong correlations between age and performance on executive function measures (Zelazo et al., 2008, Zelazo and Carlson, 2012). Sex differences in some executive functions may also exist during the same developmental period, but findings are mixed, with females outperforming males in some studies (Berlin and Bohlin, 2002, Carlson and Moses, 2001) and males outperforming females in others (Brocki and Bohlin, 2004). As such, the M-CIN may be undergoing sex-specific reorganization, particularly in the approximately 6.5–8-year-old period when the difference in the temporal parameters between sexes is most pronounced, paralleled by changes in executive function. While the plotted slopes of males and females diverged with increasing age in the current sample, it is also possible that a nonlinear pattern of development may be present over a longer period as network connections continue to be refined and shaped by experience. Further longitudinal research is necessary to address this question.

Lastly, as suggested by Tomescu et al. (2018), it is possible that microstates 1 and 2 did not show relationships with age and sex because they may represent RSNs involved in basic sensory functions that have robust functional organizations early in life. Britz et al. (2010) and Custo et al. (2017) both found that microstates 1 and 2 were related to networks responsible for auditory (i.e., pericentral network) and visual processing (i.e., occipital network), respectively. However, clear network-specific relationships were not evident in our source localization results. Since previous studies have only been performed with adults, it is plausible that the sources underlying microstates 1 and 2 found in the current study reflect ongoing patterns of neurobiological development and/or developmentally specific patterns of network relationships in young children reflecting current task demands (i.e., sit still with eyes closed). However, the present study cannot make this functional distinction, and future longitudinal work will be necessary.

4.3. Overlap of sources may reflect network flexibility and hub-like transition states

In addition to a developmental explanation, the overlap of sources and hypothesized underlying networks between microstates in the current study may reflect global brain dynamics. For example, using fMRI in adults, the M-CIN has been shown to have a stable yet highly flexible organization; functional interactions of this network are among the most spatially varied in the brain (Chen et al., 2016). Furthermore, this network may be a hub for facilitating flexible interactions across networks and has been shown to predict individual differences in cognitive flexibility (Chen et al., 2016). Another example of network flexibility comes from studies of the M-FPN, which have demonstrated its regions to dynamically switch community memberships, adapt a global configuration, and have a critical role in higher-order cognitive processing (Vatansever et al., 2015). As a result, the current source localization findings suggest that microstate analyses may similarly reflect dynamic patterns of changing connectivity between brain regions but at a finer temporal resolution. Additional studies should further investigate this possibility to determine if microstates could be used to study developmental changes in dynamic network connectivity.

Our findings also show that some sources (e.g., precuneus) are present in all microstates and may be hubs that support multiple brain networks. Although our microstate analysis backfitting procedure accounted for all the data, the first clustering stage was performed only on GFP peaks, failing to capture topographies during periods of microstate transitions. While these periods have lower GFP and signal-to-noise, they have been shown to have complex dynamics missed by routine microstate analysis (Shaw et al., 2019). It is possible that these periods reflect hub-like transition states whose sources leak into all microstates. Supporting this hypothesis, precision dynamical mapping of fMRI data at the single participant-level has revealed hub-like transition states represented by all RSNs equally (Saggar et al., 2021). Investigation of transition periods may provide a fuller understanding of the spatiotemporal dynamics captured by microstate analysis.

4.4. Strengths, limitations, and future directions

Our study, while cross-sectional, is the first to include typical children under the age of six years in a data-driven microstate analysis of resting-state EEG. With our large sample of 4–8-year-old children, we had enough variation in age to assess continuous relationships between microstate parameters and age and their interactions with sex, rather than group-level statistics between individuals grouped by specific ages. Furthermore, this is the first study to assess the underlying neural sources of microstates in children, offering promise for the utility of EEG microstates in studying functional brain development.

The lack of microstate research in typical children led this study to be exploratory rather than hypothesis-driven, and the results of this study should be interpreted with caution until replicated. The meaning of low versus high values of microstate temporal parameters is relatively unknown. Future longitudinal studies investigating the relationships between microstates and behavioral, cognitive, and clinical measures are needed to further understand the significance of the current findings for normative and atypical development.

Although source localization provides insight into the network of brain regions generating each microstate, the spatial resolution of EEG is markedly lower than fMRI. Still, the temporal resolution with which we can capture the spatiotemporal dynamics of brain activity provides unique and advantageous information that can further our developmental understanding of rapidly changing functional brain networks in children. Nevertheless, future use of individual MRI scans and EEG coordinate locations and multimodal EEG-fMRI studies may better assess the spatial overlap between EEG and fMRI RSNs.

The current study also has implications for understanding brain network development in children with psychopathology. The spatiotemporal dynamics of microstates are sensitive to psychopathology that emerges during early childhood, most notably autism spectrum disorder (ASD) and attention-deficit/hyperactivity disorder (ADHD). Interestingly, for example, prior research has identified differences in the temporal parameters of microstates C (resembling microstate 3) and D (resembling microstate 4) between children and adults with ASD or ADHD and typical controls (Das et al., 2021, D’Croz-Baron et al., 2019, Férat et al., 2021, Jia and Yu, 2019, Nagabhushan Kalburgi et al., 2020, Takarae et al., 2022). Our findings of age- and sex-related effects in the temporal parameters of these two microstates may be critical for understanding these observed differences in children with ASD and/or ADHD – which also have known sex differences in diagnosis – as well as in other forms of childhood psychopathology.

4.5. Conclusion

The current study reports novel age- and sex-related effects in the spatiotemporal dynamics of EEG microstates using a large sample of 4- to 8-year-old children. Matching previous reports in older samples, data-driven analyses indicated that a four-microstate solution best characterized resting-state EEG data at this young age. Further, using source localization techniques, we found support for attention- and control-related systems governing the topographies of age- and sex-dependent microstates. As a result, the current study provides unique insights into children’s functional brain development using the EEG microstates approach.

Data Statement

The data that support the findings of this study are available on request from the corresponding author. The data are not publicly available due to privacy or ethical restrictions.

Funding

This study was supported by the National Institute of Mental Health, USA (R01MH110488 to MSG).

CRediT authorship contribution statement

Bagdasarov: Conceptualization, Methodology, Software, Validation, Formal analysis, Data curation, Writing – original draft, Writing – review & editing, Visualization. Roberts: Software, Validation. Bréchet: Software, Validation, Writing – review & editing. Brunet: Software, Validation. Michel: Software, Validation, Writing – review & editing. Gaffrey: Conceptualization, Methodology, Resources, Writing – review & editing, Supervision, Funding acquisition.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary material

Supplementary material.

Data Availability

Data will be made available on request..