Domain-adaptive neural networks improve supervised machine learning based on simulated population genetic data

Abstract

Investigators have recently introduced powerful methods for population genetic inference that rely on supervised machine learning from simulated data. Despite their performance advantages, these methods can fail when the simulated training data does not adequately resemble data from the real world. Here, we show that this “simulation mis-specification” problem can be framed as a “domain adaptation” problem, where a model learned from one data distribution is applied to a dataset drawn from a different distribution. By applying an established domain-adaptation technique based on a gradient reversal layer (GRL), originally introduced for image classification, we show that the effects of simulation mis-specification can be substantially mitigated. We focus our analysis on two state-of-the-art deep-learning population genetic methods—SIA, which infers positive selection from features of the ancestral recombination graph (ARG), and ReLERNN, which infers recombination rates from genotype matrices. In the case of SIA, the domain adaptive framework also compensates for ARG inference error. Using the domain-adaptive SIA (dadaSIA) model, we estimate improved selection coefficients at selected loci in the 1000 Genomes CEU population. We anticipate that domain adaptation will prove to be widely applicable in the growing use of supervised machine learning in population genetics.

Introduction

Advances in genome sequencing have allowed population genetic analyses to be applied to many thousands of individual genome sequences (Auton et al. 2015; Sudlow et al. 2015; Karczewski et al. 2020). Given adequately rigorous and scalable computational tools for analysis, these rich catalogs of genetic variation provide opportunities for addressing many important questions in areas such as human evolution, plant genetics, and the ecology of non-model organisms. Deep-learning methods, already well-established in other application areas (LeCun et al. 2015), have proven to be good matches for these analytical tasks and have recently been successfully applied to many problems in population genetics (Sheehan and Song 2016; Kern and Schrider 2018; Schrider and Kern 2018; Flagel et al. 2019; Torada et al. 2019; Adrion et al. 2020; Caldas et al. 2022; Hejase et al. 2022; Korfmann et al. 2023).

The key to the success of deep learning in population genetics has been the use of large amounts of simulated data for training. Under simplifying, yet largely realistic, assumptions, evolution plays by relatively straightforward rules. By exploiting these rules and advances in computing power, a new generation of computational simulators has made it possible to efficiently produce extremely large (virtually unlimited) quantities of perfectly labeled synthetic data across a wide range of evolutionary scenarios (Haller et al. 2019; Haller and Messer 2019; Baumdicker et al. 2022). This synthetic training data serves as the foundation of the new simulate-and-train paradigm of supervised machine learning for population genetics inference (Fig. 1A, Schrider and Kern 2018^; Korfmann et al. 2023).

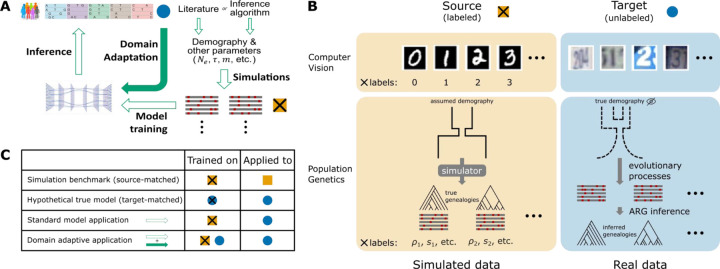
Figure 1. Unsupervised domain adaptation in the context of population genetic inference.

A) A high-level overview of the supervised machine-learning approach for population genetic inference and how domain adaptation fits into the paradigm. B) Example formulations of the unsupervised domain adaptation problem with application to computer vision and population genetics. C) Four benchmarking scenarios considered in this study. Gold squares represent source domain data, blue circles represent target domain data and crosses (x) represent labels.

At the same time, this paradigm is highly dependent on well-specified models for simulation (Korfmann et al. 2023). If the simulation assumptions do not match the underlying generative process of the real data—that is, in the presence of simulation mis-specification—the trained deep-learning model may reflect the biases in the simulated data and perform poorly on real data. Indeed, previous studies have shown that, despite being robust to mild to moderate levels of mis-specification, performance inevitably degrades when the mismatch becomes severe (Adrion et al. 2020; Hejase et al. 2022).

In a typical workflow, key simulation parameters such as the mutation rate, recombination rate, and parameters of the demographic model are either estimated from the data or obtained from the literature (e.g. Tennessen et al. 2012) (Fig. 1A). Sometimes these parameters are allowed to vary during simulation, and sometimes investigators evaluate the sensitivity of predictions to departures from the assumed range, but there is typically no way to ensure that the ranges considered are adequately large. Moreover, these benchmarks do not usually account for under-parameterization of the demographic model. Particularly in the case of non-model organisms, the quality of the estimates can be further limited by the availability of data. Overall, some degree of mis-specification in the simulated training data is impossible to avoid.

One way to mitigate the effects of simulation mis-specification would be to engineer a simulator to force the simulated data to be compatible with real data. For example, one could simulate from an overdispersed distribution of parameters followed by a rejection sampling step (based on summary statistics) as in Approximate Bayesian Computation (ABC) methods, or one could use a Generative Adversarial Network (GAN) (Wang et al. 2021) to mimic the real data. These methods tend to be costly, however. For example, ABC methods scale poorly with the number of summary statistics, and GANs are notoriously hard to train.

Here we consider the alternative approach of adopting a deep-learning model that is explicitly designed to account for and mitigate the mismatch between simulated and real data (Fig. 1A). As it happens, the task of building well-performing models for a target dataset that has a different distribution from the training dataset is a well-studied problem known as “domain adaptation” in the machine-learning literature (Csurka 2017; Wilson and Cook 2020). A typical setting of interest for domain adaptation is image classification (Fig. 1B). For example, suppose a digit recognition model is needed for the Street View House Numbers (SVHN) dataset (the “target domain”), but abundant labeled training data is only available from the MNIST dataset of handwritten digits (the “source domain”). In this case, a method needs to train on one data set and perform well on another, despite systematic differences between the two data distributions.

A variety of strategies for domain adaptation have been introduced. Early methods focused on reweighting training instances (Shimodaira 2000; Dai et al. 2007) or explicitly manipulating a feature space through augmentation (Daumé III 2009), alignment (Fernando et al. 2013; Sun et al. 2016) or transformation (Pan et al. 2011). Alternatively, domain adaptation can be incorporated directly into the process of training a neural network (deep domain adaptation). Most recent methods of this kind share the common goal of learning a “domain-invariant” representation of the data through a feature extractor neural network, for example, by minimizing domain divergence (Rozantsev et al. 2019), by adversarial training (Ganin and Lempitsky 2014; Liu and Tuzel 2016) or through an auxiliary reconstruction task (Ghifary et al. 2016). Domain adaptation so far has been most widely applied in the fields of computer vision (e.g., using stock photos for semantic segmentation of real photos) and natural language processing (e.g., using Amazon product reviews for sentiment analysis of movies and TV shows) where large, heterogeneous datasets are common but producing labeled training examples can be labor intensive (Wilson and Cook 2020). More recently, deep domain adaptation has been used in regulatory genomics to enable cross-species transcription-factor-binding-site prediction (Cochran et al. 2022).

In this work, we reframe the simulation mis-specification problem in population genetics as an unsupervised domain adaptation problem (unsupervised in the sense that data from the target domain is not labeled) (Fig. 1B). In particular, we use population-genetic simulations to obtain large amounts of perfectly labeled training data in the source domain. We then seek to apply the trained model to unlabeled real data in the target domain. We use domain adaptation techniques to explicitly account for the mismatch between these two domains when training the model.

To demonstrate the feasibility of this approach, we incorporated domain-adaptive neural network architecture into two published deep learning models for population genetic inference: 1) SIA (Hejase et al. 2022), which identifies selective sweeps based on the Ancestral Recombination Graph (ARG), and 2) ReLERNN (Adrion et al. 2020), which infers recombination rates from raw genotypic data. Through extensive simulation studies, we demonstrated that the domain adaptive versions of the models significantly outperformed the standard versions under realistic scenarios of simulation mis-specification. Our domain-adaptive framework for utilizing mis-specified synthetic data for supervised learning opens the door to many more robust deep learning models for population genetic inference.

Results

Experimental Design

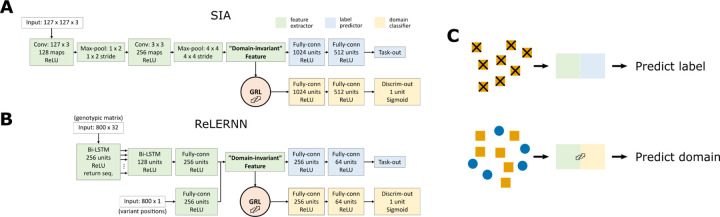
We created domain-adaptive versions of the SIA and ReLERNN models, each of which employed a gradient reversal layer (GRL) (Ganin and Lempitsky 2014) (Fig. 2A&B). As noted, the goal of domain adaptation is to establish a “domain-invariant” representation of the data (Fig. 1A). Our neural networks consist of two components: the original networks (in green and blue in Fig. 2A&B), which are applied to labeled examples from the “source” (simulated) domain; and alternative branches (in yellow in Fig. 2A&B), which use the same feature-extraction portions of the first networks but have the distinct goal of distinguishing data from the “source” (simulated) and “target” (real) domains (they are applied to both). By reversing the gradient for the second branch, the GRL systematically undermines this secondary goal of distinguishing the two domains (Fig. 2, see Methods for details), and therefore promotes domain invariance in feature extraction.

Figure 2. Neural network architecture for domain adaptation.

The model architectures incorporating gradient reversal layers (GRLs) for A) SIA and B) ReLERNN. C) When training the networks, each minibatch of training data consists of two components: (1) labeled data from the source domain fed through the feature extractor and the label predictor; and (2) a mixture of unlabeled data from both the source and target domains fed through the feature extractor and the domain classifier. The first component trains the model to perform its designated task. However, the GRL inverts the loss function for the second component, discouraging the model from differentiating the two domains and leading to the extraction of “domain-invariant” features.

We designed two sets of benchmark experiments to assess the performance of the domain-adaptive models relative to the standard models. In both cases, we tested the methods using “real” data in the target domain that was actually generated by simulation, but included features not considered by the simpler simulator used for the source domain. In the first set of experiments, background selection was present in the target domain but not the source domain. In the second set of experiments, the demographic model used for the source domain was estimated from “real” data generated under a more complex demographic model and was therefore somewhat mis-specified (see Methods and Fig. S1A for details). Below we refer to these as the “background selection” and “demography mis-specification” experiments.

Performance of Domain-Adaptive SIA Model

We compared the performance of the domain-adaptive SIA (dadaSIA) model to that of the standard SIA model on held-out “real” data, considering both a classification (distinguishing selective sweeps from neutrality) and a regression (inferring selection coefficients) task. In all cases, we focused on a comparison of the domain-adaptive model to the standard case where a model is simply trained on data from the source domain and then applied to the target domain (“standard model”; Fig. 1C). For additional context, we also considered the two cases where the training and testing domains matched (source-matched or target-matched; Fig. 1C)—although we note that these cases are not achievable with real data and provide only hypothetical upper bounds on performance.

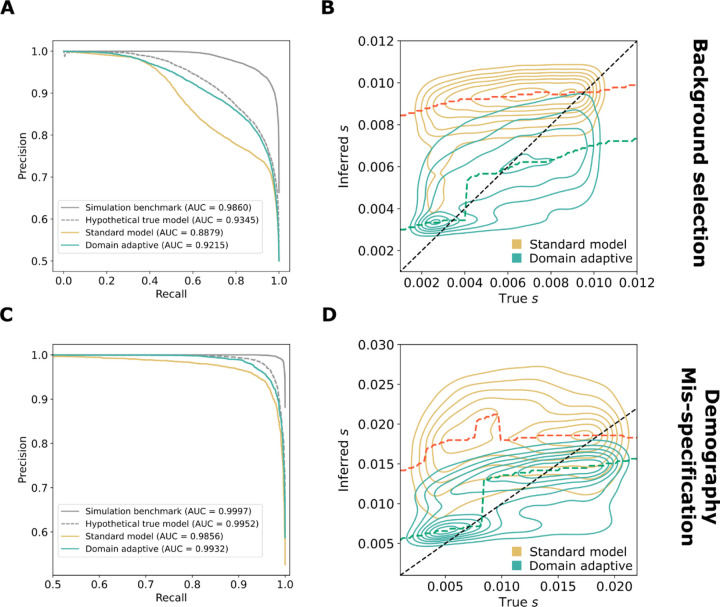
In both the background selection and demography mis-specification experiments, and in both the classification and regression tasks, the domain-adaptive SIA model substantially improved on the standard model (Fig. 3). Indeed, in all cases, the domain-adaptive model (turquoise lines in Fig. 3A&C) nearly achieved the upper bound of the hypothetical true model (dashed gray lines) and clearly outperformed the standard model (gold lines), suggesting that domain adaptation had largely “rescued” SIA from the effects of simulation mis-specification (see also Fig. S2C&D). The standard model performed particularly poorly on the regression task (Fig. 3B&D), but the domain-adaptive model substantially improved on it, reducing both the absolute error as well as the upward bias of the estimation (Fig. S2C&D).

Figure 3. Performance of domain-adaptive SIA models.

Results are shown from (A, B) the background-selection and (C, D) the demography-mis-specification experiments. (A, C) Precision-recall curves for sweep classification. (B, D) Contour plots summarizing true (horizontal axis) vs. inferred (vertical axis) selection coefficients (s) for the standard (gold) and domain adaptive (turquoise) models as evaluated on the held-out test dataset. The ridge along the horizontal axis of each contour is traced by a dashed line, representing the mode of the inferred value for each true value of s. Raw data underlying the contour plots are presented in Fig. S2. See Fig. 1C for definition of the model labels.

The comparisons with the simulation benchmark and hypothetical true model were also informative in other ways. Notice that performance in the simulation benchmark case was considerably better than that in all other cases, including the hypothetical true model. In our experiments, the ARG is “known” (fixed in simulation) in this case, whereas in the hypothetical true model it must be inferred. Thus, the difference between these two cases represents a rough measure of the importance of ARG inference error (see Discussion). In addition, note that in many studies, benchmarking of population-genetic models is performed using the same, or similar, simulations as those used for training, as in with our hypothetical true model. Thus, the difference between the hypothetical true model and the standard model is representative of the degree to which benchmarks of this kind may be overly optimistic about performance, depending on the degree to which the simulations are mis-specified.

We further investigated the effect of imbalanced training data from the target domain on the performance of the domain-adaptive model in the context of sweep classification. Despite the ability to simulate perfectly class-balanced labeled data in the source domain, in practice we have no control over whether real data are balanced. Using simulations for the background selection mis-specification experiments, we tested the performance of the domain adaptive SIA model classifying sweeps when trained with unlabeled “real” data under different proportions of sweep vs. neutral examples. While a balanced dataset yielded the best performance, significantly skewed datasets (20% or 80% sweep examples) still provided the domain adaptive model with reasonable improvement upon the standard model (Fig. S3).

Performance of Domain-Adaptive ReLERNN Model

We performed a parallel set of experiments with a domain-adaptive version of ReLERNN. In this case, the background selection experiment was essentially the same as for SIA, but we used a simpler design for the demography mis-specification experiment, following Adrion et al. (2020). Briefly, the “real” (target domain) data was generated according to the out-of-Africa European demographic model estimated by Tennessen et al. (2012). By contrast, the simulated data for the source domain simply assumed a constant-sized panmictic population at equilibrium with $N_e=\frac{{\widehat{\theta }}_W}{4\mu }$, where ${\widehat{\theta }}_W$ is the Watterson estimator obtained from the “real” data (see Methods for details).

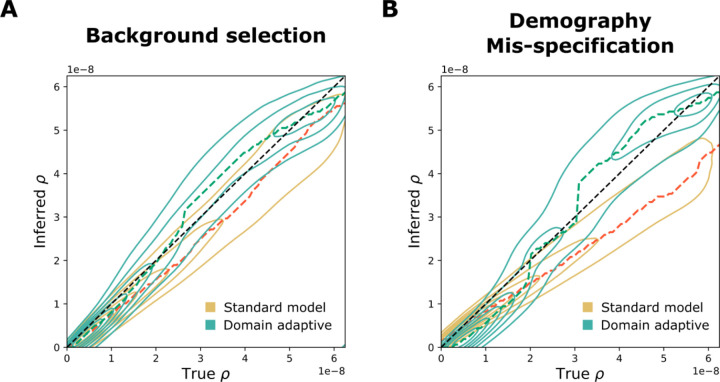
Similar to our results for SIA, the domain-adaptive ReLERNN model both reduced the mean absolute error (MAE) and corrected for the downward bias in recombination-rate estimates compared to the standard model (Fig. 4, Fig. S4). In the background-selection experiment, the standard ReLERNN model performed quite well (Fig. 4A, S4A, MAE = 5.60 × 10⁻⁹), but the domain-adaptive ReLERNN model nonetheless further reduced the MAE to 4.41 × 10⁻⁹ (Fig. S4C, Welch’s t-test: n = 25,000, t = 31.0, p < 10⁻²⁰⁸). The advantage of the domain-adaptive model was more apparent in the demography-mis-specification experiment (Fig. 4B, S4B), where it reduced the MAE from 8.06 × 10⁻⁹ to 5.45 × 10⁻⁹ (Fig. S4D, Welch’s t-test, n = 25,000, t = 72.4, p < 10⁻³²³). Notably, our results for the standard model in the demography-mis-specification experiment were highly similar to those reported by Adrion et al. (2020), including the approximate mean and range of the raw error (compare Fig. 4A from Adrion et al. 2020 and Fig. S4D), as well as the downward bias.

Figure 4. Performance of domain-adaptive ReLERNN models.

Results are shown from (A) the background-selection and (B) the demography-mis-specification experiments. Each contour plot summarizes true (horizontal axis) vs. inferred (vertical axis) recombination rates (ρ) for the standard (gold) and domain adaptive (turquoise) models as evaluated on the held-out test dataset. The ridge along the horizontal axis of each contour is traced by a dashed line, representing the mode of the inferred value for each true value of ρ. Raw data underlying the contour plots are presented in Fig. S4.

Interestingly, Adrion et al. (2020) observed that ReLERNN was sometimes more strongly influenced by demographic mis-specification than unsupervised methods such as LDhelmet, even though it still performed better in terms of absolute error. The addition of domain adaptation appears to considerably mitigate this susceptibility to demographic mis-specification, making an excellent method even stronger.

Application of Domain-Adaptive SIA to Real Data

In applications to real data, the true selection coefficient is not known, so it is impossible to perform a definitive comparison of methods. Nevertheless, it can be informative to evaluate the degree to which alternative methods are concordant, especially with consideration of their relative performance in simulation studies.

Toward this end, we re-applied our domain-adaptive SIA model (dadaSIA) to several loci in the human genome that we previously analyzed with SIA (Hejase et al. 2022), using whole-genome sequence data from the 1000 Genomes CEU population (Auton et al. 2015; see Methods). The putative causal loci analyzed included single nucleotide polymorphisms (SNPs) at the LCT gene (Bersaglieri et al. 2004), one of the best-studied cases of selective sweeps in the human genome; at the disease-associated genes TCF7L2 (Lyssenko et al. 2007), ANKK1 (Spellicy et al. 2014) and FTO (Frayling et al. 2007); at the pigmentation genes KITLG (Sulem et al. 2007), ASIP (Eriksson et al. 2010), TYR (Sulem et al. 2007; Eriksson et al. 2010), OCA2 (Han et al. 2008; Sturm et al. 2008), TYRP1 (Kenny et al. 2012) and TTC3 (Liu et al. 2010), which were also analyzed by Stern et al. (2019); and at the genes MC1R (Sulem et al. 2007; Han et al. 2008) and ABCC11 (Yoshiura et al. 2006), where SIA reported novel signals of selection.

We found that dadaSIA generally made similar predictions to SIA at these SNPs, but there were some notable differences. The seven loci predicted by SIA to be sweeps were also predicted by dadaSIA to be sweeps (Table 1), although dadaSIA always reported higher confidence in these predictions (with probability of neutrality, P_neu < 10⁻² in all cases) than did SIA (P_neu up to 0.384 for TYR). The five loci predicted by SIA not to be sweeps were also predicted by dadaSIA not to be sweeps (P_neu > 0.5). At LCT, the strongest sweep considered, the selection coefficient (s) estimated by dadaSIA remained very close to SIA’s previous estimate of s = 0.01 and also close to several prior estimates (Bersaglieri et al. 2004; Mathieson and Mathieson 2018; Mathieson 2020). In all other cases, the estimate from SIA was somewhat revised by dadaSIA, generally by factors of about 2–3. Interestingly, in all of these cases except MC1R (a novel prediction by SIA), the revision was in the direction of at least some estimates previously reported in the literature, suggesting that simulation mis-specification may have contributed to discrepancies between SIA and previous methods. Nevertheless, the estimates from dadaSIA generally remained closer to those from SIA than to previous estimates. Together, these observations suggest that the addition of domain adaptation does not radically alter SIA’s predictions for real data but may in some cases improve them.

Table 1.

Selection coefficients in the European population estimated by domain-adaptive SIA compared to previous estimates

Gene	SNP	Estimates of selection coefficient
		Domain-adaptive SIA	Standard SIA*	Previous estimates
KITLG	rs12821256	0.0035	0.0019	0.0161†
ASIP	rs619865	0.0057	0.0019	0.0974†
TYR	rs1393350	0.0028	0.0011	0.0112†
OCA2	rs12913832	0.0093	0.0056	0.002†; 0.036‡
MC1R	rs1805007	0.0027	0.0037	No selection§
ABCC11	rs17822931	0.0020	0.00035	~ 0.01 in East Asian||
LCT	rs4988235	0.0097	0.010	~ 0.01¶
TYRP1	rs13289810	Pneu > 0.5	Pneu > 0.5	No selection†
TTC3	rs1003719	Pneu > 0.5	Pneu > 0.5	No selection†
TCF7L2	rs7903146	Pneu > 0.5	Pneu > 0.5	N/A
ANKK1	rs1800497	Pneu > 0.5	Pneu > 0.5	N/A
FTO	rs9939609	Pneu > 0.5	Pneu > 0.5	N/A

^* Hejase et al. 2022

^† Stern et al. 2019

^‡ Wilde et al. 2014

^§ Harding et al. 2000

^|| Ohashi et al. 2011

^¶Bersaglieri et al. 2004; Mathieson and Mathieson 2018; Mathieson 2020

Discussion

Standard approaches to supervised machine learning rest on the assumption that the data they are used to analyze follow essentially the same distribution as the data used for training. In applications in population genetics, the training data are typically generated by simulation, leading to concerns about potential biases from simulation mis-specification when supervised machine-learning methods are used in place of more traditional summary-statistic- or model-based methods (Caldas et al. 2022; Korfmann et al. 2023). In this article, we have shown that techniques from the “domain adaptation” literature can effectively be used to address this problem. In particular, we showed that the addition of a gradient reversal layer (GRL) to two recently developed deep-learning methods for population genetic analysis—SIA and ReLERNN—led to clear improvements in performance on “real” data that differed in subtle but important ways from the data used to train the models. These improvements were observed both when the demographic models were mis-specified and when background selection was included in the simulations of “real” data but ignored in the training data.

While we observed performance improvements in all of our experiments, they were especially pronounced in the case where SIA was used to predict specific selection coefficients, rather than simply to identify sweeps. The standard model (with training on simulated data and testing on “real” data) performed particularly poorly in this regression setting and domain adaptation produced striking improvements (Fig. 3B&D). This selection-coefficient inference problem appears to be a harder task than either sweep classification or recombination-rate inference, and the performance in this case proves to be more sensitive to simulation mis-specification (cf. Fig. 3A&C). In general, we anticipate considerable differences across population-genetic applications in the value of domain adaptation, with some applications being more sensitive to simulation mis-specification and therefore more apt to benefit from domain adaptation, and others being less so.

We also observed some interesting differences in the ways SIA and ReLERNN responded to domain adaptation. For example, the performance gap between the “simulation benchmark” (trained and tested on simulated data) and “hypothetical true” (trained and tested on real data) models was considerably greater for SIA than for ReLERNN (Figs. S2C&D, S4C&D). This difference appears to be driven by ARG inference, which is required by SIA in the hypothetical true case but not the simulation benchmark case, and for which no analog exists for ReLERNN. For SIA, the uncertainty about genealogies given sequence data makes the prediction task fundamentally harder in the real world (target domain) than in simulation (source domain) (Fig. 1B). By contrast, ReLERNN does not depend on a similar inference task, and therefore the target and source domains are more or less symmetric. This same factor contributed to the much more dramatic drop in performance for SIA than ReLERNN under the “standard model,” where the model is trained on simulated data and naively applied to “real” data (Figs. 3B&D, 4). At the same time, this property means that there is more potential for improvement from domain adaptation with SIA than with ReLERNN, as indeed we do observe (Figs. 3, 4, S2, S4). In effect, in the case of SIA, domain adaptation not only mitigates simulation mis-specification but also compensates for ARG inference error. More broadly, we expect domain adaptation to be especially effective in applications that depend not only on the simulated data itself but also on nontrivial inferences of latent quantities that are known for simulated but not real data.

We used the domain-adaptive SIA model (dadaSIA) to re-analyze several loci in the human genome that we and others had previously studied. Overall, we found that dadaSIA made similar predictions to SIA at these loci, but it tended to exhibit higher confidence in its predictions, and, in some cases, it reported selection coefficients in better agreement with previous reports. In particular, at KITLG, ASIP, TYR and OCA2, dadaSIA estimated higher selection coefficients than SIA. Given that previously reported estimates of s at these loci were also higher than the original SIA estimates, it seems likely that the original model was under-estimating s due, at least in part, to simulation mis-specification, and that dadaSIA has improved the estimates (Table 1).

Although our experiments were limited to background selection and demographic mis-specification, we expect that the domain adaptation framework would also be effective in addressing many other forms of simulation mis-specification, involving factors such as mutation or recombination rates, or the presence of gene conversion. Another interesting application may be to use domain adaptation to accommodate admixed populations. Each ancestry component could be modeled as a distinct target domain using a multi-target domain adaptation technique (Isobe et al. 2021; Nguyen-Meidine et al. 2021; Roy et al. 2021). It is also worth noting that our experiments considered only one, rather simple, strategy for domain adaptation. Since the GRL was proposed, several other architectures for deep domain adaptation have achieved even better empirical performance on computer vision tasks (see: Papers with Code). Overall, there is rich potential for new work on domain adaptation to address a wide variety of model mis-specification challenges in population genetic inference.

Methods

Methodological summary of unsupervised domain adaptation

To build domain-adaptive versions of SIA and ReLERNN, we added a gradient reversal layer (GRL) to the neural network architecture for each model (Ganin and Lempitsky 2014). The GRL-containing networks consist of three components – a label predictor branch, a domain classifier branch and a feature extractor common to both branches (Fig. 2A&B). During the feedforward step, when data is fed to the neural network to obtain a prediction output, the GRL is inactive; it simply passes along any input to the next layer. However, during backpropagation, when the gradient of the loss function with respect to the weights of the network is calculated iteratively backward from the output layer, the GRL inverts the sign of any incoming gradient before passing it back to the previous layer. This operation has the effect of driving the feature extractor away from distinguishing the source and target domains, and consequently encourages it to extract “domain-invariant” features of the data. We implemented the GRLs in TensorFlow (v2.4.1) using the ‘tf.custom_gradient’ decorator. On top of each custom GRL, the rest of the model was built using the ‘tf.keras’ functional API (see the GitHub repository for details).

All models were trained with the Adam optimizer using a batch size of 64. For the domain-adaptive models, training consisted of both (1) feeding labeled data from the source domain through the label predictor and obtaining a label prediction loss; and (2) feeding a mixture of unlabeled data from both the source and target domains through the domain classifier, obtaining a domain classification loss (Fig. 2C). Training was accomplished using a custom data generator implemented with ‘tf.keras.utils.Sequence’. In this study, we simply assigned equal weights to the label-prediction and domain-classification loss functions (following Ganin and Lempitsky 2014).

Background selection experiment with SIA

To assess the robustness of domain-adaptive SIA (dadaSIA) to background selection, we simulated labeled examples (250,000 neutral and 250,000 sweep) in the source domain under demographic equilibrium with N_e = 10,000 and μ = ρ = 1.25 × 10⁻⁸/bp/gen. The sweep simulations consisted of 100kb chromosomal segments with a hard sweep at the central nucleotide having selection coefficient 𝑠 ∈ [0.002, 0.01]. The unlabeled data in the target domain (with the exception of held-out test dataset with labels retained) were simulated in a similar fashion, albeit with a 10kb segment (“gene”) under purifying selection at the center of each 100kb chromosomal segment. All mutations in the central 10kb segment that arose during the forward stage of the simulations (in SLiM) followed a DFE parameterized by a gamma distribution with a mean $\overline{s}=-0.03$, a shape parameter α = 0.2 and had dominance coefficient h = 0.25 (Boyko et al. 2008). Simulations were performed in SLiM 3 (Haller et al. 2019; Haller and Messer 2019) followed by recapitation with msprime (Baumdicker et al. 2022).

Demography mis-specification experiment with SIA

In a second set of simulations, we gauged whether domain adaptation also protects SIA against demographic mis-specification. In this case, instead of specifying the degree of mis-specification a priori, we designed an end-to-end workflow that recapitulated how demographic mis-specification arises in a realistic population genetic analysis (Fig. S1A). First, we simulated “real” data (in the target domain) using an assumed demography (Fig. S1A, loosely based on the three-population model in Campagna et al. 2022). Similar to what one would do with actual sequence data, we then used the “real” samples to infer a demography with G-PhoCS (Gronau et al. 2011), pretending that the true demography and genealogies were unknown. As shown in Fig. S1A, the inferred demography was consequently somewhat mis-specified. This mis-specified demographic model was then used to simulate labeled training data (in the source domain) for SIA.

With the goal of using SIA to infer selection in population B, we simulated a soft sweep site at the center of a 100kb chromosomal segment with selection coefficient s ∈ [0.003, 0.02] and initial sweep frequency f_init ∈ [0.01, 0.1], under positive selection only in population B. To improve computational efficiency, simulations were performed with a hybrid approach where the neutral demographic processes were simulated first with msprime (Baumdicker et al. 2022), followed by positive selection simulated with SLiM 3 (Haller et al. 2019; Haller and Messer 2019). We produced 200,000 balanced (between neutral and sweep) simulations of “peudo-real” data, 10,000 of which were randomly held out as ground-truth test data for benchmarking with their labels preserved (Fig. S1A). The rest remained unlabeled. We preserved only the sequences and used Relate (Speidel et al. 2019) to infer the ARG of population B from the “real” data. For demographic inference, we randomly downsampled 10,000 5kb loci and analyzed them with G-PhoCS, keeping 4 (diploid) individuals from population A and 16 (diploid) individuals each from populations B and C. We took the median of 90,000 MCMC samples (after 10,000 burn-in iterations) as the inferred demography (shown in Fig. S1A). The control file used to run G-PhoCS is available in the GitHub repository. We then simulated true genealogies of population B using the inferred demography, yielding 200,000 balanced samples with neutral/sweep and selection coefficient labels. All SIA models in this study used 64 diploid samples (128 taxa).

Genealogical features for the SIA model

For this study, we adopted a richer encoding of genealogies than the one used previously for SIA. Instead of simply counting the lineages remaining in the genealogy at discrete time points (Hejase et al. 2022), we fully encoded the topology and branch lengths of the tree using the scheme introduced by (Kim et al. 2020). Under this scheme, a genealogy with n taxa is uniquely encoded by an (n-1) × (n-1) lower-triangular matrix F and a weight matrix W of the same shape. Each cell (i, j) of F records the lineage count between coalescent times t_n−j and t_n−1−i, whereas each cell (i, j) of W records the corresponding interval between coalescent times, t_n−j − t_n−1−i (see Fig. S1B and Kim et al. 2020 for details). In addition, we used a third matrix R to identify the subtree carrying the derived alleles at the site of interest, following the same logic as F (see Fig. S1B for an example). The F, W and R matrices have the same shape and therefore can easily be stacked as input to a convolutional layer with three channels (Fig. 2A, 128 taxa yield a 127 × 127 × 3 input tensor).

Simulation study of recombination rate inference with ReLERNN

We conducted two sets of simulation experiments to test the same two types of mis-specification as previously described for SIA. Each simulation consisted of 32 haploid samples of 300kb genomic segment with uniformly sampled mutation rate μ ∼ U[1.875 × 10⁻⁸, 3.125 × 10⁻⁸] and recombination rate ρ ∼ U[0, 6.25 × 10⁻⁸]. To test the effect of background selection, the labeled source domain data (with true values of ρ) were simulated under demographic equilibrium with N_e = 10,000, whereas the unlabeled target domain data were simulated under the same demography, but with the central 100kb region under purifying selection, as with SIA. To test the effect of demographic mis-specification, we conducted simulations similar to those of Adrion et al. (2020) where labeled source domain data were generated under demographic equilibrium (with N_e = 6,000, calculated approximately by $\frac{{\widehat{\theta }}_W}{4\mu }$ where ${\widehat{\theta }}_W$ was estimated from the target domain data) and unlabeled target domain data were generated under a European demography (Tennessen et al. 2012). For each domain, 500,000 simulations were generated with SLiM 3 (background selection experiment) or msprime (demography experiment), and partitioned following an 88%:2%:10% train-validation-test composition. We modified the ReLERNN model to be domain-adaptive (Fig. 2B) and used the simulated data to benchmark its performance against the original version of the model.

Application of domain-adaptive SIA model to 1000 Genomes CEU population

Labeled training data (source domain) for SIA were simulated with discoal (Kern and Schrider 2016) under the Tennessen et al. (2012) European demographic model. Following Hejase et al. (2022), we simulated 500,000 100-kb regions of 198 haploid sequences. The per-base per-generation mutation rate (μ) and recombination rate (ρ) of each simulation were sampled uniformly from the interval [1.25 × 10⁻⁸, 2.5 × 10⁻⁸]; the segregating frequency of the beneficial allele (f) was sampled uniformly from [0.05, 0.95]; the selection coefficient (s) was sampled from an equal mixture of a uniform and a log-uniform distribution with the support [1 × 10⁻⁴, 2 × 10⁻²]. An additional 500,000 neutral regions were simulated to train the classification model, under the identical setup sans the positively selected site.

We curated target domain data from the 1000 Genomes CEU population to train the domain-adaptive SIA model (dadaSIA). The genome was first divided into 2Mb windows 1,111 of which passed three data-quality filters: 1) contained at least 5,000 variants, 2) at least 80% of these variants had ancestral allele information, and 3) at least 60% of nucleotide sites in the window passed both the 1000 Genomes strict accessibility mask (Auton et al. 2015) and the deCODE recombination hotspot mask (standardized recombination rate > 10, Kong et al. 2010). We randomly sampled 1,000 variants from each of these 1,111 windows and extracted genealogical features at those variants from Relate-inferred ARGs (Speidel et al. 2019), yielding around 1 million samples that constituted the unlabeled target domain data. Finally, domain-adaptive SIA models for classifying sweeps and inferring selection coefficients were trained as described previously and applied to a collection of loci of interest (Table 1).