Incorporating spatial structure into inclusion probabilities for Bayesian variable selection in generalized linear models with the spike-and-slab elastic net

Abstract

Spike-and-slab priors model predictors as arising from a mixture of distributions: those that should (slab) or should not (spike) remain in the model. The spike-and-slab lasso (SSL) is a mixture of double exponentials, extending the single lasso penalty by imposing different penalties on parameters based on their inclusion probabilities. The SSL was extended to Generalized Linear Models (GLM) for application in genetics/genomics, and can handle many highly correlated predictors of a scalar outcome, but does not incorporate these relationships into variable selection. When images/spatial data are used to model a scalar outcome, relevant parameters tend to cluster spatially, and model performance may benefit from incorporating spatial structure into variable selection. We propose to incorporate spatial information by assigning intrinsic autoregressive priors to the logit prior probabilities of inclusion, which results in more similar shrinkage penalties among spatially adjacent parameters. Using MCMC to fit Bayesian models can be computationally prohibitive for large-scale data, but we fit the model by adapting a computationally efficient coordinate-descent-based EM algorithm. A simulation study and an application to Alzheimer’s Disease imaging data show that incorporating spatial information can improve model fitness.

1. Introduction

Variable selection is a long-standing statistical problem in both classical and Bayesian paradigms, and aims to determine which variables/predictors are associated with some outcome(s). Classical statistics often relies on hypothesis testing to select predictors in a (generalized) linear model (GLM), but variability of the resulting final models can result in unacceptable generalizability, despite removing many extraneous variables. Such issues partly motivated the lasso model, which is a penalized model that implicitly performs variable selection by setting many parameter estimates to zero, and decreases the variability of the selected model compared to other common classical approaches (Tibshirani, 1996). Additionally, while traditional GLMs are not identifiable when the number of predictors exceeds the number of the observations, the lasso model is identifiable in most cases. Furthermore, while the lasso was born within a classical framework, its Bayesian interpretation is realized by placing double exponential priors on the “effect” parameters (Park and Casella, 2008).

Bayesian variable selection often employs the spike-and-slab prior framework, which models the distribution of parameters as a mixture: a wide “slab” distribution models “relevant” parameters and a narrow “spike” distribution models “irrelevant” parameters (Mitchell and Beauchamp, 1988; George and McCulloch, 1993). While initial work focused on mixtures of normal priors, other distribution choices are possible. In particular, Ročková and George (2018) introduce the spike-and-slab lasso, a mixture of double exponential priors that trades the single lasso penalty for an adaptive penalty based on the probabilities of inclusion. While the initial spike-and-slab lasso was proposed and described for normal linear regression, Tang et al. (2017) demonstrated a novel computational approach based on the EM algorithm that fits the model for GLMs. One of the primary benefits of the algorithm from Tang et al. (2017) is that it is much faster than traditional Markov Chain Monte Carlo (MCMC) methods, whose computational time can be prohibitive for large-scale data sets, like those found in genomics or neuroimaging studies.

Unlike classical GLM’s, penalized or Bayesian models are usually identifiable when predictors are highly correlated, but require suitably structured priors to use dependence structure in modeling and/or variable selection. This issue has been approached from multiple angles within genomics research. Li and Li (2008) and Pan et al. (2010) extend the lasso to use networks to describe relationships among predictors, while Li and Zhang (2010) take a graph theoretic approach while employing an Ising prior on the model space to handle dependence structures. More recently, Ročková and George (2014) discuss an EM variable selection approach based on spike-and-slab normal priors, which in part explores independent logistic regression priors and Markov random field priors to model dependence in variable selection, also inspired by genetics. Importantly, the above models use structured priors as an avenue for incorporating relevant biological information into models, making them more plausible and improving prediction accuracy.

In this work, we focus specifically on spatially structured priors in situations where it is reasonable to expect “relevant” and “irrelevant” parameters will exhibit spatial clustering, which implies the probability that a parameter should remain in the model will be similar to the respective probabilities of spatially adjacent parameters. Other works have addressed spatially structured variable selection, particularly within neuroscience and functional magnetic resonance imaging (Smith and Fahrmeir, 2007; Quirós et al., 2010; Brown et al., 2014). However, we find that these works tend to focus on using images as the outcomes of interest, e.g., activation across many voxels in the brain, whereas we want to address situations where the outcome of interest for each subject is a scalar value, while treating images/spatially structured data as the predictors rather than outcomes. For example, we may use images to predict or model whether a subject has, or will develop, dementia, which is more naturally achieved in a GLM framework. This subtle shift in focus increases the attractiveness of using penalized models like the lasso for variable selection.

The lasso has two primary downsides: when the number of predictors far exceeds the number of subjects, the number of non-zero parameters cannot exceed the number of subjects, and when predictors are correlated it tends to select one predictor and discard the rest. In part, these issues inspired the elastic net, which compromises between ridge and lasso penalties (Zou and Hastie, 2005). Unlike the ridge penalty, the elastic net solution is sparse, but unlike the lasso penalty it can include more non-zero parameters. This flexibility may be desirable when images are used as predictors, since there are often more (highly correlated) spatial measurements than subjects, and the lasso penalty may be too severe. In addition, while there are circumstances where the lasso is not uniquely identifiable, the elastic net is strictly convex and is always uniquely identifiable (Zou and Hastie, 2005).

In what follows we extend the spike-and-slab lasso to a spike-and-slab elastic net, explicitly incorporate spatial information into variable selection, and fit the model with an adaptation of the computationally efficient EM algorithm from Tang et al. (2017). Section 2 reviews the spike-and-slab lasso GLM and outlines the EM-algorithm used to fit the model. Section 3 introduces an extension of the spike-and-slab lasso GLM that generalizes the model to the elastic net and uses intrinsic autoregressions to incorporate spatial information into variable selection. Section 4 presents a simulation study to demonstrate the potential of the proposed method and examine its properties. Section 5 applies the methodology to Alzheimer’s Disease (AD) classification using data from the Alzheimer’s Disease Neuroimaging Initiative (ADNI). Finally, Section 6 summarizes the findings and discuss their implications.

2. Spike-and-slab lasso for GLM

2.1. Theory overview

GLM’s can model outcomes that are non-normal, and include the traditional linear model as a special case. The standard form of a GLM is given by:

$$g\left(\text{E}\left(y_i\mid {\mathit{X}}_i\right)\right)={\mathit{X}}_i\mathit{\beta }={\beta }_0+\sum _{j=1}^J{x}_{ij}{\beta }_j={\eta }_i,i=1,\dots ,N$$ (2.1)

where g(·) is an appropriate link function, X_i is a 1 × J subject-specific design vector, β is a J × 1 parameter vector, β₀ is an intercept, J is the total number of predictors in the model, and N is the number of observations. The joint likelihood, or data distribution, may contain an over-dispersion parameter, ϕ, and is given by:

$$p(\mathit{y}\mid \mathit{X}\beta ,\varphi )=\prod _{i=1}^{N}p\left(y_i\mid {\mathit{X}}_i\mathit{\beta },\varphi \right)$$ (2.2)

The classical lasso model is equivalent to placing double exponential priors on the β_j (Park and Casella, 2008). Thus, the spike-and-slab lasso prior is a mixture of double exponential distributions, where the narrow spike distribution shrinks “irrelevant” parameters more severely than the wider slab distribution, which allows “relevant” parameters to have estimates of larger magnitude. The model’s explicit formulation is given by (Ročková and George, 2018):

$${\beta }_j\mid {\gamma }_j,s_0,s_1~DE\left({\beta }_j\mid 0,S_j\right)=\frac{1}{2S_j}\exp \left(-\frac{\left|{\beta }_j\right|}{S_j}\right)$$ (2.3)

where S_j = (1 − γ_j)s₀ + γ_js₁, the indicator variable γ_j determines the inclusion status of the jth variable, and s₁ > s₀ > 0. In practice we do not know the value of the γ_j, and so we incorporate uncertainty with a Binomial prior:

$$p(\mathit{\gamma }\mid \theta )=\prod _{j=1}^J{\theta }^{{\gamma }_j}{(1-\theta )}^{1-{\gamma }_j}$$ (2.4)

where θ = P(γ_j = 1|θ) is a global probability of inclusion for the β_j. In Section 3 we shall discuss how to use probabilities of inclusion to incorporate spatial information, but first we will describe how to fit the model described here by assigning θ a Uniform(0, 1) prior.

2.2. The EM-coordinate descent algorithm

Bayesian analysis traditionally estimates parameters’ posterior distributions. However, for very large numbers of predictors even fast MCMC draws from the posterior distribution can impose prohibitive costs, and optimization approaches resulting solely in point estimates may be preferred in some practical settings, especially if the primary goal of analysis is prediction and/or variable selection. Tang et al. (2017) use an expectation maximization coordinate descent (EMCD) algorithm to fit the spike-and-slab lasso by treating the model inclusion indicators γ_j as missing values. The log posterior density is given by:

$$\begin{gathered} \log p(\mathit{\beta },\varphi ,\mathit{\gamma },\theta \mid \mathit{y})=\log p(y\mid \mathit{\beta },\varphi )+\sum _{j=1}^J\log p\left({\beta }_j\mid S_j\right)+\sum _{j=1}^J\log p\left({\gamma }_j\mid \theta \right)+\log p(\theta ) \\ \propto \ell (\mathit{\beta },\varphi )-\sum _{j=1}^J\frac{1}{S_j}\left|{\beta }_j\right|+\sum _{j=1}^J\left({\gamma }_j\log \theta +\left(1-{\gamma }_j\right)\log (1-\theta )\right) \end{gathered}$$ (2.5)

where ℓ(β, ϕ) = log p(y |β, ϕ). The algorithm takes the expectation with respect to the γ_j conditional on the other parameters (E-step), inputs these conditional expectations into Eq. (2.5), maximizes over the remaining parameters (M-step), and iterates until convergence.

It can be shown that the expectation of the log joint posterior density with respect to the conditional distributions of the γ_j is as follows (Tang et al., 2017):

$$\begin{gathered} p_j=p\left({\gamma }_j=1\mid {\beta }_j,\theta ,\mathit{y}\right) \\ =\frac{p\left({\beta }_j\mid {\gamma }_j=1,s_1\right)p\left({\gamma }_j=1\mid \theta \right)}{p\left({\beta }_j\mid {\gamma }_j=0,s_0\right)p\left({\gamma }_j=0\mid \theta \right)+p\left({\beta }_j\mid {\gamma }_j=1,s_1\right)p\left({\gamma }_j=1\mid \theta \right)} \end{gathered}$$ (2.6)

It follows that the conditional posterior expectation of the jth scale/penalty parameter $S_j^{-1}$ is as follows:

$$E(S_j^{-1}\mid {\beta }_j)=E\left(\frac{1}{(1-\gamma )s_0+{\gamma }_j{s}_1}\mid {\beta }_j\right)=\frac{1-p_j}{s_0}+\frac{p_j}{s_1}$$ (2.7)

It is important to note that no matter the form of the p_j, once their values are obtained the conditional expectation of the $S_j^{-1}$ immediately follows.

Eq. (2.5) shows that (β, ϕ) and θ are never within the same term simultaneously, and so can be updated separately as the following terms:

$$Q_1(\mathit{\beta },\varphi )=\ell (\mathit{\beta },\varphi )-\sum _{j=1}^J\frac{1}{S_j}\left|{\beta }_j\right|$$ (2.8)

$$Q_2(\theta )=\sum _{j=1}^J\left({\gamma }_j\log \theta +\left(1-{\gamma }_j\right)\log (1-\theta )\right)$$ (2.9)

The coordinate descent algorithm can fit GLM’s with ridge, lasso, or elastic net penalties, and Q₁(β) can be updated with this algorithm using the R package glmnet since it is equivalent to the lasso penalty with γ_j and $S_j^{-1}$ traded for their conditional posterior distributions (Zou and Hastie, 2005; Friedman et al., 2007, 2010). When θ has a uniform prior, we can use elementary calculus to update θ with $\theta =\frac{1}{J}{\sum }_{j=1}^J{p}_j$.

2.3. Extending the EMCD algorithm to incorporate spatial information

The EM algorithm described above can handle ill-posed data and highly correlated predictors, but it does not explicitly model dependence structure among parameter estimates and only allows for lasso penalties. However, in spatial settings we may expect relevant parameters to cluster, which suggests that spatially structured priors may be useful in variable selection. In addition, the correlation among predictors in spatial settings may make the lasso undesirable since it tends to pick one predictor and ignore the rest. In what follows we extend the spike-and-slab lasso GLM to address both of these issues.

3. The EMCD-IAR model

3.1. The spike-and-slab elastic net

The elastic net penalty has a Bayesian interpretation as a mixture of normal and double exponential distributions (Zou and Hastie, 2005):

$$p\left({\beta }_j\mid \lambda \right)=C(\lambda ,\xi )\exp \left[-\lambda \{(1-\xi ){\beta }_j^2+\xi \left|{\beta }_j\right|\}\right]$$ (3.1)

where the choice of ξ ∈ [0, 1] determines the compromise between ridge and lasso penalties; ξ = 0 corresponds to ridge, and ξ = 1 corresponds to lasso. Note that C(λ, ξ) is a constant depending on (λ, ξ), which in a fully Bayesian analysis is complicated to handle (Li and Lin, 2010). However, we treat ξ as tuning parameter within our EM algorithm framework, which avoids these difficulties. The elastic net is easily extended to a spike-and-slab framework:

$$\begin{gathered} p\left({\beta }_j\mid {\gamma }_j,s_0,s_1\right)=EN\left({\beta }_j\mid 0,S_j\right) \\ =(1-\xi )\exp \left(-\log \left(\sqrt{2\pi S_j}\right)-\frac{{\beta }_j^2}{S_j}\right) \\ +\xi \exp \left(-\log \left(2S_j\right)-\frac{\left|{\beta }_j\right|}{S_j}\right) \end{gathered}$$ (3.2)

where S_j = (1 − γ_j)s₀ + γ_js₁. Thus, ξ = 0 corresponds to a “spike-and-slab ridge” penalty, while ξ = 1 produces the spike-and-slab lasso described by Eq. (2.3). Note that a fully Bayesian approach to fitting the elastic net involves a normalizing constant in Eq. (3.1) that is a complicated function of λ and ξ, an issue that would follow us into Eq. (3.2) (Li and Lin, 2010). However, by using the proposed EM approach we may regard ξ as a tuning parameter and avoid issues with the complicated normalizing constant.

3.2. IAR spatial models for inclusion probabilities

The penalty $E(S_j^{-1}\mid {\beta }_j)$ determines the shrinkage severity for the β_j estimates, with variable selection arising via the many resulting zero estimates. The penalty is a function of p_j = p(γ_j = 1|β_j, θ, y), which is itself a function of the current estimate of probability of inclusion, θ. We can also allow parameter specific probabilities of inclusion, i.e., θ_j. The joint prior for γ then has the same form as Eq. (2.4):

$$p\left(\mathit{\gamma }\mid {\theta }_j\right)=\prod _{j=1}^J{\theta }_j^{{\gamma }_j}{\left(1-{\theta }_j\right)}^{1-{\gamma }_j}$$ (3.3)

where now θ_j = P(γ_j = 1|θ_j) is the prior probability of inclusion for a specific β_j and p_j = p(γ_j = 1|β_j, θ_j, y) is the conditional probability of inclusion for β_j. Thus, if a structure is imposed on the θ_j, then variable selection will implicitly depend on that structure.

Spatial processes and spatially structured priors are commonly modeled using a special case of Gaussian Markov Random Fields (GMRF) known as conditional autoregressions (CAR), which have joint multivariate Normal distributions but are specified by conditional structure (Banerjee et al., 2015; Brown et al., 2014; Cressie and Wikle, 2011; Rue and Held, 2005). The logit of the probabilities of inclusion, θ_j ∈ [0, 1], ${\psi }_j=\mathrm{logit}\left({\theta }_j\right)=\log \frac{{\theta }_j}{1-{\theta }_j}\in (-\infty ,\infty )$, has the same support as the (multivariate) Normal distribution, which enables us to use the CAR model, and after modeling the ψ_j, we can obtain θ_j = logit⁻¹(ψ_j).

A special case of the CAR model is the Intrinsic Autoregressive model (IAR), which has an improper joint distribution (Jin et al., 2005; Banerjee et al., 2015; Besag and Kooperberg, 1995):

$$\mathit{\psi }=\mathcal{N}(\mathbf{0},{[{\tau }^2(\mathit{D}-\mathit{W})]}^{-1})$$ (3.4)

where τ is a common precision parameter, D = diag(n_j) contains the number of neighbors, n_j, for each location, and W = {w_ij } is the adjacency matrix where $w_{ij}=\{\begin{array}{ll}1\hfill & j~i\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$

Despite its impotence as a data generating model, the IAR is a useful prior distribution in spatial models because each ψ_j is interpreted as varying about the mean of its neighbors rather than a global mean, and an IAR prior models stronger spatial dependence than the traditional CAR model (Besag and Kooperberg, 1995; Banerjee et al., 2015; Rue and Held, 2005). We model spatial structure in ψ_j using the following pairwise difference formulation with τ = 1, which results in interpretive and computational benefits (Besag and Kooperberg, 1995; Morris et al., 2019):

$$\log p(\mathit{\psi })\propto -\frac{1}{2}\left(\sum _{j:j~i}{\left({\psi }_j-{\psi }_i\right)}^2\right)$$ (3.5)

3.3. Derivation of the log joint posterior distribution

The EM algorithm takes the expectation of the “missing” data/parameters, replaces them with conditional expectations in the joint log likelihood, and then maximizes to obtain parameter estimates. The relevant joint log posterior extends Eq. (2.5) with IAR priors on the logit prior inclusion probabilities and an elastic net prior for the β_j:

$$\begin{gathered} \log p(\mathit{\beta },\varphi ,\mathit{\gamma },\mathit{\psi }\mid \mathit{y})\propto \underset{\log \text{likelihood}}{\underbrace{\ell (\mathit{\beta },\varphi )}}-\underset{\text{log}\text{prior}\text{for}\mathit{\beta }}{\underbrace{\sum _{j=1}^J\log EN\left({\beta }_j\mid 0,S_j\right)}} \\ +\underset{\log \text{prior}\text{for}\mathit{\gamma }}{\underbrace{\sum _{j=1}^J{\gamma }_j\log {\theta }_j+\left(1-{\gamma }_j\right)\log \left(1-{\theta }_j\right)}} \\ -\underset{\text{log}\text{prior}\text{for}{\psi }_j=\mathrm{logit}\left({\theta }_j\right)}{\underbrace{\frac{1}{2}\left(\sum _{j:j~i}{\left({\psi }_j-{\psi }_i\right)}^2\right)}} \end{gathered}$$ (3.6)

3.4. The structure of the EM algorithm

E-step

We again treat the γ_j as missing and take their conditional expectations given the other parameters in the model. Similar to Tang et al. (2017), by application of Bayes’ Rule the conditional probability that a variable should be included the model is as follows:

$$\begin{gathered} p_j=p\left({\gamma }_j=1\mid {\beta }_j,{\theta }_j,\mathit{y}\right) \\ =\frac{p\left({\beta }_j\mid {\gamma }_j=1,s_1\right)p\left({\gamma }_j=1\mid {\theta }_j\right)}{p\left({\beta }_j\mid {\gamma }_j=1,s_1\right)p\left({\gamma }_j=1\mid {\theta }_j\right)+p\left({\beta }_j\mid {\gamma }_j=0,s_0\right)p\left({\gamma }_j=0\mid {\theta }_j\right)} \end{gathered}$$ (3.7)

where p(γ_j = 1|θ_j) = θ_j, p(γ_j = 0|θ_j) = 1 − θ_j, p(β_j |γ_j = 1, s₁) = EN(β_j |0, s₁), and p(β_j |γ_j = 1, s₁) = EN(β_j |0, s₀). Given p_j, the conditional posterior expectation of $S_j^{-1}$ is the same as in Tang et al. (2017):

$$\begin{gathered} E\left(S_j^{-1}\mid {\beta }_j\right)=E\left(\frac{1}{\left(1-{\gamma }_j\right)s_0+{\gamma }_j{s}_1}\right) \\ =\frac{1-p_j}{s_0}+\frac{p_j}{s_1} \end{gathered}$$ (3.8)

Therefore, the E-step differs from Tang et al. (2017) in that there are now J prior probabilities of inclusion, θ_j, rather than a single θ. The M-step progresses by maximizing Eq. (3.6) with γ_j and $S_j^{-1}$ exchanged for their conditional expectations.

M-step

Having obtained conditional expectations of the γ_j, we plug these into the joint log posterior distribution and maximize the expression, which is again divided into two terms. Regardless of the spatial model, the first term remains Q₁(β, ϕ), similar to Eq. (2.8), but allows the full range of elastic net priors specified by ξ ∈ [0, 1]; Q₁(β, ϕ) is again maximized via cyclic coordinate descent with the R package glmnet. However, Q₂(θ) now contains an additional term corresponding to the IAR prior on the ψ_j. We maximize Q₂(θ) using a numerical optimization function within the R package rstan using STAN code based on Morris et al. (2019):

$$Q_{1,EN}=\underset{\log \text{likelihood}}{\underbrace{\ell (\mathit{\beta },\varphi )}}-\underset{\log \text{prior}\text{for}\mathit{\beta }}{\underbrace{\sum _{j=1}^J\log EN\left({\beta }_j\mid 0,S_j\right)}}$$ (3.9)

$$\begin{gathered} Q_{2,IAR}=\underset{\text{log}\text{prior}\text{for}\mathit{\gamma }}{\underbrace{\sum _{j=1}^J{\gamma }_j\log {\theta }_j+\left(1-{\gamma }_j\right)\log \left(1-{\theta }_j\right)}} \\ -\underset{\log \text{prior}\text{for}{\psi }_j=\mathrm{logit}\left({\theta }_j\right)}{\underbrace{\frac{1}{2}\left(\sum _{j:j~i}{\left({\psi }_j-{\psi }_i\right)}^2\right)}} \end{gathered}$$ (3.10)

We iterate until convergence following Tang et al. (2017) in assessing convergence by:

$$\frac{\left|d^{(t)}-d^{(t-1)}\right|}{\left(0.1+|d^{(t)}|\right)}<ϵ$$ (3.11)

where d^(t) = −2 log ℓ(β^(t),ϕ^(t)) is the estimated deviance at iteration t. A development version of an R package, ssnet, can fit these models and is available on GitHub (https://github.com/jmleach-bst/ssnet).

4. Simulations

4.1. Simulation framework

We performed a simulation study to demonstrate the methodology and explore its properties. The simulations consist of 5000 data sets containing N = {25, 50, 100} subjects where subject design vectors arise from a 32 × 32 two dimensional images generated by a multivariate Normal distribution with zero mean, unit variance, and correlation given by ${\sigma }_{j,k}={0.90}^{d_{j,k}}$, j ≠ k, where d_j,k is the Euclidean distance in 2D space between any two locations j and k for j, k = 1,..., J. The resulting images thus have J = 1024 predictors whose correlation with each other decays as distance in space increases. These images are vectorized by treating the 2D lattice as a matrix, then concatenating rows. We constructed a circular cluster of 29 non-zero parameters in the 32 × 32 two-dimensional space, which are vectorized in the same manner as the images to ensure matching indices for the J = 1024 predictor and parameter vectors, X_i and β, respectively. Binary outcomes were simulated for each of i = 1, . . ., N subjects from a Bernoulli(X_iβ) distribution for two scenarios: β_j = 0.5 and β_j = 0.1. Thus, the β_j = 0.5 and β_j = 0.1 data sets correspond to a 64.87% and 10.51% increase in odds of an “event” occurring, respectively. The data were generated using the R package sim2Dpredictr, which is available on CRAN (https://CRAN.R-project.org/package=sim2Dpredictr); example code can be found at https://github.com/jmleach-bst and example images for both subjects and parameter clustering can be found in the supplementary materials.

We analyze each dataset with both elastic net (ξ = 0.5; a halfway compromise between ridge and lasso) and lasso (ξ = 1) priors under the traditional framework, the spike-and-slab framework without spatial structure, and the spikeand-slab framework with spatial structure, using a combination of the R packages glmnet, BhGLM, and ssnet. We employ 10-fold cross validation for N = {50, 100} and 5-fold cross validation for N = 25 to estimate measures of model fit/variable selection criteria. For the traditional elastic net models we allow cv.glmnet () to internally select the optimal parameter, and for the spike-and-slab lasso models we set the slab scale parameter to s₁ = 1 and manually choose the sequence s₀ = {0.01, 0.02, 0.03, . . ., 0.3} over which to choose the value of spike parameter that minimizes cross-validated prediction error. Details and code for reproducing the simulation results can be found at https://github.com/jmleach-bst/ssen-iar-simulations. All simulations and analysis were performed in R version 3.6.0.

We report several metrics to evaluate two aspects of model performance, prediction and variable selection. Prediction accuracy is assessed with cross-validated measures of deviance, mean square error (MSE), mean absolute error (MAE), area under the ROC curve (AUC), and misclassification (MC). False discovery rate (FDR) and the proportion of true non-zero parameters remaining in a model (Power) are used to evaluate variable selection performance. Note that ideal models will have lower values for deviance, MSE, MAE, MC, and FDR, and higher values for AUC and Power. The ideal spike scale is chosen as the one whose penalty minimizes the cross-validated deviance. Deviance is defined as −2 times the log likelihood with respect to the held-out data, not the training data; i.e., it is an estimate of model fitness to independent data, rather than observed data, which can help prevent over-fitting.

4.2. Simulation results

Tables 1 and 2 show that, for each sample size and both effect sizes, within a given elastic net level the models with spatially structured priors have better cross-validated prediction errors compared to models without. Under IAR priors, the spike-and-slab elastic net (SSEN) outperforms the spike-and-slab lasso (SSL), but this difference is small compared to the difference between these models with and without IAR priors; i.e., most of the improvement in prediction error results from the IAR priors not the halfway compromise between ridge and lasso penalties. Note that SSL with IAR priors has the lowest MAE when β_j = 0.5, but along every other metric in both scenarios SSEN with IAR priors had the best performance.

Table 1.

Model performance for β_j = 0.5.

N	Model	s 0	Dev.a	AUC	MSE	MAE	MCb	FDR	Power
25	EN	0.0638	17.5657	0.9068	0.1135	0.2280	0.1655	0.7164	0.4297
	SSEN	0.2337	17.4036	0.9280	0.1058	0.2582	0.1374	0.5327	0.2508
	SSEN (IAR)	0.1177	10.2933	0.9885	0.0527	0.1659	0.0493	0.4008	0.0382
	Lasso	0.0482	19.0767	0.8906	0.1236	0.2414	0.1808	0.6774	0.0991
	SSL	0.1260	11.8960	0.9654	0.0683	0.1788	0.0854	0.2408	0.0292
	SSL (IAR)	0.1480	10.4159	0.9810	0.0569	0.1604	0.0653	0.2956	0.0299
50	EN	0.0356	25.6359	0.9560	0.0806	0.1713	0.1155	0.6931	0.5740
	SSEN	0.1539	23.3948	0.9752	0.0665	0.1781	0.0805	0.4498	0.1810
	SSEN (IAR)	0.1243	14.3074	0.9944	0.0357	0.1153	0.0346	0.3723	0.0690
	Lasso	0.0251	27.1321	0.9504	0.0857	0.1767	0.1230	0.6489	0.1753
	SSL	0.1312	20.7455	0.9746	0.0607	0.1487	0.0793	0.2082	0.0440
	SSL (IAR)	0.1690	14.5391	0.9905	0.0393	0.1108	0.0458	0.2947	0.0532
100	EN	0.0231	40.3157	0.9746	0.0624	0.1360	0.0881	0.6853	0.6879
	SSEN	0.1271	34.9221	0.9852	0.0498	0.1303	0.0632	0.4380	0.1987
	SSEN (IAR)	0.1197	22.7961	0.9952	0.0298	0.0892	0.0331	0.3872	0.1074
	Lasso	0.0160	42.0318	0.9719	0.0655	0.1385	0.0929	0.6344	0.2662
	SSL	0.1016	31.8247	0.9851	0.0468	0.1120	0.0624	0.1758	0.0710
	SSL (IAR)	0.1683	23.3564	0.9931	0.0325	0.0865	0.0405	0.3067	0.0839

^aDeviance.

^bMisclassification.

Table 2.

Model performance for β_j = 0.1.

N	Model	s 0	Dev.a	AUC	MSE	MAE	MCb	FDR	Power
25	EN	0.1978	27.1003	0.7718	0.1849	0.3551	0.2916	0.7296	0.2158
	SSEN	0.2103	25.4963	0.7924	0.1716	0.3528	0.2724	0.6714	0.1660
	SSEN (IAR)	0.1102	15.2298	0.9448	0.0906	0.2230	0.1154	0.6266	0.0230
	Lasso	0.1242	28.0742	0.7602	0.1916	0.3634	0.3033	0.7064	0.0543
	SSL	0.1644	22.0441	0.8314	0.1464	0.3066	0.2329	0.4820	0.0276
	SSL (IAR)	0.1618	16.1904	0.9286	0.0992	0.2266	0.1338	0.5531	0.0204
50	EN	0.1402	49.3439	0.8263	0.1642	0.3308	0.2455	0.7010	0.3050
	SSEN	0.1217	42.2354	0.8741	0.1366	0.2892	0.1979	0.6004	0.1140
	SSEN (IAR)	0.1072	27.6291	0.9523	0.0834	0.1924	0.1113	0.6606	0.0392
	Lasso	0.0857	50.2457	0.8197	0.1674	0.3340	0.2507	0.6813	0.0999
	SSL	0.0893	40.0524	0.8894	0.1279	0.2649	0.1822	0.3017	0.0305
	SSL (IAR)	0.1576	30.3577	0.9379	0.0938	0.2012	0.1288	0.5859	0.0336
100	EN	0.1069	92.1660	0.8594	0.1509	0.3128	0.2198	0.6531	0.3893
	SSEN	0.0728	81.1419	0.8910	0.1304	0.2683	0.1875	0.5091	0.0828
	SSEN (IAR)	0.0953	57.4810	0.9467	0.0888	0.1865	0.1228	0.7289	0.0573
	Lasso	0.0630	93.1529	0.8557	0.1528	0.3138	0.2234	0.6322	0.1554
	SSL	0.0696	79.9220	0.8946	0.1279	0.2589	0.1828	0.2923	0.0477
	SSL (IAR)	0.1366	64.1930	0.9324	0.1004	0.2025	0.1407	0.6314	0.0502

^aDeviance.

^bMisclassification.

With respect to variable selection, the traditional elastic net (EN) captures the highest proportion of true non-zero parameters for all scenarios, and for any given scenario EN captures a higher proportion of true non-zero parameters compared to the lasso. However, in most scenarios examined, the traditional elastic net also had the highest estimated FDR. In general, it appears that including the IAR priors compromises between the traditional EN/lasso and the SSEN/SSL in that it tends to have FDR and proportion of non-zero parameters discovered in between the other two frameworks. However, for all models considered both FDR and proportion of true non-zero parameters included in the model is less than what we consider optimal.

We can gain additional insight by considering summaries of parameter estimates themselves. Here we consider grouped estimates of true zero and non-zero parameters, as shown in Figs. 1 and 2, which show the mean and standard deviations for estimates of non-zero and zero parameters, respectively; note that further details and discussion, as well as tables and figures are found in the supplementary materials. Not surprisingly, the average parameter estimates increase as the sample size increases. With respect to non-zero parameters, adding spatially structured priors to the model increases the average estimate at every sample size and for both the elastic net and lasso priors. This is an interesting contrast to the proportion of true non-zero parameters captured, where the traditional methods performed best. With respect to the true zeros, as was often the case with FDR, the models with spatial structure were not as low as the spike-and-slab models without spatial structure, but they were lower than the traditional models. This sheds light on how the spatial structure is leading to improved prediction error; presumably, the spike-and-slab models are estimating closer to the “true” non-zero parameter values. The average parameter values for the true zero parameters are also fairly close to zero, and so even when they are included, i.e., leading to higher FDR, they are small relative to estimates for true non-zero parameters, and so do not introduce much noise into prediction. This is a benefit of the spike-and-slab framework, where again as advertised the spike priors shrink “unimportant” parameters more than “important” parameters, at least on average.

Fig. 1.

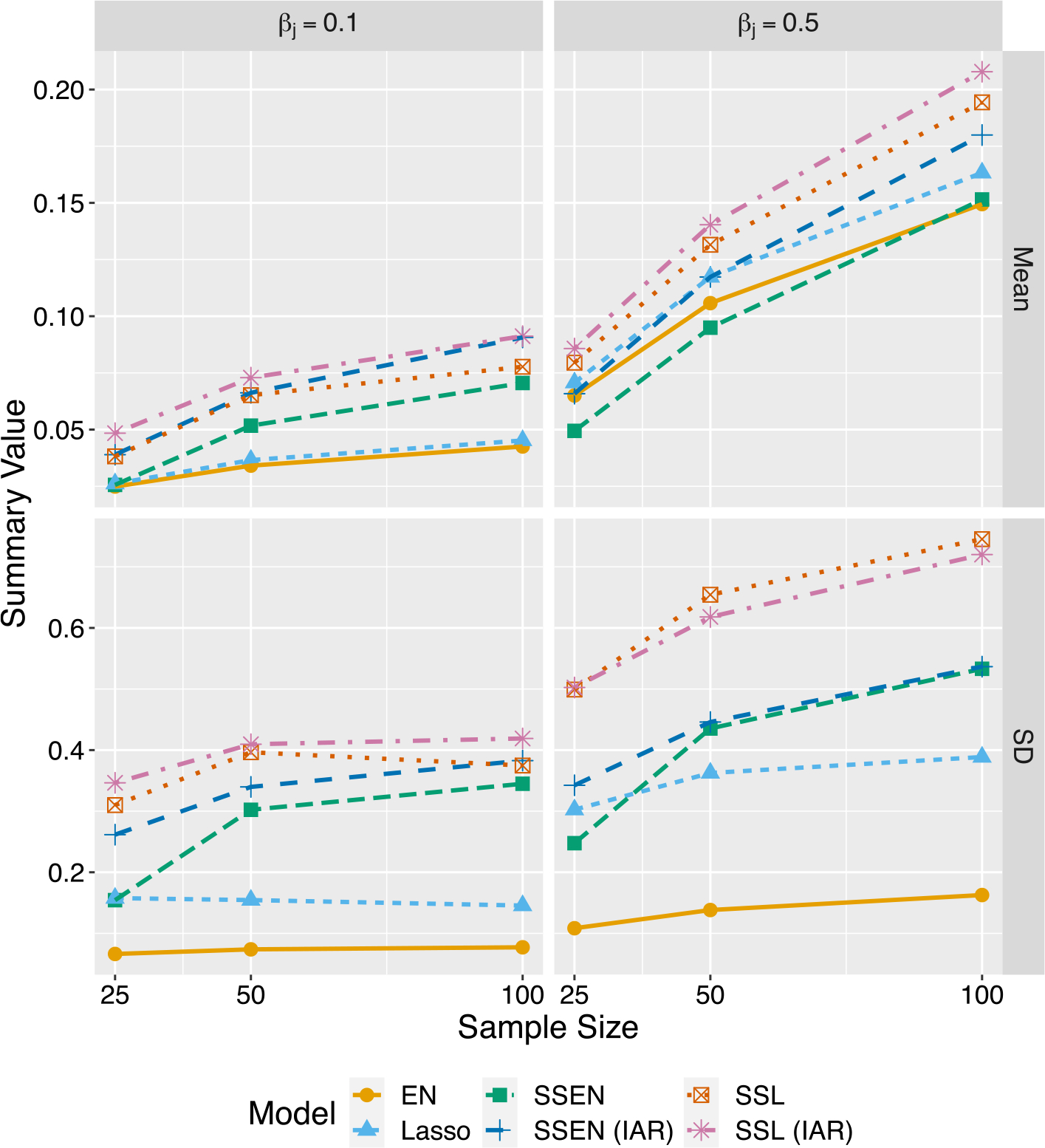
Collective average estimates for true non-zero parameters. Each dot summarizes all estimates for true non-zero parameters. SSL (IAR) usually has the least bias, but its variance is larger than most other models except SSL. Traditional models (EN and Lasso) have the lowest variance, tend to over-shrink parameters compared to the other models. SSEN (IAR) provides a best balance between bias and variance.

Fig. 2.

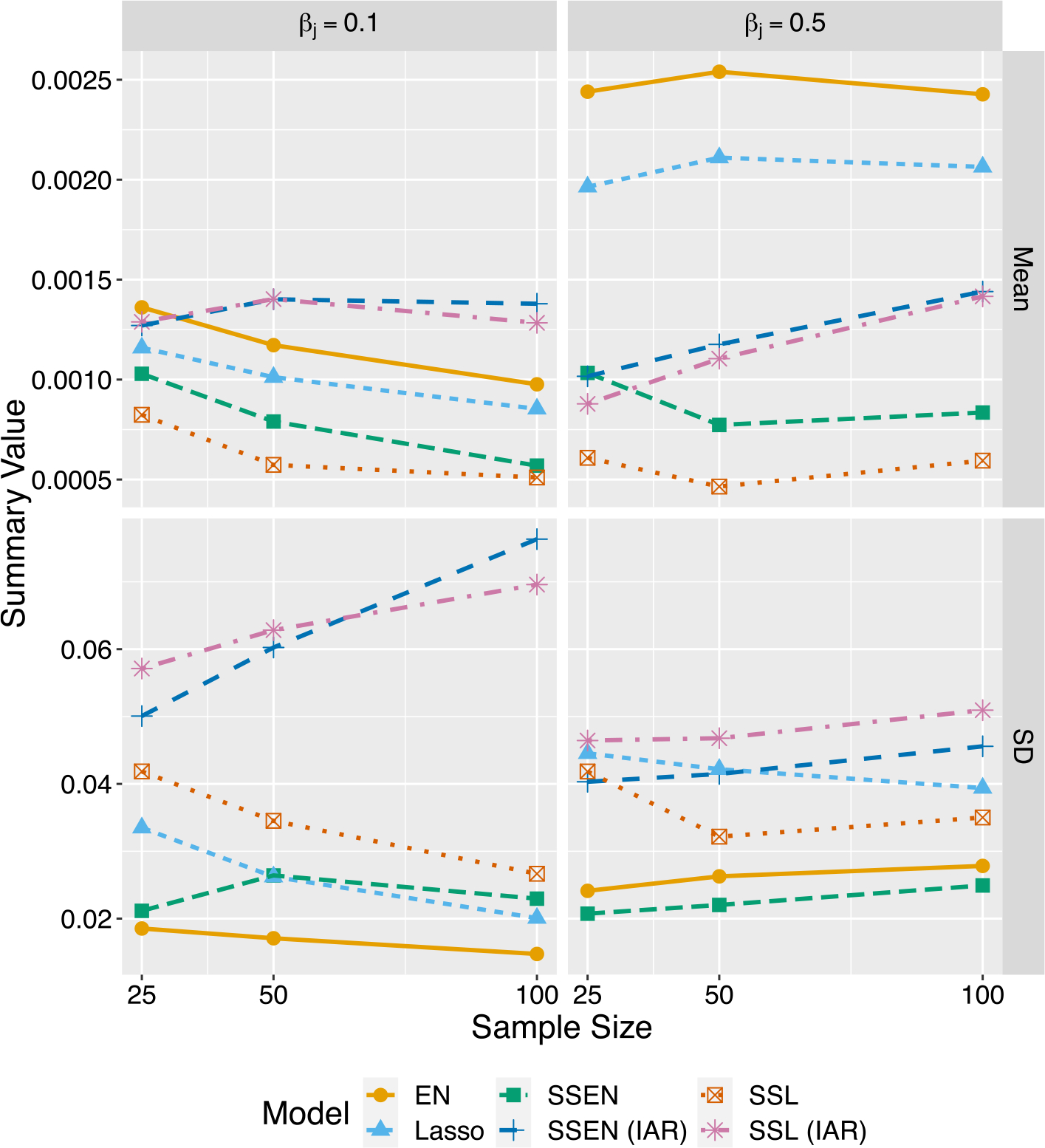
Collective average estimates for true zero parameters. Each dot is the summary measure of all estimates for true zero parameters. The β_j labels in this case correspond to the simulation scenario, but the true value for the parameters estimated here is zero. Estimates for irrelevant parameters tends to be near zero for all models. SSL and SSEN without spatial structure are the least biased, while the traditional and spatially structured models are slightly more biased. The traditional models tend to have the smallest variance, and again SSEN (IAR) appears to strike a comparatively good balance between bias and variance.

However, the mean parameter estimates do not by themselves show why the elastic with spatial structure outperforms the spike-and-slab lasso with spatial structure, but considering the variation in the estimates will help complete the story. For each prior structure, the EN version has lower variance compared to the lasso version, which implies that the bias–variance trade-off is best for the SSEN model with spatial structure and contributes to better prediction.

5. Application: Alzheimer’s disease

We also evaluated the proposed methodology using data obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (adni.loni.usc.edu). The ADNI was launched in 2003 as a public–private partnership, led by Principal Investigator Michael W. Weiner, MD. The primary goal of ADNI has been to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early Alzheimer’s disease (AD). Specifically, we modeled disease status using cortical thickness measures on the Desikan–Killiany atlas (Desikan et al., 2006); cortical thickness measures were estimated using FreeSurfer (Dale et al., 1999; Fischl et al., 1999; Fischl, 2012). The Desikan–Killiany atlas consists of 68 brain regions, 34 per hemisphere, and was used to specify the neighborhood matrix when including IAR priors on the logit inclusion probabilities. Specifically, two regions of the atlas were considered neighbors if they were in the same hemisphere and shared a border.

The analysis included 389 subjects, of which 234 (60.15%) were cognitively normal (CN), 116 (29.82%) were mildly cognitively impaired (MCI), and 39 (10.03%) had dementia. We then separately analyzed the three possible binary outcomes: CN vs. dementia, CN vs. MCI, and MCI vs. dementia. We examined model fitness for two levels of elastic net, ξ = {0.5, 1}, for the traditional models, spike-and-slab models without spatially structured priors, and spike-and-slab models with spatially structured priors. 5-fold cross validation was used to select the ideal scale parameters for both the slab (s₁ = {1, 1.5, 2, 2.5, . . ., 10}) and spike (s₀ = {0.01, 0.02, . . . 0.5}) distributions for the relevant models; for each scenario we chose the combination of s₀ and s₁ that minimized the cross validated deviance. All analyses were performed in R version 3.6.0.

Table 3 shows the estimated prediction error statistics when using cortical thickness as features. For each classification scenario, SSEN-IAR had the lowest model deviance, but in each case was closely followed by SSL-IAR. In general, model performance varied widely across outcome scenarios. The most noticeable variation was with AUC, which was above 0.95 for CN vs. dementia, between 0.62 and 0.69 for CN vs. MCI, and between 0.79 and 0.86 for MCI vs. dementia. Similar differences by classification scenario were present for MSE, MAE, and misclassification (MC).

Table 3.

Cortical thickness: Prediction error estimates.

	Model	s 0	s 1	Cross-validated average
				Dev.	AUC	MSE	MAE	MC
CN vs. Dem.	Lasso	0.002	0.002	90.321	0.952	0.046	0.094	0.063
	SSL	0.270	7.500	73.591	0.969	0.035	0.067	0.050
	SSL-IAR	0.260	6.000	70.865	0.972	0.035	0.069	0.049
	EN	0.001	0.001	84.257	0.958	0.043	0.088	0.057
	SSEN	0.260	10.000	71.964	0.970	0.036	0.077	0.051
	SSEN-IAR	0.280	10.000	67.023	0.975	0.034	0.073	0.049
CN vs. MCI	Lasso	0.007	0.007	425.341	0.622	0.208	0.414	0.289
	SSL	0.150	7.000	412.024	0.665	0.198	0.389	0.279
	SSL-IAR	0.140	4.000	402.915	0.684	0.194	0.381	0.272
	EN	0.006	0.006	423.658	0.629	0.207	0.410	0.290
	SSEN	0.140	4.500	410.785	0.665	0.198	0.392	0.278
	SSEN-IAR	0.150	7.500	399.505	0.694	0.192	0.377	0.276
MCI vs. Dem.	Lasso	0.009	0.009	140.894	0.790	0.148	0.293	0.210
	SSL	0.180	7.500	123.997	0.847	0.129	0.243	0.183
	SSL-IAR	0.140	4.000	122.383	0.849	0.126	0.244	0.172
	EN	0.006	0.006	135.305	0.813	0.142	0.278	0.205
	SSEN	0.140	7.000	120.445	0.853	0.124	0.244	0.171
	SSEN-IAR	0.140	5.500	119.196	0.856	0.123	0.246	0.165

6. Discussion

We have presented a novel approach to using the spike-and-slab prior with the elastic net when predictors exhibit spatial structure. The elastic net can be preferred to the lasso when the number of predictors far exceeds the sample size and when the predictors exhibit strong correlations. Since both the lasso and elastic net are expressible in a Bayesian framework they are reasonably amenable to a spike-and-slab prior framework, e.g., as explored in Ročková and George (2014, 2018). Our primary contributions were to incorporate spatial information into the model fitting process by placing intrinsic autoregressive priors on the logit of the probabilities of inclusion and to fit this model for GLMs by adapting the computationally efficient EM algorithm presented in Tang et al. (2017).

We explored the properties of this model using a simulation study, which while limited to only a few effect sizes and binary outcomes, yielded several important lessons. First, we demonstrated the potential for spike-and-slab models with spatially structured priors to improve upon their spatially unstructured counterparts; it is also noteworthy that the spike-and-slab models in general outperformed the traditional models with respect to cross validated prediction error, showing also that this prior framework may be fruitful for spatial data. While at least in the settings examined, the FDR and proportion of true non-zero parameters captured is not impressive for any model, and larger sample sizes would be necessary to achieve reasonable results on these metrics, the summaries for the parameter estimates themselves lend insight into why the spike-and-slab models with spatial structure are better fit. That is, in general the spike-and-slab models with spatially structured priors tend to produce estimates closer to the “true” values for “important” parameters and correspondingly shrink “unimportant” parameter estimates more strongly than do the traditional methods, which is consistent with other relevant literature and again demonstrates the power of combining spike-and-slab models with shrinkage penalties.

One might question the utility of placing IAR priors on the logit prior probabilities of inclusion in addition to an elastic net extension to the spike-and-slab lasso, given that the elastic net already encourages clustering (Zou and Hastie, 2005). The primary reason to use the IAR prior is that it can more precisely incorporate biological information about spatial structure into the model. Furthermore, in both the simulation studies and application to ADNI data, the best fitting models were those that incorporated the IAR prior and the elastic net extension, which further justifies both extensions. Moreover, model fitness was improved far more by including the IAR prior than using the elastic net penalty. That is, while SSEN (IAR) generally had the best performance, it was much closer in performance to SSL (IAR) than SSEN, as seen in Tables 1–3.

While the SSEN (IAR) models outperformed the SSL (IAR) models in the simulation studies and application presented, the difference in performance tended to be slight. However, an additional reason for preferring the SSEN (IAR) model is that it presents a better bias–variance trade off. Thus, since in practice one must usually analyze a single data set, it may be preferable to allow slightly more bias to obtain a more stable model.

While larger sample sizes may be desirable, many if not most real-world scenarios using images do not have very large sample sizes. Thus, it is relevant to probe how methods perform with smaller sample sizes and to understand what we can expect to learn in such circumstances. In addition, we showed that the improvements in model fitness were not restricted to the simulation scenarios; when applied to subjects from the ADNI data set, the best cross-validated model fits were models that included the spatially structured priors.

In the simulation study results were not sensitive to choice of s₁, and thus it was possible to follow the convention of fixing s₁ = 1. However, this was not the case in analysis of ADNI data, where model performance was sensitive to the choice of s₁. We stress that it is important to carefully choose the range of penalty parameters when applying the methodology presented in this work, and to perform sensitivity analysis to ensure that an appropriate range of values has been examined.

The proposed approaches in this work have many possible future directions and possible applications. Since the model is fit for GLM, it is amenable to the full range of non-linear outcomes ordinarily analyzed with GLM’s, and thus applications beyond Gaussian outcomes, or as shown here binary outcomes, is immediately possible without revision to the model. Given the strong performance with respect to cross validated prediction error, the algorithm may also be useful in classification problems and may be extended to handle more complex spatial relationships to better address difficult classification problems.