Automation and uncertainty analysis of a method for in-vivo range verification in particle therapy

Abstract

We introduce the automation of the range difference calculation deduced from particle-irradiation induced β⁺-activity distributions with the so-called most-likely-shift approach, and evaluate its reliability via the monitoring of algorithm- and patient-specific uncertainty factors. The calculation of the range deviation is based on the minimization of the absolute profile differences in the distal part of two activity depth profiles shifted against each other. Depending on the workflow of PET (positron emission tomography)-based range verification, the two profiles under evaluation can correspond to measured and simulated distributions, or only measured data from different treatment sessions. In comparison to previous work, the proposed approach includes an automated identification of the distal region of interest for each pair of PET depth profiles and under consideration of the planned dose distribution, resulting in the optimal shift distance. Moreover, it introduces an estimate of uncertainty associated to the identified shift, which is then used as weighting factor to “red flag” problematic large range differences. Furthermore, additional patient-specific uncertainty factors are calculated using available CT (computed tomography) data to support the range analysis. The performance of the new method for in-vivo treatment verification in the clinical routine is investigated with in-room PET images for proton therapy as well as with offline PET images for proton and carbon ion therapy. The comparison between measured PET activity distributions and predictions obtained by Monte Carlo simulations or measurements from previous treatment fractions is performed. For this purpose, a total of 15 patient datasets were analyzed, which were acquired at Massachusetts General Hospital and Heidelberg Ion-Beam Therapy Center with in-room PET and offline PET/CT scanners, respectively. Calculated range differences between the compared activity distributions are reported in a two-dimensional map in beam-eye-view. In comparison to previously proposed approaches, the new most-likely-shift method shows more robust results for assessing in-vivo the range from strongly varying PET distributions caused by differing patient geometry, ion beam species, beam delivery techniques, PET imaging concepts and counting statistics. The additional visualization of the uncertainties and the dedicated weighting strategy contribute to the understanding of the reliability of observed range differences and the complexity in the prediction of activity distributions. The proposed method promises to offer a feasible technique for clinical routine of PET-based range verification.

1. Introduction

PET-based monitoring is already clinically used for in-vivo treatment verification in proton and carbon ion tumour therapy (Enghardt et al. 2004, Hsi et al. 2009, Nishio et al. 2010, Bauer, Unholtz, Sommerer, Kurz, Haberer, Herfarth, Welzel, Combs, Debus & Parodi 2013, Min et al. 2013). The β⁺-decay of positron-emitting radionuclides, which are induced by nuclear interactions of the incoming beam with the traversed tissue can be detected with positron emission tomography (PET) during or shortly after the treatment. The comparison to predictions, typically obtained with Monte Carlo (MC) simulations, or to measurements from previous treatment fractions, may enable drawing conclusions on the consistency between planned and actual dose delivery, as well as on the reproducibility of the fractionated treatment course. So far, most of the reported clinical experiences have been limited to a qualitative comparison of two-dimensional β⁺-activity distributions sampled in different planes across the patient body, often complemented by a quantitative analysis of carefully selected depth activity profiles (Enghardt et al. 2004, Parodi et al. 2007, Knopf et al. 2008, Nishio et al. 2008, Bauer, Unholtz, Sommerer, Kurz, Haberer, Herfarth, Welzel, Combs, Debus & Parodi 2013). Recently, different strategies have been also proposed for a quantitative analysis of the activity depth profiles within the entire irradiation area (Unholtz et al. 2011, Helmbrecht et al. 2012, Min et al. 2013) or a statistical evaluation of a distal volume of interest (Kuess et al. 2012), but only tested on a restriced choice of measured and/or simulated datasets belonging to the same ion species and PET imaging strategy.

In this work, the most-likely-shift (MLS) approach is proposed for an automated in-vivo PET-based range verification using a mathematically determined criterion for identification of the distal region of interest for data analysis, and including information from the planned dose. The new method has been tested on data measured with in-room PET scans after proton treatment at MGH (Massachusetts General Hospital, Boston, MA), as well as with offline PET/CT scans after proton and carbon ion irradiation at HIT (Heidelberg Ion-Beam Therapy Center, Heidelberg, Germany). Both, the comparisons of measured data with MC simulated activity distributions and with scans from previous treatment fractions have been considered. Moreover, uncertainty factors have been introduced on the basis of available patient-specific information and a metric related to the algorithm performance, which can be visualized together or directly combined with the range difference maps in order to support the understanding and evaluate the reliability of the results from the newly developed range analysis tool.

In the following section, the basic principles of the range verification methods by (Knopf et al. 2008) and (Min et al. 2013) are reviewed, which are used in the development of the MLS approach and applied to the investigated data, respectively. Furthermore, the implementation of MLS and the calculation of all considered uncertainty factors is described. The application of the new range verification approach in comparison with calculations based on the method described in (Min et al. 2013) is given in section 3 for the irradiation of one phantom and 15 patients. Moreover, exemplary results of the uncertainty monitoring are presented. Finally, in section 4 the results of this paper are summarized and discussed.

2. Materials and methods

2.1. Range verification methods

2.1.1. Previously proposed approaches

In particle therapy facilities, different approaches for PET-based treatment monitoring are implemented. One method proposed by (Knopf et al. 2008) demonstrated the potential of considering the entire distal fall-off of two three-dimensional activity distributions for the range verification. For this analysis in the so-called “beam’s-eye-view” (BEV), at every (x, y)-coordinate the activity profiles A(z) in beam direction are normalized to their maximum and shifted against each other in order to calculate the profile difference f_diff(δ, z_min) as:

$$f_{\text{diff}}(\delta ,z_{min})=\sum _{z_k\in I}\mid A_1(z_k)-A_2(z_k-\delta )\mid ,$$ (1)

with the considered depth interval I = z_min ≤ z_k ≤ z_max, where z_min and z_max mark the depth positions of the last local maximum and the end of the activity profile, respectively. The shift between the profiles is determined as the shifting step δ, which minimizes f_diff (δ, z_min) (Knopf et al. 2008). The minimum profile difference is

$$f_{min}(z_{min})=\underset{\delta }{min}\left(f_{\text{diff}}(\delta ,z_{min})\right).$$ (2)

For reasons that will soon become apparent, we make the dependence on z_min explicit in these equations.

A different strategy to calculate the range deviation between two activity distributions is the middle point (MP) analysis by (Min et al. 2013), which is suggested to detect the range shift by defined thresholds of the distal activity fall-off. For each pair of depth profiles, the 50 % and 25 % fall-off depth positions z_0.50 and z_0.25, respectively, are determined. The middle point z_mid and the resulting range difference Δz_mid between two profiles are defined for every (x, y)-coordinate as follows (Min et al. 2013):

$$z_{\text{mid}}=(z_{0.25}+z_{0.50})/2,$$ (3)

$$\mathrm{\Delta }{z}_{\text{mid}}=z_{\text{mid},1}-z_{\text{mid},2}.$$ (4)

So far, the approach was applied to in-room PET scan results performed for several head tumour patients after proton-irradiation at MGH (Min et al. 2013).

Different methods, as reported in (Helmbrecht et al. 2012, Kuess et al. 2012) have not considered the comparison of simulated and measured proton data and are therefore not included in this study.

2.1.2. Most-likely-shift approach

The most-likely-shift approach is introduced to overcome the weakness of the method proposed by (Knopf et al. 2008), which is the somewhat arbitrary identification of the last distal maximum in PET profiles exhibiting multiple local maxima, as shown in figure 1 (a). In MLS, the original shifting method (1) is retained, but complemented by a different definition of the analysis window of the activity depth profiles. In essence, the basic idea is to introduce a suitable cut-off of the distal activity profile in order to reduce the influence of statistical noise and, more importantly, to introduce an adaptive choice of the proximal threshold z_min maximizing the reliability of the search for the most likely shift between the two distributions.

Figure 1.

Basics of range verification, exemplarily shown for the voxel coordinates (x, y) = (70,59) in patient P₃ (cf table 1). Left: β⁺-activity profiles obtained by MC simulation and in-beam PET measurement, normalized to the maximum, as well as the corresponding dose profile are shown. The blue lines denote the location of the activity maximum, the 50 % dose fall-off (vertically, left to right) and the 20 % activity limit (horizontally). Right: The profile difference D_diff is visualized as function of the profile shift for different analysis starting depths z_min.

For every (x, y)-coordinate within the treatment field, the depth interval is automatically selected. The upper boundary z_max is defined as the maximum depth between the 50 % dose fall-off, which is already deeper than the typical range definition of protons and carbon ions at the 90 % dose fall-off, and the 20 % activity fall-off, which was found to be the level below which measured activity starts to be highly sensitive to noise (Parodi et al. 2007, Knopf et al. 2008, Min et al. 2013). The lower boundary z_min is varied within I_z:

$$I_z=z_{\text{prox}}\le z_{min}\le z_{\text{dist}},$$ (5)

where z_prox gives the location of the activity maximum within the considered profile and z_dist is defined by z_dist = z_max − 5 mm, using a 5 mm margin to exclude the possibility of a comparison within a depth interval smaller than the spatial resolution of typical PET scanners. Similar to the original shifting approach, the activity profiles A₁ and A₂ are normalized to their maximum. For δ in the interval I_δ ranging from −20.0 mm to 20.0 mm in steps of 1 mm (according to the z-resolution of the data used within this work), the profile difference f_diff (1) is calculated for every z_min in I_z, also sampled at a 1 mm depth resolution. This procedure results in large uncertainties of the determined range shift in the case of a profile difference minimum with shallow gradients, but gives a more stable range deviation if a pronounced minimum is present (cf figure 1 (b)). As a measure of the “stability” or reliability of the range shift we therefore introduce the root-mean-square deviation (RMSD) D_diff between f_diff and f_min (2):

$$D_{\text{diff}}(z_{min})=\sqrt{\frac{1}{n}\sum _{\delta \in I_{\delta }}{\mid f_{\text{diff}}(\delta ,z_{min})-f_{min}(z_{min})\mid }^2},$$ (6)

where n = |I_δ| is the number of evaluated profile shifts. The best choice for z_min is the one that maximizes D_diff. We call that optimal z_min value the z_MLS:

$$z_{\text{MLS}}=\underset{z_{min}}{\text{argmax}}\left(D_{\text{diff}}(z_{min})\right).$$ (7)

Now, the profile difference calculation according to (1) within the optimized depth interval z_MLS ≤ z ≤ z_dist results in what we call the most-likely-shift δ_MLS, meaning the most probable (not in a rigorous mathematical sense) estimate of the unknown underlying shift:

$${\delta }_{\text{MLS}}=\underset{\delta }{\text{argmin}}\left(f_{\text{diff}}(\delta ,z_{\text{MLS}})\right).$$ (8)

Moreover, the steepness of the local minimum, quantified by D_diff (z_MLS), can be associated to the uncertainty, and hence reliability, of the identified shift, as discussed in the next section.

2.2. Evaluation of uncertainties

For eventual clinical application it is desirable to visualize the uncertainties associated to the identified shifts and, ideally, develop a strategy to “red flag” those range differences likely attributed to a treatment delivery problem. To this aim, we consider different factors which introduce uncertainties in the range verification, referred to as internal and external in the following investigations. External factors address the comparability of two activity distributions, including the accuracy of co-registration and the stability of the used range verification approach, especially under consideration of effects due to low counting statistics. Internal factors refer to the impact of uncertainties in the used calculation models, including effects from washout, reaction cross-sections and computed tomography (CT) range conversion, which describes the relation of CT Hounsfield units (HU) to stopping power in human tissue relative to water. This is the central information used for treatment planning on the patient model provided by the planning CT. Thus, internal factors only affect the results comparing simulated and measured data.

In order to analyze the described effects on the basis of depth profiles of different quantities, a proximal window is defined by z_min,p, the proximal depth position of 10 % of the maximum CT number, and z_prox, the depth position of the activity maximum in the considered profiles (cf section 2.1.2). Moreover, the full penetration depth is considered by the interval I_z,Full = z_min,p ≤ z_i ≤ z_dist.

2.2.1. Estimation of external factors

In the case of two different PET/CT datasets, the corresponding CT scans are overlayed and co-registered mostly based on the bony structures. A profile shifting analysis similar to (1) is performed in the proximal window between both CT datasets to detect possible discrepancies that can occur already in the entrance region, as for example due to wrong positioning. In addition, the standard deviation of the HU values along the considered profile is calculated within I_Full providing information about the inhomogeneity and the conformity of the CT images. Furthermore, the CT information is used to calculate the ratio of water-equivalent to geometrical range along the beam penetration depth for each considered lateral position in beam-eye-view.

The reliability of the range difference results depends highly on the approach used for the range verification calculations. In the case of MLS, the magnitude of D_diff (6) is directly related to the stability of the profile difference minimum and thus used for the calculation of a weighted range shift, which is performed at all x and y positions:

$${\delta }_{\text{stab}}=\mid {\delta }_{\text{MLS}}\mid ·\frac{D_{\text{diff}}}{D_{\text{diff}}^{max}},$$ (9)

where $D_{\text{diff}}^{max}$ describes the maximum D_diff of the global PET distribution. This approach basically enhances “likely true” (i.e., large weighting factor) large shifts and suppresses “likely false” (small weighting factor) large shifts, while almost not affecting unproblematic small shifts regardless of the weighting factor. Only the absolute value of δ_MLS is used, as this stability weighting specifically aims at highlighting (“red flag”) those parts of the range difference maps where critical large shifts (regardless of the sign) are reliably detected.

For the quantification of range uncertainties due to statistical effects, five reference profiles per patient with comparatively high mean activity 〈 A 〉_dist in the distal window have been selected. The profiles were reduced in amplitude by a factor of 〈 A 〉_red/〈 A 〉_dist, using different values of 〈 A 〉_red in the range from 20 Bq/ml to 1000 Bq/ml. Poisson noise was then artificially added to the reduced profiles, which were compared in range to the original profile using the MLS method. The calculation was performed in 5000 iterations by shifting the profiles normalized either to their maximum A_max, or to the mean activity around the maximum, averaged on the depth z_med = z(A = A_max) ± 2 mm.

2.2.2. Estimation of internal factors

Several intrinsic biological and physical limitations affect the simulation of activity distributions. For practical reasons addressed in section 4, this work has been focused on the impact of the CT-range calibration curve. In (Espana & Paganetti 2011, Paganetti 2012), the resulting range uncertainties are quantified as 0.2 % of the water-equivalent particle range, with additional 1.5 % caused by the effect of the mean excitation energy in tissue, confirming the reports of former studies (Schaffner & Pedroni 1998). For the calculation of the CT conversion uncertainty of every depth profile, these factors are applied on the water-equivalent range within I_z,Full, which is calculated from the CT HU values using the CT conversion calibration curve specific to the used imaging protocol.

2.3. Data analysis

The MeVisLab software framework SimInterface developed at HIT (Unholtz et al. 2011) is used for importing the different datasets to be analyzed, their co-registration matrix based on the available CT scans, and a geometrical transformation aligning the z-axis with the beam direction. In this computational environment, additional software has been coded to provide all the necessary calculations for the range verification and estimation of uncertainties, together with a graphical user interface. The data can be exported in different formats for further dedicated processing outside of the considered standard workflow. This option was also used in this work in order to perform part of the dedicated data analysis with MATLAB [MathWorks, Inc.].

In the following comparison of pairs of activity distributions, the depth profiles of every (x, y)-coordinate are investigated and only those profiles are considered, whose integrated activity is at least 20 % of the maximum profile integrated activity in the whole distribution to exclude the contribution of background as in (Min et al. 2013). Data analysis included validation of the proposed approach in cases of controlled, artificially created range shifts (cf 2.2.1), as well as clinical evaluation for patients imaged with in-room PET and offline PET/CT scanners after irradiation at different facilities with different ion species and beam delivery techniques (cf section 2.4.2). In particular, we provide comparisons of the new MLS method with the most recently proposed middle point method, including a quantitative analysis similar to (Min et al. 2013) for average range differences as well as RMSD within the selected treatment area for all the considered patient cases.

2.4. Validation and clinical evaluation

2.4.1. Controlled shift

Reliability and accuracy of the MLS detection is examined by artificially shifted distributions. A homogeneous monoenergetic proton-irradiation of a PMMA (Polymethyl Methacrylate) phantom was MC simulated as reference and artificially shifted in depth by 0.5 mm, 1.0 mm, 1.5 mm and 2.0 mm for selected regions (cf figure 3(a)). The resulting datasets created with a scoring grid of (2.0 × 2.0 × 0.5) mm³, are analyzed.

Figure 3.

Detection of simulated range deviations in activity distributions in a PMMA phantom. The shifts of the proximal edge (left) and the correlated results of the distal shift obained by the most-likely-shift (middle) and the middle point (right) analysis are shown.

To study comparable effects for human tissue, exemplary simulated and measured activity depth profiles of in-room and offline proton and offline ¹²C-ion patients are investigated with respect to the sensitivity of artificial shifts in the measured profiles starting at the 50 % and 35 % distal fall-off regions, as demonstrated in figure 2. This modification would correspond to a minor reduction of material in the beam path, masked by partial volume effects in terms of retained activity intensity. In addition, this study investigates the effect of a strong activity maximum on the range verification analysis.

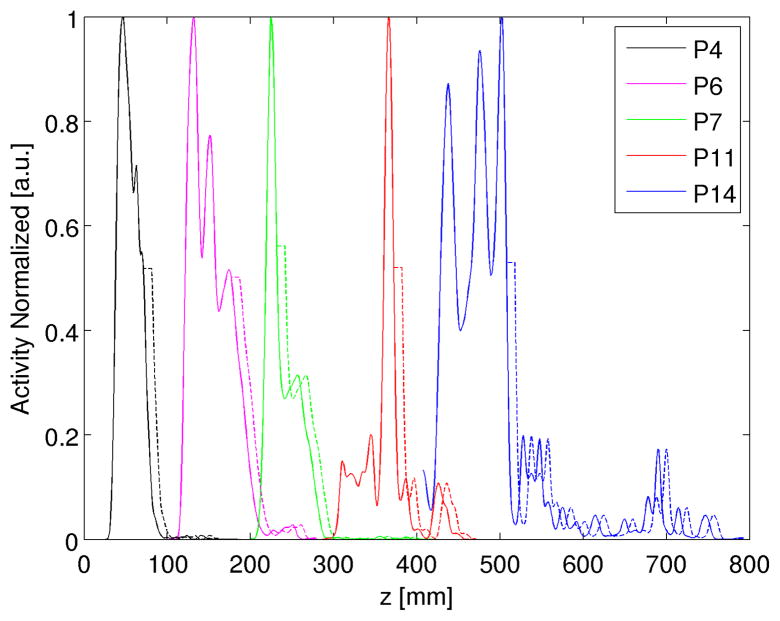
Figure 2.

Exemplary activity profiles (solid lines) obtained from in-room PET measurements of the proton patient P₄ (black) as well as from offline PET measurements of the proton patients P₆ (magenta), P₇ (green) and of the ¹²C-ion patients P₁₁ (red), P₁₄ (blue), normalized to their maximum. Starting at the 50 % activity fall-off, the profiles are shifted in depth by a constant offset (dashed lines), in the demonstrated case about 10 mm. For visualization, the original depth coordinates of the profiles are modified.

2.4.2. Patient data

For the clinical investigation, datasets of representative patient irradiation at MGH and HIT are selected, as listed in table 1. At MGH, in-room neuro PET measurements of head tumour patients are realized in the treatment room after passively scattered proton irradiation. The acquired data are compared to MC simulations performed with the Geant4 code (Agostinelli et al. 2003), as described in (Min et al. 2013). The full-ring offline PET/CT scanner at HIT enables the application of PET-based verification for several body regions, treated with scanned ion beams. Therefore, proton-irradiation induced activity in head tumours as well as ¹²C-irradiation induced activity in head, liver tumours and sacral chordoma are considered in the evaluation. In addition to measured data from multiple scans, MC simulations with the FLUKA code (Ferrari et al. 2005, Battistoni et al. 2007) are considered, which in the case of proton beams include optimized cross-sections for β⁺-reaction channels (Bauer, Unholtz, Kurz & Parodi 2013) and, for head tumours, improved tissue classification based on MR (magnetic resonance) information (Bauer, Unholtz, Sommerer, Kurz, Haberer, Herfarth, Welzel, Combs, Debus & Parodi 2013) for more accurate predictions. For all calculations, the analyzed subvolumes are interpolated to a grid of (2.0 × 2.0 × 1.0) mm³ in BEV, comparable to the typical TPS dose grid of (2.0 × 2.0 × 2.0) mm³, but ensuring an accuracy of 1 mm along the beam direction for more reliable range difference results.

Table 1.

Details on the selected patient data. For all investigated datasets from MGH and HIT, the ion species, the location of the tumour and the time structure of the performed PET measurements (M) are listed, including the irradiation time t_irr, the delay time between end of irradiation and start of PET measurement t_del and the duration of PET data acquisition t_aq. Besides, the average depth of the 50 % dose fall-off z_D,50 is given. Measurements after several fractions are numbered in brackets.

ID	Institution	Particles	Location	M	Treatment times			zD,50 [mm]
					tirr [s]	tdel [s]	taq [s]
1	MGH	protons	head		31	129	1200	88.86
2					37	114	1200	85.08
3					117	89	1200	92.04
4					90	152	1200	34.95
5					33	140	1200	57.73
6	HIT	protons	head	[1]	687	454	1800	70.25
				[2]	842	421	1800	69.19
				[3]	965	424	1800	69.06
				[4]	677	430	1800	69.83
7					329	351	1800	57.09
8					249	371	1800	77.75
9					115	538	1800	110.83
10					115	420	1800	50.00
11	HIT	12C-ions	head		431	403	1800	68.56
12					392	497	1132	56.69
13	HIT	12C-ions	liver	[1]	3638	645	1800	113.41
				[2]	4035	589	1800	110.68
				[3]	2715	727	1800	111.39
14					171	811	1800	64.65
15	HIT	12C-ions	sacral		1026	766	1800	268.35

3. Results

3.1. Range verification

3.1.1. Controlled shift

In figure 3(a), the investigated effect of simulated range shifts on proton-induced activity distributions within a homogeneous PMMA phantom is presented. Using the profile shifting method (1), the differences in the proximal window confirm the magnitude of the introduced shifts (left). For the corresponding distal shifts, both, the MLS (middle) as well as the MP (right) results show a very good agreement between artificially simulated and analyzed range differences, with more precisely reproduced lateral edges by MLS.

In the analysis of the artificially shifted profiles, a sensitivity of 1–2 mm regarding the shift in the distal fall-off could be detected by MLS for both 50 % and 35 % in the case of offline PET measurements after ¹²C-ion irradiation. The studies profiles of proton irradiation-induced activities show about 2 mm accuracy for the in-room and the offline result of P₄ and P₆, respectively, whereas a deviation of up to 5 mm has been observed in the profiles of P₇. This is most likely caused by the enhanced influence of the pronounced activity maximum, as shown in figure 2 and figure 5. It needs to be noted that the same tendency was observed by applying the range verification approach by (Knopf et al. 2008) only to the restricted fall-off region 70–40 %, according to (Helmbrecht et al. 2012). However, a fixed 70–40 % analysis window would have missed detection of changes below 35 %. Similarly, in the MP results, shifts in the distal fall-off region of < 50 % are always underestimated per construction (as one point of the analysis is fixed and one is shifted).

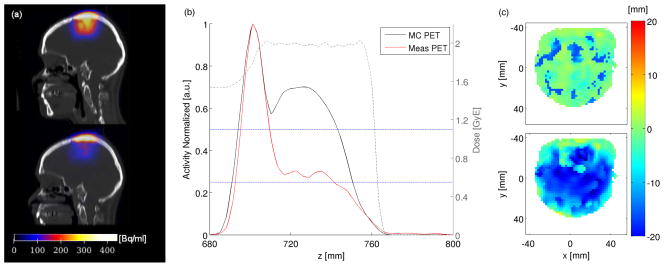
Figure 5.

Range verification of the proton-irradiation induced activity in P₇. (a) Exemplary sagittal planes of the simulation (top) and the offline PET measurement (bottom) are displayed. (b) The corresponding normalized activity depth profiles are shown together with the dose profile. The activity fall-off thresholds of 25 % and 50 % are marked by blue lines. (c) The MLS results (top) show only small deviations in most parts of the distribution compared to the MP (bottom) calculations.

3.1.2. Patient application

In this section, the results obtained from MLS as well as from MP calculations are reported for the patient cases. Range verification of proton and ¹²C-ion irradiation-induced activity is performed on the one hand between simulated and measured distributions, and on the other hand between several measured distributions obtained from PET/CT scans after different therapy fractions. The mean values and the RMSD of the detected range shifts for all investigated patients are listed in table 2. The results demonstrate the comparability of the two approaches in the case of high statistics, given by a high maximum activity in the case of in-room data acquisition for P1–P5. Low statistics and a less water-equivalent material (i.e. larger deviation between geometrical and water-equivalent depth) enhance the limitations of the MP approach, whereas the reasonable RMSD of the MLS results indicate more homogeneous results with less hotspots in the two-dimensional range difference maps. The general tendency towards negative shifts is further investigated in section 3.2.

Table 2.

Detected range shifts. The average values (Av) and the RMSDs of the calculated range deviations between the investigated datasets are presented for both, MLS and MP results. Simulated (S) and measured (M) distributions are compared. In addition, the mean values of the profile activity maxima and the ratio of geometrical depths (Geom) and water-equivalent path lengths (WEPL) are given (for both available CT data in the case of HIT data).

ID	Analysis	MLS		MP		Av Max Activity [Bq/ml]	Av WEPL/Geom
		Av [mm]	RMSD [mm]	Av [mm]	RMSD [mm]
1	S/M	−3.89	5.29	−2.50	6.80	1.25/0.59 ·103	0.91
2	S/M	−2.50	7.60	−0.55	9.09	544.24/591.65	0.89
3	S/M	0.53	7.01	5.59	8.39	625.87/654.46	0.84
4	S/M	2.78	2.98	4.04	1.87	352.62/333.08	0.78
5	S/M	−0.70	4.01	−0.78	6.48	533.51/537.25	0.86
6	S/M1	−0.45	3.11	−20.70	13.47	274.75/123.13	1.11/1.11
	M1/M2	0.20	3.13	−1.07	8.78	115.30/115.53	1.00/1.00
	M1/M3	1.15	3.85	1.18	0.95	115.30/113.36	1.00/1.00
	M1/M4	0.49	4.19	0.15	9.30	115.30/113.36	1.00/1.00
7	S/M	−3.04	5.04	−11.50	7.03	281.20/302.24	0.86/0.86
8	S/M	−4.15	4.55	−5.07	7.26	357.73/233.10	0.88/0.88
9	S/M	−4.77	8.47	−6.90	10.61	129.00/120.74	0.94/0.95
10	S/M	−1.04	3.37	−5.07	5.59	275.21/282.18	0.85/0.84
11	S/M	0.66	4.02	3.72	8.01	13.44/25.82	0.94/0.93
12	S/M	0.85	5.94	5.62	11.29	23.49/28.56	0.83/0.85
13	S/M1	−2.04	8.29	31.50	46.98	137.67/120.56	0.91/0.88
	M1/M2	0.08	7.64	7.54	52.18	126.52/107.36	1.51/1.51
	M1/M3	−3.73	8.40	7.91	62.44	126.80/92.59	1.50/1.50
14	S/M	0.32	7.41	22.77	34.05	49.71/59.07	0.92/0.91
15	SA/M	4.26	11.25	29.87	33.00	93.73/69.44	0.91/0.89
	SB/M	0.71	8.34	22.35	28.97	86.43/67.95	1.18/1.17

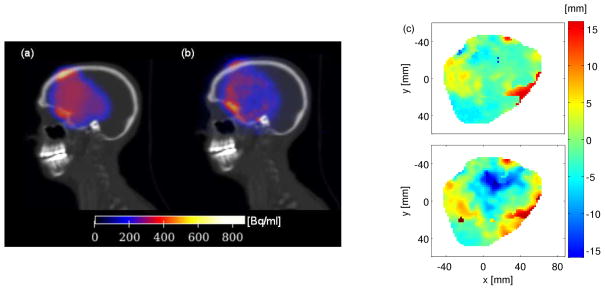
In figure 4, the isocentric slices of the simulated and in-room PET measured proton irradiation-induced activity of patient P₅ are shown. The overall agreement of the activity distributions is evident and confirmed by the range difference calculations (cf figure 4(d)). The MLS and the MP analysis show only small deviations in large parts of the distribution, but a pronounced maximum at the right edge, resulting in RMSDs of 8.47 mm and 10.61 mm, respectively. This may be caused by uncertainties in the co-registration of stand-alone PET and treatment planning CT (TP-CT) data, as reported in (Min et al. 2013). The good statistics from in-room measurements (cf table 2) leads to a generally reasonable agreement in the results of the two calculation methods with mean differences well below the RMSDs.

Figure 4.

Proton-irradiation of P₅. The isocentric sagittal slices of the simulated (a) and the in-room measured (b) activity are displayed in beam-eye-view. Furthermore, the activity range shift evaluated with MLS (top) and MP (bottom) are visualized (c).

Especially in the case of offline PET measurements after proton therapy, more fluctuations in the activity profiles due to lower statistics, as well as the larger effect of washout and the shallow distribution of the dominant ¹⁶O(p,3p3n)¹¹C reaction channel in oxygen rich tissue complicates the analysis. In figure 5, simulated and measured activity distributions for patient P₇ as well as the respective depth profiles show a clear activity maximum in skull bone and indicate a good range agreement, despite obvious limitations of washout modeling in the brain region. This is confirmed by large parts of the MLS results, while the MP approach detects a strong undershoot of the delivered field (cf figure 5(c)).

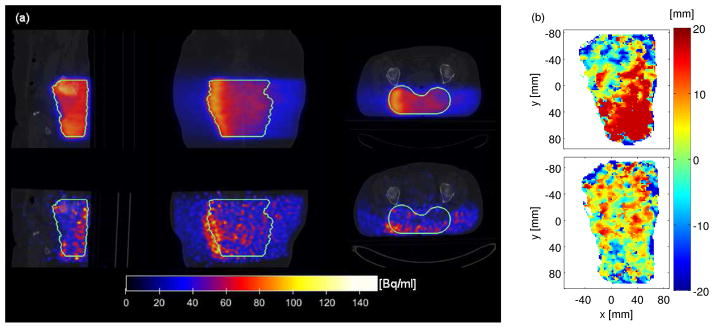
Figure 6 gives an example for the application of PET verification after carbon ion therapy. In the visualized coronal and transversal slices, a clear ¹²C-ion overshoot is detected in the measured activity distribution of patient P₁₅. This range difference is confirmed by the MLS results (cf figure 6(a)). As a consequence, the simulation was redone based on the CT obtained from the PET/CT scan after the treatment (S_B in table 2). The overshoot could be reproduced and the corresponding MLS analysis shows a good conformity of the two distributions. It has to be noted that the presented overshoot was not of clinical relevance for the patient.

Figure 6.

Comparison of carbon-ion irradiation-induced activities in P₁₅. (a) The simulated (top) and the measured (bottom) distributions at axial and horizontal planes through the target volume (contoured by the green line) are shown. (b) The most-likely-shift results are presented for the analysis of measurement against simulation S_A (top) and S_B (bottom), which are obtained based on the TP-CT and the PET/CT, respectivley.

In the case of repeated PET/CT scans at different days, the measured data can be used to check the reproducability of the delivery throughout the fractionated treatment course. In figure 7, the most-likely shifts between the activity measurements of the first and three further PET/CT scans of patient P₆ are displayed. The results show good agreement in the evaluated distributions with mean deviations of (0.61±0.23) mm.

Figure 7.

Range verification with several offline measured activity distributions after different treatment fractions of P₆. The most-likely shift for the analysis between M₁ and M₂ (a), M₁ and M₃ (b) as well as between M₁ and M₄ (c) is shown.

3.2. Estimation of uncertainties

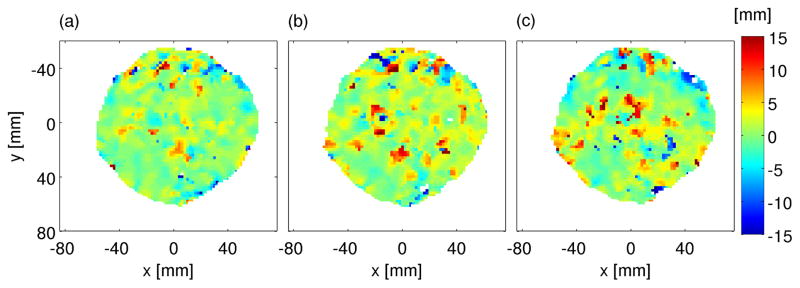
The quantification of uncertainties offers the possibility of using additional information from the evaluation method and the patient data to estimate the reliability and accuracy of detected range shifts, with the final goal of identifying delivery problems which would call for further action. This is in the following demonstrated mainly by the results based on the data from patient P₁₅. Figure 8 shows the results related to the MLS approach. The range deviation maps can be weighted with the stability metrics D_diff (6) to restrict absolute large deviations to the most-likely ones. In the considered example, the overshoot in the region of interest is confirmed to be reliable.

Figure 8.

Uncertainty of the evaluation approach applied to the datasets of P₁₅. For every x, y-coordinate, the range difference (a) is weighted with D_diff (b) to results in the stability-weighted shift map (c).

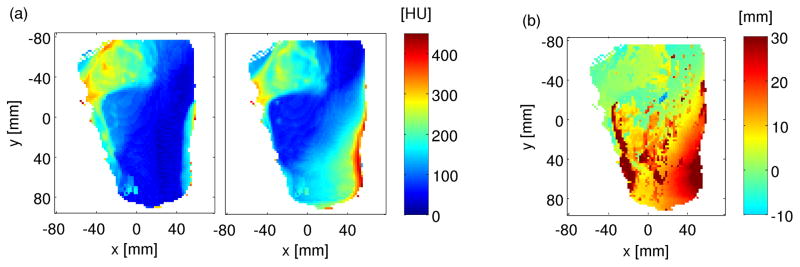
The standard deviations (σ_HU) calculated from the HU values of TP-CT and PET/CT scanner within the entire penetration depth I_z,Full (cf figure 9(a)) show an obvious difference in the same region where also a proximal shift can be detected by the shifting analysis between the CT profiles in the proximal window (cf figure 9(b)), since the analysis is performed within the same depth interval in both datasets. The reported findings indicate anatomical changes or a difference in patient positioning.

Figure 9.

CT-related monitoring of range deviations using the TP-CT and the PET/CT of P₁₅. (a) Standard deviations of HU units within the full window I_full of TP-CT (left) and PET/CT (right). (b) Shifts calculated between the CT datasets within the proximal window.

In figure 10, a dependence of the shift on the statistical mean value of the distal analysis window (cf section 2.2.1) is demonstrated for the data from several patients. The deviation between reference and modified profile from different data sets with sufficiently high statistics increases for smaller mean activity values, with a pronounced tendency towards negative shifts. This is attributed to larger influence of the statistical noise. The results improve significantly by changing the normalization of the profiles for the analysis from the activity maximum A_max to the mean activity A_med within the depth range z_med = z(A = A_max) ± 2 mm. The deviation of up to 3 mm in range, depending on the datasets, correlates to changes in the absolute value of A_med of about 3 % for both, offline and in-room results. An additional dependence of statistical uncertainties on the composition or the tissue heterogeneities as function of σ_HU was not observed. In activity distributions obtained from patient measurements, fluctuations were found to be less pronounced compared to the investigated Poisson noise on simulated data. Here, the differentiation between A_max und A_med was found to have only negligible influence on the results. This can be ascribed to the post-reconstruction filtering of the measured data, and the Gaussian smoothing of simulated distributions (Bauer, Unholtz, Sommerer, Kurz, Haberer, Herfarth, Welzel, Combs, Debus & Parodi 2013). The averages of the measured activity in the distal window and the positions of the activity maximum in the analysis of P₁₅ are very homogeneous among the different depth profiles, and do not indicate remarkable uncertainties due to very low statistics in the considered region. Besides, for the considered activity of ≈ 145 Bq/ml (cf table 2) the statistical uncertainties of figure 10 remain below the observed range deviation of ≈ 20 mm.

Figure 10.

Calculated shift between simulated profiles and manipulated profiles with artificially added noise for four exemplary head proton patients depending on their mean activity value within the distal window. For the analysis, profiles have been normalized on A_max (circles) or on A_med (crosses).

In addition to the already discussed external factors, the results of the analysis of the external and internal WEPL-based factors for patient P₁₅ are shown in figure 11. The ratio of water-equivalent and geometrical distance shows a very homogeneous distribution close to 1 (i.e., water-like tissue) and a deviation in the lower right corner that indicates a change in CT profiles obtained from the PET/CT scan compared to the one based on the TP-CT, corresponding to the shift detected in figure 9. Figure 11(b) visualizes the internal uncertainties that are caused by the conversion of the CT numbers into water-equivalent path length, according to (Paganetti 2012). This shows that the observed range shift of up to 20 mm exceeds the intrinsic uncertainty of the CT range calibration curve, thus supporting the hypothesis that the nature of the shift is rather due to external factors such as patient positioning.

Figure 11.

WEPL-related uncertainty monitoring for patient P₁₅. (a) Ratio between water-equivalent and geometrical path lengths based on both, TP-CT (left) and PET/CT (right). (b) Uncertainties caused by CT conversion.

4. Discussion

The most-likely-shift approach was introduced for an automated PET-based treatment verification and implemented as convenient user interface in MeVisLab for application in the clinical routine at HIT. The analysis between PET activity simulation and measurement as well as between several measurements was performed for different clinical cases of data acquired at different facilities with different PET scanners, ion species and beam delivery.

The approach is based on a modification of the shifting analysis of (Knopf et al. 2009), where the consideration of the entire profile fall-off compared to single point approaches was found to be almost insensitive to the influence of background noise. Moreover, it is more robust to fluctuations and to low statistics than single point approaches as MP, which is especially important for facilities using offline PET imaging strategies. With the likelihood analysis proposed in this work, the MLS approach overcomes the limitations of the original shifting approach, which was the somewhat arbitrary definition of the distal last maximum. The stability of the profile difference minimum is used for the detection of the most likely range deviation in the automatically selected analysis window, and as criteria for the reliability of the range shift results. In particular, the latter weighting factor is introduced to visually highlight and “red flag” reliably identified large shifts which are assumed to be problematic regardless of the positive or negative sign, thus offering a valuable tool to support decisions in a clinical workflow.

The proof of principle of the introduced method was shown in controlled shift applications. The accuracy of range deviations is given by the image resolution in beam direction and the influence of the activity profile maximum. Exemplary patient data from HIT and MGH were investigated with MLS and MP. The average and standard deviation of the resulting range difference maps have been calculated and demonstrate better robustness for the most-likely-shift approach. The influence of statistics was quantified by the comparison between simulated reference profiles and modified profiles with artificially added Poisson noise. It needs to be noted that, although the noise did not significantly affect the maximum of the activity profiles in the evaluated patient cases, it can explain the observed tendency towards negative shifts in table 2. In the performed sensitivity studies comparing simulated and artificially shifted measured profiles, a degradation of accuracy by about 2–3 mm for the detection of range shifts at the 50 % and 35 % activity fall-off levels was found in the presence of a strongly pronounced proximal activity maximum, as in the case of offline PET measurements after proton irradiation of P₇ (figure 5). Despite this limitation, MLS leads to more reasonable range shift results compared to MP, which in this example predicts range deviations of up to 20 mm (which do not seem to be confirmed by the data, but rather ascribed to insufficient similarity of simulated and measured profiles from deficiencies of washout models). Future work could explore a more robust normalization criterion of the activity profiles, which is so far limited to the maximum (or mean value around the maximum) in agreement with previous studies (Knopf et al. 2008, Helmbrecht et al. 2012, Min et al. 2013), as deemed less sensitive to statistical fluctuations and biological clearance. In particular, initial investigations showed encouraging results for the normalization to the profile area from z_prox to z_dist, which was found to partly overcome the encountered limitations in the presence of a pronounced activity maximum for the proton patients. Additional studies were performed concerning a modification of the distal threshold in the definition of the distal analysis window, which was solely defined by the 50 % distal dose fall-off position. The range shift results of protons and low-energy carbon ions were not affected significantly, while in the cases with a pronounced ¹²C-ion fragmentation tail deviations of about 5 % were detected. More investigations to reduce the respective effects of distal noise signals, but to improve the sensitivity of the range verification for shifts in low activity fall-off regions would be highly beneficial.

When available, CT-information obtained from the TP-CT and the PET/CT are used for the co-registration of the datasets to be compared. This CT-based image registration is performed at HIT, while the uncertainty of the co-registration based only on radioactive markers at MGH (where a PET stand-alone was clinically used so far) is estimated to be about 2 mm (Min et al. 2013). Moreover, standard deviations of HU values as well as the shift between CT profiles in the proximal window are good indicators of anatomical changes and differences in positioning between several treatment fractions or planned and actual delivery. Accounting for the CT to range conversion, the ratio of water-equivalent to geometrical depths provides information about the water-equivalence of the tissue.

The MC simulation of ion dose delivery is in general influenced by several uncertainty factors, as summarized and quantified in (Paganetti 2012) for proton beams. Restrictions in β⁺-activity predictions are additionally given by the biological washout that has an important effect on the PET distributions, especially for long delay and acquisition times. The previously performed study by (Knopf et al. 2009) with three fixed tissue-specific uncertainties for offline PET activity predictions (i.e. the distinction if the beam stops in bone or soft tissue, and in the latter case if the last activity maximum is located in bone or soft tissue) does not provide the necessary time-dependent quantification for a generalized application. The contribution of the ¹⁶O(p, 3p3n)¹¹C reaction channel, which was reported to result in larger range deviations due to inaccuracies in the cross-section calculation (Espana et al. 2011), was found to be very small for a typical treatment of human tissue and was therefore neglected for further analysis (based on the analysis of the ¹¹C and ¹⁵O contribution with related cross-section uncertainties). For the internal effects on the simulation accuracy only the CT conversion uncertainty was included in the analysis according to the findings of (Paganetti 2012). In future work addressing a more thorough uncertainty understanding, additional internal aspects need to be taken into account. Especially the washout model has a large effect on the activity distributions and would need to be investigated more precisely including its time dependence.

Concluding, we have introduced and demonstrated a new approach for automated assessment of range accuracy and reproducibility, combined with a visual quantification of uncertainties and a dedicated weighting strategy to highlight critical regions for a more reliable analysis of the identified range shifts. This method builds the basis for a decision support system, which is being developed at HIT to enable routine clinical use of PET-based treatment verification. Although so far investigated in the context of PET monitoring, our approach could also find application in other emerging areas of in-vivo range verification based on prompt gamma (Roellinghoff et al. 2014) or interaction vertex (Henriquet et al. 2012) imaging, which also require robust quantification and analysis of the relative shifts between measured and calculated profiles.