Symbiotic electroneural and musculoskeletal framework to encode proprioception via neurostimulation: ProprioStim

Summary

Peripheral nerve stimulation in amputees achieved the restoration of touch, but not proprioception, which is critical in locomotion. A plausible reason is the lack of means to artificially replicate the complex activity of proprioceptors. To uncover this, we coupled neuromuscular models from ten subjects and nerve histologies from two implanted amputees to develop ProprioStim: a framework to encode proprioception by electrical evoking neural activity in close agreement with natural proprioceptive activity.

We demonstrated its feasibility through non-invasive stimulation on seven healthy subjects comparing it with standard linear charge encoding. Results showed that ProprioStim multichannel stimulation was felt more natural, and hold promises for increasing accuracy in knee angle tracking, especially in future implantable solutions. Additionally, we quantified the importance of realistic 3D-nerve models against extruded models previously adopted for further design and validation of novel neurostimulation encoding strategies.

ProprioStim provides clear guidelines for the development of neurostimulation policies restoring natural proprioception.

Graphical abstract

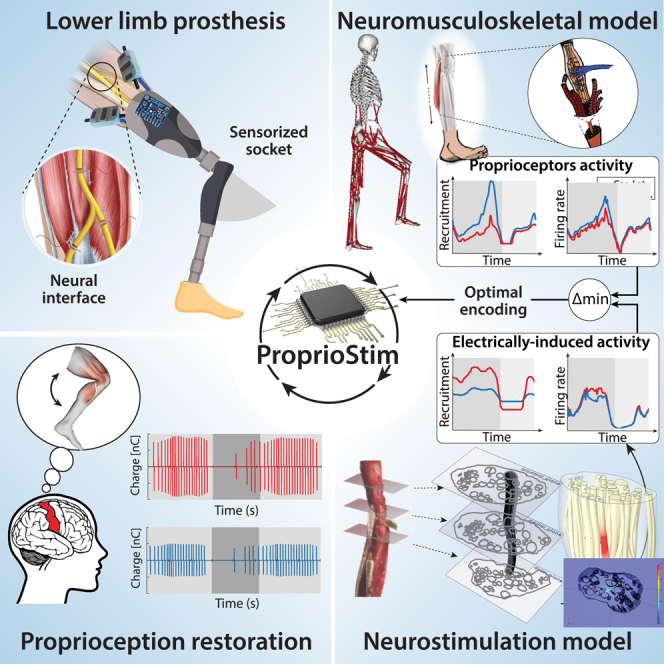
Highlights

• •ProprioStim is a model-based biomimetic encoding paradigm to restore proprioception
• •It leverages neuromusculoskeletal models and neural interface in-silico replicas
• •It is perceived more natural and accurate with respect to standard linear encodings
• •It showed potential to improve neurostimulation to restore amputee proprioception

Behavioral neuroscience; Clinical neuroscience; Bioelectronics

Introduction

In recent years, the advancement in neurotechnology has enabled scientists to pursue new ways of improving the lives of people with disabilities, such as upper- and lower-limb amputees.¹ To this day, multiple solutions that enable the subject to establish control over the prosthetic device have been presented.^2,3,4 Still, one of the main problems with conventional prostheses is the lack of sensory feedback to the user⁵ resulting in a difficult control of the prosthesis. Indeed, for the lack of feedback, the amputee perceives the prosthesis as a foreign body (low embodiment) and experiences increased mental and physical effort, all of which are often leading to prosthesis abandonment.^6,7 The need for overcoming these issues already resulted in several studies with very promising results, concerning sensory feedback restoration in both upper-^{8,9,10,11,12,13,14,15} and lower-limb amputees.^{16,17,18,19,20} In particular, transfemoral amputees suffer multiple health issues connected also to the lack of a reliable sensory feedback. They suffer from the risk of fall due to uneven terrain or obstacles,²¹ asymmetric posture, and shifted weight during standing and walking,^{22,23,24,25,26} eventually leading to pronounced fatigue, musculoskeletal disorders,^27,28 and even an increased risk of cardiovascular diseases.²⁹

In this direction, recent studies have shown that realistic artificial sensations (such as vibration, tingling, or touch) can be elicited by direct electrical stimulation of residual peripheral nerves using neural interfaces.^{5,16,20,30,31} However, restoration of natural proprioceptive sensations has never been reliably achieved using electrical nerve stimulation. Attempts in restoring proprioceptive sensations have been proposed for both invasive and non-invasive sensory restoration in limb prostheses.^32,33 This effort was justified by studies from several authors^34,35,36 among others, showing the importance of restoring proprioceptive feedback sensations. Meaningful proprioceptive restoration has been achieved through the Agonist-Antagonist Myoneural Interface.³² Although this technique elicited natural proprioceptive feeling, it cannot be performed if either agonist or antagonist are receded after the amputation. Marasco et al. achieved the restoration of hand opening and closure kinesthetic sensation through targeted muscle and targeted sensory reinnervation.^37,38 The proprioceptive feedback was obtained using kinesthetic tactor place over the reinnervated muscles. Such procedure has not yet been validated on lower limb amputees.

Thanks to the direct nerve interface with the peripheral nerves, the electrical nerve stimulation approach is not limited by the type of amputation. Notably, proprioception is a very complex sense of the somatosensory system, providing information about our own body kinematic and dynamic state. It is crucial both in subconscious and in voluntary control of body position and speed.^39,40 Its natural neural coding and processing is still under research investigation using both animal and computational models.^41,42 Since this sense is fundamental for a correct sensory-motor integration and body movements, it is necessary to design an effective encoding strategy for a more natural artificial proprioception restoration using electrical nerve stimulation.^16,17

The goal of this study is to design an optimal proprioception encoding strategy using electrical neurostimulation based on the modeling of natural behavior of proprioceptive afferents (i.e., Ia afferent fibers of muscle spindle transducers). To this day, there are no existing human realistic computational models simulating simultaneously the behavior of muscle spindles, their afferent proprioceptive fibers response, and the consequent effects of their artificial neural stimulation. Here, we implemented the Proprio-Neural Model (PNM) (Figure 1A) able to predict the natural activity of proprioceptive fibers during arbitrary movements. Then, we used it to design appropriate electrical stimulation patterns allowing the generation of congruent neural activation for encoding proprioception. In specific, the framework consists of a Neuromusculoskeletal (NMS) model coupled with emulated Ia proprioceptive fibers of muscle spindle transducers to estimate their natural activity from real kinematic and physiological measurements. Finally, we compared and validated the simulated fiber activity with human neural activity recorded using microneurography.^43,44,45 The main objective was to replicate this natural encoding through invasive neurostimulation. To this purpose, we employed an in-silico replica of an electrode-nerve interface to develop an optimal stimulation policy for biomimetic encoding of muscle kinematics. Existing peripheral nerve models replicate the tissue electrical property and axon dynamics,^19,46 but they fail to reproduce the complex longitudinal development of the curvilinear neural structures. Using sequences of histological cross-sections of the nerve, we constructed a novel realistic 3D representation of the branching nerve fascicles. This Electro-Neural Model (ENM) (Figures 1B and 2B) was used to predict fiber activity in response to electrical nerve stimulation. The validation of the ENM showed that the modeled results are in accordance with the previously acquired experimental data. Moreover, we showed the importance of morphological changes in fascicle distribution and disposition along the nerve by comparing ENM fiber recruitments with those of a conventional, simple 2D extruded model.

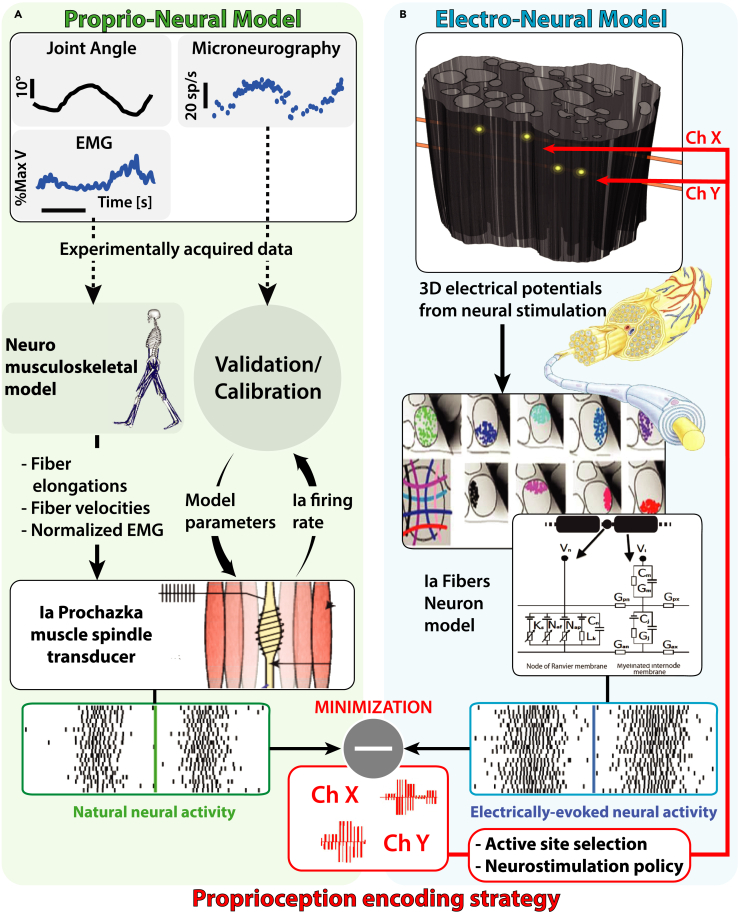
Figure 1.

Graphical representation of the proposed methodologies pipeline

(A) The Proprio-Neural Model (PNM) pipeline. Experimental data (joint angles, muscular activation, and microneurography) is used for the calibration of the modified Ia Prochazka muscle spindle transducer model on human data. Neuromusculoskeletal model (NMS) is used to estimate muscle fiber elongations and contraction velocities, that together with normalized EMG are used as input for the computation of the natural neural activity of Ia fibers through the calibrated PNM.

(B) The Electro-Neural Model (ENM) pipeline. 3D Finite Element Method modeling is used to simulate electrical nerve implant in the sciatic nerve. 3D potential distribution generated by the active site electrical stimulation is calculated for the whole structure and interpolated on multiple Ia fibers path belonging to different population distributions in the nerve fascicles. Neuron compartmental models of the Ia fibers finally simulate the depolarization caused by extracellular stimulation generating electrically evoked neural activity. In red, the final encoding strategy for the proprioception encoding strategy. Minimization between the natural and the modeled electrically evoked Ia neural activity is used to select the active site, the injected charge level, and the frequency of the neurostimulation.

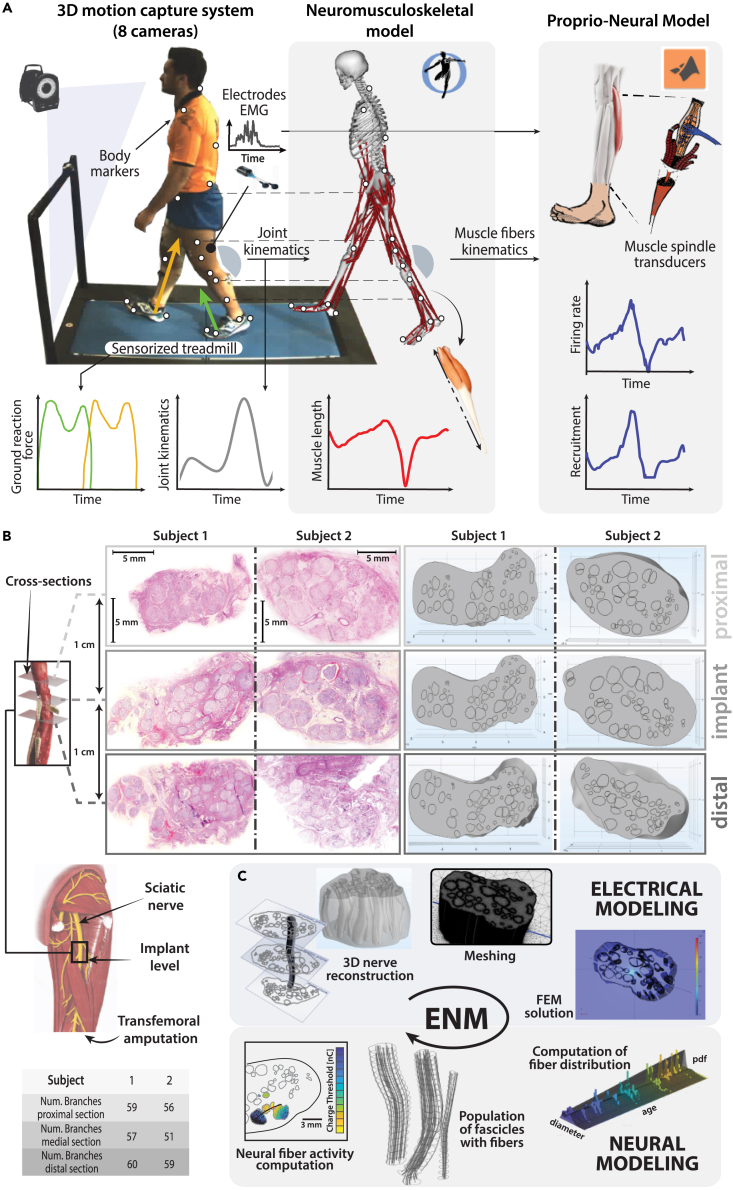
Figure 2.

Experimental acquisition for Proprio-Neural Modeling simulations and Electro-Neural Modeling of the realistic nerve structures

(A) Experimental set-up for motion acquisition during walking trials. The motion capture system acquired body markers on the subject walking on a sensorized treadmill. Computed joint kinematics from the motion capture data is then used through NMS modeling to predict muscle tendon unit kinematics. Finally, EMG muscle activity, muscle lengths, and elongation velocity are used to predict Ia afferent fiber natural activity from the modeled Ia muscle spindle transducers.

(B) Histological images taken from three cross-sectional layers of the sciatic nerves from two transfemoral amputees and the corresponding nerve segmentations based on those cross-sections (shown on the right). On the bottom, the table shows the number of fascicles visible in the histological images.

(C) A schematic view of the ENM. In Electrical modeling: a geometrical reconstruction of a curving fascicle and the complete nerve representation, based on the segmented cross-sections; the meshed nerve structure; the model of the nerve section with an implanted electrode and the electrical potentials map obtained during an active site stimulation. In Neural modeling: probability density function of fibers spatial density, based on fiber diameter and on subject age; an example of fiber distribution in the endo-fascicular space; the stimulation-driven activation of the Ia target population estimated through NEURON from the potentials produced by the FEM model, interpolated on the generated fiber paths.

The proposed modeling and encoding policy, called ProprioStim, combined PNM and ENM introducing simultaneous biomimetic modulation of charge and frequency. Testing of the novel encoding strategy during walking simulations, using experimentally acquired data, highlighted strong differences with respect to standard linear charge encoding. In fact, multichannel transcutaneous electrical nerve stimulation (TENS) on healthy subjects with PNM-driven encoded stimulation eliciting sensations of calf muscles advocated for possible increases in intuitiveness and accuracy of knee angle tracking with respect to linear encoding. However, inherent limitations (as selectivity or interface stability) of TENS indicated the necessity to employ more invasive (selective and stable) approaches to reach meaningful accuracies across the whole range of motion.

The obtained results showed, in particular, the advantage of a model-based neurostimulation strategy involving simultaneous manipulation of charge and frequency, with the objective of restoring meaningful proprioceptive sensations in multiple muscle groups. Such symbiotic somatosensory encoding is driven by our novel idea of coupling musculoskeletal and neurophysiological modeling for the restoration of the physiological activity of proprioceptive afferents.

Results

Proprio-neural model

Proprioceptive feedback is generated as summation from many different receptors (e.g., skin stretch receptors, joint receptors, tendon Golgi organ receptors, muscle spindles, and inner year organs). However, there are substantial experimental evidence that suggest muscle spindles as the major kinesthetic sensors.⁴⁷ Muscle spindles Ia fibers are able to encode movements down to 5 μm and up to 500 Hz⁴⁸: walking and other important movements are well included in such ranges. Additionally, considering the findings on both muscle spindles afferent fibers Ia and II type, it has been shown that complex illusory movements were evoked by applying patterns of muscle tendon vibration mimicking the natural Ia afferent pattern alone.⁴⁹ Therefore, considering these evidence, we chose to initially investigate only Ia fibers, since they represent the best candidate for encoding meaningful proprioceptive sensation.

According to the literature, Ia fiber afferents activity encodes the most information regarding muscle tendon unit (MTU) kinematics: i) fiber length, ii) fiber elongation velocity, iii) muscle activation.^50,51,52 These input variables can be obtained indirectly through the combination of motion acquisition and surface EMG signals, upon which the muscle kinematics and dynamics can be computed through NMS modeling (Figure 2A).⁵³ The detailed experimental pipeline is described in STAR Methods. We validated the implemented PNM on human experimental microneurography during index finger movement datasets available in literature,^43,44,45 which provided the necessary model inputs and outputs (Figure 3A). This validation is supported by evidence in the literature which found that the response of Ia fibers is not related to the type of muscle but only to the change in relative length.⁴⁸ As expected,⁵⁴ the mean firing rate from the novel model was about 40% lower with respect to (w.r.t.) the original Prochazka model, based on cat data.⁵¹ Coefficient of determination between the experimentally acquired microneurography on Ia afferent fibers of the index extensor and the PNM prediction showed a value of R² = 0.69, showing that most variance of experimental data could be fitted by the PNM response (Figure 3A). The remaining percentage could be attributed to inherent biological variability of the Ia fibers response or to measurement noise. The Root-Mean-Square Error (RMSE) was 5.26 ± 4.25 Hz on three different types of motion, suggesting a good generalization of the model on the different muscle kinematics (Figure S1).

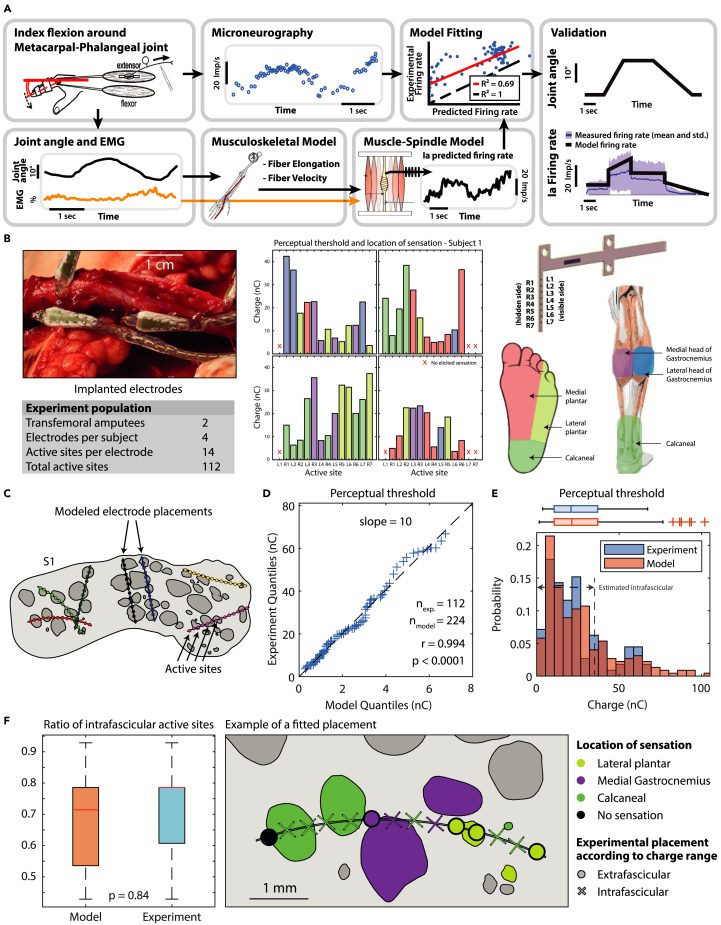
Figure 3.

Validation of PNM and ENM through experimental data

(A) Experimental data from Vallbo’s research studies^43,44,45 on index flexion around the metacarpal-phalangeal joint is used for a reparameterization of Prochazka’s Ia fibers muscle spindle transducer model. The trials are subdivided randomly in training and validation sets. From the training set, joint angles are used to compute muscle fiber elongation and contraction velocities through NMS modeling; together with EMG activity they are used as input for the Prochazka model computation. RMSE minimization between the Ia predicted firing rate and experimentally recorded microneurography is performed to adapt model parameters to human data. Final validation of the modified model is performed on the validation set. See also Figure S1.

(B) Four electrodes were implanted in each of the two amputees. The perceptual thresholds and location of the sensation within a month from implantation are hereby reported.

(C) The modeled electrode placements on subject 1.

(D) QQ-plot of experimental and model thresholds.

(E) Histogram and boxplot of experimental and model thresholds. The range of injected charges associated with intrafascicular placements in the model is marked.

(F) Boxplot of ratio of intrafascicular active sites in model and in experiment (estimated using the same charge range) and an example of the experimental results for one electrode applied on the best fitting modeled placement.

Electro-neural model

A subject-specific ENM, able to closely replicate the neural-electrical interface, was used to adjust the stimulation parameters to minimize the difference between estimated Ia natural neural activity and the electrically induced activity. To this objective, we developed models of the invasive electrode-nerve interface of two amputees who had been implanted with transverse intrafascicular multichannel electrodes (TIME). Nerve histological cross-sections have been employed for a realistic tridimensional reconstruction. The implantation of the TIME has been replicated in silico following the surgical indications (Figure 2B). Neural fiber models were defined and distributed inside the nerve structures replicating subject’s neural anatomy (Figure 2C).

The participants’ experimental perceptual thresholds and reported locations of sensation, (per each active site, of the four electrode implanted), were used for the validation of the ENM (Figure 3B).¹⁶ We compared the distribution of model-estimated recruitment thresholds^55,56,57 to the distribution of perceptual thresholds from the experiment, showing high correlation (r = 0.994). The model predicted that thresholds associated with intrafascicular and extrafascicular active sites had distinguishable distributions (Figure 3E), as expected, since it is known that intrafascicular active sites require lower injected charge to recruit a fascicle.⁴⁶

We then applied the same discriminant to the experimental charges, to estimate which active sites of the implanted electrodes were intrafascicular or extrafascicular. No statistically significant difference was found in the proportion of intrafascicular and extrafascicular active sites within the experimental data. Finally, we used this classification and the relative position of the active sites to determine which modeled placement matched experimental data the best (Figure 3F).

Realistic 3D-nerve models versus conventional extruded models

Conventional models were created by extrusion of a single histological image of the nerve (at the middle cross-section), following previously described works.^19,46 The 3D-nerve models required more mesh elements, producing longer mesh and solver computational times (respectively, 340 ± 44 vs. 145 ± 35 and 156 ± 14 vs. 44 ± 15, in minutes) w.r.t. the extruded models (Figure 4A). Figure 4C shows the comparative recruitment results for six (out of thirty-five) single-point sources (active sites), at different longitudinal distances from the middle cross-section. No significant differences were observed between the recruitment plots of the two models at the middle level (MAD 4.4 ± 3.7%), as reported in Figure 4D. However, due to the morphological changes along the longitudinal axis, pronounced differences in recruitment were found at increasing distance, reaching a MAD of 24.8% ± 18.8% at 7.5 mm distance, with a maximum of 86.9%. The mean absolute deviation of the relative recruitments for all models is shown in Figure 4D. We found that the computational cost of the novel modeling method was justifiable, since large deviations could be found for electrodes implanted even a few millimeters away from the extrusion level.

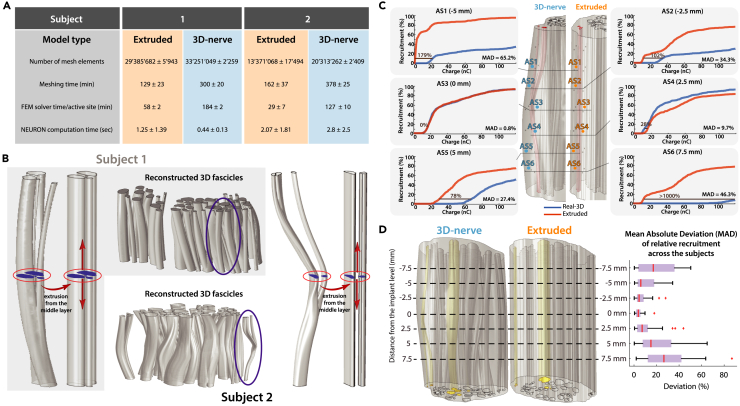
Figure 4.

A comparison: 3D-nerve vs. extruded nerve model

(A) Model computation information, with averaged values across three individual electrode positions for each subject. Computational times for the calculation of fiber recruitments were averaged across 1000 fibers.

(B) Comparative representation of fascicles for the 3D-nerve and the extruded model (the former based on the three nerve level segmentations, the latter constructed by a simple extrusion from the middle cross-section) with a magnification of an exemplary fascicle for both subjects.

(C) Visual representations of deviations of relative recruitments across 6 individual active site stimulations in one of the models.

(D) On the left: the 3D-nerve and the extruded version of the nerve model of Subject 2 as an example, with 3 highlighted fascicles chosen for the electrode structure placements and the comparisons. On the right: boxplot of the mean absolute deviation (MAD) of relative recruitment at seven different cross-sectional levels (corresponding to the electrode position levels) averaged for both subjects.

Emulating proprioceptive afferent activity

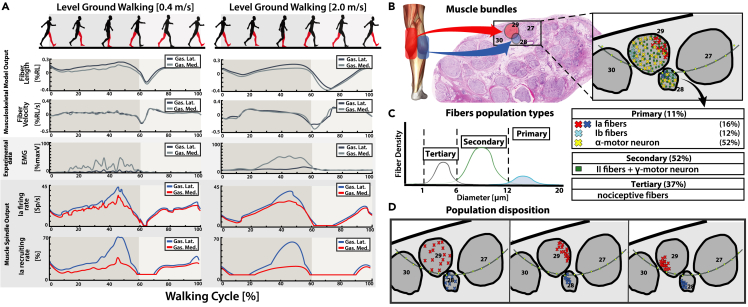
Experimental human kinematic acquisitions during locomotion were used to simulate the PNM during walking trials at three different velocities (Figure 2A). The muscle elongation on the gastrocnemius muscles —computed through NMS modeling (Figure 2A)— showed higher fiber length and contraction velocity at higher walking velocities (Figure 5A). This was compatible with greater stride length and toe-off ground reaction force (GRF), producing higher leg inertia and knee angle flexion in the swing phase. Increment of the GRF was also accompanied by higher gastrocnemius muscle contraction recorded via EMG electrodes placed on the subject calf (Figure 5A). Between the slow and fast walking velocity, different afferent activity has been predicted especially during the swing phase (Figure 5A). In fact, the increased shortening of the gastrocnemius muscles consequently produced a higher silencing of Ia fibers (low value of population recruitment and firing rate). Model prediction on the Ia afferent fibers of lateral and medial gastrocnemius muscles displayed similar behavior (Pearson’s r = 0.91). The PNM results showed that the predicted firing was inside the physiological range reported in the literature⁵⁴ (Figure 5A). The obtained natural fiber activity was assigned to Ia fibers placed in the ENM as a target for neurostimulation (Figures 5B-5D).

Figure 5.

Simulation of PNM during walking trials

(A) Results of PNM simulations during two different walking velocities; the PNM is computed on medialis and lateralis gastrocnemius muscles of the right leg. The first two rows (Musculoskeletal Model Output) plot the NMS model estimations of muscles fiber lengths and fiber elongation velocity during a gait cycle. The third row displays the normalized EMG muscular activation (Experimental data) obtained from experimental recorded data. The final two rows (Muscle Spindle Output) instead show the predicted output of the natural Ia afferent fibers recruiting rate and mean firing rate for the two simulated muscles from the PNM. PNM generated fibers activity is reconducted to implemented fibers in the Electro-Neural model.

(B) Multiple bundles are selected so that in each bundle two fascicles (one for each gastrocnemius muscles) respect appropriate dimensions and number of Ia fibers reported from literature.

(C) For each combination of fascicles, fibers are divided in three groups based on fiber diameter; Primary fibers are subsequently divided in Ia, Ib, and alpha motor neurons (percentage according to literature findings). See also Figure S3.

(D) Different dispositions of the fiber populations have been tested, the disposition of the populations can be clustered or random inside the 3D fascicular volume.

Encoding proprioception (ProprioStim)

ProprioStim consists of the optimization of stimulation parameters (charge, frequency, and active site selection) to match the electrically induced activity in Ia fibers with the lost physiological activation. This encoding strategy is obtained via the minimization of the difference between the outcome of neurostimulation, predicted by the ENM, and the natural proprioception encoding, estimated from the PNM. The combination of frequency and intensity-based feedback is an essential feature for a more complete restoration of natural proprioceptive feedback, and indeed it is a result of our modeling study: simultaneous modulation of charge and frequency allowed for the highest accuracy in replicating the natural activation of muscle spindle afferents in terms of recruitment and firing rate.

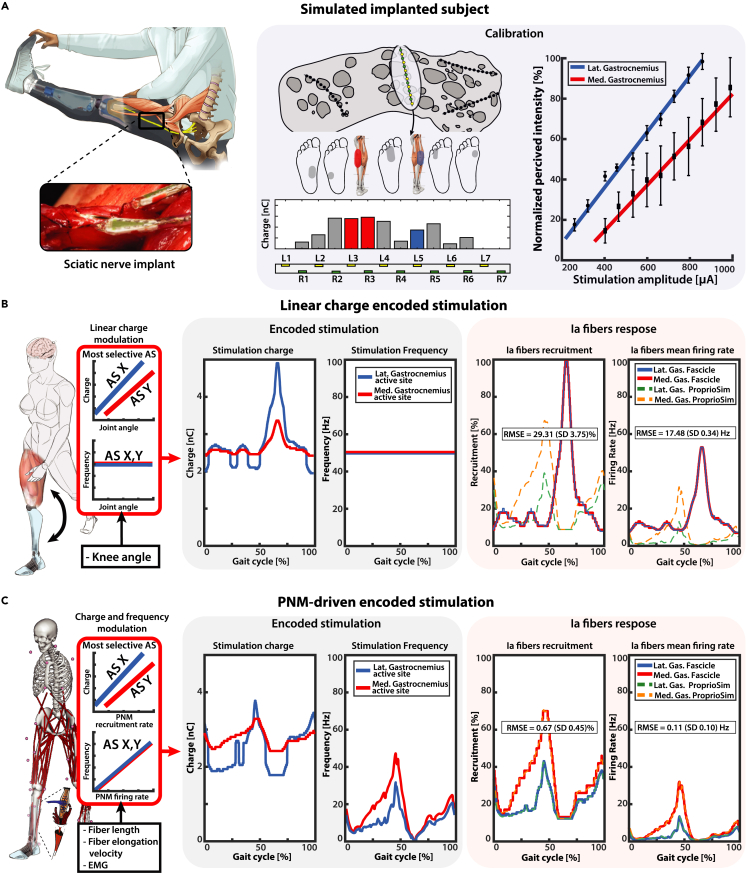
To evaluate the goodness of the proposed methodology, we decided to compare it with the encoding strategy most commonly used in the neuroprosthetic field: linear charge neuromodulation.^14,16 In fact, this kind of approach has been the most widely adopted for neuroprosthetic touch and proprioception restoration with peripheral nerve stimulation.^{15,16,17,20,31,33,36,58} Specifically for proprioception, in neuroprosthetic hands the stimulus has been linearly modulated based on the level closing/opening of the fingers,^15,33,36 while for neuroprosthetic legs the stimulus has been encoded proportional to knee joint angle.^16,17 Following results are reported from simulated implanted subjects derived from experimental data (Figure 6A).

Figure 6.

PNM-driven encoding stimulation in-silico simulations

(A) A virtual subject is modeled after the previously acquired data of Subject 2. In each modeled electrode placement, stimulation of the most selective active sites for each identified potential gastrocnemius fascicle is encoded using two different types of strategies: standard linear encoding and novel PNM-driven encoding. Calibration is performed using linear interpolation between reported percived sensations and related stimulation amplitude: the obtained calibration curve is reported on the right pannel with standard deviation for repeated measures.

(B) The recorded knee angle is used to modulate linearly the stimulation impulse charge between the minimal and maximal charge levels; stimulation impulse frequency is kept constant. The resulting time-varying charge encoding parameters are presented in the central block. On the right, Ia fiber stimulation-derived recruitments and mean firing rate are displayed and compared with the PNM estimated natural activity.

(C) The PNM estimated natural Ia fibers recruitment is used to modulate linearly the stimulation impulse charge between the minimal and maximal charge levels; stimulation impulse frequency is instead obtained by dividing the estimated mean firing rate and the fibers recruitment. The resulting time-varying charge and frequency encoding parameters are presented in the central block. On the right, Ia fiber stimulation-derived recruitments and mean firing rate are displayed and compared with the PNM estimated natural activity. The presented plots and RMSE values refer to a single fascicle combination and fiber population disposition. Comprehensive results for all the simulations are displayed in Figure S2.

The deviations (RMSE) between the Ia fiber recruitments estimated through PNM and those simulated in the ENM are 29.31 ± 3.75% and 0.67 ± 0.45%, respectively for linear charge and PNM-driven encoding. Linear charge neuromodulation scored higher deviation for the mean firing rate w.r.t. predicted Ia activity, RMSE = 17.48 ± 0.34 Hz. The same encoding algorithm scored a maximum error of 88% in the recruitments during the swing phase, with a simultaneous error of 50 Hz in frequency. The results produced with the linear charge encoding strategy modulated through kinematic data (knee angle) showed the highest discrepancy with respect to the PNM estimated natural neural activity (Figure 6B), likely to cause lower naturalness of proprioceptive feedback. This concept of biomimicry has already been shown to be valid in many applications for touch restoration,^12,59,60 even though it has never been validated for proprioception. The chosen linear charge modulation, moreover, displayed an antithetic behavior with respect to the natural Ia fiber activity. As it has been illustrated in Figure 5A, the peak activity of Ia afferent fibers occurs during stance-extension phase and the minimum in swing-flexion, in total opposition to the electrically evoked stimulus. While this could be partly compensated with a different modulation strategy, the ProprioStim encoding is able to take into consideration the highly non-linear response of the muscle spindle activity to the muscle kinematics with respect to the joint angles. The possibility to integrate the complexity of the NMS human system in the encoding algorithm enables our approach of multi-active site stimulation for different target muscles (Figure 6C), while standard techniques such as linear charge modulation¹⁷ do not consider the complementary neural activity in distinct branches separately (such as for the two gastrocnemius heads). Finally, we demonstrated that ProprioStim encoding is selective for Ia fibers with respect to secondary fibers (e.g., type II muscle spindles and touch receptors afferents), allowing for a coherent electrically evoked sensation (Figure S3). It is especially important since it has been recently shown that collateral recruitment such as of cutaneous afferents can disrupt proprioceptive information.⁶¹

TENS experimental validation

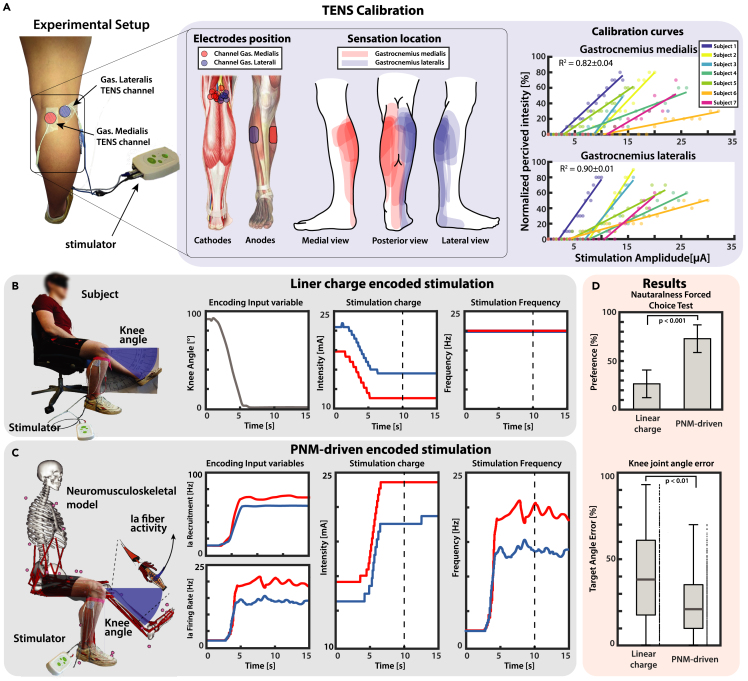
To evaluate the feasibility and performance of ProprioStim, we compared the PNM-driven and the linear charge encoding during single knee flexion extensions (see Video S1). Multichannel TENS was used on a total of 7 healthy subjects. In all subjects it was possible to elicit somatotopic sensation in the calf, placing the cathodes on the popliteal fossa over the sciatic nerve (Figure 7A). The electrode placement was carefully tailored for each subject so to obtain location and type of sensations as close as possible to the contraction of lateral and medial heads of the gastrocnemius with separate channels. For each subject, the normalized perceived sensation intensity was linearly mapped on the stimulation amplitude (Figure 7A).

Figure 7.

ProprioStim implemented via TENS

(A) Seven subjects are set up with two channels TENS targeting the sciatic nerve on the popliteal fossa. The positions of the cathodes are tailored to each subject so to make the evoked sensation as much somatotopic as possible. Calibration curves are derived linearly interpolating the normalized perceived sensation and the related stimulation amplitude.

(B and C) A knee ramp trajectory starting from flexed leg toward a defined target angle is designed and used to linearly modulate the stimulation charge while the frequency is kept constant at 20Hz. (C) A knee ramp trajectory starting from flexed leg toward a defined target angle is designed and is used as input trajectory for the neuromusculoskeletal model. The estimated fiber lengths and muscular activations are used to estimate with PNM recruitment and firing frequency of the Ia fibers of the lateral and medial gastrocnemius muscles. The dashed vertical lines in panels (B and C) mark the moment when the knee angle was measured.

(D) Results of the force choice test (mean ± SD of percentage of preferences per subject) showed that the PNM-driven encoding was considered closer to the real sensation from the pool of subjects, and knee angle matching task showed that it resulted in a higher accuracy.

See also Figures S4 and S5.

The calibration curve was then used to modulate the stimulations on 7 subjects during an exercise of knee angle matching, while receiving TENS stimulation on the contralateral leg (Figures 7B and 7C).

Results of a repeated measures ANOVA show that, in absence of any training, the subjects were able to match the perceived sensation to a particular knee angle configuration more accurately with the PNM-driven encoding with respect to the standard linear encoding (respectively 23.78 ± 3.81% and 39.79 ± 5.84% error on the target angle, F_1,6 = 25.2, p < 0.01, f = 1.034) (Figure 7D). The absolute value of error of ProprioStim resulted significantly lower than linear encoding for 0° and in range between 55° and 90° (p < 0.05 for 0° and 55°, p < 0.01 60°, and p < 0.001 between 65° and 90°). Linear encoding performed significantly better only for 30° (p < 0.05). The error did not significantly differ between encoding paradigms for the remaining angles (5°-25°, 35°-50°). The interaction between angle and paradigm did not result statistically significant (F1,6 = 1.16). Errors plotted separately for each angle are reported in Figure S4.

No evidence of habituation has been found when studying the errors in time for each subject. A Mann-Kendall test with the Bonferroni-Hochberg correction for multiple testing did not reject the hypothesis of no monotone trends of the errors in time for any subject and condition (meaning there was no habituation, which would have caused errors to decrease over time) (Figure S5).

Four subjects performed a force choice test during which they were asked to choose which of the two stimulations was closer to the real sensation of muscle contraction during knee flexion extension. The subjects indicated that the biomimetic stimulation was encoding a more natural sensation in the 73.25 ± 14.34% of the times (p < 0.001, 4 subjects, 20 repetitions, Figure 7D). These results demonstrated a higher intuitiveness of the novel encoding with respect to the standard linear charge encoding algorithms.

Discussion

We developed ProprioStim with the hypothesis that more sophisticated and bio-inspired neurostimulation policies are necessary to elicit more natural proprioceptive sensations. We demonstrated the feasibility of developing a biomimetic policy to improve traditional encoding paradigms. Differently from these, ProprioStim is able to take in consideration: firstly, the non-linear coupling and over-actuation between the joint and muscle kinematics; secondly, the non-linear dependency between the muscles elongation and the Ia muscle spindles afferents fibers firing frequency and recruiting. These non-linear transformations embed dynamic information (e.g., velocities) which are important for proprioception.⁴⁸ The simultaneously control of all the stimulation parameters (i.e., charge, frequency, and active site) is then used to replicate the estimation of the natural neural activity as close as possible (Figure 6C).

Concomitant modulation of amplitude and frequency of stimulation was indeed necessary to obtain a Ia fiber activity closer to natural activity. This essential feature was reported in previous studies where scientific findings suggested that sensations are encoded both in the number of activated fibers and in their firing patterns.⁶² This is particularly true in case of proprioception, where investigations on Ia afferent fibers showed that the stretch information is also encoded in their firing rate.^63,64

Additionally, ProprioStim supports simultaneous and biomimetic time-variant multichannel stimulation of afferent fibers originating from different muscles. This is an essential feature to restore proprioceptive feedback through electroneural stimulation, since proprioception arises from the interaction of different muscle feedback receptors involved in the joint movement. This result is in accordance with previous studies attempting to elicit proprioceptive sensations through intracortical microstimulation (ICMS), hypothesizing that spatiotemporally precise neurostimulation could improve the naturalness of elicited sensations.⁶⁵

These findings were additionally supported by comparing the two stimulation paradigms with TENS in healthy subjects. ProprioStim was able to generate a more intuitive and reliable proprioceptive sensation of knee flexion. This result might indicate that providing natural and richer proprioceptive information enhances the accuracy of the subject in the perception of knee joint configuration. This slow and stationary task was chosen because our subjects were non-amputees and their proprioceptive feedback from muscle spindle was still intact. Therefore, any movement performed with their leg (in a more dynamic scenario) would have generated a proprioceptive sensation over-imposed to or mixed with the artificial sensation generated from the transcutaneous electrical nerve stimulation. This controlled (and therefore limited) scenario represents a first step validation showing the potential of model-informed neural stimulation. It is above all a useful practical implementation that shows a possible way to use this computational model in the experimental reality, which can be exploited in other clinical trials and especially in efforts with implants. However, our validation demonstrated the limited viability of PNM modulation for TENS applications in the clinical environment due to the relatively large median error (up to 56%) at low flexion angles (Figure 7D). At the same time, the outcome of having lower errors at higher flexion angles (median error of 14% above 50°) is a promising result. Indeed, considering the proposed application with amputees, higher flexion angles are usually associated with kinematic configurations where the foot is not in contact with the terrain (it is in air), and no ground reaction force can be perceived through the socket of the prosthesis. Proprioception is indeed critical for movements such as swing during walking and climbing stairs.

Our findings advocate for future testing during natural walking in an amputees’ cohort with invasive implants. Additionally, in future experiments (best with very selective implants enabling high control of target) it could be interesting to disentangle the different contributions that amplitude and frequency modulation give to the discrimination resolution through a specifically designed paradigm. In turn, this could lead to findings for a possible model simplification.

Together with direct neuroprosthetic applicability, ProprioStim embodies a validated framework for interfacing with the human peripheral nerve. This approach can be translated into a wide range of neuroscientific applications related to the optimization of encoding strategies for human-machine interfaces. Model-based approaches have been demonstrated to be helpful in the development of interfaces in direct contact with the human nervous system, which has to deal with numerous issues. These problems are related to long and complicated animal/human trials and high cost of the materials and instrumentation. Thus, we believe that ProprioStim can be a useful instrument for reducing preclinical trial assessments, allowing preliminary investigations on application feasibility and performance.

Indeed, the ENM was employed as a cost-effective platform for the optimization and testing of stimulation paradigms. The obtained results showed the induced recruitments were strongly influenced by the curvilinear and branching morphological structure of the nerve. Therefore, the adoption of a realistic 3D reconstruction of the human nerve for simulating the electro-neural interface should have prior importance for reducing the discrepancy between the in-silico model and reality. This advocates for a more in-depth investigation to reflect on accurate representations of nerve anatomy and physiology.

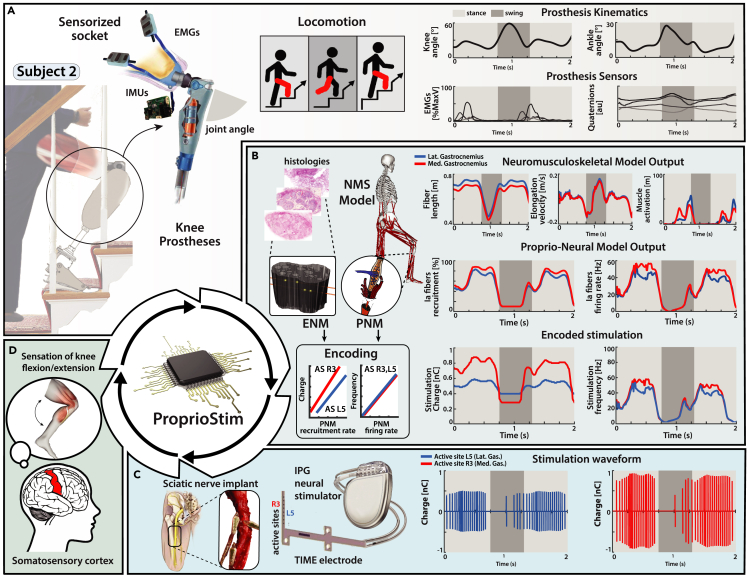
Through our TENS experimental protocol, we were able to ensure the feasibility of ProprioStim for future applications for invasive peripheral nerve interfaces. We envision that transfemoral amputees are going to be implanted with invasive electrodes for nerve stimulation, similar to the previous study conducted by Petrini et al.^16,17,20,31 (Figure 8C). The provided knee prosthesis will embed EMG and IMU sensors in the socket (Figure 8A). The collection of these signals will be used to drive our ProprioStim encoding algorithm (Figure 8B). Starting from the IMU data sensors, joint encoders of the prostheses, and EMG recordings, is it possible to estimate the lower-limb kinematics and from that compute muscular elongations and activation).⁶⁶ The subject-specific ENM would need the geometry of implant, shape, and size of nerves (e.g., from ultrasounds), alongside our averaged distribution of fascicles and axons across the nerve. Finally, depending on the motion of the leg and muscle contraction, a real-time PNM model would predict the natural activity of the Ia muscle spindles in the missing limb, and apply the stimulation parameters optimally encoding proprioception.⁶⁷ A stimulation policy, developed from the ENM with subject-specific calibration (Figure 6A), will encode the natural Ia afferent fiber activity to a corresponding stimulation (Figure 8C). The simultaneous stimulation of multiple active sites for the coactivation of Ia afferent fibers of different muscles should create a more congruent artificial sensation corresponding to the flexion and extension of the missing joints (Figure 8D).

Figure 8.

Future clinical trial overview for neuroprostheses in proprioceptive sensory restoration

(A) Virtual subject wearing knee prosthesis with sensorized socket (EMG and IMU sensors) for real-time acquisition of physiological and kinematic data.

(B) The data obtained from IMU and EMG sensors embedded in the prosthetic device allow the computation of a real-time NMS model, which predicts the MTU kinematics of muscles of interest (medial and lateral gastrocnemius). The acquired information is subsequently used as an input for the estimation of the natural Ia fibers recruitment and firing rate activity. This activity serves as a modulating variable for the subject-specific calibrated encoding strategy, which produces the real-time electrical stimulus parametrization.

(C) The subject is implanted with multiple electrodes in the tibial branch of the sciatic nerve; IPG neural stimulator applies the appropriate stimulation to the relevant active site.

(D) Biomimetic encoded electrical stimulation generates coherent Ia fibers activation with respect to natural fiber activity. Electrically driven Ia fibers activity is interpreted from the central nervous as proprioceptive feedback, allowing the subject to perceive the flexion/extension of the joint.

Developing a model-based framework represents a fundamental step in a biomimetic encoding strategy to restore natural proprioception by electrical neural stimulation (Figure 8). We propose ProprioStim as a tool for the transition toward bio-inspired encoding strategies within the next generation of neuroprosthetic interventions. To this objective, we shared a standalone distribution of ProprioStim which allows us to choose a movement from the experimental dataset with 10 different movements (e.g. walking uphill/downhill, fast/slow, and so forth), visualize body kinematics, muscle spindle activations, and compute the related stimulation parameters, allowing its custom reimplementation for any other related study or future neuroprosthetic applications.⁶⁸ This particular approach will create a more user-friendly human-machine collaboration, relieving users from non-intuitive sensory integration.

Limitations of study

Still, the presented approach has some limitations. We replicated a real peripheral neural interface through the ENM, but, as any model, it remains a limited representation of reality. Although the 3D-reconstructed nerve structures in the ENM are based on and thoroughly reflect the real human anatomy, they do not take into account the presence of non-neural tissues (i.e. fibrotic tissue, body fluids, heterogeneous surrounding tissues). The precision of the nerve reconstruction was also limited by the low number of cross-sections and would be improved by decreasing the inter-slice distances. Additionally, the PNM has been validated only through a limited dataset for upper limb muscles. Similar experimental data acquisitions should be performed for bigger muscle groups in the lower limb to consolidate the muscle spindle transducer model accuracy. It is also crucial to realize that proprioception remains a very complex sense, that arises from the interaction of numerous and different receptors, not only primary muscle spindle transducers. Future efforts must be spent to integrate additional sensory sources of proprioception, such as type II muscle spindle receptors, Golgi tendon organs, and skin stretch sensors. Finally, a complete validation of ProprioStim would need the direct assessment of the elicited sensations’ naturalness employing invasive peripheral neural interfaces in patients with a lower limb amputation. This would allow to perform more complex, real-life movements thanks to the absence of confounding proprioceptive sensations from the limb, otherwise present during experiments with healthy subjects. The reported performance in untrained joint angle discrimination with ProprioStim seems promising when compared to a previous attempt at restoring hand proprioception with invasive stimulation after training (median error of 9.1°, IQR of 14.6°),¹⁵ especially considering that the proprioceptive sensitivity of the knee is lower than of fingers.⁶⁹ Moreover, it must consider the inherent TENS limitation regarding fiber selectivity during stimulation. In fact, with this set up, we did not expect to be able to replicate the complete neural dynamics of Ia spindle afferents. This aspect is supported by Chee et al.,⁷⁰ showing TENS constraints in the selectivity and intensity encoding with respect to the invasive stimulation. Additionally, during the calibration phase, the stimulation range was limited by either strong sensations reported under the electrodes or muscle twitching, which restricts the values of both frequency and charge that could be delivered to the user. This implies that reliable testing of ProprioStim would be obtained only with invasive stimulation.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
NEURON myelinated axon model	McIntyre et al.71	ModelDB: http://modeldb.yale.edu/3810
Hybrid Electro-Neural Simulation Platform	Ciotti et al.72	Zenodo: https://doi.org/10.5281/zenodo.7639313
ProprioStim executable	Ciotti et al.68	Zenodo: https://doi.org/10.5281/zenodo.7347123 https://github.com/neuroenglab/propriostim
Software and algorithms
OpenSim 3.3	Delp et al.73	https://simtk.org/projects/opensim/
NEXUS 2.10	VICON	https://www.vicon.com/
ImageJ 1.52p	Schneider et al.74	https://imagej.net/
NeuronJ 1.4.3	Meijering et al.75	https://imagescience.org/meijering/software/neuronj/
SOLIDWORKS 2019	Dassault Systèmes	https://www.solidworks.com/
COMSOL Multiphysics 5.5	COMSOL Inc.	https://www.comsol.com/
NEURON 7.7.2	Carnevale and Hines76	https://www.neuron.yale.edu/
MATLAB 2020b	MathWorks, Inc.	https://mathworks.com/
Other
Mini Wave EMG sensors	Cometa S.r.l.	https://www.cometasystems.com/
Wave Plus Wireless receiver	Cometa S.r.l.	https://www.cometasystems.com/
Split-belt sensorized treadmill	AMTI	https://www.amti.biz/
Vero infrared cameras	VICON	https://www.vicon.com/
Vue video camera	VICON	https://www.vicon.com/

Resource availability

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by the lead contact, Stanisa Raspopovic (stanisa.raspopovic@hest.ethz.ch).

Materials availability

This study did not generate new unique materials.

Experimental model and subject details

The experimental data used to build the PNM was obtained from a healthy man (age 27 years, height 182 cm, mass 75 kg), who volunteered for this investigation and gave a written informed consent.

The comparison of ProprioStim with linear charge encoding was performed with 7 healthy human volunteers who give their written consent for the experimentation.

The single subject details are reported in Table S1.

This study was approved by ETH Zürich ethical commission (EK 2019-N-97).

Method details

Proprio-neural modeling

We recorded subject movement, applied force under the foot and EMG to compute the lower limb muscles contribution during walking using OpenSim^66,77 (Figure 2A). We used in sequence inverse kinematics, inverse dynamics, and muscle analysis tools to specifically estimate the gastrocnemius muscles elongation and activation. These variables gave us a global description of the muscle state during the entire recorded movement. To estimate Ia muscle spindle natural activation, we developed the PNM. Starting from the muscles kinematics this model was able to compute fibers recruitment and mean firing rate of the muscle spindle afferents. We based our model on previous findings on experimental recordings^43,44,45,50 and prior attempted modelization.⁵¹ In practice, the Ia fiber recruitment function was through numerical interpolation of microneurography data recorded at different gastrocnemius muscles elongations.⁵⁰ The mean population firing rate function is instead obtained through error minimization of an available animal model with human Ia fibers microneurography recordings^43,44,45(Figure 3A). We were finally able to predict the Ia afferent fibers activity from the previously computed gastrocnemius muscles kinematics and muscular activation and use them as input variables for the implemented PNM. This allowed us to obtain the Ia fibers natural activity starting from generic body movement recordings (Figure 5A). Complete details of this model are reported in the next sections.

Muscle spindles modelization

In order to characterize the response of Ia fibers muscle spindle transducers, we took into account the prior findings of Botterman et al. (1982) and Prochazka (1999), who attempted first modelization through cat experimental data on Ia fibers.^50,51 As first, Botterman et al. (1982) provided experimental measurements on cat medial gastrocnemius microneurography of Ia fibers recruitment at different muscle stretching intensities.⁵⁰ We used this data to interpolate linearly the mean Ia fiber recruitment as a function of the muscle elongation. Concerning fiber firing rate, many different formulations have been proposed in literature.^{41,51,78,79,80,81,82} Among the reviewed works, Prochazka formulation have been chosen for this study.⁵¹ Since none of the investigated models was validated on humans, our choice was mostly driven from formulation and code availability and the possibility of using the NMS model for its computation. As for Botterman et al.,⁶³ Prochazka’s formulation was based on cat experiments. Prochazka modeled both the passive fiber elongation-contraction and the active contribution of the γ-motor neurons through α-motor neuron coactivation that can be recorded through muscle activation (EMG). Using recorded muscle fiber elongations, velocities and normalized EMG as inputs, the mean firing rate frequency of the Ia neural response can be estimated. The exact formulation of the model can be found in the original publication.⁵¹ Differently from the defined recruitment function, it is well known from the literature that the Ia fibers’ mean firing rate in cats is higher than in humans.^54,83 Therefore, we proposed a reparameterization of the model using the experimental data available in literature.^43,44,45

Vallbo’s studies recorded human Ia afferent fibers firing rate activity from index extensors muscle spindles through microneurography, during index flexion around the metacarpal-phalangeal joint. While the trajectories of the finger joint were provided within the data set, no information was collected for the muscle fiber elongation. We therefore decided to use a musculoskeletal model of the hand provided with the OpenSim software to obtain the missing fiber kinematics. Scaling of the model was not required since Prochazka muscle spindle model required only relative fiber elongation. Trajectories of the metacarpal-phalangeal joint could be imposed on the model and related index extensor fiber elongation extracted. The data reported in literature^43,44,45 was divided in three trials type: ramp-and-hold, sinusoidal and random joint movement. Random eighty percent of trials, stratified among the three trial types, were used to reparametrize the model through nonlinear regression: the new coefficients were estimated using iterative least squares estimation and initial parameter values were chosen as the ones reported by Prochazka.⁵¹ Validation of the model was done on the remaining twenty percent of the available dataset: R² coefficient was computed in order to evaluate the goodness-of-fit of the new parameters.

While our application is intended for lower limb muscles, the use of data from forearm muscles for the reparameterization is supported by the fact that evidence in literature does not report any morphological or functional change of the muscle spindles depending on the body district. Indeed, the model formulation of their response is independent from the type of muscle and their shape but is only related to the relative change in length of the fibers.⁴⁸

Data-driven subject simulation

We computed the validated PNM model output using walking trial experimental acquisition performed in the Rehab Technologies Lab, Istituto Italiano di Technologia on a healthy subject. The subject was instrumented with 38 body-markers. On the left leg nine wet wireless Mini Wave EMG electrodes (Cometa S.r.l., Italy) were placed over the nine superficial muscular group in the right tibia and thigh actuating the knee joint (rectus femoris, vastus lateralis, vastus medialis, gracilis, sartorius, semitendinosus, biceps femoris, lateral and medial gastrocnemius). The electrodes were placed following SENIAM guidelines.

The EMG electrodes were connected wirelessly to Cometa Wave Plus Wireless 16 digital channels receiver. Split-belt sensorized treadmill (AMTI, Watertown, MA, United States) was used to measure the GRF during the trial execution. Body markers trajectories were obtained through motion capture system (eight Vero infrared cameras and one Vue video camera, VICON, Oxford, UK). VICON cameras (120FPS), treadmill (2000Hz) and EMG electrodes (2000Hz) recordings were synchronized through VICON NEXUS software. The GRF from the two force platforms in the sensorized treadmill were zero-phase second-order Butterworth low-pass filtered with 8 Hz cut-off frequencies. EMG signals were first band-passed filtered between 30 and 300 Hz, full-wave rectified, and zero-phase second-order Butterworth filtered at cut-off frequency of 6 Hz. Linear envelopes of each muscle were normalized for their maximum recorded value in the acquisition set.

Before starting the acquisitions, the subjects were asked to determine their slow, comfortable, and fast walking speed on the treadmill. Five trials at self-selected low walking velocity and five at self-selected high walking velocity were acquired. All trials `c3d' generated files were converted and exported to OpenSim and MATLAB compatible files.⁸⁴The subject-specific NMS model calibration has been performed through OpenSim. The OpenSim Musculoskeletal (MS) model used for these analyses is composed of twelve rigid bodies: five in each leg (toes, calcaneus, talus, tibia, and femur) and two for the main body (hips and torso). The adopted model is described by three-dimensional 37 degree of freedom. Main muscle groups are described through 92 Hill-type MTU. OpenSim software was used to calibrate the model parameters to match the subject anthropometry using static standing trials data as previously described.⁷⁷ Joint kinematics was obtained using the inverse kinematics tool. Angle joints of the calibrated model, similarly to the calibration process, were calculated solving weighted least squares problem between the virtual and the experimental markers trajectories. Finally, employing the inverse dynamics and residual reduction analysis algorithms of OpenSim, it was possible to calculate the joints torque combining the GRF measurements and inverse kinematics results.⁵³ Finally, the tool for muscle analysis was used to compute the muscle fibers lengths and elongation velocities.

The subjects from the Petrini et al. study^16,17 reported proprioceptive sensations only from the calf muscles during sensory feedback restoration. In fact, the tibial branch of the sciatic nerve innervates only the posterior muscles of the lower leg. Hence, since in our study we modeled the same nerve interface, only gastrocnemius muscles in the lower leg were investigated. Fiber lengths from lateral and medial gastrocnemius muscles and fiber elongation velocities were normalized for the muscle rest length. These muscle kinematics variables and EMGs (normalized for maximum contraction) were subdivided in gait cycles and the PNM was computed to obtain changes in recruitment and firing rate during walking in the Ia muscle spindles afferents (see Figure 5A). The estimated natural activity was finally reconducted to the selected Ia fibers in the ENM (see Figures 5B–5D).

Electro-neural modeling

We implemented a realistic 3D model for intraneural stimulation by incorporating in peripheral nerve FEM models compartmental models of axons,⁷¹ taking previous studies as reference.^{19,46,85,86,87,88} The nerve models were reconstructed tridimensionally from three histological cross-sectional images obtained from two transfemoral amputees' tibial branches of the sciatic nerve, who participated in the previously conducted sensory restoration experiments¹⁶ (Figure 2B), therefore respecting the natural longitudinal development of fascicles including branching and merging, as opposed to extruded models used in the past.^19,46,85,89 Each of the two participants was implanted with four TIME electrodes in the residual tibial nerve in order to restore the sensations in the phantom leg. We therefore placed these intraneural electrodes in several positions on the nerve models according to the experimental constraints. The fibers were placed randomly in a uniform distribution inside the defined fascicles. Their diameters and density was sampled from distributions found in literature for the human sciatic nerve.^90,91 The injection of current from the electrodes was simulated by FEM in COMSOL Multiphysics. Ultimately, the charge injection threshold for the recruitment of each axon was estimated by NEURON simulations and used to build recruitment curves and to calculate selectivity metrics. Complete details of this model are reported in the next sections.

3D nerve reconstruction

When removing the implants, three histology images were taken at the site of implantation from each subject. The distance between each of the histology levels was 1 cm for both subjects. Visible contours in nerve image cross-sections, i.e. contours of three connective tissues (endoneurium, perineurium and epineurium) served as a base for generating a 3D Computer-Aided Design (CAD) model (Figure 2B) for each subject. Segmentation of histological images was performed by identifying 2D contours of the corresponding nerve structures, manually tracing them via ImageJ with its plugin NeuronJ. For a proper 3D nerve reconstruction, it is vital to determine the arrangement of the internal structures, i.e. the position of each fascicle. As the first step in determining how each fascicle progresses along the nerve, spatial orientations, disposition, and the points in the three cross-section layers where the fascicles are passing need to be identified. Orientations and transversally similar positions of each fascicle contour as well as the individual areas they occupy are to be decided upon; blood vessels, fascicle and epineurium shapes and fascicle groups (bundles) can be used as reference points. Varying number of individual contours in the adjacent layers indicates branching of the fascicles. Once the paths of all the fascicles were determined based on the 2D reconstructions, a 3D structure was generated by connecting the cross-sections. Each fascicle was composed of two volumes: an endoneurium and a surrounding perineurium. According to Grinberg et al.⁹² the perineurium in human nerves takes the outer 3 ± 1% of the total fascicle diameter, leaving the endoneurium with the remaining inner 97 ± 1%. Encapsulating all of the defined fascicles was a volume of epineurium. We then placed electrodes in the nerve model to be as congruent as possible to the experiment and surgical procedure described in Petrini et al.¹⁶

Incorporating the electrodes into the nerve model

In order to replicate the experiment from Petrini et al.¹⁶ as closely as possible, four TIME electrodes were inserted into the nerve model. The electrodes were implemented in accordance with the real manufacturer specifications and modeled according to the procedure done in the experiments, with 14 platinum active sites, 7 on each side; their crosswise order symmetrically displaced by half the distance between the adjacent active sites on one side, as seen in Figure 3B. Since the exact positions of the experimental insertions of the electrodes were not visible in the nerve cross-sections, we chose 8 potentially realistic electrode placement for each of the two subjects (16 models in total) and first made 8 (16) corresponding models for each separate electrode position, in order to observe their individual behavior in the nerve model.

Electrode placements were chosen in accordance with the surgical procedure described by Petrini et al.¹⁶ In the procedure, the surgeon would make a small surgical window in the epineurium of the nerve, which would enable him to distinguish certain individual nerve fascicles and choose the placement for each of the electrodes. Then, a needle was used to guide the electrode through the epineurium sutures and into the position in which all the electrode’s active sites would be in contact with some of the fascicles, after which the electrode would be fixated and fastened to the epineurium. Four TIME electrodes would be placed in such a way that they cover as much of the individual fascicles, with the idea that as many fibers as possible can potentially be recruited (in order to increase the selectivity and fiber recruitments). Longitudinally, all the electrode positions chosen in the models were located at or in the near proximity of the middle level of the modeled nerve section, since we knew that this area was approximately the surgical implantation level.

An electrode would be imported from SOLIDWORKS into COMSOL Multiphysics and merged with the nerve model. To keep the representation as realistic as possible, the modeled electrodes for some of the positions were slightly bended, as they would have been due to the internal nerve structures, they would run into during the surgical procedure to maximize fascicular coverage. Surface areas of the 14 active sites of each electrode were assigned as boundary current sources. The electrical ground is instead placed on the outer faces of the external cylinder containing the whole model structure.

Bulk electrical modeling

For the next step —the calculation of the electrical potentials—, the reconstructed nerve geometry was imported into COMSOL Multiphysics. Following the approach from the previous studies,^19,46 an isotropic saline solution in a form of cylinder, which represents the surrounding tissue, was set up around the nerve model. Taking into account the frequency range used in the experiments and in the corresponding modeling method, we used a quasi-static approximation of Maxwell’s equations, expressed through a Laplace formulation for the extracellular electric potential V_e^93,94:

$$\nabla ·\sigma \nabla V_e=0\text{.}$$

Material characteristic were assigned to each of the tissue classes: epineurium with electrical conductivity (σ) of value 0.0826 S/m,^85,95 perineurium of 0.00088 S/m,⁴⁶ while endoneurium, as an anisotropic medium, had transversal conductivity of 0.0826 S/m and longitudinal conductivity of 0.571 S/m.^85,95 The material surrounding the nerve was implemented as a homogeneous saline solution, with electrical conductivity of 2 S/m.^85,95,96

Boundary conditions

In order to model appropriately the neural interface based on electrical stimulation, the electrical ground represent a critical point in model boundary conditions. In fact, applying electrostatic and electrodynamics calculations, the ground (null potential) is usually set at infinity.^46,94 Therefore, our FEM model had to consider the approximation of an infinite space in a finite volume establishing the optimal distance of the ground from the model center. That meant defining a trade-off on the saline cylinder radius to simultaneously minimize the error on the computed potentials, while maintaining a reasonable computational load. Increasing cylinder radiuses with a step of 10 mm —up to 60 mm— were tested on a single point stimulation in the nerve center in quasi static condition. For defining the optimal cylinder dimensions, we compared for each condition previously proposed indexes^46,85: correlation coefficient, magnification factor and root mean square error were compared against the computational time. For the two subjects’ model, the optimal radius value was established at 20 mm, as the cylinder length.

Meshing the model

Due to the models’ complexity and curvilinear structures, meshing optimization was required to lower the computational load. Free Tetrahedral mesh was implemented throughout the whole geometry and its quality optimized was heuristically customized for each domain. The goal was to minimize the number of mesh elements without losing mesh quality, customizing mesh element sizes by hand. A subsequent analysis on the obtained mesh was performed with the same methodology applied for the boundaries condition: single point source stimulations were computed augmenting and lowering the number of mesh elements of 20% for all the structures. Correlation coefficient, magnification factor and root mean square error showed that the original meshing was already the optimal trade-off between mesh quality and computational load.

Fiber placement and modeling

The completed geometry was then exported from COMSOL Multiphysics into MATLAB. Cross-sections of the nerve 3D structure at longitudinal distances of 100 μm were made, obtaining stacked 2D boundaries of epineuria, endoneuria, and electrodes. The outlines of the endoneuria were then used for fiber path reconstruction. The count of fibers per diameter class —discretized at 0.5 μm steps— was generated from a 2D Gaussian fiber density function based on observational studies on human peripheral nerves^90,91 depending on axonal diameter and subject age. For each fascicle, its smallest cross-section was selected as a starting point. The fibers were distributed randomly in this initial cross-section avoiding overlaps. Subsequently, their trajectory was propagated to the adjacent cross-sections, shifting their centers to assure a uniform distribution along the changing endoneurium boundary, especially in proximity of subdivision/merging of fascicles, through Delaunay triangulation and uniformization of distances between neighboring fibers and boundary of the fascicle. The total number of fibers introduced in the 3D structure was decreased by a factor of 5 in order to reduce computational cost.^46,96 The splines representing the fibers’ paths were finally partitioned into compartments.⁹⁷ Randomization of the compartments’ shift along the fiber path was additionally performed. As in the state of the art models,^19,46,85,87 all fibers were generically modeled using the McIntyre-Richardson-Grill model (MRG),⁷¹ which was developed as a myelinated, mammalian motor nerve fiber. Its compartmental nerve structure uses nonlinear modified Hodgkin-Huxley equations⁹⁸ and is composed of Ranvier nodes and inter-nodal segments.

Simulating the stimulation

Based on the electric potentials computed by solving the FEM model, scaled so they correspond to 1 nC of charge injected within a square pulse corresponding to the experimental setup (50 μs pulse width), the potentials at the fiber node with the maximum potential and up to its 20 closer neighboring nodes —including internodal compartments lying in between— were interpolated at the coordinates of the compartment centers.^19,46 In order to reduce the computational load, only fibers within a fixed range of 2000 μm around the active site were taken into account, since Raspopovic et al.⁴⁶ showed that no fibers beyond this radius from the current source were selectively activated. The resulting values were used by NEURON as extracellular potentials for each fiber’s response. A fiber was considered activated once both the middle and the proximal end node were depolarized (reached zero potential). A bisection algorithm was employed to measure the injected charge threshold for the recruitment of each fiber by scaling the electrical potential by a multiplicative factor.

3D-nerve vs. extruded nerve model

State of the art models^19,46,85,89 use extrusion of a segmented histological cross-section along the longitudinal axis for the creation of a 3D structure. The hereby presented 3D-nerve models were built instead on a sequence of three nerve cross-sections. For each of the two implanted amputees both a 3D-nerve model and a corresponding extruded model was generated. The latter is constructed using a simple linear extrusion of the middle histological cross-section (as presented in the examples in the Figures 4B and 4D). From each of the two subjects’ extruded models, 35 single source points were placed around three representative fascicles. The point current sources were positioned at 7 different longitudinal distances from the extrusion level and for each level 5 points —4 representing squares vertices and one representing the diagonals crossing point— were placed so to enclose the fascicle structure. The same active sites arrangement was replicated in the 3D-nerve model. Finally, we compared the relative recruitments of the chosen fascicles between the two types of models. The deviation between extruded and 3D-nerve models was calculated by mean absolute deviation (MAD) of recruitment curves of each fascicle by each point current source (see Figures 4C and 4D).

Electro-neural model validation

The experimental data was composed by the perceptual thresholds and reported location of sensation per active site, for the two subjects, each with four implanted electrodes (see Figure 3B).¹⁶ Since the real placement of the electrodes could not be obtained during the following histological study on the excised nerves, we performed the statistical comparison considering the placements as samples of the general population of all plausible placements. Therefore, we modeled the electrodes in several placements observing the surgical constraints of the TIME implant procedure, which require the surgeon to be able to see both the proximal and the distal end of the electrode for fixation and all the active sites to lie within the nerve (Figure 3C). Experimental perceptual thresholds and the recruitment thresholds estimated during ENM simulations for each active site have been compared using the probability plot correlation coefficient (Figure 3D). Considered the proportionality observed on the probability plot, a corrective factor 10 was applied to the model charges (Figures 3D and 3E). The recruitment threshold was defined as the injected charge necessary to recruit 10% of a fascicle, chosen based on previous investigation on animal and humans for motor fascicular invasive electrical stimulation.^55,56,57 The discrimination boundary between the distributions of the model-estimated charge thresholds between intrafascicular and extrafascicular active sites was used to classify the active sites of the implanted electrodes (Figure 3E). Finally, we compared the ratio of intrafascicular active sites in model and experiment per placement (Figure 3F).

ProprioStim encoding

While the PNM described activation of a specific subset of fibers (Ia afferent fibers), the ENM provided the entire myelinated fibers activity for the whole nerve. Therefore, in the ENM, a first fibers differentiation was done based on their diameters: primary fibers (D > 12 μm), secondary fibers (6μm < D < 12 μm), tertiary fibers (D < 6 μm). Ia muscle spindles afferent fibers belong to the primary group together with Ib fibers and α-motor neurons (Figure 5). Primary fibers were than divided respecting a ratio of 16%, 12% and 72% respectively for Ia, Ib, and motor neurons. This ratio was determined combining different studies in which muscle spindles, Golgi tendon organs and motor units have been enumerated in animal muscles.^63,99 Knowing that the correspondence between these organs and their neural fibers is 1:1 we can define the fiber ratio for the primary fibers. Target fascicles, that innervated the gastrocnemius muscles were chosen based on previous anatomical and physiological studies.^{100,101,102,103} It was than possible to discriminate combinations of two fascicles innervating the two gastrocnemius muscles, based on their size and bundles association. To make the results generalizable, all the possible fascicle combination were tested, and 10 different randomized distribution of fibers location were simulated for each one of them (Figure 5). The time-variant stimulation pulse charge and frequency were computed so to minimize the difference between the electrically-induced fiber recruitments in the ENM with respect to the natural Ia fibers recruitments predicted by the PNM. The stimulation charge is found by interpolating the Ia recruitment curve of the ENM at the recruitment level predicted by the PNM. The stimulation frequency is set to simultaneously follow the firing rate predicted by the PNM.

To evaluate the goodness of the proposed methodology for encoding proprioception, we decided to compare it with respect to the classic encoding strategy used in literature and in the previous study: linear charge encoding.¹⁶ For both encoding strategies, recruitment of Ia is computed in the model during the acquired walking cycle execution. In order to make the results comparable, the two algorithms were tuned so they have the same minimal and maximal current intensity. Charge resolution of the stimulus was of 0.4 nC (8 μA).

In case of the linear charge encoding, the stimulus pulse charge (pulse width 50 μs) was linearly mapped between the minimal and maximal charge from the recorded angle joint during the walking cycle. Frequency of the stimulus was kept constant at 50 Hz. PNM-driven encoding instead mapped linearly the estimated recruitment between the maximum and minimum charge. Stimulus frequency is obtained dividing the estimated mean frequency firing rate from PNM by the recruitment level.

Resulting recruitments and mean firing rates of the Ia lateral and medial gastrocnemius afferent fibers between the two different encoding strategies are compared by computing the RMSE. Additionally, we investigated non-target fibers recruitments such as Ib, α-motor neurons, touch, and nociceptive fibers during the same stimulus. Different recruitment distributions were compared during peak stimulation using Kruskal–Wallis test. This investigation was necessary to understand if applied stimulus was able to restore proprioception without triggering other types of sensory sensation.

Comparing PNM-driven stimulation with linear charge modulation through TENS

Seven healthy subjects (2 males, 5 females, 24.0 ±1.5 years old) were recruited for testing the two different encoded stimulations: PNM-driven and linear charge modulation. On each subject were placed initially two pairs of TENS electrodes to specifically target the sciatic nerve branch innervating the gastrocnemius muscles. The anodes (rectangular sticky patches, 4 × 3 cm) were placed on the upper frontal part of the leg on the medial and lateral side of the tibial bone. Cathodes (circular sticky patch, diameter of 1.5 cm) were instead positioned over the popliteal fossa (area where the nerve is the most superficial) so to target the two different sciatic nerve branches innervating the lateral and medial gastrocnemius muscles (Figure 7A). This anode-cathode configuration was tailored for each specific subjects shifting slightly the cathodes (Figure 7A). Final position of the cathode was chosen to maximize the somatotopy and the naturalness of the elicited sensation compatible with area innervated by the tibial nerve, and specifically to obtain the strongest sensations at the medial and lateral muscular bulges of the calf. We excluded placements that were reporting any sensation on the anterior part of leg and dorsum of the foot which would indicate recruitment of the peroneal nerve. Elastic bands were used to secure electrode position and reduce electrodes displacements.

An initial calibration phase was performed. Increasing intensity stimulation was delivered to the user to identify a reasonable range for charge modulation. Minimum charge corresponded to the threshold for evoked sensation. Maximum charge instead represented the stimulation intensity below both pain sensation and muscle contraction. Muscle contraction had to be avoided so to not confound the TENS elicited sensation with the proprioceptive response due to actual muscle contraction. Ultimately, the calibration curve was obtained by linearly fitting the reported normalized sensation obtained by delivering 20 random intensity stimuli uniformly spaced between the identified minimum and maximum charge. Mapping of the stimulus on the reported normalized sensation was moreover essential to guarantee the absence of intensity bias between the two types of encoding strategies.

After the calibration, the stimulation was delivered to the user using two types of encoding: PNM-driven and linear charge encoding modulation. The user was only informed that the received stimulation encoded a knee flexion-extension movement in a ramp shape. The user had to follow the sensation matching with the contralateral leg the perceived angle knee (Video S1). The ramp was repeated for both the two stimulation paradigms and for different ramp target angles equally distributed between 90° (flexed) and 0° (extended) with a step size of 5°. The encoded stimulation represents a knee angle ramp movement here defined: 3 seconds of static leg at 90°, 5 seconds ascending ramp from the flexed position till the target angle, 7 seconds of static position at the identified target angle.

In the case of linear charge encoding, the stimulation for the gastrocnemius lateralis and medialis were obtained transforming the knee angle trajectory into charge level with the obtained calibration curve, while the stimulation frequency was kept constant at 20 Hz (Figure 7B). In the case of PNM-driven modulation, OpenSim software was used to obtain muscle elongations and muscular activations of the selected muscles, simulating the same knee trajectories used for the linear encoding. This information is than used to compute the percentage of Ia fiber recruitment and firing rate with the PNM and subsequently use them to modulate stimulation intensity and frequency (Figure 7C). While gastrocnemius muscles are more involved in ankle movements, we chose to use knee flexion and extension for three main reasons: i) The knee closure/opening are strongly correlated to the status of those muscles. Indeed, during physiological walking, the activation of the calf muscles play a major role in the control of the knee^104,105; ii) Feedback about the knee angle is more important for the typical use of an above-knee prosthesis¹⁰⁶; iii) To obtain a fair comparison with previous literature,¹⁶ where knee joint angle was used for the modulation of the evoked proprioceptive sensation. We have however minimized the ankle influence on the overall sensation by instructing the subjects to keep the ankle fixed at 90°, so that gastrocnemius proprioceptive sensations were derived only from knee joint motion.

During the experiment the subject is comfortably seated blindfolded. The user is warned from an audio cue that the stimulation is starting and that he can move the contralateral leg with respect the stimulation to match the felt sensation. After 10 seconds, at the end of the ramp knee movement another audio cue is delivered to the subject to return in the starting position. This trial is repeated for each target angle (19 repetition), each condition (2 type of stimulations) and for 3 sessions. The trials were shuffled to avoid habituation affecting the comparison between the two encoding strategies. Between every session 5 minutes break was taken.

The measured angle was tracked through video recording. The angle was measured only at the sound of the second audio cue and compared with the target angle and normalized between maximum extension and flexion to avoid perspective distortions.

Four subjects were moreover chosen for a forced choice paradigm. The subjects received the stimulation corresponding to a fully extension and flexion of the knee joint. In each trial, both types of stimulations were performed in random order. At the end of the two stimulations the subject was asked to choose the one that generated a more natural proprioceptive sensation, i.e. the one that gave a sensation closer to what they felt during actual flexion and extension of the knee joint, which they were allowed to perform at will between trials for reference. Each trial was repeated 20 times. Binomial test was computed to calculate the statistical difference between the two response rate.

Quantification and statistical analysis

The body kinematics and EMG were synchronized with VICON NEXUS 2.10.

The musculoskeletal model was developed with OpenSim 3.3.

The histological segmentation was performed with ImageJ 1.52p and its plugin NeuronJ 1.4.3.

The volumetric nerve reconstructions were performed with SOLIDWORKS 2019.

The FEM simulations were performed on a commercially available personal computer with a 3.00 GHz Intel Core i7-9700 CPU and 32 GB RAM, with COMSOL Multiphysics 5.5.

The recruitments were calculated on a commercially available personal computer with a 4.00 GHz Intel quad-core CPU with 8 GB of RAM and on NEURON software, version 7.7.2, in parallel execution.

Numerical analyses and statistical tests were performed on MATLAB 2020b.

The comparison of the ratio of intrafascicular active sites in model and experiment per placement was performed by a Kolmogorov–Smirnov test (Figure 3F).

The recruitment between target and non-target fibers were compared using a Kruskal–Wallis test.

The absolute value of errors between the two encoding strategies during the TENS were compared using a repeated measure ANOVA with angle, encoding paradigm, and their interaction as predictors. Post-hoc correction was performed by Tukey’s honest significance test for multiple comparisons.

The response rates in the forced choice paradigm were compared by a binomial test.

Habituation was evaluated with a Mann-Kendall test with the Bonferroni-Hochberg correction for multiple testing (Figure S5).

Published: January 21, 2023

Data and code availability

• •All data reported in this paper will be shared by the lead contact upon request.
• •All original code has been deposited on Zenodo and is publicly available⁷² as of the date of publication. DOIs are listed in the key resources table. A standalone executable distribution of ProprioStim is also publicly available.⁶⁸ It allows to choose a movement form experimental dataset with 10 different movements (e.g. walking uphill/downhill, fast/slow, etc.), visualize body kinematics, muscle spindle activations, and compute the related stimulation parameters. Moreover, it includes MATLAB and NEURON source code to interactively visualize exemplary results of the presented models and allow to run neurophysiological and ProprioStim simulations under different hypotheses regarding fibers distribution, axon model, etc. A brief description of its usage is found in the README file provided with the code.
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.