Functional Protein Dynamics Directly from Sequences

Abstract

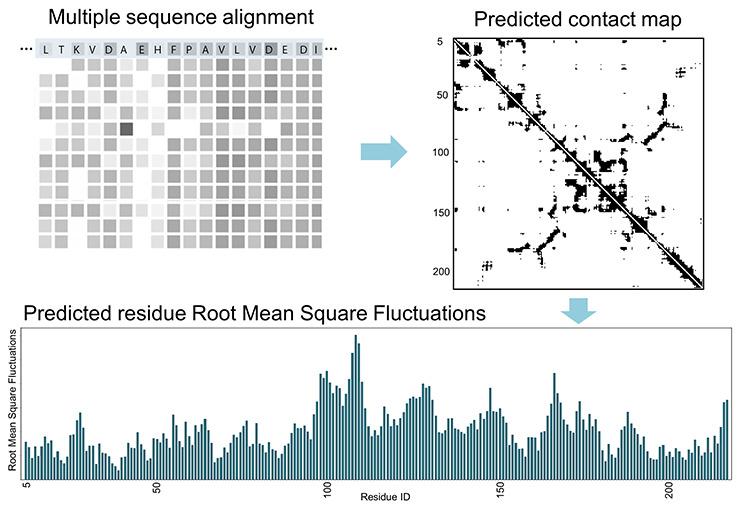
The sequence correlations within a protein multiple sequence alignment are routinely being used to predict contacts within its structure, but here we point out that these data can also be used to predict a protein’s dynamics directly. The elastic network protein dynamics models rely directly upon the contacts, and the normal modes of motion are obtained from the decomposition of the inverse of the contact map. To make the direct connection between sequence and dynamics, it is necessary to apply coarse-graining to the structure at the level of one point per amino acid, which has often been done, and protein coarse-grained dynamics from elastic network models has been highly successful, particularly in representing the large-scale motions of proteins that usually relate closely to their functions. The interesting implication of this is that it is not necessary to know the structure itself to obtain its dynamics and instead to use the sequence information directly to obtain the dynamics.

Introduction

Generally, the relationship between protein structure and dynamics is considered to be the critical information for comprehending function. However, the intention here is to demonstrate that it is possible to comprehend the dynamics even without having any structure. It may seem odd to suggest this, especially since predictions have recently proven to be so effective for protein structures whenever no experimental structure is available. AlphaFold2,¹ RosettaFold,² and ESMFold³ now present us with the possibility of having reliable structures for the majority of proteins. Why is there a need for skipping structure and going directly from sequences to functional dynamics? There are several reasons for making this direction connection: (1) comprehension of the full set of mutations is a huge task that requires rapid computations, (2) understanding the effects of all known mutations is likewise an impossible task, and (3) the growth in sequence data is huge and likely to be even more rapid in the near future, with technological developments making it ever cheaper.

Why Is This Possible?

There has been remarkable progress in understanding protein dynamics with coarse-grained elastic network models (ENM). We have demonstrated how most of the protein dynamics are captured by these coarse-grained dynamics models, with only a small overall loss.⁴ The information required by these models is the contacts between amino acid pairs. Coarse-graining of structures and the subsequent capture of dynamics have made important progress. Of course, this approach also has the advantage of more rapid computations. Usually, these approaches consider coarse-grained dynamics where each structure is represented by geometry at the level of one point representing the individual amino acids, rather than having all atoms present.

The evolution-driven mutations among residue sites of a protein family are interdependent due to the constraints on protein functions from the structure. The basis for much of the gain in recent structure predictions originates from comprehending the coevolutionary correlations in protein multiple sequence alignments that are used to predict residue-level spatial proximity or structural contacts. And the central data used for the computations of dynamics with the ENMs is the same—the structure contact matrix. So what we are proposing here is to simply skip over the step of generating the structure from the contacts and instead use the contacts directly to generate the dynamics

Using Sequence Correlations

The huge volume of sequence data presents this opportunity since sequences provide coevolutionary correlations (evolutionary couplings) for most protein families. It is widely accepted that evolution conserves the functional dynamics of proteins. It is rational to directly use the evolutionary sequence information to recover protein structural and dynamical properties. There is some previous work relating sequence correlations to protein dynamics such as that by Liu and Bahar,⁵ who used a set of 34 enzymes to analyze the connection between sequence correlation and structural dynamics. Their result showed that the structural regions are distinguished by their coevolution propensities. Gerek et al.⁶ pointed out the connection between residue flexibility and residue variability. In their work, they analyzed the functionally critical positions within 100 human proteins and found that the rate of variability at each residue position produces concordant patterns on the proteome scale. In other words, the structural dynamics flexibility is closely related to the evolution in a protein family. With the development of coevolution methods, being used to predict protein structures by exploring the evolutionary coupling for pairs of residue sites within a multiple sequence alignment, more and more evidence demonstrates that there is a distinct connection between protein sequence evolution and protein dynamics. Sutto et al.⁷ combined coevolution correlation information and molecular dynamics simulations to study protein conformational heterogeneity. One of the important findings of their research was that the various regions of the sequence display different stabilities related to multiple biologically relevant conformations and to the cooperativity of the coevolving pairs. They further proposed a protocol that can reproduce the essential features of a protein folding mechanism and account for regions involved in conformational transitions with the appropriate sampling of the conformers involved. Granata et al.⁸ showed that the network of pairwise evolutionary couplings can be analyzed to reveal communities of amino acids, which are in striking agreement with the quasi-rigid protein domains obtained from elastic network models⁹⁻¹² and molecular dynamics simulations.¹³ In their study, the communities are identified by spectral clustering based on the correlation network, which was defined by evolution couplings from direct coupling analysis (DCA).¹⁴ Tang and Kaneko¹⁵ studied the dynamics–evolution correspondence in protein structures. In their study, the elastic network model was used to quantify the dynamics of a protein structure. Principal component analysis was used for acquiring evolutionary modes from the corresponding multiple sequence alignments. Based on the analysis of 415 protein families, they found overlaps between the subspaces spanned by the dynamics and evolutionary modes, which finally suggests a universal link between the functionality and evolvability of proteins.

These previous studies have laid the foundation for establishing the connection between sequence correlation and dynamics. In this work, we evaluate the recovery of dynamics information directly from the evolutionary sequence correlations. For this purpose, we perform DCA on 4945 protein families to extract the evolutionary couplings between residue positions. Then we use two approaches to derive protein dynamics: (1) We threshold the coupling matrix into a residue contact map and then use GNM^10,16 to calculate the modes that represent the dynamics information from evolutionary couplings. (2) Inspired by Tang and Kaneko’s work,¹⁵ we normalize each coupling matrix to approximate the residue displacement correlation matrix of a protein. Then we use principal component analysis to extract the essential dynamics vectors to represent the protein dynamics.^13,17 Both “evolutionary” dynamics sets are then compared with the GNM modes calculated from the representative experimental structure. The similarity between the modes is measured with RMSIP (root mean square inner product).¹⁸⁻²⁰ The results show in general that the dynamics derived from both methods overlaps with the structural dynamics. The first approach, the contact map reconstruction method, has overall better agreement with the experimental structure dynamics than the other approach. However, the level of overlap depends strongly on the DCA performance. We categorize protein families into five classes by ranking their contact prediction accuracy. The family with the most accurate contact predictions will clearly yield better dynamics reconstruction. We also compare the contact maps between families with good dynamics reconstruction. Surprisingly, the predicted contact maps are not always in perfect agreement with the contact maps derived from the experimental structure, but they are nonetheless of sufficient quality to extract most of the important dynamics. This result may be due to the fact that the predicted contact maps often include alternative conformation information and multimer interaction information,²¹ which are also dynamics information.

Results

Contact Predictions with the Coevolution Method Applied to Large Quantities of MSA Data

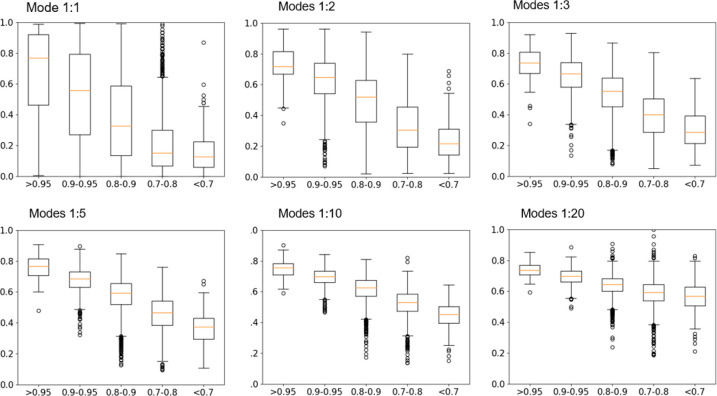
Direct coupling analysis (DCA) provides a global statistical model for analyzing multiple sequence alignment (MSA) data and evaluates the evolutionary couplings between each pair of residue positions to predict the residue contacts in the protein structure.^14,22 We apply the implementation of DCA purposed by Marks et al.²² to 4945 multiple sequence alignments of protein families from the Pfam database.²³ Each of the families has at least one experimental structure available to evaluate the DCA performance and protein dynamics. For each family, we compare the number of positions that have strong coevolution signals with the length of the protein and find that the top-ranked 10% correlated positions usually include all of the residue positions in the protein. As shown in Figure 1 A, for the top-ranked 6%, the average coverage is close to 100% but still with small deviations and many outliers. For the top 20%, the extent of deviations and the number of outliers decrease significantly. Panel A in Figure 1 demonstrates that intramolecular coevolution is ubiquitous in almost all protein families. Panel B shows the DCA performance for residue contact prediction. The distribution resembles a skewed Gaussian distribution with a mean value of 0.84. Later we separate families into different groups by their prediction accuracy to examine the dynamics representation.

Figure 1.

Coverage of strongly correlated positions and distribution of AUC for residue contact prediction for DCA for 4945 protein families. (A) Box plot showing the distribution of position coverages for different levels of top-ranked positions. The top 20% of strongly coevolved position pairs for almost all protein families is sufficient to cover all positions in each protein. (B) AUC (area under the curve) histogram for all 4945 protein families The distribution has a mean of 0.84 with a standard deviation of 0.07.

Overlaps between Dynamics Derived from Experimental Structure and Dynamics from Predicted Contacts

In this approach, we follow an intuitive approach: using cutoffs on the coevolution coupling matrix to reconstruct contact matrices by using DCA scores to predict the spatial proximity of any two residue positions. The higher the score, the closer the two positions. Therefore, converting the coupling matrix to a contact matrix will usually contain sufficient structural information for GNM to be able to calculate the dynamics. Based on the result in Figure 1 A, we reconstruct contact maps from DCA scores with a starting cutoff value of 0.05 (top 5% of ranked pairs) where residue pairs with scores larger than the cutoff are considered to be in contact. More details about contact map reconstruction are provided in the Methods and Materials section. Then the dynamics are calculated using GNM based on this reconstructed contact matrix. In order to make certain that the reconstructed contact network is a fully connected graph (needed by GNM), we iteratively increase the thresholding cutoff on coupling scores until all positions are connected in the network. For comparison, the dynamics modes from the experimental structure are calculated using standard GNM with a distance cutoff of 10 Å. The top 1, 2, 3, 5, and 20 modes from both the experimental structure and the coevolution couplings are compared, and the RMSIP (root mean square inner product)¹⁸⁻²⁰ is used as a measure of dynamics overlaps. To avoid averaging overlap values between families with accurate contact predictions and those with poor predictions, we categorize all 4945 families into 5 classes according to their contact prediction accuracy levels.

Figure 2 shows the dynamics overlaps within each class. Overall, for the most important motions (modes 1 to 5), the overlaps are highly dependent on the accuracy of the contact prediction. Families with an AUC value higher than 0.95 can reach average overlaps near 0.8. Another trend is seen in the number of modes in the comparisons. The more modes included, the less difference there is among the five categories, which means that the overlaps become less dependent on the prediction accuracy.

Figure 2.

Overlaps between the dynamics of experimental structures and the dynamics of the reconstructed contact matrix from evolutionary couplings. The top 1, 2, 3, 5, 10, and 20 modes are compared. All 4945 families are categorized into 5 classes: AUC values >0.95, 0.9–0.95, 0.8–0.9, 0.7–0.8, and <0.7. The families with higher AUC values have better dynamics overlaps. The more modes included, the smaller the differences among the five categories.

Disagreements between the two types of contact maps do not necessarily lead to very different dynamics. In this study, we often see small differences between the predicted contact map and the true contact map. Anishchenko et al.²¹ pointed out that “additional” contacts predicted by coevolution methods often correspond to alternative conformations sampled during the protein’s dynamics. The contact map based on a single experimental structure reflects only the residue contacts in a single conformational state of the protein. This means that any changes due to the dynamics may lead to changes in the contact map, with some individual contacts either missing or newly appearing. However, if two positions form contacts in any of the protein’s conformations, then they are likely to be present in the predicted contacts. Consequently, the predicted contact map based on coevolution methods and the true contact map derived from a single experimental structure will usually have some differences, but importantly, these differences actually often directly reflect the dynamics. For example, the glutamine binding protein has a typical open–closed motion where the two ends come into contact in the closed form (PDB ID: 1wdn). However, if we use an open form (PDB: 1ggg) to evaluate the contact map, then these contacts would not be present. The predicted contact map has a significant area of contacts that is not present in the contact map of the open 1ggg. In this case, the coevolution coupling predicts those contacts present in the alternative closed conformation. On the other hand, fewer contacts in the predicted contact map do not necessarily lead to dissimilar dynamics. In another study,²⁴ we coarse-grained the protein structure for different levels of coarse-graining. The results showed that even for extreme coarse-graining, which means that there are fewer contacts included, the elastic network model nonetheless is still able to derive similar large domain motions.

Overlaps between Dynamics Derived from the Experimental Structure and Principal Component Vectors of the Evolutionary Coupling Matrix

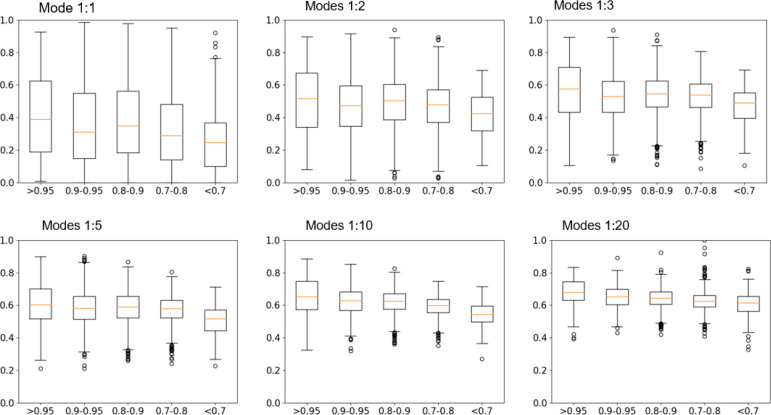
In this approach, we first convert the evolutionary coupling matrices to correlation matrices. Then we perform principal component analysis and use principal component (PC) vectors (below referred to as PC modes) to represent the dynamics modes of the protein. Finally, the overlaps between the PC modes from evolutionary couplings and GNM modes from experimental structures are measured using RMSIP. In this approach, we categorize protein families into the same five classes. Figure 3 shows the overlaps for each class and for 1, 2, 3, 5, 10, and 20 modes included. In comparison to the results of the first approach, the overall overlaps are lower. The dynamics overlaps clearly are less dependent on the contact prediction accuracy, which means that there are smaller differences among the five classes. Again, the more modes included, the higher the overlaps observed, but still some information about characteristic slow motions is lost.

Figure 3.

Overlaps between dynamics derived from experimental structures and PC modes from the evolutionary coupling matrix. The top 1, 2, 3, 5, 10, and 20 modes are compared. All 4945 families are categorized into 5 classes with AUC values >0.95, 0.9–0.95, 0.8–0.9, 0.7–0.8, and <0.7. The overlaps of the first mode are only around 0.3–0.4. With more modes included, the overlaps increase to around 0.7. The overlaps are less sensitive to the contact prediction accuracy compared to the results in Figure 2.

Next, we show in Figure 4 some examples comparing the sequence correlations and the contact maps for some individual structures. In addition, we show the similarity in the dynamics predicted from the sequence correlation matrix and the dynamics from the experimental structure contacts. This is a strong demonstration showing how reliable this approach can be. Although the focus in this figure is only on the slowest normal mode motion, other important mode motions can also be extracted from the set of contacts predicted from that sequence correlation.

Figure 4.

Validating the use of contacts predicted from sequences as a basis for generating protein dynamics, skipping over the generation of the structures. Comparisons are shown for contact map overlaps, and the first mode overlaps between experimental structures and evolutionary couplings. In each panel, the left side shows the contact maps, and the dynamics mode comparisons are shown on the right. In each contact map, the upper triangle map is from the experimental structure and the lower triangle map is from the predicted contact map. (A) Overlaps for the Cna protein B-type domain family (PF05738). The AUC value of the contact prediction is 0.86, and the first mode overlap is 0.93. (B) CHC2 zinc finger family (PF01807). The AUC value is 0.91, and the first mode overlap is 0.96. Both panels A and B demonstrate that with an accurate prediction of the contact map, the overlaps between the first mode of the PDB structure and the predicted mode are high. However, exceptions can happen. (C) Overlaps of Family 5′_3′_exonuc (PF01367). The mode overlaps are high, but the contact maps are not consistent. The contact prediction AUC value is 0.78. The mode overlap value is as high as 0.98. The reason for this is that the protein structure contains a long loop with the loop “waving” motion dominating the major motion, with other motions less important. (D) Another exception where the contact map overlaps are high (AUC 0.97) but the mode overlap for the first mode is low (0.39). Although the overall “shape” is captured by the predicted contact map, multiple extra false-positive contacts along the left side of the map affect the first mode significantly. The structures on the right sides are colored spectrally by the motion of the first mode, with red being the largest motion and blue being the smallest motion.

In Figure 4 C, we show a protein with a highly disordered segment. The dynamics overlap from the slowest (first) mode is poor. The “waving” motion of a long disordered region of the protein dominates the first mode. In fact, the Gaussian network model is not suitable for predicting the dynamics of disordered proteins due to its inability to capture the dynamic nature of these proteins, since they lack any well-defined structure, with no persistent contacts upon which to base the computation of dynamics. GNM relies on the assumption that the residue contacts capture the essential overall structural features of a protein structure. These inter-residue contacts are used directly in the dynamics calculation of the elastic network. However, disordered proteins lack well-defined structures, meaning that their structural features cannot usually be represented with a contact map. Thus, GNM cannot accurately predict the dynamics of such proteins.

Figure 4D shows an unusual example where there is strong similarity between the contact maps yet low agreement in the first mode of the dynamics. The top 1, 2, 3, 5, 10, and 20 mode overlaps of the protein are 0.39, 0.72, 0.75, 0.80, 0.77, and 0.75, respectively. The first mode has a low overlap value (0.39) with the true dynamics from the experimental structure (PDB ID: 2FF4) even when the contact prediction has a high AUC value (0.97). However, if more modes are included, for example, the top five modes, then the overall dynamics overlap is high, which means that the predicted dynamics is similar to the true dynamics.

Conclusions

We have demonstrated here the feasibility of generating reliable functional dynamics directly from sequence information. This builds upon the rapidly growing sequence data and is important if there is no available structure. Two cases come to mind where this could be useful: (1) identifying labeling sites for FRET experiments where it would help to have some knowledge of the motions and (2) investigating the effect of the many disease mutants that change a protein’s functional dynamics (requiring the use of atomic elastic network models). This relationship could be helpful in assessing the effects of a disease mutant to enable the rapid identification of the effects of critical mutations on the functional dynamics. The additional component required to put this into effect is the identification of the outliers in sequence, i.e., which mutations deviate from the usual sequence distribution for each family of proteins, that is, which mutations represent deviations from those observed sequences for a given family.

Methods and Materials

Overall Pipeline Description

In this work, we implement a pipeline that is designed to predict protein dynamics from evolutionary couplings. We first apply DCA²² to calculate the evolutionary coupling on multiple sequence alignments of 4945 protein families. Then the coupling scores are used in two ways. The first is to reconstruct the protein residue contact map and to calculate its dynamics using GNM. The second is to convert the couplings to a covariance matrix to obtain the essential dynamics of the protein. Finally, both of these results are compared against the result calculated directly from experimental structures and their contact maps using GNM.

Data Selection

The data selection process is important in order to obtain accurate results. To ensure the quality of the multiple sequence alignments and also for the purpose of ensuring the reproducibility of our work, we choose to use the MSA data from the Pfam database.²³ The Pfam database is a comprehensive source of protein family alignments and is widely used in the field of bioinformatics. The selection criteria are as follows: (1) using the full alignment data from the Pfam database and selecting families having at least 500 sequences to provide sufficient statistics for the evolutionary coupling detection and (2) having at least one experimental structure with a resolution of 3 Å or better for each family to guarantee the quality of prediction evaluations. The list of Pfam IDs and PDB IDs is provided in the Supporting Information (Table S1)

Evaluation of Coevolution Coupling Using DCA

Direct coupling analysis (DCA) is a widely used coevolution method for predicting protein residue contacts. DCA is based on the premise that residues which are located close together in the three-dimensional structure of a protein are likely to be “coupled” across evolution to maintain the same structure. DCA quantifies this coupling by analyzing the correlations between pairs of amino acid residues in the protein sequence. In this study, we adopt the DCA implementation from Sander’s group. DCA begins by assigning a probability to each aligned sequence (A₁, ..., A_L) of length L

1

where e_ij(A_i, A_j) denotes the direct coupling between amino acid A_i in position i and amino acid A_j in position j and h_i(A_i) is the local bias for only the amino acid present in a single position i. The partition function Z is used to normalize the probability. Then parameters are optimized to reproduce the empirical statistics extracted from the MSA

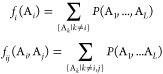2

for all positions i and j and all amino acids A_i and A_j. Here f_i(A) denotes the frequency of occurrence of amino acid A at position i and f_ij(A, B) is the fraction of sequences having A in position i and B in position j in the MSA. Parameters are estimated using the mean-field approach. To remove the sampling bias in the MSA data, a sequence reweighting scheme introduced in Marks et al.²² is applied. In the reweighting process, sequences in the MSA are clusters using a similarity cutoff of 80%, where two sequences within each cluster have no less than 80% identities. Then each sequence is assigned a weight value t equal to 1 over the number of sequences in the current cluster. Finally, the weights are normalized to be in the range of [0, 1] by dividing the summation of all weights. The summation of all weights is also used to evaluate the diversity of sequences in the MSA.

Reconstruction of the Contact Map from DCA Coupling Scores

In this approach, we reconstruct the residue contact map from the DCA coupling scores. The predicted contact map can then be input into GNM to calculate the protein dynamics. In the DCA results, the higher the score between two positions, the more likely they are to form a contact in the protein structure. We derive a contact map by thresholding the DCA coupling score matrix with score rankings. We first convert the coupling score into a ranking score where all of the scores are sorted from large to small, then we assign a rank value to each score based on the sorting, and finally, all of the rank values are normalized to a range of 0 to 1. In this way, we can threshold the score matrix by a certain percentage of the top-ranked pairs. According to the statistics shown in Figure 1, we start thresholding with a default ranking cutoff of 0.05, which means we use the top-ranked 5% of the position pairs to form the contact map. If the resulting contact map is not a connected graph, then we increase the cutoff with an interval of 0.01 until the contact map forms a connected graph.

Protein Dynamics from the Gaussian Network Model

The Gaussian network model (GNM) is a computational tool used in protein dynamics analysis. It is an elastic network model that represents a protein as an elastic mass-and-spring network to analyze protein fluctuations and collective dynamics.^10,16 The method is based on the idea that proteins vibrate about an energy minimum and that the fluctuations of these vibrations can be used to predict protein structure and dynamics. The steps in calculating dynamics with GNM are the following: (1) Generate a contact network from the 3D coordinates in the protein structure. Two residues are connected if their α-carbons are within a certain distance cutoff. (2) Derive a Kirchhoff matrix from the residue contact network. The Kirchhoff matrix is defined by eq 3,

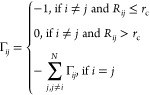3

where Γ_ij is the ijth element of the Kirchhoff matrix and r_c is a cutoff distance for spatial interactions. (3) Apply eigen decomposition to the Kirchhoff matrix. As a result, for a protein with N residues, each GNM mode k is represented by an N-dimensional eigenvector, with each element describing the displacement of residue i along the kth mode axis. The first mode is removed and represents rigid body motions. The eigenvalue describes the frequency of a model where the low-frequency modes represent the long-time large-scale motion of the protein, which is often more important in representing the dynamics. In this study, a cutoff value of 10 Å is used to define residue contacts. In this project, we use experimental protein structures to calculate the “true” dynamics information, and then we calculate the overlap of the top 1, 2, 3, 5, 10, and 20 modes between predicted dynamics and the true dynamics to evaluate the prediction performance.

Protein Dynamics from Essential Dynamics Analysis

This is an alternative approach to infer protein dynamics directly from the coevolution correlations. Tang and Kaneko showed the strong similarities between the dynamics correlation matrix and the coevolution correlation matrix of proteins, indicating that the residues with high dynamical mobility exhibit high structural variability.¹⁵ This suggests that the coevolution couplings can be treated as a residue displacement correlation matrix which can further be used in the essential dynamics analysis to infer the protein dynamics. Essential dynamics (ED)¹³ is a technique used to investigate the global conformational dynamics of proteins and to determine the most important motions of the protein. It is based on the concept that the conformational changes of a protein can be described in terms of a small number of collective variables, or “essential dynamics”. The input data for ED is often the time-dependent fluctuations of the atomic coordinates of the protein structure from a simulation. The fluctuations are usually calculated by applying principal components analysis (PCA) to the simulation data. The output principal component vectors are used to characterize the most important collective motions of the protein. If a protein has N residues, then the output vectors characterizing its dynamics also have N elements, with each element representing a small magnitude of position displacement along the direction, which is similar to the dynamics modes from GNM. In this study, we convert the coevolution coupling matrix to a correlation matrix by normalizing the scores into the [0, 1] range and assigning 1.0 to the diagonal elements. The PCA is applied directly to this converted correlation matrix to derive the principal vectors.

Comparing Predicted Dynamics with True Dynamics from Experimental Structures

To compare predicted dynamics with true dynamics, we use the root mean square inner product (RMSIP)¹⁸⁻²⁰ to quantify the similarity between two motions. RMSIP is a mathematical technique used to measure the overlap between two vectors or two spaces spanned by vectors, defined in eq 4,

4

where η_i and ν_j are the set of eigenvectors of the predicted and true dynamics vector spaces, respectively. N is the number of elements in both vectors. It is a widely accepted method for quantifying the similarities between protein dynamics.¹⁷ If the RMSIP is close to 1, then the dynamics are similar; if the RMSIP is close to zero, then the dynamics do not overlap. In this study, we compare the overlaps between the spaces spanned by the dynamics derived from an experimental structure and other predicted dynamics. One set is derived from the GNM with a reconstructed contact map, and the other set is from PCA with a converted displacement correlation matrix. The top 1, 2, 3, 5, 10, and 20 modes are used to calculate the overlaps.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcb.2c05766.

• Supplementary table lists all Pfam families used in the current work, with Pfam IDs, the number of sequences in the multiple sequence alignment, and the size of the protein domain (XLSX)

The authors declare no competing financial interest.

Special Issue

Published as part of The Journal of Physical Chemistry virtual special issue “Jose Onuchic Festschrift”.