Abstract
Rigorous physics-based methods to calculate binding free energies of protein–ligand complexes have become a valued component of structure-based drug design. Relative and absolute binding free energy calculations have been deployed prospectively in support of solving diverse drug discovery challenges. Here we review recent applications of binding free energy calculations to fragment growing and linking, scaffold hopping, binding pose validation, virtual screening, covalent enzyme inhibition, and positional analogue scanning. Furthermore, we discuss the merits of using protein models and highlight recent efforts to replace costly binding free energy calculations with predictions from machine learning models trained on a limited number of free energy perturbation or thermodynamic integration calculations thereby allowing for extended chemical space exploration.
Keywords: rational drug design, FEP, prospective prediction, lead optimization, late-stage functionalization
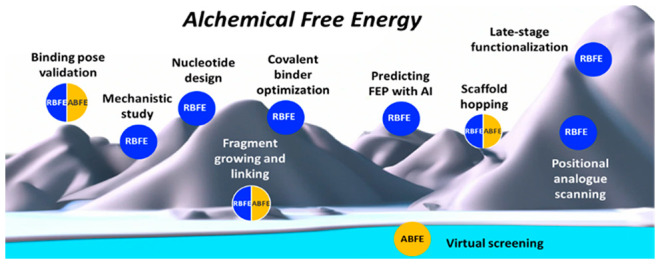
Estimating binding affinities of ligand–protein complexes on a regular basis has become a reality in many drug discovery endeavors today.1 Fueled by high-resolution protein structures derived from crystallography, cryoelectron microscopy, and deep learning methods and guided by maturing computation technologies and increasing compute resources, relative (RBFE) and absolute (ABFE) binding free energy (BFE) calculations have been utilized with more confidence and greater reliability in designing lead compounds for drug discovery.2−4 Free energy perturbation (FEP) and thermodynamic integration (TI) are two prominent algorithms used to calculate BFEs; commercial and open source implementations are available.5−7 Often the aim of using physics-based RBFE and ABFE calculations is to decide what compound to make next in the course of a multiparameter lead optimization campaign.8 However, BFE calculations are now used to support a variety of additional tasks including scaffold hopping, advancing fragments into leads, improving covalent binders, exploring alternative modalities, guiding positional analogue scanning, validating binding mode hypotheses, and making forays into virtual screening (Figure 1). In addition, results of computationally intensive RBFE calculations that can take several GPU hours to finalize can be predicted by machine learning (ML) methods allowing for the exploration of larger chemical spaces of congeneric series. In this Microperspective, we review applications of RBFE and ABFE calculations across these areas of application as they are relevant to drug discovery.
Figure 1.
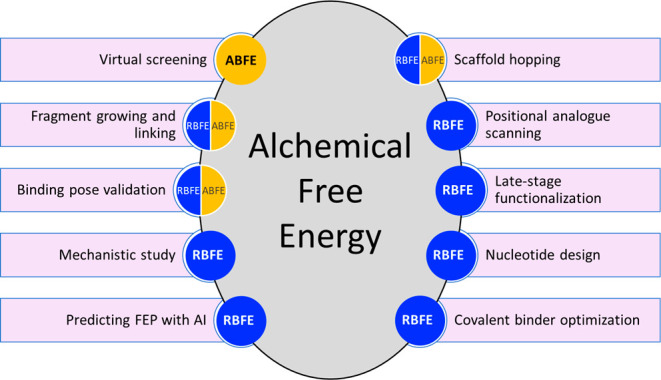
Application of alchemical RBFE and ABFE calculations to different drug design tasks.
RBFE and ABFE Calculations
While we leave a rigorous introduction to the methodology and technical aspects of RBFE and ABFE calculations to comprehensive reviews written on the subject,4,9,10 we briefly touch on the underlying alchemical nature of the BFE calculations performed in silico and how they relate to observable parameters for relative and absolute BFEs. Figure 2 illustrates the thermodynamic cycles deployed by the two methods. As free energy is a thermodynamic state function, RBFE calculations take advantage of the net zero free energy variation in a complete thermodynamic cycle. The difference of BFEs between two ligands can be calculated by alchemically changing one ligand into another in the protein binding site compared to aqueous solution. Although this process cannot be experimentally tested, it is feasible to simulate in silico and forms the basis of FEP or TI methods predominantly used to calculate RBFEs (left side of Figure 2). Following an alternative thermodynamic cycle (right side of Figure 2), an alchemical ABFE can be calculated by simulating the annihilation of a ligand in the protein binding pocket and in solvent. While FEP and TI RBFE calculations are well established and convenient software implementations are available, ABFE calculations incur higher computational costs and are less accessible, although Schrodinger recently tested an ABFE implementation.11
Figure 2.
Thermodynamic cycles of RBFE and ABFE calculations for ligand Lig. ΔΔGbindRef→Lig is the difference in BFEs between ligand Lig and a reference ligand Ref calculated by alchemically changing Ref to Lig in solvent and in the protein binding site. ΔGbind is the ABFE of Lig calculated as sum of the creation of Lig in the protein binding site (ΔGcompLig) and annihilation of Lig in the solvent (−ΔGsolv).
RBFE calculations have been successfully applied to drug discovery tasks, yet they are not a panacea. A number of practical considerations and best practices help increase the chances of success. They include appropriate protein and ligand preparation, the choice of a suitable simulation protocol and runtime assessment, validation of the protein–ligand system at hand, comparison to benchmarks, and assessing the applicability domain, statistical reliability, and reproducibility of the simulation protocol.12 General limitations of alchemical BFE calculations lie in the inadequate force field representation of molecules studied and the inability to sample large conformational changes in the allotted sampling time leading to a ∼1 kcal/mol accuracy threshold for current RBFE calculations.4
Performance of Prospective RBFE Calculations
Schindler, Kuhn, and colleagues presented a comprehensive assessment of BFE calculations in 18 drug discovery projects as well as eight benchmark systems of pharmaceutically relevant target proteins.2 An important element for assessing the suitability of a protein system for RBFE calculations is a validation step. The authors establish a root-mean-square error (RMSE) threshold of <1.3 kcal/mol between predicted and experimental RBFE for ten or more ligands with known activity to validate the FEP system. The validation succeeded for 14 out of 17 protein systems involving 21 out of 25 chemical series where sufficient ligand data and a protein–ligand cocomplex structure were available. After successful validation, the FEP system was applied prospectively to 12 targets with 19 chemical series consisting of at least 5 data points each. The authors reported an average mean unsigned error (MUE) of 1.24 kcal/mol ranging from 0.48 to 2.28 kcal/mol with the median at 1.1 kcal/mol. The average RMSE was 1.64 kcal/mol across all 19 series. Although the accuracy of the prospective calculations was lower than that of the validation set, the reported results across a number of diverse protein targets illustrate the general usefulness of RBFE calculations for drug design.
Late-Stage Functionalization
O’Donovan et al.13 applied FEP calculations prospectively to the late-stage functionalization of polycomb repressive complex 2 (PRC2) methyltransferase inhibitors. Combining FEP with late-stage functionalization allowed for the synthetic prioritization of previously unexplored regions of the embryonic ectoderm development (EED) subunit of the PRC2 complex. For a series of triazolopyrimidines, the authors predicted the potency of analogues of compound 1 (Figure 3). The hydrophilic pocket explored at R1 was challenged with functional groups of different sizes and polarities. In agreement with prospective FEP predictions, F, Cl, and NH2 substitutions yielded potent analogues. In contrast, larger moieties such as OMe led to a substantial loss of EED binding. A nitrile substitution, although requiring some induced fitting, was correctly predicted to lose 30-fold activity compared to compound 1. Several analogues were not synthesized due to predicted loss of binding illustrating the committed use of FEP calculations for synthesis prioritization.
Figure 3.
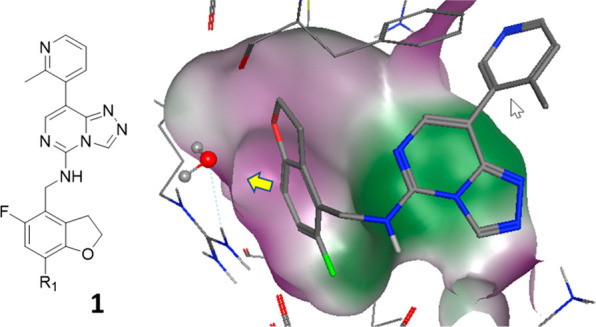
Reference compound for FEP calculations of R1-substituted analogues of EED ligands. The surface of the ligand binding site (EED protein bound to analogue of 1; PDB ID 6YVI) is colored by hydrophilicity (purple) and hydrophobicity (green). The yellow arrow illustrates the chemical space exploration vector.
Free Energy Calculations for Fragments
Fragments are valued hits for drug discovery because of their high ligand efficiency and implicit coverage of chemical space. Especially when protein structures of fragment–protein complexes are available, fragments are often considered productive starting points for hit-to-lead efforts. BFE calculation methods have been explored to guide in the growth and exploration of fragment hits. A systematic analysis involving 90 fragments studied in eight protein systems using FEP suggested that RBFE calculations are suitable to accurately predict fragment binding affinities with an RMSE of 1.1 kcal/mol,14 which is close to the generally accepted limit of ∼1 kcal/mol.4 This result is remarkable as in vitro binding experiments are often less accurate for fragments. Moreover, fragments can sometimes assume multiple binding modes more easily due to their small size compared to leadlike or druglike compounds. Even within a congeneric series, binding modes do not always stay the same when functional groups change, although methods have been devised to accommodate multiple binding modes of ligands in FEP calculations, especially when high energy barriers are encountered.15
Although different binding modes and different scaffolds add uncertainty and limit the applicability of BFE calculations, recent success has been reported in predicting the effect of fragment linking on binding affinity. When linking two fragments, the BFE is expected to gain 3.6–4.8 kcal/mol because the second fragment does not pay an entropic penalty upon protein binding when tethered to the first fragment.16 However, such gain is rarely observed. Yu et al.16 showed, for ten fragment linking cases, that entropy gains due to restricting the conformational space in the solvent or gas phase constitute only one of multiple contributions to the BFE. The configurational entropy incurred by restricting the movement of the nonlinked fragments in the receptor site is a major detrimental factor affecting the BFE by 1.7–3.9 kcal/mol. Additional factors are the changes in hydration free energy of the free and linked fragments, strain induced by the linker, and the interaction energy of the linker with the protein. While the hydration energy changes are smaller for the reported examples (0–1.8 kcal/mol), the linker–protein interaction energies span 8 kcal/mol ranging from −4.3 to 3.7 kcal/mol. In fact, throughout the ten fragment examples described by Yu et al., the linker–protein interaction energy correlates surprisingly well with the total change in BFE upon fragment linking. While the configurational restriction of the linked fragment in the binding pocket is the main reason for not gaining binding energy in most fragment linking cases, the results also suggest that the most promising path to improve BFEs of linked fragments is the choice of the right linker and its favorable interactions with the protein, a concept relevant for instance to the design of proteolysis-targeting chimeras for targeted protein degradation.
Scaffold Hopping
Changes to the chemical scaffold of a small molecule are introduced to enhance efficacy or target selectivity, improve molecular properties, or escape intellectual property space. Reliably estimating the effect of scaffold hops on binding to a protein target can reduce the risks associated with introducing ring openings, closures, or changes in linker length. Established RBFE methods are largely unsuitable due to an increased error propensity associated with changing the entire, often large, scaffold as part of the perturbation. Instead, FEP methods have been adapted to include specific bond stretch potentials to accommodate ring size changes, openings, closings, and extensions. Alternatively, auxiliary constraints can hold atoms in place during ring bond forming and breaking allowing for more complex ring modifications.
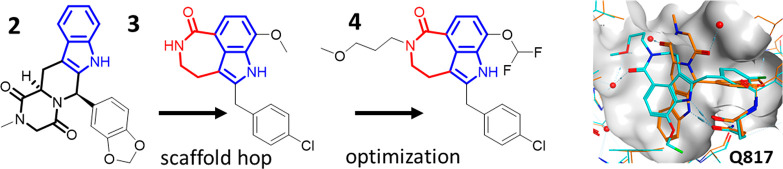
A recent example of finding novel phosphodiesterase 5 (PDE5) inhibitors using an ABFE-FEP approach was reported by Wu et al.17 Starting from compound 2, tadalafil (IC50 2 nM in a PDE enzymatic assay), and LW1607 (not shown), the authors arrived at a substantially altered scaffold (compound 3), which was adopted for further optimization (compound 4). The FEP method correctly predicted a comparable binding affinity of compound 4 to PDE5 (IC50 8 nM). The observed changes in the binding pose and interactions with PDE5 are remarkable. While a key hydrogen bond to Gln817 is maintained through the NH of an indole moiety, several other interactions as well as the water network in the active site are significantly altered (Figure 4). This outcome would have been difficult to predict without the use of a method such as MD that samples conformations of protein–ligand complexes with proper representations of relevant interaction energies.
Figure 4.
FEP-guided scaffold hopping for PDE5. Crystal structures of 2 (tadalafil; PDB ID 1XOZ, orange) and 4 (PDB ID 7FAR, cyan).
Predicted Protein Models
Small changes in protein structure, as introduced by different preparation methods of the protein, can have a significant influence on the accuracy of FEP calculations.18 Hence, one might wonder if homology models of protein structures are suitable for BFE calculations. A comprehensive study involving an induced-fit docking MD methodology compared FEP results of congeneric ligand series in 29 homology models with those obtained from crystal structures for 14 protein targets.19 For protein models built on template structures of 30–50% sequence identity, FEP results were comparable to those obtained with protein crystal structures in an impressive 86% of the cases. Likewise, AlphaFold2 models for 14 proteins structures built on templates with <30% sequence identity yielded FEP results comparable to those generated with crystal structures suggesting suitability for lead optimization purposes.20 These examples support the notion that RBFE calculations can succeed when using protein models. However, we believe that caution is still warranted because unsuccessful attempts to use model structures, as experienced on multiple occasions by us (unpublished) and others,2 are rarely advertised.
Positional Analogue Scanning
Our recent work on using RBFE calculations focused on the application of Amber GPU-TI on assessing the effect of positional analogue scans (PAS) on changes in compound potencies.21 PAS is an established strategy for lead optimization, where methine groups in aromatic and heteroaromatic ring systems are systematically exchanged with heteroatoms or other small substituents.22 PAS transformations involving only a single atom can result in significant changes in binding affinity. Three-fold changes in binding affinity occur in 30–43% of 110,000 matched molecular pairs of changing CH groups to N, CF, CMe, or COH.22 In 10–20% of these pairs a 10-fold shift was observed,21 suggesting that prospectively predicting such small changes would be quite meaningful as complete PAS can often not be performed due to time and resource constrains. Using 14 protein systems and 20 PAS sets of compounds, we showed that potency changes could be predicted with an MUE of 0.74 kcal/mol and an RMSE of 0.91 kcal/mol for 120 individual RBFE calculations. For only two compounds a large deviation of >2 kcal/mol was obtained, although the direction of the potency change was still correctly predicted. In fact, for all 66 PAS compounds and 120 individual RBFE calculations, the directions of potency changes were correct in cases where either the experiment or the prediction showed a >10-fold change in potency. The finding suggests that RBFE calculations are suitable to prioritize positional analogues for synthesis and testing.
Binding Pose Validation
Accurate BFE calculations rely on the knowledge of the binding pose of at least one ligand of a congeneric series in the receptor site. Even small deviations of the starting pose from a given experimentally confirmed binding mode can lead to reduced free binding energy prediction accuracy in FEP calculations.23 Turning this observation around, one can utilize the correct prediction of observed BFEs of a congeneric ligand series as an indicator for a correct binding mode.
An illustrative case of applying FEP to binding pose elucidation involved a series of dihydropyrimidinones as stereoselective antagonists of the human A2B adenosine receptor.24 Following a binding mode hypothesis of compound 5 in the A2A adenosine receptor, docking into a homology model of A2B adenosine receptor resulted in two different binding mode hypotheses. Both binding poses featured hydrogen bonds to Gln254 and π-stacking interactions with Phe173; however, the furyl group and proximal substitution vector R1 were situated at opposite sites (Figure 5). FEP calculations using the two different binding mode hypotheses as starting points conclusively identified the pose assumed by the green compound in Figure 5 as the correct pose.
Figure 5.
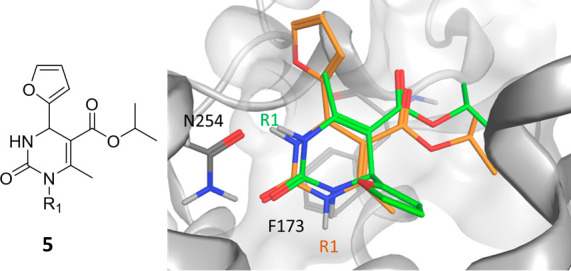
Two binding mode hypotheses (green, orange) of compound 5 in a homology model of the A2B adenosine receptor.
In another more challenging example, Shan et al.25 demonstrated for an IL-2 ligand not only that a cryptic pocket could be found through MD simulations, but also that the correct binding mode could be identified through the use of FEP calculations, further supporting the utility of FEP for such purpose.
FEP calculations not only allow for pose validation but can also provide mechanistic insight into conditional binding events. Xiaoli et al.26 reported FEP calculations for the cyclic peptide antagonist PMX53 binding to C5a anaphylatoxin chemotactic receptor 1 (C5aR1). Depending on whether the allosteric nonpeptide antagonist NTD9513727 was bound to C5aR1, binding of PMX53 to the binary or the ternary complex was favored by FEP providing energetic insights to the allosteric mechanism of NTD9513727.
Absolute Binding Free Energies and Virtual Screening
Virtual screening progresses in stages from computationally less demanding ligand-based similarity and property filtering to pharmacophore- and structure-based techniques involving molecular docking into the target protein and using rigorous physics-based methods such as BFE calculations as a final filter. RBFE calculations are not suitable to assess compounds with diverse structures. In contrast, alchemical ABFE calculations allow for comparing binding affinities across not only different chemical structures but also different targets thereby enabling ABFE calculations to predict selectivity against potential counter targets. Recent work by Feng et al.27 showed how ABFE calculations enriched known hits performing a molecular docking-based virtual screen of hundreds of actives and tens of thousands of decoy compounds against the well-studied drug targets BACE1, CDK2, and thrombin. For two of the targets, a significant improvement in the enrichment of actives in the top 1% of virtual screening hits could be observed when using ABFE calculations starting from docking poses. For BACE1 the enrichment factor increased from 8 to 28 and for CDK2 from 14 to 30. The result suggests not only that ABFE calculations are a useful last step of virtual screens but also that docking poses seem to be a useful starting point for ABFE calculations.
Covalent Inhibitors
Many drugs form a covalent complex with their target protein. Covalent inhibitors offer potential advantages of higher target selectivity, increased potency, and residence time, offsetting concerns of off-target toxicities. The covalent binding of an inhibitor to an enzyme comprises a reversible and an irreversible (unless it is a reversible covalent binder) component (eq 1). The equilibrium of the noncovalent binding (Ki) as well as the nonequilibrium kinetics of the irreversible covalent binding (kinact) need to be evaluated to determine the rate of covalent bond formation, kinact /Ki, the most relevant parameter to assess its efficiency.
| 1 |
Computational approaches to calculate the reaction kinetics of covalent binding have been devised. Yu et al. introduced a method where the transition state barrier of the rate limiting step of the ligand warhead covalently binding to the specific protein residue is calculated first using density functional theory methods.28 FEP is then used to model the interaction of ligands sharing the same warhead to the protein environment, thereby avoiding the need to calculate kinact. The approach allows for the calculation of relative binding kinetics of irreversible covalent inhibitors. It was applied to 28 ligands and four target proteins yielding a promising MUE of 0.79 log units comparing experimental and calculated Δlog(kinact/Ki). The approach has also been implemented in Schrodinger’s commercial FEP+ software. In a related approach, Mihalovits et al. calculated reaction barriers using a QM/MM approach and modeled the noncovalent binding step with TI reporting MUE < 2 kcal/mol for KRAS and EGFR inhibitors.29 For lead optimization purposes of a congeneric series, calculating relative covalent BFEs is most practical; however, absolute free energies of covalent binding were also successfully calculated for different warheads.30
In contrast to irreversible covalent binding, for reversible covalent binding the noncovalent and covalent binding states are in equilibrium. Therefore, without the need for calculating the transition barrier of the covalent binding reaction, FEP has been used to estimate how much covalent and noncovalent binding states add to the overall binding affinity of a reversible covalent ligand.31 In a recent example Bonatto et al. showed, for human cathepsin L, how FEP can be used to estimate free energy changes.32 Using a small set of nitrile-based reversible covalent cathepsin L inhibitors, the authors found that FEP to predict relative BFEs, using the covalent state, generated more predictive results than using the noncovalent state. The respective MUE and Pearson correlation coefficients were reported as 1.33 (0.92) and 0.69 (0.89) for the noncovalent (covalent) transformations. While a general conclusion that FEP calculations of reversible covalent binders are generally more dependent on the covalent state may be premature based on the limited data set, the observations provide an interesting starting hypothesis for calculations of other covalent systems.
Predicting FEP with AI
The high cost of FEP limits the number of RBFE calculations to practically less than a few hundred leaving large parts of a congeneric series unexplored. Iteratively training automated ML (AutoML) models with a limited number of RBFE calculations has been suggested as an alternative. Gusev et al.33 proposed an iterative AutoML workflow where Amber GPU-TI RBFE calculations were conducted for a small number of SARS-CoV-2 papain-like protease binders. For a focused set of 8175 potential ligands, the centroids of 45 clusters were subjected to Amber GPU-TI RBFE calculations. The calculated RBFEs were used as dependent variables of an AutoML workflow deploying a number of well-known ML algorithms including random forest, linear regression, k-nearest neighbors, support vector machines, and Gaussian processes. For five iterations, the 200 molecules with the lowest predicted RBFE were clustered and 30 structurally diverse representatives subjected to Amber GPU-TI RBFE calculations thereby increasing the training set of the AutoML approach for each subsequent iteration. In the last two iterations, a random set of 30 compounds as well as the 30 compounds with the lowest predicted RBFE were added to the TI calculations bringing the final AutoML training set to 253 compounds. Negative RBFE were computed for 53% of the TI calculations (133 compounds) compared to only 10% for compounds chosen in a random cycle illustrating the utility of the approach for the rapid exploration of large chemical spaces.
Recently, a collaboration between Google Research and Relay Therapeutics led to an exhaustive study of RBFE calculations on 10,000 congeneric tyrosine kinase 2 (TYK2) inhibitors using RDKit Morgan fingerprints as descriptors and deploying active learning (AL) strategies.34 A number of ML methods were explored, but the performance appeared to be largely independent of the specific ML algorithm used. After ten iterations of subsets sampled, only 6% of the 10,000 TYK2 inhibitors had been explicitly calculated with an FEP protocol, while the remaining compounds were predicted using the AL approach identifying 75 of the top 100 scorers. Using ML methods promises a significant speedup of RBFE predictions. However, a more rigorous test of this attractive approach as well as broader applications to diverse sets of ligands are still forthcoming.
Alchemical BFE calculations to predict binding affinities of ligands to their therapeutic targets have enjoyed continuous attention for many decades. Conducting BFE calculations has become practical in drug discovery due to increased compute power and convenient access to well-validated RBFE implementations. More recently, the use of RBFE and to a lesser extend ABFE methods has expanded to support a broader spectrum of structure-based drug discovery tasks. They include fragment growing and linking, scaffold hopping, binding pose validation, virtual screening, covalent enzyme inhibition, as well as assisting multiparameter optimization strategies such as positional analogue scanning. Recently, methods have been introduced to predict BFE calculation results using ML methods. This latest development holds great promise to expand chemical spaces accessible to RBFE calculations, otherwise restricted by time and computer cost. While many publications focused on introducing and validating BFE calculation methods using existing data sets, recent prospective studies illustrated the practical utility of alchemical BFE calculations for drug discovery.
Glossary
Abbreviations
- RBFE
relative binding free energy
- ABFE
absolute binding free energy
- BFE
binding free energy
- FEP
free energy perturbation
- TI
thermodynamic integration
- ML
machine learning
- RMSE
root-mean-square error
- MUE
mean unsigned error
- PRC2
polycomb repressive complex 2
- FED
embryonic ectoderm development
- PDE5
phosphodiesterase 5
- PAS
positional analogue scans
- C5aR1
C5a anaphylatoxin chemotactic receptor 1
- TYK2
tyrosine kinase 2
- AL
active learning
The authors declare no competing financial interest.
Special Issue
Published as part of the ACS Medicinal Chemistry Letters virtual special issue “New Enabling Drug Discovery Technologies - Recent Progress”.
References
- Meier K.; Bluck J. P.; Christ C. D.. Use of Free Energy Methods in the Drug Discovery Industry. In Free Energy Methods in Drug Discovery: Current State and Future Directions; Armacost K. A., Thompson D. C., Eds.; American Chemical Society: Washington, DC, 2021; pp 39–66. [Google Scholar]
- Schindler C. E. M.; Baumann H.; Blum A.; Bose D.; Buchstaller H. P.; Burgdorf L.; Cappel D.; Chekler E.; Czodrowski P.; Dorsch D.; Eguida M. K. I.; Follows B.; Fuchss T.; Gradler U.; Gunera J.; Johnson T.; Jorand Lebrun C.; Karra S.; Klein M.; Knehans T.; Koetzner L.; Krier M.; Leiendecker M.; Leuthner B.; Li L.; Mochalkin I.; Musil D.; Neagu C.; Rippmann F.; Schiemann K.; Schulz R.; Steinbrecher T.; Tanzer E. M.; Unzue Lopez A.; Viacava Follis A.; Wegener A.; Kuhn D. Large-Scale Assessment of Binding Free Energy Calculations in Active Drug Discovery Projects. J. Chem. Inf. Model. 2020, 60, 5457–5474. 10.1021/acs.jcim.0c00900. [DOI] [PubMed] [Google Scholar]
- Lee T. S.; Allen B. K.; Giese T. J.; Guo Z.; Li P.; Lin C.; McGee T. D. Jr.; Pearlman D. A.; Radak B. K.; Tao Y.; Tsai H. C.; Xu H.; Sherman W.; York D. M. Alchemical Binding Free Energy Calculations in AMBER20: Advances and Best Practices for Drug Discovery. J. Chem. Inf. Model. 2020, 60, 5595–5623. 10.1021/acs.jcim.0c00613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cournia Z.; Allen B.; Sherman W. Relative Binding Free Energy Calculations in Drug Discovery: Recent Advances and Practical Considerations. J. Chem. Inf. Model. 2017, 57, 2911–2937. 10.1021/acs.jcim.7b00564. [DOI] [PubMed] [Google Scholar]
- Wang L.; Wu Y.; Deng Y.; Kim B.; Pierce L.; Krilov G.; Lupyan D.; Robinson S.; Dahlgren M. K.; Greenwood J.; Romero D. L.; Masse C.; Knight J. L.; Steinbrecher T.; Beuming T.; Damm W.; Harder E.; Sherman W.; Brewer M.; Wester R.; Murcko M.; Frye L.; Farid R.; Lin T.; Mobley D. L.; Jorgensen W. L.; Berne B. J.; Friesner R. A.; Abel R. Accurate and reliable prediction of relative ligand binding potency in prospective drug discovery by way of a modern free-energy calculation protocol and force field. J. Am. Chem. Soc. 2015, 137, 2695–703. 10.1021/ja512751q. [DOI] [PubMed] [Google Scholar]
- Tsai H. C.; Lee T. S.; Ganguly A.; Giese T. J.; Ebert M. C.; Labute P.; Merz K. M.; York D. M. AMBER Free Energy Tools: A New Framework for the Design of Optimized Alchemical Transformation Pathways. J. Chem. Theory Comput. 2023, 19 (2), 640–658. 10.1021/acs.jctc.2c00725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gapsys V.; Hahn D. F.; Tresadern G.; Mobley D. L.; Rampp M.; de Groot B. L. Pre-Exascale Computing of Protein-Ligand Binding Free Energies with Open Source Software for Drug Design. J. Chem. Inf. Model. 2022, 62, 1172–1177. 10.1021/acs.jcim.1c01445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pennington L. D.; Muegge I. Holistic Drug Design for Multiparameter Optimization in Modern Small Molecule Drug Discovery. Bioorg. Med. Chem. Lett. 2021, 41, 128003. 10.1016/j.bmcl.2021.128003. [DOI] [PubMed] [Google Scholar]
- Song L. F.; Merz K. M. Jr. Evolution of Alchemical Free Energy Methods in Drug Discovery. J. Chem. Inf. Model. 2020, 60, 5308–5318. 10.1021/acs.jcim.0c00547. [DOI] [PubMed] [Google Scholar]
- Armacost K. A.; Thompson D. C.. Free Energy Methods in Drug Discovery: Current State and Future Directions; American Chemical Society: Washington, DC, 2021. [Google Scholar]
- Chen W.; Cui D.; Abel R.; Friesner R.; Wang L.. Accurate calculation of absolute protein-ligand binding free energies. ChemRxiv, 2022. 10.26434/chemrxiv-2022-2t0dq-v2 [DOI]
- Mey A.; Allen B. K.; Macdonald H. E. B.; Chodera J. D.; Hahn D. F.; Kuhn M.; Michel J.; Mobley D. L.; Naden L. N.; Prasad S.; Rizzi A.; Scheen J.; Shirts M. R.; Tresadern G.; Xu H. Best Practices for Alchemical Free Energy Calculations [Article v1.0]. Living J. Comput. Mol. Sci. 2020, 2 (1), 18378. 10.33011/livecoms.2.1.18378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’ Donovan D. H.; Gregson C.; Packer M. J.; Greenwood R.; Pike K. G.; Kawatkar S.; Bloecher A.; Robinson J.; Read J.; Code E.; Hsu J. H.; Shen M.; Woods H.; Barton P.; Fillery S.; Williamson B.; Rawlins P. B.; Bagal S. K. Free energy perturbation in the design of EED ligands as inhibitors of polycomb repressive complex 2 (PRC2) methyltransferase. Bioorg. Med. Chem. Lett. 2021, 39, 127904. 10.1016/j.bmcl.2021.127904. [DOI] [PubMed] [Google Scholar]
- Steinbrecher T. B.; Dahlgren M.; Cappel D.; Lin T.; Wang L.; Krilov G.; Abel R.; Friesner R.; Sherman W. Accurate Binding Free Energy Predictions in Fragment Optimization. J. Chem. Inf. Model. 2015, 55, 2411–20. 10.1021/acs.jcim.5b00538. [DOI] [PubMed] [Google Scholar]
- Kaus J. W.; Harder E.; Lin T.; Abel R.; McCammon J. A.; Wang L. How to deal with multiple binding poses in alchemical relative protein-ligand binding free energy calculations. J. Chem. Theory Comput. 2015, 11, 2670–9. 10.1021/acs.jctc.5b00214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu H. S.; Modugula K.; Ichihara O.; Kramschuster K.; Keng S.; Abel R.; Wang L. General Theory of Fragment Linking in Molecular Design: Why Fragment Linking Rarely Succeeds and How to Improve Outcomes. J. Chem. Theory Comput. 2021, 17, 450–462. 10.1021/acs.jctc.0c01004. [DOI] [PubMed] [Google Scholar]
- Wu D.; Zheng X.; Liu R.; Li Z.; Jiang Z.; Zhou Q.; Huang Y.; Wu X. N.; Zhang C.; Huang Y. Y.; Luo H. B. Free energy perturbation (FEP)-guided scaffold hopping. Acta Pharm. Sin. B 2022, 12, 1351–1362. 10.1016/j.apsb.2021.09.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shih A. Y.; Hack M.; Mirzadegan T. Impact of Protein Preparation on Resulting Accuracy of FEP Calculations. J. Chem. Inf. Model. 2020, 60, 5287–5289. 10.1021/acs.jcim.0c00445. [DOI] [PubMed] [Google Scholar]
- Xu T.; Zhu K.; Beautrait A.; Vendome J.; Borrelli K. W.; Abel R.; Friesner R. A.; Miller E. B. Induced-Fit Docking Enables Accurate Free Energy Perturbation Calculations in Homology Models. J. Chem. Theory Comput. 2022, 18, 5710–5724. 10.1021/acs.jctc.2c00371. [DOI] [PubMed] [Google Scholar]
- Beuming T.; Martin H.; Diaz-Rovira A. M.; Diaz L.; Guallar V.; Ray S. S. Are Deep Learning Structural Models Sufficiently Accurate for Free-Energy Calculations? Application of FEP+ to AlphaFold2-Predicted Structures. J. Chem. Inf. Model. 2022, 62, 4351–4360. 10.1021/acs.jcim.2c00796. [DOI] [PubMed] [Google Scholar]
- Hu Y.; Muegge I. In Silico Positional Analogue Scanning with Amber GPU-TI. J. Chem. Inf. Model. 2022, 62, 4448–4459. 10.1021/acs.jcim.2c00860. [DOI] [PubMed] [Google Scholar]
- Pennington L. D.; Aquila B. M.; Choi Y.; Valiulin R. A.; Muegge I. Positional Analogue Scanning: An Effective Strategy for Multiparameter Optimization in Drug Design. J. Med. Chem. 2020, 63, 8956–8976. 10.1021/acs.jmedchem.9b02092. [DOI] [PubMed] [Google Scholar]
- Cappel D.; Jerome S.; Hessler G.; Matter H. Impact of Different Automated Binding Pose Generation Approaches on Relative Binding Free Energy Simulations. J. Chem. Inf Model 2020, 60, 1432–1444. 10.1021/acs.jcim.9b01118. [DOI] [PubMed] [Google Scholar]
- Majellaro M.; Jespers W.; Crespo A.; Nunez M. J.; Novio S.; Azuaje J.; Prieto-Diaz R.; Gioe C.; Alispahic B.; Brea J.; Loza M. I.; Freire-Garabal M.; Garcia-Santiago C.; Rodriguez-Garcia C.; Garcia-Mera X.; Caamano O.; Fernandez-Masaguer C.; Sardina J. F.; Stefanachi A.; El Maatougui A.; Mallo-Abreu A.; Aqvist J.; Gutierrez-de-Teran H.; Sotelo E. 3,4-Dihydropyrimidin-2(1H)-ones as Antagonists of the Human A(2B) Adenosine Receptor: Optimization, Structure-Activity Relationship Studies, and Enantiospecific Recognition. J. Med. Chem. 2021, 64, 458–480. 10.1021/acs.jmedchem.0c01431. [DOI] [PubMed] [Google Scholar]
- Shan Y.; Mysore V. P.; Leffler A. E.; Kim E. T.; Sagawa S.; Shaw D. E. How does a small molecule bind at a cryptic binding site?. PLoS Comput. Biol. 2022, 18, e1009817. 10.1371/journal.pcbi.1009817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiaoli A.; Yuzhen N.; Qiong Y.; Yang L.; Yao X.; Bing Z. Investigating the Dynamic Binding Behavior of PMX53 Cooperating with Allosteric Antagonist NDT9513727 to C5a Anaphylatoxin Chemotactic Receptor 1 through Gaussian Accelerated Molecular Dynamics and Free-Energy Perturbation Simulations. ACS Chem. Neurosci. 2022, 13, 3502–3511. 10.1021/acschemneuro.2c00556. [DOI] [PubMed] [Google Scholar]
- Feng M.; Heinzelmann G.; Gilson M. K. Absolute binding free energy calculations improve enrichment of actives in virtual compound screening. Sci. Rep. 2022, 12, 13640. 10.1038/s41598-022-17480-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu H. S.; Gao C.; Lupyan D.; Wu Y.; Kimura T.; Wu C.; Jacobson L.; Harder E.; Abel R.; Wang L. Toward Atomistic Modeling of Irreversible Covalent Inhibitor Binding Kinetics. J. Chem. Inf. Model. 2019, 59, 3955–3967. 10.1021/acs.jcim.9b00268. [DOI] [PubMed] [Google Scholar]
- Mihalovits L. M.; Ferenczy G. G.; Keseru G. M. Affinity and Selectivity Assessment of Covalent Inhibitors by Free Energy Calculations. J. Chem. Inf. Model. 2020, 60, 6579–6594. 10.1021/acs.jcim.0c00834. [DOI] [PubMed] [Google Scholar]
- Zhou J.; Saha A.; Huang Z.; Warshel A. Fast and Effective Prediction of the Absolute Binding Free Energies of Covalent Inhibitors of SARS-CoV-2 Main Protease and 20S Proteasome. J. Am. Chem. Soc. 2022, 144, 7568–7572. 10.1021/jacs.2c00853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang H.; Jiang W.; Chatterjee P.; Luo Y. Ranking Reversible Covalent Drugs: From Free Energy Perturbation to Fragment Docking. J. Chem. Inf. Model. 2019, 59, 2093–2102. 10.1021/acs.jcim.8b00959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonatto V.; Shamim A.; Rocho F. D. R.; Leitao A.; Luque F. J.; Lameira J.; Montanari C. A. Predicting the Relative Binding Affinity for Reversible Covalent Inhibitors by Free Energy Perturbation Calculations. J. Chem. Inf. Model. 2021, 61, 4733–4744. 10.1021/acs.jcim.1c00515. [DOI] [PubMed] [Google Scholar]
- Gusev F.; Gutkin E.; Kurnikova M. G.; Isayev O.. Active learning guided drug design lead optimization based on relative binding free energy modeling. ChemRxiv, 2022. 10.26434/chemrxiv-2022-krs1t [DOI] [PubMed]
- Thompson J.; Walters W. P.; Feng J. A.; Pabon N. A.; Xu H.; Goldman B. B.; Moustakas D. T.; Schmidt M.; York F. Optimizing active learning for free energy calculations. Artificial Intelligence in the Life Sciences 2022, 2, 100050. 10.1016/j.ailsci.2022.100050. [DOI] [Google Scholar]