Deep Label Fusion: A Generalizable Hybrid Multi-Atlas and Deep Convolutional Neural Network for Medical Image Segmentation

Abstract

Deep convolutional neural networks (DCNN) achieve very high accuracy in segmenting various anatomical structures in medical images but often suffer from relatively poor generalizability. Multi-atlas segmentation (MAS), while less accurate than DCNN in many applications, tends to generalize well to unseen datasets with different characteristics from the training dataset. Several groups have attempted to integrate the power of DCNN to learn complex data representations and the robustness of MAS to changes in image characteristics. However, these studies primarily focused on replacing individual components of MAS with DCNN models and reported marginal improvements in accuracy. In this study we describe and evaluate a 3D end-to-end hybrid MAS and DCNN segmentation pipeline, called Deep Label Fusion (DLF). The DLF pipeline consists of two main components with learnable weights, including a weighted voting subnet that mimics the MAS algorithm and a fine-tuning subnet that corrects residual segmentation errors to improve final segmentation accuracy. We evaluate DLF on five datasets that represent a diversity of anatomical structures (medial temporal lobe subregions and lumbar vertebrae) and imaging modalities (multi-modality, multi-field-strength MRI and Computational Tomography). These experiments show that DLF achieves comparable segmentation accuracy to nnU-Net (Isensee et al., 2020), the state-of-the-art DCNN pipeline, when evaluated on a dataset with similar characteristics to the training datasets, while outperforming nnU-Net on tasks that involve generalization to datasets with different characteristics (different MRI field strength or different patient population). DLF is also shown to consistently improve upon conventional MAS methods. In addition, a modality augmentation strategy tailored for multimodal imaging is proposed and demonstrated to be beneficial in improving the segmentation accuracy of learning-based methods, including DLF and DCNN, in missing data scenarios in test time as well as increasing the interpretability of the contribution of each individual modality.

1. Introduction

In recent years, deep convolutional neural network (DCNN) algorithms based on the U-Net architecture (Çiçek et al., 2016; Khandelwal et al., 2021; Ronneberger et al., 2015) have been shown to outperform conventional approaches with a significant margin in segmenting anatomical structures in medical images, such as ventricles of the heart (Chen et al., 2020; Duan et al., 2019) and brain regions from MRI (Thyreau and Taki, 2020; Yushkevich et al., 2015), spine from computational tomographic (CT) images (Khandelwal et al., 2021; Kim et al., 2020; Lessmann et al., 2019; Whitehead et al., 2018) and so on. Also, when multimodal data is available, either from different imaging devices (e.g., MRI, CT, ultra-sound) or different imaging sequences of the same device [e.g., T1-weighted (T1w), T2-weighted (T2w) MRI], DCNN can efficiently be trained to make use of information from each modality. However, its generalizability, the ability to perform similarly well on data that is not well represented in the training samples, is relatively poor, especially when the training set is small or homogeneous. Improving the generalizability of deep learning methods, by applying various augmentation strategies, few-shot learning (Snell et al., 2017) in domain adaptation (Ganin et al., 2016) or domain generalization (Khandelwal and Yushkevich, 2020; Li et al., 2017), is an active area of research. Prior to the emergence of DCNN segmentation algorithms, multi-atlas segmentation (MAS) was considered a leading medical image segmentation technique, capable of achieving promising segmentation accuracy using relatively small training datasets and of good generalization to unseen patient populations and imaging protocols (Parivash et al., 2019; Sone et al., 2016). MAS consists of two steps: (1) a set of atlases, i.e., images together with manual segmentations of structures of interest, which are transformed (warped) into the space of the target image via linear and deformable registration; (2) the warped atlas segmentations are combined into a consensus segmentation of the target image using a label fusion algorithm, which typically involves weighted voting among the atlases. Majority voting (MV) (Heckemann et al., 2006) is the first and simplest MAS algorithm that gives equal weights to all the atlases. More accurate spatially varying weighted voting (SVWV) schemes (Coupé et al., 2011; Sanroma et al., 2015) assign each atlas a different weight at each location in the target image based on patch-level intensity similarity between the warped atlas image and the target image. Joint label fusion (JLF) (Wang et al., 2012) further improves label fusion accuracy by taking the correlated errors among atlases into account in weight estimation. However, conventional SVWV/JLF algorithms derive weights based on heuristic assumptions about the relationship between patch similarity and atlas suitability (e.g., negative exponential relationship). Relatedly, conventional MAS algorithms lack an optimal way to combine atlas-to-target similarity estimations across multiple modalities. These limitations may negatively impact the accuracy of conventional MAS techniques, particularly in multimodality applications.

This paper seeks to develop a hybrid method that combines the relative strengths of DCNN and MAS algorithms. Built on prior work on combining non-DCNN machine learning methods with MAS (Bai et al., 2014; Sanroma et al., 2018, 2015), several attempts that focus on using DCNN with MAS have been made. The first set of methods uses DCNN to improve atlas-target image similarity (or dissimilarity) estimation, replacing the heuristic models used in SVWV and JLF with data-driven models. Sanroma et al. (2018) and Ding et al. (2020) used neural networks to learn a non-linear embedding that transforms the image patches to a feature space in which the discriminability between atlas-target patch pairs that have the same label and that have different labels is maximized. Alternatively, Ding et al. (2019a, 2019b) and Xie et al. (2019a) directly estimated the likelihood of an atlas having an erroneous vote either for a patch (Xie et al., 2019a) or for the whole image (Ding et al., 2019b, 2019a). One common issue with these methods is that the improvement in similarity (or dissimilarity) estimation for weight computation does not fully translate to better final label fusion accuracy. Ding et al. (2019) reported that a 2% improvement in discriminating error votes results in only 0.4% increase in final segmentation accuracy, which is consistent with the results in the other two studies (Ding et al., 2020; Xie et al., 2019a). A potential way to improve final segmentation accuracy over these techniques would be to train an end-to-end DCNN-based MAS pipeline with a loss function that directly quantifies segmentation errors. Such an end-to-end pipeline was explored for the first time by Yang et al. (2018). Their pipeline consists of a DCNN-based feature extraction subnet with learnable weights and a label fusion subnet with a fixed non-learnable structure that mimics conventional label fusion. Although this pipeline is trained end-to-end, there is no modification to the label fusion process, limiting the potential improvement. Furthermore, although demonstrating consistent improvement compared to conventional MAS and DCNN-based approaches, Yang et al. (2018) only evaluated their pipeline on 2D cardiac MRI images, which limits its utility for medical image segmentation.

In this study, we build on these prior attempts to combine DCNN and MAS by developing and evaluating a 3D hybrid MAS-DCNN end-to-end pipeline that has learnable weights in the label fusion subnet and can adapt to a variable number of datasets. We hypothesize that our pipeline, named deep label fusion (DLF), will improve the segmentation accuracy and generalizability compared to MAS or DCNN alone across a range of medical image segmentation problems. This work is a follow-up study to our prior proceeding presentation at the 27^th international conference on Information Processing in Medical Imaging 2021 (IPMI 2021) (Xie et al., 2021), which proposed the first such 3D hybrid MAS-DCNN end-to-end pipeline. The following extensions are unique to the current work: (1) A more comprehensive evaluation with five datasets on different anatomical structures [medial temporal lobe (MTL) subregions and lumbar vertebrae] acquired with different imaging modalities (MRI and CT) to demonstrate the feasibility of the DLF in various applications. (2) A novel augmentation strategy that is designed specifically for training DCNN models on multimodal datasets is proposed and evaluated to show its potential utility in interpreting the contribution of individual modalities and in missing data scenarios. (3) We compare DLF with nnU-Net, the state-of-the-art DCNN segmentation pipeline, in terms of accuracy and generalizability. (4) We perform a more comprehensive evaluation on the contribution of different components of the network to segmentation accuracy and generalizability.

2. Methods and materials

2.1. Datasets

Five datasets acquired with different imaging modalities covering two different organs of interest [multimodal MRI images of human MTL subregions and computational tomography (CT) scans of human lumbar vertebrae] are used to evaluate the segmentation accuracy and generalizability of the proposed DLF. Figure 1 summarizes the experiments (cross-validation or testing for generalizability) done on these datasets and includes some examples.

Figure 1 (color figure).

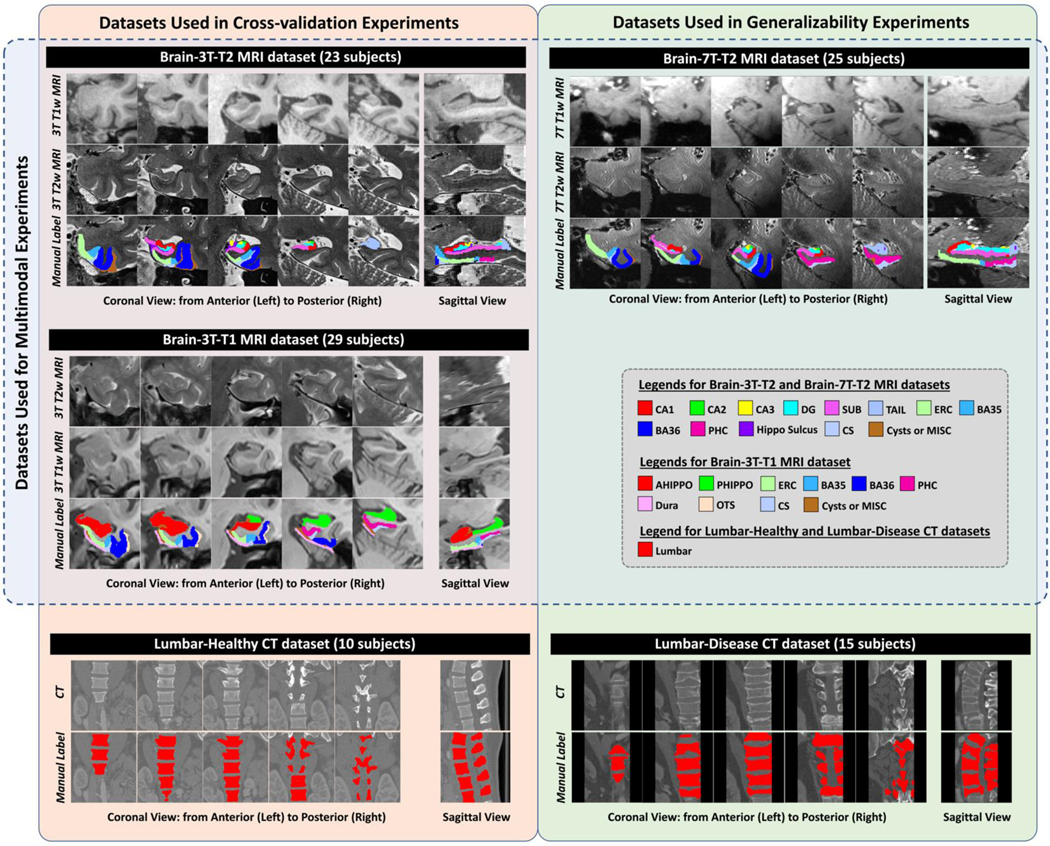
Example images and manual segmentations of the five datasets included in this study. Abbreviations: CT = computational tomography; AHippo/PHippo = anterior/posterior hippocampus; CA1–3 = cornu ammonis 1 to 3; dentate gyrus = DG; subiculum = SUB; TAIL = the tail of hippocampus; ERC = entorhinal cortex; BA35/36 = Brodmann areas 35/36; PHC = parahippocampal cortex; CS = collateral sulcus; OTS = occipitotemporal sulcus; MISC = miscellaneous label.

2.1.1. Multimodal 3T and 7T brain MRI of the hippocampal subfields and MTL cortical subregions (Brain-3T-T2 and Brain-7T-T2 datasets)

As in prior work presented in IPMI 2021, a multimodal structural 3T MRI dataset from the University of Pennsylvania (UPENN) was primarily used to develop the DLF algorithm. The dataset consists of T1w (MPRAGE sequence, 0.8×0.8×0.8 mm³) and T2w (TSE sequence, 0.4×0.4×1.2 mm³) brain MRI scans of 23 subjects from the Penn Alzheimer’s Disease Research Center (ADRC). The T2-weighted scans are optimized for imaging hippocampal subfields and adjacent MTL cortical subregions, which play related but distinct roles in memory function and are affected to different degrees by neurodegenerative diseases (Braak and Braak, 1995; Ding and Van Hoesen, 2010). Automatic segmentation of these subregions can potentially yield promising biomarkers for detecting and tracking the progression of early Alzheimer’s disease (Coupé et al., 2011; Xie et al., 2019b; Yushkevich et al., 2015). Following the anatomical protocol described in Berron et al. (2017) with some modifications (details in Supplementary Material S1), manual segmentations are generated in the space of the T2w MRI with labels including hippocampal subfields [cornu ammonis (CA) 1 to 3, dentate gyrus (DG), subiculum (SUB), the tail of hippocampus (TAIL)], MTL cortical subregions [entorhinal cortex (ERC), Brodmann areas 35 and 36 (BA35/36) and parahippocampal cortex (PHC)] together with 4 supporting non-gray-matter labels [hippocampal sulcus, collateral sulcus (CS), cysts in the hippocampus and miscellaneous voxels around the cortex]. Bilateral segmentations are available for each subject. This is a challenging dataset because the boundaries of most adjacent gray matter subregions are defined based on anatomical landmarks and geometric rules, and there is no perceivable difference in contrast between them. Spatial context is important for accurate segmentation, which makes this dataset well-suited to compare DLF with conventional MAS and general DCNN frameworks, such as the U-Net (Çiçek et al., 2016; Ronneberger et al., 2015). Since the segmentation is in the space of the 3T T2w MRI focusing on the MTL, we refer to this dataset as the Brain-3T-T2 dataset. A similar naming convention was used to name the other datasets.

A similar multimodal 7T MRI dataset from the PennADRC, which consists of T1w (the second inversion image of the MP2RAGE sequence, 0.7×0.7×0.7 mm³) and T2w (TSE sequence, 0.4×0.4×1.0 mm³) MRI scans of 25 subjects (named Brain-7T-T2 dataset), was used as an out-of-sample dataset to evaluate the generalizability of DLF trained on the Brain-3T-T2 dataset. Bilateral manual segmentations are available in the space of the 7T T2w image following the same segmentation protocol (Berron et al., 2017) as the Brain-3T-T2 dataset with the same modifications (details in Supplementary Material S1). Subtle differences in the placement of tissue boundaries between the Brain-3T-T2 and Brain-7T-T2 datasets are expected, despite following the same segmentation protocol, because tissue contrast and resolution between the two datasets are different (Figure 1). In addition, four subjects are present in both datasets and thus are excluded from training in experiments evaluating generalizability (details in Section 3).

2.1.2. Multimodal 3T brain MRI of the hippocampus and MTL cortical subregions (Brain-3T-T1 dataset)

T2w scans optimized for hippocampal subfield segmentation are not always collected in MRI studies of aging and neurodegeneration, whereas T1w MRI scans with approximately 1×1×1 mm³ are very common. Xie et al. (2019b, 2016) transferred the MTL subregion segmentations from a prior MTL subregion dataset (including hippocampal subfields and MTL cortical subregions) in the T2w MRI space (Yushkevich et al., 2015) (segmentation protocol is different from Brain-3T-T2) into the space of 3T T1w MRI of the same subjects, first upsampling these scans to 0.5.0×0.5×1.0 mm³ resolution using the non-local means algorithm (Manjón et al., 2010). Since boundaries of hippocampal subfields cannot be reliably visualized in T1w MRI (de Flores et al., 2015; Laura E. M.Wisse, Geert Jan Biessels, 2014), hippocampal subfield labels were merged into a single hippocampus label, which was then divided along the hippocampal long axis into anterior and posterior subregions. MTL cortical labels (ERC, BA35, BA36 and PHC) were retained in the T1w MRI segmentation. The non-gray-matter supporting labels were expanded to include anterior and posterior dura mater, as well as CS, occipital-temporal sulcus (OTS) and miscellaneous (i.e., cerebrospinal fluid) voxels in the hippocampus. In total, 29 subjects are available in the Brain-3T-T1 dataset.

The Brain-3T-T1 provides another dataset, in addition to Brain-3T-T2, to evaluate DLF in the context of multiple MRI modality segmentation since for each individual in the atlas set, a T2w MRI is available. A five-fold cross-validation experiment is performed using this dataset (details in Section 2.2.2.1).

2.1.3. Computational tomography scans of human lumbar vertebrae (Lumbar- Healthy and Lumbar-Disease datasets)

To evaluate the proposed algorithm in a different imaging modality and different organ of interest, two additional datasets of human lumbar vertebrae acquired using CT are included in this study. The first CT dataset is from the MICCAI Computational Spine Imaging Challenge 2014 (Yao et al., 2016). It consists of spine CT images (resolution: 0.3×0.3×1.0 mm³) of 10 healthy adults acquired in daily clinical routine work in a trauma center. Although images of the whole spine are available, we only included the area around the 5 lumbar vertebrae to be consistent with the second CT dataset described below. We perform five-fold cross-validation using this dataset to evaluate segmentation accuracy (named Lumbar-Healthy, details in Section 2.2.2.1).

The second publicly available CT dataset (resolution: 1.0×1.0×1.0 mm³), named Lumbar-Disease dataset (Ibragimov et al., 2014), consisting of lumbar vertebrae images of 15 pathological cases of vertebrae with fractures of different morphological grades and cases, is used to test the generalizability of the segmentation algorithm in unseen disease cases with large difference in image contrast and field of view (see Figure 1).

2.2. Deep label fusion

Like conventional MAS methods, DLF utilizes a set of atlases (medical images with expert segmentations of the structures of interest) that are deformed to fit each target image using non-linear diffeomorphic deformable registration. These registrations are performed using conventional variational techniques that minimize an image dissimilarity metric (normalized cross-correlation) between the target image and each atlas image. Specifics of the image registration for each dataset are provided in Section 2.2.2.2. The task of the DLF pipeline is to combine the deformed (warped) atlas segmentations into a single consensus segmentation of each target image.

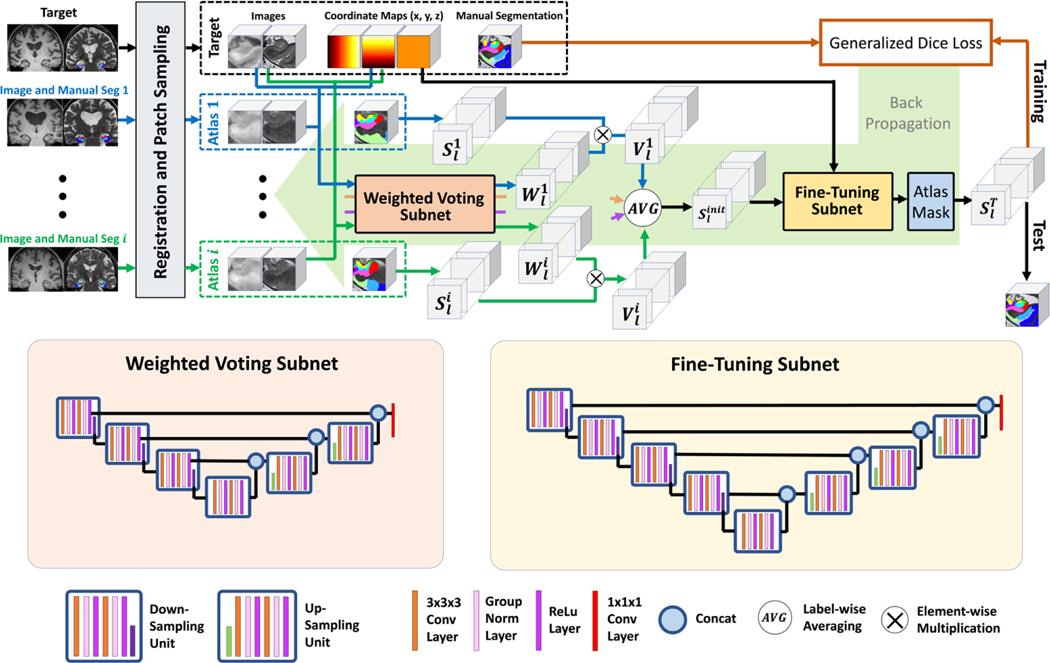
As illustrated in Figure 2, the DLF takes as inputs a target image (T) and a set of registered atlases, i.e., warped images [$A=\left\{A_i,i=1,2,\dots ,N_{atlas}\right\}$, where $N_{atlas}$ represents the number of atlases] together with the corresponding warped manual segmentations $\left[S=\left\{S_i,i=1,2,\dots ,N_{atlas}\right\}\right]$. The output of DLF is the segmentation for the target image ($S^T$). To avoid confusion, in the rest of this paper, only the registered images are referred to as “atlases” and the original expert-labeled images (before registration) in the training set are referred to as training images [$I=\left\{I_j,j=1,2,\dots ,N_{train}\right\}$, where $N_{train}$ is the number of images in the training set]. The training scheme of DLF is similar to that of DCNN networks. First, pairwise registration is done between all the training images I. Then, DLF is applied to each training image ($I_j$) and the corresponding registered atlases (the warped remaining training images) to generate an automatic segmentation. The segmentation error between the automatic and the manual segmentations, evaluated by a loss function, is then backpropagated to update the weights of DLF. This process is repeated until convergence. The details of DLF network architecture will be described in Section 2.2.1. Implementation details will be provided in Section 2.2.2.

Figure 2 (color figure).

Network architecture of the proposed deep label fusion network.

2.2.1. Network architecture

The proposed deep label fusion algorithm consists of three parts: the weighted voting subnet that estimates similarity between atlas and target images, label fusion computations that mimic the MAS algorithm, and the fine-tuning subnet that takes advantage of the U-Net to improve segmentation accuracy. The network architecture is similar to our prior work presented at IPMI 2021 (Xie et al., 2021). Figure 2 gives an overview of the network architecture and details are described below.

2.2.1.1. Weighted voting subnet

The weighted voting subnet is designed to replace the weight computation using conventional similarity metrics (e.g., sum-of-square difference) with a data-driven learning-based approach. It takes in a pair of atlas-target images together with the coordinate-maps (3 channels for coordinates in x, y, z axes, which provide spatial context) and outputs label-specific weight maps [one for each of the $N_{label}$ labels, denoted as $W^i=\left\{W_l^i,l=1,2,\dots ,N_{label}\right\}$ for atlas i with value $w_{ln}^i$ at voxel n]. The subnet has the U-Net architecture (Çiçek et al., 2016) with three levels. as shown in Figure 2 (detail of the architecture is described in Supplementary Material S3).

2.2.1.2. Label fusion computation

After applying the weighted voting subnet to all the N_atlas atlases, label fusion is performed to fuse the candidate segmentations $\left\{S^i,i=1,2,\dots ,N_{atlas}\right\}$ to generate the initial consensus segmentation $S^{init}=\left\{p_l^{init},l=1,2,\dots ,N_{label}\right\}$ with voxel value $p_{ln}^{init}$ at location n] with the following steps: (1) For the $i^{th}$ atlas-target pair$\left(i=1,2,\dots N_{atlas}\right)$, the label-specific weight maps$W^i$, outputted from the weighted voting subnet (the same network for all the atlases), is generated. (2) Then the candidate segmentation $S^i$ is converted to one-hot encoding segmentations $S^i=\left\{p_l^i,l=1,2,\dots ,N_{label}\right\}$ for each label l with voxel value $s_{ln}^i$. (3) Next the vote maps are computed for all the labels [$V^i=\{V_l^i,l=1,2,\dots ,N_{label}\}$with voxel value $v_{ln}^i$] by elementwise multiplying $W^i$ with$S^i$, i.e., $v_{ln}^i=w_{ln}^i\cdot p_{ln}^i$for all labels $l=1,2,\dots ,N_{label}$ and spatial location n. (4) For each label, the corresponding vote maps of all the atlases are averaged to generate the initial segmentation, i.e., $p_{ln}^{init}=\left(\sum _{i=1}^{N_{atlas}}{v}_{ln}^i\right)/N_{atlas}$for each n and l. Importantly, the average operation allows varying number of atlases as inputs to the network, providing flexibility in adjusting the number of atlases in training to fulfill the limit of the GPU memory capacity.

2.2.1.3. Fine-tuning subnet and atlas mask

The fine-tuning subnet, which shares a similar U-Net architecture with the weighted voting subnet (the number of levels is four instead of three), is employed to allow the network to correct for residual errors that may remain after the label fusion computation. It takes $S^{init}$ and the coordinate maps as inputs and outputs a set of feature maps that have the same dimensions as$S^{init}$. Then, a label-specific mask, generated by taking the union of all the candidate segmentations of the corresponding label (i.e., $binarze\left(\sum _{i=1}^{N_{atlas}}{p}_l^i\right)$, referred to as atlas mask), is multiplied with the corresponding channel of the fine-tuning subnet output to generate the final segmentation S_T. The atlas masking operation assumes that the truth label should be contained inside the region that has atlas votes of that label.

2.2.2. Implementation details

The model was implemented in PyTorch using functionalities from the MONAI project (Consortium, 2020), a freely available, community-supported, PyTorch-based framework for deep learning in healthcare imaging (https://monai.io/). NVIDIA Tesla P100 in Google Cloud Platform (16GB, used to conduct experiments related to Brain-3T-T2 and Brain-7T-T2 datasets) and NVIDIA RTX A5000 in local computer (24GB, used to perform experiments related to Brain-3T-T1, Lumbar-Healthy, and Lumbar-Disease datasets) were used in this project. All the models were trained using generalized Dice similarity coefficient (GDSC) loss (Sudre et al., 2017) with the Adam optimizer. Since the GDSC accounts for the volume differences of all labels, it is more suitable to evaluate the overall performance when there is a big difference in label volumes, such as in our brain MRI applications. We adopted the deep-supervision scheme (Dou et al., 2016) (four levels with weights of 1.0, 0.5, 0.2, 0.1) in the fine-tuning subnet to improve training efficiency. Due to GPU memory limitation, the proposed network was trained using image patches, obtained following steps described in Section 2.2.2.2. The batch size was set to one, constrained by GPU memory capacity.

2.2.2.1. Cross-validation experiments and parameter tuning

Since the datasets are relatively small, cross-validation experiments were performed in each of the Brain-3T-T2 (4-fold), Brain-3T-T1 (5-fold) and Lumbar-Healthy (5-fold) datasets to evaluate the segmentation accuracy of DLF. To tune DLF for each application, in each dataset, we use the first fold as the validation set and the remaining folds as the training set to determine the set of parameters that generate the optimal performance in terms of GDSC of all gray matter labels in MRI datasets and Dice similarity coefficient (DSC) of lumbar vertebrae in the CT dataset. The same set of parameters is applied in the rest of the cross-validation experiments (experiments using each of the folds other than the first fold as the validation set). To reduce potential bias, results excluding the experiment that is used to tune parameters (the one using the first fold as a validation set) are reported.

2.2.2.2. Preprocessing steps to obtain the patch-level training and validation sets

Each step of network training involves randomly selecting one of the training images in a given cross-validation fold as the “target” and selecting a random patch in the target image space. The remaining training images take the role of “atlases”. Using previously computed registrations between all image pairs, the patches corresponding to the target patch are extracted from the warped atlas images and warped atlas segmentations. These patches are input to the end-to-end network, which yields the segmentation of the target patch,$S^T$. The loss function measures GDSC between this segmentation and the ground truth segmentation of the target patch. Registration between image pairs is computed differently for different datasets, as detailed in Supplementary Material S4.

To make full use of the bilateral segmentations of the MTL datasets (Brain-3T-T2 and Brain-3T-T1) during network training, we effectively double the number of segmented images by flipping each image across the midsagittal plane, i.e., each training subject provides both left and right MTL as training images in segmenting each side of the MTL of the target image. This is not done in the Lumbar-Healthy dataset. The Greedy registration toolbox (github.com/pyushkevich/greedy) with the normalized cross-correlation metric is used in all the registration tasks.

From each training image and the corresponding registered atlases, we sampled twelve patches (10 and 2 centered on voxels with foreground and background, respectively) in the MRI datasets (Brain-3T-T2 and Brain-3T-T1) and seventeen patches (15/2 centered on foreground/background) in the Lumbar-Healthy dataset. The patch size is set to 72×72×72 voxels for the MRI datasets and 104×104×104 voxels for the Lumbar-Healthy dataset, determined in the parameter tunning stage (Section 2.2.2.1). All the patches are normalized by subtracting the mean and dividing by the standard deviation.

Following similar steps, the patch-level validation set that is used to tune parameters is generated by treating the subjects in the first fold of the cross-validation experiments (parameter tuning stage in Section 2.2.21) as the targets and all the remaining training subjects as the atlases.

2.2.2.3. Augmentation strategies

In addition to using common augmentations methods, including random flipping, random rotation (≤ 10°), random elastic deformation augmentation and random additive Gaussian noise to both the target and the atlases, we propose two novel augmentation strategies that are unique to the DLF pipeline. (1) The first strategy is related to how the atlases are sampled in patch extraction. Instead of using all the atlases in a fixed sequence, which may result in a network not being robust to different atlas combinations or different ordering of atlases as input channels to the weighted voting subnet (this is important as one more atlas will be available in the test phase), we randomly select $N_{atlas}$ out of all available atlases. To make it more robust to atlas variability, the selection is done with replacement, and we allow $N_{atlas}$ bigger than the number of available atlases, i.e., duplicated atlases may be present. This is desired as the network may learn to handle repeated/similar votes, similar to the core idea of JLF in penalizing correlated errors among the atlases (Wang et al., 2012). This process is empirically repeated three times to generate enough sample for training. (2) The second one is that we extend the random histogram shift augmentation in the DLF setting. In detail, random histogram shift is applied to the target image as well as the atlases independently with a 0.8 probability. By doing this, we allow variability in contrast between atlases and target to help the weighted voting subnet to be more sensitive to the similarity of underlying structure rather than the intensity distribution of the target image, which helps improve the generalizability.

With the advancement of medical imaging, multimodal imaging data, either from different imaging devices (e.g., MRI, CT, ultra-sound) or different imaging sequences of the same device (e.g., T1w MRI, T2w MRI), is becoming more and more common. Active research is being conducted to answer important questions such as how to effectively make full use of the complementary information provided by different modalities, how to deal with missing or corrupted data both in training and test time, how to accurately interpret the contribution of each modality. One unique characteristic of multimodal data is that the information provided by different modalities, although complementary, is highly correlated. When a DCNN model is trained directly on multiple modalities, it is unclear which modality contributes the most to successful segmentation. Furthermore, if at test time one of the modalities is missing or is corrupted by noise or artifact, a DCNN model trained on multiple modalities may be confused and produce a poor segmentation. In this paper, we propose to make our model more robust to missing/corrupted modalities using a simple modality augmentation (ModAug) strategy. When training with multimodal data (the Brain-3T-T2 and Brain-3T-T1 datasets with multiple MRI modalities in this study), we randomly (with a probability of 0.5) replace one of the channels (T1w or T2w MRI) with random white noise. By doing this, the model is forced to base its prediction on individual modalities as much as possible. The ModAug strategy is applied to both standard U-Net (StandU-Net, detailed in Section 2.3.3) and DLF training.

2.2.2.4. Inference and postprocessing

In the inference phase, either in applying the models to the validation fold in cross-validation experiments or to the out-of-sample dataset in the experiments testing generalizability, each of the test images is treated as the target and all the subjects in the training dataset are used as atlases. After performing registration following the steps in Supplementary Material S4, the sliding window inference approach is applied with spacing equal to half of the patch size to generate an automatic segmentation of each test image. A gaussian kernel (standard deviation equal to 1/5 of patch size) is multiplied by the prediction of each sliding window to give more weight to the center of the patch before fusing patch-level predictions to generate the whole-image segmentation. In the cross-validation experiments of the MRI MTL datasets, the posterior probability maps of the original and the corresponding flipped images are averaged before generating the final segmentation, which has been found to produce more accurate results.

In the parameter tuning phase, we observe that all the methods generate isolated islands of segmentation in the background in some subjects. Therefore, an additional postprocessing step is performed by multiplying the automatic segmentation with a binary mask of the largest component of the foreground labels.

2.2.2.5. Other dataset specific implementation details

Brain-3T-T2 and Brain-3T-T1:

10 atlases were selected in each patch sampling (Section 2.2.2.3). Each model converged after 20 epochs. We used a step decay learning rate scheduler with initial learning rate set to 0.0005 and was reduced by a factor of 0.2 at epochs 10, 15, and 18.

Lumbar-Healthy:

5 atlases were selected in each patch sampling. We trained the model for 35 epochs. The initial learning rate was set to 0.0005. It was reduced by a factor of 0.2 at the end of epochs 20 and 30.

2.3. Alternative methods for comparisons

2.3.1. Conventional MAS algorithms

The first set of algorithms we compared with are the conventional MAS methods, including MV, SVWV, and JLF with a neighborhood search scheme (Wang et al., 2011b). In addition, a learning-based corrective algorithm (CL) (Wang et al., 2011a), commonly used together with JLF, is applied to the JLF output (JLF+CL) to get the benchmark performance of conventional MAS algorithms. For each method, the optimal set of hyper-parameters (e.g., patch radius, search radius, and so on) are determined in the parameter tuning stage (using the first fold of the cross-validation experiment as the validation set, described in Section 2.2.2.1) by performing a grid search for the best the GDSC of gray matter labels in the MRI MTL datasets or the DSC of the lumbar vertebrae in the CT datasets.

2.3.2. nnU-Net

State-of-the-art in DCNN segmentation is represented by nnU-Net (Isensee et al., 2020), a self-adapting U-Net approach. nnU-Net has been optimized to achieve top performance in various medical imaging segmentation tasks (github.com/MIC-DKFZ/nnUNet), making it well-suited to serve as the high-performing comparison method for DLF. The algorithm is designed to be used out-of-the-box without the need for the user to choose parameters (the automatic chosen parameters of each experiment are reported in the Supplementary Material S2), to perform cross-validation experiments and to run inference. As recommended by the authors, the “3d_fullres” mode is used to generate the results. The patch sizes automatically determined by the algorithm are 208×238×196 voxels for Brain-3T-T2, 205×196×189 voxels for Brain-3T-T1 and 178×289×200 voxels for Lumbar-Healthy.

2.3.2. Standard U-Net with the comparable settings in DLF (StandU-Net)

Although nnU-Net provides state-of-the-art performance of DCNN algorithms, it has a different architecture and is trained with significantly different parameters and implementations compared to the U-Net backbone in DLF. To have a fair comparison and provide insight in whether incorporating MAS provides value in DCNN in a similar setting, we also report results of a standard 3D U-Net (Çiçek et al., 2016) with the same architecture as the fine-tuning subnet that is trained with the same set of key training parameters as DLF (i.e., augmentation methods, patch size, learning rate, optimizer, deep-super vision training, loss function and so on). This method is named StandU-Net in this paper. The StandU-Net is trained over 60 epochs with a batch size of 7 for the MRI datasets and 45 epochs with a batch size of 5 for the CT dataset. Inference and postprocessing follow the same steps as DLF described in Section 2.2.2.4.

2.3.3. Oracle experiment to evaluate label fusion performance upper bound

An ideal label fusion strategy, named oracle label fusion [inspired by Ding et al. (2019a, 2019b)], is able to find the correct label from a set of registered atlases. Such strategy provides an upper bound of label fusion method, which informs possible room for improvement and reflects the quality of registration. Therefore, segmentation accuracy using this strategy is evaluated and the results are reported in Tables 1 and 2. Specifically, for each voxel, the oracle label fusion assigns the correct label if at least 10% of the registered atlases vote for it, or otherwise the background label (0).

Table 1.

Mean (±standard deviation) Dice similarity coefficient (DSC) [or generalized DSC (GDSC) of all labels] and mean surface distance (MSD) between automatic and manual segmentations in cross-validation experiments. Volume of each label is provided for better interpretation of the DSC scores. For better interpretation, background color of each cell indicates the relative performance compared to the best (darkest red) and worst (darkest blue) performance in each row (the darker red/blue, the closer to the best/worst performance respectively, oracle experiment excluded).

		Volume (cm3)	Oracle (10%)	MV	SVWV	JLF+CL	StandU-Net (w/ ModAug)	nnU-Net	DLF (w/o ModAug)
Dice similarity coefficient	Brain-3T-T2 dataset
	GDSC	-	97.5±1.4	70.8±4.3*	75.8±3.8*	78.2±3.7*	80.1±3.7*	81.6±3.3	81.1± 3.4
	Hippo	2.8±0.5	97.9±1.0	88.5±2.1*	91.5±1.2*	93.1±1.3*	93.4±1.1*	94.2±1.1 *	93.9±1.0
	CA1	0.7±0.1	97.5±1.5	68.4±6.0*	73.3±3.9*	75.8±4.2*	78.6±3.0	79.3±3.8	79.2±3.5
	CA2	0.1±0.0	93.1±4.6	54.2±9.6*	61.3±7.4*	69.7±5.2*	72.3±3.5	74.1±4.8	72.6±4.6
	CA3	0.2±0.0	96.6±1.8	63.5±5.2*	68.1±4.5*	71.8±3.3*	74.7±4.6*	76.3±3.7	76.5±4.4
	DG	0.5±0.1	97.7±1.3	75.1±4.1*	79.9±2.8*	82.5±2.4*	82.5±1.7*	85.1±2.0 *	83.8±2.1
	SUB	1.0±0.2	98.8±1.8	75.2±7.7*	78.3±7.1*	80.4±7.2	78.2±7.2	80.9±6.5	79.3±7.7
	TAIL	0.4±0.1	98.5±0.9	79.9±3.2*	81.8±3.0*	83.3±2.9*	84.2±2.2*	84.6±2.5	84.8±2.5
	ERC	0.9±0.2	97.5±1.4	75.0±3.9*	78.6±3.7*	81.1±3.7*	84.6±4.0*	85.4±3.9	85.5±3.2
	BA35	0.6±0.1	95.4±3.3	56.8±10.1*	64.4±9.4*	66.7±8.9*	72.8±9.6	73.7±8.5	74.0±6.6
	BA36	1.7±0.6	98.3±1.0	68.7±6.4*	76.3±5.6*	78.5±5.1*	80.0±5.6*	82.0±5.6	81.7±5.3
	PHC	0.6±0.2	96.1±6.9	67.8±9.1*	71.2±7.9*	75.1±7.9*	76.5±6.9	79.3±6.8 *	77.0±7.1
	Brain-3T-T1 dataset
	GDSC	-	98.8±0.5	80.8±2.8*	82.6±2.3*	83.6±2.3*	84.7±2.1*	86.0±2.0	86.1±1.8
	Hippo	3.2±0.6	99.4±0.3	90.1±2.5*	91.9±1.5*	92.5±1.3*	91.6±2.2*	92.9±1.4	92.7±1.3
	AHippo	1.6±0.4	99.5±0.3	89.6±3.1*	91.1±2.3*	91.8±2.1*	91.2±3.0*	92.0±1.9*	92.5±1.8
	PHippo	1.5±0.2	99.3±0.4	87.2±2.7*	89.2±1.8*	90.0±1.7*	89.9±2.0*	90.8±1.6	90.8±1.4
	ERC	0.5±0.1	98.3±1.1	73.3±4.2*	74.8±3.2*	75.9±3.6*	79.7±4.1*	80.6±3.3	81.2±3.0
	BA35	0.5±0.1	97.4±2.0	66.2±9.0*	69.2±7.6*	70.6±7.1*	75.2±5.6*	75.8±6.5	76.2±5.9
	BA36	1.8±0.3	98.7±0.9	74.7±5.0*	76.8±4.8*	78.1±4.3*	79.7±3.7*	81.8±3.8	81.8±3.4
	PHC	0.9±0.2	98.3±1.5	78.0±3.8*	79.5±3.8*	80.2±4.0*	82.0±2.8*	84.4±3.2	83.8±2.8
	Lumbar-Healthy dataset
	Lumbar	269±64	99.6±0.3	86.9±2.7*	95.6±0.6*	96.0±1.9	91.1±8.0	97.1±0.8	96.4±0.9
Mean surface distance (mm)	Brain-3T-T2 dataset
	Hippo	2.8±0.5	0.21±0.06	0.45±0.09*	0.35±0.04*	0.31±0.04*	0.29±0.04	0.27±0.04	0.28±0.03
	CA1	0.7±0.1	0.13±0.06	0.71±0.15*	0.65±0.14*	0.59±0.14	0.56±0.12	0.56±0.13	0.56±0.14
	CA2	0.1±0.0	0.16±0.10	0.72±0.27*	0.61±0.23*	0.49±0.19	0.47±0.14	0.48±0.17	0.49±0.22
	CA3	0.2±0.0	0.13±0.07	0.65±0.17*	0.58±0.15*	0.51±0.11	0.48±0.11	0.45±0.09	0.47±0.18
	DG	0.5±0.1	0.13±0.07	0.60±0.12*	0.53±0.11	0.47±0.09	0.49±0.09	0.42±0.07 *	0.49±0.12
	SUB	1.0±0.2	0.09±0.09	0.78±0.24*	0.72±0.21	0.65±0.20	0.71±0.21	0.63±0.19	0.68±0.23
	TAIL	0.4±0.1	0.10±0.05	0.52±0.09*	0.50±0.09*	0.48±0.09	0.46±0.08	0.47±0.07	0.45±0.07
	ERC	0.9±0.2	0.18±0.10	0.85±0.23*	0.74±0.19*	0.68±0.20	0.55±0.19	0.56±0.22	0.54±0.21
	BA35	0.6±0.1	0.23±0.14	1.17±0.28*	1.02±0.29*	0.95±0.31*	0.79±0.26	0.79±0.26	0.81±0.25
	BA36	1.7±0.6	0.15±0.06	1.04±0.21*	0.90±0.20*	0.83±0.18*	0.79±0.17	0.74±0.24	0.74±0.19
	PHC	0.6±0.2	0.19±0.24	0.99±0.36*	0.92±0.36	0.79±0.35	0.79±0.26	0.68±0.24 *	0.81±0.34
	Brain-3T-T1 dataset
	Hippo	3.2±0.6	0.09±0.04	0.48±0.08*	0.38±0.04*	0.36±0.03	0.40±0.06*	0.34±0.03	0.35±0.04
	AHippo	1.6±0.4	0.07±0.04	0.53±0.08*	0.43±0.06*	0.41±0.06*	0.41±0.07*	0.37±0.05	0.35±0.05
	PHippo	1.5±0.2	0.08±0.04	0.50±0.10*	0.43±0.07*	0.41±0.06	0.41±0.07	0.38±0.06	0.39±0.06
	ERC	0.5±0.1	0.11±0.04	0.66±0.14*	0.64±0.14*	0.62±0.12*	0.50±0.08	0.53±0.12	0.51±0.10
	BA35	0.5±0.1	0.15±0.07	0.85±0.24*	0.79±0.20*	0.77±0.21*	0.63±0.16	0.64±0.17	0.63±0.18
	BA36	1.8±0.3	0.12±0.07	0.95±0.24*	0.91±0.23*	0.86±0.21*	0.76±0.15*	0.72±0.17	0.71±0.16
	PHC	0.9±0.2	0.13±0.07	0.65±0.18*	0.63±0.17*	0.62±0.19*	0.51±0.09*	0.47±0.12	0.48±0.09
	Lumbar-Healthy dataset
	Lumbar	269±64	0.19±0.11	1.69±0.44*	1.02±0.23*	0.84±0.24	1.34±0.42*	0.66±0.31	0.74±0.32

Note:

^*:p < 0.05 compared to DLF, tested with two-sided Wilcoxon signed rank test.

Hyper-parameters: SVWV: β = 0.05; JLF+CL: β = 2.0. The optimal patch size is 3×3×1 voxels for both SVWV and JLF+CL. The optimal search radius is 4×4×1 voxels for SVWV and 3×3×1 voxels for JLF+CL. The patch sizes of DLF and StandU-Net are 72×72×72 voxels for Brain-3T-T2 and Brain-3T-T1 and 104×104×104x voxels for Lumbar-Healthy. The patch sizes of nnU-net are 208×238×196 voxels for Brain-3T-T2, 205×196×189 voxels for Brain-3T-T1 and 178×289×200 voxels for Lumbar-Healthy, determined automatically by the nnU-Net package.

Abbreviations: MV = majority voting; SVWV = spatially varying weighted voting; JLF+CL = joint label fusion plus corrective learning; DLF = deep label fusion; Hippo = hippocampus; AHippo/PHippo = anterior/posterior hippocampus; CA1–3 = cornu ammonis 1 to 3; dentate gyrus = DG; subiculum = SUB; TAIL = the tail of hippocampus; ERC = entorhinal cortex; BA35/36 = Brodmann areas 35/36; PHC = parahippocampal cortex; ModAug = modality augmentation; w/ and w/o = with and without.

Table 2.

Mean (±standard deviation) Dice similarity coefficient (DSC) [or generalized DSC (GDSC) of all labels] and mean surface distance (MSD) between automatic and manual segmentations in experiments testing for generalizability. Volume of each label is provided for better interpretation of the DSC scores. For better interpretation, background color of each cell indicates the relative performance compared to the best (darkest red) and worst (darkest blue) performance in each row (the darker red/blue, the closer to the best/worst performance respectively, oracle experiment excluded).

		Volume (cm3)	Oracle (10%)	JLF + CL	StandU-Net (w/ ModAug)	nnU-Net	DLF (w/o ModAug)
Dice similarity coefficient	Brain-7T-T2 dataset
	GDSC	-	95.2±2.0	68.6±4.8*	69.9±5.6*	57.5±9.4*	74.5±4.0
	Hippo	2.7±0.4	96.9±1.4	89.3±1.9*	87.9±3.4*	79.1±10.6*	91.1±1.5
	CA1	0.6±0.2	96.8±2.4	72.5±3.2*	70.8±5.4*	58.1±15.1*	77.2±3.0
	CA2	0.1±0.0	92.1±4.8	60.5±7.2*	61.2±9.3*	45.3±23.6*	70.7±5.7
	CA3	0.1±0.0	94.8±2.6	61.6±7.9*	61.0±7.7*	58.2±11.9*	70.9±5.2
	DG	0.5±0.1	97.6±2.1	77.8±4.6*	75.5±4.9*	73.8±11.8*	81.6±2.4
	SUB	1.0±0.1	96.4±3.7	77.0±5.3 *	69.4±6.1*	49.7±17.8*	74.2±4.4
	TAIL	0.5±0.2	97.1±1.7	79.5±2.8*	75.8±5.9*	67.9±8.5 *	80.8±3.3
	ERC	0.7±0.1	96.2±1.7	72.6±6.4*	69.1±11.4*	69.9±10.6*	80.8±4.9
	BA35	0.5±0.1	92.9±3.8	53.9±10.9*	62.0±8.3*	49.4±13.9*	66.6±8.6
	BA36	1.4±0.4	92.4±3.8	57.1±11.6*	66.5±7.2	47.7±14.0*	66.4±9.5
	PHC	0.5±0.2	95.8±3.8	67.5±9.3*	70.9±8.5*	65.7±11.5*	75.0±7.0
	Lumbar-Disease dataset
	Lumbar	394±84	96.9±1.4	83.1±4.1	79.7±5.4*	78.8±5.6*	83.9±4.6
Mean surface distance (mm)	Brain-7T-T2 dataset
	Hippo	2.7±0.4	0.24±0.06	0.45±0.07*	0.48±0.12*	1.08±0.69*	0.37±0.06
	CA1	0.6±0.2	0.14±0.06	0.62±0.07	0.71±0.15*	1.42±1.09*	0.60±0.11
	CA2	0.1±0.0	0.16±0.07	0.55±0.10*	0.60±0.19*	1.82±1.93*	0.51±0.11
	CA3	0.1±0.0	0.14±0.04	0.63±0.22*	0.65±0.17*	1.23±1.49*	0.51±0.09
	DG	0.5±0.1	0.12±0.06	0.56±0.11	0.64±0.13*	0.88±0.80*	0.55±0.11
	SUB	1.0±0.1	0.19±0.12	0.71±0.15 *	0.90±0.24*	1.73±0.76*	0.78±0.14
	TAIL	0.5±0.2	0.15±0.05	0.56±0.10	0.69±0.16*	1.08±0.58*	0.55±0.10
	ERC	0.7±0.1	0.19±0.07	0.81±0.19*	0.82±0.31*	0.96±0.33*	0.57±0.18
	BA35	0.5±0.1	0.29±0.12	1.19±0.35*	0.93±0.21	1.54±0.78*	0.90±0.23
	BA36	1.4±0.4	0.33±0.12	1.33±0.37*	1.04±0.21	2.09±1.16*	1.05±0.24
	PHC	0.5±0.2	0.20±0.14	0.94±0.39*	0.78±0.22	1.07±0.37*	0.76±0.25
	Lumbar-Disease dataset
	Lumbar	394±84	0.71±0.28	2.57±0.61*	2.16±0.33	3.39±0.82*	2.05±0.49

Note:

^*:p < 0.05 compared to DLF, tested with two-sided Wilcoxon signed rank test. Hyper-parameters and patch sizes are the same as that in Table 1.

Abbreviations: JLF+CL = joint label fusion plus corrective learning; DLF = deep label fusion; Hippo = hippocampus; CA1–3 = cornu ammonis 1 to 3; dentate gyrus = DG; subiculum = SUB; TAIL = the tail of hippocampus; ERC = entorhinal cortex; BA35/36 = Brodmann areas 35/36; PHC = parahippocampal cortex; ModAug = modality augmentation; w/ and w/o = with and without.

2.4. Statistical analysis

The evaluation metrics are GDSC for all the labels of interests (e.g., gray matter labels in the MRI MTL datasets) and DSC for the other labels (individual labels and the compound label of hippocampus in MRI MTL datasets). In addition, we adopt the mean surface distance (MSD) metric to evaluate the segmentation quality. Compared to DSC, which is used in the loss function, MSD evaluates the accuracy of the segmentation boundaries and thus will provide a more comprehensive evaluation. Two-sided Wilcoxon signed rank test is performed to evaluate whether the segmentation accuracy (DSC/GDSC or MSD) of alternative methods (except for the oracle strategy) is significantly different from that of DLF in each experiment of each dataset. For the MRI MTL datasets with bilateral segmentations, segmentation accuracy of both sides is first averaged before being tested for significance to maintain the independence between samples.

3. Evaluation experiments and results

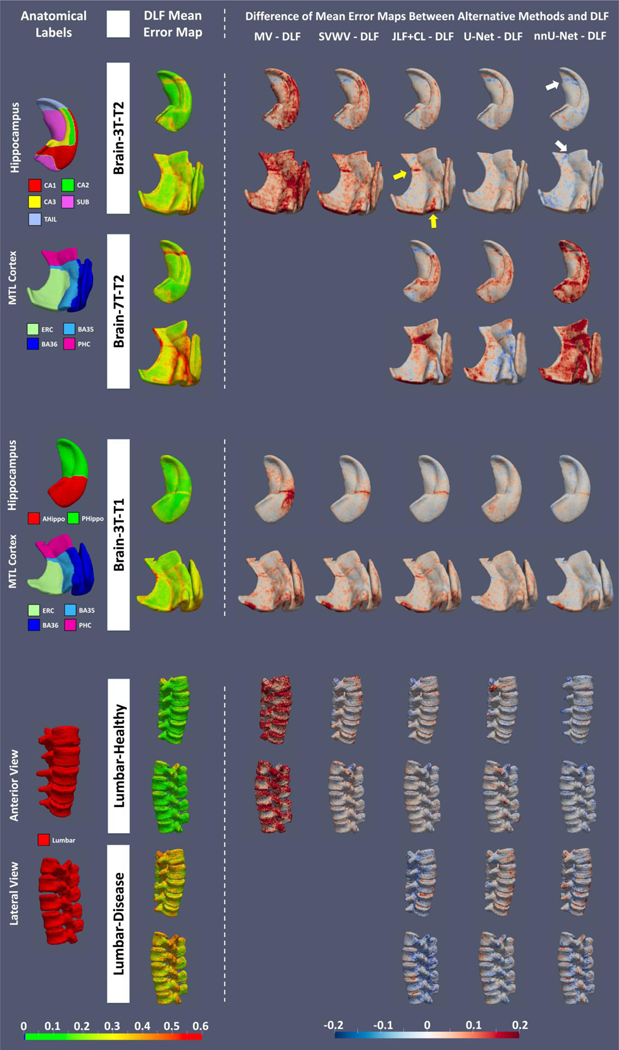
Cross-validation experiments (described in Section 2.2.2.1) and generalizability experiments are performed to evaluate the segmentation accuracy of the proposed DLF both in data with similar characteristics as the training set and in data without. Ablation experiments are also included to investigate the contribution of individual components of DLF and the modality augmentation strategy to segmentation accuracy and generalizability. To visualize the spatial error distribution of each algorithm, we generate the mean error map of each method in each dataset by warping the error maps of all the test subjects (binary maps indicating locations of disagreement between the automatic and manual segmentations) to the unbiased population template, built using manual segmentations of the corresponding training set the same as in (Xie et al., 2017). Results are shown in Figure 3. In addition, examples of typical segmentation errors of the T2-based MRI datasets (Brain-3T-T2 and Brain-7T-T2) and lumbar vertebrae datasets (Lumbar-Healthy and Lumbar-Disease) are shown in Figure 4 and Figure 5. Example segmentations errors of the Brain-3T-T1 dataset are shown in Supplementary Figure S1.

Figure 3 (color figure).

Visualization of mean spatial error distribution of all methods. Anatomical labels and mean error map of DLF are shown on the left. Difference in mean error maps between alternative methods and DLF are shown on the right with red or blue indicating the alternative methods having more or less mean errors respectively. Abbreviations: MV = majority voting; SVWV = spatially varying weighted voting; JLF+CL = joint label fusion plus corrective learning; DLF = deep label fusion; CT = computational tomography; AHippo/PHippo = anterior/posterior hippocampus; CA1–3 = cornu ammonis 1 to 3; dentate gyrus = DG; subiculum = SUB; TAIL = the tail of hippocampus; ERC = entorhinal cortex; BA35/36 = Brodmann areas 35/36; PHC = parahippocampal cortex; CS = collateral sulcus; OTS = occipitotemporal sulcus; MISC = miscellaneous label; MTL = medial temporal lobe; U-Net: StandU-Net..

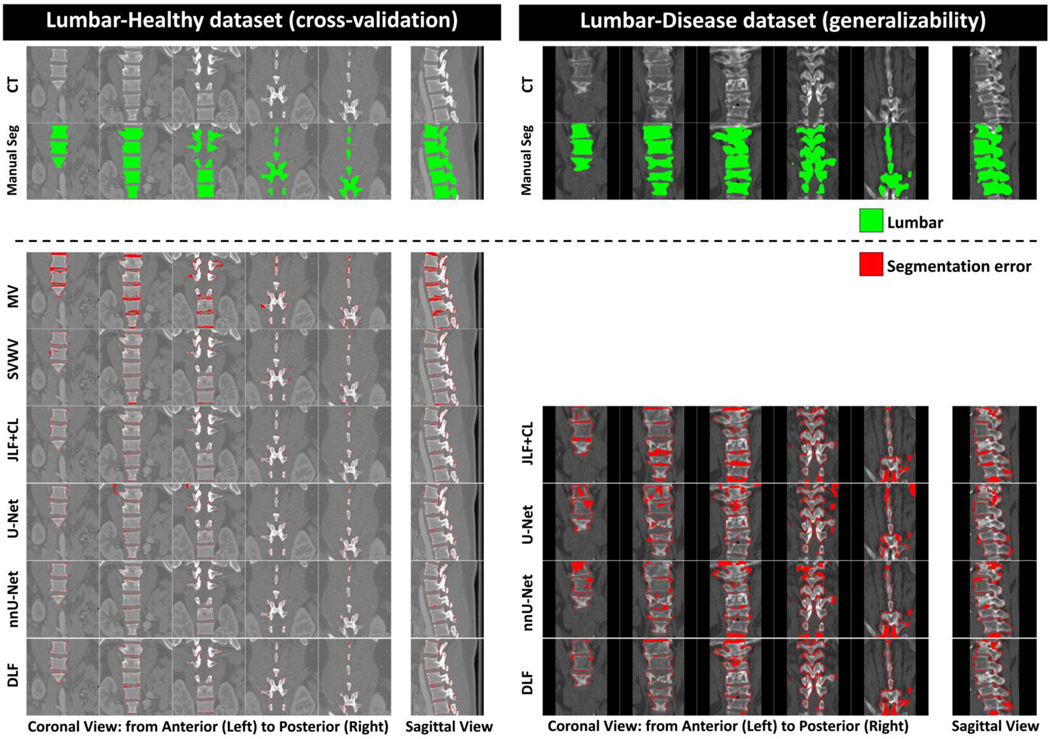
Figure 4 (color figure).

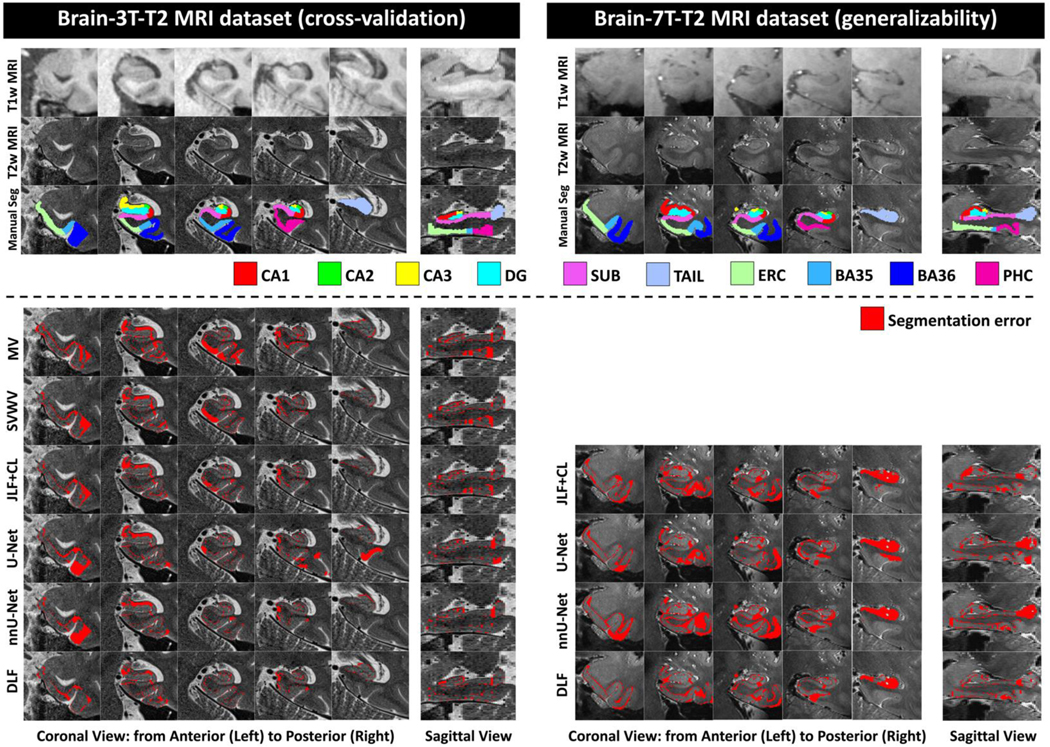
Examples of typical segmentation errors (bottom section) compared to manual segmentation (Manual Seg, top section) of different algorithms of the T2-based MRI datasets (Brain-3T-T2 and Brain-7T-T2). Example segmentations of all the methods can be found in Supplementary Figure S2. Abbreviations: MV = majority voting; SVWV = spatially varying weighted voting; JLF+CL = joint label fusion plus corrective learning; DLF = deep label fusion; CA1–3 = cornu ammonis 1 to 3; dentate gyrus = DG; subiculum = SUB; TAIL = the tail of hippocampus; ERC = entorhinal cortex; BA35/36 = Brodmann areas 35/36; PHC = parahippocampal cortex; U-Net: StandU-Net.

Figure 5 (color figure).

Examples of typical segmentation errors (bottom section) compared to manual segmentation (Manual Seg, top section) of the CT datasets (Lumbar-Healthy and Lumbar-Disease). Example segmentations of all the methods can be found in Supplementary Figure S3. Abbreviations: MV = majority voting; SVWV = spatially varying weighted voting; JLF+CL = joint label fusion plus corrective learning; DLF = deep label fusion.

3.1. Cross-validation experiments

Table 1 shows the results of cross-validation experiments with the optimal parameters of the MAS methods in the notes. Since the ModAug strategy only helps improve the segmentation accuracy for StandU-Net rather than DLF when complete data is available, which will be discussed in Section 3.3, results of StandU-Net with ModAug and DLF without ModAug are compared in this section.

• Comparison with conventional MAS methods: Consistent with prior literature, JLF+CL outperforms the other conventional MAS algorithms. DLF significantly outperforms JLF+CL in almost all the tasks (except for SUB in Brain-3T-T2). We observe the biggest improvements are in CA1–3, ERC and BA35, which are subregions of early Alzheimer’s disease research because they are affected by the earliest neurofibrillary tangle pathology. Spatially, the biggest improvements (yellow arrows in the Brain-3T-T2 dataset row in Figure 3) are located at the small stripe of BA35 between ERC and PHC as well as the boundary of BA35 and BA36.

• Comparison with StandU-Net: DLF significantly improves the segmentation accuracy for most of the tasks compared to StandU-Net. In the remaining tasks, although not significant, DLF consistently produces better results. Interestingly, as shown in Figure 3, the improvements are spatially uniform in the Brain-3T-T2 and Brain-3T-T1 datasets.

• Comparison with nnU-Net: Overall, the performance of DLF and nnU-Net are comparable with nnU-Net performing better in some tasks (significant better DSC/MSD in hippocampus, DG and PHC in Brain-3T-T2) and DLF in other tasks (significant better DSC in anterior hippocampus in Brain-3T-T1). From the error maps of the Brain-3T-T2 dataset, we can see the biggest difference is in locating the anterior boundary of the TAIL (white arrows), which is important for the accurate segmentation of other hippocampal subfields and PHC (in the manual segmentation protocol, the posterior border of PHC is one slice anterior to the anterior border of the TAIL). Interestingly, the improvement is less obvious when compared to StandU-Net trained with similar parameters as DLF. The bigger patch size of nnU-Net could potentially contribute to this difference.

To further compare the segmentation accuracy of the Lumbar-Healthy dataset with state-of-the-art algorithms in the literature, we summarize the averaged DSC scores of various methods reported in the corresponding publications in Supplementary Table S2. From this indirect comparison, we can see that the proposed DLF achieves comparable high segmentation accuracy.

3.2. Generalization to unseen datasets with different characteristics

To test the generalizability of JLF+CL (one of the best conventional label fusion methods in Table 1), StandU-Net, nnU-Net and DLF, we trained these methods on the entire Brain-3T-T2 (the 4 overlapping subjects were excluded from the training) and Lumbar-Healthy datasets and directly applied the models to the Brain-7T-T2 and Lumbar-Disease datasets respectively. Segmentation accuracy is evaluated in terms of DSC/GDSC and MSD between the automatic and manual segmentations.

The results, shown in Table 2, demonstrate the significantly better generalizability of DLF compared to all the alternative methods. nnU-Net, which has similar performance to DLF in the cross-validation experiments, produces significantly poorer segmentation results in segmenting both Brain-7T-T2 and Lumbar-Disease datasets. Compared with JFL+CL and StandU-Net, DLF significantly outperforms in most of the tasks (except for TAIL compared to JLF+CL and BA36 compared to StandU-Net). Overall, segmentation accuracy in these generalizability experiments is lower than in the cross-validation experiments. This is expected due to differences in image contrast, field of view, and diagnosis (the CT dataset). Indeed, in the Brain-3T-T2 dataset, we can see from Figure 3 that the segmentation errors are mostly located at boundaries between neighboring MTL subregions, where we expect the highest inter-rater variability, rather than gray/white matter or gray matter/CSF boundaries in the center of each label.

3.3. The effect of the modality augmentation

In this section, we evaluate the effect of the proposed modality augmentation strategy in the multimodal MRI datasets. Both StandU-Net and DLF were trained with and without the ModAug strategy in the cross-validation (Section 3.1) and applied to experiments testing generalizability (Section 3.2). At the test time, in addition to making prediction with both modalities, inputs with only one modality (either T1w MRI or T2w MRI, the other channel was replaced with random white noise) were passed to the model to make prediction to test its ability in handling missing data.

As shown in Table 3, in both StandU-Net and DLF, the ModAug strategy improves the segmentation accuracy when only one modality is available in the test time compared to the models that are trained without ModAug in both the cross-validation and the generalizability experiments (the columns for experiments with “Primary Modality Missing” and “Secondary Modality Missing”). The improvements are very large for StandU-Net models when the primary modality in a given experiment is missing (i.e., missing T2 in the T2-based MRI datasets and missing T1 in the T1-based MRI dataset).

Table 3.

Mean (±standard deviation) generalized Dice similarity coefficient (GDSC) of all gray matter labels in the MRI datasets between automatic and manual segmentations in experiments testing the effect of modality augmentation (ModAug) in standard U-Net (StandU-Net) and deep label fusion (DLF). Cells with better segmentation accuracy between models trained with and without ModAug in the same situation (applying to primary modality missing, secondary modality missing and both modalities present respectively) are highlighted with light red background. Supplementary Table S1 reports complete Dice similarity coefficient scores of individual labels.

StandU-Net
Test-time modalities	Primary Modality Missing		Secondary Modality Missing		Both Modalities Present
	w/ ModAug	w/o ModAug	w/ ModAug	w/o ModAug	w/ ModAug	w/o ModAug
Brain-3T-T2 (cross-validation experiment)
GDSC	79.9±3.5	75.2±3.6	76.6±3.6	6.1±5.1	80.3±3.4	79.5±3.8
Brain-7T-T2 (generalizability experiment)
GDSC	56.8±11.8	51.3±14.2	56.4±7.3	0.0±0.0	67.2±4.6	66.1±8.6
Brain-3T-T1 (cross-validation experiment)
GDSC	83.7±2.7	37.4±13.5	81.7±2.7	2.5±1.2	84.7±2.1	84.7±2.2
DLF
Test-time modalities	Primary Modality Missing		Secondary Modality Missing		Both Modalities Present
	w/ ModAug	w/o ModAug	w/ ModAug	w/o ModAug	w/ ModAug	w/o ModAug
Brain-3T-T2 (cross-validation experiment)
GDSC	80.7±3.5	80.1±3.4	78.6±3.5	74.9±4.1	80.9±3.6	81.1± 3.4
Brain-7T-T2 (generalizability experiment)
GDSC	66.4±4.5	64.9±4.7	71.5±3.9	71.2±4.0	71.4±3.9	71.8±3.7
Brain-3T-T1 (cross-validation experiment)
GDSC	85.6±1.9	85.0±2.3	85.2±1.7	84.0±2.5	85.9±1.7	86.1±1.8

Abbreviations: Hippo = hippocampus; AHippo/PHippo = anterior/posterior hippocampus; CA1–3 = cornu ammonis 1 to 3; dentate gyrus = DG; subiculum = SUB; TAIL = the tail of hippocampus; ERC = entorhinal cortex; BA35/36 = Brodmann areas 35/36; PHC = parahippocampal cortex; w/ and w/o = with and without.

When the complete data (both modalities are available, last two columns in Table 3) is input to the model, the ModAug strategy helps improve the segmentation accuracy of StandU-Net in the cross-validation experiments and even to a larger extent in the generalizability experiments (columns with “Both Modalities Present” in the top part of Table 3). However, DLF does not benefit from the ModAug strategy in both experiments when using complete data (last two columns of the bottom part of Table 3). Therefore, we include StandU-Net with ModAug and DLF without ModAug in Sections 3.1 and 3.2.

3.4. Ablation analysis of main DLF components

To investigate the contribution of the main DLF components (i.e., weighted voting subnet, fine-tuning subnet and atlas mask) to the segmentation accuracy within the cross-validation datasets, an ablation analysis is performed in the parameter tuning fold of each dataset (the one using the first fold as the validation fold and the rest as training folds). All the models are trained with the ModAug strategy to be consistent. As reported in Table 4, the fine-tuning subnet is the most important contributor to DLF, and the weighted voting subnet also makes a significant contribution. The atlas mask brings marginal improvement to the final segmentation in both Brain-3T-T2 and Lumbar-Healthy datasets but not in the Brain-3T-T1 dataset. Since this component benefits two out of three datasets, it is utilized in the final model.

Table 4.

Mean (±standard deviation) Dice similarity coefficient (DSC) [or generalized DSC (GDSC) of all labels] and mean surface distance (MSD) between automatic and manual segmentations of the ablation experiments in the training fold of cross-validation experiment. For better interpretation, background color of each cell indicates the relative performance compared to the best (darkest red) and darkest (most blue) performance in each row (the darker red/blue, the closer to the best/worst performance respectively).

		w/o fine-tuning subnet	w/o weighted voting subnet	w/o atlas mask	DLF
Dice similarity coefficient	Brain-3T-T2 dataset
	GDSC	73.4±6.0	78.1±4.3	79.4±4.0	79.9±4.2
	Hippo	88.0±4.0	93.9±1.1	94.0±1.1	93.9±1.1
	CA1	67.4±8.1	76.9±4.7	75.9±4.5	75.8±4.9
	CA2	56.0±17.4	74.2±3.4	72.1±4.9	72.8±5.2
	CA3	66.8±8.2	75.1±4.6	75.6±5.1	76.5±5.4
	DG	82.1±2.9	82.9±1.9	83.2±2.4	83.0±3.3
	SUB	72.1±9.5	79.2±2.9	78.6±4.3	81.4±4.7
	TAIL	80.7±2.9	83.4±3.0	82.7±2.8	83.1±3.1
	ERC	78.4±4.4	84.7±3.6	85.9±3.0	85.4±4.0
	BA35	65.6±12.9	72.9±9.2	74.7±10.2	74.4±8.6
	BA36	70.8±11.2	74.5±7.8	80.7±5.6	80.4±5.2
	PHC	69.5±9.8	72.9±9.0	70.4±8.6	73.8±8.8
	Brain-3T-T1 dataset
	GDSC	81.3±3.1	84.8±1.8	85.9±2.2	85.3±2.1
	Hippo	90.2±2.5	92.7±0.7	92.8±0.9	92.5±0.9
	AHippo	89.2±1.8	90.8±1.9	91.7±1.8	91.7±1.7
	PHippo	84.8±4.7	89.3±2.1	89.2±2.1	89.2±2.2
	ERC	77.1±4.3	78.7±1.3	81.2±2.6	80.7±2.5
	BA35	73.3±3.6	74.8±2.9	76.8±3.8	75.9±3.9
	BA36	74.1±5.9	81.5±3.6	82.5±2.9	81.6±2.9
	PHC	80.8±3.0	82.2±1.6	84.2±3.0	82.6±3.2
	Lumbar-Disease dataset
	Lumbar	91.6±3.5	96.2±0.6	97.0±0.6	97.1±0.7
Mean surface distance (mm)	Brain-3T-T2 dataset
	Hippo	0.46±0.11	0.27±0.03	0.29±0.03	0.28±0.03
	CA1	0.78±0.24	0.65±0.15	0.68±0.15	0.67±0.16
	CA2	0.72±0.31	0.51±0.07	0.57±0.12	0.55±0.14
	CA3	0.50±0.11	0.49±0.08	0.53±0.08	0.46±0.13
	DG	0.51±0.09	0.54±0.06	0.54±0.09	0.50±0.12
	SUB	0.81±0.21	0.68±0.12	0.73±0.19	0.65±0.15
	TAIL	0.63±0.14	0.56±0.12	0.59±0.11	0.56±0.11
	ERC	0.67±0.14	0.47±0.11	0.47±0.12	0.49±0.15
	BA35	0.96±0.39	0.81±0.26	0.77±0.32	0.77±0.25
	BA36	0.99±0.32	0.97±0.29	0.76±0.19	0.76±0.20
	PHC	0.93±0.30	0.94±0.30	1.00±0.26	0.92±0.28
	Brain-3T-T1 dataset
	Hippo	0.46±0.13	0.35±0.05	0.36±0.07	0.38±0.07
	AHippo	0.54±0.11	0.46±0.09	0.42±0.09	0.42±0.08
	PHippo	0.61±0.16	0.46±0.09	0.46±0.10	0.48±0.10
	ERC	0.56±0.11	0.51±0.04	0.47±0.06	0.47±0.04
	BA35	0.70±0.11	0.66±0.09	0.61±0.13	0.63±0.11
	BA36	0.97±0.20	0.72±0.18	0.70±0.10	0.71±0.11
	PHC	0.59±0.11	0.53±0.06	0.47±0.11	0.51±0.13
	Lumbar-Disease dataset
	Lumbar	1.66±0.09	0.96±0.04	0.63±0.02	0.47±0.09

Abbreviations: DLF = deep label fusion; Hippo = hippocampus; AHippo/PHippo = anterior/posterior hippocampus; CA1–3 = cornu ammonis 1 to 3; dentate gyrus = DG; subiculum = SUB; TAIL = the tail of hippocampus; ERC = entorhinal cortex; BA35/36 = Brodmann areas 35/36; PHC = parahippocampal cortex; w/ and w/o = with and without.

In addition, we applied the models from the ablation experiments directly to the corresponding out-of-sample datasets (Brain-T2–7T and Lumbar-Disease) to investigate the importance of different DLF components to the generalizability of DLF. The results show that the generalizability of the individual fine-tuning subnet and weighted voting subnet is inferior to the DLF algorithm, indicating the effectiveness of the proposed two-stage network architecture (Table 5).

Table 5.

Mean (±standard deviation) Dice similarity coefficient (DSC) [or generalized DSC (GDSC) of all labels] and mean surface distance (MSD) between automatic and manual segmentations of the ablation experiments in the unseen datasets, testing for generalizability. For better interpretation, background color of each cell indicates the relative performance compared to the best (darkest red) and worst (darkest blue) performance in each row (the darker red/blue, the closer to the best/worst performance respectively).

		w/o fine-tuning subnet	w/o weighted voting subnet	w/o atlas mask	DLF
Dice similarity coefficient	Brain-7T-T2 dataset
	GDSC	61.3±6.9	61.4±10.5	70.7±3.8	71.2±4.3
	Hippo	81.0±9.2	81.7±13.2	90.8±1.4	90.7±1.5
	CA1	58.8±14.9	65.0±13.4	75.5±3.4	75.5±3.9
	CA2	38.1±24.5	57.0±14.0	67.1±6.4	67.8±6.4
	CA3	49.1±16.5	56.4±15.5	69.3±5.5	69.6±5.6
	DG	67.2±18.4	70.3±15.0	80.9±2.0	80.6±2.6
	SUB	71.9±6.7	67.8±9.7	72.0±5.4	73.4±5.7
	TAIL	73.7±5.6	68.5±13.9	80.5±2.8	80.4±3.3
	ERC	68.8±8.7	61.6±18.8	80.2±5.0	79.5±5.7
	BA35	54.4±10.1	56.3±14.6	65.2±9.5	66.0±9.8
	BA36	57.0±10.3	56.3±15.5	66.2±7.9	67.5±8.7
	PHC	66.6±6.5	69.1±11.3	72.8±9.3	72.4±8.2
	Lumbar-Healthy dataset
	Lumbar	79.9±5.6	78.1±5.9	83.0±4.7	83.4±4.7
Mean surface distance (mm)	Brain-7T-T2 dataset
	Hippo	0.65±0.26	0.70±0.58	0.38±0.06	0.38±0.06
	CA1	0.91±0.38	1.16±1.36	0.63±0.11	0.61±0.09
	CA2	1.73±1.91	0.88±0.87	0.56±0.14	0.54±0.13
	CA3	1.17±0.93	1.05±1.13	0.55±0.11	0.54±0.11
	DG	0.77±0.42	0.97±1.09	0.55±0.07	0.57±0.09
	SUB	0.78±0.23	0.93±0.30	0.84±0.21	0.78±0.16
	TAIL	0.69±0.12	0.94±0.67	0.57±0.09	0.57±0.09
	ERC	0.82±0.20	1.13±0.88	0.61±0.18	0.60±0.19
	BA35	1.10±0.28	1.15±0.68	0.95±0.27	0.94±0.28
	BA36	1.31±0.33	1.38±0.69	1.09±0.21	1.05±0.22
	PHC	0.92±0.28	0.78±0.26	0.83±0.31	0.87±0.32
	Lumbar-Healthy dataset
	Lumbar	2.63±0.46	2.44±0.37	2.16±0.50	2.12±0.50

Abbreviations: DLF = deep label fusion; Hippo = hippocampus; AHippo/PHippo = anterior/posterior hippocampus; CA1–3 = cornu ammonis 1 to 3; dentate gyrus = DG; subiculum = SUB; TAIL = the tail of hippocampus; ERC = entorhinal cortex; BA35/36 = Brodmann areas 35/36; PHC = parahippocampal cortex; w/ and w/o = with and without.

4. Discussion

In this paper, we propose deep label fusion, or DLF, a 3D end-to-end segmentation pipeline that combines multi-atlas segmentation and deep convolutional neural network. Experiments on five diverse datasets demonstrate that, compared to U-Net based and conventional label fusion algorithms, DLF matches the state-of-the-art segmentation accuracy in cross-validation experiments while achieving significantly better generalizability in unseen data that have different image characteristics or comes from a different population.

4.1. DLF takes advantage of the high segmentation accuracy of DCNN-based methods

From the cross-validation experiments in Section 3.1, we can see that DLF outperforms conventional MAS methods by a large margin in segmenting MTL subregions. One potential reason may be because the U-Net architecture, both in the weighted voting subnet and the fine-tuning subnet, provides more flexibility to learn the optimal way in fusing the candidate segmentations. Also, the fact that the main improvements are located in the ERC/BA35/PHC boundaries and the anterior extent of the MTL cortex, highlighted by yellow arrows in Figure 3 indicates that the DCNN-based method is able to learn geometric rules better than conventional MAS methods, which are not aware of global shape.

Compared to the state-of-the-art DCNN-based method, the nnU-Net, DLF achieves comparably high segmentation accuracy when the test and training datasets match. However, it may not be a fully fair comparison as the patch size of DLF is much smaller than that in nnU-Net (Table 1). Bigger patch size, i.e., larger special coverage, allows better awareness of global shape that is crucial in localizing subregion boundaries. Indeed, better localization of the anterior border of the TAIL (white arrows in Figure 3) and posterior extent of PHC in the Brain-3T-T2 dataset, which depends heavily on the location of the uncus that is not adjacent to these boundaries (Berron et al., 2017), can be better captured when using larger patch size. Limited by the fact that DLF requires more GPU memory to train and the limitation of GPU hardware, we are not able to set patch size the same as nnU-Net. Fair comparisons using the same patch size can be done in the future with the advancement of GPU technology. As an alternative, we evaluated the StandU-Net that has the same architecture of fine-tuning subnet and was trained with the same parameters as DLF, including the same patch size, for a fair comparison. The significantly better performance compared to the StandU-Net in all three datasets in Table 1 supports that incorporating MAS improves the performance of pure U-Net based methods.

4.2. DLF achieves better generalizability

Although DLF performs comparably well compared to nnU-Net tested on data with the same characteristics as the training data (cross-validation experiments), it generalizes significantly better to out-of-sample datasets (shown in Table 2). nnU-Net, on the other hand, is potentially overfitted to the training set and thus does a worse job when applied to datasets that have different intensity distributions (Brain-7T-T2) or from a different population (Lumbar-Disease). Surprisingly, its generalizability is even worse than the StandU-Net, which is less engineered compared to nnU-Net, indicating there may be a trade-off between in-sample accuracy and out-of-sample generalizability of the U-Net architecture. Using additional samples with manual segmentations, U-Net or similar DCNN methods can be fine-tuned to a specific dataset using few-shot learning (Snell et al., 2017). However, DLF maintains the good performance in unseen data without this additional step, which is desirable and may enable broader utility and impact. Nonetheless, if necessary, the few-shot learning strategy can also be incorporated with DLF to further improve generalizability, which will be interesting to explore in future studies.

The registration and weighted voting subnet, the two additional steps of DLF compared to StandU-Net (the fine-tuning subnet is the same as StandU-Net), could be the key to the “out-of-box” generalizability of DLF. These two components may serve as preprocessing steps to generate initial label probabilities maps that are more robust to the change of data characteristics potentially due to two reasons. First, the general-purpose registration is not trained on specific data distribution to align the atlases to the target. Second, with the per-image random histogram augmentation, the weighted voting subnet is trained to be sensitive to atlas-target structural similarity rather than the appearance of the target image. It would be interesting to investigate in future studies whether the generalizability can be maintained if the conventional registration component in MAS is replaced by a learning-based deformable registration method (Balakrishnan et al., 2019). Interestingly, despite the importance of the two sub-networks, using them in isolation is not enough to achieve good generalizability as shown in Table 5. The ablation experiments indicate that all the components of the DLF network are crucial to the better generalizability performance.

4.3. Modality augmentation improves robustness to missing data and interpretability to the contribution of each individual modality

The ModAug strategy improves the segmentation accuracy when one of the modalities is not available (either T1w MRI or T2w MRI) compared to that predicted by models trained without ModAug, indicating the models based its prediction on every single modality as much as possible rather than relying on some/all of them. Interestingly, this improvement is large for StandU-Net, which shows the importance of handling correlated features in the training. On the other hand, the improvement in missing data scenarios is consistent but a lot smaller when it comes to DLF, indicating DLF is more efficient in integrating information from multiple MRI modalities.

In addition to boosting the performance of StandU-Net when we have incomplete data, ModAug also improves the accuracy (in Brain-3T-T2 and in Brain-3T-T1 datasets) and generalizability (better performance in Brain-7T-T2) of StandU-Net when both modalities are available, probably due to more efficient learning multimodal information. However, DLF trained with ModAug performs almost the same with a slight decrease in accuracy when complete data is available in test time. The reason could be that DLF is already efficient in handling multimodal information and the simple ModAug strategy proposed in this study is not sufficient to further improve this performance. This may leave opportunity for improvement with more tailored designed algorithms to further make full use the multimodal data, such as meta-learning (Khandelwal and Yushkevich, 2020) and privileged knowledge distill (Chen et al., 2021) strategies.

ModAug also helps improve the interpretability of the relative contribution of individual modalities to the task of interests. For example, if we compare the StandU-Net results with only T2w MRI (primary modality missing, GDSC=6.1), only T1w MRI (secondary modality missing, GDSC=75.2) and both T1w and T2w MRIs (both modalities are present, GDSC=79.5) in Brain-3T-T2, one may conclude that T1w and T2w MRI can only contribute 7.7% and 94.6% respectively to the segmentation. However, this is not accurate as can be seen in results trained with ModAug, T1w and T2w MRI can contribute up to 95.4% and 99.5% respectively. When trained without ModAug, the interpretation may be greatly influenced by initialization, training parameters and so on, resulting in uncertainty of interpretation. On the other hand, the design of the ModAug strategy forces the model to maximize information extracted from individual modalities, yielding more accurate and certain interpretations.

An important limitation of the ModAug analysis is that the performance with single modality reported in Table 3 only represents the situation where the other modality is missing in the model prediction stage of DLF. However, both modalities are used in the registration phase. Therefore, the DLF results with single modality should not be interpreted as the other modality being completely unavailable. Future work will investigate the performance of the proposed method when single modality is used in both registration and label fusion.

4.4. Limitations

The proposed DLF technique has limitations. First, as in all MAS methods, registration quality greatly impacts the segmentation results with DLF. Therefore, DLF is not applicable to problems in which reasonable correspondence cannot be reliably established using deformable registration. The oracle experiment (Section 2.3.3) provides a good measure of whether DLF/MAS is suitable for a specific application. Second, processing time needed to train and test the DLF model is longer than standard U-Net or similar methods because it requires additional registration, patch sampling with atlases, and has a more complicated model. The registration speed can, in principle, be increased by incorporating learning-based registration methods, such as VoxelMorph (Balakrishnan et al., 2019) into the DLF model. However, it is possible that this approach would lower generalizability. Third, although DLF improves the segmentation accuracy in terms of DSC/GDSC and MSD, the clinical significance, such as whether the improvement results in better clinical disease diagnosis and so on, is not tested in this work. Future studies applying DLF to various applications to evaluate its clinical utility are necessary.

5. Conclusions

Deep Label Fusion (DLF) is a medical image segmentation approach that combines the strengths of deformable image registration, multi-atlas label fusion, and deep-learning based segmentation using the U-Net architecture. Across multiple challenging segmentation problems, DLF matches the segmentation accuracy of the state-of-the-art nnU-Net algorithm when the characteristics of training and test datasets are similar. However, achieves significantly better generalizability than nnU-Net and multiple other algorithms in datasets that have different characteristics from the training data. In addition, we demonstrate that a modality augmentation strategy applied during model training can improve the performance of DL-based methods, including DLF, in incomplete test data scenarios and boost the interpretability of the relative contributions of individual modalities. Future work will focus on increasing the speed of DLF by replacing conventional deformable registration with learning-based ones, further evaluating DLF in a greater variety of datasets to identify its strengths and limitations, more in-depth investigation on understanding the better generalization by looking at the learnt features in latent space and applying DLF to clinical populations to demonstrate its clinical significance. We hope that this publicly available software (github.com/LongXie/DeepLabelFusion) will serve the scientific community in advancing research of generalizability of learning-based methods.

Highlights.

• Deep label fusion is the first 3D end-to-end hybrid multi-atlas and deep learning method

• Similar accuracy to state-of-the-art nnU-Net in single-dataset cross-validation experiments

• Significantly improved generalizability on unseen datasets with different characteristics

• Novel augmentation strategy to account for missing data in multimodality applications

1. Abbreviations.

DCNN

deep convolutional neural networks

MAS

multi-atlas segmentation

DLF

deep label fusion

CT

computational tomography

MV

majority voting

SVWV

spatially varying weighted voting

JLF

joint label fusion

CL

corrective learning

Hippo

hippocampus

AHippo/PHippo

anterior/posterior hippocampus

CA1–3

cornu ammonis 1 to 3

DG

dentate gyrus

SUB

subiculum

TAIL

the tail of hippocampus

ERC

entorhinal cortex

BA35/36

Brodmann areas 35/36

PHC

parahippocampal cortex

ModAug

modality augmentation

w/ and w/o

with and without

MTL

medial temporal lobe

CS

collateral sulcus

OTS

occipitotemporal sulcus

MISC

miscellaneous label

UPENN

University of Pennsylvania

MPRAGE

Magnetization Prepared RApid Gradient Echo

TSE

turble spine echo

T1w

T1-weighted

T2w

T2-weighted

DSC

Dice similarity coefficient

GDSC

generalized Dice similarity coefficient