Using Global t-SNE to Preserve Intercluster Data Structure

Abstract

The t-distributed stochastic neighbor embedding (t-SNE) method is one of the leading techniques for data visualization and clustering. This method finds lower-dimensional embedding of data points while minimizing distortions in distances between neighboring data points. By construction, t-SNE discards information about large-scale structure of the data. We show that adding a global cost function to the t-SNE cost function makes it possible to cluster the data while preserving global intercluster data structure. We test the new global t-SNE (g-SNE) method on one synthetic and two real data sets on flower shapes and human brain cells. We find that significant and meaningful global structure exists in both the plant and human brain data sets. In all cases, g-SNE outperforms t-SNE and UMAP in preserving the global structure. Topological analysis of the clustering result makes it possible to find an appropriate trade-off of data distribution across scales. We find differences in how data are distributed across scales between the two subjects that were part of the human brain data set. Thus, by striving to produce both accurate clustering and positioning between clusters, the g-SNE method can identify new aspects of data organization across scales.

1. Introduction

Dimensionality-reduction techniques have been playing essential roles for analyzing modern high-dimensional data sets. High-dimensional data, which are usually represented by high-dimensional vectors or matrices of pairwise distances, can be embedded into lower-dimensional spaces by preserving pairwise distances of embedded points as much as possible. Low-dimensional embeddings (e.g., in two or three dimensions) not only provide a way to visualize data organization but also reveal its hidden structure. t-distributed stochastic neighbor embedding (t-SNE) is a powerful nonlinear embedding technique that has been widely applied in many areas of science, from visualizing feature representations in deep learning (Mnih et al., 2015), to clustering bone marrow samples to distinguish between cancerous and healthy cells (Amir et al., 2013) and classifying neuron cells by gene expression profiles in biology (Mahfouz et al., 2015). As a neighbor embedding algorithm, t-SNE finds embedding that attempts to preserve similarity distances between points, before and after embedding, but the similarity function is strongly biased toward preserving local distances and is not sensitive to changes in distances between points with large separation in the original space (Maaten & Hinton, 2008). The neighbor embedding property makes t-SNE effective for identifying local clusters in the data, but as a result, it fails to preserve the global intercluster structure: the embedding distances among clusters have no meaning, and the global distribution of clusters is random (Wattenberg, Viégas, & Johnson, 2016). Yet the global structure of local clusters can provide significant insight into many biological systems. For example, ordering of cell clusters at different stages was found to represent a developmental trajectory (Macaulay et al., 2016) and to yield insights into cell lineages in the vertebrate brain (Raj et al., 2018). For these tasks, it is essential to preserve intercluster organization of the data at multiple scales.

Recently many algorithms have been proposed to preserve the global structure of data (Wu, Tamayo, & Zhang, 2018; Ding, Condon, & Shah, 2018; Becht et al., 2019; McInnes, Healy, & Melville, 2018; Kobak & Berens, 2018), UMAP (Becht et al., 2019) is one of the leading algorithms that can better preserve global structure than t-SNE and runs faster than algorithms for very large data set. However, the global structure preservation is not the primary goal of UMAP, as stated in McInnes et al. (2018), and further analysis shows that the global structure preservation of UMAP may not be superior to optimazed t-SNE in many other data sets (Kobak & Berens, 2018). In addition, UMAP requires large sample sizes to find manifold structure in noisy data (McInnes et al., 2018), which makes it inappropriate for small data sets. For these reasons, t-SNE and its variants are still of great interest in doing dimensionality reduction, and much effort has recently been made to overcome the weaknesses of t-SNE on running speed (Pezzotti, Höllt, Lelieveldt, Eisemann, & Vilanova, 2016; Linderman, Rachh, Hoskins, Steinerberger, & Kluger, 2019), parameter tuning (De Bodt, Mulders, Verleysen, & Lee, 2018; Belkina et al., 2018), and global structure preservation (Kobak & Berens, 2018), which makes t-SNE more applicable to large, complex biological data sets. In all these efforts, the way to calculate attractive force and repulsive force was optimized, but the form of these forces was not changed. We notice that the key reason for a lack of global structure in t-SNE is that the repulsive force in the cost function is not sensitive to large distances.

Here we propose the global t-SNE (g-SNE) algorithm based on traditional t-SNE to preserve the global structure of clusters in data. The algorithm preserves the global structure by introducing a global cost function in which the repulsive force is dominated by large distances and optimize a new cost function that is the weighted sum of global cost function and the original one. We test the algorithm on a synthetic data set and two real data sets, and demonstrate its ability to preserve both local and global organization of the data, yielding new biological insights.

2. Global t-SNE (g-SNE)

Let us consider a data set containing N data points described by D-dimensional vectors: $\left\{{\mathbf{x}}_1,{\mathbf{x}}_2,{\mathbf{x}}_3,\dots ,{\mathbf{x}}_N;{\mathbf{x}}_i\in {ℝ}^D\right\}$. The t-SNE algorithm (Maaten & Hinton, 2008) describes the similarities of two points according to the following measure:

$$p_{j\mid i}=\frac{\exp \left(-{\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert }^2/2{\sigma }_i^2\right)}{{\sum }_{k\ne i}\exp \left(-{\Vert {\mathbf{x}}_i-{\mathbf{x}}_k\Vert }^2/2{\sigma }_i^2\right)},$$ (2.1)

$$p_{ij}=\frac{p_{j\mid i}+p_{i\mid j}}{2n}.$$ (2.2)

To avoid the crowding problem in low-dimensional embedding, the heavy tailed Student t-distribution is applied within the embedding d-dimensional space where distances between points $\{{\mathbf{y}}_1,{\mathbf{y}}_2,{\mathbf{y}}_3,\dots ,{\mathbf{y}}_N;{\mathbf{y}}_i\in {ℝ}^d\}$ are defined as

$$q_{ij}=\frac{{\left(1+{\Vert {\mathbf{y}}_i-{\mathbf{y}}_j\Vert }^2\right)}^{-1}}{{\sum }_{m\ne n}{\left(1+{\Vert {\mathbf{y}}_m-{\mathbf{y}}_n\Vert }^2\right)}^{-1}}.$$ (2.3)

The Kullback-Leibler (KL) divergence between the joint probability distributions of pairwise data points $p_{ij}$ and embedding points $q_{ij}$ measures the distance discrepancies between the data and embedding points:

$$L=D_{KL}(P\parallel Q)=\sum _i\sum _j{p}_{ij}\log \left(\frac{p_{ij}}{q_{ij}}\right).$$ (2.4)

The t-SNE minimizes the KL divergence by gradient descent method. The gradient of the cost function L with respect to embedding coordinate y_i is (see section 6):

$$\frac{\partial L}{\partial {\mathbf{y}}_i}=4\sum _j\left(p_{ij}-q_{ij}\right)\left({\mathbf{y}}_i-{\mathbf{y}}_j\right){\left(1+{\Vert {\mathbf{y}}_i-{\mathbf{y}}_j\Vert }^2\right)}^{-1}.$$ (2.5)

The probability distributions of distances $p_{ij}$ and $q_{ij}$ in equations 2.2 and 2.3 are symmetric distributions that peak at 0 and decay exponentially or polynomially as the distances increase. As such, these distributions are sensitive to small pairwise distances among neighboring points but not to large distances between distant points. Minimizing the differences of probability distributions of data and embedding points can effectively capture and preserve the local structure of data and generate well-separated clusters in the embedding space. However, it fails to capture the large distances of intercluster points, so both the relative and absolute positions of the clusters are not preserved and as a result are embedded randomly (Wattenberg et al., 2016). To capture and preserve the global structure of the points and clusters, we propose the g-SNE algorithm that takes into account a new set of probability distributions for distance measures ${\widehat{p}}_{ij}$ and ${\widehat{q}}_{ij}$, which are primarily sensitive to large values:

$$\begin{gathered} {\widehat{p}}_{ij}=\frac{1+{\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert }^2}{{\sum }_{m\ne n}\left(1+{\Vert {\mathbf{x}}_m-{\mathbf{x}}_n\Vert }^2\right)}, \\ {\widehat{q}}_{ij}=\frac{1+{\Vert {\mathbf{y}}_i-{\mathbf{y}}_j\Vert }^2}{{\sum }_{m\ne n}\left(1+{\Vert {\mathbf{y}}_m-{\mathbf{y}}_n\Vert }^2\right)}. \end{gathered}$$ (2.6)

The global probability distributions ${\widehat{p}}_{ij}$ and ${\widehat{q}}_{ij}$ are also symmetric but peak at large values. Just as in equation 2.4, we can also define the global cost function $\widehat{L}$ in g-SNE:

$$\widehat{L}=D_{KL}(\widehat{P}\parallel \widehat{Q})=\sum _i\sum _j{\widehat{p}}_{ij}\log \left(\frac{{\widehat{p}}_{ij}}{{\widehat{q}}_{ij}}\right).$$ (2.7)

Minimizing the global cost $\widehat{L}$ preserves the large distances in the low-dimensional embedding. To account for both the local and global structure of the data, we define a total cost function $L_{total}$ by combining the two cost functions using a weight parameter λ:

$$L_{\mathit{\text{total}}}=L+\lambda \widehat{L}.$$ (2.8)

The gradient of the total cost function $L_{total}$ in g-SNE has a simple form:

$$\frac{\partial L_{total}}{\partial {\mathbf{y}}_i}=4\sum _j\left[\left(p_{ij}-q_{ij}\right)-\lambda \left({\widehat{p}}_{ij}-{\widehat{q}}_{ij}\right)\right]\cdot \left({\mathbf{y}}_i-{\mathbf{y}}_j\right){\left(1+{\Vert {\mathbf{y}}_i-{\mathbf{y}}_j\Vert }^2\right)}^{-1},$$ (2.9)

where the weight λ of the global cost function controls the balance between the local clustering and global distribution of the data. Large λ values lead to more robust global distributions of clusters but less clear classifications. Small λ moves back to approximate the traditional t-SNE, and will be exactly the same when λ = 0. In the next section, we apply the g-SNE algorithm to one synthetic data set and two real data sets to test its ability to preserve the local and global structures of data and compare the results with t-SNE.

3. Synthetic Data

Traditional t-SNE is powerful in generating local clustering, and it performs best in tasks where one only needs to define clusters, for example, to separate features in deep learning (Mnih et al., 2015). However, the t-SNE method does not pay attention to organization between clusters. To evaluate our new algorithm, we select the data sets that have significant structure across multiple scales.

We generate six groups of points in two-dimension planes, each group containing 50 clustered points; the six groups are hierarchically distributed in the plane (see the first column in Figure 1). First, we apply the two-dimensional multidimensional scaling (MDS; Kruskal, 1964) method to this data set, obtaining good reconstructions for the data structure (see the second column). The t-SNE generates six tightly clustered groups, but the distribution of the six clusters is random across three repeats and in consistent with the data structure (see the third column). Applying g-SNE with λ = 1 to the data yields six well-separated clusters (see the fourth column). When further increasing λ = 1 to 10, the global structure even better approximates the data (see the fifth column), with the point clouds becoming more scattered. This shows how the change of λ affects the balance of local and global structures of data. In both cases, the positioning of clusters in the g-SNE map is consistent across repeats and shows good correspondence to the original data. This test on synthetic data shows the ability of g-SNE to preserve the global structure of data.

Figure 1:

Clustering for synthetic data using MDS, t-SNE, and g-SNE with three repeats. Three rows represent three repeats of mapping. First column: Synthetic two-dimensional data containing six groups of points labeled by different colors, with 50 points in each group. Second column: MDS maps of data. Third column: t-SNE maps. Fourth column: g-SNE maps with λ = 1. Fifth column: g-SNE maps with λ = 10.

4. Biological Data

4.1. Iris Flower Data Set.

Next we apply the g-SNE algorithm to a low-dimensional real biological data set: the four-dimensional Iris flower data (Fisher, 1936). This data set has been widely used in many statistical classification algorithms as a test example. It consists of 50 samples in each of the three Iris species: setosa, virginica, and versicolor. Each sample is described by four features: the length and width of the sepals and petals measured in centimeters. We embed the four-dimensional Iris data set to two-dimensional space using MDS, t-SNE, and g-SNE (see Figure 2). The 2D MDS mapping preserves the intercluster structure of the Iris data well across three repeats (Dhillon, Modha, & Spangler, 1998) (first colunm). The three species form three clusters: the versicolor cluster (green) and virginica cluster (blue) are close to each other and far from setosa (red), but versicolor is closer to setosa than virginica. The t-SNE mapping shows the three clusters, but the intercluster distances are not preserved: the setosa cluster is too far from the other two clusters compared with the MDS mapping, and the versicolor is farther from setosa than virginica in repeat 3 (see the second column). The g-SNE with λ = 1 generates very similar intercluster structure as the MDS in all three repeats, only with different rotations of the maps (see the third column). However, g-SNE provides better cluster separation than the MDS, which reduces the noise in the data. When further increasing λ = 1 to 10, the global structure does not change much, but the points within each cluster become more scattered, showing the reduced clustering effects (see the fourth column). Therefore, the g-SNE combines both the advantages of the t-SNE in cluster separation and the ability of MDS to preserve the intercluster structure, and it performs better than any one of them with a proper λ.

Figure 2:

Clustering for Iris flower data set using MDS, t-SNE, and g-SNE with three repeats. Three rows represent three repeats of mapping. First column: MDS maps of data. Second column: t-SNE maps. Third column: g-SNE maps with λ = 1. Fourth column: g-SNE maps with λ = 10.

4.2. Human Brain Atlas Data.

We next study much more complex and high-dimensional data: the human brain transcriptome atlas (Hawrylycz et al., 2012). This data set contains microarray profiling of around 900 anatomical regions in the human brain from two donors, H0351.2001 and H0351.2002, and each sample region was profiled by 58,692 probes representing 29,191 genes. The data were already normalized using the methods in Atlas (2013) and was available in Allen Institute for Brain Science (2014). For the complex brain atlas data, MDS fails to give a good local clustering as in synthetic data or the simple Iris data. We perform MDS embeddings on the two brain data sets, and only three or four clusters can be identified from the embeddings (see Figure 1S). We quantify the local structure preservation by calculating the optimal number of clusters and Silhouette scores of the clusters (see section 6), finding that MDS gives only four clusters with very low silhouette scores (see Table S1). A nonlinear dimensionality-reduction method such as t-SNE usually performs better clustering than MDS on complex biological data. Mahfouz et al. (2015) applied BH-SNT (a fast t-SNE) to the human brain atlas data set to reduce the dimensionality of gene expression space and visualize the organization of region samples in the brain. Here, we first apply the t-SNE method to the brain atlas data to reproduce the results in Mahfouz et al. (2015). We then apply g-SNE to the same data to generate new mappings and use recent topological methods (Giusti, Pastalkova, Curto, & Itskov, 2015; Zhou, Smith, & Sharpee, 2018) to quantitatively evaluate how well both methods preserve the global structure of the data.

We apply both t-SNE and g-SNE to the gene expression profiles of brain region samples in donor H0351.2002 and plot the 2D maps of the samples with three repeats (see the first row in Figure 3A); the samples are colored by their anatomical acronyms from the Allen Reference Atlas (Allen Institute for Brain Science, 2014). We identify the 15 acronyms used in Mahfouz et al. (2015) and label other acronyms as “Other” for comparison purposes. In total, we work with 16 clusters. To view the global structure more clearly, we calculate the mean positions of samples in each cluster (with the same acronyms) as the centroid of the cluster and plot the 16 centroids with the same colors (see the second row in Figure 3A). The first repeat of the t-SNE map resembles the result shown in Mahfouz et al. (2015). However, the other two differ a lot in the global distribution of clusters (see Figure 3A). The reason is that t-SNE performs weakly in preserving large distances in data. The g-SNE with λ = 1 shows different maps of the data, and the global structures of embedding clusters are more consistent across three repeats than the t-SNE maps (see Figure 3B). g-SNE also preserves the local structure well, and it generates 11 to 16 clusters (a total of 16 clusters in data) with much higher Silhouette scores than MDS (see Table S1). We also perform UMAP embedding to the data. The global patterns in UMAP are not very consistent; for example, the relative position of GP and Cb varies across the three repeats (see Figure S2). In addition, the clusters in UMAP are not separated as well as in g-SNE (see Figure S2 versus Figure 3B). The quantitative analysis shows that UMAP embedding generates a very small number of clusters (two to three clusters; see Table S1). The evidence shows that g-SNE preserves better local structures than MDS and UMAP and preserves better global structure than t-SNE and UMAP.

Figure 3:

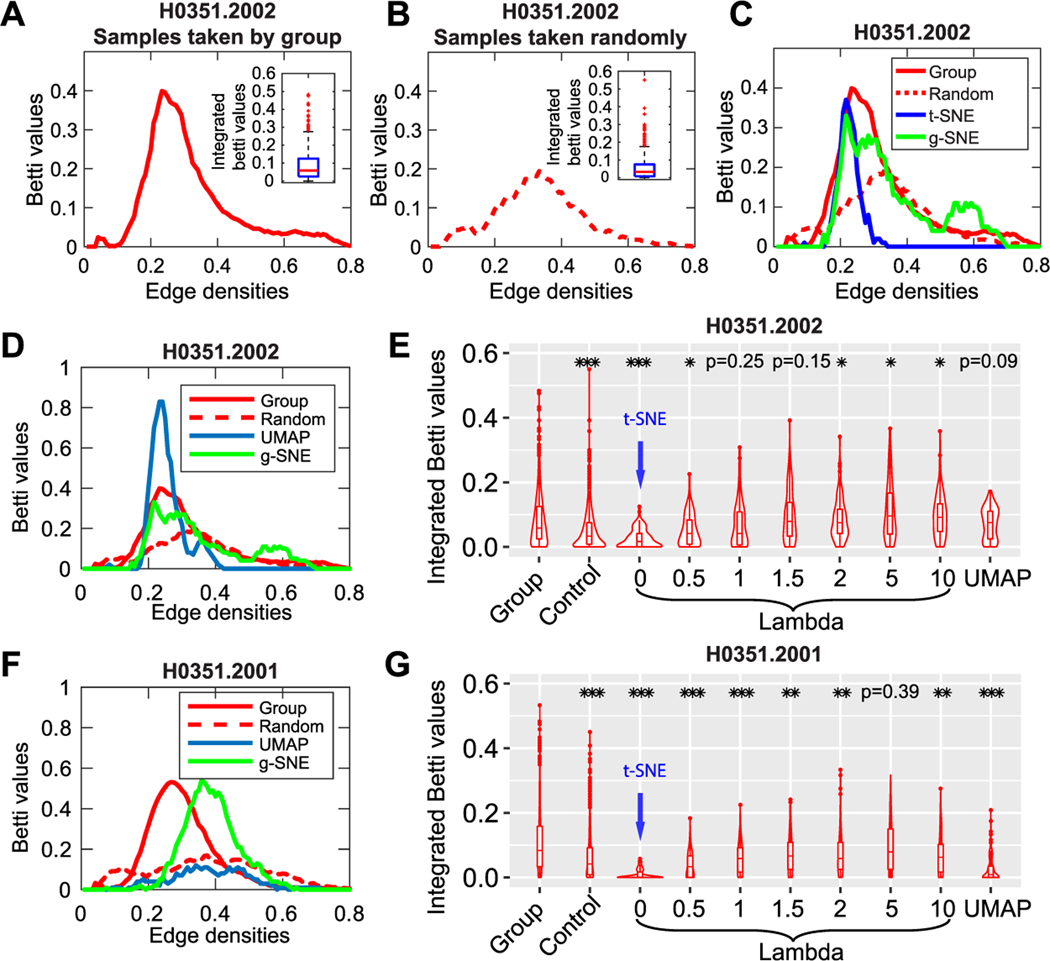
Two-dimensional embedding of gene expression profiles of donor H00351.2002 using t-SNE and g-SNE with three repeats. The brain region samples are labeled and colored by their anatomical acronyms from the Allen Reference Atlas: frontal lobe (FL), parietal lobe (PL), temporal lobe (TL), occipital lobe (OL), hippocampal formation (HiF), striatum (Str), globus pallidus (Gp), amygdala (Amg), thalamus (TH), hypothalamus (Hy), mesencephalon (MES), pons, myelencephalon (MY), cerebellum (Cb), white matter (WM) and Others. (A) Three repeats of t-SNE maps (first row) and the centroid positions of samples with the same labels (second row). (B) Three repeats of g-SNE maps with λ = 1 (first row) and centroids of the 16 anatomical groups in the maps (second row). (C) The schematic of network topology changing with the edge densities. New edges are added to the network as we decrease the connection threshold of points. The edge density ρ increases from 0.33 to 0.53, and the one-dimensional hole appears at ρ = 0.40, persists at ρ = 0.47, and vanishes at ρ = 0.53. Plotting the number of one-dimensional holes (first Betti values) against the edge densities yields the Betti curves in panels D and E. (D) Average Betti curve of the 16 centroids in 100 repeats of t-SNE maps. Insets: Box plot of integrated Betti values of the 100 repeats. (E) Average Betti curve of the 16 centroids in 100 repeats of g-SNE maps. Insets: Box plot of integrated Betti values of the 100 repeats.

Next we apply two quantitative approaches to evaluate the global structure preservation of the t-SNE, g-SNE, and UMAP algorithms. The first approach is a topological technique proposed in Giusti et al. (2015). According to this method, each pairwise distance matrix of a set of points can be quantified by the characteristic Betti curve. The Betti curves are based on computing Betti values, which represent the number of cycles of different dimensions with the set of connected points. The zeroth Betti value measures the number of connected components, whereas the first Betti value yields the number of one-dimensional “circular” holes. Points in the data set are deemed “connected” if the distance between them is less than a certain threshold. Varying this threshold changes the number of connected data points and also affects the Betti value (see Figure 3C). The Betti curve describes how the Betti value changes as a fraction of the connected points increases. Giusti et al. (2015) reported that the integral of the Betti curve, termed the integrated Betti value, was sensitive to the presence of geometrical organization in the data set, and in particular could distinguish geometrically generated data from random data sets. For the tasks at hand, we find that working with just the first integrated Betti value is sufficient to evaluate the data set structure.

To use the topological method, we generate the average Betti curves of the 16 cluster centroids from 100 t-SNE maps repeats and make the box plots of the integrated Betti values of the 100 maps (see Figure 3D). We make the same plots for 100 g-SNE maps in Figure 3E. As expected, the Betti curves of the t-SNE and g-SNE maps have different shapes, and the integrated Betti values distribution of the g-SNE maps is significantly different from the t-SNE maps (p < 0.001 in the two-sample Kolmogorov-Smirnov test). Thus, the t-SNE and g-SNE methods produce different representations of the data at the global scales.

To evaluate which of these results better reflects the organization of the original data at the global scale, we apply topological methods to the original data. We cannot directly use the mean values of gene expression of samples within each cluster to represent the 16 clusters of data. One reason is that it will smooth out gene expression patterns, and another is that it produces only one set of points and one Betti curve, which cannot be used to make statistical comparison with the results of 2D maps. To make full use of the data and generate a large number of intercluster representatives of Betti curves, we randomly select 16 anatomical samples from the 16 acronym groups and then repeatedly sample different representatives from the 16 groups 1000 times (see Figure 4A). As a control, we randomly take 16 samples from the whole brain but not based on acronym groups (see Figure 4B). After taking the samples, we can define pairwise distance matrix by the Euclidean distance of gene expression vectors and then plot the Betti curves. We show the averaged Betti curves and integrated Betti value distributions of samples taken by acronym groups (see Figure 4A) and taken randomly across the whole brain (see Figure 4B). The difference of the two integrated Betti value distributions is significant (see Figure 4E, p < 0.001 in the two-sample Kolmogorov-Smirnov test). This shows that the data set has a significant intercluster global structure. Integrating the Betti curves of data and 2D maps together shows that the Betti curves of the g-SNE map better fits the data than the t-SNE and UMAP (see Figures 4C, 4D, and 4F). The integrated Betti value distributions of data can be fitted by g-SNE with λ = 1 (p = 0.25; see Figure 4E) but not by t-SNE (p < 0.001; see Figure 4E).

Figure 4:

Betti curves of gene expression profiles of the human brain atlas and evaluation of 2D embedding maps. (A) Average Betti curves of 1000 pairwise distance matrices. Each matrix is generated from 16 anatomical region samples where each sample is randomly taken from one of the 16 acronym groups. (B) Average Betti curves of 1000 pairwise distance matrices. Each matrix is generated from 16 samples randomly taken from all the anatomical samples in the brain. The pairwise distances of samples are defined as Euclidean distances of gene expression vectors. The insets show the box plots of 1000 integrated Betti values of the Betti curves. (C) Integration of Betti curves of samples randomly taken based on acronym groups (red solid lines, “Group”), Betti curves of samples randomly taken from whole brain (red dashed line, “Random”), Betti curves of cluster centroids of t-SNE maps (blue line), and Betti curves of cluster centroids of g-SNE maps with λ = 1 (green lines). (D) The blue line indicates the result of UMAP embedding with optimal parameters instead of t-SNE. (E) Box plots of integrated Betti values of data, g-SNE with different λ, and UMAP with optimal parameters. λ = 0 is equivalent to t-SNE. The brain donor in panels A to E is H0351.2002. (F, G) The Betti curves and violin plots of integrated Betti values of data and models for donor H0351.2001. The stars in panels E and G represent the significance levels of a two-sample Kolmogorov-Smirnov test on integrated Betti value distributions of the first column (“Group”) with the rest ones: *p < 0.05, **p < 0.01, and ***p < 0.001.

For another donor H0351.2001, g-SNE with λ = 5 fits the data (p = 0.39) while neither t-SNE nor UMAP can do so (p < 0.001; see Figure 4G). Thus, g-SNE better preserves the global structure in the brain atlas data than both t-SNE and UMAP. By screening the weight parameter λ in g-SNE, we notice that there exists an optimal λ for each donor; too small or too large λ cannot fit the data (see Figures 4E and 4G). The reason may be that too small λ recovers t-SNE and cannot account for large distance distributions, while too large λ performs poorly in local clustering, which weakens the intercluster structure. We also notice that the optimal λ differs across donors, which means that optimal λ may serve as an indicator of brain states.

The second approach to evaluating the goodness of embedding is the Shepard diagram (Shepard, 1980), a plot of embedding pairwise distances against data distances. For both brain donors, g-SNE gives higher correlation coefficients for distance plots than t-SNE and UMAP (see Figure 5, R = 0.76 for H0351.2002, R = 0.77 for H0351:2001), and approximates the distance preservation in MDS (R = 0.78) in donor H0351.2002. The low correlations in the t-SNE and UMAP embeddings result from the plateaus in large distances, which indicates that the global structures of data are not well preserved. However, the g-SNE embedding gives linear relationships in all distance scales, which indicates good preservation of global structures.

Figure 5:

Quantitative evaluation of embeddings of different models. (A) The embedding distances of t-SNE, UAMP, g-SNE, and MDS are plotted against the data distances that are grouped by 50 bins. The lines in the middle and the shadows represent the median and 95% interval of the values in the bins. R is the Pearson correlation coefficient of the distances plots. The data are from brain donor H0351.2002. (B) Shepard diagram of data from brain donor H0351.2001. The optimal parameters are used in both g-SNE and UAMP for both data sets.

5. Discussion

We introduced the g-SNE algorithm by redefining the t-SNE cost function as the weighted sum of the local cost function for local classification and the global cost function for intercluster organization. With this combined cost function, the g-SNE was able to preserve the global structure of data as well as perform good local clustering. By applying the two quantitative evaluations of the Betti curves method and Shepard diagram, we show that g-SNE with optimal λ outperforms both t-SNE and UMAP in the two brain data sets.

The weight parameter λ in g-SNE balances the local and global distances preservation. The difference of optimal λ on different brain donors indicates that optimal λ is case dependent. How the optimal λ is related to the intrinsic structure of data would be an interesting problem to study in the future. In particular, it may serve as a global parameters describing different data sets with a similar data structure, for example, characterizing the human transcriptome differences across tissues and individuals (Melé et al., 2015).

In this work, we also introduced a quantitative and principled way to evaluate how unsupervised clustering methods preserve data structure across scales. The latent structure of the high-dimensional data is usually unknown, and the evaluation of low-dimensional mapping of data has always been qualitative (i.e., focusing more on separation of clusters and less on the relative positions of these clusters). The previous methods are ill suited for describing multiscale data. Here we propose a quantitative method based on Betti curves to compare the topological structure of cluster organization in low-dimensional mapping and the structure of data. In the analysis of the human brain atlas data set, the t-SNE and our algorithm generate similar local clusters with similar levels of separations (see Figures 3A and 3B). However, the global organization of the local clusters was significantly different, as revealed by the topological analyses (compare the Betti curves in Figures 3D and 3E). Unlike the t-SNE results, the proposed algorithm preserves the global topological structure of the data (see Figure 4). We show that in Figure 4C, this structure is completely missed by the regular t-SNE method.

We showed the success of g-SNE on two small data sets (N < 1000) but did not test it on very large ones; the main reason is that the current version of g-SNE was based on the original t-SNE algorithm in Maaten and Hinton (2008) without any optimization. Theoretically g-SNE has the same level of computational complexity as the original t-SNE because the information needed to calculate the global cost function is the same as in the local term; the state-of-the-art acceleration methods are based on the original cost function in t-SNE and optimize nearest neighbor searching without considering the distant points; how to integrate the acceleration methods into our g-SNE is a future direction.

6. Methods

6.1. Evaluation of Local Structure Preservation.

We evaluate the local structure preservation using two approaches: calculating the optimal number of clusters and the Silhouette scores. The optimal number of clusters describes the unsupervised clustering effects of the embedding, and the Silhouette scores measure the consistency of the clustering with the cluster labels. Together they can give reliable measurements for the quality of clustering algorithms. We use Matlab’s built-in function evalclusters to calculate the optimal number of clusters, in which we use k-means clustering and silhouette criterion and set the KList to be 1 to 16 (because the data have 16 groups). The optimal number of clusters may be different in different repeats for some inputs, so we listed a range of values for g-SNE inputs in Table S1. We use Matlab’s built-in function silhouette to calculate Silhouette scores with a Euclidean metric.

6.2. Parameters of the Algorithms.

The parameters in t-SNE are set as perplexity = 30 and exaggeration = 4. The parameters in UMAP are set as neighbors values= 50 and min dist values = 0.8. We run the t-SNE and MDS algorithms using Matlab’s R2017a.