Abstract
Objective
To compare the original synthetic control (OSC) method with alternative approaches (Generalized [GSC], Micro [MSC], and Bayesian [BSC] synthetic control methods) and re‐evaluate the impact of a significant restructuring of urgent and emergency care in Northeast England, which included the opening of the UK's first purpose‐built specialist emergency care hospital.
Data Sources
Simulations and data from Secondary Uses Service data, a single comprehensive repository for patient‐level health care data in England.
Study Design
Hospital use of individuals exposed and unexposed to the restructuring is compared. We estimate the impact using OSC, MSC, BSC, and GSC applied at the general practice level. We contrast the estimation methods' performance in a Monte Carlo simulation study.
Data Collection/Extraction Methods
Hospital activity data from Secondary Uses Service for patients aged over 18 years registered at a general practice in England from April 2011 to March 2019.
Principal Findings
None of the methods dominated all simulation scenarios. GSC was generally preferred. In contrast to an earlier evaluation that used OSC, GSC reported a smaller impact of the opening of the hospital on Accident and Emergency (A&E) department (also known as emergency department or casualty) visits and no evidence for any impact on the proportion of A&E patients seen within 4 h.
Conclusions
The simulation study highlights cases where the considered methods may lead to biased estimates in health policy evaluations. GSC was found to be the most reliable method of those considered. Considering more disaggregated data over a longer time span and applying GSC indicates that the specialist emergency care hospitals in Northumbria had less impact on A&E visits and waiting times than suggested by the original evaluation which applied OSC to more aggregated data.
Keywords: causal inference, difference‐in‐differences, new care models, observational data, policy evaluation, synthetic control
What is known on this topic
The redesign of urgent and emergency care in Northumberland, UK, increased Accident and Emergency (A&E) visits (13.6%) and reduced the proportion of patients seen within 4 h of attending A&E (6.7%).
A wide range of quasi‐experimental methods for longitudinal settings has been proposed in the literature.
Existing simulation studies have not compared methods head‐to‐head in contexts with features commonly faced in health economics and policy evaluations.
What this study adds
Our re‐evaluation finds a smaller increase in A&E visits and little evidence of an impact on the proportion of A&E patients seen within 4 h.
Our simulation demonstrates the vulnerability of the Generalized synthetic control method to serial correlation, the Micro synthetic control method to unobserved confounders that differ by the outcome, and the Bayesian synthetic control method to “non‐high frequency” settings.
1. INTRODUCTION
The increasing availability of administrative and other forms of non‐experimental data provides the opportunity for rigorous evaluations of health care interventions. In such studies, the aim is to investigate the impact of an intervention, event, or treatment on affected individuals or populations. A key threat to the validity of such evaluations is unobserved confounding when variation in outcomes between treated and control groups is driven by differences in unmeasured, or unmeasurable factors.
Difference‐in‐Differences (DID) methods are often used in these settings to control for unobserved confounding. 1 , 2 , 3 , 4 , 5 , 6 DID contrasts the changes in outcomes over time between treated and control groups assuming that in the absence of treatment, outcomes for both treatment and control groups follow “parallel trends” over time, conditional on covariates. Synthetic control approaches do not rely on parallel trends. The original synthetic control method (OSC) 7 , 8 aims to find a weighted combination of units in the control group which tracks the aggregate outcome of the units in the treated group in the pre‐treatment period. This similarity is then assumed to extend into the post‐treatment period, providing an estimate of the counterfactual outcome for the treated group in the absence of the intervention. More formally, the identifying assumption underlying OSC is that (in the absence of treatment) the units' expected outcomes in each post‐intervention period equals the weighted sum of expected outcomes for the control units for that period. OSC has been considered for the evaluation of various health policy initiatives. 9 Driven by concerns about the limitations of this approach, a plethora of alternative synthetic control approaches have been proposed. 10 , 11 , 12 , 13 , 14 , 15 , 16 , 17 , 18 , 19 , 20 , 21 , 22 , 23 , 24 , 25 , 26
OSC was used to evaluate the impact of a redesign of urgent and emergency care in Northumberland, England, on hospital use in the English National Health Service (NHS). 27 Here, we re‐evaluate the impact using three additional methods—Micro Synthetic Control (MSC), 13 Generalized Synthetic Control (GSC), 14 and Bayesian Synthetic Control (BSC) methods. 10 These methods are potentially attractive for the analysis of complex health care initiatives, where data is often highly dimensional, there are multiple treated units and outcomes, and effects are likely to be heterogenous and time‐varying.
To inform the re‐evaluation, we use Monte Carlo simulations to contrast the expected performance of OSC, GSC, MSC, and BSC under relevant scenarios. Simulation studies have compared combinations of these methods and alternative counterfactual analysis methodologies: OSC and a panel data approach 28 , 29 ; DID, OSC, and regression approaches 5 ; DID, OSC, and GSC 12 , 14 , 30 DID, OSC, and BSC 31 and DID, OSC and MSC. 13 However, the relative performance of OSC, GSC, MSC, and BSC in simulation studies has not been assessed.
2. MOTIVATING EXAMPLE: RE‐EVALUATION OF THE NORTHUMBERLAND PROGRAMME
2.1. Background
The Northumbria Specialist Emergency Care (NSEC) hospital opened in Cramlington, Northumberland, on 16th June 2015. It was the UK's first purpose‐built specialist emergency care hospital and aimed to improve care and care quality for patients through improved access to a wide range of consultants and diagnostics. After the NSEC hospital opened, three existing Accident and Emergency (A&E) departments in the region (at North Tyneside, Wansbeck, and Hexham) that provided ambulatory care services, including rapid access treatment units and short‐stay wards, were gradually refocused on providing urgent but non‐emergency care for minor injuries and illnesses. For full details see O'Neill et al. 32
The short‐term impact of these changes on the hospital use of people registered with a general practice in Northumberland Clinical Commissioning Group (CCG) was evaluated over the 12‐month period from August 2015 (allowing for a 2‐month bedding‐in period). 27 CCGs are groups of general practices which come together in areas across England to commission the best services for their patients and organize the delivery of NHS services in their local areas. The original evaluation used Northumberland CCG as a single “treated” unit and used 20 CCGs from elsewhere in the country as controls. Changes to urgent and emergency care in Northumberland were found to be significantly associated with an increase of 13.6% in Accident and Emergency (A&E) visits, and a decrease of 6.7% in the proportion of patients admitted, transferred, or discharged within 4 h of attending A&E.
In this re‐evaluation, we use different methods and, since complex changes to health care rarely have the intended impacts on outcomes in the short term, 33 a considerably longer follow‐up period, from August 2015 to March 2019. We use general practices, rather than CCGs, as our units of observation. This may be advantageous for synthetic control methods if there is heterogeneity across general practices within a CCG. In this case, the synthetic control method can select a subset of general practices within a CCG that is most informative about the treated unit(s), rather than being restricted to using full CCGs as in the original evaluation. A CCG‐level synthetic control might ignore these differences, that is, differences may “cancel out” in the pre‐intervention period and any such “canceling out” would need to persist in the post‐intervention period for the CCG‐level synthetic control to perform well.
3. METHODOLOGY
3.1. Framework
We assume there are T time periods ( before the intervention), and I units (the first are untreated). Let Y it represent one of Ms observed outcomes for unit i at time t and a treatment indicator ( if unit i is treated and 0 otherwise). Let and be the potential outcomes in unit i at time t when and respectively. The observed outcome can be written as
| (1) |
We assume that is derived linearly via the interactive fixed effects model:
| (2) |
where is an vector of observed covariates and is the vector of their unknown coefficients, is an vector of unknown factor loadings (time‐invariant unobserved confounders), an vector of unobserved common factors (time‐varying coefficients), and are unobserved idiosyncratic shocks. Assuming an additive treatment effect, the observed outcome can be written as:
| (3) |
The average treatment effect on the treated (ATT) at time t is
| (4) |
where and are the average potential outcomes for the treated units in the presence and absence of treatment, respectively.
In the post‐intervention period, whilst is observed for the treated units, , is not. Therefore, estimation of the ATT requires the counterfactual potential outcome to be estimated for and , or its average value across the treated units: for . We next describe the estimators used to do so here.
3.2. Original synthetic control
OSC 7 , 8 was designed for the case of a single treated unit, however, multiple treated units can be aggregated to create a single treated region. 34 The similarity between the treated region and the synthetic control region for the outcome is assessed based on r covariates and each of the outcomes from the pre‐intervention periods for the treated unit represented by and the untreated units . The synthetic control unit is then formed by minimizing the distance between and based on the metric
| (5) |
where V is a the diagonal matrix that captures the relative importance of the p predictors and is a vector of positive weights for the control units that sum to one. The optimal set of weights satisfies
The outcome for the “synthetic control” region defined by these weights represents the counterfactual outcome for the aggregate treated region. Hence an estimate of the ATT for is:
| (6) |
3.3. Generalized synthetic control
GSC 14 unifies OSC with an interactive fixed effects model, nesting DID as a special case. Estimation of the ATT takes place in three steps. First, an interactive fixed effects estimation approach 35 is applied to the untreated observations to obtain parameter estimates , a fixed number of latent factors , and factor loadings for the untreated units. Second, factor loadings for the treated units are estimated that minimize the mean squared error between the observed treated units' outcomes and those predicted by the interactive fixed effects model in the pre‐intervention time periods. Finally, the counterfactual for the treated unit is constructed based on , , and :
and hence an estimate of the ATT for is:
GSC has a number of attractive properties: (i) unlike OSC, it can yield counterfactual estimates when the covariates/outcomes of the treated units cannot be obtained by weighting the control units' covariates/outcomes by values between 0 and 1 (i.e., the treated units are not within the “convex hull”); (ii) it allows unobserved confounders () to have time‐varying effects () on the outcome, relaxing the parallel trends assumption; (iii) GSC can account for heterogeneous treatment effects since post‐intervention outcome data is not used within the initial estimation steps. GSC maintains the unbiasedness properties of OSC but can provide more precise estimates if the interactive fixed effects model is correctly specified.
3.4. Micro synthetic control
A limitation of OSC and GSC is that they focus on a single outcome. Applying them to multiple outcomes separately ignores the correlation between the outcomes thus foregoing potential efficiency gains. MSC 13 aims to bridge this gap by leveraging additional information from multiple outcomes to more accurately account for unobserved confounding—assuming that unobserved confounders are common to all outcomes. A calibration approach is used to determine a synthetic control region that resembles the treated unit, or the sum of multiple treated units, across multiple outcomes simultaneously. Provided the outcomes are affected by the same unobserved confounders, this approach can reduce the risk of “matching on noise” (overfitting) which can occur when OSC is applied with relatively few pre‐intervention observations. 8 , 30 However, bias may be introduced if unobserved confounders are outcome specific.
Let , where includes the pre‐intervention values for each of the outcomes. The synthetic control unit is formed by finding a vector of positive weights which satisfies a set of calibration equations
| (7) |
where , and . Note that the same vector of weights is applied to all outcomes. Given that satisfies, 8 we can estimate the average treated counterfactual value, and an estimate of the ATT for for each outcome k as:
Henceforth, we use “MSC” and “MSJ” to distinguish between the application of MSC to single and multiple outcomes respectively.
3.5. Bayesian synthetic control
BSC 10 relies on a Bayesian structural time‐series (state‐space) model to predict the counterfactual outcome for the treated unit. Here we briefly describe the BSC approach for a single (aggregated) treated unit. A state‐space model is estimated for the observed outcome of the treated unit , at time t as:
| (8) |
where includes contemporaneous control series' over the pre‐intervention period consisting of the treated unit's covariates and the control groups' outcomes and is a scalar idiosyncratic error term. The influence of the control series on the outcome for the treated unit in period t is captured by the vector , which can vary over time. 36 Thus, as in OSC, the outcome of the treated unit is assumed to be mimicked by a combination of the outcomes of control units, although here it may also depend on other covariates. The comparator series in are chosen by applying a spike‐and‐slab prior for the set of regression coefficients ()—where the “spike” reflects the probability of a particular coefficient being zero and the “slab” is the prior distribution for the regression coefficient values ‐and using model averaging over the set of controls. 37 This approach avoids the need to explicitly choose the control units used to estimate the treated units' counterfactual outcome. Unlike OSC, BSC allows the weights given to each control series to lie outside the (0, 1) interval.
The state space model is estimated using all pre‐intervention observations, The posterior distribution of the counterfactual time series is then computed using the post‐intervention observations of the control unit only. The difference between the observed and predicted counterfactual outcomes during the post‐intervention period gives a semiparametric Bayesian posterior distribution for the causal effect. The state space model in Equation (8) can be expanded in many ways, such as including local trends or dynamic coefficients.
4. MONTE CARLO SIMULATION STUDY
4.1. Data generating process
Data was simulated allowing for K = 2 outcomes with the kth outcome determined by:
where the observed covariates , influencing both outcomes, and the outcome‐specific unobserved confounders and are generated from a multivariate normal distribution. The means of and were set one standard deviation higher for the treated units than for the control units (see supplementary materials Section 5 for full details).
We considered three core scenarios: (A) parallel trends; (B) Non‐parallel trends and (C) non‐parallel trends with serially correlated errors (Table S1). We also explore a scenario where we anticipate all methods will struggle, namely where the data‐generating process for the control and treated units differ fundamentally (Scenario D). For each scenario, 3000 datasets were generated each with units (where are controls and are treated), T 0 = 96 pre‐intervention periods, T 1 = 12 post‐intervention periods, and independent unobserved confounders. Each dataset was subsetted to include only the 500 control units most similar to the 50 treated units in the pre‐intervention period as in the main analysis. To test the joint estimation of both outcomes using MSJ, simulations were repeated specifying correlated unobserved confounders. Methods were applied to estimate the effect of the intervention on the first outcome () when including each of the latest 12, 24, and 48 pre‐intervention periods in each simulated dataset. See supplementary materials Section 5 for more details.
4.2. Sensitivity analyses
To assess whether our findings are sensitive to this data‐generating process, we conducted additional simulations based on an alternative data‐generating process in which a single treated unit is formed as a weighted combination of a subset of control units (see supplementary materials Section 6). To allow for improvement in selected methods over a longer pre‐intervention term, additional estimates were made using up to T 0 = 384 pre‐intervention periods.
4.3. Implementing the methods in the re‐evaluation of the Northumberland programme
For the re‐evaluation, we considered two outcomes: the number of A&E visits (including “type 1” major consultant‐led 24‐h services and “type 3” doctor or nurse‐led A&E/minor injury services) per 1000 general practice registered patients and the proportion of A&E visits where the patient was seen, transferred or discharged within 4 h of arrival (hereafter referred to as “percentage seen within 4 h”).
4.4. Case study data
Hospital activity data were obtained from the Secondary Uses Service, a national, person‐level database that records health care data in England (see supplementary materials Section 1.1 and Table S2). Each health care record contains a wide range of information about an individual admitted to an NHS hospital including the general practice they are registered with. Additional data relating to the characteristics of CCGs and general practices were collected from publicly available sources (supplementary materials Section 1.2 and Table S3).
4.5. Treated and control groups
Practices were excluded if they closed during the study period. The treated group comprised 41 practices in Northumberland. The control group included the 500 practices most similar to the treated practices in terms of CCG and general practice characteristics (supplementary materials Section 2; Tables S4 and S5). Retaining only the control practices that are most similar to the treated practices may mitigate bias from observed confounders. 38 However, it is important to note that the remaining control practices may still differ from the treated practices in terms of unobserved variables, indeed the selection of potential controls based on the similarity of observed covariates may even exacerbate such differences if observed and unobserved confounders are negatively correlated, necessitating the use of statistical methods that attempt to control for such confounding. The validity of the resulting estimates depends crucially on the extent to which they do so.
4.6. Statistical approach to case study
Data were collected over 92 months between April 2011 and March 2019 for all patients aged over 18 years and registered at a general practice in England. Data were aggregated to general practice by month resulting in observations for each general practice for 46 pre‐intervention months (April 2011–May 2015), 2 bedding‐in months (June 2015–July 2015), and 44 post‐intervention months (August 2015–March 2019). A test for parallel trends between average outcomes in the treated and control groups was performed (supplementary materials Section 7). Each estimator was applied to each outcome in turn. All methods were applied using the default options except for BSC which was provided with a seasonal 12‐month component.
5. RESULTS
5.1. Monte Carlo simulation study
Figure 1 displays boxplots of the bias of the OSC, MSC, BSC, and GSC estimators across the core simulation scenarios. Table S6 summarizes the mean percentage bias, and root mean square error. We make the following observations:
FIGURE 1.
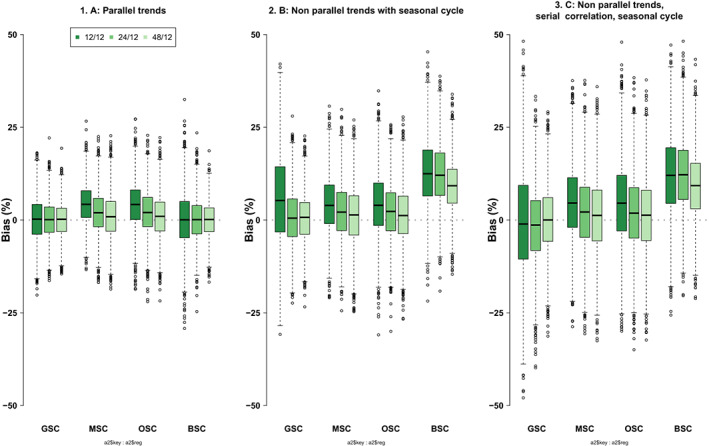
Monte Carlo simulation results for all estimators. Each plot shows boxplots of bias (%) for GSC, MSC, OSC, and BSC under scenarios, A, B, and C for 12 (darkest green), 24 (middle green), and 48 (lightest green) pre‐intervention periods and 12 post‐intervention periods across 3000 simulations with 50 treated units and 500 untreated units. BSC, Bayesian Synthetic Control; GSC, Generalized Synthetic Control; MSC, Micro Synthetic Control applied to each outcome separately; OSC, original synthetic control [Color figure can be viewed at wileyonlinelibrary.com]
Scenario A (parallel trends) (Figure 1, panel 1). GSC and BSC perform well, yielding unbiased estimates with low RMSE. MSC and OSC appear to “match‐on‐noise” 2 in shorter panels leading to bias. The lack of bias for BSC, unlike the other methods, may be explained by the fact that a simple state space model including a single control unit and an intercept is sufficient to approximate the true counterfactual well here. Increasing the number of pre‐intervention periods reduces the risk of “matching on noise” for OSC and MSC and increases efficiency in the other methods.
Scenario B (non‐parallel trends) (Figure 1, panel 2). OSC and MSC again display evidence of “matching on noise” but perform better with longer pre‐intervention periods. As in scenario A, GSC provides unbiased, relatively efficient (low RMSE) estimates for longer pre‐intervention periods. For the shorter pre‐intervention period, further inspection reveals that GSC incorrectly selects no factors (i.e., only includes two‐way fixed effects) in approximately 1/3 of runs with the short‐pre‐intervention period, while it correctly selects a single factor, (i.e., includes an interactive fixed effect in addition to the two‐way fixed effects) for 100% of runs with longer pre‐intervention periods (Table S7). This points to the difficulty of separating time‐varying and time‐invariant unobserved components when data is only available for a short period and outcomes are noisy. BSC performs poorly but improves with increasing pre‐intervention period length (Figure S1). It is important to note that BSC was proposed in the context of relatively high‐frequency data (e.g., daily data) where this may be less of a concern. Incorporating more informative priors or reducing the number of control series in may improve the performance of BSC.
Scenario C (non‐parallel trends with serially correlated errors) (Figure 1, panel 3). When serial correlation is introduced, mean bias remains largely unchanged for all methods (Table S6), in comparison to Scenario B, and the variability of estimates is increased. The ability of GSC to select the correct number of factors deteriorates when the serial correlation is introduced. We note that interactive fixed effects models tend to be more sensitive to including too few rather than too many interactive fixed effects. 39
Joint estimation. When the same unobserved confounders influence both outcomes (MSJ common confounders), there is a small improvement in bias, precision, and RMSE of the estimate of the effect of the intervention on the outcome () using MSJ in comparison to the corresponding MSC estimates (Figure 2, Table S8). However, when the confounders for the two outcomes differ (MSJ independent confounders), bias and RMSE are increased compared to the MSC estimates, except in Scenario A where parallel trends hold (i.e., the confounders are irrelevant). This suggests that while the benefits of using MSC are modest here, the potential costs may outweigh these benefits.
FIGURE 2.
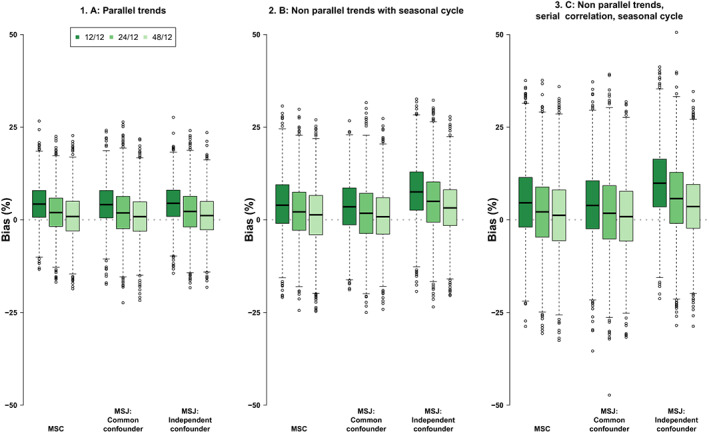
Monte Carlo simulation results for MSC and for MSJ when unobserved confounders for each outcome are either perfectly correlated (MSJ Common confounder) or uncorrelated (MSJ independent confounder). Each plot shows boxplots of bias (%) under scenarios, A, B, and C for 12 (darkest green), 24 (middle green), and 48 (lightest green) pre‐intervention periods and 12 post‐intervention periods across 3000 simulations with 50 treated units and 500 untreated units. MSC, Micro Synthetic Control applied to each outcome separately; MSJ, Micro Synthetic Control applied to both outcomes jointly. [Color figure can be viewed at wileyonlinelibrary.com]
In our additional simulations (supplementary materials Section 6), potentially favoring the original synthetic control methods, GSC continues to perform well, outperforming or performing similarly to the other methods in all scenarios. MSJ is found to perform well, however, this is attributable to the fact we include two outcomes that depend on the same observed and unobserved variables. Where this is not the case we anticipate bias as shown in the main simulations. When the same data‐generating process does not apply to treated and control groups, all methods are biased (Figure S4) albeit the direction of bias differs across the methods.
5.2. Case study
General practices in Northumberland were broadly comparable to those in the selected control group of 500 general practices (Table S4). However, Northumbrian practices tended to have larger average list sizes (8343 vs. 7354), be located in areas of lower population density (60 vs. 1314 people per km2), and have a consistently lower burden of disease and practice achievement scores. Quality and Outcomes Framework disease prevalence proportions and achievement scores were slightly lower in all categories in Northumberland. Control practices were distributed across the North, Midlands, East, and South regions in England (Table S5). Figure 3 displays the aggregate outcomes for the treated and control practices over time.
FIGURE 3.
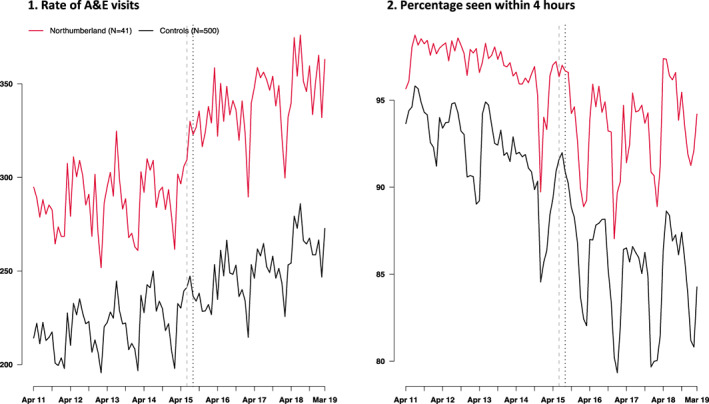
Aggregate outcomes (weighted by the relative frequency of individual practice registered population size) for the rate of A&E visits per 10,000 registered patients per month and percentage seen within 4 h in general practices in Northumberland Clinical Commissioning Group (red lines) versus the control group of size N = 500 (black lines). The vertical dashed lines indicate the bedding‐in‐period between the last pre‐intervention period and the first post‐intervention period. Test for parallel trends in the preintervention period: p = 0.314 for rate of A&E visits per 10,000 registered patients; p < 0.001 for percentage seen within 4 h [Color figure can be viewed at wileyonlinelibrary.com]
Given the long pre‐intervention period of 46 months and the results of our simulation study, we anticipate a priori that GSC will be the most reliable estimator for each of our outcomes. A summary of results for each of the methods can be found in Table 1 and Table S9. Results are illustrated in Figure 4. We make the following observations:
TABLE 1.
Impact of the opening of the Northumbria Specialist Emergency Care hospital on hospital use in the population of Northumberland Clinical Commissioning Group (CCG) from August 2015 to March 2019.
| Outcome | Northumberland clinical commissioning group, mean (SD) | Serial correlation, (ρ) a | Method | ATT | p | MSE b |
|---|---|---|---|---|---|---|
| Rate of A&E visits per 10,000 registered patients per month | 340.52 (17.8) | 0.09 | GSC | 32.3 | 0.002 | 38.4 |
| MSC | 21.6 | <0.001 | 102.9 | |||
| MSJ | −0.1 | 0.988 | 245.4 | |||
| OSC | 22.2 | <0.001 | 82.5 | |||
| BSC | 38.2 | 0.015 | 14.7 | |||
| Percentage seen within 4 h | 93.4 (2.6) | 0.38 | GSC | 0.6 | 0.486 | 0.6 |
| MSC | 2.5 | 0.022 | 1.4 | |||
| MSJ | 2.3 | 0.033 | 1.1 | |||
| OSC | 3.3 | <0.001 | 3.6 | |||
| BSC | −0.5 | 0.347 | 0.2 |
Note: Estimates of the serial correlation (r), the average treatment effect on the treated (ATT), p‐value (p), and pre‐intervention mean squared error (MSE), are shown for each outcome and method. The ATT estimates the average change in outcomes in the 41 general practices in Northumberland CCG compared to those of a synthetic control area where the synthetic control area has been estimated using 500 general practices in England that are similar to the general practices in Northumberland CCG. Estimates are risk‐adjusted as described in the text.
Abbreviations: BSC, Bayesian Synthetic Control; GSC, Generalized Synthetic Control; MSJ, Micro Synthetic Control applied to both outcomes jointly; MSC, Micro Synthetic Control applied to each outcome separately; OSC, original synthetic control; SD, standard deviation.
Serial correlation estimated from the Auto‐Regressive order 1 (AR1) process using residuals from a DID estimator and a Durbin Watson test of significance.
Mean squared error showing expected value of the squared difference between the actual and counterfactual estimates in the pre‐intervention period.
FIGURE 4.
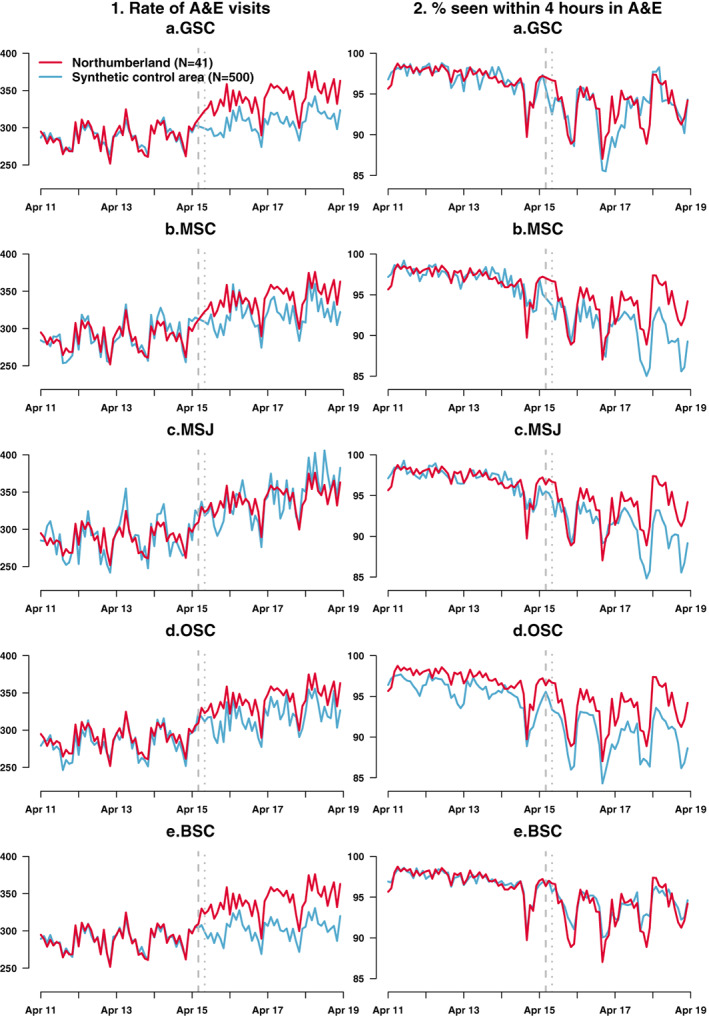
The effect of the opening of the NSEC on (column 1) the rate of A&E visits per 10,000 registered patients per month; (column 2) the percentage seen within 4 h of an A&E visit for each of the synthetic control methods (A) GSC, (B) MSC, (C) MSJ, (D), OSC and (E) BSC. Each plot shows the actual aggregated outcome (red lines) and estimated counterfactuals (blue lines). The vertical dashed lines indicate the bedding‐in‐period between the last pre‐intervention period and the first post‐intervention period. BSC, Bayesian Synthetic Control; GSC, Generalized Synthetic Control; MSJ, Micro Synthetic Control applied to both outcomes jointly; MSC, Micro Synthetic Control applied to each outcome separately; OSC, original synthetic control [Color figure can be viewed at wileyonlinelibrary.com]
5.3. Rate of A&E visits
We found little evidence for a lack of parallel trends in the rate of A&E visits (Figure 3) and the estimated serial correlation was low (ρ = 0.09) (see supplementary materials Section 8 for details of the test for parallel trends). Apart from MSJ, all estimators provide significant positive estimates of effect suggesting that the opening of the NSEC led to an increase in the rate of A&E visits. GSC estimates 32.3 (p = 0.002) more visits to A&E per 10,000 registered patients per month in Northumberland compared to the synthetic control area between August 2015 and March 2019 (Table 1). The increase in A&E visits estimated by GSC was sustained across the whole post‐intervention period (Table S9). There was greater variation in annual effects across the other methods. The estimate from the joint estimator MSJ is not statistically significant (ATT = −0.1, p = 0.988) and is vastly different from the other estimates, perhaps reflecting that the two outcomes are influenced by different unobserved confounders.
5.4. Percentage seen within 4 h
As well as a steady decline in the percentage seen within 4 h over our study period, there is also a distinct increase in seasonality in this outcome in both Northumberland and the control practices after April 2014 (Figure 3B), albeit it is more pronounced for the treated group as volatility was low in the pre‐intervention period. While A&E attendances tend to be at their lowest in the winter months (as seen in Figure 3A), the case mix tends to differ, with older and more vulnerable individuals being at increased risk of health conditions related to viruses and cold weather. This results in an increased risk of emergency admissions in the winter months, which can lead to “congestive hospital failure,” whereby as hospital beds become full, new patients cannot be cared for as quickly, leading to departments missing their 4‐h waiting time targets. As the level of A&E attendance has increased in recent years, the risk of “congestive hospital failure” may also have increased accordingly. Increases in total waiting time have been reported elsewhere during this period. 40
There was evidence of non‐parallel trends in the percentage seen within 4 h (Figure 3 and supplementary materials Section 8) and the serial correlation was modest (ρ = 0.38). This suggests that simulation scenario C is relevant here so that GSC is the most reliable and other estimators are likely to be biased. GSC reports no statistically significant impact of the opening of the NSEC on the percentage seen within 4 h during the first 4 years.
6. DISCUSSION
We used Monte Carlo simulations to compare the relative performance of four different synthetic control methods and used these methods to re‐evaluate the impact of a significant restructuring of urgent and emergency care in Northeast England.
6.1. Monte Carlo simulations
One of the most striking findings was that none of the methods dominate across all simulation scenarios considered. In line with existing simulation studies, 14 , 30 GSC performed well across a range of scenarios in the absence of serial correlation, although under serial correlation there was some evidence of bias with a short pre‐intervention period. To the best of our knowledge, this is the first simulation study to assess the performance of the method under alternative DGPs—the aforementioned studies both simulated data using IFE models. This was also the first simulation study to assess the bias in GSC that arises when the models underlying treated and control units' DGPs differ, violating the identification assumption of GSC.
Although MSC is recommended for joint estimation of effects for multiple outcomes, it may be prone to considerable bias if outcomes are influenced by different unobserved confounders, as is likely to be the case in many health policy settings. Using MSC for joint estimation requires careful consideration. However, there do appear to be some efficiency gains from using MSC in place of OSC when there is a single outcome and many controls available.
In our simulations, BSC delivered estimates that were always more variable (higher RMSE) than at least one of the competing models. However, we note that we used the default “out‐of‐the‐box” settings given in the CausalImpact R package implementation 41 and so do not specifically state space models that incorporate seasonal components, informative priors, or dynamic coefficients which may have improved performance. Also, BSC was developed in the context of higher frequency data, and we did find evidence that performance improved as the number of pre‐intervention periods increased. Hence, the method may be more suited to alternative contexts with fewer controls and longer‐pre‐intervention periods than are typically available in health policy evaluations, for example, financial evaluations, unless more informative priors are available.
In additional simulations arguably favoring OSC and MSC, GSC is the most consistent choice across all scenarios, generally outperforming or equalling the other methods. Nonetheless, there are a number of cases where we might expect GSC to perform poorly. For instance, violations of the common shock assumption (i.e., a shock specific to the treated unit in the post‐intervention period) or where the data generating process underlying the treated unit is fundamentally different from that determining the control units. Moreover, GSC requires that the number of pre‐intervention periods for which data is available to be greater than the potential number of unobserved factors
6.2. Case study
In contrast to the original evaluation, 27 we used a longer follow‐up and applied multiple methods at the level of general practice, rather than CCG. We determined that GSC was most appropriate for both outcomes studied. We estimate there were 9.5% more A&E visits (p = 0.002) in Northumberland in the first 4 years after the NSEC opened compared to the counterfactual. This can be broken down into increases of 10.4% (p < 0.001), 7.7% (p < 0.001), 10.3% (p = 0.020), and 9.9% (p = 0.002) in the first 4 financial years, 2015–2019 (Table S9). The rate for 2015–2016 is slightly lower than the increase of 13.6% reported for the same period in the earlier analysis using OSC at the CCG level. We did not find any significant evidence of an impact on the proportion of A&E patients seen within 4 h in contrast to the earlier study, which found an average increase of 7% for the first year after opening.
However, caution is advisable when directly comparing the estimates. The earlier study risk‐adjusted outcomes according to observables prior to implementing OSC and hence effects were on risk‐adjusted outcomes at the CCG level. 32 Some uncertainty associated with the risk adjustment equation is not accounted for in that analysis. In contrast, using general practice level data allowed us to control for characteristics of the general practices (see Table S5) within the methods directly. We note that for the proportion of A&E patients seen within 4 h, GSC identified nine latent factors suggesting that this outcome is subject to relatively complex patterns of unobserved confounding, while for the number of A&E visits, unobserved confounding could be captured using only one latent factor.
After the NSEC opened in June 2015, three existing departments continued to provide A&E care, alongside hospitals in surrounding areas to which some of the population of Northumberland CCG looked for treatment. This analysis looked at visits at both type 1 (24‐h consultant‐led emergency departments) and type 3 (other types of A&E/minor injury units) all departments offering A&E services, and hence the increased A&E activity likely reflects an increase in the number of departments providing A&E care, as well as perceived improvements in the quality of care provided at NSEC. From April 2017, the other departments offering A&E services to the population of Northumberland were refocused from “type 1” major consultant‐led 24‐h services to “type 3” doctor or nurse‐led A&E/minor injury services. Further work could examine the impact on visits at type 1 A&E departments over this period, which is likely to have dropped significantly from April 2017 onwards.
6.3. Limitations
The control practices selected for the re‐evaluation of the Northumberland programme may have been different from the treated practices in Northumberland at the outset of the study and so findings might be due to systematic differences between areas, rather than a change in how care was delivered. In the absence of a randomized control trial, it is not possible to eliminate this risk but we aimed to mitigate it by selecting practices for the control group with similar characteristics to those in the treated group for a range of variables including registered population size, number of general practitioners per capita and prevalence of common diseases. We also excluded general practices from the control group if they were located in CCGs also participating as new care model vanguards.
We only consider a few of the available methods in this study. Since we began our evaluation, many other methods have been proposed in the literature 11 , 16 , 17 , 20 , 21 , 23 , 42 , 43 , 44 , 45 and more work is required to assess their relative performance vis‐à‐vis the methods considered in this study. Furthermore, the data‐generating processes used for the Monte Carlo simulation may not reflect empirical scenarios and may favor some methods over others. Hence, further work should consider the performance of methods under alternative data generating process. Finally, there are a number of method and parameter choices for which we made ad hoc decisions in this study but which warrant further exploration including (i) the optimal level of aggregation of units and time periods and (ii) the optimal approach for choosing units for inclusion/exclusion in the donor pool for SC analyses.
6.4. Recommendations
Synthetic control methods are sometimes viewed as a panacea with regard to non‐parallel trends, neglecting the fact that such methods rely on alternative assumptions which may or may not hold in a given context. Moreover, as we show in scenario A, traditional synthetic control methods may introduce bias if parallel trends do not hold. Researchers should consider alternative study designs, paying close attention to their underlying assumptions. Methods, such as GSC, which nest alternative designs are attractive given their enhanced robustness. Simulation studies, such as those presented herein, can be helpful in teasing out the performance advantages of different approaches in a given context.
OSC is attractive in that it gives an easily interpretable control unit and performs relatively well when the treated units are truly a weighted average of controls. However, we note a number of cases where performance is worse than alternative methods considered, although it should also be noted that a number of extensions have been proposed to extend the usefulness of this approach which were not explored here. 8 , 10 , 40 Here, based on our simulations, we caution against the use of BSC unless data is available at very high frequency or care is taken with specifying priors since “out‐of‐the‐box” performance was poor. The use of MSC may be beneficial provided the outcomes are plausibly influenced by the same set of unobserved confounders, although the researcher should err on the side of caution given the potential for bias if this is not the case. Where this assumption is implausible, separate estimation for each outcome may be preferred. Alternatively, one might consider the approach proposed by Samartsidis et al. 46 which was not explored here, as it allows for outcome‐specific unobserved factors.
Of the methods considered here, GSC performs well across a range of settings. However, GSC has two main limitations. Firstly, when the number of pre‐intervention periods is small, this places restrictions on the number of unobserved confounders that can be captured and estimates may be biased. Secondly, GSC depends on the treated and control units sharing a common support in factor loadings but, unlike OSC, will still provide estimates if this is not the case. Hence, researchers should check that the characteristics of the treated and control groups overlap to ensure that estimates are produced by more reliable interpolations then extrapolations. Researchers should also consider whether outcomes are likely to be serially correlated since longer pre‐intervention periods are required to mitigate bias in this case.
Supporting information
Data S1. Supporting information
ACKNOWLEDGMENTS
The authors thank the wider Improvements Analytics Unit team at The Health Foundation, in particular Stefano Conti, Caroline Gori, Filipe Santos, and Arne Wolters for their support and advice on this work.
Clarke GM, Steventon A, O'Neill S. A comparison of synthetic control approaches for the evaluation of policy interventions using observational data: Evaluating the impact of redesigning urgent and emergency care in Northumberland. Health Serv Res. 2023;58(2):445‐457. doi: 10.1111/1475-6773.14126
Funding information The Health Foundation
REFERENCES
- 1. Bertrand M, Duflo E, Mullainathan S. How much should we trust differences‐in‐differences estimates? Q J Econ. 2004;119(1):249‐275. doi: 10.1162/003355304772839588 [DOI] [Google Scholar]
- 2. Jones AM, Rice N. Econometric Evaluation of Health Policies; 2012. 10.1093/oxfordhb/9780199238828.013.0037 [DOI]
- 3. Fletcher JM, Frisvold DE, Tefft N. Non‐linear effects of soda taxes on consumption and weight outcomes. Health Econ (United Kingdom). 2015;24(5):566‐582. doi: 10.1002/hec.3045 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Wen H, Hockenberry JM, Cummings JR. The effect of medical marijuana laws on adolescent and adult use of marijuana, alcohol, and other substances. J Health Econ. 2015;42:64‐80. doi: 10.1016/j.jhealeco.2015.03.007 [DOI] [PubMed] [Google Scholar]
- 5. O'Neill S, Kreif N, Grieve R, Sutton M, Sekhon JS. Estimating causal effects: considering three alternatives to difference‐in‐differences estimation. Health Serv Outcomes Res Methodol. 2016;16:1‐21. doi: 10.1007/s10742-016-0146-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Dimick JB, Ryan AM. Methods for evaluating changes in health care policy: the difference‐in‐differences approach. JAMA. 2014;312:2401. doi: 10.1001/jama.2014.16153 [DOI] [PubMed] [Google Scholar]
- 7. Abadie A, Gardeazabal J. The economic costs of conflict: a case study of the Basque country. Am Econ Rev. 2003;93(1):113‐132. doi: 10.1257/000282803321455188 [DOI] [Google Scholar]
- 8. Abadie A, Diamond A, Hainmueller J. Synthetic control methods for comparative case studies: estimating the effect of California's tobacco control program. J Am Stat Assoc. 2010;105(490):493‐505. doi: 10.1198/jasa.2009.ap08746 [DOI] [Google Scholar]
- 9. Bouttell J, Craig P, Lewsey J, Robinson M, Popham F. Synthetic control methodology as a tool for evaluating population‐level health interventions. J Epidemiol Commun Health. 2018;72:673‐678. doi: 10.1136/jech-2017-210106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Brodersen KH, Gallusser F, Koehler J, Remy N, Scott SL. Inferring causal impact using Bayesian structural time‐series models. Ann Appl Statis. 2015;9:247‐274. [Google Scholar]
- 11. Doudchenko N, Imbens GW. Difference‐in‐differences and synthetic control methods: a synthesis. Nation Bureau Econ Res Work Paper Ser. 2016;22791:1‐35. doi: 10.3386/w22791 [DOI] [Google Scholar]
- 12. Gobillon L, Magnac T. Regional policy evaluation: interactive fixed effects and synthetic controls. Rev Econ Statis. 2016;98:535‐551. doi: 10.1162/REST_a_00537 [DOI] [Google Scholar]
- 13. Robbins MW, Saunders J, Kilmer B. A framework for synthetic control methods with high‐dimensional, micro‐level data: evaluating a neighborhood‐specific crime intervention. J Am Stat Assoc. 2017;112(517):109‐126. doi: 10.1080/01621459.2016.1213634 [DOI] [Google Scholar]
- 14. Xu Y. Generalized synthetic control method: causal inference with interactive fixed effects models. Politic Anal. 2017;25(1):57‐76. doi: 10.1017/pan.2016.2 [DOI] [Google Scholar]
- 15. Abdul‐Rahman A, Syed‐Yahaya SS, Atta AMA. Robust synthetic control charting. Int J Technol. 2021;12(2):349‐359. doi: 10.14716/ijtech.v12i2.4216 [DOI] [Google Scholar]
- 16. Arkhangelsky D, Athey S, Hirshberg DA, Imbens GW, Wager S. Synthetic difference in differences. arXiv. 2018.
- 17. Ben‐Michael E, Feller A, Rothstein J. The augmented synthetic control method. J Am Stat Assoc. 2021;116(536):1789‐1803. doi: 10.1080/01621459.2021.1929245 [DOI] [Google Scholar]
- 18. Chernozhukov V, Wuthrich K, Zhu Y. Exact and Robust Conformal Inference Methods for Predictive Machine Learning With Dependent Data. eprint arXiv:180206300. Published online February 1, 2018: arXiv:1802.06300.
- 19. Powell D., Imperfect Synthetic Controls: Did the Massachusetts Health Care Reform Save Lives? 2018.
- 20. Athey S, Tibshirani J, Wager S. Generalized random forests. Ann Statis. 2019;47(2):1148‐1178. doi: 10.1214/18-AOS1709 [DOI] [Google Scholar]
- 21. Cerulli G. A flexible synthetic control method for modeling policy evaluation. Econ Lett. 2019;182:40‐44. doi: 10.1016/j.econlet.2019.05.019 [DOI] [Google Scholar]
- 22. Tanaka M. Bayesian matrix completion approach to causal inference with panel data. J Statis Theory Pract. 2021;15(2):1‐22. doi: 10.1007/s42519-021-00188-x [DOI] [Google Scholar]
- 23. Pang X, Liu L, Xu Y. A Bayesian alternative to synthetic control for comparative case studies. Political Anal. 2022;30(2):269‐288. doi: 10.2139/ssrn.3649226 [DOI] [Google Scholar]
- 24. Samartsidis P, Seaman SR, Presanis AM, Hickman M, De Angelis D. Assessing the causal effect of binary interventions from observational panel data with few treated units. Statis Sci. 2019;34(3):486‐503. doi: 10.1214/19-STS713 [DOI] [Google Scholar]
- 25. Athey S, Bayati M, Doudchenko N, Imbens G, Khosravi K. Matrix completion methods for causal panel data models. J Am Stat Assoc. 2021;116(536):1716‐1730. doi: 10.1080/01621459.2021.1891924 [DOI] [Google Scholar]
- 26. Callaway B, Karami S. Treatment effects in interactive fixed effects models with a small number of time periods. J Economet. 2022. doi: 10.1016/j.jeconom.2022.02.001 [DOI] [Google Scholar]
- 27. Stephen O, Wolters A, Steventon A. Briefing: The Impact of Redesigning Urgent and Emergency Care in Northumberland. 2017.
- 28. Gardeazabal J, Vega‐Bayo A. An empirical comparison between the synthetic control method and HSIAO et al.'s panel data approach to program evaluation. J Appl Economet. 2017;32(5):983‐1002. doi: 10.1002/jae.2557 [DOI] [Google Scholar]
- 29. Wan SK, Xie Y, Hsiao C. Panel data approach vs synthetic control method. Econ Lett. 2018;164:121‐123. doi: 10.1016/j.econlet.2018.01.019 [DOI] [Google Scholar]
- 30. O'Neill S, Kreif N, Sutton M, Grieve R. A comparison of methods for health policy evaluation with controlled pre‐post designs. Health Serv Res. 2020;55:328‐338. doi: 10.1111/1475-6773.13274 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Kinn DD. Synthetic Control Methods and Big Data. arXiv: Econometrics. 2018.
- 32. O'Neill S, Wolters A, Steventon A. The impact of redesigning urgent and emergency care in Northumberland: Health Foundation consideration of findings from the Improvement Analytics Unit. 2017.
- 33. Clarke GM, Pariza P, Wolters A. The Long‐Term Impact of New Care Models on Hospital Use; 2020.
- 34. Kreif N, Grieve R, Hangartner D, Turner AJ, Nikolova S, Sutton M. Examination of the synthetic control method for evaluating health policies with multiple treated units. Health Econ. 2015;19(11):1514‐1528. doi: 10.1002/hec.3258 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Bai J. Panel data models with interactive fixed effects. Econometrica. 2009;77(4):1229‐1279. doi: 10.3982/ECTA6135 [DOI] [Google Scholar]
- 36. Hamilton JD. Chapter 50 state‐space models. Handbook of Econometrics. Vol 4; 1994. doi: 10.1016/S1573-4412(05)80019-4 [DOI] [Google Scholar]
- 37. George EI, McCulloch RE. Variable selection via Gibbs sampling. J Am Stat Assoc. 1993;88(423):881‐889. doi: 10.1080/01621459.1993.10476353 [DOI] [Google Scholar]
- 38. Abadie A. Using synthetic controls: feasibility, data requirements, and methodological aspects. J Econ Literat. 2021;59(2):391‐425. doi: 10.1257/jel.20191450 [DOI] [Google Scholar]
- 39. Moon HR, Weidner M. Linear regression for panel with unknown number of factors as interactive fixed effects. Econometrica. 2015;83(4):1543‐1579. doi: 10.3982/ecta9382 [DOI] [Google Scholar]
- 40. Nuffield Trust. A&E waiting times. Quality Watch 2022. Accessed July 1, 2022. https://www.nuffieldtrust.org.uk/resource/a-e-waiting-times.
- 41. Brodersen KH, Hauser A, Hauser MA. Package CausalImpact. 2015.
- 42. Amjad M, Shah D, Shen D. Robust synthetic control. J Mach Learn Res. 2018;19(1):802‐852. [Google Scholar]
- 43. Cerulli G. Nonparametric synthetic control using the npsynth command. Stata J. 2020;20(4):844‐865. doi: 10.1177/1536867X20976315 [DOI] [Google Scholar]
- 44. Ferman B, Pinto C. Synthetic controls with imperfect pretreatment fit. Quant Econ. 2021;12(4):1197‐1221. doi: 10.3982/QE1596 [DOI] [Google Scholar]
- 45. Bilinski A, Hatfield LA. Nothing to see here? non‐inferiority approaches to parallel trends and other model assumptions. arXiv preprint. 2018; 1805.03273.
- 46. Samartsidis P, Seaman SR, Montagna S, Charlett A, Hickman M, De Angelis D. A Bayesian multivariate factor analysis model for evaluating an intervention by using observational time series data on multiple outcomes. J Royal Statis Soc Series A: Statist Soc. 2020;183:1437‐1459. doi: 10.1111/rssa.12569 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data S1. Supporting information


