Mitotic outcomes and errors in fibrous environments

Significance

Mitotic cells push against their environment to achieve spherical shapes for proper spindle formation and to minimize division errors. We use a model system of extracellular matrix-mimicking suspended fibers to expose the role of the geometry of the fibers on the stability of mitotic cells. By manipulating the number of fibers to which a cell is attached, we describe how the number density of adhesion-originated retraction fibers affects mitosis. Combining quantitative microscopy with analytical and computational models, we demonstrate that while bipolar mitosis is robust in a fibrous environment, subtle changes in fiber networks can cause a dramatic switch in the character of the mitotic defects. Overall, we describe how extracellular fibers in vivo might affect the fidelity of mitosis.

Abstract

During mitosis, cells round up and utilize the interphase adhesion sites within the fibrous extracellular matrix (ECM) as guidance cues to orient the mitotic spindles. Here, using suspended ECM-mimicking nanofiber networks, we explore mitotic outcomes and error distribution for various interphase cell shapes. Elongated cells attached to single fibers through two focal adhesion clusters (FACs) at their extremities result in perfect spherical mitotic cell bodies that undergo significant 3-dimensional (3D) displacement while being held by retraction fibers (RFs). Increasing the number of parallel fibers increases FACs and retraction fiber-driven stability, leading to reduced 3D cell body movement, metaphase plate rotations, increased interkinetochore distances, and significantly faster division times. Interestingly, interphase kite shapes on a crosshatch pattern of four fibers undergo mitosis resembling single-fiber outcomes due to rounded bodies being primarily held in position by RFs from two perpendicular suspended fibers. We develop a cortex–astral microtubule analytical model to capture the retraction fiber dependence of the metaphase plate rotations. We observe that reduced orientational stability, on single fibers, results in increased monopolar mitotic defects, while multipolar defects become dominant as the number of adhered fibers increases. We use a stochastic Monte Carlo simulation of centrosome, chromosome, and membrane interactions to explain the relationship between the observed propensity of monopolar and multipolar defects and the geometry of RFs. Overall, we establish that while bipolar mitosis is robust in fibrous environments, the nature of division errors in fibrous microenvironments is governed by interphase cell shapes and adhesion geometries.

The mitotic spindle is a remarkable biological machine responsible for the proper segregation of chromosomes (CHs) during cell division (1, 2). Its positioning determines the cell division axis orientation and is therefore crucial for tissue morphogenesis. Defects in spindle positioning are often implicated in developmental disorders and cancer progression (3). Mitotic spindle positioning depends on several factors, including delamination (4), cell shape (5), the spatial organization of cell–matrix focal adhesions (FAs) present during interphase (6–8), and confinement forces (9, 10). In vivo cells undergoing mitosis push on neighboring interphase cells to generate space for rounded cell shape for proper mitotic spindle positioning (11, 12). Rounded cells are held in place within tissues through basolateral septate junctions (4), actin mitotic protrusions in 3-dimensional (3D) gels (13), or the in vitro substrate via thin actin-rich structures referred to as retraction fibers (RFs) that originate from active integrin-based adhesion sites (10, 14, 15). Mitotic protrusions and RFs act as mechanical links to stabilize the orientation of the mitotic spindle (6, 10, 16) and to facilitate the spreading of daughter cells following cytokinesis through the reestablishment of FAs (14).

Cells in the body can move along or between interstitial fiber networks composed of a loose network of fibers (17). Very little is known about how mitosis proceeds in loose fibrous extracellular matrix (ECM) environments. Can the organization of ECM fiber networks direct mitotic outcomes? Central to this inquiry is the finding that cells in native fibrous 3-dimensional environments form elongated cell–matrix adhesions at their peripheries that differ significantly from the low aspect ratio (AR) adhesions formed isotropically on flat 2D surfaces (18–24). In addition, mitosis on flat 2D, and 2D adhesive micropatterns, occurs primarily in an unrestricted manner (25, 26), and we aim to answer how mitosis proceeds in a well-controlled artificial fiber network that mimics the natural interstitial ECM (23).

Fibrous ECM in vivo consists of individual fibrils and bundled fibers ranging in diameters from a few hundred nanometers to several microns (27–29) organized in a diverse range of fiber densities, pore sizes, and network architectures, including aligned configurations (30) and crossing fiber arrangements (31–34). In fibrous environments of large pore sizes, cells make contact with only a few fibers (17, 21, 35–37). Recently, intravital imaging of breast cancer cells showed the ability of cells to contact individual collagen fibers using protrusions and exert forces resulting in their deformation (38).

In this study, we used our previously reported nonelectrospinning “Spinneret based Tunable Engineered Parameters” (STEP) technique to generate aligned and crosshatch networks of suspended fibers (39, 40). We have previously shown that our model system matches behaviors reported in vivo and from studies in cell-derived 3D matrices and 3D gels. For example, we have shown that the i) migratory modes match the findings from 3D cell-derived matrices and 1D fibrillar lines (commonly used to study 3D migration) (20, 21), ii) cell protrusions applying forces on suspended fiber systems (41) as shown in vivo (38), and iii) cellular cytoskeleton cages the nuclei and has similar invaginations in the nuclei compared to cells in 3D gels (42).

In this study, we controlled the interfiber spacing of fiber networks to achieve cells in elongated and kite shapes (19, 20), with a varying number of adhesion clustering sites on fibers (two, four, and many) at the cell peripheries. RFs originating from the FAs on the fibers held rounded, mitotic cells in position, but with the freedom to move about the fiber axes due to the absence of a basal surface, a key difference with 2D culture methods. We observe that reduced orientational stability, on single fibers, results in increased monopolar mitotic defects, while multipolar defects become dominant as the number of adhered fibers increases. A stochastic Monte Carlo simulation of centrosome (CS), chromosome, and membrane interactions was developed to explain the relationship between mitotic errors and the geometry of RFs. Overall, we present a biologically relevant model system of suspended fiber networks that allows us to expose the mitotic rules and error evolution in fibrous microenvironments mimicking the ECM.

Results

FA Clustering on Fibers Controls Actin Retraction Fiber Organization.

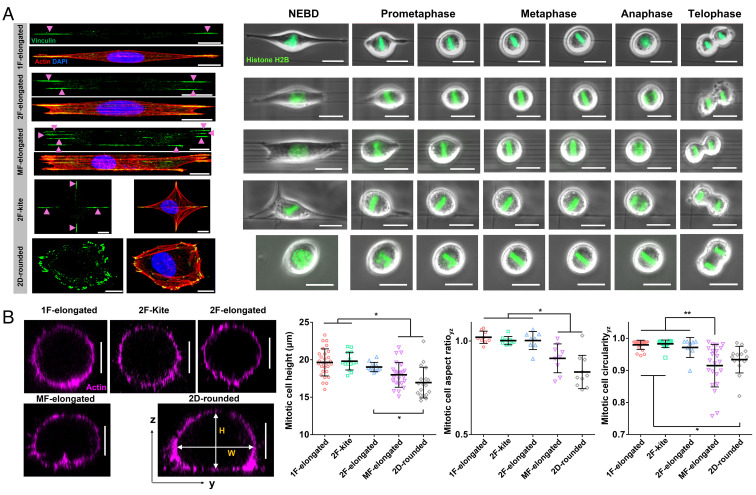
We wanted to inquire whether the FA patterns on fibers, correlating with different cell shapes and ARs, contributed to the organization of actin RFs. We generated suspended nanofiber (fiber diameter ~250 nm) networks in both aligned and crosshatch geometries to achieve control on cells of diverse AR and FA clusters to study mitosis (Fig. 1A and Movies S1–S5). Tuning the interfiber spacing (4 µm to 25 µm) in the aligned networks resulted in three elongated high AR cell shapes: i) one fiber-elongated (1F-elongated) shaped cells attached to single fibers and having two major FA clusters, ii) two fiber-elongated (2F-elongated) shaped cells attached to two fibers and having four FA clusters, and iii) multifiber-elongated (MF-elongated) shaped cells attached to ≥ three fibers with multiple aligned FA clusters. Crosshatch networks of interfiber spacing ~50 µm induced symmetric polygonal kite-shaped cells (2F-kite) with four FA clusters. Quantification of the ARs during interphase revealed the highest elongated geometries in the 1F- and 2F-elongated categories (AR ~ 9, SI Appendix, Fig. S1), followed by the MF-elongated shapes (AR ~ 5) and finally the 2F-kite shape and 2D cells on flat 2D (2D-rounded) having AR close to 1.

Fig. 1.

Cell division in suspended fiber environments. (A) Time-lapse images showing representative cases of mitotic progression starting from nuclear envelope breakdown (NEBD) to telophase corresponding to five distinct interphase cell shapes: 1F-elongated, 2F-elongated, MF-elongated (≥3 fibers), 2F-kite (2 orthogonal fibers), and 2D-rounded (glass coverslips). Interphase cells are fluorescently stained with actin (red), vinculin (green), and nucleus (blue). (Scale bars, 10 µm and 20 µm, respectively.) (B) Representative yz cross-sectional images of actin-stained cells fixed at metaphase for different substrate categories, mitotic cell height (H), mitotic cell AR (H/W), and mitotic cell circularity (4*π*area/perimeter²) for different substrate categories. No statistical differences were observed between 1F-elongated, 2F-kite and 2F-elongated categories in terms of mitotic cell height, AR and circularity. (Scale bar, 10 µm.) *, **, ***, and **** represent P < 0.05, 0.01, 0.001, and 0.0001, respectively.

As cells rounded up during mitosis, we observed that they were held in place by actin RFs originating at the FA cluster sites and connecting to the cell cortex (CRTX). We characterized the 3D shape of mitotic cells during metaphase (Fig. 1B). On flat surfaces, mitotic cells are not perfectly spherical but instead show an elliptical shape in their cross-sectional views, with ARs (cell height by width) significantly less than 1 (0.84 ± 0.09, mean ± SD, Fig. 1B). In the 1F-elongated shape, we observed almost perfectly spherical mitotic cells [AR (1.02 ± 0.03, Fig. 1B) and circularity (0.980 ± 0.014, Fig. 1B)]. Interestingly, in the multifiber category, where cells are positioned on top of the fiber layer, the mitotic cell shape is significantly more flattened [AR (0.908 ± 0.077) and a significant reduction in circularity (0.915 ± 0.066)]. Thus, cells in the MF-elongated are more similar to cells on flat 2D surfaces. Our observations are in excellent agreement with previous studies on flat 2D, which also report shorter cell heights than widths (43).

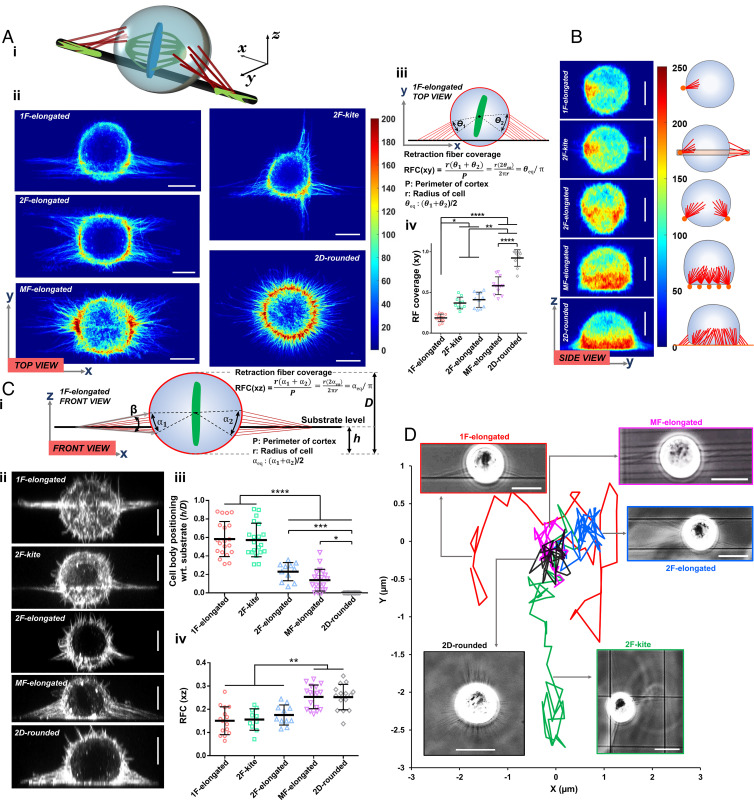
We observed rounded cells held in position by RFs (schematically shown in Fig. 2 A, i). Using confocal microscopy, we analyzed the top (xy, Fig. 2 A, ii), side (zy, Fig. 2B), and front (xz, Fig. 2 C, i and ii) views. We identified RFs to appear as actin-rich hot spots in the averaged intensity heat maps of the CRTX. 1F-elongated cells attached to single fibers through two major FA clusters during interphase were connected by two major sets of RFs during mitosis. Interestingly, 2F-kite shaped cells, despite having four FA clusters during interphase, were found to be anchored by two dominant sets of orthogonally arranged RFs in the rounded mitotic state. To quantitate the spatial localization of RFs, we introduced a new metric, RF coverage (RFC), defined as the fraction of the cortical perimeter to which RFs were connected (Fig. 2 A, iii) along two principal equatorial planes (Fig. 2 A, iv for the top view: ${\mathrm{RFC}}_{\left(\mathrm{xy}\right)} = {\theta }_{\mathit{e}\mathit{q}}/\mathrm{\pi }$  and Fig. 2 C, iv for the front view: ${\mathrm{RFC}}_{\left(\mathrm{xz}\right)} = {\alpha }_{eq}/\mathrm{\pi }$ ). The 1F-elongated cells had an RFC of only ~0.19 and 0.15, while cells on flat 2D had an average value of ~0.92 and 0.25 for top and front views, respectively. To relate the spatial arrangement of RFs and cell body with respect to the fiber axis (Fig. 2 C, i), we introduced new metrics: i) the number of major RFs associated with a single FA cluster, ii) location of rounded cell with respect to the substrate (h/D ratio, where h is the distance from the fiber plane to the bottom of the cell, and D is the height (z-dimension) of the cell in its rounded state), and iii) net included angle (β) defined as the angular spread of the RFs about their attachment sites. Quantification of the number of major RFs emanating from individual FA clusters revealed an average of 10 to 12 RFs per category (SI Appendix, Fig. S2i). We observed that rounded mitotic cells were positioned roughly in the midcortical level for 1F-elongated and 2F-kite shapes (h/D ratio ~ 0.5 to 0.6). In contrast, cells on multiple fibers typically were positioned on top of the fiber plane (h/D ratio ~ 0.1) similar to cells on flat 2D (h/D = 0, Fig. 2 C, iii). Interestingly, analysis of the cortical distribution of RFs revealed that the RFs were mainly positioned along, above, and below the nanofiber plane in 1F-elongated and 2F-kite configurations. Cells in the 2F-elongated, MF-elongated, and flat 2D cases were positioned above the substrate, causing the RFs to be organized at a steeper angle between the midcortical level of the rounded cell and the underlying substrate (SI Appendix, Fig. S2ii).

Fig. 2.

Retraction fiber-based stability and positioning of mitotic rounded cell bodies. (A, i) 3D schematic of rounded cell body held in place by RFs in a single-fiber category, (ii) average hot spots of RFs from confocal microscopy of the top view across various fiber configurations and 2D (n = 10 per category) (scale bar, 10 µm), (iii) schematic describing retraction fiber coverage metric, and (iv) retraction fiber coverage (RFC) across fiber configurations and 2D in the xy plane. (B) Average hot spots of RFs from confocal microscopy of the side view across various fiber configurations and 2D (n = 10 per category). (Scale bar, 10 µm.) (C, i) Schematic shows the retraction fiber organization from the front view of cells, (ii) representative images showing the front view of mitotic cells across various fiber configurations and 2D (scale bar, 10 µm), (iii) cell body positioning (h/D ratio defined in C, i) across all fiber configurations and 2D, h is the distance from the fiber plane to bottom of cell, and D is the height (z-dimension) of the cell in the rounded state, and (iv) RFC in the xz plane across all fiber configurations and 2D. (D) Representative cell body displacement profile during mitosis showing cells in 1F-elongated and 2F-kite shapes undergoing large displacements. (Scale bar, 20 µm.) *, **, ***, and **** represent P < 0.05, 0.01, 0.001, and 0.0001, respectively.

Increased retraction fiber coverage directly affected the rounded cell body movement observed from high-speed time-lapse videos (top view, Movies S6–S9). On flat 2D and multifiber categories, the cell body was essentially locked in place (minimal movement), while 1F-elongated and 2F-kite categories displayed significant cell body movement (Fig. 2D). Although unviewable from the front view, we expect similar trends of cell body movement in 1F- and 2F-kites due to an h/D ratio of ~0.5 to 0.6 and reduced motion for 2F-elongated categories due to the mitotic bodies resting on top of the two fibers (low h/D ratio ~ 0.22). Overall, we conclude that 1F-elongated and 2F-kite mitotic rounded bodies undergo significant 3D movement, including rotations about all axes.

Cell Shape and Retraction Fibers Regulate Mitotic Dynamics.

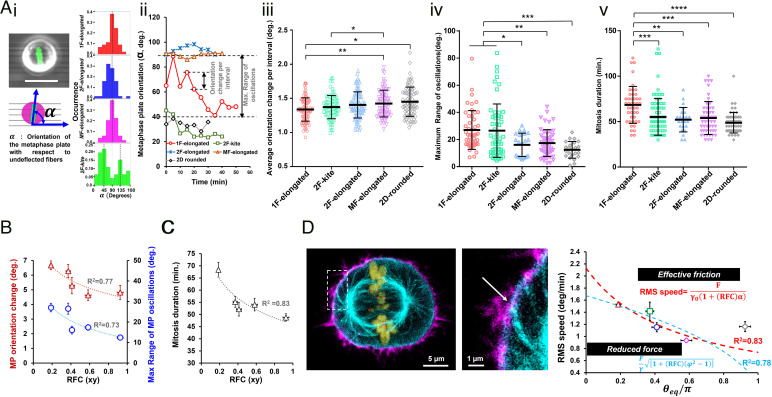
Next, we inquired how the RFC contributed to mitotic dynamics. Consistent with previously reported literature (44), we observed that the metaphase plate (MP) exhibited significant fluctuations about its mean position following mitotic entry. We characterized the fluctuations of the MP orientation (α, Fig. 3 A, i, and Movies S10–S13) and found that in aligned fiber networks, the orientation profiles were centered around 90° (i.e., orthogonal to the cell elongation during interphase) in good agreement with Hertwig’s rule (45). Interestingly, in the case of 2F-kite shaped cells, the temporal profiles (SI Appendix, Fig. S3) were mainly centered around 45° or 135°, indicating a diagonal placement of MP between the two orthogonal adhesion sites.

Fig. 3.

Retraction fiber-based mitotic dynamics. (A, i) Illustration showing convention for metaphase plate orientation (α) (scale bar, 20 µm), (ii) analysis of individual temporal profiles of metaphase plate orientation using orientation change per interval and maximum range of metaphase plate oscillations, (iii and iv) statistical comparison across all fiber configurations and 2D for metaphase plate dynamics, and (v) mitosis duration analysis showing 1F-elongated to be the slowest. (B) Metaphase plate orientation and maximum range of oscillations decrease with increasing RFC. (C) Mitosis duration decreases with increasing fiber coverage. (D) Representative image showing the mechanical linking of the astral microtubules and the CRTX at the sites of the RFs, actin (magenta), microtubules (cyan), histone H2B (olive), and kinetochore Hec1 (red). (Scale bars, 5 µm and 1 µm in the main image and Inset, respectively.) Model formulations based on increased effective friction and force for MP movements at higher retraction fiber coverage. *, **, ***, and **** represent P < 0.05, 0.01, 0.001, and 0.0001, respectively.

A closer inspection of the individual temporal profiles (Fig. 3 A, ii) indicated significant movement of MPs during mitosis. We quantified the degree of orientation changes using two metrics: i) absolute orientation change of the MP per time interval and ii) maximum angular range of MP rotations. Across all elongated shapes, we observed that the 1F-elongated shaped cells with two FA clusters demonstrated significantly larger orientation changes (Fig. 3 A, iii) and the highest angular range of MP rotations (Fig. 3 A, iv). Incidentally, similar dynamic activity levels of the MP were also observed in symmetric 2F-kite shaped cells with four FA clusters. Intrigued by the differences in MP dynamics and the curious similarity between 1F-elongated and 2F-kite shapes, next, we investigated the durations for mitosis completion (NEBD to telophase, Fig. 3 A, v). We found that 1F-elongated cells took significantly longer average times (68.4 ± 3 min, mean ± SEM) to divide as compared to other suspended cell shapes (50 to 55 min) or on traditional flat glass coverslips (48.8 ± 1.5 min).

Plotting MP orientation changes per interval and maximum angular range, as a function of RFC, demonstrated reduced MP oscillations with increasing RFCs (Fig. 3B). Coincidentally, mitosis time decreased with an increasing number of RFs, indicating a role of mechanical stability in mitosis (Fig. 3C). Imaging of single mitotic cells demonstrated colocalization of actin and the β-tubulin within the CRTX, which indicated potential force interactions between the actin cortex and the astral microtubules of the mitotic spindle. To understand such interactions and how they impact metaphase plate angular fluctuations, we developed a force/friction-based theoretical model. We present two formulations, with both models based on the force interactions between the actin cortex and astral microtubules (Fig. 3D). The first formulation considers the higher effective friction experienced by the interacting microtubules in the CRTX region covered by the RFs. Thus, the rms angular velocity of the metaphase plate (quantified from distributions of the angular velocity, SI Appendix, Fig. S4) scales with the microtubule–cortex forces (F) as $\sqrt{\langle {\text{v}}^2\rangle }= \sqrt{\langle F^2\rangle /{\gamma }^2}$ , where γ is the effective friction coefficient, which is given by γ = γ₀(1 + (RFC)α), where α > 1 denotes the higher effective friction in the cortical region attached to the RFs. Thus, the rms speed of the metaphase plate depends directly on the retraction fiber coverage as follows:

$$\sqrt{\langle {\text{v}}^2\rangle }=\frac{\text{F}}{{\text{γ}}_0(1+\left(\text{RFC}\right)\text{α})}\text{.}$$

The second formulation considers a reduction of the forces exerted by the astral microtubules on the cortex due to being “stuck” on adhesion complexes where the RFs emanate. The central approximation in this formulation is that microtubules are less mobile when in contact with a cortex area with RFs linked to it by a factor $0<\phi <1$ . Thus, the mean square force (microtubule–cortex) can be given as follows:

$$\langle F^2\rangle =[(1-\text{RFC})+\left(\text{RFC}\right){\phi }^2]F^2,$$

and the corresponding rms speed $\begin{array}{c}\sqrt{\langle {\text{v}}^2\rangle }= \sqrt{\langle F^2\rangle /{\gamma }^2}=\hfill \end{array}$$\begin{array}{c} \frac{F}{\gamma }\sqrt{\left[1+\left(\text{RFC}\right)\left({\phi }^2-1\right)\right]}\hfill \end{array}$.

Fitting this expression to the experimental results demonstrates that $\phi$ is effectively zero, which gives the dependence of the MP rms speed on the RFC in this limit: $\sqrt{\langle {\text{v}}^2\rangle }=\frac{\text{F}}{\text{γ}}\sqrt{\left[1-\left(\text{RFC}\right)\right]}$.

Both proposed models fit our experimental data reasonably well (R² = 0.83 and 0.78, respectively) and demonstrate how increasing the RFC can significantly reduce the overall movements of the metaphase plate.

Overall, we found that the spatial organization of RFs in fibrous environments regulated the 3D positioning, shape, and movement of mitotic cells and led to varying levels of mechanical stability of the metaphase plate.

Mitotic Fidelity Is Influenced by Fiber Geometry.

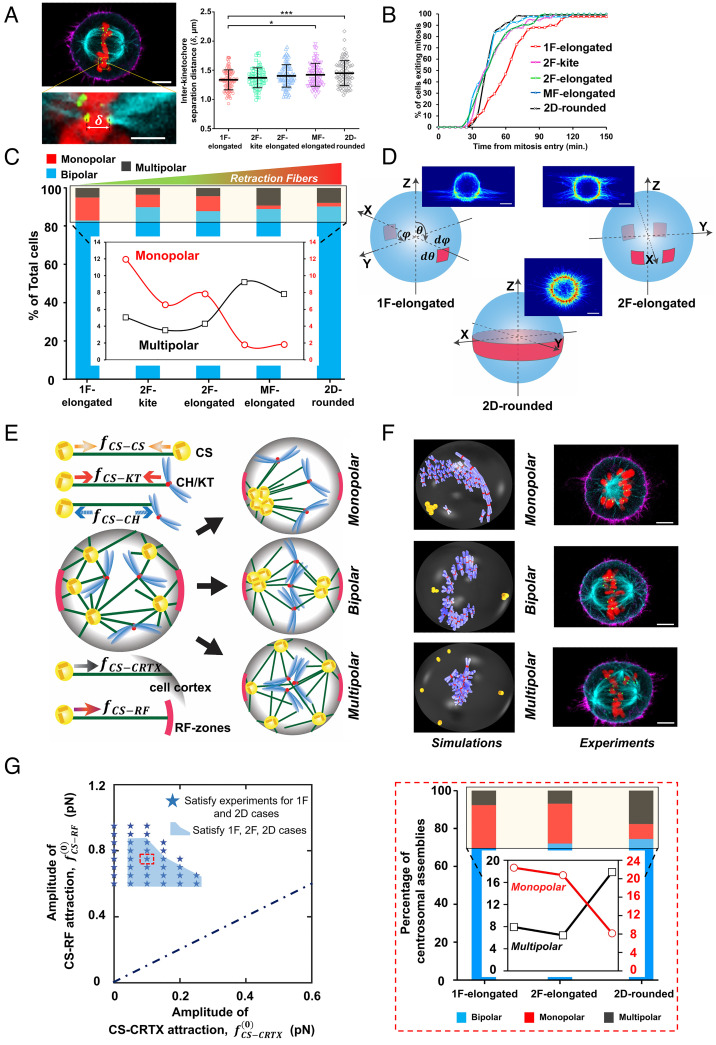
Our observations that controlling interphase cell shape and adhesion geometry can significantly affect the metaphase plate dynamics, mitotic duration, and daughter cell positioning led us to inquire whether mitotic errors were affected by fiber geometry as well. To this end, we synchronized divisions of HeLa cells by treatment and washout with the Cdk1 inhibitor RO-3306 and fixed mitotic rounded cells at metaphase (46, 47). Similar to the previously reported classification of mitotic spindles, we observed three major types of outcomes: i) bipolar (two symmetrically positioned spindle poles for normal chromosome segregation), ii) monopolar (a single spindle pole, defective chromosome segregation), and iii) multipolar (at least three spindle poles, defective chromosome segregation) (48). Treatment with the drug did not have any significant effect on spindle polarity as cells treated with RO-3306 compared to those treated with vehicle alone (DMSO) showed no statistical difference in the percentage of cells forming bipolar, monopolar, and multipolar spindles (SI Appendix, Fig. S5). We immunostained the rounded cells for different components of the mitotic spindles: microtubules (β-tubulin), kinetochores (KT) (Hec1), and the CHs (histone H2B). We quantified the net length and width of the mitotic bipolar spindles and did not observe differences between the overall spindle shape across fiber networks and conventional flat glass substrates (SI Appendix, Fig. S6). Since kinetochore stretching is directly associated with the regulation of mitotic timing (49), we wanted to estimate the extent of stretching by analyzing the interkinetochore separation distances (Fig. 4A). Our observations reveal that the interkinetochore separation distance was reduced in the 1F-elongated cells, thus potentially explaining the slower mitotic progression in these cells (Fig. 4B).

Fig. 4.

Mitotic errors in different fiber geometries: (A) Representative image showing a pair of kinetochores on the two sister chromatids of a mitotic chromosome attached to microtubules from each of the two spindle poles, and the comparison of the interkinetochore separation distance between the different cell shapes. (Scale bars, 5 µm and 1 µm in the main image and Inset, respectively.) Actin (magenta), microtubules (cyan), histone H2B (red), and KT Hec1 (green). *, **, ***, and **** represent P < 0.05, 0.01, 0.001, and 0.0001, respectively. (B) Cumulative profiles showing the mitotic timing for the different categories. (C) Relative occurrence of monopolar, bipolar, and multipolar spindles in the different fiber categories and 2D. The inset shows the percentage of total cells in the box area. Increased stability due to the increased number of RFs causes an increase in multipolar and a decrease in monopolar defects. (D) The shape and position of the RF spots considered in the simulations are based on the experimentally observed RF distributions. (Scale bar, 10 µm.) (E) Schematic of the computational model and the five main forces included in the model that predicts three possible outcomes of monopolar, bipolar, and multipolar spindles according to the experimental observations. (F) The similarity in spindle shapes between the computational model (Left) and experiments (Right). (Scale bar, 5 µm.) (G, Left) The parameter combinations satisfying the experimental findings in the phase space of CS–CRTX and CS–RF attraction. (Right) The statistics of monopolar, bipolar, and multipolar mitotic spindle outcomes for the 1F-elongated, 2F-elongated, and 2D-rounded cases qualitatively match experimental trends in C.

Next, we wanted to investigate whether the mitotic spindle assembly was affected by the underlying fiber geometry. To understand the relative occurrence of the spindle types, we sampled at least 300 cells (from multiple independent experiments) for each cell shape category. We observed that bipolar outcomes were the highest in all categories (increasing with the number of RFs), thus highlighting the robustness of the mitotic process (Fig. 4C). Unexpectedly, decreasing the mitotic cell-body movement stability during mitosis (1F-elongated and 2F-kite) resulted in a significantly higher percentage of monopolar spindles and reduced incidences of multipolar defects. Overall, we found that bipolar mitotic outcomes were robustly maintained across ECM-mimicking fibers and flat 2D, but the different retraction fiber geometries affected the spindle integrity and the characteristics of the chromosome segregation errors.

Theoretical and Computational Framework Validates Mitotic Spindle Outcomes.

To elucidate the underlying mechanisms of various spindle configurations in the presence of the RFs, we developed a computational model accounting for interaction forces between multiple CSs and CHs inside a rounded mitotic cell. The model is built upon our earlier construction (50), with additional modifications to account for the contributions from the RFs (SI Appendix, Eqs. S6 and S7). The attachments of the RF to the CRTX “hot spots” were chosen based on the experimental observations (Fig. 2). For example, we considered two diametrically opposite RF attachment spots on the cell surface for the 1F-elongated case (Fig. 4D) and four spots with two on one side and the other two on the diametrically opposite side of the cell surface for the 2F-elongated case. The RF spots are placed adjacent to the equatorial plane and extend downward from the equator in each case, following experimental observations (Fig. 2 A and C). For the 2D case, we considered a band of RF spots encircling the cell’s surface right below the equatorial plane. In all fiber cases, the width of the RF spot was kept constant as we did not observe significant changes in outcomes with a reduction in size or placement of RF attachment spots (SI Appendix, Fig. S7). However, notable changes can be seen with variations in the width of the RF band in the 2D-rounded case (SI Appendix, Fig. S8).

Our model treats CSs and CHs as particle-like objects, with the interaction between them described by pairwise isotropic forces that depend on their relative separation. The model considers five primary forces (Fig. 4E): 1) attractive forces between CSs, 2) attractive forces between CSs and KT, 3) repulsive forces between CS and CH arms, 4) short-ranged attraction between CSs and CRTX, and 5) short-ranged attractive forces acting on CSs from the RF spots. We employ exponentially decreasing spatial dependence of the force in each scenario, except for the force between the CS and KT, which is distance independent (50–52). These forces arise from molecular motors moving along MTs and due to the growth dynamics of the MTs (53). Utilizing stochastic energy minimization and computational force screening, we derive the mechanical conditions for monopolar (Movie S14), bipolar (Movie S15), and multipolar spindles (Movie S16).

RF attachment spots correlate with actin-rich regions on the cell surface, which are known to interact more strongly with astral MTs compared to the rest of the CRTX (26). Our primary objective is to determine the combinations of the amplitudes of attractive forces between the CSs and the RF spots (CS-RF) and the remaining cell cortex (CS–CRTX) that closely match the experimental predictions. Since bipolar spindles were the dominant outcomes in the experimental and computational analysis, we considered CS–CS, CS–CH, and CS–KT forces to be maintained at the base value corresponding to a bipolar majority (50), while we did a parameter sweep of CS–CRTX and CS–RF attractive forces to map the statistics for spindle outcomes in 1F, 2F, and 2D cases. The computed spindle statistics for monopolar, bipolar, and multipolar spindles qualitatively match the experimental outcomes in a particular region of the parameter space corresponding to the RF spots attracting the CSs ~4 to 10 times more strongly than the surrounding cortex (Fig. 4 F and G). This big difference is in agreement with previous studies, which associated all the forces applied on the MTs to the RF attachment spots (26). It is also in agreement with the analytic model of the MP fluctuations, which was fitted to the data based on the MTs getting stuck at the RF spots (Fig. 3D). We have included more details on the computational technique and model parameters (50) in the SI Appendix.

Our theoretical and computational framework allowed us to examine the mechanistic origins of differences in mitotic errors with the increase in RFs (stability). Since the CS–RF attraction is considered short ranged, each CS feels a stronger attraction from the proximal RF spots than the distal one (shown schematically in SI Appendix, Fig. S9). The attractive forces become stronger with increasing RFC. Aided by large CS–CH repulsions, the expelled CSs from the initial CS–CH mixture are attracted to the RF spots, which increases CSs aggregation chances into a bipolar CS assembly with the chromosomal ring formed in between (Movie S15). CSs merging into clusters cannot overcome the energy barrier created by the intermediate chromosomal ring, reducing the chances of becoming monopolar. Thus, the increasing RFC from 1F→2F→2D results in an increased bipolarity and a simultaneous decrease in the monopolarity (SI Appendix, Fig. S9A). Multipolarity occurs primarily when the CHs cluster in the middle and generate a strong repulsion to the CSs, preventing them from merging (SI Appendix, Fig. S9B). In fiber scenarios, however, each CS is strongly attracted toward the proximal RF spots, thereby reducing the number of multipolar clusters by merging those CSs moving toward the RF spots. In the 2D case, CSs are strongly connected to the surrounding RF band; therefore, they have limited capability to merge by overcoming the strong CS–RF attraction and CS–CH repulsion from the central CHs. This results in the highest percentage of multipolarity for the 2D-rounded scenario compared to the other fiber configurations.

Since 1F-elongated and 2D flat cases had near-opposing mitotic errors, we explored the mechanistic origins of mitotic errors by examining CS–CRTX versus CS–RF attraction contributions that led to contradictions with experimental observations (SI Appendix, Fig. S10). For CS–CRTX and CS–RF attractive forces smaller than the experimentally consistent parameter region of Fig. 4G (region 1 in SI Appendix, Fig. S10A with CS–RF attraction > CS–CRTX attraction), the percentage of monopolar spindles exceeds the multipolar spindles. For the weak CS–CRTX attractive force category, increasing the CS–RF values beyond the experimentally consistent region (region 2 in SI Appendix, Fig. S10B with CS–RF attraction >> CS–CRTX attraction) causes strong pulling on the CSs preventing them from merging. This generates a high proportion of multipolarity and a lower proportion of bipolarity for the 2D-rounded case compared to 1F-elongated. For high CS–CRTX attraction (far right on the x-axis of Fig. 4G) and low CS–RF attraction (region 3 in SI Appendix, Fig. S10C with CS–RF attraction < CS–CRTX attraction), the percentage of multipolar spindles is reduced in the 2D compared to 1F. We identify that the band-like arrangement of RFs in the 2D-rounded scenario with impaired CS–RF attraction facilitates segregating the CSs in each cell half (above and below the RF band) due to stronger attraction from the respective CRTX. The CSs are pulled toward the CRTX in their respective cell halves and merge into a single cluster in each cell half, thereby increasing (decreasing) the bipolarity (multipolarity). However, in the 1F-elongated case, the two small independent RF spots are incapable of segregating the CSs and generate comparatively fewer bipolar spindles and many multipolar spindles. Finally, for high CS–CRTX and CS–RF attraction (region 4 with CS–RF attraction > CS–CRTX attraction, SI Appendix, Fig. S10D), the greater RFC in the 2D causes a stronger overall pull on the CSs from the cell surface resulting in increased multipolarity that led to lower bipolarity than 1F.

While our in silico model captures a feasible parameter space that fits the experimentally observed mitotic spindle outcomes for different RF geometries, the model outcomes are sensitive to a few factors. Altering the range of interactions between two CSs and CS–CH substantially changes the parameter space satisfying the experiment (SI Appendix, Fig. S11). A short-ranged (or long-ranged) interaction between CSs and CHs shifts the parameter space to greater (or smaller) RF attraction with enhanced monopolarity (or multipolarity). The parameter space that fits all the observed data is substantially diminished when the experimental 2F-kite RF distribution is considered (SI Appendix, Fig. S12). Besides, the changes in the spindle statistics for the 1F-elongated, 2F-elongated, and 2F-kite cases are relatively small within this joint parameter regime irrespective of variation of the RF spot size.

Overall, our theoretical and computational framework qualitatively recovers the mitotic spindle outcomes observed experimentally. Mechanistically, we demonstrate that the CS–RF attraction needs to be considerably larger than the CS–CRTX attraction, thus confirming the role of RFC in directing mitotic outcomes on suspended fibers.

Dynamics of Daughter Cell Positioning.

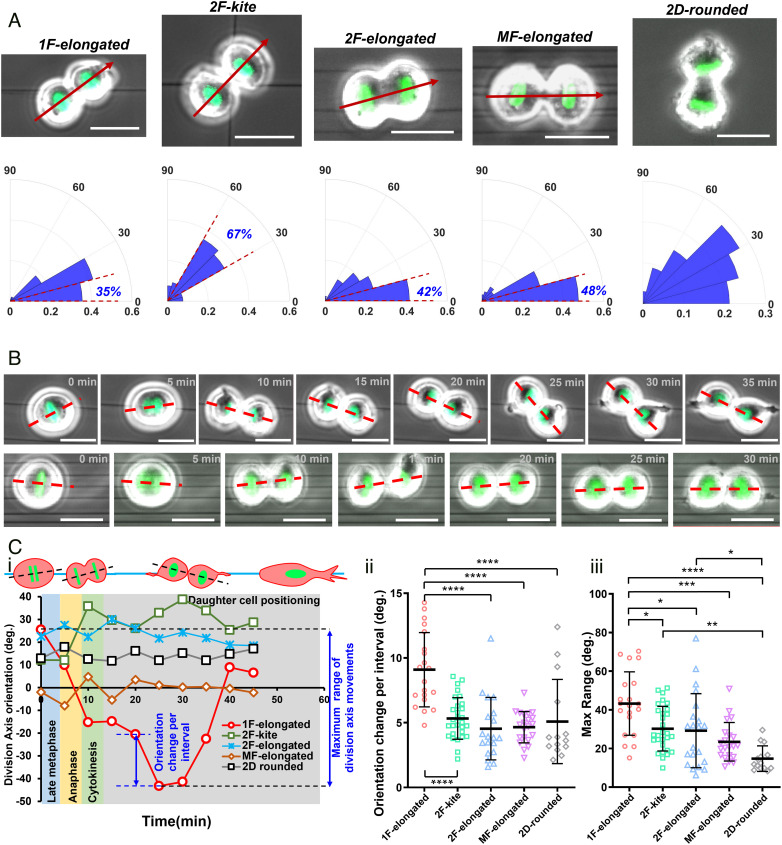
Since 3D mitotic cell body positioning, metaphase spindle dynamics, and mitotic times are governed by the organization and density of RFs, we inquired whether the orientation of the cell division axis and the subsequent positioning of the dividing daughters were also affected. We quantified the orientation of the division axis with respect to the underlying fiber orientation. Interestingly, 1F-elongated cells, the least stable cells, demonstrated the widest spread (Fig. 5A) in their division axis orientation compared to the 2F-elongated or MF-elongated cell shapes. Consistent with average metaphase plate orientations, 2F-kite shaped cells showed a distinct peak (~67%) in the 30 to 60° region, indicating the division axis to be symmetrically located between the two orthogonal focaladhesion clusters (FACs). On flat 2D substrates, due to the isotropic distribution of RFs, the division axis distribution was primarily random, in agreement with the previous reports (26). Equivalent measurement of the spindle axis orientations in our computational model correlates with the experiments (SI Appendix, Fig. S13). Since the present simulation cannot capture the cytokinesis and segregation of the daughter cells, following Hertwig’s rule, (40) we assume that the spindle axis aligns along the axis of cell division. Substantial pulling on the local CS cluster in each cell half from the proximal RF spot of the diametrically opposite two RF spot arrangement (1F-elongated case) results in the spindle axis orientated toward the fiber plane (SI Appendix, Fig. S13A). The preferred alignment of the spindle axis directly corresponds to the experimentally observed mean metaphase plate orientation at 90° in Fig. 3 A, i, which tends to form perpendicular to the spindle axis (SI Appendix, Fig. S13A). However, the isotropic RF distribution in the 2D-rounded case pulls the CS uniformly along the band favoring a random orientation of the spindle axis (SI Appendix, Fig. S13B).

Fig. 5.

Division axis orientation and daughter cell positioning on suspended fibers. (A) Polar histograms of cell division axis orientations (marked by a red arrow; division axis orientation in fiber networks is measured with respect to the undeflected horizontal fibers; for 2D-rounded category, the division axis orientation is measured with respect to the long axis of the interphase cell shape) shown for different fiber geometries; absolute acute angle magnitudes of orientation are used. n = 45, 41, 62, 105, and 33 for 1F-elongated, 2F-elongated, MF-elongated, 2F-kite, and 2D-rounded, respectively. Percentage of cells in 0 to 15° sector for aligned geometries and 30 to 60° for crosshatch geometry. (Scale bar, 20 µm.) (B) Time-lapse images showing the representative dynamics of cell division axis (red dashed line) in single fibers versus multiple fibers. (Scale bar, 20 µm.) (C, i) Representative profiles showing the variations of division axis orientation and subsequent positioning of daughter cells. (ii and iii) Statistical comparison of the orientation change per interval and maximum range of division axis movements for different substrate categories. *, **, ***, and **** represent P < 0.05, 0.01, 0.001, and 0.0001, respectively.

Additionally, following mitotic exit by the formation of the cytokinetic furrow, we observed that the orientation of the cell division axis is highly dynamic and tracked it from late metaphase (see Materials and Methods section for defining cell division axis orientation) until the time taken by daughter cells to begin spreading (Fig. 5B). As with the previous analysis (Fig. 3), we utilized two major parameters: the maximum range of orientation change in the total time period and average orientation change during individual imaging intervals (Fig. 5 C, i). In line with our analysis of the maximum 3D movement of mitotic 1F-elongated rounded bodies, we found that daughter cells of 1F-elongated cells were the most dynamic as they underwent the maximum degree of motion before spreading on fibers (Fig. 5 C, ii and iii). High-speed time-lapse microscopy demonstrated that the fluctuations in daughter cell positioning were primarily mediated by the RFs (Movies S6–S9). Not surprisingly, mitotic rounded cells essentially locked in position through the multiple retraction fiber groups on multiple fibers (MF-elongated shape) demonstrated significantly reduced fluctuations in daughter cell spreading. Overall, we found that retraction fiber-based stability directly impacted the positioning of daughter cells following mitotic exit.

Discussion

Here, we inquired about the role of cell fiber adhesion-based mechanical stability in establishing mitotic rules for cells attached to suspended ECM-mimicking nanofibers of well-controlled geometries. We designed aligned and suspended fiber networks with tunable interfiber spacing and organization to understand the interplay of interphase cell elongation and adhesion organization. Proper cell rounding from interphase shapes during mitosis plays a critical role in chromosome capture and spindle stability, allowing the spindle to locate the center of the cell accurately (54). Rounded mitotic cells retain their “memory” of their adhered interphase shape through force-bearing RFs (10) or mitotic protrusions (13). By precisely controlling the fiber networks, we were able to achieve repeatable positioning of actin-rich RFs that connect the fiber to the CRTX. These RFs applied forces on the mitotic cells, deforming them away from perfect roundness. This effect increased with the RFC of the CRTX, which increased from 1F to 2D. Our findings agree with previous studies demonstrating retraction fiber-driven sagging of rounded mitotic cells on flat surfaces, resulting in a flattened morphology (43, 55). Consistent with observations on elongated cells on micropatterns, cells on aligned fibers divided along the fiber axis (3). Our observations that the metaphase plate can undergo significant levels of oscillations are in agreement with previous studies, which also report similar movements throughout the division process (44). An increase in RFC resulted in lower MP oscillations and faster mitotic times, in agreement with a previous study demonstrating that a loss of RFs mediated by knockdown of β₅-integrins led to random orientations of the mitotic spindle and delayed mitosis (15). Here, we show that the amount of cortical coverage by RFs is determined by the geometry of the cell–ECM adhesions, which thereby critically affects the fidelity of cell division.

Recent studies have demonstrated how astral microtubules existing at either end of the mitotic spindle are mechanically linked to the CRTX and the RFs via the integrin-dependent cortical mechanosensory complex (6, 56). More recently, it has been shown that such cross talk between the mitotic spindle and the cortical motor complexes is crucial for aligning the spindle and can also impact the fidelity of the spindle assembly (57). Additionally, the tension in the astral microtubules near the CRTX depends on the contact angle between the cell surface and microtubules. For spherical cells, microtubules contacting the cortex at the shallowest angle exert the highest force (56), suggesting the possible role of friction in establishing the forces that control mitotic spindles. Our theoretical formulation of the mitotic spindle dynamics is based on mechanical interactions/links between the astral microtubules and the cortical complexes connected to RFs [integrins and other key players of the cortical mechanosensory complex, including caveolin-1, FAK, LGN-NuMA, dynein, and MISP, to the CRTX (6, 7, 53)], which presumably contribute to increased friction. Our model, therefore, predicts a constraining effect on metaphase plate movements at higher cortical coverage by RFs.

Our computational simulation elucidated the mechanical basis for the changes in spindle outcomes as RFC increased. A concomitant decrease (increase) in monopolarity (bipolarity) is observed when RFC is extended from 1F-elongated to 2D-rounded geometries. With increasing RFC, the evolving CS clusters at the opposite cell halves are efficiently pulled toward the respective CRTX, preventing them from collapsing with the CSs in the other cell half. The latter is further prevented by the repulsion from the chromosomal ring produced in between. We also found that the increased multipolarity due to increased RFs is associated with RFs strongly attracting the smaller CS clusters in the neighborhood, preventing them from merging into larger ones and increasing the multipolar centrosomal assemblies. Our observations from the computational modeling are in good agreement with another study, which also demonstrates that the adhesive pattern geometry can impact the proper assembly of the mitotic spindle, especially in the presence of two or more CSs (58).

It has been shown that for cells attached to flat 2D substrates, daughter cells spread precisely according to the mother cell adhesive patterns. Thus, the most elongated cells will have the slightest deviation in the daughter cell spreading directions (5). In contrast, we find that the most elongated shape (1F-elongated with interphase AR ~9) and kite shape on crosshatches (2F-kite with interphase AR ~1) had the widest spread in the cell division axis orientation. The cells on single fibers (1F-elongated) have two sets of RFs originating at the two peripheral FACs. In the 2F-kite category, the interphase cell is attached to four fibers (four FACs), but during mitosis, the rounded cell is located across two crossing fibers (two orthogonally located FACs). In both 1F-elongated and 2F-kite categories, the two sets of RFs cause the rounded cell bodies to have significant movement in 3D resulting in increased metaphase plate movements, mitosis duration times, and widest spread in daughter cell positioning. Cells on multiple fibers (MF-elongated) with increased stability due to a higher number of RFs match the outcomes from 2D flat control. Thus, we conclude that the interphase cell elongation factor does not completely predict daughter cell positioning in sparse fibrous environments.

In conclusion, we demonstrate the utility of our suspended fiber-based method to develop knowledge regarding mitotic progression in cells of different shapes. Our experiments and computational modeling reveal that the stability of the rounded cell body is strongly affected by the spatial organization of RFs, which is a critical property that determines mitotic outcomes and errors. The dramatic switch between monopolar and multipolar defects, as the fiber geometry changes from 1F to 2D, was unexpected. We show that it is driven by subtle changes in the RFC and geometry, which we explain mechanistically through a balance of attractive and repulsive forces applied between the CHs, MT asters, and the cell membrane. Future research may explore the impact of the switch in mitotic errors during tissue and organ development and cancer progression.

Materials and Methods

Manufacturing Nanofiber Networks.

Suspended fiber networks were generated from solutions of polystyrene (MW: 2,000,000 g/mol; category no. 829; Scientific Polymer Products, Ontario, NY, USA) dissolved in xylene (X5-500; Thermo Fisher Scientific, Waltham, MA, USA) at 7 wt% using our previously reported nonelectrospinning STEP technique (39, 40). Horizontal arrays of 250-nm fibers with interfiber spacings between 3 and 25 µm were deposited on large-diameter (~2 µm) vertical support fibers placed ~350 µm apart. Support fibers were generated from 5 wt% solutions of polystyrene (MW: 15,000,000 g/mol, Agilent Technologies) dissolved in xylene. Crosshatch networks were prepared with orthogonal layers of 250-nm fibers with an interfiber spacing of ~50 µm. Fiber networks were bonded at intersection points using a custom fusing chamber.

Cell Culturing and Cell Division Synchronization.

HeLa cells expressing histone H2B GFP cells were cultured in Dulbecco’s modified Eagle’s medium (Invitrogen, Carlsbad, CA) supplemented with 10% fetal bovine serum (Gibco, Thermo Fisher Scientific) in T25 flasks (Corning, Corning, NY, USA) and maintained at 37 °C and 5% CO₂ in a humidified incubator. Nanofiber networks were first sterilized with 70% ethanol for 10 min, followed by functionalization with 4 µg/mL fibronectin in PBS (Invitrogen, Carlsbad, CA). For select imaging experiments, fibers were coated with rhodamine-conjugated fibronectin (Cytoskeleton Inc.).

To synchronize divisions, cells were treated with 9 µM of the Cdk1 inhibitor RO-3306 for 20 h. Cells were subsequently released for division after 5 times wash with complete culture media. To capture cells at metaphase, paraformaldehyde (4%) fixation was performed ~1 h following drug washout.

Live Imaging.

Time-lapse optical imaging was performed every 5 min for extended periods of time (~12 to 16 h) to track multiple cell division events. Imaging was performed with a 20× 0.8 NA objective in a Zeiss AxioObserver Z1 microscope. GFP fluorescence was captured using a FITC filter set. Experiments were performed under incubation conditions of 37 °C and 5% CO₂ (Zeiss, Oberkochen, Germany). To capture cell body movement during mitosis, imaging was conducted at 1 to 5-s intervals at 40× 0.75 NA objective.

Immunofluorescent Staining and Imaging.

Cells were fixed with 4% paraformaldehyde for 15 min. Following 2 times PBS wash, permeabilization was performed with a 0.1% Triton X-100 solution. Permeabilized cells were washed with PBS (2×) and blocked with 5% goat serum (Invitrogen, Grand Island, NY) for 45 min. Primary antibodies were diluted in an antibody dilution buffer consisting of PBS with 1% bovine serum albumin and Triton X-100 and stored overnight at 4 °C. Primary antibodies include anti-β-tubulin (1:500, mouse monoclonal, 2 28 33, Invitrogen), anti-Hec1 (1:1,000, human monoclonal), and anti-phospho-paxillin (1:100, rabbit polyclonal, pTyr31, Invitrogen). Secondary antibodies diluted in antibody dilution buffer were added along with the conjugated Phalloidin-TRITC (Santa Cruz Biotechnology) or Alexa Fluor 647 Phalloidin (1:40 to 1:80, Invitrogen) and stored in a dark place for 45 min. Secondary antibodies include donkey anti-human IgG Alexa Fluor 555 (1:600), goat anti-mouse IgG Alexa Fluor 405 (1:500, Invitrogen), and goat anti-mouse IgG Alexa Fluor 647 (1:500, Invitrogen). Confocal microscopy was performed using a laser scanning confocal microscope (LSM 880, Carl Zeiss Inc.) with optimal imaging settings and z-slice thicknesses ranging from 0.36 to 0.5 µm.

Cell Shape Metrics.

To quantify cell shape during interphase, manual outlining of phalloidin-stained cells was performed in Image J (NIH; https://imagej.nih.gov/ij/), and AR (cell length by width) was computed using the bounding rectangle function. Cell circularity is defined by 4πA/P², where A is the spread area (μm²), and P is the perimeter (μm) of the cell. A circularity value of 1.0 was achieved for perfectly circular cells. For elongated or contoured shapes, this value is reduced and falls between 0 and 1. 3D shape characterization of mitotic cells was carried out by measuring the AR in the top view and the cross-sectional side view. Confocal z-stacks of rounded mitotic cells were utilized for the analysis, and the AR in each view was computed from the maximum intensity projection from that corresponding view.

To compute cell heights during mitosis, complete z-stacks were processed in the Zen Blue (Carl Zeiss Inc.), and orthogonal cross-sectional views (xz and yz) generated using the “ortho” function were used.

Quantification of RFs.

To quantify the number of major RFs, we have utilized confocal z-stacks of phalloidin-stained cells and have generated maximum intensity projection images. Major RFs are identified as continuous actin-rich structures emerging from the CRTX and are counted to obtain the net number associated with each interphase adhesion cluster.

Quantification of Cell Division Axis Orientation.

Orientation of the cell division axis (corresponding to Fig. 5A analysis) is quantified at the late anaphase stage. The direction of the axis is taken along the line joining the centers of the two cell lobes corresponding to daughter cells. Once daughter cells have formed, the division axis (Fig. 5 B and C) is defined by the line joining the centroids of the two daughter cells. On fiber networks, the division axis orientation is taken with respect to the undeflected horizontal fibers at all times. For cells on flat glass (2D-rounded category), the division axis orientation is taken with respect to the long axis of the interphase cell shape.

Scoring of Mitotic Defects.

Cells stained for microtubules and DNA were visually inspected under a 40× objective to categorize as bipolar, monopolar, or multipolar based on the number of spindle poles. Only cells with fully formed metaphase plates (cells which have entered metaphase) were considered for this analysis. Simultaneous staining for both microtubule arrays and CHs further enabled for differentiating between cells in prometaphase and cells which have already entered metaphase. At least 300 cells over 3 to 4 independent experiments were considered for each fiber category and flat glass, and the average proportion of observed bipolar, monopolar, and multipolar cells is reported.

Statistical Analysis.

Statistical analysis was performed in GraphPad Prism (GraphPad Software, La Jolla, CA, USA) software. Statistical comparisons among multiple groups were performed using one-way ANOVA along with Tukey’s honestly significant difference test. Pairwise statistical comparisons were performed using Student’s t test. Error bars in scatter data plots indicate SD. *, **, ***, and **** represent P < 0.05, 0.01, 0.001, and 0.0001, respectively.

Supplementary Material

Appendix 01 (PDF)

Movie S1.

HeLa cell expressing Histone H2B GFP dividing on a single fiber (timestamp-h:min) and scale bar 20 μm.

Movie S2.

HeLa cell expressing Histone H2B GFP dividing on a orthogonal arrangement of fibers (timestamp-h:min) and scale bar 20 μm.

Movie S3.

HeLa cell expressing Histone H2B GFP dividing on a fiber doublet (timestamp-h:min) and scale bar 20 μm.

Movie S4.

HeLa cell expressing Histone H2B GFP dividing on multiple fibers (timestamp-h:min) and scale bar 20 μm.

Movie S5.

HeLa cell expressing Histone H2B GFP dividing on flat glass coverslips (timestamp-h:min) and scale bar 20 μm.

Movie S6.

High-speed recording of division event of Hela cell on single fibers, showing movements of the rounded cell during metaphase (timestamp-h:min:sec) and scale bar 20 μm.

Movie S7.

High-speed recording of division event of Hela cell on crossing fibers (timestamp-h:min:sec) and scale bar 20 μm.

Movie S8.

High-speed recording of division event of Hela cell on a fiber doublet (timestamp-h:min:sec) and scale bar 20 μm.

Movie S9.

High-speed recording of HeLa division on multiple fibers (timestamp-h:min:sec) and scale bar 20 μm.

Movie S10.

Metaphase plate (MP) oscillations over the course of mitosis for HeLa cell dividing on a single fiber. Red arrow is included in the GFP channel for visual tracking of the MP oscillations (timestamp-h:min) and scale bar 20 μm.

Movie S11.

Metaphase plate (MP) oscillations for HeLa cell dividing on crossing fibers (timestamp-h:min) and scale bar 20 μm.

Movie S12.

Metaphase plate (MP) oscillations for HeLa cell dividing on fiber doublets (timestamp-h:min) and scale bar 20 μm.

Movie S13.

Reduced level of metaphase plate (MP) oscillations for HeLa cell dividing on multiple fibers (timestamp-h:min) and scale bar 20 μm.

Movie S14.

Simulation movies demonstrating the formation of a monopolar spindle in the 2D-rounded case. CSs are yellow, chromosome arms are blue, KTs are red. The region between two circular rings (colour: orange) at the equatorial area represents the RF-band.

Movie S15.

Simulation movies demonstrating the formation of a bipolar spindle in the 2D-rounded case. CSs are yellow, chromosome arms are blue, KTs are red. The region between two circular rings (colour: orange) at the equatorial area represents the RF-band.

Movie S16.

Simulation movies demonstrating the formation of a multipolar spindle in the 2D-rounded case. CSs are yellow, chromosome arms are blue, KTs are red. The region between two circular rings (colour: orange) at the equatorial area represents the RF-band.

Data, Materials, and Software Availability

Simulation code, written in C, can be accessed at https://github.com/sarkarapurba/Mitotic-outcomes-and-errors-in-fibrous-environments.git. Other study data are included in the article and/or SI Appendix.