Consistent methods for fat‐free mass, creatinine clearance, and glomerular filtration rate to describe renal function from neonates to adults

Abstract

Quantifying the effect of kidney disease on glomerular filtration rate (GFR) is important when describing variability in the clearance of drugs eliminated by the kidney. We aimed to develop a continuous model for renal function (RF) from prematurity to adulthood based on consistent models for fat‐free mass (FFM), creatinine production rate (CPR), and GFR. A model for fractional FFM in premature neonates to adults was developed using pooled data from 4462 subjects and 2847 FFM observations. It was found that girls have an FFM higher than that predicted from adult women based on height, total body mass, and sex, and boys have an FFM lower than adult men until around the onset of puberty, when it approaches adult male values. Data from 108 subjects with measurements of serum creatinine (Scr) and GFR were used to construct a model for CPR. Creatinine clearance was predicted using a model for CPR (based on FFM, postmenstrual age, and sex) and Scr that avoids discontinuous predictions between neonates, children, and adults. Individual CPR may then be used with individual Scr to predict the estimated GFR (eGFR; eGFR = CPR/Scr). A previously published model for human GFR based on 1153 GFR observations in 923 subjects without known kidney disease was updated using the model for fractional FFM to predict individual size and age‐consistent values for the expected normal GFR (nGFR). Individual renal function was then calculated using RF = eGFR/nGFR.

Study Highlights.

• WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

Fat‐free mass (FFM) is predictable from children to adults using total body mass, height, sex, and age. Creatinine‐based estimates of glomerular filtration rate (GFR) can be problematic if differences in size, body composition, and age are not accounted for appropriately.

• WHAT QUESTION DID THIS STUDY ADDRESS?

This study described a model for renal function predicted using the ratio of estimated GFR to normal GFR. This accounts for differences in size, maturation, body composition, and the effect of birth from neonates to adults.

• WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?

A method for the prediction of FFM in neonates and infants has been developed that is consistent with previous methods for children and adults. Continuous models for creatinine production rate, creatinine clearance, and GFR are described from neonates to adults. These models were used to predict renal function.

• HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?

This study provided a consistent metric describing renal function suitable for dose adjustment from neonates to adults.

INTRODUCTION

Body size is quantitatively the most important factor predicting drug clearance (CL). ¹ Size has traditionally been described using total body mass (TBM) without consideration of body composition. There is still a lack of consensus in how to describe pharmacokinetics in individuals using body composition. Normal fat mass (NFM) has been proposed because it can be parameter specific, but it relies on knowing fat‐free mass (FFM). ¹ Predictive equations for FFM have been described in adults. ² That FFM model has been extended down to children as young as 3 years of age ³ and also to include different ethnicities. ⁴ However, there is currently no continuous model predicting FFM from premature neonates to adults. Such a model would be useful to account for body composition in drug pharmacokinetics across the human age span.

Differences in the ability of the kidney to eliminate a drug or metabolites can be described using a metric that we call renal function (RF), obtained from a comparison between estimated glomerular filtration rate (eGFR) using a biomarker (e.g., serum creatinine [Scr]) and normal glomerular filtration rate (nGFR). nGFR is the expected glomerular filtration rate (GFR) in the absence of kidney disease based on size, body composition, and maturation. RF is therefore the ratio of eGFR to nGFR under the assumption that eGFR is equal to creatinine CL (CLcr). CLcr is typically calculated from Scr and an estimate of the creatinine production rate (CPR). There are two types of approaches using Scr for the estimation of GFR: mechanistic and empirical.

The first is based on mechanistic principles involving CPR and Scr to estimate CLcr (CLcr = CPR/Scr). This method is based on the relationship between the rate of elimination and the concentration that defines CL (Equation 1).

$$\text{Rate out}=\text{clearance}\times \text{concentration}$$ (1)

There are several mechanistic models for CLcr in adults ⁵ , ⁶ , ⁷ and in children. ⁸ , ⁹ , ¹⁰ These models predict CPR using covariates such as TBM (equivalent to weight), age, sex, and height and then divide by Scr to obtain CLcr.

The second approach uses empirical regression models involving similar covariates such as age, sex, race, and Scr to estimate GFR, for example, the Modification of Diet in Renal Disease (MDRD) method and the Chronic Kidney Disease Epidemiology Collaboration (CKD‐EPI) method. ¹¹ The MDRD and CKD‐EPI methods are only useful for adults and contain a race‐based covariate (skin color), which is challenging to use. ¹² , ¹³ , ¹⁴ These GFR methods implicitly use a prediction of CPR divided by Scr, although an empirical power function of Scr is typically used rather than Scr itself. Methods that scale for size, for example, per 1.73 m², need to be unscaled to obtain Clcr in the individual.

A less biased and more precise way of determining GFR is to use the gold standard measurement methods (e.g., inulin, iothalamate or iohexol CL, or radiolabeled isotope methods). However, these are seldom performed because of cost and practical difficulty. Instead, CLcr is a widely used estimate of GFR because Scr measurement is readily available in most clinical settings. eGFR equations can be implemented in pharmacokinetics studies as a quantitative way to describe kidney function. However, these equations are often developed in specific populations and may not be able to be extended down to infants and neonates when developed for adults or vice versa. This means a description of kidney function can be challenging in pharmacokinetics studies with a wide age range.

A better description of how kidney disease may affect drug disposition would be helped by consistent models for predicting differences based on factors used to calculate RF (i.e., body size, body composition, and maturation). An update to a previously published GFR model ¹⁵ has been developed using the FFM model presented in this work with a birth effect on GFR in addition to the process of maturation occurring both before and after birth. An individual with expected nGFR and no kidney disease will have an RF value of one for all combinations of size, body composition, and maturation. Typically, kidney disease will decrease RF, but values greater than one are expected with disease‐associated hyperfiltration, which has been described in septic states. ¹⁶ We describe the development of consistent FFM, CPR, and GFR models used to calculate individual RF.

METHODS

We developed a continuous model for RF comprising three submodels. For each model, the data used in its construction are presented first, followed by the calculation of the dependent variable when it is derived from other primary observations and then the model itself.

Body size

NFM ¹ is used as the descriptor for body size in the FFM, CPR, and nGFR models described in this work. NFM is an extension of the concept of predicted normal weight ¹⁷ and is a size metric derived from TBM, FFM, and theory‐based allometric concepts. NFM is calculated from FFM and TBM with an additional parameter, Ffat (Equation 2).

$$\mathrm{NFM}=\mathrm{FFM}+\text{Ffat}\times \left(\mathrm{TBM}-\mathrm{FFM}\right)$$ (2)

The influence of fat mass (TBM–FFM) combined with FFM as a predictor of theory‐based allometric size is described by Ffat. The basis of NFM is to estimate the value of Ffat, which is specific to the biological structure or function parameter being described. For example, if Ffat is estimated to be 0, then FFM alone may be used to predict size, whereas if Ffat is 1, then TBM may be used to predict size. A standard value for NFM (NFM_std) may be calculated for a male with a TBM of 70 kg, an FFM of 56.1 kg, a height of 1.76 m, and the drug parameter–specific value of Ffat (Equation 3).

$${\mathrm{NFM}}_{\mathrm{std}}=56.1+\text{Ffat}\times \left(70-56.1\right)$$ (3)

A size factor, F_size, can be obtained from NFM, NFM_std, and a theory‐based allometric exponent WBE (Equation 4). WBE is obtained from the West, Brown, and Enquist theory, which predicts an allometric exponent of 1 for structural properties (e.g., V) and ¾ for functional properties (e.g., CL). ¹⁸ NFM allows for body composition to be included in the meaning of allometric size.

$${\mathrm{F}}_{\text{size}}={\left(\frac{{\mathrm{NFM}}_{\mathrm{i}}}{{\mathrm{NFM}}_{\mathrm{std}}}\right)}^{\mathrm{WBE}}$$ (4)

Model for FFM

Data

A model to predict FFM from neonates to adults was developed using FFM observations and a published adult FFM model. ² Data were pooled from 15 studies, which included 100 mean FFM values and 2747 individual FFM observations from a total of 4462 subjects (95th percentile postmenstrual age [PMA] interval [40.6, 1134] weeks). These were used to calculate the fraction of adult‐predicted FFM (predicted from Janmahasatian et al. ² ). A data summary is presented in Table S1, and subject covariate distributions are shown in Figure S1.

Model

The dependent variable for the fractional FFM (FRFFM) model was calculated using observations of FFM from the study data (FFM_observed) and predictions of FFM from Janmahasatian et al. ² (FFM_adult) using TBM, height, and sex (Equation (5).

$$\text{FRFFM}=\frac{{\mathrm{FFM}}_{\text{observed}}}{{\mathrm{FFM}}_{\text{adult}}}$$ (5)

FRFFM is then a fraction of FFM predicted from the adult model, ² relative to the observed FFM. The FRFFM model (see Figure 1 and (Equation 6) predicts the value of FRFFM by combining a baseline (FFMIN), a component for neonates and infants (FFNEO), and a component for children (FFKID) using PMA and sex.

$$\text{FRFFM}=\text{FFMIN}+\text{FFNEO}+\text{FFKID}$$ (6)

FIGURE 1.

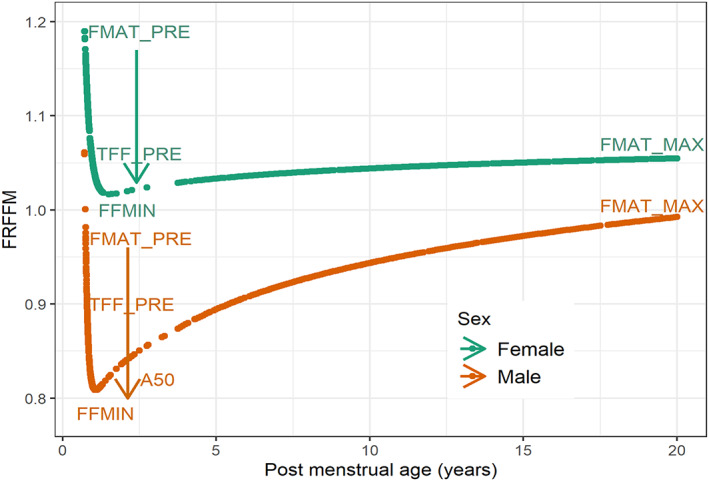
Predicted fraction of adult FFM (FRFFM) in males and females from neonates to young adults based on postmenstrual age, sex, total body mass, and height covariates in the pooled data set. The arrows show the exponential drop from FMAT_PRE to FFMIN. In males, FRFFM rises approaching adult fat‐free mass values caused by the increasing influence of the child component of the fractional model for fat‐free mass and the diminishing influence of the neonate and infant component of the fractional model for fat‐free mass. Parameter values are shown in Table 1. FFMIN, baseline component of the fractional model for fat‐free mass; FMAT_MAX, asymptotic estimate of the adult fat free mass prediction; FMAT_PRE, lower asymptote of neonate and infant component of the fractional model for fat‐free mass estimated in a 24‐week premature neonate; FRFFM, fractional model for fat‐free mass; TFF_PRE, half‐life of decrease of the neonate and infant component of the fractional model for fat‐free mass contribution to the fractional model for fat‐free mass.

The baseline, FFMIN, is obtained from FMAT_PRE, a parameter describing FRFFM in a 24‐week premature neonate, and FMAT_MAX, the asymptotic estimate of FFM_adult (Equation (7).

$$\text{FFMIN}=\text{FMAT}\_\mathrm{PRE}\times \text{FMAT}\_\mathrm{MAX}$$ (7)

The neonatal component, FFNEO, describes the exponential drop in FFM fraction from FMAT_PRE toward FFMIN. TFF_PRE is the half‐life of decrease of FFNEO, and PMAY is PMA in years (Equation 8).

$$\text{FFNEO}=\left(\text{FMAT}\_\mathrm{PRE}-\text{FFMIN}\right)\times {\mathrm{e}}^{\frac{-\log \left(2\right)}{\mathrm{TFF}\_\mathrm{PRE}\times \left(\text{PMAY}-\frac{24}{52}\right)}}$$ (8)

The child component, $\text{FFKID}$, is an asymmetrical sigmoid Emax model. $\text{FFKID}$ rises as PMA approaches adult values ($\text{FMAT}\_\mathrm{MAX}$) from baseline ($\text{FFMIN}$). $\mathrm{A}50$ is the PMAY when $\text{FFKID}$ is 50% of the adult FRFFM. The $\text{HILL}$ exponent has a different value when younger (HILL_Y) or equal to or older (HILL_O) than $\mathrm{A}50$ (Equation 9).

$$\text{FFKID}=\frac{\text{FMAT}\_\mathrm{MAX}-\text{FFMIN}}{1+{\left(\frac{\text{PMAY}}{\mathrm{A}50}\right)}^{-\text{HILL}}}$$ (9)

Each parameter of the FRFFM model is sex specific. The prediction of FRFFM is limited at 1.16 for males and 1.19 for females to avoid implausible values at very young PMA. These upper limits were obtained from the upper 95% percentile of the observed values of FRFFM. Figure 1 shows the predicted FRFFM in males and females with an indication of how the FRFFM model parameters influence the time course with increasing PMA in years.

Data from each study that provided only average measured FFM data were combined by weighting the variance of the residual error of the FFM prediction in inverse proportion to the number of subjects (Equation 10). RUV_CV is a parameter describing the proportional residual error associated with the prediction of FRFFM.

$$\mathrm{SD}=\sqrt{\frac{{\left(\text{FRFFM}\times \mathrm{RUV}\_\mathrm{CV}\right)}^2}{N_{\text{subjects}}}}$$ (10)

Model for CPR

Data

Measurements of GFR and Scr from Rhodin et al. ¹⁵ were used to construct the model for CPR. A total of 108 subjects had measurements of both GFR (not indexed to body surface area [BSA]) and Scr, with a percentile PMA interval of [27.8, 872] weeks. Covariate distributions for these subjects are shown in Figure S2. By assuming CLcr is equal to GFR, CPR can be calculated using Equation (11).

$$\mathrm{CPR}=\mathrm{GFR}\times \mathrm{Scr}$$ (11)

Assays for Scr quantitation can have poor analytical specificity, for example, the Jaffe colorimetric method. ¹⁹ , ²⁰ The Rhodin et al. ¹⁵ Scr measurements used a nonspecific Jaffe method. Plasma proteins, immunoglobulins, and other drugs (e.g., cephalosporins) are known to interfere with the Jaffe assay. ²¹ Enzymatic methods used for Scr quantitation are more accurate, have greater specificity, and are less affected by interfering substances. ²⁰ , ²² The Jaffe method for Scr determination is still widely used, which can be challenging when CPR is predicted using a more specific method. A conversion factor may be used to convert Jaffe Scr measurements to the more specific enzymatic equivalent (Equation 12). ²³

$${\mathrm{F}}_{\mathrm{Scr}}=\frac{\left(88.4-{\mathrm{NCr}}_{\mathrm{std}}\right)}{88.4}=0.748$$ (12)

The value of 88.4 is the μmol/L equivalent of 1 mg/dL. NCr_std is the offset required to make a Jaffe method measurement approximately equivalent to an enzymatic method measurement. Olympus 5400 and Roche H917 methods are corrected for noncreatinine chromogens with offsets of 26.5 and 18 μmol/L, respectively. ²³ Where the machine‐type information is not available, an average offset of 22.25 μmol/L may be used, giving an F_Scr value of 0.748. The original Rhodin et al. ¹⁵ Jaffe Scr measurements were corrected by F_Scr to approximate the more specific enzymatic measurements.

Model

CPR can be predicted using a population standard for CPR, size, and age. The model for CPR based on these factors is shown in Equation (13).

$$\mathrm{CPR}={\mathrm{CPR}}_{\mathrm{std}}\times {\mathrm{F}}_{\text{size}}\times {\mathrm{F}}_{\mathrm{MAT},\mathrm{CPR}}$$ (13)

CPR_std is the standard enzymatic equivalent CPR for a 40‐year‐old male based on the estimate for a male with 70 kg TBM (0.386 mmol/h/70 kg = 0.516 mmol/h/70 kg x ${\mathrm{F}}_{\mathrm{SCr}}$). ⁷ Size is scaled using FFM because Ffat was estimated to be close to zero. The allometric exponent for CPR uses the theory‐based value of one as CPR comes from muscle mass, which is a structural rather than a functional property. An empirical maturation function (F_MAT,CPR) based on PMA was used to describe the maturation of CPR from premature neonates to young adults. This function has three segments depending on PMA (Equations (14), (15), (16)).

After accounting for body size, when PMA is less than or equal to 37 weeks, the CPR does not seem to increase and is described by the constant CPR_int (Equation 14).

$${\mathrm{F}}_{\mathrm{MAT},\mathrm{CPR}}={\mathrm{CPR}}_{\mathrm{int}}$$ (14)

From infants to adults (PMA >37 to 1080 weeks PMA_adult/20 years postnatal age [PNA]), the CPR maturation function is describable by a linear function (${\mathrm{CPR}}_{\text{slope}}$; (Equation 15). Both the CPR_int and CPR_slope parameters are sex specific.

$${\mathrm{F}}_{\mathrm{MAT},\mathrm{CPR}}=1+\frac{{\mathrm{CPR}}_{\text{slope}}\times \left({\mathrm{PMA}}_{\text{adult}}-\mathrm{PMA}\right)}{100}$$ (15)

For adults (>20 years PNA), CPR is calculated using the Matthews et al. ⁷ modification of the Cockcroft and Gault model (Equation 16).

$${\mathrm{F}}_{\mathrm{MAT},\mathrm{CPR}}=\frac{112-\mathrm{AGE}}{\left(112-40\right)}\left(\times 0.82\text{if female}\right)$$ (16)

Low Scr concentrations in adults are more likely to be due to low CPR rather than unusually high renal function. Methods have been proposed where Scr concentrations below 0.06 mmol/L (Jaffe) are simply rounded up to 0.06 mmol/L, which ignores the actual Scr. ²⁴ , ²⁵ The Matthews et al. ⁷ method (Equation 17) does not discard information about RF contained in the Scr. It proposes a factor for CPR change with a reduction by 0.7 when Scr is less than 0.049 mmol/L (enzymatic equivalent) = 0.06 x ${\mathrm{F}}_{\mathrm{Scr}}$ mmol/L (Jaffe).

$${\mathrm{F}}_{\mathrm{MAT},\mathrm{CPR}}=\frac{119-\mathrm{AGE}}{\left(119-40\right)}\times 0.7$$ (17)

Prediction of CLcr

CLcr can then be calculated from a measurement of Scr and predicted CPR (Equation 13). This typically assumes that Scr is at steady state so that CPR (rate in) is an estimate of the rate of elimination (rate out). When GFR is changing rapidly, Scr cannot be assumed to be at steady state. Creatinine pharmacokinetics can be used to account for rapidly changing Scr by predicting the CLcr at the time of Scr measurement. Creatinine is assumed to have a single distribution volume (Vcr = 0.5 L/kg * TBM) and renal elimination CL (CLcr L/h). The creatinine elimination rate constant (Kcr; calculated from CLcr/Vcr) is then used with the observed Scr (ScrNOW) to calculate CLcr at that time. The first Scr is assumed to be at steady state to calculate the initial CLcr used to initialize the CLcrLAST variable. The time (h) of the first Scr observation is used to initialize the HLAST variable. At subsequent times (HNOW) of Scr, the CLcr (CLcrNOW) is obtained by solving the creatinine pharmacokinetic model for ScrNOW.

$$\begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}\text{DELTA}=\text{HNOW}-\text{HLAST};\text{time between}\mathrm{Scr}\text{measurements}\hfill \\ \mathrm{Kcr}=\frac{\text{CLcrLAST}}{\mathrm{Vcr}}\\ \text{ScrNOW}=\frac{\mathrm{CPR}\times \left(1-{\mathrm{e}}^{-\mathrm{Kcr}\times \text{DELTA}}\right)}{\text{CLcrNOW}}-\text{ScrLAST}\times {\mathrm{e}}^{-\mathrm{Kcr}\times \text{DELTA}}\end{array}\\ \text{CLcrNOW}=\frac{\mathrm{CPR}\times \left(1-{\mathrm{e}}^{-\mathrm{Kcr}\times \text{DELTA}}\right)}{\text{ScrNOW}-\text{ScrLAST}\times {\mathrm{e}}^{-\mathrm{Kcr}\times \text{DELTA}}}\end{array}\hfill \end{array}\hfill \end{array}$$ (18)

After each calculation (Equation 18), CLcrNOW becomes CLcrLAST and HNOW becomes HLAST to continue the algorithm. Scr is not reliable as a predictor of CLcr immediately after birth because most Scr in the neonate is derived from the mother. At this time, it is usually plausible to assume that GFR is normal. The estimate of Kcr based on nGFR and Vcr can be used to predict the creatinine half‐life and how long it will take for most of the maternally derived creatinine to have been eliminated, for example, after four creatinine half‐lives. After then, it becomes reasonable to use measured Scr in neonates to estimate CLcr.

Model for nGFR

Data

A model has been previously described for the growth of GFR based on gold standard measurements in subjects with normal kidney function. ¹⁵ These data were composed of 1153 GFR observations in 923 subjects, with a percentile PMA interval of [28.3, 1071] weeks.

Model

The Rhodin et al. ¹⁵ model describing GFR was updated using FFM as a measure of size from the FRFFM model described previously and the addition of a PNA maturation function, which describes a birth effect (Equation 21). nGFR describes GFR predicted under the assumption of normal kidney function. nGFR changes rapidly after birth due to increasing body size (growth) and increasing age (maturation). ²⁶ Theory‐based allometry and maturation models can be used to describe the impact of these processes on GFR using Equation (19).

$$\text{nGFR}={\mathrm{GFR}}_{\mathrm{std}}\times {\mathrm{F}}_{\text{size}}\times {\mathrm{F}}_{\mathrm{mat},\mathrm{PMA}}\times {\mathrm{F}}_{\mathrm{mat},\mathrm{PNA}}$$ (19)

GFR_std is the mature population estimate for GFR of a male with TBM 70 kg and height of 176 cm. NFM, specific for GFR, was used to predict F_size (Equation 4). A sigmoid Emax model was used to describe the maturation of GFR with respect to PMA. To account for maturation of GFR and the impact of birth, two maturation fractions were combined based on PMA (F_mat,PMA weeks) and PNA (F_mat,PNA days). F_mat,PMA is defined in terms of TM₅₀, the maturation half time, that is, the PMA (weeks) at 50% of the fully mature value of one, and HILL, a parameter that describes the steepness of the maturation curve (Equation (20).

$${\mathrm{F}}_{\mathrm{mat},\mathrm{PMA}}=\frac{1}{1+{\left(\frac{\mathrm{PMA}}{{\mathrm{TM}}_{50}}\right)}^{-\text{HILL}}}$$ (20)

Transition from the intrauterine to the extrauterine environment is associated with major changes in blood flow and oxygenation. This can cause changes in GFR, kidney function, and drug metabolism. ²⁷ , ²⁸ Therefore F_mat,PNA (PNA maturation) was used to describe changes in addition to those predicted from PMA alone (Equation 21).

$${\mathrm{F}}_{\mathrm{mat},\mathrm{PNA}}=1-{\mathrm{PNA}}_{\max }+{\mathrm{PNA}}_{\max }\times \left(1-{\mathrm{e}}^{\frac{-\ln \left(2\right)\times \text{PNAD}}{\text{PNAT}50}}\right)$$ (21)

PNA_max is the fractional increase relative to the completion of the birth‐associated component of maturation, PNAT₅₀ is the half time required to achieve 50% of this maturational change, and PNAD is PNA in days. F_mat,PMA and F_mat,PNA approach an asymptote of 1, signifying completion of these maturational processes.

Prediction of RF

RF is defined by the ratio of eGFR to nGFR (Equation 22). It differs from the more general term kidney function by proposing a quantitative measure of efficiency of all functions of the kidney that are linked with CLcr and GFR.

$$\mathrm{RF}=\frac{\text{eGFR}}{\text{nGFR}}$$ (22)

eGFR can be predicted using CPR and Scr with the assumption that CLcr is the same as GFR (Equation 23).

$$\text{eGFR}=\text{eCLcr}=\frac{\mathrm{CPR}}{\mathrm{Scr}}$$ (23)

This makes RF a quantity that is independent of size, body composition, maturation, and birth effects when these factors are consistently accounted for in both eCLcr and nGFR. The new models presented here for FFM, CPR, and nGFR allow a continuous function to predict RF from premature neonates to adults.

Data analysis

Data were analyzed using NONMEM (ICON Development Solutions) Version 7.5.1 and Wings for NONMEM Version 744 (http://wfn.sourceforge.net/). Population parameter estimates were obtained using NONMEM's first‐order conditional estimation method with the interaction option. The convergence criterion was 3 with tolerance SIGLEVEL = 6. Nonparametric bootstrapping was used to evaluate parameter uncertainty in each model. ²⁹ A total of 100 bootstrap replicates were used to describe the distribution of the parameter estimates and estimate the uncertainty of the prediction.

Visual predictive checks were used to evaluate the models by comparing the 5th, 50th, and 95th percentiles of the observed and model‐predicted values. ³⁰ The 95% confidence intervals were estimated from the distribution of each of the prediction percentiles. Further details on the data analysis are presented in Appendices S2 to S4.

RESULTS

Model for FFM

Sex‐specific parameter estimates for the FRFFM model are presented in Table 1. Population parameter variability (PPV) was estimated for TFF_PRE (half‐life decrease of FFNEO) and A50 (PMAY at 50% of FFKID) with the same PPV for males and females. The residual error was described using a proportional model for the random effect.

TABLE 1.

Original parameter estimates for the FRFFM model and bootstrap estimates from 100 bootstrap runs.

Parameter	Unit	Original	Bootstrap average	Bootstrap 2.5th percentile	Bootstrap 97.5th percentile	Bootstrap RSE (%)
Females
FMAT_PRE		0.837	1.33	0.850	1.76	18.5
TFF_PRE	PMA y	0.12	0.10	0.08	0.12	9.4
FFMAT		0 FIXED	0	0	0	–
FMAT_MAX		2.03	2.05	2.02	2.08	0.9
A50	PMA y	1.53	1.95	0.255	4.48	152
HILL_Y		0.0339	0.0290	0.0170	0.0386	20.1
HILL_O		0.0306	0.0249	0.0144	0.0325	20.6
PPV_TFF_PRE		0.016	0.032	0.000	0.118	110.8
PPV_A50		3.67	4.61	3.39	8.01	27.0
Males
FMAT_PRE		5.20	5.03	1.62	9.95	46.3
TFF_PRE	PMA y	0.060	0.064	0.051	0.090	16.4
FFMAT		0 FIXED	0	0	0	–
FMAT_MAX		1.74	1.72	1.68	1.75	1.1
A50	PMA y	3.54	3.27	2.34	4.06	12.8
HILL_Y		0.127	0.118	0.063	0.178	28.9
HILL_O		0.164	0.173	0.144	0.206	9.3
PPV_TFF_PRE		0.130	0.128	0.103	0.158	10.5
PPV_A50		1.015	0.964	0.767	1.125	10.0
Residual error
CV_FRFFM		0.046	0.046	0.042	0.051	4.8

Note: The bootstrap 2.5th and 97.5th percentiles form the empirical 95% confidence interval. RSE is calculated from the bootstrap standard deviation divided by the bootstrap average.

Abbreviations: A50, age at which the child component of fractional model for fat‐free mass is 50% of the adult value; CV, coefficient of variation (proportional residual error calculated from the square root of sigma); FFMAT, fraction of asymptotic estimate of the adult fat‐free mass prediction that describes the lower asymptote of the fractional model for fat‐free mass; FMAT_MAX, asymptotic estimate of the adult fat‐free mass prediction; FMAT_PRE, lower asymptote of the neonate and infant component of the fractional model for fat‐free mass estimated in a 24‐week premature neonate; FRFFM, fractional model for fat‐free mass; HILL_O, Hill exponent above or equal to the age at which the child component of fractional model for fat‐free mass is 50% of the adult value; HILL_Y, Hill exponent below the age at which the child component of fractional model for fat‐free mass is 50% of the adult value; PMA, postmenstrual age; PPV, population parameter variability calculated from the square root of omega; RSE, relative standard error; TFF_PRE, half‐life decrease of the neonate and infant contribution to the fractional model for fat‐free mass.

Girls have an FFM larger than adult‐predicted FFM (see female FRFFM predictions, Figure 1). Boys have an FFM lower than adult‐predicted FFM until about the onset of puberty, when it approaches adult values (see male FRFFM predictions, Figure 1). There is high uncertainty in the estimate of A50 in females. This is likely due to the sparse data between 1.5 and 4 years PMA. The visual predictive checks of the FRFFM model (Figure 2) show that the difference between males and females is well described by the median prediction of the observed value.

FIGURE 2.

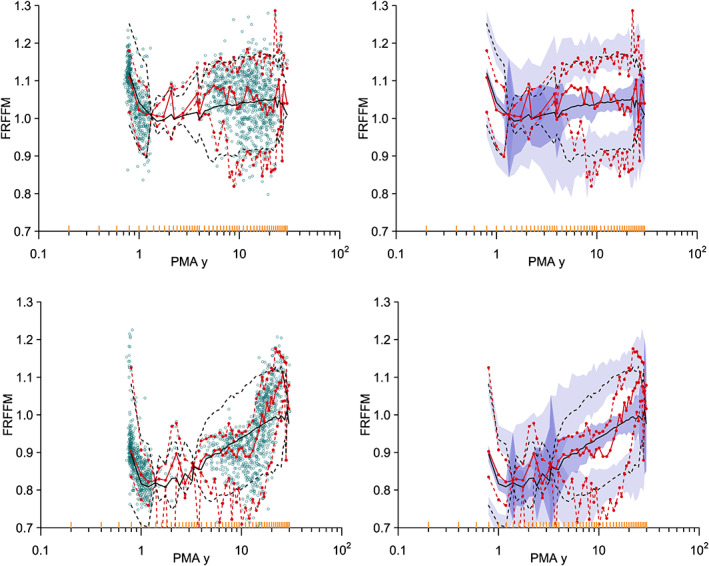
Visual predictive check for the FRFFM model in females (top) and males (bottom). The 5% percentile, median, and 95% percentile of the distribution of the observations are red, and predictions are black. The hollow circles in the left‐side plots are the individual observations. The 95% confidence intervals for the prediction percentiles are shown by the purple‐shaded areas in the right‐side plots. The yellow lines on the x‐axis show the data bins used in the construction of the visual predictive check. FRFFM, fractional model for fat‐free mass; PMA, postmenstrual age.

Model for CPR

The parameter estimates for the CPR model are shown in Table 2. FFM alone was used to predict the size for CPR based on the assumption that muscle mass (the primary source of creatinine) is not affected by fat mass, and therefore FfatCPR = 0. The residual error was described using a proportional error model for the random effect. The PPV of the coefficient of variation was estimated.

TABLE 2.

Original parameter estimates from the CPR model and bootstrap estimates from 100 bootstrap runs.

Parameter	Unit	Original	Bootstrap average	Bootstrap 2.5th percentile	Bootstrap 97.5th percentile	Bootstrap RSE (%)
Females
CPRint	mmol/h	0.720	0.700	0.609	0.822	9.3
CPRslope	mmol/h/week PMA	−0.0274	−0.0346	−0.0464	−0.0123	27.8
Males
CPRint	mmol/h	0.764	0.780	0.623	1.075	15.1
CPRslope	mmol/h/week PMA	−0.0315	−0.0358	−0.0515	−0.0217	22.3
Residual error
CV_CPR		0.228	0.213	0.169	0.255	10.1
PPV_RUV_CPR		0.503	0.522	0.037	0.820	32.2

Note: The bootstrap 2.5th and 97.5th percentiles form the empirical 95% confidence interval. RSE is calculated from the bootstrap standard deviation divided by the bootstrap average.

Abbreviations: CPR, creatinine production rate; CPR_int, maturation constant when postmenstrual age ≤37 weeks; CPR_slope, linear maturation function gradient when postmenstrual age is >37 weeks and ≤1080 weeks; CV, coefficient of variation (proportional residual error calculated from the square root of sigma); PMA, postmenstrual age; PPV, population parameter variability calculated from the square root of omega; RSE, relative standard error; RUV, residual unexplained variability.

CPR predictions from neonates to adults using data from the GAVamycin covariate database are shown in Figure S3. Comparison of CPR predictions between our model and other published models are presented in Figures S4 and S5. The visual predictive check for the CPR model (Figure 3) shows that the observed percentiles are well described by the model predictions.

FIGURE 3.

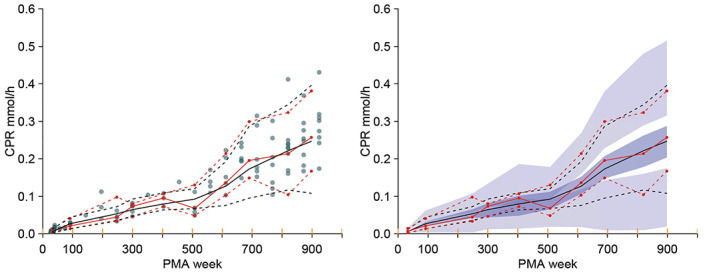
Visual predictive check for the CPR model. The 5% percentile, median, and 95% percentile of the distribution of the observations (red lines) and predictions (black lines) compare the distributions. The filled circles in the left‐side plot are the individual observations. The 95% confidence intervals for the prediction percentiles are shown by the purple‐shaded areas in the right‐side plot. The yellow lines on the x‐axis show the data bins used in the construction of the visual predictive check. Data from Rhodin et al. ¹⁵ CPR, creatinine production rate; PMA, postmenstrual age.

Model for nGFR

The parameter estimates for the updated nGFR model are shown in Table 3. Size was predicted using FFM (Ffat_GFR estimated and not distinguishable from zero) in the update to the nGFR model reported previously. ¹⁵ The maturation and postnatal effects of birth on GFR were investigated using models for PMA maturation and postnatal transition (PNT). ²⁸ The FRFFM model was used to describe GFR changes with size. An asymptotic exponential PNT maturation model (PNTexp) described the effect of birth on GFR maturation and included factors for PNT and PMA maturation. Figure S6 shows the differences in a PMA maturation model (PMAonly) compared with the PNTexp model (PMA plus PNT). Maturation was slower before birth using the PNTexp model compared with PMA maturation alone. At birth, the relative GFR estimate was 25% less using the PNTexp model compared with PMAonly, but this difference increased to 60% during the first weeks of life. The estimated GFR_std was 116 mL/min/70 kg TBM (size equivalent to 56.1 kg FFM) in a standard male. The visual predictive check for the GFR model (Figure 4) shows good agreement between the observed and predicted percentiles, confirming the assumptions of the model.

TABLE 3.

Updated parameter estimates for the GFR model using data from Rhodin et al. ¹⁵ and bootstrap estimates from 100 bootstrap runs.

Parameter	Unit	Original	Bootstrap average	Bootstrap 2.5th percentile	Bootstrap 97.5th percentile	Bootstrap RSE (%)
PMAT50	PMA week	33.6	33.7	29.5	39.1	7.2
PMAHILL		3.49	3.55	2.95	4.50	11.4
PNAMAX		0.588	0.585	0.474	0.674	9.1
PNAT50	PNA day	6.94	7.13	3.54	11.9	26.4
GFR_STD	mL/min/70 kg TBM	116	116	112	120	1.6
FFAT		0 FIXED	0	0	0	–
PPV_GFR		0.197	0.193	0.157	0.239	10.2
Residual error
CV_GFR		0.249	0.250	0.209	0.279	10.2

Note: The bootstrap 2.5th and 97.5th percentiles form the empirical 95% confidence interval. RSE is calculated from the bootstrap standard deviation divided by the bootstrap average.

Abbreviations: CV, coefficient of variation (proportional residual error calculated from the square root of sigma); GFR, glomerular filtration rate; GFR_STD, population standard glomerular filtration rate; PMA, postmenstrual age; PMAHILL, Hill exponent for the postmenstrual age maturation function; PMAT50, postmenstrual age at 50% of the fully mature value of 1; PNA, postnatal age; PNAMAX, fractional increase relative to the completion of the birth associated component of maturation; PNAT50, postnatal age required to achieve 50% of the fractional increase relative to the completion of the birth associated component of maturation; PPV, population parameter variability calculated from the square root of omega; RSE, relative standard error; TBM, total body mass.

FIGURE 4.

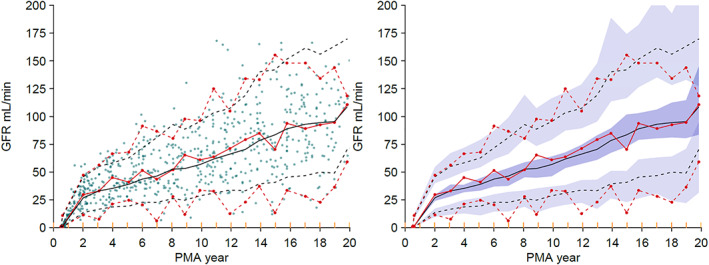
Visual predictive check for the GFR model, based on a theory‐based allometric model for size with maturation based on the postnatal transition maturation model. The 5th, median and 95thpercentiles of the distribution of the observations are shown as red lines and the predictions as black lines. The filled circles in the left‐side plot are the individual observations. The 95% confidence intervals for the prediction percentiles are shown by the purple‐shaded areas in the right side‐plot. The yellow lines on the x‐axis show the data bins used in the construction of the visual predictive check. GFR, glomerular filtration rate; PMA, postmenstrual age.

Renal function

RF was predicted using Equation (22). Evaluation of predictions of RF (Figure S7) was performed using covariates from a large population (9998 patients) treated with renally eliminated antibiotics (the GAVamycin covariate database ³¹ ).

DISCUSSION

We propose a definition of RF that is based on GFR. We use the term RF as a metric to describe kidney function. This is different to the more common use of RF, which is not necessarily quantitative. RF accounts for metrics including CPR, size, body composition, maturation, and the effect of birth—which in turn are predicted from primary observations of Scr, TBM, height, sex, and age (postmenstrual and postnatal). We developed a continuous model for RF comprising submodels of GFR (based on data from Rhodin et al. ¹⁵ ) and new models for CPR and size based on FFM.

The model for FFM described in this article extends the prediction of FFM to neonates and extends the model previously reported for children, ³ which in turn was based on extrapolation from a model developed in adults. ² Using NFM as a measure of size can be used to understand how body function is related to size and body composition. The parameter estimates for the human GFR model ¹⁵ have been updated using the fractional model for FFM extended to infants and neonates in the current analysis. We have shown that CPR from premature neonates to young adults can be predicted using FFM, PMA, and sex. The increase in CPR from premature neonates to adults is assumed to be a consequence of increasing muscle mass as opposed to the decrease in CPR associated with the loss of muscle mass that occurs with older age. Our model for CPR shows lower predictions in older individuals (Figure S5) than other published models. Empirical models for eGFR do not make the explicit assumption that CLcr = GFR, which we have used to develop a model for CPR (Equation 23) and may explain this prediction difference.

A recent publication comparing creatinine‐based methods to estimate measured GFR found a worst‐case bias of 7% and best‐case bias of 0.7% ³² when comparing unscaled estimates of CLcr and measured GFR. This is similar in magnitude to the bias reported by Soveri et al. ³³ with different methods of measuring GFR directly when compared with renal CL of inulin. Thus we think the bias in the estimation of GFR using a creatinine‐based method is clinically negligible for the purpose of calculating RF. Even if the estimate of RF is biased in relation to GFR, it does not change the usefulness of this metric for describing kidney function because differences in CPR, size, body composition, and maturation are used in a consistent and principled way. This should be contrasted with the common practice of expressing GFR as a function of estimated BSA when there is no biological link between skin and GFR. The use of BSA is widely used to standardize GFR across the human size and age range but has no rationale apart from clinical tradition derived perhaps from the misunderstanding of studies of heat loss, ³⁴ which can be plausibly linked to BSA, but not to GFR. Systematic differences in eGFR predictions have been reported with the exclusion of the race covariate from some creatinine‐based equations. ³⁵ , ³⁶ Our model for eGFR may not have this racial bias due to the theory‐based, rather than empirical, approach to GFR prediction. This could be tested but would have to be evaluated in a US population with Black individuals.

Determining drug dosage based on GFR estimates should use them in a consistent way that is adapted to all sizes, maturations, and body compositions. This is what is achieved using our model for RF. It can predict variability in renal drug elimination across a broad range of age from birth to older adulthood. Exploration of a link between RF and other covariates such as exposure to potentially nephrotoxic medication is now feasible given a consistent age and size metric for kidney function.

AUTHOR CONTRIBUTIONS

C.J.O.H. and N.H. wrote the manuscript. A.S., H.S.A.‐S., and N.H. designed the research. C.J.O.H., A.S., H.S.A.‐S., and N.H. performed the research. C.J.O.H., H.S.A.‐S., and N.H. analyzed the data.

FUNDING INFORMATION

No funding was received for this work.

CONFLICT OF INTEREST

The authors declared no competing interests for this work.

Supporting information

Appendix S1

Appendix S2

Appendix S3

Appendix S4

O’Hanlon CJ, Holford N, Sumpter A, Al‐Sallami HS. Consistent methods for fat‐free mass, creatinine clearance, and glomerular filtration rate to describe renal function from neonates to adults. CPT Pharmacometrics Syst Pharmacol. 2023;00:1‐12. doi: 10.1002/psp4.12924

DATA AVAILABILITY STATEMENT

The full data that support the findings of this study are not publicly available due to privacy or ethical restrictions. Example data fragments have been provided from the databases used in the construction of the figures in this work. All data has been deidentified with the addition of random variability to the values. The R script containing code for all models described in this work as well as for the construction of the figures has been provided. The data fragments and R script can be used together to reproduce the models and figures.