A hybrid deep forest-based method for predicting synergistic drug combinations

Summary

Combination therapy is a promising approach in treating multiple complex diseases. However, the large search space of available drug combinations exacerbates challenge for experimental screening. To predict synergistic drug combinations in different cancer cell lines, we propose an improved deep forest-based method, ForSyn, and design two forest types embedded in ForSyn. ForSyn handles imbalanced and high-dimensional data in medium-/small-scale datasets, which are inherent characteristics of drug combination datasets. Compared with 12 state-of-the-art methods, ForSyn ranks first on four metrics for eight datasets with different feature combinations. We conduct a systematic analysis to identify the most appropriate configuration parameters. We validate the predictive value of ForSyn with cell-based experiments on several previously unexplored drug combinations. Finally, a systematic analysis of feature importance is performed on the top contributing features extracted by ForSyn. The resulting key genes may play key roles on corresponding cancers.

Graphical abstract

Highlights

• •ForSyn is a deep forest-based method that predicts synergistic drug combinations
• •ForSyn handles imbalanced, high-dimensional, and medium-scale datasets
• •The predictive model is validated with cell-based assays
• •Key genes can be extracted by the model for interpretable analysis

Motivation

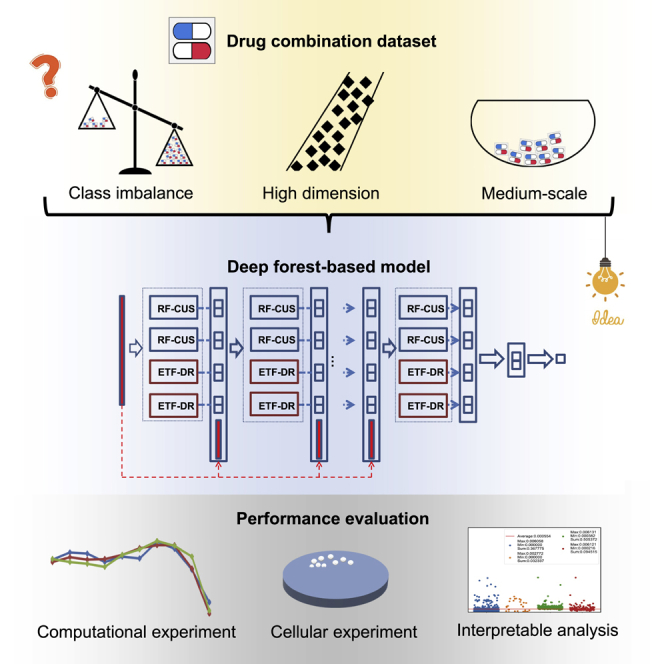
Combination therapy has shown promise as a treatment for complex diseases such as cancer. Synergistic drug combinations can offer increased therapeutic efficacy and reduce toxicity compared with single drugs. However, class imbalances in datasets have complicated the use of computational tools, such as deep learning, for synergistic drug prediction. We propose an improved deep forest-based model, ForSyn, to address the above problem on imbalanced, medium- or small-scale datasets with high dimensionality.

Wu et al. develop ForSyn, an improved, deep forest-based method that predicts synergistic drug combinations in cancer cell lines. ForSyn can effectively handle imbalanced and high-dimensional data in medium- and small-scale datasets. ForSyn predictions are validated with cell-based assays.

Introduction

There has been important progress in anticancer drugs, especially targeted therapies. However, many tumors inevitably become resistant to the single agents.^1,2,3 To overcome the limitations of monotherapy, combination therapy has been proposed as a new treatment approach. In combination therapy, multiple drugs can target multiple targets, subpopulations, or diseases simultaneously.^4,5 Compared with monotherapy, combination therapy can increase therapeutic efficacy, reduce toxic side effects, and slow down the development of drug resistance.^1,6,7,8,9 For these therapeutic benefits, combination therapy has become a standard clinical treatment strategy for several complex diseases including cancers.⁷

Systematic surveys of effective drug combinations in vitro have been proposed such as the high-throughput screening method.¹⁰ However, it is insufficient for the large-scale experiments to search across such a large drug combination space.^11,12,13 To solve these problems, some computational approaches have been proposed such as network analysis^14,15,16 and mathematical models.¹⁷ But most of them are often limited in the prior knowledge of biomedicine and the complexity of networks.¹⁴ Alternatively, deep learning, as a data-driven computing method, has been widely used in drug combination prediction because of its generality, generalization and high prediction performance. Almost all deep learning methods used in drug combination prediction are based on deep neural networks (DNNs), including feedforward neural network,^18,19 deep belief network,²⁰ autoencoder,²¹ transformer,²² and graph neural network (GNN).²³ Although these methods have achieved high overall prediction performance, the problem of class imbalance is ignored. In drug combination dataset, the number of positive samples (minority class) involving synergistic drug combinations is usually small. Although most samples are negative samples (majority class) including antagonistic, additive and slightly synergistic drug combinations, which is usually more than ten times the number of positive samples. Most previous methods are based on the assumption that the distribution of training samples in each class is balanced. In the case of imbalanced data, the classification results are usually biased toward the majority class.^24,25 That is, the model tends to predict more samples as majority (negative) class to obtain higher overall prediction accuracy, while ignoring the prediction accuracy on minority (positive) class. Especially in DNN-based methods, it is prone to over-fitting because of the samples in minority class are particularly rare. Anand et al.²⁶ explored the impact of imbalanced data on the neural network backpropagation algorithms. They showed that the majority class essentially dominates the gradient of the network and is responsible for the weight update of the model. The classification error of the majority class will rapidly decrease in the early iteration process, while the classification error of the minority class will increase and cause the network to fall into a slow convergence mode.

In addition, most previous studies only applied structural and physicochemical properties of drugs, and gene expression profiles of untreated cancer cell lines to construct the feature set. This may ignore the biological connection between drugs and cancer cells, as synergism is the response of cells to drugs.⁵ The response of cancer cells to drugs should also be considered.^27,28,29,30 Once more informative feature types are applied, the samples with missing features should be removed. The number of samples will be reduced, and the dimension of each sample’s feature will be increased. The DNN-based methods always rely on the large-scale training datasets, and it is difficult to maintain its prediction performance on a medium- or small-scale dataset. Small sample size dataset with high dimensionality has further aggravated the difficulty in drug combination prediction. This is also an inherent problem in many biomedical datasets with multi-view/multi-omics data.

Given the powerful performance of deep learning technology on classification tasks, it is of great importance to explore the application of non-neural network deep learning technology on imbalanced, medium- or small-scale datasets with high dimensionality. Zhou et al.³¹ proposed the deep forest (DF) model, which can be regarded as an alternative to DNN. DF is a multi-layer cascade structure, where each layer is composed of multiple tree-based forests. Each forest can be regarded as a unit in a cascade layer, similar to the neurons in the DNN. Compared with the DNN, the DF has the following advantages: suitable for datasets of different sizes, few hyper-parameters, and adaptive generation of model complexity.³² The model complexity of DF can be adaptively determined under sufficient training. This advantage makes DF applicable to datasets of different scales, especially medium-sized datasets.³³ Because of its advantages, DF has been widely used in many fields, such as image retrieval,³⁴ cancer sub-category identification,³⁵ online financial cash-out monitoring,³⁶ etc. In the field of drug combination prediction, Zhang et al.³⁷ proposed a DF-based model, DCE-DForest, consisting of two components, a drug Bert³⁸ and a DF model. The Bert is a pretrained neural network to obtain the representations of drugs, and a DF is used to predict drug combinations. First, the drug representations extracted by Bert cannot fully represent the multi-view (physical, biological, etc.) information of drugs. Each dimension of the representations has no specific meaning and cannot be interpreted. Second, DCE-DForest uses the original DF framework and does not consider the case of data with imbalance and high feature dimension.

To solve the above problems, we first construct a feature set consisting of physical, chemical and biological properties of drugs, in which the key features can be evaluated through ForSyn. The feature types include drug molecular fingerprints (DMFs), drug physicochemical properties (DPPs), cell line-specific drug-induced gene expression profiles (DGEs), and gene expression profiles of untreated cell lines (CGEs). The cell line-specific DGE feature can not only capture biological connection between drugs and cancer cells, but also be generalized to the study of patients.³⁹ Each dimension of the curated feature types has a specific meaning, which can facilitate the interpretable analysis to find out the key features in prediction process. Faced with this imbalanced, high-dimensional and medium-sized dataset, an improved DF-based model, ForSyn, is proposed to predict synergistic drug combinations. Two novel forest units are designed to embed in ForSyn. One is an RF based on affinity propagation (AP) clustering⁴⁰ and stratified under-sampling, which is designed to deal with the problem of class imbalance. The other is an extreme tree forest (ETF) that based on data complexity dimension reduction dealing with the problem of high-dimensional data. Then, the application of ForSyn is systematically analyzed by comparing 12 algorithms in eight datasets. The ForSyn with all the feature types wins the best performance in most cases. The performance of different configurations of ForSyn are also explored. Then, cellular experimental validation performed on a set of previously untested drug combinations further confirms the predictive ability of ForSyn. Finally, a systematic interpretable analysis of the key features extracted by ForSyn is performed.

Results

The framework of ForSyn

In this study, the drug combinations tested in different cancer cell lines are collected as the sample dataset. The effects of drug combinations can be classified as synergism and non-synergism. A total of 3,192 samples are obtained from the DrugComb,⁴¹ DrugCombDB,⁴² and AstraZeneca-Sanger Drug Combination Prediction⁴³ databases, and classified according to the scheme proposed by Malyutina et al.⁴⁴ Two hundred samples are regarded as the synergism class (minority class), and the remaining 2,992 samples are classified as non-synergism class (majority class). The imbalance rate is close to 15, which is defined as the ratio between the size of the majority class and that of the minority class. Meanwhile, feature set is composed of four feature types. The 881-dimensional DMF, 55-dimensional DPP, and 978-dimensional DGE are used as the feature of drugs, the 978-dimensional CGE are used to represent cancer cell lines. All the feature types have been proved to be effective on other drug-related prediction tasks.^{33,45,46,47,48,49} Each dimension of the curated feature types has a specific meaning, which can facilitate the interpretable analysis to find out the key features in prediction process. More specifically, each dimension in DMF, DPP, and DGE represents a substructure, physicochemical property, and gene expression values of drugs respectively.

To further investigate the influence of different representations in the classification process, eight different datasets including different feature combinations are generated (Table 1). In the training dataset of this study, a sample represent a drug combination on a particular cancer cell line (i.e., a drug combination-cell line pair). The same drug combination on different cell lines will have different effects. It is important to distinguish the drug combinations on different cell lines. In order to make the model to gain the distinguished ability, the representation of each sample is consisting of the drug feature and a cell line-specific feature. The drug feature includes DGE, DMF, and DPP. The cell line-specific features are DGE and CGE. According to the principle, eight datasets are generated and listed in Table 1.

Table 1.

Eight datasets used in this study

Dataset	Description	Dimension
Data 1	DMF + CGE	2,740
Data 2	DPP + CGE	1,088
Data 3	DGE	1,956
Data 4	DMF + DPP + CGE	2,850
Data 5	DMF + DGE	3,718
Data 6	DPP + DGE	2,066
Data 7	DMF + DPP + DGE	3,828
Data 8	DMF + DPP + DGE + CGE	4,806

In the eight datasets, the representation of each sample is the concatenation of pairwise drug feature and the cell line feature.

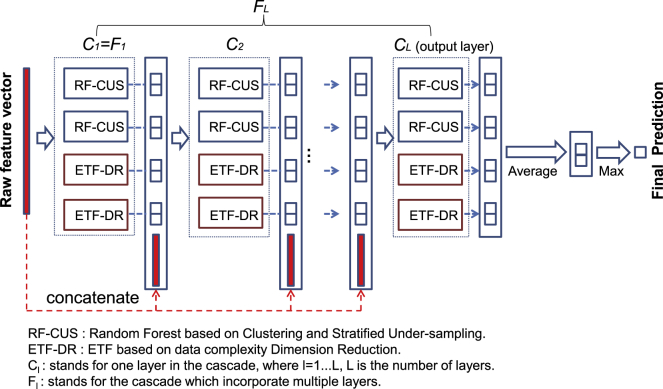
Faced with the imbalanced, high-dimensional and medium-sized datasets, we propose ForSyn, which is a multi-layer cascade structure (Figure 1). Two novel forest types are embedded as the unit in each cascade layer. One is the RF based on clustering and stratified under-sampling (RF-CSU) dealing with imbalanced data. The other is an ETF based on data complexity dimension reduction (ETF-DR) dealing with high feature dimension (details are provided in STAR Methods).

Figure 1.

The overall framework of ForSyn

RF is one of the representative algorithms of ensemble learning. It performs bootstrap sampling and random feature selection in the induction process of the base classifier. The perturbation of the feature space and the sample space ensures the diversity of the ensemble system. However, as with most traditional machine learning algorithms, the RF cannot effectively process imbalanced data. To deal with the problem of imbalanced data, the most common method is to rebalance the training set, such as randomly under-sampling the majority class. But this method always loses useful information. Some training samples that may play a key role in the classification process may be lost in the under-sampling process. To overcome this defect, we design an under-sampling method on the basis of AP clustering and stratified under-sampling, to rebalance the training set and minimize the information loss caused by random sampling. The proposed under-sampling method is combined with the standard RF framework to rebalance the training set of each decision tree.

The ETF can be regarded as a variant of RF. Different from the RF, the ETF uses all the features as candidates, and then randomly selects a feature as the split node of the tree. The tree will continuously grow until each leaf node contains samples of the same class.³² According to the properties, the ETF performs better to the imbalanced data. The pure leaf node that stores minority samples can effectively identify unknown minority samples. However, the high feature dimension and random selection of features would deepen the depth of the tree and cause over-fitting. To overcome the problem of ETF, we propose a greedy dimension reduction method, which combines a data complexity metric with the greedy algorithm. Data complexity, such as the shape of the decision boundary and the overlap between classes, is always used to describe the characteristics of the data.⁵⁰ The data complexity metrics would closely affect the predictive performance of the classifier.⁵¹ In this study, the data complexity metric is defined as the tail overlap of the conditional distribution between two classes⁵⁰ (details are provided in STAR Methods).

Performance evaluation

In this experiment, ForSyn is compared with 12 advanced algorithms on five metrics. The comparison algorithms include eight state-of-the-art deep learning-based algorithms in drug combination prediction, and four advanced machine learning algorithms. The deep learning-based algorithms are four DNN-based methods (DeepSynergy,¹⁸ MatchMaker,¹⁹ TranSynergy,²² and SynPathy⁵²), two DF-based methods (original DF³² and DCE-DForest³⁷), and two GNN-based methods (DeepDDS-GCN and DeepDDS-GAT²³). The machine learning algorithms are two ensemble learning methods (XGBoost⁵³ and RF), and two imbalance learning methods (RUSBoost⁵⁴ and balanced bagging⁵⁵). The evaluation metrics include F1 score, AUPR (area under the precision-recall curve), recall, MCC (Matthews correlation coefficient), and G-mean²⁴; the F1 value is regarded as the main evaluation metric.

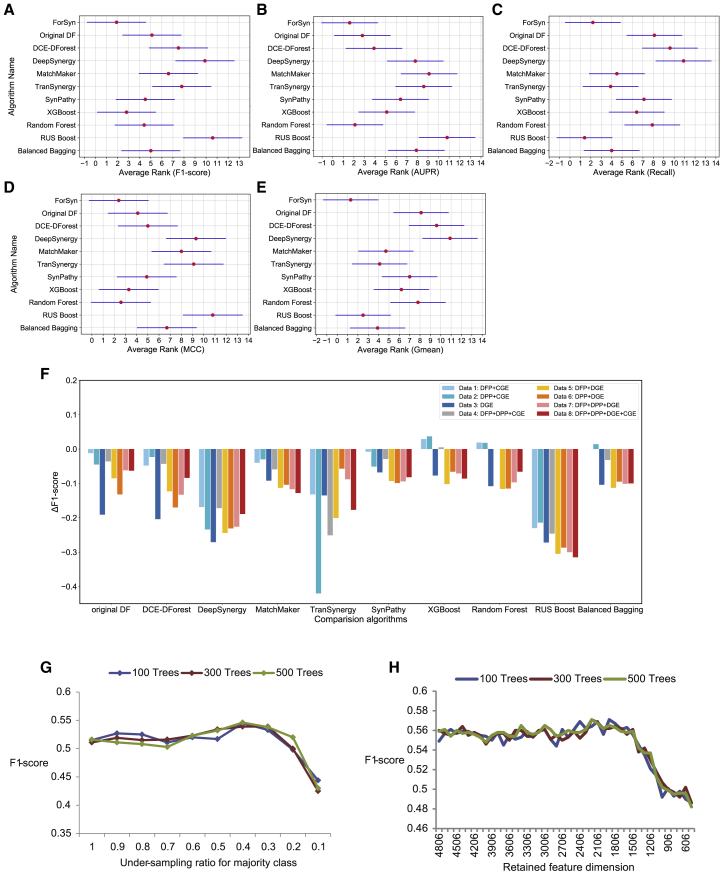
The results of all algorithms on the five metrics are shown in Tables S1–S5. The performance results are the mean value of ten-time 5-fold cross-validation (CV). In addition to the DeepDDS, other 11 algorithms are tested on eight datasets (data 1–8) composed of different feature types. The performance of DeepDDS-GCN and DeepDDS-GAT based on graph data is shown in separate rows in Tables S1–S5. In Tables S1–S5, the performance of 11 algorithms based on data 1–8 is ranked, and the ranking values are shown in parentheses. The smaller ranking value indicates better performance. Then, the Friedman test and the Nemenyi test⁵⁶ are used to analyze the performance difference among the 11 algorithms. The Friedman test compares the performance differences of multiple algorithms on multiple datasets, while the Nemenyi test is performed between pairwise algorithms. According to Equations 15 and 16 (provided in STAR Methods), the Friedman statistical values and the corresponding p values in Tables S1–S5 are 16.40 (p = 2.638 × 10⁻⁸), 55.35 (p = 5.200 × 10⁻¹¹), 37.30 (p = 1.480 × 10⁻¹⁰), 28.10 (p = 1.823 × 10⁻⁹), and 33.34 (p = 3.419 × 10⁻¹⁰), respectively (N = 8, K = 11). The distribution of F_F is based on the F distribution with 10 and 70 degrees of freedom. The critical value of F_F is 1.969 (Equation 16) with a 95% confidence level. The statistical results and p values on all the metrics reflect that there is a significant performance difference among the 11 algorithms. Next, according to Equation 17 and Table S6, CD = 5.338 is calculated with the 95% confidence level in this study. Figures 2A–2E visually show the Nemenyi test results for Tables S1–S5. The average rank of the algorithms in data 1−8 is shown as the red dot in Figures 2A–2E.

Figure 2.

Performance evaluation of ForSyn

(A–E) According to Nemenyi test, the average rank of all algorithms tested on data 1–8 and five metrics: (A) F1 score, (B) AUPR, (C) recall, (D) MCC, and (E) G-mean. The average rank of each algorithm in eight datasets is marked as a red dot, and a horizontal line crossing the red dot indicates the range of CD value in Nemenyi test. The smaller the overlap between two horizontal bars, the more significant the difference between the two algorithms.

(F) The performance difference between ForSyn and other algorithms on F1 score under data 1–8. The y axis denotes ΔF1 between ForSyn and other comparison algorithms, ΔF1 = F1_{comparison algorithms}-F1_ForSyn. A positive number indicates that the performance value of the comparison algorithm exceeds ForSyn, while a negative number indicates that ForSyn is superior to the comparison algorithm.

(G) The impact of the number of base classifiers and the under-sampling ratio on performance of ForSyn’s RF-CSU unit. The y axis represents the F1 score, and the x axis represents the under-sampling ratio for the majority class with a value range of 0.1–1. The blue, red, and green lines represent the RF-CUS unit containing 100, 300, and 500 decision trees, respectively.

(H) The impact of the number of base classifiers and the retained feature dimension on performance of ForSyn’s ETF-DR unit.

From the average rank of performance results on data 1–8 (Figures 2A–2E; Tables S1–S5), it is observed that the ForSyn ranks first on four metrics, F1 score, AUPR, MCC and G-mean, showing its superior prediction performance. In addition, ForSyn performs better than the two DeepDDS algorithms on almost all datasets (Tables S1–S5). The deep learning-based algorithms, original DF, DCE-DForest, DeepSynergy, MatchMaker, TranSynergy, SynPathy and DeepDDS, have no module for imbalanced data processing, so the performance results on the five typical evaluation metrics of imbalanced data are relatively low. For the metric of recall, the performance of ForSyn ranks second, slightly lower than that of balanced bagging (Figure 2C; Table S3). Actually, the recall metric cannot fully reflect the performance of the model, and it often conflicts with precision. According to Figure 2A and Table S1, the F1 score of balanced bagging is low. It can be inferred that the algorithm greatly sacrifices the recognition rate of the majority class samples in exchange for an improvement in the recognition rate of the minority class samples. In addition to ForSyn, the other two DF-based algorithms, original DF and DCE-DForest, have similar ranks in all metrics and get the middle rank. This shows that the innovative design of ForSyn has brought great performance improvement. Figure 2F show the performance difference between ForSyn and other algorithms on the main metric (F1 score) more intuitively. From Figure 2F, it is observed that only three algorithms, XGBoost, random forest, and balanced bagging, have slightly better performance than ForSyn on data 1, 2 and 4. In addition to the three algorithms, ForSyn outperforms other comparison algorithms on all datasets. Similar results exist in other metrics. The performance difference on other metrics is shown in Figure S1.

Next, to evaluate the generalization performance on novel unseen cell lines, drugs and drug combinations, three cross-validation strategies are performed. The training and test sets are shuffled by cell lines, drugs, or drug combinations, which are described as leave-cell-line-out CV, leave-drug-out CV and leave-drug-combination-out CV. The performance results are listed in Table S7. The result of the leave-drug-combination-out CV of all algorithms is inferior to random 5-fold cross-validation. For the leave-drug-out and leave-cell-line-out CV, the results are similar to those mentioned by Preuer et al.¹⁸ That is, all methods yield low predictive performance and thus do not generalize well on novel drugs or novel cell lines, while ForSyn has achieved the best performance in F1 score, AUPR, and MCC, followed by TranSynergy. On the metric recall, RUSBoost is still the best, which is similar to the results discussed in random CV.

Parameter analysis

Each layer of DF is the ensemble of multiple individual forests. In ForSyn, the RF-CSU unit dealing with data imbalance and the ETF-DR unit dealing with high-dimensional features are designed. This subsection will analyze the parameters that affect the performance of the RF-CUS, ETF-DR units, and ForSyn, respectively.

In the RF-CUS unit, the major parameter is the under-sampling ratio for the majority class, which is the ratio between the number of samples in the majority class before sampling and after sampling. We explore the effect of the number of base classifiers and under-sampling ratios on the performance of the RF-CSU unit. As shown in Figure 2G, the performance of the RF-CSU unit wins the best performance when the under-sampling ratio is 0.4. In addition, the increase in the number of decision trees dose not bring a significant improvement in model performance. Therefore, in the ForSyn, the number of decision trees in the RF-CSU unit is set to 100, and the under-sampling ratio for the majority class is set to 0.4.

Figure 2H shows the parameters that affect the performance of the ETF-DR unit. The longest dimension of the samples is 4,806 (data 8). We first sort all features by data complexity, and then perform a greedy backward shrinkage to iteratively reduce the feature dimension, with a step size of 300. From Figure 2H, the performance of the ETF-DR unit wins the best performance when the retained dimension is 1,806. In addition, when the number of decision trees is set to 100, the model has the best performance. Therefore, in the ForSyn, we first reduce the feature dimension of the training sample to 1,806, then train the ETF-DR unit, and set the number of base classifiers of the ETF-DR unit to 100.

Table 2 shows the F1 score of the ForSyn under different configurations. It is observed that the average ranks of ForSyn^{(RFC∗2+ETFD∗2)} and ForSyn^{(RFC∗3+ETFD∗3)} are the same, and the average rank of ForSyn^{(RFC∗4+ETFD∗4)} model is slightly lower. It is inferred that as the unit number increases, the performance of the model does not increase obviously. According to the principle of Occam’s razor (“entities should not be multiplied unnecessarily”), ForSyn^{(RFC∗2+ETFD∗2)} is chosen as the best configuration for the proposed model. In addition, by observing the performance of ForSyn^(RFC∗4) and ForSyn^(ETFD∗4), it can be inferred that the ETF-DR unit has more advantages than the RF-CUS unit when processing drug combination dataset. If ForSyn only uses a single type of unit (for example, ForSyn^(ETFD∗4)), it will cause the ensemble diversity of the cascade layer to decrease, which in turn leads to a decrease in the performance of the layer. However, the combination of different type units will promote the diversity of the cascade layer, which further improves the performance of the overall model.

Table 2.

Performance of ForSyn in different configurations under F1 score

	ForSyn(RFC∗2+ETFD∗2)	ForSyn(RFC∗3+ETFD∗3)	ForSyn(RFC∗4+ETFD∗4)	ForSyn(RFC∗4)	ForSyn(ETFD∗4)
Data 1	0.499(2.5)	0.491(4.0)	0.499(2.5)	0.341(5.0)	0.510(1.0)
Data 2	0.496(3.0)	0.525(1.0)	0.501(2.0)	0.364(5.0)	0.477(4.0)
Data 3	0.519(3.0)	0.543(1.5)	0.543(1.5)	0.327(5.0)	0.460(4.0)
Data 4	0.529(1.0)	0.524(2.0)	0.519(3.0)	0.349(5.0)	0.475(4.0)
Data 5	0.568(3.0)	0.575(1.5)	0.575(1.5)	0.335(5.0)	0.497(4.0)
Data 6	0.551(1.5)	0.539(3.0)	0.551(1.5)	0.345(5.0)	0.473(4.0)
Data 7	0.564(1.5)	0.564(1.5)	0.547(3.0)	0.354(5.0)	0.493(4.0)
Data 8	0.572(1.0)	0.556(2.0)	0.547(4.0)	0.339(5.0)	0.551(3.0)
Average rank	2.1	2.1	2.4	5.0	3.5

The value in parentheses represents the ranking value of the corresponding performance. Taking data 8 as an example, the ForSyn^{(RFC∗2+ETFD∗2)} on this dataset has the best performance (0.572) and is assigned a ranking value of 1.0. In data 6, the performance of ForSyn^{(RFC∗2+ETFD∗2)} and ForSyn^{(RFC∗4+ETFD∗4)} are the same (0.551), and they occupy the first and second positions, respectively, so their ranking values are uniformly assigned 1.5 ([1.0 + 2.0]/2). The average rank of each algorithm is defined as the average of its ranks on all datasets. RFC, RF-CUS unit; ETFD, ETF-DR unit; and the number behind each unit represents the number of units of this type on each cascade layer. For example, ForSyn^{(RFC∗2+ETFD∗2)} means that each cascade layer is placed with two RF-CUS units and two ETF-DR units.

Therefore, the optimal configuration of ForSyn is to place two RF-CUS units and two ETF-DR units in each cascade layer. Each RF-CUS unit contains 100 decision trees, and the under-sampling ratio is set to 0.4. Before training the ETF-DR unit, the proposed dimensionality reduction method is used to sort the feature space, and the first 1,806 dimensions of the sorted features are retained as the training set. The number of base classifiers in the ETF-DR unit is set to 100.

In addition, other tree-based forests are tested as the unit of ForSyn, including ADAboost (ADA), BAGging (BAG), and gradient boosting classifier (GBC). The base classifier of these models is the decision tree, and the parameters use default settings. Table 3 shows the performance comparison between the ForSyn and these derivative models. Under five evaluation metrics, the performance of the proposed ForSyn with two RF-CUS units and two ETF-DR units wins the best performance.

Table 3.

Performance comparison of deep forest embedding different units based on data 8

Configuration	F1 score	AUPR	Recall	MCC	G-mean
DF(ADA∗2+BAG∗2)	0.500	0.582	0.384	0.509	0.614
DF(ADA∗2+GBC∗2)	0.484	0.559	0.350	0.508	0.588
DF(BAG∗2+GBC∗2)	0.493	0.561	0.365	0.512	0.598
DF(RF-CUS∗2+ETF-DR∗2)	0.572	0.591	0.537	0.535	0.722

DF, deep forest; ADA, ADAboost; BAG, BAGging; GBC, gradient boosting classifier.

Subsequently, an ablation experiment on ForSyn is performed (Table S8). First, five different type units are placed on each cascade layer of DF, such as DF^{(ADA∗1+BAG∗1+GBC∗1+RF-CUS∗1+ETF-DR∗1)}, the performance of this model can be regarded as a benchmark for ablation experiment (0.562). Then the units will be removed to observe the change of performance. As shown in Table S8, when the ETF-DR unit is removed, the model performance drops the most, followed by the RF-CUS unit. It can be inferred that the two units we designed are more suitable as units in the cascade framework than other decision tree ensembles.

Cellular experiments of novel drug combinations

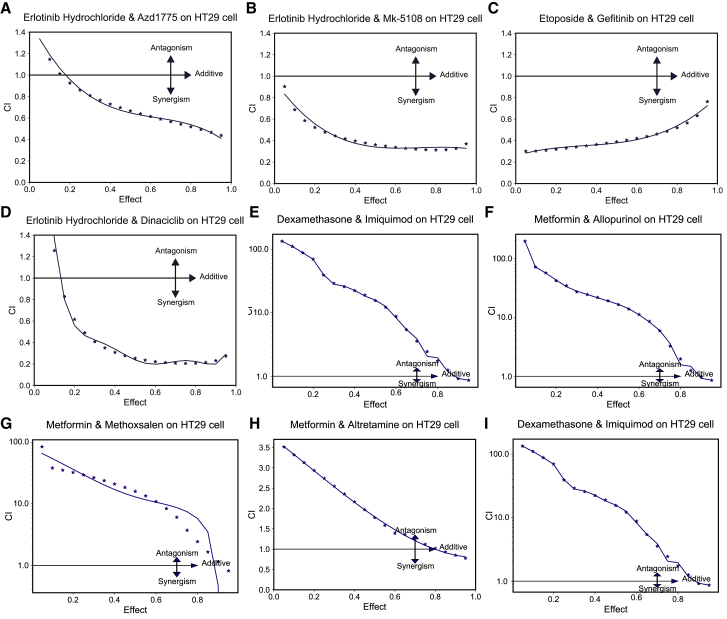
To confirm the efficacy of ForSyn, we further apply ForSyn to predict novel synergistic drug combination that have not been tested before. The cellular experiment is carried out on the predicted novel drug combinations. All drugs are combined in pairs, and the reported samples are removed. The remaining unmeasured samples are regarded as the novel drug combinations. According to the predicted probability of synergism class, eight drug combinations in the HT29 colorectal cell line with top predicted probability (Table S9) are selected to perform the cellular experiment. The synergistic potentials are observed on four drug combinations in the HT29 cell line, including erlotinib hydrochloride and AZD1775, erlotinib hydrochloride and MK-5108, etoposide and gefitinib, and erlotinib hydrochloride and dinaciclib (Figures 3A–3D).

Figure 3.

The result of cellular experiment of ForSyn

(A–D) The effect-CI plot of top predicted synergistic drug combinations tested in the HT29 cell line. CI < 1 indicates that the drug combination has synergistic effect, while CI > 1 indicates the non-synergistic effect.

(E–I) The effect-CI plot of top predicted non-synergistic drug combinations tested in the HT29 cell line.

Erlotinib hydrochloride is an inhibitor of the epidermal growth factor receptor tyrosine kinase (EGFR-TK). The EGFR has become an important therapeutic target for a variety of cancers.^57,58 The alterations of EGFR lead to cell growth, invasion, angiogenesis, and metastases. In colorectal cancer, 25%–77% of tumors overexpress EGFR.^59,60 There have been various EGFR inhibitors, such as erlotinib, an EGFR-TK inhibitor. Erlotinib has demonstrated efficacy against a range of solid tumor types including non-small-cell lung cancer (NSCLC), with more modest effects in colorectal cancer in phase I and II clinical trials.^61,62,63 Although the response rate of erlotinib is not satisfactory when used as monotherapy.⁶⁴ The combination therapy of erlotinib with other anticancer therapies should be more explored.

AZD1775 is a WEE1 inhibitor. It has been proved that the WEE1 gene could repair the DNA damage, which would limit the efficacy of DNA-damaging treatments in cancer cells.⁶⁵ The erlotinib has been found to suppress DNA damage repair in tumor cells.⁶⁴ The combination erlotinib and AZD1775 may enhance the sensitivity of tumor cells. MK-5108 is an Aurora-A kinase inhibitor. The synergistic effect has been observed in combined inhibition of the EGFR and Aurora-A pathways in cancer cells.⁶⁶ Aurora kinase inhibitors are active in combination with EGFR inhibition in a number of EGFR-mutant cell lines. Dinaciclib is a CDK inhibitor for CDK2, CDK5, CDK1, and CDK9. It has been reported that combined inhibition of EGFR and CDK9 resulted in reduced cell proliferation, accompanied by induction of apoptosis, G2-M cell-cycle arrest, inhibition of DNA replication and abrogation of CDK9-mediated transcriptional elongation, in contrast to monotherapy.⁶⁷

In addition, giving gefitinib together with etoposide may kill more tumor cells (https://clinicaltrials.gov, NCT00483561). The phase II trial is studying how well giving gefitinib and etoposide works in treating patients with advanced prostate cancer that did not respond to hormone therapy. Gefitinib may stop the growth of tumor cells by blocking some of the enzymes needed for cell growth and by blocking blood flow to the tumor. Etoposide works in different ways to stop the growth of tumor cells, either by killing the cells or by stopping them from dividing.

Moreover, to investigate the potential false negatives of ForSyn, we also pick up five drug combinations in the HT29 cell line predicted as negative (non-synergistic) with highest probability to perform the same cellular experiment. The experimental results are shown in Figures 3E–3I. It is observed that all the five samples predicted by ForSyn as negative samples are verified as negative by cellular experiments. The CI of three drug combinations even exceeded 100, indicating the strong potential of non-synergistic. This further demonstrates the prediction accuracy of ForSyn in the negative samples.

Interpretable analysis of feature importance

Model interpretation is of paramount importance in machine learning-based biomedical studies. In this study, ForSyn can evaluate the importance of each feature in the prediction process. ForSyn quantify the global relationship between each feature and the output by evaluating the feature importance value (FIV). Then, the FIVs extracted by ForSyn is analyzed from three aspects, the association with prediction process, the contribution of feature types, and the biological analysis of key features. All the FIVs are calculated on data 8 because it contains all the feature types.

Association with prediction process

First, two experiments are performed to show the relationship between FIVs and prediction process from the global and local perspectives, including the layer-by-layer error correction, and the difference of FIVs between different layers.

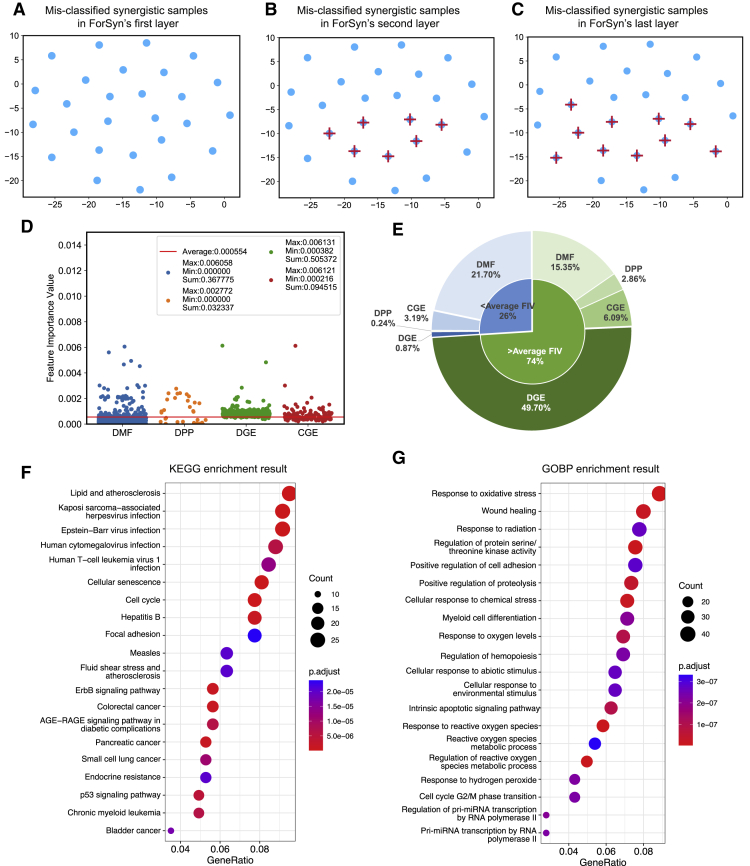
ForSyn is a deep learning method with multiple layers, which can be adaptively expanded according to the performance gain. In this section, we trained a ForSyn model with three layers, the classification results and FIVs of each layer in ForSyn are analyzed. In the first experiment, the layer-by-layer error correction capability of ForSyn is visualized in the feature space through FIVs (Figures 4A–4C). The positive samples (synergistic drug combinations) that are wrongly classified at each layer are extracted. Then the top two features on the basis of the FIVs are used to project the mis-classified samples into a two-dimensional space. Figures 4A–4C shows the error correction result of each layer. The blue dots represent the mis-classified positive samples by the first layer of ForSyn. The red “+” represents the samples that are correctly classified at the second and last layers of ForSyn. From Figures 4A and 4B, the number of red plus signs appears more, indicating that the growth of the layer brings a significant performance improvement. In Figures 4B and 4C, the number of red plus signs increases slightly, indicating that the layer stops growing and the performance gradually converges. In addition, there are samples that cannot be corrected in the final layer, some of which may be related to the correctness of labels in the dataset. There may still be several incorrectly labeled noisy samples in the dataset because of the existence of experimental noise, as mentioned by Malyutina et al.⁶⁸

Figure 4.

The interpretable analysis result of ForSyn

(A–C) The top two features sorted by FIVs are used to visualize the ForSyn’s layer-by-layer error correction of mis-classified positive (synergistic) samples. The blue dots represent the mis-classified positive samples by the first layer of ForSyn. The red plus sign represents the samples that are correctly classified at the second and last layers of ForSyn.

(D) The FIV of each feature in four feature types. The red line indicates the average FIV all features.

(E) The contribution of each feature type in two groups, which are the features that are greater than and less than the average FIV.

(F and G) The top 20 enrichment results of KEGG pathway and Gene Ontology Biological Process, which are obtained by key genes involved in the key DGE features.

In the local analysis of the association with prediction process, the difference of FIVs between different layers is evaluated. The FIV of each feature in the lth layer is calculated according to Equation 12 in STAR Methods. Then a rank vector is generated by sorting the FIVs of all features, so as to generate the rank vectors of three layers of ForSyn. Finally, the Wilcoxon signed rank test⁶⁹ is used to evaluate the significant differences between the three rank vectors. The p value for layer 1 vs. layer 2 is 0.958, and that for layer 2 vs. layer 3 is 0.972. The original hypothesis of this test is that there is no significant difference between paired vectors. Both p values are greater than 0.05, failing to reject the original hypothesis. That is, there is no significant difference between the paired FIVs’ rank vectors in the layers of ForSyn.

Contribution of feature types

The key features based on FIVs are then analyzed. The most contributing feature type is first investigated. The feature set is composed of four feature types, DMF, DPP, DGE, and CGE. When analyzing the FIVs, it should be noted that not all features participate in the whole prediction process. In the ETF-DR unit of ForSyn, a greedy dimension reduction method is applied to select 1,806-dimensional (see Parameter analysis) features to achieve the prediction task. Therefore, only the 1,806 features participate in the whole prediction process, including 1,037 DMFs, 31 DPPs, 600 DGEs, and 138 CGEs. The FIV of each feature is shown in Figure 4D. The red line in Figure 4D represents the average FIV of all features, which is 0.000554 (1/1,806). Figure 4E divides the features into two groups, the features that are greater than and less than the average FIV. It further shows the contribution of each feature type in the two groups. The contribution is calculated by summing the FIVs of features in a feature type. From Figures 4D and 4E, 768 features are greater than the average FIV, and the contributions of the 768 features are accounted for 74%. Therefore, we believe that these 768 features are top contributing features for prediction process. Among the 768 features, there are 107 DMFs, 17 DPPs, 582 DGEs, and 62 CGEs, with contributions of 15.35%, 2.86%, 49.70%, and 6.09%, respectively (Figure 4E). The results show that DGE plays a key role in the prediction process. Although there are many DMFs among 1,806 features, the contribution of most DMF features is lower than the average FIV (Figures 4D and 4E).

Biological analysis of key features

Next, the biological analysis is performed on the key DGE features extracted by ForSyn. The 479 genes (with duplication removed) involved in the 582 DGE features that are greater than the average FIV are extracted. A global analysis on the extracted genes is carried out, including two kinds of gene enrichment analysis on Kyoto Encyclopedia of Genes and Genomes (KEGG) pathway and Gene Ontology Biological Process (GOBP). Enrichment results show that these genes are significantly enriched in 67 KEGG pathways and 518 GOBPs (adjusted p < 0.01). The top 20 enrichment results are shown in Figures 4F and 4G. KEGG pathway enrichment result shows multiple significant biological pathways that are closely related to cancer (Figure 4F). According to the characteristics of these pathways, they can be divided into four categories: specific cancer pathways (colorectal cancer, pancreatic cancer, etc.), regulation process of cancer (cellular senescence, cell cycle, etc.), oncogenic virus infection (Kaposi sarcoma-associated herpesvirus infection, etc.) and immune inflammation (lipid and atherosclerosis, etc.). For enrichment result of top 20 GOBP (Figure 4G), the key genes are more concentrated in the response to stimulus, especially the response to oxidative stress.

After the global analysis of the key genes, the cancer-specific key genes in DGE in different cell lines are further investigated. Four cell lines (HT29, A549, MCF7, and PC3) with more than 500 samples are selected to train the ForSyn respectively. Then the key DGE features with top FIVs of four cell lines are obtained. The top 10 genes involved in these key DGE features may play a key role in corresponding cancer cell lines, as shown in Table S10. For example, in A549 lung cancer cell line, CCND3 and TSPAN14 genes are identified as the top contributing genes. Song et al.⁷⁰ proposed that CCND3 could serve as potential biomarkers and provide a theoretical basis for the pathogenesis of lung adenocarcinoma. And TSPAN14 gene is also proposed as an indicator of NSCLC metastasis and progression.⁷¹ In the HT29 colorectal cell line, the CAMSAP2 gene has been proved to be a promising therapeutic target for the treatment of metastatic colorectal cancer patients.⁷² PLOD3 has also been proved to be a potential biomarker for CRC diagnosis and prognosis prediction.⁷³ In MCF7 breast cancer cell and PC3 prostate carcinoma cell line, the top contributing genes, PGM1 and SPRED2, as well as SIRT3 and UFM1, are also proved to play a key role in breast and prostate cancers.^{74,75,76,77,78}

Discussion

In this study, we propose a new algorithm, ForSyn, to predict synergistic drug combinations in different cancer cell lines. Two novel forest types are designed to embed in ForSyn, including the RF-CSU unit dealing with data imbalance and the ETF-DR unit dealing with high-dimensional features. The ForSyn can effectively solve the problems of class imbalanced, and high feature dimension in the medium-scale datasets. Compared with 12 advanced algorithms on five metrics, ForSyn ranks first in four metrics, F1 score, AUPR, MCC and G-mean. Two statistical tests confirm that ForSyn perform significantly better than other algorithms in most cases. Next, the different configurations of ForSyn are analyzed. The results show that the under-sampling ratio for the majority class in RF-CSU, the feature dimension of the training sample in ETF-DR, the number of base classifiers, the types and numbers of units have influence on the performance of ForSyn. In addition, the novel synergistic drug combinations predicted by ForSyn are verified by cellular experiment, showing the predictive ability of ForSyn. Finally, a systematic interpretable analysis of the FIVs evaluated by ForSyn is performed. The layer-by-layer error correction and the difference of FIVs between different layers show the association between FIVs with prediction process. By summing the FIVs of each feature type, the DGE has been proved to play a critical role in the prediction process. Then the key genes involved in the key DGE features are explored by enrichment analysis. The key genes extracted by ForSyn may have potential effects on corresponding cancers.

Two forest types are designed in ForSyn, including RF-CSU and ETF-DR. The reason for choosing RF and ETF is that both models have their own advantages in dealing with high-dimensional and unbalanced data. The RF selects $\sqrt{d}$ (where d is the dimension of the training data) features for each decision tree. Thus, the high feature dimension will not have a great negative impact on the performance of the RF, and effectively solving the problem of data imbalance is the key factor to improve the performance of RF. In the ETF model, the tree will continuously grow until each leaf node contains samples of the same class. Thus, the ETF has some advantages when dealing with imbalanced data. For example, the pure leaf node that stores minority samples can effectively identify unknown minority samples. However, the high feature dimension and the behavior of randomly selecting the feature, which deepens the depth of the tree and easily causes over-fitting. The effective dimension reduction methods may reduce computational cost and avoid over-fitting of the ETF. Thus, to obtain an excellent model to deal with the imbalanced and high-dimensional data, we design the modules of imbalanced data process and dimensionality reduction on RF and ETF respectively.

For the input feature data, the DGE and CGE can be quickly obtained at low cost through L1000 method or published predicted models when there are new drugs and cell lines to be predicted. In this study, the DGE and CGE are obtained from the National Institutes of Health (NIH) Library of Integrated Network-Based Cellular Signatures (LINCS)⁷⁹ database. In LINCS database, the data are obtained using the L1000 method, which is a low-cost, high-throughput method and only needs 1,058 probes for 978 landmark transcripts and 80 control transcripts. The reagent cost of the L1000 assay is approximately $2. The 978 landmarks have been shown to be sufficient to recover ∼80% of the information in the full transcriptome. In addition, DGE and CGE also can be generated or predicted by machine learning models.^80,81 For example, Zhu et al.⁸⁰ have proposed a deep learning-based model, DLEPS, using SMILES of molecules to predict the 978-dimentional DGE obtained from LINCS database. DLEPS has been validated in the use of screening potential drugs in obesity, hyperuricemia and nonalcoholic steatohepatitis.

ForSyn has shown an excellent predictive performance in drug combination prediction, which is validated by computational and biological experimental results. The novel units designed in ForSyn can largely solve the problems of imbalanced and high-dimensional data. Both are common problems in the datasets of drug-related biomedical studies. We hope that the propose of ForSyn can not only apply narrow down the candidates of drug combinations for experimental validations but also provide insights for other studies in drug discovery.

Limitations of the study

Although ForSyn shows excellent prediction performance and interpretability, this study is limited by the number of training samples when using DGE and CGE as features. The importance of DGE has been shown in this study. In future work, we expect that the scale of the training dataset will expand with the accumulation of DGE, and the performance and interpretability of EC-DFR would be further improved accordingly. In addition, the predictive model cannot generalize well on novel drugs or novel cell lines, which is an inherent problem in drug combination prediction and should be explored in future work. Finally, some potential drug combinations and key genes has been found on the basis of ForSyn. The key factors should be further investigated through more biological experiments.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, peptides, and recombinant proteins
Erlotinib Hydrochloride EGFR inhibitor	MedChemExpress(MCE)	HY-12008; CAS: 183319-69-9
Gefitinib (ZD1839) EGFR inhibitor	MedChemExpress(MCE)	HY-50895; CAS: 184475-35-2
AZD1775 Wee1 inhibitor	MedChemExpress(MCE)	HY-10993; CAS: 955,365-80-7
MK-5180 Aurora A inhibitor	MedChemExpress(MCE)	HY-13252; CAS: 1010085-13-8
Etoposide Topoisomerase-II inhibitor	MedChemExpress(MCE)	HY-13629; CAS: 33419-42-0
Dinaciclib CDK inhibitor	MedChemExpress(MCE)	HY-10492; CAS: 779353-01-4
Critical commercial assays
Counting Kit-8 (CCK8) assay	Sigma-Aldrich	M5655
Deposited data
DrugComb	Zagidullin et al.41	https://drugcomb.fimm.fi/
DrugCombDB	Liu et al.42	http://drugcombdb.denglab.org/main
AstraZeneca-Sanger Drug Combination Prediction	Menden et al.43	https://www.synapse.org/#!Synapse:syn4231880/wiki/235645
LINCS L1000	Stathias et al. 81	https://lincsproject.org/LINCS/tools/workflows/find-the-best-place-to-obtain-the-lincs-l1000-data
Experimental models: Cell lines
Human:HT29	ATCC	ATCC HTB-38
Software and algorithms
ForSyn	This paper	https://doi.org/10.5281/zenodo.7562405
Original Deep Forest	Zhou et al.31	https://github.com/kingfengji/gcForest
DCE-DForest	Zhang et al.37	N/A
DeepSynergy	Preuer et al.18	www.bioinf.jku.at/software/DeepSynergy
MatchMaker	Kuru et al.19	https://github.com/tastanlab/matchmaker
TranSynergy	Liu et al.22	https://github.com/qiaoliuhub/drug_combination
SynPathy	Tang et al.52	https://github.com/TangYiChing/SynPathy
DeepDDS	Wang et al.23	https://github.com/Sinwang404/DeepDDS/tree/master
ChemmineR	Cao et al.82	https://www.bioconductor.org/packages/release/bioc/html/ChemmineR.html
OpenBabel	O'Boyle et al.83	https://openbabel.org/wiki/Category:Installation

Resource availability

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by the lead contact, Xiaochen Bo (boxc@bmi.ac.cn, boxiaoc@163.com).

Materials availability

This study did not generate new unique reagents.

Experimental model and subject details

The HT-29 cell line purchased from the American Type Culture Collection (ATCC, Manassas, VA, USA) are used for drug combination screening. The cell line is verified by Short Tandem Repeat (STR) profiling performed by Cell Line Authentication Service at ATCC. HT29 cells are cultured in McCoy’s 5A (Hyclone, Logan, UT, USA) containing 10% fetal bovine serum (FBS) (Hyclone, USA), 1% penicillin (Invitrogen, USA), and 1% streptomycin (Invitrogen, USA). The cell line is maintained at 37°C and 5% CO2 in a humidified incubator.

Method details

Drug combination dataset

In the dataset, a sample represent a drug combination on a particular cancer cell line, i.e., a drug combination-cell line pair. The samples are collected from DrugComb, DrugCombDB and AstraZeneca-Sanger Drug Combination Prediction databases. To ensure that each sample contains all the four feature types, the samples with missing features are removed. For the samples collected from DrugComb and DrugCombDB, four kinds of synergy scores (Loewe, Bliss, HSA and ZIP) are used to quantify the effects of samples. The synergy scores in replicate experiments are averaged to get a unique value for each sample. Finally, 3,192 samples are obtained, covering 77 drugs and 15 cancer cell lines.

The samples are classified according to the scheme proposed by Malyutina et al.⁴⁴ due to the noise data exists in the datasets. The 200 samples with above four synergy scores greater than five are regarded as the synergism class (minority class), the remaining 2,992 samples are classified as non-synergism class (majority class). The imbalance rate is close to 15, which is defined as the ratio between the size of the majority class and that of the minority class.

Feature set

To construct the input dataset, the representation of each sample is the concatenation of pairwise drug feature and the cell line feature. The feature vector of a single drug is composed of the 978-dimensional DGE, 881-dimensional DMF, and 55-dimensional DPP. The 978-dimensional CGE is used to represent cancer cell lines. It should be noted that the DGE and CGE features are cell line-specific, each dataset should include DGE or CGE to distinguish samples on different cell lines. To further investigate the influence of different representations in the classification process, eight different datasets including different feature combinations are generated (Table 1).

Drug-induced gene expression profiles

The 978-dimensional DGE of 15 cell lines are collected from LINCS L1000 database (Level 5).^79,82 The expression profiles of the same drug at different doses and different time points are fused by weighted average method.⁸² The 978 landmark genes and their Z values in the expression profiles are selected as the gene expression values under drug perturbation. Each gene expression value represents the relative value of gene expression level. A positive value indicates that gene expression is up-regulated and a negative value indicates that expression is down-regulated.

Chemical structure of drugs

The 881-dimensional PubChem⁸³ DMF calculated by R-package ChemmineR are used to represent the chemical structure of drugs.⁸⁴ In the binary vectors, each bit represents whether the specific substructure exists.

Physicochemical properties of drugs

The 55-dimensional DPP is calculated by ChemmineR, OpenBabel⁸⁵ and JoeLib packages. Physicochemical properties include molecular weight, solubility and hydrophobic parameters.

Gene expression profiles of untreated cell lines

The 978-dimensional CGE are also collected from the LINCS L1000 database. The transcriptional expression levels of 15 cell lines treated with dimethyl sulfoxide as solvent control are used as the feature of cell lines.

Description of ForSyn

Random Forest dealing with imbalanced data

RF performs bootstrap sampling and random feature selection in the induction process of the base classifier. However, the RF cannot effectively handle imbalanced data. To deal with the problem of imbalanced data, a stratified under-sampling based on AP clustering is designed to rebalance the training set and minimize the information loss caused by random sampling. The proposed under-sampling method is combined with the standard RF framework to rebalance the training set of each decision tree. Data S1 and Figure S2A show the training process of the proposed RF.

Figure S2B shows a diagram of stratified under-sampling based on clustering. The purpose of clustering is to make the samples with high similarity as concentrated as possible. The stratified sampling is to obtain samples from each cluster in a balanced manner. This strategy can preserve the useful information of the majority class as much as possible. Traditional clustering methods, such as K-means, need to preset the number of clusters, and randomly select the initial cluster centers in the training data. The performance of the K-means algorithm is sensitive to the initial cluster centers. It often takes multiple runs to find relatively good initial cluster centers. While AP clustering does not need to preset the number of clusters. Each sample is regarded as a node in a network. The pairwise nodes perform information exchange recursively along the edge until a set of good cluster centers and corresponding clusters appear. Compared with traditional clustering methods, AP clustering always perform better and takes less time. Next, the AP clustering results are stratified sampled to obtain more representative samples of majority class. After resampling, the number of samples of the majority class is equal to that of the minority class.

Extreme tree forest dealing with high feature dimension

Different from RF, the ETF uses all the features as candidates, and then randomly selects a feature as the split node of the tree. According to the properties, the ETF is less affected by imbalanced data compared with RF. However, the high feature dimension and random selection of features would deepen the depth of the tree and lead to over-fitting. To overcome the problem of ETF, we propose a greedy dimension reduction method and combines a data complexity metric. The data complexity metric is defined as the tail overlap of the conditional distribution between two classes.⁵⁰ For each feature in the dataset, find the maximum and minimum values of the feature in different classes, and calculate the overlap area between them (Equation 1):

$$F_i=\frac{\mathit{MIN}\left(\mathit{max}\left(f_i,c_1\right),\mathit{max}\left(f_i,c_2\right)\right)-\mathit{MAX}\left(\mathit{min}\left(f_i,c_1\right),\mathit{min}\left(f_i,c_2\right)\right)}{\mathit{MAX}\left(\mathit{max}\left(f_i,c_1\right),\mathit{max}\left(f_i,c_2\right)\right)-\mathit{MIN}\left(\mathit{min}\left(f_i,c_1\right),\mathit{min}\left(f_i,c_2\right)\right)}$$ (Equation 1)

where $\mathit{max}\left(f_i,c_j\right)$ and $\mathit{min}\left(f_i,c_j\right)$ refer to the maximum and minimum values of the i-th feature in the j-th class, i = 1 … d, d corresponds to the feature dimension. j∈[1,2] corresponds to two classes. The value range of the overlap area is [0,1]. The smaller the value indicates the smaller the overlap area of the feature between different classes. The smaller the overlapping area, the greater the contribution of the feature to the classification result.

Data S2 performs dimension reduction on the input data. First, the data complexity metric is used to evaluate the classification contribution (overlap area) of each feature. Then combines the greedy algorithm to approximate the local optimal feature subspace. Finally, the selected features are used to train the ETF. Suppose the dataset D is divided into training set T and validation set V (D = T∪V). T is used to train the ETF, and V is used to evaluate the performance of the model. The algorithm process of Data S2 can be described as follows.

• Step 1.

  Calculate $F_i$ of each feature, and then sort the feature space by ascending order of $F_i$ (Algorithm process 1–2 in Data S2).

• Step 2.

  The dataset D after the feature reordering is horizontally divided into R subsets (Algorithm process 3–4 in Data S2).

• Step 3.

  R-1 subsets are used as the training set and one subset as the verification set, to train and evaluate the performance of the ETF (Algorithm process 5–8 in Data S2).

• Step 4.

  The feature dimension is iteratively reduced, and the performance of trained ETF is checked. If the performance drops, stop iterative training and return to the dimension of the current feature subset (Algorithm process 9–18 in Data S2).

• Step 5.

  Repeat step 3 to step 4, until R-fold cross-verification training is implemented. The average dimension of R retained feature subspaces is obtained, and then the local optimal feature subspace is returned to train an ETF (Algorithm process 19–23 in Data S2).

Framework of the ForSyn

As shown in Figure 1, RF-CUS and ETF-DR are embedded as the unit in the cascade structure of the ForSyn. In the ForSyn, l represents the index of each layer, l = 1 … L. Each layer has T units, t represents the index of the unit in each cascade layer, t = 1 … T. The $p_{i,j}^{t,l}$ refers to the probability that the forest in t-th unit of the l-th layer predicts sample x_i belongs to the j-th class. In the binary classification of imbalanced data, the majority class and the minority class are represented by −1 and 1, respectively, j∈[-1,1], then:

$$p_{i,-1}^{t,l}+p_{i,1}^{t,l}=1$$ (Equation 2)

When predicting an unknown sample, each unit generates a class probability vector [$p_{i,-1}^{t,l},p_{i,1}^{t,l}$]. In one layer, the output class probability vectors of the units are concatenated with the raw feature vector as the input of the next cascade layer. Thus, the classification result of the previous layer can guide the classification process of the next layer. Assuming C_l represents the l-th layer, F_l is the cascade of the first l layers, the relationship between the layer and the cascade can be expressed as Equation 3:

$$F_l\left(x_i\right)=\{\begin{array}{cc}{C}_l\left(x_i\right)& l=1\\ C_l\left(\left[x_i,p_{i,j}^{t,l-1},t=1\dots T\right]\right)& l>1\end{array}$$ (Eqaution 3)

where $\left[x_i,p_{i,j}^{t,l-1},t=1\dots T\right]$ represents the concatenation of the raw feature vector and the output of the previous layer. Through the cascade structure, the layer-by-layer processing and in-model feature transformation are implemented for the raw data. For the unknown sample $x_i$, the output of the last cascade layer (C_L) is formulated as Equation 4:

$$C_L\left(x_i\right)={\mathit{argmax}}_{j\in \left[-\mathrm{1,1}\right]}\frac{1}{T}\sum _{t=1}^T{p}_{i,j}^{t,L}$$ (Equation 4)

In addition, the growth of the cascade layer adopts a greedy convergence mode during the training process. The number of cascade layers is adaptively determined under sufficient training.

Comparison methods

We contrast the ForSyn with 12 advanced algorithms, including eight deep learning-based state-of-the-art methods and four advanced machine learning methods. Among the deep learning-based methods, DeepSynergy, MatchMaker, TranSynergy, SynPathy are DNN-based methods for drug combination prediction. DeepSynergy is a feedforward neural network with two hidden layers, which is proposed by Preuer et al. The author claims that it is the first application of deep learning technology in drug combination prediction. MatchMaker applies three subnetworks. Two subnetworks are trained in parallel to learn the representation of drugs on a particular cell line, and then the joint representation for the combination is fed into the third network to predict the synergy score. TranSynergy is a transformer-based deep learning model with dimension reduction component. A transformer is applied to learn the representation of samples and a fully connected layer is used to predict. SynPathy is a DNN-based model with three fully connected layers. The DCE-DForest and original DF are DF-based methods. DCE-DForest is a DF-based model with four original RFs in each layer. The original DF put two RF and two ETF units in each layer. DeepDDS-GCN and DeepDDS-GAT are GNN-based methods proposed by Wang et al. It should be noted that the datasets applied by the two DeepDDS methods are different from other comparison methods. Other methods support tabular input formats, while only graph-structured data can be accepted as input of DeepDDS. To construct the dataset of graph format, the SMILES of each drug are obtained and converted to a graph using RDKit followed by the article of DeepDDS. In the graph of drug, the vertices are atoms and the edges are chemical bonds. The CGE data is used to represent the cell lines. DeepDDS applies two types of GNN, GCN and GAT, to extract the representations of drugs. Then the representations of drugs and cell lines are concatenated and input into the fully connected layers to achieve predict task.

Among the machine learning algorithms, XGBoost and RF are two advanced ensemble learning algorithms, which are representative of sequential ensemble and parallel ensemble respectively. RUSBoost and Balanced Bagging are the classical methods in imbalanced learning. Both are the combination of ensemble learning and data resampling technology. RUSBoost balances the training set by randomly under-sampling majority class, and sequentially trains decision trees. Balanced Bagging uses similar under-sampling techniques to train all decision trees in parallel. All the algorithms are implemented according to the corresponding literature or the default configuration.

Evaluation metrics

$$\mathrm{A}\mathrm{c}\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{y}=\frac{\mathrm{T}\mathrm{P}+\mathrm{T}\mathrm{N}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{N}+\mathrm{T}\mathrm{N}+\mathrm{F}\mathrm{P}}$$ (Equation 5)

$$\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}=\frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{P}}$$ (Equation 6)

$$\mathrm{R}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}=\mathrm{T}\mathrm{P}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e}=\frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{N}}$$ (Equation 7)

$$\mathrm{F}-\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}=\frac{\left(1+{\beta }^2\right)\ast \mathrm{R}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}\ast \mathrm{P}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}}{{\beta }^2\ast \left(\mathrm{R}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}+\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}\right)}$$ (Equation 8)

$$\mathrm{T}\mathrm{N}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e}=\frac{\mathrm{T}\mathrm{N}}{\mathrm{T}\mathrm{N}+\mathrm{F}\mathrm{P}}$$ (Equation 9)

$$G-Mean=\sqrt{TPrate\ast TNrate}$$ (Equation 10)

$$MCC=\frac{TP\ast TN-FP\ast FN}{\left(\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{N}\right)\left(\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{P}\right)\left(\mathrm{T}\mathrm{N}+\mathrm{F}\mathrm{P}\right)\left(\mathrm{T}\mathrm{N}+\mathrm{F}\mathrm{N}\right)}$$ (Equation 11)

There are more than 40 evaluation metrics used to deal with the problem of imbalanced data, which are introduced in a comprehensive review proposed by Branco et al.⁸⁶ In this study, five metrics are used to evaluate the performance of algorithms. The metrics including F1-score, AUPR, Recall, MCC and G-Mean. The formulas are shown in Equations 5, 6, 7, 8, 9, 10, and 11.

Accuracy (Equation 5), as a global metric, is often used to evaluate the classification performance of models. But it is not suitable for imbalanced learning. It will induce the classification result biased toward the majority class. Suppose that the proportions of the majority class and the minority class in a dataset are 95% and 5%, respectively. In this case, a classifier can obtain high Accuracy by marking all test samples as the majority class. However, the purpose of imbalanced learning is to identify unknown samples in minority class. The Accuracy cannot effectively reflect the predictive performance of the classifier on minority class samples.

Precision takes FP (False Positives) into account and is more sensitive to imbalanced data (Equation 6). But using Precision alone cannot accurately express the classification status because it ignores FN (False Negatives). The Recall is not affected by imbalanced data, because it only relies on the minority classes, but it ignores FP (Equation 7). Precision and Recall often conflict with each other. To solve this problem, F-value is defined as a trade-off between them, where β is used to adjust the relative importance between Precision and Recall (Equation 8). In the current learning, β is set to 1.

G-Mean calculates the square root of the product of TP (True Positives) rate and TN (True Negatives) rate, and pays attention to the classification result of the majority class and the minority class simultaneously (Equation 10). MCC can be regarded as a balanced metric (Equation 11). It is a correlation coefficient value between −1 and 1. 1 represents the perfect performance of the classifier, and 0 represents the performance of average random prediction, −1 means the opposite performance.

In previous studies, the authors also used the ROC curve, which plots the relationship between the true positive rate and the false positive rate. It creates a visual model that describes the trade-off between correctly classified positive samples and incorrectly classified negative samples. However, when comparing the ROC curves of multiple algorithms on the plane, it is difficult to intuitively select the best algorithm because of the overlap between the curves, unless one curve can completely outperform all other curves in the overall space. The area under the ROC curve provides a single value to measure the average performance of each algorithm. According to Davis’s research, the ROC curve expresses overly optimistic results on a highly imbalanced dataset, and the PR curve should be used instead.⁸⁷ Similar to AUC, AUPR represents the area under the PR curve.

Although Recall ignores FP, it intuitively reflects the performance of the classifier on the minority class. The remaining four metrics pay attention to the classification results of the minority class and the majority class synchronously.

Cross validations

In addition to the random 5-folds CV, three CV strategies are also performed to evaluate the generalization performance on novel unseen cell lines, drugs, and drug combinations. The training and test sets are shuffled by cell lines, drugs, or drug combinations, which are described as leave-cell-line-out CV, leave-drug-out CV and leave-drug-combination-out CV, as shown in Figure S2C. There are 15 cell lines, 77 drugs and 884 unique drug combinations (without considering cell lines) in this dataset. For leave-cell-line-out CV, the drug combinations in each cell line is regarded as the test set in turn and in the other 14 cell lines are the training set. Then, a 15-fold CV is performed. For leave-drug- out CV, we divide the 77 drugs into n = 7 groups. The drug combination samples involved in a drug group are combined as the test set, and those in the other n-1 groups are the training set. Consequently, all drug groups are regarded as test sets in turn. For the leave-drug-combination-out CV, 884 unique drug combinations (without considering cell lines) are extracted to split the training and testing data. The 884 unique drug combinations are divided into n = 8 groups. The samples (considering cell lines) involved in one drug combination group is regarded as the test set and in the other n-1 groups are the training set. Then, an 8-fold CV is performed.

Evaluation of feature importance value

ForSyn is a decision tree-based deep learning method. It contains multiple cascade layers, each of which is composed of multiple decision tree-based forests. Thus, each layer is the integration of decision trees. The decision tree is an excellent interpretable model, which quantify the global relationship between each feature and the output by evaluating the FIV. That is, the FIV can be used to represent the amount of influence a feature has over the classification process.⁸⁸

Then, ForSyn can evaluate the FIV of each feature by extracting and aggregating the FIVs of all decision trees. In each decision tree, the FIV can be evaluated by some classic data-dependent metrics, such as information gain or gini impurity.⁸⁹ Suppose a trained ForSyn has L layers, each layer contains J forests, and each forest contains T trees. Then the FIV of the d-th feature in the t-th tree of the j-th forest in the l-th layer is represented by $I_{j,t}^{d,l}$, where d = 1 … D, l = 1 … L, j = 1 … J, and t = 1 … T. $C_l^d$ represents the FIV of the d-th feature on the l-th layer, and is calculated by Equation 12. $C_d$ represents the FIV of the d-th feature in all layers (Equation 13). It can be regarded as the contribution of the d-th feature in the overall model.

$$C_l^d={\sum }_{j=1}^J{\sum }_{t=1}^T{I}_{j,t}^{d,l}$$ (Equation 12)

$$C_d=\frac{{\sum }_{l=1}^L{C}_l^d}{{\sum }_{d=1}^D{\sum }_{l=1}^L{C}_l^d}$$ (Equation 13)

Drug combination screening

The Cell Counting Kit-8 (CCK8) assay (Sigma, M5655) is performed to evaluate the synergy potential in HT29 cell line. The experimental design is adopted from Chou et al.,⁴ where 10 concentration values of drugs are set. Cells are seeded in 96-well plates (Nest, 701,001) at 4000 cells/well densities and cultured at the indicated concentrations with the solvent DMSO or drug combinations for 72 h. After 72 h of incubation, 10μL per well of CCK8 reagent is added to the plates, followed by 4 h of incubation. The luminesce of optical density value (OD) is measured using Envision plate reader (PerkinElmer) at 450 nm wavelength. The cellular proliferation inhibition rate is defined as Equation 14. Then the CI value of each drug combination is calculated by CompuSyn software⁴ to quantify the synergistic potential.

$$inhibition(\%)=(ODsample-ODNegative)/(ODPositive-ODNegative)\times 100\%$$ (Equation 14)

Quantification and statistical analysis

The Friedman test and Nemenyi test are used to analyze the performance difference among different algorithms. The Friedman test compares the performance differences of multiple algorithms on multiple datasets. Under the null hypothesis, it believes that the performances of all algorithms are equal. Equation 15 and Equation 16 show the original Friedman statistics and an improved version respectively.

$${\mathrm{X}}_{\mathrm{F}}^2=\frac{12\mathrm{N}}{\mathrm{K}\left(\mathrm{K}+1\right)}\left[\sum _{\mathrm{j}}{\mathrm{R}}_{\mathrm{j}}^2-\frac{\mathrm{K}{\left(\mathrm{K}+1\right)}^2}{4}\right]$$ (Equation 15)

$$F_F=\frac{\left(N-1\right)X_F^2}{N\left(K-1\right)-X_F^2}$$ (Equation 16)

Then, the Nemenyi test is performed to verify the performance difference between pairwise algorithms. The performances of two classifiers are significantly different if the corresponding average ranks differ by at least the critical difference (CD):

$$\mathrm{C}\mathrm{D}=q_{\alpha }\sqrt{\frac{K\left(K+1\right)}{6N}}$$ (Equation 17)

The statistical details and exact values of experiments can be found in RESULTS-Performance evaluation section.

Published: February 21, 2023

Data and code availability

• •The data reported in this paper is publicly available on GitHub (https://github.com/Lianlian-Wu/ForSyn) and Zenodo (https://doi.org/10.5281/zenodo.7562405).
• •The original code is publicly available on GitHub (https://github.com/Lianlian-Wu/ForSyn) and Zenodo (https://doi.org/10.5281/zenodo.7562405).
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.