The effect direction should be taken into account when assessing small-study effects

Abstract

Background.

Studies with statistically significant results are frequently more likely to be published than those with non-significant results. This phenomenon leads to publication bias or small-study effects and can seriously affect the validity of the conclusion from systematic reviews and meta-analyses. Small-study effects typically appear in a specific direction, depending on whether the outcome of interest is beneficial or harmful, but this direction is rarely taken into account in conventional methods.

Methods.

We propose to use directional tests to assess potential small-study effects. The tests are built on a one-sided testing framework based on the existing Egger’s regression test. We performed simulation studies to compare the proposed one-sided regression tests, conventional two-sided regression tests, as well as two other competitive methods (Begg’s rank test and the trim-and-fill method). Their performance was measured by type I error rates and statistical power. Three real-world meta-analyses on measurements of infrabony periodontal defects were also used to examine the various methods’ performance.

Results.

Based on simulation studies, the one-sided tests could have considerably higher statistical power than competing methods, particularly their two-sided counterparts. Their type I error rates were generally controlled well. In the case study of the three real-world meta-analyses, by accounting for the favored direction of effects, the one-sided tests could rule out potential false-positive conclusions about small-study effects. They also are more powerful in assessing small-study effects than the conventional two-sided tests when true small-study effects likely exist.

Conclusions.

We recommend researchers incorporate the potential favored direction of effects into the assessment of small-study effects.

INTRODUCTION

Meta-analysis is a statistical method of synthesizing results from multiple related studies to obtain an overall average effect. It has become a powerful and widely used tool in a wide range of different disciplines, including psychology, medicine, epidemiology, as well as dental research.^{1, 2} However, small studies with statistically significant results are more likely to be published than small studies with non-significant results, leading to publication bias or small-study effects.^{3, 4} This phenomenon could seriously threaten the validity of conclusions from systematic reviews. It is critical to detect small-study effects and assess their impact on the synthesized results of meta-analyses.⁵

Studies in dental research frequently have smaller sample sizes compared with many other medical specialties, possibly because dental studies are time-consuming and expensive.⁶ For example, we conducted a simple investigation of the sample sizes reported in studies from systematic reviews and meta-analyses recently published in the Journal of Evidence-Based Dental Practice (JEBDP) and The BMJ. Both journals advocate evidence-based medicine, while the former focuses on dental research and the latter is a general medical journal. The sample sizes reported in the JEBDP (median=65) are generally smaller than those in The BMJ (median=170), as shown in Figure 1. Table S1 in the Supplementary Materials presents more detailed results. The relatively small sample sizes in dental meta-analyses may be a concern for small-study effects, which can pose a nonignorable threat to the synthesis of the studies.

Figure 1. Boxplot of sample sizes of studies published in the Journal of Evidence-Based Dental Practice (JEBDP) and The BMJ.

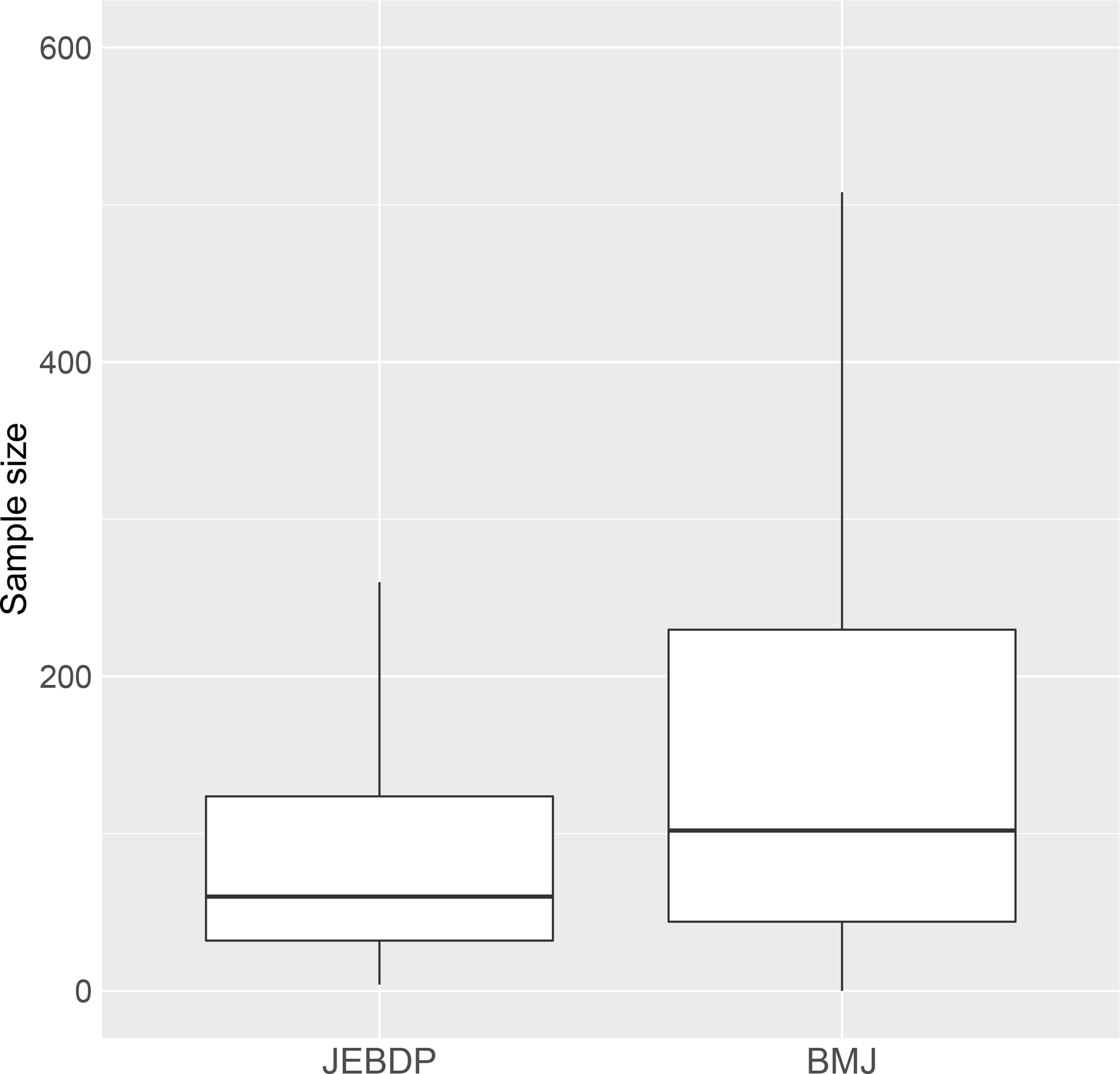
The included studies were published or available online between January 1, 2021 and August 10, 2022. In total, 519 studies from 34 systematic reviews were collected from the JEBDP, and 4449 studies from 48 systematic reviews were collected from The BMJ. Outliers are not shown in the boxplot.

A simple graph method to detect small-study effects is the funnel plot, which usually presents the effect sizes of studies on the horizontal axis against their standard errors or precisions (the inversed standard errors) on the vertical axis.⁷ It detects small-study effects by observing the asymmetry of the funnel plot: the funnel plot tends to be skewed in the presence of small-study effects. However, the visual examination may be subjective and inaccurate. Based on the funnel plot, various quantitative methods were developed for small-study effects. Begg and Mazumdar⁸ constructed a rank correlation test that examines the correlation between the effect sizes and their variances based on Kendall’s tau. Small-study effects tend to induce a strong correlation. Egger et al.⁹ proposed a simple linear regression test of the standardized effect sizes against their precisions; small-study effects will result in a non-zero regression intercept. This method is perhaps the most popular one for assessing small-study effects in the current literature of meta-analyses. However, the original version of Egger’s regression test does not account for heterogeneity as in the typical random-effects meta-analysis model.^10–12 Clinical and methodological heterogeneity is imminent in studies conducted under different protocols; this heterogeneity may also manifest as statistical heterogeneity.¹³ If heterogeneity is detected (e.g., based on the I² statistic¹⁴), Egger’s regression test can be modified to incorporate the between-study variance due to heterogeneity.¹⁰ Additionally, the trim-and-fil method is also widely used for assessing small-study effects.^{15, 16} It not only detects the occurrence of small-study effects but also adjusts the estimated overall effect size. However, the trim-and-fill method is built on the strong assumption that the asymmetry in a funnel plot is caused by the suppression of studies based only on magnitudes of effect sizes, while many other factors (e.g., p-values) are also important causes of small-study effects. This method may have low statistical power if the assumption is not fully satisfied.¹⁷

To our knowledge, except for the trim-and-fill method, the popular rank and regression methods do not account for the direction of potential small-study effects in most meta-analysis applications. However, in practice, small-study effects usually occur in a certain direction only.¹⁸ This perhaps is due to the confirmation bias,¹⁹ a bias induced by a general tendency for researchers to strongly believe in their favored hypothesis. For example, for harmful outcomes (e.g., oral infections), researchers tend to expect lower odds ratios (ORs) for new treatments, while for beneficial outcomes such as healing, small studies with higher ORs may be more likely to be published than those with lower ORs. Failing to account for an appropriate effect direction could lead to false-positive conclusions and lower statistical power for identifying true small-study effects.

To fill this gap, we propose directional tests that account for the direction of potential small-study effects. For illustrative purposes, this article primarily builds the directional tests based on Egger-type regression tests.⁹ Although Egger’s test has several drawbacks (e.g., the possible inflation of the type I error rate for ORs),²⁰ it has competitive statistical power in many settings of study suppression and remains its popularity for evidence synthesis.²¹ The idea of the directional tests similarly applies to other regression-based methods (e.g., regressions with sample sizes as predictors).^{20, 22, 23}

The rest of this article is organized as follows. We first review the existing regression tests for detecting small-study effects and then propose the directional regression tests. Simulation studies are presented to compare the statistical performance of the directional tests, conventional (undirectional) tests, and the trim-and-fill method. We also apply the various methods to three actual meta-analyses that investigate the accuracy of clinical and radiographic measurements of periodontal infrabony defects. This article concludes with a brief discussion.

METHODS

Regression Test

Suppose a meta-analysis contains n independent studies. Let y_i and s_i be the effect estimate and its standard error (SE) within study i, respectively (i = 1, 2, …, n). Egger’s test regresses the standardized effect sizes (y_i/s_i) on the reciprocals of SEs (1/s_i); that is,

$$y_i/s_i=\alpha +\mu \cdot 1/s_i+{ϵ}_i,{ϵ}_i~N\left(0,{\sigma }^2\right),$$ #(1)

where α and μ are the regression intercept and slope, respectively, and ∈_i is the regression error. If there are no small-study effects, the funnel plot should be approximately symmetric. In such a case, the intercept α should be 0, so Egger’s regression focuses on testing H₀:α = 0 vs. H₁:α ≠ 0.

The original version of Egger’s test corresponds to the conventional common-effect model, where all studies in a meta-analysis share a common underlying true effect.¹¹ In the presence of noticeable heterogeneity, we may modify the test to make it suitable for the additive random-effects setting. The random-effects model can be specified as $y_i~N\left(\mu ,s_i^2+{\tau }^2\right)$, where τ² is the between-study variance. Therefore, Egger’s regression test can be modified by using the marginal standard deviations ${\left(s_i^2+{\tau }^2\right)}^{1/2}$ to replace the s_i in its original version^{23, 24}; that is,

$$y_i/\sqrt{s_i^2+{\tau }^2}=\alpha +\mu /\sqrt{s_i^2+{\tau }^2}+{ϵ}_i,{ϵ}_i~N\left(0,{\sigma }^2\right).$$ #(2)

The modified regression test also detects small-study effects by examining whether the regression intercept α is 0.

Directional Test

Conventionally, two-sided hypothesis testing is performed for Egger’s regression (as well as its modification under the random-effects setting). The alternative hypothesis of α ≠ 0 permits both directions of small-study effects, which are not practical.

We propose to use directional tests for Egger’s regression and its random-effects modification. In the following, the new tests are referred to as one-sided Egger’s regression test and one-sided modified regression test. Specifically, we alter the alternative hypothesis from H₁:α ≠ 0 to H₁:α > 0 (or α < 0). The direction of the intercept α depends on outcomes (i.e., harmful or beneficial). A negative value of α generally indicates that studies with smaller effect sizes are more likely to be published (i.e., missing studies tend to appear on the right side of the funnel plot), and vice versa.

If the published studies tend to have negative effect sizes, the p-value of the one-sided regression test is

$$P=F_t\left(\frac{\widehat{\alpha }}{\mathrm{SE}(\widehat{\alpha })}\right).$$

Here, $\mathrm{SE}(\widehat{\alpha })$ is the SE of the estimated $\widehat{\alpha }$, and F_t(⋅) is the cumulative distribution function of the t distribution with n − 2 degrees of freedom. If the published studies tend to have positive effect sizes, the p-value is

$$P=1-F_t\left(\frac{\widehat{\alpha }}{\mathrm{SE}(\widehat{\alpha })}\right).$$

In contrast, the p-value from the conventional two-sided test for small-study effects is

$$P=2\left(1-F_t\left(\frac{\left|\widehat{\alpha }\right|}{\mathrm{SE}(\widehat{\alpha })}\right)\right).$$

When $\widehat{\alpha }$ is in the same direction as the true small-study effects, the p-value of the one-sided test is half smaller than the two-sided test. If $\widehat{\alpha }$ has a large absolute value in the opposite direction of the truth, the one-sided test could produce a larger p-value than the two-sided test.

SIMULATION STUDIES

Simulation Designs

We conducted simulation studies to investigate the performance of the directional regression test compared with the conventional two-sided regression test. Other commonly used methods for assessing small-study effects, including Begg’s rank test and the trim-and-fill method, were also considered.^{8, 16} For each simulated meta-analysis, the within-study SEs were drawn from a uniform distribution: s_i ~ U(1,4). We generated the study-specific effect sizes by $y_i~N\left({\mu }_i,s_i^2\right)$, where the true effect size for each study was μ_i ~ N(μ, τ²). Without loss of generality, the true overall effect size was set to μ = 0. The between-study standard deviation τ took values of 0, 1, and 4. The number of published studies contained in each meta-analysis was set to n = 15, 30, and 50. We considered the following two scenarios for generating small-study effects. Without loss of generality, we assumed positive effect estimates were favored, and negative effect estimates may be suppressed.

Scenario 1 considers small-study effects at the study level that assume researchers may publish their results with probabilities determined by the significance of the results and their beliefs, which are common in practice. For example, researchers may choose to give up a study if the results are not statistically significant or contradict their strong beliefs. This scenario suppresses studies based on their publication probabilities. Studies reporting significantly positive effect estimates had the highest probabilities of being published, studies reporting significantly negative effect estimates had the lowest probabilities of being published, and studies reporting non-significant effect estimates had moderate publication probabilities. The study publication status, denoted by a binary dummy variable X_i, followed a Bernoulli distribution Ber(π_i), where π_i represents the publication probability for study i. Studies with X_i = 0 were suppressed, while those with X_i = 1 were published. We continued to generate studies until n published studies were collected. We considered four different cases of publication mechanisms, varying publication probabilities π_i according to their p-values and effect estimates’ directions (Figure 2). These included the case of no small-study effects, denoted by case 0, where all studies were published (i.e., π_i = 1 for all studies). The three other cases had small-study effects, denoted by cases 1, 2, and 3. Small-study effects became more severe from case 1 to case 3.

Figure 2. Four mechanisms of generating publication probabilities.

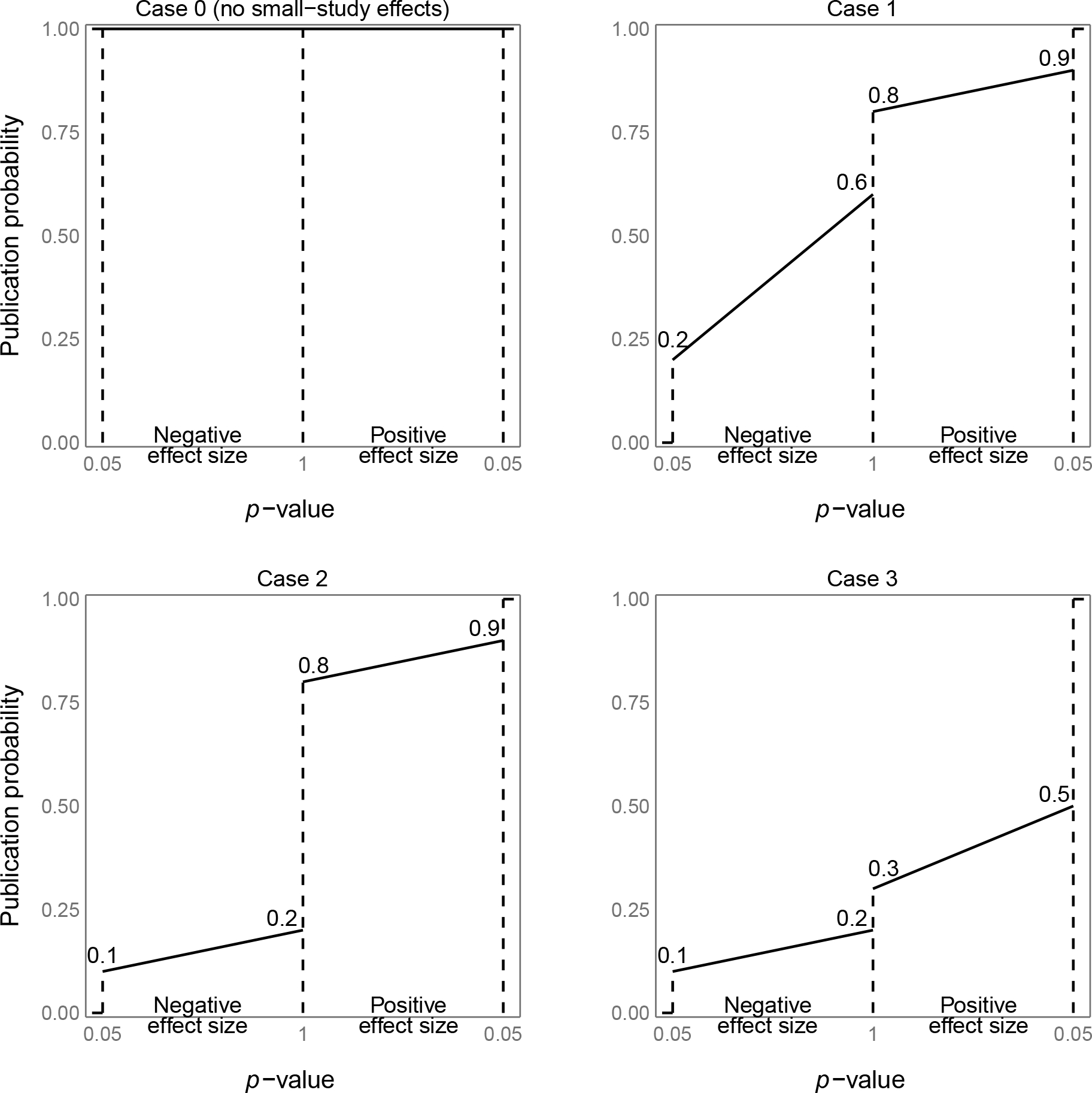
The horizontal axis represents p-values of the studies with both positive effect sizes and negative effect sizes. The vertical axis represents publication probabilities. The segments on the plots show the relationship between the p-values of the studies and their publication probabilities.

Scenario 2 considers small-study effects at the population level that assumes a proportion of all studies have been suppressed due to their results. This scenario suppresses studies with the most negative effect sizes. In addition to the p-values, studies’ suppression could also depend on the magnitudes of their effect estimates.¹⁶ For each simulated meta-analysis, n + m studies were generated. We then suppressed m studies with the most negative effect estimates, where m was set to 0, ⌊n/4⌋, ⌊n/3⌋, and ⌊n/2⌋. Here, ⌊x⌋ denotes the largest integer that is not greater than x. The case with m = 0 had no small-study effects.

In both scenarios, the proposed one-sided tests aimed at testing H₀: α ≤ 0 vs. H₁: α > 0 because the missing studies tended to have negative effect sizes. We also brought this prior knowledge to the trim-and-fill method by specifying the side of missing studies to be the left. For the other competitive methods (i.e., the conventional regression tests and Begg’s rank test), the aim was to test for H₀:α = 0 vs. H₁:α ≠ 0, which did not account for the direction.

We simulated 10,000 meta-analyses for each setting. The type I error rates and statistical power were evaluated. The nominal significance threshold was set to be 0.1 because the methods for assessing small-study effects usually have relatively low power. We used the restricted maximum likelihood (REML) method to estimate the between-study variance τ² in the random-effects setting.²⁵ The Monte Carlo SEs of all type I error rates and power were <1%.

Simulation Results

Figure 3 summarizes type I error rates under scenarios 1 and 2. Type I error rates for these two scenarios were similar as no small-study effects exist under the null; the differences between the two scenarios should be due to Monte Carlo errors. When heterogeneity was absent or moderate (τ = 0 or 1), type I error rates of most tests were controlled well. In the presence of substantial heterogeneity (τ = 4), the type I error rate of the two-sided Egger’s test was inflated, while the one-sided Egger’s regression controlled the type I error rate slightly better (Figure 3 and Tables S2 and S3 in the Supplementary Materials).

Figure 3. Type I error rates of various tests for small-study effects under scenario 1 (A) and scenario 2 (B).

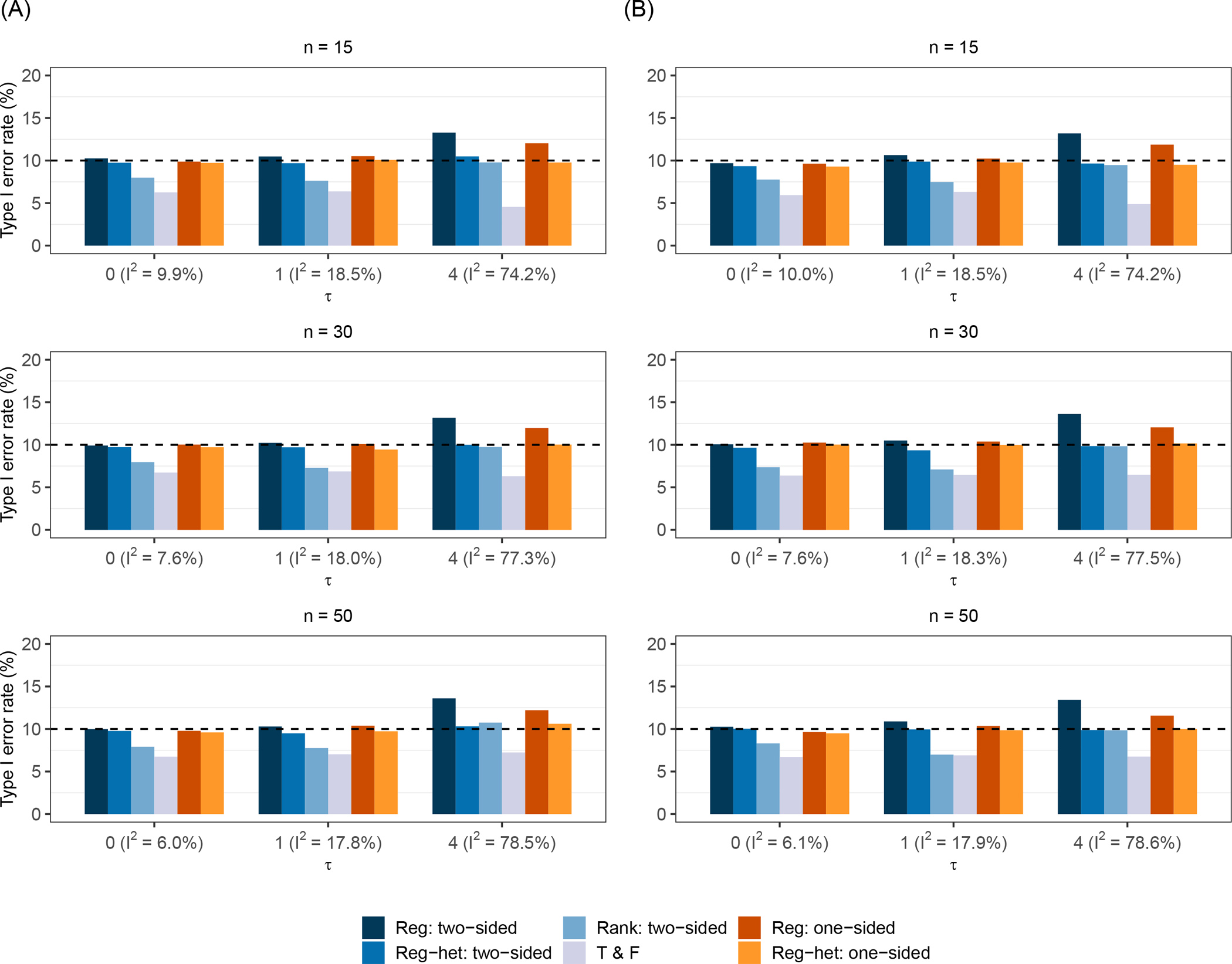
The nominal significance level is 0.1. Note: n is the number of published studies in each meta-analysis; the compared tests include the two-sided Egger’s test (Reg: two-sided), the two-sided modified regression test (Reg-het: two-sided), Begg’s rank test (Rank: two-sided), the trim-and-fill method (T & F), the proposed one-sided Egger’s test (Reg: one-sided), and the proposed one-sided modified regression test (Reg-het: one-sided).

Figure 4 presents the statistical power of different methods when the studies were suppressed based on their publication probabilities (scenario 1). The one-sided regression tests improved the statistical power through all settings. The power of both the one-sided Egger’s test and the one-sided modified regression test increased dramatically compared with the two-sided counterparts. Also, as expected, all methods became more powerful when the number of published studies in meta-analyses increased. Among the three cases of small-study effects, methods achieved the highest power when the publication probabilities were distributed evenly (case 2). When the heterogeneity was absent or moderate (τ = 0 or 1), the conventional Egger’s regression test and its modification (the method that accounted for between-study variance) had similar power. When the heterogeneity was substantial (τ = 4), the conventional Egger’s regression test achieved slightly higher power than the modified regression test, while its type I error rate was considerably inflated (Figure 3). Begg’s rank test and the trim-and-fill method were less powerful than the regression tests. The trim-and-fill method had similar performance across the three cases, and it performed poorly when the heterogeneity was strong.

Figure 4. Power of various tests for small-study effects under scenario 1.

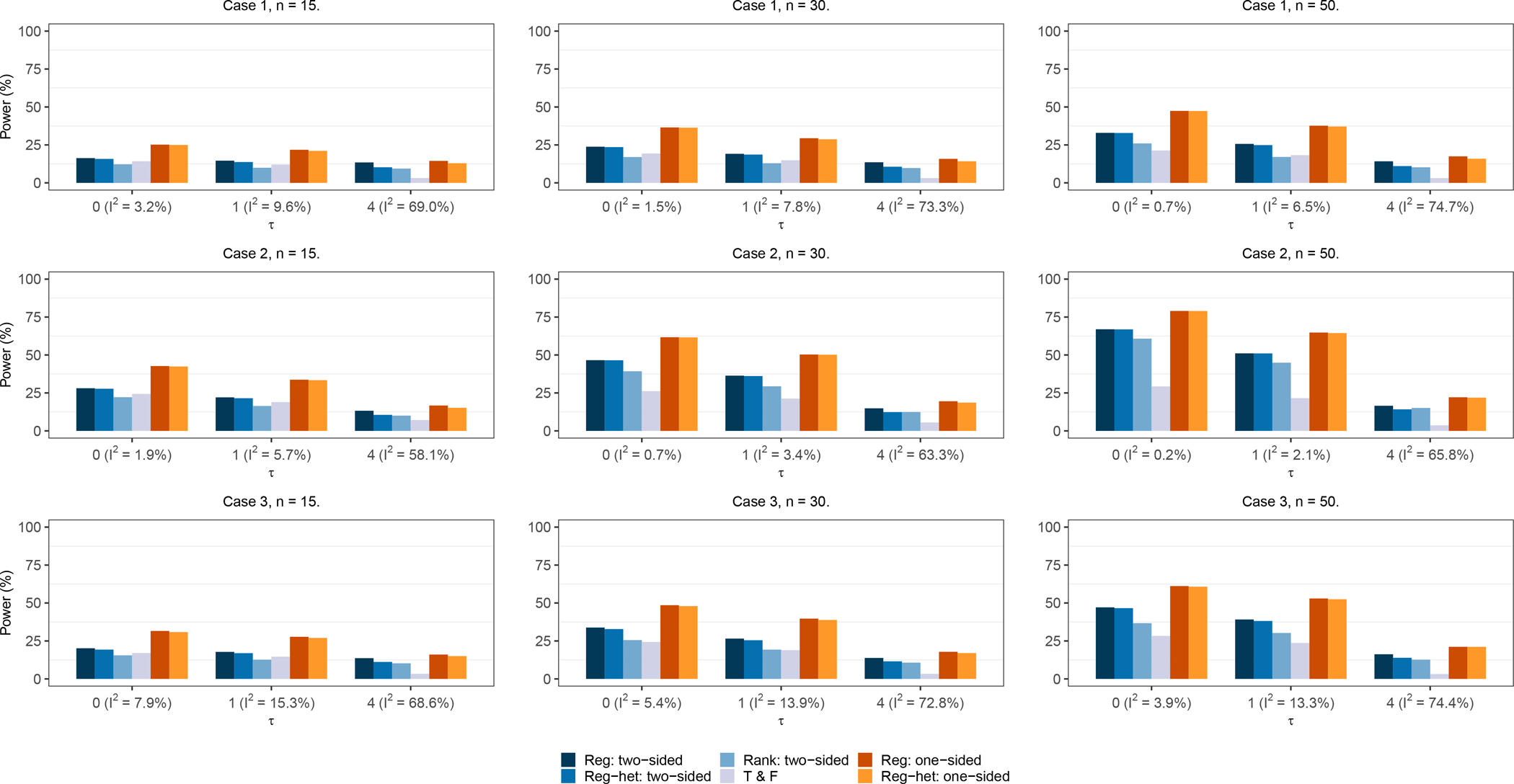
The nominal significance level is 0.1. Cases 1, 2, and 3 indicate the three study publication mechanisms with different publication probabilities. Note: n is the number of published studies in each meta-analysis; the compared tests include the two-sided Egger’s test (Reg: two-sided), the two-sided modified regression test (Reg-het: two-sided), Begg’s rank test (Rank: two-sided), the trim-and-fill method (T & F), the proposed one-sided Egger’s test (Reg: one-sided), and the proposed one-sided modified regression test (Reg-het: one-sided).

Figure 5 presents the power of these tests when the m studies with the most negative effect sizes were suppressed (scenario 2). The one-sided tests continued to be more powerful than the two-sided counterparts. Again, the power tended to be higher when more studies were suppressed. When n = 15, the trim-and-fill method seemed to have the highest power. This was likely because the assumption of the trim-and-fill method was perfectly satisfied under this scenario with sufficient numbers of published studies. The two-sided regression tests had relatively higher power than Begg’s rank test; they became similar in the presence of high heterogeneity. The one-sided tests improved the power compared to the two-sided tests, and their power approached those of the trim-and-fill method, especially when τ = 0 or 1. When n = 30 or 50, the trim-and-fill method had substantially high power, even when the studies were highly heterogeneous. Besides the trim-and-fill method, the power of Egger’s test and the modified regression test were similar; they were higher than those of Begg’s rank test when the studies were less heterogeneous. However, the power dramatically dropped when the heterogeneity became strong. Begg’s rank test performed better than the two-sided regression tests when n = 50 (Figure 5 and Table S3 in the Supplementary Materials).

Figure 5. Power of various tests for small-study effects under scenario 2.

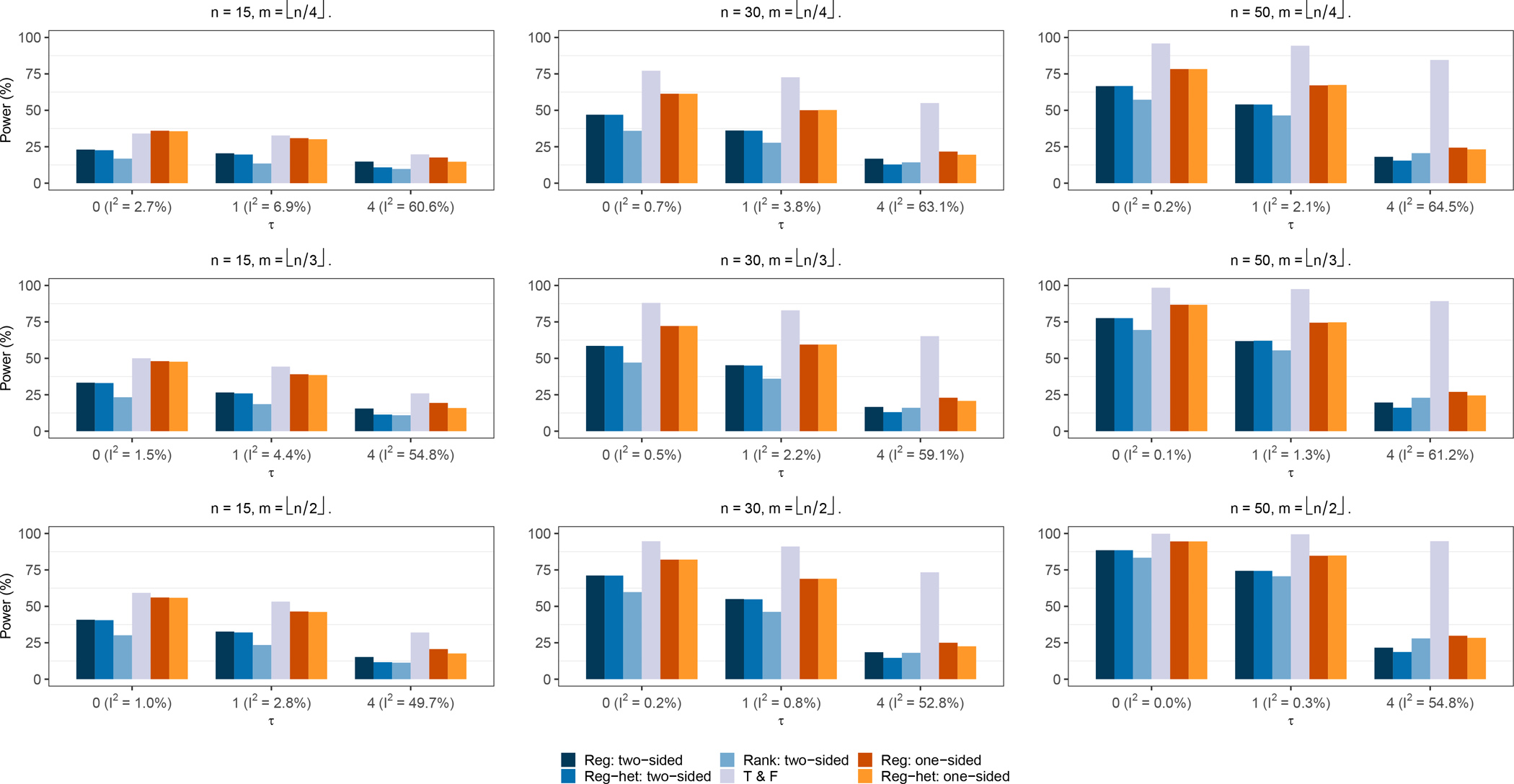
The nominal significance level is 0.1. Note: n is the number of published studies in each meta-analysis; m is the number of suppressed studies; the compared tests include the two-sided Egger’s test (Reg: two-sided), the two-sided modified regression test (Reg-het: two-sided), Begg’s rank test (Rank: two-sided), the trim-and-fill method (T & F), the proposed one-sided Egger’s test (Reg: one-sided), and the proposed one-sided modified regression test (Reg-het: one-sided).

CASE STUDIES

We illustrate the performance of the various methods for assessing small-study effects by three meta-analyses in a systematic review by Clark-Perry et al.²⁶ This review aimed to determine the accuracy of clinical attachment level (CAL) and radiographic bone level (rBL) of periodontal infrabony defects. Accurately measuring periodontal infrabony defects is important to diagnose periodontal disease, a disease that can be prevented and stabilized if diagnosed early.²⁷ The CAL measures the loss of periodontal support around a tooth by using the periodontal probe to measure the distance from the cement-enamel junction (CEJ) to the base of the pocket.^{28, 29} The rBL measures the periodontal bone loss by radiographic linear measurements from CEJ to the bottom of the defects. Even though the amount of bone loss can be accurately assessed using intraoperative bone level (iBL) that directly and physically measures the distance from CEJ to the bottom of defects following debridement, thus serving as the gold standard, it is unclear what is the accuracy of clinical and radiographic measurements. The three meta-analyses conducted by Clark-Perry et al.²⁶ compared CAL vs. iBL, rBL vs. iBL, and CAL vs. rBL. In total, they meta-analyzed 11 studies, including 17 comparisons. Each comparison was treated as a data entry in the analyses. The effect measure was the mean difference (MD). Figures S1–S3 in the Supplementary Materials show the forest plots of these meta-analyses with complete data. Both CAL and rBL measurements were found to tend to underestimate the iBL values, the gold standard for the amount of bone loss.

To evaluate small-study effects, we reperformed the three meta-analyses; the REML method was used to obtain τ² in the random-effects model. Figure 6 presents the three meta-analyses’ contour-enhanced funnel plots for visually assessing small-study effects. Different contours represent different significance levels, which could help assess whether the potentially missing studies are non-significant.³⁰ We applied the proposed one-sided regression tests along with the other competitors to assess the small-study effects; Table 1 presents the results.

Figure 6. Contour-enhanced funnel plots of the three meta-analyses in the case study.

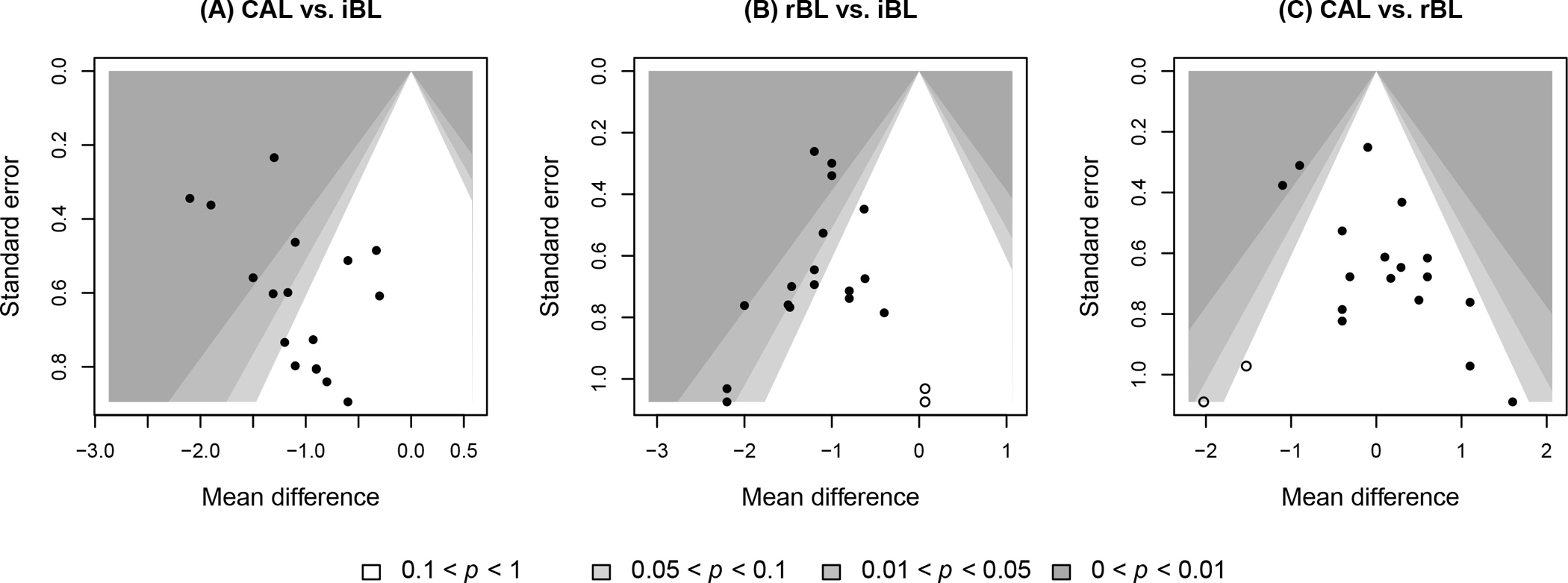
The filled points represent published data, while the unfilled points represent imputed missing studies by the trim-and-fill method.

Table 1. Results of the three meta-analyses in the case study.

The compared tests include the two-sided Egger’s test (Reg: two-sided), the two-sided modified regression test (Reg-het: two-sided), Begg’s rank test (Rank: two-sided), the trim-and-fill method (T & F), the proposed one-sided Egger’s test (Reg: one-sided), and the proposed one-sided modified regression test (Reg-het: one-sided).

	CAL vs. iBL	rBL vs. iBL	CAL vs. rBL
I2 (%)	31	0	40
Reg: two-sided (p-value)	0.056	0.234	0.016
Reg-het: two-sided (p-value)	0.046	0.234	0.005
Rank: two-sided (p-value)	0.052	0.091	0.042
T & F
Imputation side	Right	Right	Left
No. of imputed studies	0	2	2
p-value	0.500	0.125	0.125
Reg: one-sided (p-value)	0.972	0.117	0.008
Reg-het: one-sided (p-value)	0.977	0.117	0.003

For the meta-analysis comparing CAL vs. iBL, it was expected to observe negative MDs due to the underestimation of CAL. In fact, all comparisons had negative MDs (Figure S1). Therefore, we assumed that positive MDs were likely missing, and the proposed directional tests aimed to examine H₀:α ≥ 0 vs. H₁:α < 0. All two-sided tests yielded p -values <0.1, indicating the presence of small-study effects. However, this conclusion was challenged by the one-sided regression tests. Both the one-sided Egger’s test and modified regression test yielded large p-values (>0.900), indicating no evidence of significant small-study effects. The trim-and-fill method agreed with this conclusion, as no missing comparisons were imputed with a p-value of 0.500. Although the contour-enhanced funnel plot in Figure 6A shows some extent of asymmetry, it indicates a trend of missingness in areas of significance on the left side, contrary to the fact that negative MDs were favored. Thus, the small-study effects detected by conventional two-sided methods were likely false-positive conclusions.

Similarly, in the meta-analysis comparing rBL vs. iBL, negative MDs were also favored; all comparisons had negative MDs, and more than half of them were significant (Figure S2). The one-sided tests examined H₀:α ≥ 0 vs. H₁:α < 0. The REML estimate of the between-study variance was 0, so Egger’s test and the modified regression test gave the same results. For the two-sided tests, Egger’s test did not indicate significant small-study effects (p-value = 0.234), while Begg’s rank test implied significant small-study effects (p-value = 0.091). The trim-and-fill method imputed two missing comparisons on the right side of the funnel plot, with p-value = 0.125 (Figure 6B). The one-sided Egger’s test yielded p-value = 0.117, which was close to the significance level of 0.1. In this example, most methods except Begg’s rank test provided consistent results, indicating that small-study effects may not be a concern for this meta-analysis comparing rBL vs. iBL.

For the meta-analysis comparing CAL vs. rBL (Figure S3), Egger’s test implied comparisons with positive MDs were likely published, which was supported by the asymmetric pattern of the funnel plot in Figure 6C. Egger’s test and Begg’s rank test yielded significant small-study effects. The regression tests’ p-values became smaller when the heterogeneity was taken into consideration. The one-sided modified regression yielded the smallest p-value, which was 0.003. The trim-and-fill method imputed two comparisons with negative MDs, but it failed to suggest significant small-study effects (Figure 6C).

To further evaluate the broad impact of the proposed methods, we reanalyzed the additional meta-analyses on COVID-19. The Supplementary Materials present the details (Figures S4–S7 and Table S4).

DISCUSSION

The assessment of small-study effects requires both clinical and statistical perspectives. This article focuses on statistical methods for assessing small-study effects, while clinical input also plays a critical role in appraising the certainty of meta-analysis results.^{31, 32} For example, besides using statistical methods (e.g., the trim-and-fill method) to impute potential missing studies, we also suggest systematic reviewers try their best to explore unpublished resources and identify all available evidence. Such resources could come from preprints, trial preregistration servers (e.g., ClinicalTrials.gov), or other gray literature.³³ This effort is particularly important when a meta-analysis contains only a few studies (say, <10), where the results from statistical assessment might be unreliable due to large random errors.³⁴ Although the quality of unpublished data may be questionable, these data could at least offer systematic reviewers valuable information to perform sensitivity analyses by examining their impact on meta-analysis results.

This article has several limitations. For example, we built the one-sided tests based on the conventional Egger’s test, primarily because of its powerfulness and popularity. However, it is also often criticized for the inflation of its type I error rates when study-specific effect estimates are intrinsically associated with their SEs (e.g., for ORs).^{11, 20, 35} Many alternative methods are available in the literature of evidence synthesis,³⁶ and some could solve the problem of inflated type I error rates.^{20, 22, 37} The proposed framework of one-sided testing could be similarly applied to other existing two-sided tests, including Macaskill’s test,²² Peters’ test,²⁰ Harbord’s test,³⁷ and the skewness-based test.²³ In addition, this article is restricted to univariate meta-analyses, where each pair of treatments for each outcome is compared separately. Multivariate meta-analyses of multiple treatments and/or multiple outcomes have been increasingly used to better synthesize evidence.³⁸ For example, the case study in this article investigated three measures for the same outcome, and it could be performed using a network meta-analysis. Nevertheless, the methods for assessing small-study effects in multivariate meta-analyses were only investigated in a limited number of studies.^39–42 More efforts are needed in this research direction.

CONCLUSION

This article has proposed directional statistical tests to assess small-study effects. They challenge the current practice of using two-sided tests, Egger’s test and Begg’s test, in nearly all meta-analysis applications. Simulation studies showed that the one-sided tests could have considerably higher statistical power than competing methods, particularly their two-sided counterparts. Their type I error rates were generally controlled well. Three real-world meta-analyses on measurements of infrabony periodontal defects were also used to demonstrate the performance of the proposed methods. In summary, we recommend researchers incorporate the potential favored direction of effects into the assessment of small-study effects.