Abstract
Van der Waals (vdW) stacking of two-dimensional (2D) materials to create artificial structures has enabled remarkable discoveries and novel properties in fundamental physics. Here, we report that vdW stacking of centrosymmetric 2D materials, e.g., bilayer MoS2 (2LM) and monolayer graphene (1LG), could support remarkable second-harmonic generation (SHG). The required centrosymmetry breaking for second-order hyperpolarizability arises from the interlayer charge transfer between 2LM and 1LG and the imbalanced charge distribution in 2LM, which are verified by first-principles calculations, Raman spectroscopy, and polarization-resolved SHG. The strength of SHG from 2LM/1LG is of the same order of magnitude as that from the monolayer MoS2, which is well recognized with strong second-order nonlinearity. The emergent SHG reveals that the interlayer charge transfer can effectively modify the symmetry and nonlinear optical properties of 2D heterostructures. It also indicates the great opportunity of SHG spectroscopy for characterizing interlayer coupling in vdW heterostructures.
Van der Waals stacking can effectively engineer symmetry breaking and nonlinear optical properties in 2D heterostructures.
INTRODUCTION
Van der Waals (vdW) stacking of two-dimensional (2D) materials to create artificial structures (1) has enabled remarkable discoveries, which span a broad spectrum of topics central to modern solid-state physics. Following the first realization of high-quality graphene electronics using hexagonal boron nitride (h-BN) encapsulation (2), fascinating phenomena including fractal quantum Hall effect (3), band gap opening (4), Hofstadter butterfly states (3–5), and gate-tunable Mott insulator (6) have been observed in graphene/h-BN vdW heterostructures (vdWHs), which are caused by the substrate’s moiré potential. Besides h-BN, strong coupling in graphene homo-bilayers can generate flat electronic bands, which leads to correlated insulating states and superconductivity in magic-angle twisted bilayer graphene (7, 8). In addition to electrical transport, there has also been great progress in the study of the optical properties and excited-state dynamics in vdWHs (9). Interlayer excitons in hetero-bilayers of transition metal dichalcogenides (10), especially the excitons trapped in moiré potentials with inherited valley-contrasting physics (11–14), have set off a new climax in condensed matter physics. Furthermore, broad research interests have also been ignited in the interfacial interaction involving particles/quasiparticles in vdWHs, including the interlayer carrier dynamics (charge transfer and energy transfer) (9, 15), electron-phonon coupling (16, 17), and interlayer phonon interaction (18). All these discoveries act as the bedrock of fundamental physics and photonics/optoelectronics, enabling practical applications in functional devices, such as energy storage (19), photovoltaics (20, 21), photodetection (22, 23), light-emitting diodes (24), optical modulators (25), lasers (26), logic applications (27), and so on.
Here, we report that vdW stacking 2D materials with centrosymmetry into heterostructures could induce remarkable second-harmonic generation (SHG), which should only arise in materials without centrosymmetry (28). As schematically shown in Fig. 1A, although there is no SHG from the bilayer MoS2 (2LM) or monolayer graphene (1LG), strong SHG could be obtained from their vdWH. The origin of this emergent SHG is the interlayer charge transfer between these two constituents, which breaks the inversion symmetry of 2LM. The conclusions are confirmed by the first-principles calculations, Raman spectroscopy, and polarization-resolved SHG. In addition, from vdWHs of 1LG and four- or six-layer MoS2, similar phenomena of emergent SHG are observed. We note that SHG from the 2LM/1LG vdWH is close to that from the monolayer MoS2 (1LM), which is well recognized with strong second-order nonlinearity. Our results indicate that the interlayer charge transfer can effectively modify the symmetry and nonlinear optical properties of 2D materials. It also illustrates that the SHG technique could be used as reliable spectroscopy to characterize the interlayer coupling and charge distribution in the vdWH of 2D materials.
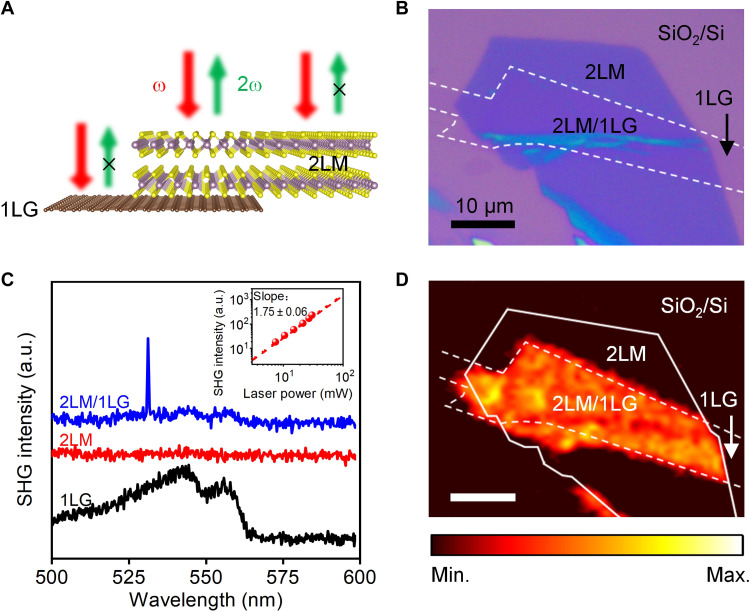
Fig. 1. Fabrication and SHG characterization of 2LM/1LG.
(A) Schematic of the emergent SHG in 2LM/1LG vdWH. Excitation at ω (red arrow) generates second-harmonic radiation at 2ω (green arrow). (B) Optical microscope image of 2LM/1LG vdWH formed by transferring 2LM on 1LG. The 1LG is marked by the white dashed line. (C) Frequency-up-converted optical spectra measured from different regions shown in (B). Inset: Log-log plot of pump power dependence of the SHG intensity. a.u., arbitrary units. (D) Spatial SHG mapping of the sample in (B) at the wavelength of 532 nm. Scale bar, 10 μm.
RESULTS
Fabrication and SHG characterization of 2LM/1LG
To fabricate the 2LM/1LG vdWH, we first mechanically exfoliated 1LG on a silicon substrate covered by a 285-nm-thick oxide layer using the standard scotch tape method (29). The 2LM flake was exfoliated on a poly(dimethylsiloxane) (PDMS) stamp, which was then transferred onto the prepared 1LG by the all-dry transfer method (30). A vacuum annealing process at 300°C was carried out for 30 min (31). As described carefully in the Supplementary Materials, this annealing process is essential for the well interlayer coupling between the 2LM and 1LG. The atomic force microscopy (AFM) characterizations before and after annealing (see fig. S1) indicate that the air gaps between 2LM and 1LG were eliminated effectively, showing a flat and smooth surface over the vdWH region. The ultralow frequency Raman spectra shown in fig. S2 present the shifted shear mode and layer-breathing mode, indicating the effective interlayer coupling as well.
Figure 1B shows the optical microscope image of one of the fabricated 2LM/1LG vdWHs. The layer numbers of the 2LM and 1LG were determined by Raman spectroscopy (see fig. S3). This 2LM/1LG vdWH was then loaded on a home-built multiphoton nonlinear optical microscopy system for SHG characterization (see fig. S4). A picosecond pulsed laser at the wavelength of 1064 nm was chosen as the fundamental pump radiation, which is vertically focused by an objective lens (100×, numerical aperture = 0.8) on the sample with a spot size of ~1 μm. The frequency-up-converted optical signal from the sample was collected by the same objective lens, which was subsequently coupled to a spectrometer mounted with a cooled silicon charge-coupled device camera.
Figure 1C shows the acquired frequency-up-converted optical spectra from different regions of the vdWH sample shown in Fig. 1B. From the region of 2LM/1LG, a sharp peak appears at 532 nm, which is exactly half of the pump wavelength. It indicates the emergence of SHG. In contrast, there is no SHG signal in the separate 1LG or 2LM regions. Only broadband nonlinear photoluminescence (NPL) was observed in 1LG, which is the result of excitation by ultrashort laser pulses (32). The sharp cut at 570 nm in the acquired spectrum is due to the dichroic mirror in our optical setup, which blocks the part of NPL with a wavelength range larger than 570 nm. We note here that the NPL from graphene in the 2LM/1LG is weakened compared with the pristine monolayer, which will be discussed later. No SHG observed in the separate 2LM agrees with the expectation that the 2H-phase 2LM belongs to the centrosymmetric D3d space group with χ(2) = 0 (33). Then, the dependence of SHG intensity from the 2LM/1LG on the pump power was measured, as shown in the inset of Fig. 1C. A linear slope of 1.75 ± 0.06 is obtained in the log-log scale, which is almost consistent with the SHG process that two photons of the fundamental laser convert into one photon of the SHG signal.
The emergent SHG from the 2LM/1LG was further illustrated by implementing its spatial mapping. The sample is mounted on a 2D piezo-actuated stage with a moving step of 500 nm. The mapping result of the signal at the wavelength of 532 nm is displayed in Fig. 1D, showing a clear and continuous region with an obvious SHG signal from the 2LM/1LG. No SHG signal is observed over the regions of separate 2LM or 1LG.
As mentioned in the above fabrication process, an annealing process was used after the stacking of 2LM and 1LG. Before the annealing, the frequency-up-converted spectra were acquired from the as-stacked 2LM/1LG, as shown in fig. S5. Only the broadband NPL was obtained from the 2LM/1LG overlapping region (green curve in fig. S5), which has the same emission spectrum as that from the separate 1LG region (black curve in fig. S5). There is no SHG peak from the as-stacked 2LM/1LG. In contrast, after the annealing, the SHG emerged from the 2LM/1LG, as shown in the blue curve in fig. S5. Considering the annealing process is essential to the good interfacial contact of vdWH (see AFM results in fig. S1 and Raman spectra in fig. S2), the zero (strong) SHG signal observed from the 2LM/1LG vdWH before (after) annealing could be attributed to the absence (emergence) of interlayer coupling.
Charge transfer and symmetry breaking in 2LM/1LG
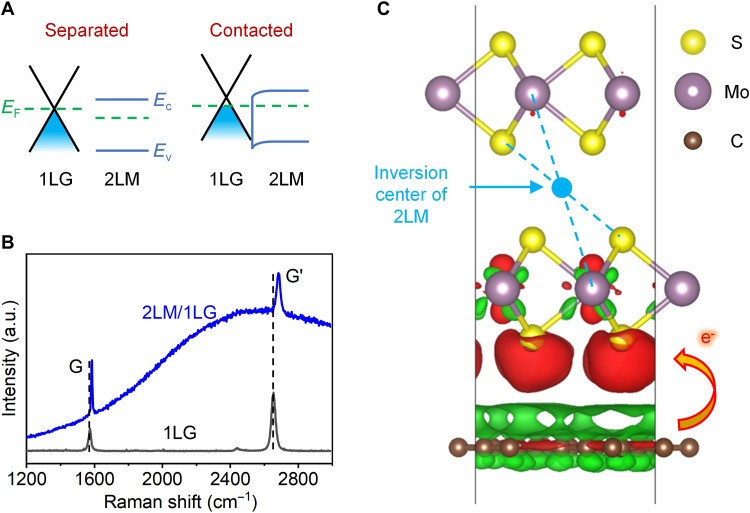
With the interlayer coupling in 2LM/1LG, the electrons in 1LG would partially transfer to 2LM because 1LG has a work function (~4.5 eV) (34) lower than that of 2LM (~5.1 eV) (35). When 1LG is in contact with 2LM, the Fermi level will shift to the same level, leading to the accumulation of negative charge in 2LM and positive charge in 1LG (36), as schematically shown in Fig. 2A. The charge transfer behavior could be proved by measuring the Raman spectra of the separate 1LG and the 1LG in the vdWH, as shown in Fig. 2B. The peak positions of the G and G′ modes in the Raman spectra of 1LG are highly sensitive to the doping level (37). For pristine 1LG, the peak positions of the G and G′ modes are 1575.0 and 2661.8 cm−1, respectively. In the 2LM/1LG vdWH, the peak positions of the G and G′ modes are shifted to 1588.0 and 2689.9 cm−1. The blue shifts of the G (13 cm−1) and G′ (28.2 cm−1) modes indicate the p-type doping of the 1LG, that is, the electrons are transferred from 1LG to 2LM. The shift of the A1g mode of 2LM shown in fig. S6 also indicates the charge transfer and interlayer coupling in 2LM/1LG (18). We note that the shift of Raman modes could also be due to strains in the material. Here, the restoration of the E2g1 mode (see fig. S6) and the absence of splitting in the G′ mode (see Fig. 2B) prove that there is no strain in 2LM or 1LG (38, 39). A detailed explanation can be seen in section S7.
Fig. 2. Charge transfer between 1LG and 2LM.
(A) Schematic illustration of band alignment and charge transfer between 1LG and 2LM before and after their vdW contact. Here, EF refers to the Fermi level. Ec and Ev refer to the conduction band and valence band of 2LM, respectively. (B) Raman spectra of the separate 1LG and the 2LM/1LG vdWH. (C) Side view of isosurface plots of the induced charge density difference for the 2LM/1LG vdWH. The isosurface is taken to be 1 × 10−4 e/Å3. The red and green regions represent the accumulation and depletion of electrons, respectively.
This ground-state charge transfer can also be proved by the power-dependent Raman spectra, where the positions of G, G′, and A1g modes show no observable variation under different incident laser powers (see fig. S7). Hence, it is unexpected that the emergent SHG from the 2LM/1LG is caused by the photo-induced charge transfer. The broadband background in the spectrum of 2LM/1LG vdWH is the photoluminescence of the 2LM (40). In addition, as indicated in Fig. 1C, the NPL from the 1LG is degraded remarkably after its vdW stacking with the 2LM. Considering the strong doping-dependent property of the NPL in 1LG (41), the weakened NPL in the 2LM/1LG vdWH verifies the charge transfer between 2LM and 1LG as well. This charge transfer could induce the broken inversion symmetry in the 2LM/1LG vdWH for the emergent SHG.
To intuitively describe the inversion symmetry breaking by the vdW stacking and the origin of SHG, we carried out the first-principles calculations on the 2LM/1LG. A √7 × √7 supercell of graphene (14 carbon atoms) was chosen to match a 2 × 2 supercell of 2LM (8 molybdenum and 16 sulfur atoms). Figure 2C shows the calculated charge density differences over the 2LM and 1LG after they form the 2LM/1LG vdWH. The red isosurface regions indicate the gain of electrons, while the green ones indicate the loss of electrons. In the 2LM/1LG vdWH, to reach an electrostatic equilibrium state, electrons transfer from 1LG to 2LM (~0.04 electrons per cell are transferred), leaving the positive 1LG and negative 2LM. The transferred electrons are mainly concentrated near the lower sulfur (S) atom on the bottom MoS2 layer, and the charge distribution of the upper MoS2 layer is almost not affected.
As indicated in Fig. 2C, although there is an inversion symmetry center in the intrinsic 2LM, the imbalanced charge distribution over the 2LM induced by the charge transfer in the 2LM/1LG vdWH makes it lose the inversion symmetry, which could yield an effective second-order hyperpolarizability and SHG (28). Note that, as shown in Fig. 2C, the charge transfer in 2LM/1LG vdWH also gives rise to the presence of charge inhomogeneity in 1LG. In this case, the π electrons in the 1LG lose the horizontal mirror plane and the inversion symmetry, and the 1LG is isomorphic to the point group C6v (42). However, since electric-dipole-allowed SHG is not sensitive to the presence of a Cn rotation symmetry operation with n > 3 (43), no SHG signal is expected from the 1LG layer in the 2LM/1LG vdWH. In future work, it is interesting to calculate the emergent second-order nonlinear susceptibility and its dispersion property with the first-principles calculations by considering the charge transfer-assisted interband and intraband transition in the 2LM/1LG vdWH (44).
Polarization-resolved SHG in 2LM/1LG
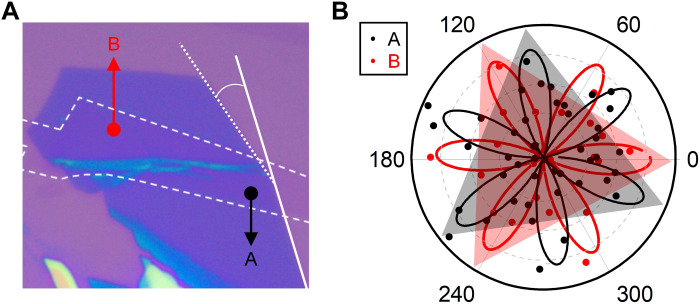
The above analysis that the emergent SHG in 2LM/1LG vdWH arises from its 2LM layer could be further verified experimentally by measuring the polarization-resolved SHG. As discussed above, the transferred electrons lead to the imbalanced charge distribution in 2LM, which transforms it from the centrosymmetric D3d point group to the noncentrosymmetric C3v point group (45, 46). The polarization-resolved SHG pattern of the C3v point group would have a sixfold with respect to the laser polarization, which is determined by I2ω ∝ sin2(3θ), where θ is the angle between the armchair direction of 2LM and the pump laser polarization (33, 47, 48). In the fabrication of the 2LM/1LG vdWH shown in Fig. 1B, the annealing process twists part of the 2LM layer and leaves a wrinkle in it, as displayed in the AFM images of the 2LM/1LG vdWH before and after annealing (see fig. S1). To facilitate the discussion, we denote the regions of the 2LM/1LG at the two sides of the wrinkle as A and B, as shown in Fig. 3A. By measuring the rotating angle of the straight edges of the 2LM in the two regions (the dotted line and the solid line), the twisted angle is estimated as 15° (also shown in fig. S1). We measured the polarization-resolved SHG from region A and region B, as shown in Fig. 3B. Both of them have the sixfold pattern, which agrees with I2ω ∝ sin2(3θ). What’s more, the patterns from the two regions have a twist angle of around 19°, which is almost consistent with the twist of the 2LM. The slight difference may be due to the fitting error and large sampling interval. Considering the bottom 1LG is uniform over the whole vdWH, it is concluded that the SHG in 2LM/1LG originates from the 2LM.
Fig. 3. Polarization-resolved SHG in 2LM/1LG.
(A) Optical microscope image of the 2LM/1LG. (B) Polar plots of the polarization-resolved SHG intensity measured from regions A and B in (A). The two triangles overlapping with the patterns serve as guides to the eye.
Note that it is necessary to exclude the possibility of the twisting between the two layers of the 2LM, which could also induce SHG due to symmetry breaking. We examine it by monitoring the shear mode in the Raman spectra of separate 2LM and 2LM/1LG (see fig. S6). The nonvariation indicates the absence of interlayer twisting in the 2LM (49).
Gate-tunable SHG in 2LM/1LG
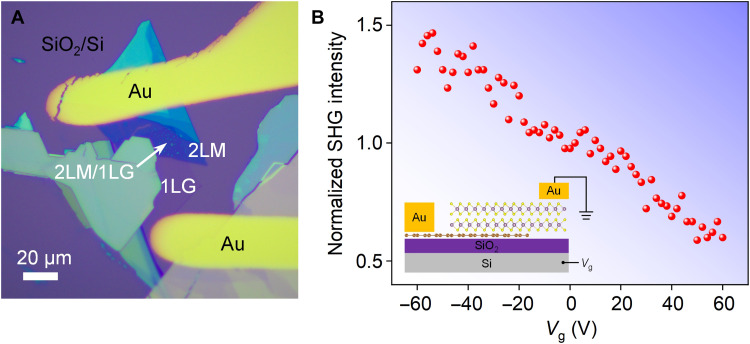
To further prove the mechanism of the emergent SHG in 2LM/1LG vdWH, we also performed electrically tuned SHG in another fabricated 2LM/1LG vdWH with metal electrodes (see Fig. 4A) by applying back gate voltage (Vg). With the application of varied Vg, the SHG intensity from the vdWH region varies from 50 to 150% with Vg changed from 60 to −60 V, as shown in Fig. 4B. To facilitate the explanation of this result, the Vg-dependent Raman spectra of the 2LM/1LG vdWH were evaluated (see fig. S8, B and C). The G and G′ modes of the 1LG and A1g mode of the 2LM show no shift with the variation of Vg, which indicates that the charge transfer between 2LM and 1LG is not modulated by the Vg. That is, the ground-state charge transfer between 2LM and 1LG has been determined when the heterostructure is formed. However, the applied Vg can change the charge distribution in the heterostructure, affecting the symmetry and SHG intensity, based on our first-principles calculations (see fig. S8, D and E).
Fig. 4. Gate-tunable SHG in 2LM/1LG.
(A) Optical microscope image of the device. (B) Vg-dependent SHG intensity in 2LM/1LG. Inset: Schematic illustration of the device.
When the Vg is applied, the resulted external electric field drives the charge to redistribute in the 2LM. As we can see in fig. S8D, compared with the situation when Vg = 0 V (Fig. 2C), the accumulation of electrons at the top of the MoS2 bilayer may cancel out effective second-order hyperpolarizability for SHG in 2LM with the increasing Vg. This may be the reason why the SHG strength in 2LM/1LG decreases with the increase of the positive Vg. In another case, when Vg is applied along the negative direction, the depletion of electrons at the top of the MoS2 bilayer may enhance the effective second-order hyperpolarizability for SHG in 2LM (see fig. S8E), giving rise to the increased SHG intensity. Above all, although the charge transfer between 1LG and 2LM may not be effectively tuned by the Vg, the Vg-induced electric field can redistribute the charges in 2LM and alter the effective second-order hyperpolarizability. This gate-tunable SHG further verifies that the charge transfer-induced symmetry breaking and effective second-order hyperpolarizability in 2LM give rise to the emergent SHG in 2LM/1LG vdWH. Here, to avoid the breakdown of the SiO2 dielectric layer, the Vg is limited to 60 V (−60 V). It is expected that zero SHG or even stronger SHG could be achieved if the amplitudes of Vg were increased further.
SHG in vdWHs of 1LG and other even number–layered MoS2
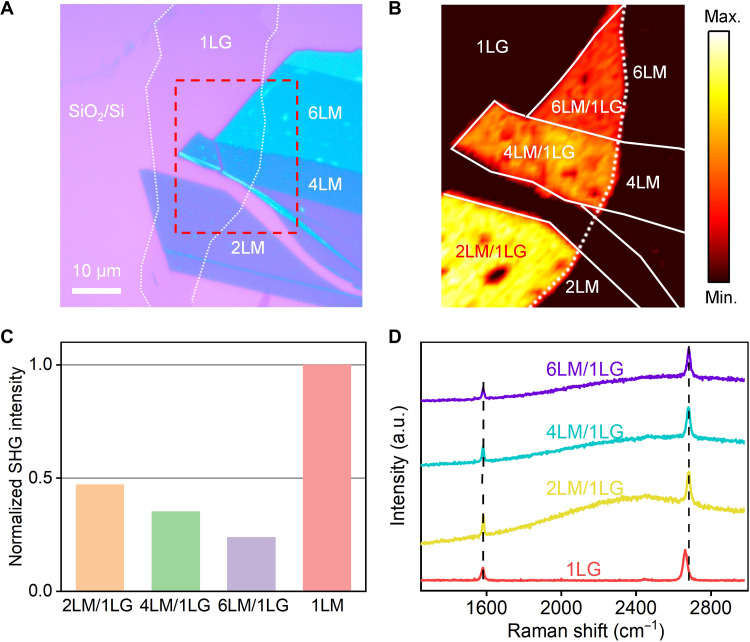
To further confirm the vdW stacking-induced SHG in the centrosymmetric MoS2 and graphene, we fabricated more vdWHs by stacking 1LG with other even number-layered MoS2. Figure 5A displays the optical microscope image of a fabricated device, where a 1LG was vdW contacted with bilayer, four-layer, and six-layer MoS2, denoted as 2LM, 4LM, and 6LM, respectively. The SHG behaviors of the vdWHs were examined by the SHG spatial mapping and polarization-resolved SHG, as shown in Fig. 5B and fig. S9. Clear SHG signals are observed from the vdW stacking regions of 2LM/1LG, 4LM/1LG, and 6LM/1LG. However, there is no SHG signal over the separate 2LM, 4LM, and 6LM. On the bare 1LG, there is no SHG either. These emergent SHGs from 4LM/1LG and 6LM/1LG could be explained with the mechanism discussed above on the 2LM/1LG. In brief, with the vdW contact of the 1LG and 4LM (6LM) in their vdWHs, the electrons in 1LG transfer to 4LM (6LM) due to the band alignment. The transferred electrons are mainly concentrated near the lower sulfur (S) atom on the bottom MoS2 layer (see fig. S10), and the charge distribution of the upper MoS2 layers is almost not affected, resulting in imbalanced charge distribution over the 4LM (6LM). As a result, the intrinsically centrosymmetric 4LM (6LM) loses its inversion symmetry, which could yield an effective second-order hyperpolarizability and SHG. It will be discussed later in detail with the polarization-resolved SHG, layer-dependent Raman spectra, and the re-absorption of SHG by the multilayer MoS2. Especially, the polarization-resolved SHG patterns of 4LM/1LG and 6LM/1LG in fig. S9 all have sixfold to the pump laser polarization, which proves the mechanism discussed above.
Fig. 5. SHG in 2LM/1LG, 4LM/1LG, and 6LM/1LG vdWHs.
(A) Optical microscope image of 2LM/1LG, 4LM/1LG, and 6LM/1LG vdWHs. The 1LG is marked by the white dotted line. (B) SHG spatial mapping of the sample marked by the red dashed box in (A). (C) Normalized SHG intensities from 2LM/1LG, 4LM/1LG, 6LM/1LG, and 1LM. (D) Raman spectra from the 2LM/1LG, 4LM/1LG, 6LM/1LG vdWHs, and 1LG in (A).
The mapping results also reveal that though the SHG over each vdWH region has a uniform value, the SHG signal from 2LM/1LG (6LM/1LG) is the strongest (weakest). To evaluate the efficiencies of SHGs from the vdWHs, in Fig. 5C, we plot their values by comparing them with the SHG intensity from the 1LM, which was acquired with the same experimental conditions. The SHG intensities of 2LM/1LG, 4LM/1LG, and 6LM/1LG are about 47, 35, and 23% of that of the 1LM. Considering the moderately large χ(2) in 1LM (50), the vdW stacking could be recognized as an effective technique to induce χ(2) from centrosymmetric materials.
Here, the decrease of SHG intensity as the thickness of MoS2 increases could be attributed to the re-absorption of SHG by the multilayer MoS2. As illustrated by the charge distribution in 2LM/1LG (see Fig. 2C), the transferred electrons are mainly concentrated on the S atoms in the bottom MoS2 layer, and there is almost no variation of charge distribution in the top MoS2 layers. Similarly, if 4LM or 6LM were stacked on 1LG, then the charge transfer would only take place between the 1LG and the bottom MoS2 layer (see fig. S10). The charge concentrations in other MoS2 layers would not be changed. Hence, in the vdWHs, the effective second-order hyperpolarizability for SHG would only be generated between the bottom two MoS2 layers. For the 4LM (6LM), the top two (four) MoS2 layers would not contribute any second-order hyperpolarizability. In addition, as indicated by the Raman spectra shown in Fig. 5D, the shift of the G′ band in the 2LM/1LG, 4LM/1LG, and 6LM/1LG is the same relative to that of the separate 1LG, implying that the p-type doping level of 1LG by MoS2 layers is almost same in these vdWHs. This further proves that charge transfer occurs at the interface between MoS2 and graphene, which is independent of the increased number of MoS2 layers. This charge transfer behavior is also consistent with the previously reported first-layer effect in graphene-enhanced Raman scattering (51) where charge transfer usually occurs at a distance level below 1 nm and decays quickly with the increase of the distance. As a consequence, the 2LM/1LG, 4LM/1LG, and 6LM/1LG, should have the same effective second-order hyperpolarizability and therefore yield the same SHG radiation powers. However, the top two (four) MoS2 layers in 4LM (6LM) would absorb the SHG signal generated in the bottom two MoS2 layers, considering the energy of SHG photons (about 2.33 eV) is larger than the band gap of few-layer MoS2 (<1.6 eV) (52). The corresponding absorption properties of these even number-layered MoS2 are extracted from their differential reflection spectra (see fig. S11). Hence, SHG from 6LM/1LG (2LM/1LG) is the weakest (strongest) one due to the largest absorption of SHG (absence of SHG absorption).
DISCUSSION
We have demonstrated the emergence of SHG from centrosymmetric 2D materials (e.g., 2LM, 4LM, 6LM, and 1LG) by vdW stacking them into the heterostructure. Assisted by the first-principles calculations, Raman spectroscopy, polarization-resolved SHG, the underlying mechanism of the emergent SHG in vdWH is attributed to the interlayer charge transfer, which gives rise to imbalanced charge distributions in the MoS2 multilayers and breaks the inversion symmetry for yielding second-order hyperpolarizability. We also verify this emergent SHG from centrosymmetric materials induced by interlayer charge transfer by vdW stacking other 2D materials without intrinsic SHG, including a vdWH of 1LG and bilayer WSe2 (see fig. S12) and a vdWH of monolayer ReS2 and 2LM (see fig. S13). Although there is no SHG in these separate 2D materials, their vdWHs present clear SHG signals. In previously reported works, in a vdWH of two 2D materials with intrinsic SHGs, modulations of their SHGs by the interlayer charge transfer were studied using a pump-probe technique, which could be considered as an ingenious all-optical method to dynamically characterize the charge transfer (53). However, limited by the weak electric field induced by the separated photoinduced carriers at the interface, the modulation is about two orders of magnitude smaller than the original SHG. In our experiment, the SHG strength from the 2LM/1LG vdWH is as strong as that from the monolayer MoS2, indicating that the interlayer charge transfer in the as-formed vdWH can effectively modify the symmetry and nonlinear optical properties of 2D materials.
Our results are expected to reveal new physics and important techniques for the development of 2D materials. It provides a possible strategy to engineer symmetry breaking of 2D materials, which may boost enchanting physical phenomena like valley-contrasting physics (54), spin-orbit physics (55), and unconventional Ising superconductivity (56). Our work also proves that SHG is an effective means to characterize interlayer couplings in vdW-stacked heterostructures. Compared with the complex Raman and pump-probe spectroscopy, the SHG spectroscopy revealed in this work could judge the interlayer coupling using the emergence of SHG intensity or not, which is more straightforward. What’s more, besides the implication of charge transfer in vdWH, which was also realized by the Raman or pump-probe methods, the SHG spectroscopy could also indicate the imbalanced charge distributions around the interface of the vdWH.
MATERIALS AND METHODS
Fabrication of the 2LM/1LG vdWHs
First, we mechanically exfoliated 1LG on a silicon substrate covered by a 285 nm thick oxide layer using the standard scotch tape method (29). Then, the 2LM flake was exfoliated on a PDMS stamp. Next, we transferred 2LM onto the prepared 1LG by the all-dry transfer method (30). Last, the 2LM/1LG was annealed in a vacuum furnace at 300°C for 30 min.
Characterizing the 2LM/1LG vdWHs
For Raman characterization, all Raman spectra are recorded at room temperature in the air using the confocal WiTec Alpha 300R Raman microscope where the Raman signal is collected in reflection geometry. The excitation wavelength is 532 nm. For SHG characterization, we choose the picosecond pulsed laser at the wavelength of 1064 nm as the fundamental pump. A detailed description and a schematic representation of the system are shown in the Supplementary Materials.
The first-principles calculation
The charge density difference between the MoS2 bilayer and graphene is calculated by VASP (57) with PBE (58) functional and PAW (59) potential based on the density functional theory. The heterostructure is built by using 2 × 2 × 1 MoS2 supercell and √7 × √7 × 1 graphene supercell. The energy cutoff is set to 500 eV. The atomic structures are relaxed until the force is less than 0.01 eV/Å. The k-point grid of 6 × 6 × 1 is used to sample the first Brillouin zone. The vdW interactions between these layers are described by DFT-D3 (60).
Acknowledgments
Funding: This work was supported by National Key R&D Program of China (grant nos. 2022YFA1404800 and 2018YFA0307200), National Natural Science Foundation of China (grant nos. 91950119, 61905196, 62104198, and 62090033), and Key Research and Development Program in Shaanxi Province of China (grant nos. 2020JZ-10).
Author contributions: X.G. conceived and supervised the project. M.Z., J.Z., J.W., and X.C. contributed to the sample preparation, characterization, vdWH fabrication, measurements, and data analysis. N.H. carried out first-principles calculations. The manuscript was written through the contributions of all authors. All authors have approved the final version of the manuscript.
Competing interests: The authors declare that they have no competing interests.
Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials.
Supplementary Materials
This PDF file includes:
Supplementary Text
Sections S1 to S13
Figs. S1 to S13
REFERENCES AND NOTES
- 1.Geim A. K., Grigorieva I. V., Van der Waals heterostructures. Nature 499, 419–425 (2013). [DOI] [PubMed] [Google Scholar]
- 2.Dean C. R., Young A. F., Meric I., Lee C., Wang L., Sorgenfrei S., Watanabe K., Taniguchi T., Kim P., Shepard K. L., Hone J., Boron nitride substrates for high-quality graphene electronics. Nat. Nanotechnol. 5, 722–726 (2010). [DOI] [PubMed] [Google Scholar]
- 3.Dean C. R., Wang L., Maher P., Forsythe C., Ghahari F., Gao Y., Katoch J., Ishigami M., Moon P., Koshino M., Taniguchi T., Watanabe K., Shepard K. L., Hone J., Kim P., Hofstadter’s butterfly and the fractal quantum Hall effect in moiré superlattices. Nature 497, 598–602 (2013). [DOI] [PubMed] [Google Scholar]
- 4.Hunt B., Sanchez-Yamagishi J. D., Young A. F., Yankowitz M., LeRoy B. J., Watanabe K., Taniguchi T., Moon P., Koshino M., Jarillo-Herrero P., Ashoori R. C., Massive Dirac fermions and Hofstadter butterfly in a van der Waals heterostructure. Science 340, 1427–1430 (2013). [DOI] [PubMed] [Google Scholar]
- 5.Ponomarenko L. A., Gorbachev R. V., Yu G. L., Elias D. C., Jalil R., Patel A. A., Mishchenko A., Mayorov A. S., Woods C. R., Wallbank J. R., Mucha-Kruczynski M., Piot B. A., Potemski M., Grigorieva I. V., Novoselov K. S., Guinea F., Fal’ko V. I., Geim A. K., Cloning of Dirac fermions in graphene superlattices. Nature 497, 594–597 (2013). [DOI] [PubMed] [Google Scholar]
- 6.Chen G., Jiang L., Wu S., Lyu B., Li H., Chittari B. L., Watanabe K., Taniguchi T., Shi Z., Jung J., Zhang Y., Wang F., Evidence of a gate-tunable Mott insulator in a trilayer graphene moiré superlattice. Nat. Phys. 15, 237–241 (2019). [Google Scholar]
- 7.Cao Y., Fatemi V., Fang S., Watanabe K., Taniguchi T., Kaxiras E., Jarillo-Herrero P., Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018). [DOI] [PubMed] [Google Scholar]
- 8.Cao Y., Fatemi V., Demir A., Fang S., Tomarken S. L., Luo J. Y., Sanchez-Yamagishi J. D., Watanabe K., Taniguchi T., Kaxiras E., Ashoori R. C., Jarillo-Herrero P., Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 556, 80–84 (2018). [DOI] [PubMed] [Google Scholar]
- 9.Jin C., Ma E. Y., Karni O., Regan E. C., Wang F., Heinz T. F., Ultrafast dynamics in van der Waals heterostructures. Nat. Nanotechnol. 13, 994–1003 (2018). [DOI] [PubMed] [Google Scholar]
- 10.Rivera P., Schaibley J. R., Jones A. M., Ross J. S., Wu S., Aivazian G., Klement P., Seyler K., Clark G., Ghimire N. J., Yan J., Mandrus D. G., Yao W., Xu X., Observation of long-lived interlayer excitons in monolayer MoSe2–WSe2 heterostructures. Nat. Commun. 6, 6242 (2015). [DOI] [PubMed] [Google Scholar]
- 11.Seyler K. L., Rivera P., Yu H., Wilson N. P., Ray E. L., Mandrus D. G., Yan J., Yao W., Xu X., Signatures of moiré-trapped valley excitons in MoSe2/WSe2 heterobilayers. Nature 567, 66–70 (2019). [DOI] [PubMed] [Google Scholar]
- 12.Jin C., Regan E. C., Yan A., Utama M. I. B., Wang D., Zhao S., Qin Y., Yang S., Zheng Z., Shi S., Watanabe K., Taniguchi T., Tongay S., Zettl A., Wang F., Observation of moiré excitons in WSe2/WS2 heterostructure superlattices. Nature 567, 76–80 (2019). [DOI] [PubMed] [Google Scholar]
- 13.Tran K., Moody G., Wu F., Lu X., Choi J., Kim K., Rai A., Sanchez D. A., Quan J., Singh A., Embley J., Zepeda A., Campbell M., Autry T., Taniguchi T., Watanabe K., Lu N., Banerjee S. K., Silverman K. L., Kim S., Tutuc E., Yang L., MacDonald A. H., Li X., Evidence for moiré excitons in van der Waals heterostructures. Nature 567, 71–75 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Alexeev E. M., Ruiz-Tijerina D. A., Danovich M., Hamer M. J., Terry D. J., Nayak P. K., Ahn S., Pak S., Lee J., Sohn J. I., Molas M. R., Koperski M., Watanabe K., Taniguchi T., Novoselov K. S., Gorbachev R. V., Shin H. S., Fal’ko V. I., Tartakovskii A. I., Resonantly hybridized excitons in moiré superlattices in van der Waals heterostructures. Nature 567, 81–86 (2019). [DOI] [PubMed] [Google Scholar]
- 15.Hu Z., Liu X., Hernández-Martínez P. L., Zhang S., Gu P., Du W., Xu W., Demir H. V., Liu H., Xiong Q., Interfacial charge and energy transfer in van der Waals heterojunctions. InfoMat 4, e12290 (2022). [Google Scholar]
- 16.Jin C., Kim J., Suh J., Shi Z., Chen B., Fan X., Kam M., Watanabe K., Taniguchi T., Tongay S., Zettl A., Wu J., Wang F., Interlayer electron–phonon coupling in WSe2/hBN heterostructures. Nat. Phys. 13, 127–131 (2017). [Google Scholar]
- 17.Lin M.-L., Zhou Y., Wu J.-B., Cong X., Liu X.-L., Zhang J., Li H., Yao W., Tan P.-H., Cross-dimensional electron-phonon coupling in van der Waals heterostructures. Nat. Commun. 10, 2419 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Li H., Wu J.-B., Ran F., Lin M.-L., Liu X.-L., Zhao Y., Lu X., Xiong Q., Zhang J., Huang W., Zhang H., Tan P.-H., Interfacial interactions in van der Waals heterostructures of MoS2 and graphene. ACS Nano 11, 11714–11723 (2017). [DOI] [PubMed] [Google Scholar]
- 19.Pomerantseva E., Gogotsi Y., Two-dimensional heterostructures for energy storage. Nat. Energy 2, 17089 (2017). [Google Scholar]
- 20.Furchi M. M., Zechmeister A. A., Hoeller F., Wachter S., Pospischil A., Mueller T., Photovoltaics in Van der Waals heterostructures. IEEE J. Sel. Top. Quantum Electron. 23, 106–116 (2017). [Google Scholar]
- 21.Paul K. K., Kim J. H., Lee Y. H., Hot carrier photovoltaics in van der Waals heterostructures. Nat. Rev. Phys. 3, 178–192 (2021). [Google Scholar]
- 22.Massicotte M., Schmidt P., Vialla F., Schädler K. G., Reserbat-Plantey A., Watanabe K., Taniguchi T., Tielrooij K. J., Koppens F. H. L., Picosecond photoresponse in van der Waals heterostructures. Nat. Nanotechnol. 11, 42–46 (2016). [DOI] [PubMed] [Google Scholar]
- 23.Zhang K., Zhang T., Cheng G., Li T., Wang S., Wei W., Zhou X., Yu W., Sun Y., Wang P., Zhang D., Zeng C., Wang X., Hu W., Fan H. J., Shen G., Chen X., Duan X., Chang K., Dai N., Interlayer transition and infrared photodetection in atomically thin type-II MoTe2/MoS2 van der Waals heterostructures. ACS Nano 10, 3852–3858 (2016). [DOI] [PubMed] [Google Scholar]
- 24.Withers F., Del Pozo-Zamudio O., Mishchenko A., Rooney A. P., Gholinia A., Watanabe K., Taniguchi T., Haigh S. J., Geim A. K., Tartakovskii A. I., Novoselov K. S., Light-emitting diodes by band-structure engineering in van der Waals heterostructures. Nat. Mater. 14, 301–306 (2015). [DOI] [PubMed] [Google Scholar]
- 25.Guo X., Liu R., Hu D., Hu H., Wei Z., Wang R., Dai Y., Cheng Y., Chen K., Liu K., Zhang G., Zhu X., Sun Z., Yang X., Dai Q., Efficient all-optical plasmonic modulators with atomically thin van der Waals heterostructures. Adv. Mater. 32, 1907105 (2020). [DOI] [PubMed] [Google Scholar]
- 26.Paik E. Y., Zhang L., Burg G. W., Gogna R., Tutuc E., Deng H., Interlayer exciton laser of extended spatial coherence in atomically thin heterostructures. Nature 576, 80–84 (2019). [DOI] [PubMed] [Google Scholar]
- 27.Huang M., Li S., Zhang Z., Xiong X., Li X., Wu Y., Multifunctional high-performance van der Waals heterostructures. Nat. Nanotechnol. 12, 1148–1154 (2017). [DOI] [PubMed] [Google Scholar]
- 28.R. W. Boyd, Nonlinear Optics (Elsevier, 2020);https://linkinghub.elsevier.com/retrieve/pii/C20150055101.
- 29.Novoselov K. S., Geim A. K., Morozov S. V., Jiang D., Zhang Y., Dubonos S. V., Grigorieva I. V., Firsov A. A., Electric field effect in atomically thin carbon films. Science 306, 666–669 (2004). [DOI] [PubMed] [Google Scholar]
- 30.Castellanos-Gomez A., Buscema M., Molenaar R., Singh V., Janssen L., Van Der Zant H. S. J., Steele G. A., Deterministic transfer of two-dimensional materials by all-dry viscoelastic stamping. 2D Mater. 1, 011002 (2014). [Google Scholar]
- 31.Tongay S., Fan W., Kang J., Park J., Koldemir U., Suh J., Narang D. S., Liu K., Ji J., Li J., Sinclair R., Wu J., Tuning interlayer coupling in large-area heterostructures with CVD-grown MoS2 and WS2 monolayers. Nano Lett. 14, 3185–3190 (2014). [DOI] [PubMed] [Google Scholar]
- 32.Liu W. T., Wu S. W., Schuck P. J., Salmeron M., Shen Y. R., Wang F., Nonlinear broadband photoluminescence of graphene induced by femtosecond laser irradiation. Phys. Rev. B - Condens. Matter Mater. Phys. 82, 081408 (2010). [Google Scholar]
- 33.Li Y., Rao Y., Mak K. F., You Y., Wang S., Dean C. R., Heinz T. F., Probing symmetry properties of few-layer MoS2 and h-BN by optical second-harmonic generation. Nano Lett. 13, 3329–3333 (2013). [DOI] [PubMed] [Google Scholar]
- 34.Yu Y. J., Zhao Y., Ryu S., Brus L. E., Kim K. S., Kim P., Tuning the graphene work function by electric field effect. Nano Lett. 9, 3430–3434 (2009). [DOI] [PubMed] [Google Scholar]
- 35.Wang X., Kim S. Y., Wallace R. M., Interface chemistry and band alignment study of Ni and Ag contacts on MoS2. ACS Appl. Mater. Interfaces 13, 15802–15810 (2021). [DOI] [PubMed] [Google Scholar]
- 36.Sun X., Zhang B., Li Y., Luo X., Li G., Chen Y., Zhang C., He J., Tunable ultrafast nonlinear optical properties of graphene/MoS2 van der Waals heterostructures and their application in solid-state bulk lasers. ACS Nano 12, 11376–11385 (2018). [DOI] [PubMed] [Google Scholar]
- 37.Das A., Pisana S., Chakraborty B., Piscanec S., Saha S. K., Waghmare U. V., Novoselov K. S., Krishnamurthy H. R., Geim A. K., Ferrari A. C., Sood A. K., Monitoring dopants by Raman scattering in an electrochemically top-gated graphene transistor. Nat. Nanotechnol. 3, 210–215 (2008). [DOI] [PubMed] [Google Scholar]
- 38.Wang Y., Cong C., Qiu C., Yu T., Raman spectroscopy study of lattice vibration and crystallographic orientation of monolayer MoS2 under uniaxial strain. Small 9, 2857–2861 (2013). [DOI] [PubMed] [Google Scholar]
- 39.Yoon D., Son Y.-W., Cheong H., Strain-dependent splitting of the double-resonance raman scattering band in graphene. Phys. Rev. Lett. 106, 155502 (2011). [DOI] [PubMed] [Google Scholar]
- 40.Splendiani A., Sun L., Zhang Y., Li T., Kim J., Chim C. Y., Galli G., Wang F., Emerging photoluminescence in monolayer MoS2. Nano Lett. 10, 1271–1275 (2010). [DOI] [PubMed] [Google Scholar]
- 41.Huang D., Jiang T., Zhang Y., Shan Y., Fan X., Zhang Z., Dai Y., Shi L., Liu K., Zeng C., Zi J., Liu W.-T., Wu S., Gate switching of ultrafast photoluminescence in graphene. Nano Lett. 18, 7985–7990 (2018). [DOI] [PubMed] [Google Scholar]
- 42.Malard L. M., Guimarães M. H. D., Mafra D. L., Mazzoni M. S. C., Jorio A., Group-theory analysis of electrons and phonons in N-layer graphene systems. Phys. Rev. B Condens. Matter Mater. Phys. 79, 125426 (2009). [Google Scholar]
- 43.Dean J. J., Van Driel H. M., Second harmonic generation from graphene and graphitic films. Appl. Phys. Lett. 95, 261910 (2009). [Google Scholar]
- 44.He C., Wu R., Qi M., Huang Y., Zhou Y., Zhang S., Zhao Q., Xu X., Dispersion property and evolution of second harmonic generation pattern in type-I and type-II van der Waals heterostructures. ACS Appl. Mater. Interfaces 13, 27334–27342 (2021). [DOI] [PubMed] [Google Scholar]
- 45.Klein J., Wierzbowski J., Steinhoff A., Florian M., Rösner M., Heimbach F., Müller K., Jahnke F., Wehling T. O., Finley J. J., Kaniber M., Electric-field switchable second-harmonic generation in bilayer MoS2 by inversion symmetry breaking. Nano Lett. 17, 392–398 (2017). [DOI] [PubMed] [Google Scholar]
- 46.Lee J., Mak K. F., Shan J., Electrical control of the valley Hall effect in bilayer MoS2 transistors. Nat. Nanotechnol. 11, 421–425 (2016). [DOI] [PubMed] [Google Scholar]
- 47.Malard L. M., Alencar T. V., Barboza A. P. M., Mak K. F., De Paula A. M., Observation of intense second harmonic generation from MoS2 atomic crystals. Phys. Rev. B Condens. Matter Mater. Phys. 87, 201401 (2013). [Google Scholar]
- 48.Zhang M., Han N., Wang J., Zhang Z., Liu K., Sun Z., Zhao J., Gan X., Strong second harmonic generation from bilayer graphene with symmetry breaking by redox-governed charge doping. Nano Lett. 22, 4287–4293 (2022). [DOI] [PubMed] [Google Scholar]
- 49.Lin M.-L., Tan Q.-H., Wu J.-B., Chen X.-S., Wang J.-H., Pan Y.-H., Zhang X., Cong X., Zhang J., Ji W., Hu P.-A., Liu K.-H., Tan P.-H., Moiré phonons in twisted bilayer MoS2. ACS Nano 12, 8770–8780 (2018). [DOI] [PubMed] [Google Scholar]
- 50.Woodward R. I., Murray R. T., Phelan C. F., De Oliveira R. E. P., Runcorn T. H., Kelleher E. J. R., Li S., De Oliveira E. C., Fechine G. J. M., Eda G., De Matos C. J. S., Characterization of the second- and third-order nonlinear optical susceptibilities of monolayer MoS2 using multiphoton microscopy. 2D Mater. 4, 011006 (2017). [Google Scholar]
- 51.Ling X., Zhang J., First-layer effect in graphene-enhanced Raman scattering. Small 6, 2020–2025 (2010). [DOI] [PubMed] [Google Scholar]
- 52.Lee H. S., Min S. W., Chang Y. G., Park M. K., Nam T., Kim H., Kim J. H., Ryu S., Im S., MoS2 nanosheet phototransistors with thickness-modulated optical energy gap. Nano Lett. 12, 3695–3700 (2012). [DOI] [PubMed] [Google Scholar]
- 53.Yao P., He D., Zereshki P., Wang Y., Zhao H., Nonlinear optical effect of interlayer charge transfer in a van der Waals heterostructure. Appl. Phys. Lett. 115, 263103 (2019). [Google Scholar]
- 54.Xu X., Yao W., Xiao D., Heinz T. F., Spin and pseudospins in layered transition metal dichalcogenides. Nat. Phys. 10, 343–350 (2014). [Google Scholar]
- 55.Yuan H., Bahramy M. S., Morimoto K., Wu S., Nomura K., Yang B. J., Shimotani H., Suzuki R., Toh M., Kloc C., Xu X., Arita R., Nagaosa N., Iwasa Y., Zeeman-type spin splitting controlled by an electric field. Nat. Phys. 9, 563–569 (2013). [Google Scholar]
- 56.Lu J. M., Zheliuk O., Leermakers I., Yuan N. F. Q., Zeitler U., Law K. T., Ye J. T., Evidence for two-dimensional Ising superconductivity in gated MoS2. Science 350, 1353–1357 (2015). [DOI] [PubMed] [Google Scholar]
- 57.Kresse G., Furthmüller J., Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B Condens. Matter Mater. Phys. 54, 11169–11186 (1996). [DOI] [PubMed] [Google Scholar]
- 58.Perdew J. P., Burke K., Ernzerhof M., Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996). [DOI] [PubMed] [Google Scholar]
- 59.Kresse G., Joubert D., From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B Condens. Matter Mater. Phys. 59, 1758–1775 (1999). [Google Scholar]
- 60.Grimme S., Antony J., Ehrlich S., Krieg H., A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 132, 154104 (2010). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Text
Sections S1 to S13
Figs. S1 to S13