Quantifying the impact of COVID-19 on essential health services: a comparison of interrupted time series analysis using Prophet and Poisson regression models

Abstract

Background

Coronavirus disease 2019 (COVID-19) altered healthcare utilization patterns. However, there is a dearth of literature comparing methods for quantifying the extent to which the pandemic disrupted healthcare service provision in sub-Saharan African countries.

Objective

To compare interrupted time series analysis using Prophet and Poisson regression models in evaluating the impact of COVID-19 on essential health services.

Methods

We used reported data from Uganda’s Health Management Information System from February 2018 to December 2020. We compared Prophet and Poisson models in evaluating the impact of COVID-19 on new clinic visits, diabetes clinic visits, and in-hospital deliveries between March 2020 to December 2020 and across the Central, Eastern, Northern, and Western regions of Uganda.

Results

The models generated similar estimates of the impact of COVID-19 in 10 of the 12 outcome-region pairs evaluated. Both models estimated declines in new clinic visits in the Central, Northern, and Western regions, and an increase in the Eastern Region. Both models estimated declines in diabetes clinic visits in the Central and Western regions, with no significant changes in the Eastern and Northern regions. For in-hospital deliveries, the models estimated a decline in the Western Region, no changes in the Central Region, and had different estimates in the Eastern and Northern regions.

Conclusions

The Prophet and Poisson models are useful in quantifying the impact of interruptions on essential health services during pandemics but may result in different measures of effect. Rigor and multimethod triangulation are necessary to study the true effect of pandemics on essential health services.

INTRODUCTION

The coronavirus disease 2019 (COVID-19) pandemic has caused variations in healthcare utilization patterns including but not limited to non-COVID hospital admissions, emergency department visits, and elective surgeries.^1,2 These were occasioned by a myriad of factors such as the implementation of nonpharmaceutical interventions (NPIs) including lockdowns and restrictions of movement, health workforce redeployment, and individual fear of the contagion.³ Accordingly, efforts to uncover the impact of COVID-19 and related NPIs would help health service providers and policymakers, particularly in resource-constrained settings, implement plausible mitigation measures and improve preparedness for future pandemics.

To quantify the extent to which COVID-19-related disruptions impacted the provision of health services, researchers have employed several qualitative, quantitative, and mixed methods approaches.^3–9 In particular, the interrupted time series (ITS) analysis design is a quasiexperimental study design that has increasingly become popular for evaluating the true impact of COVID-19 disruptions since randomization is not possible in such settings. For example, Doubova et al¹⁰ used the technique to estimate the overall effect of COVID-19-related disruption of essential health services in Mexico and found that up to 8.74 million patient visits were lost in the period between April and December 2020. Similarly using the ITS design, Hatageka et al¹¹ found an estimated 16% decline in hypertension visits and a 39% decline in diabetes visits in public health facilities in Kinshasa, the Democratic Republic of the Congo. Interestingly, Namumanga et al¹² did not find any major impact of COVID-19 on routine malaria indicators in rural Uganda, suggesting the differential impact of the pandemic across measures and outcomes.

While ITS studies are useful, evidence from the literature suggests that the quality of such studies is limited by heterogeneity in their conduct and bias in their reporting.^13–15 To this end, recommendations have been made to introduce formal methodological and reporting guidelines when conducting such studies.^13,15 However, little research has been done to evaluate the use of the ITS design in investigating the impact of the COVID-19 pandemic and related NPIs in sub-Saharan countries and similar settings. Furthermore, most applications of ITS analysis in this context involve single statistical analysis methods, and little has been done to compare different methods for quantifying the extent to which the pandemic disrupted healthcare service provision. It is, therefore, not clear to stakeholders which ITS models are preferable in different contexts, and how contradictory findings from different methods can be addressed. Specifically, concerning our study, no work has compared “effects measures” of the impact of the COVID-19 pandemic derived from ITS analyses using Prophet^16,17 and Poisson¹⁸ models, two regression models that are increasingly becoming popular for their ease of use and interpretability.

This study compared ITS analysis with the Prophet and Poisson regression models in evaluating the impact of COVID-19 on essential health services. We applied the two approaches to model the extent to which new clinic visits, diabetes clinic visits, and in-hospital deliveries across the Central, Eastern, Northern, and Western regions of Uganda changed at the onset of the COVID-19 pandemic. Our key contributions include: (1) the validation of Prophet and Poisson regression models in quantifying the potential impact of the COVID-19 pandemic on essential health services and (2) the comparison of insights derived from Prophet and Poisson models to demonstrate how different methods could lead to differing conclusions, hence the need for more rigor when conducting ITS analyses in global health settings.

METHODS

Design

A time series is a continuous sequence of observations repeatedly collected from a population at multiple intervals over time. ITS analysis refers to the analysis of a time series outcome to establish if the level and underlying trend of the outcome were changed by a particular intervention at a known point in time.¹³ ITS designs model a counterfactual (hypothetical) scenario with the assumption that the level and trend of a given outcome measure would have remained the same if there was no intervention.¹³

In this study, we applied the ITS analysis design using the Prophet^16,17 and Poisson¹⁸ time series models. We chose the Prophet model to capitalize on its ability to automatically deal with seasonal effects, missing data, outliers, and shifts in trends, making it ideal for a wider audience including non-expert analysts. We chose the Poisson model since we dealt with counts that were strictly non-negative and followed a Poisson distribution. The Poisson model is also more robust to sparse data sets with fewer time series variables and observations.

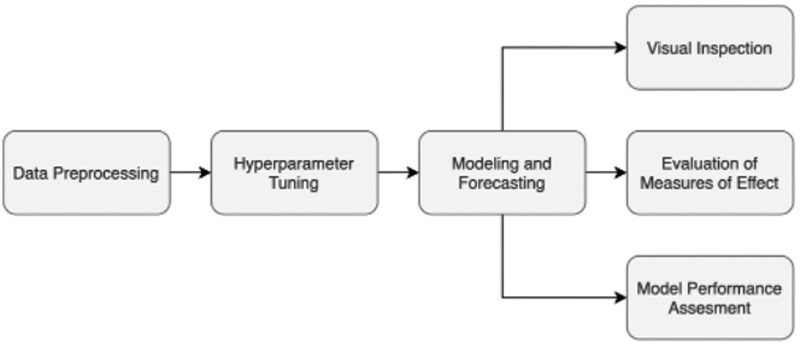
We separately trained the two models and used them to evaluate the impact of the pandemic disruption by comparing the evolution of the outcomes under the predicted (counterfactual) scenario to the observed (actual) scenario using 95% confidence intervals (CIs) and P-values ($\le .05$) as measures of significance. Figure 1 illustrates the analytic pipeline implemented in this study to analyze a single outcome in a specific region and one postintervention period.

Figure 1.

The pipeline for interrupted time series (ITS) analysis for a single outcome in a single region.

Outcomes

We evaluated 3 outcomes across the 4 geopolitical regions in Uganda (Central, Eastern, Northern, and Western). The outcomes included new clinic visits defined as the number of outpatient department clinic visits per month, diabetes clinic visits defined as the number of outpatient diabetes clinic visits per month, and in-hospital deliveries defined as the number of in-hospital newborn deliveries. These outcomes are examples of the World Health Organization indicators of essential health service delivery¹⁹ that were readily available for illustrating the methods in our study. For each region, we normalized each outcome by the population size of the region and analyzed counts per 100 000 population.

Intervention

We defined the intervention as the implementation of NPIs in response to the COVID-19 epidemic in Uganda. We assumed that the interruptions due to the pandemic started in March 2020 when the COVID-19 NPIs were first introduced in Uganda. Accordingly, given the data we had at hand, we defined the preintervention period as February 2018 to February 2020 and the postintervention period as March 2020 to December 2020. For both the Prophet and Poisson regression models, we conducted separate analyses to determine the effect of the pandemic with the assumption that the interruptions started in April 2020 (and not March 2020). In these analyses, we defined the preintervention period as February 2018 to March 2020 and the postintervention period as April 2020 to December 2020.

Data preprocessing

Our raw data consisted of monthly counts of outcomes per healthcare facility as captured in Uganda’s Health Management Information System.²⁰ We began by aggregating the facility-level data to arrive at monthly counts of each outcome for each of the 4 geopolitical regions in Uganda. After the aggregation, we noticed that the data for the months of January and December 2019 months were missing, while there was significant underreporting in the month of January 2020 across all regions and outcomes. We also noticed a few instances of over-reporting. We addressed these problems by treating them as missing values (ie, dropping the data) and then using quadratic (order = 2) spline interpolation²¹ to impute the missing values.

Hyperparameter tuning

This step involved using grid search cross-validation to choose an optimal set of hyperparameters for modeling the outcome using the Prophet model. Of note is that for the Poisson model, this step was skipped as the model does not have any hyperparameters.

Modeling and forecasting

This step involved separately fitting Prophet and Poisson models and using the fitted models to forecast outcomes in the postintervention period. By default, the Poisson and Prophet models return predicted values and the uncertainty intervals of the predicted values.

ITS modeling with Prophet regression

Prophet is a modular additive regression time series regression model developed by Meta.¹⁷ It allows for adjustable model parameters that use time as a regressor and then fit both linear and nonlinear functions of time. Prophet uses a decomposable time series model with three main components as follows:

$$y\left(t\right)=g\left(t\right)+s\left(t\right)+h\left(t\right)+\mathrm{ }{ϵ}_t$$ Equation 1

Here, g(t) is the trend function (models nonperiodic changes), s(t) represents seasonality (models periodic changes), h(t) represents the effects of holidays and events, and ϵ_t is an error term that models idiosyncratic changes and is assumed to be normally distributed. Taylor and Letham,¹⁶ the authors of the Prophet model, explain in detail how the trend, seasonality, and holiday effects are modeled along with the assumptions of the underlying processes.

To conduct ITS analysis with Prophet regression, we first tuned 3 parameters: the changepoint_prior_scale that determines the flexibility of the trend, the seasonality_prior_scale that determines the flexibility of the seasonality, and the seasonality_mode which models seasonality as additive or multiplicative.¹⁷ We selected the optimal parameters for the model by evaluating the root mean squared error over a 3-month horizon. Next, we trained a Prophet model using the optimal parameters on observed data in the preintervention period and used it to predict outcomes in the postintervention period. We then compared the predicted outcomes to the actual outcomes in the postintervention period. All analyses were done using the Python programming language.

ITS modeling with Poisson regression

The Poisson regression model is a generalized linear model that requires 3 main variables: (1) $T$, the unit representing time series intervals (eg, month), (2) $X_t$, a dummy binary variable at time t representing the preintervention period ($X_t$=0) and the postintervention period ($X_t$=1), and (3) $Y_t$, the outcome at time $t.$¹⁸ Of note is that additional harmonic terms are used to adjust for seasonality. In this study, the Poisson regression was modeled as follows:

$$Y_t={\beta }_0+{\beta }_{1}T+\mathrm{ }{\beta }_2{X}_t+{\beta }_3{H}_1+{\beta }_4{H}_2+{\beta }_5{H}_3+{\beta }_6{H}_4$$ Equation 2

Here, ${\beta }_0$ is the baseline at $T=0$, ${\beta }_1$ is the change in outcome per unit increase in time, ${\beta }_2$ is the level change due to the intervention. ${\beta }_3$, ${\beta }_4$, ${\beta }_5$, and ${\beta }_6$ are the coefficients of the harmonic terms for adjusting seasonality. We used 4 harmonic terms specifying 2 sine and cosine pairs over a 12-month period. These harmonic terms are periodic functions (Fourier terms) based on trigonometric sine and cosine functions of time that capture the seasonal rise and decline over an underlying period that reflects a seasonal cycle.^22,23

To conduct ITS analysis with Poisson regression, we implemented the steps suggested by Bernal et al¹⁸ using the generalized linear model in the statsmodels²⁴ package in Python. We trained a step change Poisson model using count data and with an indicator variable representing the pre- and postintervention periods. We included standardized population as an offset variable in the model to adjust for changes in population over time. To generate the predicted outcomes, we first created new data as if the COVID-19 interruption never occurred and used the trained model to generate predictions under this counterfactual scenario. We then compare the predicted outcomes to the actual outcomes in the postintervention period.

Visual inspection

This step involved plotting the model predictions alongside the actual observations and making deductions according to the visualizations. It also involved examining scatter plots of the time series to check for trends, seasonal patterns, and outliers.

Evaluation of measures of effect

We computed a metric that compared the evolution of the actual and counterfactual outcomes in the postintervention period. We used the mean of the percent change in outcome counts per 100 000 population assuming the predicted counts as the baseline (Equation 3).

$$\mathrm{Percent}\mathrm{ }\mathrm{change}=\frac{1}{N}\mathrm{ }{\sum }_{i=1}^N\frac{(y_i-{\widehat{y}}_i)}{{\widehat{y}}_i}$$ Equation 3

In Equation 3, $i$ represents a given month in the postintervention period, $y_i$ is the actual outcome at month $i$, and ${\widehat{y}}_i$ is the counterfactual outcome at month $i$. $N$ is the total number of months in the postintervention period. We also computed measures of significance based on 95% CIs of the percent change and P-values derived from the Wilcoxon signed-rank test.^25,26

Model performance assessment

In this step, we used cross-validation to evaluate the performance of the Prophet model.¹⁷ The model performance results are available in the Supplementary Material.

RESULTS

Visual inspection

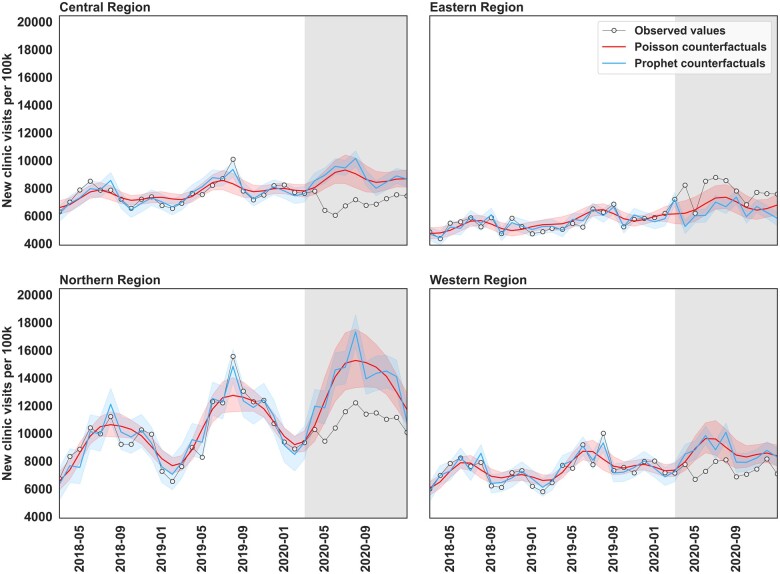
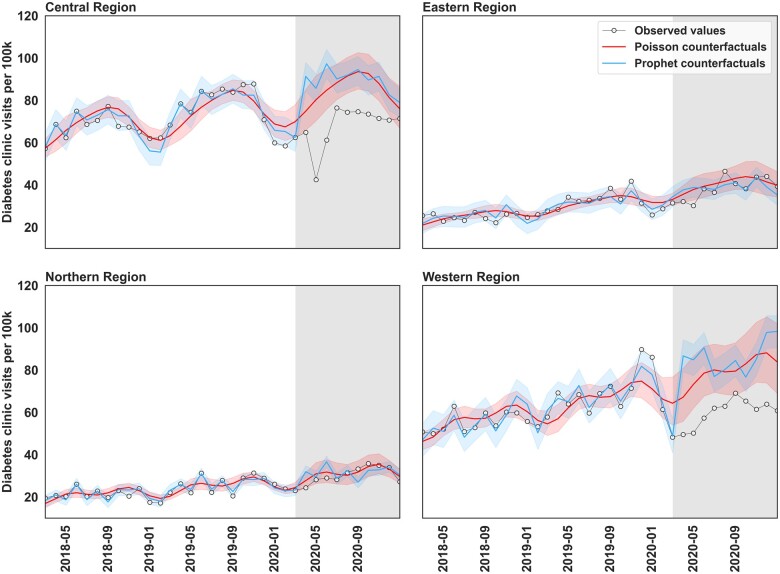
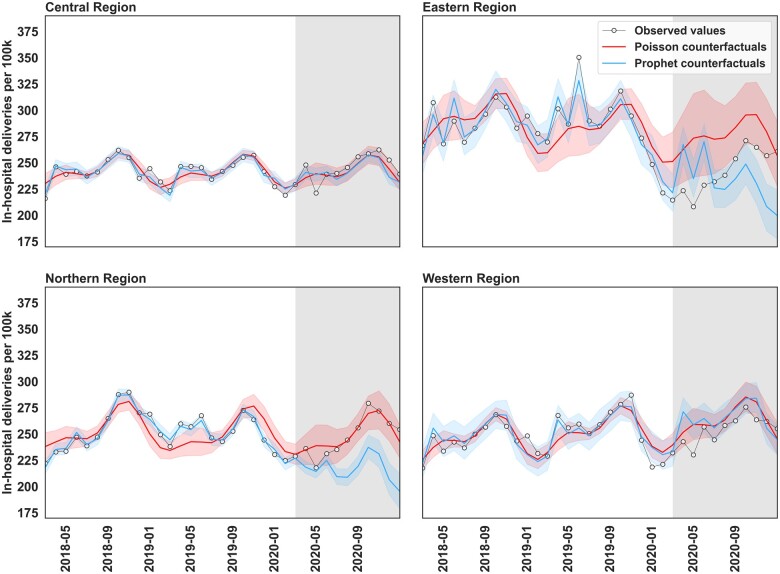
Figures 2, 3, and 4 illustrate the time series of the actual values and the counterfactual predictions by the Prophet and Poisson regression models for the considered outcomes. In each figure, the x-axis is the time in months between February 2018 to December 2020 and the y-axis is the respective count per 100 000 persons. The grey background represents the postintervention period from March 2020 to December 2020. For each region, the joined scatter plot represents actual observations. The red line and band represent the counterfactual values and 95% CI of the counterfactual values from the Poisson regression model. The blue line and band represent the counterfactual values and 95% CI of the counterfactual values from the Prophet model.

Figure 2.

Time series of the observed values and model-generated counterfactual predictions of new clinic visits per 100 000 persons across 4 regions in Uganda.

Figure 3.

Time series of the observed values and model-generated counterfactual predictions of diabetes clinic visits per 100 000 persons across 4 regions in Uganda.

Figure 4.

Time series of the observed values and model-generated counterfactual predictions of in-hospital deliveries per 100 000 persons across 4 regions in Uganda.

Visual inspection of Figure 2 suggests a gentle upward trend in the number of visits over time across the 4 regions along with seasonal effects characterized by higher midyear visits and lower end-year visits. In the postintervention period of all the regions, we notice that the CI bands of the two models overlap, implying similarity in their predictions and possibly effect estimates. Both models suggest that the pandemic could have reduced the number of new clinic visits in the Central, Northern, and Western regions as evidenced by the actual values in the postintervention period being less than the model-predicted counterfactual values. Interestingly, both models also suggest a possible increase in the number of visits in the Eastern Region since the actual values are higher than the model-predicted counterfactual values.

Figure 3 shows a gentle increase in the number of diabetes clinic visits over time, with the Central Region having the highest counts. Of note is that in all the regions, the CIs of the Poisson and Prophet regression models have a high degree of overlap. Both models suggest that the pandemic reduced the number of outpatient diabetes clinic visits in the Central and Western regions, with no significant changes in the Eastern and Northern regions.

In Figure 4, we can see region-specific seasonal patterns with minimal change in temporal trends across all 4 regions. The Central, Northern, and Western regions appear to have regular consistent seasonal patterns, while the Eastern Region appears to have an irregular pattern. In the postintervention period, there is a high degree of overlap in the predictions of the Prophet and Poisson regression models in the Central and Western Region, but little to no overlap in Eastern and Northern regions. Both models suggest that there were no significant changes in in-hospital deliveries in the Central and Western regions. However, the Prophet model suggests no change in Eastern Region and a drop in the Northern Region, while the Poisson regression model suggests a drop in the Eastern Region and no change in Northern Region.

Comparisons of Prophet and Poisson regression effect measures

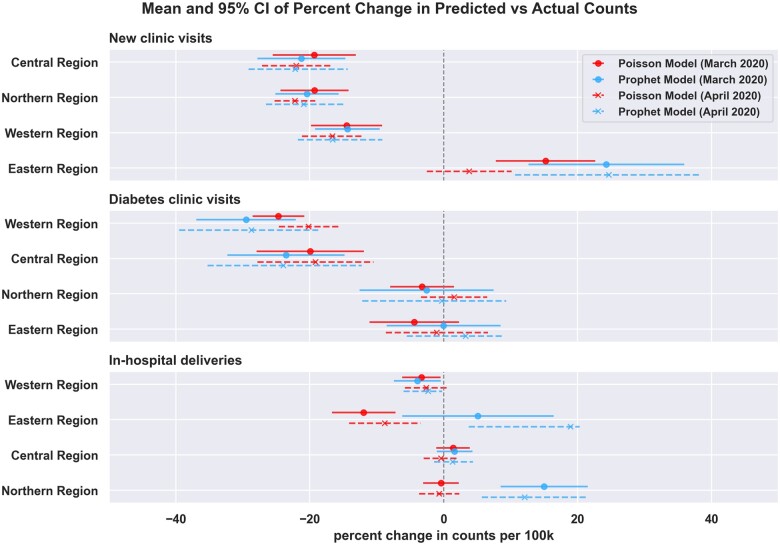
Figure 5 illustrates the mean and the 95% CI of the percent change in the predicted versus the actual counts per 100 000 persons of the three outcomes. Interestingly, if we assume that the postintervention period started in March 2020 (continuous lines), the Prophet and Poisson regression results for new clinic visits and diabetes clinic visits are similar for all regions. We confirm, by way of examining overlaps in the 95% CI bands, that the Prophet and Poisson regression models generated effect estimates that overlap in 10 out of the 12 ITS analysis tasks.

Figure 5.

Mean and 95% CI of the percent change in counts per 100 000 persons of new clinic visits, diabetes clinic visits, and in-hospital deliveries across the 4 regions investigated based on modeling the postintervention period from March 2020 to December 2020 (continuous lines) and the postintervention period from April 2020 to December 2020 (dotted lines).

Concerning new clinic visits, we confirm that both models estimated significant drops in the Central, Northern, and Western regions, and a significant increase in the Eastern Region. Concerning diabetes clinic visits, both models also suggest significant reductions in diabetes clinic visits in the Central and Western regions, and that the changes in the Eastern and Northern regions were not statistically significant. For in-hospital deliveries, both models estimate a slight drop in the Western Region and no statistically significant changes in the Central Region. However, we can see that in the Eastern and Northern regions, the model estimates are contradictory. The Poisson model estimates a significant drop in the Eastern Region, while the Prophet model estimates a significant rise in Northern Region.

Sensitivity analyses

As also illustrated in Figure 5, if we assume that the postintervention period started in April 2020 and ended in December 2020 (dotted lines), the effect estimates were similar in 9 out of 12 ITS analysis tasks. Both models estimated significant drops in new clinic visits in the Central, Northern, and Western regions. Both models suggest significant drops in diabetes clinic visits in the Central and Western regions, with no changes in the Eastern and Northern regions. Furthermore, both models suggest that in-hospital deliveries in the Western and Central regions did have significant changes.

Interestingly, the models gave contradictory estimates for new visits in the Eastern Region, and in-hospital deliveries in the Eastern and Northern regions. The Prophet model estimated a significant increase in new clinic visits in the Northern Region while the Poisson regression model estimated no changes in this region. Similarly, the Prophet model estimated a significant increase in in-hospital deliveries in the Northern Region while the Poisson regression model estimated no changes in this region. Lastly, the Prophet model estimated an increase in the in-hospital deliveries in the Eastern Region, but the Poisson model estimated a decline in the same region.

DISCUSSION

Principal findings

This study compared ITS analysis with the Prophet and Poisson regression models in evaluating the impact of COVID-19 on selected essential health services in Uganda. We found that in most cases, the Prophet and Poisson models generated similar estimates of the impact of the pandemic across the 3 outcomes (new clinic visits, diabetes clinic visits, and in-hospital deliveries) and the 4 regions geopolitical regions in Uganda studied. However, in some cases, the two models generated contradictory effect estimates. This suggests caution in the interpretation of the results generated by a single model as well as the need for methodological triangulation to arrive at the true estimates of the impact of the pandemic on essential health services.

The disagreements between the two models, if true, could be plausibly due to a variety of reasons. For example, data inconsistencies could have affected the performance of the models, suggesting that COVID-19 researchers must ensure that they have high-quality data and use appropriate analytic methods.²⁷ The observation could also be due to differences between Prophet’s and Poisson’s modeling of the seasonality of outcomes. More importantly, the few data points in the postintervention period likely resulted in high variances in the predictions by the two models. This suggests the need for more frequently collected data such as daily or weekly data rather than monthly data. Researchers could also explore upsampling techniques to increase the frequency of their samples before analysis.²⁸

At the onset of the COVID-19 pandemic in Uganda, the government of Uganda instituted several NPIs including nighttime curfews, suspension of public transportation, suspension of mass gatherings, and border closure.²⁹ It is plausible that the strict implementation of movement-related NPIs resulted in changes in the use of essential services. Of note, however, is that our study focused on comparing two ITS models. We do not make conclusions about the impact of the pandemic or describe factors contributing to the heterogeneity observed in this study. Instead, as part of future work, our research team will report on a more comprehensive multimethod approach involving both qualitative and quantitative techniques to fully understand the true impact of the disruption of essential health services delivery in Uganda and selected sub-Saharan African countries.

Comparison to related work

There are several techniques for conducting ITS analysis including autoregression methodologies such as the Auto-Regressive Integrated Moving Average (ARIMA),³⁰ generalized linear models such as Poisson regression, generalized additive models such as Prophet,¹⁷ and deep-learning approaches such as long short-term memory.³¹ We chose to focus on the Prophet and Poisson regression methods as they are quick to model and easier to interpret. Of note, however, is that both models have their inherent limitations. For example, the Prophet model has been criticized for prioritizing ease of use and tuning over model performance, leading to poorer performances compared to ARIMA and deep learning models.³² On the other hand, Poisson regression assumptions of data having a Poisson distribution and observation being independent are often violated, leading to challenges such as incorrect estimation of standard errors and autocorrelation.¹⁸ Furthermore, both Prophet and Poisson models do not account for unmeasured or unknown time-varying confounders that require more sophisticated causal inference techniques.¹⁸

ITS analyses are one of the most robust evaluation methods when randomization is not possible. They are particularly useful as they can analyze any given time series data and generate insights that are easy to interpret.¹⁸ However, due to the possibility of erroneous conclusions based on model specification and confounding, caution must be taken when employing and interpreting the findings of a single ITS analysis technique.¹⁸ It is, therefore, critical that researchers take precautionary measures such as specifying models and assumptions a priori. Furthermore, there is a need for research on the use of ensemble multi-method approaches to improve the robustness of ITS analyses.

Limitations of the study

There are several limitations to this study. First, the inconsistency in data reporting across regions could have affected the validity of the generated insights. Indeed, in our preliminary investigations, we noticed that certain facilities did not report data consistently across time as other facilities. To address this, we imputed data for regions and timesteps where we found obvious missingness and underreporting. Second, we worked with monthly data spanning a period of 3 years. Access to additional data spanning multiple years at more granular time intervals could have improved our understanding of the seasonal and long-term trends in the data. Third, we only applied two techniques and analyzed univariate outcomes. Further investigations using other ITS models as well as investigation of other factors beyond COVID-19 and related NPIs are, therefore, warranted. Lastly, this study did not compare the effects of data quality on the performances of the evaluated models. Further investigations are, therefore, warranted to compare how robust the two models are with respect to aspects such as the granularity of data, missingness of data, and presence of outliers.

CONCLUSIONS

ITS analysis methods are critical in quantifying the impact of COVID-19 and related interventions on essential health services in sub-Saharan Africa and similar settings. The Prophet and Poisson regression models, if correctly specified, could generate similar findings on the effects of the COVID-19 pandemic on essential health services. Regardless of the method selected, the implementation of the method must be rigorous, such as by having model specifications a priori and addressing possible confounding. However, different ITS analysis approaches may still result in different measures of effect. We, therefore, encourage stakeholders investigating the true impact of COVID-19 on essential health services to use ITS models while ensuring standardized handling of biases in data, appropriate model specification, quantification of uncertainty in reported estimates, and consideration of multi-method triangulation to generate more robust effect estimates.

FUNDING

This work was supported by the Bill and Melinda Gates Foundation, grant number 019972.

AUTHOR CONTRIBUTIONS

WO and VA proposed the idea of using the Prophet and Poisson models, respectively for analyzing the essential health service data from Uganda. IW and SK acquired and formatted the raw data analyzed. WO, VA, and CW performed the analysis. All coauthors discussed the results and contributed to the manuscript. WO, GAT, IW, SK, VA, and AW reviewed and revised the manuscript based on peer review feedback.

SUPPLEMENTARY MATERIAL

Supplementary material is available in the Journal of the American Medical Informatics Association online.

CONFLICT OF INTEREST STATEMENT

None declared.

DATA AVAILABILITY

The data underlying this article were derived from the Uganda National Health Management Information System by permission. The data will be shared on reasonable request to the corresponding author with the permission of the Makerere University School of Public Health.