Abstract
Emerging evidence has shown that functional connectivity is dynamic and changes over the course of a scan. Furthermore, connectivity patterns can arise from short periods of co-activation on the order of seconds. Recently, a dynamic co-activation patterns (CAPs) analysis was introduced to examine the co-activation of voxels resulting from individual timepoints. The goal of this study was to apply CAPs analysis on resting state fMRI data collected using an advanced multiband multi-echo (MBME) sequence, in comparison with a multiband (MB) sequence with a single echo. Data from 28 healthy control subjects were examined. Subjects underwent two resting state scans, one MBME and one MB, and 19 subjects returned within two weeks for a repeat scan session. Data preprocessing included advanced denoising namely multi-echo independent component analysis (ME-ICA) for the MBME data and an ICA-based strategy for Automatic Removal of Motion Artifacts (ICA-AROMA) for the MB data. The CAPs analysis was conducted using the newly published TbCAPs toolbox. CAPs were extracted using both seed-based and seed-free approaches. Timepoints were clustered using k-means clustering. The following metrics were compared between MBME and MB datasets: mean activation in each CAP, the spatial correlation and mean squared error (MSE) between each timepoint and the centroid CAP it was assigned to, within-dataset variance across timepoints assigned to the same CAP, and the between-session spatial correlation of each CAP. Co-activation was heightened for MBME data for the majority of CAPs. Spatial correlation and MSE between each timepoint and its assigned centroid CAP were higher and lower respectively for MBME data. The within-dataset variance was also lower for MBME data. Finally, the between-session spatial correlation was higher for MBME data. Overall, our findings suggest that the advanced MBME sequence is a promising avenue for the measurement of dynamic co-activation patterns by increasing the robustness and reproducibility of the CAPs.
Keywords: Resting-state functional MRI, Multiband, Multi-echo, Co-activation patterns, Functional connectivity, Dynamic
1. Introduction
For nearly three decades, resting-state functional MRI (rs-fMRI), where images are collected while the participant does not perform a specific task, has been used to extract distinct brain networks (Biswal et al., 1995; Fox et al., 2005). For the most part, these studies have assumed these brain networks were static over time and examined functional connectivity by identifying brain regions where the entire time series was in sync. More recent work, however, has shown this may not be the case, and functional connectivity is dynamic, even changing throughout the course of a single scan (Allen et al., 2014; Chang and Glover, 2010; Liu et al., 2013; Liu and Duyn, 2013; Sakoglu et al., 2010).
For example, Chang and Glover performed a time-frequency coherence analysis using wavelet transform coherence, allowing coherence and phase differences between two time series to be evaluated in time-frequency space (Chang and Glover, 2010). They found significant variability in both coherence and phase between the posterior cingulate cortex (PCC) and the task-positive networks. They also performed a sliding window analysis, wherein the correlation is computed between subsets, or windows, of the time series. These windows are then moved forward in time along the time series, and a correlation coefficient is obtained for each window. That analysis identified several brain regions exhibiting variable connectivity with the PCC. Another study used the sliding window approach to evaluate the correlation between 50 brain networks, identified using group independent component analysis (gICA) in a group of control subjects (Allen et al., 2014). Thus, a 50 × 50 correlation matrix was computed for each window. Then, a k-means clustering algorithm identified different correlation patterns or states, and windowed correlation matrices were each assigned to one of the states. These results identified organized connectivity patterns that varied across time in individual subjects, repeated over time, and existed across subjects. Damaraju et al. (2014) applied this technique in patients suffering from schizophrenia. They found that patients spent less time in states with higher, widespread connectivity and had overall reduced connectivity in these states.
Other studies have examined activation patterns related to single timepoints, based on the idea that patterns of connectivity can arise from short co-activation periods lasting mere seconds (Chen et al., 2015; Liu et al., 2013; Liu and Duyn, 2013). These studies showed that a particular brain region can be co-active with brain regions in different networks at different timepoints. Different co-activation patterns (CAPs) can be identified by looking at individual timepoints and identifying brain regions with concurrent high (or low) signal intensity, and then using a clustering algorithm to identify distinct CAPs. Each timepoint is then assigned to a CAP based on its spatial similarity.
In addition to advances in dynamic functional connectivity analyses, technical improvements in echo-planar imaging (EPI) image acquisition have greatly improved functional connectivity estimation. For example, multiband (MB) imaging, where multiple slices are acquired simultaneously, permits increased spatial and/or temporal resolution (Feinberg et al., 2010; Moeller et al., 2010; Setsompop et al., 2012). Moreover, multi-echo (ME) EPI imaging involves collecting images at several echo times (TEs) in a single shot. Multi-echo imaging provides increased fMRI sensitivity (Fernandez et al., 2017; Kundu et al., 2012; Poser and Norris, 2009; Poser et al., 2006; Posse et al., 1999), but it also suffers from decreased spatial and temporal resolution due to the increased echo train length required to collect additional echoes.
Recent studies have combined the MB and ME techniques in a single MBME acquisition (Boyacioglu et al., 2015; Olafsson et al., 2015). Increasing literature has begun to systematically evaluate the benefits of MBME imaging for fMRI studies (Cohen et al., 2021a,2021b,2021c). For the rs-fMRI application, Cohen et al. (2021c) directly compared an MBME sequence with an MB sequence and found higher functional connectivity strength and extent for the MBME data. They also found better reproducibility of rs-fMRI metrics in a subset of subjects with repeat imaging. To date, there remains a lack of dynamic analyses, specifically utilizing CAPs, using MBME imaging.
In this study, MBME and MB rs-fMRI scans were collected in a group of healthy volunteers, with a subset returning within two weeks for repeat imaging. A CAPs analysis was conducted and measures of activation strength, goodness of fit, and reproducibility were compared between the MBME and MB datasets.
2. Methods
2.1. Subjects
All subjects provided written informed consent prior to participation in this study, which was approved by the Medical College of Wisconsin Institutional Review Board and conducted in accordance with the Declaration of Helsinki. In total, 28 healthy volunteer subjects (Mean Age = 28.0 Range 20 – 46, 9 Male, 19 Female) participated in this study. Among them, 19 subjects (Mean Age = 27.2 Range 20 – 46, 7 Male, 12 Female) returned within two weeks to repeat the study. Subjects were instructed to refrain from caffeine and tobacco for six hours prior to imaging.
2.2. MR imaging
MR Imaging was performed at 3T (Signa Premier, GE Healthcare, Waukesha, WI) with a body transmit coil and a 32-channel NOVA (Nova Medical, Wilmington, MA) receive head coil. The maximum gradient strength was 70 mT/m and the maximum slew rate was 170 mT/m/ms. First, a high-resolution 3D T1-weighted magnetization-prepared rapid acquisition with gradient echo (MPRAGE) anatomical image was acquired with TR/TE = 2200/2.8 ms, FOV = 24 cm, matrix size = 512 × 512 × 256, slice thickness = 0.5 mm, voxel size = 0.47 × 0.47 × 0.5 mm, and flip angle (FA) = 8°.
Each subject then underwent two gradient-echo EPI rs-fMRI acquisitions: one MBME scan and one MB scan, as described previously (Cohen et al., 2021c). The MBME scan had the following parameters: TR/TE = 900/11,30,49 ms (three echoes), FOV = 24 cm, matrix size = 80 × 80 with slice thickness = 3 mm (3 × 3 × 3 mm voxel size), 11 slices with multiband factor = 4 (total slices 44), FA = 60°, and partial Fourier factor = 0.85. Both MB and MBME scans utilized in-plane acceleration (R) = 2. The MB scan had the following parameters: TR/TE = 650/30 ms, FOV = 24 cm, matrix size = 80 × 80 with slice thickness = 3 mm (3 × 3 × 3 mm voxel size), 11 slices with multiband factor = 4 (total slices 44), FA = 60°, and partial Fourier factor = 0.85. Resting state scans lasted six minutes each resulting in 400 volumes for the MBME scans and 554 volumes for the MB scans. During the resting state scans, subjects were instructed to close their eyes, but remain awake, refrain from any motion, and not think about anything in particular.
Reconstruction was performed online using a modified multiband EPI reconstruction to support the multi-echo acquisition (Cohen et al., 2021a,2021b,2021c). Multiband unaliasing was accomplished using Autocalibrating Reconstruction for Cartesian Imaging (ARC) reconstruction technology with a blipped-controlled CAIPI shift = 4 (Setsompop et al., 2012). Zero-filling was used during reconstruction for the partial Fourier data.
2.3. Data preprocessing
A combination of AFNI (Cox, 1996, 2012), FSL (Jenkinson et al., 2012), and Matlab (The Mathworks, R2018a) were used for the data analysis. Image preprocessing was conducted based on the HCP minimal preprocessing pipeline (Glasser et al., 2013), available at https://github.com/Washington-University/HCPpipelines, modified in-house to account for multi-echo data (Cohen et al., 2021a,2021b,2021c).
2.3.1. Anatomical processing
Anatomical processing used the PreFreeSurferPipeline.sh scripts from the HCP pipeline. First, the anatomical image was aligned with line between the anterior commissure (AC) and posterior commissure (PC) using aff2rigid in FSL. Next, a brain mask was created using FNIRT-based brain extraction. For this process, first, the MPRAGE image was linearly registered to MNI space using flirt in FSL with 12° of freedom (Jenkinson et al., 2002). Then, fnirt in FSL was used to non-linearly refine the registration. A masked reference image in MNI space was inverse warped back to native space using the transformations determined above and used to mask the MPRAGE. Finally, the MPRAGE brain-only image was registered to MNI space using flirt with 12° of freedom followed by fnirt.
2.3.2. Functional preprocessing
For both the MBME and MB datasets, the first 16 volumes were discarded to allow the signal to reach equilibrium. Next, both the MBME and MB datasets were volume registered to the first volume using mcflirt in FSL and the six rigid-body motion parameters were output. For the MBME data, only the first echo was registered. Subsequent echoes were registered using the transformation matrices from the first echo. In addition, framewise displacement (FD) was calculated using fsl_motion_outliers in FSL (Power et al., 2012).
MBME preprocessing and denoising:
The MBME data was denoised using multi-echo independent component analysis (ME-ICA) (Kundu et al., 2013,2012) and the open-source python script tedana.py version 0.0.9 (Ahmed et al., 2020). The three echoes were first combined using the T2* -weighted approach (Posse et al., 1999). The combined-echo data was then denoised using ME-ICA. The ME-ICA technique, described in detail elsewhere (Ahmed et al., 2020; Kundu et al., 2013,2012), classifies independent components as BOLD or non-BOLD based on whether or not their amplitudes are linearly dependent on TE, respectively (Kundu et al., 2013,2012; Olafsson et al., 2015). Components classified as non-BOLD are regressed out of the combined ME data using general linear regression, resulting in a denoised dataset. The denoised MBME dataset was then registered to the ACPC-aligned MPRAGE image using epi_reg in FSL, and subsequently registered to MNI space using the anatomical transformations computed in Section 2.3.1. Finally, the data was smoothed using a 4 mm full width at half maximum (FWHM) Gaussian kernel.
MB preprocessing and denoising:
The MB data was registered to the AC-PC aligned MPRAGE image using epi_reg in FSL. Then, the MB data was registered to MNI space using the anatomical transformations computed in Section 2.3.1. The data was then smoothed using a 4 mm FWHM Gaussian kernel and denoised using an ICA-based strategy for Automatic Removal of Motion Artifacts (ICA-AROMA) with automatic dimensionality estimation and non-aggressive denoising (Dipasquale et al., 2017; Pruim et al., 2015). ICA-AROMA is a data-driven technique that removes motion-related components from the data.
2.3.3. CAPs analysis
The denoised and smoothed data was then used for the CAPs analysis, which was conducted using the TbCAPs toolbox (https://c4science.ch/source/CAP_Toolbox.git) (Bolton et al., 2020). Separate analyses were performed for the MB and MBME datasets. In addition, the data was split into training and test datasets. The training data set consisted of the nine subjects with only one session and five randomly selected subjects with two sessions and was used to determine the optimal cluster sizes and generate the CAPs. The remaining 14 subjects, all with two sessions, comprised the test dataset. For both the training and test datasets the data was masked using a template gray matter (GM) mask and then temporally z-scored so the temporal mean = 0 and temporal standard deviation = 1.
Seed-based approach:
Next, the timepoints for the CAPs analysis were selected. To ensure the robustness of the results, two analyses were conducted. First, a single seed, the posterior cingulate cortex (PCC) was used. This seed was obtained from the AAL2 brain atlas, including voxel values of 39 and 40 (Rolls et al., 2015). The PCC was chosen because it is a hub in the extensively studied default mode network (DMN) (Chang and Glover, 2010). For all datasets, the mean temporally z-scored signal was extracted from the PCC seed. Frames with signal intensity in the top 30% were retained. In addition, frames with FD > 0.5 were excluded.
The optimal number of CAPs and the CAPs themselves were determined using only the training data. As mentioned previously, CAPs were determined separately for the MB and MBME data. To generate CAPs the data from the whole gray matter volume, at the thresholded frames from the PCC seed, were clustered using k-means clustering. First, the optimal number of clusters was determined using consensus clustering (Monti et al., 2003) as implemented in the TbCAPs toolbox (Bolton et al., 2020). Briefly, k-means clustering was run across 20 folds for cluster numbers (K) ranging from 2 to 12, randomly selecting a 80% of the data for each fold. In the ideal case, data points should regularly be clustered together or clustered separately across folds. The optimal K is the one for which the proportion of ambiguously clustered pairs (PAC) (i.e. sometimes clustered together and sometimes separately) is minimized (Senbabaoglu et al., 2014). The stability was defined as 1 – PAC. Once the optimal K was determined, k-means clustering was run using the training data using that cluster number. For all datasets, each surviving frame was assigned to one of the CAPs based on their spatial similarity.
Since CAPs were computed separately for the MB and MBME datasets, the centroid CAPs were visually inspected and matched between MB and MBME datasets. CAPs that did not have a counterpart in the other dataset were not included in further comparisons between datasets. The surviving frames from the subjects in the test dataset were then assigned to one of the CAPs by spatially correlating each frame with each CAP and assigning the frame to the CAP with the highest correlation.
Seed-free approach:
analysis was then repeated using a seed-free approach where all frames were included in the analysis except frames with FD > 0.5. Consensus clustering was once again used to determine the optimal number of clusters for the MB and MBME datasets separately using the training dataset. Resulting CAPs were visually compared between MB and MBME datasets and CAPs that did not appear for both were excluded from further analyses. Finally, in the same manner as the seed-based approach, timepoints from subjects in the test dataset were assigned to one of the CAPs.
For the seed-free method, several additional metrics were computed including the number of occurrences of and number of entries into each CAP, the probability of remaining in a CAP between timepoints (resilience), betweenness centrality, the likelihood of entering a specific CAP from any other CAP (in-degree), and the likelihood of leaving a specific CAP towards another CAP (out-degree). The number of occurrences of and number of entries into each CAP for the MB data were scaled by the ratio of timepoints in the MBME data to number of timepoints in the MB data (384 and 538, respectively).
2.3.4. Goodness of Fit
Goodness of fit metrics were computed for the test dataset. The goodness of fit of each of the CAPs was estimated by computing the spatial correlation and mean squared error (MSE) between each frame and the centroid CAP it was assigned to. The MSE was computed by averaging the squared difference between the volume at each frame and the centroid CAP to which it was assigned.
The within-dataset variance (Vwin) was extracted by computing the voxelwise variance across all frames assigned to each of the CAPs separately for each dataset (i.e. single scan). The Vwin was then averaged across voxels to obtain one value per dataset.
2.3.5. Test-retest
Test-retest similarity was also computed for the test dataset. To estimate test-retest similarity of the CAPs, for each dataset the frames assigned to each CAP were averaged resulting in one volume for each CAP for the MB or MBME dataset. The spatial correlation was then computed between scan session 1 and scan session 2 for each subject for the MBME and MB datasets.
2.3.6. Comparisons between MBME and MB sequences
The mean and maximum FD were compared between the MB and MBME datasets using a paired t-test across subjects. In addition, the mean and maximum FD were compared across CAPs using an ANOVA and between MB and MBME datasets for each CAP using a paired t-test.
For each CAP, the voxel-wise mean CAPs (averaged within each dataset) were compared between MBME and MB test datasets using the paired t-test option of 3dttest++ in AFNI. Multiple comparisons correction was accomplished using the 3dClustSim feature in 3dttest++. Resulting z-score maps were thresholded at p< 0.001 with minimum cluster sizes ranging from 80 to 90 voxels (α< 0.05).
The following comparisons were all made on the test dataset only. For the spatial correlation and MSE metrics, timepoints were grouped by CAP and sequence (MBME or MB) across subjects and sessions. Since the number of timepoints for each CAP differed across datasets, spatial correlation and MSE were compared between MBME and MB datasets using a two-sample t-test for each CAP separately. For Vwin, each dataset had one value. Thus, a paired t-test was used to compare MBME and MB datasets across subjects for each CAP. Similarly, for the test-retest analysis, the spatial correlation between sessions was compared between the MBME and MB datasets using a paired t-test across subjects for each CAP. All results were Bonferroni corrected for multiple comparisons, and a corrected p < 0.05 was considered significant.
3. Results
3.1. Head motion
No significant difference was found between MB and MBME scans for mean FD (0.52 ± 0.43 vs. 0.40 ± 0.37, respectively, p= 0.09) or maximum FD (0.096 ± 0.042 vs. 0.101 ± 0.036 respectively, p = 0.24). In addition, there was no significant difference between number of scrubbed frames between MB and MBME datasets. Finally, no significant differences in FD were seen between CAPs and between MB and MBME datasets for each CAP for both the seed-based and seed-free approaches (Supplementary Fig. S1).
3.2. Number of clusters
For the MB data the number of clusters (K) was chosen to be five for the seed-based and seed-free analyses as a clear local maximum in the stability metric was observed for both. The results weren’t as clear for the MBME case. For the seed-based approach a small local maximum was observed at five clusters, however, there was no local maximum for the seed-free case. As a result, different numbers of clusters were tried. It was found that for K> 5 there were very few timepoints (< 1%) from the test dataset assigned to clusters 6 and above. Thus, five clusters were chosen for all datasets. Plots of stability as a function of cluster size are shown in Supplementary Fig. S2.
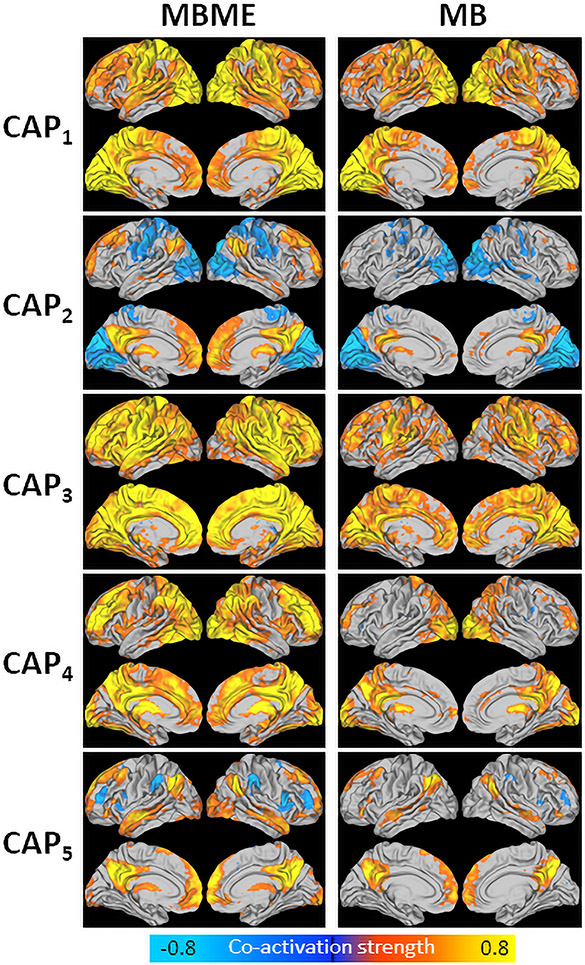
3.3. PCC seed
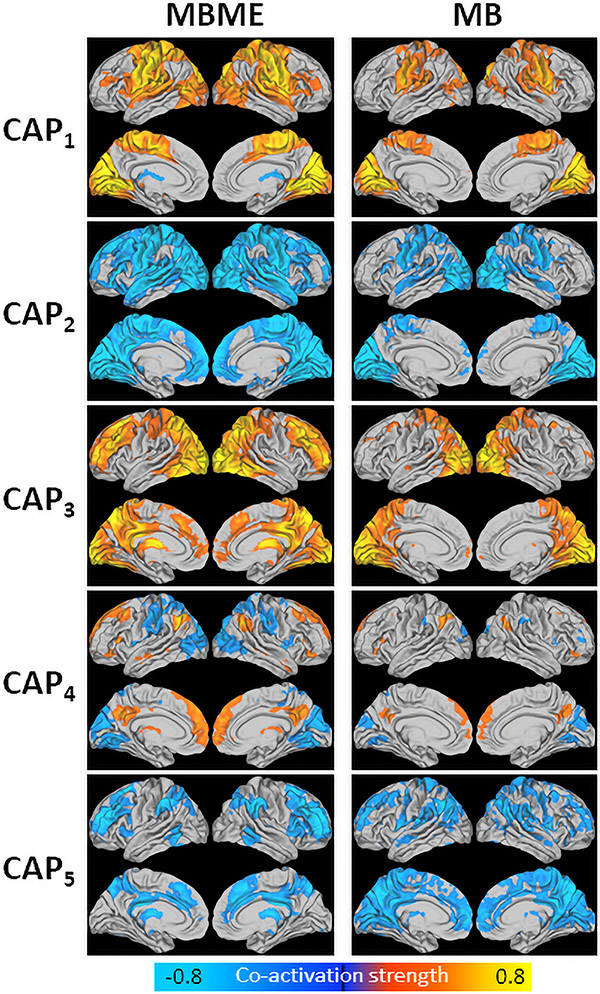
Fig. 1 shows the five centroid CAPs extracted using the training dataset. Each CAP in the MB dataset was matched with its corresponding CAP in the MBME dataset. In general, CAP1 showed strong co-activation mainly in the visual and motor cortices. CAP2 showed higher co-activation in the DMN and negative co-activation in the visual and motor cortices.. CAP3 showed high co-activation globally, especially for the MBME dataset, with areas of heightened co-activation in the motor cortices, default mode network (DMN), frontoparietal network, and salience network (i.e. insula). CAP4 showed higher co-activation in the DMN, some frontal and temporal regions. Finally, CAP5 showed heightened co-activation in the DMN.
Fig. 1.
Centroid CAPs for the MBME (left) and MB (right) data for the seed-based analysis. Centroid CAPs were generated separately for the MBME and MB data using the training dataset. Similar CAPs were matched between the MBME and MB datasets. All five CAPs had a corollary between datasets. CAP3 showed the highest activity with high co-activation throughout much of the gray matter. CAP1 showed higher co-activation in the motor cortex and visual cortex. CAP4 showed higher co-activation in parietal, visual, frontal and subcoritical regions. Finally, CAPs 2 and 5 showed higher co-activation in the default mode network, along with some subcoritcal area.
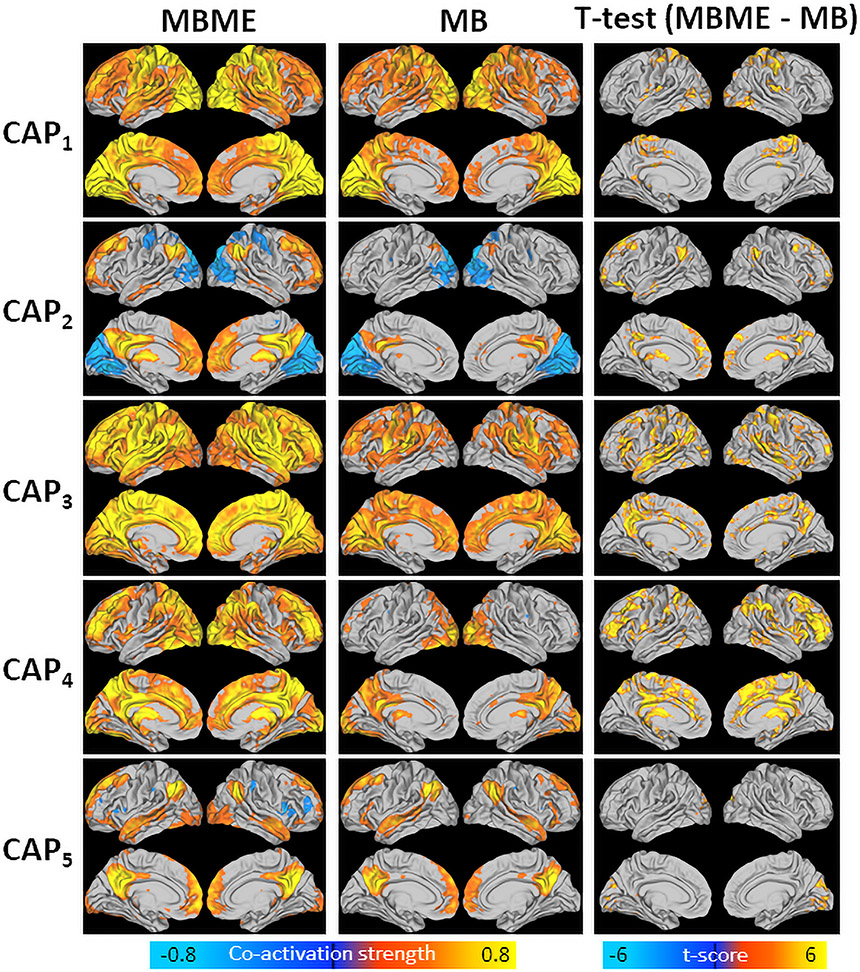
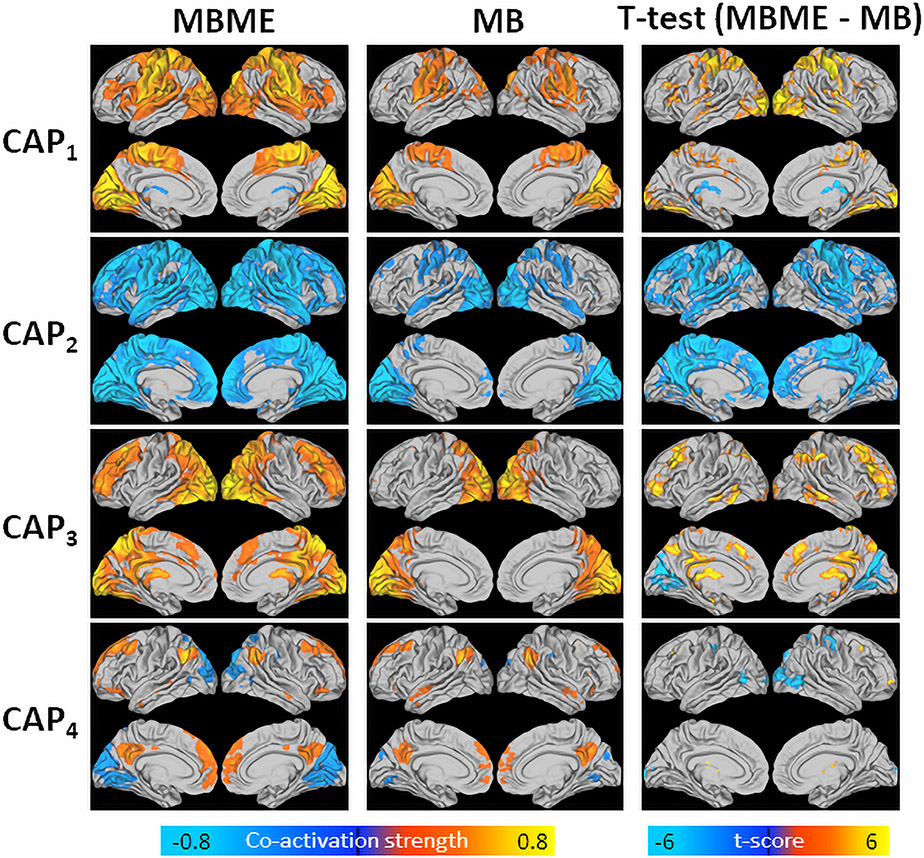
Fig. 2 shows mean CAPs for the test dataset for the MBME (left) and MB (middle) datasets. Overall, significantly higher co-activation was seen for the MBME data compared to the MB data for all five CAPs, as evidenced by the voxel-wise paired t-test results (p< 0.001, cluster size corrected) (Fig. 2, right). No area showed higher co-activation for any of the five CAPs for the MB data in comparison with the MBME data.
Fig. 2.
Mean CAPs evaluated for MBME (left) and MB (middle) data separately and t-test results comparing MBME and MB data (right) for the seed-based analysis. CAPs were determined using the test dataset by assigning each frame to a CAP based on spatial similarity. Thus, mean CAPs closely match the centroid CAPs determined from the training data. While the patterns of co-activation are similar for the MBME and MB datasets, significantly higher co-activation was observed for the MBME data compared to the MB data for all five CAPs (p < 00.001, cluster-size corrected). No region showed higher co-activation in the MB data compared to the MBME data.
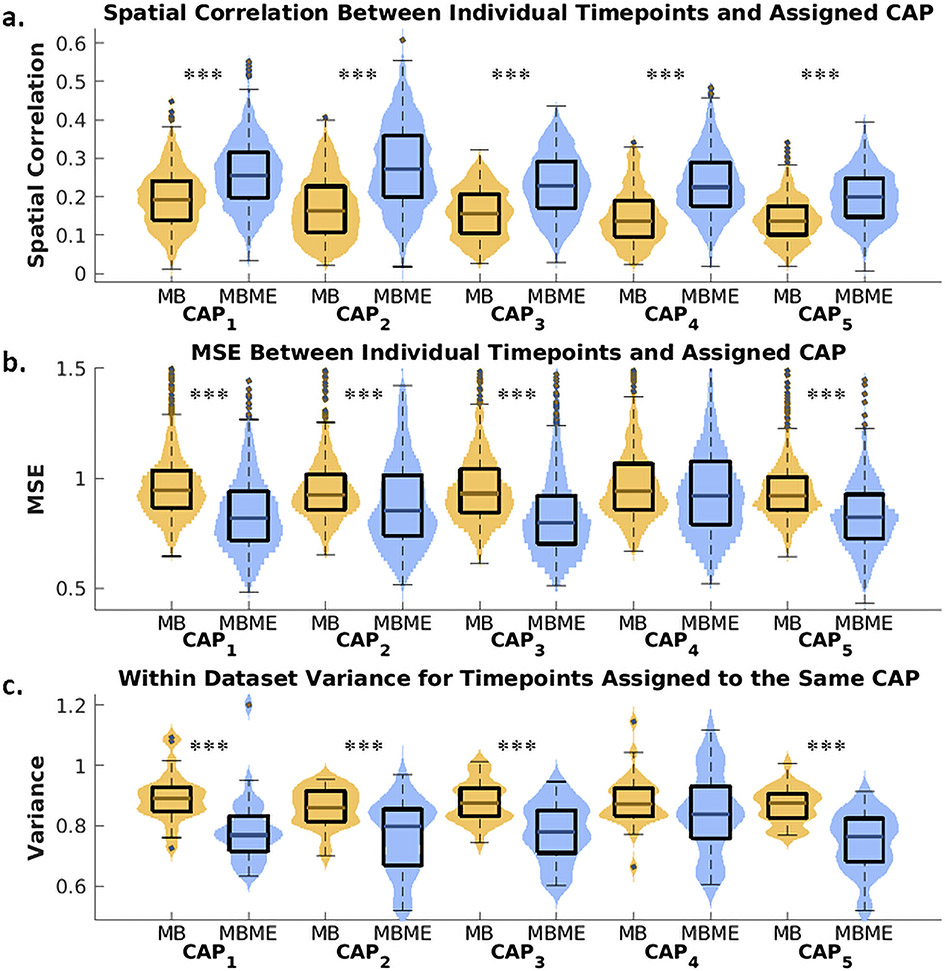
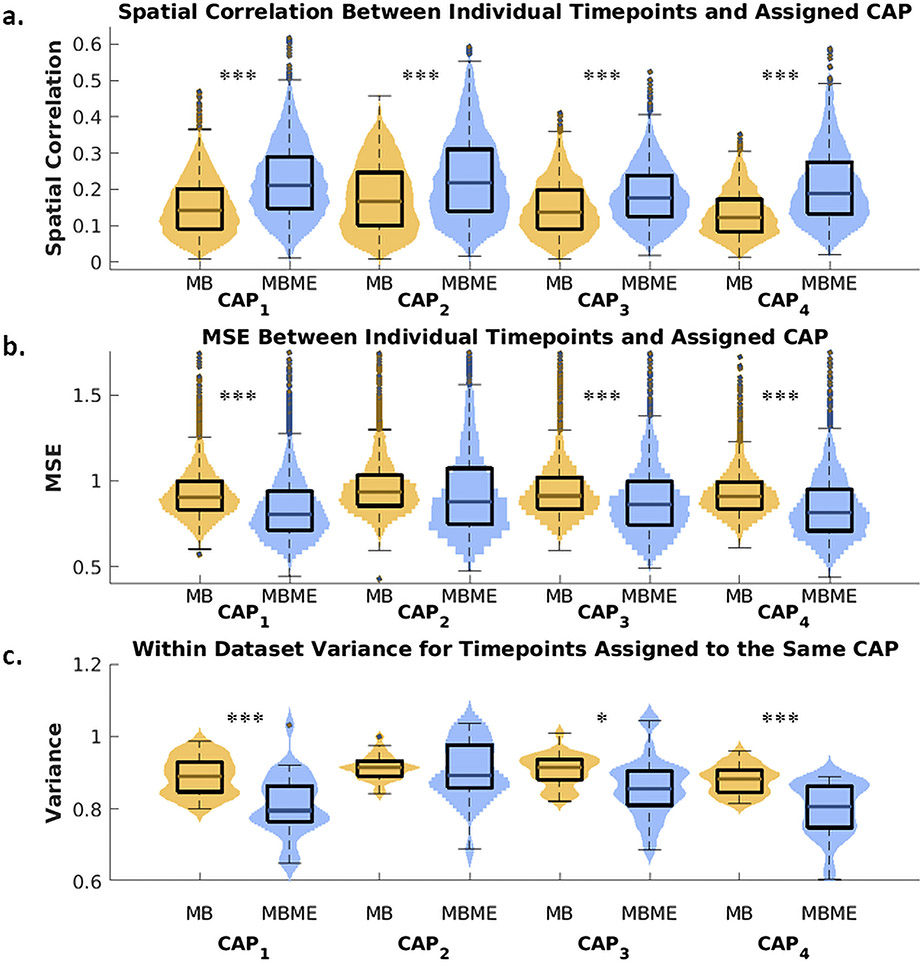
Fig. 3 shows box plots of the goodness of fit metrics and within-dataset variance compared between MBME and MB datasets for all five CAPs. Mean spatial correlation between each timepoint assigned to a CAP and the corresponding centroid CAP was significantly higher for the MBME data than the MB data for all five CAPs (Fig. 3a, p < 0.001, Bonferroni-corrected). The MSE between each timepoint assigned to a CAP and the corresponding centroid CAP was significantly lower for MBME vs. MB data for CAPs 1 – 3 and 5 (Fig. 3b, p < 0.001, Bonferroni-corrected). Similarly, the within-dataset variance across timepoints assigned to each CAP was significantly lower for MBME vs. MB data for CAPs 1 – 3 and 5 (Fig. 3c and 4, p< 0.001, Bonferroni-corrected).
Fig. 3.
Violin plots of the goodness of fit and CAP robustness metrics for the seed-based analysis. All plots were generated using the test dataset. Spatial correlation (a) and mean squared error (MSE) (b) between individual timepoints and their assigned centroid CAP were computed separately for MBME and MB datasets (MB: yellow color; MBME: blue color). The spatial correlation was significantly higher for MBME vs. MB datasets for all five CAPs, while MSE was significantly lower for MBME vs. MB datasets for all CAPs except CAP4. Within-dataset variance (c), calculated across timepoints assigned to the same CAP for each subject, session, and sequence, was significantly lower for MBME data compared to MB data for all CAPs except CAP4. Note: on each box, the central mark indicates the median, and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively. *** p < 00.001, ** p < 00.01, * p < 00.05, Bonferroni-corrected.
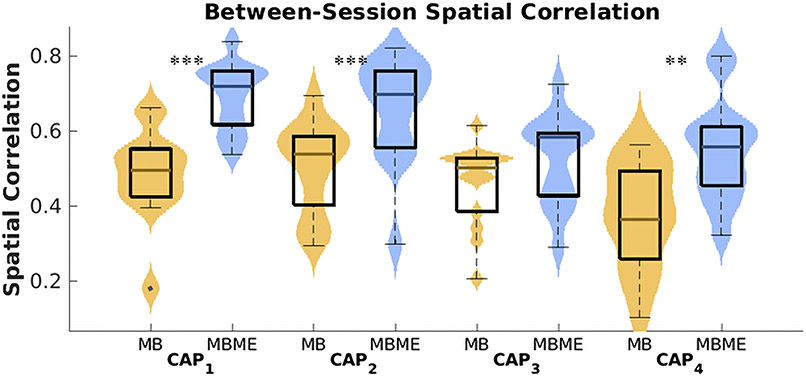
Fig. 4.
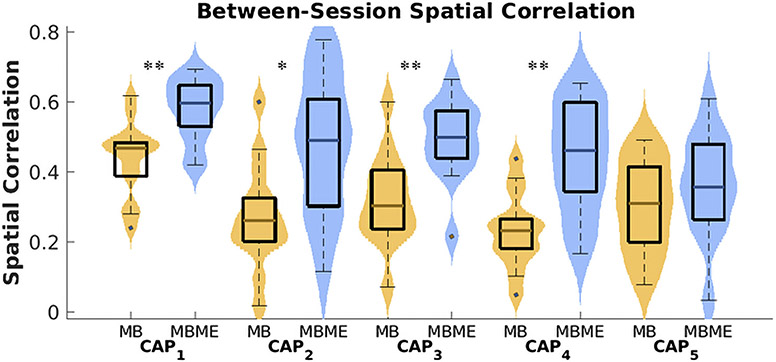
Violin plot of CAP reproducibility for the seed-based case. Between-session spatial correlation was calculated for the test dataset using the mean of all timepoints assigned to each CAP for each subject and sequence. CAPs 1 – 4 showed significantly higher spatial correlation for the MBME vs. MB data (MB: yellow color; MBME: blue color). Note: on each box, the central mark indicates the median, and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively. *** p < 0.001, ** p < 0.01, * p < 0.05, Bonferroni-corrected.
Furthermore, the spatial correlation between sessions 1 and 2 for each CAP was compared between the MBME and MB data. Between-session spatial correlation was significantly higher for MBME data vs. MB data for CAPs 1 – 4 (CAP1 : p= 0.003; 5CAP2: p= 0.013; CAP3: p= 0.003; CAP4 : p= 0.003; all Bonferroni-corrected).
3.4. Seed-free
A total of five centroid CAPs were extracted from the training data for the seed-free approach. Overall, four of the five CAPs matched between the MB and MBME datasets, while CAP5 differed (Fig. 5). CAP1 showed areas of heightened co-activation in the visual and motor cortices. CAP2 showed largely global negative co-activation for the MBME data with heightened negative co-activation mainly in the visual and motor areas. CAP3 showed higher co-activation in the visual network and frontoparietal network. CAP4 showed higher co-activation in the DMN.
Fig. 5.
Centroid CAPs for the seed-free analysis calculated using the training dataset for the MBME (left) and MB (right) data separately. CAPs were visually matched between the MBME and MB data. CAPs 1 – 4 matched while CAP5 differed. CAP1 showed areas of heightened co-activation in the visual and motor cortices. CAP2 showed largely global negative co-activation for the MBME data with heightened negative co-activation focused in the visual and motor cortices. CAP3 showed higher co-activation in the visual network, frontoparietal network, and subcoritcal region. CAP4 showed higher co-activation in the DMN and negative co-activation in the visual cortex.
Fig. 6 shows mean CAPs for the test dataset for the MBME and MB datasets for the four CAPs that matched between the MB and MBME datasets. In general, significantly higher co-activation, both in the positive and negative direction, was seen for the MBME data compared to the MB data for the four CAPs, as evidenced by the voxel-wise paired t-test results (p< 0.001, cluster size corrected) (Fig. 6, right). For example, for CAP2, a more negative co-activation strength was seen for the MBME data compared to the MB data throughout the brain. For CAP3 there was an area of lower co-activation in the visual cortex.
Fig. 6.
Mean CAPs evaluated for MBME (left) and MB (middle) data separately and t-test results comparing MBME and MB data (right) for the seed-free analysis for the four CAPs that matched between MBME and MB data. CAPs were determined using the test dataset by assigning each frame to a CAP based on spatial similarity. Thus, mean CAPs closely match the centroid CAPs determined from the training data. As with the seed-based case, the patterns of co-activation are similar for the MBME and MB datasets; however, in general, significantly higher co-activation, both in the positive and negative direction, was seen for the MBME data compared to the MB data for the four CAPs (p < 0.001, cluster-size corrected).
The goodness of fit metrics and within-dataset variance were compared between MBME and MB datasets for the four matched CAPs (Fig. 7). Mean spatial correlation between each timepoint assigned to a CAP and the corresponding centroid CAP was significantly higher for the MBME data compared to the MB data for all four CAPs (Fig. 7a, p< 0.001, Bonferroni-corrected). The MSE between each timepoint assigned to a CAP and the corresponding centroid CAP was significantly lower for MBME vs. MB data for all CAPs 1, 2, and 4 (Fig. 7b, p < 0.001, Bonferroni-corrected). Finally, the within-dataset variance across timepoints assigned to each CAP was significantly lower for MBME vs. MB data for all CAPs 1,3, and 4 (Fig. 7c, CAP1 : p< 0.001; CAP3 : p = 0.02; CAP4 : p< 0.001; all Bonferroni-corrected).
Fig. 7.
Violin plots of the goodness of fit and CAP robustness for the seed-free analysis for the four CAPs that matched between the MBME and MB data. Metrics were computed using the test dataset. Spatial correlation (a) was higher for MBME vs. MB datasets for all four CAPs, while MSE (b) was lower for MBME vs. MB datasets for all CAPs except CAP2. Within-dataset variance (c) was also lower for MBME data compared to MB data for all CAPs except CAP2. Note: on each box, the central mark indicates the median, and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively. *** p < 0.001, ** p < 0.01, * p < 0.05, Bonferroni-corrected.
The spatial correlation between sessions 1 and 2 for each CAP for the MBME and MB data was also evaluated (Fig. 8). Between-session spatial correlation was significantly higher for MBME data vs. MB data for CAPs 1,2, and 4 (CAP1 : p< 0.001; CAP2: p < 0.001; CAP4: p= 0.009;, Bonferroni-corrected).
Fig. 8.
Violin plot of CAP reproducibility for the seed-free analysis using the test dataset for the four CAPs that matched between MBME and MB datasets. Between-session spatial correlation was computed using the mean of all timepoints assigned to each CAP for each subject and sequence. CAPs 1, 2, and 4 showed significantly higher spatial correlation for the MBME vs. MB data. Note: on each box, the central mark indicates the median, and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively. *** p < 0.001, ** p < 0.01, * p < 0.05, Bonferroni-corrected.
In addition, results of seed-free analyses for the other summary metrics, including the number of occurrences of each CAP, number of entries into each CAP, resilience, betweenness centrality, CAP in-degree, and CAP out-degree are presented as Supplementary Material (Fig. S3).
4. Discussion
In this study, a CAPs analysis was conducted on rs-fMRI data acquired using MBME and MB sequences. Various metrics were compared between MBME and MB datasets in a group of control subjects imaged twice over a span of two weeks. Overall, co-activation using seed-based (PCC) or seed-free approaches was higher for the MBME sequence vs. MB sequence. In addition, individual frames were more strongly spatially correlated with their assigned CAP centroid and had lower variance within datasets for the MBME data. Finally, the between-session spatial correlation was higher for MBME data for most CAPs.
A very limited number of studies have used a multi-echo sequence for dynamic analyses of rs-fMRI data. One study used a single band ME sequence to examine the variability of DMN connectivity in depression (Wise et al., 2017). They found higher variability in the medial prefrontal cortex and PCC in major depression subjects using a sliding window approach. Another study used an MBME sequence and a sliding window approach to examine the relationship between dynamic functional connectivity and mindfulness, assessed using the Child and Adolescent Mindfulness Measure (CAMM), in children and adolescents (Marusak et al., 2018). They found no significant effects between static connectivity and mindfulness, but found mindful participants changed states more throughout the scan and spent more time in a state characterized by positive default mode network connectivity with central executive networks. Although neither study compared ME to single echo approaches, they indicate the potential for using ME approaches in the clinical realm.
In this study, the CAPs method was used. In contrast to more conventional approaches focusing on correlating rs-fMRI time series across time (i.e. static or sliding window connectivity), the CAPs method focuses on single timepoints (Bolton et al., 2020). As described by Liu et al., time series approaches might have several disadvantages (Liu et al., 2018). First, brain networks comprise thousands of voxels while correlations are computed over tens or hundreds of timepoints, potentially leading to covariation across many voxels. Similarly, rs-fMRI data has orders of magnitude more voxels than timepoints leading to rank-deficient matrices. The CAPs method builds off previous work using point process analyses (PPA), with timepoints defined by the sequence of timepoints that crosses a defined threshold from below (Tagliazucchi et al., 2012). Tagliazucchi et al. showed averaging these high amplitude timepoints in the BOLD signal results in similar results to standard connectivity analyses using continuous data, and distinct groups of brain voxels are co-active over very short timescales (Tagliazucchi et al., 2012). These methods can evaluate the codependence in activity over more than two brain regions (Liu et al., 2018). The CAPs method expands on this by clustering high intensity voxels, extracted from the time series of a spec-fied seed region (or using all frames), based on spatial similarity. The CAPs method has shown distinct spatial patterns both within and outside of the DMN that would not be expected using static or sliding window correlation techniques (Liu et al., 2013).
Nevertheless, our results align with our previous studies evaluating static rs-fMRI connectivity using MBME and MB sequences (Cohen et al., 2017,2021c). For example, Cohen et al showed higher functional connectivity strength and extent for MBME vs. MB scans for seed-based and whole-brain parcellation-based methods. They also found MBME scans to be more reproducible using the Dice coefficient. Dipasquale et al. (2017) showed higher connectivity strength using ME approaches compared to single echo approaches especially after denoising using ME-ICA. It is important to distinguish the current study with these eariler studies evaluating static connectivity (Cohen et al., 2017, 2021c). Those studies mainly evaluated correlations between time series. In contrast, the CAPs approach treats each time point separately as independent data points. Thus, it was not trivial whether the results of the static connectivity analysis would translate to the dynamic CAP analysis.
Anytime data is being clustered, the number of clusters to choose is paramount as the “correct” number of clusters is often not known a priori. Two common methods used in dynamic rs-fMRI studies are the elbow criterion (Allen et al., 2014; Damaraju et al., 2014; Espinoza et al., 2019; Rabany et al., 2019) and silhouette criterion (Fiorenzato et al., 2019; Kim et al., 2017; Shakil et al., 2016). For the elbow criterion, a cluster validity index (i.e. the ratio of within to between cluster distances) is computed for a range of cluster numbers. The cluster number at the elbow of the cluster validity index vs. cluster size graph is chosen. For the silhouette criterion (Rousseeuw, 1987), the similarity of a point to points in its own cluster compared to points in other clusters is computed across clusters, and the cluster size with the maximum is selected. In this study, consensus clustering was used (Monti et al., 2003) as implemented in the TbCAPs toolbox. It works well for datasets with large dimensionality and, as described in the TbCAPs manual, has been successfully applied to selecting cluster numbers for generating functional brain networks with large scales (Bolton et al., 2020; Zöller et al., 2018). While cluster number is important, previous work has shown that CAP patterns did not depend on the number of clusters, and the majority of clusters found for lower cluster numbers were also found for higher cluster numbers (Liu and Duyn, 2013).
There was an overlap in the location of CAPs found using the seed-based seed-free approaches. For example, CAP2 and CAP4 for the seed-free approach matched CAP4 and CAP3 for the seed-based approach, respectively. This was somewhat expected as the PCC frames used for the single seed analysis were a subset of the seed-free case. However, in general, the intensity of the seed-based CAPs was higher compared to the seed-free CAPs. This is also unsurprising as the seed-based case only used frames in the top 30% of intensity. Finally, there were two all-negative CAPs for the seed-free approach. The seed-free approach used all frames and, since the data was z-scored, this included ~~50% of voxels with intensity < 0. While the implication of these negative CAPs remains to be further explored, they still have shown improved goodness of fit and reproducibility metrics for the MBME compared to MB data.
This study focuses on co-activation maps from individual timepoints and their relationship with the centroid CAPs. There are several other, more global metrics that can be assessed using the CAPs method including the number of occurrences of and the number of entries into each CAP, the probability of remaining in a CAP between timepoints (resilience), betweenness centrality, the likelihood of entering a specific CAP from any other CAP (in-degree), and the likelihood of leaving a specific CAP towards another CAP (out-degree). These metrics are presented as supplementary material and were not the main focus of the paper. One reason was that the brain might have been in different states during different scans, potentially biasing the results. The MB scans in this study always occurred following the MBME scans, which could have introduced bias into these metrics. For example, if the subject became fatigued throughout the course of the scan, it could have altered their brain state. For example, one study evaluated CAPs during four states of consciousness (Amico et al., 2014). They found, while the overall CAP patterns were maintained, some regions were no longer coactivated when consciousness was reduced. Another study evaluated patients with unresponsive wakefulness syndrome (UWS) and found reduced occurrences of CAPs associated with the DMN in UWS patients (Di Perri et al., 2018). In addition, these metrics are only presented for the seed-free case as timepoints were skipped in the seed-based analysis making these measures difficult to interpret.
One advantage of ME scans is that a short echo time (< 15 ms) image can be acquired. Since the signal from the first echo will be weighted more heavily in the T2* -weighted echo combination scheme, BOLD contrast will be maximized in voxels with short T2*. In addition, the signal is higher at shorter echo times. Thus, the collection of short TE images reduces susceptibility-induced signal dropout (Cohen et al., 2021a; Fernandez et al., 2017). This can particularly be observed for CAP2 for the seed-based analysis, which had higher co-activation in the orbitofrontal cortex for the MBME data compared to the MB data.
More subcortical co-activation was found for the MBME data, specifically in CAPs 2 and 4 for the seed-based analysis and CAP3 for the seed-free analysis. This finding is in line with previous work by Cohen et al., where subcortical-cortical were higher for MBME scans vs. MB scans for both whole-brain parcellation analysis and seed-based analyses using the hippocampus as the seed for the functional connectivity analysis (Cohen et al., 2021a,2021c). Kundu et al. (2012) found similar results for ME compared to single-echo data by using a hippocampus seed.
Both the MB and MBME data were preprocessed using advanced ICA-based denoising techniques, namely ICA-AROMA for MB and ME-ICA for MBME. Both methods involve regressing noise ICA components from the data. A recent study by Dipasquale et al. (2017) compared a variety of denoising techniques for multi-echo and single echo datasets . Their results suggest that ICA-AROMA is best for single echo data and ME-ICA is best for multi-echo data (Dipasquale et al., 2017). It was assumed the majority of researchers would process their fMRI data with advanced denoising approaches, and our results would be more useful to readers. More importantly, ME scans also allow for the estimation of T2* and the combination of echoes prior to ME-ICA (Kundu et al., 2013,2012). ME-ICA removes the artifactual non-BOLD signal from the data including R2* effects, motion artifacts, and physiological noise (Kundu et al., 2013,2012,2017; Olafsson et al., 2015), reducing variations in these signals across scan sessions automatically and resulting in a more stable signal over time. This can account for the higher between-session spatial correlation and lower within-dataset variance for the MBME data vs. the MB data, which will have important implications for further applications (Elliott et al., 2021).
While a powerful denoising technique, Power et al. have pointed out that whole-brain respiratory artifacts are not adequately removed by techniques such as ME-ICA (Power et al., 2018). This leaves open the possibility that CAPs may be influenced by these artifacts. Techniques such as global signal regression (GSR) could be used to mitigate these effects, but the use of GSR has been hotly debated in the fMRI community and would add additional confound to the analysis (Marshall et al., 2020; Murphy et al., 2013). Moreover, the CAPs analysis tends to be less susceptible to global artifacts compared to correlation-based metrics. For example, Liu and Duyn (2013) found that global signal regression did not strongly impact spatial patterns derived by CAPs. Our study did find CAPs that appear more global in nature, especially for the MBME data (see CAP3 for the PCC seed). However, the majority of CAPs are specific and appear neural in nature, and the MBME data was improved in those CAPs compared to the MB data. Thus, we do not feel the primary differences between the MBME and MB sequences are due to brain-wide respiratory artifacts. Since CAPs analysis temporally decomposes the data into point-wise patterns, one would therefore expect global effects to be largely relegated to a subset of CAPs, with the others relatively unaffected (Nalci et al., 2017). Further, Nalci et al. (2017) showed that global signal regression acts largely as a temporal down-weighting process, attenuating specific timepoints with large global signal amplitudes. Therefore, we did not apply GSR in the current work following previous CAPs studies (Chen et al., 2015; Marshall et al., 2020).
Parameters were identical between the MB and MBME acquisitions except for the TR (900 ms for MBME and 650 ms for MB). This was done intentionally to evaluate each sequence as researchers were likely to use them. One advantage of the single echo approach is lower minimal TRs compared to the multi-echo approach. However, it leads to the question of whether differences in CAP characteristics could be attributed to the different sampling rate between the sequences. Previous work showed MBME data had a temporal SNR (tSNR) 1.18 times higher than the MB data for the same scan protocols used in this study ((Cohen et al., 2021a). One may argue that the increased tSNR from the longer TR for the MBME data is somewhat mitigated by the increase in the number of timepoints for the shorter TR MB data (Smith et al., 2013). Furthermore, a previous study has shown improvements in static functional connectivity for MBME compared to single-echo MB data with identical TR and other scan parameters (Cohen et al., 2017).
Moreover, one may speculate how our results would compare to the single-band ME acquisition. Increased TR of single-band TE would lead to fewer frames collected in the same scan time potentially leading to a lower optimal number of CAPs. On the other hand, MB acquisitions come with increased reconstruction (g-factor) artifacts potentially leading to more noise associated CAPs. In this study, no noise CAPs were detected for five CAPs.
This study had some limitations in addition to those mentioned above. First, only young healthy controls were included in this study. Comparisons should be made in patient populations. Also, as mentioned previously, the MB scans always occurred after the MBME scans, which could potentially lead to participant fatigue during the later acquisitions. These scans both occurred in the first half of the scan session so those effects should be diminished. Also, we found no significant differences in head motion, measured with framewise displacement, between the MB and MBME scans or between CAPs. It should also be noted that temporal z-scoring on a scan-to-scan basis was performed in the initial CAP and point-process studies (Liu and Duyn, 2013; Liu et al., 2018; Tagliazucchi et al., 2012). We have carried out this z-scoring step in our analysis to be consistent with the literature.
In conclusion, a CAPs analysis showed higher co-activation across CAPs for MBME scans compared to MB scans. MBME CAPs were more similar to the centroid CAPs and MBME CAPs were more reliable across scan sessions compared to MB scans.
Taken together, MBME is a promising avenue for CAPs analyses in future applications.
Supplementary Material
Acknowledgments
This work was funded by a research grant from GE Healthcare to Y.W.
Abbreviations
- rs-fMRI
resting-state functional magnetic resonance imaging
- BOLD
blood oxygenation level dependent
- CAPs
co-activation patterns
- MB
multiband
- ME
multi-echo
- MBME
multiband multi-echo
- EPI
echo planar imaging
- ME-ICA
multi-echo independent component analysis
- ICA-AROMA
ICA-based strategy for automatic removal of motion artifacts
- TE
echo time
- TR
repetition time
- FOV
field of view
- FA
flip angle
- FWHM
full width at half maximum
- PCC
posterior cingulate cortex
- AAL2
anatomical atlas version 2
- DMN
default mode network
Footnotes
Data and code availability statement
This study was funded by GE Healthcare. According to the research agreement between MCW and GE Healthcare for this study, data published in this paper will be available via a formal request to the authors and a data sharing agreement should be signed by both parties.
Credit authorship contribution statement
Alexander D. Cohen: Conceptualization, Methodology, Software, Investigation, Formal analysis, Writing – original draft, Writing – review & editing. Catie Chang: Conceptualization, Writing – review & editing, Supervision. Yang Wang: Conceptualization, Resources, Methodology, Investigation, Formal analysis, Writing – review & editing, Supervision.
Supplementary materials
Supplementary material associated with this article can be found, in the online version, at doi:10.1016/j.neuroimage.2021.118555.
References
- Ahmed Z, Bandettini PA, Bottenhorn KL, Caballero-Gaudes C, Dowdle LT, DuPre E, Handwerker D, Heunis S, Kundu P, R LA, Markello R, Markiewicz CJ, Maullin-Sapey T, Moia S, Salo T, Staden I, Teves J, Uruñuela E, Vaziri-Pashkam M, Whitaker K, 2020. ME-ICA/tedana: 0.0.9 https://zenodo.org/record/4509480. [Google Scholar]
- Allen EA, Damaraju E, Plis SM, Erhardt EB, Eichele T, Calhoun VD, 2014. Tracking whole-brain connectivity dynamics in the resting state. Cereb. Cortex 24, 663–676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amico E, Gomez F, Di Perri C, Vanhaudenhuyse A, Lesenfants D, Boveroux P, Bonhomme V, Brichant JF, Marinazzo D, Laureys S, 2014. Posterior cingulate cortex-related co-activation patterns: a resting state FMRI study in propofol-induced loss of consciousness. PLoS ONE 9, e100012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biswal B, Yetkin FZ, Haughton VM, Hyde JS, 1995. Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magn. Reson. Med 34, 537–541. [DOI] [PubMed] [Google Scholar]
- Bolton TAW, Tuleasca C, Wotruba D, Rey G, Dhanis H, Gauthier B, Delavari F, Morgenroth E, Gaviria J , Blondiaux E , Smigielski L, Van De Ville D, 2020. Tb-CAPs: a toolbox for co-activation pattern analysis. Neuroimage 211, 116621. [DOI] [PubMed] [Google Scholar]
- Boyacioglu R, Schulz J, Koopmans PJ, Barth M, Norris DG, 2015. Improved sensitivity and specificity for resting state and task fMRI with multiband multi-echo EPI compared to multi-echo EPI at 7 T. Neuroimage 119, 352–361. [DOI] [PubMed] [Google Scholar]
- Chang C, Glover GH, 2010. Time-frequency dynamics of resting-state brain connectivity measured with fMRI. Neuroimage 50, 81–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen JE, Chang C, Greicius MD, Glover GH , 2015. Introducing co-activation pattern metrics to quantify spontaneous brain network dynamics. Neuroimage 111, 476–488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen AD , Jagra AS, Visser NJ, Yang B, Fernandez B, Banerjee S, Wang Y, 2021a. Improving the breath-holding CVR measurement using the multiband multi--echo EPI sequence. Front. Physiol 12, 619714 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen AD, Jagra AS, Yang B , Fernandez B, Banerjee S, Wang Y , 2021b. Detecting task functional MRI activation using the multiband multiecho (MBME) echo-planar imaging (EPI) sequence. J. Magn. Reson. Imaging 53, 1366–1374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen AD, Nencka AS, Lebel RM , Wang Y , 2017. Multiband multi-echo imaging of simultaneous oxygenation and flow timeseries for resting state connectivity. PLoS ONE 12, e0169253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen AD, Yang B, Fernandez B, Banerjee S, Wang Y, 2021c. Improved resting state functional connectivity sensitivity and reproducibility using a multiband multi-echo acquisition. Neuroimage 225, 117461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox RW, 1996. AFNI: software for analysis and visualization of functional magnetic resonance neuroimages. Comput. Biomed. Res 29, 162–173. [DOI] [PubMed] [Google Scholar]
- Cox RW, 2012. AFNI: what a long strange trip it’s been. Neuroimage 62, 743–747 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- Damaraju E, Allen EA, Belger A, Ford JM, McEwen S, Mathalon DH, Mueller BA, Pearlson GD, Potkin SG, Preda A, Turner JA , Vaidya JG, van Erp TG, Calhoun VD, 2014. Dynamic functional connectivity analysis reveals transient states of dysconnectivity in schizophrenia. Neuroimage Clin. 5, 298–308 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- Di Perri C, Amico E, Heine L, Annen J, Martial C, Larroque SK, Soddu A, Marinazzo D, Laureys S, 2018. Multifaceted brain networks reconfiguration in disorders of consciousness uncovered by co-activation patterns. Hum. Brain Mapp 39, 89–103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dipasquale O, Sethi A, Lagana MM , Baglio F, Baselli G, Kundu P, Harrison NA, Cercignani M, 2017. Comparing resting state fMRI denoising approaches using multi- and single-echo acquisitions. PLoS ONE 12, e0173289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elliott ML, Knodt AR , Hariri AR, 2021. Striving toward translation: strategies for reliable fMRI measurement. Trends Cogn. Sci 25, 776–787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Espinoza FA , Liu J, Ciarochi J, Turner JA, Vergara VM, Caprihan A, Misiura M, Johnson HJ, Long JD, Bockholt JH, Paulsen JS, Calhoun VD, 2019. Dynamic functional network connectivity in Huntington’s disease and its associations with motor and cognitive measures. Hum. Brain Mapp 40, 1955–1968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feinberg DA, Moeller S, Smith SM, Auerbach E, Ramanna S, Gunther M, Glasser MF, Miller KL, Ugurbil K, Yacoub E, 2010. Multiplexed echo planar imaging for sub-second whole brain FMRI and fast diffusion imaging. PLoS ONE 5, e15710 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fernandez B, Leuchs L, Samann PG, Czisch M , Spoormaker VI, 2017. Multi-echo EPI of human fear conditioning reveals improved BOLD detection in ventromedial prefrontal cortex. Neuroimage 156, 65–77. [DOI] [PubMed] [Google Scholar]
- Fiorenzato E, Strafella AP, Kim J, Schifano R, Weis L , Antonini A, Biundo R, 2019. Dynamic functional connectivity changes associated with dementia in Parkinson’s disease. Brain 142, 2860–2872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox MD, Snyder AZ, Vincent JL, Corbetta M , Van Essen DC, Raichle ME, 2005. The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proc. Natl. Acad. Sci 102, 9673–9678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glasser MF, Sotiropoulos SN , Wilson JA, Coalson TS, Fischl B, Andersson JL, Xu J, Jbabdi S, Webster M, Polimeni JR, Van Essen DC, Jenkinson M, Consortium, W.U.M.H. , 2013. The minimal preprocessing pipelines for the Human Connectome Project. Neuroimage 80, 105–124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkinson M, Bannister P, Brady M , Smith S, 2002. Improved optimization for the robust and accurate linear registration and motion correction of brain images. Neuroimage 17, 825–841. [DOI] [PubMed] [Google Scholar]
- Jenkinson M, Beckmann CF, Behrens TE, Woolrich MW, Smith SM , 2012. FSL. Neuroimage 62, 782–790. [DOI] [PubMed] [Google Scholar]
- Kim J, Criaud M, Cho SS, Diez-Cirarda M, Mihaescu A, Coakeley S, Ghadery C, Valli M, Jacobs MF, Houle S , Strafella AP, 2017. Abnormal intrinsic brain functional network dynamics in Parkinson’s disease. Brain 140, 2955–2967 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kundu P, Brenowitz ND, Voon V, Worbe Y, Vertes PE, Inati SJ, Saad ZS, Bandettini PA, Bullmore ET, 2013. Integrated strategy for improving functional connectivity mapping using multiecho fMRI. Proc. Natl. Acad. Sci. U. S. A 110, 16187–16192 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kundu P, Inati SJ, Evans JW, Luh WM, Bandettini PA, 2012. Differentiating BOLD and non-BOLD signals in fMRI time series using multi-echo EPI. Neuroimage 60, 1759–1770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kundu P, Voon V, Balchandani P, Lombardo MV, Poser BA , Bandettini PA, 2017. Multi-echo fMRI: a review of applications in fMRI denoising and analysis of BOLD signals. Neuroimage 154, 59–80. [DOI] [PubMed] [Google Scholar]
- Liu X, Chang C, Duyn JH, 2013. Decomposition of spontaneous brain activity into distinct fMRI co-activation patterns. Front. Syst. Neurosci 7, 101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu X, Duyn JH, 2013. Time-varying functional network information extracted from brief instances of spontaneous brain activity. Proc. Natl. Acad. Sci. U. S. A 110, 4392–4397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu X, Zhang N, Chang C, Duyn JH, 2018. Co-activation patterns in resting-state fMRI signals. Neuroimage 180, 485–494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marshall E, Nomi JS, Dirks B, Romero C, Kupis L, Chang C, Uddin LQ, 2020. Coactivation pattern analysis reveals altered salience network dynamics in children with autism spectrum disorder. Netw. Neurosci 4, 1219–1234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marusak HA, Elrahal F, Peters CA, Kundu P , Lombardo MV, Calhoun VD, Goldberg EK, Cohen C, Taub JW, Rabinak CA, 2018. Mindfulness and dynamic functional neural connectivity in children and adolescents. Behav. Brain Res 336, 211–218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moeller S, Yacoub E, Olman CA, Auerbach E, Strupp J, Harel N, Ugurbil K, 2010. Multiband multislice GE-EPI at 7 tesla, with 16-fold acceleration using partial parallel imaging with application to high spatial and temporal whole-brain fMRI. Magn. Reson. Med 63, 1144–1153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monti S, Tamayo P, Mesirov J, Golub T, 2003. Consensus clustering: a resampling-based method for class discovery and visualization of gene expression microarray data. Mach. Learn 52, 91–118. [Google Scholar]
- Murphy K, Birn RM, Bandettini PA, 2013. Resting-state fMRI confounds and cleanup. Neuroimage 80, 349–359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nalci A, Rao BD, Liu TT, 2017. Global signal regression acts as a temporal down-weighting process in resting-state fMRI. Neuroimage 152, 602–618. [DOI] [PubMed] [Google Scholar]
- Olafsson V, Kundu P, Wong EC, Bandettini PA, Liu TT, 2015. Enhanced identification of BOLD-like components with multi-echo simultaneous multi-slice (MESMS) fMRI and multi-echo ICA. Neuroimage 112, 43–51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poser BA, Norris DG, 2009. Investigating the benefits of multi-echo EPI for fMRI at 7 T. Neuroimage 45, 1162–1172. [DOI] [PubMed] [Google Scholar]
- Poser BA, Versluis MJ, Hoogduin JM, Norris DG, 2006. BOLD contrast sensitivity enhancement and artifact reduction with multiecho EPI: parallel-acquired inhomogeneity-desensitized fMRI. Magn. Reson. Med 55, 1227–1235. [DOI] [PubMed] [Google Scholar]
- Posse S, Wiese S, Gembris D, Mathiak K, Kessler C, Grosse-Ruyken ML, Elghahwagi B, Richards T, Dager SR, Kiselev VG, 1999. Enhancement of BOLD-contrast sensitivity by single-shot multi-echo functional MR imaging. Magn. Reson. Med 42, 87–97. [DOI] [PubMed] [Google Scholar]
- Power JD, Barnes KA, Snyder AZ, Schlaggar BL, Petersen SE, 2012. Spurious but systematic correlations in functional connectivity MRI networks arise from subject motion. Neuroimage 59, 2142–2154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power JD, Plitt M, Gotts SJ, Kundu P, Voon V, Bandettini PA, Martin A, 2018. Ridding fMRI data of motion-related influences: removal of signals with distinct spatial and physical bases in multiecho data. Proc. Natl. Acad. Sci. U. S. A 115, 2105–2114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pruim RHR, Mennes M, van Rooij D, Llera A, Buitelaar JK, Beckmann CF, 2015. ICA-AROMA: a robust ICA-based strategy for removing motion artifacts from fMRI data. Neuroimage 112, 267–277. [DOI] [PubMed] [Google Scholar]
- Rabany L, Brocke S, Calhoun VD, Pittman B, Corbera S, Wexler BE, Bell MD, Pelphrey K, Pearlson GD, Assaf M, 2019. Dynamic functional connectivity in schizophrenia and autism spectrum disorder: convergence, divergence and classification. NeuroImage Clin. 24, 101966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rolls ET, Joliot M, Tzourio-Mazoyer N, 2015. Implementation of a new parcellation of the orbitofrontal cortex in the automated anatomical labeling atlas. Neuroimage 122, 1–5. [DOI] [PubMed] [Google Scholar]
- Rousseeuw PJ, 1987. Silhouettes: a graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math 20, 53–65. [Google Scholar]
- Sakoglu U, Pearlson GD, Kiehl KA, Wang YM, Michael AM, Calhoun VD, 2010. A method for evaluating dynamic functional network connectivity and task-modulation: application to schizophrenia. MAGMA 23, 351–366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Senbabaoglu Y, Michailidis G, Li JZ, 2014. Critical limitations of consensus clustering in class discovery. Sci. Rep 4, 6207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Setsompop K, Gagoski BA, Polimeni JR, Witzel T, Wedeen VJ, Wald LL, 2012. Blipped-controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g-factor penalty. Magn. Reson. Med 67, 1210–1224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shakil S, Lee CH, Keilholz SD, 2016. Evaluation of sliding window correlation performance for characterizing dynamic functional connectivity and brain states. Neuroimage 133, 111–128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Beckmann CF, Andersson J, Auerbach EJ, Bijsterbosch J, Douaud G, Duff E, Feinberg DA, Griffanti L, Harms MP, Kelly M, Laumann T, Miller KL, Moeller S, Petersen S, Power J, Salimi-Khorshidi G, Snyder AZ, Vu AT, Woolrich MW, Xu J, Yacoub E, Ugurbil K, Van Essen DC, Glasser MF, Consortium, W.U.-M.H., 2013. Resting-state fMRI in the human connectome project. Neuroimage 80, 144–168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tagliazucchi E, Balenzuela P, Fraiman D, Chialvo DR, 2012. Criticality in large-scale brain FMRI dynamics unveiled by a novel point process analysis. Front. Physiol 3, 15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wise T , Marwood L, Perkins AM, Herane-Vives A , Joules R, Lythgoe DJ, Luh WM, Williams SCR, Young AH, Cleare AJ, Arnone D, 2017. Instability of default mode network connectivity in major depression: a two-sample confirmation study. Transl. Psychiatry 7, e1105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zöller DM, Bolton TA, Karahanoğlu FI, Eliez S, Schaer M, Van De Ville D, 2018. Robust recovery of temporal overlap between network activity using transient-in-formed spatio-temporal regression. IEEE Trans. Med. Imaging 38, 291–302. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.