Abstract
Optical coherence tomography (OCT) images of ex vivo human brain tissue are corrupted by multiplicative speckle noise that degrades the contrast to noise ratio (CNR) of microstructural compartments. This work proposes a novel algorithm to reduce noise corruption in OCT images that minimizes the penalized negative log likelihood of gamma distributed speckle noise. The proposed method is formulated as a majorize-minimize problem that reduces to solving an iterative regularized least squares optimization. We demonstrate the usefulness of the proposed method by removing speckle in simulated data, phantom data and real OCT images of human brain tissue. We compare the proposed method with state of the art filtering and non-local means based denoising methods. We demonstrate that our approach removes speckle accurately, improves CNR between different tissue types and better preserves small features and edges in human brain tissue.
Keywords: Speckle, Optical coherence tomography, Multiplicative noise, Artifact correction, Majorize minimize, Gamma distribution, Human brain, Tissue imaging
1. Introduction
Optical coherence tomography (OCT) is an imaging technique that uses low temporal coherence light to obtain cross sectional images of an object at 1−20 μm resolution.In addition, block-face imaging of OCT enables large volumetric reconstruction (tens of cubic centimeters) of ex vivo human brain tissues, by combining with serial sectioning using a vibratome (Magnain et al., 2014). The high resolution of OCT images and its ability to image in three dimensions makes OCT an attractive imaging modality to study 3D brain anatomy at microscopic resolution. Microstructural compartments attenuate the light propagating in the tissue with a rate determined by its scattering coefficient. The variations in tissue optical properties lead to variation of contrast in OCT images (Goodman, 1975, 1976). Scattering coefficients have been related to brain tissue properties such as cell and myelin density (Farhat et al., 2011; Vermeer et al., 2014; Wang et al., 2017). OCT images have also been used to study pathological features in lesion, tumor, and neurodegenerative diseases (van Manen et al., 2018; Zysk et al., 2007). Recent studies have also shown that the intrinsic optical properties of ex vivo human brains provide distinctive identification of neuroanatomical features (Magnain et al., 2015a; 2015b; Wang et al., 2017).
Contamination of OCT images by speckle noise is a well known problem that results in reduced contrast visibility and inaccurate optical property estimation (Kirillin et al., 2014; Lindenmaier et al., 2013; Schmitt et al., 1999). Speckle is a form of multiplicative noise that occurs in laser based imaging modalities due to the interference of scattering waves from surrounding regions (Goodman, 1975, 1976, 1985; Lim and Nawab, 1981; Tur et al., 1982). In ex vivo brain OCT images speckle results from scattering interference of the microstructural medium. Destructive interference reduces the OCT intensity, while constructive interference increases the intensity, giving speckle a high contrast appearance. Speckle significantly degrades the contrast-to-noise-ratio (CNR) between tissue structures and masks features that are similar in size to it, dramatically reducing the accuracy of quantitative analysis.
Speckle noise is typically eliminated by averaging over multiple OCT acquisitions with uncorrelated speckle patterns (Bashkansky and Reintjes, 2000; Desjardins et al., 2007). In ex vivo imaging, since fixed tissue lacks dynamic processes, uncorrelated speckle patterns are created with different incident wavefronts, angular compounding, frequency compounding or combining polarization modes. In a recent study, we used the average of 50% overlapping tiles to reduce speckle noise and achieve large volumetric reconstructions of ex vivo human brain tissue (Magnain et al., 2014; Wang et al., 2018a). The resulting reduced speckle contrast was inversely proportional to the square root of the number of images used to average. However, this type of speckle reduction method suffers from substantially increased acquisition time. For example, acquiring 50% overlapped data takes four times longer than acquiring non-overlap data.
Several post processing tools that apply denoising algorithms to the acquired OCT data have been developed. The high-contrast appearance of speckle has led to the usage of filtering-based methods (Bernstein, 1987; Frost et al., 1982; Lee, 1980; Ramos-Llordén et al., 2015; Salinas and Fernandez, 2007; Yu and Acton, 2002) to remove speckle. Filtering methods generally work well in homogeneous regions but can distort tissue boundaries and blur structures, reducing the effective resolution of the image. Another class of denoising methods include additive noise removal methods applied to the logarithm of the OCT image. These methods are based on the assumption that, with averaging, the speckle distribution of log-transformed OCT intensity images approaches the Gaussian distribution (Xie et al., 2002). State of the art log transformation based denoising methods include non-local means (NLM) (Aum et al., 2015; Buades et al., 2010; Coupé et al., 2009; Fischl and Schwartz, 1999; Yu et al., 2016; Zhou et al., 2020), block matching 3D (BM3D) (Dabov et al., 2007), wavelet shrinkage denoising (Chong and Zhu, 2013; Mayer et al., 2012; Zaki et al., 2017) and constrained optimization (e.g. total variation constraint) methods (Fang et al., 2012; Feng et al., 2014; Gong et al., 2015; Wang et al., 2018b; Wong et al., 2010). One drawback of these approaches is that most of them assume zero mean noise, which does not hold for the log transformed speckle distribution, leading to a mean bias in the denoised result (Arsenault and April, 1976; Gong et al., 2015; Xie et al., 2002).
The advent of deep learning technology has also resulted in a number of promising learning based denoising methods. While these denoising methods have largely focused on removing additive noise, there is recent work in removing speckle in both supervised (Akter et al., 2020; Devalla et al., 2019; Menon et al., 2020; Qiu et al., 2020) and unsupervised manner (Huang et al., 2021; Mao et al., 2019) from OCT images. The supervised learning techniques rely on finding the mapping between averaged ground truth and noisy data. The unsupervised methods utilize noise2noise approach (Krull et al., 2018; Lehtinen et al., 2018) that trains on paired sets of noisy images. However, the generalizability of these methods remains untested for human brain imaging that differs in tissue contrast (signal intensities), image features, imaging resolutions, and signal to noise ratio. We are also limited in training these methods for human brain OCT due to the lack of available training data.
The final class of denoising methods remove multiplicative noise by optimizing a speckle distribution model. Speckle has been shown to be gamma distributed on OCT intensity images (Feng et al., 2014; Gong et al., 2015; Kirillin et al., 2014). Speckle in uniform media is modeled by the negative exponential distribution, a special case of the gamma distribution (Goodman, 1975). The speckle distribution of OCT amplitude, which is the square root of measured OCT intensity, is modeled by Rayleigh or Nakagami distributions (Karamata et al., 2005; Pircher et al., 2003; Yin et al., 2013), which are related to the square-root of the gamma distribution. OCT studies have also reported high goodness of fit for the generalized gamma distribution in applications such as cornea and skin imaging (Farhat et al., 2011; Jesus and Iskander, 2017; Raju and Srinivasan, 2002). While the gamma speckle model fits OCT data well, it is complicated and non-trivial to optimize. Log transformed denoising and the BM3D algorithm have been extended to use the gamma distributed multiplicative speckle noise model to denoise synthetic aperture radar (SAR) images (Bioucas-Dias and Figueiredo, 2010; Parrilli et al., 2012).
In this study we propose a new approach to optimize the gamma distribution speckle model and remove multiplicative speckle noise from OCT images of ex vivo human brain tissue. The proposed method minimizes the negative log likelihood (NLL) of the gamma distribution penalized with a spatial regularization constraint. We provide novel theoretical understanding into the convexity of different terms forming the gamma NLL cost. We take advantage of this new insight to propose a majorize-minimize framework (Hunter and Lange, 2004; de Leeuw and Heiser, 1977) based method that optimizes the complicated cost function using simpler surrogate functions. The proposed minimization reduces to solving an iterative regularized least squares problem, which decreases the computation time compared to the existing NLM state of the art methods. We compare the performance of our technique with filtering methods, log-normal approximation method, NLM and SAR BM3D, and demonstrate the improvement in overall denoising accuracy, CNR between tissue types and in preservation of small features and edges of human brain tissue. We also demonstrate the generalizability of our approach in removing speckle across multiple tissue types and multiple imaging resolution scales, and its flexibility to work with convex regularization functions.
The work is organized as follows: we briefly describe the background on speckle likelihood, derive the proposed algorithm called MM-despeckle, demonstrate speckle removal results, discuss implications of our approach and present the conclusions.
2. Background
2.1. Speckle distribution in OCT images
Speckle noise in OCT intensity images (Goodman, 1976) is a form of multiplicative noise that is well described at an arbitrary voxel as
| (1) |
where y is the measured OCT amplitude and its square is the measured OCT intensity, x is the true OCT amplitude and s is the speckle noise corrupting the OCT intensity (i.e. the squared amplitude). The probability density function (PDF) describing the spatial distribution of speckle noise in OCT intensity data is modeled with a gamma distribution (ps(s; α, β)) (Feng et al., 2014; Gong et al., 2015; Goodman, 1975; Kirillin et al., 2014):
| (2) |
with s > 0, α > 0 and β > 0. Here is the gamma function, α is the shape parameter and β is the rate parameter of the gamma distribution.
2.2. Maximum likelihood estimation (MLE) for denoising
MLE is a commonly used procedure to denoise data. The main assumption for MLE methods is that we can model the likelihood distribution of the acquired data. MLE methods find an estimate of the true signal x from the measured data y by maximizing the likelihood distribution. This is generally achieved by minimizing a penalized negative log likelihood (P-NLL) cost function
| (3) |
where R(x) is a regularization or penalty function and λ is the regularization parameter. The penalty is put in place to constrain the generally ill-posed nature of the negative log likelihood minimization.
2.3. Majorize-minimize optimization framework
In this work we propose an optimization algorithm based on the majorize-minimize (MM) framework (Hunter and Lange, 2004) to minimize the P-NLL cost of OCT speckle. The MM framework can be used to minimize a complicated cost function indirectly by sequentially minimizing simpler convex functions that are tangential to, and greater than or equal to, the cost function. The tangential functions are referred to as majorants. A majorant of a cost function , tangential to it at , satisfies the following two criteria:
The cost and the majorant meet only at a single point .
The majorant function is greater than the cost function otherwise: .
These conditions theoretically guarantee that the sequential minimization of the majorant function also monotonically decreases and minimizes the cost . In this work we find convex majorants for the gamma P-NLL cost function that can be minimized by solving least squares or a regularized least squares problems.
3. Theory
3.1. Negative log likelihood cost function
The likelihood of the OCT amplitude is defined as the conditional probability of the measured amplitude y given the true signal amplitude x. The likelihood can be derived using the probability transformation rule as
| (4) |
where we have substituted from Eq. (1) into the speckle PDF (Eq. (2)). The derivative , also follows from the multiplicative relationship in Eq. (1). Expanding the PDF and the derivative, the likelihood is derived as:
| (5) |
In this paper we assume prior knowledge of gamma distribution parameters (α and β), and drop these terms from the likelihood notation to simplify it. Assuming all voxels to be independently distributed samples of the likelihood distribution, the joint likelihood can be derived as
| (6) |
where M is the number of measurements (or voxels), m is the voxel index, is the vectorized measured OCT amplitude image of length M and is the vectorized true OCT amplitude image of length M.
The P-NLL cost for speckle noise follows as
| (7) |
where is composed of constants that do not depend on x and are ignored in the minimization.
3.2. Majorant to the P-NLL cost function
The negative log likelihood (NLL) of the gamma distribution (Eq. (7)) for an arbitrary voxel is the sum of a logarithm function and the squared function . We assume in our derivations because OCT amplitude and intensity are positive valued signals (Izatt et al., 2015). The logarithm term is strictly concave with a negative second derivative of . Similarly, the squared term is strictly convex with a positive second derivative of . Gamma NLL is thus non-convex and the sum of a strictly convex and a strictly concave function.
We take advantage of the property that the tangent to a strictly concave function majorizes the function (Hunter and Lange, 2004). We derive a convex majorant function by the summing the convex term with the tangent to the concave logarithm term. The logarithm tangent at is derived in Appendix A as . Let be the majorant function that is tangential to the gamma NLL at . The majorant function reduces to
| (8) |
The gamma majorant function is the sum of two convex functions. The minimum of the majorant can be analytically evaluated as by equating its derivative to 0 (see Appendix B for derivation).
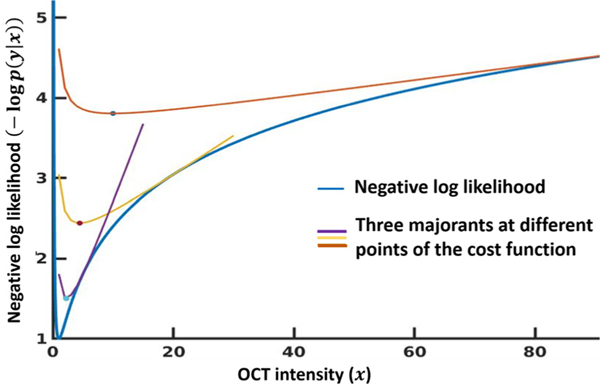
Fig. 1 plots three example tangential majorant functions ( from Eq. (8)) for a 1D gamma negative log likelihood cost function with parameters α = β = 1. The true intensity (x) was set to 1, and we see the NLL is minimum at x = 1. The majorants are convex and their minima (Appendix B) is marked in the figure. As the minimum of the majorants moves from the red to the purple curve, the estimation gradually approaches the minimum of the NLL cost function.
Fig. 1.
Example majorants of gamma distribution. We show three tangential majorants of the gamma negative log likelihood distribution with true intensity x = 1. The distribution parameters (α, β) were set to 1. The minimum of the each majorant is also marked.
Now consider the following least squares problem :
| (9) |
| (10) |
Note that while is not a tangential majorant of the gamma NLL, it shares the same minimum as the majorant can be used to find the majorant minimum and can be solved using a least squares algorithm. In addition, combined with spatial regularization functions can be solved with standard regularized least square solvers (Barrett et al., 1994; Chambolle and Pock, 2011; Rudin et al., 1994).
Lastly, we have derived similar majorant expressions for the negative exponential distribution and the generalized gamma distribution, which are related to the gamma distribution in Appendix C and Appendix D respectively.
3.3. MM-despeckle algorithm to optimize gamma P-NLL cost
We propose a new majorize-minimize algorithm MM-despeckle that minimizes P-NLL majorants iteratively to indirectly minimize the gamma P-NLL cost. The minimization at each iteration is formulated as a regularized least squares problem by combining Eq. (9) with a regularization function R(x) :
| (11) |
| (12) |
The method estimates the OCT amplitude . The input to the algorithm is the noisy OCT amplitude image y obtained by taking the square root of the measured OCT intensity image. Please note that the OCT amplitude is positive, and thus the square root mapping is a one-to-one function. Eq. (12) can be solved using standard regularized least squares algorithms such as (Chambolle and Pock, 2011; Rudin et al., 1994) for total variation regularization or Barrett et al. (1994) for quadratic smoothness regularization. The algorithm reduces to the following steps:
Initialize
{k + 1}th iteration: minimize the P-NLL majorant , where is the minimum solution of {k} th iteration.
If not converged: and repeat steps 2–3, Otherwise exit
The denoised amplitude is squared to calculate the OCT intensity image.
We evaluated to determine convergence.
4. Experiments
We describe the imaging experiments conducted to acquire OCT images to evaluate the proposed MM-despeckle method.
4.1. OCT system description
We used a spectral domain OCT to image the human brain samples (Magnain et al., 2014). Briefly, the broadband light source is a superluminescent diode (LS2000B SLD, Thorlabs Inc., Newton, New Jersey) with a center wavelength of 1310 nm, spectral bandwidth of 170 nm and an axial resolution of 3.5 μm in tissue. The spectrometer consisted of a 1024-pixel InGaAs line scan camera (Thorlabs Inc.), providing an acquisition rate of 46kHz per A-line and a depth of field of 1.5 mn in tissue. Three lenses (10 × water immersion objective, 10 × air objective, and 5 × air objective) were used in the sample arm, yielding a lateral resolution of 3.5 μm, 3.5 μm and 6 μm, respectively. To cover the large area of sample, the tissue was imaged in consecutive tiles. An overlap was used between tiles to perform registration and stitching.
4.2. Phantom samples and imaging description
We imaged a scattering phantom made by suspensions of monodisperse polystyrene microspheres with a refractive index of 1.57 at 1300 nm wavelength and a mean diameter of 1 μm. The solution was diluted with five concentrations, representing scattering coefficients of 2 mm−1, 4 mm−1, 6 mm−1, 8 mm−1 and 10 mm−1 respectively. The range of phantom scattering coefficients matched the range of scattering coefficients of gray and white matter in ex vivo human brain samples. We measured the phantom samples with the 10 × air coupled objective. Each measurement consisted of a cross-sectional image with 5000 A-lines, spanning a scanning range of 1.5 mm.
4.3. Ex vivo human brain imaging experiments
We describe the human brain tissue experiments and the denoising analysis in this section.
4.3.1. Brain samples
We obtained three postmortem human brain tissue samples from the Massachusetts General Hospital Autopsy Suite. Tissue blocks included hippocampus, visual cortex and cerebellum regions of the brain. This study and its use of postmortem tissue was approved by the Internal Revenue Board of the Massachusetts General Hospital. The samples had been fixed with 10% formalin for two months. The postmortem interval did not exceed 24 h. The sample was mounted in a water bath and submerged in distilled water during OCT imaging.
4.3.2. Hippocampus imaging experiment
We imaged a hippocampal tissue block with serial sectioning using the 10x water immersion objective (Wang et al., 2018a). One volume consisting of 512 × 512 A-lines covered a field of view (FOV) of 1.5 × 1.5 mm. We imaged the tiles with 90% overlap, which resulted in each voxel measured 100 times. While it is uncommon to use such a big overlap between tiles, we intentionally performed this acquisition to obtain a high number of averages on each xy-location. Since the speckle patterns of adjacent tiles are uncorrelated, we achieved a 10 fold reduction in speckle contrast after 100 times averaging (Magnain et al., 2016), which provided a high quality reference image to compare with the proposed method. We stitched the 90% overlap tiles to reconstruct the full section of the hippocampal tissue. We also stitched the tiles with no averaging and gave this as input to the denoising methods. We used serial sectioning to cover the entire volume of the sample block (Wang et al., 2018a).
4.3.3. Cerebellum imaging experiment
We imaged the human cerebellum tissue block using the 5 × objective. One volume consisting of 450 × 450 A-lines covered a field of view (FOV) of 2.5 × 2.5 mm. We imaged the tiles with a 50% overlap (4 averages per voxel) and stitched the tiles to construct the full sample.
4.3.4. Visual cortex vessel imaging experiment
We imaged the human visual cortex tissue block used the 10 × water immersion objective. One volume consisting of 512 × 512 A-lines covered a field of view (FOV) of 1.5 × 1.5 mm. We imaged the tiles with a 50% overlap (4 averages per voxel) and stitched the tiles to construct the full sample. We additionally averaged the neighbouring voxels to a 20 μm isotropic voxel size.
5. OCT denoising analyis
We evaluated the denoising performance of the proposed method with simulations, phantom images and ex vivo human brain tissue images. This section describes parameter selection and evaluation methods and criteria.
5.1. Gamma distribution parameter fitting
We fit the gamma distribution parameters (α and β) to the images of uniform phantoms with scattering coefficients spanning from 4 mm−1 to 10 mm−1 (as described in Section 4.2). These values span typical ranges measured for gray matter and white matter tissue in the brain (Wang et al., 2017). Our fits showed that α varied between 0.99 to 1.2 and β varied between 0.78 and 1. Based on these estimates we chose an average parameter value of 1 for both parameters to remove speckles in ex vivo brain images. In our simulation we evaluated denoising performance with gamma distribution parameters covering this range, with both parameters set to 0.5, 1 and 1.5.
5.2. Simulation setup
We evaluated our method with simulations. We simulated noisy images for this experiment by generating gamma distributed speckle and multiplying it with the standard Shepp-Logan phantom image. We simulated 100 speckle realizations for three different gamma distributions with (α, β) parameters: (0.5, 0.5), (1, 1) and (1.5, 1.5). We set the maximum amplitude of the ground truth to 80 dB and speckle size to match with that observed in ex vivo brain images with 3 μm isotropic resolution. We compared the performance of the proposed MM-despeckle method with averaging, 2D median filtering, Lee-diffusion filter (Yu and Acton, 2002), wavelet filtering (Thakur and Anand, 2005; Zhang et al., 2016), optimized Bayesian NLM (OBNLM) for speckle removal (Coupé et al., 2009), BM3D applied to log transformed image (Dabov et al., 2007), BM3D for multiplicative noise used to remove speckle (SAR BM3D) (Parrilli et al., 2012) and MLE method to remove speckle with log-normal distribution assumption (Log Normal TV). We used total variation regularization for the MM-despeckle (MM-despeckle TV) and Log Normal TV method due to its ability to preserve edges well (Rudin et al., 1994):
| (13) |
where Dh and Dv are first order finite difference matrices in the horizontal and vertical direction respectively and m is the voxel index.
5.3. Simulation evaluation
We evaluated the denoising performance of all methods in our simulation using peak signal-to-noise ratio (PSNR) and compared their edge preservation capability using structural similarity index (SSIM) (Wang et al., 2003):
| (14) |
and
| (15) |
where is the ground truth reference image, is the speckle removed denoised image, is the maximum possible intensity, M is the total number of image voxels, (, ) and (, ) are the mean and standard deviation of the reference and denoised images respectively, is the covariance between reference and denoised image, and c1 and c2 are constants to stabilize the division.
PSNR and SSIM require a ground truth image for their calculation. However, ground truth is seldom known for real OCT images and reference free metrics such as contrast to noise ratio (CNR) and speckle contrast (SC) are commonly used to evaluate performance. Therefore we also calculated CNR and SC for our simulated data. Let (, ) and (, ) be the mean and standard deviation of OCT intensity in two regions of interest (ROIs). CNR and SC are defined as
| (16) |
and
| (17) |
We chose input method parameters that resulted in the highest PSNR across all 100 noisy images of the simulated speckle distributions. These parameters included: regularization parameter for MM-despeckle and Log Normal TV methods, filter size for median filtering, neighbourhood size for Lee-diffusion filtering, number of iterations for wavelet and Lee-diffusion filtering, noise variance for BM3D, kaiser window parameter and search area diameter for SAR BM3D, and smoothing parameter for OBNLM. Other parameters were set to the same values as used in the respective papers for each method.
We implemented and tested MM-despeckle and Log Normal TV on MATLAB 2018b. We used MATLAB 2018b medfilt2 and ddencmp functions for median and wavelet filtering implementation. We used MATLAB software implementations of BM3D (Dabov et al., 2007), SAR BM3D (Parrilli et al., 2012), Bayesian NLM (Coupé et al., 2009) and Lee-diffusion filter (Loizou et al., 2014) made available by authors.
5.4. Ex vivo human brain denoising analysis
We despeckled the OCT en-face images using the 2D MM-despeckle method and compared the performance with Lee-diffusion filtering and SAR BM3D methods. Lee diffusion filter and SAR BM3D were selected as they performed best amongst the filtering and data driven methods, respectively, in our simulations. We evaluated the contribution of TV regularization by additionally comparing MM-despeckle TV with Log Normal TV in the hippocampus imaging experiment (Section 5.4.1). The results in the following sections are displayed on en-face images unless otherwise stated.
5.4.1. Hippocampus denoising evaluation
We segmented the noisy hippocampal image into gray matter (GM) and white matter (WM) by thresholding a median filter corrected image. We used a 3 × 3 2D median filter that covered 9 μm in x and y directions. The voxels above a manually selected threshold were labeled as GM and those below the threshold were labeled as WM. The same thresholding process was used to mark GM and WM ROIs in the reference image. We calculated the GM-WM CNR and the average SC for GM and WM ROIs to evaluate the denoising methods.
For each denoising method we chose input parameters that resulted in the least difference in average SC between the denoised image and the reference. We then compared the CNR and the PSNR of the denoised outputs. PSNR was calculated with the 100-average image as reference. Since speckle noise is multiplicative, the ratio of the denoised image with the reference image is a good measure of intensity bias caused by the denoising methods. Ideally, we expect this ratio to be close to 1. Any deviation from that value is a measure of bias in the intensity estimates. We evaluated the intensity bias in the denoised images by calculating the ratio of the denoised image with the reference image. We then evaluated the shape and median intensity of the histogram of the ratio image to study intensity bias.
In addition, we calculated a reference-free correlation based edge preservation index (EPI) (Sattar et al., 1997) to compare the ability of the methods to preserve microstructural features. EPI was defined as the correlation between the Laplacian of the original noisy image In and the Laplacian of the denoised image Id (Sattar et al., 1997) and gives an estimate of the number of edges preserved after denoising:
| (18) |
where and Δ is the Laplacian operator. For the purpose of EPI comparison we chose another set of input parameters that resulted in the same average SC across the two ROIs for all the methods. Specifically, we tuned MM-despeckle’s regularization parameter and Lee-diffusion filter’s neighborhood size and number of iterations to match the average SC of SAR BM3D with default parameters from Parrilli et al. (2012). We matched SC to allow us to assume that the uncorrected speckle level and its contribution to the EPI metric is the same for all methods. This enables us to deduce that the EPI differences we observe originate from differences in tissue edges and not uncorrected speckle. Lastly, we also compared computation time for all methods.
5.4.2. Cerebellum denoising evaluation
We manually selected GM and WM ROIs in the cerebellum image where we expect relatively uniform intensity, and chose input parameters for all the methods that resulted in the same CNR across the two ROIs. Here too we tuned the input parameters of MM-despeckle and Lee-diffusion filter to match the CNR of SAR BM3D with default parameters from Parrilli et al. (2012). We then compared the speckle contrast in GM and WM ROIs and the computation time. In addition, we segmented the image into GM and WM by manually thresholding the SAR BM3D corrected image. The voxels above the threshold were labeled as GM and those below the threshold were labeled as WM. We compared the GM - WM CNR of all the corrected methods with the new labels.
5.4.3. Vessel preservation evaluation
The visual cortex image was acquired to segment the vessels in GM and WM. Our goal here was to compare the quality of vessel preservation post denoising. Here we chose input parameters for MM-despeckle and Lee-diffusion filter that matched in speckle contrast with SAR BM3D. Matching speckle contrast ensured that we were removing the same amount of speckle in all the three methods. We compared the quality of vessel preservation in the corrected images by visual inspection across the three methods. We calculated EPI to quantify edge preservation in each image. We also compared CNR between the GM and WM regions of the tissue.
5.5. Optical property estimation analysis
We denoised the phantom image from Section 4.2 using 1D MM-despeckle (along x-axis) with a quadratic smoothness (Tikhonov) regularization (MM-despeckle QS)
| (19) |
where matrix calculates the finite difference along the x-axis. We chose to use a smoothness based Tikhonov regularization here because the phantom is uniform with no edges. We also denoised the phantom image using 1D median (6 μm and 60 μm filter size) and 1D Lee-diffusion filter (60 μm neighborhood size). A 6 μm median filter is in the range of what is generally used to denoise microstructure images. Filter size of 60 μm are large filters that are not practical to use with human brain OCT images that have fine edges because they will blur the structure. However, for a uniform phantom we could test with larger filter sizes and give the filtering methods an advantage to learn from more voxels. We selected the MM-despeckle regularization parameter that resulted in least mean squared scattering coefficient error with ground truth coefficient. Data driven methods such as BM3D and NLM methods that are implemented for images with 2 or higher dimensions were not applicable for this phantom experiment.
We estimated pixel-wise scattering coefficients using a single scattering model based approximation method (Vermeer et al., 2014). The method approximates the scattering coefficient at a voxel with x-axis coordinate m and z-axis (depth or slice direction) coordinate z0 as
| (20) |
where is the OCT intensity at the voxel, z describes the z-axis coordinate, Z is the total number of voxels along the z-axis. We estimated the scattering coefficients for the original image without speckle reduction, median filtering result, lee-diffusion filtering result and the proposed MM-despeckle QS method results. We compared the mean percentage error of the estimated coefficient with the ground truth across all five phantoms for all the denoising methods.
6. Results
In this section we compare and analyze MM-despeckle performance for all experiments. The images presented in the human brain tissues were en-face planes at a certain depth unless otherwise stated.
6.1. Simulation results
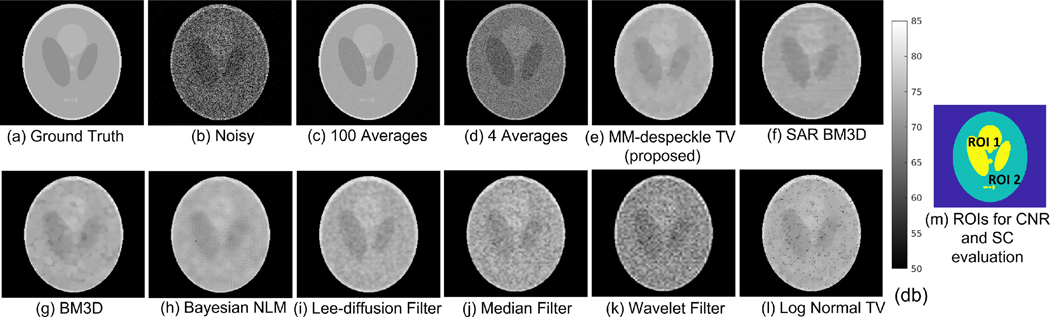
We present results of denoising simulated images that were corrupted by three different gamma distributions. Fig. 2 shows the (Fig. 2 a) ground truth phantom image, (Fig. 2 b) noisy image corrupted with gamma distributed speckle (α and β set to 0.5), (Fig. 2 c, d) average of 100 and 4 noisy images, (Fig. 2 e–l) denoised images of different algorithms with input parameters that resulted in overall highest PSNR, and (2 m) the two ROIs that were used to evaluate CNR and SC. The 100 average image removes speckle the best but requires hundred times more time to acquire in a real imaging setting making it impractical for large-scale imaging applications. The 4 average case is commonly acquired in real imaging scenarios. We observe unresolved speckle in the average using 4 images wavelet-denoised images and in the log-transform methods including BM3D, Bayesian-NLM and the Log Normal TV method. The Log Normal TV method uses the same TV regularization as MM-despeckle, but fails to correct speckle due to mismatch in the noise model. Data-driven methods (BM3D, Bayesian NLM, SAR BM3D), median filtering and wavelet filtering show ringing and edge or line artifacts in their results, while the Lee-diffusion filtering result suffers from blurring. MM-despeckle TV is able to remove speckle and denoise the image without introducing significant artifacts or resolution reduction. SAR BM3D and Lee-diffusion filter perform the best amongst the data-driven and filtering methods respectively, with the least artifacts, although still inferior to the results of MM-despeckle.
Fig. 2.
Simulation results comparing denoising performance of the proposed method with averaging, filtering methods, data driven NLM methods and other likelihood based denoising methods. The ground truth image for this example was corrupted by gamma distributed speckle noise with both parameters set to 0.5.
We confirm our qualitative observation by evaluating quantitative metrics that contribute to SNR, CNR and edge preservation (SSIM). Table 1 summarizes the mean and standard deviation values of PSNR, SSIM, CNR and SC calculated across all the denoised images. Here too the 100-average image demonstrates best PSNR, SC and SSIM. However, MM-despeckle, all the data driven methods, Lee-diffusion filter and Log Normal TV outperform the 100 average CNR. MM-despeckle TV denoising leads to the highest mean PSNR, CNR and SSIM, and the lowest SC amongst the denoised images and the 4 average image. Our current results show that TV’s edge preservation along with accurate modeling of the speckle distribution have improved all four factors. The metrics also confirm that Lee-diffusion filter and SAR BM3D outperforms other filtering and data driven methods respectively. Based on this evaluation we compare real data results with SAR BM3D, Lee-diffusion filter and Log Normal TV in later sections.
Table 1.
Mean and standard deviation values of PSNR, SSIM, CNR and SC calculated for all methods compared in the simulation. The mean and standard deviation were calculated across the results of the three gamma distributions that were simulated.
| Methods | PSNR | SSIM | CNR | SC |
|---|---|---|---|---|
| Noisy Data | 12.77 ± 0.83 | 0.05 ± 0.02 | 0.09 ± 0.02 | 1.15 ± 0.31 |
| 100 Averages | 31.83 ± 2.43 | 0.21 ± 0.01 | 0.26 ± 0.01 | 0.23 ± 0.03 |
| 4 Averages | 13.6 ± 5.00 | 0.08 ± 0.05 | 0.15 ± 0.04 | 0.61 ± 0.16 |
| MM-despeckle TV | 22.1 ± 1.97 | 0.13 ± 0.03 | 0.35 ± 0.05 | 0.33 ± 0.04 |
| SAR BM3D | 20.65 ± 4.11 | 0.13 ± 0.03 | 0.3 ± 0.03 | 0.35 ± 0.07 |
| BM3D | 20.16 ± 1.5 | 0.11 ± 0.03 | 0.32 ± 0.01 | 0.34 ± 0.05 |
| Bayes-NLM | 20.49 ± 2.08 | 0.1 ± 0.03 | 0.32 ± 0.02 | 0.34 ± 0.06 |
| Lee-diffusion filter | 21.92 ± 0.98 | 0.13 ± 0.01 | 0.32 ± 0.01 | 0.35 ± 0.03 |
| Median filter | 18.59 ± 1.6 | 0.08 ± 0.03 | 0.25 ± 0.04 | 0.48 ± 0.12 |
| Wavelet filter | 15.84 ± 0.75 | 0.05 ± 0.01 | 0.23 ± 0.05 | 0.68 ± 0.17 |
| Log Normal TV | 21.12 ± 2.17 | 0.12 ± 0.03 | 0.35 ± 0.1 | 0.35 ± 0.13 |
6.2. Hippocampus imaging results
In this section we present the results of denoising OCT images of the human hippocampus sample. We show a hippocampus OCT image slice at 145 micron depth from the surface in Fig. 3. We found the following parameters to be the best choice when matching the speckle contrast of denoised image with the reference: (i) regularization parameter of 3600 for MM-despeckle TV, (ii) regularization parameter of 2.5 for Log Normal TV, (iii) neighborhood size of 14 μm and 5 iterations for Lee-diffusion filter, and (iv) search area of 117 μm and Kaiser window parameter of 2 for SAR BM3D. These optimal values reduced to 2200 (MM-despeckle TV regularization), 0.9 (Log Normal TV regularization), 9 um (Lee-diffusion neighborhood) and 3 iterations (Lee-diffusion) when matched to SAR BM3D’s speckle contrast for EPI calculation.
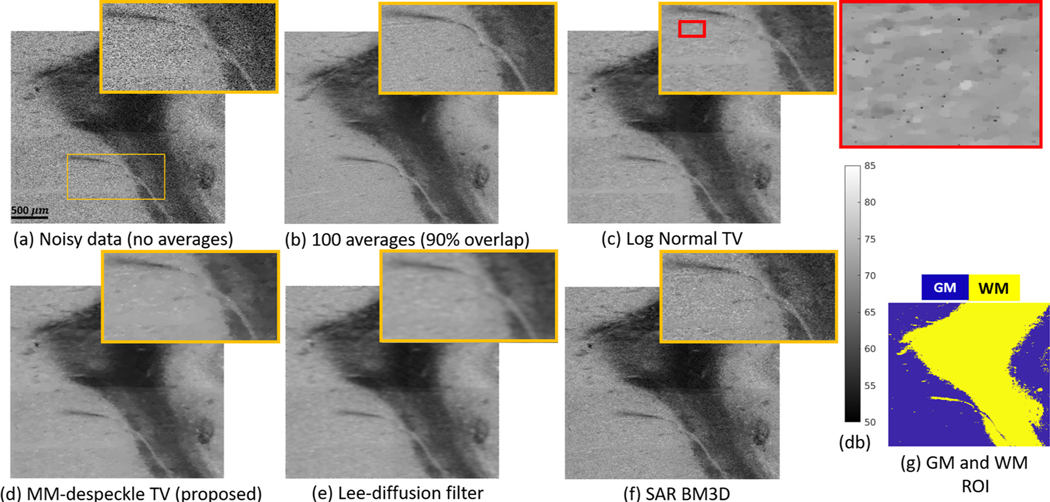
Fig. 3.
Performance of Log Normal TV, MM-despeckle TV, Lee-diffusion filter and SAR BM3D denoising methods when applied to remove speckle from human hippocampus OCT data at 2.9 μm isotropic voxel size. MM-despeckle preserves edges better that Lee-diffusion filter and reduces speckle better than Log Normal TV and SAR BM3D.
Fig. 3 a is the noisy OCT image acquired with no averages and (Fig. 3b) is the 100-average reference image.We show the result of denoising the noisy image in Fig. 3a using Log Normal TV, MM-despeckle TV, Lee-diffusion filter and SAR BM3D methods in Fig. 3c–f respectively. Fig. 3g shows the segmentation of GM and WM used for CNR calculation. We have zoomed into a region containing gray and white matter, and also containing low and high contrast edges in each of the images to qualitatively demonstrate edge preservation performance.
SAR BM3D and Log Normal TV were unable to effectively remove speckle resulting in a noisy image, while the Lee-diffusion filter blurred the edges in the image, as can be seen in the zoomed region. Log Normal TV method resulted in pepper noise that can be seen in the additional zoomed in image with red border. In contrast, the MM-despeckle TV method was able to remove speckle and preserve both low and high contrast edges.
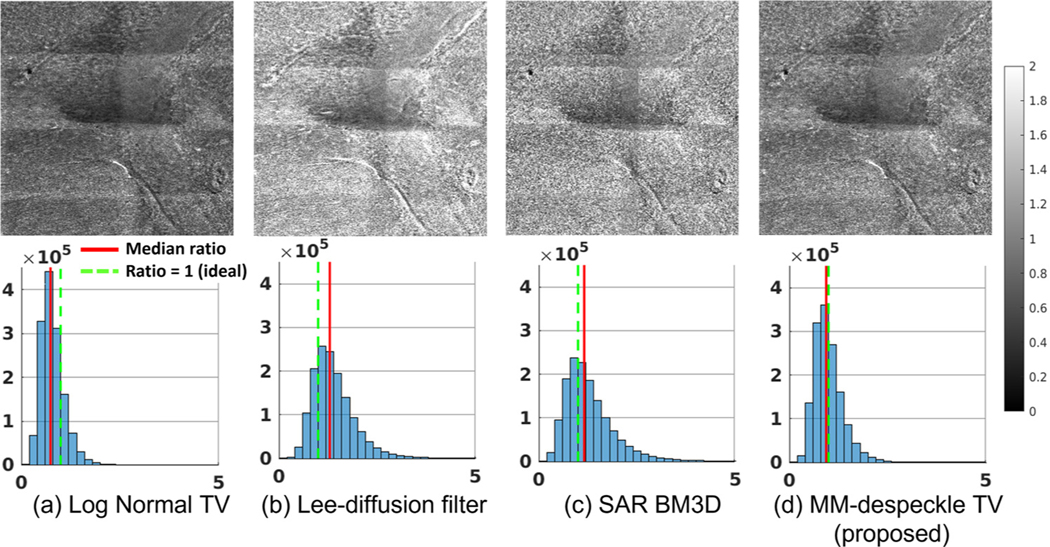
Fig. 4 shows the ratio images (top) and the associated histogram (bottom) for all the methods. The green line in the histogram marks ratio =1, when the average and denoised image intensity match, while the red line is the median of the ratio image. Prevalence of intensity bias (including reduction in dynamic range) will shift the histogram from a center value of 1. Changes in dynamic range will also be visible as an altered shape of the histogram that is deviated from a delta function at 1 (e.g. skewed or widened distribution). TV based methods lower the intensity resulting in a median value lower than 1. Lee-diffusion filter and SAR BM3D increase the intensity resulting in a median value higher than 1. The ratio image median was shifted by 26%, 30%, 15% and 7% for Log Normal TV, Lee-diffusion filter, SAR BM3D and MM-despeckle TV (proposed) respectively. MM-despeckle adds the least intensity bias compared to all methods. We also observe a larger tail in the histograms of Lee-diffusion filter and SAR BM3D suggesting altered dynamic range compared to the reference image.
Fig. 4.
Intensity bias evaluation: The images show ratio of denoised result with 100-average reference image. The red solid line is the median ratio value and green broken line is the ideal ratio = 1 line. MM-despeckle demonstrates the least intensity bias. Log Normal TV reduces the intensity while Lee-diffusion filtering and SAR BM3D increases the intensity.
Table 2 summarizes the metrics calculated to quantitatively evaluate the denoising performance of Fig. 3. SAR BM3D result had the lowest CNR and highest SC amongst the denoising methods because it was unable to remove speckle well. Lee-diffusion filter did not preserve edges well as it smoothed the images and had the lowest EPI. Log Normal TV was unable to remove all speckles resulting in higher SC and also relies more on TV resulting in smoothing of edges (i.e. low EPI) compared to MM-despeckle TV. MM-despeckle TV outperformed other methods in intensity bias, SC, edge preservation and PSNR. In addition, MM-despeckle TV along with Lee-diffusion filter and Log-Normal TV resulted in higher CNR than the reference image. Log-Normal TV demonstrates marginally higher CNR than other methods. It is important to point out that when images are smoothed then CNR and SC can increase at the cost of blurring edge structures. Thus there is a trade-off between the CNR/SC and the EPI metric. The high CNR observed in Lee-diffusion filter and Log-Normal TV filter comes at the cost of higher smoothing of edges in the images. However, MM-despeckle TV is able to retain edges better and increase CNR, demonstrating overall superior performance.
Table 2.
Quantitative metrics (CNR, SC, EPI and computation time) evaluating denoising performance of MM-despeckle TV, Lee-diffusion filter and SAR BM3D methods when applied to hippocampus image in Fig. 3.
| Methods | CNR | SC | EPI | PSNR | Time (s) |
|---|---|---|---|---|---|
| Noisy Data | 0.82 | 1.47 | - | 19.33 | - |
| 100-avg Data | 2.15 | 0.7 | - | - | - |
| MM-despeckle TV | 2.8 | 0.7 | 0.75 | 28.13 | 284.72 |
| SAR BM3D | 1.55 | 0.9 | 0.53 | 25.11 | 452.07 |
| Lee-diffusion filter | 2.77 | 0.71 | 0.08 | 27.61 | 8.53 |
| Log Normal TV | 2.92 | 0.73 | 0.62 | 26.76 | 12.76 |
Importantly, MM-despeckle TV demonstrated higher CNR and matched the SC value of the reference OCT image that took 100× longer to acquire. High CNR between tissue types, high EPI and low SC in an image facilitates tissue segmentation and analysis algorithms. Our results strongly suggest that we can reduce the overall acquisition time by using MM-despeckle TV to effectively reduce speckle and improve CNR in original no-average data, instead of acquiring multiple averages. Lastly, Lee-diffusion filtering and Log Normal TV are faster than MM-despeckle TV, followed by SAR BM3D.
6.3. Cerebellum imaging results
Fig. 5 a shows a noisy cerebellum OCT image tile at a 520 μm depth that was acquired with a 6.5 μm resolution.The two boxes in the noisy image are the two manually chosen ROIs in GM (yellow) and WM (blue) that were used to evaluate speckle contrast and to choose CNR-matched input parameters for all methods. SAR BM3D with 39 voxel (253.5 μm) search area and Kaiser window parameter of 2 resulted in a CNR of 2.85 between the GM and the WM ROI. We found MM-despeckle TV regularization of 2000 and Lee-diffusion filter neighborhood size of 32.5 μm and 5 iterations to be optimal to achieve same CNR as SAR BM3D. The cerebellum tissue had deposits of unknown cause that showed up as high intensity features in the image (an example is marked with a green arrow). Fig. 5 b–d show the denoising results for the three methods. As expected from the results, Lee-diffusion smooths the deposit leading to a blooming effect, while both MM-despeckle TVs and SAR BM3D preserve this feature well. We also observe that SAR BM3D result suffers from edge artifacts (red arrows), giving rise to spurious edges where none exist.
Fig. 5.
Denoising performance comparison in cerebellum images. We compared MM-despeckle TV, Lee-diffusion filter and SAR BM3D methods. ROIs in (a) are in locally smooth GM and WM regions, whose CNR was matched across all denoising methods. The same ROIs were used to evaluate SC. Labels in (d) were used to evaluate overall GM-WM CNR.
We evaluated denoising performance by comparing SC calculated for ROIs in Fig. 5 a, and overall GM-WM CNR using labels shown in Fig. 5 e. Table 3 summarizes our evaluation. MM-despeckle TV demonstrated the highest reduction (86%) in SC compared to other methods. MM-despeckle TV is the only method that improved the overall CNR while the other two methods reduced the CNR. We attribute the reduction in CNR in SAR BM3D to edge artifacts that lead to non-smooth intensities in otherwise locally smooth regions. The reduction in CNR in Lee-diffusion performance is likely due to excess smoothing that led to the displacement of GM into WM regions, making WM more non-uniform and bringing its mean intensity closer to GM. Blurring and edge artifacts drastically affect CNR in this dataset compared to hippocampus data (see Table 2) because the signal intensity and true GM-WM CNR is lower in the cerebellum. In addition, as the cerebellum image is from a deeper depth than the hippocampus image in Fig. 3, the SNR was also lower, making the denoising more challenging. MM-despeckle TV demonstrates better performance than SAR BM3D and Lee-diffusion filter for cerebellum denoising. We also report computation time in Table 3, where, similar to our previous results, MM-despeckle is in the middle - faster than SAR BM3D but slower than Lee-diffusion filtering.
Table 3.
Quantitative metrics (SC, CNR and computation time) evaluating denoising performance of MM-despeckle TV, Lee-diffusion filter and SAR BM3D methods when applied to cerebellum image in Fig. 5.
| Method | SC | CNR | Time (s) |
|---|---|---|---|
| Noisy Data | 0.86 | 0.14 | - |
| MM-despeckle TV | 0.12 | 0.22 | 32.97 |
| SAR BM3D | 0.13 | 0.13 | 76.75 |
| Lee-diffusion filter | 0.16 | 0.12 | 4 |
6.4. Vessel preservation results
Fig. 6 shows a noisy visual cortex image with 20 μm resolution and speckle contrast matched denoising results of the MM-despeckle TV, Lee-diffusion filter and SAR BM3D methods. The low intensity region is the WM, while the high intensity region is the cortical ribbon of the GM. Vessels show up as bright thin edges with dark end points in WM and are smaller low intensity spots in the GM. The GM vessels can be similar in size to the speckle (some are highlighted with arrows in the zoomed in image) and challenging to preserve with denoising. We evaluate how well the vessels were preserved after denoising with each of the methods. SAR BM3D with default parameters of 39 voxel (780 μm) search area and Kaiser parameter of 2 resulted in a SC value of 0.32. We found MM-despeckle TV regularization of 300 and Lee-diffusion filter neighborhood size of 60 μm and 5 iterations to be optimal to achieve same SC as SAR BM3D. Here we calculated SC in manually labeled GM and WM regions.
Fig. 6.
OCT image of vessels in the visual cortex and the corresponding denoised images for MM-despeckle TV, Lee diffusion filter and SAR BM3D methods. GM ROI is zoomed in to highlight the smallest vessels with radius of 20–40 μm and to evaluate their preservation post denoising.
In WM, the Lee-diffusion filter result is blurry, while MM-despeckle TV and SAR BM3D denoise and preserve vessels well. We highlight the GM performance in the zoomed in ROI images. The Lee-diffusion filter and SAR BM3D are unable to preserve smaller vessels that are 20 −30 μm in diameter and are blurred out in the images shown. In contrast, MM-despeckle TV denoises the GM and preserves the smaller vessels. We have also highlighted two vessels (red arrows) closer to GM-WM boundary, where thin high intensity streaks are visible. Our method is the only one that preserves such low contrast features. Overall, MM-despeckle TV demonstrated the best vessel preservation in both GM and WM.
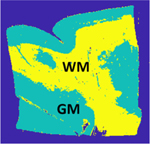
Table 4 reports the GM-WM CNR and EPI calculated for images in Fig. 6. The first column shows the GM and WM ROI in the imaged slice that was used for CNR evaluation. All images were matched to an SC value of 0.32. The CNR of all methods is similar with SAR-BM3D and Lee-diffusion filter being marginally better than MM-despeckle TV. However, in confirmation with our qualitative assessment, EPI of MM-despeckle TV is substantially higher than other methods demonstrating the best preservation of edge features such as vessels.
Table 4.
Quantitative metrics (CNR and EPI) evaluating denoising performance of MM-despeckle TV, Lee-diffusion filter and SAR BM3D methods in Fig. 6. Average speckle contrast of all three methods was matched to 0.32.
| ROI | Method | CNR | EPI |
|---|---|---|---|
|
Noisy Data | 1.39 | - |
| MM-despeckle TV | 1.5 | 0.7 | |
| SAR BM3D | 1.52 | 0.34 | |
| Lee-diffusion filter | 1.53 | 0.2 |
6.5. Scattering coefficient results in phantom
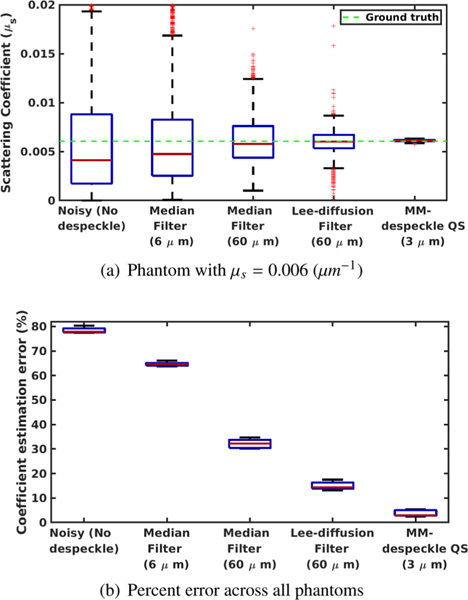
Fig. 7 compares the ground truth scattering coefficient (μs) with that estimated from phantom data. We compare estimates from four methods : (1) without speckle reduction, (2) median filtering (6 μm and 60 μm filter sizes), (3) Lee-diffusion filtering (60 μm neighborhood size) and (4) the proposed MM-despeckle QS.
Fig. 7.
Scattering coefficient estimation: We compared the accuracy of the scattering coefficient estimate of MM-despeckle QS with Tikhonov regularization, median filtering with 6μm and 60 μm filter sizes and Lee-diffusion filter with 60 μm neighborhood size, in a uniform phantom with scattering coefficient 6 mm−1 in (a). We plot the mean percent error calculated across all phantoms with different scattering coefficients in (b).
We show the comparisons for the 6 mm−1 coefficient phantom in Fig. 7 a. We mark the ground truth coefficient that was estimated from the mean of 5000 A-lines in the plot to demonstrate that the coefficient estimation method from Vermeer et al. (2014) predicts the theoretical ground truth with high accuracy. The median of the noisy estimate and the 6 μm median filter estimate suffer from a 33% and 17% error. The median of MM-despeckle QS and the 60 μm filtering methods match the ground truth well with less than 2% error. However, MM-despeckle QS outperforms the filtering methods by demonstrating a much smaller variance in the estimate. Thus, the proposed method was consistently able to estimate the coefficient for all A-lines.
Fig. 7 b. plots the mean percent error for the coefficient estimates of all five phantoms. MM-despeckle QS (2.97% median error) demonstrates an order of magnitude lower error across all phantoms compared to noisy estimate (77.85% median error), median filtering (6 μm – 64.74 % and 60 μm – 32.21 % median error) and Lee-diffusion filtering (14.32% median error). We also want to note that the filtering accuracy was higher with a 60 μm filter compared to 6 μm filter here because we are using a uniform phantom (no edges). However, such large filter sizes are unsuitable to use in biological microstructure imaging because it substantially smooths boundaries and features that are smaller than the filter size. In contrast, MM-despeckle QS smooths within a 3 μm radius and is therefore more applicable for preserving microstructure as well.
7. Discussion
In this work we proposed a new majorize-minimize-based optimization method called MM-despeckle to remove gamma distributed multiplicative speckle noise from OCT images. There are three major contributions in this work.
We provided novel theoretical insight into the non-convex structure of gamma NLL by breaking it down into a sum of a convex and a concave function. Based on this theoretical result MM-despeckle minimized the gamma P-NLL cost function by solving a series of regularized least-squares problems.
We demonstrated that MM-despeckle removes speckle and preserves microstructure in OCT images of human brain samples. This model and the proposed framework is also applicable to other OCT images contaminated by speckle noise.
We also showed that MM-despeckle results in high-quality images that are comparable to ones that would otherwise require 90 times longer acquisition time in ex vivo OCT imaging, demonstrating the potential of MM-despeckle to reduce acquisition time as well.
MM-despeckle minimizes a P-NLL based cost function that is standard for statistical estimation problems. We showed results from both total variation regularization (MM-despeckle TV) and quadratic smoothness-based spatial regularization (MM-despeckle QS). This demonstrates the flexibility of our method to integrate seamlessly with convex regularization functions relevant to speckle removal. However, care should be taken to tune the regularization parameters to the dataset being denoised because the optimum value will depend on the experimental settings such as spatial resolution and selective depth, and on the tissue being imaged. We have matched metrics like speckle contrast and CNR between methods or with a reference to select the regularization parameter for denoising tissue data. When a reference is unknown edge preservation metric like EPI could be used to find a suitable SC/CNR threshold that reduces speckle while preserving tissue structures. In addition, one could also make use of automated regularization parameter selection methods based on local variance estimators, L-curve trade-off and generalized cross-validation criteria (Dong et al., 2011; Kilmer and O’Leary, 2001)
The second input to MM-despeckle is the choice of gamma distribution parameters (α and β). In the real data experiments presented we set these parameters to 1 because that matched the fits reported in literature (Goodman, 1975) as well as those obtained by uniform phantoms with scattering coefficients spanning 4 mm−1 to 10 mm−1. We demonstrated successful denoising of gray matter and white matter tissue from multiple human brain areas using this assumption. However, prior literature has reported statistically significant differences in gamma parameters between normal and pathological tissue (Kirillin et al., 2014). This work suggests that multiple tissue types with vastly different parameters could exist where choosing a constant parameter, as we have done, might not work well. For such cases MM-despeckle could also be extended to incorporate different gamma parameters for each tissue region instead of a constant value, where the parameters can be fit to each tissue region (Kirillin et al., 2014).
Deep learning methods to remove speckle show promise in denoising OCT images. Existing methods have shown comparable and in some cases improved denoising performance compared to NLM and BM3D approaches (Huang et al., 2021; Menon et al., 2020) when applied to applied to OCT images such as those of retina and cornea. However, those methods do not utilize the speckle noise model or the OCT physics based model to denoise. It is also unclear how well they generalize to higher resolutions and ex vivo human brain OCT images. The resolution generalization is specifically interesting because we observed worse performance of data driven methods such as SAR BM3D with increasing image resolutions where the SNR is lower and microstructure intensity is more varying. We view combining optical and speckle modeling with deep learning based optimization as an interesting future direction that could benefit both accuracy and computational speed of OCT postprocessing methods. In addition, we have demonstrated that MM-despeckle generalizes well across varying tissue contrast, features and imaging resolutions. Our approach might also be useful in the future to generate training data or to compare against when testing for generalizability of deep learning methods.
We also demonstrated in our phantom experiment that denoising with MM-despeckle prior to scattering coefficient estimation improves estimation accuracy by a large margin, reducing both bias and variance of the estimates. This is a promising result because scattering coefficients are important biomarkers for disease and related to tissue properties such as myelin density. We will further perform detailed coefficient analysis on tissue images in future work to study if the improvement in accuracy is retained in images with microstructure edges.
Finally, while the examples in this paper primarily focus on OCT imaging, MM-despeckle is relevant and potentially applicable to several other applications such as RADAR, SONAR and other optical imaging modalities where gamma distribution-based speckle noise has been shown to be problematic.
Acknowledgments
Support for this research was provided in part by the BRAIN Initiative Cell Census Network grant U01MH117023 (National Institute of Mental Health), the National Institute for Biomedical Imaging and Bioengineering (P41-EB030006, P41EB015896, 1R01EB023281, R01EB006758, R21EB018907, R01EB019956, R00EB023993A, U01EB026996), the National Institute on Aging (1R56AG064027, 1R01AG064027, 5R01AG008122, R01AG016495), the National Institute of Diabetes and Digestive and Kidney Diseases (1-R21-DK-108277-01), the National Institute for Neurological Disorders and Stroke (R01NS0525851, R21NS072652, R01NS070963, R01NS083534, 5U01NS086625,5U24NS10059103, R01NS105820), Eunice Kennedy Shriver National Institute of Child Health and Human Development (R21HD106038, R01HD102616) and was made possible by the resources provided by Shared Instrumentation Grants 1S10RR023401, 1S10RR019307, and 1S10RR023043. Additional support was provided by the NIH Blueprint for Neuroscience Research (5U01-MH093765), part of the multi-institutional Human Connectome Project. In addition, BF has a financial interest in CorticoMetrics, a company whose medical pursuits focus on brain imaging and measurement technologies. BF’s interests were reviewed and are managed by Massachusetts General Hospital and Partners HealthCare in accordance with their conflict of interest policies.
Appendix
Here we derive expressions for tangent to the logarithm function, minimum of the gamma distribution majorant, the negative exponential majorant and generalized gamma distribution majorant.
Appendix A. Tangent to the logarithm part of the majorant
We define the tangent with a general equation of a straight line: , where t is the slope of the tangent and c is the y-intercept point. The slope of the tangent to at is the value of the gradient at and is calculated as
| (A.1) |
The y-intercept can be calculated by plugging in the slope and a point on the tangent into the tangent line equation and solving for c. The point (, ) can be used to find the y-intercept because it lies on the tangent and meets at . We derive the y-intercept as
| (A.2) |
| (A.3) |
| (A.4) |
| (A.5) |
The tangent equation after substituting for slope and y-intercept from Eqs. (B.1) and (B.5) is given by
| (A.6) |
Appendix B. Gamma distribution majorant minimum
We equate the partial derivative of the majorant (Eq. (8)) w.r.t xm to zero and solve for the minimum. The derivative is given by
| (B.1) |
The minimum can be calculated as
| (B.2) |
| (B.3) |
| (B.4) |
Appendix C. Negative exponential distribution (NED)
Gamma distribution reduces to the negative exponential distribution when its parameters α = β = 1,
| (C.1) |
We derive the likelihood, the P-NLL cost and the majorant for the NED distribution by substituting α = β = 1 in Eqs. (2), (7) and (8) respectively:
NED joint likelihood:
| (C.2) |
NED P-NLL cost:
| (C.3) |
where .
NED majorant:
| (C.4) |
Appendix D. Generalized Gamma distribution (GGD)
Probability density function of a generalized gamma distribution is given by,
| (D.1) |
where α and are shape parameters and β is the rate parameter. All three GGD parameters are positive: α > 0, β > 0 and . The gamma distribution is a special case of the GGD with . We derive analytical expressions of joint likelihood, P-NLL cost and majorant of GGD in the same way we solved for gamma distribution. The three quantities reduce to:
GGD joint likelihood:
| (D.2) |
| (D.3) |
GGD P-NLL cost:
| (D.4) |
where .
GGD majorant:
| (D.5) |
Footnotes
Credit authorship contribution statement
Divya Varadarajan: Methodology, Software, Writing – original draft. Caroline Magnain: Data curation, Methodology, Writing – original draft. Morgan Fogarty: Data curation. David A. Boas: Methodology, Writing – original draft. Bruce Fischl: Methodology, Writing – original draft. Hui Wang: Methodology, Writing – original draft.
References
- Akter N, Perry S, Fletcher J, Simunovic M, Roy M, 2020. Automated artifacts and noise removal from optical coherence tomography images using deep learning technique. In: 2020 IEEE Symposium Series on Computational Intelligence. SSCI 2020, pp. 2536–2542. doi: 10.1109/SSCI47803.2020.9308336. [DOI] [Google Scholar]
- Arsenault HH, April G, 1976. Properties of speckle integrated with a finite aperture and logarithmically transformed. J. Opt. Soc. Am 66 (11), 1160–1163. doi: 10.1364/JOSA.66.001160. [DOI] [Google Scholar]
- Aum J, Kim J. h., Jeong J, 2015. Effective speckle noise suppression in optical coherence tomography images using nonlocal means denoising filter with double Gaussian anisotropic kernels. Appl. Opt 54 (13), D43. [Google Scholar]
- Barrett R, Berry M, Chan TF, Demmel J, Donato J, Dongarra J, Eijkhout V, Pozo R, Romine C, van der Vorst H, 1994. Templates for the solution of linear systems: building blocks for iterative methods. Soc. Ind. Appl. Math doi: 10.1137/1.9781611971538. [DOI]
- Bashkansky M, Reintjes J, 2000. Statistics and reduction of speckle in optical coherence tomography. Opt. Lett 25 (8), 545–547. [DOI] [PubMed] [Google Scholar]
- Bernstein R, 1987. Adaptive nonlinear filters for simultaneous removal of different kinds of noise in images. IEEE Trans. Circuits Syst 34 (11), 1275–1291. [Google Scholar]
- Bioucas-Dias JM, Figueiredo MA, 2010. Multiplicative noise removal using variable splitting and constrained optimization. IEEE Trans. Image Process 19 (7), 1720–1730. doi: 10.1109/TIP.2010.2045029. [DOI] [PubMed] [Google Scholar]
- Buades A, Coll B, Morel JM, 2010. Image denoising methods. a new nonlocal principle. SIAM Rev. 52, 113–147. [Google Scholar]
- Chambolle A, Pock T, 2011. A first-order primal-dual algorithm for convex problems with applications to imaging. J. Math. Imaging Vis 40, 120–145. [Google Scholar]
- Chong B, Zhu Y-K, 2013. Speckle reduction in optical coherence tomography images of human finger skin by wavelet modified BM3D filter. Opt. Commun 291, 461–469. [Google Scholar]
- Coupé P, Hellier P, Kervrann C, Barillot C, 2009. Nonlocal means-based speckle filtering for ultrasound images. IEEE Trans. Image Process 18 (10), 2221–2229. doi: 10.1109/TIP.2009.2024064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dabov K, Foi A, Katkovnik V, Egiazarian K, 2007. Image denoising by sparse 3-{D} transform-domain collaborative filtering. IEEE Trans. Image Process 16, 2080–2095. [DOI] [PubMed] [Google Scholar]
- Desjardins AE, Vakoc BJ, Oh WY, Motaghiannezam SMR, Tearney GJ, Bouma BE, 2007. Angle-resolved optical coherence tomography with sequential angular selectivity for speckle reduction. Opt. Express 15 (10), 6200–6209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Devalla SK, Subramanian G, Pham TH, Wang X, Perera S, Tun TA, Aung T, Schmetterer L, Thiéry AH, Girard MJ, 2019. A deep learning approach to denoise optical coherence tomography images of the optic nerve head. Sci. Rep 9 (1), 1–13. doi: 10.1038/s41598-019-51062-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dong Y, Hintermüller M, Rincon-Camacho MM, 2011. Automated regularization parameter selection in multi-scale total variation models for image restoration. J. Math. Imaging Vis 40 (1), 82–104. doi: 10.1007/s10851-010-0248-9. [DOI] [Google Scholar]
- Fang L, Li S, Nie Q, Izatt JA, Toth CA, Farsiu S, 2012. Sparsity based denoising of spectral domain optical coherence tomography images. Biomed. Opt. Express 3 (5), 927–942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farhat G, Czarnota GJ, Kolios MC, Yang VXD, 2011. Detecting cell death with optical coherence tomography and envelope statistics. J. Biomed. Opt 16 (2), 26017. [DOI] [PubMed] [Google Scholar]
- Feng W, Lei H, Gao Y, 2014. Speckle reduction via higher order total variation approach. IEEE Trans. Image Process 23 (4), 1831–1843. [DOI] [PubMed] [Google Scholar]
- Fischl B, Schwartz EL, 1999. Adaptive nonlocal filtering: a fast alternative to anisotropic diffusion for image enhancement. IEEE Trans. Pattern Anal. Mach. Intell 21 (1), 42–48. [Google Scholar]
- Frost VS, Stiles JA, Shanmugan KS, Holtzman JC, 1982. A model for radar images and its application to adaptive digital filtering of multiplicative noise. IEEE Trans. Pattern Anal. Mach. Intell PAMI-4 (2), 157–166. doi: 10.1109/TPAMI.1982.4767223. [DOI] [PubMed] [Google Scholar]
- Gong G, Zhang H, Yao M, 2015. Speckle noise reduction algorithm with total variation regularization in optical coherence tomography. Opt. Express 23 (19), 24699–24712. [DOI] [PubMed] [Google Scholar]
- Goodman JW, 1975. Statistical properties of laser speckle patterns. In: Dainty JC (Ed.), Laser Speckle and Related Phenomena, pp. 9–75. [Google Scholar]
- Goodman JW, 1976. Some fundamental properties of speckle ∗. J. Opt. Soc. Am 66 (11), 1145–1150. [Google Scholar]
- Goodman JW, 1985. Statistical Optics. Wiley Series in Pure and Applied Optics. Wiley, New York. [Google Scholar]
- Huang Y, Zhang N, Hao Q, 2021. Real-time noise reduction based on ground truth free deep learning for optical coherence tomography. Biomed. Opt. Express 12 (4), 2027–2040. doi: 10.1364/boe.419584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hunter DR, Lange K, 2004. A Tutorial on {MM} Algorithms. Am. Stat 58, 30–37. [Google Scholar]
- Izatt JA, Choma MA, Dhalla AH, 2015. Theory of optical coherence tomography. In: Optical Coherence Tomography: Technology and Applications, Second Edition. Springer International Publishing, pp. 65–94. [Google Scholar]
- Jesus DA, Iskander DR, 2017. Assessment of corneal properties based on statistical modeling of OCT speckle. Biomed. Opt. Express 8 (1), 162–176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karamata B, Hassler K, Laubscher M, Lasser T, 2005. Speckle statistics in optical coherence tomography. J. Opt. Soc. Am. A 22 (4), 593–596. doi: 10.1364/JOSAA.22.000593. [DOI] [PubMed] [Google Scholar]
- Kilmer ME, O’Leary DP, 2001. Choosing regularization parameters in iterative methods for ill-posed problems. SIAM J. Matrix Anal. Appl 22 (4), 1204–1221. [Google Scholar]
- Kirillin MY, Farhat G, Sergeeva EA, Kolios MC, Vitkin A, 2014. Speckle statistics in OCT images: Monte Carlo simulations and experimental studies. Opt. Lett 39 (12), 3472. doi: 10.1364/ol.39.003472. [DOI] [PubMed] [Google Scholar]
- Krull A, Buchholz T-O, Jug F, 2018. Noise2Void - learning denoising from single noisy images. In: Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2019-June, pp. 2124–2132. [Google Scholar]
- Lee J-S, 1980. Digital image enhancement and noise filtering by use of local statistics. IEEE Trans. Pattern Anal. Mach. Intell PAMI-2 (2), 165–168. [DOI] [PubMed] [Google Scholar]
- de Leeuw J, Heiser WJ, 1977. Convergence of correction matrix algorithms for multidimensional scaling. In: Lingoes J. (Ed.), Geometric Representations of Relational Data. Mathesis Press, Ann Arbor, Michigan, pp. 735–753. [Google Scholar]
- Lehtinen J, Munkberg J, Hasselgren J, Laine S, Karras T, Aittala M, Aila T, 2018. Noise2Noise: learning image restoration without clean data. In: 35th International Conference on Machine Learning, vol. 7. ICML 2018, pp. 4620–4631. [Google Scholar]
- Lim JS, Nawab H, 1981. Techniques for speckle noise removal. Opt. Eng 20 (3), 472–480. doi: 10.1117/12.7972744. [DOI] [Google Scholar]
- Lindenmaier AA, Conroy L, Farhat G, DaCosta RS, Flueraru C, Vitkin IA, 2013. Texture analysis of optical coherence tomography speckle for characterizing biological tissues in vivo. Opt. Lett 38 (8), 1280. doi: 10.1364/ol.38.001280. [DOI] [PubMed] [Google Scholar]
- Loizou CP, Theofanous C, Pantziaris M, Kasparis T, 2014. Despeckle filtering software toolbox for ultrasound imaging of the common carotid artery. Comput. Methods Programs Biomed 114 (1), 109–124. doi: 10.1016/j.cmpb.2014.01.018. [DOI] [PubMed] [Google Scholar]
- Magnain C, Augustinack JC, Konukoglu E, Boas D, Fischl B, 2015. Visualization of the cytoarchitecture of ex vivo human brain by optical coherence tomography. In: Optics in the Life Sciences, p. BrT4B.5. [Google Scholar]
- Magnain C, Augustinack JC, Konukoglu E, Frosch MP, Sakadzic S, Varjabedian A, Garcia N, Wedeen VJ, Boas DA, Fischl B, 2015. Optical coherence tomography visualizes neurons in human entorhinal cortex. Neurophotonics 2 (1), 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magnain C, Augustinack JC, Reuter M, Wachinger C, Frosch MP, Ragan T, Akkin T, Wedeen VJ, Boas DA, Fischl B, 2014. Blockface histology with optical coherence tomography: a comparison with Nissl staining. Neuroimage 84, 524–533. doi: 10.1016/j.neuroimage.2013.08.072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magnain C, Wang H, Sakad ž i ć S, Fischl B, Boas DA, 2016. En face speckle reduction in optical coherence microscopy by frequency compounding. Opt. Lett 41 (9), 1925–1928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Manen L, Dijkstra J, Boccara C, Benoit E, Vahrmeijer AL, Gora MJ, Mieog JSD, 2018. The clinical usefulness of optical coherence tomography during cancer interventions. J. Cancer Res. Clin. Oncol 144 (10), 1967–1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mao Z, Miki A, Mei S, Dong Y, Maruyama K, Kawasaki R, Usui S, Matsushita K, Nishida K, Chan K, 2019. Deep learning based noise reduction method for automatic 3D segmentation of the anterior of lamina cribrosa in optical coherence tomography volumetric scans. Biomed. Opt. Express 10 (11), 5832–5851. doi: 10.1364/boe.10.005832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mayer MA, Borsdorf A, Wagner M, Hornegger J, Mardin CY, Tornow RP, 2012. Wavelet denoising of multiframe optical coherence tomography data. Biomed. Opt. Express 3 (3), 572–589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Menon SN, Vineeth Reddy VB, Yeshwanth A, Anoop BN, Rajan J, 2020. A novel deep learning approach for the removal of speckle noise from optical coherence tomography images using gated convolution–deconvolution structure. In: Advances in Intelligent Systems and Computing, Vol. 1024, pp. 115–126. [Google Scholar]
- Parrilli S, Poderico M, Angelino CV, Verdoliva L, 2012. A nonlocal SAR image denoising algorithm based on LLMMSE wavelet shrinkage. IEEE Trans. Geosci. Remote Sens 50 (2), 606–616. doi: 10.1109/TGRS.2011.2161586. [DOI] [Google Scholar]
- Pircher M, Gotzinger E, Leitgeb RA, Fercher AF, Hitzenberger CK, 2003. Speckle reduction in optical coherence tomography by frequency compounding. J. Biomed. Opt 8 (3), 565–569. doi: 10.1117/1.1578087. [DOI] [PubMed] [Google Scholar]
- Qiu B, Huang Z, Liu X, Meng X, You Y, Liu G, Yang K, Maier A, Ren Q, Lu Y, 2020. Noise reduction in optical coherence tomography images using a deep neural network with perceptually-sensitive loss function. Biomed. Opt. Express 11 (2), 817–830. doi: 10.1364/boe.379551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raju BI, Srinivasan MA, 2002. Statistics of envelope of high-frequency ultrasonic backscatter from human skin in vivo. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 49 (7), 871–882. [DOI] [PubMed] [Google Scholar]
- Ramos-Llordén G, Vegas-Sánchez-Ferrero G, Martin-Fernandez M, Alberola-López C, Aja-Fernández S, 2015. Anisotropic diffusion filter with memory based on speckle statistics for ultrasound images. IEEE Trans. Image Process 24 (1), 345–358. doi: 10.1109/TIP.2014.2371244. [DOI] [PubMed] [Google Scholar]
- Rudin LI, Osher S, Fatemi E, 1994. Nonlinear total variation based noise removal algorithms. Physica D 60, 677–686. [Google Scholar]
- Salinas HM, Fernandez DC, 2007. Comparison of PDE-based nonlinear diffusion approaches for image enhancement and denoising in optical coherence tomography. IEEE Trans. Med. Imaging 26 (6), 761–771. [DOI] [PubMed] [Google Scholar]
- Sattar F, Floreby L, Salomonsson G, Lövström B, 1997. Image enhancement based on a nonlinear multiscale method. IEEE Trans. Image Process 6 (6), 888–895. doi: 10.1109/83.585239. [DOI] [PubMed] [Google Scholar]
- Schmitt JM, Xiang SH, Yung KM, 1999. Speckle in optical coherence tomography. J. Biomed. Opt 4 (1), 95. doi: 10.1117/1.429925. [DOI] [PubMed] [Google Scholar]
- Thakur A, Anand RS, 2005. Image quality based comparative evaluation of wavelet filters in ultrasound speckle reduction. Digit. Signal Process 15 (5), 455–465. doi: 10.1016/j.dsp.2005.01.002. [DOI] [Google Scholar]
- Tur M, Chin KC, Goodman JW, 1982. When is speckle noise multiplicative? Appl. Opt 21 (7), 1157. doi: 10.1364/ao.21.001157. [DOI] [PubMed] [Google Scholar]
- Vermeer KA, Mo J, Weda JJA, Lemij HG, de Boer JF, 2014. Depth-resolved model-based reconstruction of attenuation coefficients in optical coherence tomography. Biomed. Opt. Express 5 (1), 322–337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang H, Magnain C, Sakadzic S, Fischl B, Boas DA, 2017. Characterizing the optical properties of human brain tissue with high numerical aperture optical coherence tomography. Biomed. Opt. Express 8 (12), 5617–5636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang H, Magnain C, Wang R, Dubb J, Varjabedian A, Tirrell LS, Stevens A, Augustinack JC, Konukoglu E, Aganj I, Frosch MP, Schmahmann JD, Fischl B, Boas DA, 2018. as-PSOCT: volumetric microscopic imaging of human brain architecture and connectivity. Neuroimage 165, 56–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang S, Huang T-Z, Zhao X-L, Mei J-J, Huang J, 2018. Speckle noise removal in ultrasound images by first- and second-order total variation. Numer. Algorithms 78 (2), 513–533. [Google Scholar]
- Wang Z, Simoncelli EP, Bovik AC, 2003. Multi-scale structural similarity for image quality assessment. In: Conference Record of the Asilomar Conference on Signals, Systems and Computers, Vol. 2, pp. 1398–1402. doi: 10.1109/acssc.2003.1292216. [DOI] [Google Scholar]
- Wong A, Mishra A, Bizheva K, Clausi DA, 2010. General Bayesian estimation for speckle noise reduction in optical coherence tomography retinal imagery. Opt. Express 18 (8), 8338–8352. doi: 10.1364/OE.18.008338. [DOI] [PubMed] [Google Scholar]
- Xie H, Pierce LE, Ulaby FT, 2002. Statistical properties of logarithmically transformed speckle. IEEE Trans. Geosci. Remote Sens 40 (3), 721–727. [Google Scholar]
- Yin D, Gu Y, Xue P, 2013. Speckle-constrained variational methods for image restoration in optical coherence tomography. J. Opt. Soc. Am. A 30 (5), 878–885. doi: 10.1364/JOSAA.30.000878. [DOI] [PubMed] [Google Scholar]
- Yu H, Gao J, Li A, 2016. Probability-based non-local means filter for speckle noise suppression in optical coherence tomography images. Opt. Lett 41 (5), 994. doi: 10.1364/ol.41.000994. [DOI] [PubMed] [Google Scholar]
- Yu Y, Acton ST, 2002. Speckle reducing anisotropic diffusion. IEEE Trans. Image Process 11 (11), 1260–1270. doi: 10.1109/TIP.2002.804276. [DOI] [PubMed] [Google Scholar]
- Zaki F, Wang Y, Su H, Yuan X, Liu X, 2017. Noise adaptive wavelet thresholding for speckle noise removal in optical coherence tomography. Biomed. Opt. Express 8 (5), 2720–2731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang J, Lin G, Wu L, Cheng Y, 2016. Speckle filtering of medical ultrasonic images using wavelet and guided filter. Ultrasonics 65, 177–193. doi: 10.1016/j.ultras.2015.10.005. [DOI] [PubMed] [Google Scholar]
- Zhou Q, Guo J, Ding M, Zhang X, 2020. Guided filtering-based nonlocal means despeckling of optical coherence tomography images. Opt. Lett 45 (19), 5600. doi: 10.1364/ol.400926. [DOI] [PubMed] [Google Scholar]
- Zysk AM, Nguyen FT, Oldenburg AL, Marks DL, Boppart SA, 2007. Optical coherence tomography: a review of clinical development from bench to bedside. J. Biomed. Opt 12 (5), 51403–514021. [DOI] [PubMed] [Google Scholar]