SAGE: SLAM with Appearance and Geometry Prior for Endoscopy

Abstract

In endoscopy, many applications (e.g., surgical navigation) would benefit from a real-time method that can simultaneously track the endoscope and reconstruct the dense 3D geometry of the observed anatomy from a monocular endoscopic video. To this end, we develop a Simultaneous Localization and Mapping system by combining the learning-based appearance and optimizable geometry priors and factor graph optimization. The appearance and geometry priors are explicitly learned in an end-to-end differentiable training pipeline to master the task of pair-wise image alignment, one of the core components of the SLAM system. In our experiments, the proposed SLAM system is shown to robustly handle the challenges of texture scarceness and illumination variation that are commonly seen in endoscopy. The system generalizes well to unseen endoscopes and subjects and performs favorably compared with a state-of-the-art feature-based SLAM system. The code repository is available at https://github.com/lppllppl920/SAGE-SLAM.git.

I. Introduction

Endoscopy is a technique allowing inspection, manipulation, and treatment of internal organs using devices from a distance of the target organs without a large incision. Nowadays, the quality of an endoscopic procedure is directly related to the attitude and level of skills of the person who drives the endoscope [1]. When inspection or surgeries are performed, there is a risk of iatrogenic perforations [2]. In cases where critical structures below the surface get damaged, the consequence can be detrimental. One of these is endoscopic endonasal surgery (ESS), which requires a thorough knowledge of anatomy, in particular, the relationship of the nose and sinuses to adjacent vulnerable structures such as the orbit or base of the skull. However, malformations, previous operations, and massive polyposis may interfere greatly with the intra-operative orientation of surgeons and this leads to major risks, such as loss of vision, diplopia, injury to the carotid artery, etc., for patients [3]. Having a surgical navigation system that tracks the endoscope and shows the spatial relationship between the scope and the surrounding anatomy can greatly reduce the risk.

Many marker-based navigation systems have been developed and commercialized to provide such information. Nevertheless, visual-based navigation systems have been preferred compared to marker-based ones because the former do not interrupt the clinical workflow and is robust to the relative movement between the observed anatomy and the patient. One critical component of such a system is to track the endoscope and estimate the geometry of the observed anatomy from a video stream. The surface geometry from a video can be aligned with a pre-operative model, e.g., one from Computed Tomography (CT), with a registration method. The spatial relationship between the endoscope and the surrounding structures will then be known. A typical choice for endoscope tracking is a Simultaneous Localization and Mapping (SLAM) system. Many systems [4]–[6] only provide sparse geometry, which mainly serves as a map to track the endoscope but is not sufficient to register against the pre-operative model and also not useful for other clinical applications (e.g., anatomical shape analysis). The accuracy and robustness of such systems are also limited in endoscopy because of the scarce textures that lead to less repeatable keypoint detections across frames. For previous works that estimate dense geometry [7], the accuracy of the estimated surface models is not evaluated and the generalizability of such a system on unseen subjects is unknown.

In this work, to robustly track the endoscope and obtain accurate surface geometry of the observed anatomy with a monocular endoscope, we develop a SLAM system that combines the expressivity of deep learning and the rigorousness of non-linear optimization. Specifically, we exploit learning-based appearance and optimizable geometry priors and factor graph optimization. Based on our evaluation, the proposed SLAM system generalizes well to unseen endoscopes and subjects and performs favorably compared with a state-of-the-art feature-based SLAM system [8]. The contributions of this work are as follows: 1) A SLAM system with learning-based appearance and geometry priors for monocular endoscopy. 2) An end-to-end training pipeline to explicitly learn the appearance and geometry priors that are suitable for handling the task of pair-wise image alignment.

II. Related Work

A. Representation Learning for Visual Tracking and Mapping

In recent years, researchers have worked on exploiting prior information learned from data to improve the performance of SLAM and Visual Odometry (VO). Different forms of depth priors have been used, such as fixed depth estimate [7], [9], [10], self-improving depth estimate [11], depth estimate with uncertainty [12], and depth estimate with optimizable code [13]–[15]. Appearance priors have been studied to replace the role of color images in vision-based methods, which enlarges the convergence basin of optimization and enables scenarios with no photometric constancy. BA-Net [14] proposed representation learning with differentiable BA-related loss. DeepSFM [16] extracted implicit representation with joint depth and pose estimation. In this work, we integrate both appearance and optimizable depth priors into the SLAM system. There are also works exploiting other forms of priors for the VO and SLAM systems. For example, Yang et al. [12] exploit a pose prior to enable better convergence and mitigate the scale-drift issue; Zhan et al. [17] estimate dense optical flow to gain more robustness towards camera tracking.

B. Simultaneous Localization and Mapping in Endoscopy

Many SLAM systems have been developed for the general scene [8], [9], [11], [13], [15], [18]–[25]. In endoscopy, additional challenges exist compared with other scenarios such as driving scenes, which are illumination changes, scarce textures, deformation, etc. Feature-based SLAM [4], [5], [26] has been developed for its robustness to illumination changes. To deal with the scarce texture that causes inaccurate estimates, works have been proposed using either hardware [27] or algorithmic [7], [28], [29] solutions. Deformation happens in endoscopy, especially in certain cases such as laparoscopy and when surgical operations are applied, and there are works developed to confront this challenge [23], [30]–[32]. In this work, we exploit deep priors and dense geometry to improve the robustness of the system to illumination changes and scarce texture.

III. Representation Learning

A. Network Architecture

Two separate networks are used to learn geometry and appearance representations, respectively. In terms of geometry, a depth network produces an average depth estimate, which is correct up to a global scale, and depth bases. The average depth estimate captures the expectation of the depth estimate based on the input color image. However, the task of depth estimation from a single image is ill-posed and therefore errors are expected. The depth bases consist of a set of depth variations that could be used to explain the variation of geometry given the appearance of the input. Such bases provide a way to further refine the depth estimate, with additional information, during the SLAM optimization. The network is close to UNet [33] with partial convolution [34], where an endoscope mask is used so that blank regions do not contribute to the final output. There are two output branches, where one, with absolute as output activation, predicts the average depth estimate, and the other produces depth bases with hyperbolic tangent as output activation. Please refer to the code repository for the architecture of the depth network used for depth training.

In terms of appearance, a feature network produces two sets of representations. One set, named descriptor map, is used as descriptors in pair-wise feature matching that are involved in the Reprojection Factor and Sparse Matched Geometry Factor, described in Sec. IV-B. A similar training approach as [29] is used. The other set, named feature map, is used for the computation of the Feature-metric Factor as a drop-in replacement of the color image. This is because, in the image, the illumination of the same location of the scene changes as the viewpoint varies, which is caused by the lighting source moving with the camera. On the other hand, feature maps can be robust to illumination and viewpoint changes, if the feature network is trained correspondingly. In this work, we use the task of pair-wise image alignment with differentiable non-linear optimization to train both the appearance and geometry representations, with more details in Sec. III-D. The network architecture for the feature network is the same as the depth network, except for the two output branches. The sizes of channel dimension for the three layers in both the descriptor map and feature map output branches (from hidden to output) are 64, 64, and 16; the output activation functions are both hyperbolic tangent.

B. Differentiable Optimization

To make the networks learn to master the task of pairwise image alignment, a differentiable non-linear optimization method is required. In this work, we use Levenberg-Marquardt (LM) algorithm as the optimization solver. LM is a trust-region algorithm to find a minimum of a function over a space of parameters. The design is based on Tang et al. [14], with modifications to increase memory and computation efficiency. In the computation graph of network training, all accepted steps in the optimization process are connected, while the decision stage and rejected steps in LM are not involved. We apply gradient checkpoint technique [35] to largely increase the allowed number of accepted steps in the graph.

C. Loss Design

For each iteration, when the LM optimization converges, several outputs before, during, and after the optimization process will be involved in the loss computation for the network training. The groundtruth data required for training are relative camera pose, camera intrinsics, binary video mask to indicate valid region, dense depth map, and dense 2D scene flow map that can be generated with the data before. The average and the optimized depth estimate should agree with the groundtruth depth map up to a global scale. We do not let the depth network try to predict the correct scale and instead leave it to the optimization during SLAM running because predicting a correct depth scale from a monocular endoscopic image is nearly impossible. Therefore, a scale-invariant loss is used for this objective. With a predicted depth map $\mathit{D}\in {ℝ}^{1\times H\times W}$, the corresponding groundtruth depth map $\tilde{\mathit{D}}\in {ℝ}^{1\times H\times W}$, and the binary video mask $\mathit{V}\in {ℝ}^{1\times H\times W}$, the loss is defined as

$${ℒ}_{\text{si}}=\frac{\sum {\mathit{D}}_{\text{ratio}}^2}{\sum \mathit{V}}+\frac{{\left(\sum {\mathit{D}}_{\text{ratio}}\right)}^2}{{\left(\sum \mathit{V}\right)}^2},$$ (1)

where ${\mathit{D}}_{\text{ratio}}=\log (\mathit{V}\mathit{D}+ϵ)-\log (\mathit{V}\tilde{\mathit{D}}+ϵ)$. $ϵ\in ℝ$ is a small number to prevent logarithm over zero. To guide the intermediate depth maps during optimization, we additionally use an adversarial loss [36]. In this loss, a discriminator is used to distinguish real samples from fake ones. The real sample for the GAN will be a color image and the corresponding normalized groundtruth depth map; the fake sample will be the color image and the corresponding normalized depth estimate. For normalization, these depth maps are divided by their maximum value so that the discriminator judges the fidelity of the sample pair based only on the relative geometry and not on the scale.

For the descriptor map, the RR loss proposed in [29] is used. Because a descriptor map is also used for loop closure detection, besides producing good feature matches on images with large scene overlap, having dissimilar descriptions for images with small or no scene overlap is also desired. A triplet histogram loss is used to make sure the similarity between histograms of descriptor maps for the source and target images is higher than that for the source and far images. The definitions of these three images are in Sec. III-D. The triplet histogram loss is defined as

$$\begin{gathered} {ℒ}_{\text{hist}}=\frac{1}{C}\sum _{i\in \{1,\dots ,C\}}\min (\frac{1}{K}{d}_{\text{EMD}}\left({\mathit{h}}_i^{\text{src}},{\mathit{h}}_i^{\text{tgt}}\right)- \\ \frac{1}{K}{d}_{\text{EMD}}\left({\mathit{h}}_i^{\text{src}},{\mathit{h}}_i^{\text{far}}\right)+{\eta }_{\text{hist}},0)\text{, } \end{gathered}$$ (2)

where $d_{\text{EMD}}\left({\mathit{h}}_1,{\mathit{h}}_2\right)={‖\mathrm{CDF}\left({\mathit{h}}_1\right)-\mathrm{CDF}\left({\mathit{h}}_2\right)‖}_2^2$ measures the earth mover’s distance between two histograms. CDF is the operation to produce cumulative density function (CDF) from a histogram. ${\mathit{h}}_i^{\text{src}}\in {ℝ}^K$ is the soft histogram of elements from source descriptor map ${\mathit{I}}^{\text{src}}\in {ℝ}^{C\times H\times W}$ along the i^th channel, which is ${\mathit{I}}_i^{\text{src}}\in {ℝ}^{1\times H\times W}$; K is the number of bins in each CDF and C is the channel size of the descriptor map; ${\eta }_{\text{hist}}\in ℝ$ is a constant margin. To compute the CDF differentiably, we refer to the method in [37] and describe it in the code repository.

After the optimization process in Sec. III-B, the source image should be warped to the target frame with good alignment, using the estimate of status. Such a warping process can be described with a 2D scene flow. Therefore, to guide the learning process to produce better image alignment, another loss is to encourage the similarity between the groundtruth 2D scene flow, and the one estimated from the optimization process. The flow loss is defines as

$${ℒ}_{\text{flow}}=\frac{1}{{\omega }^{\text{s}\to \text{t}}\sum \mathit{V}}\sum \mathit{V}{\left({\tilde{\mathit{W}}}^{\text{s}\to \text{t}}-{\mathit{W}}^{\text{s}\to \text{t}}\right)}^2,$$ (3)

where ${\tilde{\mathit{W}}}^{\text{s}\to \text{t}}\in {ℝ}^{2\times H\times W}$ and ${\mathit{W}}^{\text{s}\to \text{t}}\in {ℝ}^{2\times H\times W}$ are the groundtruth and estimated 2D scene flows from source to target frame, respectively. ${\omega }^{\text{s}\to \text{t}}\in ℝ$ is a normalization factor, defined as ${\omega }^{\text{s}\to \text{t}}=\frac{1}{2}\sum \mathit{V}\left({\left({\tilde{\mathit{W}}}^{\text{s}\to \text{t}}\right)}^2+{\left({\mathit{W}}^{\text{s}\to \text{t}}\right)}^2\right)$. The estimated flow ${\mathit{W}}^{\text{s}\to \text{t}}$ at 2D location x^src is defined as

$${\mathit{W}}^{\text{s}\to \text{t}}\left({\mathit{x}}^{\text{src}}\right)=\pi \left({\mathit{p}}^{\text{s}\to \text{t}}\right)-{\mathit{x}}^{\text{src}}\text{, where}$$ (4)

$${\mathit{p}}^{\text{s}\to \text{t}}=T_{\text{src}}^{\text{tgt}}{\pi }^{-1}\left({\mathit{x}}^{\text{src}},{\mathit{D}}^{\text{src}}\left({\mathit{x}}^{\text{src}}\right)\right).$$ (5)

${\mathit{p}}^{\text{s}\to \text{t}}\in {ℝ}^3$ is the 3D location of the lifted source 2D location ${\mathit{x}}^{\text{src}}\in {ℝ}^2$ in the target coordinate system. π and π⁻¹ are the project and unproject operation of the camera geometry. These two operations are the same for all keyframes because camera intrinsics are assumed to be fixed throughout the video. ${\mathit{T}}_{\text{src}}^{\text{tgt}}={\left({\mathit{T}}_{\text{tgt}}^{\text{wld}}\right)}^{-1}{\mathit{T}}_{\text{src}}^{\text{wld}}$ is the relative pose between target and source. ${\mathit{D}}^{\mathrm{src}}\left({\mathit{x}}^{\text{src}}\right)\in ℝ$ is the depth estimate at 2D location x^src based on the current estimate of depth scale and depth code. It is defined as ${\mathit{D}}^{\text{src}}\left({\mathit{x}}^{\text{src}}\right)=s^{\text{src}}\left({\overline{\mathit{D}}}^{\text{src}}\left({\mathit{x}}^{\text{src}}\right)+{\left({\mathit{c}}^{\text{src}}\right)}^{\mathbf{\top }}{\widehat{\mathit{D}}}^{\text{src}}\left({\mathit{x}}^{\text{src}}\right)\right)$. The source average depth estimate and depth bases are ${\overline{\mathit{D}}}^{\text{src}}\in {ℝ}^{1\times H\times W}$ and ${\widehat{\mathit{D}}}^{\text{src}}\in {ℝ}^{B\times H\times W}$. the source depth scale, depth code, and camera pose matrix are $s^{\text{src}}\in ℝ$, ${\mathit{c}}^{\text{src}}\in {ℝ}^B$, and ${\mathit{T}}_{\text{src}}^{\text{wld}}\in \text{SE}$ (3), respectively.

D. Training Procedure

In each iteration, three images are used for training, which are the source, target, and far images. Source and target are two images with a large scene overlap, while the far image has a small or no scene overlap with the source. The network training consists of two stages. At the first stage, the depth and feature networks are trained separately with the scale-invariant loss and RR loss, respectively. After both networks are trained to a reasonable state, the training moves to the second stage, where the networks are jointly trained with the scheme below. The task for training becomes pair-wise image alignment which can be handled well only if networks produce good representations. The variables that are optimized over are relative camera pose, depth scale, and depth code of the source image. And the factors involved are pair-wise factors, FM, SMG, and GC, and prior factors, SC and CD, which are introduced in Sec. IV-B. A random relative camera pose and all-zero depth code are initialized. The source depth scale is computed to match the scale of the target depth map.

The optimization in Sec. III-B is then applied to minimize the objective described by the factors and the networks are updated afterward with the losses described in Sec. III-C. A GAN training cycle [36] is also involved because of the adversarial loss.

IV. Simultaneous Localization and Mapping

A. Overview

The SLAM system modules are organized into frontend and backend threads. Frontend consists of Camera Tracking and Keyframe Creation modules. When a new frame comes in, the Camera Tracking is used to track it against a reference keyframe. The Keyframe Creation module then handles keyframe creation and temporal keyframe connection. For each keyframe, a bag-of-words vector is created for global loop detection in the Loop Closure module. Backend threads run Loop Closure and Mapping modules. The Loop Closure module constantly detects both local and global connections between all keyframe pairs. Whenever a global connection is detected, a lightweight pose-scale graph optimization will be applied to close the loop by adjusting depth scales and camera poses of all keyframes. The Mapping module constantly optimizes all depth codes, depth scales, and camera poses with factors described in Sec. IV-B. The overall diagram of the SLAM system is shown in Fig. 1.

Fig. 1: Overall diagram of SLAM system.

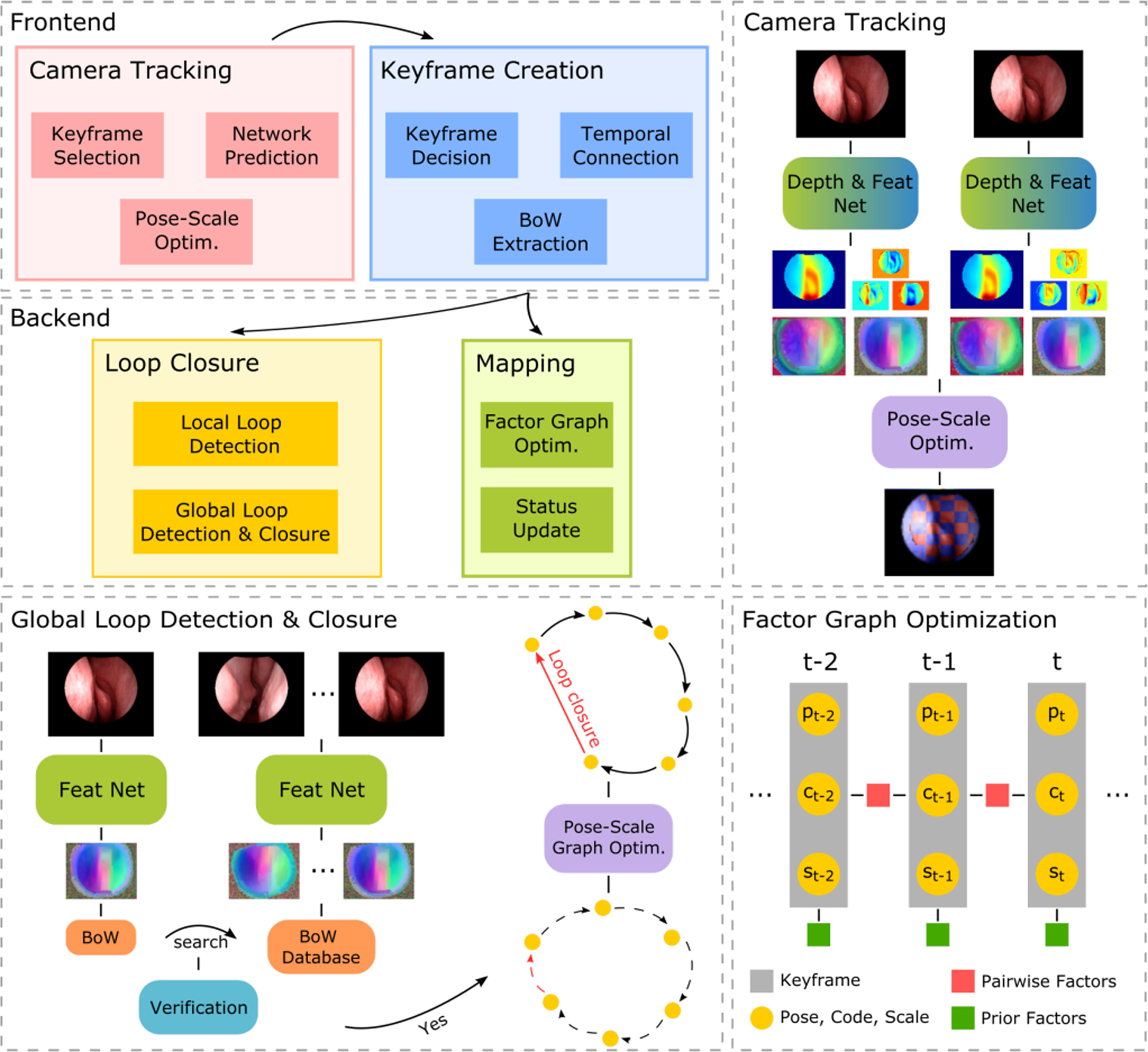
The top left shows the module relationship in our SLAM system. The top right demonstrates the network prediction and pose-scale optimization within the Camera Tracking module. The bottom left shows the process of global loop detection and closure within the Loop Closure module. The bottom right demonstrates the optimization in the Mapping module, where pair-wise factors between non-adjacent keyframes are not shown. More details are described in Sec. IV.

B. Factor Design

Feature-metric Factor (FM).

This factor uses the feature map from the feature network as the appearance prior of a frame for reasons in Sec. III-A. The feature map is processed to form a Gaussian pyramid with a specified number of levels to increase the convergence basin. To build a level of the pyramid, the Gaussian smoothing operation with a specified size and sigma, and 2-time downsampling will be applied to the map in the previous level. The source feature map pyramid is defined as ${ℱ}^{\text{src}}=\left\{{\mathit{F}}_i^{\text{src}}\mid i=1,\dots ,L\right\}$, where L is the number of levels and ${\mathit{F}}_i^{\text{src}}\in {ℝ}^{C\times H/2^{i-1}\times W/2^{i-1}}$ is the feature map at pyramid level i; The objective of this factor is defined as

$$\begin{array}{l}{ℒ}_{\text{fm}}=\frac{1}{L}\sum _{i=1}^L\frac{1}{\left|{\text{Ω}}_{\text{src},\text{tgt}}\right|}\sum _{{\mathit{x}}^{\text{src}}\in {\text{Ω}}_{\text{src},\text{tgt}}}\Vert {\mathit{F}}_i^{\text{tgt}}\left(\pi \left(p^{\text{s}\to \text{t}}\right)\right)-\\ {\mathit{F}}_i^{\text{src}}\left({\mathit{x}}^{\text{src}}\right){\Vert }^2,\end{array}$$ (6)

where ${\text{Ω}}_{\text{src},\text{tgt}}$ is the set of source 2D locations that can be projected onto the target mask region given the estimates.

Sparse Matched Geometry Factor (SMG).

With only FM, the convergence basin is relatively small, which is common for the appearance-warping-based objectives [38]. The descriptor map from the feature network can be used to estimate 2D point correspondences between images through feature matching. This enables the objective to have global convergence characteristics. Because in this work, each keyframe has a depth estimate, the 2D correspondences can be replaced with 3D ones. Compared with 2D, the 3D ones should contain fewer outliers because 3D point cloud alignment [39] is used to remove outliers, which has less ambiguity than the common 2D filtering method based on epipolar geometry. The definition of this factor is:

$$\begin{array}{l}{ℒ}_{\text{smg}}=\frac{1}{\left|ℳ\right|}\sum _{\left({\mathit{x}}^{\text{src}},{\mathit{x}}^{\text{tgt}}\right)\in ℳ}{\rho }_{\text{fair}}\left(\Vert {\mathit{p}}^{\text{s}\to \text{t}}-\right.\\ \left.{\pi }^{-1}\left({\mathit{x}}^{\text{tgt}},{\mathit{D}}^{\text{tgt}}\left({\mathit{x}}^{\text{tgt}}\right)\right){\Vert }^2;{\delta }_{\text{smg}}^{\text{src}}\right),\end{array}$$ (7)

where $ℳ$ is a set of feature matches consisting of pairs of 2D locations $\left({\mathit{x}}^{\text{src}},{\mathit{x}}^{\text{tgt}}\right)\in {ℝ}^2\times {ℝ}^2$, and ${\delta }_{\text{smg}}^{\text{src}}=\frac{{\sigma }_{\text{smg}}}{\left|{\text{Ω}}^{\text{src}}\right|}{\sum }_{\mathit{x}\in {\text{Ω}}^{\text{src}}}{\overline{\mathit{D}}}^{\text{src}}(\mathit{x})$, which is the mean value of the source average depth estimate multiplying a constant factor ${\sigma }_{\text{smg}}\in ℝ$. The outlier-robust “Fair” loss [40] is used, which is defined as ${\rho }_{\text{fair}}(a;b)=2(\sqrt{a/b}-\ln (1+\sqrt{a/b}))$.

Reprojection Factor (RP).

This factor behaves similarly to SMG except that the objective is changed from minimizing the average distance of 3D point sets to that of the corresponding projected 2D locations. The factor is defined as:

$$\begin{array}{l}{ℒ}_{\text{rp}}=\frac{1}{\left|ℳ\right|}\sum _{\left({\mathit{x}}^{\text{src}},{\mathit{x}}^{\text{tgt}}\right)\in ℳ}\\ {\rho }_{\text{fair}}\left({‖\pi \left({\mathit{T}}_{\text{src}}^{\text{tgt}}{\pi }^{-1}\left({\mathit{x}}^{\text{src}},{\mathit{D}}^{\text{src}}\left({\mathit{x}}^{\text{src}}\right)\right)\right)-{\mathit{x}}^{\text{tgt}}‖}^2;{\sigma }_{\text{rp}}{W}^2\right),\end{array}$$ (8)

where ${\sigma }_{\text{rp}}\in ℝ$ is a multiplying factor and W is the width of the involved depth map.

Geometric Consistency Factor (GC).

This factor enforces geometric consistency by encouraging the source depth estimate transformed to the target coordinate to have consistent values as the target depth estimate. The factor is defined as:

$$\begin{array}{l}{ℒ}_{\text{gc}}=\frac{1}{\left|ℳ\right|}\sum _{\left({\mathit{x}}^{\text{src}},{\mathit{x}}^{\text{tgt}}\right)\in ℳ}{\rho }_{\text{cauchy}}\left(\parallel z^{\text{s}\to \text{t}}-\right.\\ \left.{\mathit{D}}^{\mathrm{tgt}}\left(\pi \left({\mathit{p}}^{\text{s}\to \text{t}}\right)\right){\parallel }^2;{\delta }_{\text{gc}}^{\text{src}}\right),\end{array}$$ (9)

where $z^{\text{s}\to \text{t}}$ is the z-axis component of ${\mathit{p}}^{\text{s}\to \text{t}}$; ${\delta }_{\text{gc}}^{\text{src}}$ is the same as ${\delta }_{\text{smg}}^{\text{src}}$, except that σ_gc is used instead of σ_smg. Cauchy loss [40] is used to increase the robustness of this factor, which is defined as ${\rho }_{\text{cauchy}}(a;b)=\ln (1+a/b)$.

Relative Pose Scale Factor (RPS).

This factor is used in the graph optimization for the global loop closure in Sec. IV-C. The error value for the pair-wise factors above will not change if the depth scales and relative camera pose are scaled jointly. During a global loop closure, all frame pairs except the newly detected global loop should have reasonably variable estimates. Therefore, this factor is to keep variables in the previous links unchanged up to a global scale and encourage the new global link to reach the goal. The factor is defined as follows:

$$\begin{array}{l}{ℒ}_{\text{rps}}={‖\frac{{\mathit{t}}_{\text{src}}^{\text{tgt}}}{s^{\text{src}}}-\frac{{\tilde{\mathit{t}}}_{\text{src}}^{\text{tgt}}}{{\tilde{s}}^{\text{src}}}‖}_2^2+{\omega }_{\text{rot}}{‖\log \left({\mathit{R}}_{\text{src}}^{\text{tgt}}\right)-\log \left({\tilde{\mathit{R}}}_{\text{src}}^{\text{tgt}}\right)‖}_2^2+\\ {\omega }_{\text{scl}}{\left(\log \left(\frac{s^{\text{tgt}}}{s^{\text{src}}}\right)-\log \left(\frac{{\tilde{s}}^{\text{tgt}}}{{\tilde{s}}^{\text{src}}}\right)\right)}^2,\end{array}$$ (10)

where ${\mathit{t}}_{\text{src}}^{\text{tgt}}\in {ℝ}^3$ and $R_{\text{src}}^{\text{tgt}}\in \text{SO}$ (3) are the translation and rotation components of the relative pose ${\mathit{T}}_{\text{src}}^{\text{tgt}}$ described above, respectively. Note that the logarithm operation on the rotation components is the matrix logarithm of SO (3). ${\omega }_{\text{rot}}\in ℝ$ and ${\omega }_{\text{scl}}\in ℝ$ are the weights for the rotation and scale components of this factor, respectively. In this equation and the ones below, every symbol with ~ on top represents the target counterpart of the one without it.

Code Factor (CD).

This is used to keep the depth code of a keyframe within a reasonable range. It is defined as

$${ℒ}_{\text{code}}=\frac{1}{B}‖{\mathit{c}}^{\text{src}},-,{\tilde{\mathit{c}}}^{\text{src}}‖{ }_2^2.$$ (11)

Scale Factor (SC).

This is to make the depth scale of a keyframe close to the goal. It is defined as

$${ℒ}_{\text{scale}}={\left(\log \left(s^{\text{src}}\right)-\log \left({\tilde{s}}^{\text{src}}\right)\right)}^2.$$ (12)

Pose Factor (PS).

It is used in the first keyframe to anchor the trajectory of the entire graph, which is defined as

$$\begin{array}{l}{ℒ}_{\text{pose }}={‖{\mathit{p}}_{\text{src}}^{\text{wld}}-{\tilde{\mathit{p}}}_{\text{src}}^{\text{wld}}‖}_2^2+\\ {\omega }_{\text{r}}{‖\log \left({\mathit{R}}_{\text{src}}^{\text{wld}}\right)-\log \left({\tilde{\mathit{R}}}_{\text{src}}^{\text{wld}}\right)‖}_2^2,\end{array}$$ (13)

where ${\omega }_{\text{r}}\in ℝ$ is the weight of the rotation component.

C. Module Design

Camera Tracking.

This module is used to track a new frame against a reference keyframe. The reference is the spatially closest one against the last frame, which is verified based on appearance similarity. Camera tracking is solved with LM optimization over the relative camera pose, ${\mathit{T}}_{\text{src}}^{\text{tgt}}$, between the new frame and the reference, where factors FM and RP are involved. The termination of optimization is based on several criteria, which are the maximum number of iterations, parameter update ratio threshold, and gradient threshold. Once the optimization finishes, the pose of the new frame can then be computed correspondingly.

Keyframe Creation.

For every tracked new frame, this module first determines if a new keyframe is needed. Because the scale of the entire graph is ambiguous due to the scale ambiguity of monocular depth estimation, no absolute distance threshold can be relied on. Instead, we use a set of more intuitive criteria that directly relate to the information gain of a new frame, which are scene overlap, feature match inlier ratio, and the average magnitude of 2D scene flow. Scene overlap measures the overlap between two frames and reflects how much new region is observed from a new frame. Feature match inlier ratio is the ratio of inlier matches over all the feature match candidates. This reflects how dissimilar the two frames are in terms of appearance, which may be due to a small region overlap, a dramatic texture change, etc. The average magnitude of 2D scene flow measures how much movement the content of a frame has. This is to track the camera movement of keyframes more continuously and to produce more consistent descriptors and feature maps between keyframes. For each keyframe, a bag-of-words vector is computed from the descriptor map and added to a database for global loop indexing in Sec. IV-C. Connections consisting of keyframes within a temporal range will be added to the new keyframe. At least one keyframe will be connected to the new one and extra ones, up to a specified number, will be added only if the appearance is similar to the new keyframe. The pair-wise factors involved in the keyframe connections are FM and GC. For the first keyframe, prior factors, CD, SC, and PS, are integrated into the factor graph and only CD will be included for the other keyframes.

Mapping.

The mapping is constantly running at the backend, where the framework of optimization is ISAM2 [41]. The factor graph consisting of pair-wise and prior factors from all keyframes is optimized in this module and Fig. 1 shows an example of such a graph. The variables jointly optimized are camera poses, depth scales, and depth codes of all keyframes.

Loop Closure.

This module constantly tries to search for local or global loop connections through all keyframes and handles the closure correspondingly. For local loop detection, the keyframes within a specified temporal range for each searched keyframe are considered. A verification based on filtering, appearance, and geometric, which is described with more details in the code repository, is applied to select the best local loop candidate. The selected local connection is then linked with pair-wise factors same as the temporal connections. Another part of this module is global loop connection and closure, as shown in Fig. 1. Global loop detection searches for keyframe pairs whose interval is beyond a specified temporal range and first applies appearance verification. The descriptor map from the feature network describes the appearance distinctively and those from the training set are used to build a bag-of-words place recognition model [42]. When a global loop connection is searched for a query keyframe, the database will be searched through with the query bag-of-words vector. A specified number of keyframes that are the most similar to the query keyframe in terms of bag-of-words description will be selected as candidates. Then the appearance and geometric verification, which is described in the code repository, is applied to select global loop candidates. The drifting error for the global connection is often large. Therefore, it is slow to rely on the full graph optimization in the Mapping module to close the gap. To this end, we design a lightweight pose-scale graph optimization for the global loop closure, where all camera poses and depth scales are optimized jointly. In this graph, a set of lightweight factors are used. For the new global loop pair, SC and RPS are used, where the target camera poses and depth scales come from the geometric verification above; For all other keyframe connections, RPS is used, where the values of the current estimates are used as the target in the factors. The graph optimization terminates if the maximum number of iterations is reached or the number of updates with no relinearization reaches a threshold.

V. Experiments

A. Cross-Subject Evaluation

Please refer to the code repository for the experiment setup in terms of parameter setting. For all studies in this work, the metrics used for camera trajectory evaluation are Absolute Trajectory Error (ATE) and Relative Pose Error (RPE) [43]. Note that only the frames that are treated as keyframes by the SLAM system will be evaluated in terms of both trajectory error and depth error. Therefore, synchronization needs to be done to first associate the trajectory estimate with the groundtruth one. The trajectory estimate will then be spatially aligned with the groundtruth trajectory, where a similarity transform is estimated [43]. To evaluate depth estimates, Absolute Relative Difference (ARD) and Threshold [38] are used. Before computing metrics, different pre-processing is applied for two sets of metrics, which are ARD_traj and Threshold_traj, and ARD_frame and Threshold_frame. For the first set, the estimated depth per keyframe is scaled with the scale component in the similarity transform obtained from the trajectory alignment above. For the other set, each depth estimate is scaled with the median value of ratios between the corresponding groundtruth one and the estimate. Please find definitions of these metrics in the code repository. To evaluate the performance of the SLAM system on endoscopic videos from unseen subjects, we run a cross-validation study. Four models are trained with different train/test splits on 11 subjects in total, where each test split has 3 subjects and the rest are used for training. For evaluation, the proposed SLAM is run on all sequences, with runtime performance of around 5.5 FPS, and generates estimates of camera poses and dense depth maps for all keyframes. Note that the value of each metric is averaged over all the sequences from all subjects, where each subset of the sequences is evaluated with the corresponding trained model so that all the sequences are unseen during training. We also compare against ORB-SLAM3 [8]. We adjust its parameters so that more keypoint candidates can be detected per frame. We conduct the paired t-test analysis between results from ORB-SLAMv3 and the proposed system. Evaluation results are shown in Table I, where the values with ***, **, and * stand for p-value smaller than 0.001, 0.01, and 0.05, respectively. The proposed system outperforms ORB-SLAM3 on all metrics with statistical significance except for the RPE_rot where p = 0.12.

TABLE I:

Cross-subject evaluation on SLAM systems.

Metrics / Methods	ATEtrans (mm)	ATErot (°)	RPEtrans (mm)	RPErot (°)	ARDtraj	ARDframe	Thresholdtraj $\left(\theta =1.25\right)$	Thresholdframe $\left(\theta =1.25\right)$	Thresholdtraj $\left(\theta ={1.25}^2\right)$	Thresholdframe $\left(\theta ={1.25}^2\right)$
Ours	1.6 ± 1.4	22.2 ± 15.1	1.5 ± 0.6	5.5 ± 2.4	0.36 ± 0.16	0.17 ± 0.03	0.42 ± 0.17	0.73 ± 0.08	0.74 ± 0.21	0.95 ± 0.04
ORB-SLAM v3 [8]	4.7 ± 4.2***	62.5 ± 55.5***	3.5 ± 2.5***	6.3 ± 3.6	1.76 ± 1.49***	24.27 ± 42.07**	0.17 ± 0.18***	0.37 ± 0.13***	0.31 ± 0.25***	0.56 ± 0.15***

B. Ablation Study

We evaluate the contributions of several SLAM components by disabling some in different runs. The components for ablation are FM in the Camera Tracking and Mapping modules (FMT and FMM), RP in the Camera Tracking module (RPT), local loop detection in the Loop Closure module (Local), and global loop detection and closure in the Loop Closure module (Global). All metrics described in Sec. V-A are evaluated and results are provided in the code repository. The overall observation is, FM has a large impact on both trajectory and trajectory-scaled depth metrics; RP mainly affects trajectory metrics; the Loop Closure module mainly affects the trajectory metrics ATE_trans and ATE_rot.

C. Evaluation with CT

This study uses the average residual error between the registered surface reconstruction and the corresponding CT model as the evaluation metric. Before computing the residual error, the depth fusion method in [44] is first applied to obtain a surface reconstruction from SLAM output. Then a point cloud registration algorithm based on [45] is applied between the surface reconstruction and the CT surface model, where a similarity transform is estimated. Lastly, the residual error is computed between the registered surface reconstruction and the CT surface model. In this study, we evaluate the accuracy of surface reconstructions from the videos of 4 cadavers, where for each subject, the metrics of all the sequences are averaged over to report here. The average residual errors for subject 7, 9, 10, and 11 are 0.83, 0.88, 0.78, and 0.86 mm, respectively.

VI. Conclusion

In this work, we propose a SLAM system, integrated with learning-based appearance and optimizable geometric priors, that can track the endoscope and reconstruct dense geometry of the anatomy from a monocular endoscopic video stream. An effective end-to-end training pipeline is developed to learn such priors by explicitly mastering the task of pair-wise image alignment. Based on the experiments, the system is shown to be robust to texture-scarce and illumination-varying scenarios and generalizable to unseen endoscopes and patients. To serve as a brief discussion, the accuracy of the proposed SLAM system depends on the generalizability of networks, and thus a representative collection of data for network training is important. Currently, the system cannot recover from a spurious global loop connection, which might be enabled with [20], and therefore the global loop detection criteria need to be strict to keep the false positive rate to zero. The current system is designed for static scenes, though having additional variables to model deformation (e.g., deformation-spline [46]) could also make the system suitable for deformable environments.