Reproductive Risk Estimation Calculator for Balanced Translocation Carriers

Abstract

Balanced translocation carriers experience elevated reproductive risks, including pregnancy loss and children with anomalies due to generating chromosomally unbalanced gametes. While understanding the likelihood of producing unbalanced conceptuses is critical for individuals to make reproductive decisions, risk estimates are difficult to obtain as most balanced translocations are unique. To improve reproductive risk estimates, Drs. Trunca and Mendell created models based on a logistic regression analysis of a dataset of over 6000 individuals from over 1000 translocation families. While risk assessments using these models have been offered as a free service for years, this protocol aims to create a sustainable model for genetics professionals to obtain risk estimates for their patients directly. This protocol guides the user through collecting clinical information, using a risk-generating Java program based on the models, and interpreting the program outputs. A practice tutorial is provided to ensure competency in interpretation prior to use.

Basic Protocol 1:

Estimation of reproductive risks for balanced translocation carriers

Basic Protocol 2:

Practical examples of typical patient encounters with instructive interpretations

INTRODUCTION

A reciprocal or balanced translocation is defined as a chromosome rearrangement in which end segments of chromosomes have exchanged positions. Carriers of reciprocal translocations are found in the newborn population with a frequency of approximately 0.14% (Nielsen & Wohlert, 1991). While balanced translocation carriers are at a small risk for developmental, congenital, and other genetic disorders because genes can be disrupted or dysregulated at breakpoints of the translocation (Higgins et al., 2008; Redin et al., 2017; Schilit et al., 2020), most carriers are healthy. However, carriers of balanced translocations risk having pregnancy loss or congenitally abnormal children as a direct result of producing chromosomally unbalanced gametes.

Understanding the risk of producing unbalanced conceptuses is critical for a balanced translocation carrier to make reproductive decisions. While historical studies have determined a general empirical abnormal segregation risk of 10% to 20% for female carriers and 5% to 10% for male carriers (Lejeune, Dutrillaux, & de Grouchy, 1970), this implies that translocations can be treated as a homogeneous class. However, the behavior of translocated chromosomes during meiosis depends on several factors, including the relative sizes and centromere positions of the chromosomes involved in the translocation, the lengths of the interchanged segments, and the frequency and distribution of chiasmata between the rearranged chromosome pairs (Jalbert, Sele, & Jalbert, 1980). Moreover, the viability of an unbalanced conceptus will depend on the size and genomic content of the chromatin imbalance (Cohen, Cans, Mermet, Demongeot, & Jalbert, 1994).

Specific risk figures based on empirical data for having a liveborn aneuploid child exist for the most common rearrangements like the der(14;21)(q10;q10) Robertsonian translocation (Chen, 2006) and the relatively common t(11;22)(q23;q11) translocation (Fraccaro, Lindsten, Ford, & Iselius, 1980). However, because most balanced translocations are unique, empirical risk estimates are impossible to obtain. While understanding the favored unbalanced outcome (as a result of adjacent-1, adjacent-2, or 3:1 segregation) is helpful, neither the probability of that occurring nor the likely viability of the unbalanced outcomes is known (McKinlay, Gardner & Amor, 2018).

To improve reproductive risk estimates, Carolyn Trunca, a clinical cytogeneticist and PhD medical geneticist, and Nancy Mendell, a biostatistician, developed three models to estimate the risk of having a miscarriage or a liveborn baby with an unbalanced chromosome complement for any balanced autosomal translocation carrier. The models are based on a logistic regression analysis of a dataset of 6227 individuals from 1079 translocation families collected between 1977 and 2012 from the literature and Dr. Trunca’s clinical practice. To avoid ascertainment bias, all probands were eliminated from the dataset. In addition, individuals whose chromosome complement provided evidence that one of the untested parents was an obligate carrier were not included in the dataset to avoid over-counting carriers. Others in the sibship were included.

In the early stages of this project, the collected data were analyzed to determine which variables were likely to be important for predicting reproductive risk. The results of that analysis are included in the “Data Collection and Analysis” section of this protocol. The analysis showed that the important variables were the chromosomes involved in the rearrangement, the translocation breakpoints (which determine the sizes of the exchanged and non-exchanged segments), the lengths from the breakpoints to the centromeres, the sex of the carrier, and how the family was ascertained.

A brief description of the logistic regression analysis is described in the “Statistical Analysis” section below. In addition, the risk equation and c-value for each model are provided in that section.

Dr. Trunca has offered these risk assessments as a free clinical service through http://www.thegeneticscenter.com/transrsk.htm since 1991 at a volume of approximately 600 inquiries per year. The goal of this protocol is to create a more sustainable model for disseminating reproductive risk estimates for balanced translocation carriers. This resource is intended to teach medical genetics professionals how to use the provided risk-generating software and interpret the risk estimates appropriately. The protocol outlines how to collect clinical information, use a custom Java program with the reproductive risk models, and interpret the program outputs. This protocol also includes practice problems that a medical geneticist might encounter during a risk assessment to ensure proper input of values into the program and interpretation of risk outputs.

Basic Protocol 1

ESTIMATION OF REPRODUCTIVE RISKS FOR BALANCED TRANSLOCATION CARRIERS

Three logistic regression models were developed to provide the relevant risk estimates to a carrier of any balanced autosomal translocation: one to calculate the estimated miscarriage risk and two to calculate the risk for a liveborn child with an unbalanced translocation. These models are the basis for the risk-generating software included in this publication. This protocol is designed to instruct genetics professionals on using the translocation risk calculator (Translocation Risk Estimates v5.1.jar program). It outlines what clinical information to collect, how to input it into the custom Java program containing the reproductive risk models, and how to interpret the program output.

Materials

Computer (Windows or Mac)

Access to the internet

Java program (download is freely available at https://www.java.com/en/download/manual.jsp)

Custom Translocation Risk Estimates v5.1.jar program that uses the logistic regression-based models to generate risk estimates (available as a supplemental file on the Current Protocols in Human Genetics webpage or from GitHub at https://github.com/sschilit/Translocation-Risk-Estimates.git).

Published rates of miscarriage by maternal age (Table 1) (adapted with permission from Figure 2 of Magnus, Wilcox, Morken, Weinberg, and Håberg, 2019).

• 1On a computer, download Java from the internet. The download is freely available at https://www.java.com/en/download/manual.jsp. Access the Translocation Risk Estimates v5.1.jar software link and download the file. This is available as a supplemental file on the Current Protocols in Human Genetics webpage or from GitHub at https://github.com/sschilit/Translocation-Risk-Estimates.git (click: Go to file → Translocation Risk Estimates v5.1.jar → Download).
• 2Obtain clinical cytogenetic information for the balanced translocation carrier, including the chromosomes involved in the translocation and their breakpoints at 400-band level resolution. For example, 4q13.2 indicates that a 550-band level was achieved, and the breakpoint is in the long arm of chromosome 4 at region 1, band 3, sub-band 2. The same breakpoint designation at the lower 400-band level resolution would be 4q13. Band information past the decimal is not included (refer to the International System for Human Cytogenomic Nomenclature [ISCN] (McGowan-Jordan, Hastings, Moore, 2020)).
• 3Obtain the age of the female carrier or the female partner of a male carrier. Estimate the age-related miscarriage risk using published data (Table 1) (Magnus et al., 2019).

The risk estimate requires information about the two individuals contributing genetic material to the conceptus and the types of gametes they produce. For this protocol, the term “female” describes the individual contributing ova, the term “male” describes the individual contributing sperm, and “partner” refers to the second individual contributing genetic material.

• 4Obtain a three-generation pedigree with special emphasis on reproductive history (see genetic counseling protocol (Brock, Allen, Keiser, & Langlois, 2010)).
• 5Use the pedigree to determine how the translocation was ascertained. Typically, the reasons for ascertainment are: 1) a carrier has a liveborn child with an unbalanced translocation; 2) a carrier or carrier’s partner has a history of multiple miscarriages/stillbirths or infertility; or 3) fortuitously (i.e., cytogenetic studies were performed for any other reason, e.g., prenatal diagnosis due to advanced maternal age).

Fortuitous ascertainment should be reserved for families in which there are multiple carriers with few, if any, adverse reproductive outcomes. Please note that the correct ascertainment category may not always be why the patient sought genetic counseling. For example, if an individual’s translocation were identified during pregnancy after undergoing prenatal diagnosis for advanced maternal age, and subsequent family history revealed that the translocation was inherited, and the individual’s parents had three miscarriages in addition to three normal pregnancies, the ascertainment category should be multiple miscarriages even if the patient has not personally had any miscarriages.

• 6Open the Translocation Risk Estimates v5.1.jar program and input the chromosome numbers and breakpoints (arm and band), the sex of the carrier, and the ascertainment category. Note that if the software closes unexpectedly, the band information is incorrect, and the band does not exist in the dataset. Reopen the file and enter the correct band information. Breakpoints at the centromere must be entered as p11 or q11, not p10 or q10.

The software contains a file that internally generates the lengths of the involved chromosomes’ short (p) and long (q) arms, the distances between the breakpoints and the non-centromere-containing terminal ends (N1 and N2), the distances between the breakpoints and the centromere-containing terminal ends (C_1 and C_2), and the lengths from the breakpoints to the centromeres (I1 and I2) (Fig. 1). The lengths are determined by measurement, in arbitrary units, of the published diagrams in Figure 5 from the Paris Conference (1971) representing chromosomes at the 400-band level (Paris Conference (1971): Standardization in human cytogenetics, 1972) (Fig. 2). For more information, please refer to the “Data Collection and Analysis” section below.

If you have trouble opening the program, please see the “Troubleshooting” section below.

• 7Press “Calculate Risk.” The following three risk estimates will appear: the estimated miscarriage risk, a likely underestimate of the risk for a child with an unbalanced translocation (low estimate), and a likely overestimate of the risk for a child with an unbalanced translocation (high estimate). The “high estimate” is based on a total dataset that includes individuals documented to have an unbalanced translocation and those indicated as having phenotypic abnormalities that may or may not be related to having an unbalanced translocation. The “low estimate” is based on the same dataset but only includes individuals with phenotypic abnormalities documented to have an unbalanced translocation and omits individuals with abnormalities who may have unbalanced translocations but for whom chromosome studies were never performed.
• 8Interpret the results. While the output provides risk estimates to two decimal places, this indicates a precision that is not achieved in these estimates. To avoid an assumption of precision, round the risk numbers up or down according to rounding rules before providing risk estimates to patients. The miscarriage risk is the probability that a recognized pregnancy will end in a miscarriage or stillbirth for a carrier or female partner of a carrier who is 34 years old or younger. It includes the general population miscarriage risk of 12% (the risk of any pregnancy ending in miscarriage) and the added risk due to the balanced translocation. If the female carrier or the female partner of a carrier is 35 years old or older, the miscarriage risk must be recalculated using the generated estimate and the published maternal age-specific miscarriage risk (Table 1) (Magnus et al., 2019). The method for that calculation is illustrated in the first example in “Basic Protocol 2.” The risk for a child with an unbalanced translocation is presented as an underestimate and an overestimate. The best risk estimate is most likely within the range of those two values.

Table 1.

Approximate Miscarriage Risk by Maternal Age (Adapted with permission from Figure 2 of Magnus et al., 2019)

Maternal age (years)	Miscarriage risk (%)
Younger than 35	12 (Background risk)
35	14
36	15
37	17
38	19
39	22
40	27
41	31
42	35
43	39
44	46
45 and older	57

Figure 1.

A pachytene diagram of a balanced translocation on which the N1 and N2 lengths (the distances from the breakpoint to the end of the arm in which the break occurred), C_1 and C_2 lengths (the distances from the breakpoint to the end of the other centromere-containing arm), and I1 and I2 lengths (the distances from the breakpoint to the centromere) are indicated. These measurements were used to determine whether the structural characteristics of a reciprocal translocation influence the type of segregation and the viability of the unbalanced segregants. Circles represent the centromeres of the chromosomes involved in the translocation.

Figure 2.

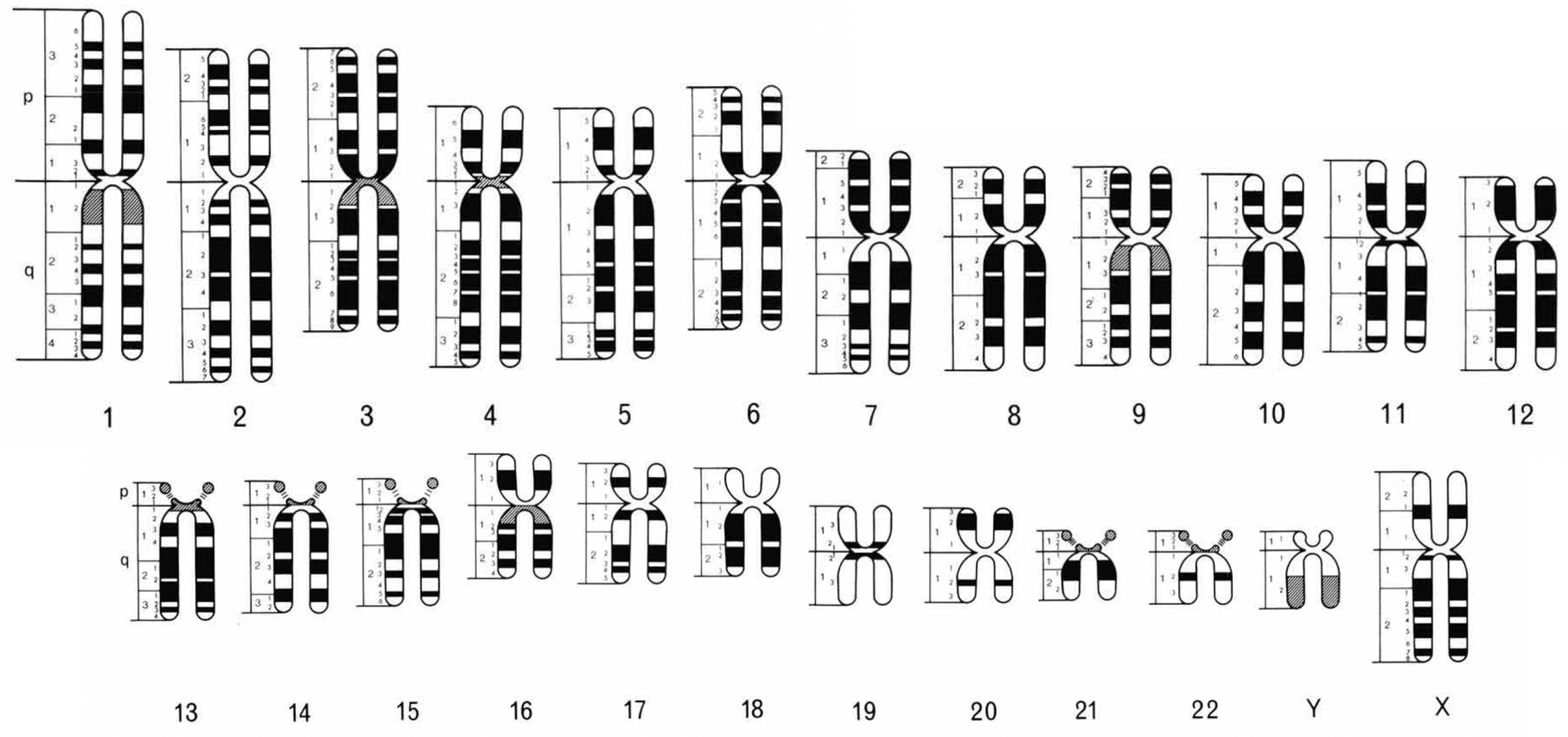
The chromosome ideogram adapted from Figure 5 in the Paris Conference (1971) representing chromosomes at the 400-band level (Paris Conference (1971): Standardization in human cytogenetics, 1972). White indicates negative or pale staining Q and G bands or positive R bands, black indicates positive Q and G bands or negative R bands, and gray indicates variable bands. The band measurements used to calculate the N1, N2, C_1, C_2, I1, and I2 lengths (Fig. 1) were made using this ideogram. Used with permission from S. Karger AG, Basel.

Basic Protocol 2

PRACTICAL EXAMPLES OF TYPICAL PATIENT ENCOUNTERS WITH INSTRUCTIVE INTERPRETATIONS

This section presents scenarios a medical genetics professional might encounter during a risk assessment. It describes, in a step-by-step manner, the proper approach for calculating appropriate risk estimates in situations that are not completely straightforward. It is recommended that all users test themselves with these practice examples before calculating reproductive risk estimates for their patients to ensure comprehension of Basic Protocol 1 and competency in proper interpretation.

• 1
  Pedigree of a 40-year-old female with a t(1;16)(p36.1;q21) and two children whose karyotypes were interpreted to be normal. Her mother, a known carrier, had three miscarriages.

  • Program output when multiple miscarriages/infertility is the ascertainment category and 1p36.1 is represented as 1p36 after removing the sub-band (number after the decimal point) to comply with 400-band resolution:

    • Miscarriage risk = 47.18%
    • Risk for a liveborn child with an unbalanced translocation (low estimate) = 2.8%
    • Risk for a liveborn child with an unbalanced translocation (high estimate) = 4.21%

Interpretation:

For this individual, the estimated risk for a miscarriage, given a recognized pregnancy, is 56% and not 47% (the output) because the 40-year-old carrier has an additional age-related risk of miscarriage. To calculate a miscarriage risk that incorporates advanced maternal age, the following must be understood. The miscarriage risk output is the result of what can be assumed to be two independent risks for fetal loss: all conceptuses that have miscarried due to the translocation and all those that have miscarried due to non-translocation reasons, such as aneuploidy. There are also conceptuses miscarried for both reasons, but these are only included once in the risk output.

In general terms, the miscarriage output risk (M) = T (translocation-related risk) + N (non-translocation-related risk) − (T × N), where (T × N) is the probability that a miscarriage occurs as a result of both risks. To proceed further, the risk specific to the translocation (T) must be calculated as follows.

47% (miscarriage output risk) = T (translocation-related risk) + 12% (background non-translocation-related risk) − (T × 12%). Then solve for T by subtracting to get 35% = 88%T and then dividing to get T = 40%. In other words, T = (M − N) / (1 − N).

Now that T is known (40%) and the risk for a non-translocation-related miscarriage for a 40-year-old carrier (B) is known (27%) (Table 1), this patient’s age-adjusted miscarriage risk (A) is calculated as A = T + B − (T × B).

40% (translocation-related risk) + 27% (background and age-related risk) − (40% × 27%) = 67% − 11% = 56%. The 11% must be subtracted to avoid double counting conceptuses that have both a translocation-related and an age-adjusted non-translocation reason for miscarrying.

Another way to calculate this patient’s miscarriage risk (A) is to calculate the probability of a live birth (100% − the probability of a miscarriage) for each miscarriage reason (T and B), multiply them together, and subtract that joint probability from 100%, i.e., A = 1 − ((1 − T) × (1 − B)). In this case, it would be 100% − (60% × 73%) = 56%.

While subtracting the background risk from the output and adding the age-specific risk to the result may seem simpler, it incorrectly increases the actual risk because it fails to subtract the miscarriages due to both reasons.

The estimated risk for a liveborn child with an unbalanced chromosome complement is between 2.8% and 4.21%, rounded to 3%–4%.

• 2
  Pedigree of a 37-year-old male with a t(13;15)(q13.2;q12) whose 29-year-old partner had a liveborn child with an unbalanced translocation.

  • Program output using child with unbalanced chromosomes as the ascertainment category and when 13q13.2 is represented as 13q13 after removing the sub-band (number after the decimal point) to comply with 400-band resolution:

    • Miscarriage risk = 44.74%
    • Risk for a liveborn child with an unbalanced translocation (low estimate) = 5.46%
    • Risk for a liveborn child with an unbalanced translocation (high estimate) = 9.68%

Interpretation:

For this family, the risk of miscarriage, given a recognized pregnancy, is 45%. This includes a background risk of approximately 12%. As the patient’s partner is 29 years old, there is no additional age-related risk. The chance that a liveborn child will have an unbalanced translocation is between 5% and 10%.

Please note that the risk of a miscarriage and the risk of a liveborn child with an unbalanced translocation cannot be added together because the risks refer to two different datasets. Using 45% for the miscarriage risk and 8% for the risk of having a liveborn child with an unbalanced translocation, it is not true that this carrier has a 47% chance of having a liveborn child with normal or balanced chromosomes. If the patient asks for the probability, from the moment of conception, that they will have a liveborn child with normal or balanced chromosomes, the answer in this case would be 51%. This is calculated as 55% (the probability of having a liveborn child) × 92% (the probability of that child not having an unbalanced translocation) = 51%. If the patient asks for the probability, from the moment of conception, that they will have a liveborn child with an unbalanced translocation, the answer in this case would be 4%; that is, 55% (the probability of having a liveborn child) × 8% (the probability of that child having an unbalanced translocation) = 4%. If a patient asks for the probability that a phenotypically normal child will carry the translocation, the theoretical answer is 50% and this was confirmed in our dataset.

• 3Pedigree of a 32-year-old female with a t(4;20)(q31.1;q11.2) detected prenatally when her mother had a prenatal diagnosis for advanced maternal age. She has one normal child and two brothers, neither of whom has had children. Her now-deceased parents never had chromosome studies.
  There is not enough reproductive information from this family to be sure of the appropriate ascertainment category, so it is prudent to look at the risk estimates generated for each ascertainment category and determine a range for the risk estimates.

  • Program output using child with unbalanced chromosomes as the ascertainment category when 4q31.1 and 20q11.2 are represented as 4q31 and 20q11 after removing the sub-bands (numbers after the decimal point) to comply with a 400-band resolution:

    • Miscarriage risk = 37.39%
    • Risk for a liveborn child with an unbalanced translocation (low estimate) = 19.73%
    • Risk for a liveborn child with an unbalanced translocation (high estimate) = 30.08%
  • Program output using multiple miscarriages/infertility as the ascertainment category:

    • Miscarriage risk = 52.11%
    • Risk for a liveborn child with an unbalanced translocation (low estimate) = 3.58%
    • Risk for a liveborn child with an unbalanced translocation (high estimate) = 8.92%
  • Program output using fortuitously as the ascertainment category:

    • Miscarriage risk = 37.39%
    • Risk for a liveborn child with an unbalanced translocation (low estimate) = 1.42%
    • Risk for a liveborn child with an unbalanced translocation (high estimate) = 5.1%

Interpretation:

With so little reproductive history from a known carrier, the risk estimates cannot be very specific. If one looks across all ascertainment groups, the patient’s risk for a miscarriage, given a recognized pregnancy, would range from 37% to 52%, which includes a background risk of 12%. Because the patient is 32 years old, there is no additional age-related risk. The risk for a child with an unbalanced translocation would range from 1% to 30%. If, in the future, the family history changes, more specific risk estimates should be generated.

• 4Pedigree of a 25-year-old female with a t(7;10)(p11;p11) who has two normal children and who terminated a fetus that was prenatally diagnosed with an unbalanced translocation.
  As the fetus was terminated, the outcome of the pregnancy is unknown. It is possible the fetus could have been born alive or died prior to birth.

  • Program output for child with unbalanced chromosomes ascertainment:

    • Miscarriage risk = 25.99%
    • Risk for a liveborn child with an unbalanced translocation (low estimate) = 10.3%
    • Risk for a liveborn child with an unbalanced translocation (high estimate) = 13.23%
  • Program output using multiple miscarriages/infertility as the ascertainment category:

    • Miscarriage risk = 39.02%
    • Risk for a liveborn child with an unbalanced translocation (low estimate) = 1.71%
    • Risk for a liveborn child with an unbalanced translocation (high estimate) = 3.35%

Interpretation:

Ascertainment matters in risk assessment. If the fetus with an unbalanced translocation had been born alive (not terminated), the risk for a miscarriage, given a recognized pregnancy, would be 26%, which includes a background risk of 12%. Because the patient is 25 years old, there is no additional age-related risk. In addition, the chance that a liveborn child will have an unbalanced translocation would be 10% to 13% using this ascertainment category. On the other hand, if the appropriate ascertainment category is miscarriages (i.e., this pregnancy resulted in a miscarriage or stillbirth), the risk for a miscarriage, given a recognized pregnancy, would be 39% and the chance that a liveborn child will have an unbalanced translocation would be reduced to 2% to 3%.

• 5
  Pedigree of a 23-year-old female with a t(5;18)(q12;q21.2) and her male partner with a t(9;11)(q22.1;q23.2). The female had a sister who died at two months with an unbalanced translocation, and the male’s mother had three miscarriages. Together the couple has had two miscarriages.

  • Program output for the female with t(5;18)(q12;q21.2) using child with unbalanced chromosomes as the ascertainment category when 18q21.2 is represented as 18q21 after removing the sub-band (number after the decimal point) to comply with a 400-band resolution:

    • Miscarriage risk = 23.26%
    • Risk for a liveborn child with an unbalanced translocation (low estimate) = 5.25%
    • Risk for a liveborn child with an unbalanced translocation (high estimate) = 11.65%
  • Program output for the male with t(9;11)(q22.1;q23.2) using multiple miscarriages/infertility as the ascertainment category when 9q22.1 and 11q23.2 are represented as 9q22 and 11q23, respectively, after removing the sub-bands (numbers after the decimal point) to comply with a 400-band resolution:

    • Miscarriage risk = 35.16%
    • Risk for a liveborn child with an unbalanced translocation (low estimate) = 0.91%
    • Risk for a liveborn child with an unbalanced translocation (high estimate) = 3.78%

Interpretation:

Information from families where two translocations are segregating was not included in the dataset, so specific estimates provided by the models are not available for this family. While the following approach is likely to provide reasonable estimates, there is enough uncertainty due to lack of empirical data that the following risk estimates must be regarded as educated conjecture, understanding that the real risks for a fetal loss or for a liveborn child with an unbalanced chromosome complement may be higher or lower than the suggested risks.

The risk for a miscarriage, given a recognized pregnancy, involves the background risk (12%) and the additional risks conferred by the t(5;18)(q12;q21.2) and t(9;11)(q22.1;q23.2) translocations. First, the translocation risks must be calculated using the equation derived in practical example 1: T = (M − N) / (1 − N), where T = translocation-related risk, M = miscarriage output risk, and N = non-translocation-related risk. The additional risk conferred by the t(5;18) is T1 = (23% − 12%) / (100% − 12%) = 11% / 88% = 13%. The additional risk conferred by the t(9;11) is T2 = (35% − 12%) / (100% − 12%) = 23% / 88% = 26%. Thus, an estimate of this couple’s risk for a miscarriage is 100% minus the product of the probabilities of not having a miscarriage due to the background risk or either translocation ((100% − 12%) × (100% − 13%) × (100% − 26%)) = 100% − (88% × 87% × 74%) = 100% − 57% = 43%.

The chance that a liveborn child will have one or more unbalanced translocations is 100% minus the probability that the conceptus receives normal or balanced chromosomes from both parents. Use the averages of the high and low estimates as the likelihood that a liveborn child will have an unbalanced translocation (8.5% from the female and 2.5% from the male). The estimate that a liveborn child will have received normal or balanced chromosomes from the female is 91.5% (100% − 8.5%) and the estimate that a liveborn child will have received normal or balanced chromosomes from the male is 97.5% (100% − 2.5%). Thus, the probability that the conceptus will be born alive having received normal or balanced chromosomes from both parents is 89% (91.5% × 97.5% = 89%). Consequently, the chance that a liveborn child will have one or more unbalanced translocations is 11% (100% − 89% = 11%). Although the numbers appear the same in this example after rounding, this calculation will result in a value less than what would result from adding the estimated risks together because it avoids double counting conceptuses that inherited unbalanced derivative chromosomes from both parents. In addition, note that such a conception might not become a recognized pregnancy, or it might result in a miscarriage with a higher frequency than a conception with only one unbalanced translocation, so this risk estimate is likely an overestimate. The same approach would apply to an individual with two translocations. Once again, while this approach is likely to provide a reasonable estimate of the risk, lacking real data produces enough uncertainty that the risk estimates must be regarded as educated conjecture.

COMMENTARY

Background Information

Historical Background for the Development of Models for Estimating Reproductive Risk for Translocation Carriers

Direct observations of meiosis in organisms other than humans and indirect observations of the results of meiosis in human gametes indicate that the behavior of a balanced translocation during meiosis depends on the chromosomes involved in the translocation and their breakpoints because these two factors determine the structural characteristics of the pachytene cross and the position and likelihood of chiasmata formation in diplotene (Benet, Oliver-Bonet, Cifuentes, Templado, & Navarro, 2005; Burnham, 1962; Goldman & Hulten, 1993; Jalbert & Sele, 1979; Lewis & John, 1963; Yakut, Ercelen, Acar, Kimya, & Egeli, 2006). Both direct and indirect observations confirm that meiosis in balanced translocation carriers proceeds according to the following principles.

1. At pachytene, each segment of the rearranged chromosomes pairs with the homologous segment of the normal chromosomes, forming a pachytene cross.

2. At diplotene, chiasmata appear where crossing over has occurred. The number of chiasmata is positively correlated to the length of the arms of the pachytene cross. It is possible that an arm may have no chiasmata.

3. At diakinesis and first metaphase, the four chromosomes are associated either as a ring (having at least one chiasma in each arm); a chain (having at least one chiasma in three of the four arms); or are separated into two bivalents, a univalent and a trivalent, two univalents and a bivalent, or even four univalents (resulting from the failure of chiasma formation in two or more arms).

4. At anaphase, there are three ways that the four chromosomes associated as a ring or chain can orient concordantly so that two go to each pole of the spindle:

   1. Alternate: alternate centromeres in a ring or chain pass to the same pole so that all gametes are genetically balanced, with 50% containing the two normal chromosomes and 50% containing the two translocated chromosomes;
   2. Adjacent-1: adjacent non-homologous centromeres pass to the same pole, so that all gametes are genetically unbalanced; or
   3. Adjacent-2: adjacent homologous centromeres pass to the same pole, so that all gametes are genetically unbalanced.

5. At anaphase, two bivalents will segregate independently, so 50% of the gametes are genetically balanced and 50% are unbalanced.

6. At anaphase, if a univalent and a trivalent have occurred, 3:1 disjunction may result and then all gametes will be unbalanced.

Data Collection and Analysis

To determine what variables influence the type of segregation that occurs during meiosis in human translocation carriers and the resulting reproductive outcomes, a dataset containing 6227 individuals from 1079 translocation families was analyzed. The data were collected between 1977 and 2012 from both the literature as well as Dr. Trunca’s clinical practice. Probands and carriers who demonstrated that an untested parent is an obligate carrier were eliminated from the dataset to avoid ascertainment bias. The dataset includes the chromosomes and breakpoints involved in the translocation; the sex of the carrier; whether offspring of the carrier were liveborn or had been miscarried or stillborn; if liveborn, whether they were normal or had abnormalities; and if abnormal, whether it was the result of having inherited an unbalanced translocation.

In addition, the following lengths for both chromosomes in a translocation were calculated:

1. the lengths of the short arms (p1 and p2) and the long arms (q1 and q2);

2. the distances from the breakpoint to the end of the arms in which the break occurred (terminal distances N1 and N2);

3. the distances from the breakpoint to the end of the other centromere-containing arm (terminal distances C_1 and C_2); and

4. the distances from the breakpoint to the centromere (interstitial distances I1 and I2) (Fig. 1).

These lengths were determined by measurement, in arbitrary units, from the diagrammatic representation of human chromosome bands in Figure 5 published by the Paris Conference (1971) (Paris Conference (1971): Standardization in human cytogenetics, 1972) (Fig. 2). Although this figure was not based on extensive measurements, the bands correspond reasonably well to the actual position observed with G-banding. The distances were calculated assuming the break was at the midpoint of the band.

Hypotheses were tested to determine whether structural factors influence the type of segregation (hypothesis A); whether there are selection differences between chromosomally unbalanced eggs and sperm (hypothesis B); whether the way a family is ascertained may give some indication of the viability of an unbalanced segregation—that is, the likelihood of an unbalanced segregation resulting in a liveborn child versus a fetal death (hypothesis C); and whether particular chromosomes and breakpoint locations increase or decrease risk (hypotheses D and E, respectively).

• Hypothesis A

  • Hypothesis: If structural factors influence the type of segregation that occurs during meiosis in humans, the following statements should be true:

    1. If large chromosome segments are exchanged, the translocation is predisposed to undergo alternate segregation, and the likelihood of a conceptus inheriting an unbalanced translocation is small.
    2. If very small chromosome segments are exchanged, the translocation is predisposed to undergo independent assortment, and 50% of the gametes will be genetically unbalanced. Therefore, the likelihood of a conceptus inheriting an unbalanced translocation is high.
  • Methods: After classifying all translocations according to their structural characteristics, the rates of liveborn offspring with an unbalanced translocation were calculated for carriers of translocations in structurally different groups.
  • Results: When large chromosome segments were exchanged, the risk of having a child with an unbalanced translocation was 1.6% ± 1.1% (N = 127). When small chromosome segments were exchanged, the risk of having a child with an unbalanced translocation was 25.1% ± 2.2% (N = 375) (chi-square = 33.85, p < 0.00001).
  • Conclusion: There is a highly significant relationship between the structural characteristics of a balanced translocation and having a liveborn child with an unbalanced translocation.
• Hypothesis B

  • Hypothesis: There are differences in reproductive risk between female and male translocation carriers.
  • Methods: Observed rates of liveborn offspring with an unbalanced translocation from male and female carriers were studied.
  • Results: For male carriers, the risk of having a child with an unbalanced translocation was 6.95% (N = 1510) and for female carriers, the risk of having a child with an unbalanced translocation was 10.15% (N = 2405) (chi-square = 17.91, p < 0.0001).
  • Conclusion: The relationship between the sex of the carrier and the risk of having a liveborn child with an unbalanced translocation is highly significant. Female carriers have a higher risk than male carriers of having a liveborn child with an unbalanced translocation.
• Hypothesis C

  • Hypothesis: There are differences in reproductive risk for carriers who were ascertained for different reasons.
  • Methods: Observed rates of liveborn offspring with an unbalanced translocation and observed rates of miscarriage or stillbirth by ascertainment group were studied.
  • Results: The risk of having a child with an unbalanced translocation was 12.78% (N = 2606) for the group ascertained by having a child with an unbalanced translocation, 1.85% (N = 701) for the group ascertained by miscarriages/infertility, and 0.49% (N = 608) for the group ascertained fortuitously (chi-square value = 144.04, 2df, p < 0.00001). The risk of miscarriage or stillbirth was 29.87% (N = 4078) for the group ascertained by having a child with an unbalanced translocation, 44.35% (N = 1301) for the group ascertained by miscarriages/infertility, and 27.12% (N = 848) for the group ascertained fortuitously (chi-square value = 107.34, 2df, p < 0.00001).
  • Conclusion: Overall, the relationship between pregnancy outcome and method of ascertainment is highly significant (p < 0.00001). However, pairwise comparisons indicate that the fetal death rate in the fortuitously ascertained group was not significantly different from that in the group ascertained through a liveborn child with an unbalanced translocation (p = 0.12). Only those in the group ascertained because of a history of multiple miscarriages/infertility had a higher fetal death rate. Pairwise comparisons of the observed rates of liveborn offspring with an unbalanced translocation were significantly different. Carriers ascertained through a liveborn child with an unbalanced translocation had the highest rate of recurrence. Fortuitously ascertained families had the lowest observed rates for fetal death and for having a liveborn child with an unbalanced translocation. Therefore, ascertainment category is a strong predictor of the viability of an unbalanced translocation.
• Hypothesis D

  • Hypothesis: There is random involvement of chromosomes in balanced translocations.
  • Methods: Chromosome involvement in translocations was analyzed for overrepresentation and underrepresentation of particular chromosomes in the entire dataset and for each ascertainment group.
  • Results: Statistical analysis of the entire dataset indicated that chromosomes are not involved in translocations at random, and the difference is highly significant. In the group ascertained through a liveborn child with an unbalanced translocation (N = 557), chromosomes 9, 11, 13, 18, 21, and 22 were overrepresented and chromosomes 1, 2, 3, 6, 7, and 19 were underrepresented. Chromosome 22 was overrepresented, and no chromosomes were underrepresented in the group ascertained because of a history of multiple miscarriages/infertility (N = 89). No chromosomes were overrepresented or underrepresented in the group ascertained fortuitously (N = 123). The level of significance for enrichment or depletion is p < 0.002 or p < 0.05 upon adjusting for multiple comparisons.
  • Conclusion: These results indicate that breakage and, therefore, chromosome involvement in translocations does occur randomly (no chromosome is either overrepresented or underrepresented) in the group ascertained fortuitously. The significant differences from random involvement of chromosomes in translocations found in the families ascertained because of an abnormal child are the result of differences in risk. Carriers of translocations involving chromosomes 9, 11, 13, 18, 21, and 22 are more likely to have a liveborn child with an unbalanced translocation and are, therefore, more likely to be included in the dataset. The reverse is true for translocations involving chromosomes 1, 2, 3, 6, 7, and 19. Likewise, carriers of translocations involving chromosome 22 are more likely to have multiple miscarriages or infertility. Therefore, the chromosomes involved in a translocation are predictors of risk.
• Hypothesis E

  • Hypothesis: Breaks are distributed at random within a given chromosome.
  • Methods: The entire dataset and the three ascertainment groups were compared separately against a uniform probability distribution in which the proportion of breaks within a particular band equals the length of the band divided by the total length of the chromosome.
  • Results: The combined dataset gives a poor fit to random allocation of breaks for essentially every chromosome. In addition, the distribution of breakpoints differs significantly between ascertainment groups. Using chromosome 1 to demonstrate the ascertainment group differences for essentially all chromosomes, the distribution of breaks in chromosome 1 is uniform (p = 0.1) in the fortuitously ascertained group while the distribution of breaks in chromosome 1 is highly significantly different (p = 0.0004) in the group ascertained through a liveborn child with an unbalanced translocation. In general, the distribution of breaks in all chromosomes from the group ascertained through a liveborn child with an unbalanced translocation showed a clustering of breakpoints toward the ends of the chromosome arms resulting in short terminal lengths. In the group ascertained through multiple miscarriages/infertility, the breaks occur more medially, increasing the mean terminal length.
  • Conclusions: The results suggest that terminal distance is another important factor in determining reproductive risk and carriers of translocations with breaks near the terminal ends are at an increased risk of having a liveborn child with an unbalanced translocation. Carriers of translocations with breaks that are more medially placed are at an increased risk of having a miscarriage or stillbirth. This is not surprising because it is reasonable to expect that the smaller the genetic imbalance in an unbalanced translocation, the higher the likelihood that it will lead to a liveborn but abnormal child. Conversely, when an abnormal segregation occurs in a translocation that involves a breakpoint or breakpoints more medially placed, the genetic imbalance is increased. Therefore, the likelihood that it results in fetal loss is increased.

The variables shown to be predictors of the risks for having a child with an unbalanced translocation or a miscarriage include: 1) the sex of the carrier, 2) the way the family was ascertained, and 3) the chromosomes and breakpoints involved in the translocation. Therefore, these variables were used to develop our logistic regression models for estimating the reproductive risks for balanced translocation carriers.

Critical Parameters

Eligibility criteria

The reproductive risk estimation calculator can only be used for individuals with balanced autosomal rearrangements. Robertsonian translocations, balanced rearrangements involving sex chromosomes, unbalanced translocations, inversions, insertions, and complex rearrangements including three-way translocations are not included in the models. Similarly, cytogenetic data from preimplantation studies prior to in vitro fertilization cannot be used for obtaining risk estimates because the models are based on data from post-implantation pregnancies where the outcome is known.

Information obtained

The estimates cannot predict the phenotype of a child with an unbalanced chromosome complement. In addition, as discussed in the fifth practice example, risk estimates must only be considered educated conjecture when calculated for the presence of two familial reciprocal translocations, as these scenarios were not captured in the dataset.

Troubleshooting

The program must be used on a Windows or Mac computer, not a mobile device. Mac computers may show an error message stating that the Translocation Risk Estimates v5.1.jar file “cannot be opened because it is from an unidentified developer.” This can be overridden by opening the Apple menu and clicking System Preferences → Security & Privacy → General → Open Anyway → Open.

Statistical Analysis

Logistic regression is used to determine whether specific factors are related to the presence of some characteristic, such as whether a balanced translocation carrier having chromosome 7 in the translocation is predictive of having a liveborn child with an unbalanced translocation. Like linear regression, logistic regression produces a prediction equation. However, unlike linear regression, which can be solved explicitly with an algebraic formula, logistic regression is based on maximum likelihood estimation. The response variable that characterizes logistic regression is an indicator of the presence or absence of a characteristic, that is, a binary “yes or no” variable. For example, did the pregnancy end in a miscarriage/stillbirth? A predictor variable is a factor that may affect the outcome of the response variable (e.g., ascertainment category).

A logistic regression equation does not directly predict the probability of an occurrence. The output of a logistic regression analysis is a constant and a coefficient for each predictor variable. Each coefficient represents the change in the response (e.g., the increase or decrease in log odds of risk) per unit change in the predictor (e.g., the change from male to female carrier). While a result in log odds, at first, does not seem very helpful, it can be directly transformed from log odds of risk to a risk probability.

The risk equations for each of the three models, which are the outputs of each logistic regression analysis, are included below:

• The equation to calculate the log odds of the risk of miscarriage is:

  −1.67+.57*C1+.27*C2+.38*C4+.66*C6+.25*C7+.19*C8+.22*C10+.22*C11+.38*C12+ .5*C13+.41*C14+.59*C15+.15*C16+.42*C17+.33*C18+.48*C20+.44*C21+.13*VSEX−.0019*N1+.0047*N2+.0022*I1+.0026*I2−.0019*C_1+.6*VASG2. (c-value = 0.62)

• The equation to calculate the log odds of the risk for a child with an unbalanced translocation (low estimate) is:

  −4.36+.33*C4+.2*C9−.78*C11−.45*C12+.63*C13−.32*C18−.89*C19+.36*C21+.32*VSEX−.29*ACRO−.0085*N1−.0135*N2−.0048*I2+2.84*VASG1+.95*VASG2. (c-value = 0.74)

• The equation to calculate the log odds of the risk for a child with an unbalanced translocation (high estimate) is:

  −2.98+.46*C2+.32*C3+.64*C4+.26*C5+.23*C8+.24*C9−.21*C11+.9*C13+.31*C14−.97*C19+0.28*C20+.68*C21+.12*VSEX−.42*ACRO-.0082*N1−.0127*N2−.0022*I1−.0033*I2+2.08*VASG1+.6*VASG2. (c-value = 0.73)

In the above models, VSEX = 1 if male, VSEX = 2 if female; ACRO = 1 if one or both chromosomes in the translocation is an acrocentric (13, 14, 15, 21, or 22), otherwise ACRO = 0; VASG1 = 0 and VASG2 = 0 if ascertained fortuitously, VASG1 = 1 and VASG2 = 0 if ascertained through child with an unbalanced translocation, VASG1 = 0 and VASG2 = 1 if ascertained through multiple miscarriage or infertility; N1 and N2 = chromosome lengths from the breakpoint to the non-centromere-containing terminal end, I1 and I2 = lengths from the breakpoint to the centromere, and C_1 and C_2 = lengths from the breakpoint to the centromere-containing terminal end. Terms “_1” and “_2” refer to the first and second chromosomes involved in the translocation. C(1–22) refers to the chromosomes involved in the translocation. For example, for a translocation involving chromosome 3 and chromosome 10, C3 and C10 each = 1, and all others = 0. In addition, the c-value, or concordance statistic, indicates how strong a model is at predicting outcomes correctly.

From the results of these equations (in log odds), the probability of a miscarriage, the probability of a liveborn child with an unbalanced translocation (low estimate), and the probability of a liveborn child with an unbalanced translocation (high estimate) for any translocation carrier can be calculated as follows:

• Log odds: log[odds] = log_e[p/(1−p)]

• Given the log odds: odds = exp[log odds]

• Given the odds: probability (p) = odds/(1+odds) because odds = p/(1−p)

Understanding Results

Upon completion of this protocol, medical genetics professionals will be able to provide a balanced autosomal translocation carrier with estimates of the reproductive risks of miscarriage/stillbirth or of having a liveborn child with an unbalanced chromosome complement related to the balanced translocation.

The risk estimates must be understood as estimated probabilities that are “in the ballpark” rather than precise. The c-value associated with each of the models indicates how strong each model is in predicting the outcome. Values for this measure range from 0.0 to 1.0, where a value of 0.5 indicates that the model is no better at predicting an outcome than the observed rate of that outcome in the entire dataset and a value of 1.0 indicates that the model predicts an outcome perfectly (unlikely to ever be achieved) (Hosmer & Lemeshow, 2000). While there are varying opinions, logistic regression models are typically considered good when the c-value is higher than 0.7 and strong when it exceeds 0.8. The two models that were developed to predict the log odds of risk of having a liveborn child with an unbalanced translocation are considered good (c-values are equal to 0.74 and 0.73 for the low and high estimate, respectively). The model that predicts the log odds of the risk of having a miscarriage is less robust (c-value is 0.62), but it provides valuable information because the model, which incorporates significant factors, is better than using the rate of fetal loss to predict the risk of fetal loss. To illustrate, the rate of fetal loss in the entire dataset is 33%, while in the group ascertained due to multiple miscarriage/infertility it is 44%, and in the group ascertained fortuitously it is 27%. Method of ascertainment is only one of several significant factors incorporated in the model for predicting fetal loss and each factor affects the prediction.

Risk estimates are challenging to validate as most balanced translocations are unique, family sizes are small, and generation times are long. Therefore, checking prospectively to see whether the predictions are accurate is basically impossible. However, for the well-known recurrent constitutional t(11;22)(q23;q11) where empirical risk estimates for a child with an unbalanced chromosome complement, based on small samples, have been published (Fraccaro et al., 1980), the estimates are similar to the ones generated by the models. Fraccaro et al. reported a recurrence risk of 5.7% for female carriers and 4.3% for male carriers. Using the model that only includes individuals where the karyotype is known (low estimate of risk) because that was the case for the individuals included in the Fraccaro et al. study, the recurrence risk for females is 6.4% and the recurrence risk for males is 4.73%.

Time Considerations

Once the cytogenetic information and three-generation pedigree is obtained, entering that data into the risk-generating software takes a minute. Interpreting the risk estimates is dependent on the complexity of the clinical situation. In most cases, however, the interpretation should take no more than 15 min.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.