Dynamic Biophysical Responses of Neuronal Cell Nuclei and Cytoskeletal Structure Following High Impulse Loading

Abstract

Cells are continuously exposed to dynamic environmental cues that influence their behavior. Mechanical cues can influence cellular and genomic architecture, gene expression, and intranuclear mechanics, providing evidence of mechanosensing by the nucleus, and a mechanoreciprocity between the nucleus and environment. Force disruption at the tissue level through aging, disease, or trauma, propagates to the nucleus and can have lasting consequences on proper functioning of the cell and nucleus. While the influence of mechanical cues leading to axonal damage has been well studied in neuronal cells, the mechanics of the nucleus following high impulse loading is still largely unexplored. Using an in vitro model of traumatic neural injury, we show a dynamic nuclear behavioral response to impulse stretch (approaching 150% strain per second) through quantitative measures of nuclear movement, including tracking of rotation and internal motion. Differences in nuclear movement were observed between low and high strain magnitudes. Increased exposure to impulse stretch exaggerated the decrease in internal motion, assessed by particle tracking microrheology, and in intranuclear displacements, assessed through high-resolution deformable image registration. An increase in F-actin puncta surrounding nuclei exposed to impulse stretch additionally demonstrated a corresponding disruption of the cytoskeletal network. Our results show direct biophysical nuclear responsiveness in neuronal cells through force propagation from the substrate to the nucleus. Understanding how mechanical forces perturb the morphological and behavioral response can lead to a greater understanding of how mechanical strain drives changes within the cell and nucleus, and may inform fundamental cellular behavior that directs pathogenesis following traumatic brain injury.

Statement of Significance

The nucleus of the cell has been implicated as a mechano-sensitive organelle, courting molecular sensors and transmitting physical cues in order to maintain cellular and tissue homeostasis. Disruption of this network due to disease or high velocity forces (e.g., trauma) can not only result in orchestrated biochemical cascades, but also biophysical perturbations. Using an in vitro model of traumatic neural injury, we aimed to provide insight into the neuronal nuclear mechanics and biophysical responses at a continuum of strain magnitudes and after repetitive loads. Our image-based methods demonstrate mechanically-induced changes in cellular and nuclear behavior after high intensity loading and have the potential to further defined mechanical thresholds of neuronal cell injury.

1. INTRODUCTION

Biomechanical cues guide and regulate cellular behavior including nuclear mechanics, gene expression, and tissue homeostasis [1–3]. Global forces that act upon tissues during normal physical loading or trauma transfer to the cell and organelles through physical links and biochemical signaling. Alterations in nuclear envelope mechanics, chromatin organization, and gene expression have demonstrated the response of the nucleus to changes in the microenvironment [4,5]. How cells integrate cues from the mechanical environment and respond through changes in the cell phenotype is known as mechanoreciprocity. Directed by mechanosensors in the cell membrane, cytoskeleton, and nuclear envelope, mechanoreciprocity is necessary for mechanical stability in the extracellular environment and intracellular compartments [3,6–8]. For example, biochemical signals observed in disease or during prolonged inflammation effect the constituents of the microenvironment over time, which can lead to increases in cell and nuclear stiffness [9,10]. Similarly, microenvironments in which constant mechanical signaling is applied also demonstrate alterations in tissue, cellular, and nuclear stiffness with changes in mechanical differentials over time [11]. However, during short-term mechanical loading, high intensity forces can cause excessive strain (e.g., tensile stretch) and immediate disruption of regulatory pathways in the cell and nucleus, and in turn can lead to cellular and nuclear mechanical instability [12].

One physiological example of immediate mechanical failure within the cell due to impulse loading is traumatic brain injury (TBI), which affects 1.7 million people each year in the United States alone [7,13,14]. The complex nature of TBI arises from a combination of mechanical insult (i.e., primary injury) and activation of biochemical cascades (i.e., secondary injury). On a cellular level, the sequelae of TBI is frequently associated with diffuse axonal injury, characterized by axonal blebbing and neurite swelling [15]. These hallmark morphological features represent disruption in the cytoskeletal network of the neuronal axon. Additionally, in vitro studies varying strain and rates of strain during mechanical loading have provided insight into mechanisms of neuron activity and death [16–19], including axonal damage [15,17,20,21]. However, the extent that axonal and related damage extends or transfers to the nucleus has received less attention.

Studies of neuronal axonal injury typically only examine the axon and dendrites before and after mechanical loading without considering the mechanical load experienced by the soma or internal organelles like the nucleus. Earlier work has shown that the soma and axon have different material properties [22] and responses after applied forces [23]. Furthermore, it is well established that alterations in the microenvironment influence axonal length and growth cone extension in neuronal cultures [24,25], demonstrating the mechanoreciprocity of the neuron within its environment. During traumatic loading, it was hypothesized that the soma of the neuron might receive a majority of the dissipating energy during axonal injury [7,23]. However, how this mechanical energy affects nuclear mechanics and directs behavior is still unclear.

In our lab, we have explored mechanoreciprocity and noted that while environmental and extracellular matrix stiffness affected cellular stiffness, changes in cell mechanics did not reciprocally influence matrix stiffness [10]. Additionally, we showed that disruption of the native tissue (extracellular) environment propagates to the plasma membrane and interior nuclear envelope structures of viable cells [9], and that environmental stiffening or disruption of complexes of the linker of nucleoskeleton and cytoskeleton influence nuclear mechanics and cellular behavior [4,26–28]. In our studies, we demonstrate how biophysical perturbations in the microenvironment have an immediate influence on nuclear mechanics [4,5,29]. Consequently, we were motivated to explore nuclear responses in neuronal cells to impulse loading in light of pathologies resulting from traumatic brain injury.

Several studies have shown that characterization of biophysical perturbations of the cell and nucleus may better depict the underlying collective molecular responses [30–32]. Here we use nuclear movement and temporal tracking of biophysical features to better understand neuronal nuclear biomechanics after high intensity loading. We hypothesized that single and multiple impulse loading, leading to substrate and cellular stretching would result in nuclear architecture remodeling. Temporal analysis of the nuclear behavior revealed the mechanosensitive nature of the neuronal nucleus and provides insight into the damage response of the soma following impulse loading.

2. METHODS

2.1. Neural Cell In Vitro Co-Culture:

Neural cells were obtained from B6.Cg-Tg (HIST1H2BB/EGFP) 1Pa/J mice (Stock No: 006069, Jackson Laboratory). Mice were maintained in specific pathogen-free, temperature-controlled housing with 12 hour light cycles, and received food and water ad libitum. All animal procedures were performed following Institutional Animal Care and Use Committee approval. Primary neural co-cultures were derived from the neocortices of embryonic (E18.5) H2B-eGFP mice, which enabled us to visualize time-course changes in nuclear organization without the use of exogenous staining (e.g. DAPI). Isolated neocortices were washed in ice-cold HBSS (Gibco, 14175103) and added to a digestion cocktail of Papain (2 mg/ml, Sigma P4762) and DNase I (100μg/ml, Sigma D4263). Tissue was chemically digested for 30 mins at 37°C with continuous shaking. After digestion, tissue was triturated 10 times through a full diameter, then half diameter fire-polished Pasteur pipette [33]. Cellular suspension was washed in 5% Neuronal Culture Medium (5% NCM: Neurobasal medium (Gibco, 12348017), 1× Pen/Strep (Gibco, 151250122), 1× Glutamax (Gibco, 30050061), 2× B27 Supplement (Gibco, 17504044), 5% Heat-Inactivated Fetal Bovine Serum (Gibco, 26140079)) [19]. The suspension was filtered through a 40μm cell strainer and counted. Cells were plated at 350×10³ cells/mL on 50μg/mL fibronectin coated soft PDMS substrates in a custom-designed well. After 24 hours in vitro, cultures were washed twice in warmed 1× HBSS, and 5% NCM was added back to the well. Cultures were fed every 3–4 days with a 50/50 medium change, and maintained in a 37°C incubator with 5% CO for up to 14 days. Cultures were used for experiments between days 10–14 in vitro.

2.2. Substrate Preparation, Well Assembly, and Device Design:

2.2.1. Substrate Preparation and Well Assembly:

Thin and transparent silicone membranes (SMI, 127μm thickness, gloss) were cut into 22×22mm squares and coated with a 100μm thick layer of soft (~13kPa) PDMS (Syglard 527 1:1, Part A to Part B). PDMS-coated membranes were degassed and cured overnight at 80°C. Once cured, the 100μm thick PDMS-coated membranes were sandwiched between custom-made polyether ether ketone (PEEK) or polysulfone (PS) cylinders into an acrylic base as a well for the neural cells cultures (Figure 1). Wells were cleaned in a sterile environment with 70% ethanol and rinse three times in PBS prior to coating. Once dry, the soft PDMS substrate was coated with 50μg/mL Fibronectin (Sigma, F1141) for 12–16 hours at 37°C prior to the experiment.

Figure 1: A custom device was designed for controlled mechanical stretch of primary neural cultures.

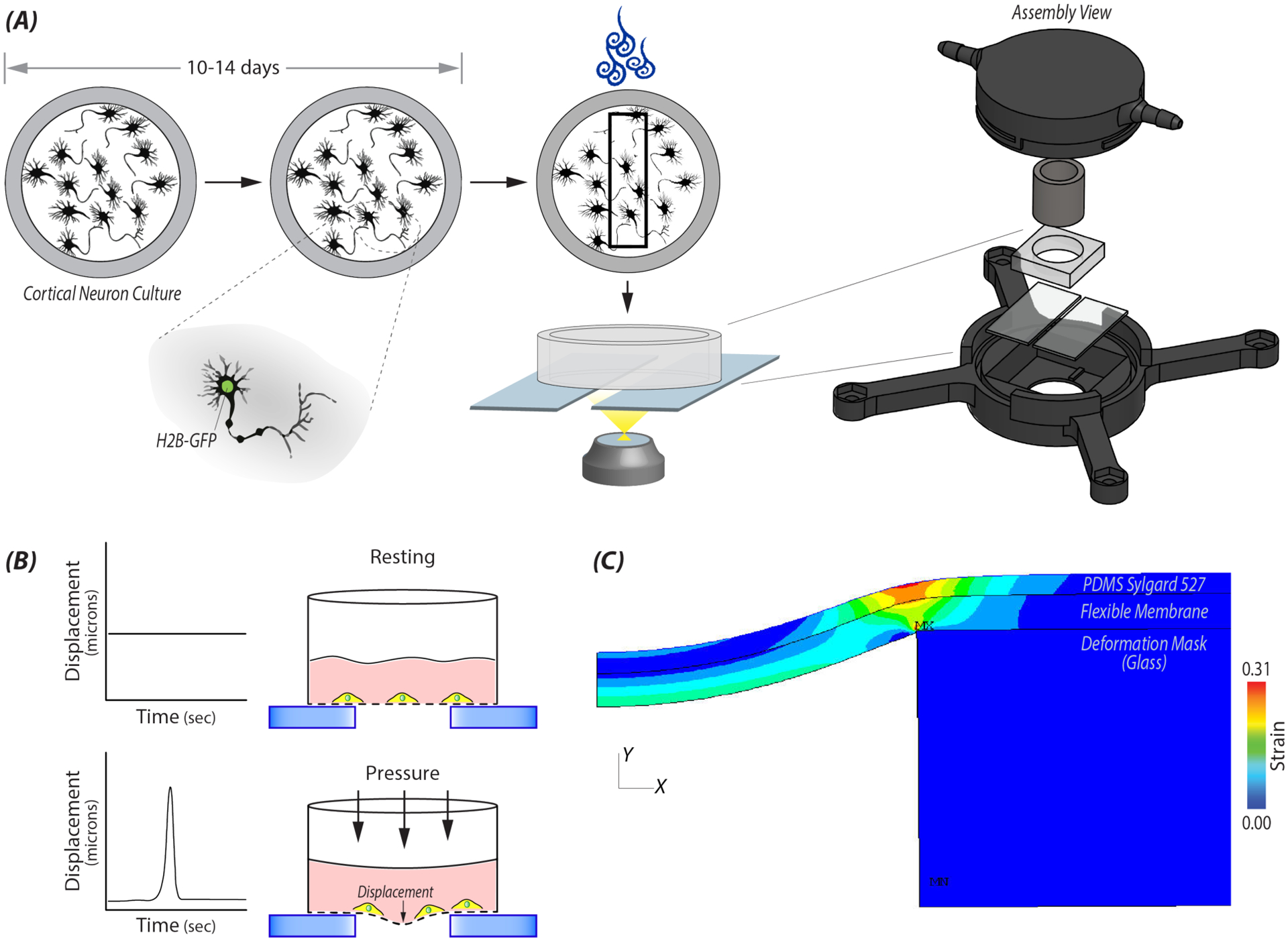
A) Custom machine wells constructed out of PEEK or PS were used to culture primary embryonic (E18.5) cortical neural cultures from H2B-eGFP mice. On days 10–14, a single well was added into a 3D printed pressure chamber that attached to the automatic stage of a Nikon A1R confocal. Within a given location of a well, 20 cells were selected and imaged at selected time steps before and after applying a high intensity load. B) Cartoon depicting the displacement of the flexible membrane and in turn the neural cells adherent to the membrane, during the high impulse load. C) Finite element analysis (FE) model was used to determine strain and rate of strain at a specified locations in the well during a 500ms impulse from the electro-pneumatic device. During the impulse, the flexible elastic membrane on which the cells were plated deformed into a 2mm gap between two glasses slides. Cells within the specified location received uniaxial stretch.

2.2.2. Live Cell Imaging Device Design:

Short-duration loading was delivered through a controlled pressure pulse from an electro-pneumatic device [34] (Figure 1). The device consisted of a pneumatic servo-valve (QB1T, Proportion Air), solenoid valves (NVKF334V, SMC Pneumatics), and a commercially available compressor (Black-Porter). A basic breadboard and power source were used for building a circuit connecting the components. A computer running a custom LabView (National Instruments, 2019) code provided control through a NI-DAQ board (USB-6341, National Instruments) for release and timing of impulses. The solenoid valve was connected to a 3D printed pressure chamber which was secured onto the motorized stage of a Nikon A1R confocal microscope. A secondary pressure sensor confirmed pressure within the chamber (leading to membrane stretch that the cells experienced). The chamber housed a single assembled well and rested on up two glass slides 2 mm apart.

2.3. FE Model and Calculation of Substrate Strain/Strain Rate:

2.3.1. FE Model:

We created and solved a finite element (FE) model of the pressure chamber and culture well in Ansys Mechanical APDL 19.2 to estimate the distributions in strain and strain rate acting on the cells. Our two-dimensional, plane-strain model included 36,500 2-D, 4-Node structural solid elements (type=plane182) and 36,714 nodes. We also included 2-node surface elements (type=surf153) with zero stiffness to extract the solution along the membrane surface. In solving the model, we accounted for large deformations and transient (mass/inertia) effects. In light of the variability in the culture wells, we adjusted the geometry and material properties of the substrates until the maximum deflection of both the membrane within the gap and the glass support structure matched (to within ~10%) those measured experimentally, at both minimum (0.0119 MPa) and maximum (0.0320 MPa) applied pressures. For the PDMS (~13kPa) substrate, we then solved the model for all combinations of applied pressure (0.0119, 0.0184, 0.0253, 0.0320 MPa) for a total of four simulations. For each simulation, we estimated the distributions in local membrane strain and strain rate from the center of the membrane to ~2 mm from this center using a custom macro written in APDL. Beyond 2 mm from the center of the membrane, the local membrane strain was nearly zero.

2.3.2. Strain Calculation:

From the x-y coordinates of each nucleus and using the glass edge of the deformation mask, a distance was calculated for each nucleus. We then reference the location of the nucleus to coordinates provided by the FE results which specified the strain magnitude and strain rate at that specific location with a given pressure. Only cells that were in tension were used in the analysis. Based on the maximum applied pressure (0.0320 MPa), the trackable cells could experience up to 25% strain magnitude and rates of strain approaching 150%/sec.

2.4. Image Acquisition for Time-Course Nuclear Movement and Actin Visualization:

2.4.1. Live Cell Imaging:

On Days 10–14 in vitro, wells were added to the pressure chamber mounted on the stage of a Nikon A1R confocal microscope. Results from the FE model allowed us to only select cells within the very center of the well and not close to the edges where plane-strain assumptions broke down. Twenty cells were selected per well for imaging based on cellular morphology using the transmitted light, and Pre-pulse images of the nucleus (z-stack, 3 images, 1.5μm steps) were acquired with an ELWD40× objective (25×25mm² FOV, 512×512 pixel, 0.06 μm/pixel) in the 488 channel (GFP) every 10 min. Due to the restrictions of our imaging system, the shortest time step possible was 10 min. After collecting the Pre-pulse image, a pressure was applied using the electro-controlled pneumatic device. Depending on the loading scheme (Figures 2A and 4A), a 500ms impulse at 0.0253 MPa or 0.0320 MPa was applied once, twice or four times. Z-stack images were collected every 10 min per nucleus for up to 1 hour. For two impulses, a Pre-pulse image was collected, followed by application of a 500ms impulse, acquisition of a z-stack imaged for all nuclei, application of a second 500ms impulse, and then imaging of nuclei for an additional 40 min with z-stack images acquired every 10 min. The four impulse treatment was imaged in the same order, except two impulses twice were applied instead of a single impulse twice (Figure 4A). Control nuclei were imaged for the same duration of time without receiving an impulse. Immediately after imaging, wells were removed from the chamber and fixed in 4% sucrose (Sigma, S7903) with 4% paraformaldehyde (Electron Microscopy Sciences, 15714-S) in PBS for 45 mins at 4°C.

Figure 2: Nuclear movement was quantified after high impulse mechanical loading.

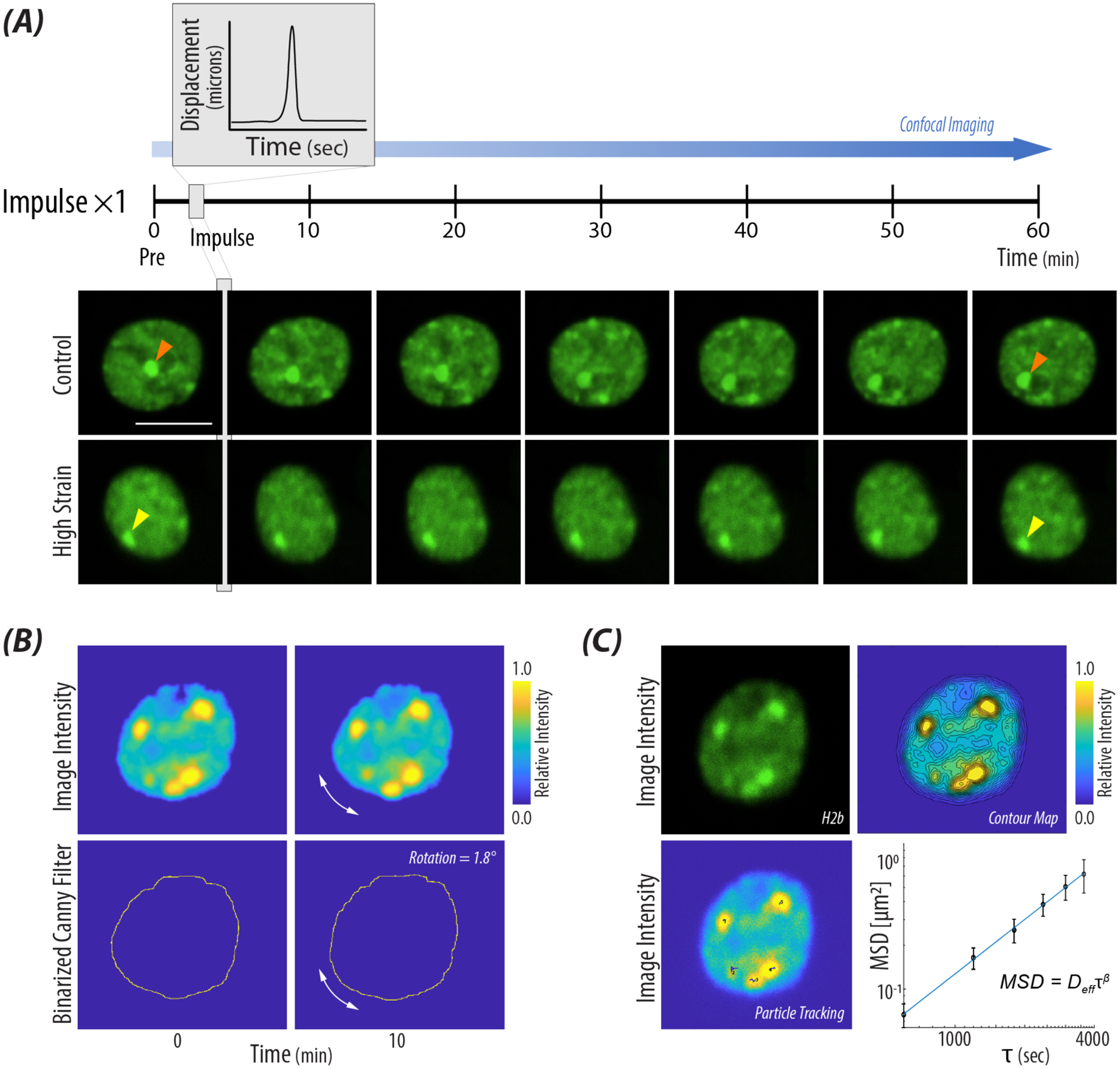
A) Representative images of two nuclei, control and a nucleus which received 21% strain. A z-stack image of the nucleus was taken prior to and then at ten minutes time steps after a high impulse load. The orange arrow tracks large intranuclear displacement over time, while the yellow arrow identifies an H2B-eGFP cluster with minimal movement after receiving a single high impulse. scale bar = 10μm B) Nuclear rotation was quantified using cross spectral power analysis in the Fourier domain and summing the degrees rotated through time steps Pre (pulse) up to 40 min. Representative images show the input images from the custom MATLAB code and the degrees rotated through a single time step. C) Nuclear internal motion was quantified through tracking H2B-eGFP clusters and calculating the ensembled-averaged mean squared displacement for a single nucleus. Contour maps were used to find high intensity areas of H2B for the particle tracking algorithm. Derived values of D_eff and β were calculated using the power law behavior of MSD (Equation 2).

Figure 4: Increased repetitive mechanical impulse loading influences intranuclear movement.

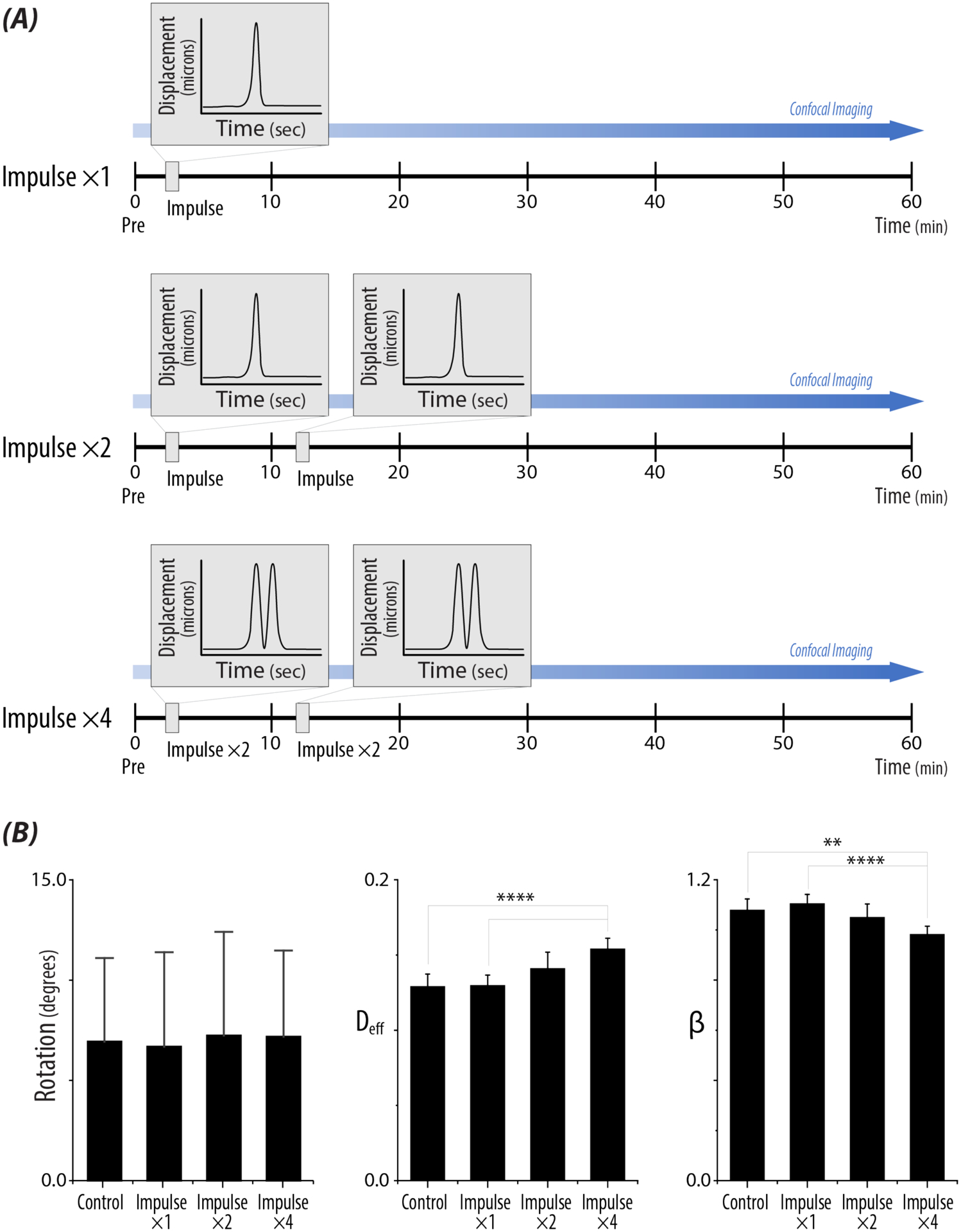
A) Repetitive loading schematic for two (×2) and four (×4) 500ms impulses. Nuclei were imaged prior to (Pre), in between impulses (10 min), after the second impulse (20 min), and up to 60 min. B) Bar plots represent rotational values, D_eff, and β, for each loading treatment. Increased repetitive loading did not have a significant effect on rotation, regardless of strain. With repetitive high intensity loading, D_eff significantly increased compared to controls and single impulse nuclei. β significantly decreased for 2 and 4 impulses compared to controls and a single impulse. n >80 nuclei/loading treatment, N>5 animals. Bonferroni adjusted p-values :*p < 0.008833, ** p < 0.0017, *** p < 0.00017, **** p <0.000017.

2.4.2. Actin Imaging:

Fixed wells were permeabilized in 0.2% PBX (PBS + 0.2% Triton-X) and stained with Phalloidin Texas-Red (1:400) for visualization of actin. Wells were incubated for 45 mins at room temperature before washing, and store in PBS. For improved resolution, each fixed well was mounted on a 22×22 mm coverslip with Sylgard 184 (10:1, base:curing agent) and allowed to cure overnight. The following day the membrane was cut from the well and wells were preserved in DAKO Mounting Medium (Aglient, S3023). Mounted wells were flipped and imaged (z-stack, 3 images, 0.5μm steps) immediately on a Nikon A1R using a 40× oil objective (1024 × 1024, 25×25mm² FOV, 0.06 μm/pixel).

2.5. Calculation of Nuclear Movement and Actin Morphology:

2.5.1. Rotation:

Using a custom MATLAB (Mathworks, 2018b) code, each z-projected image slice was corrected for translational drift, histogram normalized, median filtered, and binarized. MATLAB’s built-in Canny edge detector was used to create an outline before processing using the Fourier transform (Figure 2B). In the frequency domain, cross-spectral power analysis was performed between subsequent time steps up to the fourth time step (30 min) [35,36]. It was assumed if the nucleus began rotating at or after 40 mins of imaging, the rotation may be due to another condition and not the mechanical stimulus. The degrees of rotation were summed from the four images for a total amount of rotation. The algorithm was validated using 12 different nuclei at various strains and simulating rotation of 23° in MATLAB. Additionally, the influence of noise was assessed by adding random noise to the image, rotating 23°, and then running it through the algorithm again (Supplemental Figure 1).

2.5.2. Internal Motion:

Nuclear image stacks were adjusted in ImageJ (NIH) to remove artifacts of rotation and translation using the StackReg plugin in ImageJ. Fluorescent foci in the nucleus from clusters of H2B-eGFP were used as trackers from a custom particle tracking MATLAB code. Due to the more diffuse fluorescence of the endogenous GFP, we generated contour maps of the nucleus to identify local regions of high intensity. Only foci which could be tracked through all timeframes were kept and use to calculate the mean squared displacement (Equation 1),

$$MSD\left(\tau \right)=\langle {\left(x_{t+\tau }-x_t\right)}^2+{\left(y_{t+\tau }-y_t\right)}^2\rangle .$$ (1)

The ensembled-averaged mean squared displacement was graphed versus lag time, tau (τ), to quantify the power-law behavior using Equation 2 [37].

$$MSD=D_{eff}{\tau }^{\beta }$$ (2)

As each individual nucleus had only 2–15 foci which could be tracked, it was recognized that the calculated diffusive exponent could have increased error for single nucleus calculations (Figure 3A). For nuclear groups, (either strain categories or number of impulses), the effective diffusivity, D_eff, and the diffusive exponent, β, were calculated using ensembled-averaged mean squared displacements of the respective group. The calculation of D_eff was performed by normalizing to the imaging time step of ten minutes [38]. 95% confidence intervals were derived from the fitted equation.

Figure 3: A single high impulse load alters nuclear rotation and intranuclear movement.

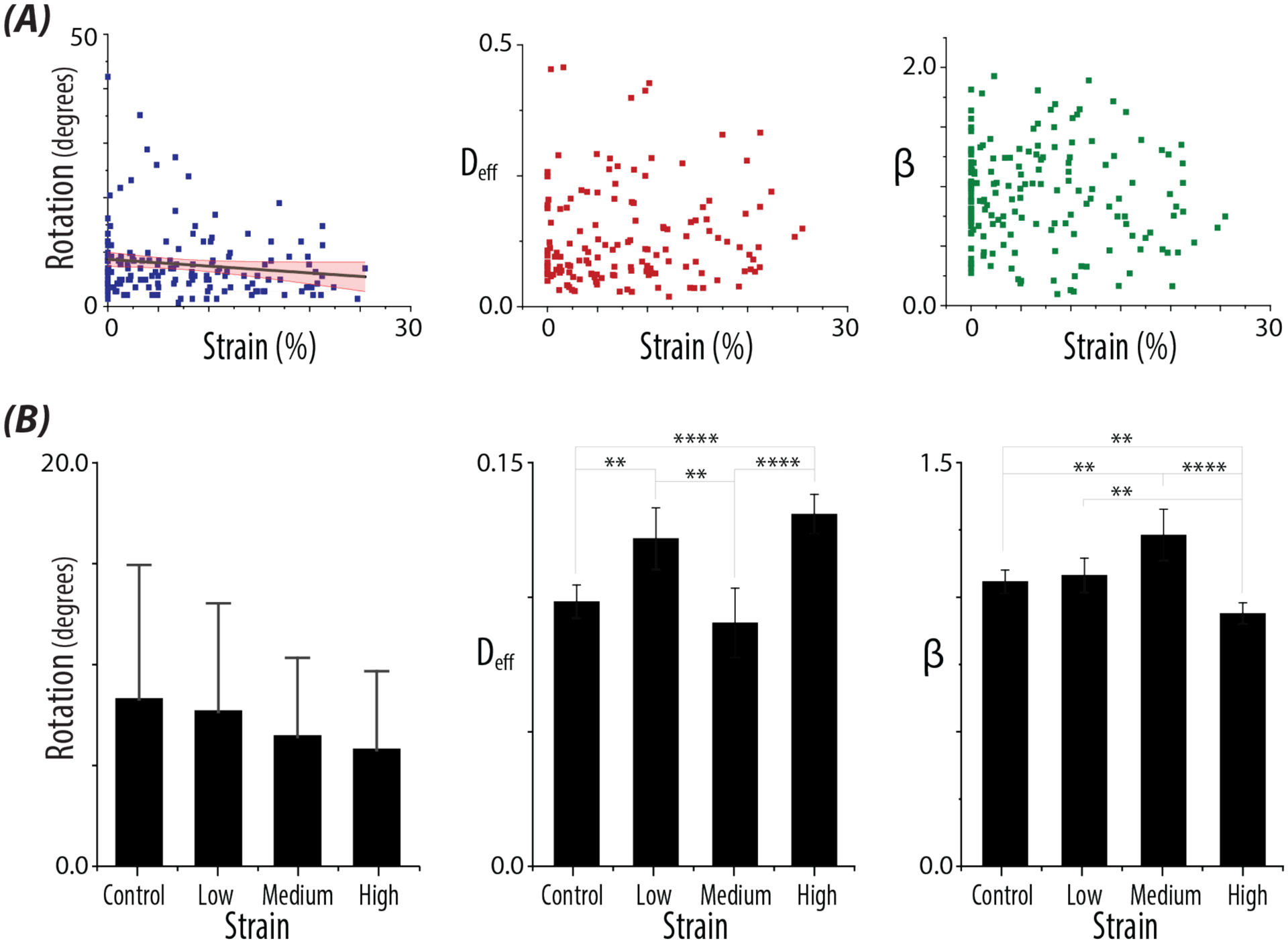
A) Quantified values of nuclear behavior. Plots show the quantified values of Rotation (p=0.03), and the derived parameters, D_eff and β, with continuous models of the experienced strain magnitudes. Confidence interval of the fitted line (95%) in red. Control nuclei are represented in the plots as having 0% strain. B) Bar plots of Rotation, D_eff, and β for control nuclei, nuclei which received Low (0–2%), Medium (9–15%), and High (>18%) strain. Errors bars represent SD for Rotation. Error bars represent 95% confidence intervals for D_eff and the β. n > 17 nuclei/strain level, N >5 animals. Bonferroni adjusted p-values :*p < 0.008833, ** p < 0.0017, *** p < 0.00017, **** p <0.000017.

2.5.3. Determining Nuclear Movement:

A histogram of the summed rotation values for each nucleus and internal motion values (β) were plotted for 91 nuclei (Supplemental Figure 2). Examining the histogram of all rotational values showed two distributions where a cutoff value of 5 degrees was determined to be the cutoff between “No Rotation” and “Rotation”. Examining a histogram of all the diffusive exponent values (β) showed two distributions where a cutoff value of 0.8 (dimensionless) was determined to be “No Internal Motion” versus “Internal Motion”. To validate the methods used to determine rotation and internal motion, three independent persons examined each nucleus and categorized the nuclei into “Rotation” or “No Rotation” and “Internal Motion” or “No Internal Motion” (Supplemental Figure 1).

For strain level categorization, literature reports have shown distinct morphological and biophysical alteration, including axonal blebbing and cytoskeletal damage at defined strain ranges in neuronal cells [15–17]. Using the single impulse nuclei (Figure 3), we grouped nuclei based off 3 defined strain levels from the literature [15–17]. We further examined nuclei only within the 3 strain levels: 0–2% (Low, n = 21), 9–15% (Medium, n = 30), and >18% (High, n = 17) plus controls (n=36).

2.5.4. Deformation Microscopy:

Greater than twenty nuclei per loading treatment were randomly selected that experienced either low strain (0–2%) or high strain (>18%). Z-projected images of each nucleus from selected time steps, Pre-pulse images, and images acquired after 10 min, 20 min, and the final timepoint (60 min), were compared using image registration methods to map intranuclear deformation [26]. The calculated relative difference from the displacement matrices in the x and y directions were calculated for each pair of images.

2.5.5. Morphological Analysis of Nuclei and F-actin:

For morphological analysis, images were corrected for translational drift in ImageJ using the StackReg plugin (Fiji). Nuclei were analyzed for morphological features including kurtosis, skewness, area, and chromatin condensation after histogram normalization of the GFP intensity using a custom MATLAB code. All data was graphed in OriginPro (OriginLab, 2019b). For F-actin analysis, z-projected images of cells (Phalloidin, 561nm; H2B-eGFP, 488nm) were histogram normalized, cropped, and Phalloidin intensity peaks counted using FastPeakFind (v.1.7), that surrounded the nucleus.

2.6. Statistical Analysis:

Linear mixed effects models were used for single impulse experiments to compare strain versus rotation or internal motion were run in R (RStudio, Version 1.2.1335; R, Version 3.6.1). To test for a relationship between D_eff or β and strain or repetitive loading, we used one-way ANOVAs and post-hoc t-tests with Bonferroni corrections for multiple comparisons. To test for relationships between relative displacement or F-actin analysis and loading treatment, linear mixed effects models (nlme package, Version 3.1–140) and one-way ANOVA were used. Post-hoc tests were performed with the emmeans package using Tukey’s HSD corrections for multiple comparisons (Version 1.4.3.01). Normality assumptions required for ANOVA were validated by testing the residuals of the model with the Shapiro-Wilk test and visual examination of qq-plots.

3. RESULTS

3.1. Validation of Device and Culture System

In order to test our hypothesis that high impulse loading would result in nuclear architecture remodeling, and would be correlated with alterations in biophysical features, we successfully implemented and achieved a damage model using custom culture wells, and a pressure chamber with a pneumatic loading device (Figure 1A). During the applied impulses, the thin PDMS-coated silicone membrane deflected into the gap between the glass coverslips with controlled strain magnitudes (approaching 25%) and rate of strain (approaching 150%/sec). The displacement of the membrane was dependent on the magnitude of the applied air pressure pulse (Figure 1B). An FE model estimated the strain of the substrate, which we assumed was transferred to the attached cells at defined locations (Figure 1C). Importantly, the system enabled the cell culture population to be exposed to a well-defined gradient of strain values, which further allowed us to track individual cells at specified locations and study the continuum of strains influencing cell and nuclear responses.

3.2. Quantitative Single Cell Measures of Nuclear Movement

Using a transgenic mouse in which the H2B histone is fluorescently tagged by GFP, we were able to image the nucleus of the neuronal cell without the addition of an exogenous fluorescent reporter (e.g. DAPI). We performed live cell imaging of neuronal nuclei prior to and every ten minutes after the high impulse load (Figure 2A). After a single impulse, we observed a subset of nuclei that experienced increased strain magnitudes also displayed lower nuclear movement when compared to controls, motivating additional methods to quantify behavior at both population and single-cell levels. Since we were observing alterations in nuclear movement through fluorescent intensity using the H2B-eGFP marker of the chromatin, we were unable to use current methods to quantify nuclear rotation [39,40]. Additionally, we noticed deformation of the nucleus and irregular movement of H2B-eGFP clusters which violated angular tracking algorithms. Instead, we were able to utilize edge detection and Fourier domain-based analysis [35,36], which enabled quantification of rotation (Figure 2B, Supplemental Figure 2A). Quantification of internal motion was accomplished using particle tracking methods of H2B-eGFP clusters visible via fluorescence microscopy (Figure 2C). The heterochromatin clusters were easily identified with the 10 min time step which was defined by the resolution of imaging system (Figure 2A, orange and yellow arrows). To validate our methods of nuclear movement, we binned and classified the nuclei in to Rotation/No Rotation and Internal Motion/No Internal Motion groups (Supplemental Figure 2A). Comparing our assessment of nuclear movement (i.e. rotation and internal motion) with three independent persons, we found our quantifications of nuclear movement to closely correlate (Supplemental Figure 1A).

3.3. Nuclear Movement Altered with Increasing Strain

When we examined rotational values of the nucleus compared to strain magnitudes, we observed a significant decreased in rotation with increased strain (p = 0.03), but not D_eff (p = 0.2) or β (p = 0.3) (Figure 3A). However, when the same nuclei were binned according to strain levels expected to impact axons in neuronal injury [15–17], we found significant increases in D_eff (p < 0.0001) and decreases in β (p = 0.0017) between control nuclei and those nuclei at the high strain level. While we had significant differences in D_eff and β between the strain levels, the derived parameters did not show trends with increased strain magnitudes (Figure 3B).

3.4. Repeated High Impulse Loading Increases Dynamic Behavior of the Nucleus

To further investigate the observed nuclear behavior, neuronal nuclei were subjected to repetitive high impulse loads under the same experimental design (Figure 4A). Quantified values of rotation did not show significant differences with repetitive loading (p = 0.5) (Figure 4B, Supplemental Figure 3B) However, D_eff and β showed a load-dependent response independent of strain magnitudes. D_eff showed a significant increase in the Impulse ×4 treatment compared to control nuclei (p < 0.0001), and additionally to the Impulse ×1 treatment (p < 0.0001). Likewise, a significant decrease in β was observed between the Impulse ×4 treatment compared to control nuclei (p = 0.0009), and compared to the Impulse ×1 treatment (p < 0.0001) (Figure 4B). Further morphological analysis of nuclei which received high strain (>18%), did not show alterations in biophysical features at different time steps (Supplemental Figure 4).

3.5. Repeated Loading Decreased Intranuclear Movement within the Nucleus

Intranuclear movement assessed by deformation microscopy decreased inversely with increased repetitive loading (Figure 5A and B). Comparing the three loading treatments to control nuclei after the first impulse (10 min), decreased displacement of chromatin movement was observed for all nuclei (Figure 5C). A significant decrease in displacement was found between Impulse ×4 and controls for all time steps analyzed (p = 0.04).

Figure 5: Deformation microscopy reveals decreased chromatin displacement over time after high impulse loading.

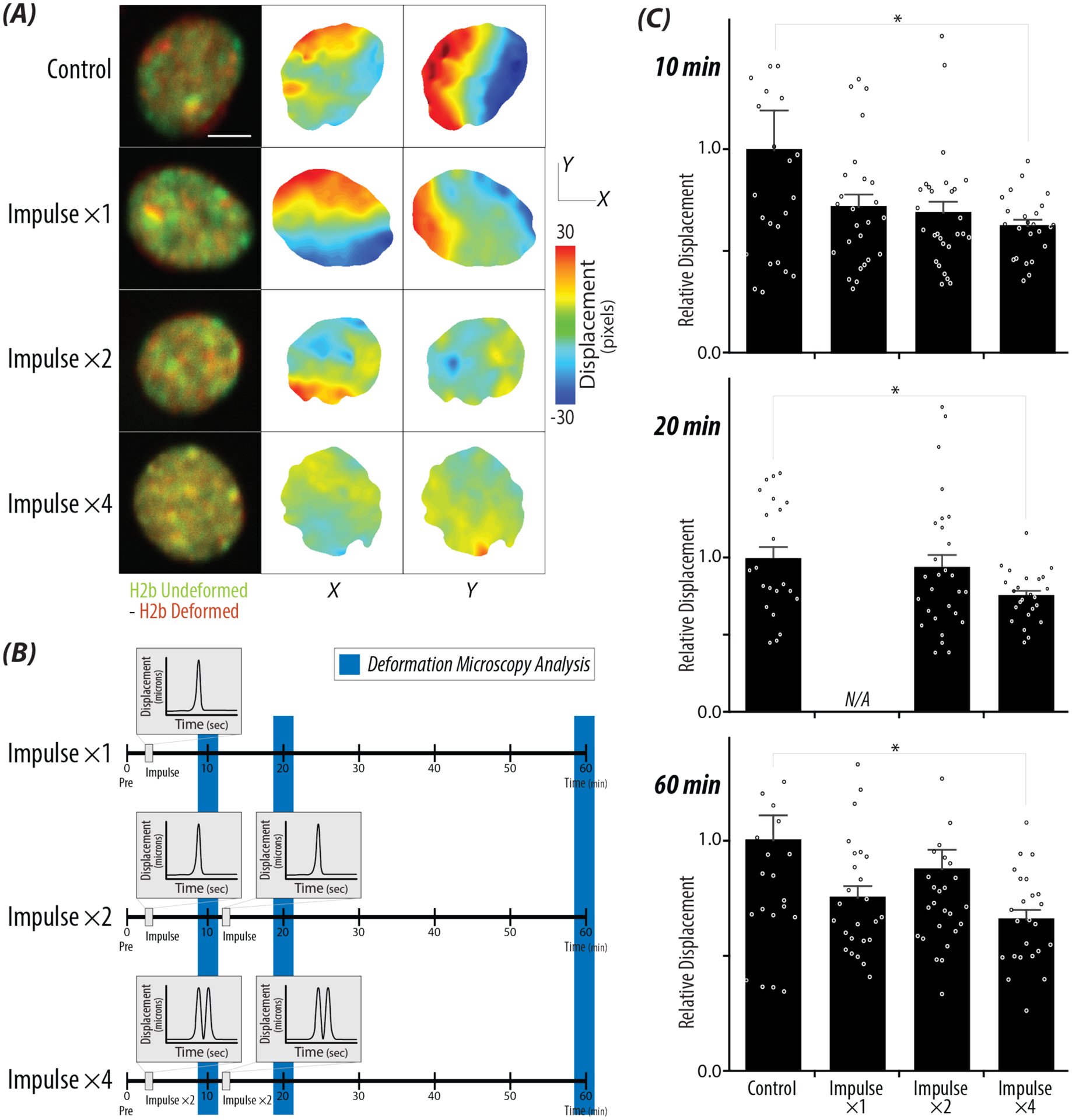
A) Overlayed represented images of control nuclei and nuclei that received high strain (>18%) at time steps: Pre (green) vs 60 min (red). Displacement maps in the x and y directions were generated using deformation microscopy, showing decreased displacement between the four loading treatments (Control, ×1, ×2, ×4), scale bar = 5μm. B) Repetitive loading schematic with blue bars represents the time steps that correspond to the bar graphs in Figure 5C. C) Relative displacements calculated from the sum of the xy displacement values of each nucleus comparing the Pre image to the selected timepoints: 10 min, 20 min, and 60 min. A significant decrease in the absolute displacement for Impulse ×4 compared to control cells for all timepoints. Error bars = SEM, n>20 nuclei/treatment, N > 4 animals. *p < 0.05.

3.6. Altered Microenvironment Surrounding the Nucleus

Having observed decreased nuclear movement with increase loading and high strains, we examined mechanisms of force transmission into the nucleus. After receiving a high impulse load, neuronal nuclei had increased F-actin (Phalloidin) intensity and increased F-actin puncta surrounding the nucleus, represented by white arrows (Figure 6A). Interestingly, F-actin puncta counts showed a dose-dependent response to repetitive loading regardless of strain magnitudes. Compared to control nuclei, significant increases in puncta were observed at all treatment levels (Impulse ×1, p = 0.0001; Impulse ×2, p <0.0001; Impulse ×4 p <0.0001) (Figure 6B). Furthermore, among the repetitive loading groups, Impulse ×1 and Impulse ×4 also demonstrated a significant (p = 0.02) dose-dependent increase with loading.

Figure 6: Repetitive loading results in increased F-actin puncta surrounding the nucleus regardless of strain.

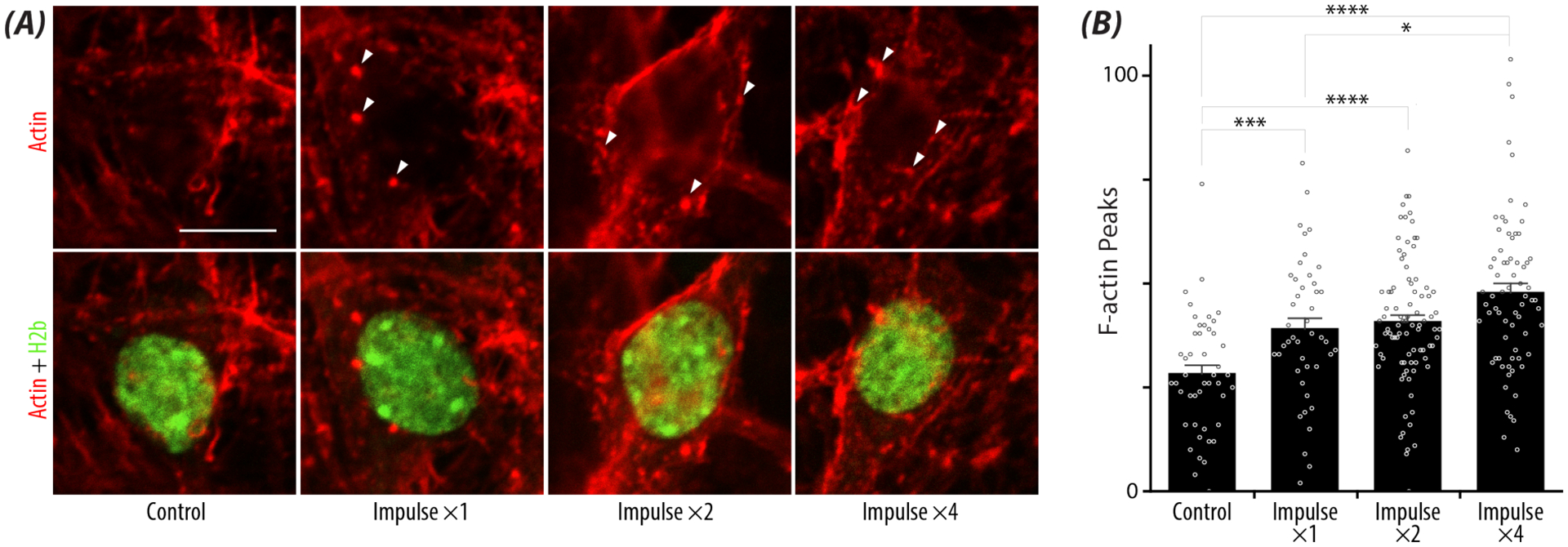
A) Representative images depicting F-actin puncta (Phalloidin Texas-Red, white arrows) surrounding the nucleus (GFP) at high strain (>18%) with repetitive high intensity loading. scale bar = 10μm. B) Bar plot represents the increased F-actin puncta surrounding the nucleus with repetitive loading compared to controls. Error bars = SEM. n> 44 nuclei/loading treatment, N = 3 animals. *p < 0.05, **p < 0.01, ***p < 0.001, ****p<0.0001

4. DISCUSSION

In this study, we present collective nuclear responses through a custom designed pneumatic system to observe biophysical perturbations in response to high intensity applied loads. This device allowed us to explore the mechanosensitive nature of the neuronal nucleus, in addition to the extent that mechanoreciprocity between the nucleus and environment exists or is stabilized following mechanical impulse. Using imaging methods, we present a combination of imaging techniques for quantitative assessment of nuclear behaviors in a physiological model of high intensity loading to neuronal cells. We reveal an altered nuclear behavior through quantitative measures of rotation and internal motion at higher strain magnitudes, and found this response to be exaggerated with repetitive loading regardless of strain. Mapping chromatin movement or reorganization using deformation microscopy, we further examined decreased intranuclear movement with increasing numbers of mechanical impulses. Examining the cytoskeletal network surrounding the nucleus, we observed increased F-actin puncta with repetitive loading independent of strain magnitude.

High intensity loading revealed that the neuronal nucleus demonstrates altered nuclear behavior in response to both strain magnitude and repetitive loading. Comparing low strain versus high strain magnitudes for a single impulse, we found decreased rotation, an increased in effective diffusivity (D_eff) and a decrease in the diffusive exponent (β). Examining the nuclear behavior with repetitive loading regardless of strain magnitude, we observed an increased in the effective diffusivity, a decrease in the diffusive exponent, and decreased in total chromatin movement using deformation microscopy. Together these results show distinct patterns of how mechanical energy dissipation during neuronal cell stretching influences nuclear mechanics. At high strain magnitudes and increased loading, the nucleus became more diffuse and decreased movement of heterochromatin domains within the nucleus. The increases in the effective diffusivity and decreased diffusive exponent could mean a softening of the nucleus and more elastic response after high impulse loading [38,41]. High resolution image registration further revealed that even if intranuclear movement was observed, there was a decrease in chromatin reorganization (measured by displacement) within the nucleus. The quantification of these four parameters could indicate a potential protective mechanism of energy conservation used by the nucleus to dissipate the mechanical energy after cellular stretch [2,23].

Rotation and intranuclear movement (i.e. internal motion) have mainly been described as healthy part of cellular activity [42–44]. In oocytes, nuclear rotation is observed in areas within the ovary that experience large mechanical stresses (compression) from tightly packed cellular areas with increased F-actin stress fibers [44]. At the same time, in 2D monolayer culture, manipulation nuclear mechanics though designed mutations in the nuclear lamina impedes nuclear rotation and results in an altered cellular environment through uncoordinated motion [45]. Taken together, these reports demonstrate continue crosstalk between the surrounding environment and nuclear behavior. Additionally, studies of intranuclear movement with neuronal interphase nuclei show that rotational nuclear actions (spin) were described to be sensitive to cellular calcium [46]. During traumatic neural injury, large calcium fluxes have been reported in response to cytoskeletal damage and plasma membrane disruptions [7,47]. Given these large influxes of extracellular calcium, it might be expected that increased nuclear movement should occur. However, responses of neuronal cells have shown to not elicit the same biochemical response (measured through calcium influx) at same strain magnitudes and can have transient activation within the different regions of the cell in response to applied force [48,49]. This heterogeneity in response to applied loading could partially explain the different nuclear behaviors of the neuronal cells observed in our study.

Depending on the nature of the mechanical load, the soma could experience both the high mechanical energy from axonal stretch and disruptions in membrane integrity. To prevent further secondary damage, nuclear movement involving molecular trafficking and stress response repair processes may help alleviate additional damage. We did not observe significant cell death or nuclear collapse (data not shown) within our system at either high strain magnitudes or repetitive loads. However, other studies using in vitro models of axonal damage haven seen delayed cellular death over the course of hours in response to both high strain magnitudes and strain rates [19,47], beyond the 60 minute window of observation utilized in our study. Increased incubation time after axonal injury might have revealed a correlation between altered nuclear behavior and cellular death. At the same time, increased incubation time after loading would have introduced secondary biochemical effects and which could have influenced or confounded our understanding of cellular instability within the cultures.

The cytoskeleton is responsible for transmitting force directing from the microenvironment into the nucleus with direct linkage to the nuclear envelope resulting in both morphological alterations and fluctuations in nuclear movement [29,38]. These movements have been linked with a “push-pull theory” involving cytoskeletal proteins that allow the nucleus to translocate within the cell [42,50]. Within neurons, actin is found in mainly in the dendrites, adjacent to the plasma membrane, and supports part of the tensile load [7]. In migrating neurons, researchers demonstrated that disruptions of the actin cytoskeleton and depolymerization of the microtubules separately abrogated nuclear rotation and translation [40]. In non-migrating cells, actin has been suggested to play a role in both rotation and internal motion [51]. As the nucleus is directly tethered to the extracellular environment though the cytoskeletal connections with integrins, we postulated that disruption of the actin cytoskeleton as seen by the F-actin puncta might explain this divergent nuclear response. Additionally, in vitro models of axonal stretch injury have shown low strain (<5%) and repetitive loading correlating to mild axonal injury has large effects on F-actin stabilization within the neuron [52].

Large heterogeneities have been described in both neuronal culture systems and in the neuronal cell morphology themselves. Morphological analysis of the cell shape and profile can differ greatly within the same culture [47]. More specifically in our in vitro damage model, differences in cellular orientation in relation to the direction of the uniaxial stretch might explain some of the quantified variance of nuclear behavior at the same strain magnitude. If the cell was oriented in the direction of uniaxial stretch, or alternatively if the axon experienced a higher load, the nucleus may have displayed decreased movement. At the same time, if the cell was perpendicular to the uniaxial stretch, the nucleus and axon may receive similar and comparatively lower stain magnitudes leading to energy dissipation in the soma, and attenuation of high strains transferred to the nucleus. Even within the nucleus, we observed heterogeneity of the heterochromatin H2B-eGFP cluster displacement with time in response to mechanical loading. Explanation for this intranuclear fluctuation mainly at higher strain magnitudes could be due to a DNA damage response within particular H2B-eGFP (heterochromatin) clusters. DNA damage in transcriptionally repressed chromatin foci were shown to have a time-dependent and increased intranuclear movement compared to bulk chromatin motion [53], which could form the focus of future studies.

It should be noted that the collective response captured in this work only examined the immediate nuclear behavioral response within 60 minutes of high intensity loading, and nuclear movement might have resumed if monitored for a longer time duration. While the single impulse data displayed trends of decreased intranuclear movement at high strain magnitudes, there was large variance in nuclear response on the single cell level. Additionally, with the categorical strain levels for a single high intensity load, increasing the sample sizes of nuclei per strain level (n>17 nuclei/strain level) could improve the observed effects of significance with the decreased nuclear movement.

Categorizing intranuclear movement through rotation and internal motion at a single cell level did present limitations in defining nuclear behavior in response to loading. Large alterations due to nuclear shape changes increased variances at all strain magnitudes in response to high impulse loads. While endogenous GFP signal in the nucleus allowed for us to observe nuclear movements free of the addition of dyes or fluorescent probes, the more diffusive GFP signal resulted in fewer (e.g. 2–15) H2B-eGFP clusters available for particle tracking, which could be improved for a more detailed movement analysis in nuclei. However, at a population level we found these methods captured the decreases in intranuclear movement we had observed visually. Used together, the derived parameters from the power law equation and deformation microscopy provide a powerful tool for defining nuclear mechanics.

While there are clear trends of collective nuclear responses to high intensity loads, there exists heterogeneity in the results, especially when analyzing results at specific strain magnitudes. As this research aimed to quantify biophysical nuclear perturbations in response to mechanical loading, it was necessary to only examine strain magnitudes and strain rates that have been shown to elicit a cellular response and not cellular death. Given the complex nature of TBI and the resulting cellular damage, understanding how different regions of the cell receive mechanical loads could provide further insight into the ensembled stress response. Quantified mechanically-induced alterations in nuclear behavior help to further define nuclear biomechanics, and more specifically in this study, in the context of trauma or injury. In conclusion, we present several methods for quantitative assessment of nuclear behaviors, responses, and mechanics in a physiological model of traumatic neural injury. This study may provide additional insight into damage mechanisms that could persist after a mechanical insult and contribute to secondary injuries after trauma.