Experimental validation of Monte Carlo dosimetry for therapeutic beta emitters with radiochromic film in a 3D‐printed phantom

Abstract

Purpose

Validation of dosimetry software, such as Monte Carlo (MC) radiation transport codes used for patient‐specific absorbed dose estimation, is critical prior to their use in clinical decision making. However, direct experimental validation in the clinic is generally not performed for low/medium‐energy beta emitters used in radiopharmaceutical therapy (RPT) due to the challenges of measuring energy deposited by short‐range particles. Our objective was to design a practical phantom geometry for radiochromic film (RF)‐based absorbed dose measurements of beta‐emitting radionuclides and perform experiments to directly validate our in‐house developed Dose Planning Method (DPM) MC code dedicated to internal dosimetry.

Methods

The experimental setup was designed for measuring absorbed dose from beta emitters that have a range sufficiently penetrating to ∼200 μm in water as well as to capture any photon contributions to absorbed dose. Assayed ¹⁷⁷Lu and ⁹⁰Y liquid sources, 13–450 MBq estimated to deliver 0.5–10 Gy to the sensitive layer of the RF, were injected into the cavity of two 3D‐printed half‐cylinders that had been sealed with 12.7 μm or 25.4 μm thick Kapton Tape. A 3.8 × 6 cm strip of GafChromic EBT3 RF was sandwiched between the two taped half‐cylinders. After 2–48 h exposures, films were retrieved and wipe tested for contamination. Absorbed dose to the RF was measured using a commercial triple‐channel dosimetry optimization method and a calibration generated via 6 MV photon beam. Profiles were analyzed across the central 1 cm² area of the RF for validation. Eleven experiments were completed with ¹⁷⁷Lu and nine with ⁹⁰Y both in saline and a bone equivalent solution. Depth dose curves were generated for ¹⁷⁷Lu and ⁹⁰Y stacking multiple RF strips between a single filled half‐cylinder and an acrylic backing. All experiments were modeled in DPM to generate voxelized MC absorbed dose estimates. We extended our study to benchmark general purpose MC codes MCNP6 and EGSnrc against the experimental results as well.

Results

A total of 20 experiments showed that both the 3D‐printed phantoms and the final absorbed dose values were reproducible. The agreement between the absorbed dose estimates from the RF measurements and DPM was on average −4.0% (range −10.9% to 3.2%) for all single film ¹⁷⁷Lu experiments and was on average −1.0% (range −2.7% to 0.7%) for all single film ⁹⁰Y experiments. Absorbed depth dose estimates by DPM agreed with RF on average 1.2% (range −8.0% to 15.2%) across all depths for ¹⁷⁷Lu and on average 4.0% (range −5.0% to 9.3%) across all depths for ⁹⁰Y. DPM absorbed dose estimates agreed with estimates from EGSnrc and MCNP across the board, within 4.7% and within 3.4% for ¹⁷⁷Lu and ⁹⁰Y respectively, for all geometries and across all depths. MC showed that absorbed dose to RF from betas was greater than 92% of the total (betas + other radiations) for ¹⁷⁷Lu, indicating measurement of dominant beta contribution with our design.

Conclusions

The reproducible results with a RF insert in a simple phantom designed for liquid sources demonstrate that this is a reliable setup for experimentally validating dosimetry algorithms used in therapies with beta‐emitting unsealed sources. Absorbed doses estimated with the DPM MC code showed close agreement with RF measurement and with results from two general purpose MC codes, thereby validating the use of this algorithms for clinical RPT dosimetry.

1. INTRODUCTION

Nuclear medicine clinics worldwide are seeing an increase in the number of available radiopharmaceutical therapy (RPT) options. ¹ , ² In addition to the well‐established ⁹⁰Y microsphere radioembolization (RE) for hepatic malignancies, ¹⁷⁷Lu peptide receptor radionuclide therapy (PRRT) for neuroendocrine tumors and ¹⁷⁷Lu radioligand therapy for prostate cancer have both been recently approved. Even new applications of ¹³¹I, the classical therapy radionuclide used for decades in radioiodine therapy, are emerging. ³ Alongside the rise of these new therapeutic applications comes a renewed interest in individualized dosimetry‐guided treatment planning. Accurate absorbed dose data is also required for answering key questions that remain in the field; such as what absorbed dose–response relationships exist, what scale of dosimetry is necessary, and how spatial distribution affects outcomes. ⁴

RPT, unlike brachytherapy or external beam radiotherapy (EBRT), commonly relies on ligand or antibody uptake in the specific cancer cell, or its close neighbors, in order to deliver a therapeutic dose of radiation. This process is inherently dependent on the cell function and distribution on a microscopic level and absorbed dose may be very nonuniform over even a couple of millimeters. This is in stark contrast to EBRT where the known beam geometry covers a much larger area, and any given pulse of radiation can be relativity flat across the beam. Even in brachytherapy, the applicators are, relative to the size of a cell, quite large and absorbed dose approximations can be made reliably, as the radiation is applied using a fixed geometry. The dependence on a nonuniform, microscopic geometry paired with short‐range beta emitters in RPT increases the need to validate the absorbed dose calculation software at very short distances.

Experimental absorbed dose validation for radionuclides such as ⁶⁰Co or ¹³⁷Cs used in EBRT has been widely achievable with the use of ionization chambers or thermoluminescent dosimeters (TLD), ⁵ , ⁶ due to the photon component being used for therapy. Radionuclides with less penetrating radiations, such as ¹⁷⁷Lu used in radiopharmaceutical therapies, require geometries and methods not commonly available in commercial systems in order to directly measure the beta contribution of the absorbed dose. Low energy betas may lack the penetration distance necessary for ion chamber measurement and the liquid nature of the therapeutic agents makes contamination an additional challenge that must be overcome when using TLD's or similar detectors.

In order to directly and reliably measure the beta contribution of absorbed dose a detector must be placed sufficiently close to a liquid source and have a repeatable geometry. Both RF and gel dosimetry can fit this niche need. Gel dosimetry has been shown to be a viable measurement system for beta particles from ⁹⁰Y brachytherapy seeds, ⁷ and further investigation may be warranted in future studies. For a much simpler, more accessible, and less costly measurement, film dosimetry has proven to be a reliable method of acquiring high resolution data one plane at a time. Film dosimetry has a rich history in EBRT measurements with its use in a variety of applications from megavoltage beam commissioning to small field and in‐vivo measurements. ⁸ Given the thin (∼25 μm) active layer, high resolution, and low dependence on absorbed dose‐rate and particle energy, ⁹ RF can also be easily extended for use in beta measurements relevant to RPT.

The ongoing interest in these low energy beta measurements has prompted other experiments with Tiwari et al., ¹¹ demonstrating the use of RF measurement for ⁹⁰Y and ¹⁷⁷Lu at distances between 1 mm and 15 mm from the source, although the first 1–2 mm of the film was impacted by delamination. Their experimental configuration showed good correlation with GEANT4 Application for Tomographic Emission (GATE) ¹² MC at these distances and incorporated direct measurement of the beta, gamma, and bremsstrahlung portions of the deposited dose. The experimental geometries and materials used for their research allowed for effective measurement of absorbed dose from the ⁹⁰Y beta in all three of the common clinical mediums: soft tissue, lung, and bone; however, direct measurement of ¹⁷⁷Lu was restricted to only lung equivalent materials due to the significantly shorter maximum beta range, 1.8 mm in tissue for ¹⁷⁷Lu versus 11 mm ¹³ in tissue for ⁹⁰Y. As many of the currently used or experimental beta emitters have low average electron energies (Table 1), the majority of their absorbed dose will be deposited in path lengths shorter than 1.5 mm, and a different geometry is required for comprehensive absorbed dose validation work in this space.

TABLE 1.

Beta emitters of interest in RPT and their physical characteristics ¹⁰

Nuclide	Half‐life	Mean beta energy (keV)	Maximum beta energy (keV)	CSDA range for maximum beta energy (mm)
177Lu	6.71 d	133	497	1.8
124I	4.18 d	188	610	2.3
131I	8.02 d	182	606	2.3
153Sm	46.3 h	225	705	2.8
186Re	3.72 d	323	1070	4.4
89Sr	50.5 d	583	1490	7.1
188Re	17.0 h	765	2120	10
90Y	2.67 d	934	2280	11

Note: Continuous slowing down approximation (CSDA) range is an approximation of the average distance traveled by a charged particle. The displayed CSDA range only includes the range of the highest energy beta for the radionuclide.

Villarreal‐Barajas et al. ¹⁴ attempted RF measurement of betas at distances as short as 104 μm from a liquid ¹⁵³Sm source in an acrylic phantom. Their experimental results showed excellent agreement with film measurement with depths between 416 μm and 832 μm, having agreement within 5%. They noted that films closer than 416 μm ended up damaged during removal from the phantom, which highlights the complexity involved in both being close to a liquid source and avoiding contamination or other damage when doing so.

The MC method is a valuable tool for radiopharmaceutical therapy dosimetry, especially when voxel‐level estimates are of interest. As detailed in a recent publication, ¹⁵ there are multiple general purpose and specialized MC codes that can be used for dosimetry with explicit radiation transport using the patient's own anatomical and emission images as well as for generating the kernels for dose kernel convolution methods. ¹⁶ , ¹⁷ While direct MC radiation transport is generally accepted as superior to convolution using MC‐derived dose kernels, it is computationally very demanding and can be associated with long simulation times to obtain good statistics when general purpose codes (e.g., MCNP, EGSnrc, and GATE) are used.

To overcome this, the specialized MC code Dose Planning Method (DPM) ¹⁸ was originally developed at the University of Michigan for fast absorbed dose estimation in EBRT. DPM achieves its significant speed‐up over conventional MC via special transport mechanics that permits long transport steps across heterogeneous boundaries. The accuracy of DPM at energies and geometries relevant to EBRT has previously been demonstrated by benchmarking against measurements. ¹⁹ , ²⁰ Since DPM was optimized specifically for absorbed dose computations in voxel geometries, in particular, those derived from CT scans, it is perfectly suited for patient‐specific absorbed dose estimation in RPT. Therefore, we previously adapted DPM for RPT applications by sampling decay locations internally within the voxelated geometry. ²¹ We have previously demonstrated the use of DPM for efficiently performing direct MC dosimetry in patients undergoing ¹³¹I radioimmunotherapy, ²² , ²³ radioiodine therapy, ^{24 90}Y radioembolization, ²⁵ and very recently ¹⁷⁷Lu‐DOTATATE peptide receptor radionuclide therapy. ²⁶ Thus far, DPM benchmarking for RPT consisted of comparison with estimates from EGS4 and OLINDA. ²¹ , ²² Although some initial measurements with TLDs were performed to experimentally validate the photon contribution, ²¹ no experimental validation of the beta component of DPM was undertaken at the time, due to the challenges associated with the short range. To our knowledge, prior experimental studies undertaken by others have also not attempted to directly measure absorbed dose deposition in water equivalent or high‐density mediums by beta emitters that have a range as low as that of the betas associated with ¹⁷⁷Lu.

Motivated by the recent surge in interest in RPT dosimetry and the scarcity of experimental measurements relevant to validating dosimetry calculations in RPT, our goal was to design a practical and reproducible experimental setup for measuring the absorbed dose deposited in water/tissue by beta emitting therapy radionuclides. We then use our experimental setup to perform a full (electron + photon components) validation of our in house DPM MC code for ⁹⁰Y and ¹⁷⁷Lu. Secondary benchmarking of Monte Carlo N‐Particle version 6.2 ²⁷ (MCNP6) code as well as the general purpose EGSnrc ²⁸ against the experimental results was also performed, as both are widely available/used for RPT dosimetry.

2. MATERIALS AND METHODS

2.1. Experiments

Two types of measurements were performed with the RF. The first was a measurement of absorbed dose to a single sheet of film (SF) and the second was measurement of radionuclide depth dose (DD) curves using a stack of films. Absorbed doses were measured for ¹⁷⁷Lu (in the form of ¹⁷⁷Lu DOTATATE) and ⁹⁰Y (in the form of ⁹⁰YCl₃) in saline (S) and a bone (B) equivalent solution. Two different thicknesses of tape (used between the film and the radioactive solution) were tested for ¹⁷⁷Lu. The nomenclature used to identify each experiment is indicated in the last column of Table 2.

TABLE 2.

Variations in experimental setup parameters

Radionuclidea	Measurement type	Liquid solution	Measurement depth (mm)	Kaptonb Tape Thickness		Repeat measurements	Experimental setup name
177Lu	Single Film	Saline	0.2032		25.4μm	4	Lu177SF,S,25.4
	Single Film	Saline	0.1651		12.7μm	2	Lu177SF,S,12.7
	Single Film	Liquid bone	0.2032		25.4μm	3	Lu177SF,B,25.4
	Depth dose	Saline	0.2032–1.3152		25.4μm	2	Lu177DD,S,25.4
90Y	Single film	Saline	0.2032		25.4μm	4	Y90 SF,S,25.4
	Single Film	Liquid bone	0.2032		25.4μm	2	Y90 SF,B,25.4
	Depth dose	Saline	0.2032‐2.7052		25.4μm	3	Y90 DD,S,25.4

^a177Lu DOTATATE [Novartis], ⁹⁰Y Chloride [Eckert & Ziegler]

^bUsed to seal the solution

2.1.1. Phantom design

The main challenges with experimental measurements that are relevant to RPT dosimetry are the short beta particle ranges and the need to have the radioactive material in liquid form. These considerations were key to our final design of the phantom, which is shown in Figures 1 and 2.

FIGURE 1.

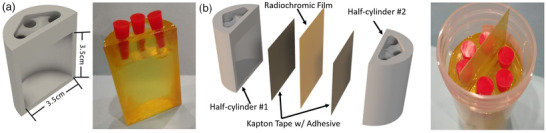
3D CAD cross‐sectional and photo views of a phantom half‐cylinder (a) alongside entire assembly views of the taped and filled finished product with exploded CAD model (b). Three filling ports with corks for sealing (red objects in (a and b)) were used to facilitate the filling process and reduce back pressure.

FIGURE 2.

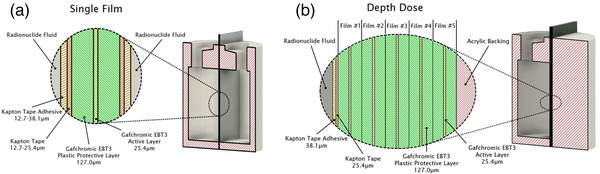
Cross‐sectional view of each material layer at the center of the single film phantom to measure absorbed dose‐to‐closest‐layer phantom (a) and stacked film phantom to measure absorbed depth dose (b). Five and 10 film layers were used for ¹⁷⁷Lu and ⁹⁰Y, respectively.

The phantom was modeled using computer aided design (CAD) software and 3D‐printed utilizing a Form 2 printer using stereolithography in a photopolymer resin. Each phantom was designed as a half‐cylinder with an open cavity and three top holes used for filling the volume with the radioactive liquid as seen in Figure 1. The phantom cavity size was chosen to provide a smooth absorbed dose distribution across the center 1 cm × 1 cm area of the film measurement. External dimensions were modeled to fit inside a standard 90 ml urine sample container, commonly found at most hospitals, in order to contain inadvertent leakage.

After printing, the model was allowed to dry for 24 h. All excess support structures were manually removed, and the front face of the phantom was sanded with a 400 grit diamond plate to improve tape to surface adhesion. A 3.8 cm by 6 cm length of Kapton tape ²⁹ was mounted across the front of the phantom to enclose the cavity. These taped phantoms were used as the core component in all validation procedures and allowed for a wide variety of experiments to be performed (Table 2) with consistent reproducibility.

Gafchromic EBT3 was cut into 3.8 cm × 6.0 cm strips using a Full Spectrum Laser Hobby Series 20×12 CO Laser Cutter, and a small watermark was cut into the top right corner to provide consistent orientation during post‐exposure film scanning. Strips were sandwiched in between two taped half‐cylinder phantoms before insertion into the standard specimen container per Figure 2.

2.1.2. Activity measurement and solution preparation

The ¹⁷⁷Lu and ⁹⁰Y activities used for the different experiments ranged from 13 MBq to 450 MBq. Injected activity levels were selected to minimize both exposure during phantom handling and cost while providing absorbed dose in the sensitive range for EBT3 ⁹ in each configuration. Prior to each experiment, the necessary exposure time was estimated by scaling the Monte Carlo predicted dose rate for each geometry by a number of decays until the film absorbed dose was within this sensitive range. This total number of decays was combined with the available radionuclide activity to estimate the required exposure time. Activities were measured in a Capintec 15R dose calibrator within a 10 cc syringe. The dial setting used was 55 × 10 for ⁹⁰Y ³⁰ and 48 × 10 for ¹⁷⁷Lu. The setting for ¹⁷⁷Lu was determined by a dial setting transfer performed in house to match activity readings for a 10 cc syringe and for a Schott vial with the NIST recommended setting ³¹ of 449 × 10. The activity solutions were combined in a 60 cc syringe with either ∼30 cc of saline or bone equivalent liquid that included ethylenediaminetetraacetate (EDTA) to avoid any potential absorption from heavy metal radionuclides into the walls of the container.

The bone equivalent liquid was prepared by combining deionized water with K₂HPO₄ salt at a ratio of 100 g for salt per 67 g water, which results in density and linear attenuation coefficient close to that of cranial bone. ³² The phosphate‐buffered saline mixture was assembled with 1× PBS at 7.3 pH with EDTA added until a concentration of 2.5‐μM EDTA ³³ was reached. For the bone equivalent solution, the EDTA salt was mixed directly into the solution until a concentration of 2.5‐μM was reached.

2.1.3. Measuring absorbed dose to closest layer using a single film

A single strip of 3.8 cm by 6.0 cm Gafchromic EBT3 film was placed between the two phantom halves and then secured in a standard specimen container. A cross‐sectional view of each material layer is shown in Figure 2a. Two phantom halves were each enclosed with Kapton tape (12.7 or 25.4 μm) and filled with radioactive solution. The entire center cavity of each phantom half was filled for a total of ∼33 cc of fluid, ∼16.5 ml in each half. The semiclear nature of the 3D print material allowed for visual confirmation of the solution level in each phantom during filling. Precise solution volumes were calculated from calibrated digital scale measurements of the empty, filled, and residual syringes as well as the empty and full phantoms. Phantoms were shielded and secured in locked facilities for 3–47 h before the film was removed.

2.1.4. Measuring absorbed depth dose using stacked films

Measurement of radionuclide‐absorbed depth dose curves was also completed using a very similar phantom setup, except that only one phantom half was used in this case. The single phantom half was enclosed with 25.4 μm thick Kapton tape and filled with radioactive solution. The cavity of the single phantom half was filled full, resulting in a total of ∼16.5 ml of solution. Five (for ¹⁷⁷Lu measurements) to 10 (for ⁹⁰Y measurements) 3.8 cm by 6.0 cm Gafchromic EBT3 films were placed in between the single phantom half and a backscatter stack of water equivalent acrylic and then secured in a standard specimen container. A cross‐sectional view of the layers are shown in Figure 2b. Phantoms were shielded and secured in locked facilities for 20–48 h before the stack of films was removed.

2.2. Film analysis

Post‐exposure optical film scanning was done on an EPSON XL10000 flatbed scanner at 200 dpi with all image correction features turned off. All films were centered in the middle one‐fourth of the scanner to avoid lateral response artifacts, and a glass compression plate was used to prevent deformation of the film during scanning.

2.2.1. Calibration films

Calibration films were created on a Varian TrueBeam Linear Accelerator that was calibrated per TG‐51 standards ⁵ using a 6 MV photon beam. Ten calibration films were created over a 0–1850 cGy range with a geometric dose sequence at 0, 79.7, 159.5, 319.0, 478.4, 717.7, 877.1, 1116.4, 1594.8, and 1834.0 cGy. Eight additional calibration films were created at the same time as a secondary validation set for checking the accuracy of the final fits. The average difference between our calibration curve and the calibration check films in our measured range was 0.1%, and the maximum difference for a single film was 2.2%.

The 10 original calibration films were optically scanned and used to fit a continuous calibration curve for each of the red, blue, and green color channels. Triple‐channel dosimetry optimization methods ³⁴ were used to help correct the scanned images for all measurements. The reported absorbed dose values were computed from the triple‐channel optimization reported red channel values. The calibration fits were created in FilmQA Pro ³⁵ using their color rational cubic fit shown in Equation (1) and Figure 3 where X(D) is the color channel value, A, B, C, E, and F are the cubic fit parameters, and D is the known delivered dose.

$$X\left(D\right)=\frac{\left(A+BD+C{D}^2+E{D}^3\right)}{\left(D+F\right)}$$ (1)

FIGURE 3.

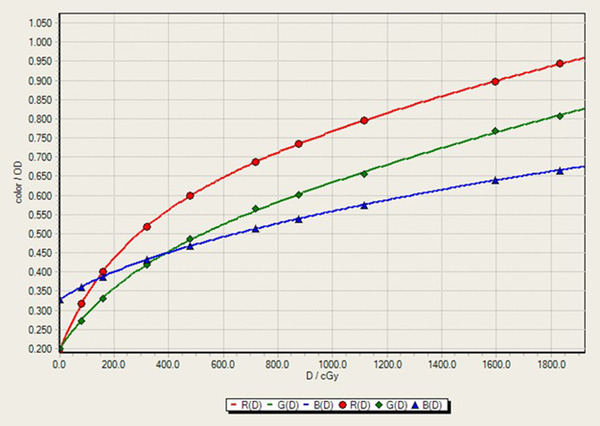
Rational cubic film calibration curve 150 h after initial exposure.

2.2.2. Experimental film analysis

Film analysis was performed using FilmQA Pro software. Each experimental film was optically scanned with both the measurement film and an unexposed film strip from the same sheet of EBT3 in a single session. All experimental film measurements were analyzed using a film calibration from the same film production batch as the experiment. An average over the 1 cm × 1 cm square at the center of the exposed film area was used to calculate the mean dose to the film.

Compensation for post exposure film darkening, ³⁶ often accomplished by using the single scan protocol, ³⁷ was instead corrected by closely matching the post‐exposure optical scan time between the calibration strips and the experimental measurements as well as using the dose shift single point recalibration provided by Ashland. ³⁸ Equation (2) gives the dose shift single point recalibration with X(D) being the RGB value, D as the original dose, and x and a as scaling factors calculated from the differences between the experimental scan's unexposed film and the calibration scan's unexposed film.

$$X\left(D\right)=x\left(a+D\right)$$ (2)

All ⁹⁰Y experiments were allowed between 145 h and 176 h for development while ¹⁷⁷Lu films were measured between 45 and 100 h. Calibration curves were rescanned to match the experimental film development time with no more than a 4% difference in total film development time for the ¹⁷⁷Lu and a maximum 11% development time difference for ⁹⁰Y.

2.3. Monte Carlo simulations

Simulations of the experiments were performed using our in‐house DPM program as well as two general purpose MC codes: MCNP and EGSnrc. A computational phantom for DPM, MCNP, and EGSnrc was created based on the material and geometry specifications of the 3D‐printed phantom, the Kapton tape and manufacturers specifications for Gafchromic film. The material compositions were obtained from Compendium of Material Composition Data for Radiation Transport Modeling ³⁹ and RADIOCHROMIC FILM: Role and Applications in Radiation Dosimetry ⁹ and are given in Table A5. As DPM is designed to perform dose transport on voxelized geometries (for example, patient PET/CT or SPECT/CT images), the phantom design was voxelized. The voxel size was chosen to be 1.25 × 1.25 × 0.0127 mm to model the thin film layers, while keeping the total calculation time and memory requirements reasonable. No attempt was made to match the simulation voxel size to the flatbed scanner pixel dimensions, as the average over the 1 cm² center of the film was well sampled in both situations and finer MC binning would significantly increase runtimes. This voxelization caused only <1.2% difference in the film thickness and <5.2% difference in the Kapton tape thickness (TablesA2 and A3). The voxelization of the phantom also caused all computational phantom material thicknesses to be somewhere between the average physically measured dimensions and the manufacturers specified thicknesses; therefore, we have high confidence in the final model.

The simulated phantom was specified as filled to 3.5 cm high, reaching the bottom of the insertion holes, with water (Figure 1). This filled water volume in the phantom was used to define the volume containing the radioactive solution with a uniform activity distribution throughout.

The beta energy spectra for all simulations were those generated by BetaShape software version 1.0 available from the Laboratoire National Henri Becquerel. ⁴⁰ Photon, X‐ray, auger electron, and electron capture spectrums were acquired from NuDat 3.0 via Brookhaven National Laboratory. ⁴¹ Simulations for ⁹⁰Y included only the beta energy spectrum, and no transport was attempted on any X‐ray, auger, or conversion electron portions of ⁹⁰Y decay due to their minimal contribution to absorbed dose. Simulation for ¹⁷⁷Lu did include modeling of X‐rays and monoenergetic electrons. No attempt was made to model absorbed dose contribution from contaminants that may be present in the radionuclide solution, such as ^177mLu in ¹⁷⁷Lu DOTATATE, ⁴² or ⁹⁰Sr in ⁹⁰Y‐Cl₃, ⁴³ depending on the method used to produce the radionuclide.

In the DPM simulations, low energy beta and photon cutoffs were set to 20 keV and 4 keV, respectively, and the energy of source betas and/or X‐rays born below or reaching the respective cutoffs was deposited locally. To test the validity of this assumption, we started with a much higher beta cutoff (100 keV) and re‐ran with lower cutoff values until the difference in absorbed dose‐rate values was <0.5%. With the mean free path of ∼0.1 mm for a 4 keV photon in tissue being less than the minimum distance from the fluid to the active layer of the radiochromic film (∼150 μm) and only ∼7% of the total absorbed dose coming from photons, we did not observe meaningful differences when lowering the cutoff under 4 keV. A total of 8 billion decays spread uniformly throughout the solution were simulated, giving an uncertainty of <0.5% in the center 1 cm² of the first film of each simulation. Run times varied depending on the isotope from 13 h to 90 h of CPU time on a 2.7 GHz Intel Xeon E5‐2697v2.

MCNP calculations were defined in the same way as the DPM setup, with a few exceptions. Instead of a uniform voxel distribution, the geometry was defined via MCNP's macrobody and universe style definitions. The same beta and photon spectra and electron yields described above for DPM were included for transport in MCNP. Energy cutoffs were matched to the DPM run. MCNP simulations were run for 1 billion histories, due to the much longer run times of a general purpose MC code, giving an uncertainty of <1.0% in the center of each film. Run times varied, depending on the isotope from 880 to 3690 h of CPU time on a 3.4 GHz AMD Threadripper 1950x. MCNP simulations were run on 16 processors to obtain results in <10 days.

EGSnrc calculations were also defined as close to the DPM setup as possible. Instead of a uniform voxel distribution, the geometry was defined via EGSnrc's C++ geometry module. The same beta and photon spectra and electron yields described above for DPM were included for dose transport in EGSnrc. Energy cutoffs and number of histories were matched to the DPM run. This gave an uncertainty of <0.5% in the center of each film. Run times varied depending on the isotope from 46 h to 562 h of CPU time on a 3.4 GHz AMD Threadripper 1950x.

3. RESULTS

A total of 55 films were analyzed over the course of 20 experiments. The first plot in Figure 4 shows all experimental absorbed dose readings versus the DPM predictions across a wide range of dose (41.7–1561.6 cGy). The central plot in Figure 4 shows experiment versus MCNP calculations for all experimental configurations, and the final plot shows experiment versus EGSnrc.

FIGURE 4.

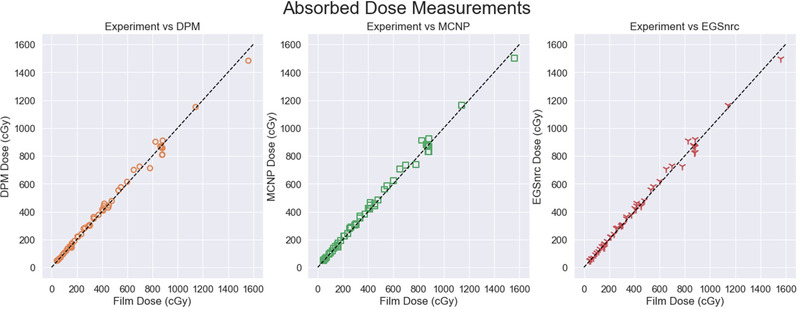
Complete experimental absorbed dose comparisons across all doses, measurements, and computation engines. Identity line shown in black.

Horizontal and vertical profiles from all MC simulations as well as experimental measurement from our single film geometry, Figure 5, show the design provides a uniform absorbed dose region across the center film planes.

FIGURE 5.

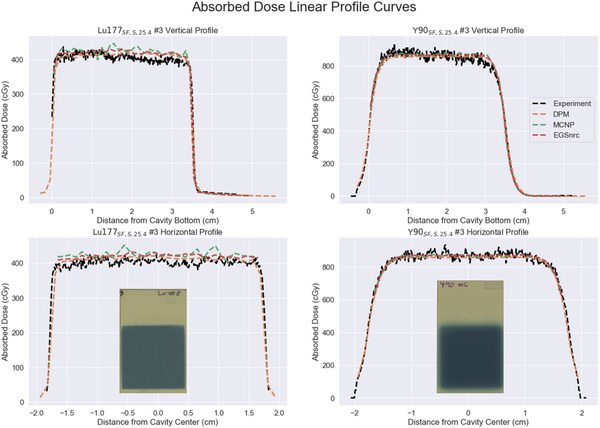
Vertical and horizontal linear profiles for both evaluated radionuclides. Profiles were obtained from single film experimental geometries with a saline medium. Scanned images of representative exposed films are inset under each horizontal profile.

3.1. Single film results: Dose to closest layer

The agreement between measurement and each of the three MC estimated absorbed doses are given in Table 3 for the different single film experiments. The agreement between the absorbed dose estimates from the RF measurements and DPM was on average −4.0% (range −10.9% to 3.2%) for all single film ¹⁷⁷Lu experiments and was on average −1.0% (range −2.7% to 0.7%) for all single film ⁹⁰Y.

TABLE 3.

Average value of differences between absorbed doses from experimental measurement and estimates by DPM, MCNP, and EGSnrc MC codes for the single film setup. The standard deviation in the dose rate is calculated across repeat measurements for each film setup

Experiment	Repeat measurements	Measurement depth (mm)	Experiment dose rate (μGy/GBq × s)	DPM vs. Experiment (%)	MCNP vs. experiment (%)	EGSnrc vs. Experiment (%)
Lu177SF,S,25.4	4	0.2032	123.1 ± 4.1	−1.1	1.4	1.1
Lu177SF,S,12.7	2	0.1651	153.3 ± 1.2	−0.6	1.7	1.3
Lu177SF,B,25.4	3	0.2032	96.9 ± 1.2	−10.2	−6.8	−8.2
Y90SF,S,25.4	4	0.2032	3495.3 ± 51.1	−1.2	0.0	0.1
Y90SF,B,25.4	2	0.2032	2438.9 ± 26.8	−0.4	1.5	1.1

The contribution from the beta emissions to the total absorbed dose deposited in the single films was calculated with MC, which showed that the primary contribution to the absorbed dose was indeed the beta particles for all configurations. Absorbed dose to the Lu177 _SF,S,25.4 film was 93% from the beta, Lu177 _SF,S,12.7 was 94%, and Lu177 _SF,B,25.4 was 90%. The conversion electrons and auger electrons contributed <0.15% of dose to the first layer of the film. The rest of the contribution (7 to 10%) in the ¹⁷⁷Lu experiments is from photons (X‐rays and gamma‐rays), which are dominated by the emissions at 113 keV and 208 keV. ⁴¹ Dose from ⁹⁰Y experiments was considered to be effectively 100% from the betas as no other starting particles were simulated due to their negligible dose contributions. All dose from secondary particles, that is, Bremsstrahlung, was grouped as part of the starting particle dose estimate in the MC simulation tallies.

3.2. Stacked film results: Depth dose

The agreement between measurement and DPM, EGSnrc, and MCNP estimated absorbed doses is given in Table 4 as well as Figures 6 and 7 for the different stacked film experiments. Depth dose estimates by DPM agreed with RF measurement on average 1.2% (range −8.0% to 15.2%) across all depths for ¹⁷⁷Lu and on average 4.0% (range −5.0% to 9.3%) across all depths for ⁹⁰Y. At the deepest measured depth (1.3152 mm), the ¹⁷⁷Lu film measurement received only 5.9% of the absorbed dose that the shallowest film (0.2032 mm) received.

FIGURE 6.

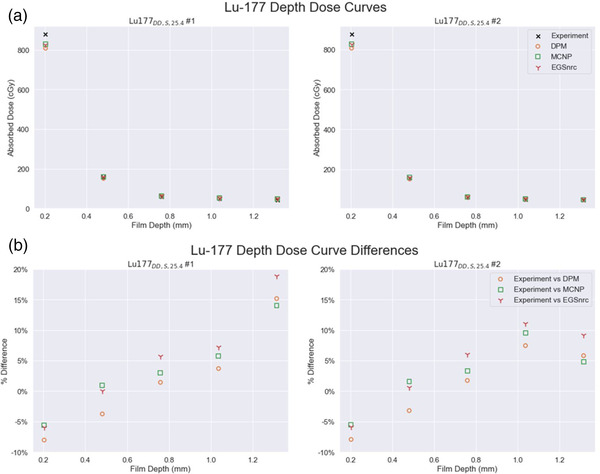
Depth dose curves for both ¹⁷⁷Lu depth dose experiments showing (a) absolute absorbed dose values (b) percentage differences relative to experiment

FIGURE 7.

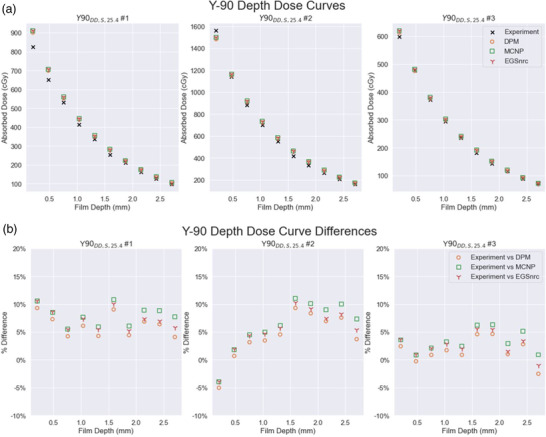
Depth dose curves for three ⁹⁰Y depth dose experiments showing (a) absolute absorbed dose values and (b) percentage differences relative to experiment

MC simulations predicted that absorbed dose from betas was 92.8%, 63.5%, 13.2%, 1.6%, and 1.2% of the total (betas + others) going from the film closest to the ¹⁷⁷Lu solution to the furthest as seen in Figure 8, indicating a large component of the beta dose was measured across our design.

FIGURE 8.

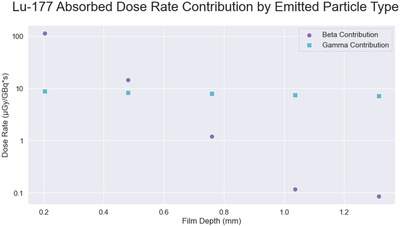
Absorbed dose contribution from beta and gamma. Values calculated in DPM for the Lu177_DD,S,25.4 experimental geometry

The measured absorbed doses for ⁹⁰Y showed closer agreement to the MC code estimates than the ¹⁷⁷Lu across all 10 depths. Absorbed dose to the 10th film (2.7052 mm) was 11.4% of the dose to the shallowest (0.2032 mm). Due to the longer range of the ⁹⁰Y beta, complete measurement across the entire beta range was not attempted with this phantom geometry.

MC calculations done using EGSnrc, MCNP, and DPM agreed with each other across the board, within 4.7% and within 3.4% for ¹⁷⁷Lu and ⁹⁰Y, respectively, for all geometries and across all depths.

3.3. Uncertainty estimation

Overall uncertainty in the measurement was determined by evaluating the level of reproducibility across repeated experiments. Table 2 shows each of the seven experimental setups along with the number of times each experiment was attempted, with two to four repetitions for any given configuration. The coefficient of variation of the absorbed dose rate across all the runs of each setup was between 0.0% and 4.5% for the¹⁷⁷Lu experiments and 1.0–6.0% for the Y‐90 experiments. The coefficient of variation for single films was 0.5–3.0% (Table 3) and for the depth dose measurements 0.0–6.0% (Table 4).

TABLE 4.

Average value of differences between absorbed doses from experimental measurement and estimated by DPM, MCNP, and EGSnrc MC codes for the depth dose setup. The standard deviation in the dose rate is calculated across repeat measurements for each film depth

Experiment	Repeat measurements	Depth (mm)	Experiment dose rate (μGy/GBq × s)	DPM vs. Experiment (%)	MCNP vs. Experiment (%)	EGSnrc vs. Experiment (%)
Lu177DD,S,25.4	2	0.2032	132.1 ± 0.1	−8.0	−5.6	−5.9
		0.4812	23.6 ± 0.1	−3.5	1.3	0.3
		0.7592	8.9 ± 0.0	1.6	3.2	5.9
		1.0372	7.2 ± 0.2	5.6	7.6	9.1
		1.3152	6.6 ± 0.4	10.5	9.4	14.0
Y90DD,S,25.4	3	0.2032	3371.2 ± 237.6	2.2	3.4	3.5
		0.4812	2601.4 ± 102.3	2.6	3.7	3.8
		0.7592	2050.9 ± 34.4	2.7	4.0	4.0
		1.0372	1614.3 ± 34.2	3.8	5.3	5.0
		1.3152	1290.7 ± 25.8	3.2	4.8	4.4
		1.5932	983.5 ± 24.5	7.6	9.4	8.6
		1.8712	791.1 ± 16.3	5.8	7.5	6.6
		2.1492	626.2 ± 20.7	4.9	6.9	5.4
		2.4272	483.7 ± 11.5	5.6	8.0	6.2
		2.7052	384.4 ± 14.3	1.8	5.3	3.4

Although individual components contributing to the uncertainty in the recorded dose‐rates are difficult to measure and uncertainty propagation challenging, some estimates can be made. The use of the Capintec 15R dose calibrator for each of the radionuclide activity measurements provides a high degree of accuracy. Zimmerman et al. ³⁰ gives ∼1–2% uncertainty for a ⁹⁰Y Capintec 15R measurement using a 10 ml syringe and Denis E. Bergeron and Jeffrey T. Cessna ³¹ estimate their dose calibration uncertainty at ∼1%. The geometry dependence of the dose calibrator reading was also verified to have a minimal impact on our activity measurement (Figure A2), and a sensitivity analysis was completed to estimate potential error in activity measurement across both dose calibrators and dial settings (Table A1). The uncertainty in the phantom fluid‐volume measurement that also contributes to the uncertainty in the activity is expected to be negligible based on the scale validation data given in Figure A1.

Variability in experimental geometry for any given experiment was evaluated by repeated caliper measurements of the 3D‐printed phantom, Kapton tape, and RF. Agreement between the 3D print and the CAD design was within ∼3% (Table A4), except for wall thickness, which is not expected to impact the overall dose‐rate measurement. Variation in Kapton film thickness was 4–5% (Table A3) and RF layer thicknesses was ∼1% (Table A2).

Among factors associated with RF measurement/calibration uncertainty are calibration curve fitting and postexposure film darkening. The uncertainty associated with film calibration curve fitting is estimated as 0.1% on average and up to 2.2% for any given film (Section 2.2.2). Variations in postexposure film darkening were evaluated across multiple postexposure timepoints from 1 to 400 h for a subset of the experiments. Both calibration films and experimental films were rescanned at eight postexposure timepoints, and dose to the central 1 cm² was measured to quantify the variation in only using a single recalibration film strip. This rescanning protocol also evaluates the overall film analysis repeatability by including variation in flatbed scanner light/heat levels, film position on the scanner, among other things. A standard deviation of 4.4% was found across the varied postexposure readout film subset, giving us high confidence in the repeatability of the film analysis procedures.

Statistical uncertainties associated with the MC simulations were well under 0.5% according to the estimates provided by all three MC codes, with the shorter 1 billion history MCNP runs having the highest uncertainties. Potential uncertainty in the simulations due to parameters such as photon or electron cutoffs, step size, and the voxelization sizes are expected to be larger contributions than statistical uncertainty and are estimated at ∼0.5% (Section 2.3)

4. DISCUSSION

Experimental validation of the absorbed dose estimation step is critical for clinical translation of dosimetry‐guided RPTs. This is, however, rarely undertaken due to the challenges of measuring dose deposited in tissue by short‐range particles such as the betas associated with ¹⁷⁷Lu. In this study, we design, construct, and test a simple phantom for RF film‐based measurement of beta and gamma components of ¹⁷⁷Lu and ⁹⁰Y absorbed doses, which is then used to validate our in‐house developed DPM MC dosimetry code. The single film geometry provided for a wide variety of experiments to be performed, allowing for several aspects of the setup to be tested independently without substantial increases in time or experimental complexity. Variations on the transport medium, either saline or bone equivalent fluid, and depth to the film, via Kapton tape thickness, were easily implemented. Further changes to the 3D‐printed cavity height, depth, or shape for any given radionuclide have not been evaluated yet, but the platform we have developed will allow such evaluation in the future. The depth dose measurements showed the high level of agreement between DPM and experiment in regions both dominated by beta energy deposition and by photon deposition. Figures 6b and 7b show the relative differences between DPM, MCNP, and EGSnrc versus the experiment. When the DPM versus experiment difference increases, the MCNP versus experiment difference and EGSnrc experiment difference also increase, and vice versa. While the magnitude of the difference for each comparison varies, the overall trends match across all three MC simulations.

Dose to film for both measured radionuclides showed excellent agreement with DPM regardless of experimental setup, with an average of −4.0% for all single film ¹⁷⁷Lu experiments, 1.2% for depth dose ¹⁷⁷Lu, −1.0% for single film ⁹⁰Y, and 4.0% for depth dose ⁹⁰Y (Tables 3 and 4). The average difference between measurement and simulation was within the overall measurement uncertainty estimated from the repeats. While four of the five single film experimental geometries showed an average agreement of <2% with DPM, the bone liquid experiment (Lu177 _SF,B,25.4) was an outlier with a 10.2% difference between measurement and simulation. With both MCNP and EGSnrc also showing relatively large discrepancies compared with experiment, 6.8% and 8.2%, respectively, experimental setup variation associated with the challenges of working with the bone liquid is likely the primary factor for this disagreement. Additional investigation using FilmQA Pro revealed larger nonuniformities in the vertical and horizontal film profiles than was seen in other experimental setups. Mixing of the thick bone solution with the ¹⁷⁷Lu DOTATATE may have been insufficient during the filling procedure, potentially creating nonuniform distributions within the phantom volume. We did not see mixing issues with the ⁹⁰Y chloride in bone solution; however, the chloride's yellow tint helped verify the solution was uniformly mixed, whereas the DOTATATE was translucent.

When validating Monte Carlo codes, multiple factors such as step size, cutoff energies, material/geometry specifications can contribute to the difference between experiment and simulation. While specifications for the composition of the phantom material, RF and the Kapton tape were available, ⁹ , ³² the composition of the silicone adhesive on the tape was not provided by the vendor and was estimated using the entry for silicone. However, the impact of the adhesive material composition appears to be minimal, because the percent difference between absorbed dose‐rates from experiment and simulation were very similar when using a much thinner tape/adhesive combination in the ¹⁷⁷Lu experiments (Table A3). Additionally, micrometer measurements of multiple film sheets and measurements within any given sheet of RF show close manufacturing tolerances within the film itself, measuring within 3 μm of specification for the film base, active layer, and total thickness (Table A2). Similar evaluation of the 3D‐printed phantoms also provided good agreement in every batch of 3D prints (Table A4).

The radiochromic film energy dependence between the 6 MV calibration energy and the much lower energy betas of ¹⁷⁷Lu and ⁹⁰Y is expected to be minimal as the electron restricted stopping power ratios between EBT3 and water over the 10 keV–10 MeV range show minimal variation. ⁴⁴ A 6 MV photon beam was chosen due to the extensive validation of absorbed dose delivery, and because such beams should be readily available at other institutions. Other photon energies may be used for calibration ⁸ ; however, use of low energy photon sources (<50 keV) may need alternative procedures or calibration factors. The dose‐rate dependence for EBT3 is minimal, ⁹ and prior studies with beta‐emitting eye plaques have successfully irradiated RF to 30 Gy over 1 week, ⁴⁵ which is ∼18 cGy/h compared to the ∼1–100 cGy/h used in our study.

The use of relatively low activity radionuclide sources resulted in long exposure times (3–48 h) for the validation measurements in our study. A portion of the polymerization process that would typically be considered “post‐exposure” is now taking place alongside the experimental polymerization, as the absorbed dose slowly builds up over a course of days. As the postexposure polymerization can be approximated by logarithmic fits, ³⁶ the majority of the additional development happens in the first 24–48 h. In addition, the rate of change in net optical density is dependent on the initial deposited dose, with higher doses having significantly higher rates of postexposure polymerization. This makes matching calibration curve postexposure time development to experimental postexposure time development in RPT applications more complicated than in traditional EBRT film studies. We have chosen to extend our calibration and experimental scan times to help compensate for any initial changes in optical densities, but this is an issue that may need further investigation in the future.

Prior work on experimental measurement of short‐range beta emitters has shown the viability of using RF as an effective measurement tool for these radionuclides but lacks the capability to reliably measure at short distances, where a large portion of the dose is deposited for many radionuclides of interest. Tiwari et al. ¹¹ was able to measure beta energy deposition above 1 mm, and Villarreal‐Barajas et al. ¹⁴ showed the potential to measure at 0.104 mm, but found damage to their first three layers of RF, and recorded their first clean measurement at 0.416 mm. It is unclear if the geometry proposed by Villarreal‐Barajas et al. would be reliable at 0.416 mm or at any lower distances as only a single measurement appears to have been attempted. The 3D‐printed phantom developed for this study has shown the ability to both place the RF within 0.1651 mm cleanly and repeatedly.

Future refinements for the phantom would include optimizing the cavity shape/volume for different radionuclides and for depth dose measurements would include using less sensitive film (EBTXD) closer to the source and more sensitive (EBT3) further away. Our work could also be extended to other radionuclides not evaluated in the current study including alpha particle emitters. With thinner Kapton tape and delaminated RF, one can measure the absorbed dose from particles with ranges below 100 μm.

5. CONCLUSION

The experimental measurements presented in this work validates both electron and photon components of our in‐house DPM internal dosimetry code, which we had previously only performed for photons using TLDs. Furthermore, the experimental setup we present can be used in other clinics for validating their internal dosimetry calculations/software. Despite the extensive checks and verifications completed while performing the absorbed dose measurements the overall process is straightforward and able to be completed in any hospital that has access to RF dosimetry equipment. The level of repeatable results using this relatively simple inexpensive design across experiments was encouraging for future endeavors. The 20 experiments performed in this setup showed that the combination of 3D printing and film measurement can provide a viable base for inexpensive repeatable measurements that could be used for one time validation or continued (annual) quality assurance in almost any clinic. For short‐range radionuclide that have increased sensitivity to any variation in experimental setup, we were able to obtain measurements with low standard deviations.

Validation of DPM showed remarkably good agreement with experimental measurement, for both single and depth dose geometries, between experiment and DPM, with an average difference of <4%. Experiments that did show higher variation from the DPM calculated values also showed high deviation with the two other MC codes, indicating DPM's transport methodology was likely not the source of disagreement. With the consistent repeatability of experimental setup and measurement, the low level of differences between DPM, MCNP, and EGSnrc, and the high level of agreement between MC and experiment, DPM has shown itself to be a reliable dose transport engine for photons and short/medium range betas relevant to RPT.

CONFLICT OF INTEREST

The authors have no conflicts to disclose.

A. VERIFICATION OF EXPERIMENTAL PARAMETERS

When using experimental measurement to validate MC simulation, it is imperative that physical properties such as material composition, material thicknesses, and injected activities used in the MC model be highly accurate. For this work, we carefully verified these parameters as shown below.

A1. Activity Verification

Activity measurements used in this study were taken using a Capintec 15R dose calibrator. For Y‐90, the Capintec 15R activity measurements were checked against two other dose calibrators in our pharmacy. A sensitivity analysis was completed to estimate potential error in activity measurement across both dose calibrators and dial settings Table A1. All activity measurements were taken in a 10 cc syringe placed in the center of the dose calibrator holder

A2. Activity/experimental process verification

The phantom radionuclide activity was calculated based on the weight of the saline injected into the phantom. These injections ranged between 30 ml and 35 ml per experiment and was measured on an available digital scale. We performed a calibration for the scale, which is shown in Figure A1. Calibration was completed across the 1–50 g range, and no major deviations were seen over the measured range.

The syringe used for activity injection into each phantom was also checked to make sure the dose calibrator activity in the syringe was consistent over the entire range of 0–10 ml for ¹⁷⁷Lu. Figure A2 shows the dose calibrator reading from <0.5 ml to >9.5 ml and which has good linearity over the whole range, so no additional calibration curve was applied to the dose calibrator readings.

A3. Physical model dimension verification

Both Gafchromic EBT3 film and Kapton tape thickness measurements were acquired using a Mitutoyo 293‐344‐30 micrometer. Three sets of measurements were taken at different points across three reference film cutouts to measure the total thickness and then the film was carefully peeled apart and each layer was measured individually. Results showed an active layer thickness of 25.1 μm and a base thickness of 128μm, very close to the values used in our simulation models, 25.4 μm and 127 μm respectively. These results are presented in Table A2.

Kapton tape thickness was measured at five locations across multiple strips of tape and averaged values are reported in Table A3. The tape is composed of two materials, a layer of Kapton film and a layer of silicone adhesive. Two tape thicknesses were used in our experiments: a 25.4 μm thick Kapton tape with a 38.1 μm thick adhesive layer, and a 12.7 μm thick Kapton tape with a 12.7 μm thick adhesive layer. Manual verification of the overall thickness of each tape strip showed close agreement with the manufacturer's listed thicknesses with ∼4–5% difference.

The 3D‐printed phantom was also measured using the same micrometer to verify printing tolerances. Three different phantoms were randomly selected, and four sections of the phantom were measured; the thickness of the top, the radial width, the thickness of the bottom and the side wall thickness. Table A4 shows the results with only the sidewall thickness showing a substantial deviation from the modeled values. This may be due to the interaction between the curvature of the wall and the micrometer's flat sensor face. It is not expected that the wall thickness will substantially affect the results in any way for this experimental design as the overall change in volume is negligible and any displaced fluid is not in near proximity to the film measurement.

A4. Simulation Material Compositions

Material compositions and densities for each simulation have been included in this appendix for future reference and/or result reproducibility.

FIGURE A1.

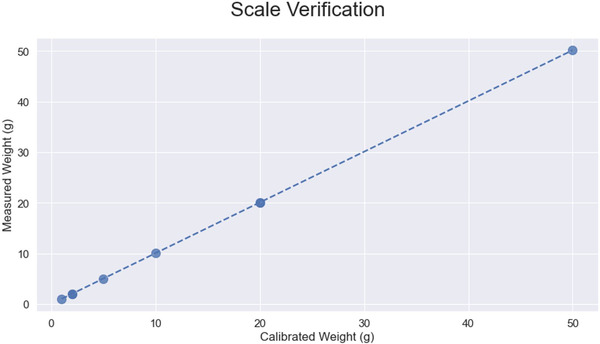
Measurement of scale linearity from 1 to 50g using calibrated weights.

FIGURE A2.

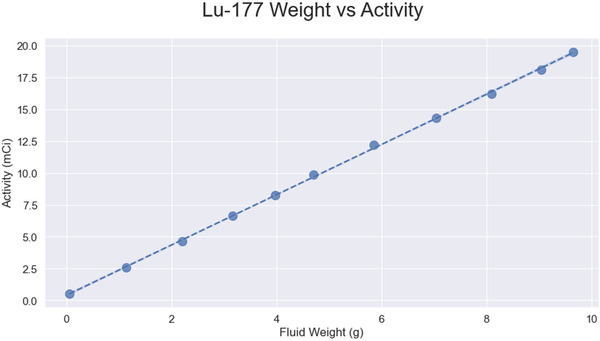
Variation in dose calibrator readout for ¹⁷⁷Lu 10cc syringe. Linear response across entire range of radionuclide fill level within syringe.

TABLE A1.

Sensitivity analysis for Capintec dose calibrators for Y‐90 syringe activity measurements

	Dose calibrator setting
	45	48	51	55	59	62
Capintec 15	0.43	0.43	0.42	0.41	0.39	0.38
Capintec 55	0.43	0.419	0.411	0.398	0.388	0.378
Capintec 55	0.413	0.404	0.395	0.383	0.373	0.363

TABLE A2.

Measured variation in EBT3 film layer thicknesses. Values averaged over three different films with three positions measured for each variable

	Measured Thickness (μm)	Manufacturer specification (μm)	DPMvoxelized thicknesses (μm)	% Difference MC modeled thickness vs. measured thickness
Base	128.0	125.0	127	0.78
Active	25.1	28.0	25.4	1.19
Total	281.8	278.0	279.4	0.85

TABLE A3.

Measured variation in Kapton tape with silicone adhesive. Values averaged over two different films with three positions measured for each thickness

	Measured thickness (μm)	Manufacturer specification (μm)	DPMVoxelized Thicknesses (μm)	% DifferenceMC modeled thickness vs. Measured thickness
25.4 μm Kapton	60.4	63.5	63.5	5.13
12.7 μm Kapton	26.4	25.4	25.4	3.79

TABLE A4.

Measured variation in 3D‐printed phantom thicknesses. Values averaged over three different phantoms with three positions measured for each variable

	Measured (mm)	Designed (mm)	% Difference
Radial depth	20.503	20.358	0.71
Wall thickness	3.318	3.000	10.61
Top thickness	11.861	11.500	3.13
Base thickness	3.969	4.000	0.78

TABLE A5.

Simulation materials and densities

Material	Density (g/cc)	Element	Atomic fraction
Water	0.998	H	0.333
		O	0.666
Polyester film base	1.20	H	0.364
		C	0.455
		O	0.182
Active film layer	1.35	H	0.568
		Li	0.006
		C	0.276
		O	0.133
		Al	0.016
Kapton polyimide film	1.42	H	0.256
		C	0.564
		N	0.051
		O	0.128
Kapton adhesive (rubber, silicon)	1.02	H	0.597
		C	0.199
		O	0.104
		Si	0.099
Liquid bone	1.55	H	0.509
		O	0.382
		P	0.036
		K	0.073

Van B, Dewaraja YK, Niedbala JT, et al. Experimental validation of Monte Carlo dosimetry for therapeutic beta emitters with radiochromic film in a 3D‐printed phantom. Med Phys. 2023;50:540–556. 10.1002/mp.15926