Bayesian Graphical Regression

Abstract

We consider the problem of modeling conditional independence structures in heterogeneous data in the presence of additional subject-level covariates – termed Graphical Regression. We propose a novel specification of a conditional (in)dependence function of covariates – which allows the structure of a directed graph to vary flexibly with the covariates; imposes sparsity in both edge and covariate selection; produces both subject-specific and predictive graphs; and is computationally tractable. We provide theoretical justifications of our modeling endeavor, in terms of graphical model selection consistency. We demonstrate the performance of our method through rigorous simulation studies. We illustrate our approach in a cancer genomics-based precision medicine paradigm, where-in we explore gene regulatory networks in multiple myeloma taking prognostic clinical factors into account to obtain both population-level and subject-level gene regulatory networks.

1. Introduction

Basic inferential problem.

Graphical models have been widely applied to investigate conditional (in)dependence structures in multivariate data in different domains and contexts. Specifically, for a p-dimensional random vector X = (X₁, …, X_p), a graphical model for X is defined by a tuple: ${\mathcal{G}}_X=\{G,\mathcal{P}(X)\}$, consisting of a graph G and an associated probability distribution $\mathcal{P}(X)$ (e.g., Gaussian distribution for continuous variables), respecting the conditional independence encoded by G. In many scientific contexts, it is possible that the graph structure G of the primary variables of interest (X) can change as extraneous factors change (e.g., experimental conditions). In this paper, we propose methods for modeling the conditional independence structure of X given another m-dimensional random vector U = (U₁,…, U_m), termed external covariates. The model thus defined as ${\mathcal{G}}_X(U)=\{G(U),\mathcal{P}(X\mid U)\}$ is treated as a regression function of the external covariates U (or simply covariates hereafter); hence, we have graphical regression such that the conditional independence structure is allowed to vary arbitrarily with different realizations of U. Concisely stated, the main inferential goals are (i) evaluate how graph topology changes over different realizations of U; (ii) select covariate (sub-)sets in U that have major impact on the graph topology; and (iii) allow for prediction, at both the node and graph structure levels, in the support of U. The conceptual frameworks introduced in this paper are generally applicable to any class of graphical models (undirected or directed) – the methodology we develop particularly targets directed graphical models.

The concept is illustrated through a toy example in Figure 1, where the directed graphs have p = 4 nodes and m = 2 covariates of which U₁ is continuous (horizontal axis) and U₂ is binary (vertical axis). For each column, the two graphs have both common and differential edges that correspond to the binary variable. For each row, the graphs are “evolving” with respect to the values of U₁. Figure 1 shows a snapshot of the “evolution” in the continuous space of U₁ at four arbitrary values. The thickness of the edge is proportional to its strength (e.g., posterior probability/partial correlation).

Figure 1:

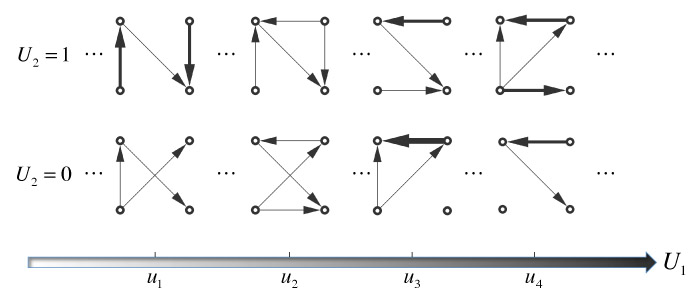
Toy example of directed graphs with four nodes and two external covariates. U₁ is continuous and U2 is binary. The edge thickness is proportional to its strength of association.

Scientific motivation.

The scientific motivation of this work stems from the fact that cancer is a heterogeneous disease at different molecular, genomic and clinical levels (Heppner and Miller, 1983). Thus, the paradigm in cancer treatment has shifted from the traditional “one-size-fits-all” approach towards developing personalized treatments that account for individual variability in genes and in clinical and environmental characteristics for each person – termed precision medicine (De Bono and Ashworth, 2010). In the context of clinical genomics, the development and progression of cancer is driven by sub-networks within the functional regulatory networks of genes and their products, which undergo changes in response to different patient-specific characteristics such as clinical prognostic factors and/or environmental stress conditions (Luscombe et al., 2004; Bandyopadhyay et al., 2010). To this end, recovering both population-level and subject-level gene regulatory networks and monitoring the changes in gene regulatory relationships as a function of a given patient’s clinical characteristics may assist in developing personalized treatment regimes that target specific pathway disruptions – and is, perhaps one of the most pertinent and pressing quantitative problems in molecular biology. Statistically, the challenge is to integrate the additional patient-level information (e.g., prognostic factors) for assessing the conditional independence structures in multivariate genomic data (e.g., gene expression data), as alluded to in the previous paragraph (Section 5 provides a more detailed exposition).

Existing approaches and limitations.

Traditional graphical models (Lauritzen, 1996) typically assume i.i.d. sampling and thus do not account for subject-specific heterogeneity. However, several attempts have been made to model the conditional independence structure in this challenging setting. For external covariates with discrete support, Oates et al. (2014) and Yajima et al. (2015) developed group-specific directed acyclic graphs (DAGs) to estimate differential networks for several related groups. Similarly, Guo et al. (2011), Danaher et al. (2014) and Peterson et al. (2015) studied group-specific graphical models for the undirected case. Geiger and Heckerman (1996) studied a context-specific DAG model in which the space of one node is partitioned, and each subspace defines a different DAG structure. In a similar spirit, Nyman et al. (2014) developed a context-specific undirected graphical model in which the structure changes with discrete nodes. Liu et al. (2010) proposed a graph-valued regression that discretizes the continuous covariate space into a finite number of subspaces by classification and regression trees and fits a separate undirected graph for each subspace. In essence, the infinite dimensional problem is reduced to a finite dimensional one. However, the estimated graphs may be unstable and lack similarity for close covariates due to the separate graph estimation, as reported by Cheng et al. (2014). In summary, these approaches allow graph structure to vary with an external covariate/node which must be discrete. Kolar et al. (2010a) proposed a penalized kernel smoothing approach for conditional Gaussian graphical models in which the precision matrix varies with the continuous covariates. Cheng et al. (2014) developed a conditional Ising model for binary data where the dependencies are linear functions of additional covariates. Although the methods of Kolar et al. (2010a) and Cheng et al. (2014) allow the edge strength to vary with the covariates, neither approach deals with a graph structure that changes with the covariates. From a machine learning perspective, Zhou et al. (2010) and Kolar et al. (2010b) proposed interesting time-varying undirected graph algorithms for time series data. The graph structure is allowed to change over time by borrowing strength from “neighboring” time points via kernel smoothing. The graph estimation problem is essentially broken down to separate estimation for each time point, for which the joint distribution is not well-defined. It is not straightforward to extend their methods beyond univariate case due to the curse of dimensionality of kernel methods (Scott, 2008), that is, “neighboring” points quickly become “distant” as dimensionality increases. In addition, extending to discrete covariates is also unclear with kernel-based methods.

Brief outline of our method.

In this paper, we overcome the challenges described above and propose a novel class of graphical models, graphical regression (GR), which has six major axes of innovation. (1) Non-stationarity: we allow both the edge strength and the structure of the graph to vary simultaneously with multiple covariates, which can be either continuous, discrete or a mixture of both. This allows the edge strength to vary smoothly with continuous covariates, which encourages similar graphs for similar covariate realizations. (2) Sparsity in both edge and covariate selection: sparsity is a critical assumption in a high-dimensional setting where the number of parameters is much larger than the sample size. Here, we impose two levels of sparsity: (i) sparsity in edge selection and (ii) sparsity in the relationship between edges and covariates. We select relevant edges through a thresholding parameter and select relevant covariates for each edge through a spike-and-slab prior formulation. (3) Functional nonlinearity in edge-covariate relationships: the relationships between edges and covariates are allowed to be nonlinear and are modeled using spline-based semiparametric representations. This allows the model to distinguish the functional form of the relationships (linear vs. nonlinear) through suitable orthogonal basis decompositions. (4) Accounting for subject-specific heterogeneity: the regression formulation of GR conveniently allows us to construct graphs that are subject-specific, which is often more appropriate than single (population-level) graphs in some contexts. For example, due to tumor heterogeneity, even patients with the same type of cancer are expected to have different structural changes in their molecular signaling pathways that are determined by their specific clinical characteristics. Hence, personalized gene networks recovered by GR may assist in developing precision medicine (tailored therapies) for treatment. (5) Prediction: our regression-based framework allows us to predict network structures for new patients. In doing so, we do not require new node-level data (e.g., gene expressions); rather, new covariates (e.g., prognostic factor levels) will suffice. (6) Selection theoretical justifications: our thresholded prior formulations for the edge/covariate selection connects to the spike-and-slab prior, a commonly used prior for Bayesian variable selection. Moreover, the “slab” part is shown to be equivalent to a non-local prior (Johnson and Rossell, 2010). Non-local priors tend to shrink small effect to zero which is desirable in our setting where we are only interested in edges with moderate to strong strength/effect. We show under certain conditions that the proposed prior achieves model selection consistency.

In essence, GR can be thought of as an infinite dimensional generalization of an ordinary DAG model that admits a fairly wide class of models. Special cases of GR include ordinary, conditional, time-varying, group- and context-specific DAG models (see detailed list at the end of Section 2.1). We compare GR to alternative and existing methods with extensive simulation studies and establish its superiority in terms of both model selection and prediction. We apply GR to multiple myeloma gene expression data and construct a subject-specific graph by incorporating important prognostic factors. While some of our results are confirmed by the existing biological literature, several interesting findings are potential targets for future validation studies. Furthermore, we develop an interactive web application to visualize and interpret the varying graph structures. Finally, we discuss the possibilities as well as challenges of extension to the undirected case in Section 6.

We remark that there is also a rich machine learning literature on dynamic Bayesian networks for time series data and causal inference (DBNs, Ghahramani (1998); Murphy (2002); Song et al. (2009); Robinson and Hartemink (2010); Grzegorczyk and Husmeier (2011); Dondelinger et al. (2013)) which is orthogonal to this work. DBNs focus on modeling temporal networks between time points and leave the network structure within each time slice unmodeled or fixed, which in our case is explicitly modeled by GR.

2. Model

2.1. Graphical regression

A DAG, G = (V, E), contains a set of nodes V = {1,…,p} and a set of directed edges E ⊂ V × V that does not contain any directed cycles. We denote a directed edge from node j to node h by h ← j. A DAG model ${\mathcal{G}}_X=\{G,\mathcal{P}(X)\}$ for X is a pair consisting of a graph G, for which the nodes V represent random variables X = X_V and an associated probability distribution $\mathcal{P}(X)$, respecting the conditional independence encoded by G. The joint distribution of X admits a convenient factorization $\mathcal{P}(X)={\prod }_{h=1}^p\mathcal{P}(X_h\mid X_{\mathit{pa}(h)})$, where pa(h) denotes the parent set of node h. Assuming that X follows a multivariate normal distribution, each conditional distribution $\mathcal{P}(X_h\mid X_{\mathit{pa}(h)})$ can be modeled by a linear regression, $X_h={\sum }_{j\in \mathit{pa}(h)}{X}_j{\beta }_{\mathit{hj}}+{ϵ}_h$ with ${ϵ}_h\sim N(0,{\sigma }_h^2)$ and β_hj ≠ 0 if and only if j ∈ pa(h). We assume that X is arranged according to a prior ordering such that β_hj = 0 for all h ≥ j, then pa(h) = {j ≥ h + 1: β_hj ≠ 0}. Without an ordering, DAGs within the same Markov equivalence class (i.e. DAGs with the same conditional independence structure) cannot be distinguished. In GR, we consider DAG ${\mathcal{G}}_X(U)=\{G(U),\mathcal{P}(X\mid U)\}$ and assume that $\mathcal{P}(X\mid U)$ factorizes according to a DAG,

$$\mathcal{P}(X\mid U)=\prod _{h=1}^p\mathcal{P}(X_h\mid X_{\mathit{pa}(h\mid U)},U),$$ (1)

where pa(h∣U), depending on covariates U, is the parent set of node h in graph G(U). In what follows, we call U the external covariates (or simply the covariates) and X the nodes. Each conditional distribution $\mathcal{P}(X_h\mid X_{\mathit{pa}(h\mid U)},U)$ is then modeled by

$$X_h=\sum _{j\in \mathit{pa}(h\mid U)}{X}_j{\beta }_{\mathit{hj}}(U)+{ϵ}_h.$$ (2)

We define B_hj(U) as a conditional independence function (CIF) since the event I{β_hj(U) = 0} determines the DAG structure which in turn encodes the conditional independence of X as a function of U. This is stated formally in the following lemma.

Lemma 1 (Functional Directed Pairwise Markov Property). Assuming the conditional distribution of X given U satisfies (1) and (2) and h < j. If I{β_hj(U) = 0} = 1, then X_h ⫫ X_j∣X_pa(h), U.

The proof of lemma 1 follows from the fact that I{βhj(U) = 0} = 1 implies there is a missing edge between h and j given U, which in turn implies that X_h ⫫ X_j∣X_pa(h), U by the directed pairwise Markov property (Lauritzen, 1996). GR is a fairly flexible class of models and has at least five special cases:

• (1)If U is empty, then GR reduces to the case of the ordinary Gaussian DAG model.
• (2)If U is discrete (e.g., binary/categorical group indicator), then β_hj(U) is group-specific and GR is a group-specific DAG model.
• (3)If U is taken to be the last node X_p, then GR can be interpreted as a context-specific DAG (Geiger and Heckerman, 1996) where the graph structure varies with X_p.
• (4)If the distribution of β_hj (U) is absolutely continuous with respect to Lebesgue measure, then GR is a conditional DAG model in which the strength of the graph varies continuously with the covariates but the structure is constant.
• (5)If U is univariate time points, then GR can be used for modeling time-varying DAGs. Given the CIFs β_hj (U), the likelihood of a GR can be expressed as

$$\mathcal{P}(\mathit{x}\mid \mathit{u},\beta ,{\sigma }^2)=\prod _{i=1}^n\prod _{h=1}^p{(2\pi {\sigma }_h^2)}^{-1∕2}\text{exp}\left[-\frac{1}{2{\sigma }_h^2}{\left\{x_{\mathit{ih}}-\sum _{j=h+1}^p{x}_{\mathit{ij}}{\beta }_{\mathit{hj}}({\mathit{u}}_i)\right\}}^2\right],$$ (3)

where β = (β_hj), ${\sigma }^2={({\sigma }_1^2,\dots ,{\sigma }_p^2)}^T$ and x, u are the n samples of X, U. In the following sections, we detail a methodological framework with the aim of making inference on the CIFs and consequently on a graphical regression model ${\mathcal{G}}_X(U)$.

2.2. Modeling the conditional independence function

We parameterize the CIF for a given edge h ← j as a product of two component functions, thresholding function,

$${\beta }_{\mathit{hj}}(U)=\underset{\text{smooth function}}{\underbrace{{\theta }_{\mathit{hj}}(U)}}\times \stackrel{\text{thresholding function}}{\overbrace{I\{\mid {\theta }_{\mathit{hj}}(U)\mid >t_{\mathit{hj}}\}}}$$ (4)

where the two components are (1) a smooth function θ_hj(·) of U to allow for both linear and nonlinear covariate effects and (2) a hard thresholding function, through a thresholding parameter t_hj to induce sparsity in the resulting graph structures. We discuss the need for and construction of the two components in detail below.

(1). Smooth function:

The parameterization of the CIF (β_hj) for a given edge in terms of a smooth function encapsulates the fact that we expect the presence of an edge and its corresponding strength to vary similarly for similar covariate values. This fact is captured through the smoothness of θ_hj(·) that encourages similar graphs for close realizations of covariates. In principle, the smooth function θ_hj(·) can be either specified by a parametric (e.g., linear) function or modeled semiparametrically or nonparametrically; we choose the latter to achieve greater flexibility by letting the model choose the appropriate structural form. Specifically, suppose U = (Z, W) consists of discrete covariates (with appropriate coding) Z = (Z₁,…, Z_r) and continuous covariates W = (W₁,…, W_q) with r + q = m. We construct θ_hj(·) through a structured additive model as

$${\theta }_{\mathit{hj}}(U)=\sum _{l=1}^r{\mathit{Z}}_l{\varphi }_{\mathit{hjl}}+\sum _{k=1}^q{f}_{\mathit{hjk}}(W_k),$$ (5)

where φ_hjl is the effect between the discrete covariate Z_l and the edge h ← j and f_hjk(·) is the functional relationship between the continuous covariate W_k and the edge h ← j. We assume f_hjk(·) to be smooth and do not specify a specific (parametric) functional form of f_hjk(·). In principle, f_hjk(·) can be modeled with any nonlinear functional representation, depending on the context of the application. For example, if the relationship follows a very localized (“spiky”) behavior, one could choose wavelets for f_hjk(·); similarly if the relationship follows a periodic pattern, Fourier bases could potentially be used. However, in the absence of such information, we model f_hjk(·) via spline-based semiparametric representations which allows graph structure to vary smoothly with external covariates. We defer the explicit formulation to Section 2.3 after we introduce the thresholding function.

(2). Thresholding function:

Now that we have defined θ_hj(U) as a smooth function of U, the solution is not sparse for any given realization of U (i.e., producing exact zeros). In other words, unconstrained estimation of θ_hj(·) might result in the graph structure having too many edges, some with very small magnitudes, which hinders both inference and interpretations (e.g., increased false positive edges). To account for this, we introduce an explicit thresholding mechanism through a parameter t_hj that admits sparsity, allowing the structure of β_hj to vary with U. This edge-specific parameter can be interpreted as a minimum effect size of the CIF. The thresholding mechanism is conceptually depicted in Figure 2, where the solid curve represents β(U), the dashed lines indicate the threshold t and the dotted curves are the part of θ(υ) that is thresholded to zero. Note that we do not fix the threshold t_hj a priori but instead estimate it a posteriori by imposing a prior distribution, which we discuss in Section 2.4. Other thresholding functions including soft thresholding and nonnegative garrote thresholding have been studied in different contexts. A soft thresholding (Donoho and Johnstone, 1995) has advantage of continuous shrinkage over hard thresholding. However, it also introduces a constant bias/deviation. A nonnegative garrote thresholding (Gao, 1998) is a compromise between soft and hard thresholding. It is continuous like soft thresholding and has less bias than soft thresholding. Our choice of using hard thresholding in this paper is mainly motivated by the theoretical property of its connection to non-local prior as described in Section 3.

Figure 2:

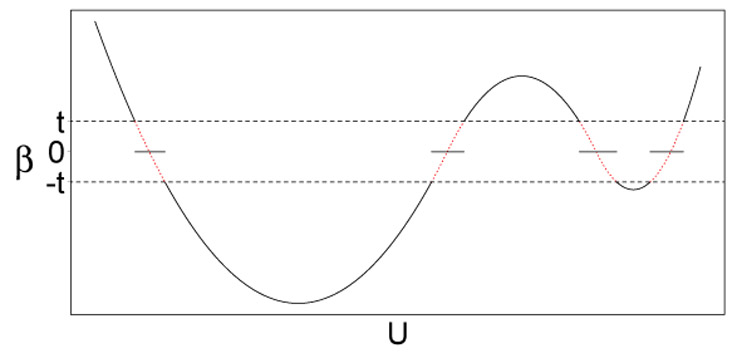
Example plot of the conditional independence function (CIF). Solid curve represents the CIF β(U); dashed lines indicate the threshold t; dotted curves are thresholded to zero.

In theory, one can use any Bayesian variable selection technique to obtain a sparse estimator of β_hj(U), for example, a spike-and-slab prior (George and McCulloch, 1993; Ishwaran and Rao, 2005). However, in order to allow the sparsity to vary with subject-specific external covariates U, we need to introduce a latent indicator for each potential edge and each subject, which would greatly increase the model complexity and hence reduce the scalability. For example, in our application with multiple myeloma dataset, the spike-and-slab construction would need n × p × (p–1)/2 = 173712 latent indicators whereas our model only needs p × (p — 1)/2 = 1128 thresholding parameters and this number can be further reduced to p = 48 (Section 2.4). In addition, while our model can perform graph structure prediction (Supplementary Material B), it is not straightforward to do so with spike-and-slab prior.

In the context of a single regression, the varying-coefficient model (VCM, Hastie and Tibshirani (1993)) can be viewed as a special case of the model defined by equations (2) and (4) with t_hj = 0 for all j = 1,…, p. In VCM, the regression coefficients vary smoothly with the covariates but the sparsity/structure of the model remains constant. We compare GR with VCM in simulation studies (Section 4).

2.3. Bayesian orthogonal basis p-splines

In this section, we specify the functional form of the relationship between the continuous covariates and edges. Our construction allows us to distinguish the functional form of the edge-covariate relationship, which generates more interpretable results in our application. In particular, we take a semiparametric approach and model the smooth function f_hjk(·) by cubic b-splines $f_{\mathit{hjk}}({\mathit{w}}_k)={\tilde{\mathit{w}}}_k{\alpha }_{\mathit{hjk}}$, where w_k denotes n samples of W_k, ${\tilde{\mathit{w}}}_k$, represents the design matrix of the spline bases for W_k, and α_hjk is the corresponding spline coefficient. We choose a large enough number of knots/bases to capture the local features in the functions. To prevent overfitting, we use p-splines (Eilers and Marx, 1996; Lang and Brezger, 2004) which restrict the influence of α_hjk by a roughness penalty. P-splines can be treated as a mixed model or equivalently a Bayesian hierarchical model (Ruppert et al., 2003) by assuming α_hjk ~ N(0, sK⁻ with the singular penalty matrix K constructed from the second order differences of the adjacent spline coefficients. The coefficients that parameterize the constant and linear trends of f_hjk(·) are in the null space of K and hence are not penalized. Also, notice that equation (4) is not identifiable because adding a constant to f_hjk(·) and subtracting it from f_hjk′(·) does not change the equation. Following Scheipl et al. (2012), we take a spectral decomposition of the covariance of ${\tilde{\mathit{w}}}_k{\alpha }_{\mathit{hjk}}$,

$$\mathit{cov}({\tilde{\mathit{w}}}_k{\alpha }_{\mathit{hjk}})=s{\tilde{\mathit{w}}}_k{\mathit{K}}^{-}{\tilde{\mathit{w}}}_k^T=s[{\mathit{u}}_k\ast ]\left[\begin{array}{cc}\hfill {\mathit{d}}_k\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right]{[{\mathit{u}}_k\ast ]}^T$$

where u_k is the orthonormal matrix of eigenvectors associated with positive eigenvalues in the diagonal matrix d_k. Let ${\mathit{w}}_k^{\ast }={\mathit{u}}_k{\mathit{d}}_k^{\frac{1}{2}}$ be the orthogonal basis and ${\alpha }_{\mathit{hjk}}^{\ast }\sim N(0,{\tau }_h{\sigma }_h^2\mathit{I})$, then ${\mathit{w}}_k^{\ast }{\alpha }_{\mathit{hjk}}^{\ast }$ has a proper normal distribution that is proportional to that of the partially improper prior of ${\tilde{\mathit{w}}}_k{\alpha }_{\mathit{hjk}}$. Note that the prior of ${\alpha }_{\mathit{hjk}}^{\ast }$ will be extended to a spike-and-slab prior in Section 2.4 for covariate selection.

In short, we have decomposed $f_{\mathit{hjk}}({\mathit{w}}_k)=f_{\mathit{hjk}}^{\mathit{pen}}({\mathit{w}}_k)+f_{\mathit{hjk}}^0({\mathit{w}}_k)$ into a penalized part $f_{\mathit{hjk}}^{\mathit{pen}}(\cdot )$ and an unpenalized part $f_{\mathit{hjk}}^0(\cdot )$ and reparameterized $f_{\mathit{hjk}}({\mathit{w}}_k)={\mathit{w}}_k^{\ast }{\alpha }_{\mathit{hjk}}^{\ast }+{\mathit{w}}_k{\alpha }_{\mathit{hjk}}^0$, where ${\alpha }_{\mathit{hjk}}^0$ is the coefficient of the linear term w_k, which allows us to put separate shrinkage/selection priors on ${\alpha }_{\mathit{hjk}}^0$ and ${\alpha }_{\mathit{hjk}}^{\ast }$ and to differentiate between linearly and nonlinearly varying effects (Section 2.4). The intercept term is merged into the global intercept μ_hj,

$${\theta }_{\mathit{hj}}(\mathit{w},\mathit{z})={\mu }_{\mathit{hj}}{1}_n+\sum _{k=1}^q{\mathit{w}}_k^{\ast }{\alpha }_{\mathit{hjk}}^{\ast }+\sum _{k=1}^q{\mathit{w}}_k{\alpha }_{\mathit{hjk}}^0+\sum _{l=1}^r{\mathit{z}}_l{\varphi }_{\mathit{hjl}},$$ (6)

where θ_hj = (θ_1hj,…,θ_nhj)^T and z_l are samples of Z_l. In practice, we retain only the first several eigenvectors and eigenvalues that explain most (e.g., 99%) of the variability of f_hjk(w_k). This leads to a great dimension reduction of ${\mathit{w}}_k^{\ast }$ (for example, with 20 bases, the dimension of ${\mathit{w}}_k^{\ast }$ is usually reduced to around 10) and hence efficient computation. Note that this construction of the orthogonal spline basis requires specification of both the order and number of basis functions. We provide detailed discussion of the specification and sensitivity analyses to both in Supplementary Materials A and E, respectively.

2.4. Parameter priors and covariate selection

In this section, we detail a set of priors that are instrumental in defining an efficient computational approach for posterior sampling (Supplementary Material B). In Section 3, we outline the connection between these priors and the non-local priors (Johnson and Rossell, 2010, 2012) and ascertain their theoretical properties.

The CIF consists of a smooth function component and a thresholding component (as described in Section 2.2), which define three sets of parameters: (1) edge-covariate-specific parameters μ_hj, ${\alpha }_{\mathit{hjk}}^0$, ${\alpha }_{\mathit{hjk}}^{\ast }$ and φ_hjl; (2) edge-specific parameter t_hj; and (3) node-specific parameter ${\sigma }_h^2$. Hereafter, we discuss the priors and hyper-priors for all the parameters of the two components with three objectives: (1) encourage sparsity in both graph structure and edge-covariate relationships; (2) improve computational efficiency; and (3) achieve the theoretical properties.

Priors for smooth function.

The smooth function is parameterized by the constant effect μ_hj; linear effect ${\alpha }_{\mathit{hjk}}^0$; nonlinear effect ${\alpha }_{\mathit{hjk}}^{\ast }$; and discrete effect φ_hjl for h = 1,…, p ‒ 1, j = h + 1,…,p, k = 1,…,q and l = 1,…,r. For simplicity, we first describe the prior for ${\alpha }_{\mathit{hjk}}^{\ast }$; the priors for μ_hj, ${\alpha }_{\mathit{hjk}}^0$, φ_hjl are analogously defined later. We expand ${\alpha }_{\mathit{hjk}}^{\ast }={\eta }_{\mathit{hjk}}{\xi }_{\mathit{hjk}}$ to be a product of a scalar η_hjk and a vector ξ_hjk with the same size as ${\alpha }_{\mathit{hjk}}^{\ast }$. The parameter expansion technique (Gelman et al., 2008) improves the mixing of the MCMC algorithm, which has also been observed by Scheipl et al. (2012) and Ni et al. (2015). We consider the case in which some of the covariates may contribute to only a few CIFs (i.e., we expect a sparse solution for ${\alpha }_{\mathit{hjk}}^{\ast }$). The scalar η_hjk is assigned a spike-and-slab prior η_hjk ~ N(0, s_hjk) with s_hjk = γ_hjkν_hjk with ν_hjk ~ IG(a_ν, b_ν) and γ_hjk ~ ρ_hδ₁(γ_hjk) + (1 – ρ_h)δ_ν0 (γ_hjk). The hyper-parameter v₀ is a very small, pre-specified number. Such a setting implies that the binary variable γ_hjk indicates the importance of η_hjk and hence ${\alpha }_{\mathit{hjk}}^{\ast }$. If γ_hjk = 1 (slab), ${\alpha }_{\mathit{hjk}}^{\ast }$ is non-zero, which suggests that there exists a nonlinear effect between the edge h ← j and the continuous covariate W_k. If γ_hj (spike), the effect of η_hjk is almost negligible and can be safely treated as zero (i.e., ${\alpha }_{\mathit{hjk}}^{\ast }=0$), which in turn implies that there is no nonlinear effect between the edge h ← j and the covariate W_k. The variance parameter v₀ can also be set to zero. Using a small but positive v₀ was first proposed by George and McCulloch (1993) to exclude nonsignificant nonzero effects. It also allows us to avoid trans-dimensional MCMC which may mix poorly in moderate to high dimensional problem. Similar strategy is also used in recent Bayesian variable selection literature (Scheipl et al., 2012; Ročková and George, 2014). We assume a beta hyper-prior for ρ_h ~ Beta(a_ρ, b_ρ), which automatically adjusts for multiplicity (Scott et al., 2010). Finally, ${\xi }_{\mathit{hjk}}=({\xi }_{\mathit{hjk}}^{(i)})$ distributes η_hjk across the entries of ${\alpha }_{\mathit{hjk}}^{\ast }$ and ${\xi }_{\mathit{hjk}}^{(i)}$ is assumed to follow a mixture of two normal distributions, ${\xi }_{\mathit{hjk}}^{(i)}\sim N(m_{\mathit{hjk}}^{(i)},1)$ with $m_{\mathit{hjk}}^{(i)}\sim 0.5{\delta }_1(m_{\mathit{hjk}}^{(i)})+0.5{\delta }_{-1}(m_{\mathit{hjk}}^{(i)})$. The bimodal nature discourages small absolute values for ${\alpha }_{\mathit{hjk}}^{\ast }$ and hence has better separation between zero and non-zero effects. The induced prior on ${\alpha }_{\mathit{hjk}}^{\ast }$ is called the parameter-expanded normal-mixture-of-inverse-gamma (peNMIG) distribution (Scheipl et al., 2012). Similarly, we assume peNMIG priors for μ_hj, ${\alpha }_{\mathit{hjk}}^0$, φ_hjl. This allows us to investigate: (1) whether there exists an edge h ← j; (2) if true, whether the edge h ← j is constant or not; (3) if not, which set of covariates affect the edge; and (4) whether the relationship between the edge and a continuous covariate is linear or nonlinear.

Priors for thresholding.

The thresholding parameter t_hj controls the sparsity of the graphs. In the limit, as t_hj → 0 all nodes are fully connected for all subjects while as t_hj → ∞ all nodes are disconnected. We remark that t_hj is not fully identifiable. For example, when μ_hj, ${\alpha }_{\mathit{hjk}}^0$, ${\alpha }_{\mathit{hjk}}^{\ast }$, Φ_hjl all equal 0, t_hj can take any positive value since β_hj is always zero. We resolve this issue by assuming t_hj = t_h, ∀j which enforces the identifiability of t_h as long as not all β_hj’s are zero. We impose a uniform prior on t_h ~ U(0, t_max) (sensitivity analyses on the choice of t_max are provided in Supplementary Material E). In our experience, due to faster mixing, peNMIG needs only 1/4 of the iterations to achieve the same performance as the prior in Section 3. Therefore, we use peNMIG in the simulations and application.

We complete the prior specifications by assuming an inverse-gamma prior for residual variance ${\sigma }_h^2\sim \mathit{IG}(a_{\sigma },b_{\sigma })$. The choice of hyperparameters and a schematic of the complete hierarchical formulation of GR are provided in Supplementary Material A. We use an MCMC algorithm to sample all the parameters from their posterior distributions; details are given in Supplementary Mateiral B where we also discuss the process of using posterior samples for predictions. We consider two types of predictions, node and graph structure predictions. Node prediction, in which the goal is to impute the missing observation of some node X_h, is common in graphical models; whereas graph structure prediction, to the best of our knowledge, is novel. The idea is to predict the graph structure for a new subject based on the external covariates.

3. Theoretical properties

In this section, we first present a general result of the connection between our thresholded prior and the discrete mixture of a point mass at 0 and a non-local prior and then discuss the model selection consistency in Supplementary Material C. A non-local prior assigns a vanishing density to the neighborhood of the null hypothesis. In model selection, the density vanishes around 0 and therefore shrinks small effect to zero, which is appealing because we are interested in a parsimonious estimation of the graph (i.e., a sparse network). Several proposals of the theoretical properties of non-local priors have been published (Johnson and Rossell, 2010, 2012; Rossell and Telesca, 2015; Shin et al., 2015).

Consider a general hard thresholding mechanism, β = θI(∣θ∣ > t) for t ≥ 0, where $\theta \sim {\mathcal{P}}_{\theta }(\theta )$ and $t\sim {\mathcal{P}}_t(t)$. The following proposition shows that with a fairly wide range of prior distributions, ${\mathcal{P}}_{\theta }(\cdot )$ and ${\mathcal{P}}_t(\cdot )$, the marginal prior of β can be expressed as a discrete mixture of a point mass at 0 and a non-local prior.

Proposition 1. Suppose ${\mathcal{P}}_{\theta }(\cdot )$ is bounded near 0 and Pr(t = 0) = 0. Then

$$\mathcal{P}(\beta \mid \psi )=\psi {\mathcal{P}}_1(\beta )+(1-\psi ){\delta }_0(\beta ),$$

where the latent variable ψ ~ Bernoulli(p_ψ) and ρ_ψ = E_t[P_r(∣θ∣ > t∣t∣)]. Moreover,

$${\mathcal{P}}_1(\beta )={\mathcal{P}}_{\theta }(\beta )\frac{\mathit{Pr}(\mid \beta \mid >t\mid \beta )}{E_t[\mathit{Pr}(\mid \theta \mid >t\mid t)]}\to 0\mathit{as}\beta \to 0.$$

The proof is given in Supplementary Material C. It is straightforward to generalize proposition 1 to an independent multivariate case where $\theta =({\theta }_1,\dots ,{\theta }_p)\sim {\prod }_{j=1}^p{\mathcal{P}}_{\theta }({\theta }_j)$, $\mathit{t}=(t_1,\dots ,t_p)\sim {\prod }_{j=1}^p{\mathcal{P}}_t(t_j)$ and β = (β₁,…, β_p) with β_j = θ_jI(∣θ_j∣ > t_j).

Corollary 1. Assume the conditions of proposition 1 apply. Then $\mathcal{P}(\beta \mid \psi )={\prod }_{\{j:{\psi }_j=1\}}{\mathcal{P}}_1({\beta }_j)$, where ψ_j ~ Bernoulli(ρ_ψ) and ψ = (ψ₁, …, ψ_p). Moreover, $\mathcal{P}(\beta \mid \psi )\to 0$ as α_j → 0 for some j = 1, …, p.

One specific example of proposition 1 and corollary 1 is the exponential moment (eMOM) prior and the product eMOM (peMOM) prior, which under mild regularity conditions leads to Bayes factor consistency in a linear model when p ≤ n (Rossell and Telesca, 2015).

Example 1. Let ${\mathcal{P}}_{\theta }(\theta )=N(\theta \mid 0,\tau {\sigma }^2)$ and let ${\mathcal{P}}_t(t)$ be the Fréchet/inverse-Weibull distribution with density ${\mathcal{P}}_t(t)=2\tau {\sigma }^2{t}^{-(2d+1)}\text{exp}\left(-\frac{\tau {\sigma }^2}{t^{2d}}\right)$. Then ${\mathcal{P}}_1(\beta )=c\text{exp}\left(-\frac{\tau {\sigma }^2}{{\beta }^{2d}}\right)N(\beta \mid 0,\tau {\sigma }^2)$ is the eMOM prior with order d = 1, 2,… and $\mathcal{P}(\beta \mid \psi )$ is the peMOM prior. When d = 1, the normalizing constant $c=e^{\sqrt{2}}$ and mixture weight ${\rho }_{\psi }=E_t[\mathit{Pr}(\mid \theta \mid >t\mid t)]=1∕c=e^{-\sqrt{2}}$.

Another example of corollary 1 is the modified peMOM prior, which provides model selection consistency even when p increases sub-exponentially with n (Shin et al., 2015).

Example 2. Let ${\mathcal{P}}_{\theta }(\theta )=N(\theta \mid 0,{\tau }^{(n,p)}{\sigma }^2)$ and ${\mathcal{P}}_t(t)=2{\tau }^{(n,p)}{t}^{-3}\text{exp}(-\frac{{\tau }^{(n,p)}}{t^2})$, where $\log p\prec {\tau }^{(n,p)}\prec n$. Then $\mathcal{P}(\beta \mid \psi )\propto {\prod }_{\{j:{\psi }_j=1\}}\text{exp}\left(-\frac{{\beta }_j^2}{2{\sigma }^2{\tau }^{(n,p)}}-\frac{{\tau }^{(n,p)}}{{\beta }_j^2}\right)$ is the modified peMOM.

Our thresholding procedure extends the results in Rossell and Telesca (2015), where they prove the equivalence between the marginal density of truncation mixtures and nonlocal priors. In our construction, we threshold the parameter itself rather than truncate its density. Hence, the resulting marginal prior of Rossell and Telesca (2015) is a non-local prior while ours is a discrete mixture of the non-local prior and point mass at 0. The priors of thresholding/truncation parameters from the two approaches are also very different in order to achieve the same non-local prior. For example, to obtain eMOM, we assume ${\mathcal{P}}_t(t)$ to be inverse-Weibull while Rossell and Telesca (2015) sets ${\mathcal{P}}_t(t)=\mathit{Pr}(e^{\sqrt{2}-\frac{\tau {\sigma }^2}{{\theta }^2}}>t\mid t)$, which is not analytically available. We discuss the circumstances under which the model selection consistency results for linear regression (Shin et al., 2015) can be applied to GR in Supplementary Material C.

4. Simulation studies

In this section, we empirically illustrate the performance of GR in terms of edge selection, covariate selection, node prediction and structure prediction. To the best of our knowledge, there are no alternative approaches that can perform DAG inference allowing graph structure to vary with both continuous and discrete covariates; therefore we compare GR to two types (Bayesian and non-Bayesian) of VCMs and to a group-specific DAG model (i.e., with categorical covariates), since both methods are a special case of GR as described in Sections 2.1 and 2.2. Throughout the simulations, we choose B = 20 spline bases and set the hyperparameters as v₀ = 2.5 × 10⁻⁴, t_max = 1, (α_σ, b_σ) = (10⁻⁴, 10⁻⁴), (a_v, b_v) = (5,100) and (a_ρ, b_ρ) = (0.5, 0.5) so that the priors have large variance. For Bayesian methods, we run 100,000 MCMC iterations, discard the first 50,000 iterations as burn-in and retain every 5th sample. For each scenario, we report the results on 50 simulated datasets. In addition, even though the focus of this paper is on DAG, we also compare GR to two state-of-the-art methods for group-specific undirected graphical models (see Supplementary Material D). We perform a sensitivity analysis on the number B of spline bases and all the hyperparameters t_max, (α_σ, b_σ), (a_ν, b_ν), (α_ω, b_ω) and v₀ in Supplementary Material E, which shows that our method is robust to the choice of number of bases and hyperparameters.

4.1. Case I: single regression

We first compare GR with both Bayesian and frequentist VCM models in the single regression setting. Bayesian VCM (BVCM) is implemented using GR with t deterministically set to 0. For the frequentist approach, we choose recent work by Fan et al. 2014, iterative nonparametric independence screening (INIS). Since INIS only works on a univariate continuous covariate, we set q = 1 and r = 0.

Low-dimensional scenarios.

We set n = 200, p = 50 and generate the data from the following model

$$\begin{array}{cc}\hfill & Y=X_1{\beta }_1(U)+X_2{\beta }_2(U)+X_3{\beta }_3(U)+ϵ\text{with}ϵ\sim N(0,1)\hfill \\ \hfill & {\beta }_1(U)\equiv 1,{\beta }_j(U)={\theta }_j(U)I(\mid {\theta }_j(U)\mid >t)\text{for}j=2,3\hfill \\ \hfill & {\theta }_2(U)=-2U,{\theta }_3(U)=U^2-1,\hfill \end{array}$$

with one constant effect, one linearly varying effect and one nonlinearly (quadratically) varying effect. We draw (X₁,…, X₅₀, U) from N(0, I₅₁). The true threshold t is set at 0.5 and 0. We also generate an independent test dataset with 200 samples for prediction.

We assess the performances in terms of prediction and of the selection of the true X’s. Specifically, we report the true positive rate (TPR), false discovery rate (FDR), Matthews correlation coefficient (MCC) and mean squared prediction error (MSPE) in Supplementary Material D. We do not report the area under the ROC curve because INIS does not have a tuning parameter that needs to be set by users. MCC is a balanced measure of binary classification that takes values between −1 (total disagreement) and +1 (perfect classification). GR performs the best in terms of both variable selection and prediction when t = 0.5. MCC is 0.960, 0.890 and 0.796 and the MSPE is 1.899, 1.927 and 6.941 for GR, BVCM and FDM, respectively. When t = 0, GR is still much better than INIS and comparable to BVCM (slightly lower MCC but also slightly lower MSPE). Note that the operating characteristics for INIS are calculated on the basis of only 2 or 3 simulated datasets (out of 50) because for the majority of the simulated datasets, INIS does not select any variables; this issue is probably due to relatively low signals and sample size.

High-dimensional scenarios.

We consider high-dimensional cases for which INIS is originally designed. We adopt the following data generating process (Fan et al., 2014):

$$\begin{array}{cc}\hfill & Y=X_1{\beta }_1(U)+X_2{\beta }_2(U)+X_3{\beta }_3(U)+X_4{\beta }_4(U)+ϵ\text{with}ϵ\sim N(0,1)\hfill \\ \hfill & {\beta }_1(U)\equiv 2,{\beta }_j(U)={\theta }_j(U)I(\mid {\theta }_j(U)\mid >t)\text{for}j=2,3,4\hfill \\ \hfill & {\theta }_2(U)=3U,{\theta }_3(U)=U^2+1,{\theta }_4=\frac{4\sin (2\pi U)}{2-\sin (2\pi U)}.\hfill \end{array}$$

We generate X₁,…,X_p from a standard normal distribution and U from a standard uniform distribution. Six scenarios are considered: (1) n = 200, p = 50, t = 0.5; (2) n = 200, p = 50, t = 0; (3) n = 200, p = 200, t = 0.5; (4) n = 200, p = 200, t = 0; (5) n = 400, p = 1000, t = 0.5; and (6) n = 400, p = 1000, t = 0. Notice that scenario (6) is exactly the same as example 3 of Fan et al. (2014).

The operating characteristics are also reported in Supplementary Material D. In terms of selecting the X’s, GR outperforms BVCM and INIS for all cases. For example, when n = 200, p = 200 and the true model is VCM (i.e., t = 0), the values of MCC for GR, BVCM and INIS are 0.961, 0.903 and 0.826, respectively. The better MCC for GR is mostly due to its better control of false positives (with FDR = 0.037) through thresholding. However, we observe that in the high-dimensional setting (especially when n = 400, p = 1000), sometimes a low FDR is achieved at the price of a relatively low TPR because of an over-estimated thresholding parameter. As a result, the prediction is somewhat undermined. This may explain the unstable prediction performance of GR. We point out that the typical application of GR involves only a moderate number of variables (48 in our case study) and variable selection rather than prediction is of key interest in graphical models.

4.2. Case II: graphical model

The goal of this simulation study is to illustrate the selection performance of GR. INIS is not considered because of its poor performance in the single regression case and its inability to handle multivariate covariates and covariate selection. We consider two examples: (1) group-specific DAG (q = 0, r = 1) and (2) general GR (q, r > 0).

Group-specific DAG.

We first study the case where we only have one categorical covariate (i.e., q = 0, r = 1). As mentioned in Section 2.1, GR, in this case, is reduced to the group-specific DAG model. We set p = 20, n = 40 and assume two groups, z ∈ {0, 1}ⁿ, with equal size. The true thresholding parameter t is set to 0.5. We assume the sparsity of the edge-covariate relationship is 0.2 (i.e., γ ~ Bernoulli(0.2)). The non-zero covariate coefficient φ is generated from N(0, 0.7²) for the first group. Then we add a normal noise level to φ for the second group. We vary the level of noise to achieve five scenarios with different percentages (10%, 30%, 50%, 80%, 100%) of differential edges. The error term ϵ is drawn from standard normal distribution. For comparison, we apply the Bayesian linear model selection method, SSVS (George and McCulloch, 1993) separately to each group.

In Figure 3, we plot the FDR and MCC of GR and SSVS for different scenarios. We do not show the TPR because it is nearly the same for the two methods (~0.6 across five scenarios). Overall, GR performs better than SSVS. This is expected since GR is a joint approach that pools the information from two groups while SSVS makes separate estimations for each group and is expected to lose efficiency. Not surprisingly, as the percentage of differential edges increases, the performance of SSVS becomes closer to that of GR. When the two groups have completely different edge sets, SSVS slightly outperforms GR.

Figure 3:

Matthews correlation coefficient (solid lines) and false discovery rate (dashed lines) are plotted against percentages of differential edges. The triangle markers represent GR; circle markers represent SSVS.

General GR.

We compare GR with BVCM in terms of both edge and covariate selection when covariates contain both continuous and discrete variables. We let n = 200, p = 50 and consider two scenarios: (i) q = r = 2 and (ii) q = r = 3. The sparsity of the edge-covariate relationship is assumed to be 0.015. The non-zero discrete covariate effect φ is generated from a standard normal distribution and the function f (·) of the significant continuous covariates is either linear or nonlinear with equal probability. Nonlinear functions are further randomly selected from f(x) = sin(8π/7x), f(x) = sin(4π/7x), f(x) = exp(x) – 1 and f(x) = x² – 1. The continuous covariates w are drawn from a standard normal distribution and the discrete covariates z are randomly generated from {0, 1, 2}.

In Table 1, we calculate the TPR, FDR and MCC for the selection of continuous covariates (with prefix c), discrete covariates (with prefix d) and network edges (with prefix e). For both scenarios, the difference in covariate selection between GR and BVCM is almost negligible and can be explained by the trade-off between TPR and FDR. But in terms of edge selection, GR outperforms BVCM. For example, the eMCCs for GR and BVCM are 0.823 and 0.626. Moreover, GR is capable of predicting the network structure for new observations. We generate independent test data w* and z* with sample size 200. We show TPR, FDR and MCC for the predictive network (with prefix p) in Table 1. The performance is nearly the same as the estimation with the training data. On an AMD 2.2 GHz processor, the average computation times are 15.6 and 20.5 hours for scenarios (i) and (ii), which can be greatly reduced by parallelizing our algorithm via the factorization (2).

Table 1:

Networks with n = 200, p = 50. Prefixes: e-edge, c-continuous (covariates), d-discrete (covariates), p-predictive network. The numbers are calculated on the basis of 50 repetitions; standard deviations are given within parentheses.

	q = r = 2		q = r = 3
	GR	BVCM	GR	BVCM
eTPR	0.895 (0.031)	0.985 (0.012)	0.854 (0.029)	0.988 (0.007)
eFDR	0.120 (0.027)	0.398 (0.030)	0.180 (0.033)	0.555 (0.038)
eMCC	0.881 (0.024)	0.755 (0.022)	0.823 (0.023)	0.626 (0.033)
cTPR	0.967 (0.024)	0.985 (0.017)	0.955 (0.026)	0.989 (0.012)
cFDR	0.336 (0.056)	0.303 (0.041)	0.490 (0.039)	0.467 (0.065)
cMCC	0.797 (0.037)	0.825 (0.026)	0.691 (0.031)	0.719 (0.051)
dTPR	0.770 (0.068)	0.826 (0.060)	0.769 (0.039)	0.828 (0.025)
dFDR	0.128 (0.058)	0.143 (0.078)	0.169 (0.049)	0.202 (0.080)
dMCC	0.817 (0.053)	0.838 (0.052)	0.796 (0.035)	0.809 (0.047)
pTPR	0.889 (0.031)	-	0.851 (0.029)	-
pFDR	0.115 (0.027)	-	0.175 (0.034)	-
pMCC	0.880 (0.023)	-	0.824 (0.023)	-

Sensitivity analysis of ordering misspecification.

One assumption of our model is the knowledge of a prior ordering of the nodes. Here we investigate the sensitivity of our approach to the ordering misspecification. This analysis is performed following the criteria in Altomare et al. (2013) and Shojaie and Michailidis (2010). We apply GR to the data simulated under scenario (i) q = r = 2, assuming misspecified orderings. To quantify the distance between the misspecified ordering (used to fit the data) and the true ordering (used to generate the data), we compute the normalized Kendall’s tau distance which is the ratio of the number of discordant pairs over the total number of pairs. The Kendall’s tau lies between 0 and 1, with 0 indicating a perfect agreement of the two orderings and 1 indicating a perfect disagreement. Since GR is not able to learn the ordering, we will ignore the directions of the edges in reporting the graph structure learning performance in Table 2. The performance of GR under ordering misspecification can be also affected by the average number of v-structures across subjects for both the true ordering and the prior ordering which is also reported in Table 2. As expected, the performance deteriorates as the Kendall’s tau becomes larger. However, it remains reasonable (MCC= 0.74) when Kendall’s tau= 0.25 whereas for extreme scenario when Kendall’s tau= 1, MCC decreases to 0.51.

Table 2:

Sensitivity of misspecified ordering when q = r = 2. The columns under label “Misspecified ordering” are simulations with misspecified prior orderings; the last column reports the performance of GR using orderings estimated by order-MCMC. Directions of the edges are ignored. The standard error for each statistic is given in parentheses.

	Misspecified ordering				order-MCMC
Kendall’s tau	0.00	0.25	0.51	1:00	0.15(0.05)
V-structures (prior)	56	56	48	50	53(4)
V-structures (shared)	56	37	18	0	41(7)
TPR	0.895 (0.031)	0.799(0.025)	0.725(0.030)	0.601(0.032)	0.820(0.037)
FDR	0.120 (0.027)	0.286(0.028)	0.399(0.031)	0.509(0.031)	0.232(0.062)
MCC	0.881 (0.024)	0.740(0.022)	0.638(0.024)	0.514(0.028)	0.781(0.047)

Although in our application the ordering is naturally retrieved from the reference signaling pathway, there are cases where such ordering is completely unknown or impractical to obtain. In these situations, the problem is usually decomposed into two sub-problems: (1) learn the ordering; and (2) given the ordering, learn the network structure. The first sub-problem can be solved by using an ordering learning algorithm such as order-MCMC (Friedman and Koller, 2003) which is an efficient MCMC algorithm over the ordering space with parameters and graph marginalized out. Here, we perform a simulation to study the performance of GR in conjunction with order-MCMC. We first apply order-MCMC (implemented by Kuipers and Moffa (2016)) to the data generated under scenario (i) for 100,000 iterations starting from a random ordering. Upon completion, the algorithm outputs a posterior sample of the orderings based on which we calculate the posterior mean ordering. Then we apply GR using the mean ordering as our prior ordering. The performance (Table 2) is quite reasonable compared to the results under the true ordering. For instance, the MCC of GR with order-MCMC (MCC=0.781) is between that of GR with the true ordering (MCC=0.881) and with slightly misspecified ordering (Kendall’s tau=0.25, MCC=0.740).

Scalability of number of covariates.

Our application considers m = 2 covariates. We conduct a simulation study (details provided in Supplementary Material D) to investigate the scalability of GR with respect to m = 6, 12, 18, 24. We find GR scales reasonably well in terms of both structure learning performance and computation time (scales linearly in m).

Comparison of different thresholding functions.

We focus on hard thresholding in this paper due to its appealing theoretical property. However, it is straightforward to extending our method to other thresholding functions such as soft thresholding and nonnegative garrote thresholding and it is interesting to empirically compare them. We carry out a simulation study for such comparison in Supplementary Material D. The results show very comparable performance among the three thresholding functions.

Sensitivity analysis of distribution misspecification.

We conduct a simulation study where the data are generated from a non-Gaussian distribution. The inference under GR is robust to distribution misspecification. Details are reported in Supplementary Material E.

5. Application

In the United States, it has been estimated that more than 26,000 new cases of multiple myeloma occurred and that multiple myeloma caused 11,000 deaths in 2015 (Siegel et al., 2015). Multiple myeloma is a late-stage malignancy of B cells in the bone marrow. According to the International Staging System (Greipp et al. 2005), multiple myeloma is classified into three stages by two important prognostic factors, serum beta-2 microglobulin (Sβ₂M) and serum albumin: stage I, Sβ₂M < 3.5 mg/L and serum albumin ≥ 3.5 g/dL; stage II, neither stage I nor III; and stage III, Sβ₂M ≥ 5.5 mg/L. Multiple myeloma is known to exhibit great genomic heterogeneity and therefore many current research efforts have shifted their focus from traditional therapies to precision medicine for patients diagnosed with multiple myeloma on the basis of genomically defined pathways (Lohr et al., 2014). Our data consist of gene expressions and matched clinical information collected by the Multiple Myeloma Research Consortium, which can be downloaded from the Multiple Myeloma Genomic Portal (https://www.broadinstitute.org/mmgp/home). We focus on the genes mapped to the five critical signaling pathways identified by previous multiple myeloma studies (Boyd et al., 2011): The (1) Ras/Raf/MEK/MAPK pathway, (2) JAK/STAT3 pathway, (3) PI3K/AKT/mTOR pathway, (4) NF-κB pathway and (5) WNT/β-catenin pathway. After removing samples with missing values, we have n = 154 samples and p = 48 genes with q = 2 continuous covariates. Our goal is to reconstruct both population-level and subject-level gene regulatory networks, monitor the changes in gene regulatory relationships guided by prognostic factors and assess the contribution of prognostic factors to the varying networks. We obtain a prior ordering of genes from the reference signaling pathway for multiple myeloma (Boyd et al., 2011). In particular, we put gene i before gene j in the ordering if there is a directed path from gene j to gene i in the reference network. For genes that are not connected by a directed path, the ordering of them is arbitrary. We run two separate MCMCs, each with 500,000 iterations, discard the first 50% as burn-in and thin the chains by taking every 25th sample. The Markov chains exhibit good mixing by MCMC diagnostics. Model checking shows no significant evidence for lack of fit and model assumption violation. Details provided in Supplementary Material F.

Population-level network.

The inferred network is shown in Figure 4. We find

• (i)38 positive constant edges/effects (solid lines): positive constant effect μ_hj > t_h, no linear effect ${\alpha }_{\mathit{hjk}}^0=0$ and no nonlinear effect ${\alpha }_{\mathit{hjk}}^{\ast }=0$ for all k = 1,…, q;
• (ii)20 negative constant effects (dashed lines): μ_hj < −t_h, ${\alpha }_{\mathit{hjk}}^0=0$, ${\alpha }_{\mathit{hjk}}^{\ast }=0$, ∀k = 1,…, q;
• (iii)2 linearly varying effects (dotted lines): ${\alpha }_{\mathit{hjk}}^0\ne 0$ and ∣θ_hj(w_i)∣ > t_h for some k and i;
• (iv)9 nonlinearly varying effects (waves): ${\alpha }_{\mathit{hjk}}^{\ast }\ne 0$ and ∣θ_hj(w_i)∣ > t_h for some k and i. The thickness of the solid or dashed line is proportional to its posterior probability and the node size is proportional to its degree. Some regulatory relationships are consistent with those reported in the existing biological literature. For example, NRAS/HRAS activating MAP2K2 is part of the well-known MAPK cascade, which participates in the regulation of fundamental cellular functions, including proliferation, survival and differentiation. Mutated regulation is a necessary step in the development of many cancers (Roberts and Der, 2007). We also observe that IL6R activates PIK3R1, which together with its induced PI3K/AKT pathway plays a key role in protection against apoptosis and the proliferation of multiple myeloma cells (Hideshima et al., 2001). Moreover, we find two driver/hub genes (degree≥ 8, hexagons in Figure 4), FLT4 and MAP2K3 with degrees 9 and 8, both of which play important roles in multiple myeloma. FLT4, also known as VEGFR3, is responsible for angiogenesis for multiple myeloma (Kumar et al., 2003) and MAP2K3 contributes to the development of multiple myeloma through MAPK cascades (Leow et al., 2013).

Figure 4:

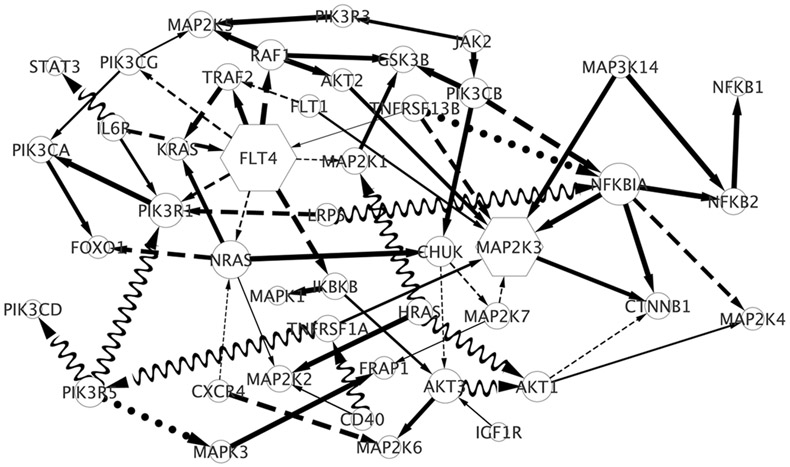
The recovered gene regulatory network in Multiple Myeloma data integrating the prognostic factors: Sβ₂M and serum albumin. The solid lines indicate positive constant effects; dashed lines indicate negative constant effects; dotted lines indicate linearly varying effects; waves indicate nonlinearly varying effects; the width of the solid or dashed line is proportional to its posterior probability; the node size is proportional to its degree. Hexagons are hub genes.

Subject-level network.

We provide six personalized (sub-)networks that correspond to different realizations of the covariates in Figure 5, two for each cancer stage. The prognostic factor levels are shown as black dots on the left and the background is color coded according to the cancer stage: white (stage I), grey (stage II) and black (stage III). Edges affected by Sβ₂M are represented in solid lines; those affected by serum albumin are shown in dashed lines. The dotted lines are constant edges. These “personalized” networks at the patient-level can potentially aid in developing precision medicine strategies using drugs that target specific disruptions in these signaling pathways.

Figure 5:

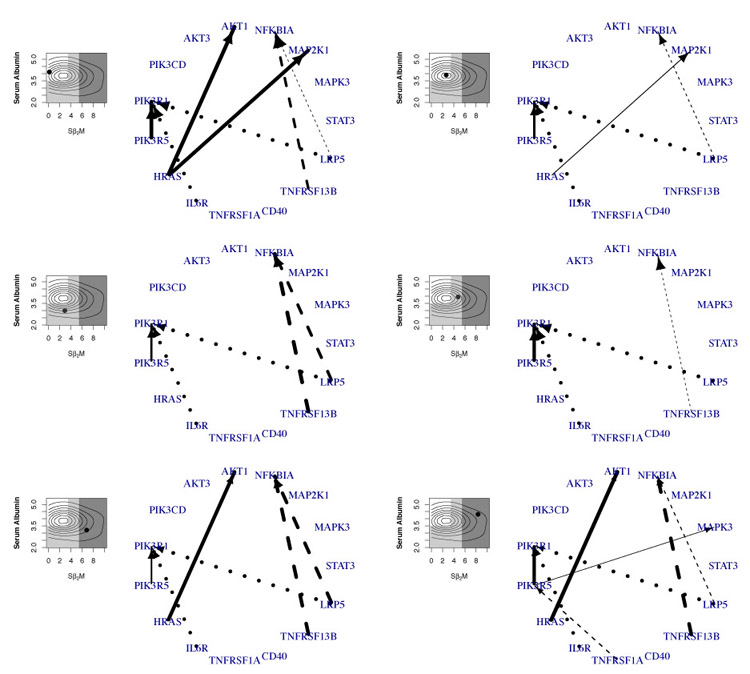
Sub-networks with varying structure. The prognostic factor level is shown as the black dot on the left panel for each plot together with the kernel density (Sβ₂M on the x-axis and serum albumin level on the y-axis). The background is color coded according to cancer stage: white (stage I), grey (stage II) and black (stage III). Edges affected by Sβ₂M are represented in solid lines; those affected by serum albumin are dashed lines. The dotted lines are constant edges. The edge width is proportional to its posterior probability.

Using the R package shiny, we develop an interactive web application (https://nystat.shinyapps.io/MMCR-app) to visualize the varying structure of the network. The application interactively displays the varying sub-network in response to the user’s input of the desired values of Sβ₂M and serum albumin; a feature enabled by graph structure prediction. We provide screenshots of the application in Supplementary Material G.

Varying gene regulatory relationships.

In Figure 6, we present 9 nonlinearly varying effects. Three of them (top panel of graphs) vary with serum albumin concentrations and the rest vary with Sβ₂M. The fitted curve and 95% credible bands are shown in the top portion of each graph; posterior edge inclusion probabilities are shown in the bottom portion. Red lines and curves indicate that the effect is significant. Some of these regulatory relationships are noteworthy. For example, we observe an interesting trend between HRAS and AKT1 (bottom left graph in Figure 6). It has been found that RAS has the potential to activate the PI3K/AKT signaling pathway in multiple myeloma (Hu et al., 2003). Our study shows that HRAS activates AKT1 when Sβ₂M< 2.64 or Sβ₂M> 5.70 but the regulatory relationship is almost negligible when Sβ₂M∈ (2.64, 5.70), which is close to the interval (3.5, 5.5) that is used for staging and corresponds to stage II multiple myeloma. In addition, we find some interesting connections for linearly varying effects (Figure 7). Many studies in multiple myeloma have revealed the importance of NF-κB activation, the inhibitor of which, NFKBIA, is degraded by TNFRSF (Silke and Brink, 2010). Our analysis (left graph in Figure 7) confirms the regulatory relationship between TNFRSF13B (a member of TNFRSF) and NFKBIA. Interestingly, the sign of the regulation switches at around the cutoff (3.5 g/dL) of serum albumin that distinguishes between stages I and II and, as expected, when serum albumin concentrations become higher, which suggests more advanced multiple myeloma, the inactivation becomes stronger.

Figure 6:

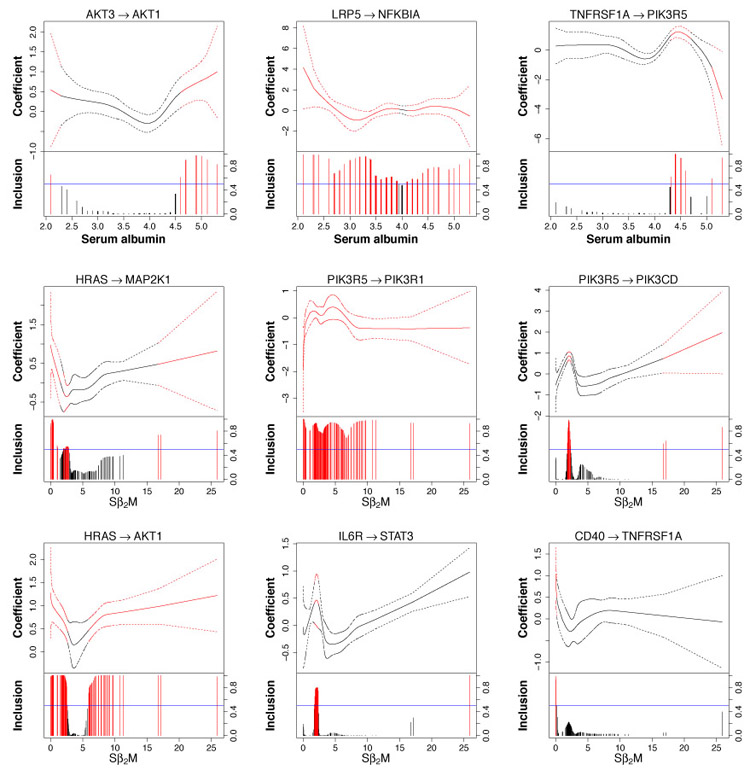
Nonlinearly varying effects. Top three graphs: CIFs vary with serum albumin concentrations. Bottom six graphs: CIFs vary with Sβ₂M. For each graph, the fitted curve (solid) with 95% credible bands (dashed) are shown in the top portion and marginal posterior inclusion probabilities are shown in the bottom portion. Blue horizontal line is the 0.5 probability cutoff. Red lines and curves indicate significant coefficients.

Figure 7:

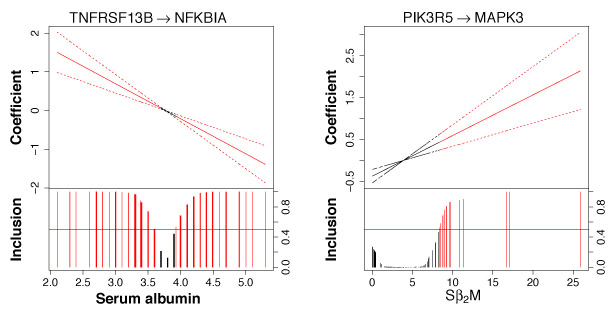
Linearly varying effects. Fitted curve (solid) with 95% credible bands (dashed) are shown in the top portion and marginal posterior inclusion probabilities are shown in the bottom portion. Blue horizontal line is the 0.5 probability cutoff. Red lines and curves indicate significant coefficients.

We assess the overall contribution of prognostic factors (Sβ₂ M and serum albumin) on the varying networks across patients using a score defined in Supplementary Material F. The resulting scores are C₁ = 6.5% and C₂ = 5.9%, i.e., 6.5% (5.9%) of the total posterior edge inclusion probability is explained by Sβ₂M (serum albumin) – thus Sβ₂M has a marginally stronger effect on varying network topology than serum albumin.

6. Discussion

We have introduced a novel class of graphical models, GR, to estimate varying structure networks by incorporating additional covariates. We assume the relationships between edges and covariates are sparse and could be nonlinear. Our thresholded prior is equivalent to a mixture of a unit point mass and a non-local prior. Under the special case in which covariates are discrete, we show model selection consistency under such a prior. Empirically, GR exhibits good performance compared to VCM. We apply GR to multiple myeloma gene expression data, taking important prognostic factors as covariates, which reveals several interesting findings that include the patient-specific networks.

GR assumes a prior ordering of the nodes, which could be thought of as a limitation of our model. However, it is a common assumption of many recent DAG approaches (Shojaie and Michailidis, 2010; Altomare et al., 2013; Ni et al., 2015). Our sensitivity analysis shows reasonable performance of GR when there is moderate ordering misspecification. We provide a discussion on how to obtain a prior ordering in practice in Supplementary Material H including when the ordering is completely unknown a priori, one can first use an ordering learning algorithm and then apply GR given the estimated ordering. We test this strategy in simulation (Section 4.2) which shows satisfactory performance. Alternatively, one may want to fit an undirected graph instead. A straightforward way to apply GR for undirected graphs is through neighborhood selection (Meinshausen and Bühlmann, 2006): each node is regressed on all the other nodes instead of its parent set, and variable selection is applied to infer graph structure. The asymmetry is mediated by taking the union or intersection of the edges. However, although asymptotically it is a legitimate procedure, the asymmetry means that there is no well-defined joint distribution, hence posterior distribution, for finite samples. Therefore, we can obtain only a point estimator based on the marginal distribution of GR, but are not able to compute the posterior distribution. An alternative approach might be to focus on a decomposable graph. With this assumption, an undirected graph can be equivalently modeled as a DAG given a perfect ordering (Stingo and Marchetti, 2015). However, in the case of GR, it is not a trivial problem because the perfect ordering may change across subjects. We plan to address this issue in future work. Another direction of future work can be developing the theoretical property of GR when the covariates are continuous. One difficulty is the singularity of the joint distribution of θ_hj (w, z), which we hope to circumvent in the future.