Propensity Scores: Confounder Adjustment When Comparing Nonrandomized Groups in Orthopaedic Surgery

Abstract

Many studies in arthroplasty research are based on nonrandomized, retrospective, registry-based cohorts. In these types of studies, patients belonging to different treatment or exposure groups often differ with respect to patient characteristics, medical histories, surgical indications, or other factors. Consequently, comparisons of nonrandomized groups are often subject to treatment selection bias and confounding. Propensity scores can be used to balance cohort characteristics, thus helping to minimize potential bias and confounding. This article explains how propensity scores are created and describes multiple ways in which they can be applied in the analysis of nonrandomized studies. Please visit the following (https://www.youtube.com/watch?v=sqgxl_nZWS4&t=3s) for a video that explains the highlights of the paper in practical terms.

Visual Abstract

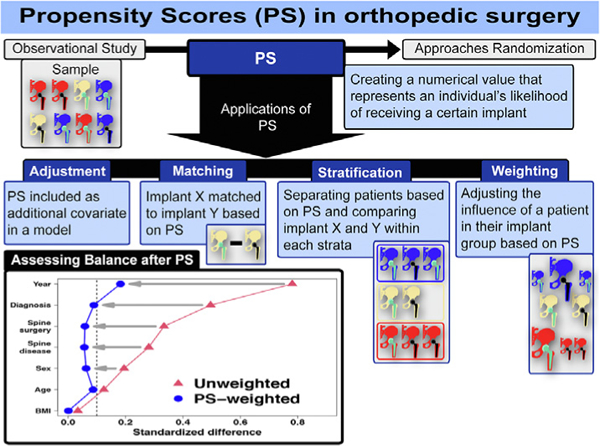
In orthopaedic clinical research, the primary goal often involves comparing 2 or more groups in terms of implant type, surgical procedures, or certain patient characteristics. While many approaches can be used, the benchmark study design for such comparisons is the randomized controlled trial (RCT), which is considered to provide the highest level of evidence for effectiveness and safety [1]. In RCTs, subjects are randomly assigned to one group versus another; as a result, the risk of confounding and treatment selection bias (ie, confounding by indication) is minimized, and on average, subjects in comparison groups will not differ systematically with respect to any measured or unmeasured baseline factors. Thus, the direct comparison of the study groups in an RCT of sufficient power provides an unbiased estimate of the average treatment effect [2]. However, due to a number of factors, such as costs, time constraints, logistical challenges, and ethical concerns, RCTs are not always practical or feasible [3]. Therefore, most clinical studies in orthopaedics rely on retrospective, nonrandomized observational studies, which are prone to treatment selection bias and confounding. It is important that bias and confounding in these types of studies are not only recognized and acknowledged, but that steps are taken to address these issues. A propensity score is a valuable tool that can be used to mitigate treatment selection bias and confounding and improve balance between non-randomized cohorts. In this article, we provide an introduction to propensity scores, describe their creation and methods of application, as well as their strengths and limitations, and offer guidelines to researchers for utilizing propensity scores in orthopaedic research.

The Basics of Propensity Scores

A propensity score is a single numerical value that represents an individual’s likelihood of receiving a given surgical procedure, medical intervention, or exposure as opposed to another procedure or exposure based on a given set of baseline characteristics [4]. Conditional on the propensity score, the distribution of measured baseline variables will be similar between individuals undergoing procedure A and those undergoing procedure B [2]. In other words, subjects who have similar propensity scores will have similar baseline characteristics. Propensity scores can be used to balance the distribution of baseline variables between subjects receiving different procedures or interventions and thus eliminate the confounding and selection bias due to the differences in the observed baseline variables used to calculate the propensity score [4]. This balancing of the baseline variables of individuals in the different exposure groups approximates the effect of randomization. However, it is important to note that balance is achieved only for those baseline variables that were measured (ie, captured as part of the study data collection process); residual confounding due to unmeasured covariates may still exist. In contrast, true randomization will balance on both measured and unmeasured covariates [5]. Hence, if a researcher is considering the use of a propensity score, careful consideration should be given to the selection of variables to make sure that, to the extent possible, all the important confounders are included in the propensity score.

Consider the following example. In a retrospective cohort study, the primary goal is to compare the postoperative infection rate of patients undergoing primary total hip arthroplasty (THA) who received an extended course of antibiotic prophylaxis to patients who received standard antibiotic prophylaxis. In this non-randomized, retrospective study, the decision to treat patients with standard or extended antibiotic prophylaxis may have been influenced by many factors, including patient characteristics, institutional protocols, and/or surgeon preferences. Therefore, a direct comparison of these 2 groups would likely be biased. In order to minimize or eliminate this bias, a propensity score could be developed based on measured factors that might influence the choice of standard versus extended antibiotic treatment, including patient age, sex, body mass index, American Society of Anesthesiologist score, history of tobacco use, baseline comorbidities, and history of previous surgery. The resulting propensity score would represent the probability that a patient received extended antibiotic prophylaxis, conditional on those variables used to calculate the propensity score. In this example, patients who have similar propensity scores would have similar distributions of the baseline variables used to create the propensity score, regardless of which type of antibiotic treatment they received, thus approximating the effect of randomizing patients to either extended antibiotic prophylaxis or standard prophylaxis.

Propensity Score Creation

Various statistical methods are available to calculate propensity scores, but the most common approach utilizes logistic regression [2]. Using this approach, the dependent variable in the model is the factor representing the surgical procedure, medical intervention, exposure, or study groups that will be compared. For example, in the above study comparing different antibiotic prophylaxis regimens, the dependent or outcome variable in the logistic regression model would be the receipt of extended prophylaxis versus standard prophylaxis. In a study comparing outcomes of patients undergoing primary THA who have a dual-mobility design to patients undergoing primary THA with a standard liner, the outcome variable would be dual-mobility design versus standard liner design. The independent variables in the model should include any covariates that may influence whether a patient is in the dual mobility or standard liner group and that also may be associated with the study outcome. These may include patient demographics, past medical histories, comorbidities, surgeon characteristics, years of surgery, etc. The selection of these variables should be made with input from an experienced orthopaedic surgeon with subject matter expertise. It is important to remember that the goal of a propensity score is to eliminate confounding, not merely to predict the exposure or treatment group [6]. Therefore, variables that are associated with the treatment or exposure but not with the study outcome should be avoided, because the inclusion of these types of variables adds noise to the propensity score and may result in an increase in variability without decreasing the bias. Consequently, patients may be poorly matched or randomly misclassified [7].

The ultimate balance between the study groups achieved by the propensity score is conditional on the model used to develop it. Therefore, careful consideration should be given to the selection of variables to be included in the model to make sure that potentially important variables are not overlooked or excluded. Generally, overfitting is not an issue when developing a propensity score, and researchers should not be concerned with limiting the number of variables in the model [8]. Rather than striving for a parsimonious model, it is better to err on the side of being overly inclusive, because the goal is to estimate the probability of being in one group versus the other. In fact, high-dimensional propensity scores with hundreds of variables have been used to reduce bias in studies using large administrative databases [9–11]. The resulting logistic regression model generates a predicted probability for each patient representing that patient’s likelihood of being in the treated or exposed group e this is the propensity score.

Applications of Propensity Scores

After the propensity score has been calculated, the researcher has several options for how to utilize the score. These methods include covariate adjustment, stratification, matching, and weighting. Each of these approaches is described below.

Covariate Adjustment

A relatively simple application of a propensity score is covariate adjustment in a regression model (eg, linear, logistic, or time-to-event). This is accomplished by including the propensity score as an additional covariate in a model containing the study outcome as the dependent variable and the group or treatment indicator as an independent variable. Because the propensity score is the probability that a given patient received one treatment versus another, including it as a term in a model is approximately adjusting for the variables included in the development of the propensity score. This can be advantageous compared to directly adjusting by including several covariates in a model, especially when the number of outcome events is too low to support the number of adjusting variables. However, there are limitations to the use of propensity score covariate adjustment. These limitations include the inability to assess for balance between study groups and the potential for bias and increased residual confounding compared to other methods of propensity score use [5]. Therefore, using the propensity score for covariate adjustment is generally considered to be inferior to other applications, such as weighting, as described below.

Stratification

This method involves comparing patients in the treated group to those in the untreated group separately within strata based on the propensity score. To do this, all patients in the overall study sample are first sorted by the value of their individual propensity scores. They are then divided into unique groups using cutpoints based on percentiles of the propensity score distribution. There is no absolute number of strata to use, and the choice may be influenced by the number of observations being studied, particularly if the sample size is modest. However, dividing the sample into quintiles (ie, 5 strata) is perhaps the most common and has been shown to result in substantial bias reduction [2,12]. Within each resulting strata, patients in the treated and untreated groups will have similar propensity score values, meaning that they will be balanced with respect to the variables used to develop the propensity score. For example, Table 1 shows a summary of patients who underwent THA using a dual mobility construct and patients who received a standard cup and liner, stratified by quintiles of the propensity score. Relative to the overall distribution, the within-strata summaries are more balanced between the 2 groups. Comparisons of the study groups are then performed separately within each stratum, and an overall estimate is generated by taking a weighted average of the stratum-specific results. Stratification allows flexibility in the analysis and may reveal patterns among the strata that are unnoticeable by other methods. Stratification also utilizes all the study data, unlike matching, which may exclude some patients. However, there are disadvantages to this approach, including the complexity of combining the stratum-specific estimates and the limited bias reduction compared to other propensity score methods [13,14].

Table 1.

Propensity Score Stratification Demonstrating Within-Strata Covariate Balance Between Patients With a Dual-Mobility Cup (DM) and Patients With a Standard Construct (Std).

Characteristic	Overall		Stratum 1		Stratum 2		Stratum 3		Stratum 4		Stratum 5
	Std	DM	Std	DM	Std	DM	Std	DM	Std	DM	Std	DM
N	7,009	367	1,462	12	1,452	25	1,423	52	1,394	82	1,278	196
Age (median)	65	68	65	66	64	61	65	62	65	65	68	70
Women (%)	52	61	45	33	48	40	47	40	52	65	67	68
BMI (median)	29.2	29.4	28.7	29.8	29.1	29.7	29.3	29.3	29.4	30.9	29.7	29.1
Indication other than OA (%)	15	36	2	0	14	8	14	26	10	16	36	46
Spine disease (%)	8	18	3	0	6	0	7	4	7	10	20	26
Spine surgery (%)	6	16	1	0	5	8	5	4	4	0	15	26
Year of surgery (median)	2013	2017	2008	2008	2011	2012	2014	2014	2017	2016	2017	2018

BMI, body mass index; OA, osteoarthritis.

Matching

To perform propensity score matching, patients in the treated group are matched to patients in the untreated group by the value of their propensity scores. Thus, each matched pair constitutes a mini stratum in which the 2 patients will have similar propensity score values and, therefore, will be likely to have similar values of the variables used in the creation of the propensity score. As an example, Table 2 shows a summary of patients who underwent THA using a dual mobility cup that have been matched 1:1 on the value of their propensity score to patients who received a standard cup and liner. The matched groups are much more closely balanced than the unmatched groups. The 2 matched groups are then directly compared to each other with respect to the study outcome. While this approach has an intuitive appeal, it is not without limitations. For example, matching results may not be consistent across all treated/untreated pairs. Some matched pairs may be more closely matched than others resulting in less balance. The researcher must decide the degree of difference to allow in the propensity score matching and may possibly exclude some pairs that are not well-matched, potentially introducing selection bias and model dependence [15].

Table 2.

Propensity Score Matching of Patients With a Dual Mobility Cup (DM) to Patients With a Standard Construct (Std).

Characteristic	Overall		Matched
	Std	DM	Std	DM
N	7,009	367	367	367
Age (median)	65	68	67	68
Women (%)	52	61	63	61
BMI (median)	29.2	29.4	28.7	29.4
Indication other than OA (%)	15	36	36	36
Spine disease (%)	8	18	18	18
Spine surgery (%)	6	16	12	16
Year of surgery (median)	2013	2017	2017	2017

BMI, body mass index; OA, osteoarthritis.

Weighting

There are several different propensity score-weighting strategies available. We will focus on inverse probability of treatment weighting (IPTW) and overlap weighting. As the name implies, the IPTW approach weights patients by the inverse of the probability of receiving one treatment versus another. For example, if the propensity score is the probability that a patient received a dual-mobility liner as opposed to a standard liner, then patients in the dual mobility group will be weighted by$\frac{1}{propensityscore}$, and patients in the standard liner group will be weighted by $\frac{1}{\left(1-propensityscore\right)}$. As a result, patients in a given group that have a high probability of being in that group will have relatively small weights, and patients in a given group that have a low probability of being in that group will have relatively large weights. In other words, patients less likely to be treated are up-weighted, and patients more likely to be treated are down-weighted, effectively balancing the influence of individual characteristics and other factors on patient selection and reducing bias. If good balance is achieved, the resulting weighted sample approximates the effect of randomization.

It should be noted that propensity scores that are very close to either 0 or 1 will yield large inverse probability of treatment weights for the treated and untreated groups, respectively. Extremely large weights may have a negative impact on the analysis results, including bias and increased variability of the estimated treatment effect [16,17]. These issues can be successfully resolved by modifying the weights. One such modification is trimming of extreme IPTW values. In this method, patients who have extreme weights are either excluded from the analysis, or alternatively, extreme IPTW values are truncated. This entails replacing any weights beyond a certain limit with the value of that limit. Typically, this is done symmetrically so that both extremely large and small weights are trimmed. The choice of the truncation threshold may be based on the values of the weights themselves (eg, 1.01 and 10) but is more commonly based on percentiles. For instance, after examination of the distribution of IPTW values in a study comparing extended antibiotic prophylaxis to standard antibiotic prophylaxis, a researcher may opt to eliminate observations with weights greater than the 99th percentile or truncate weights greater than the 99th percentile to the value of the 99th percentile. Likewise, the same is done for weights smaller than the 1st percentile.

Another approach involves stabilizing the weights. This is accomplished by multiplying the IPTW by the probability of being in either of the 2 study groups [16,18]. For example, in a study comparing dual-mobility liners to standard liners, the IPTW of patients who received dual-mobility liners will be multiplied by the proportion of patients in the overall study sample who received dual-mobility liners. Likewise, the IPTW of patients who received standard liners will be multiplied by the proportion of patients in the overall sample who received standard liners. While trimming and stabilization are often used independently, they may be used in concert, such that the IPTW are first stabilized, then trimmed, if necessary.

An alternative to inverse probability weighting that is gaining attention is overlap weighting. This method weights patients by the probability of being in the opposite group [19]. For example, if the propensity score is the probability that a patient undergoing primary THA received extended antibiotic prophylaxis versus standard prophylaxis, then patients in the extended prophylaxis group will be weighted by 1 – propensity score and patients in the standard prophylaxis group will be weighted by the propensity score. Like inverse probability weighting, overlap weighting down-weights patients that are highly likely to be treated, and up-weights patients that are unlikely to be treated. However, by design, overlap weights do not yield extremely large values in the way that inverse probability weighting might. Thus, the results are not as strongly influenced by unusual patients, and the relative contribution of patients that are likely to be in either group is much larger, providing good balance between the groups [17,20].

Assessing Balance

After the propensity score has been created and applied using either stratification, matching, or weighting, it is important to assess the improvement in the balance between the study groups. Typically, this is accomplished by calculating the standardized differences between the study groups for each variable that are used to create the propensity score. Differences are calculated separately before and after applying the propensity scores. For continuous variables, the standardized difference is the between-group difference in means divided by the standard deviation. For categorical variables, this is the difference in proportions between the groups divided by the standard deviation [21,22]. Standardized differences less than 0.1 (or 10%) are generally considered to indicate good balance. It is often helpful to visualize this graphically. Figure 1 shows the standardized differences between patients who received a dual mobility cup and those who received a standard cup before (solid triangles) and after (hollow dots) propensity score weighting.

Fig. 1.

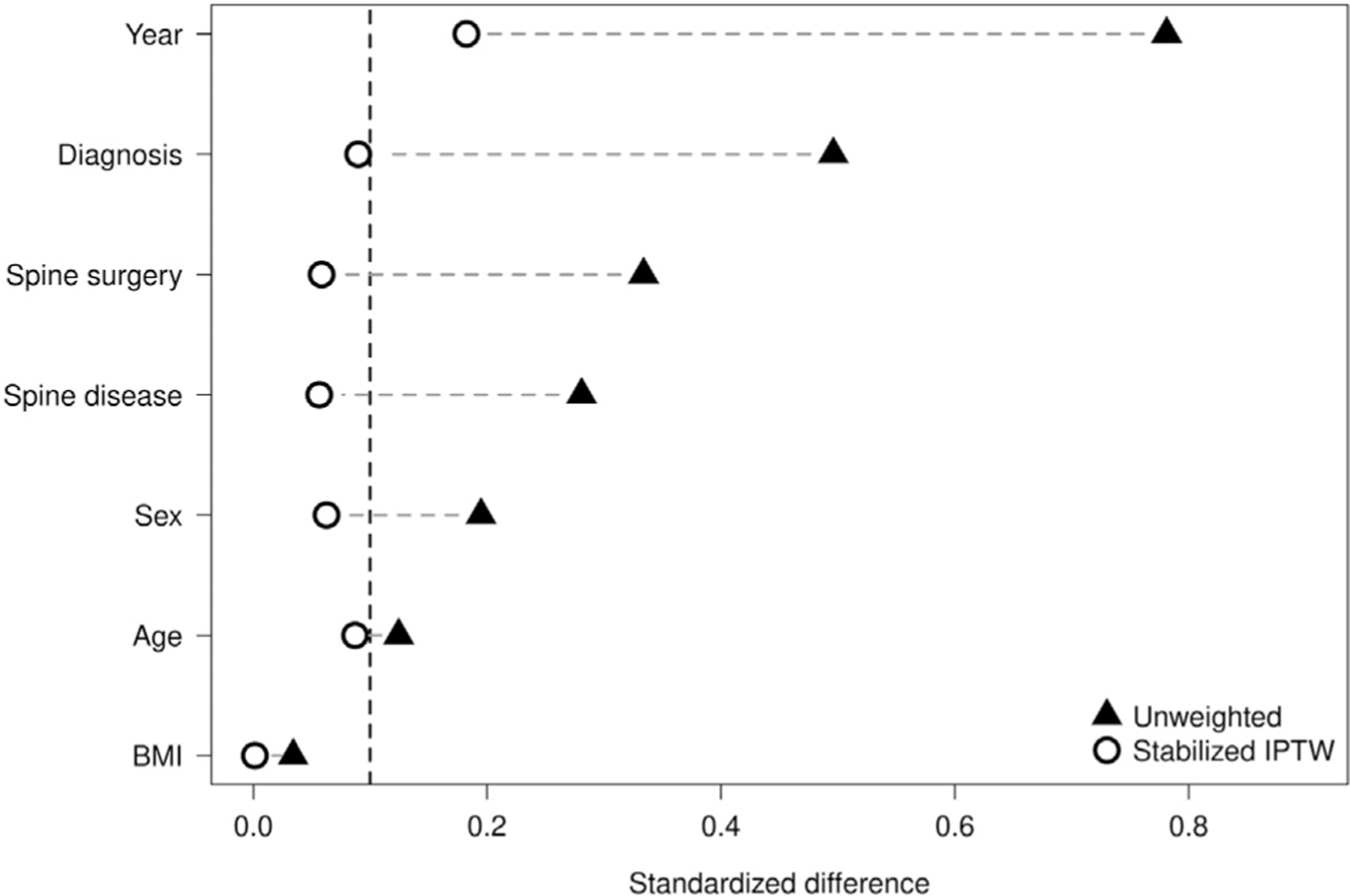
Standardized differences between patients before (solid triangles) and after (hollow dots) propensity score weighting.

Guidelines for the Researcher and Reviewer

1. If a study involves the comparison of nonrandomized groups, potential sources of confounding and bias should be identified and acknowledged.

2. The creation and use of a propensity score should be considered as a possible tool to minimize confounding and treatment selection bias in studies comparing nonrandomized groups.

3. When developing the propensity score model, all measured patient characteristics and baseline characteristics with potential for confounding influence on the inclusion of a patient into one exposure or treatment group versus another and the study outcome should be included in the model, without concern for overfitting.

4. The most important aspect of propensity score creation is the selection of the variables used to create it. First and foremost, variables included in the propensity score should have been measured at baseline. Also, subject matter expertise from an orthopaedic surgeon is essential when selecting the variables for inclusion in the propensity score. In addition, they should be associated with both treatment selection and the outcome (ie, confounders). Variables that are only associated with treatment selection but not the outcome should be avoided. Reviewers are advised to pay attention to the explanation of how propensity score variables were selected, and in particular, whether investigators took into account the association of propensity score variables with treatment, outcome, or both.

5. There are several options for applying the propensity score in the analysis; weighting is perhaps the most flexible and should be considered as a primary option. While IPTW are the most common weighting technique, overlap weights have some advantages, particularly when a number of subjects have a high probability of being in one group versus the other which would result in extreme values of IPTW.

6. Conduct the proper diagnostic assessments to make sure the issue of unbalanced groups is resolved before comparing the treatment groups in terms of the outcome of interest. Balance of the patient characteristics and baseline data used in the propensity score should be assessed prior to and after application of the propensity score. Standardized differences less than 0.1 (10%) indicate good balance.

7. Be sure to use proper analysis techniques that are appropriate for the type of propensity score application that was used (eg, weighted models or stratified analyses).

Conclusion

Retrospective, nonrandomized studies are prone to selection bias and confounding. In order to generate accurate results and conclusions from nonrandomized studies, it is important that these issues are identified and addressed. A propensity score is a valuable tool that can be used to mitigate treatment selection bias and confounding and to improve balance between comparison groups in nonrandomized studies.