Residue-Wise Local Quality Estimation for Protein Models from Cryo-EM Maps

Abstract

An increasing number of protein structures are being determined by cryogenic electron microscopy (cryo-EM). Although the resolution of determined cryo-EM density maps is improving in general, there are still many cases where amino acids of a protein are assigned with different levels of confidence. Here we developed a method that identifies potential misassignment of residues in the map, including residue shifts along an otherwise correct main-chain trace. The score, named DAQ, computes the likelihood that the local density corresponds to different amino acids, atoms, and secondary structures, estimated via deep-learning, and assesses the consistency of the amino acid assignment in the protein structure model with that likelihood. When DAQ was applied to different versions of model structures in PDB that were derived from the same density maps, a clear improvement of DAQ was observed in the newer versions of the models. DAQ also found potential misassignment errors in a substantial number of deposited protein structure models built into cryo-EM maps.

An increasing number of cryo-electron microscopy (cryo-EM) reconstructions have been determined in recent years and used to model the tertiary structures of biological macromolecules. It is also notable that the resolutions of the reconstructions are quickly improving. Currently in the Electron Microscopy Data Bank (EMDB)¹, 58% of the maps have a nominal resolution of 4 Å or better, compared to only 31% in 2017. For the majority of these high resolution maps, atomic structures of biomolecules were modeled and deposited to Protein Data Bank (PDB)².

In protein structure modeling into a cryo-EM map correct amino acid assignments can be challenging even in maps with high reported resolution because the resolution can differ locally in a map. Such errors are in addition to human errors that occur regardless of map quality. Rigorous validation of the resulting atomic model is therefore required if one wants to produce the most accurate model possible from the data in hand.

To date, several validation metrics have been proposed and can be generally categorized into two groups³. Those in the first category (map-model scores) assess how well the model fits into the map. The second category (model-coordinate scores) evaluates geometrical features of the model based on the statistics of known protein structures. Existing map-model scores include atom inclusion⁴, EMRinger⁵, Q-score⁶, and correlation-based scores, e.g., cross-correlation coefficient and Segment-based Manders’ Overlap Coefficient (SMOC) in the TEMPy package⁷, which is included in CCP-EM⁸, and Phenix⁹. The goal of model-coordinates scores is to find geometric outliers in a structure model but do not consider the model’s fitness to the map density. Model-coordinate scores include those used in Molprobity¹⁰ and CaBLAM¹¹. MolProbity evaluates stereochemical properties of structure models, including atom clashes, Ramachandran outliers, bond lengths, and angles. CaBLAM detects outliers of Cα-geometry using two Cα-pseudo dihedrals and another dihedral angles that connect carbonyl oxygens.

Proper validation of an atomic model built from an EM map requires evaluation by both categories of scores discussed above. This is because during model refinement, optimizing a model in terms of a map-model score, for example, may lead to a stereochemically incorrect structure while still achieving better map-model correlation. However, map-model scores are naturally affected by the resolution of the local density at the position of a residue in a map and hence difficult to use in evaluating the local quality of an atomic model. Thus, structure model validation for cryo-EM is still evolving and needs further development.

Here, we present a new approach, Deep-learning-based Amino acid-wise model Quality (DAQ) score, for cryo-EM protein model validation that uses information inherent in the cryo-EM map to assess the likelihood of each modeled position in a structural model. We used deep learning because it was now established that underlined molecular structure in an EM map can be detected by deep learning^12–14 from map density and such information is also useful to guide protein structure modeling¹⁵. In computing DAQ scores, local density features in an EM map specific for protein secondary structures, amino acid type, and Cα atoms, detected by deep learning are compared with amino acids in the model built from the EM map. DAQ score can indicate if an amino acid residue assigned to a local density is likely to be incorrect, even in cases where the protein sequence is misaligned along an otherwise correct main-chain trace. Incorrect amino acid assignment can happen even when the residue has reasonably high local density cross-correlation and appropriate stereochemical geometry.

Results

Deep learning-based residue-wise model quality score

The DAQ score examines how well residues in an atomic model agree with the local density of their positions in the cryo-EM density map. To characterize the local density at each residue position, we used deep learning.

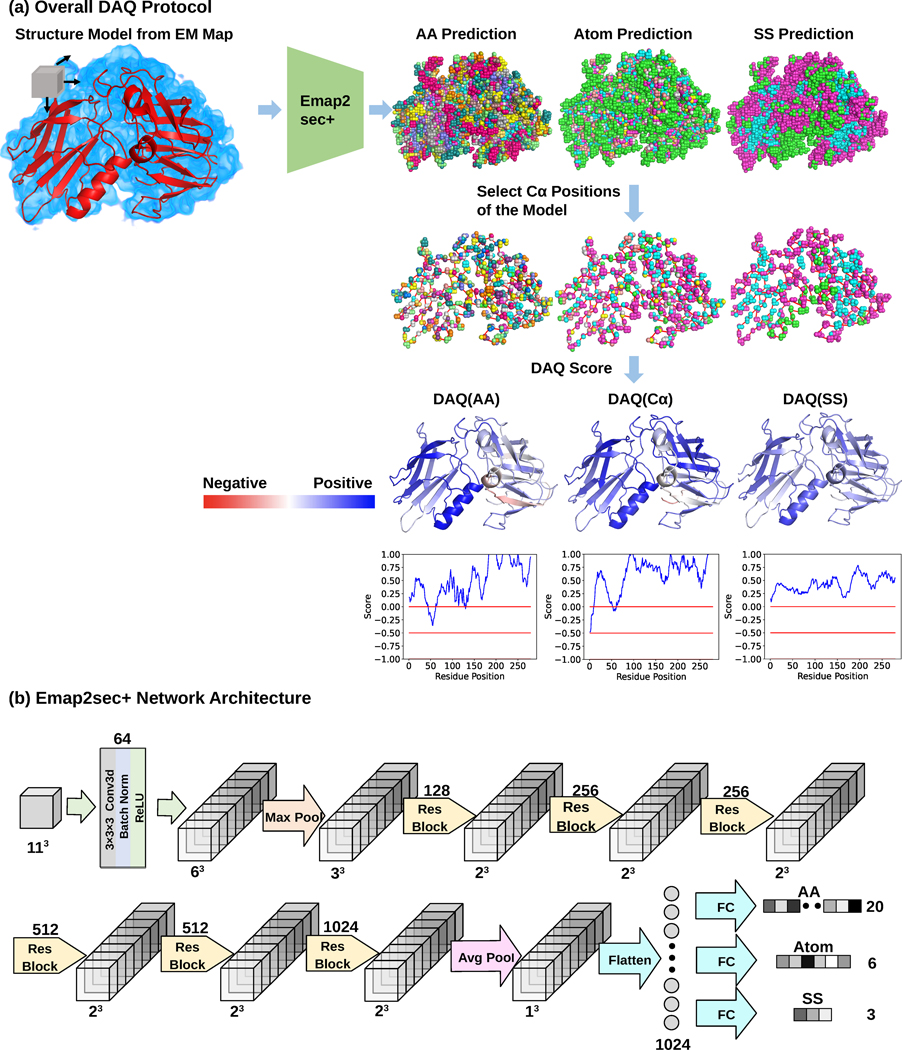
The overall process of computing DAQ for a structure model is illustrated in Fig. 1a. The deep learning method (Emap2sec+¹² in the diagram; see Methods) scans a target EM map and computes probabilities that each grid point in the map (at intervals of 1 Å) corresponds to (1) one of three secondary structure types (helix, sheet, and other); (2) one of twenty amino-acid types; and (3) Cα atoms. The probabilities for the center grid point of a box of a 11³ ų size are computed from density distribution within a box. Using these computed probability values, the DAQ score for the secondary structure, DAQ(SS), is computed for each Cα atom of residue i in the model using the following equation:

$$DAQ\left(SS\right)\left(i\right)=\sum _{ss\in H,E,C}{Pseq}_{ss}\left(i\right)\mathrm{l}\mathrm{o}\mathrm{g}\left(\frac{P_{ss}\left(i\right)}{\sum _j\raisebox{1ex}{$P_{ss}\left(j\right)$}\!\left/ \!\raisebox{-1ex}{$N$}\right.}\right)$$ (Eq. 1)

where H, E, C are a helix, extended conformation (β strand), and coil (other). Pseq_ss(i) is the probability of secondary structure ss for amino acid residue i predicted from the protein sequence using SPOT1D¹⁶, a protein secondary structure prediction program. P_ss(i) is the probability of the secondary structure ss computed by the deep learning for the nearest grid point in the map to the Cα atom of the residue i in the model. P_ss(i) is normalized by the reference probability of ss, which is the average probability of ss across all the atom positions in the model. N is the number of all the atoms j in the map. Thus, DAQ(SS)(i) is a log-odds score of secondary structures of the current position of residue i weighted by predicted secondary structure probability of the residue.

Fig. 1. Overview of DAQ.

DAQ is a residue-wise local quality estimation for protein models from cryo-EM maps based on upgraded Emap2sec+. The example used here is the rNLRP1-rDPP9 complex (PDB-ID: 7CRW, chain A) and the EM map from which the structure was built (EMD-30458). a. DAQ protocol. Emap2sec+ scans an EM map with a box of a 11*11*11 ų size with a stride of 1 Å and outputs the probabilities of amino acid type, atom type, and secondary structure type for the center position of the box. Next, the probabilities at Cα positions of the structure model are gathered. Then, DAQ(AA), DAQ(Cα), and DAQ(SS) are further calculated as log-odds scores using the average probability for the corresponding property across the entire model. In this figure, higher values (blue) indicate higher quality indicated by DAQ, while red indicate lower quality of the local structures by DAQ. b. a detailed network architecture of upgraded Emap2sec+, which were used to compute the probability values. It has 6 residual blocks and outputs the amino acid, atom, and secondary structure probability for an input box.

Similarly, DAQ score for amino-acid type, DAQ(AA)(i), for amino acid residue i is computed as:

$$DAQ\left(AA\right)\left(i\right)=\mathrm{l}\mathrm{o}\mathrm{g}\left(\frac{P_{aa\left(i\right)}\left(i\right)}{\sum _j\raisebox{1ex}{$P_{aa\left(i\right)\left(j\right)}$}\!\left/ \!\raisebox{-1ex}{$N$}\right.}\right)$$ (Eq. 2)

where aa(i) is the amino acid type of residue i, P_aa(i)(i) is the computed probability for amino acid type aa(i) for the nearest grid point to the Cα atom of residue i. The probability of residue i is normalized by the average probability of amino acid type aa(i) across over all atom positions j in the map.

Finally, Cα score of amino acid residue i, DAQ(Cα)(i), is computed as the log-odds score of the Cα atom of residue i being Cα relative to all atom positions j in the map:

$$DAQ\left(\mathrm{C}a\right)\left(i\right)=\mathrm{l}\mathrm{o}\mathrm{g}\left(\frac{P_{Ca}\left(i\right)}{\sum _j\raisebox{1ex}{$P_{Ca\left(j\right)}$}\!\left/ \!\raisebox{-1ex}{$N$}\right.}\right)$$ (Eq. 3)

DAQ(SS), DAQ(AA), and DAQ(Cα) will be positive values if the predicted probability values for the local position are higher than the average. Thus, a residue in a model that does not agree well with the predicted features derived from the EM map will have a negative value and will be flagged.

The accuracies of detecting secondary structures, Cα atoms, and amino acids were 77.3%, 51.5%, and 28.2%, respectively (Supplementary Table 1). Note that these accuracies do not need to be perfect for model validation so long as the correct residue has a positive DAQ score for the position in the map. A positive DAQ score indicates that amino acid type (or the secondary structure type, Cα atoms) fits at that position in the map better than the average (Eqs. 1, 2, 3). Indeed, it is the case - as shown the distribution of DAQ(SS), DAQ(AA), and DAQ(Cα) of Cα atom of correctly assigned residues in Supplementary Fig. 1 and Supplementary Table 2, most residues have positive scores. The fraction of positive scores for correctly assigned residues substantially increased when a local window average score was considered (Supplementary Fig. 1b, Supplementary Table 2).

In Fig. 1b, the network architecture the deep learning method used is illustrated. We used the same network architecture as our previous work, Emap2sec+¹², but re-trained on a different dataset to output probabilities of the three different types of features. The network takes density values in an input box, which are processed through 6 Residual Network¹⁷ blocks. Then, the embedded features are passed to a fully-connected network, which outputs probabilities of amino acids, secondary structures, and Cα atom (Methods).

The average DAQ(AA) score relative to EM map resolution is shown in Supplementary Fig. 2. The average DAQ(AA) score are not much influenced by the map resolution up to around 3 Å. Then, the score decreases as the map resolution lowers. But the average DAQ(AA) score stays around 0 for maps at around 4–5 Å, which indicates that the fit of amino acids in these maps are at a similar level to the average of all the atom positions in the maps. Exceptions are two maps, which showed negative average scores. The two maps are EMD-10290 (resolution: 4.2 Å) and EMD-10294 (resolution: 4.6 Å), where over 88.8% and 94.1% of residues, respectively, have no amino acid type assigned (UNK in the PDB files). In Supplementary Fig. 2, FSC-Q score and Q-score distribution on the same dataset are compared. In Supplementary Table 3, we show DAQ(AA) scores of five amino acids in apoferritin maps of different resolution. Consistent with Supplementary Fig. 2, the score decreases as the map resolution become lower.

DAQ applied to first and revised structure models in PDB

First, from a total of 13,279 EMDB entries at 5 Å resolution or better, we identified those in which there exist two versions of the deposited structure in the associated wwPDB database (ftp-versioned.wwpdb.org). We then selected for analysis those in which the Cα-RMSD between the first and the revised version of the deposited structure model was 1.0 Å or larger, leaving 15 EMDB entries, which contained 35 protein chains in total (see Methods). We call this dataset as the PDB2Ver dataset (Supplementary Table 4). Next, we classified residues, more precisely their Cα atoms, in the first version of the structure into inconsistent and consistent categories. A Cα atom in the first-version model was labeled as inconsistent with the revised model if the distance between the corresponding Cα atoms from the first and the revised models was larger than 2.0 Å. Otherwise, it was labeled as consistent. Each inconsistent residue was further classified into misaligned or mispositioned (Supplementary Fig. 3). A misaligned residue in the first-version model is the one that locates within 2.0 Å to a different amino acid in the revised-version model. Such a misalignment occurred when the assigned sequence shifted along the backbone of the original model. A mispositioned residue occurs if a Cα atom in the first version does not exist within 2.0 Å to any Cα atom in the revised-version model. There were 15,124 consistent and 3,388 inconsistent (2,005 misaligned, and 1,383 mispositioned) Cα atoms in the resulting dataset.

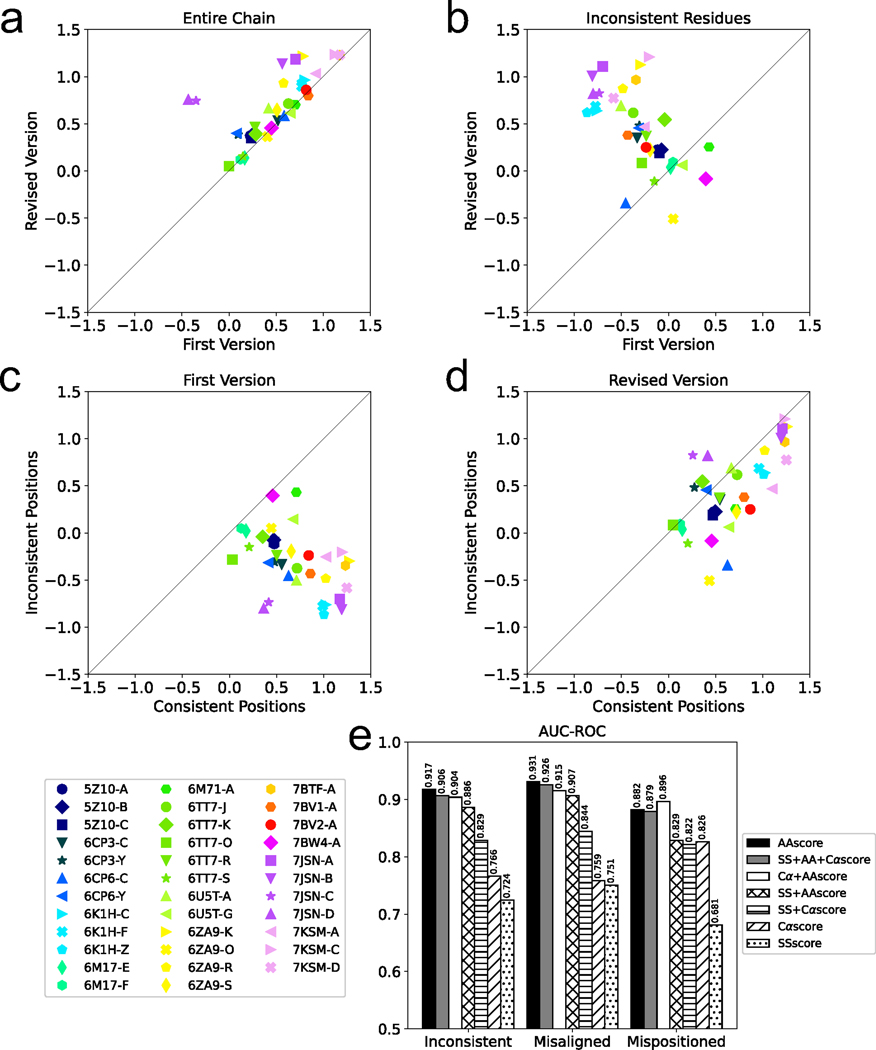
In Fig. 2a and 2b, we compared the DAQ(AA) score of the first and revised versions for the 35 protein chains. Fig. 2a shows the average score over all the residues in the models while Fig. 2b shows scores averaged only over inconsistent residues between the two models. In Fig. 2a, for 29 chains (82.9%) the revised model had a higher score than the first-version model, indicating that the revised version has a higher agreement with the EM map than the first. For the remaining 6 chains, although the scores of the first-version models were higher, the margin was small (an average difference of 0.025). When only the inconsistent residues were evaluated (Fig. 2b), revised models had a higher DAQ(AA) score for 31 (88.6%) cases and the scores were more distinct between two versions. There are four maps, EMD-30127, EMD-11127, EMD-20655, and EMD-30226, for which the revised model has a lower DAQ(AA) score. The DAQ(AA) score in fact went negative for EMD-11127 and EMD-30226. The revised regions of these models correspond to regions of the maps that were noisy, and the revised models have more exposed side-chains from the density than the first model. We further examined the score of the inconsistent residues of the first-version models (Fig. 2c) and the revised models (Fig. 2d) relative to the consistent residues, which were not modified in the model revision. Inconsistent regions have a lower score than the other parts of the models in the first-version models (Fig. 2c). After the model revision, for the 88.6% of the cases the same regions improved their scores to a similar level as the other regions of the model (Fig. 2d).

Fig. 2. Comparison of DAQ scores between first and revised protein models in the same PDB entry.

a. Comparison of DAQ(AA) scores between the first and revised protein models averaged over the entire chain. b. DAQ(AA) scores of the first and revised protein models averaged over inconsistent residues. The symbols denote PDB IDs of the protein chains. c. the average DAQ(AA) score of inconsistent residues relative to the scores of consistent residues in the first-version models. d. the average DAQ(AA) score of inconsistent residues relative to the scores of consistent residues in the revised models. A window size of 1 was used for panels a-d. e. AUC-ROC of different combinations of terms used to compute the DAQ score.

In Fig. 2e, we evaluated the performance of DAQ score in finding the inconsistent residues in protein models. For the first version model of each of the 35 protein chains, we computed the average DAQ score in sliding windows along the protein sequence. Then, we sorted the residues in the model from those with the smallest DAQ score in an ascending order and asked if the score was detecting inconsistent residues. Fig. 2e shows the Area Under the Curve of Receiver Operator Characteristic (AUC-ROC) (Methods) with a window size of 19. Seven combinations of the three component terms, DAQ(AA), DAQ(SS), and DAQ(Cα) score were compared. The results show that DAQ(AA) alone showed the highest AUC-ROC values for detecting inconsistent and misaligned residues, and the second best to the DAQ(AA) + DAQ(Cα) combination for detecting mispositioned residues. The AUC-ROC values observed by DAQ(AA) were very high, 0.917, 0.931, and 0.882, for inconsistent, misaligned, and mispositioned residues, respectively. Results for individual chains are provided in Supplementary Table 5. Results with different window sizes are provided in Supplementary Fig. 4. Using a single amino acid (i.e. a window of 1) showed a high AUC-ROC of 0.78. It further increased by using a larger window size because using a window allows detecting regions which are consistently in a low quality in its local sequential neighbors, systemically in error, such as during misalignment. We also computed the area under the precision-recall curve in Supplementary Fig. 5. The results were consistent with DAQ(AA) score performing best overall. We therefore used DAQ(AA) score, and a window size of 19 in the subsequent analyses.

Case study of a revised model

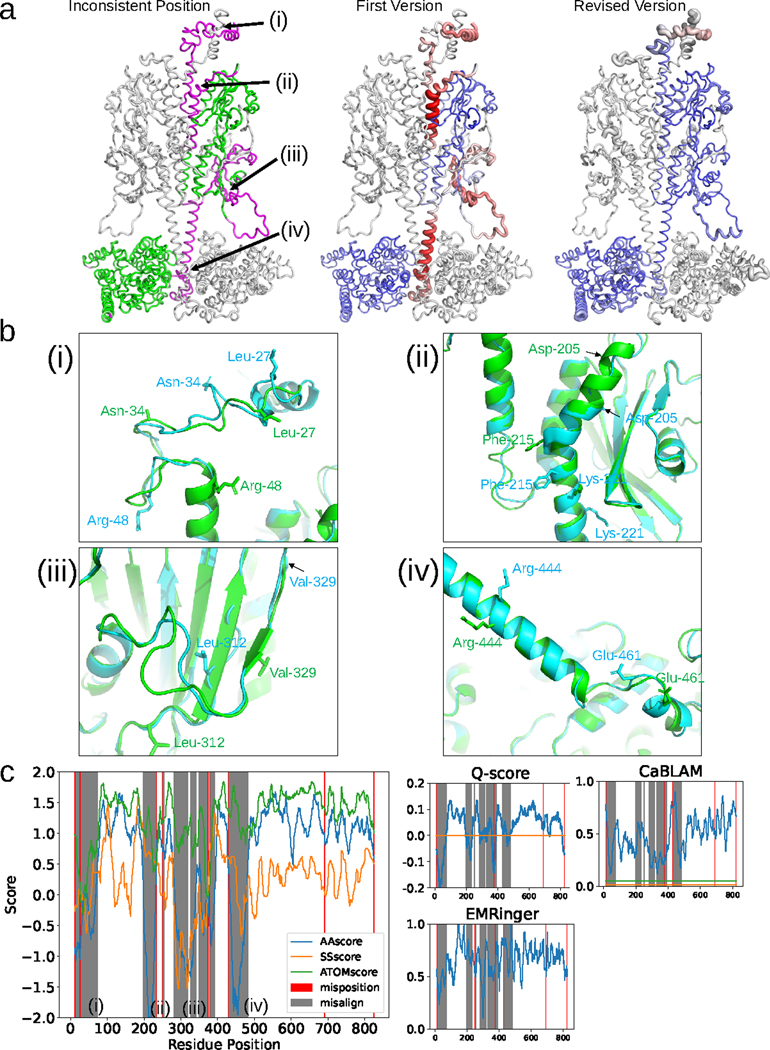
As an example, we compare the first and the revised version models of cGMP-specific 3’,5’-cyclic GMP phosphodiesterase 6 (cGMP phosphodiesterase 6) subunit β (PDB ID: 7JSN-B)¹⁸. The models were built from the 3.2 Å EM map of EMD-22458. The first model was released from PDB on October 21, 2020, and was later revised on March 31, 2021¹⁹. There are four regions (i to iv) where large deviations over 4.0 Å were observed between the two models (Fig. 3a, left). All four regions in the first version of the model were characterized by low negative DAQ(AA)-scores. The corresponding regions in the revised model reverted the DAQ score to high positive values, indicating substantial improvement, except for the region (i) at the top of the structure as portrayed in Fig. 3a (middle and right).

Fig. 3. Analysis of the DAQ score distribution for PDB entry 7JSN-B (EMD-22458).

a, Validation of the two versions of chain B deposited for entry 7JSN. Left: first version colored according to the deviation of the same Cα atom position in the revised version. Colors are scaled from green (deviation < 1.0 Å) to magenta (deviation > 4.0 Å). Middle and right: Structures of the first and revised versions, respectively. DAQ(AA) scores along the chain are shown in a color scale from red (DAQ(AA) < −2.0) to blue (DAQ(AA) > 2.0) with the width of the ribbon representation proportional to the absolute value of the DAQ(AA) score when it is negative. b, Four regions that exhibit large deviations between the two models are detailed. The first and revised versions of 7JSN chain B are shown in cyan and green, respectively. (i), residues 11–73. Three residues (Leu-27, Asn-34, and Arg-48) are highlighted with stick side chains to highlight their misplacement in the first version. (ii), residues 198–233. Three residues (Asp-205, Phe-215, and Lys-221) are shown with stick side chains as reference points to highlight misalignment. (iii), residues 282–391. Two residues (Leu-312 and Val-329) are shown with stick side chains to highlight misalignment. (iv), residues 431–483. Two residues (Arg-444 and Glu-461) are shown with stick side chains to highlight misalignment. c, DAQ scores and other validation metrics are shown as a function of sequence position. Left, three DAQ component scores are shown: DAQ(AA) (blue), DAQ(SS) (orange), and DAQ(Cα) (green). Misaligned and mispositioned residues are shaded gray and pink in the panel, respectively. The right three plots show results from three different validation scores: Q-score with the horizontal line of the expected Q-score (orange) for maps of this resolution, EMRinger, and CaBLAM with the outlier cutoff at the bottom 1% (orange) and the disfavored cutoff at bottom 5% (green), using a 19-residue sliding window.

Region (i) includes many mispositioned residues as the conformations of the two models are different. The other three regions, (ii), (iii), and (iv), have consistent backbone conformations (except for some loop regions), but misaligned residues (Fig. 3b). The DAQ score distribution also indicates that region (i) has many mispositioned residues by the fact that all three component scores, DAQ(AA), DAQ(SS), and DAQ(Cα), exhibit drops in quality (Fig. 3c, left). Notably, regions (ii) and (iv), which have misaligned positions in the first version, showed a substantial drop of only DAQ(AA). DAQ(Cα) did not drop, because the Cα positions themselves in those regions were correct, and DAQ(SS) was relatively unaffected because in both regions the backbone is α-helical. In region (iii), a large residue shift between the two models caused inconsistency in the secondary structure as well, and that was detected by a decrease of DAQ(SS). Comparison of DAQ(AA) with DAQ(ATOM) and DAQ(SS) demonstrates that DAQ(AA) captured all four inconsistent regions (the left panels in Fig. 3c). The right three panels in Fig. 3c show three other scores, Q-score, EMRinger (map-model scores), and CaBLAM (a model-coordinate score), on the same target as reference. Two other examples of DAQ(AA) score evaluation for different versions of a model for the same EM map are shown in Supplementary Fig. 6. In these examples, inconsistent regions in the two versions of the model are clearly detected by DAQ(AA) score.

To summarize, the three scores in DAQ have complementary nature. DAQ(Cα) identifies Cα atoms that are likely modeled incorrectly, whereas DAQ(SS) can identify inconsistencies in assigned secondary structure. Thus, these two scores are adept at detecting mispositioned residues. In contrast, DAQ(AA) examines characteristic local density features of amino acid residues, thus able to detect misaligned residues along otherwise correctly modelled backbone structure.

Comparison with other local quality assessment scores

In Table 1, we compared DAQ(AA) score with Q-score, EMRinger, and CaBLAM for the ability to detect inconsistent residues in the 35 first version models of the PDB2Ver dataset. Performance was evaluated using AUC-ROC and AUC of Precision-Recall (Fig. 2 and Supplementary Figs. 4 and 5). Four different sizes of the sliding averaging window (1, 3, 11, and 19 residues) were used. For each metric, two types of values are shown, one that averaged over values computed first for each PDB entry separately (e.g. Average AUC-ROC) and the other that considered all the PDB entries together (e.g. AUC-ROC All). The former examines the ability of a score to rank residues by their fit to the map within each model, whereas the latter tends to examine the ability of a score to identify potentially mismodelled residues by their absolute level of fit (Methods). DAQ(AA) showed the highest value for all the evaluations in Table 1 and also in AUC-ROC All and AUC-PrecRec All, which means DAQ(AA) score identifies mismodelled residues by absolute fit, but not by comparing with other residues in the same model. Q-score showed the second highest value for most of the evaluations. A window size of 19 gave the best performance among the four sizes used to test the various scores. This is because the large window size captures stretches of amino acid positions that have consistently low scores.

Table 1.

AUC-ROC and AUC-PrecRec of identifying inconsistent positions

	Average AUC-ROC				Average AUC-PrecRec				AUC-ROC All				AUC-PercRec All
Window Size	1	3	11	19	1	3	11	19	1	3	11	19	1	3	11	19
DAQ(AA)	0.76	0.84	0.90	0.92	0.41	0.55	0.70	0.73	0.78	0.88	0.95	0.96	0.44	0.63	0.81	0.85
Q-score	0.72	0.77	0.81	0.83	0.41	0.47	0.53	0.55	0.66	0.70	0.73	0.74	0.36	0.38	0.37	0.36
EMRinger	0.55	0.58	0.62	0.63	0.22	0.24	0.31	0.33	0.56	0.59	0.66	0.69	0.15	0.17	0.23	0.27
CaBLAM	0.66	0.69	0.72	0.73	0.33	0.38	0.48	0.48	0.63	0.65	0.68	0.70	0.28	0.30	0.37	0.39

Performance in detecting inconsistent residue positions in 35 first version models of the PDB2Ver dataset was evaluated for four validation scores: DAQ(AA), Q-score, EMRinger, and CaBLAM. Average AUC-ROC and Average AUC-PrecRoc, values were computed for each model separately and then averaged over the models. The latter two evaluations, AUC-ROC All and AUC-PrecRoc All, considered the 35 models altogether (Methods). Four window sizes (1, 3, 11, and 19 residues) were used to average scores. The largest values in each column are indicated in bold. Supplementary Figure 7 shows the score distributions for inconsistent and consistent residue positions.

Supplementary Fig. 7 shows the score distributions of consistent and inconsistent residues in the models using the four sliding window sizes. DAQ(AA) score showed a more distinct separation between the two groups of residues, particularly with a window size of 19, relative to the other scores. Also, DAQ(AA) scores of inconsistent positions distribute around zero, indicating that the inconsistent positions in the first version models are indistinguishable from the reference (i.e. denominators of Eqns. 1–3).

Inconsistent protein model pairs of high sequence identity

We next extended the analysis to 399 protein structure model pairs from different PDB entries derived from cryo-EM maps of a resolution between 1.5 Å to 5.0 Å. Pairs were selected that have over 90% sequence identity with each other yet have a Cα RMSD of 1.0 Å or higher and have at least four contiguous potentially misaligned residues in their entries. These “misaligned” residues are corresponding residues in the two models that are more than 2.0 Å away from each other and close to different residues when the two models are superimposed. Thus, these protein structure pairs have a notable difference in local regions when they are expected to have almost identical structures with each other considering their high sequence identity. We refer to this as the PDBNR90 dataset (Supplementary Table 6).

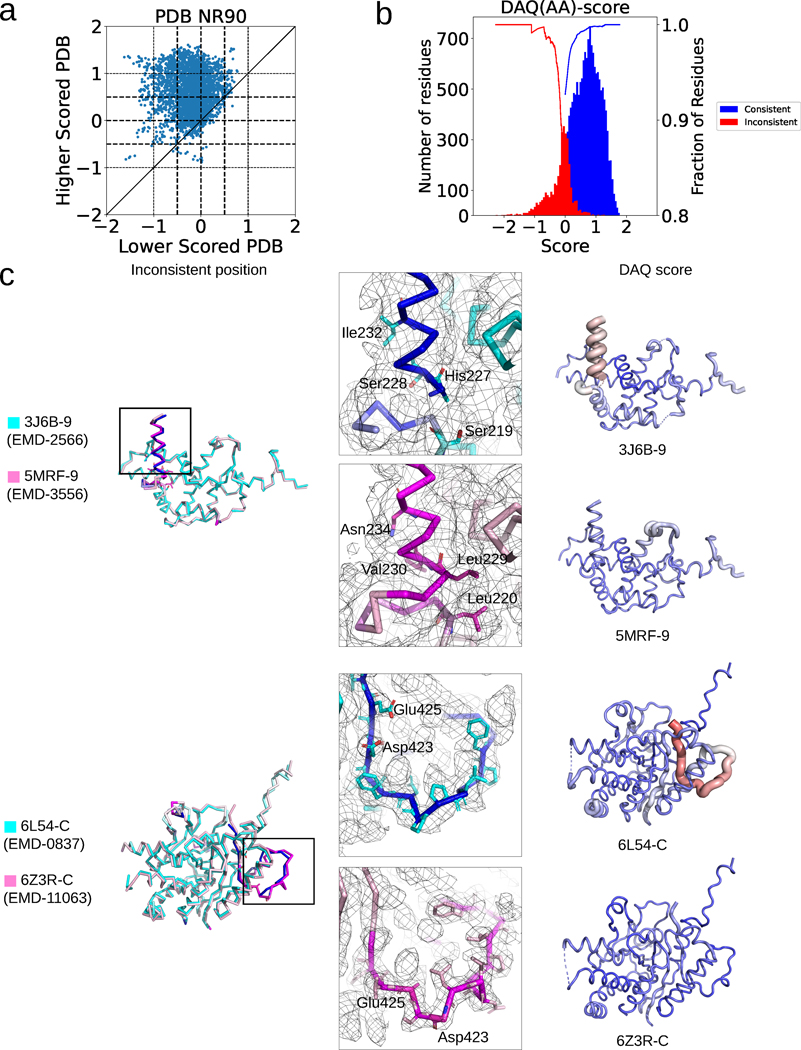
Although these model pairs have inconsistent residue assignments between each other, it is possible that both models in this dataset are correct because the two proteins have highly similar but distinct sequences. If that is the case, both models should have similarly high positive DAQ(AA) scores. However, it turned out that DAQ(AA) score prefers one model over the other in most of the cases. In Fig. 4a, we computed the average DAQ(AA) score of inconsistent residues between the structure pairs using a 19-residue sliding window. For 65.0% of the cases the inconsistent region of one model has a positive DAQ(AA) score whereas the other had a negative one. Among them, 12.2% of the pairs have a large score separation, where one model is assigned with a low DAQ(AA) less than −0.5 and another one with over +0.5. In the PDB2Ver dataset discussed in the previous section, 98.6% of residues with a DAQ(AA) lower than −0.5 are inconsistent residues in the first model which were later modified in the revised model. Likewise, 99.2% of residues with higher than 0.5 DAQ(AA) score are consistent residues in PDB2Ver. As a reference we show the distribution of scores for consistent and inconsistent residues in the PDB2Ver dataset in Fig. 4b. Therefore, it is highly likely that the regions with the lower score are misaligned or mispositioned.

Fig. 4. DAQ score analysis of misaligned residues in the PDBNR90 dataset.

a. Comparison of the average DAQ(AA) score of inconsistent regions within 399 model pairs in the PDBNR90 dataset. A 19-residue-long window was used. b. DAQ(AA) score distribution of inconsistent (red) and consistent residues (blue) in the first version models in the PDB2Ver dataset. The inconsistent residues are residues that were modified in the revised model in PDB entries and thus more likely to be incorrect in one of the models. The two curves show the fraction of inconsistent residues with a score at a negative score cutoff or below (red) and the fraction of consistent residues with a positive score at the score cutoff or higher (blue) for the data in PDBNR90. c. Two examples of protein model pairs that have a large score difference. The left column shows the superposition of the pairs (cyan and pink). Inconsistent Cα atom positions (deviation > 4.0 Å) between the two models are indicated in blue and magenta in the cyan and pink models, respectively. Models in the middle and right columns correspond to the lower and higher scored PDB models, respectively. Surface meshes represent the EM map at author recommended contour levels. In models in the right column, DAQ(AA) score is indicated in colors from red (DAQ(AA) < −2.0) to blue (DAQ(AA) > 2.0) and by the radius of the tube (thicker being more negative).

Fig. 4c shows two examples of model pairs that have large score differences. The first example compares chain 9 of the Ribonuclease III domain from PDB entries 3J6B and 5MRF^20,21. The sequence identity of these pairs is 99.5% measured by the align command in Pymol²². In the 3.2 Å resolution EM map (EMD-2566, 3J6B), density for the terminal helix region (Ser228-Val237) is not of high enough quality on its own to confirm choices on residue or atom identity. His227, Leu229, Asn231, Asn234-Lys241 are truncated as alanine, which underscore the lack of interpretability in this region. There are, however, telltale signs that there is misalignment, such as hydrophobic side-chains exposed to solvent (Ile-232 in 3J6B, which aligns with Asn-234 in 5MRF) and polar residues packed into the core of the fold (His-227 in 3J6B, which aligns with hydrophobic core residue Leu-229 in 5MRF; Ser-228 in 3J6B, which aligns with Val-230 in 5MRF; and Ser-219 in 3J6B, which aligns with Leu-220 in 5MRF). At these positions, side chains in 5MRF fit the environment well. For these reasons, 5MRF chain 9 has a better fit for both deposited EM maps, consistent with the DAQ(AA) score.

The second example is a comparison of 6L54 chain C (EMD-0837, 3.43 Å resolution) and 6Z3R chain C (EMD-11063, 2.97 Å resolution) for the protein SMG9^23,24. The sequence identity of the two proteins is 100%. In the full wwPDB EM validation report, there are an unusually large number of clashes/bad contacts (2308) listed for 6L54. In comparison, 6Z3R has 225. With respect to chain C, 6L54 is likely out of register at position Thr-405 through Leu-428 (Phe-433 in 6Z3R), and implausible side-chain packing is observed throughout this region. For example, Asp-423 and Glu-425 side chains are directed into the hydrophobic core in 6L54, but these residues are exposed to solvent in 6Z3R. In Supplementary Fig. 8, we discussed two more examples.

Validation for 4,485 non-redundant PDB models by DAQ

The above sections demonstrated that DAQ score can identify potential mismodelled residues in deposited PDB models by comparing pairs of protein structures. This brings up the question of how many models built from EM maps, without comparable structures, have potentially mismodelled regions? To answer this, we applied DAQ(AA) score to 4,485 PDB-chain models built from EM maps with resolution better than 5.0 Å. These protein models, the PDBNR1Å dataset, are non-redundant in terms of sequence and structure, having less than 90% sequence identity or more than 1.0 Å Cα RMSD with other entries (Supplementary Table 7). The data selection procedure is detailed in the Methods.

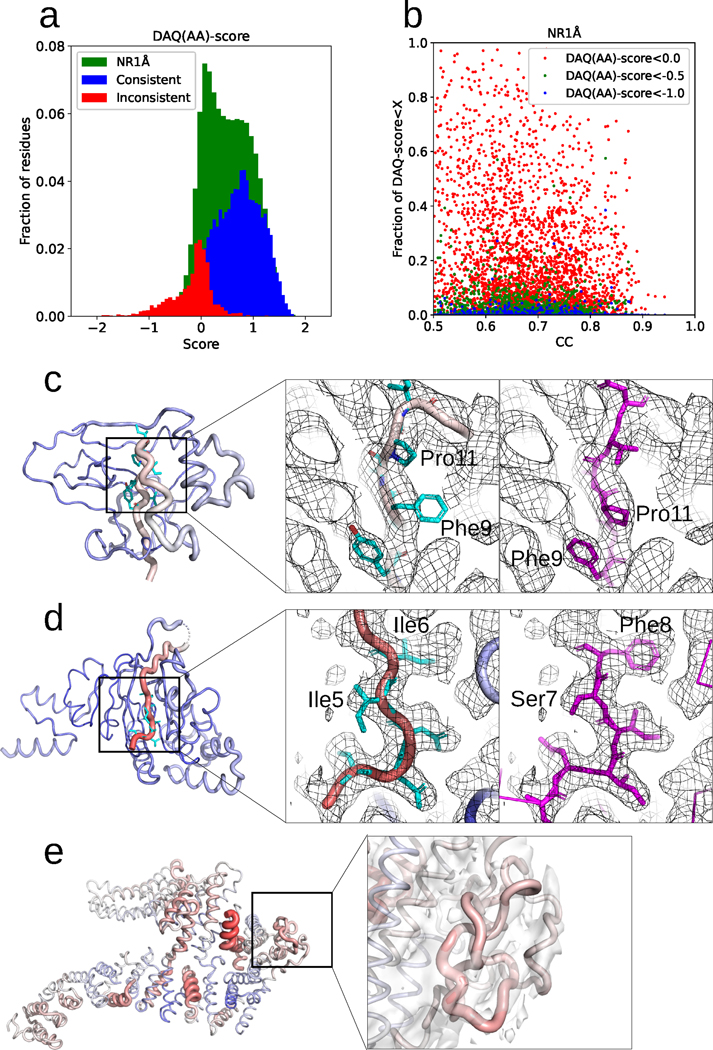
Fig. 5a shows the score distribution of residue positions for all models in PDBNR1Å in green. For reference, consistent and inconsistent residues in the first-version models for the 35 protein chains in PDB2Ver are shown in blue and red, respectively. The distribution of PDBNR1Å overlaps well with the distribution of inconsistent (red) residues. As strong negative values in the inconsistent residues generally indicated modeling problems, the result suggests that negative scoring residues in the PDBNR1Å dataset would also need attention.

Fig. 5. Analysis of 4,485 non-redundant PDB chain models in PDBNR1Å by DAQ score.

a. Distribution of DAQ(AA) score with a 19-residue sliding window. Green bars represent the distribution of the PDBNR1Å dataset. For comparison, the score distributions of consistent (blue) and inconsistent (red) residues in the PDBVer2 dataset are also shown. b. The fraction of residue positions with a low DAQ(AA) score in structure models (y-axis) were plotted relative to cross-correlation between the models and the corresponding EM maps (x-axis). The fraction (y-axis) is defined by the number of residues that have DAQ score below three cutoff values, red: 0.0, green: −0.5, and blue: −1.0, relative to the length of the protein chain. c. DAQ(AA) score mapped on PDB entry, 6S8B chain L associated with EM map (EMD-10117) determined at a 2.41 Å resolution. The chain is colored according to the DAQ(AA) score from red (DAQ(AA) score < −2.0) to blue (DAQ(AA) score > 2.0). The width of the ribbon is proportional to the absolute value of the DAQ(AA) score when it is negative. The middle panel shows the model from the PDB entry. The main chain is shown in tube with color showing DAQ(AA) score. Sidechains discussed are in cyan The right panel shows the Alphafold2 predicted model in magenta. d. DAQ(AA) score mapped on PDB entry 7NNU chain A associated with EM map (EMD-12487) determined at a 2.7 Å resolution. The middle panel shows the PDB model. This region has a strong negative DAQ(AA) score as shown in red. The right panel shows the Alphafold2 predicted model. e. DAQ(AA) score mapped on PDB entry 6TNI chain A. Its associated EM map (EMD-10534) is shown as a transparent envelope at the recommended contour level. The right panel highlights two entangled regions, Val-661 to Gln-709 and Leu-758 to Lys-778.

Fig. 5b examines correlation between the fraction of residues with a low DAQ(AA) score and cross-correlation of map density. Three different cutoff values were used to define a low DAQ(AA) score: 0.0, −0.5, and −1.0. No clear correlation was observed between the cross-correlation and the amount of the low-scoring residues, which indicates that misassignments also occurred in models that fit overall well to density maps. Using the lowest cutoff of −1.0 to define potentially misassigned residues, 173 maps among 4,485 maps (3.9%) have at least 1 misassigned residue and 6 maps (0.1%) have more than 10% misassigned residues. With a −0.5 cutoff, 89 chains have more than 10% misassigned residues (Supplementary Table 8). If we use 0.0 as the cutoff, surprisingly, 335 PDB chains (7.5%) have more than 50% of residues with a negative DAQ(AA) score. Thus, misassignment of residues in structure models constructed from EM maps may be more prevalent than we think.

Fig. 5c to 5e show examples that have low DAQ(AA) score. In the first example (Fig. 5c) (EMD-10117, 2.41 Å; PDB 6S8B chain L), residues Ser-2 through Ile-16 have a low DAQ(AA) score of −0.17 to −0.35. Throughout this region, the side chain density is inconsistent with the model. For example, the density for modeled residue Phe-9 is more consistent with that expected for proline. We remodeled this region with AlphaFold2²⁵, which is shown in the right panel. The Alphafold2 model is consistent with this interpretation. In the second example (EMD-12484, 2.7 Å; PDB 7NNU chain A), DAQ(AA) score showed strong negative values, −0.36 to −1.29, for residues Gly-1 through Thr-12. The density and residue environments are once again incompatible with the deposited structure. For example, residues Ile-5 and Ile-6 is better modeled as Ser-7 and Phe-8. Modeling by AlphaFold2 (the right panel) also suggests a two-residue shift towards the N-terminus. The last example (Fig. 5e) is the structure of the FANCD2 homodimer (EMD-10534, 3.4 Å; PDB 6TNI chain A). The model has more than 10 % of positions with a DAQ(AA)-score lower than −0.5. Overall, the EM map does not support the amino acid assignment in the PDB model, and many regions were modeled as poly-alanine. The regions Val-661 to Gln-709 and Leu-758 to Lys-778 are entangled with implausible steric collisions between backbone atoms.

Computational Time

We provided the computational time of running DAQ for maps with various sizes in Supplementary Fig. 9. It takes less than 30 min on for maps with proteins of up to 2,000 amino acid residues on a machine with 4 Intel(R) Xeon(R) 3.60GHz CPU cores, a NVIDIA RTX 2080Ti GPU and 64GB memory. In the figure, we tested three stride values (the grid interval used to scan the map), 1, which is the default that was used in the results of this work, 2, and 4. Compared to using a stride of 1, using 2 reduces the computational time about eight-fold. The accuracy of detecting inconsistent residues did not deteriorate with a stride of 2 (Supplementary Table 9) but dropped substantially with a stride of 4.

Discussion

The DAQ score we propose here is different and complementary to existing map-model scores and model-coordinate scores. The DAQ score detects local density features from cryo-EM maps that are specific to amino acids, Cα atoms, and secondary structures and identify amino acid residues that are unlikely to be positioned in this local density. DAQ score will be low, usually with a large negative value, if a wrong amino acid is assigned to a position in a map. Also, DAQ score tends to be low when the local resolution of the map is low. In this case, DAQ is usually close to 0, indicating that the fit of the residue at that position is not better than the average across all the positions in the map. DAQ is designed to compare the local map density distribution and the model structure and examines if they are compatible regardless of how the map is generated or if the map is modified by a map sharpening tool or not.

There are limitations of the DAQ score. This score currently only provides scores to protein models and cannot handle other molecules, such as DNA/RNA, stereochemical compounds, and water molecules. DAQ is a residue-wise score, and thus does not provide scores for individual atoms. Also, the targeted map resolution for DAQ score is 2.5 Å to 5.0 Å because this was the resolution range of maps in the training set, although DAQ seem to work fine for maps at a higher resolution (Supplementary Fig. 2). For a map with a worse resolution (> 5.0 Å), we observe cases that local density features are not sufficient to distinguish individual amino acids, and DAQ score values go down around 0 (neutral). Each of these characteristics of DAQ score is complementary to atom level scores, such as Q-score, therefore, we recommend to use a proper validation score depending on the needs. As we have shown above, DAQ is very efficient at identifying misalignments.

The current DAQ uses a convolutional neural network with a fixed box size to scan a map. The current scanning box size is adopted from our previous work¹². It may be worthwhile to optimize the box size specifically for DAQ and to explore different network architectures^26,27 to seek for further improvement of the performance.

Validation tools including DAQ, Q-score, EMRinger, do not fix the model itself but help researchers to identify potential problems in a structure model and guide them to fix the problems. We suggest that an accurate quality assessment method such as the DAQ score should be an integral part of the validation process for models being deposited in the PDB and for evaluations by peer reviewers prior to publication. It would also be very useful for end-users to detect potential errors in deposited structures, or at least regions of low confidence, before they use these atomic models for further computational or experimental studies. Finally, such high-fidelity assessments are fundamentally important for developing de-novo modeling methods and refinement methods.

Methods

Prediction of local properties by Emap2sec+ from an EM map

DAQ score uses the probability of secondary structure types, amino acid types, and atom types computed at each grid point of an input EM density map using an upgraded version of Emap2sec+. The original Emap2sec+ was trained for medium to low resolution maps determined at ~5 to 10 Å resolution. The current upgraded version was trained on maps of 2.5 to 5.0 Å resolution. In this work, we focused on this range because maps at higher resolution do not tend to have many modeling errors and maps at a resolution lower than 5.0 Å may have errors but correct residue types are difficult to detect from the density features. The deep neural network architecture of the original Emap2sec+ has two phases, the first-phase network with ResNet blocks, which outputs the probability of secondary structure classes, and the second phase that refines them. For DAQ, we only used the first-phase network because the performance was not much improved by the second phase.

Training and validation datasets of experimental maps for Emap2sec+

We first chose all cryo-EM maps determined at a resolution between 2.5 and 5.0 Å that have corresponding PDB entries. We removed maps if the corresponding PDB entries include a protein with unknown residues. To ensure that EM maps and associated PDB structures have sufficient overlap and align properly with each other, we examined the cross-correlation of densities between the map and a simulated map from the PDB entry at the map’s resolution. Maps were not considered if the cross-correlation was less than 0.65. The alignment between the map and the associated PDB entry was also manually checked. To assure non-redundancy of the dataset, if two maps had at least one protein chain pair with more than 25% sequence identity between each other, one map was removed. Applying these steps resulted in 237 cryo-EM maps. Among them, 197 maps remained for training and validation while 40 maps were reserved for testing Emap2sec+. We further compared the 197 maps with the PDB2Ver dataset we applied DAQ score to, which consisted of 15 EM Maps with 35 protein chains. A map was removed if it has at least one chain with more than 25% sequence identity with any protein chains in the PDB2Ver dataset. Finally, 183 maps remained for training and validation. This dataset construction process is illustrated in Supplementary Fig. 10a.

The selected EM maps underwent three pre-processing steps. First, the grid size of the maps was adjusted to 1.0 Å by trilinear interpolation. Then, density values in a map were normalized to [0.0, 1.0] with a min-max normalization. Negative density values were set to 0, and 0 was used as the minimum value. For the maximum value, we used the 98% percentile score as the maximum value, and any density values above that were normalized to 1.0. Then, we collected boxes of a size of 11³ ų by scanning across a map along three axes with a stride of 2.0 Å. Then, as ground truth for a box for training the neural network, we assigned an atom, a residue type label, and the secondary structure that were taken from the closest residue located within 1 Å to the center of the box in the corresponding protein tertiary structure from the PDB entry. The secondary structure was assigned to each residue in a protein structure using the DSSP program²⁸.

Training the deep neural network of Emap2sec+

We trained one network which computes probabilities of three secondary structure types, twenty amino acid types, and six atom types, Cα, Cβ, main-chain N, C, and O, and other heavy atom types. Note that Emap2sec+ predicts probabilities of the six atom types but only Cα atom probability is used in DAQ score. The architecture of the network is the same as the original Emap2sec+, which consists of a 3D convolutional block, a max-pooling layer, six 3D residual blocks, and a fully connected layer. The only difference between the two networks is the output layers. The network uses three softmax functions, each of which outputs probabilities of secondary structures, twenty amino acid types, and atom types, respectively, which sum up to 1.0 within each category.

From the 183 maps in the training set, we collected around 1.1 million boxes from 146 maps for training and 0.22 million boxes from 37 maps for validation. For each iteration of the training, we randomly sampled 256 boxes as input. Boxes were randomly rotated for data augmentation to achieve good generalization. In total, we ran training for 30 epochs for the network and kept the model that performed best on the validation set as our final model. We tested combinations of learning rates from [2e-5, 2e-4, 0.002, 0.02, 0.2] using the Adam optimizer²⁹ with L2 regularization with weight values of [1e-6, 1e-5, 1e-4, 0.001, 0.01, 0.1]. Among the combinations tested, the learning rate of 0.002 with LR regularization parameter of 1e-5 showed higher box-based accuracy on the validation set. The training and validation loss values with these hyperparameters along epochs are provided in Supplementary Fig. 11, which shows no trace of overfitting to the training set. Hence, we adopted these hyper-parameter combinations for the test set of 40 maps. Supplementary Fig. 10b illustrates the model training process.

The network (Fig. 1b) has three main components: input convolutional block with around 1K parameters, 6 residual blocks with around 6.47 million parameters in total, and a fully connected layer with around 60K parameters. Thus, in total, there are about 6.5 million parameters to train in the network. On the other hand, the training set has 1.1 million boxes, and for each box the network outputs 29 probability values, which are for 20 amino acids, 6 atoms, and 3 secondary structures. Thus, in total, there were 31.9 million values (1.1 million x 29) to predict.

Supplementary Table 1 shows the accuracy of Emap2sec+ on the 40-map testing dataset. To evaluate structure feature detection by Emap2sec+ to an EM map, first correct labels were assigned to each grid point in a map: According to each residue in the corresponding protein structure for the map, amino acid and secondary structure labels were assigned to grid points that were within 1.0 Å to any heavy atoms of the residue. Then, a label assignment for the residue by Emap2sec+ was considered as correct if the Emap2sec+’s assignment to the majority of the grid points with the labels from the residue were correct. The atom detection accuracy was computed in the same way.

Three datasets of cryo-EM maps and protein models examined with DAQ score

Apart from the training and validation set for Emap2sec+, we prepared three datasets for application and analysis of DAQ score. The first dataset for analysis is a set of EMDB entries determined at 5 Å resolution or better and have an associated PDB entry with two versions of the deposited protein structural models. We then selected PDB entries where the two versions of models have a Cα-RMSD of 1.0 Å or higher. The same cross-correlation criterion as mentioned above was used to ensure that protein models have sufficient overlap with the corresponding EM map. This was defined as the PDB2Ver dataset. In the end, there were 15 EMDB entries, containing 35 protein chains in total (Supplementary Table 2).

The next evaluation dataset, named PDBNR90, contains pairs of PDB chains that (1) have over 90% sequence identity between each other; (2) are at least 100 residues long; (3) have a Cα RMSD of 1.0 Å or higher; (4) have at least four continuous residues of “misaligned” positions between the two models; (5) were constructed from cryo-EM maps and the model has at least 50% of volume overlap with the maps; and (6) have at least 0.5 cross-correlation coefficients between the EM map (computed by TEMPy package³⁰). Misaligned positions in a protein structure model pair were identified from a structural alignment with the Combinational Extension (CE) algorithm³¹ and their sequence alignment. A misaligned position was defined as a Cα position that was aligned within 1.0 Å by CE, which was not aligned in the sequence alignment. To remove ambiguity in judging difference between two models, we only considered regions with at least four continuous misaligned positions. A CE alignment also revealed residue pairs in two models that were more than 2.0 Å apart and were not close enough to any other residues, which would be categorized as “mispositioned” residues. However, we did not consider mispositioned residues and only focused on misaligned residues in the analysis because both residues in a mispositioned pair could be correct in this dataset because the two models were constructed from different EM maps. If selected proteins have 25% or higher sequence identity to any proteins in the training or validation set of Emap2sec+, they were removed. The PDBNR90 dataset consists of 399 pairs and a total of 3,596 misaligned residues (Supplementary Table 5).

The third dataset, named PDBNR1Å, includes 4,485 PDB chain models. To construct this dataset, first we clustered protein chains in PDB with a 90% sequence identity cutoff. Then within each cluster, we computed Cα RMSD between structure model pairs and one of the structures was removed if they had a Cα RMSD of less than 1.0 Å. Thus, chain models, in general, have less than 90% sequence identity between each other, but if model pairs with more than 90% identity were structurally different by more than 1.0 Å in Cα RMSD, both of them were kept. Then, we further applied the following four criteria and kept protein models that satisfy all the conditions: (1) at least 200 residues long; (2) were constructed from cryo-EM maps and the model has at least 50% of volume overlap with the maps; (3) have at least 0.5 cross-correlation coefficients between the EM map; and (4) do not have 25% or more sequence identity to any proteins in the 183 training/validation set of Emap2sec+. The models consisted of a total of 2,157,911 residues. The entries are listed in Supplementary Table 6.

Area Under the Curve of Receiver Operator Characteristic (AUC-ROC)

In Fig. 2c and Table 1, AUC-ROC were computed. To obtain AUC-ROC, first we computed the DAQ score with a sliding window along the protein sequence of each of the 35 protein chains in the PDB2Ver dataset. Then, residues were sorted from the lowest DAQ score to the largest, i.e. in an ascending order. Since inconsistent residues are expected to have low DAQ scores, inconsistent residues appear earlier in the rank if the score is working. Using this sorted list of residues, a ROC curve was created by plotting the true positive rate (TPR) (the y-axis) against the false positive rate (FPR) at various top x ranks on the x-axis³². TPR is defined as (the number of inconsistent residues within the top x ranks)/(Total number of inconsistent residues in the dataset). Thus, true positives are inconsistent residues that are identified within top x ranks. FPR is defined as (the number of consistent, i.e. not inconsistent residues within the top x ranks)/(total number of consistent residues in the dataset). Supplementary Fig. 12 shows an example of ROC curve used to plot Fig. 2c. Once a curve is drawn, the Area Under the Curve (AUC) of the ROC (the gray area) quantifies the performance of the DAQ score. AUC-ROC ranges from 0 to 1. A high AUC value indicates that the score ranks inconsistent residues high with a low DAQ values relative to consistent residues. If the prediction of inconsistent residues is almost random by the DAQ score, the ROC curve will be close to a diagonal line and the AUC value will be around 0.5. On the other hand, a large ROC value close to 1.0 indicates that prediction is near perfect.

Similarly, for computing the Area Under the Curve of Precision-Recall curve (AUC-PrecRec), precision (the y-axis) and recall (x-axis) are plotted at various top x ranks. Precision is defined as (the number of inconsistent residues within the top x ranks)/(Total number of residues within top x, i.e. x). Recall is defined as (the number of inconsistent residues within the top x ranks)/(Total number of inconsistent residues in the dataset).

For Table 1, we computed two types of AUC-ROC, “Average AUC-ROC” and “AUC-ROC All”. The average AUC-ROC is the average of AUC-ROC computed for the 35 models. Thus, for each model, AUC-ROC was separately computed and then averaged over models. In contrast, the latter “AUC-ROC All” considered all the residues in the 35 models altogether, sorted them by the DAQ score and computed an AUC-ROC value once. Although they are similar, these two approaches have notable differences. The average AUC-ROC will be high if a score is able to sort residues within each model by their quality and if all the models have a similar fraction of inconsistent residues. On the other hand, because AUC-ROC All sorts all residues from all models, it tends to examine if absolute values of the score (but not relative within each model) can tell inconsistent residues or not.

Other model evaluation methods

All the following programs were used with default parameters.

Q-score.

We used the mapq_cmd.py script downloaded from https://github.com/gregdp/mapq. We subtracted the expected Q-score at a given resolution from the raw residue Q-score.

EMRinger.

We used the emringer_rolling.py script downloaded from https://github.com/fraser-lab/EMRinger.

CaBLAM.

We used the phenix.cablam_validate command in the Phenix package (version 1.19.2–4158). It was downloaded from https://phenix-online.org/.

Data availability

The list of PDB and EMDB entries used in the datasets are available in Supplementary Table 2, 3, 5, and 6.