Evolutionary game theory and the adaptive dynamics approach: adaptation where individuals interact

Abstract

Evolutionary game theory and the adaptive dynamics approach have made invaluable contributions to understanding how gradual evolution leads to adaptation when individuals interact. Here, we review some of the basic tools that have come out of these contributions to model the evolution of quantitative traits in complex populations. We collect together mathematical expressions that describe directional and disruptive selection in class- and group-structured populations in terms of individual fitness, with the aims of bridging different models and interpreting selection. In particular, our review of disruptive selection suggests there are two main paths that can lead to diversity: (i) when individual fitness increases more than linearly with trait expression; (ii) when trait expression simultaneously increases the probability that an individual is in a certain context (e.g. a given age, sex, habitat, size or social environment) and fitness in that context. We provide various examples of these and more broadly argue that population structure lays the ground for the emergence of polymorphism with unique characteristics. Beyond this, we hope that the descriptions of selection we present here help see the tight links among fundamental branches of evolutionary biology, from life history to social evolution through evolutionary ecology, and thus favour further their integration.

This article is part of the theme issue ‘Half a century of evolutionary games: a synthesis of theory, application and future directions’.

1. Introduction

Owing to exponential growth, a population whose members survive and reproduce independently from one another either rapidly goes extinct, or eventually fills the universe [1–3]. Our world, however, is not limitless. Individuals therefore inevitably interact with one another, either directly, such as through fights to control breeding territories or cooperative behaviours to exploit the environment more efficiently, or indirectly, as via the consumption of a common resource or the sharing of a common predator. When individuals vary in heritable traits that influence such interactions, those traits that are better adapted, in other words those that are associated with greater reproductive success, become more common. This sets in motion Darwinian evolution and ultimately leads to the apparent ‘fitness of form and function’ [4] that characterizes the natural world.

While it should be easy to conceive how natural selection shapes organisms to become adapted to an environment that is determined by exogenous factors (e.g. level of precipitation, pressure or temperature), it is less straightforward when the environment is dynamic and endogenous, made up of conspecifics whose evolving traits influence an individual’s reproductive success. Understanding adaptation when reproduction and survival depend on interactions among individuals has been one of the driving goals of evolutionary game theory and adaptive dynamics [5–9]. Such dependency on interactions can be organized in two categories: (i) an individual’s ability to reproduce may be influenced by population density, in particular, reproduction must eventually be curtailed by density (density-dependence); (ii) the reproductive success of an individual depends on the traits expressed by other individuals in the population and on their frequency (frequency-dependence, [10] for further considerations). Traditional evolutionary game theory has mainly focused on understanding the consequences of frequency-dependence through direct interactions among individuals, such as helping or harming ([11,12], for textbooks). The adaptive dynamics approach grew out of evolutionary game theory to focus mostly on the gradual evolution of quantitative traits (so when traits are subject to rare mutations with small phenotypic effects) that experience both density- and frequency-dependent selection, where frequency-dependence is typically due to indirect interactions mediated by the environment or ecology, such as apparent competition ([13–15], for textbooks).

Irrespective of the specific point of focus, evolutionary game theory and the adaptive dynamics approach agree on how to characterize adaptation: a population that is adapted should be uninvadable, i.e. be resistant to invasion by any rare mutant strategy [7–9,16–22]. This is made formal using what is commonly referred to as invasion fitness, which in a population reproducing and censused at discrete time points, is the geometric growth rate of a rare mutant coding for a strategy alternative to those in the resident population [21–27]. A strategy that maximizes invasion fitness when the resident population is at the uninvadable state can be considered as optimal: it is an end-point where evolution comes to a halt [7,16–19,21]. Building on evolutionary game theory, the approach of adaptive dynamics has laid a framework based on invasion fitness to understand how a population may become uninvadable under gradual evolution. In particular, this approach determines whether an uninvadable population consists of individuals all expressing the same strategy (i.e. is monomorphic) or, owing to frequency-dependence and disruptive selection, consists of multiple coexisting strategies (i.e. is polymorphic; the set of such coexisting strategies is sometimes referred to as an evolutionarily stable [4] or steady [3] coalition). The framework of adaptive dynamics is thus particularly useful to investigate the conditions that favour the emergence of phenotypic variation in the form of adaptive polymorphism, and in the context of evolutionary games, of variation in social behaviour.

More broadly, analyses of selection based on invasion fitness have made the study of adaptation possible under an extraordinarily wide range of scenarios where frequency- and density-dependence arise (e.g. competition for resources or mates, sex allocation, altruism, warfare, state-dependent life histories, phenotypic plasticity, social learning; [11,12,28–33], for overviews). While the range of social and ecological scenarios afforded by this approach may seem limitless, using invasion fitness from first principles is not always straightforward owing to two reasons [22]. The first is conceptual. Loosely speaking, invasion fitness is a gene- or replicator-centred measure of reproductive success [34,35]. But the fundamental unit of behavioural and evolutionary ecology is typically the individual organism [11,36]. It is therefore desirable to understand adaptation at this level. A second issue is computational. In heterogeneous populations (e.g. where individuals vary in age or size and this variation influences the effects of traits on reproduction), invasion fitness turns out to be the dominant eigenvalue of a matrix which can be large and complicated [37–42]. Analysing this eigenvalue mathematically is often cumbersome, limiting analysis and obscuring biological interpretation.

Here we review key equations that resolve some of these issues. Our goal is twofold: to facilitate the interpretation of natural selection in terms of the individual and to collect together simple formulae to investigate gradual evolution in class- and group-structured populations (e.g. where individuals vary in age, sex or physiology and interact in small social groups). In particular, we provide expressions for directional and disruptive selection that are sufficient to determine whether gradual evolution leads a population to a monomorphic uninvadable state or to become polymorphic under the adaptive dynamics framework. Most of the formulae presented here are currently disseminated in the literature (sometimes derived via other frameworks, such as population or quantitative genetics), some we re-derive using invasion analysis and also extend (in our electronic supplementary material, appendix). Ultimately, we aim to provide a point of entry for other evolutionary biologists interested in modelling Darwinian evolution in non-homogeneous populations, where social and ecological interactions lead to density- and frequency-dependence and possibly adaptive polymorphism.

2. The basics

First, we go over the basics of invasion analysis and how it can be used to model gradual evolution within the framework of adaptive dynamics.

(a) . Invasion fitness and uninvadability

Suppose we are interested in the evolution of a quantitative trait, such as the extraction rate on a resource, the investment into parental care or the proclivity to disperse. We focus our attention to scalar-valued traits for now, but later consider traits whose expression can change over ontogeny and plastic traits (see also [43–47] for the joint evolution of multiple traits). We first assume that the individuals of a large asexual population of haploid individuals all express the same value z ∈ Z for this trait (where $Z\subseteq \mathbb{R}$ is the space of all strategies; table 1 for a list of key symbols). If this monomorphic resident population experiences ecological or demographic changes, we wait enough time for these changes to reach a stationary state, e.g. for the population to reach an equilibrium size or for its resource to reach a stable density (this stationary state may be more complicated like a limit cycle if there are deterministic fluctuations; or a probability distribution if there are stochastic effects). Such ‘ecological’ attractor we can denote by $\hat{n}(z)$ to highlight that it may depend on the resident trait. Against this background, we introduce a single copy mutation that causes the expression of an alternative trait value z_m ∈ Z (with subscript ‘m’ for mutant). Over time, this copy may create a lineage whose members reproduce such that on average, they more than replace themselves. In this case, the mutant has a chance to invade and fix, which would lead to trait evolution and in turn potential ecological changes (as z_m substitutes z and ecology changes to $\hat{n}(z_{\mathrm{m}})$).

Table 1.

Key general symbols.

zm, z	mutant and resident traits, respectively ($z_{\mathrm{m}},z\in Z\subseteq \mathbb{R}$, where Z is the space of all possible strategies)
ρ(zm, z)	invasion fitness or geometric growth rate of a mutant allele coding for trait zm in a resident population that is monomorphic for z (i.e. per capita per-time-step number of mutant copies produced by the mutant lineage, $\rho \hspace{0.17em}:\hspace{0.17em}Z\times Z\to \mathbb{R}$ and twice differentiable)
w(zm, z)	individual fitness of a mutant carrier with trait value zm when the rest of the population expresses z (i.e. expected number of direct descendants produced over one time step by this individual, $w\hspace{0.17em}:\hspace{0.17em}Z\times Z\to \mathbb{R}$ and twice differentiable); in a homogeneous and well-mixed population, w(zm, z) = ρ(zm, z), otherwise not necessarily
s(z)	directional selection gradient (equation (2.3))
h(z)	disruptive selection (equation (2.3))
z*	singular strategy: trait value such that when expressed by the resident population, there is no directional selection (i.e. such that s(z*) = 0)

To formalize the above, we define the invasion fitness ρ(z_m, z) of a mutant z_m in a resident population z as its geometric growth rate, i.e. as the per capita per-time-step number of mutant copies produced by the mutant lineage ([21–25,27,48–50]; as the mutant is rare, its ecological background is set by the resident so ρ(z_m, z) will also typically depend on $\hat{n}(z)$, but we do not write such dependency for ease of presentation). From the theory of branching processes [51,52], it follows that the mutant goes extinct with probability 1 if, and only if, ρ(z_m, z) ≤ 1, i.e. if on average the mutant at most replaces itself. Otherwise, there is a non-zero probability that the mutant persists indefinitely. The definition of uninvadability can be derived from this [21]: a population monomorphic for z_u is said to be uninvadable when

$$\rho (z_{\mathrm{m}},z_{\mathrm{u}})\le 1\text{for all}\hspace{0.17em}{z}_{\mathrm{m}}\in Z,$$ 2.1

such that it is protected against invasion from all possible mutants. Using the fact that a neutral mutant has invasion fitness equal to 1 (i.e. that ρ(z, z) = 1), uninvadability equation (2.1) of a population monomorphic for z_u can also be expressed as $z_{\mathrm{u}}\in \arg \underset{z_{\mathrm{m}}\in Z}{max}\rho (z_{\mathrm{m}},z_{\mathrm{u}})$, i.e. z_u maximizes invasion fitness when the resident is at the uninvadable state [21].

(b) . Local analysis and gradual evolution

A related but different question is whether a population can become uninvadable through gradual evolution, to which the adaptive dynamics approach provides an answer. The main assumption behind this approach is that mutations are rare, so that a population monomorphic for z has time to reach its ecological equilibrium $\hat{n}(z)$ before a mutant appears. Assuming further that mutations have weak unbiased phenotypic effects (i.e. following the continuum of allele model [53–56] with $ϵ=z_{\mathrm{m}}-z$ small), invasion fitness can be Taylor expanded in z_m around z_m = z as

$$\rho (z_{\mathrm{m}},z)=1+s(z)(z_{\mathrm{m}}-z)+\frac{1}{2}h(z){(z_{\mathrm{m}}-z)}^2+O({ϵ}^3),$$ 2.2

where

$$s(z)={\frac{\mathrm{\partial }\rho (z_{\mathrm{m}},z)}{\mathrm{\partial }{z}_{\mathrm{m}}}|}_{z_{\mathrm{m}}=z}\text{and}h(z)={\frac{{\mathrm{\partial }}^2\rho (z_{\mathrm{m}},z)}{{\mathrm{\partial }{z}_{\mathrm{m}}}^2}|}_{z_{\mathrm{m}}=z}$$ 2.3

are two key functions that, respectively, capture directional and disruptive selection, which can be used to characterize gradual evolution.

The function s(z), which is sometimes referred to as the selection gradient or local fitness gradient [9], gives the direction of selection. It tells us that selection favours mutants that increase the trait value (z_m > z) when s(z) > 0, and conversely mutants that decrease the trait value (z_m < z) when s(z) < 0. A trait value z* is called a singular strategy when it is such that when expressed by the whole population, there is no directional selection, i.e.

$$z^{\ast }\text{is a singular strategy if}\hspace{0.17em}s(z^{\ast })=0.$$ 2.4

When the population is away from a singular strategy (z ≠ z*), s(z) is sufficient to determine whether a nearby mutant goes extinct with certainty or whether it has a chance to invade (as we can ignore terms of order (z_m − z)² and above in equation (2.2) when z_m − z is small). If such a mutant invades, then the mutant eventually fixes and thus replaces the resident. This ‘invasion implies substitution’ result, which has been proven to hold under a wide range of situations [29,57–62], means that there exists a regime of rare mutation with weak effects such that evolution proceeds by a trait substitution sequence whereby the population can be thought of as transiting from one monomorphic state to another [3]. A singular strategy z* is then approached gradually via such a sequence when

$$s^{\prime }(z^{\ast })={\frac{\mathrm{d}s(z)}{\mathrm{d}z}|}_{z=z^{\ast }}=h(z^{\ast })+{\frac{{\mathrm{\partial }}^2\rho (z_{\mathrm{m}},z)}{\mathrm{\partial }{z}_{\mathrm{m}}\mathrm{\partial }z}|}_{z_{\mathrm{m}}=z=z^{\ast }}<0$$ 2.5

[63–66]. A singular strategy z* satisfying equation (2.5) is thus an attractor of selection and said to be convergence stable.

Once the population has evolved to express a singular strategy z*, selection is determined by h(z*) (see equation (2.2) with s(z*) = 0). In particular, all nearby mutants are counter-selected when

$$h(z^{\ast })<0.$$ 2.6

In this case, the population is locally uninvadable and selection on the trait is stabilizing for z* (figure 1a; [7,64]). By contrast, any mutant can invade when h(z*) > 0. In fact, when h(z*) > 0 and the singular strategy z* is convergence stable (equation (2.5) holds), selection is frequency-dependent and disruptive such that the population becomes polymorphic through a process referred to as evolutionary branching whereby the population trait distribution goes from unimodal to bimodal (figure 1b; [8,9,14,29,67,68]). Evolutionary branching, which has been found to occur under a wide range of ecological and social interactions (like mutualism, helping or competition [30]), can help understand how adaptive polymorphism gradually emerges in populations that are initially monomorphic.

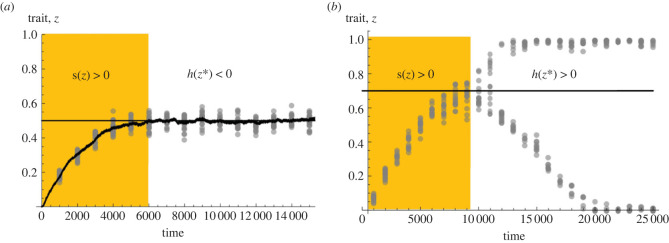
Figure 1.

Trait evolution under stabilizing and disruptive selection. (a) Evolution under recurrent mutations when selection is stabilizing. First, the population evolves under directional selection (shaded region) gradually converging to the singular strategy z*. Once the population expresses z*, stabilizing selection (h(z*) < 0) maintains the population monomorphic for z*. Simulations are shown for the biological scenario given in electronic supplementary material, appendix A.1 (parameters used: γ = 0.0005, μ = 0.8, f₀ = 2, B₁ = 2, B₂ = −2, B₃ = 0, and with mutations occurring with probability 0.01 in offspring and whose effects on the trait have mean 0 and standard deviation 0.02). Each grey dot is the trait expressed by an individual (we randomly sampled 25 individuals every 1000 generations), thick black line is the population average, and thin black line is the convergence stable and uninvadable strategy z*. (b) Evolution under disruptive selection and the emergence of polymorphism (same model as in (a) with B₁ = 1.35, B₂ = 0.5 and B₃ = 1). The population first converges to z* under directional selection (shaded region) and then becomes dimorphic owing to disruptive selection. (Online version in colour.)

Together, the functions s(z) and h(z) thus determine whether gradual evolution leads a population to a monomorphic uninvadable state under stabilizing selection or to become polymorphic due to disruptive selection (figure 1). There exist techniques based on invasion analysis to model the long-term fate of adaptive polymorphism (e.g. how many morphs eventually coexist, their trait values and frequencies [9]) but here we focus on whether polymorphism emerges or not.

(c) . All is well in a well-mixed and homogeneous world

One fundamental aspect of s(z) and h(z) to keep in mind is that they are defined from a mutant’s invasion fitness (equation (2.3)), which is a measure of reproductive success at the level of the gene or the replicator that causes the expression of the mutant phenotype. On conceptual and empirical grounds, it is however often desirable to understand selection at the level of the individual. In populations that are homogeneous and well mixed (i.e. where variation in reproductive success is only associated with variation at the locus underlying the evolving trait and where individuals interact and compete at random such that a rare mutant only ever interacts with residents), this is not a problem as invasion fitness is equal to individual fitness. To see this, let N_t be the number of mutant individuals at some demographic time point t. Invasion fitness is defined by the dynamical equation N_t+1 = ρ(z_m, z)N_t (as invasion fitness is the geometric growth rate). But this dynamical equation can equivalently be written as

$$N_{t+1}=w(z_{\mathrm{m}},z)N_t,$$ 2.7

where w(z_m, z) is individual fitness: the expected number of direct descendants produced between two time points by a mutant with trait value z_m, when the resident population expresses z. It is typically only a matter of bookkeeping to piece together such an individual fitness function w(z_m, z) for a given scenario, including where interactions are frequency- and density-dependent. This in turn allows us to straightforwardly proceed with the analysis described in §2(b) and gain insights into the outcome of evolutionary dynamics, in particular whether disruptive selection leads to the emergence of polymorphism (see electronic supplementary material, appendix A.1 for a worked out example).

The equivalence between invasion and individual fitness means that in an uninvadable population, the expressed strategy maximizes individual fitness (against itself, as in equation (2.1)). This offers a clear view on adaptation in well-mixed and homogeneous populations: selection leads to the expression of genetic traits that maximize the reproductive success of its bearer (in the absence of genetic conflicts). In fact, if individual fitness increases with a single intermediate quantity, such as fecundity, or in the context of evolutionary games—material payoff resulting from social interactions—then any z* that maximizes payoff also maximizes individual fitness, having

$$\begin{array}{rl}s(z)& ={\frac{\mathrm{\partial }w(z_{\mathrm{m}},z)}{\mathrm{\partial }{z}_{\mathrm{m}}}|}_{z_{\mathrm{m}}=z}\propto {\frac{\mathrm{\partial }\pi (z_{\mathrm{m}},z)}{\mathrm{\partial }{z}_{\mathrm{m}}}|}_{z_{\mathrm{m}}=z}\\ \text{and}h(z)& ={\frac{{\mathrm{\partial }}^{2}w(z_{\mathrm{m}},z)}{{\mathrm{\partial }{z}_{\mathrm{m}}}^2}|}_{z_{\mathrm{m}}=z}\propto {\frac{{\mathrm{\partial }}^2\pi (z_{\mathrm{m}},z)}{{\mathrm{\partial }{z}_{\mathrm{m}}}^2}|}_{z_{\mathrm{m}}=z},\end{array}$$ 2.8

where π(z_m, z) is the payoff obtained by a mutant individual in a resident population (electronic supplementary material, appendix A.2 for details). This is the basis of many optimization models in evolutionary ecology, which rather than seeking maximums of individual fitness, seek maximums of such fitness proxies, like fecundity or prey caught or rate of calorie intake (e.g. [69,70]). Equation (2.8) is also useful from an empirical point of view. As individual fitness is hard to estimate in natural populations, assays typically turn to fitness proxies, such as body weight, number of females mated, clutch size or number of seeds produced. According to equation (2.8), information on the nature of selection can be yielded by performing a quadratic regression of such proxies on individual trait values (with directional selection given by the linear term and disruptive selection by the quadratic term of the regression [71,72]).

Notwithstanding remaining technical challenges for adaptive dynamics in homogeneous and well-mixed populations [73], the equivalence between fitness at the level of the gene and at the level of the individual yields many insights into trait evolution and its resulting ecological or demographic transformations (electronic supplementary material, appendix A.3 for an example of such insight). Most natural populations, however, are not homogeneous or well-mixed. In the next two sections, we review how invasion analyses can be performed for more complex populations. In particular, we provide expressions for directional (s(z)) and disruptive selection (h(z*)) in terms of individual fitness to be compared with equation (2.8). This aims to facilitate cross-talk among models with individual fitness as common vocabulary, and ultimately aid with the interpretation of adaptation.

3. Class-structured populations: reproductive values as the exchange rate between fitness components

Populations often show heterogeneity among individuals: there can be males and females, individuals of different ages or stages, individuals in different physiological states or individuals living in different habitats. This is more generally referred to as class-structure and such structure is relevant for evolution when the fitness effect of evolving traits depends on the class of the individual expressing it. In this section, we collect together existing equations as well as present some new ones for understanding selection under three common types of class-structure (but where the population is still well-mixed such that a rare mutant only ever interacts with residents). We assume that trait expression is fixed across classes so that there is no class-specificity in trait expression (though see box 1). Technical details can be found in electronic supplementary material, appendix B.

Box 1. Directional selection on age- and state-dependent expression: the moulding of plastic traits.

The selection gradient in equation (3.12) gives the fitness effect of a mutant trait z_m (e.g. the proportion of resources allocated to growth) that influences a fitness-relevant state x(a) (e.g. size at age a) that changes with the age a of an individual (according to a dynamical system equation (3.9)). The trait z_m, however, is assumed to be fixed over an organism’s lifetime in equation (3.12). A more complicated problem is when the evolving trait z is itself a function, either of age (so-called ‘open-loop controls’; e.g. age-dependent resource allocation to growth) or of both age and state (‘closed-loop controls’; e.g. size-dependent aggression level). Such traits are more colloquially said to be plastic ([74]; or function-valued, e.g. [75–80]). As it turns out, directional selection on such traits takes a similar form to equation (3.12), revealing that singular strategies must satisfy the following balance condition at each age a:

$$\begin{array}{rl}& \frac{\mathrm{\partial }b(z_{\mathrm{m}}(a),z(a),x^{\circ }(a))}{\mathrm{\partial }{z}_{\mathrm{m}}(a)}={\tilde{v}}^{\circ }(a)\frac{\mathrm{\partial }\mu (z_{\mathrm{m}}(a),z(a),x^{\circ }(a))}{\mathrm{\partial }{z}_{\mathrm{m}}(a)}-\frac{\mathrm{\partial }{\tilde{v}}^{\circ }(a)}{\mathrm{\partial }{x}^{\circ }(a)}\frac{\mathrm{\partial }g(z_{\mathrm{m}}(a),z(a),x^{\circ }(a))}{\mathrm{\partial }{z}_{\mathrm{m}}(a)},\end{array}$$ I.A

where z_m(a) is trait expression at age a of a mutant (and z(a) of a resident), which may be written as a function of age only, say z_m(a) = u(a) for open-loop controls, or of both age and state, say z_m(a) = u(a, x(a)) for closed-loop controls (equation (B-150) in electronic supplementary material, appendix B.3.7; eqn (29) in [81]). Condition equation (I.A) reveals for instance that selection favours an increase in current reproduction (left-hand side) only if it exceeds the expected loss in future reproduction (right-hand side) due to an increase in current mortality and a decrease in the current rate of change of internal state (e.g. increasing fecundity by investing less into cellular repair and growth). In contrast to equation (3.12), selection on age a is independent from the probability of surviving to that age, meaning that where possible, selection favours traits that optimize life history for each age a.

Interestingly, strategies that are age- and state-dependent (i.e. open- and closed-loop controls) evolve to produce the same plastic phenotypes in well-mixed populations (given the environment is deterministic) [81]. By contrast, in group-structured populations where individuals interact locally through their state (e.g. size-dependent competition for light in plants), age- and state-dependent strategies can lead to different traits. This is because when individuals are able to respond to their own state and that of others, selection favours anticipating the future actions of others (e.g. when growing larger others might respond by growing even larger). This ‘anticipation’ is taken into account in the term $\mathrm{\partial }{\tilde{v}}^{\circ }(a)/(\mathrm{\partial }{x}^{\circ }(a))$ in the selection gradient (electronic supplementary material, appendix B.3.7; [81] for more details; also [41,81–83] for models with state-modulated local interactions). We only present results regarding directional selection of plastic traits here as disruptive selection for these traits has not yet been worked out, needing careful consideration of the nature of phenotypic deviation ([78] for further discussion).

(a) . Matrix population models

We first consider a population that is divided into a finite number M of discrete classes (e.g. males and females, juvenile and mature individuals, or subordinate and dominant individuals) such that mutant dynamics can be modelled by a matrix equation

$${\mathit{N}}_{t+1}=\mathit{W}(z_{\mathrm{m}},z)\cdot {\mathit{N}}_t,$$ 3.2

where entry i ∈ {1, …, M} of the vector ${\mathit{N}}_t$ gives the number of mutants in class i at some time t, and the (i, j)-entry of the M × M matrix, $\mathit{W}(z_{\mathrm{m}},z)$, which we denote by w_ij(z_m, z), is the expected number of mutants in class i produced by a mutant in class j between two time points (see table 2 for key symbols used in §§3 and 4). The matrix $\mathit{W}(z_{\mathrm{m}},z)$ is sometimes referred to as the mean matrix in the theory of multi-type branching process. From this theory, we know that invasion fitness ρ(z_m, z) is given by the leading eigenvalue of matrix $\mathit{W}(z_{\mathrm{m}},z)$ (i.e. the mutant goes extinct with probability 1 if and only if this eigenvalue is less or equal to 1 [51]). While direct analysis of this eigenvalue is possible (at least numerically), it does not afford much interpretation as is.

Table 2.

Key symbols for the different models of population structure.

	Class-structure (§3(a))
$M\in {\mathbb{Z}}_{+}$	number of classes (e.g. M = 2 for a model with males and females)
wij(zm, z)	expected number of mutants in class i ∈ {1, …, M} produced by a mutant in class j ∈ {1, …, M} over one time step
$\mathit{W}(z_{\mathrm{m}},z)$	mean matrix: M × M matrix with (i, j)-entry wij(zm, z); invasion fitness ρ(zm, z) is given by the leading eigenvalue of this matrix
$\mathit{q}(z_{\mathrm{m}},z)$	asymptotic frequency distribution of mutants across classes (right eigenvector of $\mathit{W}(z_{\mathrm{m}},z)$, normalized such that entries sum to one, $\sum _{\hspace{0.17em}j=1}^M{q}_j(z_{\mathrm{m}},z)=1$); denoted by ${\mathit{q}}^{\circ }=\mathit{q}(z,z)$ under neutrality
${\mathit{v}}^{\circ }$	normalized reproductive values, i.e. $v_i^{\circ }$ is the relative asymptotic demographic contribution of an individual in class i to the future of the population in the absence of selection; given by the left eigenvector of ${\mathit{W}}^{\circ }=\mathit{W}(z,z)$ and normalized such that ${\mathit{v}}^{\circ }\cdot {\mathit{q}}^{\circ }=1$
	Age-structure (in discrete-time, §3(b))
$M\in {\mathbb{Z}}_{+}$	maximum lifespan
ba(zm, z)	fecundity of a mutant at age a ∈ {1, …, M}, i.e. expected number of offspring of age 1 produced by a mutant of age a; under neutrality, $b_a^{\circ }=b_a(z,z)$
μa(zm, z)	probability of death of a mutant at age a.; under neutrality, ${\mu }_a^{\circ }={\mu }_a(z,z)$
la(zm, z)	probability that a mutant survives at least to age a; under neutrality, $l_a^{\circ }=l_a(z,z)$
T°	generation time in a population monomorphic for z, i.e. the expected age of a parent
${\tilde{v}}_a^{\circ }$	current reproductive value, i.e. expected number of offspring that an individual produces over the rest of its lifetime given it has survived to age a in a population monomorphic for z (equation (3.6)), proportional to normalized reproductive value, $v_a^{\circ }=(L^{\circ }/T^{\circ }){\tilde{v}}_a^{\circ }$ where $L^{\circ }=\sum _{\hspace{0.17em}j=1}^M{l_j}^{\circ }$, is the expected lifespan of a resident
	Physiological structure (in continuous-time, §3(c))
$M\in {\mathbb{R}}_{+}$	maximum lifespan (M = ∞ when lifespan is endogenously determined)
x(a), x°(a)	‘internal states’, or ‘states’ for short (e.g. size, skill), of a mutant and of a resident at age 0 ≤ a < M, respectively
g(zm, z, x(a))	rate of change of the state of a mutant in state x(a) (equation (3.9))
b(zm, z, x(a))	fecundity rate of a mutant in state x(a)
μ(zm, z, x(a))	death rate of a mutant in state x(a)
l(a), l°(a)	probabilities that a mutant and a resident survive at least until age a, respectively (equation (3.10))
${\tilde{v}}^{\circ }(a)$	current reproductive value, i.e. expected number of offspring that an individual produces over the rest of its lifetime given it has survived to age a in a population monomorphic for z (equation (3.11))
	Group-structure (§4)
$z_{\bullet }$	trait of a focal individual ($z_{\bullet }\in \{z_{\mathrm{m}},z\}$)
$\overline{z}$	average trait expressed by the neighbours of the focal individual (i.e. all members of the group except the focal individual)
$\omega (z_{\bullet },\overline{z})$	expected number of offspring produced by the focal individual over one time step
$R^{\circ }$	neutral relatedness: probability that in a population monomorphic for the resident z, an individual randomly sampled among the neighbours to a focal individual belong to the same lineage as the focal (i.e. are identical-by-descent)
R(zm, z)	mutant relatedness: probability that a randomly sampled neighbour to a mutant individual with trait zm in a resident population with trait z is also mutant (i.e. are identical-by-descent); under neutrality, $R(z,z)=R^{\circ }$
$K^{\circ }$	probability that two individuals, randomly sampled with replacement among the neighbours to a focal individual, are identical-by-descent to the focal (in a population monomorphic for z)

To gain greater biological traction, we first introduce the right eigenvector $\mathit{q}(z_{\mathrm{m}},z)$ of $\mathit{W}(z_{\mathrm{m}},z)$, normalized such that its entries sum to 1 ($\sum _{\hspace{0.17em}j=1}^M{q}_j(z_{\mathrm{m}},z)=1$), in which case q_j(z_m, z) corresponds to the asymptotic frequency of mutants in class j. Second, we let ${\mathit{v}}^{\circ }$ be the left eigenvector of the mean matrix ${\mathit{W}}^{\circ }=\mathit{W}(z,z)$ under neutrality (whose (i, j)-entry gives the expected number of individuals in class i produced by an individual in class j in the resident population at demographic equilibrium). Throughout, a superscript ° indicates neutrality, i.e. when z_m = z. Quantities with a superscript ° should thus be read as functions of the resident trait z (e.g. ${\mathit{v}}^{\circ }$ is a function of z) but we do not write such dependency explicitly to avoid notational clutter. We normalize ${\mathit{v}}^{\circ }$ such that ${\mathit{v}}^{\circ }\cdot {\mathit{q}}^{\circ }=1$, where ${\mathit{q}}^{\circ }$ is the right eigenvector of the neutral mean matrix ${\mathit{W}}^{\circ }$. The i-entry of the left eigenvector ${\mathit{v}}^{\circ }$ can then be thought of as the ‘normalized reproductive value’ of an individual in class i: it is its relative asymptotic demographic contribution to the future of the population in the absence of selection (this left eigenvector ensures that the invasion fitness of a neutral mutant is equal to 1, i.e. that ρ(z, z) = 1; electronic supplementary material, appendix B.1.1 for more details).

With the above notation, it turns out that the selection gradient can be expressed as

$$s(z)=\sum _{i=1}^M\sum _{\hspace{0.17em}j=1}^M{v}_i^{\circ }\frac{\mathrm{\partial }{w}_{ij}(z_{\mathrm{m}},z)}{\mathrm{\partial }{z}_{\mathrm{m}}}{q}_j^{\circ },$$ 3.3

(here and hereafter when s(z) is on the left-hand side of an equation, the derivatives on the right-hand side are evaluated at the resident, z_m = z; e.g. [25,29,84,85]; electronic supplementary material, appendix B.1.2 here for derivation). Equation (3.3) is most easily read from right to left, starting with $q_j^{\circ }$, which is the probability that a randomly sampled individual from a resident lineage (i.e. whose members express z) is in class j. The fitness derivative meanwhile is the effect of a substitution from resident to mutant trait in an individual of class j on the expected number of offspring in class i produced by this individual (including itself if it survives and changes class when i ≠ j). Finally, each offspring is weighted by its reproductive value $v_i^{\circ }$, which is its asymptotic contribution to the future of the population (and thus takes into account the demographic consequences of such offspring).

The implications of equation (3.3) are intuitive: selection favours most the expression of traits that increase the production of offspring with high reproductive value in individuals that are more common. Take for instance, a situation in which individuals are of either high or low condition. Suppose this is randomly determined at birth with the probability of low condition being greater (so that low condition is more common), but that individuals in high condition have greater fecundity (so that they have greater reproductive value). Gradual evolution in this case will tend to shape traits that favour most the production of high condition offspring by low condition individuals. Conversely, selection is weakest on traits that increase the production of low condition offspring by high condition individuals in this scenario. In the context of social interactions, these considerations and equation (3.3) are most relevant in the study of asymmetric games where class determines the payoff consequences of different actions by different players (e.g. [86,87]).

Once a population expresses a singular strategy z*, selection may be stabilizing or disruptive depending on h(z*), which we show in electronic supplementary material, appendix B.1.3 can be decomposed as the sum of two biologically relevant terms,

$$h(z^{\ast })=\underset{\begin{array}{rl}& \mathrm{nonlinear}\\ & \text{fitness effects}\end{array}}{\underbrace{h_{\mathrm{w}}(z^{\ast })}}+\hspace{0.17em}2\times \underset{\begin{array}{rl}& \mathrm{context}\times \mathrm{fitness}\\ & \mathrm{synergy}\end{array}}{\underbrace{h_{\mathrm{q}}(z^{\ast })}},$$ 3.4

with

$$\begin{array}{rl}{h}_{\mathrm{w}}(z^{\ast })& ={\displaystyle \sum _{i=1}^M{\displaystyle \sum _{\hspace{0.17em}j=1}^M{v}_i^{\circ }\frac{{\mathrm{\partial }}^2{w}_{ij}(z_{\mathrm{m}},z)}{{\mathrm{\partial }{z}_{\mathrm{m}}}^2}{q}_j^{\circ }}}\\ \mathrm{and}{h}_{\mathrm{q}}(z^{\ast })& ={\displaystyle \sum _{i=1}^M{\displaystyle \sum _{\hspace{0.17em}j=1}^M{v}_i^{\circ }\frac{\mathrm{\partial }{w}_{ij}(z_{\mathrm{m}},z)}{\mathrm{\partial }{z}_{\mathrm{m}}}\times \frac{\mathrm{\partial }{q}_j(z_{\mathrm{m}},z)}{\mathrm{\partial }{z}_{\mathrm{m}}},}}\end{array}$$ 3.5

where here and hereafter, the derivatives and other terms that characterize the components of h(z*) are evaluated at the singular resident z_m = z = z* (see [25,42,88], for other ways of expressing quadratic selection in matrix populations models). The first term, h_w(z*), is conceptually equivalent to disruptive selection in a homogeneous population (equation (2.8)), saying that selection tends to be disruptive when the fitness of an individual increases more than linearly with the expression of its own trait. Under class-structure however, these effects depend on the frequency of the individuals that express them and the reproductive value of their offspring (as in equation (3.3)). The second term of equation (3.4), h_q(z*), is unique to class-structured populations. It reveals that disruptive selection may be driven by the combined effects of a trait change on: (i) the fitness of a focal individual in a given class (say j, ∂w_ij(z_m, z)/(∂z_m)) and (ii) on the probability that the mutant causing this trait change is in an individual in that class (∂q_j(z_m, z)/(∂z_m)). More intuitively perhaps, h_q(z*) says that disruptive selection may occur when carrying the mutant simultaneously increases (i) the probability of being in a certain class j and (ii) fitness in that class j. Disruptive selection may thus be driven by synergistic effects between the context in which the mutant is expressed and fitness in that context. The polymorphism that emerges under such disruptive selection is expected to lead to the coexistence of different morphs that specialize in different classes. This will be made more explicit in the next section where we focus on age-structure.

(b) . Age-structure

For many animals, especially endotherms like humans, a major axis of variation is age which is associated with many physiological, behavioural and morphological differences [25,49,89]. In discrete time, evolution in age-structured populations can be modelled using the formalism summarized in the preceding section. Since offspring are all born the same age and age increases linearly with time, the matrix $\mathit{W}(z_{\mathrm{m}},z)$ in equation (3.2) becomes a Leslie matrix (electronic supplementary material, appendix B.2.1), whose special form leads to further insights that we review here.

We first introduce some notation to describe evolution in an age-structured population. Let b_a(z_m, z) be the expected number of offspring of age 1 produced by a mutant of age a ∈ {1, …, M} with trait z_m in a resident population with trait z (where M is maximum age); p_a(z_m, z) be the probability that a mutant survives from age a to a + 1 (so that μ_a(z_m, z) = 1 − p_a(z_m, z) is the probability that it dies); l_a(z_m, z) = p₁(z_m, z)p₂(z_m, z) … p_a−1(z_m, z) be the probability that a mutant survives at least until age a; $T^{\circ }=\sum _{a=1}^{M}a{l_a}^{\circ }{b}_a^{\circ }$ be the generation time in a population monomorphic for z, i.e. the expected age of a parent; and finally,

$${\tilde{v}}_a^{\circ }=\sum _{k=a}^M\frac{l_k^{\circ }}{l_a^{\circ }}{b}_k^{\circ },$$ 3.6

be the expected number of offspring that an individual produces over the rest of its lifetime given it has survived to age a in a population monomorphic for z. This ${\tilde{v}}_a^{\circ }$ is proportional to normalized reproductive value in age-structured populations, $v_a^{\circ }$ (specifically, $v_a^{\circ }=(L^{\circ }/T^{\circ }){\tilde{v}}_a^{\circ }$, where $L^{\circ }=\sum _{\hspace{0.17em}j=1}^M{l_j}^{\circ }$, is the expected lifespan of a resident; equation (B.43) in electronic supplementary material, appendix B.2.2 for details). In fact, ${\tilde{v}}_a^{\circ }$ is often simply referred to as ‘reproductive value’ following Fisher’s seminal work [90]. To distinguish between both definitions, we refer to ${\tilde{v}}_a^{\circ }$ as ‘current reproductive value’ here.

Using the above notation, the selection gradient can be expressed as

$$s(z)=\frac{1}{T^{\circ }}\sum _{a=1}^M[\frac{\mathrm{\partial }{b}_a(z_{\mathrm{m}},z)}{\mathrm{\partial }{z}_{\mathrm{m}}}-{\tilde{v}}_{a+1}^{\circ }\frac{\mathrm{\partial }{\mu }_a(z_{\mathrm{m}},z)}{\mathrm{\partial }{z}_{\mathrm{m}}}]l_a^{\circ }$$ 3.7

([49,91]; electronic supplementary material, appendix B.2.3 here for derivation). This shows that, as expected, selection favours an increase in the fecundity (b_a(z_m, z)) and a decrease in mortality (μ_a(z_m, z)) at each age a. The strength of selection on these age-specific fitness components, however, is proportional to the probability of surviving till that age under neutrality, $l_a^{\circ }$, which can be thought of as the probability that the effect of a mutant at age a is expressed and thus exposed to selection ($l_a^{\circ }$ is in fact proportional to $q_a^{\circ }$, the probability that a resident individual is of age a; equation (B.36) in electronic supplementary material, appendix B.2.2 for connection). Since $l_a^{\circ }$ always decreases with a, selection tends to be weaker on later acting than on early acting mutants [91]. This is always true for mutants affecting fecundity (b_a(z_m, z)). For mutants affecting mortality (μ_a(z_m, z)), selection strength is further proportional to the remaining number of offspring that an individual is expected to produce if it survives to the next age, ${\tilde{v}}_{a+1}^{\circ }$ (i.e. the current reproductive value, equation (3.6)). This quantity may in fact increase with age, for instance when maturity occurs later in life. Selection on a mutant that reduces mortality may therefore become stronger as its effects get closer to age at maturity. These well-known results lay the basis of the evolution of life-history traits, especially of senescence [49,89,91], and are relevant to age-specific social behaviour (e.g. [92]).

Less well-trodden is disruptive selection in an age-structured population, which in fact we have not seen anywhere expressed as equation (3.4), together with

$$\begin{array}{rl}& h_{\mathrm{w}}(z^{\ast })=\frac{1}{T^{\circ }}{\displaystyle \sum _{a=1}^M[\frac{{\mathrm{\partial }}^2{b}_a(z_{\mathrm{m}},z)}{{\mathrm{\partial }{z}_{\mathrm{m}}}^2}-{\tilde{v}}_{a+1}^{\circ }\frac{{\mathrm{\partial }}^2{\mu }_a(z_{\mathrm{m}},z)}{{\mathrm{\partial }{z}_{\mathrm{m}}}^2}]l_a^{\circ }}\\ \mathrm{and}& h_{\mathrm{q}}(z^{\ast })=\frac{1}{T^{\circ }}{\displaystyle \sum _{a=1}^M[\frac{\mathrm{\partial }{b}_a(z_{\mathrm{m}},z)}{\mathrm{\partial }{z}_{\mathrm{m}}}-{\tilde{v}}_{a+1}^{\circ }\frac{\mathrm{\partial }{\mu }_a(z_{\mathrm{m}},z)}{\mathrm{\partial }{z}_{\mathrm{m}}}]\frac{\mathrm{\partial }{l}_a(z_{\mathrm{m}},z)}{\mathrm{\partial }{z}_{\mathrm{m}}}}\end{array}$$ 3.8

(electronic supplementary material, appendix B.2.3 for derivation; e.g. [93] for other approaches to disruptive selection in age-structured populations). The term h_w(z*) depends on how age-specific fitness components change nonlinearly with trait (with age-specific effects weighted accordingly, as in equation (3.7)). The second term h_q(z*) depends on how fecundity and mortality change with trait expression at a given age a (the term within square brackets), multiplied to the trait effect on the probability of surviving till that age (∂l_a(z_m, z)/(∂z_m)). To see the potential relevance of this, consider a scenario where there are two age classes and the evolving trait z is the effort invested into fecundity at age 1. Suppose that expanding more effort diverts resources from other fitness components, leading to increased mortality at age 1 and decreased fecundity at age 2. An increase in z thus results in a decrease in both the probability of surviving till age 2 (i.e. ∂l₂(z_m, z)/(∂z_m) < 0) as well as fecundity at that age (i.e. ∂b₂(z_m, z)/(∂z_m) < 0), so that ∂l₂(z_m, z)/(∂z_m) × ∂b₂(z_m, z)/(∂z_m) > 0 causing an increase in h_q(z*) and thus in disruptive selection. In fact, we show in electronic supplementary material, appendix B.2.5 that polymorphism may emerge in this scenario when individuals compete within age-class. Disruptive selection in that case leads to the coexistence of two highly differentiated morphs: one that reproduces at age 1 and then dies, and another that reproduces only at age 2. Beyond this specific scenario, equation (3.8) reveals how age-structure opens pathways for disruptive selection and thus for the maintenance of genetic variation within populations.

(c) . Physiological structure

The way a trait affects fitness at a given age is often mediated by some other characteristic, such as size, knowledge or more generally physiology. These characteristics can depend on an organism’s past behaviour, environment or ontogeny. To characterize trait evolution in such cases, let $x(a)\in \mathbb{R}$ denote the ‘internal state’ of a mutant individual at age a and let age $a\in {\mathbb{R}}_{\ge 0}$ now be a continuous variable (we use continuous time here as it connects more straightforwardly to existing models and methods). The state x(a) could be the size of this individual, its foraging skill or its investment into cooperation at age a. These individual characteristics develop over time in a way that depends on an individual’s traits or behaviours. To model such ontogeny, let us assume all individuals are born with the same initial state x(0), which then develops with age according to a differential equation,

$$\frac{\mathrm{d}x(a)}{\mathrm{d}a}=g(z_{\mathrm{m}},z,x(a)),$$ 3.9

where the function g(z_m, z, x(a)) gives the rate of change in the internal state of a mutant. This rate of change may depend on the trait z_m expressed by the mutant, the traits of others it interacts with (i.e. the resident z), and its current state x(a). Equation (3.9) also allows the rate of change of the internal state to depend on the entire distribution of resident individuals across states via the resident trait z (e.g. the distribution of sizes in the resident population). A wide range of models in behavioural ecology and life-history theory can be captured conceptually by equation (3.9) (e.g. behavioural response rules, learning rules, neural networks [81–83,89,94–105]). Some of these models conceive the evolving trait z itself as a function of age or state (e.g. writing z(a, x(a)) and letting this function evolve); we focus here on the case where the trait z is fixed throughout an individual’s lifetime (but see box 1 for directional selection on age- and state-dependent traits).

The continuous-time nature of age calls for several modifications in the way relevant quantities are defined (in contrast to §3.2 where age is discrete). First, the fecundity and mortality of an individual at a given age are now rates. These rates can depend on an individual’s trait, that of conspecifics, and the individual’s current state, and so are written as b(z_m, z, x(a)) and μ(z_m, z, x(a)) for a mutant at age a (like equation (3.9), these may also depend on the distribution of resident individuals across states through the dependence on resident z). Survival l(a) to age a is then defined according to a differential equation,

$$\frac{\mathrm{d}l(a)}{\mathrm{d}a}=-\mu (z_{\mathrm{m}},z,x(a))l(a),\text{with}\hspace{0.17em}l(0)=1.$$ 3.10

Generation time in the resident monomorphic population now reads as $T^{\circ }={\int }_0^{M}a\hspace{0.17em}b(z,z,x^{\circ }(a))l^{\circ }(a)\mathrm{d}a$, where x°(a) and l°(a) are the internal state and survival of resident individuals at age a, obtained by evaluating equation (3.9) and (3.10) at monomorphic resident population for z. We also define

$${\tilde{v}}^{\circ }(a)\equiv {\tilde{v}}^{\circ }(a,x^{\circ }(a))={\int }_a^M\frac{l^{\circ }(a^{\prime })}{l^{\circ }(a)}b(z,z,x^{\circ }(a^{\prime }))\mathrm{d}{a}^{\prime },$$ 3.11

as current reproductive value, i.e. the expected number of offspring that a resident individual produces over the rest of its lifetime given it has survived to age a and is in state x°(a). This is conceptually equivalent to equation (3.6), except that here, current reproductive value depends on state x°(a). In fact, a change in state x°(a) at age a influences current reproductive value at that age, ${\tilde{v}}^{\circ }(a,x^{\circ }(a))$, by affecting jointly future survival l°(a′) (via equation (3.10), with a′ > a) and future fecundity b(z, z, x°(a′)) (via x°(a′)). For presentation purposes though, we do not write the dependence of current reproductive value on x°(a) and use ${\tilde{v}}^{\circ }(a)$ for short (electronic supplementary material, appendix B.3.2 for details on current reproductive value).

Using these definitions and methods from optimal control theory [81,103,106,107], directional selection on a trait z that influences how an individual’s internal state develops with age (according to equation (3.9)) can be decomposed as

$$\begin{array}{rl}s(z)& =\frac{1}{T^{\circ }}{\int }_0^M(\frac{\mathrm{\partial }b(z_{\mathrm{m}},z,x^{\circ }(a))}{\mathrm{\partial }{z}_{\mathrm{m}}}\\ & -{\tilde{v}}^{\circ }(a)\frac{\mathrm{\partial }\mu (z_{\mathrm{m}},z,x^{\circ }(a))}{\mathrm{\partial }{z}_{\mathrm{m}}}+\frac{\mathrm{\partial }{\tilde{v}}^{\circ }(a)}{\mathrm{\partial }{x}^{\circ }(a)}\frac{\mathrm{\partial }g(z_{\mathrm{m}},z,x^{\circ }(a))}{\mathrm{\partial }{z}_{\mathrm{m}}})l^{\circ }(a)\mathrm{d}a,\end{array}$$ 3.12

(eqn 19 in [83] for the more general case in group-structured population and electronic supplementary material, appendix B.3 here for derivation). The first two terms of equation (3.12) are conceptually similar to equation (3.7), giving directional selection on age-specific fecundity and mortality. More interestingly, the last term within brackets of equation (3.12) reveals that selection now also depends on how the trait influences the instantaneous rate of change in the internal state (∂g(z_m, z, x°(a))/(∂z_m)), and in turn how a change in internal state affects current reproductive value ($\mathrm{\partial }{\tilde{v}}^{\circ }(a)/(\mathrm{\partial }{x}^{\circ }(a))$). To intuit the relevance of this, it is useful to see $\mathrm{\partial }{\tilde{v}}^{\circ }(a)/(\mathrm{\partial }{x}^{\circ }(a))$ as a measure of the fitness value of future reproduction relative to current reproduction owing to a change in internal state at age a. The last term of equation (3.12) then says that in a situation where, for example, x(a) is size at age a and z controls the investment into growth at each age, selection favours greater investment into growth even at the expense of fecundity when one unit invested into growth yields greater future reproduction relative to that unit invested into current reproduction (i.e. when $\mathrm{\partial }{\tilde{v}}^{\circ }(a)/(\mathrm{\partial }{x}^{\circ }(a))\times \mathrm{\partial }g(z_{\mathrm{m}},z,x^{\circ }(a))/$ $(\mathrm{\partial }{z}_{\mathrm{m}})>-\mathrm{\partial }b(z_{\mathrm{m}},z,x^{\circ }(a))/(\mathrm{\partial }{z}_{\mathrm{m}})$). In the context of social interactions, equation (3.12) would for instance be useful to understand directional selection on reactive strategies [108,109], where x(a) is the level of cooperation at age a and the trait z_m determines how an organism reacts to cooperation by its social partners. The last term of equation (3.12) in this example would capture how selection at age a depends on the future benefits of an increase in cooperation at that age.

Disruptive selection, meanwhile, can be decomposed as equation (3.4), with

$$\begin{array}{rl}& h_{\mathrm{w}}(z^{\ast })=\frac{1}{T^{\circ }}{\displaystyle {\int }_0^M(\frac{{\mathrm{\partial }}^{2}b(z_{\mathrm{m}},z,x^{\circ }(a))}{{\mathrm{\partial }{z}_{\mathrm{m}}}^2}-{\tilde{v}}^{\circ }(a)\frac{{\mathrm{\partial }}^2\mu (z_{\mathrm{m}},z,x^{\circ }(a))}{{\mathrm{\partial }{z}_{\mathrm{m}}}^2}+\frac{\mathrm{\partial }{\tilde{v}}^{\circ }(a)}{\mathrm{\partial }{x}^{\circ }(a)}\frac{{\mathrm{\partial }}^{2}g(z_{\mathrm{m}},z,x^{\circ }(a))}{{\mathrm{\partial }{z}_{\mathrm{m}}}^2})l^{\circ }(a)\mathrm{d}a}\\ \mathrm{and}& h_{\mathrm{q}}(z^{\ast })=\frac{1}{T^{\circ }}{\displaystyle {\int }_0^M[\underset{\mathrm{change}\hspace{0.17em}\mathrm{in}\hspace{0.17em}\mathrm{age}}{\underbrace{(\frac{\mathrm{\partial }b(z_{\mathrm{m}},z,x^{\circ }(a))}{\mathrm{\partial }{z}_{\mathrm{m}}}-{\tilde{v}}^{\circ }(a)\frac{\mathrm{\partial }\mu (z_{\mathrm{m}},z,x^{\circ }(a))}{\mathrm{\partial }{z}_{\mathrm{m}}})\frac{\mathrm{\partial }l(a)}{\mathrm{\partial }{z}_{\mathrm{m}}}}}+\underset{\mathrm{change}\hspace{0.17em}\mathrm{in}\hspace{0.17em}\mathrm{state}}{\underbrace{h_{\mathrm{q},\mathrm{x}}(a)\frac{\mathrm{\partial }x(a)}{\mathrm{\partial }{z}_{\mathrm{m}}}}}]\mathrm{d}a}\end{array}$$ 3.13

(electronic supplementary material, appendix B.3.5 for derivation). At a broad level, h_w(z*) and h_q(z*) in equation (3.13) have the same interpretation as h_w(z*) and h_q(z*) in equation (3.5) or (3.8): h_w(z*) depends on the nonlinear effects of the trait on individual fitness components, while h_q(z*) depends on how the trait affects both (i) the proclivity of having a certain age and internal state, and (ii) fitness when in that state. Both h_w(z*) and h_q(z*) however contain extra terms in comparison to the scenario where only age matters (equation (3.8)). This is because in addition to age, an individual’s state now also depends on x(a), which opens new pathways for disruptive selection. The extra term in h_w(z*) in equation (3.13) (the last term within the brackets) depends on how fitness changes nonlinearly with trait expression via a change in state dynamics. This reveals for instance that disruptive selection may be driven by accelerating effects of a trait change on state dynamics at a certain age (∂² g(z_m, z, x°(a))/(∂z_m)² > 0, e.g. because an extra unit of resources invested in growth at age a generates a greater than linear increase in growth rate) when such a change improves current reproductive value ($\mathrm{\partial }{\tilde{v}}^{\circ }(a)/(\mathrm{\partial }{x}^{\circ }(a))>0$).

The first part of h_q(z*) in equation (3.13), labelled ‘change in age’, is conceptually equivalent to h_q(z*) in equation (3.8), i.e. capturing the effect of change in representation in a given age class a (through ∂l(a)/(∂z_m)) but with internal state dynamics left unchanged (so with x(a) of a resident: x°(a)). The effect of changing internal state is contained in the second term of h_q(z*) in equation (3.13), labelled ‘change in state’. This consists of the product between how a trait change influences the internal state at age a, ∂x(a)/(∂z_m), with h_q,x(a), which can be thought of as the second-order fitness effect of a change in internal state at age a (see equation (II.A) in box 2 for details). As described in box 2, there are several ways that state can influence fitness in a physiologically structured population, such as via interaction effects between trait and state on vital rates. This suggests that disruptive selection can readily emerge owing to a change in state and its knock-on fitness effects. Such disruptive selection would favour polymorphism in the evolving trait z and as a result, also in internal state across ages (x(a)).

Box 2. Second-order fitness effects of a state change in physiologically structured populations.

Disruptive selection in physiologically structured populations (equation (3.13), §3) depends on the product between the effect of a change in trait expression on internal state at age a (∂x(a)/(∂z_m)) and

$$\begin{array}{rl}{h}_{\mathrm{q},\mathrm{x}}(a)& =(\frac{\mathrm{\partial }b(z,z,x(a))}{\mathrm{\partial }x(a)}-{\tilde{v}}^{\circ }(a)\frac{\mathrm{\partial }\mu (z,z,x(a))}{\mathrm{\partial }x(a)})\frac{\mathrm{\partial }l(a)}{\mathrm{\partial }{z}_{\mathrm{m}}}\\ & +(\frac{{\mathrm{\partial }}^{2}b(z_{\mathrm{m}},z,x(a))}{\mathrm{\partial }{z}_{\mathrm{m}}\mathrm{\partial }x(a)}-{\tilde{v}}^{\circ }(a)\frac{{\mathrm{\partial }}^2\mu (z_{\mathrm{m}},z,x(a))}{\mathrm{\partial }{z}_{\mathrm{m}}\mathrm{\partial }x(a)}+\frac{\mathrm{\partial }{\tilde{v}}^{\circ }(a)}{\mathrm{\partial }{x}^{\circ }(a)}\frac{{\mathrm{\partial }}^{2}g(z_{\mathrm{m}},z,x(a))}{\mathrm{\partial }{z}_{\mathrm{m}}\mathrm{\partial }x(a)})l^{\circ }(a)\\ & +\frac{1}{2}(\frac{{\mathrm{\partial }}^{2}b(z,z,x(a))}{{\mathrm{\partial }x(a)}^2}-{\tilde{v}}^{\circ }(a)\frac{{\mathrm{\partial }}^2\mu (z,z,x(a))}{{\mathrm{\partial }x(a)}^2}+\frac{\mathrm{\partial }{\tilde{v}}^{\circ }(a)}{\mathrm{\partial }{x}^{\circ }(a)}\frac{{\mathrm{\partial }}^{2}g(z,z,x(a))}{{\mathrm{\partial }x(a)}^2})\frac{\mathrm{\partial }x(a)}{\mathrm{\partial }{z}_{\mathrm{m}}}{l}^{\circ }(a),\end{array}$$ II.A

where each line corresponds to a different fitness effect of a change in internal state x(a) at age a. (i) The first line of h_q,x(a) depends on how a change in state at age a affects fecundity and mortality at that age, multiplied to the effect of a trait change on the probability of surviving till then (∂l(a)/(∂z_m)). Consider for instance a model where x(a) is size and z_m controls the investment into growth. Under the assumption that growth trades off with survival (so that ∂l(a)/(∂z_m) × ∂x(a)/(∂z_m) < 0), this first line multiplied to ∂x(a)/(∂z_m) would be positive and thus favour disruptive selection when vital rates decrease with size at the singular strategy (so that the term within brackets in the first line of equation (II.A) is negative). (ii) The second line of h_q,x(a) depends on the interaction effects of the evolving trait and internal state on fitness (captured by the cross derivatives with respect to z_m and x(a)). To illustrate the potential implications of this, let us continue with the previous example where x(a) is size and z_m controls the investment into growth. Disruptive selection could occur because the fitness cost of investing resources into growth decreases with size (so that the term within brackets in the second line of equation (II.A) is negative and its product with ∂x(a)/(∂z_m) < 0 is positive). (iii) The third line of h_q,x(a) depends on the nonlinear effects of a change in state on fitness components. With x(a) as size, for example, the third line would be positive where mortality decreases with body size in an accelerating manner (such that ∂²μ(z_m, z, x(a))/(∂x(a))² < 0, e.g. because individuals are increasingly better at fending off predators with size). More broadly, equation (II.A) shows there are multiple ways for state to influence fitness and thus potentially favour disruptive selection.

We have illustrated equation (3.13) (and equation (II.A) in box 2) with examples from life history such as resource allocation problems as those are the most straightforward applications. But since all vital rates (fecundity b, mortality μ and growth g) depend on both mutant and resident traits (z_m and z), equations (3.13) and (II.A) can of course be used to understand disruptive selection on traits that influence social interactions. In fact, since the vital rates may depend on the resident internal state and its distribution across resident individuals, equations (3.13) and (II.A) can be applied to social interactions mediated by internal state, such as where larger individuals are more likely to win contests for resources.

(d) . Disruptive selection in class-structured populations

Together, the equations for disruptive selection that we have collected in this section (equations (3.5), (3.8) and (3.13)) reveal how there are several alternative non-exclusive paths for a trait to become polymorphic in heterogeneous populations, and how these paths depend on the nature of the heterogeneity. In particular, population heterogeneity creates conditions such that individuals may specialize in different contexts (class, age, size, habitat) when trait expression simultaneously increases the proclivity of being in a certain context and fitness in that context (what we have labelled as context × direct synergy in equation (3.4)). This may help explain within-population diversity in traits, such as life history, sexual development or habitat choice, that influence the context an individual finds itself in, as well as diversity in social behaviours that are mediated by such heterogeneity.

4. Interactions under limited dispersal: the inevitable rise of relatedness

So far, all the scenarios we have explored assume that individuals interact and compete randomly such that a rare mutant only ever interacts with residents. This facilitates analysis because mutant–mutant interactions can be ignored. In reality, carriers of a rare mutation may often interact with other carriers. This is obviously true for within-family interactions, such as parental care or sib competition, but more generally whenever dispersal is limited (i.e. whenever individuals have a non-zero probability of reproducing close to where they were born [110]). As a consequence of limited dispersal, individuals that are physically closer to one another, and thus more likely to interact, are also more likely to share alleles that are identical-by-descent at homologous loci than individuals sampled at random in the population [111]. This inevitably leads to interactions among rare mutants and to what is referred to as kin selection, which occurs whenever a trait expressed by a focal individual affects the fitness of others who are genetically related to the focal at the loci determining the trait [11,29,111,112].

In this last section, we review directional and disruptive selection when dispersal is limited under the light of kin selection. We consider the case where the population is subdivided among a large (effectively infinite) number of groups which can be arbitrarily small. The main assumption is that these groups are equally connected to one another (so that there is no isolation-by-distance): if an individual disperses and leaves its natal group, it is equally likely to immigrate into any other group (as in the homogeneous island model of dispersal of [113], and see [114] for its ecological equivalent). We focus on where there are no exogenous differences among groups (e.g. no differences in environmental condition; see [115] for an analysis of this).

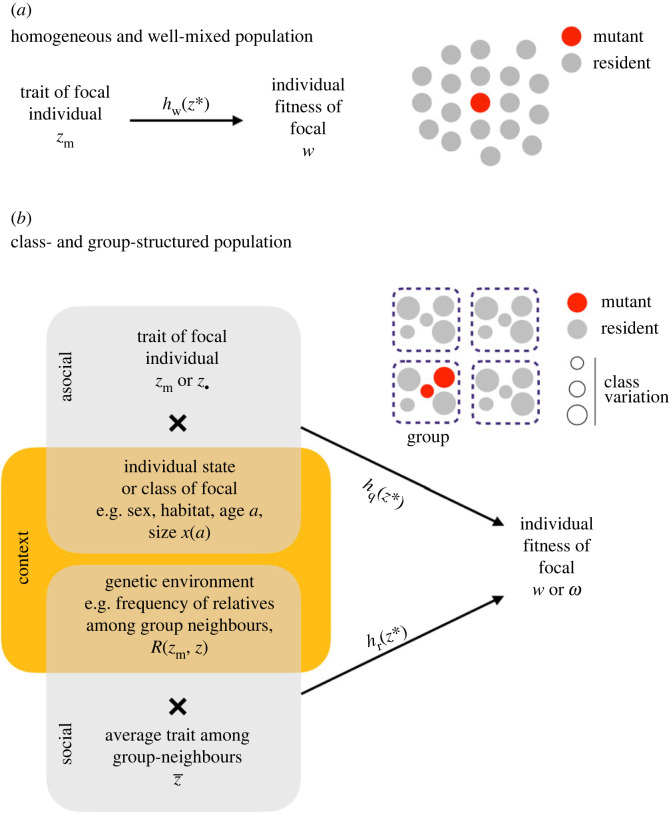
The simplest model is where groups are all of the same fixed size n, and where other than expressing the mutant or resident trait, individuals within groups are homogeneous. We detail the life cycle events that the model can consider in electronic supplementary material, appendix C.1.1 and simply note here that as long as groups have constant size, variation in several life cycle events are allowed, such as overlapping versus non-overlapping generations and dispersal via the ‘migrant pool’ versus ‘propagule pool’ model (in the former, individuals disperse independently from one another whereas, in the latter, individuals disperse in groups as part of a propagule [116]). Describing selection in this model requires an individual fitness function that takes into account group structure. We let $\omega (z_{\bullet },\overline{z})$ be this function, which gives the expected number of offspring produced by a focal individual with trait $z_{\bullet }\in \{z_{\mathrm{m}},z\}$ over one demographic time period, when its group-neighbours on average express $\overline{z}$ (all groups other than the one in which the focal individual lives can be considered monomorphic for the resident z in an invasion analysis but we do not write this dependency on z in $\omega (z_{\bullet },\overline{z})$ for simplicity). In writing fitness in terms of the average trait among its neighbours, we are assuming that the focal plays the field within its group. As a more general alternative, fitness may depend on the trait of each individual neighbour, in which case $\omega (z_{\bullet },\overline{z})$ is a first-order approximation in $ϵ=z_{\mathrm{m}}-z$ to this more complicated fitness function (electronic supplementary material, appendix C.1.2 for details).

Invasion fitness can be expressed in terms of the individual fitness function $\omega (z_{\bullet },\overline{z})$ (equation (C.12) in electronic supplementary material, appendix C.1.2), from which we readily obtain the selection gradient

$$s(z)=\underset{{\displaystyle \mathrm{direct}\hspace{0.17em}\mathrm{effect},-C}}{\underbrace{\frac{\mathrm{\partial }\omega (z_{\bullet },\overline{z})}{\mathrm{\partial }{z}_{\bullet }}}}+\underset{{\displaystyle \mathrm{relatedness}}}{\underbrace{R^{\circ }}}\times \underset{{\displaystyle \mathrm{indirect}\hspace{0.17em}\mathrm{effect},\hspace{0.17em}B}}{\underbrace{\frac{\mathrm{\partial }\omega (z_{\bullet },\overline{z})}{\mathrm{\partial }\overline{z}}}},$$ 4.1

where $R^{\circ }$ is the probability that in a population monomorphic for the resident z, an individual randomly sampled among the neighbours to a random focal individual belongs to the same lineage as the focal (i.e. are identical-by-descent; electronic supplementary material, appendix C.1.3 for derivation). $R^{\circ }$ thus corresponds to the standard coefficient of pairwise relatedness [29]. We can recognize in equation (4.1) the well-known inclusive fitness effect or Hamilton’s rule in gradient form [11,20,29,31,32]: the sum of (i) the direct fitness effect, i.e. the effect of a trait change in a focal individual on its own fitness (which in a well-mixed population is the only effect that matters, equation (2.8), and which in Hamilton’s rule is typically written as a cost −C); and (ii) relatedness-weighted indirect fitness effect, i.e. the effect of a trait change in neighbours on focal fitness (written as a benefit B in Hamilton’s rule), weighted by the probability that a neighbour and the focal both carry the same mutation (under neutrality). Relatedness in equation (4.1) thus quantifies mutant–mutant interactions and highlights their well-known evolutionary significance: interactions among relatives tend to favour the evolution of prosocial traits (i.e. traits such that $\mathrm{\partial }\omega (z_{\bullet },\overline{z})/(\mathrm{\partial }\overline{z})>0$, [11,29,111]). The selection gradient equation (4.1), which is written in terms of the individual fitness function $\omega (z_{\bullet },\overline{z})$ where individuals play the field within groups, also holds more generally for the case where individual fitness depends on the trait of each individual neighbour (electronic supplementary material, appendix C.1.3 for details).

For group-structured populations, the selection gradient as in equation (4.1) is significantly easier to handle mathematically than working from first principles with invasion fitness (or other proxies such as the metapopulation number, [117,118]). This is because invasion fitness depends on the entire probability distribution that a mutant is in a group with a given number of other mutants ([22,41,45,117,118]; equation (C5) in electronic supplementary material, appendix here). Equation (4.1), by contrast, depends only on neutral relatedness, which is just one moment of this distribution assuming the mutant and resident have the same traits. There are at least two advantages to this. First, there exist standard techniques coming from coalescent theory to compute such a relatedness coefficient ([29]; electronic supplementary material, appendix C.1.6 here for an example of such argument). Second, it is perhaps the only evolutionary parameter presented in this review that can be easily and systematically estimated in natural populations. In fact, $R^{\circ }$ in equation (4.1) can be connected to the well-known F_ST measure of genetic differentiation [119], which can be estimated from neutral markers [120]. Owing to its simplicity, empirical connections and the biological insights it affords, equation (4.1) has been one of the most widely used expressions to understand directional selection on an array of social behaviours, such as cooperation, sex ratio, dispersal and many more [31].

More seldom seen is disruptive selection in terms of relatedness coefficient [45,47,115,121–125]. Under the assumption that individual fitness can be written as $\omega (z_{\bullet },\overline{z})$, we show in electronic supplementary material, appendix C.1.4 that disruptive selection is given by

$$h(z^{\ast })=\underset{\begin{array}{rl}& \mathrm{nonlinear}\\ & \text{fitness effects}\end{array}}{\underbrace{h_{\mathrm{w}}(z^{\ast })}}+2\times \underset{\begin{array}{rl}& \mathrm{social}\hspace{0.17em}\mathrm{context}\times \\ & \text{fitness synergy}\end{array}}{\underbrace{h_{\mathrm{r}}(z^{\ast })}}$$ 4.2

where

$$\begin{array}{rl}& h_{\mathrm{w}}(z^{\ast })=\frac{{\mathrm{\partial }}^2\omega (z_{\bullet },\overline{z})}{{\mathrm{\partial }{z}_{\bullet }}^2}+2R^{\circ }\frac{{\mathrm{\partial }}^2\omega (z_{\bullet },\overline{z})}{\mathrm{\partial }{z}_{\bullet }\mathrm{\partial }\overline{z}}+K^{\circ }\frac{{\mathrm{\partial }}^2\omega (z_{\bullet },\overline{z})}{{\mathrm{\partial }\overline{z}}^2}\\ \mathrm{and}& h_{\mathrm{r}}(z^{\ast })=\frac{\mathrm{\partial }\omega (z_{\bullet },\overline{z})}{\mathrm{\partial }\overline{z}}\frac{\mathrm{\partial }R(z_{\mathrm{m}},z)}{\mathrm{\partial }{z}_{\mathrm{m}}}\end{array}$$ 4.3

in which $K^{\circ }$ is the probability that two individuals, randomly sampled with replacement among the neighbours to a focal individual, are identical-by-descent to the focal (in a population monomorphic for the resident z). $K^{\circ }$ can thus be thought of as the tendency of interacting with more than one relative under neutrality. The quantity R(z_m, z), meanwhile, is the probability that a randomly sampled neighbour to a mutant individual with trait z_m in a resident population with trait z is also mutant (note how this measure of genetic structure is no longer under neutrality and depends on the mutant trait z_m). If individual fitness more generally depends on the trait of each individual neighbour (so if individuals do not play the field and individual fitness cannot be written simply as $\omega (z_{\bullet },\overline{z})$), then h_w(z*) consists of extra terms (as in e.g. [45,122,123]; electronic supplementary material, appendix C.1.5 for details).

Equation (4.2) highlights how disruptive selection can emerge from two pathways in group-structured populations. The first, given by h_w(z*), depends on three second-order effects of traits on fitness among relatives: (i) ${\mathrm{\partial }}^2\omega (z_{\bullet },\overline{z})/{(\mathrm{\partial }{z}_{\bullet })}^2$ is how focal fitness changes nonlinearly with its own trait (as in well-mixed populations, equation (2.8)); (ii) ${\mathrm{\partial }}^2\omega (z_{\bullet },\overline{z})/(\mathrm{\partial }{z}_{\bullet }\mathrm{\partial }\overline{z})$, weighted by relatedness $R^{\circ }$, is how focal fitness changes with joint changes in its own trait and in the average trait among its neighbours; and (iii) ${\mathrm{\partial }}^2\omega (z_{\bullet },\overline{z})/{(\mathrm{\partial }\overline{z})}^2$, weighted by $K^{\circ }$, is how focal fitness changes nonlinearly with the average trait in neighbours. These two latter terms capture how trait expression by different individuals within groups can influence focal fitness in a synergistic way (synergy among the focal and the average neighbour with ${\mathrm{\partial }}^2\omega (z_{\bullet },\overline{z})/(\mathrm{\partial }{z}_{\bullet }\mathrm{\partial }\overline{z})$; and synergy among two average neighbours with ${\mathrm{\partial }}^2\omega (z_{\bullet },\overline{z})/{(\mathrm{\partial }\overline{z})}^2$; see [47] for further considerations on these). To see the possible relevance of such synergy, consider for example a scenario where individuals can cooperate with one another and the evolving trait is the amount invested into cooperation and that joint cooperation has antagonistic effects on payoff (such that ${\mathrm{\partial }}^2\omega (z_{\bullet },\overline{z})/(\mathrm{\partial }{z}_{\bullet }\mathrm{\partial }\overline{z})<0$ as in e.g. the Snowdrift game). In this case, interactions among relatives tend to inhibit disruptive selection (i.e. h(z*) decreases with $R^{\circ }$ [123]). Put differently, kin selection favours the evolution of equal contribution among social partners in this scenario (electronic supplementary material, appendix C.1.6 for analysis; [47,121,122] for a similar inhibitory effect of limited dispersal in other models).

The second pathway that can contribute to disruptive selection in group-structured populations, h_r(z*), depends on the product of two quantities: (i) how a trait change in neighbours increases the fitness of the focal individual ($\mathrm{\partial }\omega (z_{\bullet },\overline{z})/(\mathrm{\partial }\overline{z})$), with (ii) how a trait change increases the probability of interacting with other individuals also expressing this change, i.e. with relatives (∂R(z_m, z)/(∂z_m)). This reveals that selection favours mutants that either: (i) increase the fitness of neighbours and the probability that these neighbours are also mutants or (ii) decrease the fitness of neighbours and the probability that these neighbours are also mutants. This effect of selection can thus be seen as the social equivalent of synergy among context and fitness obtained in heterogeneous populations (h_q(z*) in equation (3.4)). In contrast to §3 where context is the individual state (e.g. sex, age, size or habitat) the mutant can be in, context here is the social environment, i.e. the frequency of relatives in the group. To illustrate such synergy, we explore in electronic supplementary material, appendix C.1.7 an example where the evolving trait is the amount invested into a common good that benefits the whole group but that such an investment leads to a decreased propensity to disperse (e.g. due to functional trade-offs). As a result, a mutant that invests more resources into cooperation disperses less and thus is more likely to interact with relatives. We show that such a scenario readily leads to the emergence of two social morphs: one that cooperates and tends to remain philopatric, and another that defects and disperses. These two are maintained due to the association between social and dispersal behaviours allowing cooperators to preferentially benefit relatives and defectors to preferentially harm non-relatives. Beyond this specific example, h_r(z*) suggests that when mutants can preferentially interact with other mutants (or residents), disruptive selection favours diversity in social behaviours [45,75,124,126,127].

Many social groups are not homogeneous. Colonies of eusocial insects have queens and workers, matriarchal societies of killer whales are composed of multiple generations, and primate groups are often governed by complex dominance hierarchies. We discuss directional and disruptive selection in populations that are subdivided into social groups, and where individuals belong to different classes within groups, in boxes 3 and 4, respectively.

Box 3. Directional selection in heterogeneous social groups: ‘How to make a kin selection model’ [128].

Consider a population subdivided into social groups and where individuals belong to M different classes within groups (e.g. age, sex, social rank as in §3.1). To describe the fitness of a focal individual in this model, we first denote by ${\overline{z}}_k$ the average trait expressed among the neighbours to this focal that belong to class k. For short, we collect these averages in the vector $\overline{\mathit{z}}=({\overline{z}}_1,\dots ,{\overline{z}}_M)$. We then let ${\omega }_{ij}(z_{\bullet },\overline{\mathit{z}})$ be the expected number of offspring in class i produced by a focal individual in class j with trait $z_{\bullet }$ when its group-neighbours express $\overline{\mathit{z}}$ on average (electronic supplementary material, appendix C.2.1 for details). As shown previously [22,29,128], the selection gradient for this model can be expressed as

$$s(z)=\sum _{i=1}^M\sum _{\hspace{0.17em}j=1}^M{v}_i^{\circ }[\frac{\mathrm{\partial }{\omega }_{ij}(z_{\bullet },\overline{\mathit{z}})}{\mathrm{\partial }{z}_{\bullet }}+\sum _{i^{\prime }=1}^M\frac{\mathrm{\partial }{\omega }_{ij}(z_{\bullet },\overline{\mathit{z}})}{\mathrm{\partial }{\overline{z}}_{i^{\prime }}}{R}_{i^{\prime }|j}^{\circ }]q_j^{\circ },$$ III.A

where $v_i^{\circ }$ is the reproductive value of individuals in class i, $R_{i^{\prime }|j}^{\circ }$ is the probability that a randomly sampled neighbour in class i′ to a focal individual in class j is identical-by-descent to the focal, and $q_j^{\circ }$ is the probability that a randomly sampled individual is in class j (all three quantities in a population monomorphic for the resident z; see electronic supplementary material, appendix C.2.2 for our derivation of equation (III.A)). In a well-mixed population (where $R_{i^{\prime }|j}^{\circ }=0$ for all i′ and j), the selection gradient reduces to the one for class-structured populations (equation (3.3)), as expected. With limited dispersal and interactions among relatives, selection further depends on indirect fitness effects ($\mathrm{\partial }{\omega }_{ij}(z_{\bullet },\overline{\mathit{z}})/(\mathrm{\partial }{\overline{z}}_{i^{\prime }})$). As highlighted by equation (III.A), these indirect fitness effects tend to favour prosocial behaviours, in particular towards individuals that produce offspring with high reproductive value. More generally, equation (III.A) allows us to understand social evolution within heterogeneous groups and thus under asymmetric interactions which can lead to counterintuitive situations (i.e. where payoff depends on class, e.g. [86,87,129,130]).

Box 4. Disruptive selection in heterogeneous social groups: where individual and social context can drive polymorphism.

Like directional selection (equation (III.A)), disruptive selection in heterogeneous social groups combines elements from class- and group-structure (i.e. from equation (3.5) and (4.3) [115]). In fact, under the assumption that the expected number of offspring in class i produced by a focal individual in class j with trait $z_{\bullet }$ can be written as ${\omega }_{ij}(z_{\bullet },\overline{\mathit{z}})$, where $\overline{\mathit{z}}=({\overline{z}}_1,\dots ,{\overline{z}}_M)$ collects the average trait ${\overline{z}}_k$ among neighbours in class k (i.e. under the assumption that individuals play the field within groups), disruptive selection can be decomposed into

$$h(z^{\ast })=h_{\mathrm{w}}(z^{\ast })+2h_{\mathrm{r}}(z^{\ast })+2h_{\mathrm{q}}(z^{\ast }),$$ IV.A

(electronic supplementary material, appendix C.2 for our derivation; [115] for derivation with more general fitness function). Briefly, the first term consists of second-order fitness effects weighted by reproductive value and relatedness,

$$\begin{array}{rl}& h_{\mathrm{w}}(z^{\ast })=\sum _{i=1}^M\sum _{\hspace{0.17em}j=1}^M{v}_i^{\circ }[\frac{{\mathrm{\partial }}^2{\omega }_{ij}(z_{\bullet },\overline{\mathit{z}})}{{\mathrm{\partial }{z}_{\bullet }}^2}+2\sum _{i^{\prime }=1}^M\frac{{\mathrm{\partial }}^2{\omega }_{ij}(z_{\bullet },\overline{\mathit{z}})}{\mathrm{\partial }{z}_{\bullet }\mathrm{\partial }{\overline{z}}_{i^{\prime }}}{R}_{i^{\prime }|j}^{\circ }+\sum _{i^{\prime }=1}^M\sum _{i^{″}=1}^M\frac{{\mathrm{\partial }}^2{\omega }_{ij}(z_{\bullet },\overline{\mathit{z}})}{\mathrm{\partial }{\overline{z}}_{i^{\prime }}\mathrm{\partial }{\overline{z}}_{i^{″}}}{K}_{i^{\prime },i^{″}|j}^{\circ }]q_j^{\circ },\end{array}$$ IV.B

where $K_{i^{\prime },i^{″}|j}^{\circ }$ is the probability that in a population monomorphic for the resident z, two individuals in classes i′ and i″ randomly sampled with replacement among the neighbours to a random focal individual in class j are identical-by-descent to the focal. The second term,

$$h_{\mathrm{r}}(z^{\ast })=\sum _{i=1}^M\sum _{\hspace{0.17em}j=1}^M\sum _{i^{\prime }=1}^M{v}_i^{\circ }\frac{\mathrm{\partial }{\omega }_{ij}(z_{\bullet },\overline{\mathit{z}})}{\mathrm{\partial }{\overline{z}}_{i^{\prime }}}\frac{\mathrm{\partial }{R}_{i^{\prime }|j}(z_{\mathrm{m}},z)}{\mathrm{\partial }{z}_{\mathrm{m}}}{q}_j^{\circ },$$ IV.C

depends on the trait’s effect on relatedness, as R_i′|j(z_m, z) is the asymptotic probability that a randomly sampled neighbour in class i′ to a mutant individual in class j with trait z_m in a resident population with trait z is also mutant. Finally, the third term participating to disruptive selection,

$$h_{\mathrm{q}}(z^{\ast })=\sum _{i=1}^M\sum _{\hspace{0.17em}j=1}^M{v}_i^{\circ }[\frac{\mathrm{\partial }{\omega }_{ij}(z_{\bullet },\overline{\mathit{z}})}{\mathrm{\partial }{z}_{\bullet }}+\sum _{i^{\prime }=1}^M\frac{\mathrm{\partial }{\omega }_{ij}(z_{\bullet },\overline{\mathit{z}})}{\mathrm{\partial }{\overline{z}}_{i^{\prime }}}{R}_{i^{\prime }|j}^{\circ }]\frac{\mathrm{\partial }{q}_j(z_{\mathrm{m}},z)}{\mathrm{\partial }{z}_{\mathrm{m}}},$$ IV.D

depends on the trait’s effect on the probability on being in a certain class, $\mathrm{\partial }{q}_j(z_{\mathrm{m}},z)/(\mathrm{\partial }{z}_{\mathrm{m}})$. All three terms thus have similar interpretations than those emerging in models of just class- or just group-structure (equations (3.5) and (4.3)). In particular, h_w(z*) reveals that disruptive selection can come about when fitness changes nonlinearly with trait expression within and between individuals of the same group (as in equation (4.3) but here weighted by reproductive value); h_r(z*), when trait expression increases both the likelihood of being in a certain social environment and fitness in that environment; and finally h_q(z*), when trait expression augments jointly the probability of being in a given individual state and fitness in that state (both via direct and indirect fitness effects owing to group-structure; see [115] for further considerations).

The expressions for selection in such heterogeneous social groups combine those of models of class- (equations (3.3)–(3.5)) and group-structure (equations (4.1)–(4.3)). In particular, disruptive selection can emerge owing to the synergy of fitness with asocial as well as social context (box 4), laying the ground for the coexistence of morphs that specialize in both types of contexts and thus for adaptive polymorphisms of many different natures.

5. Concluding remarks

Understanding phenotypic evolution when individuals interact has been at the core of evolutionary game theory and of the theory of adaptive dynamics. These research programmes have led to a well-established and robust set of tools based on evolutionary invasion analyses that can tackle a wide range of questions in evolutionary biology. Here, we reviewed two important pieces of this toolbox, directional s(z) and disruptive h(z) selection, which determine whether gradual evolution leads a population to an uninvadable (i.e. evolutionarily stable) monomorphic state where all individuals express the same trait, or to become polymorphic through adaptive diversification (figure 1). As such, they constitute a useful platform to understand the conditions that favour phenotypic variation in the form of adaptive polymorphism.

With the aim of facilitating connections between models and biological interpretation, we collected together expressions of s(z) and h(z) in terms of individual fitness, extending reviews that focus on directional selection (e.g. [29,31–33] for s(z) in structured populations, including under isolation-by-distance). Interpreting disruptive selection in terms of individual fitness brings together what we see as the strong points of the related branches of theoretical evolutionary biology that are evolutionary game theory and adaptive dynamics. The former has a long tradition of decomposing selection in a way to understand the different forces at play in the evolution of social and life-history traits [5,6,29,31,91,111,128]. Most investigations of complex populations, however, stop at directional selection and do not determine whether polymorphism emerges. By contrast, adaptive dynamics models typically study such emergence as well as its maintenance (how many morphs, the traits they express, and their frequency, e.g. [9,75,131–134]). But the complexity of the mathematical procedures involved in such studies and the fitness measures used often leave little room for interpretation. In decomposing disruptive selection in biologically relevant components, we thus hope to motivate yet further research to understand phenotypic variation in non-homogeneous populations, especially in life-history traits and social behaviours that act either via direct interactions, or through indirect ecologically mediated interactions.

Linking invasion fitness, which is a measure of fitness at the level of the gene (or replicator) [34], to individual fitness in heterogeneous and non-randomly mixed populations requires taking into account the fact that a gene may find itself in carriers in different states, who can in turn interact with other carriers and impact their reproductive success. This is achieved by expressing invasion fitness of a mutant as a weighted average of individual fitness over the distribution of states that a carrier of the mutant can be in ([22,41,128]; electronic supplementary material, appendix C here). With class-structure, the appropriate weights turn out to be reproductive values [84], while the averaging in group-structured populations invariably leads to the notion of relatedness as a measure of interactions among carriers of genes that are identical-by-descent [29,111]. Remarkably, it is sufficient to consider these summary statistics in the resident population (i.e. under neutrality) to investigate the direction of selection s(z): ‘a gift from God’ [135] that bypasses many computational headaches. To characterize disruptive selection h(z), however, requires considering how the mutant perturbs the distribution of states an individual carrier can be in (e.g. [45,115,122,123]). As we hope to have conveyed here, these perturbations inform on the nature of disruptive selection. In fact, we suggest that there are two main pathways that can favour polymorphism in trait expression: (i) when individual fitness increases more than linearly with trait expression (h_w(z), which is the only pathway in well-mixed and homogeneous populations); (ii) when trait expression simultaneously increases the probability that an individual is in a given context (e.g. a given age, sex, habitat, size or social environment) and fitness in that context (h_q(z) and h_r(z); figure 2 for a summary). Population-structure thus opens novel pathways for the operation of disruptive selection, leading to polymorphisms that have characteristics unique to these populations. More specifically, class- and group-structure lay the ground for the coexistence of genotypes that specialize in the different contexts that a genotype can be in, be it the individual state (e.g. its age, sex or size), or the socio-genetic environment of its carrier (e.g. with or without relatives).

Figure 2.

The different paths for disruptive selection. (a) In a homogeneous and well-mixed population, the only relevant effect for disruptive selection is how trait expression by an individual influences its own fitness, specifically whether fitness increases more than linearly with trait expression (h_w(z*), equation (2.8)). (b) In class- and/or group-structured populations, disruptive selection can also be due to trait expression simultaneously increasing the probability that a focal individual is in a certain context and individual fitness in that context. Such context × fitness synergy can be decomposed into two types: (i) asocial, where the context is the state (or class) of the focal (h_q(z*), equation (3.5)); and (ii) social, where the context is the genetic environment of the focal (h_r(z*), equation (4.3)). (Online version in colour.)

Concerning polymorphism, we have focused our attention on disruptive selection h(z), as this constitutes the more recent advances in the literature. It is however important to keep in mind that for phenotypic diversity to emerge, it is also necessary that the population first converges to a singular strategy, i.e. that condition equation (2.5) holds. This condition, together with h(z*) > 0, highlights that polymorphism requires ∂²ρ(z_m, z)/(∂z_m∂z) to be sufficiently negative (when z_m = z = z*). Similar changes in mutant and resident traits must thus lead to a decrease in mutant fitness at the singular strategy. More intuitively perhaps, interactions among mutants and residents must have antagonistic effects on mutant fitness, leading to negative-frequency dependence (which for instance is the case when interactions have payoffs that follow the Snowdrift or Hawk–Dove game).

Owing to time and space constraints, many other results that are relevant to the adaptive dynamics of social behaviour had to be left out. We have for instance ignored the effect of changing or stochastic environments and oscillatory or chaotic population dynamics and finite population sizes (e.g. [24,136–141]). We have also largely left out the influence of trait evolution on ecological or demographic variables that can feedback on selection and lead for instance to evolutionary suicide (though see electronic supplementary material, appendix A.3; [14,142–144]). These feedbacks are particularly relevant under limited dispersal as they lead to inter-temporal mutant–mutant interactions (e.g. when individuals deplete local resources and this disproportionately influences relatives in the future through ecological inheritance [145–147]), whose implications are best understood under the light of kin selection (e.g. [145,148–154]). With regard to physiological and age-structure, we have not addressed the complications that arise when individuals can be born in different initial internal states (e.g. [155]). Finally, following most of adaptive dynamics literature, we have focused on haploid asexuals. Under random mating and additive genetic effects on traits, directional and disruptive selection are not affected by diploidy and sexual reproduction [29,156,157]. This is because, when rare, a mutant allele is only ever found in heterozygotic form under random mating (so that the relevant fitness measure is simply the expected number of heterozygotes produced by a heterozygote). But in the presence of inbreeding, whether due to selfing or mating within dispersal-limited groups [117], a rare mutant allele will also appear in homozygotic form. In that case, the machinery described above for class-structure can readily be used to infer evolution (where heterozygotes and homozygotes for the mutant allele constitute two classes [29,32]).

These omissions and many others aside, we hope this review provides a basic introduction on how to model and understand Darwinian evolution in non-trivial populations, where density- and frequency-dependence interactions inevitably take place. More broadly, the forms of directional and disruptive selection presented here should help see the connections between fundamental branches of evolutionary biology, from life history and evolutionary developmental biology, to social evolution and evolutionary ecology, and thus ultimately facilitate further the integration of these branches.

Data accessibility

This article has no additional data. The data are provided in electronic supplementary material [158].

Authors' contributions

P.A.: conceptualization, formal analysis, investigation, writing—original draft, writing—review and editing; C.M.: conceptualization, formal analysis, investigation, supervision, visualization, writing—original draft, writing—review and editing.

All authors gave final approval for publication and agreed to be held accountable for the work performed therein.

Conflict of interest declaration

We declare we have no competing interests.

Funding

This study was funded by the Swiss National Science Foundation (grant no. PCEFP3181243 to C.M.).