Recent advances in density functional theory approach for optoelectronics properties of graphene

Abstract

Graphene has received tremendous attention among diverse 2D materials because of its remarkable properties. Its emergence over the last two decades gave a new and distinct dynamic to the study of materials, with several research projects focusing on exploiting its intrinsic properties for optoelectronic devices. This review provides a comprehensive overview of several published articles based on density functional theory and recently introduced machine learning approaches applied to study the electronic and optical properties of graphene. A comprehensive catalogue of the bond lengths, band gaps, and formation energies of various doped graphene systems that determine thermodynamic stability was reported in the literature. In these studies, the peculiarity of the obtained results reported is consequent on the nature and type of the dopants, the choice of the XC functionals, the basis set, and the wrong input parameters. The different density functional theory models, as well as the strengths and uncertainties of the ML potentials employed in the machine learning approach to enhance the prediction models for graphene, were elucidated. Lastly, the thermal properties, modelling of graphene heterostructures, the superconducting behaviour of graphene, and optimization of the DFT models are grey areas that future studies should explore in enhancing its unique potential. Therefore, the identified future trends and knowledge gaps have a prospect in both academia and industry to design future and reliable optoelectronic devices.

Highlights

• •Overview of the historical background of graphene and its derivatives.
• •Advances in the properties of graphene and its distinctive atomic behaviour.
• •The significance of the high thermal conductivity in graphene for optoelectronics.
• •The optoelectronic phenomena revealed by the electronic transition in graphene.
• •Challenges and future direction in engineering the properties of graphene via DFT.

1. Introduction

Almost every facet of our civilization is governed by the continual discovery of novel materials with specified functions and performances [[1], [2], [3]]. Today, the computational density functional theory technique has substantially expanded the materials design process, either alone or in tandem with experimental research, owing to the relatively complex level of concepts and computer modelling [[1], [2], [3]]. Moreover, at the turn of the last decade, graphene, a single layer of graphite exfoliated by Geim and co-workers, became the focus of intense research due to its remarkable physical properties [[4], [5], [6]]. Since its discovery, several 2D materials have been synthesized, including hexagonal boron nitride, silicene, transition metal dichalcogenide, antimonene, and phosphorene [[7], [8], [9], [10], [11]]. The properties of these materials are markedly different from those of the parent compound due to changes in the size of the crystal structure and quantum confinement [12,13].

Despite the surge in 2D materials, graphene stands out among them for having exceptional electronic, optical, and thermal properties [14,15]. It has very high carrier mobilities ($\sim$200,000 ${\mathrm{c}\mathrm{m}}^2{\mathrm{V}}^{-1}{\mathrm{S}}^{-1}$) [[16], [17], [18]], unusual linear dispersion around the Dirac point [19,20], ultrahigh thermal conductivities ($\sim 5000\mathrm{W}/\mathrm{m}\mathrm{k}$) [[21], [22], [23]], room temperature ballistic carrier transport [24,25], large surface area (2630 ${\mathrm{m}}^2/\mathrm{g}$) [[26], [27], [28]], a Young's Modulus of 1 TPa [29,30], broadband optical absorbance (2.3%) [[31], [32], [33]], and a robust crystal structure, all of which reveal the material's high quality and suggest its prospects for future optoelectronic devices [[34], [35], [36]]. However, its use in optoelectronics is limited due to its zero bandgap and relatively poor structural tunability [[37], [38], [39]]. Therefore, several reports have established different approaches to induce a sizeable band gap and efficiently modulate the intrinsic properties of graphene by stacking configuration, mechanical strain, electric and magnetic fields, and heteroatom chemical doping via DFT methods for next-generation electronics with designer functionalities [[40], [41], [42]].

In this paper, we present an extensive review of heteroatom doping of graphene employing the DFT within the last decade as well as the recently introduced data-driven ML-DFT models because these are regarded as the most effective method of manipulating the properties of graphene [[43], [44], [45]]. Moreover, these modifications in the properties of graphene are largely determined by the types of dopant atoms, their percentages, and the doping sites [42]. Additionally, these heteroatoms can either be electron acceptor (p-type) or electron donor (n-type) systems when substituted into graphene, depending on the number of valence electrons in the dopant atom [[46], [47], [48]]. Therefore, a comprehensive catalogue of the methods and results will provide insights into the achievements, present status, and shortfalls in the research area. To that end, in Section 2.1, we present an overview of the heritage of graphene as well as an in-depth review of the electronic and optical properties calculated using the density functional approach. Section 3.1 is dedicated to the models and implementation platforms for both traditional DFT and ML-DFT for the electronic structure calculation of graphene. Lastly, this section is concluded by revealing some knowledge gaps and future trends in the literature on the study of graphene. Section 4 presents a concluding remark.

2. Overview of the heritage of graphene and selected properties

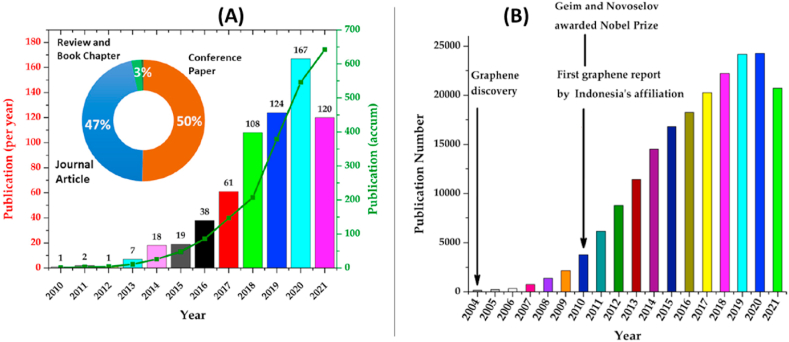
Graphene has remained the “de facto” and most studied 2D material for almost two decades, with its discovery changing the dynamics of the materials world [49,50]. In 2013, about two scientific articles on the application of graphene were published every 96 min, which was over forty journals every 24 h [51]. Interestingly, graphene research has further advanced, Fig. 1(a–b) reveals the status of the globally published related material and graphene research publication per year from 2010 to 2021.

Fig. 1.

Fig. 1: (a) The Schematic illustration of Graphene's globally published research articles from 2004 to 2021 and (b) graphene's related publications from 2004 to 2021. Figure remodified from Ref. [52].

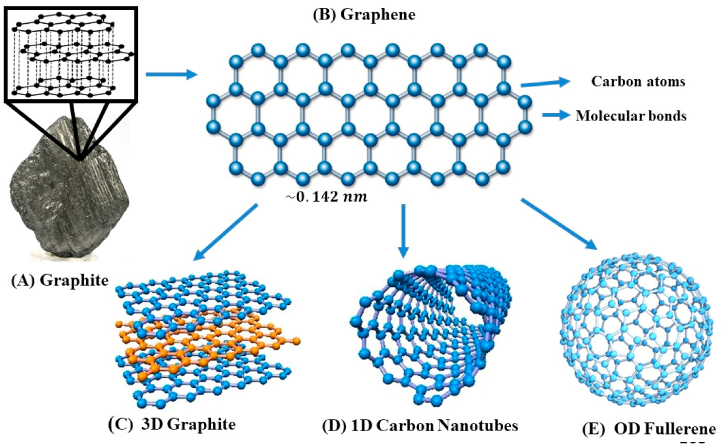
More broadly, graphene is the first of a large family tree of 2D nanomaterials as shown in Fig. 2 which includes a plethora of different carbon materials ranging from fullerenes (0D), carbon nanotubes (1D), graphene oxide (GO) to graphene quantum dots (GQDs), and other derivatives introducing physics for low-dimensional systems which have never ceased to amaze, proving to usher in a new generation system [53]. The earliest evidence of graphene was reported when Benjamin Brodie created carbonic acid in the second millennium, which he hypothesized was a new form of carbon and proposed the name “graphon”. In the ensuing century, only a few studies have described the layered structure of graphite oxide, which was shown to contain distinct atomic planes [54]. The discovery of graphite oxide paper was reported by Kohlschutter and Haenni [55,56] and subsequently, in the mid-‘90s, Ruess and Vogt [57] employed a transmission electron microscope to observe graphite oxide flakes with a thickness of a few nanometers that were produced by the evaporation of a suspension droplet placed on the TEM grid [55,56]. Meanwhile, Boehm et al. [58] initiated the chemical method of reducing graphite oxide in a diluted alkaline solution of hydrazine and hydrogen sulphide under proper conditions a few years later and subsequently proposed the term “graphene” in the late twentieth century to designate a variety of carbon-based compounds, which enables the isolation of mono and few layers graphitic layers [58,59]. However, Wallace [60] was the first to propose graphene as a theoretical construct to aid in the calculation of graphite's band structure [61]. Moreover, a decade earlier, it was demonstrated that a 2D crystal could not exist because the system was not in equilibrium [62]. The idea was later expanded with a plethora of experimental evidence [62,63]. It was not until nineteen years ago that a successful method for separating graphene from graphite by mechanical exfoliation with scotch tape was discovered in Manchester [64,65]. This discovery sparked widespread interest in graphene, and numerous experts around the world have since conducted extensive research on this ubiquitous material [66]. Its large honeycomb network serves as the foundation for several other allotropes, as displayed in Fig. 2(a)–(e). This one-atom-thick layer of graphite called graphene demonstrates an extremely strong absorption for a monolayer atom that is wavelength-independent [39]. However, graphene has a gapless band structure, and the total absorption and quantum efficiency are still poor. Therefore, for graphene to realize its potential a sizeable band gap must be created to enhance the optical properties for application in electronic devices with optimized stability and performance while widening the scope for novel electronic designs [[67], [68], [69], [70], [71]].

Fig. 2.

The Schematic illustration of the Origin and the transformation of graphite to graphene's atomic structure. The transformation process shows that graphene, a 2D basic unit of carbon can be folded into (C) 3-D Graphite (D) rolled into 1-D nanotubes (E) and folded into 0-D Fullerene. Figure remodified from Ref. [80].

2.1. The structural properties of pure graphene material

Graphene is a remarkably 2D layer with a C–C bond length of 1.420 Å, as displayed in Fig. 2b, (the simplest and most important crystalline allotrope of carbon atoms), which originates in a tightly packed hexagonal lattice with a purely sp2 orbital hybridization at ambient temperature [72,73]. This $\sigma$ bond results in some impressive mechanical properties [74]. A three-sided network with a two-atom basis for each cell makes up the structure. The graphene lattice vectors in Eq. (1) are expressed as follows [69]:

$$a_1=\frac{a}{2}\left(3,\sqrt{3}\right),a_2=\frac{a}{2}\left(3,-\sqrt{3}\right)$$ (1)

The distance between near-set neighbor atoms is expressed as $a=1.42\mathrm{\AA }$. The vectors of the reciprocal-lattice in Eq. (2) are determined by:

$$b_1=\frac{2\pi }{3a}\left(1,\sqrt{3}\right),b_2=\frac{2\pi }{3a}\left(1,-\sqrt{3}\right)$$ (2)

The sp² hybridization consists of orbitals from the S, $P_x$ and $P_z$ families. In the hexagonal phase, three different carbon atoms form covalent bonds with one other, leaving one free electron for each carbon atom. This free electron is held in the $P_z$ orbital, which is above the plane and creates the π bond. Moreover, the exceptional properties of this 2D nanomaterial rely heavily on this free radical [75,76]. The half-filled π band allows the highly mobile non-bonding electrons to travel easily in graphene. Therefore, the π -band reduces at half-filling to two inequivalent locations at the corners of the first Brillouin zone, resulting in Dirac cones [77]. Furthermore, in the bilayer and multilayer graphene, the π-bonds produce a van der Waals interconnection with the layers of graphene [78,79].

2.2. The electronic properties of pure graphene

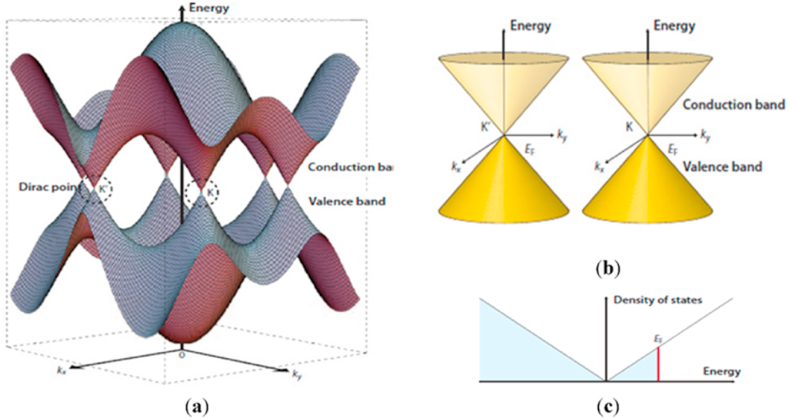
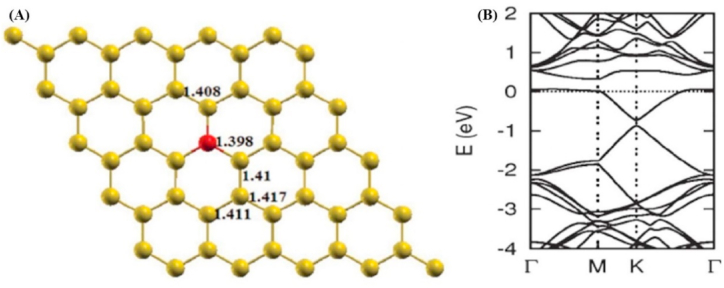
The tight-binding method was employed by Wallace in investigating the electronic band structure of a monolayer of graphite [60,81,82]. And subsequently, Castro Neto and others have also reported graphene's electronic properties and discussed how these properties are determined by stacking graphene layers [69,83]. Thus, graphene has drawn so much research interest for optoelectronic applications due to its high electron mobilities (15,000 ${\mathrm{c}\mathrm{m}}^2/\mathrm{V}$) at room temperature and unusual electronic behaviours such as the quantum hall effect (QHE), which mimics massless transportation, leading to its high superconductivity [84]. The QHE is further discussed later in this section. Moreover, it's worth noting that structural holes allow phonons to pass through unhindered, resulting in high thermal conductivity in graphene. Additionally, graphene displays a semi-metallic behaviour; the band structure reveals the unoccupied (π*) and occupied (π) bands overlap at the same K point just below the Fermi energy level with linear dispersion near it. In addition, the density of states contains the valence and conduction bands, with a disappearing density at the Fermi level, which is mostly generated by π states, as displayed in Fig. 4(c) [[85], [86], [87]]. Moreover, the schematic illustration of the formation process based on the basic elements of graphene's bonding properties, the honeycomb structure, the SEM image of graphene's single layer and the calculated band structure of graphene is displayed in Fig. 3(a–f).

Fig. 4.

(a) Schematic illustration of the energy bands near the Fermi level in graphene. The horizontal plane in the first Brillouin zone of graphene. The conduction and valence band meets at the K and K′ points in the Dirac cone. (b) The conic energy bands near the K and K′ points. (c) The density of states with the fermi energy near the Fermi level. Figure remodified from Ref. [91].

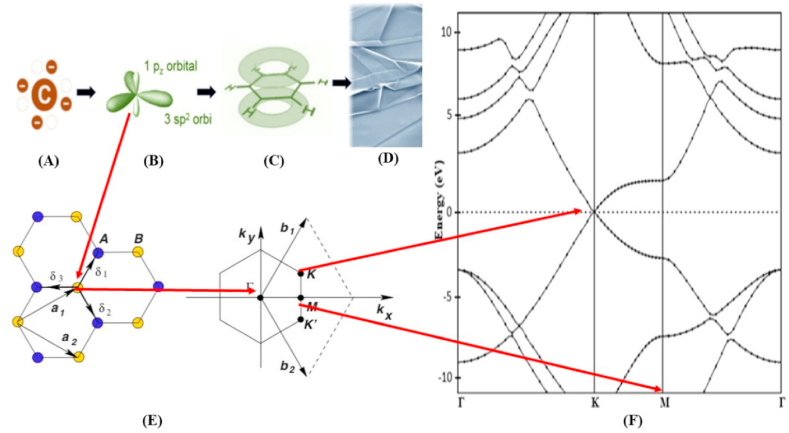
Fig. 3.

(a–c) Schematic illustration of the formation process from the basic element of graphene bonding properties and (d) the mono-layer graphene SEM image (e) the honeycomb lattice and its Brillouin zones. The L.H.S. reveals the interpenetrating triangular lattices that make up the lattice structure of 2D graphene. The vectors of the closest neighbors are represented by ${\delta }_{i,}$ = 1, 2, 3 and $a_1$ and $a_2$ unit is the lattices respectively. The R.H.S reveals the Dirac Cone which is created by the valence and conduction band crossing at the K and $K^{\prime }$ point This is indicated in (f) the band structure of pure graphene. Figure remodified from Ref. [88].

Furthermore, the upper side of the linear dispersion curve shown in Fig. 3(f), describes the π* (upper conduction) energy anti-bonding band, and the bottom side, which defines the energy bonding band. At the Dirac point k, the π* and π band are reduced, indicating that pure graphene is a two-dimensional gapless semimetal [88]. The charge carriers in graphene are generally defined by the Dirac equation and not the Schrodinger equation due to the uniformity of the crystal lattice, which comprises two identical carbon sublattices A and B.

Moreso, the electronic sub-bands consisting of a mixture of equal and unequal wave functions for the two sublattices overlap at the Brillouin zone's edge, giving rise to a cone shape around the Dirac point describing the electron dynamics as the energy and the quasi momentum lies in the same plane i.e., the dispersion relationship in metals and semiconductors is shaped like a parabola as displayed in Fig. 4(a) and (b) [89]. The Dirac points at the edge of the graphene Brillouin zone are very critical for the graphene physics as displayed in Fig. 4(a). The placements of these objects in momentum space are determined by Eq. (3) [90].

$$K=\left(\frac{2\pi }{{3a}_1},\frac{2\pi }{{5.196a}_1}\right),K^{\prime }=\left(\frac{2\pi }{3a},-\frac{2\pi }{{5.196a}_1}\right)$$ (3)

The three nearest-neighbor vectors in Eq. (4) are expressed as follows in real space:

$${\delta }_1=\frac{a_1}{2}\left(1,1.732\right){\delta }_2=\frac{a_1}{2}\left(1,-1.732\right){\delta }_3=-a_1\left(1,0.00\right)$$ (4)

while in Eq. (5), the six closest neighbors are situated at:

$${\delta }_1=\pm a_1,{\delta }_2=\pm a_2,{\delta }_3=\pm \left(a_2-a_1\right)$$ (5)

2.2.1. The quantum Hall effect of graphene material

Edwin Hall hypothesized that the magnetic field caused a transverse voltage in the wire when he reported the classical Hall-effect in the late 19th century. An electron gas with a strong magnetic field splits into Landau levels because of the magnetic field. The orbital for each level is described in Eq. (6) [92]:

$$D=\sqrt{2\pi eB/\hslash c}\left(\frac{L}{2\pi }\right)={\left(\frac{eB{L}^2}{hc}\right)}^{1/2}$$ (6)

Graphene's highly unique charge carriers exhibit massless relativistic behaviour and are one of the material's most fascinating features, i.e., the Dirac fermions as displayed in Fig. 5. When confined to magnetic fields, Dirac fermions act in a manner that is significantly aberrant in the energy spectra of the Landau levels compared to electrons, as demonstrated by the anomalous integer quantum Hall effect [93]. The Landau energy levels of graphene can be written as:

$$E_j=\pm \left(j\right)V_F{\left(2e\hslash \left|j\right|B\right)}^{1/2}$$ (7)

Fig. 5.

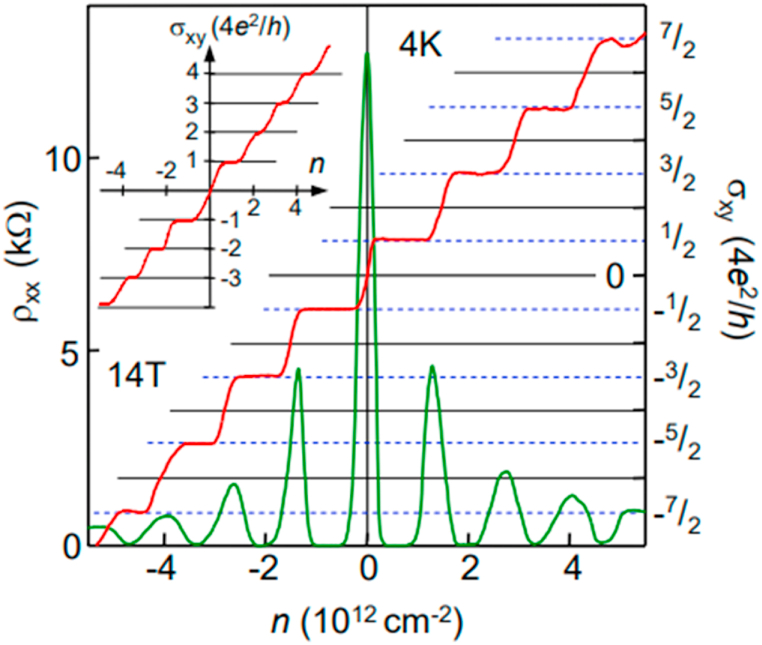
The QHE for massless fermions in monolayer graphene. Hall Conductivity ${\sigma }_{xy}$ and longitudinal resistivity ${\rho }_{xx}$ of graphene as a function of their concentration at $B=14TandT=4.K{\sigma }_{xy}=\left(2e/\sqrt{h}\right)V^{\frac{1}{2}}$ is determined from the measured dependencies of ${\rho }_{xy}\left(V_g\right)$ and ${\rho }_{xx}$ ($V_g$) as ${\sigma }_{xy}={\rho }_{xy}/{(\rho }_{xy}^2+{\rho }_{xx}^2)$. The nature of $1/{\rho }_{xy}$ is similar but shows a discontinuity at $V_g\approx 0$, which was avoided by plotting ${\sigma }_{xy}$. The quantization sequence in the two-layer graphene's inset displays the ${\sigma }_{xy}$ at integer j, where it is normal. Figure remodified from Ref. [102].

Therefore, Eq. (7) provides the clearest proof for the non-interacting Dirac fermion model [92]. Therefore, $j=0,\pm 1,\pm 2\text{,}$ The Fermi velocity is represented by $V_F$, $e$ is the elementary charge, where $\hslash$ the reduced Planck's constant is and can be expressed as $\hslash =\frac{h}{2\pi }$ and B represents the magnetic field.

However, the chiral quasiparticles show that graphite possesses a Berry phase 2 that is dominated by a parabolic dispersion and a double-degenerate zero-energy. The Landau level contains two distinct orbital states (${K-K}^{\prime }\mathrm{p}\mathrm{o}\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{s})$ with the same energy, i.e., both the electrons and holes share the same level [93,94]. This reveals the anomalous integer QHE where Eq. (8) describes the Hall conductivity [93]:

$${\sigma }_{xy}=\pm \frac{\left(4j+2\right)e^2}{h}$$ (8)

The electronic structure of graphene, however, exhibits an anomalous quantization that is replaced by a non-empty, half-integer Berry's phase. The quantum Hall effect in a single layer of graphene is sharply different from the standard QHE for both holes and electrons. This sets graphene apart from other traditional 2D carbon-based electronic materials with a definite carrier mass [95,96]. The anomalous quantum hall-effect was first reported by Novoselov et al. [96] which is illustrated in Fig. 5a. This is calculated at $\mathrm{{\rm B}}=\mathrm{{\rm T}}$ and T = 4 K [96]. As a result, the charge Hall conductance is precisely quantized as described in Eq. (9), when the Fermi level is in the energy gap [93]:

$${\sigma }_{xy}=\frac{2e^2}{h}$$ (9)

Furthermore, Qiao et al. [97] reveal that Rashba spin-orbit coupling, and exchange fields can cause graphene to develop a visible gap. Furthermore, a gap as large as 5.5 meV appeared at the Dirac points, resulting in a topological effect using first-principles calculations. This further validates the anomalous QHE in graphene [98]. Thus, a Dirac cone is created by plotting the energy of the topological electrons against momentum indicating graphene has a very high thermal conductivity [99,100]. Moreover, Cynse et al. [101] discovered a fourfold splitting in the Coulomb interaction for quantum hall. It is possible to produce a Hamiltonian that only contains graphene and correctly depicts the impurity by using first-principles calculations and a genetic algorithm technique. The physics of graphene exhibits a pronounced breaking of the structure for lower Landau levels, high magnetic fields, and fast-moving electrons, and this disorder exponentially increases with the magnetic field.

2.3. The optical properties of pure graphene material

Electronic transitions are fundamental for the optical properties of solids in general. They are inextricably linked to their electronic structures and are crucial to their application. As a result, optical anisotropy has been observed in graphene superlattices, with the level of anisotropy being determined by the thickness of the graphene layer and not the composition [103] Furthermore, the empirical results have demonstrated that the optical and energy loss spectra of graphene indicate a redshift of absorption bands and the π + σ electron plasmon, as well as the removal of mass plasmons, as contrasted to graphite [104,105]. The optical properties, absorption coefficient, reflectivity, complex refractive index, dielectric function, etc. Have been investigated in several studies. The dielectric function specifies the features of electromagnetic waves as they flow through a medium by describing the linear response of the medium to electromagnetic radiation [[106], [107], [108], [109]]. The complex dielectric function is expressed in Eq. (10) below:

$$\epsilon \left(\omega \right)={\epsilon }_1\left(\omega \right)+i{\epsilon }_2\left(\omega \right)$$ (10)

Hence, $\omega$ is the photon frequency, ${\epsilon }_1\left(\omega \right)\mathrm{a}\mathrm{n}\mathrm{d}{\epsilon }_2\left(\omega \right)$ are the real and imaginary parts of the complex dielectric function in Eq. (10), respectively [110]. In more detail, Fermi's golden rule is as follows in Eq. (11) because of the direct inter-band transition [111]:

$${\epsilon }_2\left(\omega \right)=\frac{{2e}^2\pi }{\mathrm{\Omega }{\epsilon }_0}\sum _{k,c,v}\left|({\mathrm{\Psi }}_k^c|u•r\right|{\mathrm{\Psi }}_k^v\left){|}^2\delta \right(E_k^c-E_k^v-E)$$ (11)

$\omega =$ The electromagnetic radiation's frequency, $\mathrm{\Omega }$ = volume of the cell, ${\epsilon }_0=$ permittivity of free space, $c=$ conduction band, $v=$ valence band, $u=$ vectors characterized by the polarization of the incident electric field, and $r=$ vector location.

The real and imaginary parts ${\epsilon }_2\left(w\right)$ of a dielectric function ${\epsilon }_1\left(\omega \right)$ can be compared using the Kramers-Kroing relation in Eq. (12) [111].

$${\epsilon }_1\left(\omega \right)=\frac{1}{\pi }P{\int }_{-\infty }^{\infty }{\epsilon }_2\frac{{\omega }^{\prime }}{{\omega }^{\prime }-\omega }d{\omega }^{\prime }$$ (12)

P represents the integral's primary value.

The amount of energy lost by the wave when it passes through a solid is indicated by the light absorption coefficient [111]. Moreover, despite its high absorption coefficient, one-atom-thick graphene absorbs only 0.023 of visible light and has a reflectance of less than 0.001 of infrared light, according to several experimental findings [[112], [113], [114]]. This is due to the linear dispersion of the electron, which causes it to behave like a massless material, which is amazing for a monolayer material [[115], [116], [117]]. However, this is rather poor for applications in photodetection [118,119]. Hence, the absorbed white light is determined by the atomic structure and not the properties of the material [120]. The amount of white light absorbed increases linearly [121,122]. In addition, graphene is a promising candidate for sensing broadband in the terahertz and infrared ranges, but this results in its short exciton lifetime, which is harmful to exciton splitting and high photoresponsivity [[123], [124], [125]]. Moreover, graphene's absorption spectrum is empty in the ultraviolet region, ranging from (900–300) × ${10}^{-9}\mathrm{m}$, with a maximum absorption peak about 270 nm [126]. In summary, several studies established that graphene has a Drude-like intra-band conductivity based on Ω = 0, followed by an area of reduced conductivity at higher energies before a sudden rise to a steady comprehensive framework value of ${\sigma }_0=\raisebox{1ex}{${\pi e}^2$}\!\left/ \!\raisebox{-1ex}{$2h$}\right.$ indicating that graphene exhibits semi-metallic behaviour [125,127,128]. The transitions between the fully filled valence band and the unfilled conduction band are known as inter-band transitions, and this accounts for its optical sensitivity [[129], [130], [131], [132]]. However, an extensive study is required on the optical properties of graphene employing the density functional calculations to tailor it for applications in optoelectronics.

2.4. Modification of the electronic and optical properties of graphene by chemical doping

This is employed to modify the intrinsic behaviour of graphene to achieve optimized performance by doping a controlled percentage of foreign atoms in its symmetry [133,134]. The formation energy, bond length and band gap of the different doped graphene structures reported in literature are displayed in Table 1. Meanwhile there are two methods reported for the chemical doping of graphene generally: (1) The adsorption of specified materials such as gases, chemicals, metals among others into the graphene surface. (2) Foreign atoms are substituted into graphene, replacing the C atom. Therefore, the substitution of heteroatoms for the carbon atoms in graphene induces structural and electronic changes, contributing to the modifications of the system's thermal, carrier mobility, fermi level, electronic and optical properties [[135], [136], [137]]. This can result in either a nucleophile (electron donor), an n type or an electrophile (electron acceptor), a p type semiconductor. Nitrogen (n-type) and boron (p-type) are the most studied dopant atom because of their similar atomic radii to carbon, with nitrogen having an extra electron and boron being electron-deficient [[138], [139], [140]]. However, nitrogen has attracted more interest than boron due to its ease of substitution into graphene [141,142]. Moreover, the Graphitic-N (sp² hybridization), pyridinic (sp² hybridization), and pyrrolic N (sp³ hybridization) are the three most common N bonding configurations [143]. Studies shows that the pyridinic-N bonding configuration is relatively stable in the presence of mono-vacancy while pyrrolic bonding energetically favours divacancy defect [[144], [145], [146]]. The graphitic configuration favours an n-type while both pyrrolic and pyridinic favours a p-type doping [147]. Fig. 6(a) and (b) reveals the structural and electronic band change of a N/G graphene. Moreover, Rafique et al. [148] observed that nitrogen doping preserves linear energy dispersion around graphene's Dirac cone using the ab initio method. The studies on N-doped graphene have focused on the influence of the total percentage of N-doping in graphene, while few studies have investigated the positions of the N-dopant atom and the impact of the different C–N bonding configurations. However, B-doped graphene, as revealed by Beheshti and his colleagues, results in an electron-deficient structure [148].

Table 1.

The calculated parameters for pure and different doped graphene systems.

System (%)	Band Gap (eV)	Bond length ($\mathbf{\AA }$)	Formation energy (eV)	References
Graphene	0.00	1.42	NA	[[155], [156], [157]]
Beryllium doped Graphene (12.50)	1.44	1.56	25.56	[158,159]
Beryllium doped Graphene (12.50)	1.44 0.89	1.46	2.96	[160,161]
Beryllium doped Graphene (25.00)	1.42	1.55	5.19 25.56	[110,162]
Boron doped Graphene (12.00)	0.32	1.42	1.42	[163,164]
Boron doped Graphene	0.30	1.47	3.46	[[165], [166], [167]]
Boron doped Graphene	0.32	1.49	−27.30	[168]
Sulphur doped Graphene	0.57	1.62	8.33	[162,169]
Silicon doped Graphene (6.25)	0.70	1.65	−0.87	[170]
Silicon doped Graphene	2.00	1.91	NA	[171]
Nitrogen doped graphene	1.30	1.39	0.32	[172,173]
Nitrogen doped Graphene	0.21	1.39	−6.63	[157,174]
Phosphorous doped Graphene (3.13)	0.32	1.77	−6.42	[[175], [176], [177]]
Aluminium doped Graphene	0.40	1.73	9.86	[157,169]
Iron doped Graphene	1.70	1.67	7.24	[174,178,179]
Nitrogen-Aluminium doped Graphene	0.47	1.69	13.5 13.4	[157]
Beryllium–Nitrogen doped Graphene (25.00)	1.54	1.75	13.54	[158,180]
Beryllium-Sulphur doped Graphene	0.58	(Be) 1.53–1.54 (S) 1.36–1.38	2.45	[162]
Beryllium-Sulphur doped Graphene	0.37	NA	4.85	[181]

Fig. 6.

The (a) optimized geometry and (b) the electronic band structure of Nitrogen-doped graphene. The Nitrogen atom is symbolized by the red ball and the bond lengths indicated in the rings are measured in Å. Figure remodified from Ref. [107]. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)

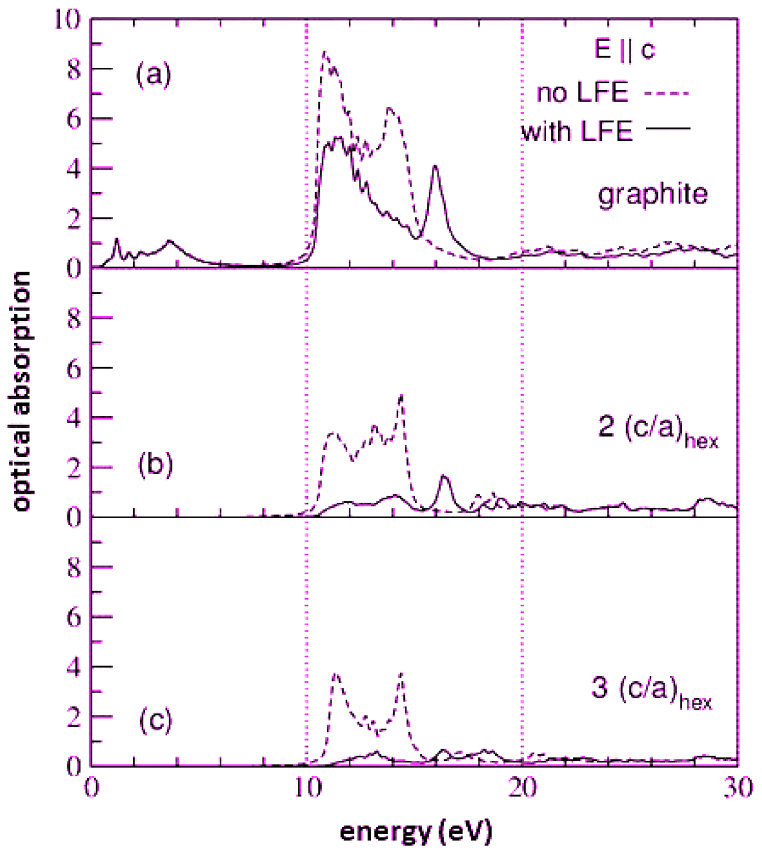
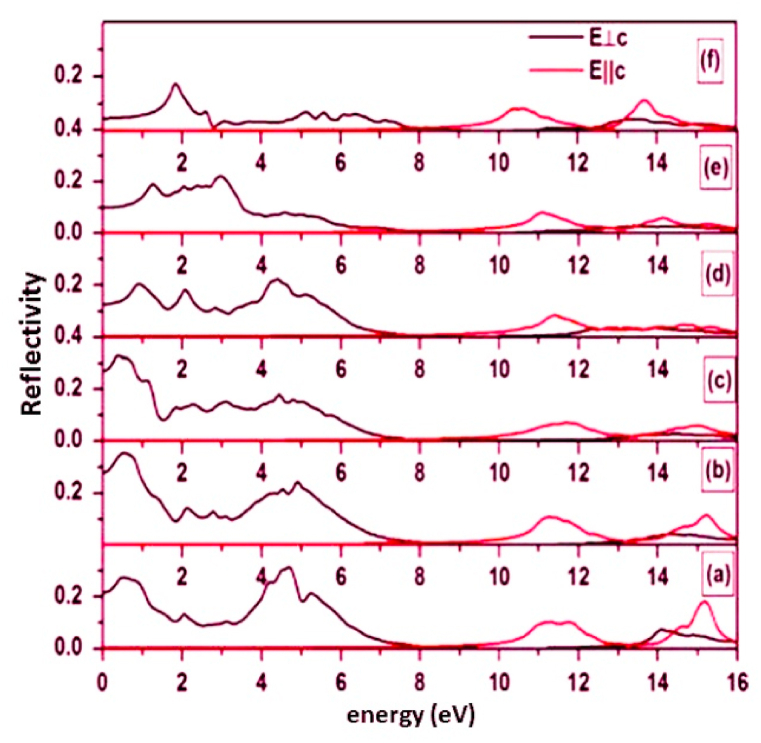
Likewise, Be-doped graphene are reported in literature. However, despite its physical and electronic potentials as indicated by density functional approach, it suffers from very high formation energy which has limited its viability for synthesis compared to the N-and B-doped graphene [110]. Nonetheless, atomic elements with larger atomic radii than carbon such as silicon, sulphur, germanium are being substituted into graphene lattice to modify its intrinsic properties [[149], [150], [151]]. Moreover, Marinopoulos et al. [152] reports that the graphite's absorption spectra for the light parallel to the c axis and the increasing of interlayer spacing resulted in the stacking of the graphene layers unit cell with less intense mutual interaction [152]. The absorption spectra of the graphene sheet structures are displayed in Fig. 7b and (c). At the same time, Nath et al. [153] compared the reflectivity of pure graphene to that of B/N doped graphene and observed a redshift of the main peak at higher doping concentration (See Fig. 8) [154]. However, despite the potentials of employing ab initio studies to chemically dope graphene reported in literature several discrepancies exist in their results (see Table 1, Table 2, Table 3, Table 4, Table 5) which may be as a result of the choice of the exchange correlations functionals, and basis set as well as wrong input parameters. Meanwhile, in the next section, a brief discussion of the different generations of exchange correlation functionals employed in density functional theory is presented. We have also surveyed machine learning, which was recently proposed as a way of improving density functional theory models by employing a large amount of training data from first principles calculations to accurately predict and tailor the properties of graphene for optoelectronics.

Fig. 7.

(a) Graphite and (b) graphene sheet geometries with 2(c/a)_hex and (c) 3(c/a)_hex for ${\mathrm{E}\perp }_{\mathrm{C}}$ optical absorption spectrum. Figure remodified from Ref. [152].

Fig. 8.

The reflectivity for pristine graphene (a) as compared with graphene dual doped at different percentages of BN in increasing order of concentrations of boron at different percentages (b), 12.75% (c) 18.75% (d) and 37.5% (e) and 75% respectively for perpendicular and parallel polarization. Figure remodified from Ref. [154].

Table 2.

A summary of the applications and gaps of doped graphene systems in literature.

Focus of Study	Comments/Inference	Prospects	Gaps	Reference
DFT study of CO adsorption in Boron-doped and Nitrogen-doped graphene (B/NG)	1.The stabilities of Nitrogen and Boron showed an anisotropy behaviour and response to CO adsorption 2.B/NG doping is a more effective gas detector due to its high sensitivity. 3.B/NG improves adsorption energy.	Chemical Sensor of toxic gases	1.Limited theoretical studies in relation to doping sites on the composition of co-doping of B/NG 2.Reduced Charge transfer	[[182], [183], [184]]
DFT study of the adsorption of boron doped graphene (B/G)	1.It turns to a less electronegative network. 2.It is an efficient storage material for Li-Ion batteries 3.Induces P-type conductivity	Li-ion Batteries	1.Broken symmetry which implies structural deformities 2.Different doped graphene structures are not stable.	[185,186]
First principles calculations of calculations of calcium decorated boron doped graphene	1.Boron doping limits clustering problem by increasing metal adsorption strength on graphene compared to Transition metal coated graphene	Hydrogen Storage	1.Individual Calcium atoms are not stable on graphene. 2.Weaker bond observed in the B-doped graphene system	[187]
Ab initio calculations of the electronic structure of Boron and Nitrogen doped graphene sheets	1.Graphene changed from a semi-metal to semiconductor with an increasing number of dopants. 2.The size of the band gap is determined by the lattice position of the dopant atoms.	Polymer-based electrolytic fuel cells	1.There are variations in the stability of the doped systems.	[107]
Ab initio studies of the geometry, and electronic properties of Beryllium and Boron doped graphene	1.The percentage and the position of the dopants is important in modifying the band structure of graphene. 2.The band gap created can be used to design transistor devices. 3.Hexagonal doping was reported to be superior to rectangular doping due to its higher band gap	Electronic devices	1.Rectangular doping engineered a lower band gap. 2.At higher doping percentage the symmetry was broken and a decrease in the cohesive energy	[159]
Ab initio study of doping of Alkaline earth (Be, Mg, Ca, and Sr) metals on graphene	1.A full electron transfer of $a+1.6e^{-}$ was observed for Be/G. 2.Spin polarized electronic structures and ionic bonding observed in (Mg, Ca, Sr) indicating magnetic properties. 3.They are energetically stable revealing its viability as a doping motif	Magnetic Semiconductors	1.Be/G does not exhibit any magnetic properties. 2.Inconsistency in the charged transfer compared to existing results	[188]

Table 3.

A summary of the different doping types, applications, and gaps of doped graphene systems in literature.

System	Doping Type	Applications	Gaps in Literature	References
1.Dissociation of ${\mathrm{H}}_2\mathrm{S}$ on Fe-doped graphene 2.Adsorption of NO on Fe-doped graphene.	N-type Semiconductor	Sensors Low dimensional materials	1.In adsorption with ${\mathrm{H}}_2\mathrm{S}$ the impact of Fe with S is weak at certain distances 2.Instability in the interactions between the adsorbent and adsorbate which results in the desorption process due to the positive electric fields	[178,189]
Aluminium doped graphene	N-type Semiconductor	Sensors	1.Less efficient than Beryllium doped graphene in terms of electronic engineering 2.High formation energy associated with its unusual reactivity. 3.Low rate of absorption in the Visible light range.	[157,190]
Sulphur doped graphene	N-type Semiconductor	Electronic devices	1.Decrease in the work function and band gap at higher doping concentration. 2.It has poor magnetic moment 3.Large formation energy which affects the ease of substitution into graphene when compared into nitrogen dopants.	[191,192]
Platinum doped graphene	N-type Semiconductor	Electronics, Optoelectronics, and sensors.	1.Structural deformities in graphene 2.Rare atomic elements 3.Limited theoretical and experimental studies	[193]

Table 4.

A summary of the different doping types, applications, and gaps of doped graphene systems in literature.

System	Doping Type	Applications	Gaps in Literature	References
Pure graphene	NA	Electronics, Photonics, Optoelectronic devices, etc.	1.Its intrinsic electrical conductivity and very high resistivity limit its rate of absorption. 2.Zero-band gap	[[194], [195], [196]]
Beryllium doped graphene. Be-decorated Fullerenes.	P-type Semiconductor	Nano-electronics and Optoelectronic devices Hydrogen Storage Transistors	1.Very large formation energy, and poor stability. 2.Reduced charge transfer 3.Decrease in the volume of ${\mathrm{H}}_2$ adsorbed due to the dissociation of ${\mathrm{H}}_2$ molecule. 4.No record of its experimental synthesis in literature based on our knowledge.	[158,159,197]
Boron doped graphene	P-type Semiconductor	Electronic devices. Optoelectronic devices Li-ion batteries Circuits, Memory devices	1.Less effective in engineering the band structure of graphene 2.In the long wavelength limit for parallel polarization, the static dielectric constant depends on the impurity concentration. 3.No absorption at high doping percentage. 4.Poor catalytic activity in Non-aqueous Li-ion batteries	[159,163,165,168,[198], [199], [200]]
Hydrogen adsorption on Nitrogen-doped graphene.	N-type Semiconductor (Graphitic) P-type semiconductor (pyrrolic and pyridinic)	Optoelectronics devices	1.The role of each of the C–N bonding configuration remain elusive 2.There was a rapid decrease in the absorption coefficient in the visible light range.	[13,46,172,[201], [202], [203]]
Silicon doped graphene	P-type Semiconductor	Semiconducting devices	1.Lower effective masses for the carriers of siliphene compared to traditional semiconductors such as Si and GaAs 2.Very wide band gap may not be suitable for field effect transistors 3.Clustering of silicon atom in graphene at higher doping concentration.	[169,171,[204], [205], [206]]

Table 5.

A summary of the different doping types, applications, and gaps of doped graphene systems in literature.

System	Doping Type	Applications	Gaps in Literature	References
1.B-/N doped graphene	N-type Semiconductor	Fast Computer Processors, Circuits	1.Weak contributions of the $\pi$ electrons resulting in decrease in the electronic conductivity 2.Large redshift in the absorption coefficient towards the visible light spectrum 3.Torsional deformation at the main peak	[107,172,202,[207], [208], [209], [210]]
Be-/N doped graphene	P-type semiconductor	Nano-electronics and optoelectronic devices	Beryllium still has large formation energy although much reduced despite co-doping with Nitrogen and decrease in stability despite indicating the possibilities of being synthesized at high doping concentrations.	[110]
Be-/S doped graphene	N-type semiconductor	Electronic and Optoelectronic devices	1.The system's stability falls with an increase in the dopants concentration which is evidenced by the defects formed in the system. 2.Reduced optical peak intensities at higher doping concentration.	[211,212]
N–Al doped graphene	N-type Semiconductor	Electronic devices	Large formation energy impedes its stability. Poor optical absorption	[213]

3. Overview of DFT models for the optoelectronic properties of graphene

3.1. Density functional models employed for predicting properties of graphene

It is one of the most popular computational approaches applied in condensed matter physics and quantum chemistry and is based on the concept that electron density can be employed as a basic variable to solve the electronic structure problem of materials as well as the total electronic energy [[214], [215], [216], [217], [218], [219]]. It relies on the Hohenberg-Kohn's theorem and gives completely quantum solutions to solving the Schrodinger equation, by mapping the many body systems of interacting electrons into a simplified single-particle problem [[220], [221], [222]]. The Born-Oppenheimer approximation is used to represent the degenerate N-ground system's state energy as illustrated in Eqn. (13), which is a special functional of the electron density [223]:

$$E\left[\rho \left(r\right)\right]=F\left[\rho \left(r\right)\right]+J\left[\rho \left(r\right)\right]+Q_{ee}\left[\rho \left(r\right)\right]$$ (13)

where the overall functional $F\left[\rho \left(r\right)\right]$ is given by the sum of the kinetic energy functional $T\left[\rho \left(r\right)\right]$ and the nuclear-electron interaction energy functional represented by $V_{en}\left[\rho \left(r\right)\right]$ and the quantum electron-electron energy represented by $Q_{ee}\left[\rho \left(r\right)\right]$. Furthermore, the first attempts at density functionals were made in the early twentieth century by Thomas and Fermi theory, which predicted mutually independent movements of the electrons and a local density approximation characterizing the kinetic energy associated with the motion [[224], [225], [226], [227]]. Moreover, this functional failed miserably in regions with large spatial changes in electron density [228]. However, about four decades later, Kohn and Sham demonstrated in their paper that the problem of electron kinetic energy using a basis set can be accurately approximated by a single slater determinant to represent an imaginary system of non-interacting electrons (columbic interaction ignored), with the same ground state density as the exact correlation functional [223,229,230].

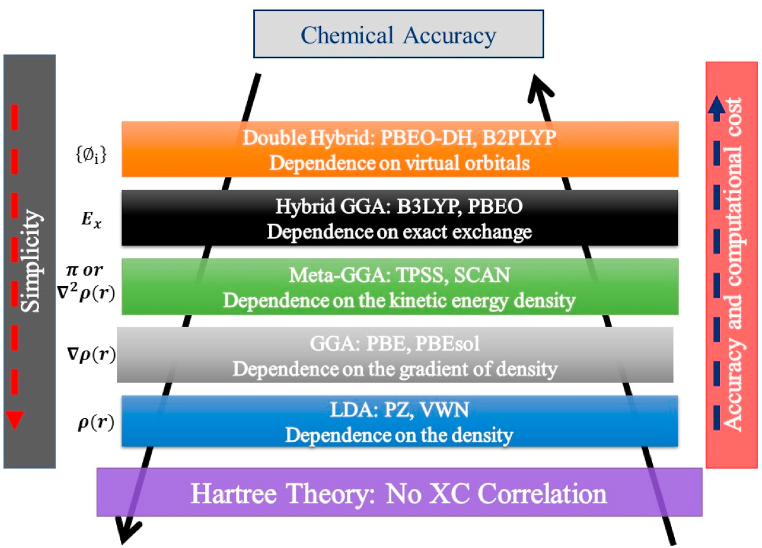
The literature has reported over 300 functionals over the last three and a half decades, and with the current trend, it is expected to double in the next ten years [215,231]. These are the semi-empirical and non-empirical functionals, which envelope parameters fitted from data and free parameters deduced by fitting standard specifications, respectively [223,232,233]. A few examples of semiempirical functionals include B3LYP, ωB97X-2, B 97, while non-empirical functionals include PBE, TPSS, SCAN, etc. However, for a detailed presentation, see Refs. [223,[234], [235], [236], [237], [238]]. Regardless, the five distinct classifications of the XC functionals are displayed in Fig. 9. This is a progressive illustration known as Jacob's ladder, which demonstrates that each rung corresponds to functionals that elicit a certain kind of approximation with the chemical accuracy increasing by moving up the ladder and is more advanced [[239], [240], [241], [242]]. However, the top rung has a higher computational cost [243,244]. Moreover, the precision of the energies and electron densities increases with each step until the turn of the century [[244], [245], [246]]. However, the energies have continued to advance while the accuracy of the electron density is declining [247]. This could be because conventional fitting ignores characteristics with high density dependencies. However, this is debatable [247].

Fig. 9.

The Jacob's Pardew ladder rung describing the hierarchy of the XC functionals. Figure remodified from Ref. [317,318].

Additionally, the orbital shell describes the characteristics of solids. As a result, Herring postulated that an orbital's base during World War II is an orthogonalized plane wave, which is a linear combination of core and plane waves (OPW) [248,249]. Convergence restrictions were present in this model, although this was overcome by using secular determinants in the OPW and pseudopotentials developed by Philip and Kleinman [250,251]. The pseudopotentials describe the interaction between the nuclei and the core electrons and enable the modelling of crystals such as graphene with any atomic element on the periodic table [[252], [253], [254], [255]]. Examples of widely used pseudopotentials embedded in simulation software for calculating and modelling graphene with any atomic element are the projected augmented plane waves and ultrasoft pseudopotentials [[256], [257], [258]].

Moreover, the first implementations of DFs employed LDA functionals [259,260]. However, this functional is plagued with controversies due to systematic errors and the overestimation of the interaction energies. The limitation was circumvented by GGA approximations, which consider spatial variation and not only the spin densities [261,262]. However, this failed to accurately define the localized states; it underestimates the band structure and phonon properties of crystals, even in graphene. This has resulted in the development of more advanced XC functionals, such as Meta-GGAs and hybrid functionals, which incorporate the reliance on K.E. densities and Hartree Fock, respectively, to reach chemical accuracy heaven [248,263,264]. This is displayed in Table 6, highlighting their distinguishing features. In summary, DFT is widely recognized for calculating the electronic structure of graphene due to its well-proven theories, which have been extensively validated, and an increasing volume of papers in the literature has greatly contributed to its acceptance in the scientific community [[265], [266], [267]]. Furthermore, the different simulation codes and platforms employed for DFT calculations are displayed in Table 7. However, density functional calculations may not accurately reflect the electronic properties of large and complex systems with strong electronic correlation or non-local effects, which is where ML-DFT functionals are handy [218,220,261]. Therefore, an overview of this newbie in computational material science is presented in the following sub-section.

Table 6.

A summary of the different XC functionals employed in density functional calculations.

Functional	Description	Strengths	Weakness	Uncertainties	References
Local Density Approximation (LDA)	It makes an approximation of the XC energy, which depends on the electron density at defined points	It gives a solid representation of the chemical bond and electronic properties of graphene. Moreso, it is more efficient than the self-consistent field HF	The calculated band gap is underestimated and has poor accuracy.	The calculated results of the LDA are generally considered to be less accurate than the GGA or hybrid functionals	[[268], [269], [270], [271], [272]]
Generalized Gradient Approximation (GGA)	It relies on the local electron density gradient and the electron density	It corrects the underestimation of the calculated band gap with LDA	The calculated band gap is overestimated	They are seen as being more accurate than LDA. However, they are less reliable than the hybrid functionals	[[273], [274], [275], [276]]
Hybrid Functionals	It combines the Hartree-Fock (HF) exchange integral and the exchange functional	In terms of the band gap and electronic structure of graphene, it outperforms both the LDA and GGA XC functionals	It's application in large systems is constrained by the exact exchange's expensive cost, which scales with the number of electrons	Predictions may have fewer uncertainties. However, they are more computationally expensive	[[277], [278], [279], [280], [281]]
Meta-GGA functionals	It employs the electron density, its gradient, and the K.E. density to distinguish between single orbital and orbital overlap regions	It accurately describes the electronic structure and normalizes LDA/GGA's under and overestimation of the calculated band gap	It is computationally more expensive than LDA and GGA	It has considerably larger uncertainties compared to both the LDA and GGA potentials. These are evident in the total energies, geometries, and electronic structure	[[282], [283], [284]]
Double hybrid Functionals	It contains a virtual K–S orbitals, in which non-local Fock exchange substitutes a portion of the semi local DFT exchange, as well as non-local effect	Better precision for molecular structures and binding energies It provides a more accurate account of the effects of long-range electron correlation caused by London dispersion forces	It is computationally more expensive than LDA and GGA Some of them have intrinsic deficiencies, such as the large basis set superposition error and missing London dispersion effects	It is laborious to determine its uncertainties because the accuracy relies on the exact functionals and system under study Undefined DF or atomic or atomic basis set combination can introduce systematic error into the system	[285,286]

Table 7.

A summary of the DF's simulation codes based on their basis types.

Name	Software	License	References
Plane-waves basis sets	CASTEP	Commercial	[[10], [11], [12], [13]]
	VASP	Commercial	[[14], [15], [16]]
	ABINIT	General Public License	[[17], [18], [19]]
	BigDFT	General Public License	[297,298]
Linearized augmented plane wave	WIEN2K	Commercial	[[299], [300], [301]]
	FLEUR	Massachusetts Institute of Technology	[[302], [303], [304]]
Atom centered basis set	SIESTA	General Public License	[[305], [306], [307]]
	ORCA	free	[308,309]
	Gaussian	Commercial	[[310], [311], [312]]
	Q-Chem	Commercial	[313,314]
Real-space grids	GPAW	General Public License	[315,316]

3.2. Machine learning models for predicting the properties of graphene

Machine learning (ML), a form of computer pattern recognition that automatically improves with experience, has had a substantial impact on several fields of science during the last decade [[319], [320], [321], [322]]. Moreover, in the late 20th century, Doren and co-workers noted that ML had evolved into a technique for the design of atomistic potentials by leveraging it to approximate unknown factors [323]. However, despite the challenging task of distinguishing between machine learning, a branch of artificial intelligence, and ab initio DFT-based calculation without some measure of arbitrariness [324,325].

The convergence of these two major fields has resulted in a new direction of deep learning first-principles calculations in computational material science and chemistry for developing systems affecting our daily lives, such as flexible electronic devices, voice recognition, and self-driving cars, among other things [324]. As a result, a variety of ML-potentials, including neural network potentials (NNPs) [[326], [327], [328], [329]], Gaussian approximate potentials (GAP) [330,331], moment tensor potentials (MTP) [332,333], and kernel ridge regression (KRR) [334,335], have been reported in the literature for this purpose [[336], [337], [338], [339]] A brief description of a few of the potentials used in machine learning DFT and their applications, is given in Table 8. A review of all the ML potentials is beyond the scope of this study. The potentials generate a force field or potential energy surface, which is the atomic localization of potential energy and atomic forces [340]. Furthermore, the Born-Oppenheimer approximation defines the potential energy surface (PES) [341,342]. Therefore, the training data, such as their corresponding energies, forces, and stress, can be employed to execute the Molecular dynamics simulations in determining the electronic structure with precision comparable to the ab initio approach without incurring a large computing burden [343,344]. The earliest potential, the neural network, is confined to low-dimensional systems, while the second variant is known as the high-dimensional neural network [343,345]. Here, the maximum atomic energy contributions induced by the energy vary depending on the local environment, which is characterized by atom-centered symmetry function descriptors [343,346]. This ensures that the requirement for the linear, rotational, and permutation invariance for many body systems of any configurations is met [[347], [348], [349]]. The descriptors are the central element of the ML model, which has to do with an iterative process known as the numerical encoding of the input cases or materials [350].

Table 8.

Summary of description and applications of ML potentials.

Machine Learning Potentials	Descriptions	Applications	References
Neural Network	The neural networks are used widely in ML potentials to calculate energy and forces from atomic locations. The conventional neural networks are characterized using feed forward neural networks which can be enhanced physically to offer extrapolation capabilities outside the scope of the training data. However, it can only be employed in low dimensional systems	To predict the energetics of lithium intercalation into graphite with accuracy comparable to DFT models To enhance the rate of convergence and prediction accuracy for the inverse optical design of inverse optical design of graphene-based metamaterials	[370,372,373]
Gaussian approximate potentials (GAP)	The total energy disintegrates into local atomic contributions which are determined using the gaussian process regression from ab initio data	It creates the graphene interatomic potential To predict finite temperature phonon spectra and the thermal expansion of graphene	[218,344,374,375]
Moment Tensor potentials	It is an active learning approach that is analogous to GAP, and has descriptors based on tensor operations that essentially approximate any PES. It induces less energy and force test errors at greater precision and speed of calculation	It is trained to modeled atomic interactions To calculate thermal and mechanical properties	[369,376]

Moreover, the prediction scheme should possess a numerical encoding to be considered quantitative [351,352]. However, a sufficient understanding of the problems and goals is essential in the right selection of the numerical encoding which considers the materials properties related to the intended property [352]. The descriptor may need to incorporate important information regarding the atomic level elements that may govern these behaviours since the accuracy required of the predictions depends on the relevant characteristics or a specified property of a 2D material, such as the optical properties of graphene [353]. Moreover, the common descriptor is the electronic property obtained without complicated calculations, while more accurate descriptors that include the valence band in the d-band core are computationally expensive. This implies striking a balance between the cost and prediction accuracy [354,355]. Today, the third and fourth variant descriptors were able to describe long-range interactions beyond the local chemical environments but relies on the local charges [343].

However, the predictions of the ML potentials are subject to uncertainties which are challenging to verify due to the approximate models of the real bonding physics of the system. These can either be numerical, structural, and parametric [[356], [357], [358], [359]]. The factors that the numerical uncertainty considers are the size of the computational domain, and the set-up time for the input. The structural and parametric uncertainties that relate to the accuracy of the ML potentials are more burdensome [359,360]. The Bayesian approaches, the gaussian process regression offer a logical route for measuring the prediction's level uncertainty [361,362]. The Bootstrapping is an alternative, simple and flexible approach to access the uncertainties [363]. There are other approaches, but they come at a substantial additional expense. Moreover, the uncertainty can be utilized to gradually and constantly enhance prediction models which may be achieved by optimizing the costs between exploration and exploitation [364]. The uncertainty and the strength of some of these potentials are revealed in Table 9.

Table 9.

The strength, weakness, and uncertainties of ML potentials.

Name	Strength	Weakness	Uncertainties	References
Neural Network	Their non-linear functional is flexible which enables accurate and faster electronic structure calculations	1.Identifying its hyperparameters and developing training regimens that prevent overfitting can be difficult 2.Interpretability and explainability is lacking for practically accurate results for large time data	The uncertainty in the construction of the potential energy surface of graphene relies on the efficiency of the training set essential for improved transferability required of NN potential	[322,324,377]
Gaussian Approximation Potential	It is faster than first principles approach and is independent of the size of the training set.	1.For huge data, the inference stage of GAP requires matrix inversion which increases the computing cost 2.Overfitting of the models which has resulted in unphysical behaviours 3.It fails to capture the interlayer interactions; it is not applicable to multilayer graphene structures	The transferability of GAP has a high degree of uncertainty to accurately predict outside the training set. Moreover, the specific implementation and the training set relies on the accuracy of GAP	[378,379]
Moment Tensor Potentials	It is computationally cheaper and save more time than DFT calculations.	The learning algorithm is built through a time-consuming trial and error cycles in which the trained potential efficiency is manually evaluated	This is currently being investigated and has not been completely established. However, its accuracy might be affected by the size of the configuration domain and the input data.	[380,381]

The ML algorithm can be grouped into supervised modelling, unsupervised modelling [365], semi-supervised modelling [366], and reinforcement modelling. The supervised learning contains both the input and the output data, i.e., label data. Unsupervised modelling is used on unlabeled data with no inherent ground truth. In addition, the se mi-supervised models have a larger input than output as they combine the strengths of supervised and unsupervised models [367,368], and the reinforcement models do not require previous knowledge and instead acquire knowledge and experience via interaction with the environment.

It is important to note that the role of model selection is to determine the best approach and parameters for a particular task [364]. Thus, the label of the input data sets, and the known physical image of descriptors and properties of interest heavily influence the selection of the most suitable approach, which is the heart of the selection process [354]. Therefore, for a comprehensive description of ML and its applications in DFT, consult refs, [218,[369], [370], [371]]. However, despite the exciting prospects of ML-DFT, we observed that it has not yet been widely applied to graphene in the literature, which may be a result of insufficient data sets which is required for obtaining accurate results and the complexity of the electronic structure of graphene, etc. Moreover, the existing knowledge gap in the literature, which will provide meaningful insights into the future trends and directions in study of graphene for applications in optoelectronics, are presented in the following sub-section.

3.3. Knowledge gaps of graphene research

Despite the expanding scope of density functional theory and the emerging ML-DFT approach in providing an enormous understanding of the electronic structure at absolute temperature and optical excitations of graphene, some grey areas remain unresolved.

• 1.Band gap calculation: The band gap calculation of graphene structures is a controversial topic in the literature, with different exchange-correlation functionals employed in ab initio studies predicting different values due to imbalances in the delocalization, static correlation error, and the wrong selection of parameters, making the choice of XC functionals system dependent. Moreover, the lack of training data for ML models has restricted their applications in predicting the electronic properties of graphene [323].
• 2Van der Waals (vdW) interactions: The inability of the XC functionals employed in the ab initio studies to describe long-range electron correlations for the properties of graphene Thus, the lack of dispersion forces is one of the most significant problems in first principles calculations [382]. Moreover, training of the non-local ML potential is system-specific, and to accurately describe the non-local functional with different parameters, a large amount of training data is required [383].
• 3Vibration and Temperature Effects: The effects of the vibrations from DFT calculations are not defined for both the band structure and spectroscopy level in graphene. This limits the role of polaronic effects, including the effect of temperature, which is important for optoelectronic applications that are frequently temperature dependent.
• 4Modelling of graphene-based heterostructures: There are limitations in the accurate modelling of graphene-based heterostructures, such as the graphene-hBN layer and graphene silicon heterostructures. This is due to the complexity of their systems, which involve the interaction of different parameters. This has restricted the modelling of the interactions and the properties of these heterostructures, resulting in discrepancies in the calculations of their electronic and optical properties. Moreover, ML potentials require a large time series of data to accurately predict these properties.

3.4. Future trends of graphene research

Graphene's electronic properties have received most of the interest in research to this point, whereas few models have been developed on its thermal conductivities from different illustrations of phonons and even from density functional theory, molecular dynamics simulations, and ML training data to accurately determine its phonon transport. This will improve the imagination and provide comprehensive information on graphene's phonon scattering [384]. Moreover, by exploring its thermal conductivity, it can help solve the heat dissipation problem in electronic devices and aid in the design and commercialization of high-performance future optoelectronic and thermodynamic devices, e.g., heat engines, with optimized performance and stability.

Recently, graphene/hBN heterostructures have been considered the foundation for next-generation optoelectronics due to their high electron mobilities and tunable band structure. Currently, graphene-based heterostructures are being tested in optical communication satellites, superfast electronics, and photodetectors [171]. However, accurate and transferable DFT and ML models to determine the strong anisotropic tensor in the overall optical response of graphene heterostructures are required to facilitate their implementation in real-world optical systems [385,386].

Graphene has been reported to display inherent superconducting and nonconducting behaviour by creating a superlattice of two graphene layers rotated at a magic angle of 1.1°. Therefore, employing traditional DFT and ML-DFT to accurately predict the unconventional superconducting and insulating nature of large and complex graphene are essential in the near future for the design and fabrication of nano-superconducting quantum optical devices and nano-superconducting transistors [387].

Moreso, graphene is regarded as the thinnest and strongest 2D material, which highlights its prospects for application in ultrathin and ultralight aviation composite materials. Interestingly, it also has the potential to reduce the weight of the aircraft by 1%, saving almost $1 billion in fuel usage. Moreover, graphene-based coatings with distinct electronic properties might use electricity to generate thermal energy and transport it to the external surface, or they could improve conductivity and electromagnetic shielding to guard against lightning strikes. Therefore, optimization of the DFT and ML-DFT frameworks in future studies to modify graphene's structural and electronic properties is critical for the design and large-scale manufacturing of these graphene-based devices [388,389].

4. Conclusions

This review presents a detailed theoretical foundation, models employed in density functional theory, and recent research efforts in computational material science with the aid of machine learning to accurately predict the properties of graphene. The electronic and optical properties of the chemically doped graphene systems using the DFT approach were extensively discussed, with special emphasis on their prospects, doping type, and reported gaps in the literature. Moreover, these gaps can be associated with the choice of the exchange correlation functionals, basis sets, and wrong inputs of parameters, which affect the accuracy of its predictions. Despite this, traditional DFT models are at the heart of the electronic structure calculation of graphene, and the results are validated experimentally. Similarly, recent advances in machine learning have demonstrated tremendous potential for speeding up and improving the accuracy of DFT predictions of long-range electron correlations of graphene properties. However, the results obtained from ML-DFT have not been validated experimentally yet. Hence, the marriage of these two approaches is projected to play a key role in addressing the knowledge gaps in the study of graphene and ensuring it fulfills its promise.

Author contribution statement

All authors listed have significantly contributed to the development and the writing of this article.

Funding statement

A. L. Olatomiwa acknowledges Malaysia International Scholarship (MIS) for funding his Master of Science (MSC) in Nanomaterial Engineering at the Institute of Nano Electronic Engineering, Universiti Malaysia Perlis, Malaysia.

Data availability statement

Data will be made available on request.

Declaration of interest's statement

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.