Abstract
Microbial communities are highly dynamic and sensitive to changes in the environment. Thus, microbiome data are highly susceptible to batch effects, defined as sources of unwanted variation that are not related to and obscure any factors of interest. Existing batch effect correction methods have been primarily developed for gene expression data. As such, they do not consider the inherent characteristics of microbiome data, including zero inflation, overdispersion and correlation between variables. We introduce new multivariate and non-parametric batch effect correction methods based on Partial Least Squares Discriminant Analysis (PLSDA). PLSDA-batch first estimates treatment and batch variation with latent components, then subtracts batch-associated components from the data. The resulting batch-effect-corrected data can then be input in any downstream statistical analysis. Two variants are proposed to handle unbalanced batch x treatment designs and to avoid overfitting when estimating the components via variable selection. We compare our approaches with popular methods managing batch effects, namely, removeBatchEffect, ComBat and Surrogate Variable Analysis, in simulated and three case studies using various visual and numerical assessments. We show that our three methods lead to competitive performance in removing batch variation while preserving treatment variation, especially for unbalanced batch  treatment designs. Our downstream analyses show selections of biologically relevant taxa. This work demonstrates that batch effect correction methods can improve microbiome research outputs. Reproducible code and vignettes are available on GitHub.
treatment designs. Our downstream analyses show selections of biologically relevant taxa. This work demonstrates that batch effect correction methods can improve microbiome research outputs. Reproducible code and vignettes are available on GitHub.
Keywords: microbiome data, multivariate, non-parametric, dimension reduction, batch effect correction
Introduction
Investigating the link between microbial composition and phenotypes, including human diseases, is the main goal of microbiome research. The disruption of gut microbial communities has been linked to varieties of diseases and sub-health status, ranging from inflammatory bowel disease [1], diabetes [2] to obesity [3] and malnutrition [4].
However, microbiome research faces the challenges of data reproducibility and replicability that invalidate statistical results. Because microbial communities are highly dynamic [5], microbiome data are highly susceptible to batch effects, that is, any unwanted sources of variation that are unrelated to and obscure the biological factors of interest [6]. Microbiome studies affected by batch affects are increasingly abundant in the literature: unwanted variation can be introduced by changes in technical procedures including sample collection, shipping and processing [7–9] or from independent studies [10]. Other confounding factors including geography, age, sex, stress and diet also introduce batch effects to the composition of the host microbiota [11–14]. These batch effects often mask the biological effects of interest. Batch effect management is therefore critical to improve the validity of microbiome studies’ results.
Two types of approaches exist to handle batch effects [6]: methods that correct for batch effects consist in removing batch variation from the data; methods that account for batch effects include batch effects as covariates in the statistical model. Evaluating the effectiveness of the former is easier than the latter through numerical and graphical analyses [6].
Methods that account for batch effects are often restricted to differential abundance analysis with models that hold strong assumptions about data distribution. They include zero-inflated Gaussian model [15] and Bayesian Dirichlet multinomial regression [16].
Methods that correct for batch effects are the most flexible and any type of downstream analysis can be applied to the resulting batch-effect-corrected data, including dimension reduction, visualization and clustering. However, for microbiome studies, these methods are challenged by small sample sizes, which increase the uncertainty of batch effect estimation [17]. In addition, batch effect correction methods assume that batch and treatment effects are independent, requiring a balanced batch  treatment design [6]. However, microbiome experiments often result in unbalanced designs where batch and treatment effects are partly confounded, leading to the loss of treatment variation during the batch effect correction process.
treatment design [6]. However, microbiome experiments often result in unbalanced designs where batch and treatment effects are partly confounded, leading to the loss of treatment variation during the batch effect correction process.
The multivariate method Remove Unwanted Variation (RUV) has been recently adapted for microbiome data [18, 19], but requires negative control variables and technical sample replicates that capture batch variation, which are not often available in microbiome studies. Two methods percentile-normalization [20] and NetMoss [21] were developed to remove batch effects for microbial studies, but are only valid for case-control studies, which narrow the scope of their application.
Several batch effect correction methods have been developed for gene expression data [22, 23]. However, they are challenged by the inherent characteristics of microbiome data including zero inflation, uneven library sizes and compositional structure (even if data are transformed beforehand, for example, with centred log ratio transformation). Univariate methods disregard the inter-dependent relationships between microrganisms [24]. They also assume that batch effects are systematic and thus have a homogeneous influence on all microbial variables, which was found to be unlikely [6]. When non-systematic batch effects are mistakenly treated as systematic, biological variation of interest might be removed from the data, or the batch variation may remain during the batch effect correction process.
Promising methods have been proposed in other fields of application, such as single-cell RNA-sequencing. Seurat V3 [25], mnnCorrect [26], scmerge [27], zinbwave [28] assume a zero-inflated distribution but are only effective for very large sample size.
We propose novel approaches to correct for batch effects in microbiome data based on Partial Least Squares Discriminant Analysis (PLSDA [29]). PLSDA-batch is highly suitable for microbiome data as it is non-parametric, multivariate and allows for ordination and data visualization. Latent components related to treatment and batch effects are estimated to remove batch variation in the data while preserving biological variation of interest. Two other variants are proposed for unbalanced batch  treatment designs and to select discriminative microbial variables among treatment groups. We assess the performance of PLSDA-batch in extensive simulation studies and three case studies that investigate microbial communities in sponge tissues, anaerobic digestion conditions and diet types in mice. We compare the efficiency of our approaches in removing batch effects and uncovering treatment effects with popular linear methods that have been previously applied in microbial studies [30–32], such as ComBat and removeBatchEffect. As our approach shares some similarities with Surrogate Variable Analysis (SVA), besides the fact that it accounts, rather than corrects for batch effects, we include some comparisons in the simulation studies.
treatment designs and to select discriminative microbial variables among treatment groups. We assess the performance of PLSDA-batch in extensive simulation studies and three case studies that investigate microbial communities in sponge tissues, anaerobic digestion conditions and diet types in mice. We compare the efficiency of our approaches in removing batch effects and uncovering treatment effects with popular linear methods that have been previously applied in microbial studies [30–32], such as ComBat and removeBatchEffect. As our approach shares some similarities with Surrogate Variable Analysis (SVA), besides the fact that it accounts, rather than corrects for batch effects, we include some comparisons in the simulation studies.
Methods
Our three approaches are derived from PLSDA [29] to correct batch effects. We first give a brief description of the core method Partial Least Squares (PLS [33]), and its PLSDA extension for classification problems. We will use the following notations: 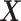 denotes an
denotes an 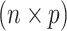 explanatory data matrix with
explanatory data matrix with 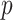 microbial variables and
microbial variables and 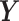 an
an 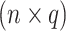 data matrix with
data matrix with 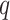 response variables. Both datasets match on the same
response variables. Both datasets match on the same 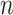 samples. We denote the matrix transpose by
samples. We denote the matrix transpose by 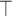 . The
. The 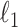 norm of a random vector
norm of a random vector 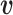 (
(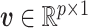 ) is defined as
) is defined as 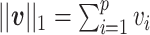 and the
and the 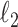 norm is
norm is 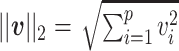 .
.
PLS and sparse PLSDA
PLS, a.k.a Projection to Latent Structures is an orthogonal component-based regression method commonly used to model the covariance structure between explanatory (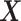 ) and response (
) and response (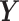 ) matrices in large datasets. The optimization problem to solve is
) matrices in large datasets. The optimization problem to solve is
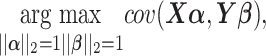 |
(1) |
where 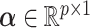 and
and 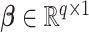 represent the loading vectors of
represent the loading vectors of 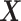 and
and 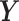 , respectively. The aim of PLS is to find the linear transformations (
, respectively. The aim of PLS is to find the linear transformations (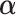 and
and 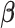 ) of
) of 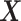 and
and 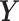 that maximize the covariance between their latent components denoted as
that maximize the covariance between their latent components denoted as 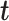 and
and 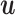 , respectively, with
, respectively, with 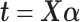 and
and 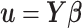 ,
, 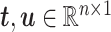 . After the first pair of latent components (
. After the first pair of latent components (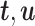 ) is obtained, the residual matrix is calculated via matrix deflation as
) is obtained, the residual matrix is calculated via matrix deflation as
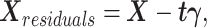 |
(2) |
where 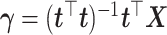 .
. 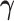 represents the regression coefficient vector for each variable in
represents the regression coefficient vector for each variable in 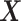 on
on 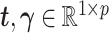 . Similarly, we can calculate the residual matrix
. Similarly, we can calculate the residual matrix 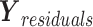 by deflating the matrix
by deflating the matrix 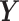 with
with 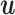 . The deflated matrices are then used as updated
. The deflated matrices are then used as updated 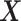 and
and  for the next PLS dimension. The deflation steps ensure that the latent components associated with each PLS dimension are orthogonal.
for the next PLS dimension. The deflation steps ensure that the latent components associated with each PLS dimension are orthogonal.
PLSDA is an adaption of PLS for classification and discrimination, where the response matrix 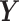 is a dummy matrix transformed from a categorical outcome variable. Each column in
is a dummy matrix transformed from a categorical outcome variable. Each column in 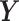 indicates the group membership of each sample: If sample
indicates the group membership of each sample: If sample 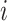 belongs to group
belongs to group 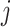 , then
, then 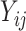 equals 1, otherwise 0. For each dimension
equals 1, otherwise 0. For each dimension 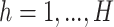 , the latent components
, the latent components 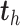 and
and 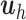 are calculated as shown earlier in Eq.(1).
are calculated as shown earlier in Eq.(1). 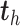 summarizes the variation from
summarizes the variation from 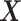 that is associated with
that is associated with 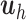 , whereas
, whereas 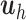 is a linear combination of the dummy outcomes in
is a linear combination of the dummy outcomes in 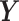 . Thus, the
. Thus, the 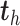 component is mostly relevant to explain the discrimination between sample groups.
component is mostly relevant to explain the discrimination between sample groups.
In PLSDA, we need to specify the optimal number of components 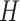 . It can be chosen using repeated cross-validation to estimate the classification error rate on each component
. It can be chosen using repeated cross-validation to estimate the classification error rate on each component 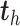 . As PLSDA is an iterative process based on deflated matrices, the
. As PLSDA is an iterative process based on deflated matrices, the 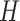 components that yield the lowest error rate correspond to the overall performance of the PLSDA model [34].
components that yield the lowest error rate correspond to the overall performance of the PLSDA model [34].
sparse PLSDA (sPLSDA) uses 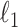 penalization on the loading vectors
penalization on the loading vectors 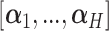 in PLSDA to select variables [35]. During the regression step, for each component
in PLSDA to select variables [35]. During the regression step, for each component 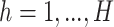 , the penalty is solved with soft-thresholding in Eq.(1):
, the penalty is solved with soft-thresholding in Eq.(1):
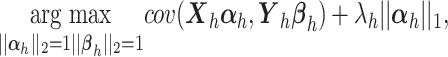 |
(3) |
where 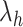 is a non-negative parameter that controls the amount of shrinkage on the loading vector
is a non-negative parameter that controls the amount of shrinkage on the loading vector 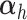 and thus the number of non-zero loadings. The latent component
and thus the number of non-zero loadings. The latent component 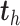 is therefore calculated based on a subset of variables that are deemed most discriminative to classify the sample groups.
is therefore calculated based on a subset of variables that are deemed most discriminative to classify the sample groups.
Two types of parameters need to be specified in sPLSDA: the number of components 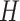 and the number of variables to select on each component, which corresponds to the shrinkage coefficient
and the number of variables to select on each component, which corresponds to the shrinkage coefficient 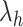 . Both parameters can be chosen simultaneously using repeated cross-validation by evaluating the classification error rate on a grid of number of variables to select on each component [34].
. Both parameters can be chosen simultaneously using repeated cross-validation by evaluating the classification error rate on a grid of number of variables to select on each component [34].
PLSDA-batch
PLSDA-batch aims to estimate and remove batch variation while preserving treatment variation. We use additional notations as we include in the model two different types of sample information, treatment and batch, denoted 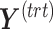 and
and 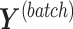 , respectively. The matrices
, respectively. The matrices 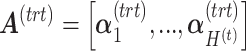 and
and 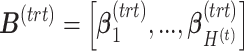 include the loading vectors associated with
include the loading vectors associated with 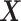 and
and 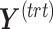 , respectively, where
, respectively, where 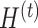 is the number of components associated with the treatment variation. The corresponding latent components are denoted
is the number of components associated with the treatment variation. The corresponding latent components are denoted 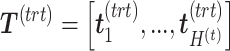 and
and 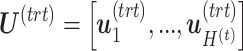 . Similar notations are used for the loading vectors and latent components associated with the batch effect across
. Similar notations are used for the loading vectors and latent components associated with the batch effect across 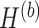 components. We will use simplified notations without superscript, such as
components. We will use simplified notations without superscript, such as 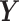 ,
, 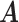 ,
, 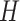 and
and 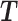 that are related to either treatment or batch variation when there is not ambiguity.
that are related to either treatment or batch variation when there is not ambiguity. 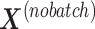 is the matrix from which the batch effect is removed, and similarly
is the matrix from which the batch effect is removed, and similarly 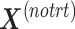 for the treatment effect.
for the treatment effect.
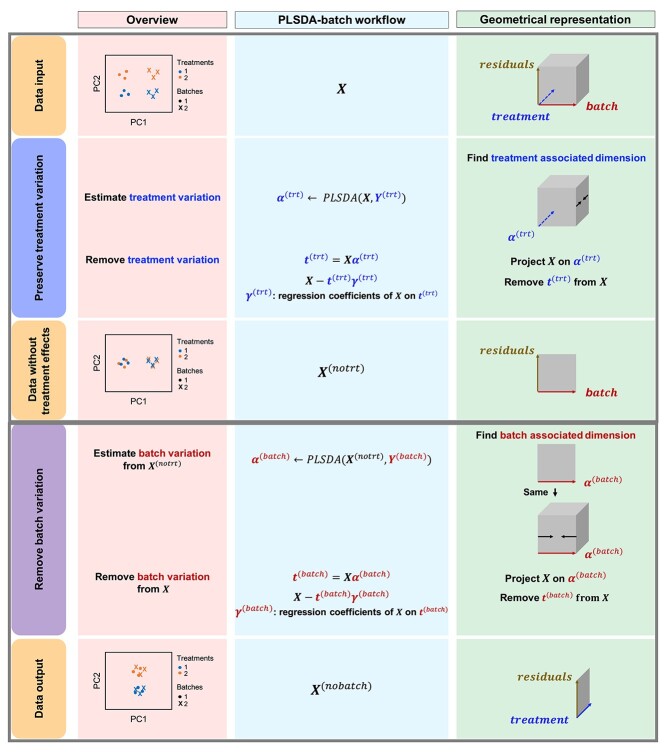
Overview
The general concept of PLSDA-batch is shown in the first column of Figure 1. Assuming 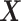 includes both treatment and batch effects, the samples projected onto a Principal Component Analysis (PCA) plot would be segregated according to both treatment and batch information. In a first step, PLSDA-batch estimates the treatment variation with the components
includes both treatment and batch effects, the samples projected onto a Principal Component Analysis (PCA) plot would be segregated according to both treatment and batch information. In a first step, PLSDA-batch estimates the treatment variation with the components 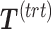 , which are extracted from
, which are extracted from 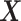 to obtain
to obtain 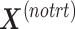 , so that only batch variation remains. The second step estimates the batch associated components
, so that only batch variation remains. The second step estimates the batch associated components 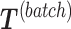 from
from 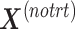 . The original dataset
. The original dataset 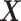 is then deflated with
is then deflated with 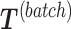 to obtain the final matrix corrected for batch effects while preserving the treatment variation
to obtain the final matrix corrected for batch effects while preserving the treatment variation 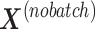 .
.
Figure 1.
PLSDA-batch framework. From left to right columns: Visualization with Principal Component Analysis sample plots; Workflow describing each step of Algorithm 1 and Geometrical representation of the approach via projections and deflation. For illustrative purpose, we only represent one component associated with either treatment or batch effects.
Algorithmic and geometrical point of views
The remaining columns in Figure 1 further describe the approach. For illustrative purposes, we only depict the case where only one component is associated with either treatment or batch effects rather than several components. The data matrix 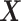 with both treatment and batch effects can be decomposed into three major sources of variation: treatment, batch and residuals. All these sources are assumed to be independent but in practice, treatment and batch sources are likely to be correlated to some extent. This motivated our approach to first estimate the treatment variation to avoid over-estimating the batch variation and losing substantial treatment variation.
with both treatment and batch effects can be decomposed into three major sources of variation: treatment, batch and residuals. All these sources are assumed to be independent but in practice, treatment and batch sources are likely to be correlated to some extent. This motivated our approach to first estimate the treatment variation to avoid over-estimating the batch variation and losing substantial treatment variation.
In the first step, we apply PLSDA to 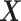 and
and 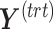 to identify the dimension of treatment effects
to identify the dimension of treatment effects 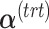 from
from 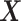 (see Algorithm 1 ‘Estimation of latent dimensions’).
(see Algorithm 1 ‘Estimation of latent dimensions’). 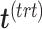 is then calculated using a scalar projection of
is then calculated using a scalar projection of 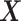 onto
onto 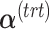 . Therefore, the treatment variation of all variables in
. Therefore, the treatment variation of all variables in 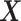 is summarized in the component
is summarized in the component 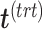 . We then calculate the matrix without treatment effects
. We then calculate the matrix without treatment effects 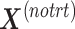 by deflating
by deflating 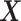 with
with 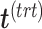 . In the second step, we identify the batch-associated dimension
. In the second step, we identify the batch-associated dimension 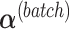 from
from 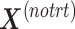 , then calculate
, then calculate 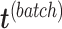 by projecting
by projecting 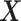 onto
onto 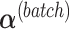 . The batch variation
. The batch variation 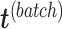 is then removed from
is then removed from 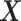 via matrix deflation while ensuring the treatment effects are fully preserved. Since the components
via matrix deflation while ensuring the treatment effects are fully preserved. Since the components 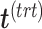 and
and 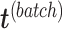 are orthogonal, we could also deflate
are orthogonal, we could also deflate 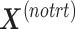 with respect to
with respect to 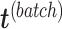 but such alternative would require adding the treatment variation back.
but such alternative would require adding the treatment variation back.

Weighted PLSDA-batch
A balanced batch 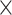 treatment design is an experimental design where samples within each treatment group are evenly distributed across batches [6]. Because of experimental constraints, a batch
treatment design is an experimental design where samples within each treatment group are evenly distributed across batches [6]. Because of experimental constraints, a batch 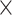 treatment design may be unbalanced, resulting in treatment and batch effects that are correlated and not separable. In PLSDA-batch, latent components associated with either treatment or batch effects are assumed to be orthogonal, thus ignoring the correlation between these two effects. The consequences might be over-estimation of the treatment variation as well as insufficient removal of the batch variation. Weighted PLSDA-batch (wPLSDA-batch) is inspired from weighted PCA to account for unbalanced designs [36], but in the case of PLSDA-batch the weight is defined accordingly. Further details on defining the weights are described in the Supplemental Section S2. Each sample
treatment design may be unbalanced, resulting in treatment and batch effects that are correlated and not separable. In PLSDA-batch, latent components associated with either treatment or batch effects are assumed to be orthogonal, thus ignoring the correlation between these two effects. The consequences might be over-estimation of the treatment variation as well as insufficient removal of the batch variation. Weighted PLSDA-batch (wPLSDA-batch) is inspired from weighted PCA to account for unbalanced designs [36], but in the case of PLSDA-batch the weight is defined accordingly. Further details on defining the weights are described in the Supplemental Section S2. Each sample 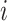 is assigned a weight
is assigned a weight 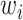 to take into account the number of samples within each batch and treatment:
to take into account the number of samples within each batch and treatment:
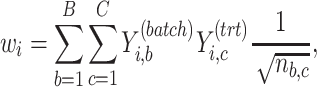 |
(4) |
where 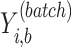 represents the indicator value (0 or 1) of sample
represents the indicator value (0 or 1) of sample 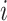 and batch
and batch 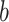 in the dummy matrix
in the dummy matrix 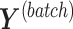 , and similarly for
, and similarly for 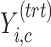 .
. 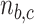 represents the sample size in batch
represents the sample size in batch 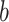 and treatment group
and treatment group 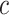 .
. 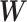 is a diagonal matrix that includes
is a diagonal matrix that includes 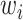 ,
, 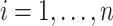 . We obtain the weighted explanatory and response matrices
. We obtain the weighted explanatory and response matrices 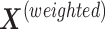 and
and 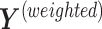 by multiplying
by multiplying 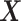 and
and 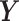 with
with 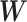 , respectively. The batch-effect-corrected data
, respectively. The batch-effect-corrected data 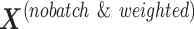 resulting from the calculation on the weighted matrices using PLSDA-batch are then multiplied by
resulting from the calculation on the weighted matrices using PLSDA-batch are then multiplied by 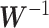 to remove the influence of weights.
to remove the influence of weights.
Sparse PLSDA-batch
In PLSDA-batch, the latent components are calculated based on all variables, thus assuming that all microorganisms are affected by the treatment (e.g. antibiotics). In most microbial studies, we can instead make the assumption that only a small number of microorganisms are affected by the treatment [37]. In that case, the batch-effect-corrected matrix 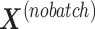 may not be accurate as it depends on the calculation of the treatment components
may not be accurate as it depends on the calculation of the treatment components 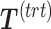 . These components are most likely to be affected by batch-related variables, especially when batch effect variability is high among samples.
. These components are most likely to be affected by batch-related variables, especially when batch effect variability is high among samples.
To avoid overfitting when we estimate the treatment components, we apply 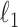 -penalty to each treatment associated loading vector (see Eq. (3)) to select variables. Thus, variables with no treatment effect are assigned a zero loading value and are not included in the calculation of a component. Batch effects are assumed to be less microorganism specific than treatment effects. Thus, to ensure that the batch variation is fully captured, no variable selection is performed on the batch components.
-penalty to each treatment associated loading vector (see Eq. (3)) to select variables. Thus, variables with no treatment effect are assigned a zero loading value and are not included in the calculation of a component. Batch effects are assumed to be less microorganism specific than treatment effects. Thus, to ensure that the batch variation is fully captured, no variable selection is performed on the batch components.
Parameter tuning
In PLSDA-batch, we need to specify the optimal number of components associated with either treatment or batch effects (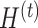 or
or 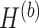 ). To choose this parameter, we estimate the variance explained in the outcome matrix
). To choose this parameter, we estimate the variance explained in the outcome matrix 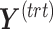 on each treatment component
on each treatment component 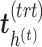 ,
,  and similarly for the batch-associated outcome matrix and components. We choose the optimal number of components that explain 100% variance in either
and similarly for the batch-associated outcome matrix and components. We choose the optimal number of components that explain 100% variance in either  or
or 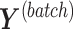 . The remainder components should only explain some (unknown) noise.
. The remainder components should only explain some (unknown) noise.
In sPLSDA-batch, in addition to the parameter above, we also need to specify the optimal number of variables to select on each treatment component. For this purpose, we calculate the balanced classification error rate BER = 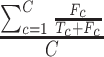 ), where
), where 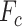 and
and 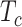 represent the number of false and truly classified samples in the treatment group
represent the number of false and truly classified samples in the treatment group 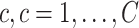 , where
, where 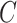 represents the total number of treatment groups [38]. The BER is evaluated through repeated cross-validation using the ‘maximum’ prediction distance as described in [34] on a proposed grid of number of variables to select on each treatment component. The number of variables yielding the lowest BER is the optimal parameter.
represents the total number of treatment groups [38]. The BER is evaluated through repeated cross-validation using the ‘maximum’ prediction distance as described in [34] on a proposed grid of number of variables to select on each treatment component. The number of variables yielding the lowest BER is the optimal parameter.
Simulation and case studies
Simulation study
Microbiome data are multivariate with inherent correlation structure between microbial variables. The data are over-dispersed with a distribution close to a negative binomial distribution [39, 40]. Inspired by [41], we simulated data from multivariate negative binomial distribution achieved with quantile–quantile transformation between multivariate normal and negative binomial distributions. To add treatment and batch effects, we used matrix factorization to simulate the mean for modelling negative binomial distribution as a matrix
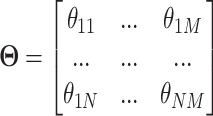 |
for 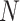 samples and
samples and 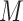 microbial variables as follows:
microbial variables as follows:
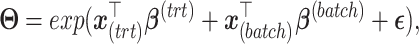 |
(5) |
where 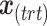 and
and 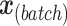 represent the design vectors of treatment and batch effects, respectively, for each sample.
represent the design vectors of treatment and batch effects, respectively, for each sample. 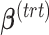 and
and 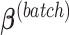 represent the regression coefficients of treatment and batch effects for each microbial variable, and
represent the regression coefficients of treatment and batch effects for each microbial variable, and 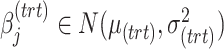 ,
, 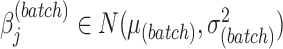 .
. 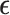 contains the random noise that is independent and identically distributed (i.i.d) and
contains the random noise that is independent and identically distributed (i.i.d) and 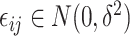 , in which
, in which 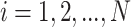 samples,
samples, 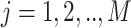 variables.
variables.
The probability matrix
 |
for modelling negative binomial distribution is calculated as
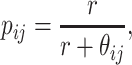 |
(6) |
where 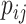 and
and 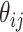 represent the probability of success in each trial and the mean for negative binomial distribution of sample
represent the probability of success in each trial and the mean for negative binomial distribution of sample 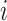 and microbial variable
and microbial variable 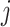 , and
, and 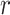 is the dispersion parameter representing the number of successes.
is the dispersion parameter representing the number of successes.
We then simulated a data matrix based on multivariate normal distribution with mean 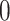 and correlation matrix
and correlation matrix 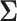 :
:
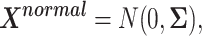 |
(7) |
where the correlation matrix 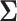 was simulated with the strategy adapted from [42] as follows: We first generated a lower triangular matrix
was simulated with the strategy adapted from [42] as follows: We first generated a lower triangular matrix 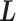 , in which the diagonal elements follow
, in which the diagonal elements follow 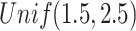 , and the other elements
, and the other elements 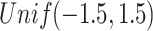 . We randomly set the elements outside the diagonal of
. We randomly set the elements outside the diagonal of 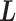 to zero with probability
to zero with probability 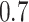 . A precision matrix, which is the inverse of covariance matrix, was created as
. A precision matrix, which is the inverse of covariance matrix, was created as 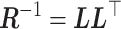 . The corresponding correlation matrix
. The corresponding correlation matrix 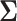 to
to 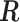 was then obtained. These parameters were set according to [42].
was then obtained. These parameters were set according to [42].
Thereafter we used Cumulative Distribution Function (CDF) to achieve quantile–quantile transformation as
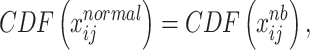 |
(8) |
where 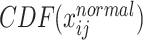 represents the cumulative probability of
represents the cumulative probability of 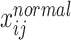 for sample
for sample 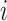 and variable
and variable 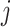 that belongs to matrix
that belongs to matrix 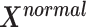 from multivariate normal distribution as Eq.(7).
from multivariate normal distribution as Eq.(7). 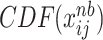 represents the cumulative probability of each
represents the cumulative probability of each 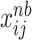 in matrix
in matrix 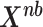 from negative binomial distribution as Eq.(9).
from negative binomial distribution as Eq.(9).
Based on the cumulative probability from Eq.(8), we can simulate a data matrix 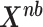 with multivariate negative binomial distribution:
with multivariate negative binomial distribution:
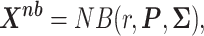 |
(9) |
where 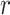 represents the dispersion parameter,
represents the dispersion parameter, 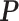 represents the probability matrix and
represents the probability matrix and 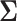 the correlation matrix explaining the dependence structure between microbial variables.
the correlation matrix explaining the dependence structure between microbial variables.
We simulated datasets with different parameters including amount of batch and treatment effects (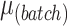 ,
, 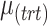 ) and variability among variables (
) and variability among variables (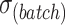 ,
, 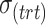 ), number of variables with batch and/or treatment effects (
), number of variables with batch and/or treatment effects (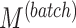 ,
, 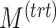 and
and 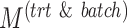 ), balanced and unbalanced batch
), balanced and unbalanced batch 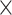 treatment designs, as summarized in Table 1. The microbial variables with treatment or batch effects were randomly indexed in the data with non-zero
treatment designs, as summarized in Table 1. The microbial variables with treatment or batch effects were randomly indexed in the data with non-zero 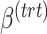 or
or 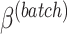 . The background noise
. The background noise 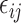 was randomly sampled from
was randomly sampled from 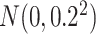 , reflecting real microbiome datasets.
, reflecting real microbiome datasets.
Table 1.
Summary of simulation scenarios (two batch groups). For a given choice of parameters reported in this table, each simulation was repeated 50 times. 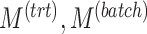 and
and 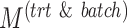 represent the number of variables with treatment, batch or both effects, respectively. Simulation 6 includes parameters likely to represent real data according to our experience in analysing microbiome datasets.
represent the number of variables with treatment, batch or both effects, respectively. Simulation 6 includes parameters likely to represent real data according to our experience in analysing microbiome datasets.
| Parameters |
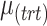
|
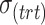
|
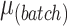
|
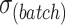
|
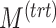
|
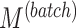
|
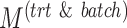
|
|---|---|---|---|---|---|---|---|
| Simulation 1 | 3 | 1 | 7 | {1,4,8} | 60 | 150 | 0 |
| Simulation 2 | {3,5,7} | 1 | 7 | 8 | 60 | 150 | 0 |
| Simulation 3 | 3 | {1,2,4} | 7 | 8 | 60 | 150 | 0 |
| Simulation 4 | 3 | 2 | 7 | 8 | {30,60,100,150} | 150 | 0 |
| Simulation 5 | 3 | 2 | 7 | 8 | 60 | {30,60,100,150} | 0 |
| Simulation 6 | 3 | 2 | 7 | 8 | 60 | 150 | {0,18,30,42,60} |
We also simulated datasets with different number of batch groups:
(1) Two batch groups: Each dataset included 300 variables and 40 samples grouped according to two treatments (trt1 and trt2) and two batches (batch1 and batch2). The balanced batch
 treatment experimental design included 10 samples from two batches, respectively, in each treatment group. The unbalanced design included 4 and 16 samples from batch1 and batch2, respectively, in trt1, 16 and 4 samples from batch1 and batch2 in trt2 (see Table 2).
treatment experimental design included 10 samples from two batches, respectively, in each treatment group. The unbalanced design included 4 and 16 samples from batch1 and batch2, respectively, in trt1, 16 and 4 samples from batch1 and batch2 in trt2 (see Table 2).(2) Three batch groups: Each dataset included 300 variables and 36 samples grouped according to two treatments (trt1 and trt2) and three batches (batch1, batch2 and batch3). The balanced batch
 treatment experimental design included six samples from three batches, respectively, in each treatment group. The unbalanced design included 2, 10 and 2 samples from batch1, batch2 and batch3, respectively, in trt1, 10, 2 and 10 samples from batch1, batch2 and batch3 in trt2 (see Table 3).
treatment experimental design included six samples from three batches, respectively, in each treatment group. The unbalanced design included 2, 10 and 2 samples from batch1, batch2 and batch3, respectively, in trt1, 10, 2 and 10 samples from batch1, batch2 and batch3 in trt2 (see Table 3).
Table 2.
Unbalanced batch  treatment design in the simulation study for two batch groups
treatment design in the simulation study for two batch groups
| Trt1 | Trt2 | |
|---|---|---|
| Batch1 | 4 | 16 |
| Batch2 | 16 | 4 |
Table 3.
Unbalanced batch 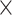 treatment design in the simulation study for three batch groups
treatment design in the simulation study for three batch groups
| Trt1 | Trt2 | |
|---|---|---|
| Batch1 | 2 | 10 |
| Batch2 | 10 | 2 |
| Batch3 | 2 | 10 |
In addition, we simulated a ground-truth dataset that only included treatment effects and background noise without batch effects to evaluate batch effect correction methods.
Our simulations generate over-dispersed count data with batch and treatment effects as well as correlation structure among variables, but without any compositional structure. We therefore only applied natural log transformation to the simulated data prior to analysis.
In these simulation scenarios, for PLSDA-batch we set 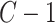 (or
(or  ) components associated with treatment (or batch) effects (where
) components associated with treatment (or batch) effects (where 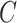 and
and 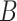 represent the total number of treatment and batch groups respectively) as
represent the total number of treatment and batch groups respectively) as 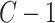 (
( ) components are likely to explain 100% variance in
) components are likely to explain 100% variance in 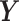 . The number of variables with a true treatment effect (
. The number of variables with a true treatment effect (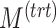 ) is set as the optimal number to select on each treatment component in sPLSDA-batch.
) is set as the optimal number to select on each treatment component in sPLSDA-batch.
Case studies
We analysed three 16S rRNA amplicon datasets at the operational taxonomic unit (OTU). The count data were filtered to alleviate sparsity and transformed with Centered Log Ratio (CLR) transformation [43]. CLR is a pragmatic way to handle both uneven library sizes and compositional structure in real data [37]. It also helps reducing skewness in the data.
Sponge A. aerophoba. This study investigated the relationship between metabolite concentration and microbial abundance on specific sponge tissues [44]. The dataset includes the relative abundance of 24 OTUs and 32 samples collected from two tissue types (Ectosome versus Choanosome) and processed on two separate denaturing gradient gels in electrophoresis. The tissue variation is the effect of interest, while the gel variation is the batch effect. This study includes a batch effect with similar variation to the treatment effect, and a completely balanced batch x treatment design. The sponge study enables us to assess the efficacy of batch effect correction methods in such circumstance.
Anaerobic digestion. This study explored the microbial indicators that could improve the efficacy of anaerobic digestion (AD) bioprocess and prevent its failure [45]. The dataset includes 231 OTUs and 75 samples treated with two different ranges of phenol concentration (effects of interest). These samples were processed at five different dates corresponding to batch effects. This study includes a strong batch effect compared with the treatment effect, with an approximately balanced batch x treatment design. The AD dataset enables us to assess whether batch effect correction methods are able to remove sufficient batch variation in this case.
High fat high sugar diet. This study aimed to investigate the effect of high fat high sugar (HFHS) diet on the mouse microbiome [37]. This dataset includes 515 OTUs and 149 samples collected at day 1, 4 and 7 from the mice treated with two types of diets (HFHS versus normal). The diet variation is the treatment effect, while the day variation constitutes a potential batch effect, which is actually weak. The HFHS study enables us to assess whether batch effect correction methods are able to preserve treatment variation when batch effects are small.
For the PLSDA-batch analyses, we chose the number of components that explained 100% variance in 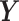 associated with either treatment or batch effects (Sponge data: one treatment component, one batch component; AD data: one treatment component, four batch components and HFHS data: one treatment component, two batch components). For sPLSDA-batch, we chose the number of variables to select on each treatment component that yielded the lowest BER from repeated cross-validation with four folds and 50 repeats (Sponge data: one variable; AD data: 100 variables and HFHS data: two variables).
associated with either treatment or batch effects (Sponge data: one treatment component, one batch component; AD data: one treatment component, four batch components and HFHS data: one treatment component, two batch components). For sPLSDA-batch, we chose the number of variables to select on each treatment component that yielded the lowest BER from repeated cross-validation with four folds and 50 repeats (Sponge data: one variable; AD data: 100 variables and HFHS data: two variables).
Benchmarking and assessment of batch effect removal
We compared our approaches with removeBatchEffect, ComBat and SVA. These methods are univariate and were originally developed for gene expression data from microarray or RNA-sequencing. They have been used extensively in microbiome studies [30–32, 46, 47] even though they would require further developments to be adapted to the inherent characteristics of microbiome data. These methods’ limitations include the inability to deal with non-Gaussian distribution, small sample sizes and dependence between microbial variables. Similar to the aim of our proposed methods, RemoveBatchEffect and ComBat correct for batch effects to generate batch effect-free data for downstream analysis, while SVA accounts for batch effects. Both our approaches and SVA attempt to preserve treatment variation prior to batch effect management to avoid information loss, but the algorithms used to achieve this purpose differ. However, SVA estimates and accounts for unknown batch effects, which may result in overfitting the data, compared with our approaches. Further details on these methods are described in the Supplemental Section S1. We used a wide range of performance measures to evaluate whether these methods are effective in managing batch effects while preserving treatment effects. These include classical accuracy measures used in simulation studies where we know the ground-truth, that is, we know which variables include batch and/or treatment effects [16], as well as multivariate and univariate approaches to measure the proportion of variance explained by batch and treatment effects after batch effect removal.
Accuracy measures (simulation study only)
We identified variables with a true treatment effect after correcting or accounting for batch effects using two approaches:
(1) Univariate one-way analysis of variance ANOVA) [48] to identify differentially abundant taxa between treatment groups (Benjamini–Hochberg adjusted P-value
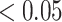 ) followed by accuracy measures described below,
) followed by accuracy measures described below,(2) Multivariate sparse PLSDA to identify taxa that discriminate treatment groups followed by Area Under the Curve of Receiver Operating Characteristics (AUC-ROC).
We measured the accuracy of the selected variables from one-way ANOVA using Precision (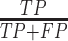 ), Recall (
), Recall (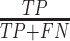 ) and
) and 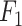 score (
score (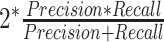 ), where
), where 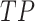 is the number of true positives—the variables assigned with treatment effects in the simulation and correctly identified;
is the number of true positives—the variables assigned with treatment effects in the simulation and correctly identified; 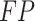 the number of false positives—the variables without treatment effects but wrongly identified;
the number of false positives—the variables without treatment effects but wrongly identified; 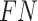 the number of false negatives—the variables with treatment effects that were not identified. A high precision indicates an accurate model with a low number of false positives, while a high recall indicates a sensitive model with a low number of false negatives. The
the number of false negatives—the variables with treatment effects that were not identified. A high precision indicates an accurate model with a low number of false positives, while a high recall indicates a sensitive model with a low number of false negatives. The 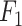 score balances both precision and recall, with a high score indicating a model with good accuracy and sensitivity.
score balances both precision and recall, with a high score indicating a model with good accuracy and sensitivity.
We measured the accuracy of the selected variables from sPLSDA using AUC-ROC. As SVA does not generate batch-effect-corrected data, we only considered the Precision, Recall and 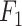 score for this approach.
score for this approach.
Proportion of explained variance across all variables
We used the multivariate method partial redundancy analysis (pRDA) in the batch-effect-corrected data to calculate the proportion of variance explained by treatment, batch effects and, most importantly, their intersection [6, 49]. The intersectional variance quantifies the unbalance in the batch 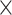 treatment design. A null value indicates a completely balanced design.
treatment design. A null value indicates a completely balanced design.
Proportion of explained variance for each variable
We used the 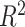 value estimated with one-way ANOVA to calculate the proportion of variance explained by treatment or batch effects for each variable. The
value estimated with one-way ANOVA to calculate the proportion of variance explained by treatment or batch effects for each variable. The 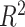 values with either treatment or batch effects were then visualized with boxplots. We also considered the sum of all the
values with either treatment or batch effects were then visualized with boxplots. We also considered the sum of all the 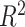 values to compare the methods globally.
values to compare the methods globally.
Principal Component Analysis (case studies only)
We investigated the variance structure of the data before and after batch effect correction using PCA. If batch effects account for the largest proportion of variance in the data, we expect a separation of the samples from different batches on the first component [6].
Alignment scores (case studies only)
We used the alignment score proposed for single-cell RNA-seq datasets integration [50]. We extended the approach that was originally developed based on canonical correlation analysis for PCA. This score complements the qualitative results from PCA to evaluate the degree of mixing samples from different batches in the batch-effect-corrected data. The alignment score ranges from 0 to 1 (poor to excellent mixing samples among the different batches). We first perform a PCA on a given batch-effect-corrected matrix to calculate a sample dissimilarity matrix based on the principal components that explained at least 95% of the total variance. Based on this dissimilarity matrix, the alignment score is defined as
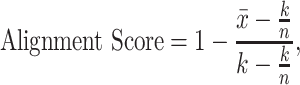 |
(10) |
where 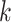 represents the number of nearest neighbours and
represents the number of nearest neighbours and 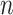 represents the sample size.
represents the sample size. 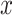 is the number of each sample’s
is the number of each sample’s 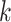 nearest neighbours that belong to the same batch and
nearest neighbours that belong to the same batch and 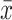 represents the average of all
represents the average of all 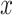 . In our case studies, we chose
. In our case studies, we chose 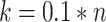 , a value deemed reasonable for the sample size of our data.
, a value deemed reasonable for the sample size of our data.
Note that this score relies on PCA projection to calculate the nearest neighbours. It is only relevant to compare several PCA dissimilarity matrices (resulting from the batch-effect-corrected matrices with different methods) where the samples have similar sample distribution in their PCA projection.
Results
We benchmarked our three PLSDA-batch methods with removeBatchEffect, ComBat and SVA on the simulated datasets, then against the former two on the three case studies.
Simulation studies
We first describe the results from a single simulation scenario with two batch groups where parameters were representative of real data, namely, 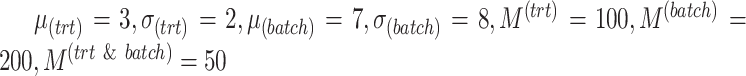 . The results for the other scenarios are summarized in Supplemental Figures S1–S6.
. The results for the other scenarios are summarized in Supplemental Figures S1–S6.
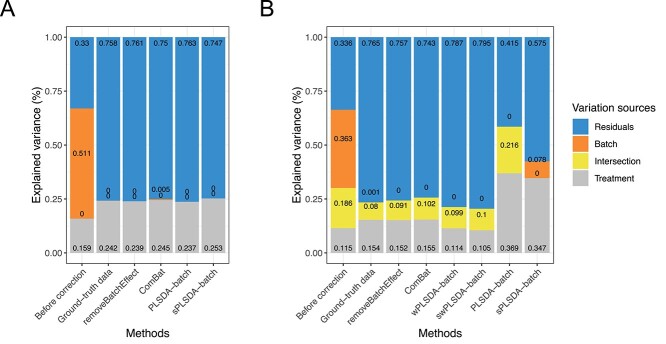
pRDA assessment
Efficient batch effect correction methods should generate data with a null proportion of variance explained by batch effects, and a proportion of variance explained by treatment that is larger compared with the original data, as shown in Figure 2A original data and ground-truth data.
Figure 2.
Simulation studies (two batch groups): comparison of explained variance before and after batch effect correction for (A) balanced and (B) unbalanced batch 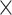 treatment designs. The method pRDA estimated the proportion of variance explained by (from top to bottom) residuals, batch effects, intersection of batch and treatment effects and treatment effects. All methods performed equally well in removing batch variance for a balanced design except ComBat, while in an unbalanced design, our weighted variants wPLSDA-batch and swPLSDA-batch performed better than their unweighted counterparts.
treatment designs. The method pRDA estimated the proportion of variance explained by (from top to bottom) residuals, batch effects, intersection of batch and treatment effects and treatment effects. All methods performed equally well in removing batch variance for a balanced design except ComBat, while in an unbalanced design, our weighted variants wPLSDA-batch and swPLSDA-batch performed better than their unweighted counterparts.
For a balanced batch 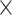 treatment design, we observed no intersection shared between treatment and batch variance, as expected. All methods successfully removed batch variance and preserved (or slightly increased) treatment variance (sPLSDA-batch), with the exception of ComBat where a very small amount of batch variance remained.
treatment design, we observed no intersection shared between treatment and batch variance, as expected. All methods successfully removed batch variance and preserved (or slightly increased) treatment variance (sPLSDA-batch), with the exception of ComBat where a very small amount of batch variance remained.
For a strong unbalanced batch 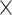 treatment design (Figure 2B), we observed the presence of intersectional variance explained by both batch and treatment effects, as expected. This source of variance is also present in the ground-truth data but should be smaller compared with the uncorrected data. Both unweighted PLSDA-batch and sPLSDA-batch performed poorly for such design—for PLSDA-batch the intersectional variance increased, while for sPLSDA-batch the batch variance was not entirely removed. The other methods were successful in removing batch variance. removeBatchEffect and ComBat explained a proportion of variance by treatment similar to the ground-truth data, while wPLSDA-batch and swPLSDA-batch explained slightly less treatment variance.
treatment design (Figure 2B), we observed the presence of intersectional variance explained by both batch and treatment effects, as expected. This source of variance is also present in the ground-truth data but should be smaller compared with the uncorrected data. Both unweighted PLSDA-batch and sPLSDA-batch performed poorly for such design—for PLSDA-batch the intersectional variance increased, while for sPLSDA-batch the batch variance was not entirely removed. The other methods were successful in removing batch variance. removeBatchEffect and ComBat explained a proportion of variance by treatment similar to the ground-truth data, while wPLSDA-batch and swPLSDA-batch explained slightly less treatment variance.
 assessment
assessment
We estimated the proportion of variance explained by treatment and batch effects for each variable using the 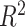 value.
value.
In the balanced batch  treatment design (Figure 3A), removeBatchEffect and PLSDA-batch had the best performance, with results very similar to the ground-truth data. ComBat retained more batch variance of variables with batch effects only, and with both batch and treatment effects, indicating an incomplete removal of batch effects. This result is in agreement with the overall pRDA evaluation described earlier. For sPLSDA-batch, variables with no treatment effect (batch effects only) included a slight amount of (spurious) treatment variance. This was also observed in pRDA evaluation. However, sPLSDA-batch performed as well as PLSDA-batch when the simulated data did not include variables with both batch and treatment effects.
treatment design (Figure 3A), removeBatchEffect and PLSDA-batch had the best performance, with results very similar to the ground-truth data. ComBat retained more batch variance of variables with batch effects only, and with both batch and treatment effects, indicating an incomplete removal of batch effects. This result is in agreement with the overall pRDA evaluation described earlier. For sPLSDA-batch, variables with no treatment effect (batch effects only) included a slight amount of (spurious) treatment variance. This was also observed in pRDA evaluation. However, sPLSDA-batch performed as well as PLSDA-batch when the simulated data did not include variables with both batch and treatment effects.
Figure 3.

Simulation studies (two batch groups): 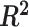 values for each microbial variable before and after batch effect correction for (A) balanced and (B) unbalanced batch
values for each microbial variable before and after batch effect correction for (A) balanced and (B) unbalanced batch  treatment designs. Each box represents a summary of
treatment designs. Each box represents a summary of 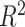 values for variables simulated with the associated effects (batch or/and treatment effects). Each
values for variables simulated with the associated effects (batch or/and treatment effects). Each 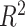 value was fitted for each variable from a one-way ANOVA with a treatment effect or batch effect as covariate (x-axis). The colours indicate the effects assigned to each variable. In both designs, ComBat did not remove enough batch variation. For the balanced design, sPLSDA-batch generated slightly spurious treatment variation for the variables with batch effects only. For the unbalanced design, wPLSDA-batch and swPLSDA-batch generated data with less treatment variation for the variables with both treatment and batch effects compared with the ground-truth data.
value was fitted for each variable from a one-way ANOVA with a treatment effect or batch effect as covariate (x-axis). The colours indicate the effects assigned to each variable. In both designs, ComBat did not remove enough batch variation. For the balanced design, sPLSDA-batch generated slightly spurious treatment variation for the variables with batch effects only. For the unbalanced design, wPLSDA-batch and swPLSDA-batch generated data with less treatment variation for the variables with both treatment and batch effects compared with the ground-truth data.
We observed similar performance for removeBatchEffect and ComBat for the unbalanced design (Figure 3B). With wPLSDA-batch and swPLSDA-batch, variables with both treatment and batch effects explained less treatment variance after correction, compared with the ground-truth data. However, for the other variables, wPLSDA-batch and its sparse version performed as similar as the ground-truth data.
The sum of all the 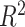 values showed similar results (Supplemental Figure S7).
values showed similar results (Supplemental Figure S7).
Accuracy measures
The results from the accuracy measures combined with variable selection highlight the importance of removing batch effects as both F1 score and AUC largely improved compared with the original data (Table 4).
Table 4.
Simulation studies (two batch groups): summary of accuracy measurements before and after batch effect correction. The proportion of correctly identified microbial variables with a true treatment effect was assessed with Precision, Recall, F1 score (using one-way ANOVA as variable selection procedure) and AUC (using sPLSDA as variable selection procedure). Each value is the mean (or standard deviation) over 50 repeats.
| Before correction | ground-truth data | SVA | removeBatchEffect | ComBat | PLSDA-batch | sPLSDA-batch | ||
|---|---|---|---|---|---|---|---|---|
| Balanced | Precision | 0.984 (0.04) | 0.952 (0.08) | 0.957 (0.06) | 0.950 (0.09) | 0.952 (0.08) | 0.952 (0.08) | 0.807 (0.11) |
| Recall | 0.674 (0.03) | 0.900 (0.03) | 0.934 (0.03) | 0.910 (0.03) | 0.911 (0.03) | 0.910 (0.03) | 0.910 (0.03) | |
| F1 | 0.799 (0.02) | 0.923 (0.05) | 0.944 (0.04) | 0.927 (0.05) | 0.929 (0.05) | 0.929 (0.05) | 0.851 (0.06) | |
| AUC | 0.944 (0.02) | 0.964 (0.02) | / | 0.968 (0.02) | 0.968 (0.02) | 0.969 (0.01) | 0.954 (0.02) | |
| Before correction | ground-truth data | SVA | removeBatchEffect | ComBat | wPLSDA-batch | swPLSDA-batch | ||
| Unbalanced | Precision | 0.385 (0.01) | 0.973 (0.05) | 0.401 (0.02) | 0.901 (0.09) | 0.834 (0.08) | 0.943 (0.05) | 0.943 (0.05) |
| Recall | 0.825 (0.03) | 0.895 (0.03) | 0.918 (0.03) | 0.910 (0.03) | 0.919 (0.03) | 0.888 (0.03) | 0.862 (0.03) | |
| F1 | 0.525 (0.01) | 0.932 (0.03) | 0.558 (0.02) | 0.903 (0.05) | 0.873 (0.05) | 0.914 (0.03) | 0.900 (0.03) | |
| AUC | 0.704 (0.06) | 0.967 (0.02) | / | 0.963 (0.02) | 0.962 (0.01) | 0.965 (0.01) | 0.954 (0.02) |
In the balanced design, starting from the original data compared with the ground-truth data, selected variables had a higher precision, lower recall and lower AUC, indicating a smaller number of variables selected with an actual treatment effect. Combined with univariate one-way ANOVA, SVA performed best with the highest, and sometimes greater, accuracy measurements than the ground-truth data, as we discuss below. The other methods led to similar performance with the exception of sPLSDA-batch, which selected more false positives than the other methods. PLSDA-batch led to a slightly better AUC than the other methods.
In the unbalanced design, the precision of SVA is low and very similar to the original data, indicating that the performance of SVA heavily depends on the experimental design and is likely to overfit. This may explain the somewhat inflated results of SVA in the balanced design case. wPLSDA-batch performed best with results close to those from the ground-truth data.
We observed similar results but with higher resolution of these accuracy measures for the other simulation scenarios presented in Supplemental Figures S1–S6 and discussed in the Supplemental Section S3.1. For simulations with three batch groups (parameters 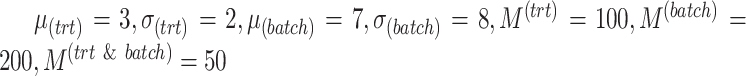 ), we also observed similar results as the two batch group cases (Supplemental Figures S8, S9 and S10 and Table S1).
), we also observed similar results as the two batch group cases (Supplemental Figures S8, S9 and S10 and Table S1).
Summary of the simulation results
Our extensive simulation studies showed that weighted PLSDA-batch was essential for an unbalanced batch 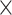 treatment design, compared with its unweighted counterpart. Our PLSDA-batch method preserved similar or slightly smaller proportion of treatment variance compared with the other batch effect correction methods, but achieved a higher F1 score and AUC especially in an unbalanced design. When there was no variables with both treatment and batch effects in the data, sPLSDA-batch- and PLSDA-batch-corrected data were close to the ground-truth data. However, when some variables included both these effects, sPLSDA-batch performed slightly worse than PLSDA-batch. Our results also suggested that SVA had a tendency to overfit the data, while ComBat was not able to completely remove batch variation. removeBatchEffect was not able to preserve enough treatment effects for accurate variable identification.
treatment design, compared with its unweighted counterpart. Our PLSDA-batch method preserved similar or slightly smaller proportion of treatment variance compared with the other batch effect correction methods, but achieved a higher F1 score and AUC especially in an unbalanced design. When there was no variables with both treatment and batch effects in the data, sPLSDA-batch- and PLSDA-batch-corrected data were close to the ground-truth data. However, when some variables included both these effects, sPLSDA-batch performed slightly worse than PLSDA-batch. Our results also suggested that SVA had a tendency to overfit the data, while ComBat was not able to completely remove batch variation. removeBatchEffect was not able to preserve enough treatment effects for accurate variable identification.
Case studies
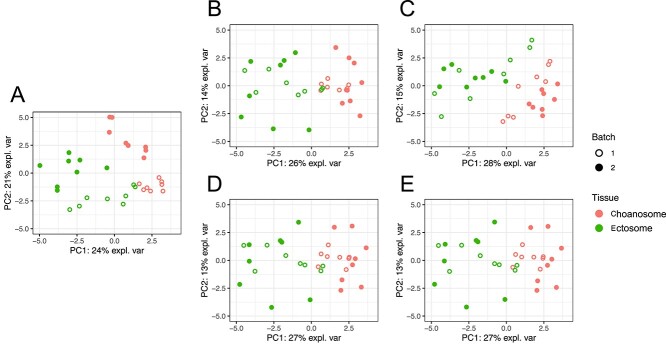
PCA
In the sponge data (Figure 4A), 24% of the total data variance was explained by the first principal component, which highlighted a strong difference of samples across different tissues (the effect of interest). The batch variation accounted for 21% of the total variance in the second component. Thus, in this study, batch effects are smaller than the treatment effects. After batch effect correction, the difference between batches became barely distinct (Figure 4B–E), except for ComBat-corrected data where a clear separation of the samples from two batches for the Choanosome tissue could still be observed. The variance explained by the first principal component that separated the different tissue types was increased in all of the corrected data, with PLSDA-batch and sPLSDA-batch resulting in the second highest proportion of variance (27%) next to ComBat (28%).
Figure 4.
PCA sample plots of the sponge data (A) before or after batch effect correction using (B) removeBatchEffect, (C) ComBat, (D) PLSDA-batch or (E) sPLSDA-batch. The colours represent the effect of interest (tissue types), and shapes the batch types. ComBat did not remove enough batch variation, as samples still present a batch separation within the cluster of Choanosome.
In the AD study (Supplemental Figure S11), batch variation was removed after correction from all methods. PLSDA-batch performed the best as the proportion of variance explained by the first component that was highly relevant to treatment variation was larger than the explained variance for any other method.
In the HFHS data, the PCA plot indicated that batch variation was only observed in one treatment group and was very weak (Supplemental Figure S12). After batch effect correction, the batch difference was removed and the proportion of variance explained by the first component (related to treatment effects) was slightly improved, indicating that treatment variation was still preserved. This case study shows that batch effect correction methods are still relevant when batch effects are very weak. However, sPLSDA-batch performed the worst with a loss of treatment variance, indicating this method is not appropriate to correct for very weak batch effects.
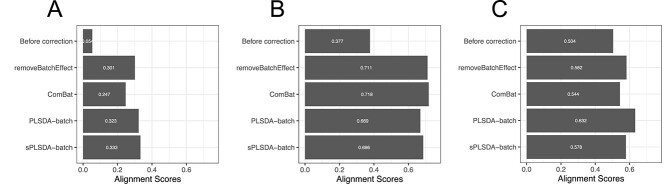
Alignment scores
The alignment scores complement the PCA results when batch effect removal is difficult to assess on PCA sample plots. In Figure 5, we observed that the samples across different batches were better mixed after batch effect correction with different methods compared with the original data.
Figure 5.
Comparison of alignment scores for (A) sponge data, (B) AD data and (C) HFHS data before and after batch effect correction using different methods. A large alignment score indicates that samples from different batches are well mixed based on the PCA dissimilarity matrix. The alignment scores between methods can only be compared when samples have similar sample distribution in their PCA projection, i.e. for sponge and HFHS data. In these two case studies, our method PLSDA-batch had a better performance than the univariate methods ComBat and removeBatchEffect.
In the sponge study, the data corrected using PLSDA-batch and sPLSDA-batch had higher alignment scores than using removeBatchEffect and ComBat, indicating a better performance in removing batch variation. The ComBat-corrected data had the lowest alignment score, which was consistent with PCA that the data still had residual batch variation remaining.
In the AD data, the alignment scores of the data corrected with PLSDA-batch and sPLSDA-batch led to a poorer performance than removeBatchEffect and ComBat. This may result from the difference in the PCA sample projections of the batch-effect-corrected matrices, as we discussed in the Methods section. The data corrected with removeBatchEffect and ComBat had a large variance in their PCA projection, while PLSDA-batch- and sPLSDA-batch-corrected data had a small variance. A small variance projection results in a small alignment score, as it is easy to locate the samples from the same batch as nearest neighbours. In fact, pRDA presented below quantitatively confirmed that both PLSDA-batch and sPLSDA-batch entirely removed the batch variance.
For the weak batch effect in the HFHS data, PLSDA-batch performed best with the highest alignment score compared with the other methods. We did not face the same issue as the AD data as the sample distribution in projection was similar across all datasets.
pRDA assessment
We next focused on estimating the proportion of variance explained by treatment and batch effects globally for the batch-effect-corrected data using pRDA.
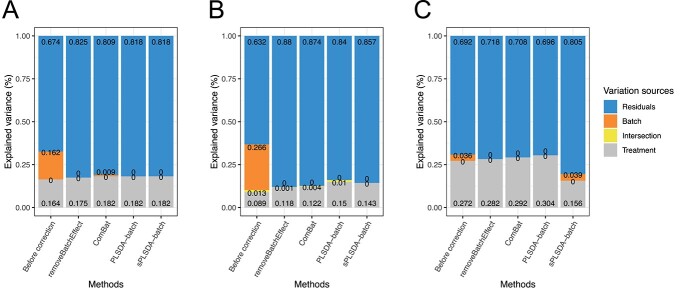
In the sponge data (Figure 6A), the different methods preserved similar proportion of treatment variance (removeBatcheffect: 17.5%, ComBat: 18.2%, PLSDA-batch: 18.2%, sPLSDA-batch: 18.2%) and removed all batch variance, with the exception of ComBat that still retained 0.9% of batch variance.
Figure 6.
Explained variance before or after batch effect correction for (A) sponge data, (B) AD data and (C) HFHS data. In sponge data (A), ComBat-corrected-data still included batch associated variance. In AD data (B), sPLSDA-batch-corrected data included a higher treatment variance and lower intersectional variance compared with the data corrected from the other methods. In HFHS data with weak batch effects (C), PLSDA-batch-corrected data preserved the largest amount of treatment variance.
In the AD data (Figure 6B), we observed a small amount of intersectional variance (1.3%) due to the unbalanced batch  treatment design. As the intersection was small, unweighted PLSDA-batch and sPLSDA-batch were still applicable, and thus the weighted versions were not used. PLSDA-batch preserved the largest proportion of variance explained by treatment effects, and also the largest proportion of intersectional variance. sPLSDA-batch-corrected data led to a higher proportion of treatment variance than the two univariate methods. sPLSDA-batch is a shrinkage version of PLSDA-batch, thus the proportion of treatment variance preserved by sPLSDA-batch should be nearly the same as or slightly smaller than PLSDA-batch, as we observed for this study.
treatment design. As the intersection was small, unweighted PLSDA-batch and sPLSDA-batch were still applicable, and thus the weighted versions were not used. PLSDA-batch preserved the largest proportion of variance explained by treatment effects, and also the largest proportion of intersectional variance. sPLSDA-batch-corrected data led to a higher proportion of treatment variance than the two univariate methods. sPLSDA-batch is a shrinkage version of PLSDA-batch, thus the proportion of treatment variance preserved by sPLSDA-batch should be nearly the same as or slightly smaller than PLSDA-batch, as we observed for this study.
In the HFHS data where batch effects are weak, we detected 3.6% of the variance explained by batch effects (Figure 6C). PLSDA-batch performed the best as the corrected data preserved the highest proportion of treatment variance and a complete removal of batch variance. sPLSDA-batch performed the worst as the method did not remove sufficient batch variance and lost some treatment variance. This result is consistent with the previous results that sPLSDA-batch-corrected data had a lower alignment score (related to batch variation) and lower variance explained by the first PCA component (related to treatment variation) than the other methods.
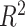 assessment
assessment
The 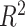 values representing the variance explained by batch or treatment effects for each variable estimated with one-way ANOVA are displayed in Figure 7 for the AD study. The corrected data from ComBat still included a few variables with a large proportion of batch variance. The overall sum of
values representing the variance explained by batch or treatment effects for each variable estimated with one-way ANOVA are displayed in Figure 7 for the AD study. The corrected data from ComBat still included a few variables with a large proportion of batch variance. The overall sum of 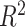 values indicated that removeBatchEffect removed slightly more batch variance (removeBatchEffect: 1.70, PLSDA-batch: 12.40, sPLSDA-batch: 9.25) but preserved less treatment variance (removeBatchEffect: 31.75, PLSDA-batch: 40.00, sPLSDA-batch: 36.22) than our proposed approaches (Supplemental Figure S13). We observed similar results with the sponge data (Supplemental Figures S14, S15). In the HFHS study, we did not observe any variables with a large proportion of batch variance in the ComBat corrected data (Supplemental Figure S16), but the total amount of treatment variance summed from all variables was smaller than with PLSDA-batch. We reached similar conclusions for remove batch-effect-corrected data (Supplemental Figure S17).
values indicated that removeBatchEffect removed slightly more batch variance (removeBatchEffect: 1.70, PLSDA-batch: 12.40, sPLSDA-batch: 9.25) but preserved less treatment variance (removeBatchEffect: 31.75, PLSDA-batch: 40.00, sPLSDA-batch: 36.22) than our proposed approaches (Supplemental Figure S13). We observed similar results with the sponge data (Supplemental Figures S14, S15). In the HFHS study, we did not observe any variables with a large proportion of batch variance in the ComBat corrected data (Supplemental Figure S16), but the total amount of treatment variance summed from all variables was smaller than with PLSDA-batch. We reached similar conclusions for remove batch-effect-corrected data (Supplemental Figure S17).
Figure 7.
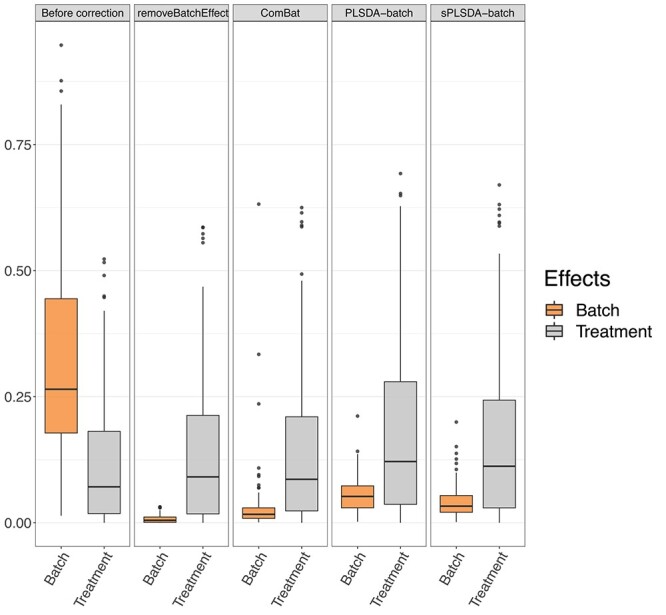
AD study:  values for each microbial variable before and after batch effect correction. Each box represents a summary of
values for each microbial variable before and after batch effect correction. Each box represents a summary of  values fitted for variables from a one-way ANOVA with a treatment effect or batch effect as covariate (x-axis). The colours indicate the fitted effects in ANOVA. The Combat-corrected data included some variables with a large proportion of batch variance (outliers). removeBatchEffect removed slightly more batch variance, but preserved less treatment variance than our proposed PLSDA-batch and sPLSDA-batch.
values fitted for variables from a one-way ANOVA with a treatment effect or batch effect as covariate (x-axis). The colours indicate the fitted effects in ANOVA. The Combat-corrected data included some variables with a large proportion of batch variance (outliers). removeBatchEffect removed slightly more batch variance, but preserved less treatment variance than our proposed PLSDA-batch and sPLSDA-batch.
Biological interpretation
We applied sPLSDA to select 20% of the total number of OTUs in the anaerobic digestion (46) and the HFHS diet (103) studies, but we excluded the sponge study from this analysis as it includes only a small number of OTUs. We then compared the OTU selections before and after batch effect correction with different methods.
Anaerobic digestion. When comparing the variable selections before and after batch effect correction, five OTUs were uniquely selected in the original uncorrected data and belonged to the family Spirochaetaceae (order Spirochaetales), Synergistaceae (order Synergistales) and three different families of the order Clostridiales. Both of Spirochaetaceae and Synergistaceae have been reported to be associated with methanogenesis. The former can ferment glucose to acetate and ethanol which are utilized by methanogenic communities [51], while the latter is associated with hydrogenotrophic methanogens in a syntrophic manner [52]. Members of the order Clostridiales have been recognized to hydrolyse a variety of polysaccharides by different mechanisms [53]. After batch effect correction, we observed an overlap of 32 out of 46 OTUs (69.6%) that were selected from the data uncorreted and corrected with different methods, showing a good agreement among all methods. We also identified 17 OTUs that were only selected from the corrected data compared with the uncorrected data. Among these OTUs, one from the family Christensenellaceae was only selected with removeBatchEffect, while one from the family Peptococcaceae and two from the family Synergistaceae were selected with both removeBatchEffect and ComBat. The family Christensenellaceae includes saccharolytic fermentative anaerobes [54], while members of the family Peptococcaceae are acetogen/syntrophic bacteria in natural and methanogenic environments [55]. Another eight OTUs among these 17 were only selected with PLSDA-batch or/and sPLSDA-batch. The families of these eight taxa included Ruminococcaceae (3), Syntrophomonadaceae (1), Peptococcaceae (1), Clostridiales vadinBB60 group (1) from the order Clostridiales and Thermoplasmatales Incertae Sedis (1) from the order Thermoplasmatales and Marinilabiaceae (1) from the order Bacteroidales. Ruminococcaceae can decompose a wide variety of recalcitrant substrates like cellulose and hemicellulose to produce small molecules of acids, such as acetic acid and butyric acid involved in the process of anaerobic digestion [56, 57]. The family Syntrophomonadaceae is responsible of the acetate production from butyrate and in a syntrophic relationship with hydrogenotrophic methanogens [58]. Clostridiales vadinBB60 group plays an important role in carbohydrate fermentation and short-chain fatty acid production [59]. Thermoplasmatales Incertae Sedis includes methanogens [60]. Marinilabiaceae can ferment various substrates with the production of propionate, acetate, and succinate [61]. The rest five OTUs were selected with removeBatchEffect, ComBat, sPLSDA-batch and/or PLSDA-batch. Four out of the five were from the order Clostridiales (family Christensenellaceae (2), Ruminococcaceae (1) and Family XIV (1)), and only one was from the family Marinilabiaceae of the order Bacteroidales. To summarize, from the data corrected with our PLSDA-batch and sPLSDA-batch approaches, we identified more taxa within the order Clostridiales than with removeBatchEffect and ComBat. Our approaches selected a larger number of unique OTUs compared with the two univariate methods, and these OTUs are highly relevant to the AD process. This study also shows that our approaches were successful at preserving treatment variation for the data that included a strong batch effect.
(High fat high sugar diet). For this study, we did not include the selection from sPLSDA-batch-corrected data, which did not preserve enough treatment variation inferred from previous assessments. When comparing the original data with the batch-effect-corrected data, three OTUs selected were from the family S24-7 (order Bacteroidales), family Lachnospiraceae and Ruminococcaceae (order Clostridiales), respectively, that were not selected after batch effect correction. The family S24-7 is closely related to carbohydrate metabolism [62], while the family Lachnospiraceae plays a key role in the metabolism of undigested carbohydrates [63], and Ruminococcaceae can decompose a wide variety of recalcitrant substrates like cellulose and hemicellulose to short-chain fatty acids, including butyrate [56, 57]. Among all different datasets, 91 out of 103 OTUs (88.3%) were commonly selected. We identified 12 OTUs that were uniquely selected from the data corrected with particular methods, including one OTU from the family Lachnospiraceae selected from the ComBat. Another six OTUs were only selected from our PLSDA-batch approach and belonged to the family Erysipelotrichaceae (2) (order Erysipelotrichales), Desulfovibrionaceae (2) (order Desulfovibrionales), Coriobacteriaceae (1) (order Coriobacteriales) and an unknown family (1) of order Clostridiales. The family Erysipelotrichaceae is highly correlated with cholesterol metabolism [64], while the family Desulfovibrionaceae is positively correlated with glucose and lipid metabolism [65] and the family Coriobacteriaceae increases the level of short-chain fatty acids including acetic acid, propionic acid and butyric acid and is related to impaired glucose metabolism [66]. The rest five out of these 12 OTUs selected with ComBat, PLSDA-batch and/or removeBatchEffect were from the family S24-7 (1) (order Bacteroidales), Lachnospiraceae and three unknown families from the order Clostridiales. To summarize, in the HFHS data that include weak batch effects, over 88% of the selected microbial variables from different batch-effect-corrected data were in common with the original uncorrected data. However, from the data after our PLSDA-batch correction, we selected additional OTUs highly relevant to the HFHS diet compared with the other datasets including removeBatchEffect, ComBat corrected data and the original data.
Discussion
In this article, we introduced PLSDA-batch to correct for batch effects in a multivariate fashion while preserving treatment variation. We also proposed two additional variant methods weighted PLSDA-batch that includes group size weight to handle unbalanced batch  treatment designs, and sparse PLSDA-batch that includes variable selection when estimating treatment components. In this article we referred to microbiome data as microbial metataxonomic data and analysed datasets at the OTU level. However, our methods are also suitable for the metagenomic data and datasets considered at any other level of taxonomy.
treatment designs, and sparse PLSDA-batch that includes variable selection when estimating treatment components. In this article we referred to microbiome data as microbial metataxonomic data and analysed datasets at the OTU level. However, our methods are also suitable for the metagenomic data and datasets considered at any other level of taxonomy.
We compared our proposed methods with existing removeBatchEffect, ComBat and SVA. The former two are univariate methods that correct for known batch effects, while SVA is a hybrid method that estimates unknown batch effects with a multivariate strategy and accounts for the estimated batch effects in a univariate manner. All methods assume each variable follows a Gaussian distribution and do not consider the dependent structure between variables. In addition, ComBat assumes that all variables are affected by batch effects in a systematic manner. This assumption does not hold true in practice [6]. Our approach PLSDA-batch has a relaxed assumption about data distribution and thus is more suitable for microbiome data, even after CLR transformation. The multivariate nature of our approach also enables to model the correlation structure between variables and handle non-systematic batch effects.
Our simulation studies showed that SVA had a tendency to overfit the data; ComBat was not able to completely remove batch variation and removeBatchEffect was not able to preserve enough treatment effects for accurate variable identification.
Across most simulation scenarios, PLSDA-batch led to a high performance in terms of F1 score and AUC, especially in an unbalanced design where weighted PLSDA-batch was preferable to its unweighted version. PLSDA-batch performed better than sPLSDA-batch in the case where variables had both treatment and batch effects. Our simulations under a negative binomial distribution did not emphasize on the performance of sPLSDA-batch compared with PLSDA-batch, as sPLSDA-batch lacked the appropriate fit in component estimation and removed excessive amount of batch variation, resulting in spurious treatment variation. Further simulations (Supplemental Figures S18–S25) under a Gaussian distribution demonstrated a better performance of sPLSDA-batch. This was also reflected in the case studies, suggesting that the count data after CLR transformation may approximate a Gaussian distribution. The distribution of real microbiome data is often debatable, thus may not be strictly negative binomial. Some studies have discussed that microbiome data may follow instead a zero-inflated lognormal distribution [67], which was confirmed to some extent in our results.
In the case studies of sponge and anaerobic digestion, PLSDA-batch and sPLSDA-batch performed similarly. These two studies include a strong batch effect, and all performance criteria we used indicated that PLSDA-batch and sPLSDA-batch outperformed ComBat, which removed an insufficient amount of batch variation (sponge and AD data) and preserved insufficient treatment variation (AD data). The data corrected with removeBatchEffect resulted in a smaller proportion of treatment variance compared with our methods. When performing variable selection on the data corrected for batch effects with our approaches, we selected a larger number of unique OTUs relevant to anaerobic digestion than with the other batch effect correction approaches. Regarding the HFHS data that include a weak batch effect, the data corrected with sPLSDA-batch lost certain amount of treatment variance as it did not estimate the treatment associated component well, indicating sPLSDA-batch is not suitable for weak batch effects. We observed a large overlap of OTUs when performing variable selection before and after batch effect correction by the different methods, but from the data corrected by PLSDA-batch we selected additional OTUs highly relevant to HFHS diet, suggesting that batch effect correction is still beneficial when batch effects are weak. Due to the limited resolution of taxonomic information with 16S rRNA sequencing, our biological interpretation was limited to family level. Deeper resolution obtained with whole genome sequencing would give more insight into the biological meaning of the additional OTUs that were selected with our approaches.
Based on our results, we propose the following guidelines to choose the best method that achieves maximum batch effect removal: (1) when the proportion of treatment variance after batch effect correction is larger than from the original data, it is best to choose the method that preserves a smaller treatment variance that is likely to be not spurious; (2) on the opposite, when the proportion of treatment variance after correction is smaller than from the original data, it is best to choose the method that preserves the larger treatment variance.
We have identified several limitations in our proposed framework that will warrant further investigations. Our methods currently require pre-defined batch group information. If the batch information is unknown, we recommend assigning the samples to batches identified with PCA or any clustering methods. While wPLSDA-batch showed a good performance, the presence of an interaction effect between batch and treatment on microbial variables still remains a challenge, most likely because this interaction is non-linear. When batch and treatment effects are collinear, only methods which account for batch effects but do not correct for them would be suitable, such as linear regression [6]. In addition, PLSDA methods are linear techniques, where both explanatory and response components are constructed based on a linear combination of variables, and where we model the linear relationship between components. It is highly possible that variables in microbiome data interact non-linearly. As such, non-linear approaches based on PLS kernel could also be expanded in our framework [68].
Conclusions
Our multivariate approach PLSDA-batch aims to estimate and remove batch variation while preserving treatment variation for microbiome data. The batch-effect-corrected data can then be used as input in any downstream analyses, such as dimension reduction, visualization, clustering or variable selection. In our study, we showed that when some variables included both treatment and batch effects or when batch effects were very weak, PLSDA-batch was more suitable than the sparse version. For unbalanced batch  treatment designs, the weighted PLSDA-batch led to superior results to disentangle correlated batch and treatment effects. On both simulation and case studies, our methods resulted in a superior performance compared with existing methods based on both visual and quantitative assessments. The taxa selected in the downstream analysis were biologically relevant. Our work is an important step to raise awareness for managing batch effects and ensure reliable downstream statistical analyses to ultimately facilitate microbial studies.
treatment designs, the weighted PLSDA-batch led to superior results to disentangle correlated batch and treatment effects. On both simulation and case studies, our methods resulted in a superior performance compared with existing methods based on both visual and quantitative assessments. The taxa selected in the downstream analysis were biologically relevant. Our work is an important step to raise awareness for managing batch effects and ensure reliable downstream statistical analyses to ultimately facilitate microbial studies.
Key Points
We developed a set of three multivariate and non-parametric batch effect correction methods for microbiome data to estimate and remove batch variation while preserving treatment variation.
The methods were specifically designed to handle unbalanced batch x treatment designs (weighted PLSDA-batch) and to avoid overfitting in components estimation with variable selection (sparse PLSDA-batch).
The application of our methods to both simulated and real case studies showed competitive performance to existing methods, especially for unbalanced batch x treatment designs.
Various visual and numerical assessments for batch effect detection and removal are available.
Data availability
The R package ‘PLSDAbatch’ along with the case study datasets, simulations and all analyses are fully reproducible and available on GitHub: https://github.com/EvaYiwenWang/PLSDAbatch.
Supplementary Material
Acknowledgments
We thank A/Prof Olivier Chapleur from INRAE for his help in interpreting the variable selection results from the AD data.
Author Biographies
Yiwen Wang is currently a research fellow at the Shenzhen Branch, Guangdong Laboratory of Lingnan Modern Agriculture, Genome Analysis Laboratory of the Ministry of Agriculture and Rural Affairs, Agricultural Genomics Institute at Shenzhen, Chinese Academy of Agricultural Sciences. She graduated with a Ph.D degree from Melbourne Integrative Genomics, School of Mathematics and Statistics, University of Melbourne. Her research focuses on developing methods for microbiome data analysis.
Kim-Anh Lê Cao is a professor in statistical genomics at the University of Melbourne. Her lab focuses on the development of computational and integrative multivariate methods for feature selection in biological data, with a particular interest for microbiome and multi-omics studies.
Contributor Information
Yiwen Wang, Shenzhen Branch, Guangdong Laboratory of Lingnan Modern Agriculture, Genome Analysis Laboratory of the Ministry of Agriculture and Rural Affairs, Agricultural Genomics Institute at Shenzhen, Chinese Academy of Agricultural Sciences, 97 Buxin Rd, Shenzhen, 518000, Guangdong, China; Melbourne Integrative Genomics, School of Mathematics and Statistics, The University of Melbourne, 30 Royal Parade, Melbourne, 3052, VIC, Australia.
Kim-Anh Lê Cao, Melbourne Integrative Genomics, School of Mathematics and Statistics, The University of Melbourne, 30 Royal Parade, Melbourne, 3052, VIC, Australia.
Funding
This work was supported by the China Scholarship Council - University of Melbourne PhD Scholarship [201707510003], the fellowship of China Postdoctoral Science Foundation [2022TQ0370] and the Young Scientists Fund of the National Natural Science Foundation of China [32200077] to Y.W; and the National Health and Medical Research Council (NHMRC) Career Development fellowship [GNT1159458] to K-A.LC.
Authors’ contributions
YW developed, implemented and benchmarked the methods, and wrote the manuscript. K-ALC supervised YW and edited the manuscript.
Abbreviations
RUV: Remove Unwanted Variation SVA: Surrogate Variable Analysis PLS: Partial Least Squares, a.k.a Projection to Latent Structures PLSDA: Partial Least Squares Discriminant Analysis sPLSDA: sparse Partial Least Squares Discriminant Analysis PLSDA-batch: Partial Least Squares Discriminant Analysis for batch effect correction PCA: Principal Component Analysis wPLSDA-batch: weighted PLSDA-batch sPLSDA-batch: sparse PLSDA-batch BER: Balanced classification Error Rate CLR: Centered Log Ratio OTU: Operational Taxonomic Unit AD: Anaerobic Digestion HFHS: High Fat High Sugar diet pRDA: partial Redundancy Analysis
References
- 1. Zuo T, Ng SC. The gut microbiota in the pathogenesis and therapeutics of inflammatory bowel disease. Front Microbiol 2018;9:2247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Sharma S, Tripathi P. Gut microbiome and type 2 diabetes: where we are and where to go? J Nutr Biochem 2019;63:101–8. [DOI] [PubMed] [Google Scholar]
- 3. Gérard P. Gut microbiota and obesity. Cell Mol Life Sci 2016;73(1):147–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Alou MT, Million M, Traore SI, et al. . Gut bacteria missing in severe acute malnutrition, can we identify potential probiotics by culturomics? Front Microbiol 2017;8:899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Schloss PD. Identifying and overcoming threats to reproducibility, replicability, robustness, and generalizability in microbiome research. MBio 2018;9(3):e00525–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Wang Y, Lê Cao K-A. Managing batch effects in microbiome data. Brief Bioinform 2020;21(6):1954–70. [DOI] [PubMed] [Google Scholar]
- 7. Goffau MC, Stephen Charnock-Jones D, Smith G, et al. . Batch effects account for the main findings of an in utero human intestinal bacterial colonization study. Microbiome 2021;9(1):1–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Randall DW, Kieswich J, Swann J, et al. . Batch effect exerts a bigger influence on the rat urinary metabolome and gut microbiota than uraemia: a cautionary tale. Microbiome 2019;7(1):1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Morrow JD, Castaldi PJ, Chase RP, et al. . Peripheral blood microbial signatures in current and former smokers. Sci Rep 2021;11(1):1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Wang Z, Yang Y, Yan Z, et al. . Multi-omic meta-analysis identifies functional signatures of airway microbiome in chronic obstructive pulmonary disease. ISME J 2020;14(11):2748–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Porras AM, Shi Q, Zhou H, et al. . Geographic differences in gut microbiota composition impact susceptibility to enteric infection. Cell Rep 2021;36(4):109457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Janiak MC, Montague MJ, Villamil CI, et al. . Age and sex-associated variation in the multi-site microbiome of an entire social group of free-ranging rhesus macaques. Microbiome 2021;9(1):1–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Almand AT, Anderson AP, Hitt BD, et al. . The influence of perceived stress on the human microbiome. BMC Res Notes 2022;15(1):1–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Leeming ER, Johnson AJ, Spector TD, et al. . Effect of diet on the gut microbiota: rethinking intervention duration. Nutrients 2019;11(12):2862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Paulson JN, Colin Stine O, Bravo HC, et al. . Differential abundance analysis for microbial marker-gene surveys. Nat Methods 2013;10(12):1200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Dai Z, Wong SH, Jun Y, et al. . Batch effects correction for microbiome data with Dirichlet-multinomial regression. Bioinformatics 2019;35(5):807–14. [DOI] [PubMed] [Google Scholar]
- 17. Debelius J, Song SJ, Vazquez-Baeza Y, et al. . Tiny microbes, enormous impacts: what matters in gut microbiome studies? Genome Biol 2016;17(1):217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Hardwick SA, Chen WY, Wong T, et al. . Synthetic microbe communities provide internal reference standards for metagenome sequencing and analysis. Nat Commun 2018;9(1):1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Moskovicz V, Ben-El R, Horev G, et al. . Skin microbiota dynamics following b. subtilis formulation challenge: an in vivo study in mice. BMC Microbiol 2021;21(1):1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Gibbons SM, Duvallet C, Alm EJ. Correcting for batch effects in case-control microbiome studies. PLoS Comput Biol 2018;14(4):e1006102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Xiao L, Zhang F, Zhao F. Large-scale microbiome data integration enables robust biomarker identification. Nature Computational Science 2022;2(5):307–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Evan Johnson W, Li C, Rabinovic A. Adjusting batch effects in microarray expression data using empirical Bayes methods. Biostatistics 2007;8(1):118–27. [DOI] [PubMed] [Google Scholar]
- 23. Ritchie ME, Phipson B, Di W, et al. . Limma powers differential expression analyses for RNA-sequencing and microarray studies. Nucleic Acids Res 2015;43(7):e47–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Ramette A. Multivariate analyses in microbial ecology. FEMS Microbiol Ecol 2007;62(2):142–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Stuart T, Butler A, Hoffman P, et al. . Comprehensive integration of single-cell data. Cell 2019;177(7):1888–902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Haghverdi L, Lun ATL, Morgan MD, et al. . Batch effects in single-cell rna-sequencing data are corrected by matching mutual nearest neighbors. Nat Biotechnol 2018;36(5):421–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Lin Y, Ghazanfar S, Wang KYX, et al. . Scmerge leverages factor analysis, stable expression, and pseudoreplication to merge multiple single-cell rna-seq datasets. Proc Natl Acad Sci 2019;116(20):9775–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Risso D, Perraudeau F, Gribkova S, et al. . A general and flexible method for signal extraction from single-cell rna-seq data. Nat Commun 2018;9(1):1–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Barker M, Rayens W. Partial least squares for discrimination. Journal of Chemometrics: A Journal of the Chemometrics Society 2003;17(3):166–73. [Google Scholar]
- 30. Kubinski R, Djamen-Kepaou J-Y, Zhanabaev T, et al. . Benchmark of data processing methods and machine learning models for gut microbiome-based diagnosis of inflammatory bowel disease. Front Genet 2022;13:784397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Hong BY, Paulson JN, Stine OC, et al. . Meta-analysis of the lung microbiota in pulmonary tuberculosis. Tuberculosis 2018;109:102–8. [DOI] [PubMed] [Google Scholar]
- 32. Jing W, Peters BA, Dominianni C, et al. . Cigarette smoking and the oral microbiome in a large study of american adults. ISME J 2016;10(10):2435–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Wold S, Sjöström M, Eriksson L. Pls-regression: a basic tool of chemometrics. Chemom Intel Lab Syst 2001;58(2):109–30. [Google Scholar]
- 34. Rohart F, Gautier B, Singh A, et al. . Mixomics: an r package for ‘omics feature selection and multiple data integration. PLoS Comput Biol 2017;13(11):e1005752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Lê Cao K-A, Boitard S, Besse P. Sparse pls discriminant analysis: biologically relevant feature selection and graphical displays for multiclass problems. BMC bioinformatics 2011;12(1):253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Holmes S, Huber W. Modern statistics for modern biology. United Kingdom: Cambridge University Press, 2018. [Google Scholar]
- 37. Susin A, Wang Y, Lê Cao K-A, et al. . Variable selection in microbiome compositional data analysis. NAR Genomics and Bioinformatics 2020;2(2):lqaa029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Tharwat A. Classification assessment methods. Applied Computing and Informatics 2021;17(1):168–92. [Google Scholar]
- 39. McMurdie PJ, Holmes S. Waste not, want not: why rarefying microbiome data is inadmissible. PLoS Comput Biol 2014;10(4):e1003531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Quinn TP, Erb I, Richardson MF, et al. . Understanding sequencing data as compositions: an outlook and review. Bioinformatics 2018;34(16):2870–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Hawinkel S, Mattiello F, Bijnens L, et al. . A broken promise: microbiome differential abundance methods do not control the false discovery rate. Brief Bioinform 2019;20(1):210–21. [DOI] [PubMed] [Google Scholar]
- 42. McGregor K, Labbe A, Greenwood CMT. Mdine: a model to estimate differential co-occurrence networks in microbiome studies. Bioinformatics 2020;36(6):1840–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Lê Cao K-A, Costello M-E, Lakis VA, et al. . Mixmc: a multivariate statistical framework to gain insight into microbial communities. PloS one 2016;11(8):e0160169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Sacristán-Soriano O, Banaigs B, Casamayor EO, et al. . Exploring the links between natural products and bacterial assemblages in the sponge aplysina aerophoba. Appl Environ Microbiol 2011;77(3):862–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Chapleur O, Madigou C, Civade R, et al. . Increasing concentrations of phenol progressively affect anaerobic digestion of cellulose and associated microbial communities. Biodegradation 2016;27(1):15–27. [DOI] [PubMed] [Google Scholar]
- 46. Ho EXP, Cheung CMG, Sim S, et al. . Human pharyngeal microbiota in age-related macular degeneration. PloS One 2018;13(8):e0201768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Thompson KJ, Ingle JN, Tang X, et al. . A comprehensive analysis of breast cancer microbiota and host gene expression. PloS One 2017;12(11):e0188873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Law CW, Chen Y, Shi W, et al. . Voom: precision weights unlock linear model analysis tools for rna-seq read counts. Genome Biol 2014;15(2):R29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Borcard D, Legendre P, Drapeau P. Partialling out the spatial component of ecological variation. Ecology 1992;73(3):1045–55. [Google Scholar]
- 50. Butler A, Hoffman P, Smibert P, et al. . Integrating single-cell transcriptomic data across different conditions, technologies, and species. Nat Biotechnol 2018;36(5):411–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Dollhopf S, Hashsham S, Dazzo F, et al. . The impact of fermentative organisms on carbon flow in methanogenic systems under constant low-substrate conditions. Appl Microbiol Biotechnol 2001;56(3):531–8. [DOI] [PubMed] [Google Scholar]
- 52. Wang H, Li J, Zhao Y, et al. . Establishing practical strategies to run high loading corn Stover anaerobic digestion: methane production performance and microbial responses. Bioresour Technol 2020;310:123364. [DOI] [PubMed] [Google Scholar]
- 53. Poirier S, Déjean S, Chapleur O. Support media can steer methanogenesis in the presence of phenol through biotic and abiotic effects. Water Res 2018;140:24–33. [DOI] [PubMed] [Google Scholar]
- 54. Goodrich JK, Waters JL, Poole AC, et al. . Human genetics shape the gut microbiome. Cell 2014;159(4):789–99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Singh A, Müller B, Schnürer A. Profiling temporal dynamics of acetogenic communities in anaerobic digesters using next-generation sequencing and t-rflp. Sci Rep 2021;11(1):1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Wang R, Zhang J, Liu J, et al. . Effects of chlortetracycline, cu and their combination on the performance and microbial community dynamics in swine manure anaerobic digestion. J Environ Sci 2018;67:206–15. [DOI] [PubMed] [Google Scholar]
- 57. Fan Y, Niu X, Zhang D, et al. . Analysis of the characteristics of phosphine production by anaerobic digestion based on microbial community dynamics, metabolic pathways, and isolation of the phosphate-reducing strain. Chemosphere 2021;262:128213. [DOI] [PubMed] [Google Scholar]
- 58. Liu Y, Wachemo AC, Yuan HR, et al. . Anaerobic digestion performance and microbial community structure of corn Stover in three-stage continuously stirred tank reactors. Bioresour Technol 2019;287:121339. [DOI] [PubMed] [Google Scholar]
- 59. Oakley BB, Lillehoj HS, Kogut MH, et al. . The chicken gastrointestinal microbiome. FEMS Microbiol Lett 2014;360(2):100–12. [DOI] [PubMed] [Google Scholar]
- 60. Wojcieszak M, Pyzik A, Poszytek K, et al. . Adaptation of methanogenic inocula to anaerobic digestion of maize silage. Front Microbiol 2017;8:1881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Poirier S, Madigou C, Bouchez T, et al. . Improving anaerobic digestion with support media: mitigation of ammonia inhibition and effect on microbial communities. Bioresour Technol 2017;235:229–39. [DOI] [PubMed] [Google Scholar]
- 62. Ormerod KL, Wood DLA, Lachner N, et al. . Genomic characterization of the uncultured bacteroidales family s24-7 inhabiting the guts of homeothermic animals. Microbiome 2016;4(1):1–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63. Vacca M, Celano G, Calabrese FM, et al. . The controversial role of human gut lachnospiraceae. Microorganisms 2020;8(4):573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64. Martínez I, Perdicaro DJ, Brown AW, et al. . Diet-induced alterations of host cholesterol metabolism are likely to affect the gut microbiota composition in hamsters. Appl Environ Microbiol 2013;79(2):516–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65. Zhou L, Xiao X, Zhang Q, et al. . Improved glucose and lipid metabolism in the early life of female offspring by maternal dietary genistein is associated with alterations in the gut microbiota. Front Endocrinol 2018;9:516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66. Liu H, Hou C, Li N, et al. . Microbial and metabolic alterations in gut microbiota of sows during pregnancy and lactation. FASEB J 2019;33(3):4490–501. [DOI] [PubMed] [Google Scholar]
- 67. Weiss S, Zhenjiang Zech X, Peddada S, et al. . Normalization and microbial differential abundance strategies depend upon data characteristics. Microbiome 2017;5(1):1–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68. Nguyen TT, Tsoy Y. A kernel pls based classification method with missing data handling. Statistical Papers 2017;58(1):211–25. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The R package ‘PLSDAbatch’ along with the case study datasets, simulations and all analyses are fully reproducible and available on GitHub: https://github.com/EvaYiwenWang/PLSDAbatch.