Generating Anthropomorphic Phantoms Using Fully Unsupervised Deformable Image Registration with Convolutional Neural Networks

Abstract

Purpose:

Computerized phantoms have been widely used in nuclear medicine imaging for imaging system optimization and validation. Although the existing computerized phantoms can model anatomical variations through organ and phantom scaling, they do not provide a way to fully reproduce the anatomical variations and details seen in humans. In this work, we present a novel registration-based method for creating highly anatomically detailed computerized phantoms. We experimentally show substantially improved image similarity of the generated phantom to a patient image.

Methods:

We propose a deep-learning-based unsupervised registration method to generate a highly anatomically detailed computerized phantom by warping an XCAT phantom to a patient CT scan. We implemented and evaluated the proposed method using the NURBS-based XCAT phantom and a publicly available low-dose CT dataset from TCIA. A rigorous trade-off analysis between image similarity and deformation regularization was conducted to select the loss function and regularization term for the proposed method. A novel SSIM-based unsupervised objective function was proposed. Finally, ablation studies were conducted to evaluate the performance of the proposed method (using the optimal regularization and loss function) and the current state-of-the-art unsupervised registration methods.

Results:

The proposed method outperformed the state-of-the-art registration methods, such as SyN and VoxelMorph, by more than 8%, measured by the SSIM and less than 30%, by the MSE. The phantom generated by the proposed method was highly detailed and was almost identical in appearance to a patient image.

Conclusions:

A deep-learning-based unsupervised registration method was developed to create anthropomorphic phantoms with anatomies labels that can be used as the basis for modeling organ properties. Experimental results demonstrate the effectiveness of the proposed method. The resulting anthropomorphic phantom is highly realistic. Combined with realistic simulations of the image formation process, the generated phantoms could serve in many applications of medical imaging research.

I. Introduction

Computerized phantoms for nuclear medicine imaging research have been built based on anatomical and physiological models of human beings. They have played a crucial part in evaluation and optimization of medical image reconstruction, processing and analysis methods^1,2,3,4. Since the exact structural and physiological properties of the phantom are known, they can serve as a gold standard for the evaluation and optimization process. The 4D extended cardiac-torso (XCAT) phantom⁵ was developed based on anatomical images from the Visible Human Project data. This realistic phantom includes parameterized models for anatomy, which allows the generation of a series of phantoms with different anatomical variations. These phantoms have been used in Nuclear Medicine imaging and CT research^{6,7,8,9,10,11,12}, as well as in various applications of deep learning^13,14,15.

In the XCAT phantom, changing the values of parameters that control organ anatomy can be used to vary the volumes and shapes of some tissues. However, the scaling of organs, even when different factors are used in orthogonal directions, does not fully and realistically capture the anatomical variations of organs within different human bodies. However, for many applications, having a population of phantoms that models the variations in patient anatomy and, in nuclear medicine, uptake realization is essential for comprehensive validation and training of image processing and reconstruction algorithms. To solve this, in¹⁶, Segars et al. used a deformable image registration technique to map phantom labels to segmented patient images; the resulting deformation fields were then applied to the phantom, thus creating a population of new XCAT models that capture the anatomical variability among patients. This method relies on the segmentation of patient images, which is tedious and time consuming. In this work, we propose an approach based on Convolutional neural networks (ConvNets) to perform phantom to patient registration without requiring the patient segmentation. The resulting deformation field can then be applied to organ label maps to generate a gold-standard segmentation for the deformed phantom image.

Deformable Image registration is a process of transforming two images into a single coordinate system, where one image is often referred to as the moving image, denoted by I_m, and the other is referred to as the fixed image, denoted by I_f. Traditional methods formulate registration as a variational problem for estimating a smooth mapping, ϕ, between the points in one image and those in another. They often tend to iteratively minimize the following energy function (eq. 1) on a single image pair¹⁷:

$$E=E_{sim}\left(I_m\circ \varphi ,I_f\right)+R(\varphi ),$$ (1)

where, E_sim measures the level of alignment between the transformed moving image, I_m ◦ϕ, and the fixed image, I_f. Some common choices for E_sim are mean squared error (MSE) or the squared L² norm of the difference¹⁸, sum of squared differences (SSD)¹⁹, cross-correlation (CC)²⁰, and mutual information (MI)²¹. The transformation, ϕ, at every point is defined by an identity transformation with the displacement field u, or ϕ = Id + u, where Id represents the identity transform²². The second term, R(ϕ), is referred to as the regularization of the deformation, ϕ, which enforces spatial smoothness. Many regularization designs have been proposed previously based on different applications and prior knowledge about the deformation field. However, they are usually characterized by the gradients of u. In some applications, regularizers were designed to take sliding organs into account^23,24,25, where instead of enforcing global smoothness, they preserve motion discontinuities allowing multiple organs to move independently. In most applications, a common assumption is that similar structures are present in both moving and fixed images. Hence, a continuous and invertible deformation field (a diffeomorphism) is desired, and the regularization term, R(ϕ), is designed to enforce or encourage this. Diffeomorphisms can be essential in some studies, for which the registration field is analyzed further. However, in the application of registration-based segmentation, the quality of the segmentation propagation is more critical than the diffeomorphic property of the underlying deformation fields²⁶. In this study, due to the large interior and exterior shape variations between digital phantoms and patients, diffeomorphism is less important. However, we show that by introducing various regularizers to the proposed model, the number of non-invertible voxel transformations in the resulting deformation field can be substantially reduced.

Recently, many deep learning-based methods have been proposed to perform registration tasks (summarized in Table 1). Some of the methods rely on ground truth deformation fields^27,28,29, which are often obtained by simulated deformations or applying classical registration algorithms on a pair of images. However, ground truth registration fields are time-consuming to obtain and can limit the types of deformations that are learned. While other methods, such as^{22,30,31,32,33,34}, were introduced as unsupervised (or more percisely, self-supervised) techniques, but they still require a prior training stage with a large amount of training data. These methods assume that neural networks can provide a universal and generalized model for image registration by minimizing the registration energy function over a dataset of images. This is a common assumption with deep-learning-based approaches. Yet, such an assumption could be unreliable according to a recent study from Zhang et al.³⁵, where they showed that a well-generalized CNN classifier trained by a large dataset can still easily overfit a random labeling of the training data. Other studies on fooling deep neural networks (DNNs) with adversarial images also suggest that the well-trained networks can be unstable to small or even tiny perturbations of the data^{36,37,38,39,40}. On the other hand, the proposed registration method is fully unsupervised, meaning that no previous training is required. Instead of following the conventional pattern of training a network on a large dataset of training images, we show that a CNN can estimate an optimal deformation field for a single image pair by minimizing the energy function described in eq. 1 iteratively. This idea was inspired by Lempitsky et al.’s work on the Deep Image Prior⁴¹ (DIP), where they showed that learning from a large amount of data is not necessary for building useful image priors, but the structure of a ConvNet itself is sufficient to capture image statistics. They treated the training of ConvNets with random initialization as a regularization prior, and in order to achieve good solutions in their application of image denoising, determining early stopping points was often required. Whereas in image registration, instead of starting from a random initialization (i.e., random noise images), it makes logical sense to initialize the ConvNet with a moving image. Since one would like to transform the moving image so that it is similar to a target image as possible, early stopping is not desired. In this work, we treat ConvNet as an optimization tool, where it generates a deformation field that minimizes the difference between deformed moving and fixed images by updating its parameter values in each iteration. The deformation is realized with a spatial transformer constructed based on the spatial transformer networks⁴² and VoxelMorph²². It differs from the B-Spline grids used in^29,31,32, which are only demonstrated on sub-regions (patches) of images, support only small transformations, and impose implicit regularization defined by interpolation methods^22,33. On the contrary, the control points of the spatial transformer used in this work were applied to all the pixel locations. This, thus, enables large deformations and allows for external regularization.

Table 1:

Conceptual comparisons among various registration methods and the proposed method (UnsupConvNet).

Registration Methods	DNN-based	Supervision	Operating mode
VoxelMorph22,30,33	Yes	Self-supervised	Whole image
DLIR32	Yes	Self-supervised	Patch-based
DIRNet31	Yes	Self-supervised	Patch-based
FAIM62	Yes	Self-supervised	Whole image
RegNet29	Yes	Supervised	Patch-based
RobustRegNet28	Yes	Supervised	ROI-based
SyN20	No	Unsupervised	Whole image
LDDMM18	No	Unsupervised	Whole image
UnsupConvNet	Yes	Unsupervised	Whole image

II. Materials and Methods

II.A. Computerized Phantom Generation

The phantom used in this study was created from the 3D attenuation distribution of the realistic NURBS-based XCAT phantom⁴³. Attenuation values were computed based on the material compositions of the materials and the attenuation coefficients of the constituents at 140 keV, the photon energy of Tc-99m. This single 3D phantom image was deformed to multiple patient CT images. The simulated attenuation map image can be treated as the template image, and phantom label map can then be thought of as the atlas in the traditional paradigm of medical image registration. The aim is to first register the phantom attenuation map image to patient CT images. Next, the registration parameters would be applied to the XCAT phantom label map (used to define organs and thus the activity distribution) to create new anthropomorphic phantoms. For the nuclear medicine imaging application, new images would be generated from the resulting phantoms using conventional physics-based simulation codes^{44,45,46,47,48,49}.

II.B. Image Registration with ConvNet

Let the moving image be I_m, and the fixed image be I_f; we assume that they are grayscale images defined over a n-dimensional spatial domain Ω ⊂ ℛⁿ and affinely aligned. This paper primarily focuses on the 2D case (i.e., n = 2), but the implementation is dimension independent (Notice that for n > 2 cases, the required GPU memory will be significant increased). We model the computation of the displacement field, ϕ, given the image pair, I_m and I_f, using a deep ConvNet with parameters θ, i.e., f_θ(I_m, I_f) = ϕ. Fig. 1 describes the architecture of the proposed method; it consists of a ConvNet that outputs a registration field, and a B-spline spatial transformer. First, the ConvNet generates the ϕ for the given image pair, I_m and I_f. Second, the deformed moving image is obtained by applying a B-spline spatial transformer that warps I_m with ϕ (i.e., I_m ◦ ϕ). Finally, we backpropagate the loss computed from the similarity measure between I_m ◦ ϕ and I_f to update θ in the ConvNet. The steps are repeated iteratively until the loss converges; the resulting ϕ then represents the optimal registration field for the given image pair. The loss function (ℒ) of this problem can be formulated mathematically as:

$$\begin{gathered} ℒ\left(I_m,I_f,\varphi ;\theta \right)={ℒ}_{\text{sim }}\left(I_m\circ \varphi ,I_f;\theta \right)+\lambda R(\varphi ;\theta ) \\ ={ℒ}_{\text{sim }}\left(I_m\circ f_{\theta }\left(I_m,I_f\right),I_f;\theta \right)+\lambda ℛ\left(f_{\theta }\left(I_m,I_f\right),\theta \right). \end{gathered}$$ (2)

where ℒ_sim is the image similarity measure and ℛ represents the regularization of ϕ Then, the parameters θ that generate the optimal registration field can be estimated by the minimizer:

$${\theta }^{*}=\underset{\theta }{\text{arg min }}ℒ\left(I_m,I_f,\varphi ;\theta \right),$$ (3)

and the optimal ϕ is then given by:

$${\varphi }^{*}=f_{{\theta }^{*}}\left(I_m,I_f\right).$$ (4)

Different choices of image similarity metrics and registration field regularizers (R(ϕ)) were also studied in this work, and they are described in detail in a later section. The next subsection describes the design of ConvNet architecture.

Figure 1:

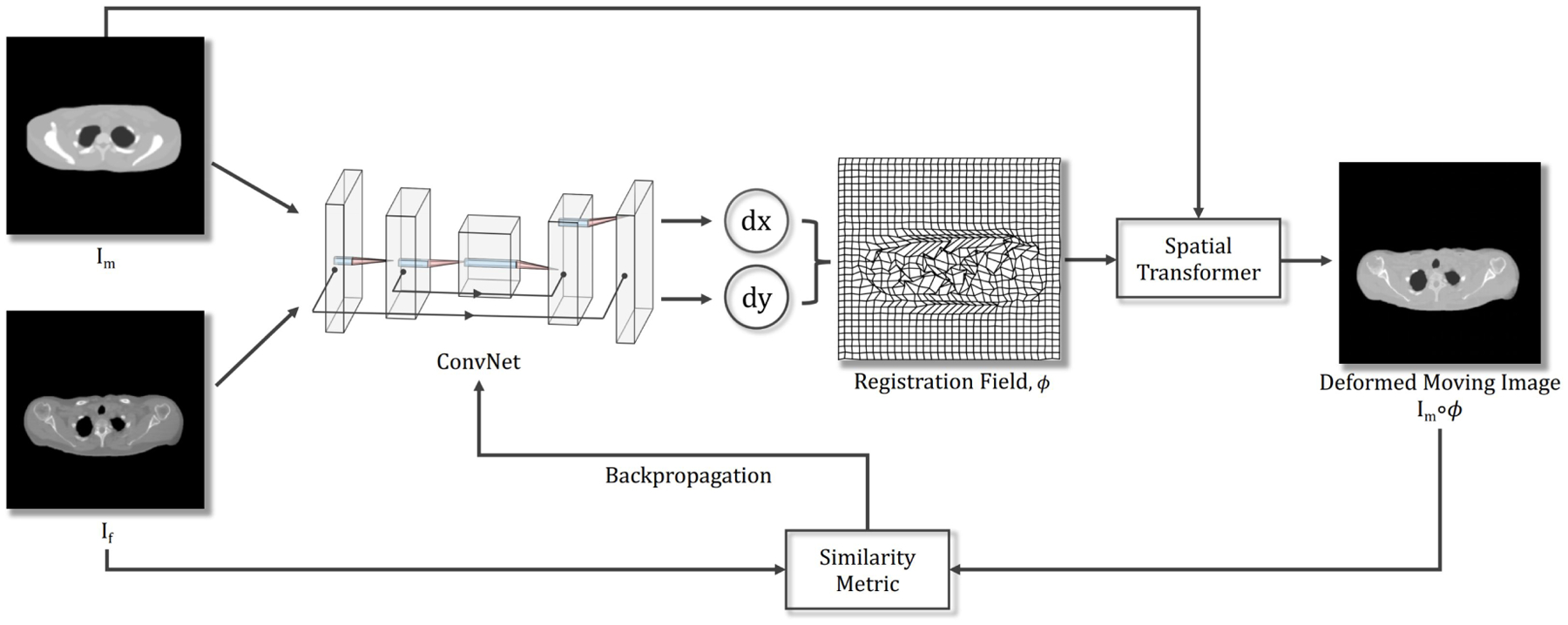
Schematic of the proposed method. The network takes a pair comprised of one moving and one fixed image as its inputs. The ConvNet learns from a single image pair and generates a deformation field, ϕ. We then warp the moving image I_m with ϕ using a B-spline spatial transformer. The loss determined by the image similarity measure between I_m ◦ ϕ and I_f is then backpropagated to update the parameters in the ConvNet. Since no aspect of the ConvNet is learned from a prior training stage, the method follows a fully unsupervised paradigm.

II.B.1. ConvNet Architecture

The ConvNet had a U-Net-like ”hourglass” architecture⁵⁰. The network consisted of one encoding path, which takes a single input formed by concatenating the moving and fixed images into a 2 × M × M volume, where M × M represents the shape of one image. Each convolutional layer had a 3×3 filter followed by a rectified linear unit (ReLU), and the downsampling was performed by 2×2 max pooling operations. In the decoding stage, the upsampling was done by ”up-convolution”⁵⁰. Each of the upsampled feature maps in the decoding stage was concatenated with the corresponding feature map from the encoding path. The output registration field, ϕ, was generated by the application of sixteen 3×3 convolutions followed by two 1×1 convolutions to the 16 feature maps. This is a relatively small network with 98,794 trainable parameters in total. The network architecture is shown schematically in Fig. 2.

Figure 2:

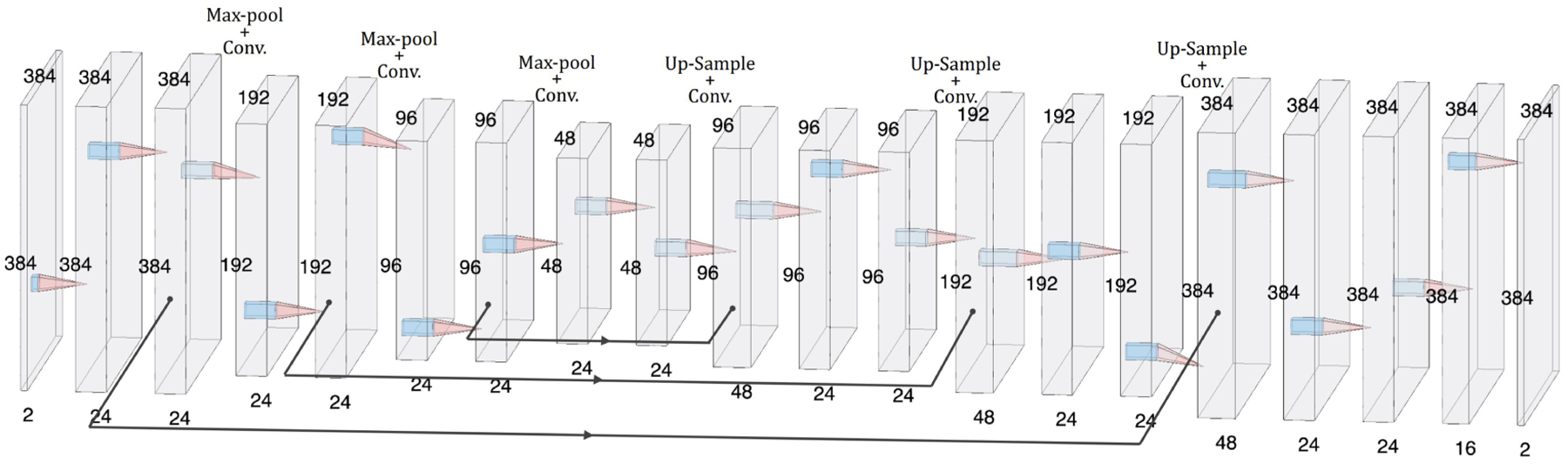
The ConvNet has a U-Net-like architecture.

II.B.2. Spatial Transformer

The spatial transformer was implemented on the basis of the spatial transformer networks⁴², which applies a non-linear warp to the moving image, where the warp is determined by a flow field of displacement vectors (u) that define the correspondences of pixel intensities in the output image to the pixel locations in the moving image. The number of control points in the flow field, (u), is equal to the image’s size; thus, the spacing of the control points grid is 1. The intensity at each pixel location, p, in the output image, I_m ◦ ϕ(p), is defined by:

$$I_m\circ \varphi (p)=I_m(p-u(p)).$$ (5)

Notice that p − u(p) is not necessarily an integer, and pixel intensities are only defined at integer locations in the image. Therefore, the value of I_m ◦ ϕ(p) was obtained by applying interpolation methods to the nearest pixels around p − u(p):

$$I_m\circ \varphi (p)=\sum _{q\in 𝓏\left(p^{\prime }\right)}{I}_m(q)\prod _{d\in \left\{x,y\right\}}k\left(p_d^{\prime }-q_d\right),$$ (6)

where p′ = p−u(p), Ƶ(p′) represents the neighboring pixels of p′, d iterates over dimensions of the spatial domain Ω, and k() is a generic sampling kernel, which defines the image interpolation. We used, respectively, bi-linear and nearest-neighbor interpolation to obtain pixel values in the deformed XCAT attenuation map and the deformed organ labels. The nearest-neighbor interpolation reduces (6) to:

$$I_m\circ \varphi (p)=\sum _{q\in 𝓏\left(p^{\prime }\right)}{I}_m(q)\prod _{d\in \{x,y\}}\delta \left(\lfloor p_d^{\prime }+0.5\rfloor -q_d\right),$$ (7)

where δ() represents the Kronecker delta function, and $\lfloor p_d^{\prime }+0.5\rfloor$ rounds $p_d^{\prime }$ to nearest integer value. If k() is a bi-linear sampling kernel, (6) is reduced to:

$$I_m\circ \varphi (p)=\sum _{q\in 𝓏\left(p^{\prime }\right)}{I}_m(q)\prod _{d\in \left\{x,y\right\}}\left(1-\left|p_d^{\prime }-q_d\right|\right).$$ (8)

II.B.3. Image Similarity Metrics

Over the years, considerable effort has been expended designing image similarity metrics. We mentioned some of the metrics that have been widely adopted in image registration in the previous section. In this work, we studied the effectiveness of five different loss functions, we also propose a new ℒ_sim that combines the advantages of both Pearson’s Correlation Coefficient (PCC) and the Structural Similarity Index (SSIM). In the following subsections, we denote the deformed moving image as I_d (i.e., I_d = I_m ◦ ϕ) for simplicity.

Mean Squared Error (MSE)

MSE is a measurement of fidelity, and indicates the degree of agreement of intensity values in images; it is applicable when I_f and I_m have similar contrast and intensity distributions. The loss function is defined as ℒ_sim(I_m, I_f, ϕ;θ) = MSE(I_d, I_f).

Local Cross Correlation (CC)

Another popular image similarity metric is CC, due to its robustness to intensity variations between images^20,33,51. Since CC ≥ 0, we minimize the negative CC, the loss function is ℒ_sim(I_m, I_f, ϕ; θ) = −CC(I_d, I_f).

Mutual Information (MI)

MI was first applied to image registration in⁵². It measures the statistical dependence between the intensities of corresponding pixels in both moving and fixed images. Let $p_{I_f}(a)$ and $p_{I_d}(b)$ be the marginal probability distributions of the fixed and deformed moving images. MI is a measure of the Kullback-Leibler Divergence⁵³ between the joint distribution $p_{I_f{I}_d}(a,b)$ and the distribution associated with the case of complete independence $p_{I_f}(a)\cdot p_{I_d}(b)$⁵²:

$$\text{MI}\left(I_d,I_f\right)=\sum _{a,b}{p}_{I_f{I}_d}(a,b)\text{ log}\frac{p_{I_f{I}_d}(a,b)}{p_{I_f}(a)\cdot p_{I_d}(b)}.$$ (9)

The joint distribution, $p_{I_f{I}_d}(a,b)$, can be computed as:

$$p_{I_f{I}_d}(a,b)=\frac{1}{\Omega }\sum _{i\in \Omega }\delta \left(a-I_f(i)\right)\delta \left(b-I_d(i)\right),$$ (10)

Notice that the Kronecker delta function, δ(), is not differentiable. Therefore, the resulting loss cannot be back-propagated in the network. To solve this issue, we approximate $p_{I_f{I}_d}(a,b)$ with the Parzen windowing functions as described by Mattes et al. in⁵⁴:

$$p_{I_f{I}_d}(a,b)=\alpha \sum _{i\in \Omega }\psi \left(a-I_f(i)\right)\chi \left(b-I_d(i)\right),$$ (11)

where α is a normalization factor that ensures $\sum p_{I_f{I}_d}(a,b)=1$, and ψ() and χ() are kernel functions of Parzen window. There is a broad choice for kernel functions, such as the first order or the third order B-Spline kernel⁵⁴, and Gaussian kernel²¹. Since Cubic B-Spline has a close relationship with Gaussian functions^55,56, we chose ψ() and χ() to be Gaussian kernels in this work. The joint distribution, (11), can be rewritten as:

$$p_{I_f{I}_d}(a,b)=\alpha \sum _{i\in \Omega }\frac{1}{\Delta w_d\Delta w_m\pi }{e}^{\frac{{\left(a-I_f(i)\right)}^2}{2\Delta w_f^2}}{e}^{\frac{{\left(b-I_d(i)\right)}^2}{2\Delta w_d^2}},$$ (12)

where Δw_f and Δw_d are the widths of each intensity bin in image I_f and I_d. A larger bin width potentially leads to an improvement in computational efficiency, because the number of intensity bins used in the estimation of the marginal probability distributions could be reduced. Finally, the two marginal probability distributions can be derived using $p_{I_f{I}_d}(a,b)$. Maximizing MI is equivalent to minimizing the negative of the MI. Thus, the loss function is formulated as ℒ_sim(I_m, I_f, ϕ; θ) = −MI(I_d, I_f).

Pearson’s Correlation Coefficient (PCC)

PCC measures the linear correlation between two images. Unlike MSE, PCC is less sensitive to linear transformations of intensity values from one image to another. Its application to medical image registration is described in⁵⁷. PCC is defined as the covariance between images divided by the product of their standard deviations:

$$\text{PCC}\left(I_d,I_f\right)=\frac{{\sum }_{i\in \Omega }\left(I_f(i)-{\overline{I}}_f\right)\left(I_d(i)-{\overline{I}}_d\right)}{\sqrt{{\sum }_{i\in \Omega }\left(I_f(i)-{\overline{I}}_f\right)}\sqrt{{\sum }_{i\in \Omega }\left(I_d(i)-{\overline{I}}_d\right)}}$$ (13)

where ${\overline{I}}_f$ and ${\overline{I}}_d$ represent the mean intensities. PCC has a range from −1 to 1, where 0 implies that there is no linear correlation, and −1 and 1 correspond, respectively, to the maximum negative and positive correlations between two images. Since a positive correlation is desired, we can define the loss function to be: ℒ_sim(I_m, I_f, ϕ; θ) = 1 − PCC(I_d, I_f).

Structural Similarity Index (SSIM)

SSIM was proposed in⁵⁸ for robust image quality assessments based on the degradation of structural information. Within a given image window, SSIM is defined by:

$$\text{SSIM}\left(I_d,I_f\right)=\frac{\left(2{\mu }_{I_d}{\mu }_{I_f}+C_1\right)\left(2{\sigma }_{I_f{I}_d}+C_2\right)}{\left({\mu }_{I_f}^2+{\mu }_{I_d}^2+C_1\right)\left({\sigma }_{I_f}^2+{\sigma }_{I_d}^2+C_2\right)},$$ (14)

where C₁ and C₂ are small constants needed to avoid instability, ${\mu }_{I_f}$ and ${\mu }_{I_d}$, and ${\sigma }_{I_f}$ and ${\sigma }_{I_d}$ are local means and standard deviations of the images I_f and I_d, respectively. The SSIM has a range from −1 to 1, where 1 indicates a perfect structural similarity. Thus, ℒ_sim(I_m, I_f, ϕ; θ) = 1 − SSIM(I_d, I_f).

PCC + SSIM

While PCC is robust to noises, it was also found to be less sensitive to blurring. A motivating example is shown in Fig. 3, where in (b), the ”Shepp-Logan” phantom image⁵⁹ was corrupted with Gaussian noise, and in (c), the image was blurred by a Gaussian filter. Both (b) and (c) yield a lower SSIM and a higher PCC. If we think of (a) as a moving image, and (b) and (c) as fixed images, SSIM would impose the ConvNets to model the details, including noises and artifacts. Whereas, using PCC alone as the loss function might converge to a less accurate result. Hence, there is a need to balance the two similarity measures. Both PCC and SSIM are bounded with a range from −1 to 1, where 1 indicates the most similar. Thus, we propose to combine SSIM and PCC with an equal weight:

$${ℒ}_{sim}\left(I_m,I_f,\varphi ;\theta \right)=0.5*\left(1-\text{SSIM}\left(I_d,I_f\right)\right)+0.5*\left(1-\text{PCC}\left(I_d,I_f\right)\right)$$ (15)

Figure 3:

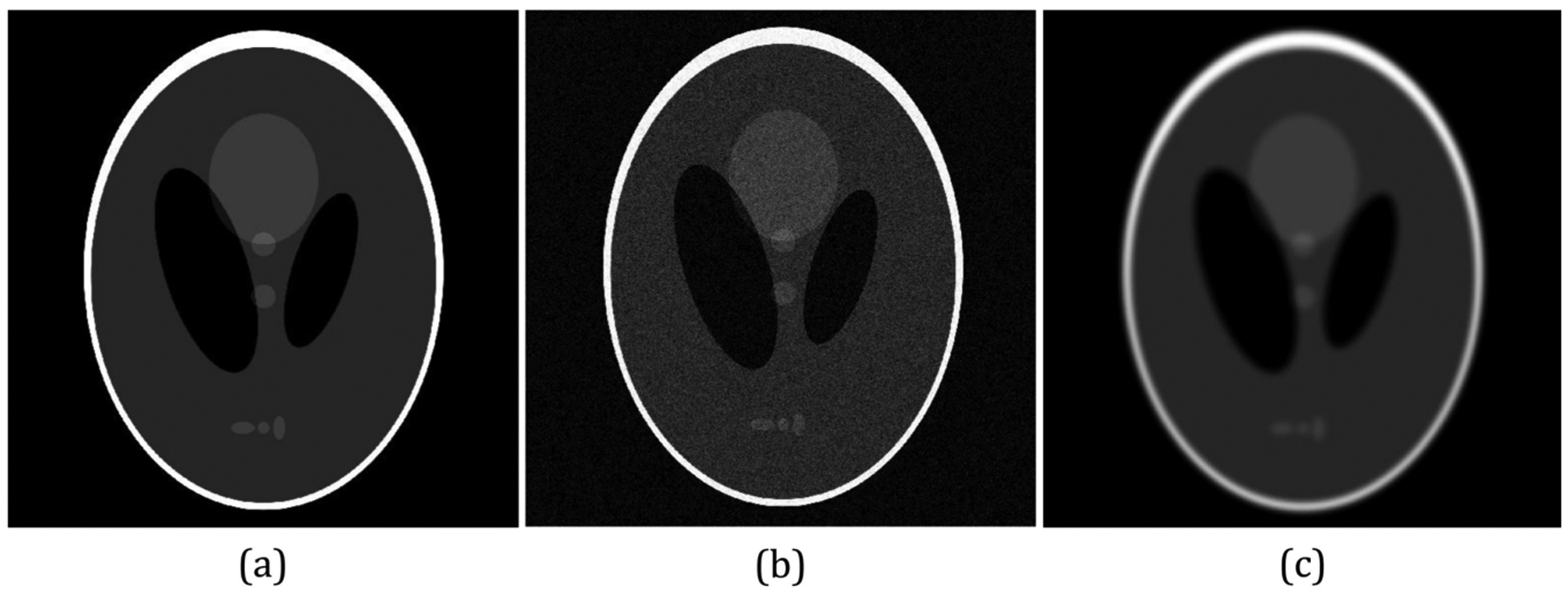
Comparison of ”Shepp-Logan” phantom images⁵⁹ with different types of distortions. (a) Original Image. (b) Image corrupted by Gaussian noise. SSIM: 0.14, PCC: 0.96. (c) Gaussian blurred image. SSIM: 0.9, PCC: 0.94.

II.C. Deformation Regularization

The spacing of the control point grid is 1 pixel, thus the spatial transformer does not implicitly enforce any regularization (i.e., smoothness of the deformation field). Because each pixel can move freely, optimizing the image similarity metrics solely would encourage the deformed moving image, I_f, to be as close as possible to the fixed image, I_m. However, the resulting deformation field might not be smooth or realistic. To impose smoothness and weakly enforce diffeomorphism in the deformation field, we tested several different regularizers.

II.C.1. Diffusion Regularizer

Balakrishnan, et al. used a diffusion regularizer in a ConvNet-based image registration model, VoxelMorph²². In this method, the regularization is applied on the spatial gradients of the displacement field u:

$${ℛ}_{\mathit{\text{Diffusion}}}(\varphi ;\theta )=\sum _{i\in \Omega }\parallel \nabla u(i){\parallel }^2,$$ (16)

where the spatial gradients are approximated by the forward difference, that is ∇u(i) ≃ u(i+1)−u(i). Minimizing this the value of this regularizer leads to smaller spatial variations in the displacements, resulting in a smooth deformation field.

II.C.2. Total Variation Regularizer

Instead of using the squared L² norm as the diffusion regularizer, the total variation norm regularizes the L¹ norm on the spatial gradients of u⁶⁰:

$${ℛ}_{TV}(\varphi ;\theta )=\sum _{i\in \Omega }\parallel \nabla u(i){\parallel }_1$$ (17)

Penalizing the TV of the displacement field constrains its spatial incoherence without forcing it to be smooth. Detailed properties of TV regularization of displacements were studied by Vishnevskiy et al. in⁶¹.

II.C.3. Non-negative Jacobian

The determinants of the Jacobian represent the amount of transformation under a certain deformation. In⁶², Kuang et al. proposed a regularizer that specifically penalizes ”folding” or non-invertable deformations, that is, the spatial locations where the Jacobian determinants are less than 0. This regularizer is formulated as:

$${ℛ}_{\mathit{\text{Jacobian}}}(\varphi ;\theta )=\sum _{i\in \Omega }\left(\left|det\left(J_{\varphi }(i)\right)\right|-det\left(J_{\varphi }(i)\right)\right).$$ (18)

Combined this with diffusion regularization to constrain the overall smoothness results in a regularizer that produces deformations with fewer folded pixels:

$${ℛ}_{reg}(\varphi ;\theta )={ℛ}_{\mathit{\text{Diffusion}}}(\varphi ;\theta )+\alpha {ℛ}_{\mathit{\text{Jacobian}}}(\varphi ;\theta ),$$ (19)

where α is a weighting parameter.

II.C.4. Gaussian Smoothing

A direct way to constrain a deformation field to be smooth is to convolve the displacements with a Gaussian smoothing filter parameterized by its standard deviation, σ³⁴:

$$\widehat{u}=G_{\sigma }*u,$$ (20)

where a larger σ gives a smoother deformation, and vice versa.

II.D. Registration Procedure

The overall algorithm for the proposed method is shown in Algorithm. 1. In the beginning, we initialized an untrained ConvNet (f_θ) for a given pair of moving and fixed images, I_m and I_f. First, the untrained f_θ produces an initial deformation field, ϕ. Second, we deform the moving image with ϕ (i.e., I_m ◦ ϕ). Then, the registration loss is computed as:

$$\ell ={ℒ}_{sim}\left(I_d,I_f;\theta \right)+\lambda ℛ(\varphi ;\theta ),$$ (21)

where ℒ_sim represents the similarity measure between I_d and I_f, ℛ represents the value of the regularizer applied to the deformation field, and λ is a user-defined weighting parameter to control the effectiveness of ℛ. The loss is back-propagated to update the parameters in f_θ. The above procedure is repeated for a pre-specified number of iterations.

Since no information other than the given image pair is needed, the proposed method requires no prior training and is thus fully and truly unsupervised. The ConvNet is capable of learning an ”optimal” deformation from a single pair of images. In the next section, we discuss a series of experiments that were performed to study the effectiveness of the proposed method.

II.E. Experiments

The goal of this work was to create anthropomorphic phantoms by registering the XCAT phantom attenuation map with patient CT images, and then using the deformed of XCAT phantom label map. Nine clinical low-dose whole-body CT patient scans were used in this study; for those, only the torso part of the scans was extracted, resulting in 1153 2D-transaxial slices in total. We resampled the 2D slices into the size of 384 × 384 using bi-linear interpolation to match the size of an XCAT slice. The proposed method was implemented using Keras⁶³ with a Tensorflow⁶⁴ backend on an NVIDIA Quadro P5000 GPU (with 16 GB memory). We applied the proposed method to register a pair of 2D XCAT and CT images slice by slice. The required GPU memory to register a pair of 2D slices was 2,693 MB. The patient CT data was obtained from a publicly available dataset (NaF Prostate,⁶⁵) from The Cancer Imaging Archive (TCIA,⁶⁶). The dataset contains 44 baseline and follow-up studies of nine patients, where we randomly extracted one PET/CT scan from the studies of each nine patients to form the dataset used in this work. We first compared the performance produced by the ConvNets with different image similarity metrics. Then, we compared the proposed method to state-of-the-art registration algorithms: the symmetric image normalization method (SyN)²⁰ from the ANTs package⁶⁷, and a learning-based self-supervised method, VoxelMorph^22,33.

II.F. Evaluation Metrics

We used the following metrics to evaluate the quality of the registration:

• Mean Squared Error: MSE is measured as the mean squared difference between every pixel in I_d and the corresponding pixel in I_f.

• Structural Similarity Index: SSIM indicates the average of perceived change in structural information between the I_d and I_f.

• Number of Non-positive Jacobian Determinants: J_ϕ gives the portion of the registration transformation that resulting from the deformation, ϕ. The quantity measurement of the non-positive |J_ϕ| indicates the number of pixel transformations that are not inveratible. A small number of non-positive |J_ϕ| means a smoother deformation, and vice versa.

III. Results

We first compared the effectiveness of different loss functions (without any regularization) in section III.A.. Then, we showed that some qualitative results generated by different regularizers in section III.B.. Finally, we comprehensively studied the proposed method and compared it to several state-of-the-art registration methods. The corresponding empirical results are shown in section III.C..

III.A. Loss Function Comparisons

Some examples of the registered XCAT phantom attenuation map images resulting from the six loss functions are shown in Fig. 4. Images (a) and (h) represent the same moving image, and (b) and (i) are the target images from the same CT slice, where the later was blurred by a low-pass Gaussian filter to reduce the effects streaking artifacts. The images in both (c)-(h) and (k)-(p) show results from using, respectively, PCC, SSIM, PCC+SSIM, MSE, CC, and MI. As highlighted in the boxes, MSE, CC, and MI all failed in leading to acceptable results. Whereas, the results produced by SSIM+PCC exhibits fewer image artifacts and provided the best structural match to the target image (as shown in (m)). Combined with the Gaussian pre-filtering to suppress streaking artifacts in the target image, SSIM+PCC generated the best qualitative results among the loss functions evaluated.

Figure 4:

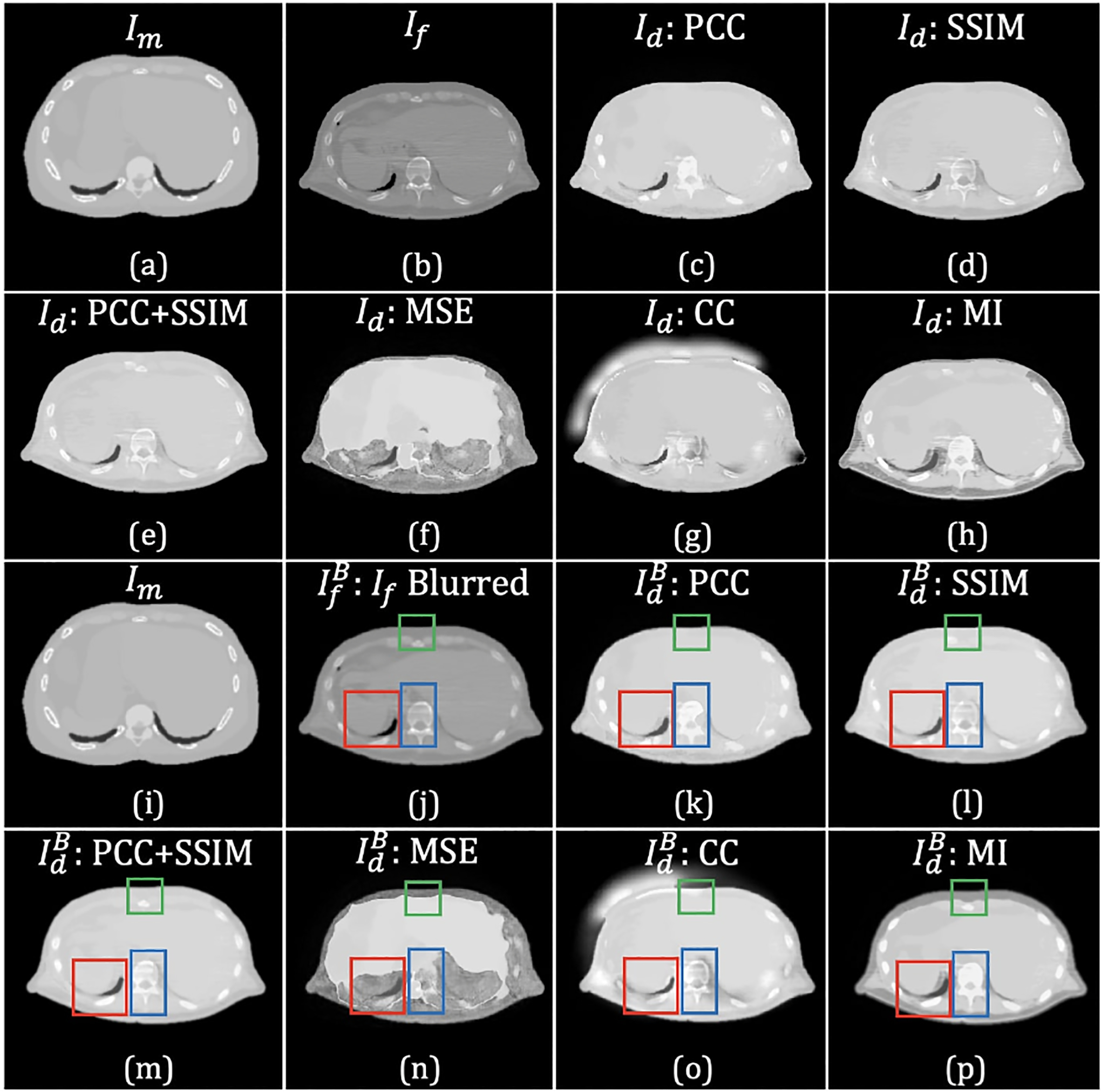
In comparing registered XCAT attenuation map images generated using different loss functions (without any regularization), some differences are highlighted by colored rectangles. The top two rows show the results generated without pre-filtering the fixed image; the bottom two rows show the results generated using the pre-filtered fixed image. The images in (a) and (i) exhibit the same slice of the attenuation map generated from the XCAT phantom, which served as the moving image, I_m; (b) and (j) are the same patient CT images, but prior to use in the registration. Image (j) is (b) blurred with Gaussian filter (σ = 0.8) to reduce noise and artifacts. The images in (b) and (j) were used as the fixed image, I_f. Images shown in (c)-(h) and (k)-(p) resulted from applying the ConvNet using 6 different loss functions: (c) and (k) PCC; (d) and (l) SSIM; (e) and (m) PCC+SSIM; (f) and (n) MSE; (g) and (o) CC; and (h) and (p) MI.

III.B. Regularization Comparisons

Fig. 5 shows results generated using different regularizers. The three images in the first column are a slice of the XCAT attenuation map (moving image), a slice of patient CT image (fixed image), and a slice of the XCAT label map. The second through last columns show the deformed moving image (first row), transformed labels (second row), and deformed grids (last row) by using no regularization, diffusion regularization, TV regularization, diffusion with none-negative Jacobian regularization, and Gaussian smoothing, respectively. The deformed moving image using no regularization had a virtually identical appearance compared to the fixed image. However, the deformed label maps were unrealistic: in the regions highlighted in rectangles, the bone marrow appeared outside of the cortical bone. Applying regularization to the deformation field helped with this issue, but there was a clear trade-off between the similarity to the fixed image and the smoothness of the deformation field. This trade-off was quantitatively studied, and the results are discussed in the next section. We specifically quantifed the regularity of the field by counting all the pixel deformations for which the transformation was not diffeomorphic (i.e., folding or |J_ϕ| ≤ 0)^22,68.

Figure 5:

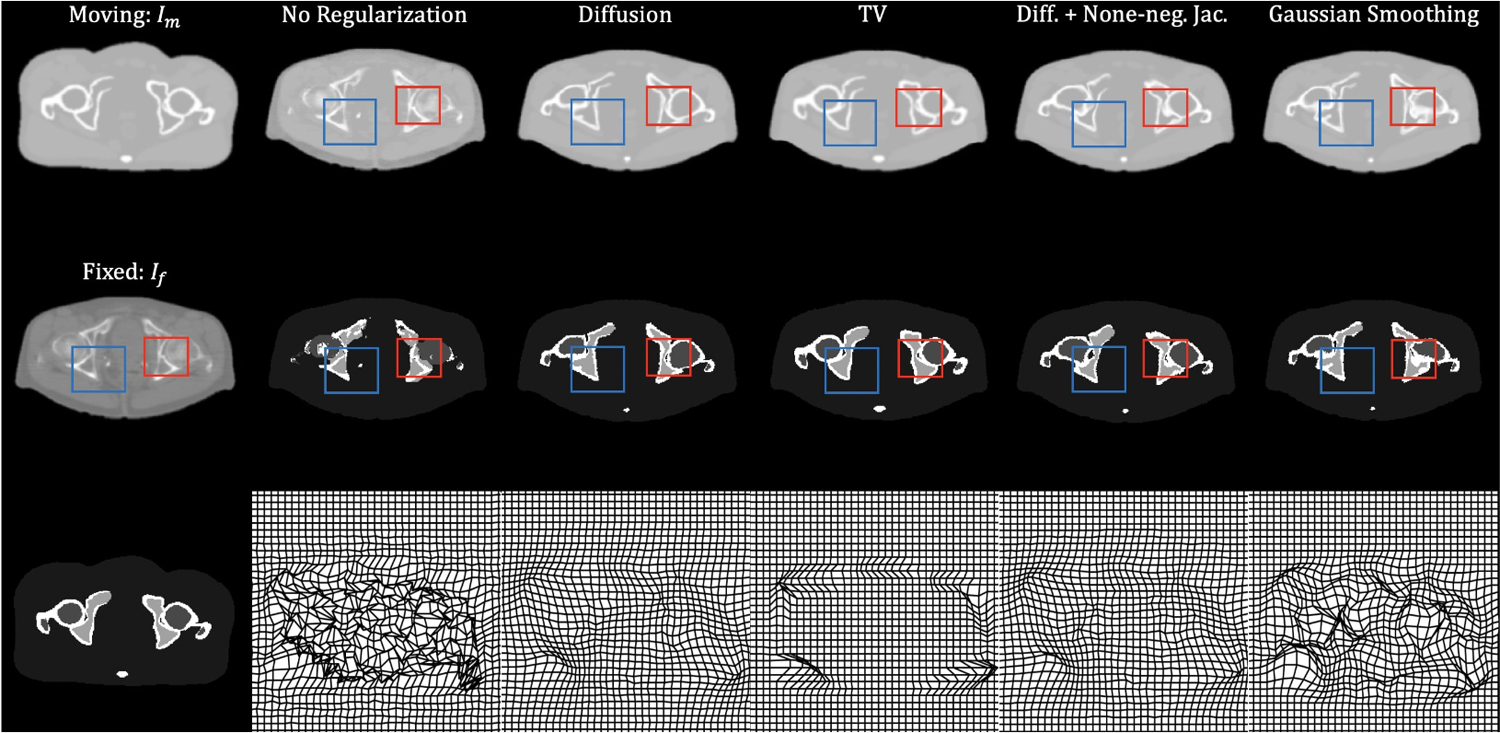
Example results from different regularization techniques. The three figures in the first column represent moving image, fixed image, and the corresponding label map, respectively. The second to last column shows deformed images: the first row shows the deformed XCAT phantom, the second row shows the deformed label map, and the last row shows the deformed grid.

III.C. Registration Performance Comparisons

In this subsection, we compared the proposed method with the SyN²⁰ and VoxelMorph^22,33 algorithms. Since VoxelMorph requires prior training, it was evaluated using a leave-oneout method: images from eight patients were used for training (~1024 2D slices), and images from one patient were treated as the test set (~128 2D slices). Then, we altered patients whose image was used for training and testing, rendering 9 possible combinations of the patient images. Figs. 6 and 7 show comparisons of the proposed method with different regularizations, the SyN, and the VoxelMorph methods, respectively. The first column shows the moving and fixed images. The second to the last column shows the deformed XCAT images (upper row) and deformed labels (lower row), respectively. Based on these qualitative results, the proposed method provides a more detailed deformation than other methods, especially in terms of the anatomy of the bone structures and soft tissues. Since a gold-standard bone segmentation was not available for the NaF Prostate dataset⁶⁵, the registration performance was evaluated quantitatively based on MSE and SSIM between I_m ◦ϕ and I_f. The results are shown in Table. 2. Without any regularization of the deformation field, the proposed method gave a mean SSIM of 0.955 and a mean MSE of 37.340, which outperformed the SyN and VoxelMorph by a significant margin (with p-values < 0.0001 from the paired t-test).

Figure 6:

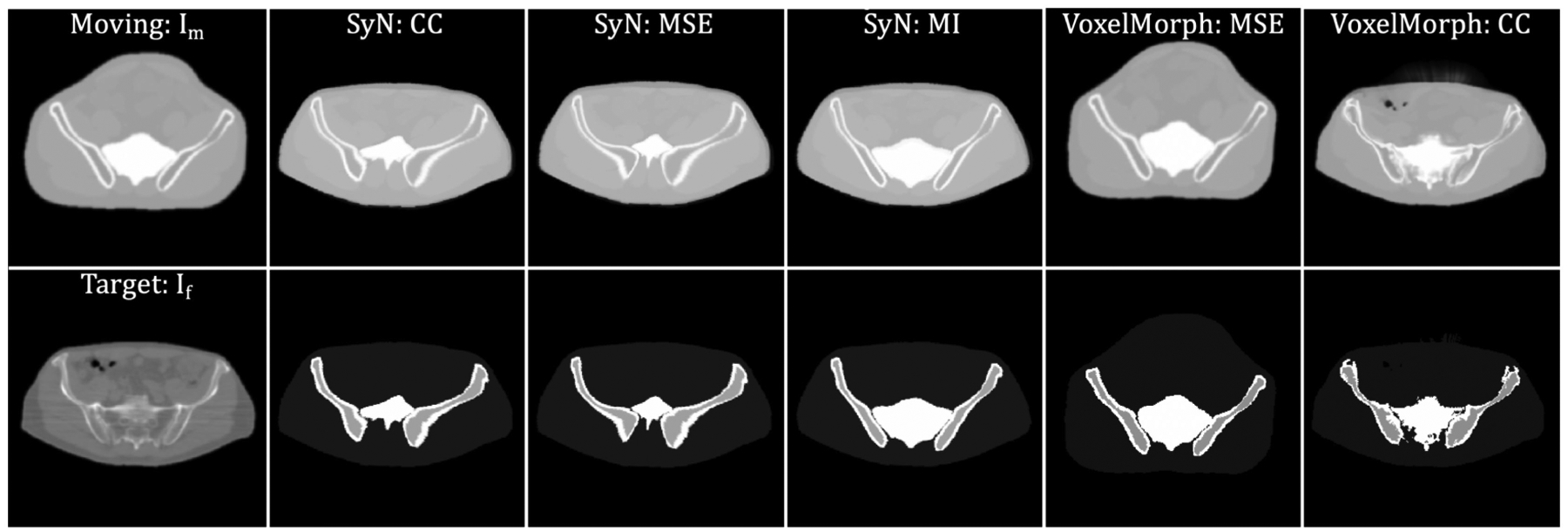
Example results generated by two baseline methods, SyN and VoxelMorph. The 1^st column: moving (the XCAT attenuation map) and target image (patient CT). For the second to the last column, the first row corresponds to the deformed moving images, and the second row shows the deformed label map. The 2^nd through 4^th columns show results from SyN using CC, MSE, and MI. The 5^th column through the last column shows results from VoxelMorph using MSE and CC.

Figure 7:

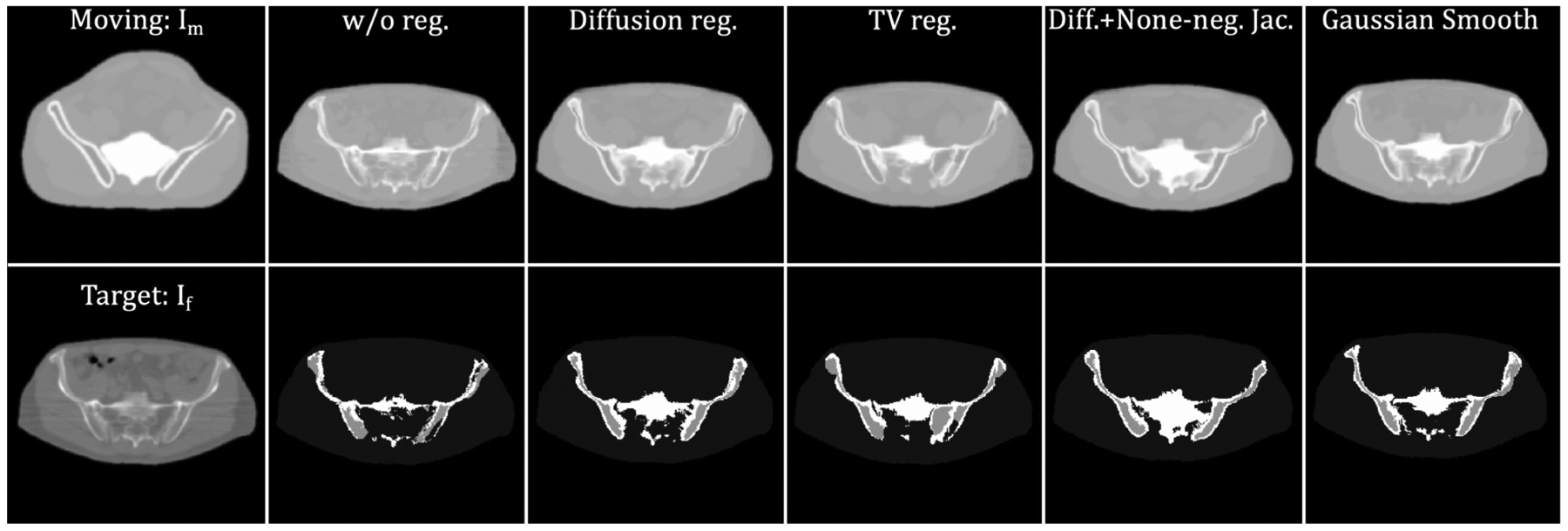
Example results generated by the proposed method with different regularization techniques. The 1^st column exhibits moving (XCAT attenuation map) and target image (patient CT). The 2^nd column to the last column display the deformed results. These correspond, respectively, to no regularization, diffusion regularization, TV norm, diffusion with none-negative Jacobian regularization, and Gaussian smoothing.

Table 2:

Comparison of SSIM, MSE, and the number and percentage of pixel locations with non-positive Jacobian determinant among the proposed method (UnsupConvNet), SyN, and VoxelMorph. The top three results in SSIM and MSE are shown in bold, underline, and italics, respectively. Evaluations were done on 2D images with size 384 × 384.

Method	SSIM	MSE	|Jϕ| ≤ 0 (counts)	% of |Jϕ| ≤ 0 (%)
Affine only	0.83 ± 0.008	69.2 ± 2.7	-	-
VoxelMorph (MSE)22	0.88 ± 0.003	47.0 ± 2.4	685 ± 185	0.5 ± 0.1
VoxelMorph (CC)22	0.92 ± 0.006	43.5 ± 4.8	2754 ± 370	1.9 ± 0.3
SyN (MSE)20	0.88 ± 0.011	52.0 ± 4.1	-	-
SyN (MI)20	0.88 ± 0.011	55.1 ± 4.0	-	-
SyN (CC)20	0.89 ± 0.011	52.8 ± 4.1	-	-
UnsupConvNet (w/o regularization)	0.96 ± 0.007	37.3 ± 5.1	21082 ± 3938	14.3 ± 2.7
UnsupConvNet (w/ diffusion regularization)	0.93 ± 0.008	42.6 ± 5.4	1202 ± 225	0.8 ± 0.1
UnsupConvNet (w/ diff. + None-neg. Jac. reg.)	0.92 ± 0.009	44.8 ± 4.9	518 ± 74	0.4 ± 0.1
UnsupConvNet (w/ TV regularization)	0.87 ± 0.030	54.7 ± 9.3	659 ± 459	0.4 ± 0.3
UnsupConvNet (w/ Gaussian filtering)	0.94 ± 0.008	41.5 ± 5.4	8500 ± 1829	5.7 ± 1.3

The plots in Fig. 8 exhibit the impact of different regularization parameters on the SSIM, MSE, and the number of folded pixels. A decreasing trend in registration accuracy and the number of folded pixels was generally seen with increasing weighting parameter values (λ and σ) for regularizers. Among the different regularization methods, the diffusion regularizer (column 1 in Fig. 8) with λ = 1 yielded the best balance between registration accuracy and the number of folded pixels. Overall, the method achieved comparable performances to VoxelMorph in terms of deformation regularity (as measured by the number of pixels where there was folding) while providing better registration accuracy.

Figure 8:

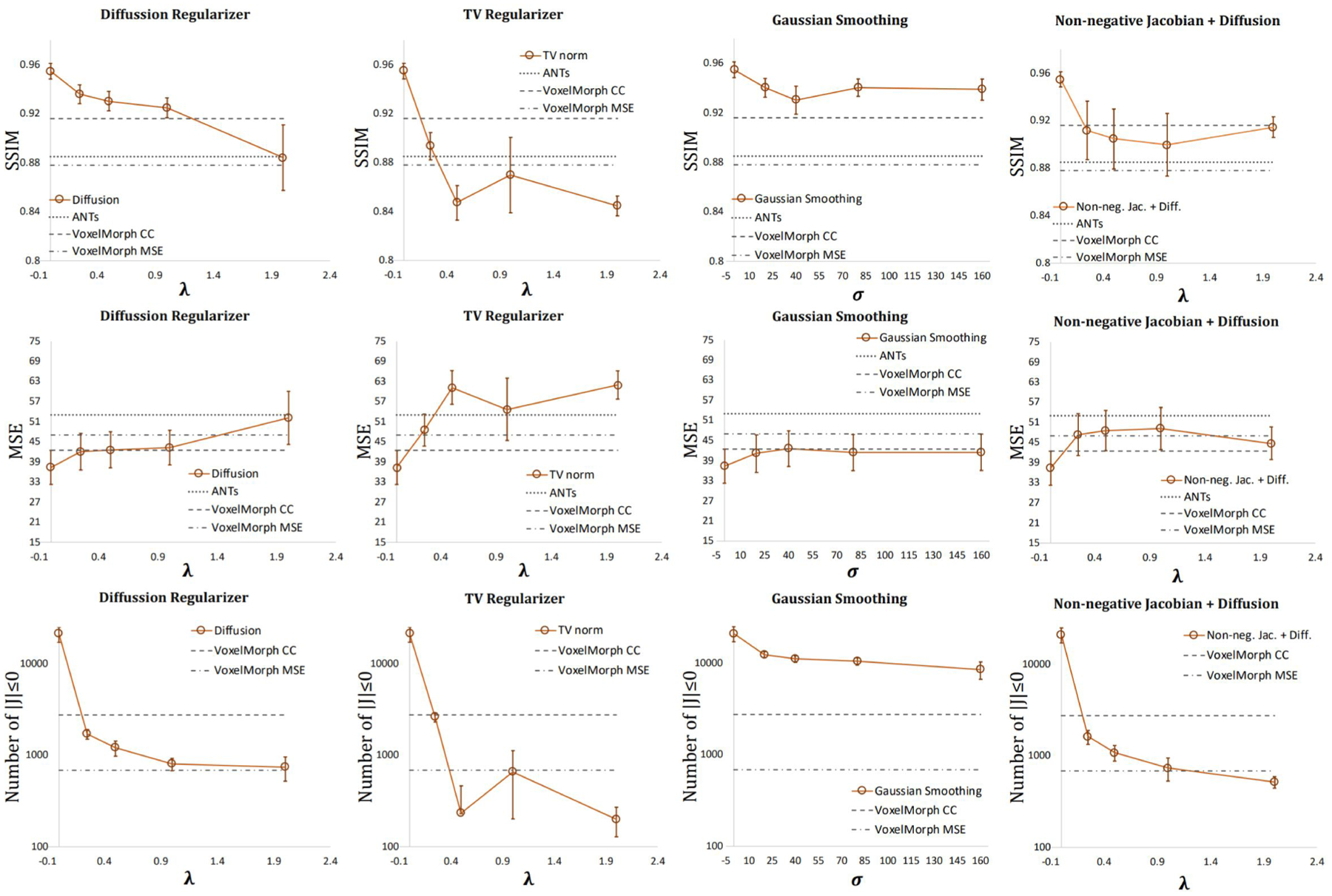
The effect of different regularization parameters on the registration accuracy (SSIM and MSE), and deformation regularity (number of folded pixels, i.e. where the determinant of Jacobian was ≤ 0). First to last rows indicate the performances in SSIM, MSE, and number of folded pixels, respectively. The columns, from left to right, are the results generated using the diffusion regularizer, TV regularizer, Gaussian smoothing, and non-negative Jacobian + diffusion regularizer, respectively.

IV. Discussion

IV.A. Fully Unsupervised ConvNet

We have developed a fully unsupervised U-Net-based registration framework for generating highly-detailed, anatomically-realistic phantoms. The proposed method works on an image pair consisting of the XCAT attenuation map and patient CT. Thus, it does not require prior training using a large dataset. This makes the proposed method different from the previously proposed self-supervised ConvNet-based registration algorithms, such as VoxelMorph^22,30,33, DIRNet³², or DLIR³¹, which require a training stage. However, while the proposed method does not demand training data, there is a trade-off: like traditional techniques^18,20, the proposed method minimizes a loss function iteratively for the given inputs, which leads to the increased computational time and complexity. The runtime for performing registration on a pair of 3D volumes (with size 192×192×128) is roughly an hour on an NVIDIA Quadro P5000 GPU. The computational time may be reduced either by using a smaller ConvNet (i.e., few trainable parameters) or using a faster GPU.

IV.B. Loss Function Choice

We demonstrated in the previous sections that the proposed SSIM-based loss function yielded the best qualitative performance and thus was more suitable for XCAT-to-CT registration. While other loss functions, MSE, CC, or MI, are commonly used in other image registration tasks, they all performed poorly in this task. Specifically, the failure of MSE is likely due to the lack of spatial information, and it is sensitive to linear transformations of the mean intensity values (as shown in the third to last column in Fig. 4). Another commonly used metric, CC, also produced sub-optimal results that exhibited image artifacts (as shown in the seventh column in Fig. 4). We also showed that using PCC or SSIM alone did not produce good results: while PCC loss was robust to image artifacts, it produced ”discretized” results around the spine (see the regions highlighted in rectangles in (c) and (j) in Fig. 4). On the other hand, the SSIM loss function produced an image that reproduced even the noise and artifacts in the target image (as shown in (d) in Fig. 4).

IV.C. Regularization Choice

Despite the fact that the proposed method without any regularization generated a deformed image that was almost identical in appearance to the fixed image, the warped label maps were not realistic (see the second column in Fig. 7). This was mainly caused by the non-smooth and non-invertible deformation field that produced a large number of folded pixels. Adding a regularizer to the loss function enforced the smoothness in the deformation field, and thus produced more realistic warped label maps. However, as shown in Fig. 8 and Fig. 9, a decreasing trend in the similarity measure to the fixed image was observed with improved deformation regularity (i.e., a decrease in the number of non-positive Jacobian determinants). Images in (b), (f), and (j) in the right panel of Fig. 9 show the deformed XCAT attenuation map using different weights, λ, of the diffusion regularization. For λ = 0 (no regularization), the soft-tissue components (e.g., liver) in (b) showed good alignment with those in the target image ((c) in the left panel of Fig. 9). When λ was increased (as shown in the second and the last row in the right panel of Fig. 9), the smoothness of the resulting deformation fields gradually improved (as shown in (d), (h), and (I)). However, the mismatch between the soft-tissue components in the deformed and the fixed image began to appear, while regions with higher contrast (e.g., bone and outer surface) retained the good alignment. The experimental results in Fig. 8 show that the diffusion regularization worked best among the regularizers investigated. It sacrificed a modest amount of image similarity (0.93 in mean SSIM and 42.6 in mean MSE) in exchange for smoother deformation fields with a smaller number of non-positive Jocobian determinants (< 0.8% of pixel transformations were noninvertible). It should be noted that the regularizers used in this work only consider global smoothing, thus we did not allow motion discontinuities between organs. Regularization methods that preserve sliding-motion^23,24,25 could be included in the future to address the problem of sliding organs.

Figure 9:

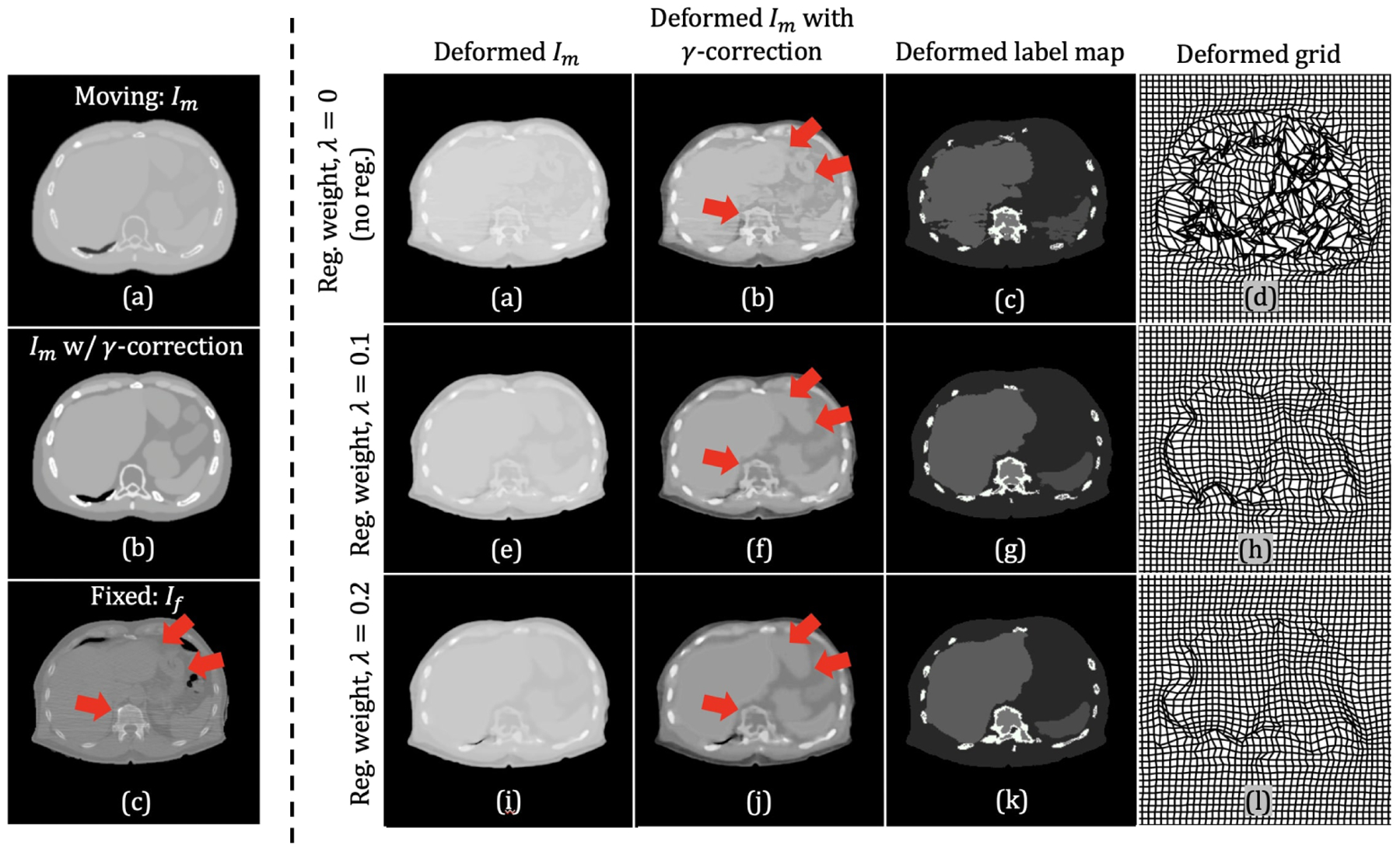
Visual effects of the diffusion regularization on the deformed image. Left panel: Images in (a), (b), and (c) corresponds to, respectively, moving image, moving image with Gamma-correction (γ = 1.8), and fixed image. Right panel: Each row represents the results obtained using different regularization weights. The first through last columns, from left to right, represent deformed moving image, deformed moving image with Gamma-correction, deformed label map, and the corresponding deformation field.

IV.D. Example Application: SPECT simulations

In this section, we demonstrate a 3D application of the proposed method to generate realistic medical image simulations. We employed the proposed registration method to map the 3D volume of the XCAT attenuation map to a 3D patient CT scan acquired from a clinical bone SPECT/CT acquisition. We then generated a realistic simulated SPECT image on the basis of the resulting deformed XCAT attenuation map as described below. The patient scan was acquired using a clinical whole-body SPECT/CT scan protocol; the CT scan was a low-dose one designed to provide an attenuation map. Both SPECT and CT images were reconstructed using scanner software. Two sample coronal slices of the patient scans are shown in the second and the third columns of the left panel in Fig. 10; the second and third columns show the CT and SPECT images, respectively. We used the proposed method with a diffusion regularizer (λ = 1) to perform the 3-dimensional registration. We resampled the image volumes to a size of 192×192×128 in order to fit into the GPU memory of 16 GB. The memory required to perform this 3D registration was 15 GB. The resulting deformed XCAT attenuation map and the corresponding SPECT simulation are shown in the fourth and the fifth columns, respectively. We then added several artificial lesions to the phantoms, and two example slices of the resulting SPECT simulation are shown in the last column. SPECT projections were simulated by an analytic projection algorithm that realistically models attenuation, scatter, and the spatially-varying collimator-detector response^47,48. We computed attenuation values on the basis of the material compositions and the attenuation coefficients of the constituents at 140 keV, the photon energy of Technetium-99m. We inserted several artificial sclerotic bone lesions to random bone regions with increased attenuation coefficient and radio-pharmaceutical uptake. The cortical and trabecular bones had an uptake of, respectively, 12.6 and 23.2 times that of the soft-tissue background, and bone lesions had an uptake of 3.5–4.5 times that of normal bone. These scale factors were computed based on the patient SPECT scan. SPECT simulations were reconstructed using a the ordered subsets-expectation maximization algorithm (OS-EM)^{69 70} using 5 iterations and 10 subsets. The figure on the right panel in Fig. 10 shows three transverse slices of the patient SPECT (top row) and the simulated SPECT (bottom row). Because the deformed XCAT phantom was able to successfully capture the anatomical structures in the patient scan, when combined with realistic physics models of image formation processing, the resulting SPECT simulation appears quite realistic compared to the patient SPECT scan. In addition, the relationship between the generated phantom activity distribution and the projection data is quantitatively realistic because of the method used to generate the projections. Fig. 11 shows some additional SPECT simulations (with lesions added to various bone locations) generated using the proposed method with the 9 clinical CT scans from the TCIA dataset. In that figure, each row represents a different patient.

Figure 10:

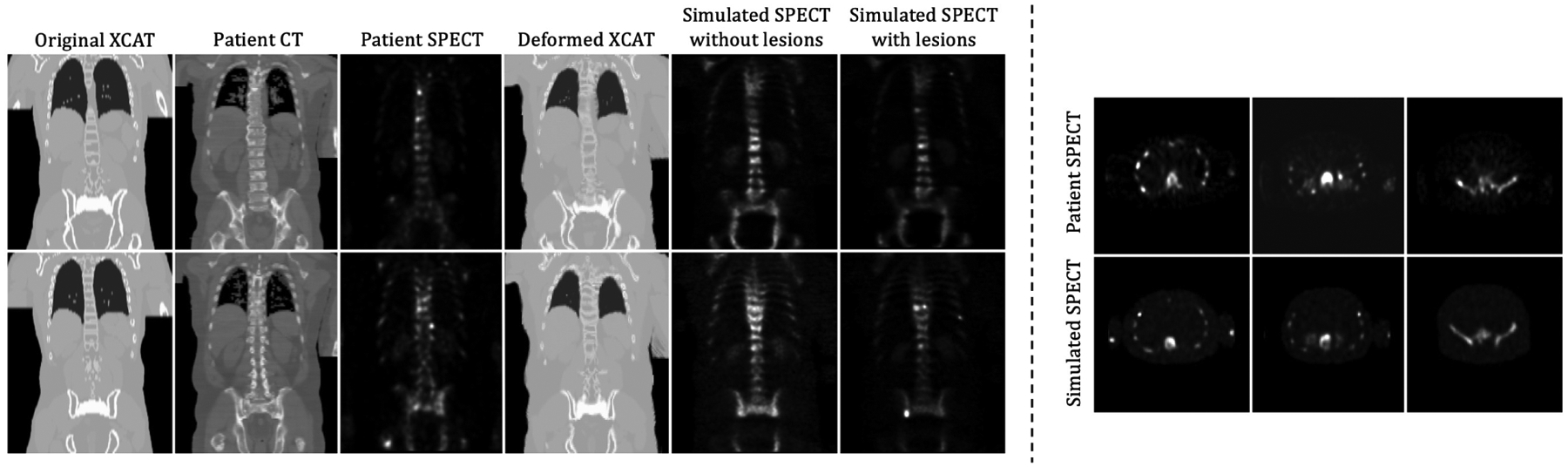
Visualization of the deformed XCAT attenuation map and SPECT simulations. Left: Two coronal slices of the original XCAT, patient CT and SPECT scans, the registered XCAT, the SPECT simulation, and the simulated SPECT with lesion added. Right: Comparison of transverse slices between patient SPECT scan and SPECT simulation.

Figure 11:

Example coronal slices of the SPECT simulations generated by the proposed method, where each row represents a different patient.

V. Conclusion

We have developed a method to create anthropomorphic phantoms using an unsupervised, ConvNet-based, end-to-end registration technique. Unlike existing deep-learning-based registration methods, the proposed method requires no prior training. While classical registration methods also do not require training data, they work in a lower-dimensional parameter space; the proposed approach operates directly in the high-dimensional parameter space common to deep-learning-based methods but without any prior training. Compared to the commonly used loss functions in ConvNet-based registration, we demonstrated that the registration performance can be improved by use of the combination of SSIM and PCC as a loss function for updating the parameters in the ConvNet. The proposed method was evaluated for the application of registering the XCAT attenuation map with real patient CT scans as part of a process to simulate realistic nuclear medicine images. We compared the registration performance of the proposed technique in terms of SSIM and MSE to conventional stateof-the-art image registration methods. Both quantitative and qualitative analyses indicated that the proposed method provided the best registration results. We also demonstrated that the proposed method, combined with accurate simulation tools, provided a highly realistic anthropomorphic medical image with known truth that faithfully represents the image formation process and qualitatively matches the appearance of a real patient image.