Abstract
Neurons in the primary visual cortex (V1) receive excitation and inhibition from distinct parallel pathways processing lightness (ON) and darkness (OFF). V1 neurons overall respond more strongly to dark than light stimuli, consistent with a preponderance of darker regions in natural images, as well as human psychophysics. However, it has been unclear whether this “dark-dominance” is because of more excitation from the OFF pathway or more inhibition from the ON pathway. To understand the mechanisms behind dark-dominance, we record electrophysiological responses of individual simple-type V1 neurons to natural image stimuli and then train biologically inspired convolutional neural networks to predict the neurons' responses. Analyzing a sample of 71 neurons (in anesthetized, paralyzed cats of either sex) has revealed their responses to be more driven by dark than light stimuli, consistent with previous investigations. We show that this asymmetry is predominantly because of slower inhibition to dark stimuli rather than to stronger excitation from the thalamocortical OFF pathway. Consistent with dark-dominant neurons having faster responses than light-dominant neurons, we find dark-dominance to solely occur in the early latencies of neurons' responses. Neurons that are strongly dark-dominated also tend to be less orientation-selective. This novel approach gives us new insight into the dark-dominance phenomenon and provides an avenue to address new questions about excitatory and inhibitory integration in cortical neurons.
SIGNIFICANCE STATEMENT Neurons in the early visual cortex respond on average more strongly to dark than to light stimuli, but the mechanisms behind this bias have been unclear. Here we address this issue by combining single-unit electrophysiology with a novel machine learning model to analyze neurons' responses to natural image stimuli in primary visual cortex. Using these techniques, we find slower inhibition to light than to dark stimuli to be the leading mechanism behind stronger dark responses. This slower inhibition to light might help explain other empirical findings, such as why orientation selectivity is weaker at earlier response latencies. These results demonstrate how imbalances in excitation versus inhibition can give rise to response asymmetries in cortical neuron responses.
Keywords: dark dominance, neurophysiology, receptive field, system identification, V1, visual cortex
Introduction
The early thalamocortical visual system is separated into two distinct pathways: an ON pathway, which responds more to lighter parts of images; and an OFF pathway, which encodes darker image regions. Neurons in primary visual cortex (V1) combine inputs from these two pathways, but the nature of this integration is still poorly understood.
V1 neurons evidently receive asymmetrical inputs from the two pathways, since they are on average more responsive to dark than light stimuli (Jin et al., 2008; Yeh et al., 2009), especially at low spatial frequencies (Kremkow et al., 2014; Jansen et al., 2019) and shorter time latencies (Komban et al., 2014). This asymmetry is presumably adaptive because of the preponderance of dark regions in natural images (Ratliff et al., 2010), which is also more pronounced at lower spatial frequencies (Cooper and Norcia, 2015). These asymmetries may influence human perception, since dark stimuli are processed faster and more reliably than light stimuli (Buchner and Baumgartner, 2007; Komban et al., 2011).
There are more OFF than ON excitatory inputs from the LGN to layer 4 of V1, which could help explain why responses to dark stimuli are stronger in V1 (Jin et al., 2008). However, this does not explain why more dark-dominant neurons are found in layers 2/3 than in layer 4 (Yeh et al., 2009). This discrepancy could be explained by stronger ON than OFF intracortical inhibition within V1 (Tucker and Fitzpatrick, 2006; Xing et al., 2014; Taylor et al., 2018). Hence, whether dark-dominance is mostly because of excitation to dark stimuli or inhibition to light stimuli remains unclear. Here we develop a novel machine learning approach to disambiguate excitation from inhibition in extracellular recordings, which allows us to make quantitative inferences about how cortical neurons integrate ON and OFF inputs.
To better understand how visual stimuli drive V1 responses, we predict the responses of recorded neurons to natural images with a simple, biologically inspired convolutional neural network. This neural network processes the natural images' light (ON) and dark (OFF) information in two distinct pathways. The first layer of each pathway consists of a convolution with a parametrized 2D Gaussian spatial filter, which represents the responses of LGN neurons (omitting the weaker surrounds) (Croner and Kaplan, 1995). The second layer is a linear-weighted sum of the excitatory or inhibitory contributions of each pathway, which then sum to provide the model's output. From these estimated weights, we can infer functional excitation and inhibition from each pathway; that is, how light and dark stimuli increase or decrease a neuron's firing rate at every spatial location and temporal lag of a V1 cell's receptive field. While functional excitation and inhibition might not necessarily represent a neuron's synaptic inputs (see Discussion), they reflect how a neuron integrates ON and OFF thalamocortical inputs.
Using this approach, we find the dark-dominance phenomenon in V1 neurons to only occur at the early response latencies. We show these stronger dark responses to be predominantly driven by a lack of functional inhibition to dark stimuli at early latencies. We also find that this slower inhibition to dark stimuli is associated with less orientation selectivity (OS) in neurons' early responses (Ringach et al., 1997; Shapley et al., 2003). These findings suggest that slower functional inhibition to dark than to light stimuli plays a crucial role in the dark-dominance found in primary visual cortex.
Materials and Methods
Animal preparation
Anesthesia in adult cats was induced by isoflurane-oxygen (3%-5%) inhalation, followed by intravenous cannulation and bolus injection of propofol (5 mg/kg). Surgical anesthesia was maintained with supplemental doses of propofol. Glycopyrrolate (30 μg) and dexamethasone (1.8 mg) were administered, and a tracheal cannula or intubation tube was inserted. Throughout the surgery, body temperature was thermostatically maintained and heart rate was monitored (Vet/Ox Plus 4700).
The animal was then positioned in a stereotaxic apparatus and connected to a ventilator (Ugo Basile 6025). Cortical Area 17 was exposed by a craniotomy (P3/L1) and a small durotomy, and the cortical surface protected with 2% agarose capped with petroleum jelly. Local injections of bupivacaine (0.50%) were administered at all surgical sites. During recording, anesthesia was maintained by infusion of propofol (5.3 mg·kg−1·h−1), and in addition, remifentanil (initial bolus injection, 1.25 μg·kg−1, then infusion, 3.7 µg·kg−1·h−1) and O2/N2O (30:70 ratio) delivered through the ventilator. Paralysis was produced with a bolus intravenous injection of gallamine triethiodide (to effect), followed by infusion (10 mg·kg−1·h−1). Throughout subsequent recording, expired CO2, EEG, ECG, body temperature, blood oxygen, heart rate, and airway pressure were monitored and maintained at appropriate levels. Intramuscular glycopyrrolate (16 μg) and dexamethasone (1.8 mg) were also administered daily.
Corneas were initially protected with topical carboxymethylcellulose (1%) and subsequently with neutral contact lenses. Spectacle lenses were selected with slit retinoscopy to produce emmetropia at 57 cm, and artificial pupils (2.5 mm) were provided. Topical phenylephrine hydrochloride (2.5%) and atropine sulfate (1%), or cyclopentolate (1.0%) in later experiments, were administered daily.
All animal procedures were approved by the McGill University Animal Care Committee and are in accordance with the guidelines of the Canadian Council on Animal Care.
Extracellular recording
Recordings were performed using 32-channel silicon probes (NeuroNexus), in most cases polytrodes (A1x32-Poly2-5 mm-50s-177) or occasionally linear arrays (A1x32-6 mm-100-177), advanced with a stepping motor microdrive (M. Walsh Electronics, uD-800A). Raw electrophysiological signals were acquired with a Plexon Recorder (3 Hz to 8 kHz; sampling rate, 40 kHz), along with supplementary signals from a small photocell placed over one corner of the visual stimulus CRT, which were used for temporal registration of stimuli and spikes, and to verify the absence of dropped frames. Spike waveforms were carefully classified from the recorded multichannel data into single units, using Spikesorter (Swindale and Spacek, 2014). Only clearly sorted units were used for further analysis.
In total, 110 single units from 37 penetrations in 8 cats (4 males, 4 females) were analyzed. These recording experiments involved laboratory personnel working on other projects. Of these neurons, 6 were rejected because part of their receptive fields was outside the screen, and 33 were rejected because the predictive performance of the fitted model was too low (see Model architecture). The sample size included the remaining 71 neurons.
Visual stimuli
Visual stimuli were presented on a γ-corrected CRT monitor (NEC FP1350, 20 inches, 640 × 480 pixels, 150 Hz, 36 cd/m2) at a viewing distance of 57 cm. Stimuli were produced by an Apple Macintosh computer (MacPro, 2.66 GHz, 6 GB, MacOSX version 10.6.8, NVIDIA GeForce GT 120) using custom software written in MATLAB (version 2012b) with the Psychophysics Toolbox (version 3.0.10) (Brainard, 1997; Pelli, 1997; Kleiner et al., 2007). We selected a channel with good spike responses to hand-held bar stimuli, which we used to determine the dominant eye (with the nondominant eye subsequently occluded), and to position the CRT monitor to be approximately centered around the population receptive field.
Visual stimuli were ensembles of 375 natural images taken from the McGill Calibrated Color Image Database (Olmos and Kingdom, 2004), cropped to 480 × 480, converted to monochrome 8-bit integers, as in Talebi and Baker (2012) but with a higher RMS contrast. We randomly presented each ensemble at 75 images per second (i.e., every 13.33 ms) in short movies of 5 s each. These stimuli were not “natural movies,” to avoid their strong temporal correlations, which would lead to substantially biased receptive field estimates using our methodology. We have observed such biases in simulated experiments on known models, which can even lead to spatiotemporal receptive field estimates with responses at negative latencies (see, e.g., Parker et al., 2022). We separated the ensembles into three sets, to evaluate predictive performance independently from overfitting. The training set had 20 movies which were presented 5 times each, while the validation and testing sets each had 5 movies which were presented 20 times each. The validation and testing sets were presented more often to provide less noisy estimates of the fitted model's predictive performance. Instances of these three subsets of movies were quasi-randomly interleaved throughout the 45 min recording session.
For the subsequent data analysis (described below), all images were resized from 480 × 480 to 40 × 40 before training (see below) to avoid overparameterization of the fitted model. Resizing was done using the Image module from the Python Image Library (Umesh, 2012).
Model architecture
The model architecture we use here is abstracted from known visual circuitry (see Fig. 1), and has parameters optimized to best predict a recorded cortical neuron's mean spiking responses to the natural image ensembles. We model LGN receptive fields as parametrized 2D isotropic gaussians, acting convolutionally on the stimulus images. The antagonistic surrounds are neglected, so there is only a pair of Gaussian width parameters, for the ON and OFF pathways, to be estimated. The connections between the Gaussian operators and the model cortical neuron are a pair of linear-weighted sums, or spatiotemporal filters, of rectified responses of the Gaussian operators, across a series of time lags. Each of these spatiotemporal filter acts like a “dense layer” in machine learning, but there is not a subsequent rectification. The output of each spatiotemporal filter might be thought of as a presynaptic membrane potential contribution, from its respective ON or OFF pathway.
Figure 1.
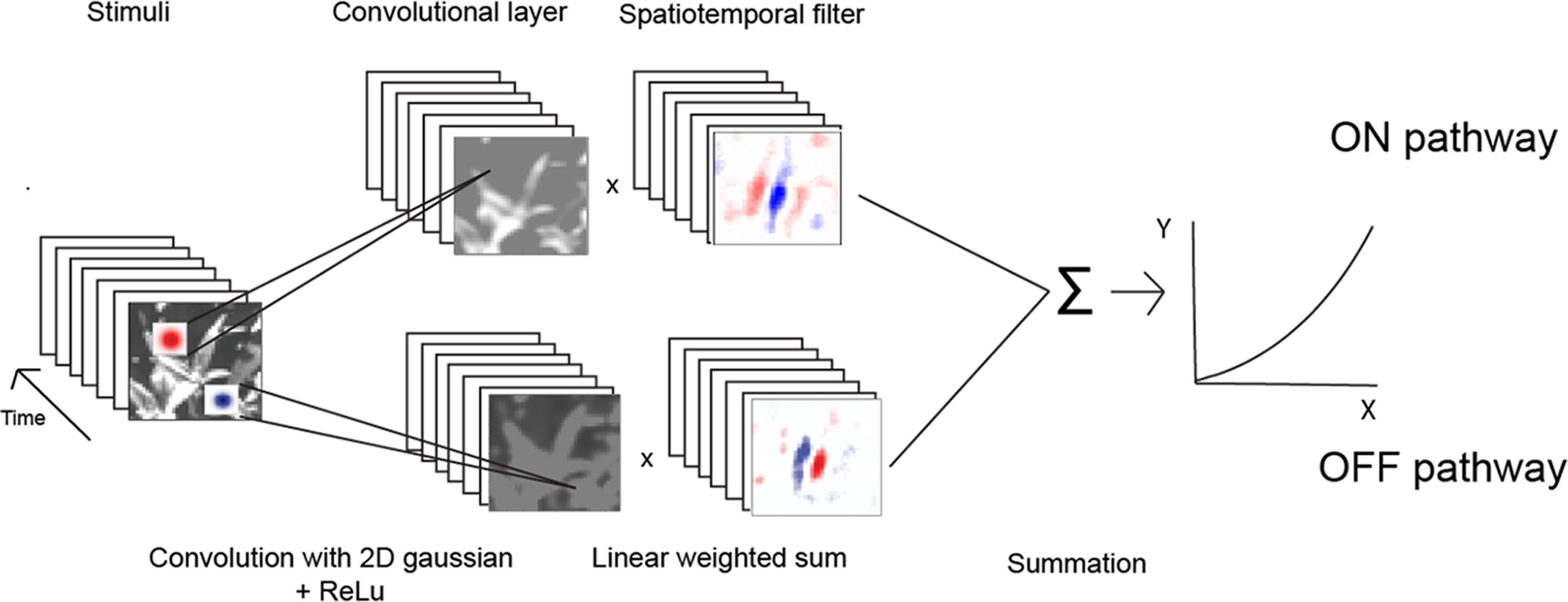
Model architecture for responses of a cortical neuron to visual stimuli, such as natural images. Light (ON pathway) and dark (OFF pathway) image regions are encoded as rectified responses of convolution with positive (light) and negative (dark) spatial gaussians, respectively. The output of this convolutional layer is then multiplied with a spatiotemporal filter of the same pathway that represents excitatory (red) and inhibitory (blue) weights for each spatiotemporal location. These linear-weighted sums are separately taken for each pathway and summed, followed by a half-power pointwise nonlinearity. A machine learning algorithm estimates the sizes of the parameterized Gaussian operators, and the two sets of spatiotemporal filters, for each of a series of latencies.
The inputs to the model are the pixel luminance values of the natural image stimuli (cropped, and spatially downsampled to 40 × 40 pixels, as described below). The mean of the inputs is centered at zero by subtracting the overall mean across all images within an ensemble. To model the neuron's temporal processing, the inputs to the estimated model (see below) are composed of the preceding 7 images, each of which was presented for 13.33 ms. The model output is the neuron's response, with spike times collected into time bins of 13.33 ms each (duration of each stimulus image frame).
The stimulus images are then convolved with a pair of parametrized 2D Gaussian filters (with positive or negative polarity for the ON and OFF pathways, respectively), each followed with a half-wave rectification. The 2D gaussians represent receptive fields of LGN neurons in which the weaker surrounds (Croner and Kaplan, 1995) are neglected, as follows:
| (1) |
where h and v are the horizontal and vertical distances between a pixel and the center of the Gaussian, respectively, and σ represents the SD (i.e., width) and α the amplitude (i.e., the height) of the 2D Gaussian. The σ parameter is estimated separately for each pathway (p). To allow each pathway to selectively process light or dark information, α is set to 1 for the ON pathway and −1 for the OFF pathway. The convolution of the 2D Gaussian with the inputs is half-wave rectified to mimic spike frequency responses of LGN neurons (Persi et al., 2011) as follows:
| (2) |
where i and j are the horizontal and vertical coordinates of the center of the 12 × 12 2D Gaussian, x is the luminance of a specific pixel (resized to a grid of 40 × 40), t is the number of time bins between the shown image and the recorded response (latency), and k is the time bin of the neuron's response. The convolution with the 2D gaussians is implemented with zero-padding and a “stride” of 1. Because of the first rectification, the ON-pathway encodes luminance above (lighter than) the mean, and the OFF-pathway luminance below (darker than) the mean.
For each of the ON- or OFF-pathways, the model then takes a linear-weighted sum of the convolution outputs from the respective rectified gaussians, with each weight notionally representing the excitatory or inhibitory inputs from an array of LGN cells to the cortical neuron. The sum of responses from these spatiotemporal filters is followed by a rectified power law output nonlinearity, which forms the final output of the model and the prediction of the neuron's mean spiking response as follows:
| (3) |
| (4) |
where w represents the spatiotemporal filter weights is the prediction of a neuron's response for the kth time bin, b is the exponent of the rectified power nonlinearity, and a is a scale (gain) factor.
To estimate the proportion of the variance in a neuron's response that is accounted for by the model's predictions, we calculate a variance-accounted-for (VAF) index by taking the square of the Pearson correlation coefficient between y (neuron's response) and (model's predictions). To ensure that the estimated weights are representative of each neuron's responses to visual stimuli, we excluded neurons with a VAF <10% in the testing set (see below). Based on this criterion, we excluded 33 neurons, which resulted in a sample size of 71 neurons for the remaining analysis.
Multifilter models (Gollisch and Meister, 2008) have also previously been used to infer ON and OFF inputs from neurons' responses. The machine learning model we use is conceptually similar; the main differences are that the convolution filters are parametrized as positive or negative 2D gaussians instead of being composed of free parameters, and that we use backpropagation instead of spike-triggered covariance to estimate the model's parameters. These differences have two key advantages compared with multifilter models. The first advantage is that backpropagation can more readily handle responses to natural images compared with spike-triggered covariance. The second advantage is that our model can estimate a significantly larger number of parameters because of the parameterization of the convolution filters and the use of regularization techniques, such as L2 and dropout.
Optimization and regularization
To characterize a neuron's receptive field, we find the model parameters which minimize the difference between its recorded responses and the responses predicted by the model of Equation 3, which requires fitting a total of 2 × 40 × 40 × 7 = 22,400 spatiotemporal filter weights, and 2 parameters () for the 2D gaussians (fitting of the two parameters for the output nonlinearity, Eq. 4, is described below). To minimize overfitting because of the large number of parameters, we use L2 regularization by penalizing the squared amplitude of the spatiotemporal filter weights (Hoel and Kennard, 1970), implemented by minimizing a loss function in which the first term is the squared error of the model prediction and the second term the regularization penalty as follows:
| (5) |
where is the neuron's recorded response, the model's predicted response for the kth time bin, wi,j,t,p the spatiotemporal filter weights (for the p-th On/Off stream, t-th latency, and i,j-th spatial position), and the L2 regularization hyperparameter. Based on pilot results from a representative subset of neurons, the hyperparameter is set to 5 × 10−6 in a first pass and 2 × 10−6 in a second pass (see below, three-pass training procedure). In the third pass, we train the model with different values of [1, 2, 4, 8, 16] × 10−6, and choose the value giving the best model performance on the validation dataset for each neuron.
This loss function is minimized using the Adam optimization algorithm (Kingma and Ba, 2014) with mini-batch gradient descent (M. Li et al., 2014). To further reduce overfitting, we apply dropout during training to both the convolutional and spatiotemporal filters with a probability of 50% (Srivastava et al., 2014).
The data are separated into training, validation, and test sets, corresponding to the three sets of stimulus movies. The model parameters are fit to the training set using a mini-batch size of 100 stimulus–response pairs. As an additional regularization measure, training is stopped if there is no improvement on the validation set in the preceding 50 epochs; then we use the model at its peak performance (i.e., 50 epochs before training stops) in subsequent analyses. We use a third, separate test set to obtain an unbiased estimate of predictive performance.
Three-pass training procedure
Because V1 receptive fields usually only occupy a small subset of the displayed visual stimulus images, it would be detrimental to optimize each neuron's model based on the full extent of the images. Doing so would entail a very high overparameterization, or a loss of spatial resolution because of excessive downsampling of the stimulus images, in either case yielding poorer predictive performance. To address this issue, we use a three-pass training procedure, with each pass improving the spatial resolution of the receptive field estimate. In the first pass, we optimize the model parameters using the full 480 × 480 stimulus images downsampled to 40 × 40. We then manually designate a square cropping window that encloses an area slightly larger than the apparent receptive field. Next, we crop the stimulus images within that window, and rescale each image within it to 40 × 40. Because of the resizing, this cropped image then has much better spatial resolution than the 40 × 40 image from the first pass. This image is used to retrain the model in the second pass, where we repeat the procedure, but with the cropped image. In the third pass, we further adjust the cropping window based on the model estimate obtained in the second pass. This third pass provides much higher accuracy in identifying the boundaries of the receptive field, and gives us the final model fits that we use for the remaining analysis. This three-pass training procedure allows us to characterize a neuron's receptive field with high resolution and substantially increases predictive performance.
Output nonlinearity
A cortical neuron's spike frequency response has often been modeled with a final output nonlinearity, consisting of a rectified power law (Heeger, 1991; Anzai et al., 1999; Persi et al., 2011). However, it has proven problematic to simultaneously estimate the power law exponent with the other parameters using the backpropagation algorithm employed here. This problem is most likely due in part to the “exploding gradient” problem (Pascanu et al., 2012). To resolve this issue, we initially set a power-law exponent value of unity (1.0), and wait 100 epochs into the training algorithm, to get a rough estimate of the other parameter values. We then pause the model optimization, to fit the two parameters of the output nonlinearity to the predicted versus measured neuron responses, and then resume full model parameter optimization, keeping the output nonlinearity parameters fixed.
To address the heavily uneven distribution of the measured firing rates, we bin the predicted responses into 100 bins of 75 responses each, and compute the mean measured response for each bin, a modification of the method used by Anzai et al. (1999). We then fit a scaling factor 'a' and an exponent 'b' (Eq. 4) to minimize the difference between the binned predicted responses and the measured spike rates y, using python scipy's 'optimize.curve_fit'.
Estimating functional excitation and inhibition
The spatiotemporal properties of each of the ON and OFF pathways in the fitted model depend on both the spatiotemporal filter weights and estimated 2D gaussians (which may differ in width for the ON and OFF pathways). To incorporate both in our analysis, for each of the ON and OFF pathways, we convolve the 2D Gaussian with the corresponding dense weights, to produce a 40 × 40 × 7 spatiotemporal filter for each pathway (ONRecon and OFFRecon). This “reconstructed” receptive field represents the neuron's responsiveness to either light or dark stimuli. For further analyses, we estimate the overall amount of functional excitation and inhibition from the filter for each pathway and time lag, by taking the sum of all positive or negative values in either the ON or OFF reconstructed receptive field. This procedure provides an inference of the total amount of ON excitation, ON inhibition, OFF excitation, and OFF inhibition contributing to each neuron's response as follows:
| (6) |
| (7) |
| (8) |
| (9) |
where ONRecon represents the contribution of the ON pathway to the estimated relationship between (light) stimuli and the neuron's responses (and similarly for OFFRecon). ONRecon and OFFRecon are estimated from the convolution of the spatiotemporal weights, wp,t, with the Gaussian layer, gp,t for p = 1 (and similarly for OFFRecon for p = 2) as follows:
| (10) |
| (11) |
Parts of our analysis are based on each neuron's peak latency of responsiveness, determined as the latency having the greatest variance in the sum of the reconstructions from each pathway as follows:
| (12) | (12) |
where
| (13) |
| (14) |
The latency t with the highest will be referred to as T.
The model architecture we use assumes no luminance adaptation; we define lights (positive values) and darks (negative values) by normalizing the inputs to a mean of 0 across all (cropped) images. Since this normalization determines what values are positives and negative, it also influences parameter estimation (e.g., ONexcit vs OFFexcit
The primary reason we did not model light adaptation is because it seems likely that the temporal dynamics of adaptation are much slower than 13.3 ms, with even fast adaptation having a decay time of ∼100 ms (Geisler, 1983). Since each stimulus is only shown for 13.3 ms, each neuron should adapt over the mean luminance of several past stimuli; because images are sampled randomly, the average of these previous images should be somewhat close to zero.
However, if this assumption is incorrect and these neurons do adapt quickly to changes in local luminance, this would have the potential to influence our results, especially because of the asymmetric distribution between lights and darks in natural images (Ratliff et al., 2010). To address this possibility, we reran the analysis with a simple model of adaptation, in which we normalize each cropped image (which is roughly the size of each neuron's receptive field) relative to its mean. The results we get are very similar to the ones shown below (see Figs. 2–7). Therefore, we think it is very unlikely that our findings are because of adaptation and the uneven distribution of lights and shadows in natural images.
Figure 2.
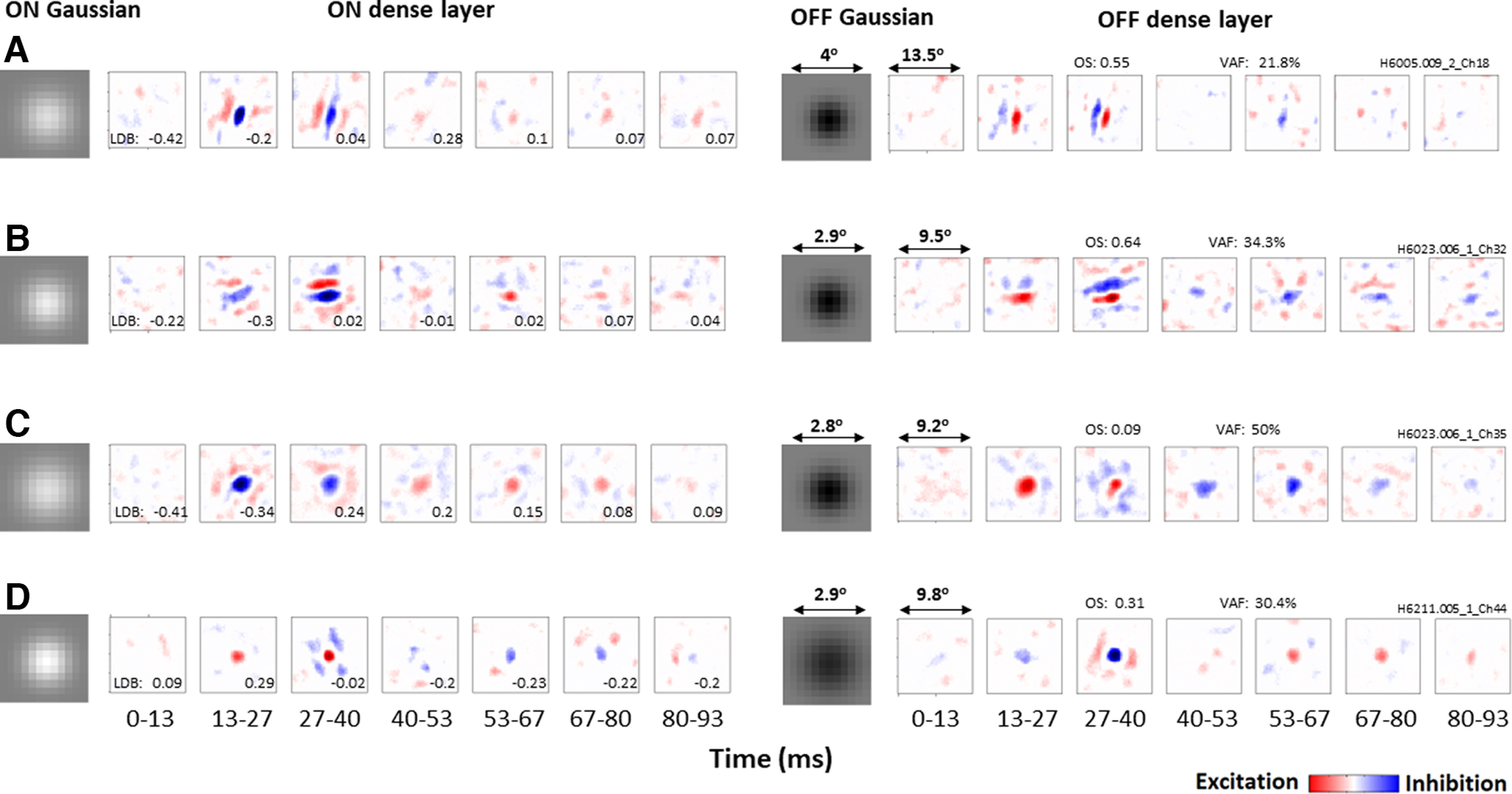
Gaussian and spatiotemporal filters estimated for four example neurons, one in each row. Left, Elements of ON pathway. Right, Elements of OFF pathway. Each spatiotemporal filter is shown as a series of latencies ranging from 0–13 to 80–93 ms, with neurons being most responsive at the 13–27 and 27–40 ms latencies. Red represents positive values (excitation). Blue represents negative values (inhibition). OS and VAF are indicated for each neuron, and LDB values for each latency. A, B, Both neurons respond more strongly to dark stimuli (LDB < 0) at the 13–27 ms latency, and become more balanced (LDB ∼ 0) at the 27–40 ms latency. C, Neuron is also dark-dominant at the 13–27 ms latency but responds more strongly to light at the 27–40 ms latency. D, Neuron that is instead light-dominant at the 13–27 ms latency, and balanced at the 27–40 ms latency.
Figure 7.
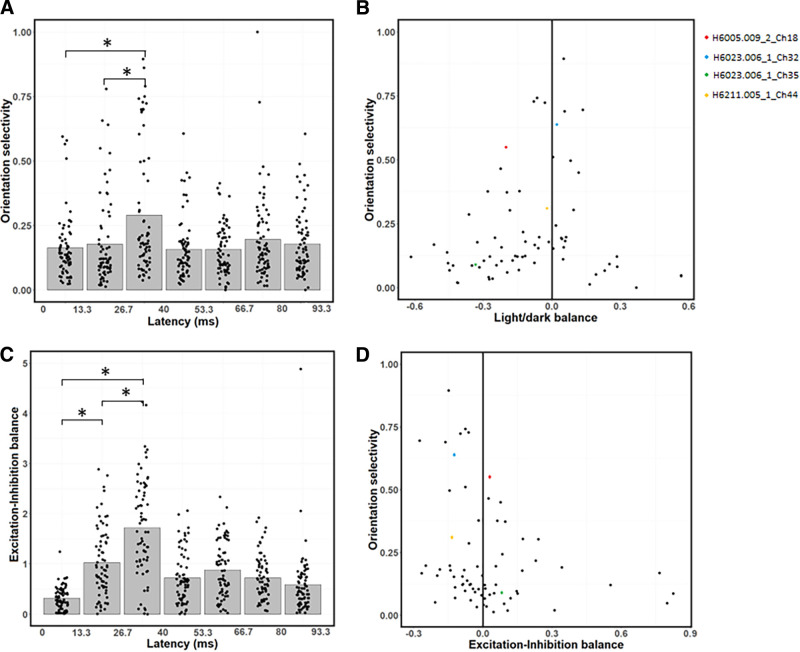
Changes in OS and EIB across latencies. A, Average OS peaks at the 26.7–40 ms latency, and is relatively low at the 0–13.3 and 13.3–26.7 ms latencies. B, Relationship between OS (ordinate) and LDB (abscissa). Neurons with higher OS tend to be more balanced. C, EIB index as a function of latency. Excitation is stronger than inhibition at the 0–13.3 and 13.3–26.7 ms latencies, while excitation and inhibition are relatively balanced at the 26.7–40 ms latency. D, Relationship between OS (ordinate) and EIB (abscissa). Neurons with stronger excitation than inhibition tend to be less orientation-selective. B, D, *p < 0.0167, significant paired t tests (with Bonferroni correction) between the first three latencies (0-40 ms).
Light/dark balance (LDB)
To quantify the extent to which individual neurons are light- or dark-dominated, we use an LDB index to indicate the relative influence of a neuron's light and dark weights as follows:
| (15) |
where
| (16) |
| (17) |
This index varies from −1.0 to 1.0, with positive LDB values indicating a neuron is light-dominated, and negative values that it is dark-dominated.
Excitation/inhibition balance (EIB)
The EIB index is similar to LDB but contrasts excitation with inhibition instead of light with dark as follows:
| (18) |
where
| (19) |
| (20) |
This index varies from −1 to 1, with positive EIB values indicating a neuron's response reflects relatively stronger excitation, and negative EIB values stronger inhibition. One neuron was excluded from this analysis for having an EIB value >3 SDs away from the mean.
Simulated responses to artificial stimuli
To better understand how dark-dominance influences neurons' responses to visual stimuli, we simulated the estimated models' responses to four different stimulus conditions. The 40 × 40 stimuli were tailored to each neuron's spatial receptive field, which we estimated by using Recon(i,j,T) (Eq. 13) at each neuron's peak latency T (see above). The four stimulus conditions (see Fig. 6) are the following: light falling on light-driven regions (LL), dark on dark-driven regions (DD), light on light-driven and half of dark-driven regions (LLHD), and dark on dark-driven and half of light-driven regions (DDHL) as follows:
where i and j index the spatial location of the image pixels, T is each neuron's peak latency, and b is a random value (either 0 or 1) drawn from an equiprobable Bernoulli distribution. The first two stimulus conditions (LL and DD) are designed to only recruit excitation, while the latter two conditions recruit a mixture of both excitation and half as much inhibition. We used the estimated model of each neuron to simulate its response to each of these four stimulus conditions at different latencies. (This procedure is equivalent to simulating the neuron's impulse response to each stimulus.) The average simulated responses across the entire sample at each latency are shown in Figure 6.
Figure 6.
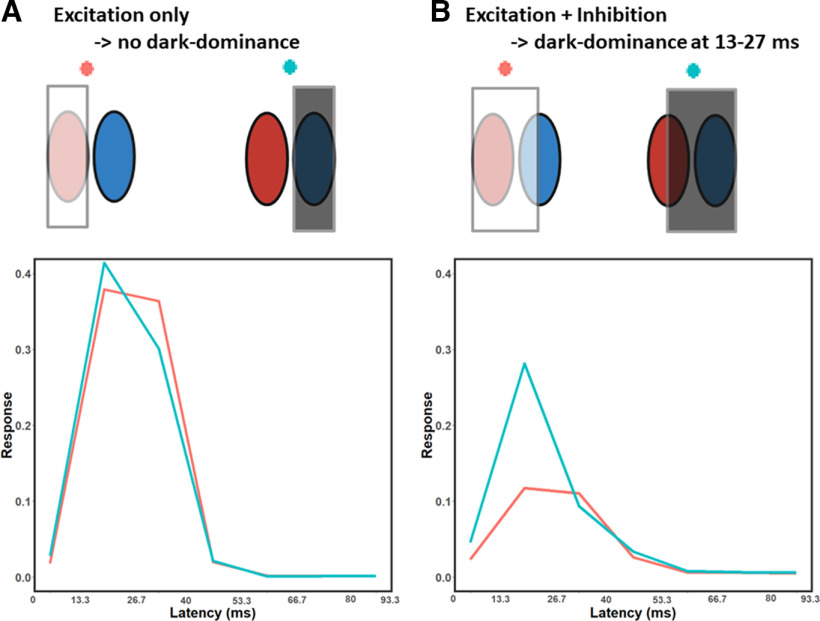
Average simulated temporal impulse responses to different stimuli. The stimuli were tailored to each neuron's receptive field and are presented here in a schematic form. A, Red represents the simulated responses to light stimuli on the light-driven regions of each neuron's receptive field. Blue represents the simulated response to dark stimuli on the dark-driven regions of each receptive field. The two responses are similar, suggesting responses to light and dark stimuli are relatively balanced across latencies. B, Red represents the simulated responses to light stimuli falling on the light-driven regions, and also on half of the dark-driven regions. Blue represents the simulated responses to dark stimuli on the dark-driven regions, plus on half of the light-driven regions. As expected, the responses are weaker than in A, and this decrease is much less pronounced for the dark stimulus (blue line) at the 13–27 ms latency. These results suggest that dark-dominance predominantly occurs when measured with stimuli that recruit both the excitatory and inhibitory regions of a neuron's receptive field.
OS
To better understand the relationship between dark-dominance and OS, we simulated the estimated models' responses to static sinewave gratings at each of 36 orientations (with increments of 5 degrees), 56 spatial frequencies (equally spaced from 0.0667 to 0.143 cycles per image), and 36 phases (increments of 5 degrees). These responses were used to compute the OS of each neuron using a vector summation method (Wörgötter and Eysel, 1987; Swindale, 1998) as follows:
| (21) |
with
| (22) |
| (23) |
where N is the number of sinewave gratings, xi is the orientation angle, and R(xi) represents the simulated responses. The OS index was computed separately for each latency in individual neurons.
Experimental design and statistical analyses
Most statistical tests here are paired t tests, to compare whether there is a significant difference between the means of two groups. We also use one-sample t tests to assess whether means differ significantly from zero, and perform linear regression to test the correlation between two sets of values. We adjust for multiple comparisons with Bonferroni corrections, where the significance threshold α of 0.05 is divided by the number of comparisons (e.g., Fig. 3C has 6 comparisons: α = 0.05/6 = 0.0083). Because visual responses are much weaker for latencies longer than 40 ms (see Fig. 2), statistical tests are only performed for the first three latencies in Figures 5 and 7, with the correction for multiple comparisons adjusted accordingly.
Figure 3.
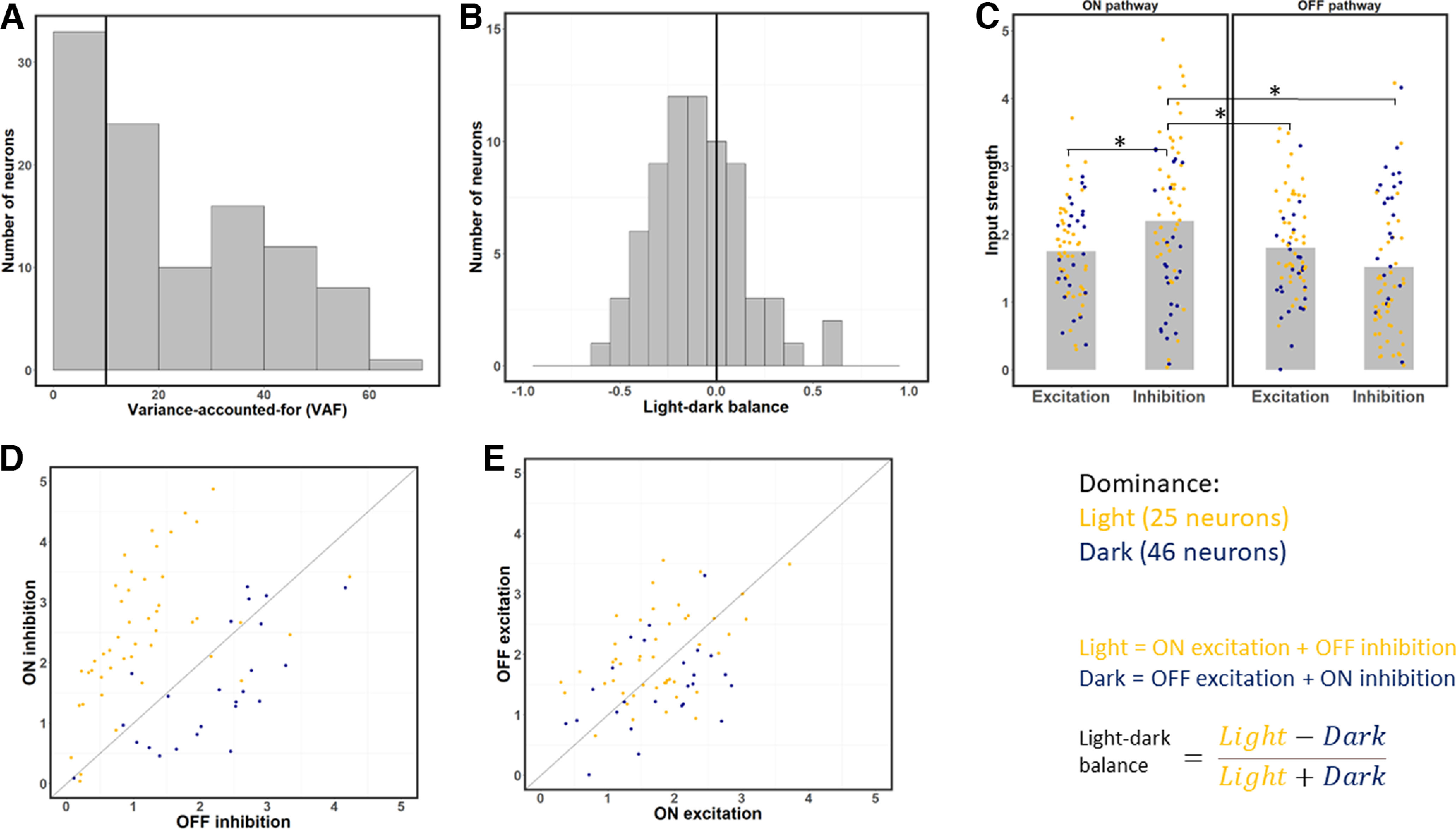
Strengths of excitation and inhibition from the ON and OFF pathways at each neuron's optimal time lag. A, Distribution of VAF values across the sample. Neurons with a VAF <10% were excluded from the rest of the analysis. B, Distribution of LDB index values for each neuron at its optimal latency. This index is on average negative, which indicates neurons respond more strongly to dark than light stimuli. C, Strength of excitation and inhibition across the ON and OFF pathways for each neuron. Gray bars represent average values. ON inhibition is the strongest input on average. Yellow dots represent light-dominant neurons. Blue dots represent dark-dominant neurons. *p < 0.0083, significant paired t tests (with Bonferroni correction). D, Scatterplot of ON versus OFF inhibition, for each of the 71 neurons. Most neurons have stronger ON inhibition, and whether ON or OFF inhibition is stronger is correlated with light- and dark-dominance. E, same as in C, but for ON and OFF excitation. Unlike the result for inhibition (C), ON and OFF excitation have relatively similar strength on average.
Figure 5.
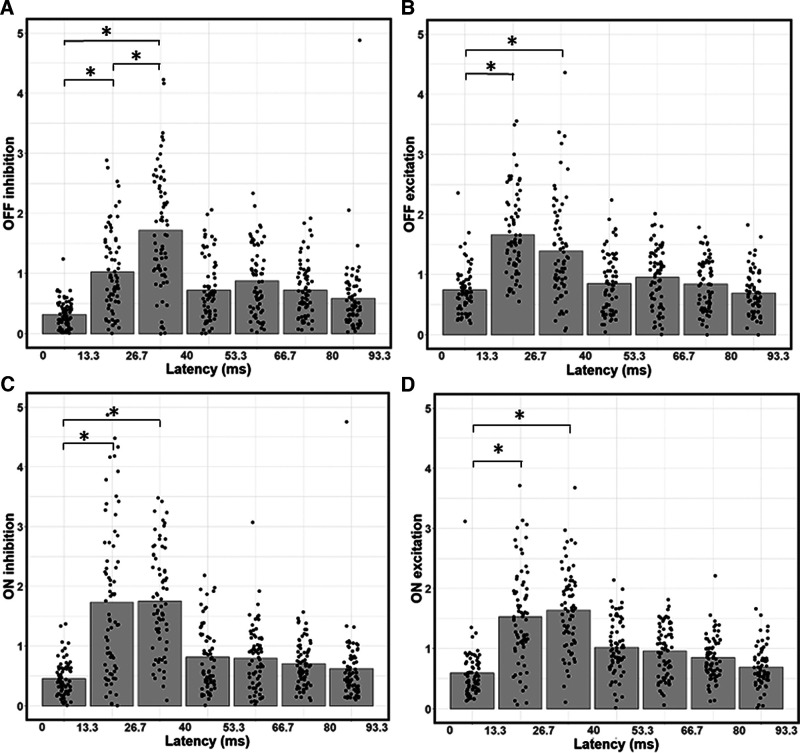
Temporal dependence of contributions from ON/OFF excitation and inhibition. A, Bar graph of average OFF inhibition strength across time lags, with data points indicating values for individual neurons. OFF inhibition is weaker at the 13.3-26.7 ms latency than at the 26.7-40 ms latency. B, Same as in A, but for OFF excitation. C, Same as in A, B, but for ON inhibition. D, Same as in A–C, but for OFF excitation. *p < 0.0167, significant paired t tests between the first three latencies. OFF inhibition (A) is the only input type to significantly vary in strength between the 13.3-26.7 and 26.7-40 ms latencies. Input strength at the 0-13.3 ms latency is always significantly weaker than at the 13.3-26.7 and 26.7-40 ms latencies.
Results
As described in Materials and Methods, a simple neural network model (Fig. 1) was fit to responses from individual neurons, to estimate 2D gaussians and 3D spatiotemporal filters separately for ON and OFF inputs, as well as a power law output nonlinearity. Figure 2 shows these estimated model parameters for four example neurons, which all had peak responses at the 13–27 or 27–40 ms latency. As we observed more generally, the early ON and OFF Gaussian filters for a given neuron were about the same size, but opposite in polarity. And for each neuron, the spatiotemporal filters were largely similar, both spatially and temporally, but opposite in polarity.
Many of the neurons had Gabor-like receptive fields that are orientation-selective (Hubel and Wiesel, 1962), like the one shown in Figure 2A (with OS = 0.55). At the 27–40 ms latency, this neuron has balanced light and dark responses for both the ON (left) and OFF (right) pathways (LDB = 0.04). This balance does not occur at the 13–27 ms latency, where the neuron responds more strongly to dark stimuli (LDB = −0.2). This bias is because of the OFF pathway having stronger functional excitation (red) than inhibition (blue), with the ON pathway being balanced.
Another neuron (Fig. 2B) is also orientation-selective (OS = 0.64), balanced (LDB = 0.02) at the 27-40 ms latency, and exhibits a bias toward dark responses (LDB = −0.3) at the 13–27 ms latency. However, for this neuron, the 27–40 ms latency is imbalanced because of both the ON and OFF pathways, with the ON pathway having weaker excitation and the OFF pathway having weaker inhibition.
The neuron shown in Figure 2C differs from the previous examples in that it has low OS (0.09) because of its isotropic receptive field, which has a dark center and an opposite-polarity surround. At the 13–27 ms latency, this neuron is dark-dominant (LDB = −0.34) because of its weaker surround, especially in the OFF pathway. Contrary to the above two example neurons, at the 27-40 ms latency, this neuron is not balanced but light-dominant because of stronger functional inhibition than excitation in the OFF pathway.
Not all neurons are dark-dominant; for example, the neuron in Figure 2D is light-dominant at the 13–27 ms latency (LDB = 0.29) because of its Gaussian-like receptive field with a light-responsive center and a weak surround. Similar to previous results, this neuron is balanced at the 27–40 ms latency (LDB = −0.02). However, as we shall see below, there is a tendency for most neurons to, on average, have stronger responses to dark stimuli at the 13–27 ms latency, and to have stronger responses to light stimuli or to be balanced at the 27–40 ms latency.
It is interesting to note that the 13.3–40 ms peak response times we find are faster than the ∼60 ms found in some previous studies of cat primary visual cortex (e.g., DeAngelis et al., 1993). This discrepancy might be because of our very short presentation of each natural image (13.3 ms), which could circumvent neurons' temporal integration from reaching maximal peak responses. In contrast, DeAngelis et al. (1993) used reverse correlation with a longer stimulus presentation of 40 ms. Other studies (Komban et al., 2014; Talebi and Baker, 2016) that use shorter image presentations (13.3–16.7 ms) with temporally uncorrelated stimuli, such as white noise or natural images, find peak responses times that are more similar to ours (∼ 30 ms).
Population responses
Figure 3A shows a histogram of VAF values, which represents the proportion of variance in a neuron's response the model predicts on the testing set. We excluded 33 neurons that were poorly predicted by the model (VAF < 10%) to get a more accurate estimate of functional excitation and inhibition across the population of neurons. The performance of the estimated models on the remaining 71 neurons was good, with an average VAF of 31.02%, with values ranging from 10.5% to 65.3%. This range of performance is similar to those in previous system identification studies of V1 neurons (e.g., David et al., 2004; Fournier et al., 2014; Vintch et al., 2015).
To investigate the patterns of light and dark response strength across the sample of 71 neurons, we computed the sums of the four types of inputs for each neuron's optimal time lag (see Materials and Methods). Neurons had an optimal time latency of either 13.3–26.7 ms (38 neurons), 26.7–40 ms (32 neurons), or 53.3–66.7 ms (1 neuron). As described in Materials and Methods, we estimated the overall amount of functional excitation and inhibition from the ON and OFF pathways, and also used these values to calculate an index of light-vs-dark balance, LDB. We classified each neuron as dark-dominated (LDB < 0) or light-dominated (LDB > 0) depending on whether it was more responsive to dark (OFF excitation and ON inhibition) or light (ON excitation and OFF inhibition) at its optimal time latency. Across our population of 71 neurons, we found 46 neurons (64.78%) to be dark-dominated (LDB < 0) and 25 neurons (35.21%) to be light-dominated (LDB > 0) at their optimal latencies, similar to Yeh et al. (2009). The neurons in our sample had a wide range of LDB values (Fig. 3B; minimum = −0.62, maximum = 0.57, median = −0.12), but were on average dark-dominated, with an average LDB of −0.098 (Fig. 3B; one-sample t test: t = −3.48, df = 70, p = 0.00087).
To better understand why cortical neurons are on average more responsive to dark than light stimuli, we next compare the four types of inputs at each neuron's optimal latency (Fig. 3C). ON pathway inhibition is the strongest type of input on average, and is significantly stronger than the other three. ON inhibition is on average significantly stronger than ON excitation (paired t tests with Bonferroni correction: t = 4.61, df = 70, p = 1.79 × 10−5), OFF excitation (paired t test: t = 3.50, df = 70, p = 0.000812), and OFF inhibition (paired t test: t = 3.86, df = 70, p = 0.00025). In contrast, OFF inhibition is on average the weakest type of input. While it has previously been suggested that stronger OFF than ON excitation could underlie stronger dark responses (Jin et al., 2008), the overall dark-dominance effect we observe at the optimal latency instead seems to be because of a strong imbalance between ON and OFF inhibition: while inhibition is on average 39.3% stronger from the ON than from the OFF pathway (Fig. 3D), there is no significant difference between excitation from the ON and OFF pathways (Fig. 3E; paired t test: t = 0.62, df = 70, p = 0.54). The difference between ON and OFF inhibition (Fig. 3D) is also significantly stronger (paired t test: t = 3.05, df = 70, p = 0.0033) than the difference between ON and OFF excitation (Fig. 3E).
In addition, whether a given neuron is light- or dark-dominated is strongly related to whether ON inhibition exceeds OFF inhibition (Fig. 3C, yellow points above 1:1 line vs blue points below). However, the imbalance of ON versus OFF excitation poorly predicts whether a neuron is light or dark-dominant (Fig. 3D). Overall, these results suggest the dark-dominance effect to be more driven by an imbalance in ON/OFF inhibition than by an imbalance in ON/OFF excitation.
Time dynamics
Since responses to dark stimuli have previously been found to have shorter latencies than responses to light stimuli (Komban et al., 2014), we suspected the above results might vary as a function of response latency. The dependence of LDB is shown for each of the measured latencies in Figure 4A, with data points for each sampled neuron, and gray bars indicating their averages. The dark-dominance effect is especially predominant at the 0–13.3 ms (one-sample t tests with Bonferroni correction: t = −7.73, df = 70, p = 5.76 × 10−11) and 13.3–26.7 ms latencies (one-sample t test: t = −4.19, df = 70, p =7.99 × 10−5). The dark-dominance effect disappears at the 26.7–40 ms latency, with slightly stronger average responses to light than dark, although the difference is not significant (one-sample t test: t = 1.90, df = 70, p = 0.069). At the longer latencies, there is no significant average light- or dark-dominance (one-sample t tests: all p > 0.12). These findings suggest that, while V1 neurons are on average biased toward dark responses in their short latencies, the dark-dominance effect disappears at the 27–40 ms latency.
Figure 4.
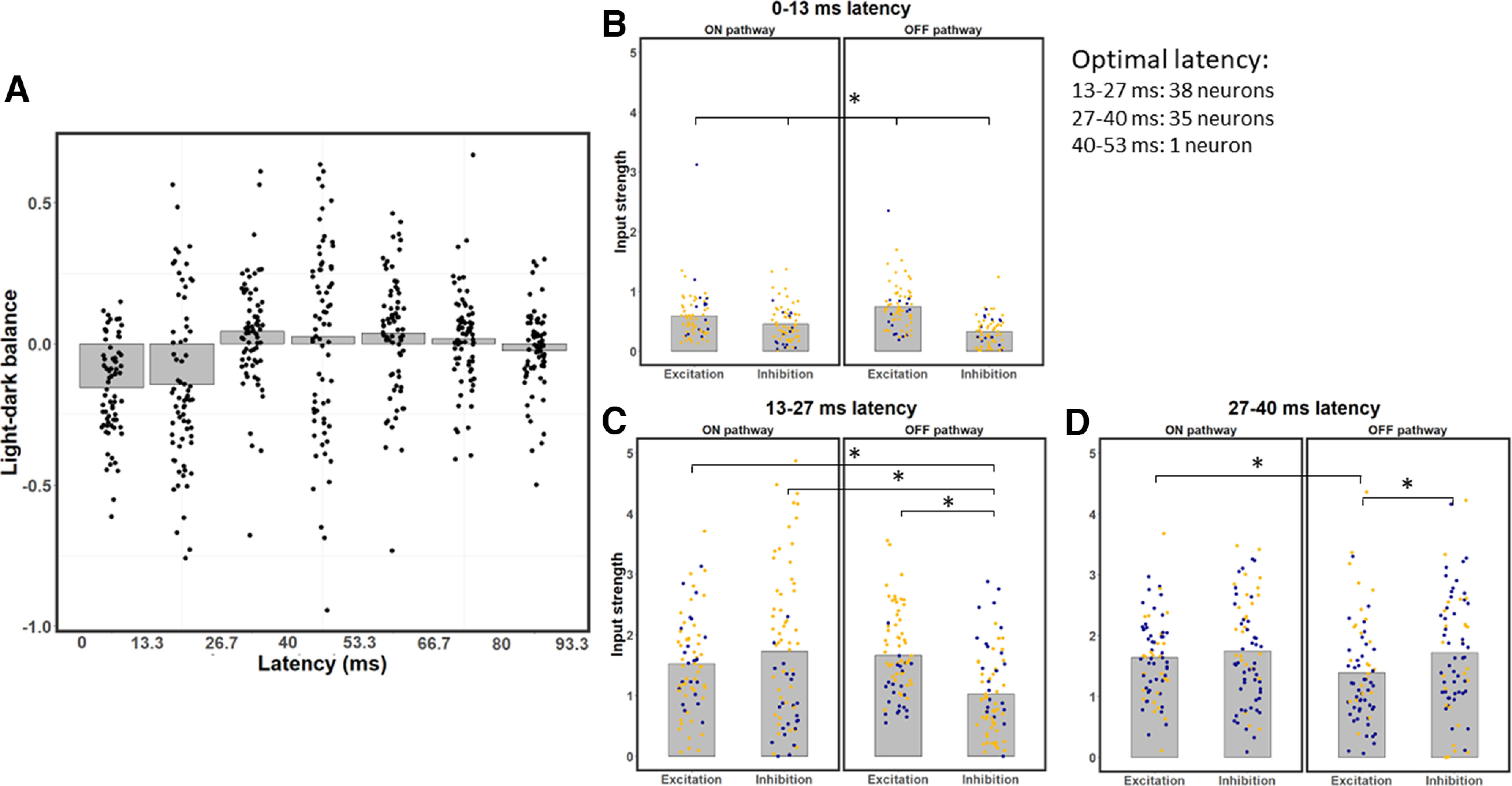
LDB index and strength of excitation/inhibition of ON and OFF pathways for all neurons, across different latencies. A, LDB index values, shown as bar graph of average values for each latency, with superimposed data points for individual neurons. The 0-13.3 and 13.3-26.7 ms latencies exhibit dark-dominance, the 26.7-40 ms latency shows a slight bias toward light-dominance and the later latencies are relatively balanced. B, Excitation and inhibition from the ON and OFF pathways for each neuron at the 0-13.3 ms latency. OFF excitation is stronger than ON excitation on average, and inhibition is significantly weaker than excitation at this latency. C, Same as in B, but for the 13.3-26.7 ms latency; note the relatively balanced values on average, except for OFF inhibition, which is significantly weaker than the other three types of input. D, Same as in B, C, but for the 26.7-40 ms latency; note the significantly weaker OFF excitation on average compared with the other three types of input. B–D, *p < 0.0083, significant paired t tests (with Bonferroni correction). All of the pairwise comparisons are significantly different in D.
To understand why neurons are dark-dominated in their early latencies, we investigate how the strength of each input type varies as a function of time. Because neurons are most responsive up until a latency of 40 ms, the following sections focus on the first three latencies. As we can see in Figure 4B, at a latency of 0-13.3 ms, OFF excitation is the strongest input on average: it is 26.0% stronger than ON excitation (paired t tests with Bonferroni correction: t = 5.03, df = 70, p = 3.7 × 10−6). Inhibition is significantly weaker than excitation, both in the ON (paired t test: t = 3.15, df = 70, p = 0.0024) and OFF (paired t test: t = 10.76, df = 70, p < 2.2 × 10−16) pathways. This discrepancy is stronger in the OFF than in the ON pathway (paired t test: t = 7.32, df = 70, p = 3.28 × 10−10). Inhibition is on average 41.6% stronger from the ON than from the OFF pathway (paired t test: t = 5.82, df = 70, p = 1.65 × 10−7), thereby contributing to stronger dark responses. Weaker inhibition than excitation at the shortest latency could be explained by inhibition having to go through at least one more synapse than excitation to reach V1 neurons (Ferster and Lindström, 1983; Martin and Whitteridge, 1984; Montero, 1986). These results are also consistent with findings from Jin et al. (2008), who demonstrated stronger OFF than ON excitation from the LGN to be an important mechanism contributing to the dark-dominance phenomenon. However, while stronger OFF than ON excitation might explain dark-dominance at the 0–13.3 ms latency, the overall dark/light dominance of neurons will be more related to the considerably stronger responses at the 13.3–26.7 and 26.7–40 ms latencies.
Responses at the 13.3–26.7 ms latency are also stronger to dark stimuli (Fig. 4C), but for a different reason. OFF excitation is not significantly stronger than ON excitation at the 13.3–26.7 ms latency (paired t tests with Bonferroni correction; t = 1.53, df = 70, p = 0.131). Instead, dark-dominance at this latency is because of weaker OFF inhibition compared with the other three types of inputs. Inhibition from the OFF pathway is on average 40.64% weaker than inhibition from the ON pathway (paired t test; t = 4.88, df = 70, p = 6.47 × 10−6). OFF inhibition is also on average 32.89% weaker than ON excitation (paired t test; t = 7.52, df = 70, p = 1.37 × 10−10) and on average 38.35% weaker than OFF excitation (paired t test; t = 5.90, df = 70, p = 1.16 × 10−7). No other pair of inputs are significantly different from each other (paired t tests: all p > 0.065 with a threshold of α = 0.0083 because of the Bonferroni correction) at the 13.3–26.7 ms latency, further strengthening the idea that the imbalance between light and dark responses at this latency is because of weaker OFF inhibition. These results are consistent with the idea that V1 neurons receive stronger inhibition to light than dark stimuli (Xing et al., 2014).
Contrary to the results for the earlier latencies, the 26.7-40 ms latency does not show dark-dominance (Fig. 4D). The only significant differences are OFF excitation being both 19.19% weaker than OFF inhibition (paired t tests with Bonferroni correction: t = −3.23, df = 70, p = 0.0019) and 20.54% weaker than ON inhibition (paired t test: t = −4.00, df = 70, p = 0.00,015). No other pair of inputs differ significantly (paired t tests: p < 0.0083) at this latency. Thus, different types of input are relatively more balanced at this latency compared with the previous ones.
To further understand the time dynamics of dark and light responses, we next analyze how the strength of each type of input changes across latencies (Fig. 5). Because all input types are much weaker at the 0-13.3 ms latency compared with the 13.3–26.7 and 26.7–40 ms latencies (Fig. 5), we focus our analysis on comparing the two latencies with the strongest responses (13.3–26.7 and 26.7–40 ms). Consistent with the above results, OFF inhibition is 40.4% weaker at 13.3–26.7 ms than at 26.7–40 ms (Fig. 5A; paired t tests with Bonferroni correction: t = 7.06, df = 70, p = 9.75 × 10−10), and is the only input type to differ significantly in strength between these two latencies. OFF excitation is 16.4% weaker at 26.7–40 ms than at 13.3–26.7 ms, but this difference is not significant (Fig. 5B; paired t test: t = 1.99, df = 70, p = 0.05). There are no significant differences between the 13.3–26.7 and 26.7–40 ms latencies for both ON inhibition (Fig. 5C; paired t test: t = 0.133, df = 70, p = 0.895) and ON excitation (Fig. 5D; paired t test: t = 1.08, df = 70, p = 0.283). These findings suggest that inhibition is slower to dark than light stimuli, which leads to dark-dominance at the 13.3–26.7 ms latency.
The results so far suggest that dark-dominance occurs at the 13-27 ms latency because of more functional inhibition to light than dark stimuli. Because of those results, we hypothesized that the dark-dominance effect would depend on how much functional inhibition a neuron receives, which in turn depends on the relationship between the stimuli and a neuron's receptive field. There should be little or no dark-dominance from excitation alone, for example, if we compare the responses to light stimuli falling on the ON-excitation region to dark stimuli on the OFF-excitation region. Dark-dominance also cannot occur from inhibition alone, since the spontaneous firing rate is close to zero. Instead, dark-dominance should occur when a stimulus triggers both excitation and inhibition, for example when either light or dark stimuli fall on both the light and dark-driven regions of a neuron's receptive field.
To test this hypothesis, we simulated responses of the estimated models to four different stimulus conditions tailored to the receptive field of each neuron (see Materials and Methods): (1) light stimuli on light-driven regions; (2) dark stimuli on dark-driven regions; (3) light stimuli on light and (half of) dark-driven regions; and (4) dark stimuli on dark and (half of) light-driven regions (Fig. 6, top parts). The averages of the four responses were taken across the entire sample of 71 neurons (Fig. 6, bottom plots). As expected, the simulation shows little or no dark-dominance when only the excitatory region is stimulated (Conditions 1 and 2; Fig. 6A). But as we hypothesized, we do obtain dark-dominance at the 13-27 ms latency with stimuli that both excite and inhibit the neuron's response (Conditions 3 and 4; Fig. 6B). These results support the idea that dark-dominance occurs when measured with stimuli that recruit both the excitatory and inhibitory regions of a neuron's receptive field.
OS
Previous studies demonstrated that V1 neurons are less orientation-selective in their early responses (Ringach et al., 1997; Shapley et al., 2003). Since we have found early latencies to respond more strongly to dark stimuli, we wondered whether the stronger dark-dominance might be related to weaker OS. To infer OS, we next simulate the responses of the neurons' fitted models to static sinewave grating stimuli with a series of orientations, spatial frequencies, and phases. For each latency, we select the sinewave grating with the best phase and spatial frequency for each orientation. We then use each model's simulated responses to these sinewave gratings to measure an index of OS, using a conventional vector summation method (Wörgötter and Eysel, 1987; Swindale, 1998) (see Materials and Methods), as a function of latency. This OS index for a given neuron typically peaks at the 26.7–40 ms latency (Fig. 7A). More specifically, across the population, the OS is significantly higher at 26.7–40 ms than at both 13.3-26.7 ms (paired t test with Bonferroni correction; t = 5.68, df = 70, p = 2.8 × 10−7) and 0-13.3 ms (paired t test: t = 4.76, df = 70, p = 1.01 × 10−5). There is no significant difference in OS between the 0-13.3 and 13.3-26.7 ms latencies (paired t test: t = 0.83, df = 70, p = 0.41). These results suggest that OS is most prominent at the 26.7-40 ms latency, where it is also the first latency where light and dark responses are relatively balanced.
We next investigate the relationship between OS and LDB at each neuron's optimal latency, which can be seen in Figure 7B. Neurons having high dark dominance (LDB ≪ 0) or high light dominance (LDB ≫ 0) tend to have low OS, while those that are more orientation-selective are more often LDBd (LDB ∼ 0). This apparent relationship is confirmed statistically: there is a significant negative relationship (r = −0.46) between OS and absolute values of LDB (linear regression test: t = −4.35, df = 69, p = 4.7 × 10−5). These results suggest that a response bias toward dark stimuli might reduce a neuron's OS (Fig. 7B), especially at the 0-13.3 and 13.3-26.7 ms latencies (Fig. 7A).
Another possible explanation for weaker OS at early latencies could be faster excitation than inhibition (Ringach et al., 1997; Shapley et al., 2003). Figure 7C shows the relative amount of excitation versus inhibition (EIB index; see Materials and Methods) at each latency. Excitation is stronger than inhibition at the 0-13.3 ms (paired t test: t = 10.83, df = 70, p < 2.2 × 10−16) and 13.3-26.7 ms latencies (paired t test: t = 4.88, df = 70, p = 6.54 × 10−6), while there is no significant difference between excitation and inhibition at the 26.7–40 ms latency (paired t test: t = −1.93, df = 70, p = 0.058). This bias toward excitation weakens over time, with lower EIB values for the 13.3–26.7 than for the 0–13.3 ms latency (paired t test: t = −4.42, df = 70, p = 5.59 × 10−5). EIB values are also lower for the 26.7–40 than for the 13.3-26.7 ms latency (paired t test: t = −6.86, df = 70, p = 2.28 × 10−9). Also consistent with Ringach et al. (1997) and Shapley et al. (2003), we find a negative correlation of r = −0.26 between OS and EIB (Fig. 7D; linear regression test: t = −2.26, df = 68, p = 0.027). Overall, these results suggest that both dark-dominance and stronger excitation contribute to weaker OS at early latencies. However, another interpretation might be that weaker OFF inhibition is responsible for all of the above phenomena at early latencies: stronger dark responses, weaker overall inhibition, and weaker OS (see Discussion).
Discussion
Using a novel model-fitting approach to natural image responses, we find V1 neurons respond more strongly to dark than to light stimuli at early but not at later latencies, because of slower functional inhibition to dark than light stimuli. Dark-dominance occurs when functional inhibition is differentially recruited, for example, when there is a light stimulus on the dark-driven region of a neuron's receptive field (or vice-versa). As can be seen in Figure 6, our results suggest little difference in the average neuron's firing rate when a light stimulus only covers the light-excited region of the receptive field (Fig. 6A, red) compared with when a dark stimulus only covers the dark-excited region of the receptive field (Fig. 6A, blue). At the 13.3–26.7 ms latency, stronger responses to dark stimuli are instead observed when light (Fig. 6B, red) or dark (Fig. 6B, blue) stimuli cover both the light and dark regions of a neuron's receptive field. These results could help explain why dark-dominance increases at lower spatial frequencies (Jansen et al., 2019), since a given light or dark band of a low-frequency grating may cover more than one region of a receptive field.
Inference of excitation and inhibition from model-fitting
We use a machine learning algorithm to fit a model based on separate ON and OFF retinogeniculate inputs to V1, each composed of linear filters followed by half-wave rectification. The weaker surrounds of LGN neurons (e.g., Croner and Kaplan, 1995) are omitted to enable robust convergence on a set of fitted parameter values. Using this approach, we can distinguish between functional excitation and inhibition to light and dark stimuli across spatial receptive field locations and temporal lags to investigate how ON and OFF pathways contribute to the dark-dominance effect.
It is important to note that the functional excitation and inhibition we estimate do not necessarily reflect direct LGN inputs. For example, V1 does not receive direct inhibitory inputs from the LGN (Ferster and Lindström, 1983; Martin and Whitteridge, 1984; Montero, 1986), but rather from local inhibitory interneurons, which in turn may relay geniculate inputs or be driven by other V1 neurons (Isaacson and Scanziani, 2011). Although V1 neurons directly receive geniculate excitation, there is also intracortical excitation within V1 (Douglas et al., 1995). Moreover, what we estimate does not necessarily reflect the synaptic excitatory or inhibitory inputs a neuron directly receives. For example, a neuron could decrease its firing rate in response to light because its excitatory inputs are inhibited by light. Consequently, functional excitation and inhibition should best be interpreted as a measure of how a neuron's response varies as a function of light and dark stimuli, and not simply as synaptic weighting.
Distinguishing excitation to dark from inhibition to light (and vice-versa) has been enabled by the use of rich stimuli, such as natural images, combined with our simple model architecture. Had we attempted to make the model more complex and biologically realistic, the results we obtain from the analysis might be more dependent on the particular sort of model we use and thus become problematic to interpret. Natural image stimuli lead to more robust system identification than with synthetic stimuli (Talebi and Baker, 2012), and perhaps more importantly, they ensure that neurons simultaneously receive visual stimuli that both increase and decrease their firing rate in different parts of their receptive fields; this allows the machine learning algorithm to distinguish between excitation from one pathway and inhibition from the other.
Dark-dominance because of weaker inhibition from dark stimuli
Dark-dominance in V1 has previously been thought to originate from relatively greater lateral geniculate excitation from the OFF pathway (Jin et al., 2008). However, it has also been suggested that intracortical inhibition is stronger to lights than darks (Xing et al., 2014), which has recently been confirmed by intracellular recordings (Taylor et al., 2018). At each neuron's optimal latency, our results show ON inhibition to be much stronger than OFF inhibition, while we do not find a significant difference between ON and OFF excitation.
These findings support the idea that dark-dominance is strongest in layer 2/3 of primate V1 (Yeh et al., 2009). If dark-dominance were principally because of stronger lateral geniculate excitation from the OFF pathway, we would expect dark-dominance to be at least as strong in layer 4 than in the other layers, since this is where most LGN neurons synapse. While two-thirds of the neurons in primate layer 4 show dark-dominance, this effect is much stronger in layers 2/3 where almost every neuron is dark-dominant (Yeh et al., 2009). This laminar difference might be because of pyramidal neurons in primate layers 2/3 receiving extensive inhibition, as has been shown in the mouse (Kätzel et al., 2011) and tree shew (Tucker and Fitzpatrick, 2006), with inhibition being stronger to light than dark stimuli (Taylor et al., 2018).
Since this study used recordings from polytrodes that did not extend across all the cortical layers, a laminar analysis was not feasible. A useful future direction could be to replicate this experiment with linear-array probes to obtain simultaneous recording across all V1 layers, to investigate the laminar dependence of dark-dominance.
Time dynamics of dark-dominance
A novel finding of this study is how the dark-dominance changes as a function of latency. We observe the dark-dominance effect at the 0–13.3 and 13.3–26.7 latencies, but instead find a slight light-dominance at the 13.3–26.7 latency. We were able to find this relationship between latency and dark-dominance because we estimate light and dark responses at every latency for each neuron. Other studies have focused on each neuron's optimal latency (e.g., Yeh et al., 2009), which here still clearly shows the dark-dominance effect (Fig. 3), but neglect the effect of latency on the strength of dark responses. Here we find dark-dominant responses are specific to the earlier latencies.
This relationship between dark-dominance and latency should not be too surprising, considering dark-dominant V1 neurons respond 3–6 ms faster than light-dominant neurons (Komban et al., 2014). These faster dark responses in V1 have been attributed to faster OFF than ON LGN responses (Jin et al., 2008, 2011). While we do find the 0–13.3 ms latency to be dark-dominant because of stronger OFF than ON excitation (Fig. 4B), most neurons have poor responses at this latency. The dark-dominance effect is most salient at the 13.3–26.7 ms latency, when response strength peaks and dark-dominance is because of weaker functional inhibition to dark stimuli (Fig. 4C). These results are consistent with findings from Taylor et al. (2018), who found intracortical inhibition to be stronger for light than for dark stimuli, and with Xing et al. (2014), who showed V1 neurons to have more transient responses to light than dark stimuli. Therefore, we interpret the dark-dominance results at each neuron's optimal time lag from Yeh et al. (2009) and Jansen et al. (2019) as mostly because of weaker functional inhibition rather than stronger functional excitation to dark stimuli.
Relationship to OS
This study also brings a new perspective on the intracortical mechanisms of OS, and helps explain why V1 neurons are less orientation-selective in their early time lags (Ringach et al., 1997; Shapley et al., 2003). Because of the absence of direct inhibition from the LGN to V1 (Ferster and Lindström, 1983; Martin and Whitteridge, 1984; Montero, 1986), the lagged onset of OS was previously attributed to the delay imposed by the necessity of intracortical inhibitory interneurons (Ringach et al., 1997; Shapley et al., 2003). We do find inhibition strength to be positively correlated with OS (Fig. 7D) (see G. Li et al., 2008). However, we also find neurons with higher OS to have more balanced light/dark responses (Fig. 7B). Consistent with these results, responses from 0–26.7 ms, which are lower in OS (Fig. 7A), are also biased toward dark stimuli (Fig. 4A) and have stronger excitation than inhibition (Fig. 7C). In contrast to the first two latencies, the 26.7–40 ms latency has high OS (Fig. 7A) and relatively balanced responses between light and dark stimuli (Fig. 4A,D). Because both dark-dominance and stronger inhibition at the 13.3–26.7 latency are because of slower inhibition to dark stimuli (Fig. 4C), the reason why neurons are less orientation-selective at the 13.3–26.7 than at the 26.7–40 ms latency could be because of this slower inhibition to dark stimuli. These results are consistent with theoretical models of cortical development in V1 (Najafian et al., 2022), which have suggested that balanced ON/OFF responses lead to higher OS.
In conclusion, we have used a novel machine learning approach to bring new insights to the phenomenon of stronger dark responses in visual cortex neurons. We find the dark-dominance effect only occurs in the early latencies, and is because of slower inhibition to dark stimuli. We also show how weaker average inhibition to dark stimuli is related to reduced OS in the early latencies. The nature of the slower inhibition to dark than to light stimuli, and whether these findings vary across laminae, could be fruitful subjects of future investigation.
Footnotes
This work was supported by Canadian Institutes of Health Research Grant MOP-119498 to C.L.B. We thank Guangxing Li for contributions to software and technical support in experiments; and Philippe Nguyen and Amol Gharat for important contributions to data collection and spike-sorting.
The authors declare no competing financial interests.
References
- Anzai A, Ohzawa I, Freeman RD (1999) Neural mechanisms for processing binocular information: I. Simple cells. J Neurophysiol 82:891–908. 10.1152/jn.1999.82.2.891 [DOI] [PubMed] [Google Scholar]
- Brainard DH (1997) The Psychophysics Toolbox. Spat Vis 10:433–436. [PubMed] [Google Scholar]
- Buchner A, Baumgartner N (2007) Text–background polarity affects performance irrespective of ambient illumination and colour contrast. Ergonomics 50:1036–1063. 10.1080/00140130701306413 [DOI] [PubMed] [Google Scholar]
- Cooper EA, Norcia AM (2015) Predicting cortical dark/bright asymmetries from natural image statistics and early visual transforms. PLoS Comput Biol 11:e1004268. 10.1371/journal.pcbi.1004268 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Croner LJ, Kaplan E (1995) Receptive fields of P and M ganglion cells across the primate retina. Vision Res 35:7–24. 10.1016/0042-6989(94)E0066-T [DOI] [PubMed] [Google Scholar]
- David SV, Vinje WE, Gallant JL (2004) Natural stimulus statistics alter the receptive field structure of v1 neurons. J Neurosci 24:6991–7006. 10.1523/JNEUROSCI.1422-04.2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeAngelis GC, Ohzawa I, Freeman RD (1993) Spatiotemporal organization of simple-cell receptive fields in the cat's striate cortex: I. General characteristics and postnatal development. J Neurophysiol 69:1091–1117. 10.1152/jn.1993.69.4.1091 [DOI] [PubMed] [Google Scholar]
- Douglas RJ, Koch C, Mahowald M, Martin KA, Suarez HH (1995) Recurrent excitation in neocortical circuits. Science 269:981–985. 10.1126/science.7638624 [DOI] [PubMed] [Google Scholar]
- Ferster D, Lindström S (1983) An intracellular analysis of geniculo-cortical connectivity in area 17 of the cat. J Physiol 342:181–215. 10.1113/jphysiol.1983.sp014846 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fournier J, Monier C, Levy M, Marre O, Sári K, Kisvárday ZF, Frégnac Y (2014) Hidden complexity of synaptic receptive fields in cat V1. J Neurosci 34:5515–5528. 10.1523/JNEUROSCI.0474-13.2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geisler WS (1983) Mechanisms of visual sensitivity: backgrounds and early dark adaptation. Vision Res 23:1423–1432. [DOI] [PubMed] [Google Scholar]
- Gollisch T, Meister M (2008) Modeling convergent ON and OFF pathways in the early visual system. Biol Cybern 99:263–278. 10.1007/s00422-008-0252-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heeger DJ (1991) Nonlinear model of neural responses in cat visual cortex. In: Computational models of visual processing (Landy MS, Movshon JA, eds), pp. 119–133. The MIT. [Google Scholar]
- Hoel AE, Kennard RW (1970) Ridge regression biased estimation for nonorthogonal problem. Technometrics 12:55–67. 10.1080/00401706.1970.10488634 [DOI] [Google Scholar]
- Hubel DH, Wiesel TN (1962) Receptive fields, binocular interaction and functional architecture in the cat's visual cortex. J Physiol 160:106–154. 10.1113/jphysiol.1962.sp006837 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Isaacson JS, Scanziani M (2011) How inhibition shapes cortical activity. Neuron 72:231–243. 10.1016/j.neuron.2011.09.027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jansen M, Jin J, Li X, Lashgari R, Kremkow J, Bereshpolova Y, Swadlow HA, Zaidi Q, Alonso JM (2019) Cortical balance between ON and OFF visual responses is modulated by the spatial properties of the visual stimulus. Cereb Cortex 29:336–355. 10.1093/cercor/bhy221 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin J, Weng C, Yeh CI, Gordon JA, Ruthazer ES, Stryker MP, Swadlow HA, Alonso JM (2008) On and off domains of geniculate afferents in cat primary visual cortex. Nat Neurosci 11:88–94. 10.1038/nn2029 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin J, Wang Y, Lashgari R, Swadlow HA, Alonso JM (2011) Faster thalamocortical processing for dark than light visual targets. J Neurosci 31:17471–17479. 10.1523/JNEUROSCI.2456-11.2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kätzel D, Zemelman BV, Buetfering C, Wölfel M, Miesenböck G (2011) The columnar and laminar organization of inhibitory connections to neocortical excitatory cells. Nat Neurosci 14:100–107. 10.1038/nn.2687 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kingma DP, Ba J (2014) Adam: a method for stochastic optimization. arXiv:1412.6980. [Google Scholar]
- Kleiner M, Brainard D, Pelli D (2007) What's new in Psychtoolbox-3? Perception 36:1–16. [Google Scholar]
- Komban SJ, Alonso JM, Zaidi Q (2011) Darks are processed faster than lights. J Neurosci 31:8654–8658. 10.1523/JNEUROSCI.0504-11.2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Komban SJ, Kremkow J, Jin J, Wang Y, Lashgari R, Li X, Zaidi Q, Alonso JM (2014) Neuronal and perceptual differences in the temporal processing of darks and lights. Neuron 82:224–234. 10.1016/j.neuron.2014.02.020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kremkow J, Jin J, Komban SJ, Wang Y, Lashgari R, Li X, Jansen M, Zaidi Q, Alonso JM (2014) Neuronal nonlinearity explains greater visual spatial resolution for darks than lights. Proc Natl Acad Sci USA 111:3170–3175. 10.1073/pnas.1310442111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li G, Yang Y, Liang Z, Xia J, Zhou Y (2008) GABA-mediated inhibition correlates with orientation selectivity in primary visual cortex of cat. Neuroscience 155:914–922. 10.1016/j.neuroscience.2008.06.032 [DOI] [PubMed] [Google Scholar]
- Li M, Zhang T, Chen Y, Smola AJ (2014) Efficient mini-batch training for stochastic optimization. Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp 661–670. 10.1145/2623330.2623612 [DOI] [Google Scholar]
- Martin KA, Whitteridge D (1984) Form, function and intracortical projections of spiny neurones in the striate visual cortex of the cat. J Physiol 353:463–504. 10.1113/jphysiol.1984.sp015347 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Montero VM (1986) The interneuronal nature of GABAergic neurons in the lateral geniculate nucleus of the rhesus monkey: a combined HRP and GABA-immunocytochemical study. Exp Brain Res 64:615–622. 10.1007/BF00340502 [DOI] [PubMed] [Google Scholar]
- Najafian S, Koch E, Teh KL, Jin J, Rahimi-Nasrabadi H, Zaidi Q, Kremkow J, Alonso JM (2022) A theory of cortical map formation in the visual brain. Nat Commun 13:1–20. 10.1038/s41467-022-29433-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olmos A, Kingdom FA (2004) A biologically inspired algorithm for the recovery of shading and reflectance images. Perception 33:1463–1473. 10.1068/p5321 [DOI] [PubMed] [Google Scholar]
- Parker PR, Abe ET, Leonard ES, Martins DM, Niell CM (2022) Joint coding of visual input and eye/head position in V1 of freely moving mice. Neuron 110:3897–3906.e5. 10.1016/j.neuron.2022.08.029 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pascanu R, Mikolov T, Bengio Y (2012) Understanding the exploding gradient problem. CoRR abs/1211.5063 2:417. [Google Scholar]
- Pelli DG (1997) The VideoToolbox software for visual psychophysics: transforming numbers into movies. Spat Vis 10:437–442. [PubMed] [Google Scholar]
- Persi E, Hansel D, Nowak L, Barone P, Van Vreeswijk C (2011) Power-law input-output transfer functions explain the contrast-response and tuning properties of neurons in visual cortex. PLoS Comput Biol 7:e1001078. 10.1371/journal.pcbi.1001078 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratliff CP, Borghuis BG, Kao YH, Sterling P, Balasubramanian V (2010) Retina is structured to process an excess of darkness in natural scenes. Proc Natl Acad Sci USA 107:17368–17373. 10.1073/pnas.1005846107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ringach DL, Sapiro G, Shapley R (1997) A subspace reverse-correlation technique for the study of visual neurons. Vision Res 37:2455–2464. 10.1016/S0042-6989(96)00247-7 [DOI] [PubMed] [Google Scholar]
- Shapley R, Hawken M, Ringach DL (2003) Dynamics of orientation selectivity in the primary visual cortex and the importance of cortical inhibition. Neuron 38:689–699. 10.1016/s0896-6273(03)00332-5 [DOI] [PubMed] [Google Scholar]
- Srivastava N, Hinton G, Krizhevsky A, Sutskever I, Salakhutdinov R (2014) Dropout: a simple way to prevent neural networks from overfitting. J Machine Learn Res 15:1929–1958. [Google Scholar]
- Swindale NV (1998) Orientation tuning curves: empirical description and estimation of parameters. Biol Cybern 78:45–56. 10.1007/s004220050411 [DOI] [PubMed] [Google Scholar]
- Swindale NV, Spacek MA (2014) Spike sorting for polytrodes: a divide and conquer approach. Front Syst Neurosci 8:6. 10.3389/fnsys.2014.00006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Talebi V, Baker CL (2012) Natural versus synthetic stimuli for estimating receptive field models: a comparison of predictive robustness. J Neurosci 32:1560–1576. 10.1523/JNEUROSCI.4661-12.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Talebi V, Baker CL Jr (2016) Categorically distinct types of receptive fields in early visual cortex. J Neurophysiol 115:2556–2576. 10.1152/jn.00659.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor MM, Sedigh-Sarvestani M, Vigeland L, Palmer LA, Contreras D (2018) Inhibition in simple cell receptive fields is broad and OFF-subregion biased. J Neurosci 38:595–612. 10.1523/JNEUROSCI.2099-17.2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tucker TR, Fitzpatrick D (2006) Luminance-evoked inhibition in primary visual cortex: a transient veto of simultaneous and ongoing response. J Neurosci 26:13537–13547. 10.1523/JNEUROSCI.3723-06.2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Umesh P (2012). Image processing in Python. CSI Commun 23. [Google Scholar]
- Vintch B, Movshon JA, Simoncelli EP (2015) A convolutional subunit model for neuronal responses in macaque V1. J Neurosci 35:14829–14841. 10.1523/JNEUROSCI.2815-13.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wörgötter F, Eysel UT (1987) Quantitative determination of orientational and directional components in the response of visual cortical cells to moving stimuli. Biol Cybern 57:349–355. 10.1007/BF00354980 [DOI] [PubMed] [Google Scholar]
- Xing D, Yeh CI, Gordon J, Shapley RM (2014) Cortical brightness adaptation when darkness and brightness produce different dynamical states in the visual cortex. Proc Natl Acad Sci USA 111:1210–1215. 10.1073/pnas.1314690111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeh CI, Xing D, Shapley RM (2009) Black responses dominate macaque primary visual cortex v1. J Neurosci 29:11753–11760. 10.1523/JNEUROSCI.1991-09.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]