Abstract
Alzheimer's disease (AD) and frontotemporal dementia (FTD) are common causes of dementia with partly overlapping, symptoms and brain signatures. There is a need to establish an accurate diagnosis and to obtain markers for disease tracking. We combined unsupervised and supervised machine learning to discriminate between AD and FTD using brain magnetic resonance imaging (MRI). We included baseline 3T‐T1 MRI data from 339 subjects: 99 healthy controls (CTR), 153 AD and 87 FTD patients; and 2‐year follow‐up data from 114 subjects. We obtained subcortical gray matter volumes and cortical thickness measures using FreeSurfer. We used dimensionality reduction to obtain a single feature that was later used in a support vector machine for classification. Discrimination patterns were obtained with the contribution of each region to the single feature. Our algorithm differentiated CTR versus AD and CTR versus FTD at the cross‐sectional level with 83.3% and 82.1% of accuracy. These increased up to 90.0% and 88.0% with longitudinal data. When we studied the classification between AD versus FTD we obtained an accuracy of 63.3% at the cross‐sectional level and 75.0% for longitudinal data. The AD versus FTD versus CTR classification has reached an accuracy of 60.7%, and 71.3% for cross‐sectional and longitudinal data respectively. Disease discrimination brain maps are in concordance with previous results obtained with classical approaches. By using a single feature, we were capable to classify CTR, AD, and FTD with good accuracy, considering the inherent overlap between diseases. Importantly, the algorithm can be used with cross‐sectional and longitudinal data.
Keywords: Alzheimer's disease, frontotemporal dementia, machine learning, magnetic resonance imaging, neuroimaging markers
We use machine learning tools in a multidisease approach to assess differential discrimination of Alzheimer's disease and frontotemporal dementia. Importantly, our approach includes a feature reduction strategy, making it computationally efficient and it also considers the study of associated brain patterns to gain explainability of the algorithm.
1. INTRODUCTION
Alzheimer's disease (AD) and frontotemporal dementia (FTD) are common forms of dementia, with different, but partly overlapping, symptoms, and brain signatures. This complicates the differential diagnosis and might lead to misdiagnosis (Balasa et al., 2011; Mendez, 2006). On the other hand, accurate characterization of longitudinal trajectories is needed for prognosis and disease tracking purposes. In recent years, clinical studies have been complemented with automated or semiautomated algorithms, which hold promise toward computer‐aided diagnosis. In this line, machine learning (ML) techniques use clinical and biomarker data to learn patterns that can be used as an aid for differential disease diagnosis and tracking.
Magnetic resonance imaging (MRI) has been widely used to detect disease‐specific brain changes across different neurodegenerative disorders. Concretely, using structural MRI, studies have described patterns of cortical thickness (CTh) and gray matter (GM) volume loss both in AD and FTD when compared separately with healthy populations (Bocchetta et al., 2021; Canu et al., 2017; Contador et al., 2021; Möller et al., 2013). In addition, in a previous study including both diseases, we showed that distinct brain atrophy patterns could potentially help in differentiating AD and FTD (Falgàs et al., 2020). More recently, measures derived from MRI have been used within ML algorithms to differentiate these diseases (Bron et al., 2017; Li et al., 2021; Möller et al., 2016; Penny et al., 2007). These approaches have shown good results. However, the large number of features needed can result in computationally expensive methods that are difficult to implement in a clinical setting. In addition, obtaining spatial patterns of the features driving classification can be challenging in some cases. These two issues limit the applicability and interpretability of the algorithms.
Besides the description of atrophy patterns at a specific time point, longitudinal neuroimaging studies have gained popularity in AD and FTD (Bejanin et al., 2020; Irish et al., 2018; Sintini et al., 2020). Using structural MRI, studies have described the trajectories of GM volume and CTh loss with time, providing valuable information on the characterization of disease trajectories and validation of prognostic biomarkers (Risacher et al., 2010; Storsve et al., 2014). When compared with cross‐sectional studies, longitudinal designs can explore the large heterogeneity of the effect of between‐subject brain changes which requires repeated measures and longitudinal designs (Bernal‐Rusiel et al., 2013; Thompson et al., 2011). Thus, while cross‐sectional studies depict patterns of differential or overlapping brain atrophy, longitudinal studies are needed to understand the differences in disease trajectories. In the context of ML, although longitudinal data are sometimes used for diagnostic confirmation and/or for exploring the predictive values of baseline acquisitions, few approaches include longitudinal data in the training to improve the models.
In this study, we developed a classification algorithm using cross‐sectional and longitudinal MRI data from 399 subjects, including AD and FTD patients and healthy controls (CTR). We implemented a feature reduction algorithm using unsupervised techniques followed by a widely used classifier, namely the support vector machine (SVM). Besides maximizing classification performance, by studying the weights of the features from the unsupervised part, we aimed to investigate the brain patterns that collected a higher amount of variance for the different classification settings, thus providing interpretability to our results.
2. MATERIALS AND METHODS
2.1. Participants
We selected 339 subjects prospectively recruited from the Alzheimer's disease and other cognitive disorders unit of the Hospital Clínic de Barcelona (HCB), all having a complete clinical work‐up and at least one 3T high‐resolution structural MRI scan. Additionally, a subset of subjects underwent a second acquisition after ~2 years. Participants were classified into three groups:
AD: patients who presented AD biomarker profiles suggesting underlying AD neuropathology (abnormal amyloid and tau, A + T+) with neurodegeneration (N+) according to National Institute on Aging/Alzheimer Association Research Framework 2018 (Jack et al., 2018) and Mini‐Mental State Examination (MMSE) ≥ 18. They also fulfilled diagnostic criteria for mild cognitive impairment due to AD or AD mild dementia (Albert et al., 2011; McKhann et al., 2011).
FTD: patients who met diagnostic criteria for either behavioral variant frontotemporal dementia (bvFTD) or primary progressive aphasia (PPA), including semantic variant PPA (svPPA), and nonfluent variant PPA (nfvPPA) (Gorno‐Tempini et al., 2011; Rascovsky et al., 2011). FTD showed normal values for AD cerebrospinal fluid (CSF) biomarkers.
CTR: healthy adults having cognitive performance within the normative range (cutoff 1.5 SD from the normative mean) and normal levels of AD CSF biomarkers.
Subjects were collected as part of other ongoing and past studies within the HCB. All were approved by the HCB Ethics Committee and all participants gave written informed consent.
2.2. MRI acquisition
A high‐resolution 3D structural data set (T1‐weighted, MP‐RAGE, repetition time = 2.300 ms, echo time = 2.98 ms, 240 slices, field‐of‐view = 256 mm, voxel size = 1 × 1 × 1 mm) was acquired for each individual at each time point in a 3T Magnetom Trio Tim scanner (Siemens Medical Systems, Germany) or in a 3T Prisma scanner (Siemens Medical Systems, Germany) at HCB using equivalent acquisition protocols. Before these analyses, we performed tests to evaluate the interscanner variability (results can be found in Supplementary Material S1), and we found low variability induced by the scanner.
2.3. MRI processing
We used the processing stream available in FreeSurfer version 6.0 (http://surfer.nmr.mgh.harvard.edu.sire.ub.edu/) to perform cortical reconstruction and volumetric segmentation of the T1‐weighted acquisitions. For longitudinal data, we used the longitudinal stream in FreeSurfer. All FreeSurfer preprocessing steps are reported in detail elsewhere (Fischl & Dale, 2000; Fischl et al., 2004; Reuter et al., 2012). Briefly, FreeSurfer allowed us to generate automated CTh maps and segmentation of the subcortical structures. From reconstructed data, we obtained global measures of mean CTh and GM volumes of the left and right hemispheres (lh and rh). In addition, we used the summary measures of mean CTh in 68 cortical parcellations and GM volumes of 17 subcortical structures, all derived from atlases available in FreeSurfer (Desikan et al., 2006; Seidman et al., 1997). Volume measures were normalized by the estimated intracranial volume. All images and individual segmentations were visually inspected and manually corrected if needed.
2.4. Cross‐sectional study: Brain signatures and classification performance
We used all the CTh values and subcortical volumes at baseline obtained with FreeSurfer to create our ML pipeline. We introduced the global and regional measures of both hemispheres (rh and lh) separately leading to a total of 103 values per subject. Subcortical regions were normalized using the intracranial volume and then all values (subcortical volumes and CTh measures) were converted to z‐score. Therefore, the features of our ML algorithm were the subcortical volumes and the CTh measures transformed to z‐scores obtained after processing the T1‐weighed MRI images.
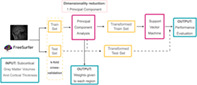
Firstly, we performed a principal component analysis (PCA) to reduce the number of regional measures (all CTh measures and all volumetric values) to a single feature, by keeping only the first principal component (PC). The first PC is the one with the highest value of explained variance, so it is the best choice to study the weights used in the transformation while keeping good classification accuracy. The weights to obtain this first PC will be used to provide a regional interpretation of the classification results. Second, this feature was introduced into a SVM algorithm to perform classifications between the three groups and between pairs of groups. Eventually, the weights of the PCA were used to create disease‐specific patterns. These patterns, allow having an interpretable ML algorithm that returns the accuracy and the associated patterns of the classification between groups. So, the proposed pipeline is not only focused on obtaining the best accuracy, but it also focuses on giving explainability to the ML algorithm.
To address circularity in the PCA and to avoid overfitting, we implemented all the steps in a cross‐validated setting, in which train data was used in the entire PCA + SVM, and a group of subjects was hold‐out to be used as test data. For testing, original data were projected into the PCA space to obtain the unique feature and this was used in the SVM classification. Overall performance was assessed using k‐fold cross‐validation with 20 iterations of the procedure explained above. Figure 1 shows a schematic representation of the algorithm. Additionally, the SVM hyperparameters: kernel (options: linear, rbf, and polynomial), C (values = [0.1,1, 10, 100, and 1000]), and gamma (values = [1, 0.1, 0.01, and 0.001]) were introduced with a Grid Search using an additional cross‐validation of 10, with the train set. The algorithm was implemented in Python version 3.8 (www.python.org), and we used the library scikit‐learn (Pedregosa et al., 2011) for PCA, Grid Search, and SVM.
FIGURE 1.
Machine Learning Algorithm scheme
To assess the effect of age in the classification, we performed two complementary analyses: (1) we evaluated if age itself was able to classify the different groups; (2) We repeated all analyses by adding age as a feature together with all the regions. To assess the effect of sex in the classification we repeated all analyses by adding sex as a feature together with all the regions.
2.5. Longitudinal study: Brain signatures and classification
We used all global and regional volumes and CTh measures derived from the FreeSurfer longitudinal stream for the longitudinal classification analysis. As in the cross‐sectional analysis, we introduced the measures of both hemispheres (rh and lh) separately, subcortical regions were divided by intracranial volume, and all values were converted to z‐score.
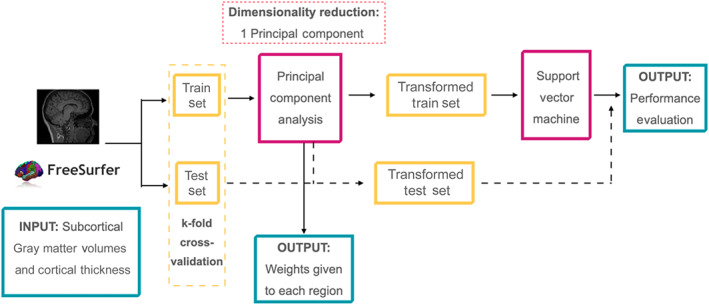
Here, the overall pipeline also consisted of an unsupervised algorithm followed by an SVM classification. For the unsupervised part, we performed a multiple factor analysis (MFA), which is a generalization of PCA. MFA allows implementing a factor analysis with repeated samples (i.e., the same measures for different time points for each subject; Abdi et al., 2013). As before, we only kept the first component. We kept the first component with the same objective as we did with the PCA in the cross‐sectional analyses. The weights to obtain this first component will give us the interpretability of the classification results of the algorithm. Then, this first component was introduced to the SVM algorithm. Here, the use of MFA facilitates the creation of a longitudinal ML in the SVM context, while keeping the interpretability of results. As before, overall performance was assessed using k‐fold cross‐validation with k = 20, in which test data was not included in any of the procedures within the pipeline (MFA and SVM). As an internal quality control, we revised the number of subjects included in the train/test set for each iteration, and we observed that they were equally distributed across iterations. Figure 2 shows a scheme of the algorithm.
FIGURE 2.
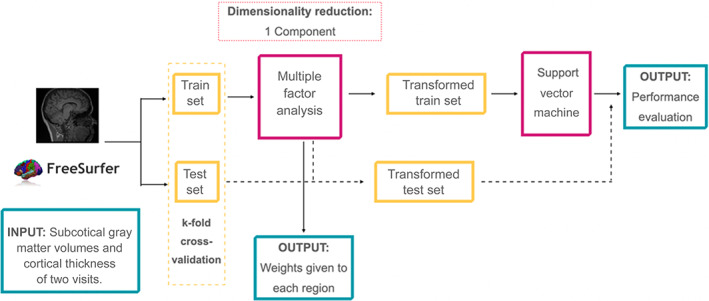
Longitudinal Machine Learning Algorithm scheme
With the objective to study how the longitudinal data can help to improve the classification in ML algorithms and how should be introduced to the algorithm, different settings were considered for the longitudinal analysis: (1) including all regional measures from time point 1 and time point 2 as different observations for each subject in the MFA decomposition. (2) including all measures from each time point together with a change variable (computed as time point2–time point1) for each region in the MFA decomposition. (3) using only the change variable in a standard PCA analysis. So, this setting will be the equivalent of a study with longitudinal data but analyzed at a cross‐sectional level. In addition, to allow comparison with the cross‐sectional analysis we performed a PCA decomposition of the data from time point 1 with the subsample having a longitudinal acquisition.
Finally, for each of the four decomposition settings mentioned above, we used the weights of the obtained component from the MFA/PCA to create disease‐specific patterns. The SVM optimal parameters were obtained with a Grid Search with cross‐validation of 10, with the train set.
The algorithm was implemented in Python version 3.8 we used the libraries prince (https://pypi.org/project/prince/) for MFA and scikit‐learn (Pedregosa et al., 2011) for PCA, Grid Search, and SVM.
3. RESULTS
3.1. Sample demographics
Of the 339 subjects included in the analyses, 153 were AD patients (n = 20 with longitudinal data); 87 were FTD (n = 26 with longitudinal data), and 99 were CTR (n = 68 longitudinal). The FTD group included subjects with 49 bvFTD patients (n = 14 longitudinal data), 20 svPPA patients (n = 7 longitudinal data), 17 nfvPPA patients (n = 4 longitudinal data), and 1 unspecified PPA patient (n = 1 longitudinal data). Demographic information and group statistics are shown in Table 1. In summary, there was a significantly greater proportion of men in the FTD group compared with the AD and CTR groups. In addition, CTR subjects were slightly younger than AD and FTD groups (p < 0.05) at the first visit. However, there were no differences in age for the second visit. The time between scanners was lower in the FTD group compared with AD and CTR (p < .0001) but did not differ between AD and CTR.
TABLE 1.
Group summaries are given as the mean and the SD of each measure.
| CTR | AD | FTD | CTR–AD | CTR–FTD | AD–FTD | |
|---|---|---|---|---|---|---|
| p‐value | p‐value | p‐value | ||||
| N at first MRI | 99 | 153 | 87 | — | — | — |
| N at second MRI | 68 | 20 | 26 | — | — | — |
| Sex at first MRI, men/women | 30/69 | 59/94 | 47/40 | .22 | .005 | .03 |
| Sex at second MRI, men/women | 18/50 | 10/10 | 15/11 | .09 | .02 | .77 |
| Age at first MRI, years (SD) | 60.2 (10.5) | 64.3 (9.7) | 63.6 (8.3) | .003 | .03 | .5 |
| Age at second MRI, years (SD) | 65.0 (7.2) | 62.1 (4.5) | 63.8 (5.9) | .3 | .5 | .5 |
| Time between MRIs, years (SD) | 2.1 (0.4) | 1.9 (0.3) | 1.4 (0.5) | .3 | 2.5 e‐9 | 4.7 e‐5 |
Note: Differences between groups are calculated using Fisher test for sex and the ANOVA test for the rest of the variables. Significant group differences are highlighted in bold, and pairwise differences were measured with Benjamini–Hochberg correction (p‐values threshold .05).
Abbreviations: AD, Alzheimer's disease; CTR, controls; FTD, frontotemporal dementia; MRI, magnetic resonance imaging.
3.2. Cross‐sectional analyses: Classification
Our algorithm had an accuracy of 83.3% ± 12.7% in the CTR versus AD classification, 82.1% ± 14.7% for CTR versus FTD, 63.3% ± 9.1% for AD versus FTD, and 60.7% ± 12.7% when discriminating the three groups. Including age or sex in the algorithm led to similar results (see Supplementary Material S1)
3.3. Cross‐sectional analyses: Brain patterns and relevant features
The weights of each of the regional measures (CTh cortical regions and GM volumes for subcortical regions) were obtained as their contribution to the main feature (i.e., the first component). Figure 3 shows these PCA weights for the separate analysis of CTR versus AD and CTR versus FTD. As all algorithms were cross‐validated using k‐fold, these patterns show the mean weights obtained with all the train sets across iterations.
FIGURE 3.
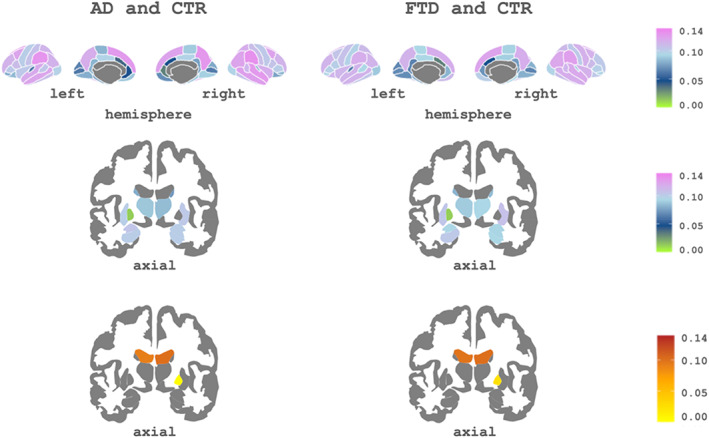
Subcortical and cortical patterns of the first principal component's weights associated with Alzheimer's disease (AD) and frontotemporal dementia (FTD). Top: Cortical regions of interest (ROIs) included in the component. Bottom: subcortical ROIs of the component. The cool color scale represents negative weights, and the warm scale represents positive weights within the component
As can be seen in Figure 3, for AD, the three most important regions were rh supramarginal, lh supramarginal, and rh precuneus. For the FTD group, these were rh supramarginal, rh superior frontal, and rh inferior parietal. The complete list of regions with their associated weights for each setting is shown in Supplementary Material S1.
3.4. Longitudinal analyses: Classification
First, when using the two time points separately for each subject in the MFA, we obtained an accuracy of 90.0% ± 14.7% in the CTR versus AD classification, 88.0% ± 16.4% for CTR versus FTD, 75.0% ± 36.9% for AD versus FTD, and 71.3% ± 13.1% for the three‐group classification (Table 2)
TABLE 2.
Classification performance of the different approaches.
| Longitudinal reduced sample | |||||
|---|---|---|---|---|---|
| Cross‐sectional all subjects (%) | Tp1, Tp2 (%) | Tp1, Tp2, change (%) | Only change (%) | Baseline of the longitudinal sample | |
| CTR vs. AD | 83.3 ± 12.7 | 90.0 ± 14.7 | 94.5 ± 11.8 | 86.5 ± 13.2 | 79.5 ± 9.8 |
| CTR vs. FTD | 82.1 ± 14.7 | 88.0 ± 16.4 | 87.8 ± 17.8 | 80.0 ± 15.4 | 81.0 ± 16.0 |
| AD vs. FTD | 63.3 ± 9.1 | 75.0 ± 36.9 | 60.8 ± 33.4 | 58.3 ± 32.2 | 67.5 ± 32.2 |
| CTR vs. AD vs. FTD | 60.7 ± 12.7 | 71.3 ± 13.1 | 77.7 ± 19.0 | 46.7 ± 21.2 | 59.7 ± 10.4 |
Note: The best accuracy for each group is highlighted in bold.
Abbreviations: AD, Alzheimer's disease; CTR, controls; FTD, frontotemporal dementia, Tp1, timepoint 1; Tp2, timepoint 2.
Including change as an additional measure for each subject and region led to higher classification scores for CTR versus AD and the three‐group classification. The accuracies were 94.5% ± 11.8% in the CTR versus AD classification, 87.8% ± 17.8% for CTR versus FTD, 60.8% ± 33.4% for AD versus FTD, and 77.7% ± 19.0% when discriminating the three groups. Interestingly, including change in the algorithm increased the accuracy for CTR versus AD and decreased the accuracy for CTR versus FTD. Including age or sex in all the longitudinal analyses led to similar results (see Supplementary Material S1)
When including only change as a feature for each region (i.e., without the individual time point data), we obtained lower classification scores compared with the full‐longitudinal setting. The classification scores were: 86.5% ± 13.2% in the CTR versus AD classification, 80.0% ± 15.4% for CTR versus FTD, 58.3% ± 32.2% for AD versus FTD, and 46.7% ± 21.2% for the three‐class classification. This result indicates that this variable is not the unique source of discrimination power across groups. However, we observed that including it in the longitudinal study together with the measures at each time point was beneficial for classification
Finally, to be able to directly compare the two approaches, we repeated the cross‐sectional analyses for the baseline data of the subjects that had longitudinal data available. We obtained a cross‐sectional accuracy of 79.5% ± 9.8% in the CTR versus AD classification, 81.0% ± 16.0% for CTR versus FTD, 67.5% ± 32.2% for AD versus FTD, and 59.7 ± 10.4% for the three‐class classification. These results highlight the increase in performance for the longitudinal approach when compared with a cross‐sectional approach with an equivalent sample. Table 2 shows a summary of all the accuracies for each analysis and comparison
3.5. Longitudinal analyses: Brain patterns and relevant structures
The contributions of each brain region (CTh cortical regions and GM volumes for subcortical regions) to the first MFA component are shown in Figure 4. Using these weights, we created a pattern for each comparison and visit: CTR versus AD and CTR versus FTD. As before, patterns were obtained with the mean weights obtained with all train sets across iterations.
FIGURE 4.

Subcortical and cortical patterns of the contributions of the first component associated with Alzheimer's disease (AD) and frontotemporal dementia (FTD) for both visits. The cool color scale represents negative weights, and the warm scale represents positive weights within the component
As can be seen in Figure 4, for the longitudinal analysis the most important regions for differentiating AD were rh pars triangularis, rh entorhinal, and lh transverse temporal from Visit 1, and rh paracentral, rh inferior temporal, and rh amygdala from Visit 2. For FTD, these were rh pars triangularis, lh pars orbitalis, and lh rostral anterior cingulate from Visit 1 and rh temporal pole, rh inferior temporal, and rh bankssts from Visit 2. The complete list of features and associated weights for each comparison can be found in Supplementary Material S1.
4. DISCUSSION
In this study, we show the utility of machine learning approaches for the differential diagnosis of AD and FTD. We used a combination of unsupervised and supervised techniques that allowed (1) reducing all subcortical GM volumes and CTh measures from MRI into a single feature and (2) obtaining blind classifications from MRI data while providing meaningful atrophy patterns at the group level using the weights of the unsupervised part of the algorithm. We implemented two equivalent algorithms for cross‐sectional and longitudinal data, and we observed that longitudinal approaches outperformed cross‐sectional analyses in differentiating AD and FTD.
At the cross‐sectional level, we demonstrated that ML can be used to support clinical diagnosis using a method that is not computationally expensive. Previous ML neuroimaging studies with cross‐sectional structural MRI data have shown accuracies between 80% and 95% for AD versus CTR, 72%–88% for FTD versus CTR, and 69%–89% for AD versus FTD (Bron et al., 2017; Klöppel et al., 2008; Möller et al., 2016). In the case of the three‐class classification, Bron et al. (2017) reported an accuracy of 70%. In our cohort, we obtained accuracy scores that are in agreement with these studies. Our study has a higher sample size than those mentioned above and differs in two important methodological aspects: first, we used a feature reduction algorithm that results in a single component being fed into the classification stage. This component encompasses information from all CTh values and GM volume measures. Even if there is an obvious risk of losing information in this step, we demonstrated that it is still useful for discrimination, while reducing the computational cost. Second, our FTD group included patients with both PPA and bvFTD variants, not only bvFTD patients as in some of the abovementioned studies. Even if further studies with similar algorithms should attempt to differentiate disease subtypes, we believe that our approach can be very useful to support differential diagnosis across diseases. Noteworthy, the wide range of misclassified subjects both in ours in previous studies suggests that some heterogeneities and overlaps need to be further explored (Habes et al., 2020).
We developed an algorithm that used longitudinal data for training the classification models, which resulted in a noticeable increase in classification accuracy for all comparisons, increasing up to 15% of the overall accuracy score. Only a few studies have used longitudinal data in ML algorithms. For example, previous studies reported accuracies between 80% and 94% for AD versus CTR (Gavidia‐Bovadilla et al., 2017; Guo et al., 2020; Zhang et al., 2017). In our cohort, we obtain accuracy scores of 90% and 95% for this specific comparison, outperforming previous approaches. To our knowledge, no previous studies have used longitudinal data to differentiate FTD versus CTR or AD versus FTD. Our approach uses the MFA decomposition, which captures the variance of the data while modeling intra‐subject variability.
The accuracy obtained in all the longitudinal experiments suggests that the proposed methodology is useful to support the diagnosis problem of distinguishing AD from FTD. Longitudinal analyses allowed studying disease change and disease trajectories. Here, we first applied the ML algorithm combining all longitudinal data in a repeated measures fashion (Visit 1 plus Visit 2). We then tested the algorithm using the longitudinal data (Visit 1 and Visit 2) in combination with the variable change that was the difference between both visits. We observed that including the change variable in the algorithm boosted the accuracy for CTR versus AD and worsened the accuracy for CTR versus FTD. This could indicate that in AD patients the change variable has higher discriminative power. On the contrary, in FTD the change variable did not add discriminative power (indeed, there is a slight decrease in accuracy), indicating that the patterns themselves provide more discriminability than the change. This finding could be associated with the fact that FTD patients could show floor effect in atrophy rates due to an advanced stage of disease, while AD patients included in this study might be in a less advanced stage (Pankov et al., 2016). Finally, as regards the abovementioned results, we acknowledge that the change variable, computed as a difference, might add collinearity to the algorithm. However, by including it, we were able to make guesses about the different spatial patterns being important for classification.
Besides maximizing performance, we were interested in depicting the spatial patterns that drive accuracy for each classification setting. In ML, this represents a crucial step for developing algorithms that are interpretable at the biological and pathological levels (Stiglic et al., 2020). Here, we used the weights of the PCA/MFA components to identify the regions that contributed the most to the group variances. To add explainability to our algorithm, we studied the most important regions providing classification between pathologies. In general, we found widespread brain patterns of variance, with common AD/FTD regions appearing within the ones on the top of the lists, depicting pathological patterns in concordance with the literature (Möller et al., 2016; Rabinovici et al., 2008). However, our classification feature was obtained from the PCA, and therefore it includes contributions across all brain regions, accounting for both overlapping and differential patterns across disorders. ML techniques search for robust interactions between features (in our case the brain regions), so it is plausible that AD and FTD patterns present both differential and overlapping regions. Previous works (Davatzikos et al., 2008; Falgàs et al., 2020; Laakso et al., 2000) have also found some overlapping patterns of degeneration across disorders. Overall, we believe that the joint analysis of overlapping patterns (i.e., indicating common neurodegeneration) and specific regional alterations will be crucial in future works investigating differential diagnosis.
We developed an ML algorithm for differential diagnosis of FTD and AD with good to excellent accuracy. Our algorithm combines unsupervised and supervised methodologies. In addition, we adapted our algorithms to longitudinal data, which was not included in previous works in the field (Bron et al., 2017; Chagué et al., 2021; Klöppel et al., 2008; Möller et al., 2016). Therefore, the main novelty is the combination of advanced methods (PCA/MFA and SVM) together with the use of longitudinal data, a key point to understanding neurodegenerative diseases (Clifford et al., 1999). Moreover, the PCA was not only used for the feature reduction step, as in previous studies (Bachli et al., 2020; Davatzikos et al., 2008; Kim et al., 2019), but also for obtaining the weights of the features for interpreting the findings.
Our study has some limitations. Regarding the sample size: First, it is important to consider that our sample size at baseline, is lower compared with the sample size which can be obtained in a multicentric study. However, all the data has been acquired in the same center, allowing us to have the same MRI scanner protocol and the same clinical criteria for the diagnosis. Another limitation is the relatively small sample size at the follow‐up visit, in some analyses, especially for the comparison between AD and FTD, the number of subjects was low, due to the difficulty of obtaining longitudinal samples in these dementias. Regarding the MRI data, it is known that the combination of different modalities of MRI, such as diffusion tensor imaging (DTI), resting‐state, amyloid positron emission tomography, or arterial spin labeling could improve the accuracy scores (Agostinho et al., 2022; Bron et al., 2014, 2017), while in our case we only used structural MRI. Thus, as future work, we could include some of these image modalities in our algorithm. Finally, the different clinical variants in the FTD group (bvFTD and PPA) were studied as a single group and there is the possibility that our results are biased by the different FTD atrophy patterns. Due to sample size limitations, it was impossible to subdivide the FTD group to study in detail the different variants of the pathology. Future studies taking into consideration this point should be considered.
In our study, we focused on differentiating AD and FTD using ML on MRI data. Other studies have reported differences between these pathologies using a wide range of methods and MRI sequences. For example, the work of Du et al. (2007) used structural MRI to compare regional CTh between AD and FTD and their relationship with neuropsychological scores at a vertex‐wise level. They found that FTD patients, compared with AD patients, had a thinner cortex in parts of the bilateral parietal and precuneus regions. Similarly, Steketee et al. (2016) used perfusion and structural MRI to differentiate AD and FTD. They studied the sensitivity, specificity, and diagnostic performance of the different regions and found that AD patients, compared with FTD patients, showed hypoperfusion in the posterior cingulate cortex. However, they also found that regional atrophy did not differ between AD and FTD. In this sense, we could differentiate AD and FTD with atrophy values, suggesting that ML techniques, that incorporate information across the whole brain, might be more sensitive. Finally, Avants et al. (2010) used sparse canonical correlation analysis with DTI and T1‐weighed MRI data to identify patterns of reduced white matter (WM) integrity for AD and FTD. They found that, in FTD, frontal and temporal degeneration is correlated across modalities. In AD, they reported a significant association between CTh and WM in parietal and temporal regions. Considering all these studies, in future work, we aim to add different MRI modalities and other clinical variables to our algorithm.
5. CONCLUSION
In conclusion, our study leads to three important points: First, the combination of PCA or MFA and SVM successfully separates patients with AD or FTD from CTR subjects. Second, they perform well in the differential diagnosis of two pathologies (AD vs FTD). Thirdly, the follow‐up visits are beneficial in ML algorithms to distinguish these pathologies, especially AD. All these points suggest an important breakthrough in computer‐aided diagnostic image analysis for clinical research and practice.
AUTHOR CONTRIBUTIONS
Agnès Pérez‐Millan, Laia Borrell, Raquel Sánchez‐Valle, and Roser Sala‐Llonch contributed to the design of the study. Agnès Pérez‐Millan, José Contador, Jordi Juncà‐Parella, and Beatriz Bosch contributed to the analyses of the data. Agnès Pérez‐Millan, José Contador, Albert Lladó, Raquel Sánchez‐Valle, and Roser Sala‐Llonch contributed to the interpretation of the data. Agnès Pérez‐Millan, José Contador, Raquel Sánchez‐Valle, and Roser Sala‐Llonch contributed to the draft of the article. Jordi Juncà‐Parella, Beatriz Bosch, Laia Borrell, Adrià Tort‐Merino, Neus Falgàs, Sergi Borrego‐Écija, Nuria Bargalló, Lorena Rami, Mircea Balasa, and Albert Lladó revised the article critically for important intellectual content and approved the final version of the article. All authors contributed to the article and approved the submitted version.
CONFLICT OF INTEREST
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supporting information
Appendix S1: Supplementary Information.
ACKNOWLEDGMENTS
The authors thank patients, their relatives, and healthy controls for their participation in the research. This work was supported by Instituto de Salud Carlos III, Spain (grant no. 20143810 and PI20/0448 to Dr. Raquel Sánchez‐Valle), Spanish Ministry of Science and by Instituto de Salud Carlos III (ISCIII) and co‐funded by the European Union (project PI19/00449 to Dr. Albert Lladó and project PI19/00198 to Dr. Mircea Balasa), by Department de Salut – Generalitat de Catalunya (PERIS 2016–2020 SLT008/18/00061 to Dr. A. Lladó) and by Spanish Ministry of Science and Innovation (PID2020‐118386RA‐I00/AEI/10.13039/501100011033 to Dr. R. Sala‐Llonch) and María de Maeztu Unit of Excellence (Institute of Neurosciences, University of Barcelona) MDM‐2017‐0729. Dr. S. Borrego‐Écija is a recipient of the Joan Rodés Josep Baselga grant from FBBVA. Dr. Neus Falgàs recipient of Rio Hortega grant (CM21/00024).
Pérez‐Millan, A. , Contador, J. , Juncà‐Parella, J. , Bosch, B. , Borrell, L. , Tort‐Merino, A. , Falgàs, N. , Borrego‐Écija, S. , Bargalló, N. , Rami, L. , Balasa, M. , Lladó, A. , Sánchez‐Valle, R. , & Sala‐Llonch, R. (2023). Classifying Alzheimer's disease and frontotemporal dementia using machine learning with cross‐sectional and longitudinal magnetic resonance imaging data. Human Brain Mapping, 44(6), 2234–2244. 10.1002/hbm.26205
Raquel Sánchez‐Valle and Roser Sala‐Llonch contributed equally to this work.
Funding information Department de Salut – Generalitat de Catalunya, Grant/Award Numbers: PERIS 2016‐2020, SLT008/18/00061; Instituto de Salud Carlos III (ISCIII), Grant/Award Numbers: 20143810, PI20/0448, PI19/00198, PI19/00449; Spanish Ministry of Science and Innovation, Grant/Award Number: PID2020‐118386RA‐I00/AEI/10.13039/501100011033; María de Maeztu Unit of Excellence (Institute of Neurosciences, University of Barcelona, Grant/Award Number: MDM‐2017‐0729; Joan Rodés Josep Baselga grant FBBVA; Rio Hortega, Grant/Award Number: CM21/00024
DATA AVAILABILITY STATEMENT
The data that support the findings of this study are available from the corresponding author upon reasonable request.
REFERENCES
- Abdi, H. , Williams, L. J. , & Valentin, D. (2013). Multiple factor analysis: Principal component analysis for multitable and multiblock data sets. Wiley Interdisciplinary Reviews: Computational Statistics, 5, 149–179. 10.1002/wics.1246 [DOI] [Google Scholar]
- Agostinho, D. , Caramelo, F. , Moreira, A. P. , Santana, I. , Abrunhosa, A. , & Castelo‐Branco, M. (2022). Combined structural MR and diffusion tensor imaging classify the presence of Alzheimer's disease with the same performance as MR combined with amyloid positron emission tomography: A data integration approach. Frontiers in Neuroscience, 15, 638175. 10.3389/fnins.2021.638175 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Albert, M. S. , DeKosky, S. T. , Dickson, D. , Dubois, B. , Feldman, H. H. , Fox, N. C. , Gamst, A. , Holtzman, D. M. , Jagust, W. J. , Petersen, R. C. , Snyder, P. J. , Carrillo, M. C. , Thies, B. , & Phelps, C. H. (2011). The diagnosis of mild cognitive impairment due to Alzheimer's disease: Recommendations from the National Institute on Aging‐Alzheimer's association workgroups on diagnostic guidelines for Alzheimer's disease. Alzheimer's Dement, 7, 270–279. 10.1016/j.jalz.2011.03.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avants, B. B. , Cook, P. A. , Ungar, L. , Gee, J. C. , & Grossman, M. (2010). Dementia induces correlated reductions in white matter integrity and cortical thickness: A multivariate neuroimaging study with sparse canonical correlation analysis. NeuroImage, 50, 1004–1016. 10.1016/j.neuroimage.2010.01.041 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bachli, M. B. , Sedeño, L. , Ochab, J. K. , Piguet, O. , Kumfor, F. , Reyes, P. , Torralva, T. , Roca, M. , Cardona, J. F. , Campo, C. G. , Herrera, E. , Slachevsky, A. , Matallana, D. , Manes, F. , García, A. M. , Ibáñez, A. , & Chialvo, D. R. (2020). Evaluating the reliability of neurocognitive biomarkers of neurodegenerative diseases across countries: A machine learning approach. NeuroImage, 208, 116456. 10.1016/j.neuroimage.2019.116456 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balasa, M. , Gelpi, E. , Antonell, A. , Rey, M. J. , Sánchez‐Valle, R. , Molinuevo, J. L. , & Lladó, A. (2011). Clinical features and APOE genotype of pathologically proven early‐onset Alzheimer disease. Neurology, 76, 1720–1725. 10.1212/WNL.0b013e31821a44dd [DOI] [PubMed] [Google Scholar]
- Bejanin, A. , Tammewar, G. , Marx, G. , Cobigo, Y. , Iaccarino, L. , Kornak, J. , Staffaroni, A. M. , Dickerson, B. C. , Boeve, B. F. , Knopman, D. S. , Gorno‐Tempini, M. , Miller, B. L. , Jagust, W. J. , Boxer, A. L. , Rosen, H. J. , & Rabinovici, G. D. (2020). Longitudinal structural and metabolic changes in frontotemporal dementia. Neurology, 95, E140–E154. 10.1212/WNL.0000000000009760 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernal‐Rusiel, J. L. , Greve, D. N. , Reuter, M. , Fischl, B. , & Sabuncu, M. R. (2013). Statistical analysis of longitudinal neuroimage data with linear mixed effects models. NeuroImage, 66, 249–260. 10.1016/j.neuroimage.2012.10.065 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bocchetta, M. , Todd, E. G. , Peakman, G. , Cash, D. M. , Convery, R. S. , Russell, L. L. , Thomas, D. L. , Eugenio Iglesias, J. , van Swieten, J. C. , Jiskoot, L. C. , Seelaar, H. , Borroni, B. , Galimberti, D. , Sanchez‐Valle, R. , Laforce, R. , Moreno, F. , Synofzik, M. , Graff, C. , Masellis, M. , … Zulaica, M. (2021). Differential early subcortical involvement in genetic FTD within the GENFI cohort. NeuroImage Clinical, 30, 102646. 10.1016/j.nicl.2021.102646 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bron, E. E. , Smits, M. , Papma, J. M. , Steketee, R. M. E. , Meijboom, R. , de Groot, M. , van Swieten, J. C. , Niessen, W. J. , & Klein, S. (2017). Multiparametric computer‐aided differential diagnosis of Alzheimer's disease and frontotemporal dementia using structural and advanced MRI. European Radiology, 27, 3372–3382. 10.1007/s00330-016-4691-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bron, E. E. , Steketee, R. M. E. , Houston, G. C. , Oliver, R. A. , Achterberg, H. C. , Loog, M. , van Swieten, J. C. , Hammers, A. , Niessen, W. J. , Smits, M. , Klein, S. , & for the Alzheimer's Disease Neuroimaging Initiative . (2014). Diagnostic classification of arterial spin labeling and structural MRI in presenile early stage dementia. Human Brain Mapping, 35, 4916–4931. 10.1002/hbm.22522 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Canu, E. , Agosta, F. , Mandic‐Stojmenovic, G. , Stojković, T. , Stefanova, E. , Inuggi, A. , Imperiale, F. , Copetti, M. , Kostic, V. S. , & Filippi, M. (2017). Multiparametric MRI to distinguish early onset Alzheimer's disease and behavioural variant of frontotemporal dementia. NeuroImage Clinical, 15, 428–438. 10.1016/j.nicl.2017.05.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chagué, P. , Marro, B. , Fadili, S. , Houot, M. , Morin, A. , Samper‐González, J. , Beunon, P. , Arrivé, L. , Dormont, D. , Dubois, B. , Teichmann, M. , Epelbaum, S. , & Colliot, O. (2021). Radiological classification of dementia from anatomical MRI assisted by machine learning‐derived maps. Journal of Neuroradiology, 48, 412–418. 10.1016/j.neurad.2020.04.004 [DOI] [PubMed] [Google Scholar]
- Clifford, J. R. , Petersen, R. C. , Xu, Y. C. , O'Brien, P. C. , Smith, G. E. , Ivnik, R. J. , et al. (1999). Prediction of AD with MRI‐based hippocampal volume in mild cognitive impairment. Neurology, 52, 1397–1403. 10.1212/wnl.52.7.1397 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Contador, J. , Pérez‐Millán, A. , Tort‐Merino, A. , Balasa, M. , Falgàs, N. , Olives, J. , Castellví, M. , Borrego‐Écija, S. , Bosch, B. , Fernández‐Villullas, G. , Ramos‐Campoy, O. , Antonell, A. , Bargalló, N. , Sanchez‐Valle, R. , Sala‐Llonch, R. , Lladó, A. , & Alzheimer's Disease Neuroimaging Initiative . (2021). Longitudinal brain atrophy and CSF biomarkers in early‐onset Alzheimer's disease. NeuroImage Clinical, 32, 102804. 10.1016/j.nicl.2021.102804 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davatzikos, C. , Resnick, S. M. , Wu, X. , Parmpi, P. , & Clark, C. M. (2008). Individual patient diagnosis of AD and FTD via high‐dimensional pattern classification of MRI. NeuroImage, 41, 1220–1227. 10.1016/j.neuroimage.2008.03.050 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desikan, R. S. , Ségonne, F. , Fischl, B. , Quinn, B. T. , Dickerson, B. C. , Blacker, D. , Buckner, R. L. , Dale, A. M. , Maguire, R. P. , Hyman, B. T. , Albert, M. S. , & Killiany, R. J. (2006). An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. NeuroImage, 31, 968–980. 10.1016/j.neuroimage.2006.01.021 [DOI] [PubMed] [Google Scholar]
- Du, A. T. , Schuff, N. , Kramer, J. H. , Rosen, H. J. , Gorno‐Tempini, M. L. , Rankin, K. , Miller, B. L. , & Weiner, M. W. (2007). Different regional patterns of cortical thinning in Alzheimer's disease and frontotemporal dementia. Brain, 130, 1159–1166. 10.1093/brain/awm016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Falgàs, N. , Ruiz‐Peris, M. , Pérez‐Millan, A. , Sala‐Llonch, R. , Antonell, A. , Balasa, M. , Borrego‐Écija, S. , Ramos‐Campoy, O. , Augé, J. M. , Castellví, M. , Tort‐Merino, A. , Olives, J. , Fernández‐Villullas, G. , Blennow, K. , Zetterberg, H. , Bargalló, N. , Lladó, A. , & Sánchez‐Valle, R. (2020). Contribution of CSF biomarkers to early‐onset Alzheimer's disease and frontotemporal dementia neuroimaging signatures. Human Brain Mapping, 41, 2004–2013. 10.1002/hbm.24925 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl, B. , & Dale, A. M. (2000). Measuring the thickness of the human cerebral cortex from magnetic resonance images. Proceedings of the National Academy of Sciences of the United States of America, 97, 11050–11055. 10.1073/pnas.200033797 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl, B. , van der Kouwe, A. , Destrieux, C. , Halgren, E. , Ségonne, F. , Salat, D. H. , et al. (2004). Automatically Parcellating the human cerebral cortex. Cerebral Cortex, 14, 11–22. 10.1093/cercor/bhg087 [DOI] [PubMed] [Google Scholar]
- Gavidia‐Bovadilla, G. , Kanaan‐Izquierdo, S. , Mataroa‐Serrat, M. , & Perera‐Lluna, A. (2017). Early prediction of Alzheimer's disease using null longitudinal model‐based classifiers. PLoS One, 12, e0168011. 10.1371/journal.pone.0168011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gorno‐Tempini, M. L. , Hillis, A. E. , Weintraub, S. , Kertesz, A. , Mendez, M. , Cappa, S. F. , Ogar, J. M. , Rohrer, J. D. , Black, S. , Boeve, B. F. , Manes, F. , Dronkers, N. F. , Vandenberghe, R. , Rascovsky, K. , Patterson, K. , Miller, B. L. , Knopman, D. S. , Hodges, J. R. , Mesulam, M. M. , & Grossman, M. (2011). Classification of primary progressive aphasia and its variants. Neurology, 76, 1006–1014. 10.1212/WNL.0b013e31821103e6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo, M. , Li, Y. , Zheng, W. , Huang, K. , Zhou, L. , Hu, X. , Yao, Z. , & Hu, B. (2020). A novel conversion prediction method of MCI to AD based on longitudinal dynamic morphological features using ADNI structural MRIs. Journal of Neurology, 267, 2983–2997. 10.1007/s00415-020-09890-5 [DOI] [PubMed] [Google Scholar]
- Habes, M. , Grothe, M. J. , Tunc, B. , McMillan, C. , Wolk, D. A. , & Davatzikos, C. (2020). Disentangling heterogeneity in Alzheimer's disease and related dementias using data‐driven methods. Biological Psychiatry, 88, 70–82. 10.1016/j.biopsych.2020.01.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Irish, M. , Landin‐Romero, R. , Mothakunnel, A. , Ramanan, S. , Hsieh, S. , Hodges, J. R. , & Piguet, O. (2018). Evolution of autobiographical memory impairments in Alzheimer's disease and frontotemporal dementia – A longitudinal neuroimaging study. Neuropsychologia, 110, 14–25. 10.1016/j.neuropsychologia.2017.03.014 [DOI] [PubMed] [Google Scholar]
- Jack, C. R. , Bennett, D. A. , Blennow, K. , Carrillo, M. C. , Dunn, B. , Haeberlein, S. B. , et al. (2018). NIA‐AA research framework: Toward a biological definition of Alzheimer's disease. Alzheimer's Dementia, 14, 535–562. 10.1016/j.jalz.2018.02.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim, J. P. , Kim, J. , Park, Y. H. , Park, S. B. , Lee, J. S. , Yoo, S. , Kim, E. J. , Kim, H. J. , Na, D. L. , Brown, J. A. , Lockhart, S. N. , Seo, S. W. , & Seong, J. K. (2019). Machine learning based hierarchical classification of frontotemporal dementia and Alzheimer's disease. NeuroImage Clinical, 23, 101811. 10.1016/j.nicl.2019.101811 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klöppel, S. , Stonnington, C. M. , Chu, C. , Draganski, B. , Scahill, R. I. , Rohrer, J. D. , Fox, N. C. , Jack, C. R., Jr. , Ashburner, J. , & Frackowiak, R. S. (2008). Automatic classification of MR scans in Alzheimer's disease. Brain, 131, 681–689. 10.1093/brain/awm319 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laakso, M. P. , Frisoni, G. B. , Könönen, M. , Mikkonen, M. , Beltramello, A. , Geroldi, C. , Bianchetti, A. , Trabucchi, M. , Soininen, H. , & Aronen, H. J. (2000). Hippocampus and entorhinal cortex in frontotemporal dementia and Alzheimer's disease: A morphometric MRI study. Biological Psychiatry, 47, 1056–1063. 10.1016/S0006-3223(99)00306-6 [DOI] [PubMed] [Google Scholar]
- Li, B. , Jang, I. , Riphagen, J. , Almaktoum, R. , Yochim, K. M. , Ances, B. M. , Bookheimer, S. Y. , Salat, D. H. , & For the Alzheimer's Disease Neuroimaging Initiative . (2021). Identifying individuals with Alzheimer's disease‐like brains based on structural imaging in the human connectome project aging cohort. Human Brain Mapping, 42, 5535–5546. 10.1002/hbm.25626 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKhann, G. M. , Knopman, D. S. , Chertkow, H. , Hyman, B. T. , Jack, C. R. , Kawas, C. H. , Klunk, W. E. , Koroshetz, W. J. , Manly, J. J. , Mayeux, R. , Mohs, R. C. , Morris, J. C. , Rossor, M. N. , Scheltens, P. , Carrillo, M. C. , Thies, B. , Weintraub, S. , & Phelps, C. H. (2011). The diagnosis of dementia due to Alzheimer's disease: Recommendations from the National Institute on Aging‐Alzheimer's association workgroups on diagnostic guidelines for Alzheimer's disease. Alzheimer's Dementia, 7, 263–269. 10.1016/j.jalz.2011.03.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mendez, M. F. (2006). The accurate diagnosis of early‐onset dementia. International Journal of Psychiatry in Medicine, 36, 401–412. 10.2190/Q6J4-R143-P630-KW41 [DOI] [PubMed] [Google Scholar]
- Möller, C. , Pijnenburg, Y. A. L. , van der Flier, W. M. , Versteeg, A. , Tijms, B. , de Munck, J. C. , Hafkemeijer, A. , Rombouts, S. A. , van der Grond, J. , van Swieten, J. , Dopper, E. , Scheltens, P. , Barkhof, F. , Vrenken, H. , & Wink, A. M. (2016). Alzheimer disease and behavioral variant frontotemporal dementia: Automatic classification based on cortical atrophy for single‐subject diagnosis. Radiology, 279, 838–848. 10.1148/radiol.2015150220 [DOI] [PubMed] [Google Scholar]
- Möller, C. , Vrenken, H. , Jiskoot, L. , Versteeg, A. , Barkhof, F. , Scheltens, P. , & van der Flier, W. M. (2013). Different patterns of gray matter atrophy in early‐ and late‐onset Alzheimer's disease. Neurobiology of Aging, 34, 2014–2022. 10.1016/j.neurobiolaging.2013.02.013 [DOI] [PubMed] [Google Scholar]
- Pankov, A. , Binney, R. J. , Staffaroni, A. M. , Kornak, J. , Attygalle, S. , Schuff, N. , Weiner, M. W. , Kramer, J. H. , Dickerson, B. C. , Miller, B. L. , & Rosen, H. J. (2016). Data‐driven regions of interest for longitudinal change in frontotemporal lobar degeneration. NeuroImage Clinical, 12, 332–340. 10.1016/j.nicl.2015.08.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pedregosa, F. , Varoquaux, G. , Gramfort, A. , Michel, V. , Thirion, B. , Grisel, O. , et al. (2011). Scikit‐learn: Machine learning in python. Journal of Machine Learning Research, 12, 2825–2830 Retrieved from October 22, 2019 http://jmlr.csail.mit.edu/papers/v12/pedregosa11a.html [Google Scholar]
- Penny, W. , Friston, K. , Ashburner, J. , Kiebel, S. , & Nichols, T. (2007). Statistical parametric mapping: The analysis of functional brain images. Elsevier Ltd. 10.1016/B978-0-12-372560-8.X5000-1 [DOI] [Google Scholar]
- Rabinovici, G. D. , Seeley, W. W. , Kim, E. J. , Gorno‐Tempini, M. L. , Rascovsky, K. , Pagliaro, T. A. , Allison, S. C. , Halabi, C. , Kramer, J. H. , Johnson, J. K. , Weiner, M. W. , Forman, M. S. , Trojanowski, J. Q. , DeArmond, S. J. , Miller, B. L. , & Rosen, H. (2008). Distinct MRI atrophy patterns in autopsy‐proven Alzheimer's disease and frontotemporal lobar degeneration. American Journal of Alzheimer's Disease and Other Dementias, 22, 474–488. 10.1177/1533317507308779 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rascovsky, K. , Hodges, J. R. , Knopman, D. , Mendez, M. F. , Kramer, J. H. , Neuhaus, J. , van Swieten, J. C. , Seelaar, H. , Dopper, E. G. P. , Onyike, C. U. , Hillis, A. E. , Josephs, K. A. , Boeve, B. F. , Kertesz, A. , Seeley, W. W. , Rankin, K. P. , Johnson, J. K. , Gorno‐Tempini, M. L. , Rosen, H. , … Miller, B. L. (2011). Sensitivity of revised diagnostic criteria for the behavioural variant of frontotemporal dementia. Brain, 134, 2456–2477. 10.1093/brain/awr179 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reuter, M. , Schmansky, N. J. , Rosas, H. D. , & Fischl, B. (2012). Within‐subject template estimation for unbiased longitudinal image analysis. NeuroImage, 61, 1402–1418. 10.1016/j.neuroimage.2012.02.084 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Risacher, S. L. , Shen, L. , West, J. D. , Kim, S. , McDonald, B. C. , Beckett, L. A. , et al. (2010). Longitudinal MRI atrophy biomarkers: Relationship to conversion in the ADNI cohort. Neurobiology of Aging, 31, 1401–1418. 10.1016/j.neurobiolaging.2010.04.029 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seidman, L. J. , Faraone, S. V. , Goldstein, J. M. , Goodman, J. M. , Kremen, W. S. , Matsuda, G. , Hoge, E. A. , Kennedy, D. , Makris, N. , Caviness, V. S. , & Tsuang, M. T. (1997). Reduced subcortical brain volumes in nonpsychotic siblings of schizophrenic patients: A pilot magnetic resonance imaging study. American Journal of Medical Genetics Part B. Neuropsychiatric Genetics, 74, 507–514. [DOI] [PubMed] [Google Scholar]
- Sintini, I. , Graff‐Radford, J. , Senjem, M. L. , Schwarz, C. G. , Machulda, M. M. , Martin, P. R. , Jones, D. T. , Boeve, B. F. , Knopman, D. S. , Kantarci, K. , Petersen, R. C. , Jack, C. R., Jr. , Lowe, V. J. , Josephs, K. A. , & Whitwell, J. L. (2020). Longitudinal neuroimaging biomarkers differ across Alzheimer's disease phenotypes. Brain, 143, 2281–2294. 10.1093/brain/awaa155 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steketee, R. M. E. , Bron, E. E. , Meijboom, R. , Houston, G. C. , Klein, S. , Mutsaerts, H. J. M. M. , Mendez Orellana, C. P. , de Jong, F. J. , van Swieten, J. C. , van der Lugt, A. , & Smits, M. (2016). Early‐stage differentiation between presenile Alzheimer's disease and frontotemporal dementia using arterial spin labeling MRI. European Radiology, 26, 244–253. 10.1007/s00330-015-3789-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stiglic, G. , Kocbek, P. , Fijacko, N. , Zitnik, M. , Verbert, K. , & Cilar, L. (2020). Interpretability of machine learning‐based prediction models in healthcare. WIREs Data Mining and Knowledge Discovery, 10, e1379. 10.1002/widm.1379 [DOI] [Google Scholar]
- Storsve, A. B. , Fjell, A. M. , Tamnes, C. K. , Westlye, L. T. , Overbye, K. , Aasland, H. W. , & Walhovd, K. B. (2014). Differential longitudinal changes in cortical thickness, surface area and volume across the adult life span: Regions of accelerating and decelerating change. The Journal of Neuroscience, 34, 8488–8498. 10.1523/JNEUROSCI.0391-14.2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson, W. K. , Hallmayer, J. , & O'Hara, R. (2011). Design considerations for characterizing psychiatric trajectories across the life span: Application to effects of APOE‐ε4 on cerebral cortical thickness in Alzheimer's disease. The American Journal of Psychiatry, 168, 894–903. 10.1176/appi.ajp.2011.10111690 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, J. , Liu, M. , An, L. , Gao, Y. , & Shen, D. (2017). Alzheimer's disease diagnosis using landmark‐based features from longitudinal structural MR images. IEEE Journal of Biomedical and Health Informatics, 21, 1607–1616. 10.1109/JBHI.2017.2704614 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix S1: Supplementary Information.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.


