Phase-independent thermometry by Z-spectrum MR imaging

Abstract

Purpose:

Z-spectrum imaging, defined as the consecutive collection of images after saturating over a range of frequency offsets, has been recently proposed as a method to measure the fat–water fraction by the simultaneous detection of fat and water resonances. By incorporating a binomial pulse irradiated at each offset before the readout, the spectral selectivity of the sequence can be further amplified, making it possible to monitor the subtle proton resonance frequency shift that follows a change in temperature.

Methods:

We tested the hypothesis in aqueous and cream phantoms and in healthy mice, all under thermal challenge. The binomial module consisted of 2 sinc-shaped pulses of opposite phase separated by a delay. Such a delay served to spread out off-resonance spins, with the resulting excitation profile being a periodic function of the delay and the chemical shift.

Results:

During heating experiments, the water resonance shifted downfield, and by fitting the curve to a sine function it was possible to quantify the change in temperature. Results from Z-spectrum imaging correlated linearly with data from conventional MRI techniques like T₁ mapping and phase differences from spoiled GRE.

Conclusion:

Because the measurement is performed solely on magnitude images, the technique is independent of phase artifacts and is therefore applicable in mixed tissues (e.g., fat). We showed that Z-spectrum imaging can deliver reliable temperature change measurement in both muscular and fatty tissues.

1. Introduction

Temperature is a key player in body homeostasis and a relevant indicator of systemic health and local tissue conditions. Measuring temperature changes in biological tissue is a nontrivial challenge, and there is a need for the development of ever more robust methods.

MRI has become the noninvasive tool of choice for thermometry.^1–7 Currently, MRI is used to monitor clinical thermal therapies efficacy.¹ Several proton magnetic resonance parameters are temperature dependent; the resonance frequency or chemical shift, the relaxation times,^2–7 the equilibrium magnetization,^8,9 and the diffusion coefficient.^10,11 Although the latter 3 parameters are interdependent and conflate into the signal amplitude, the chemical shift associates with the proton frequency alone. It does not rely on the other factors or the signal intensity. The temperature effect on the chemical shift is known as the proton resonance frequency shift (PRFS), where the water resonance shifts proportionally to the temperature increase. When temperature increases, the electron clouds of water hydrogens are stretched, leading to higher magnetic shielding of the nuclei and a lower resonance frequency. Water PRFS-based temperature measurements are very convenient for many reasons: the implementation is relatively simple, it has a relatively high sensitivity (−0.01 ppm/°C), the proportionality is linear in a wide temperature range, and, perhaps most importantly, it is relatively constant across many biological tissues.^1,12

The PRFS can be measured directly by ¹H-MR spectroscopy. The water peak is detected directly, and the spectrum from other molecules with non-shifting protons like methyl and methylene protons is used as reference.^13,14 However, as with all spectroscopic methods, it suffers from low spatial resolution and coverage or impractically long acquisition times, which curtail its use. Alternatively, the temperature change can be derived from the phase difference between images, typically gradient echoes, acquired at different thermal states.^15,16 Despite being the most widely used method for assessing temperature in medical research, phase mapping techniques are not free from many confounding factors that can corrupt the measurement. Chiefly, the phase difference changes when the magnetic field,¹⁷ the tissue susceptibility,^18,19 or other tissue properties^20,21 strongly modify the local environment. In addition, the PRFS described above is specific to protons in hydrogen bonds, that compose the water molecules, but does not apply for different atomic configurations. Other chemical species (e.g., fat) have protons that undergo different shift mechanisms; when present in the voxel with water, an ambiguity in the determination of phase is introduced, causing artifacts in the final image.^22,23 Selective saturation to exclude the contribution of such sources is a possible improvement, but it is practically unfeasible to take into account multiple fat resonances and variation in B₀ field. Other proposed strategies attempt at estimating variations in the phase by acquiring multiple baseline images or evaluating the field map from non-fat-containing voxels.^24–26 Alternatively, schemes combining aqueous and non-aqueous tissue measurements have been designed, like the joint PRFS and T₁-mapping. Relaxation time-based methods have been demonstrated in both animal and human studies, but their feasibility is cumbersome in that it requires calibration for each different tissue imaged.^27–31

Recently, Z-spectrum imaging (ZSI) has been used to measure the fat–water fraction (FWF) in brown adipose tissue by the simultaneous measurement of fat and water resonances. This technique has the potential to provide information about the frequency offset of all the species in the voxel while at the same time being independent of phase artifacts encountered in mixed tissues.^32,33 These qualities can bring a novel perspective in the field, and we decided to further explore the potential of this method. In this work, we aimed to refine the technique by combining the Z-spectrum imaging sequence with a spectrally selective preparation based on a binomial pulse. Frequency shifts can, therefore, be measured directly from the magnitude images, which translates to a high sensitivity thermal measurement applicable in aqueous and fatty tissues.

2. Methods

2.1. Z-spectrum for temperature

The PRFS effect allows deriving the information on local temperature from the water Larmor frequency in the voxel. Therefore, any sequence that can selectively tag the water resonance and monitor its traveling in the frequency domain is theoretically amenable to temperature measurement. Z-spectrum imaging fits the description: a series of images acquired after saturating a spectrum of frequencies off-resonance around water. In the resulting pixelwise spectra, the water offset is identified by the center of the Lorentzian curve representing the direct saturation of the bulk water protons. When the temperature changes, we can observe the curve shifting, and is, therefore, possible to measure the thermal differential after fitting the curve at 2-time points.^33,34 The accuracy of the thermal measurement depends on the precision of the resonance shift assessment. Besides the SNR and fitting model, which can be optimized, another critical source of indetermination in the spectral measurement is the broad linewidth of the direct saturation curve. This can be minimized by improving the local shim or reducing the intensity of the saturation, which has to be traded for enough signal over the background noise. However, even after optimizing these factors, the linewidth is inherently limited by the T₂ of the bulk water pool; our previous experimental methods could not accurately detect resonance shifts below 0.04 ppm, which translates to 4°C in aqueous tissues. Although this delta is perfectly adequate for monitoring thermal ablation therapies, it might not be suitable for more subtle physiological processes. In other words, Z-spectrum imaging, because of its spectrally selective framework, is a natural platform for the measurement of frequency shifts, but lacks the accuracy to provide fine quantifications. A remedy rests on the modification of the preparation pulse.

2.2. Binomial preparation pulse

Binomial pulses have been introduced several decades ago, and a great deal of development focused around their use for solvent suppression in MR spectroscopy, thanks to their exceptional spectral selectivity.^35–39

The excitation profile in the frequency domain can be predicted by the Fourier transform of the RF perturbation in the time domain.³⁵ The magnetization at the frequency offset Δω can be expressed as

$$M\left(\Delta \omega \right)=i\gamma M_0\left(\Delta \omega \right)F{T}^{-}\left[H_1\left(t-t_0\right)\right],$$ (1)

where the function H₁(t) is the perturbation profile of the RF irradiation and it is assumed to be much shorter than the relaxation time T₂. The RF pulse that produces a frequency profile proportional M(Δω) can be inferred by inverting the equation. Here, we want an excitation profile that allows a high spectral resolvability to measure fine frequency shifts: a sinusoidal pattern is well suited to this task. Remembering that a cosine function in the frequency domain is the Fourier transform of 2 delta functions, we can design a preparatory module made of 2 short pulses separated by a delay. If we consider 2 sinc pulses t_s long separated by a lag time τ, so that t_s << τ, we have:

$$H_1\left(t\right)=\text{sinc}\left(t\right)\cdot \frac{1}{2}\left[\delta \left(t-\tau \right)+\delta \left(t+\tau \right)\right].$$ (2)

The Fourier transform of this function, for the convolution theorem, corresponds to the convolution of the Fourier transforms of the individual functions:

$$M\left(f\right)=\frac{\pi }{2}\mathit{\text{rect}}\left(\Delta f\right)*\text{cos}\left(2\pi \tau f\right),$$ (3)

which represents a sinusoidal pattern oscillating within a window related to the parameters of the pulse. The periodicity of the function is dependent on the delay between the pulses. It is therefore possible to modulate the periodicity and therefore the spectral resolvability, by choosing a long enough delay τ.

This can perhaps be better pictured in the classical description of the magnetization vector. The excitation module that we will use is the jump and return sequence^36–39 and features 2 hard pulses along the y-axis with opposite polarity. The equilibrium magnetization along the z-axis is flipped by the first pulse, allowed to evolve during the delay τ, and then flipped back to the yz-plane by the second pulse irradiated along −y. On-resonance protons do not evolve in the rotating frame, and their magnetization will be fully flipped back onto the z-axis. Off-resonance spins instead will dephase during τ according to their chemical shift and will have reduced magnetization available during the readout. In the proximity of the central frequency, the net excitation profile will resemble a sinusoidal function of the chemical shift Δω, with null/maxima values determined by the delay-resonance product Δω×τ. When temperature changes, the water resonance ω₀ = Δω − ω shifts (with ω being the saturated offset) and with it the curve. By fitting the curve with a sine function of (Δω×τ), it is possible to keep track of the shift and therefore of the temperature changes (Figure 1).

Figure 1.

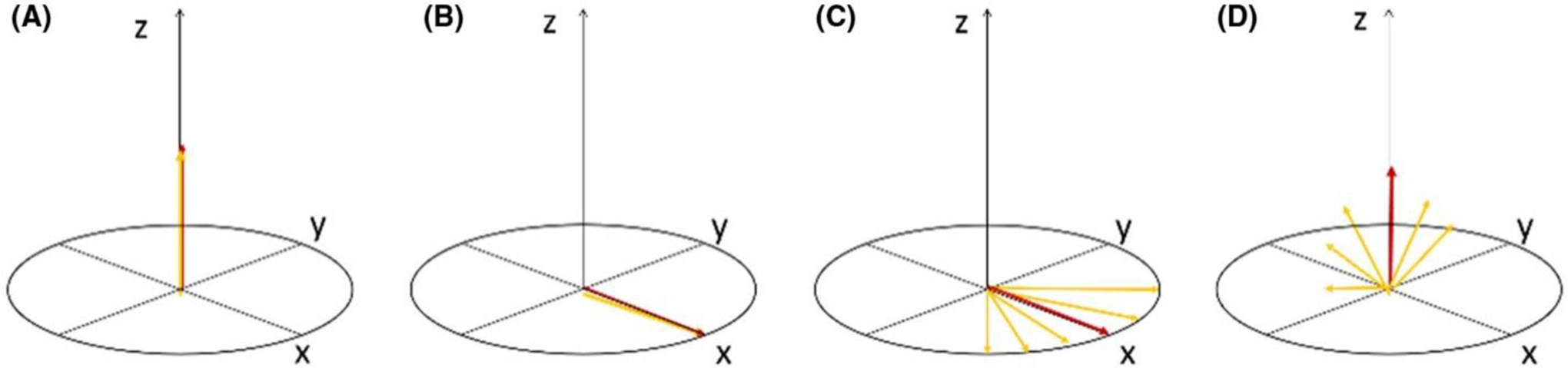
Scheme of the magnetization vector traveling during the binomial pulse. (A) At equilibrium, all spins are aligned along z. (B) After the first pulse along y-axis, the spins are tilted along the x-axis. (C) After the delay τ, the off-resonance spins fan out, depending on the frequency difference with respect to the central on-resonance frequency, which is stable. (D) The second pulse along –y, tilts back the spins on the yz plane. The more the magnetization is off-resonance, the more has fan out and produces less signal. The final pattern near the resonance is a sine function of chemical shift.

2.3. In vitro experiments

As a proof of concept, experiments were first carried out on a phantom containing a phosphate buffer sodium solution (PBS) on a 9.4 T preclinical animal scanner (Agilent, Santa Clara, CA). Temperature in the phantom was increased from 16 to 31°C by regulating the air flow temperature in the scanner bore. An MRI- compatible physiological monitoring system with the temperature sensor tip inserted in the phantom was used to monitor the thermal changes in real-time. The sequence consisted of a preparatory module of 2 90° sinc pulses each 0.3 ms long with opposite phase (i.e., along y and –y axes), separated by a 3 ms long delay. The module repeated at several frequency offsets to sample the spectrum: from −1 to 1 ppm with 0.025 ppm steps. After each repetition, a fast spin-echo readout with 2 consecutive segments with a 32 × 32 matrix collected the signal for a total scan time of 3 min. The entire series was repeated to monitor the temperature going up and down as controlled by the airflow. A diagram of the sequence is in Figure 2.

Figure 2.

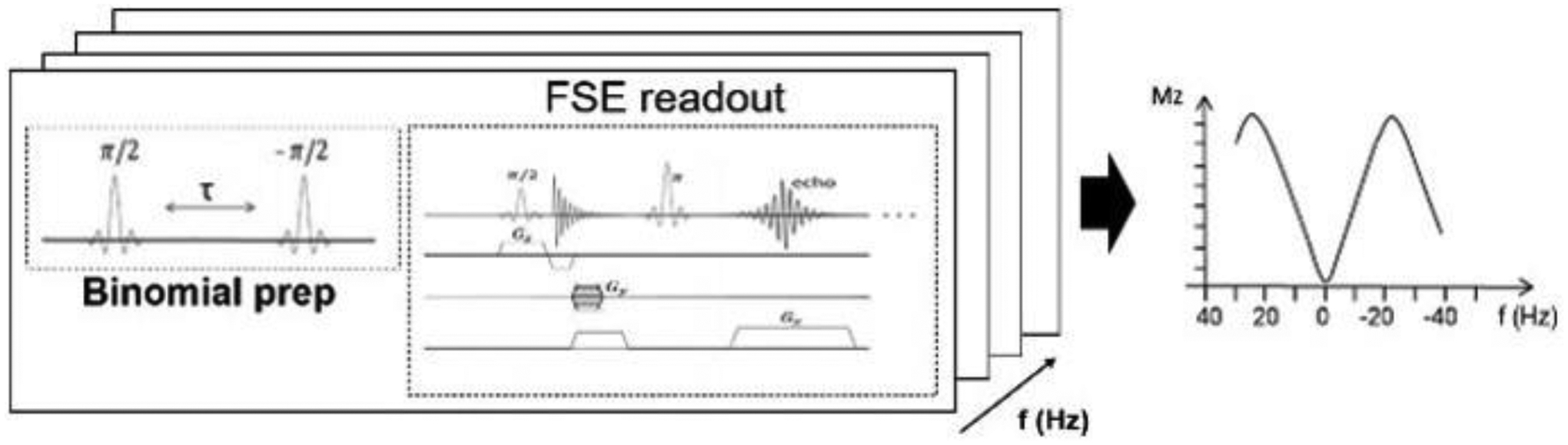
Diagram of the ZSI sequence with binomial pulse preparation. Two sinc pulses with opposite polarity and separated by a delay encode the phase accrue into the magnitude signal subsequently detected with a fast spin echo readout. The sequence is repeated at several offsets, resulting in a sinusoidal excitation profile, shown on the right of the figure.

Interleaved with the binomial-ZSI acquisitions, conventional temperature mapping gradient echo sequences (min TE = 0.85 ms, 15 echoes, ΔTE = 0.9 ms, 1.05 min scan time) were acquired, and temperature variation derived from the phase differences.^{4, 12}

After the proof of concept in the aqueous phantom, the protocol was then tested on a phantom containing heavy whipped cream (commercial kitchen cream, fat content ~25%) undergoing the same temperature variations, with the intent of showing the efficacy of the method in mixed composition tissues.

To further demonstrate the capacity of the technique to withstanding harsh environment conditions, we repeated the experiment in cream phantom while artificially introducing a large magnetic field inhomogeneity by manually altering the shimming gradients in the field of view. We also placed the imaging slice coplanar to the metallic tip of the temperature sensor, so to introduce susceptibility variation in the field. Both ZSI and spoiled GRE were acquired under thermal challenge in these conditions.

2.4. In vivo experiments

The sequence was then tested in vivo on three 7-week-old healthy male C57BL/6 mice. All studies were performed according to protocols approved by the Institutional Animal Care and Use Committee.

Anesthesia was induced by 3.5% isoflurane and oxygen mix and maintained during imaging at 1%–1.5% in 100% O₂ using a nose cone with spontaneous respiration throughout the experiment. During the MR study, temperature ranging from 27°C to 36°C in ascending and then descending order were set by heating the airflow into the scanner bore. Five minutes of delay were introduced before acquiring each image set to allow for some temperature stabilization. An MRI-compatible physiological monitoring system (Model 1025, SA Instruments, Stony Brook, NY) recorded the respiratory pattern and the body temperature through a rectal probe sensor registering the thermal changes in real time. The imaging field of view was selected as the inguinal area because of its close proximity to the sensor probe. The imaging plane was placed just above the position of the sensor tip, to avoid susceptibility artifacts. Both muscle and fat depots were included in the field of view. MRI was carried out on an Agilent Varian 9.4T preclinical scanner with a 39-mm proton volume coil. First and second-order shimming was performed to minimize B₀ field inhomogeneity. Water saturation shift referencing (WASSR) sequences³² at the beginning and the end of the experiment were carried out to assess the B₀ inhomogeneity and correct it by manually adjusting the central frequency. T₂-weighted images were obtained for anatomic reference. As in the in vitro experiments, the binomial-ZSI was carried out by a sequence with a preparatory module consisting of 2 opposite phase sinc-shaped π/2 pulses, each 0.5 ms long, separated by a 5-ms delay. The readout involved a fast spin-echo sequence with 4 segments over a rectangular 128 × 64 matrix and a 40 × 20 mm² FOV, producing square pixels sized 0.64 × 0.64 mm and 1-mm thickness. The preparation was repeated over 41 offsets around the water resonance, from −0.25 to 0.5 ppm with 0.025 ppm steps. The entire protocol was repeated without interruption throughout the thermal challenge. Interleaved to the binomial-ZSI, spoiled GRE sequences with 20 echoes, a minimum TE of 1.47 ms and ΔTE = 1.55 ms were acquired as references, and the phase difference between consecutive repetitions was used to compute temperature change in every pixel.

To study the variation in fatty tissue, where it is expected that gradient echo sequences will suffer from phase artifacts, a series of T₁ mapping sequences was acquired interleaved to ZSI in another experiment. Eleven inversion times ranging from 100 ms to 7 s were used in an inversion recovery-type sequences for 5 min and a reduced matrix: 64 × 32. Because the calibration coefficients for each mouse tissue at 9.4T were not known, only relative T1 variations, proportional to true temperature variations, were considered.^5,30

2.5. Image processing

Data from each ZSI repetition were pooled together and fitted to a function of the chemical shift:

$$S\left(f\right)=a\left|1-\text{sin}\left(2\pi \tau \left(f-f_0\right)\right)\right|,$$ (4)

where a is a scaling factor constant overall repetitions, the saturation offset frequencies are expressed in Hertz and the delay in seconds. The absolute value was considered because the fit was performed on the magnitude images. The only variable changing over time was the water resonance frequency f₀. It is possible to derive the temperature changes as:

$$\Delta T=\frac{\Delta f_0}{\alpha },$$ (5)

where Δf₀ is the shift of the water resonance at a given time point and the coefficient α = −0.01°C/ppm.^4,12 For the study in mixed and fatty tissue, the fitting model was the sum of 2 sine functions (for fat and water protons) with a starting relative frequency difference of f₀ − f_F = −3.5 ppm × 400 MHZ/ppm.

$$S\left(f\right)=\left|a\left[1-\text{sin}\left(2\pi \tau \left(f-f_0\right)\right)\right]+b\left[1-\text{sin}\left(2\pi \tau \left(f-f_F\right)\right)\right]\right|$$ (6)

In this case, the system reduced to 2 variables constant over time a, b, and 2 time-varying frequencies for water and fat pools, respectively, f₀, f_F.

The reference temperature was derived from the difference Δφ in the phase images of GRE sequences over time, according to:

$$\Delta T=\frac{\Delta \phi }{\gamma B_{0}TE\alpha },$$ (7)

where the echo time TE was chosen when fat and water were in-phase.

In the last experiment on fat tissue in vivo, temperature changes were proportional to the relative differences in T₁ relaxation times.^5,30

2.6. Statistical analysis

All data are presented as mean ± standard deviation. If specified, plots of Z-spectra and trends over time correspond to pixel values or small regions of interest. Regions of interest of inguinal visceral fat were drawn in areas identified as hyperintensity on T₂-weighted images. Muscular areas were analogously identified on the same images, excluding voxel covering bones and mixed tissues. Correlation analyses among temperature values derived from the different imaging techniques were carried out by linear regressions of the mean ROI values. Significance was reached for p < 0.05. All analyses were performed in MATLAB (The MathWorks, Natick, MA).

3. Results

3.1. Phantoms at varying temperature

The signal in the PBS phantom behaved as expected, oscillating as a function of the frequency offset in the observed range. The sinusoidal fit predicted the behavior of the signal with a least-square coefficient R² > 0.97 (Figure 3, top). When temperature changed inside the phantom, the curve shifted toward lower frequencies according to the PRFS effect (Figure 3, bottom).

Figure 3.

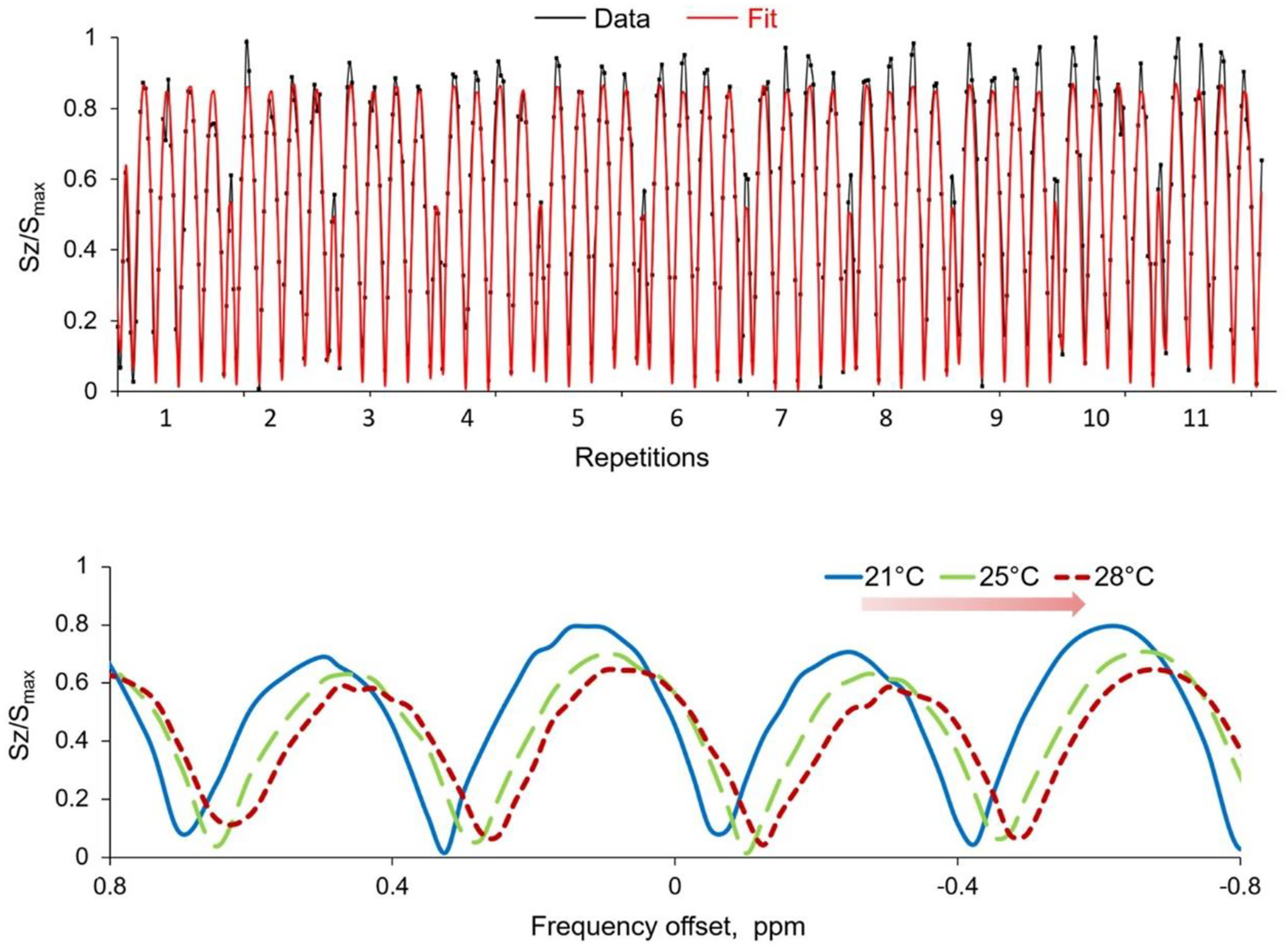
Representative Z-spectra and fitting curves. Upper row: Z-spectra from a PBS phantom concatenated over several repetitions and normalized to the maximum value S_max. The signal (blue line) oscillates sinusoidally and is well fitted by a sine function (red line). Lower row: signal modulation over frequency offsets at different temperatures. The proton resonance frequency shifts downfield at increasing temperature, observed through the binomial-ZSI in PBS phantom heated by flowing hot air

The voxelwise curve fitting produced colormaps of temperature change, computed for the initial time point. The protocol tested in the whipped cream phantom also delivered an accurate measurement of temperature change over time (Figure 4). The thermal variation obtained from the frequency shift correlated with the ground truth measurement from the temperature sensor, with a coefficient R² > 0.99 (Figure 4B). The temperature derived from the GRE phase differences, instead, produced as expected variable trends depending on the TEs adopted (green lines, Figure 4A). Phase changes were measured reliably only when fat and water protons were exactly in-phase (green squares, Figure 4).

Figure 4.

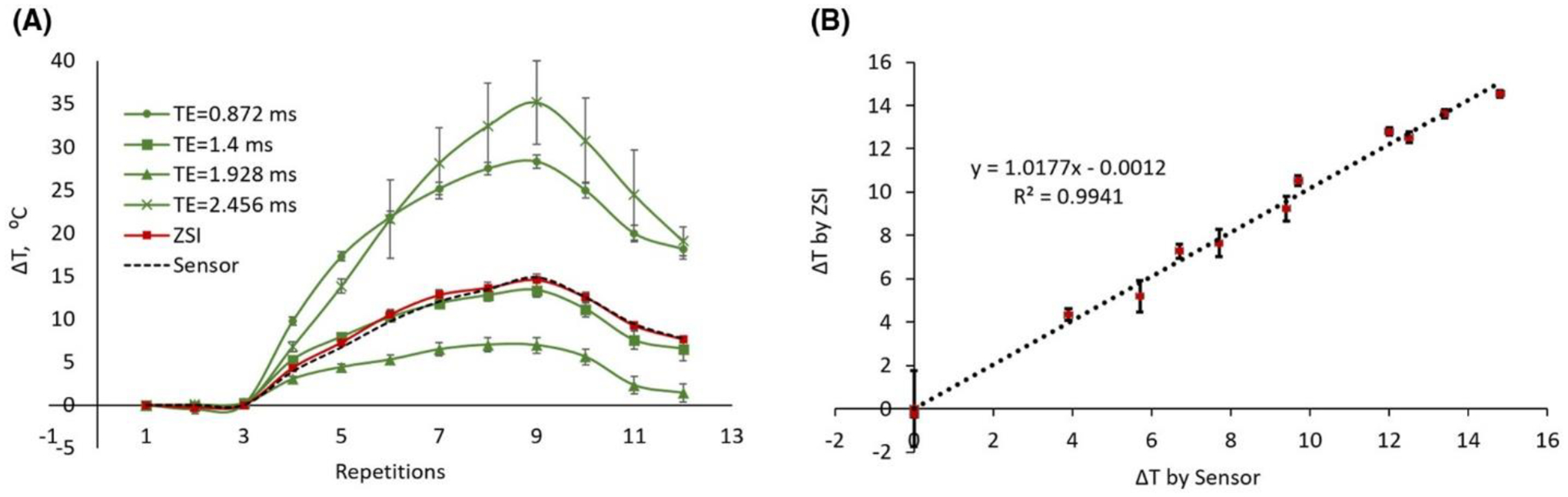
Temperature changes in cream phantoms. (A) The measurement by ZSI (red line) followed the ground truth measurement by the thermal electrode directly inserted in the phantom (black dotted line). Phase differences from GRE data resulted in varying trends depending on the TE (green lines), with accurate results only when fat and water were in phase (squares). (B) The temperature from ZSI in the cream phantom correlated well with the sensor probe measurement.

The temperature assessment was homogeneous across the field of view and independent of B₀ inhomogeneity. Even in case of large field inhomogeneity (range 2 ppm as seen in the B₀ map in Figure 5), the ZSI technique reproduced homogeneous frequency shift maps that reflected the nominal temperature measured by the probe, whereas GRE suffered from induced artifacts, at any chosen TE.

Figure 5.

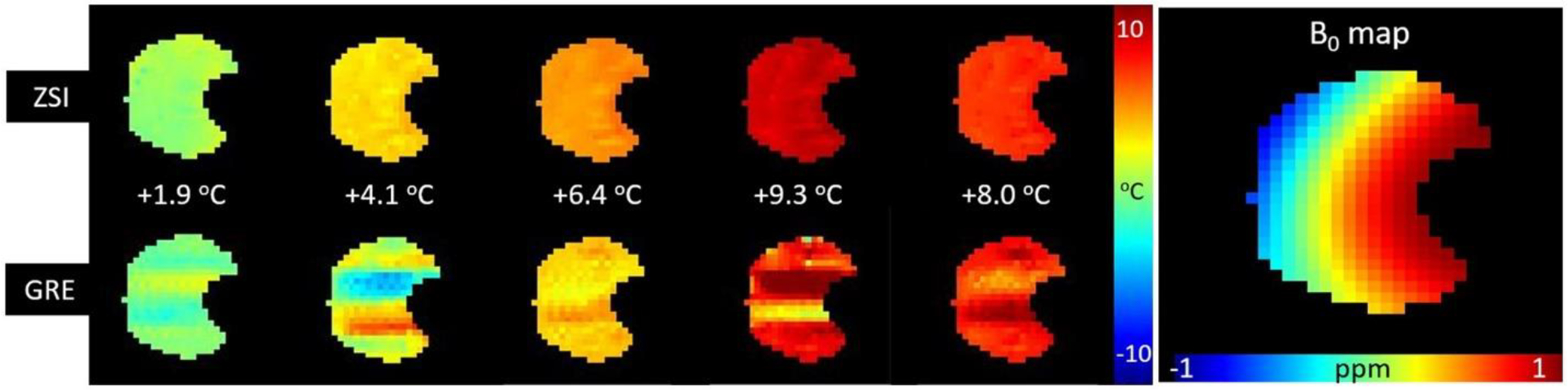
Comparison of ZSI and GRE temperature measurements in cream under non-ideal field conditions. The distribution of temperature across the imaged slice as measured by ZSI is homogeneous, even when large B0 variations (2 ppm range) are present. The presence of the metallic tip of the sensor probe (masked out from image) also might contribute to the susceptibility artifacts degrading the GRE maps.

3.2. In vivo experiment

The study in the mice ventral area showed clear trends of the proton resonance frequency shift at varying temperatures. The changes estimated by ZSI reflected the temporal and spatial distribution of the ones measured by the conventional GRE sequence (Figure 6).

Figure 6.

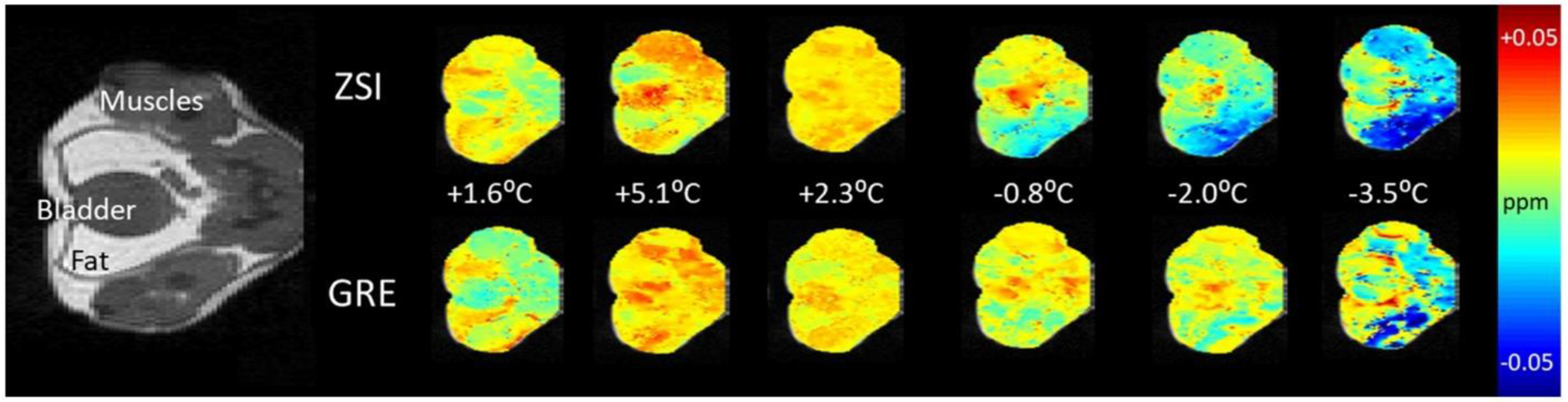
PRFS maps from healthy mouse. Comparison of proton resonance frequency shift measured by ZSI and phase difference from GRE sequences for an exemplary mouse undergoing thermal challenge. The body temperature measured by the rectal probe is indicated for each time point.

The good agreement between the techniques qualitatively observed in the colormaps was confirmed by the quantitative region of interest analysis (Figure 7).

Figure 7.

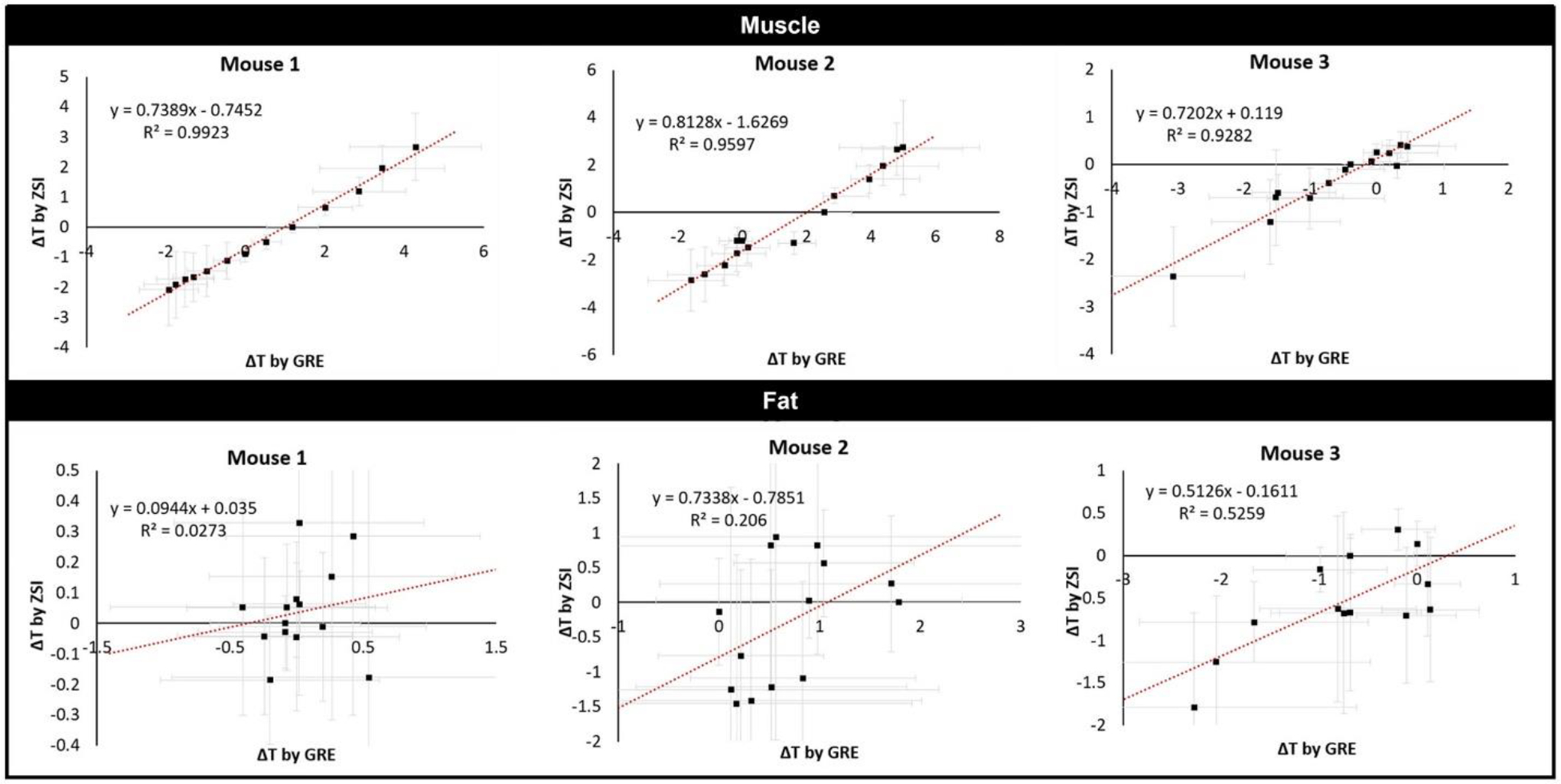
Correlations between GRE and ZSI. The temperature changes measured by the binomial ZSI and the phase difference from GREs correlated linearly in all studied mice in the muscle areas (top). Fat areas failed to return the same good correlations between techniques (bottom).

In all 3 mice, the correlation between the temperature measured in the muscle region by ZSI and the phase difference from the GRE was linear (Pearson’s correlation >0.95 in all cases). Despite trends, in fat areas the comparison did not produce consistent significant correlations (Pearson’s <0.5). When ZSI was compared to T₁ mapping, instead, we found a good linear correlation between the techniques in both muscles and fat (Pearson’s coefficient 0.90 and 0.92, respectively).

4. Discussion

Herein, we reported the successful design and implementation of a temperature-sensitive modification of the Z-spectrum imaging technique. After demonstrating the proof of concept in an aqueous solution, the protocol was applied on a whipped cream phantom exposed to heated air. Whipped cream filled the role of a generic tissue with homogeneously mixed composition. Although it might not reflect the distribution of lipid droplets in cells, the co-presence of fat and water components within the voxel constitute a valid model for the technique’s demonstration. Finally, the technique was also tested in vivo in muscular and fatty tissue of healthy mice. We measured temperature change in all tissues through ZSI and demonstrated a linear relationship with conventional methods.¹² In all experiments, it was possible to produce colormaps of frequency shift distribution, independent of field inhomogeneity assessed by B₀ maps. Notably, the results were reliable even in cases of large field shifts, whereas conventional spoiled GRE can suffer. In the in vivo thermal challenge, it is possible to notice the spatial variability of water resonance shift in the ZSI-derived colormaps. This variability is likely caused by the different level of exposure to the air flow because of the mouse position on the holder. Such variability cannot be captured by the measurement performed with the rectal probe, at a single point source, and in a specific physical compartment, measuring the core temperature. This observation reiterates the need for a thermometric method with broad coverage and high resolution. Therefore, the colormaps derived from the phase difference serve as a more apt comparison in our study. In fact, the variability observed on the ZSI colormaps corresponded to the distribution shown in the GRE-derived maps. On a more quantitative level, the correlation analysis demonstrated that the average values in the muscle region were in high agreement between the 2 techniques, with coefficient R² > 0.9 in all cases (Figure 7).

It is interesting to note that the same analysis in areas containing fat failed to produce consistent significant correlations. This was found true both in vitro, where a large B₀ shift and the proximity to the metallic sensor probe caused inhomogeneity and susceptibility artifacts in the cream phantom under GRE study, and in vivo, where tissues with large majority fat content did not provide only a single pool of protons, that is, water for classic PRFS. Although it is commonly assumed that fat proton should not be significantly affected by electronic shielding stretching, because the characteristic constant in lipids is an order of magnitude lower compared to water, σF = 0.002 versus σW = 0.01/°C,¹² it has been reported that changes in temperature in fat lead to significant variation in the susceptibility of the tissue.^28,31 Current approaches address this phenomenon by estimating forward the expected change in the field and computing the associated change in susceptibility. However, to do so, an important assumption has to be established about the geometry of the susceptibility distribution and the expected change in temperature, which is previously assessed by alternative methods, like T₁ mapping.^30,31 Therefore, we decided to compare the ZSI results to T₁ mapping directly. Here, we found an excellent linear relationship between the techniques, in both muscular and fatty tissue (Figure 8). We demonstrated that our approach is feasible and reliable in vivo, producing comparable results to standard methods but without relying on a priori calibrations and with a shorter sequence than conventional relaxation times-based method.

Figure 8.

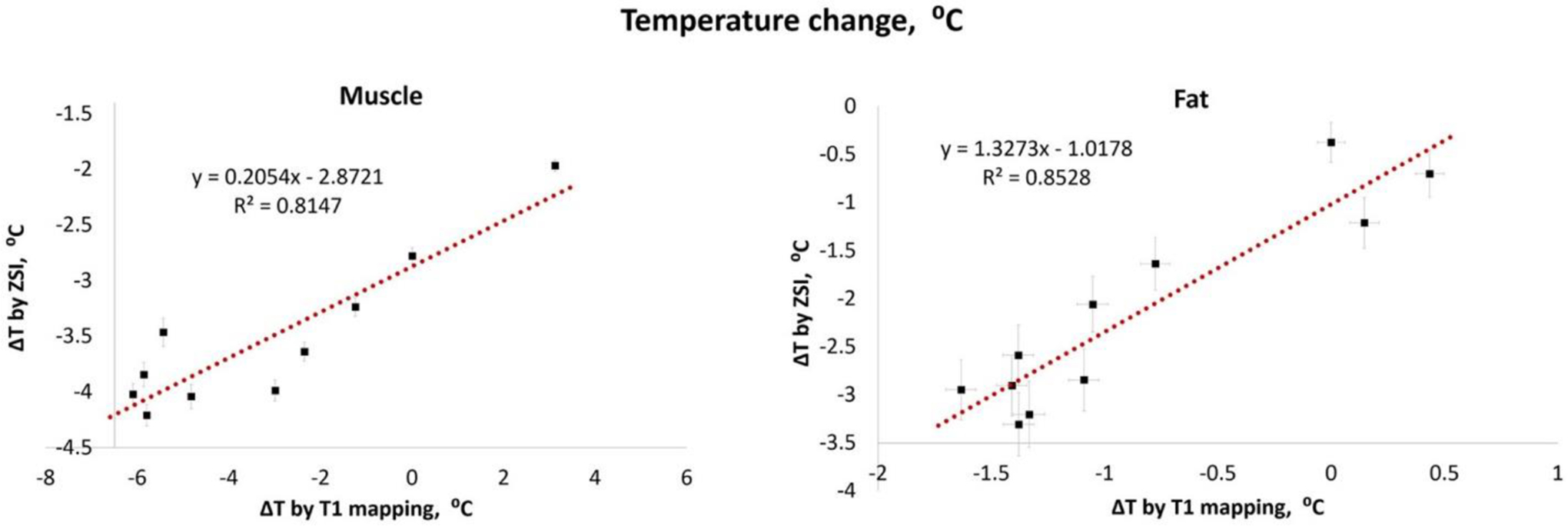
Comparison between ZSI and T₁ mapping. The temperature changes derived from the binomial ZSI and T₁ mapping linearly correlated in both muscle and fat regions of interest.

We must clarify here that the relationship between the susceptibility change and the detectable frequency shift in the case of fatty tissues is not fully understood. The most thorough description of the phenomenon has been reported by Baron et al⁸ through simulation and ex vivo experiments. In particular, they showed how a local heating through HIFU sonication at the interface between fat and aqueous tissue results in a field change with a dipole-like spatial distribution. More generally, the conclusion reached by the authors is that the field (and, consequently, the frequency) spatial pattern is dependent on the orientation of the heating source and the geometry of the tissue and interface. In our experiment, we see a somewhat homogeneous effect across the entire fat depot, and little field spillover in the interfacing muscle. We can certainly draw several critical distinctions between the studies: a diffuse heating versus a point source, a slow, mild heating delta versus a fast and intense one, and an in vivo systemic active reaction versus an ex vivo passive heating accumulation. Nevertheless, the impact of any and all these factors is unknown and the specific way the heat-induced change in susceptibility translates to the frequency change that we were able to successfully measure remains an open question.

Two great advantages derive from our newly developed technique. First, all results are derived from magnitude images. The sampling at different offsets combined to the spin echo based readout, allowed to encode the phase difference accrued during the delay time into the longitudinal magnetization. No phase component of the signal being required, no ambiguity in mixed tissues was registered, unlike when other techniques are used.^4,12 In our test, in fact, the phase difference from gradient echo sequences returned variable results depending on the TE adopted and underperformed in less than ideal field conditions. Current strategies to address phase and field heterogeneity mainly revolve around separating the components through chemical shift encoded techniques, to which iterative reconstruction and regularization algorithms have been added to estimate the field impact.¹² Far from underplaying the salience of these strategies, we just note that their complexity and effectiveness varies among studies. Instead, we offer a straightforward and easily implementable approach that avoids the phase problem altogether.

A second advantage relies on the ability to control the thermal sensitivity of the technique. The key is the parameter τ: by choosing larger delays, the periodicity of the sine function representing the signal over the frequency offsets will decrease.^36,37 With a narrower curve, it is possible to measure smaller shifts, therefore, finer temperature changes. The practical sensitivity limit will therefore, depend on the spectral periodicity, given by Δf = 1/4τ and by the amplitude of the curve, which is proportional to the flip angle of the saturation. Although a rigorous analysis of the signal was outside the goal of this work, we nevertheless were able to reach a thermal sensitivity below 1°C, which is among the best provided by current MRI methods to date.^4,12 We expect the sensitivity floor to lie even below what we presented here.

The pulse used in this work, featuring 2 hard pulses,³⁶ is the simplest version of binomial pulse. Many more sophisticated combinations have been developed and can be used for the same purpose. The choice in the current work was driven by the higher signal and stable phase across the spectrum with respect to other pulses in the binomial series.^35–39 The choice of a flip angle of 90° and the sinc shape for the RF pulses was in line with the objective of obtaining an excitation profile that offered the most straightforward interpretation. Different pulse parameters will introduce features that can add specificity to the model and possibly facilitate the fit adherence.

The binomial pulse produces a signal that is dependent on relaxation times. With a total duration of few milliseconds, the influence from T₁ and T₂ is expected to be negligible, whereas $T_{*}^2$ can have a more significant impact on the magnetization between the 2 pulses. The scaling parameter in the fitting model includes such dependency, and in future applications, an analysis of its behavior in different tissues under thermal stress will need to be investigated. Analogously, the same factor is also affected by proton density and the abundance of the species under investigation. In the case of fatty tissues, this will correspond to the fat fraction in the voxel. Although we did not expect a significant change in these factors in this experiment, because the variation of temperature was slight, it is worth considering the possibility of deriving both types of information from 1 fitting. Structural information from the fat fraction and a metabolic one related to the temperature: such prospect is particularly alluring for the investigation of brown adipose tissue, which features characteristic cellular composition and thermogenic properties.

A potential limitation of the binomial ZSI arises when considering its clinical translation. At lower fields, the spectral selectivity will be degraded, and with it the thermal sensitivity. Such loss can be ameliorated by increasing the interpulse delay, which will in turn expose the signal to relaxation effects. The scanning time can also be a concern because multiple repetitions after saturating several offsets are required. Although the clinical application is not the focus of this work, we think it is important to admit that at the present stage, imaging fast cycle therapies like tumor ablation is out of reach. However, other applications, in which the temperature variation occurs on a slower scale, might provide a more suitable context: examples can be hyperthermia treatments, or the aforementioned thermogenic activation of brown adipose tissue. A rigorous selection and minimization of the number of sampled offsets will allow to reduce the duration of the experiment. In the present study, in 3 min, we collected 40 points per voxel, which covered 3 complete sine periods of the signal oscillation, all the while maintaining a SNR >10 per single in vivo image. Combination with fast readout techniques, undersampling, or reduced field of view methods will drive the acquisition time within clinically feasible scanning times.

In conclusion, this work served as the demonstration that the binomial-ZSI technique can reliably measure temperature changes. The high sensitivity and the feasibility in adipose tissue make it an accessible option for the monitoring of subtle thermal changes in fat containing tissues like the breast. Another interesting possibility is merging structural and metabolic contrasts for the study of thermogenic brown adipose tissue, a feat that our technique is uniquely suited to perform.