The impact of the COVID-19 pandemic on global GDP growth

Abstract

This paper describes one of the first attempts to gauge the effect of the COVID-19 pandemic on the global trajectory of real GDP over the course of 2020 and 2021. It is also among the first efforts to distinguish between the role of domestic variables and global trade in transmitting the economic effects of COVID-19. We estimate panel data regressions of the quarterly growth in real GDP on pandemic variables for 90 countries over the period 2020 Q1 through 2021 Q4. We find that readings on the number of COVID-19 deaths had a very small effect in our aggregate sample. On the other hand, changes in the stringency of the lockdown measures taken by governments to restrict the spread of the virus were an important influence on GDP. The economic effects of the pandemic differed between rich and poor countries: COVID-19 deaths exerted a somewhat greater drag on GDP in advanced economies, although this difference was not statistically significant, whereas lockdown restrictions were more injurious to economic activity in emerging and developing economies. In addition to these domestic pandemic effects, global trade represented a significant channel through which the economic effects of the pandemic spilled across national borders. This finding underscores how globalization makes each country vulnerable not only to medical contagion from the COVID-19 pandemic, but to economic contagion as well.

1. Introduction

The COVID-19 pandemic triggered the sharpest downturn in the world economy since the Great Depression, with global GDP declining 3.0 percent in 2020 compared to a rise of 2.8 percent in 2019 (IMF 2022). While it is obvious that COVID-19 was the cause of this downturn, there are critical questions about the channels through which the pandemic depressed economic activity: Was it mainly through lockdowns or voluntary social distancing? How did the economic effects of the pandemic differ among different economies? How large a role was played by the collapse in global trade?

As discussed in Section 2, a plethora of studies have emerged to address these questions, using a wide range of different methodologies: production-based or computable general equilibrium (CGE) models, epidemiological models, event studies, and broader panel data analyses. But only a few of these papers (IMF 2020; Maloney and Taskin 2020; Furceri et al., 2021; König and Winkler 2021a,b; Deb et al., 2022a,b) draw on the full range of economic experiences around the world, and, aside from Furceri et al. (2021) and König and Winkler (2021a,b), these focus mainly on daily proxies for economic activity—e.g., atmospheric emissions and cellphone-based mobility data—rather than actual production measures.

By contrast, our paper focuses on how the pandemic has influenced the evolution of real GDP growth around the world. Real GDP is available on a quarterly basis. With as many as 8 quarters of data during the pandemic available for 90 countries, this is sufficient to identify the links between the spread of the virus, lockdown measures, and real GDP. Moreover, our data allows us to distinguish the effects on GDP of domestic pandemic variables from those exerted by movements in global trade also caused by COVID-19. Previous studies have not explored this important distinction.

In our paper, we estimate panel data regressions of the quarterly growth in real GDP on several measures of the pandemic for 90 countries over the period of 2020 Q1 through 2021 Q4. The domestic pandemic measures include deaths per 100,000 of the population and a measure of the stringency of lockdown restrictions, the Oxford Stringency Index (OSI). All else equal, a rise in pandemic deaths would be expected to lower GDP, both by inducing supply shortages and by prompting an increase in social distancing that leads production to be scaled back. Similarly, an increase in lockdown restrictions would also be expected to lower GDP. However, both variables could in principle be subject to reverse causality: a shock to GDP that affects the extent of social distancing could lead to changes in COVID-19 cases, deaths, and OSI, biasing the coefficients. Accordingly, we use a two-stage procedure, described below, to address this source of endogeneity.

A central feature of the economic impact of the pandemic was the collapse in world trade. In consequence, even countries that were not hard-hit by the virus itself might have suffered from economic fallout through a decline in export demand. To measure this effect, we include global goods and services imports as an explanatory variable in our model, taking care to exclude from this variable the imports of any individual country in the panel data regression.

The goal of our study is not just to measure the response of GDP growth to its various determinants but also to use those estimates to decompose the overall trajectory of GDP over the course of the first two years of the pandemic into the contributions made by those determinants. To our knowledge, this is the first study to apply such an exercise to a direct measure of global economic activity. In so doing, we apply this decomposition both to our complete country sample and, separately, to the countries in the advanced and the emerging/developing economies.

Our basic findings are as follows:

• •Changes in COVID-19 deaths, lockdown restrictions (OSI), and exports all affected GDP growth and generally to a statistically significant extent, although the size of these effects varied depending on the economies and time periods considered.
• •Using the estimated model to decompose the trajectory of GDP growth over the course of the pandemic into the contributions of the explanatory variables, we find that the key factors accounting for the collapse in GDP in the first half of 2020 were increases in the stringency of lockdown restrictions and the collapse in global trade. By the same token, it was reversals in these factors that accounted for most of the rebound in GDP growth in the following couple of quarters. COVID-19 deaths had a negligible influence on the pattern of growth. In 2021, quarter-to-quarter movements in both GDP growth and the explanatory variables were much less variable, and the model's tracking of economic growth is less consistent.
• •The size and statistical significance of the coefficients on the COVID-19 variables in our model (deaths, OSI) are greatest when estimated over the 2020 period alone and smaller and insignificant when estimated over the 2021 period. This likely reflects a couple of factors: Businesses and households learned to adjust to the pandemic; and with much smaller variability in GDP growth and its determinants in 2021, it was likely more difficult to identify the statistical relationships.
• •The size and statistical significance of the coefficients also differed, depending on whether countries were advanced economies (AEs) or emerging market or developing economies (EMDEs). COVID-19 deaths exert greater effects on GDP in advanced economies than in EMDEs; although the difference between the estimated effects in AEs and EMDEs is not statistically significant, this is a plausible result, since the poor are less capable of stopping work to weather the pandemic (Dingel and Neiman 2020). OSI is significant in nearly all samples, but it exerts stronger effects in EMDEs, with the difference being statistically significant at the 10 percent level of confidence. Accordingly, for the AEs, variations in COVID deaths contributed slightly to the collapse in GDP in 2020 and the subsequent rebound, whereas no such effect was calculated for the EMDEs.

Perhaps the most distinctive finding of our study is the outsized role that global trade has played in the impact of the pandemic on economic activity, especially in the world's poorest countries. This meant that even in countries where COVID-19 numbers were subdued and lockdowns were less restrictive, the hit to GDP in 2020 H1 and the subsequent support for the rebound in 2020 H2 was substantial. The recovery of global trade continued to provide stimulus through most of 2021. Even though the poorest economies lagged the advanced economies in vaccinations, they benefitted from the further recovery of aggregate demand and imports by the advanced economies. Our findings underscore how globalization makes each country vulnerable not only to the medical contagion of the COVID-19 pandemic, but to the economic contagion as well.

The plan of the paper is as follows. Section 2 reviews past research on this topic, and Section 3 describes the data used in this project. Section 4 describes the results of estimating our basic panel regression model, and Section 5 uses these results to decompose the movements in GDP over the course of 2020 and 2021. Section 6 concludes.

2. Literature review

Only about three years have passed, at the time of this writing, since the coronavirus emerged on the global scene, yet there already exists a broad literature on the impact of the virus on the economy. While there is research on the impact of previous pandemics on the United States and global economies (Barro 2022; Barro et al., 2022; Beach et al., 2022; Cooper 2006; Dixon et al., 2010; James and Sargent 2006; Ma et al., 2020; McKibbin and Sidorenko 2006), it is unclear to what extent the findings of this research carry over to the current situation.1 Below, we review the attempts to measure the impact of the COVID-19 crisis on the economy.

One approach to measuring this impact is based on production or general equilibrium models. These models are shocked using estimates of the initial direct effects of COVID-19 shutdowns on spending and/or production, and then the simulated effects of these shutdowns are traced through to the broader economy. For example, Mandel and Veetil (2020) use a multi-sector open economy model based on input-output data for 44 countries, and incorporating supply-chain linkages among countries, to simulate a virus-related lockdown. Similar approaches are taken by Barrot et al. (2021) and Inoue and Todo (2020). Some studies exploit DSGE and CGE models to gauge the effect on output of the virus, including Cho and Kim (2021), Maliszewska et al. (2020), Malliet et al. (2020), McKibbin and Fernando (2020), and Walmsley et al. (2020).

Another strain of models integrates epidemiological insights to explicitly model the interrelation between the virus, lockdowns, and economic activity. For instance, Eichenbaum et al. (2021) embed a Susceptible-Infected-Recovered (SIR) model in a macroeconomic model; they find that strict lockdowns lead to larger recessions initially but may be socially optimal because they save so many lives. Cakmakli et al. (2020) embed an SIR model in a general equilibrium framework, calibrated to the case of Turkey. They find that stricter lockdowns lead to smaller reductions in GDP because they limit the spread of the virus. Alvarez et al. (2021), Acemoglu et al. (2021), Alon et al. (2020), and Scherbina (2021) are additional examples of this approach, all emphasizing the medium-term benefits of strict lockdowns. Fukao and Shioji (2021) use an SIR model and the empirical relationship between mobility, infections, and government restrictions to evaluate public policy and individual behavior in New York, London, and Tokyo. Crucially, the output-infection tradeoff does not hold in the long run. Hosono (2021) explicitly models the relationship between mobility, infection rate, and consumer spending, internalizing a reverse causality between economic performance and infections.

Model-based analyses of the effect of COVID-19 have the virtue of highlighting the channels of transmission of the disease through the economy, thus supporting analysis of alternative policy responses. However, their results depend heavily on the calibration of the models and the assumptions about how pandemic-respondent policies affect economic behavior. Accordingly, these analyses have been usefully complemented by more empirical approaches.

Some researchers have adopted an event study framework, examining the movement of proxies for economic activity following lockdown announcements. For example, Alexander and Karger (2021), utilizing US county-day level data, find that lockdown announcements were followed by declines in mobility2 and small business revenue; however, these measures were falling even before the announcements, likely reflecting voluntary social distancing measures. Watanabe and Yabu (2021) use daily data from Japanese prefectures to show that emergency announcements increased the number of people staying at home, as did higher infection rates. Arnon et al. (2020) use US county-level data for an event study of the effect of lockdowns on mobility and employment, and they then embed the results of this analysis into an epidemiological model to examine the joint behavior of restrictions, COVID-19 cases, and employment.3 As before, employment was found to be falling both ahead of and after the announcement of any government policies. Chen et al. (2020), examining the variation across US counties and European countries, also find that lockdown measures explained only part of the pandemic recession. However, Baker et al. (2020) find household spending dropped more in US states imposing lockdowns.

Useful as they are, it is difficult to pin down the precise impacts of the pandemic using event studies, as they do not quantify the magnitude of COVID-19 cases or the stringency of lockdown measures, nor do they allow one to identify the separate, independent effects of these variables on economic outcomes. It is also difficult to control for the influence of related factors such as fiscal/monetary policies or international developments.

An alternative approach that better addresses these issues is the estimation of panel data regressions of economic outcomes on pandemic variables and relevant controls. Data on COVID-19 cases, deaths, and lockdown measures are available on a daily basis, but most data on economic activity, such as GDP or industrial production, are only available at lower frequencies. Accordingly, researchers using this approach have generally focused on higher-frequency proxies for economic activity. Deb et al. (2022a) exploit a multi-country dataset of atmospheric NO₂ concentrations, which are significantly correlated with industrial production. They show that a full lockdown would have a 30-day cumulative impact on NO₂ emissions equivalent to a 15% drop in industrial production. Similarly, Roidt et al. (2020) and Fezzi and Fanghella (2020) find pandemic lockdowns depress water and energy consumption in Europe. Verschuur et al. (2021) find that the pandemic reduced global maritime trade by 7.0 to 9.6 percent during the first eight months of 2020.

Other panel data analyses have used mobility data as an economic proxy—these data, derived from cellphone apps such as Google Maps, aggregate people's movements and have been shown to be strongly correlated with GDP, consumption, and/or employment (Chen and Spence 2020; Baker et al., 2020). The IMF (2020) finds that “mobility declines by 28 percent a week after the introduction of a lockdown; and a doubling of COVID-19 deaths leads to a reduction in mobility by 1.2 percent after 30 days.” Maloney and Taskin (2020) also conduct a multi-country panel analysis of Google data, finding that voluntary distancing (as reflected in the effect of cases) accounts for more of the decline in mobility than lockdowns, except for low-income countries. Consistent with that, Goolsbee and Syverson (2021), using Safegraph data on mobile phone usage for US counties, find that legal shutdown orders account for only a modest share of the massive decline in mobility observed in the first few months of the pandemic. Conversely, Coibion et al. (2020), studying US county-level data, found lockdowns to be more important than COVID-19 cases in depressing employment and spending. Chetty et al. (2020) develop a zip-code level proxy for US economic activity and, while not distinguishing between the effects of voluntary social distancing and lockdowns, document a strong contractionary impact of the spread of COVID-19. Milani (2021) uses VAR models to analyze the dynamics of social distancing and Google unemployment searches during the pandemic. Deb et al. (2022b) examine the effect of infections and vaccinations on Google mobility indexes and atmospheric emissions, finding significant impacts on both proxies for economic activity.

While studies of the effect of pandemic variables on the daily evolution of economic-activity proxies such as atmospheric emissions or mobility data are undoubtedly informative, their mapping to more traditional measures of economic activity remains uncertain.4 Furceri et al. (2021) address this issue by examining the fall in GDP during the first two quarters of 2020 across a large sample of economies. They find that output losses were greater among countries that were poorer, experienced more deaths and lockdowns, and were more dependent on tourism, among other factors. However, owing to the paucity of more recent GDP data at the time of analysis, their research is confined to cross-sectional analysis and cannot examine the evolution of economic activity over time. König and Winkler (2021a,b) use panel regressions to determine if differences in government containment strategies resulted in divergences in quarterly GDP growth across countries in 2020. But even these analyses involve relatively few time-series observations.

Accordingly, our paper makes an important contribution to the literature by analyzing the impact of pandemic variables on an actual measure of economic activity—real GDP—over the course of 2020 and 2021, across a wide range of economies, and across a number of waves of the COVID-19 virus. Using real GDP for systematic data analysis has only become possible recently, as sufficient numbers of quarterly observations have become available, and it still requires us to analyze a large multi-country dataset, as in Deb et al., 2022a, Deb et al., 2022b, IMF (2020), Maloney and Taskin (2020), and König and Winkler (2021a,b). But doing so will enable us to answer a number of important questions regarding the direct and indirect impacts of COVID-19 on a direct measure of economic activity and how those impacts might differ across countries.

3. Data

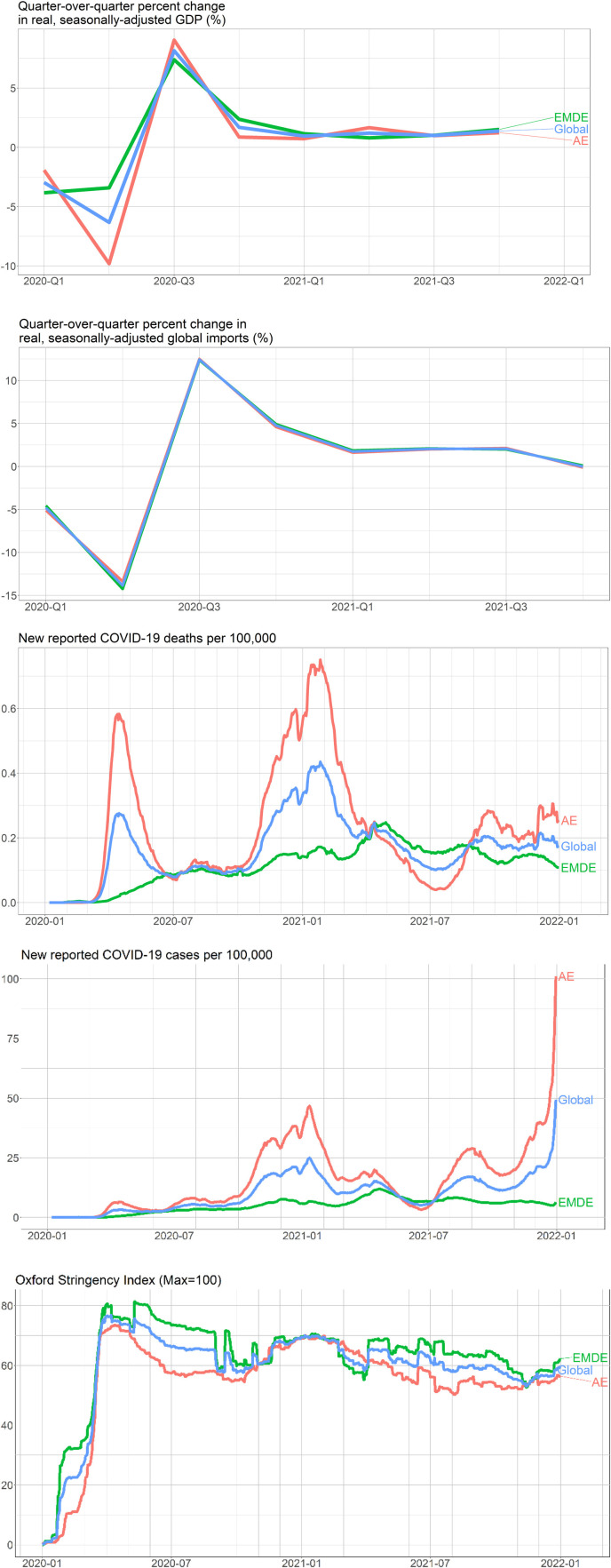
For this paper, we assemble a comprehensive panel dataset encompassing variables relating to COVID-19, government policies, and global trade. To match with GDP, most variables are averaged quarterly. Our unbalanced panel includes entries for 90 countries from 2020 Q1 through 2021 Q4. The average paths, weighted by 2019 PPP GDP, of these variables during the course of the pandemic are charted in Fig. 1 .

Fig. 1.

Key Variables during the COVID-19 pandemic.

Note: This figure presents quarter-over-quarter growth real GDP, growth in real world imports, daily reported COVID-19 deaths and cases per 100,000 people, and the level of the Oxford Stringency Index. Global, advanced economy (AE), and emerging market and develop economy (EMDE) aggregates are averages of the individual countries weighted by 2019 PPP GDP (IMF 2021). Country groups are defined in Appendix Table 1. This figure uses data from CEIC, Ritchie et al. (2020), Dong et al. (2020), Hale et al. (2021), IMF (2021), and IFS (2022a, 2022b).

3.1. Coronavirus cases and deaths

Data relating to the virus are sourced from Johns Hopkins University, which provides daily figures for officially-reported cases and deaths for 192 countries starting on January 22, 2020.5 For each country, we calculate the average daily number of new cases and deaths per 100,000 population for each quarter.

3.2. Excess deaths

Excess mortality is defined as the total number of deaths above the ‘expected’ (i.e., historical average) death toll in a given time frame. We gather our data from The Economist (2022)’s excess mortality tracker.6 The Economist uses weekly or monthly death totals from 2015 to 2019 to calibrate expected deaths for 199 countries and uses those estimates to calculate excess deaths per 100,000 people beginning on January 1, 2020.

3.3. Government restrictions (Oxford Stringency Index)

Information on the stringency of government restrictions is obtained from Oxford's COVID-19 Government Response Tracker4 (OxCGRT).7 This source provides daily index values of government restrictions for 184 countries since January 6, 2020. OxCGRT averages policy stringency across eight dimensions: school closures; workplaces closures; public event cancellations; gathering restrictions; public transportation closures; stay-at-home orders; restrictions on internal movement; and international travel bans. This variable ranges from 0 (no restrictions) to 100 (the highest possible level of restrictions across all eight dimensions). Given the subjective element in assigning ratings, one should not place too much weight on the precision of this measure. Nevertheless, it is the best measure available to assess lockdown restrictions on an internationally-consistent basis.

3.4. Real GDP

Data on real GDP are drawn from CEIC's database of quarterly real, seasonally-adjusted, non-annualized GDP. Our sample includes 90 countries, all but 10 of which provide quarterly GDP data through 2021 Q4. The countries in our sample account for 94.3 percent of world GDP at PPP exchange rates.

3.5. Global

For each country, the trajectory of real imports of goods and services is calculated over the pandemic period, indexed so that 2019 Q1 equal to 100, based on data from the IMF's International Financial Statistics. These index numbers, drawn for each country for which the IMF data are available, are then aggregated to the global level based on each country's share of world imports in 2019. Quarter-to-quarter growth rates in this global import index are calculated. A different global imports aggregate is constructed separately for each country by subtracting that country's imports growth—more specifically, the growth of that country's imports weighted by their trade share—from the total.8

Exports as a share of GDP are defined as the total exports of goods and services as a share of that country's 2019 nominal GDP (World Bank 2022). Manufacturing and services values as a share of GDP are similarly defined by the World Bank (2022).

3.6. Other characteristics

Data on the contribution of tourism spending to the total economy in 2019 is drawn from the World Trade & Tourism Council (2019). The World Bank (2022) provides data on the share of the population with internet access in 2019. The United Nations Population Division (2015) publishes data on life expectancy at age 10. Data on the share of jobs that can be done via telework are drawn from Dingel and Neiman (2020).

4. A regression model for GDP growth

4.1. Basic regression model with domestic pandemic variables

We estimate panel regressions of quarter-to-quarter percent changes in real GDP on the potential determinants discussed above. Table 1 presents estimation results for the domestic COVID-related explanatory variables: COVID deaths and the stringency of lockdown restrictions (OSI). In principle, the number of COVID cases should also influence GDP. We exclude this variable for several of reasons. First, our earlier research indicates that the coefficient on this variable is often estimated with the wrong—that is, positive—sign, suggesting that greater pandemic spread actually raises GDP (Kamin and Kearns 2021). Second, as will be discussed below, the number of new cases may be endogenous with respect to economic activity, which might account for the wrong sign.

Table 1.

Quarter-on-quarter Real GDP Growth – Domestic Variables Only.

	OLS			2SEC
	2020–21	2020	2021	2020–2021	2020	2021
	(1)	(2)	(3)	(4)	(5)	(6)
(Intercept)	0.58*	1.82⁎⁎⁎	2.25⁎⁎⁎	0.29	0.39	2.30⁎⁎⁎
	(0.33)	(0.62)	(0.27)	(0.25)	(0.26)	(0.27)
Δ Daily Deaths per 100K	−0.85	−2.24	−0.59	−1.57*	−6.09⁎⁎⁎	0.05
	(0.53)	(1.86)	(0.56)	(0.83)	(2.06)	(0.70)
Δ Quarterly OSI	−0.07⁎⁎⁎	−0.10⁎⁎⁎	−0.02	−0.07⁎⁎⁎	−0.11⁎⁎⁎	−0.02
	(0.02)	(0.03)	(0.01)	(0.02)	(0.03)	(0.01)
Lagged Dependent Variable	−0.35⁎⁎⁎	−0.41⁎⁎⁎	−0.24⁎⁎⁎	−0.35⁎⁎⁎	−0.42⁎⁎⁎	−0.25⁎⁎⁎
	(0.03)	(0.04)	(0.05)	(0.03)	(0.04)	(0.05)
R2	0.72	0.77	0.25	0.72	0.78	0.23
Time and country FE?	Y	Y	Y	Y	Y	Y
First-stage F-statistic	N/A	N/A	N/A	364.95⁎⁎⁎; 30,072.58⁎⁎⁎	167.22⁎⁎⁎; 99,999.00⁎⁎⁎	183.14⁎⁎⁎; 2925.20⁎⁎⁎
Num. obs.	692	358	334	692	358	334

Note: This table uses data from CEIC, Ritchie et al. (2020), Dong et al. (2020), and Hale et al. (2021). Columns 4 through 6 apply a two-stage process. In a first stage, deaths and OSI are separately regressed on cases. In the second stage, the residuals from these regressions are substituted for deaths and OSI in the regressions for GDP growth. Time and country fixed effects are used in the second stage. First-stage F-statistics for Columns 4 through 6 show the F-stat for regressions of actual changes in deaths and OSI on residuals from our first-stage process. Since variation in cases only explains 1 percent of variation in OSI, F-statistics for OSI residuals are mechanically large. Robust standard errors (in parentheses) are clustered at the country level.

^⁎p < 0.10;

^⁎⁎p < 0.05;.

^⁎⁎⁎p < 0.01.

Turning to the dynamic specification of the model, the level of real GDP in a quarter is likely to be related to the number of new COVID deaths registered in that quarter, which will encourage social distancing and perhaps disrupt supply, and the level of stringency of lockdown restrictions (OSI). Accordingly, to explain the quarter-to-quarter percent change in GDP, we use the quarter-to-quarter arithmetic change in COVID deaths and OSI. (Because these variables start out at zero for most countries in the sample, we do not use percent changes in deaths and OSI.) We also include the lagged dependent variable as well as country and time fixed effects. Appendix Table 1 lists the countries in the sample.

Starting with the full-sample estimates in Column 1, the coefficient on deaths is negative, as expected, albeit not statistically significantly different from zero. The coefficient on OSI is also negative, and it is highly statistically significant. The estimates suggest that a rise of one daily death per 100,000 in a quarter leads to a 0.85 percentage point decline in GDP growth. This may seem like a lot, but insofar as daily global deaths per 100,000 have averaged around 0.14 through the end of 2021 and tended not to move by more than 0.24 (its mean country-specific standard deviation), the impact is not all that large. A rise of 1 in the OSI pushes down growth by 0.07 percentage point; this seems small, but OSI rose from a median average of 17 in 2020 Q1 to 75 in the Q2, implying a hit to GDP growth of 4.3 percentage points. The coefficient on lagged GDP growth is negative and statistically significant, suggesting that impacts of the COVID variables on GDP are partially reversed in the next quarter.

Columns 2 and 3 restrict the estimation sample to 2020 and 2021, respectively. As discussed in the introduction, the impacts of the COVID variables are much larger in 2020 than in 2021, although the coefficient on deaths is still statistically insignificant. The larger effect in the first year likely reflects both that the economies managed to adjust to the pandemic by 2021, and that there was greater variability in both the dependent variable and the independent variables during the first year.

4.2. Addressing potential endogeneity problems

The equations discussed above are potentially subject to endogeneity problems. Consider, for example, a mine shutdown that leads both to reduced GDP and, by reducing opportunities for workers to spread the disease to each other, reduced cases and deaths; this could in turn could motivate a loosening of COVID-19 restrictions, depressing OSI. Alternatively, an exogenous decrease in voluntary social distancing—for example, induced by crazy political behavior—could lead both to increased cases and deaths, on the one hand, and to higher GDP, on the other; OSI might also rise if the government tried to contain the erosion of social distancing. In either case, the result would be coefficients on deaths and OSI that were biased upwards (that is, less negative).

To address this concern, we estimate a two-stage regression. In the first stage, we separately regress changes in both deaths and OSI on changes in cases in the same quarter. The residuals from these regressions would represent changes in deaths or OSI not caused by changes in contemporaneous cases, and thus would be exogenous to the effects of changes in economic activity or social distancing referenced above. Any number of factors could lead to changes in deaths and OSI not associated with changes in cases, such as new variants that alter the severity of COVID-19, changes in medical treatments of the disease (e.g., vaccinations that reduce mortality without providing substantial immunity), or shocks to the supply of medical treatments (e.g., running out of ventilators).

In the second stage, we substitute those residuals for the actual values of deaths and OSI, and re-estimate the regressions for GDP growth. We refer to this procedure as a “two-stage endogeneity correction,” or 2SEC. It is similar to the more standard two-stage least squares (2SLS) procedure, except that in the second stage, instead of regressing the dependent variable on the fitted values from the first-stage regression, we regress it on the residuals. Below, we describe similar results garnered using a more standard 2SLS approach.

The 2SEC equations are shown in Columns 4 through 6 of Table 1. The first-stage F-statistics indicate that the residuals are strong predictors of the endogenous variables.9 The second-stage results indicate more negative coefficients on deaths compared with the OLS equations, with that for 2020 becoming highly significant, but almost no change in the coefficients on OSI.10

4.2.1. Inverse hyperbolic sine transformation

The equations shown in Table 1 assume a linear relationship between deaths and real GDP growth. It is possible that the relationship may be non-linear, but taking logs of deaths is not possible because of zero deaths for some countries in some quarters.11 Goolsbee and Syverson (2021) and Watanabe and Yabu (2021) transform infections and/or deaths data using the inverse hyperbolic sine, which turns the data into a more logarithmic-like form. We apply the same transformation to our cases and deaths data and present the result regression estimates in Appendix Table 2. The new estimates present less significant coefficients on deaths and no increase in explanatory power. Accordingly, we stick with the linear deaths data used for Table 1.

4.2.2. Adding lags of the explanatory variables

The use of the lagged dependent variable in Table 1 imposes the restriction that the dynamics of response of real GDP growth to deaths and OSI are identical. In Appendix Table 3, we relax that restriction and add a one-quarter lag of changes in deaths and OSI. The coefficients on the additional lags are generally not significant and do not boost the explanatory power of the equations. Accordingly, we stick with the more parsimonious specification in Table 1.

4.2.3. Alternative simultaneity correction

As explained above, deaths and OSI are likely to respond to changes in cases, which in turn are endogenous with respect to economic activity. We correct for this potential source of endogeneity by using a 2SEC procedure in which only those parts of deaths and OSI that are orthogonal to contemporaneous cases are used as explanatory variables for GDP growth. An alternative way of addressing the simultaneity problem is to use the changes in deaths and OSI occurring just in the first month of each quarter as instruments in a more standard 2SLS procedure. Evidence suggests that increases in cases do not filter through to deaths until some two to eight weeks later (Testa et al., 2020); moreover, there is likely a lag between changes in economic activity and changes in cases. Accordingly, deaths and OSI in the first month of the quarter are unlikely to reflect changes in GDP in that quarter, while at the same time they should have some predictive power for deaths and OSI in the quarter as a whole.

This 2SLS approach may also be useful to address an additional source of endogeneity, which is that policymakers might relax stringency restrictions in response to disappointing GDP growth. It is unclear how consequential this concern is in practice, since even with the most timely data, it is difficult for policymakers to assess GDP in real time and then respond with commensurately rapid alterations in lockdown rules. However, to the extent that such reverse causation was present, it could bias upwards (less negative) the coefficient on OSI using our baseline 2SEC approach, whereas our alternative 2SLS approach—using as instruments deaths and OSI from only the first month of each quarter—would be less vulnerable to this issue.

Appendix Table 4 compares our 2SEC results described earlier with those generated using this alternative 2SLS specification that uses the first-month changes in OSI and average daily deaths as instruments. The first-stage F-statistic for the full sample in Column 4 (321.16) indicates that the change in the first month is a strong predictor for the full quarter. Despite this, the results generated are similar to those from our preferred model and offer no material improvement in explanatory power. Accordingly, we stick with our original 2SEC specification.

4.3. Addressing mismeasurement problems

It is well-known that in many countries, cases and deaths are significantly undercounted. Table 2 , Columns 1–3 repeats our equation estimates using reported deaths—these use the same data as in Table 1, but with the sample countries restricted to the 76 countries for which estimates of excess deaths are available. Columns 4–6 present estimates in which deaths have been replaced as an explanatory variable by the excess deaths data described in Section 3.12 Comparing Columns 1–3 (which use reported deaths) with Columns 4–6 (using excess deaths), the magnitudes of the deaths coefficients in the latter columns are actually lower than those in the former columns, and the R²s for the regressions are unchanged. It thus appears that even if the higher level of excess deaths is more accurate than the level of official deaths, the results provide no reason to believe that quarterly changes in excess deaths provide a better read on COVID-19 deaths than the official count. Accordingly, we stick with reported deaths for this research.

Table 2.

Quarter-on-quarter Real GDP Growth – Reported and Excess Deaths.

	Reported Deaths			Excess Deaths
	2020–2021	2020	2021	2020–2021	2020	2021
	(1)	(2)	(3)	(4)	(5)	(6)
(Intercept)	0.86⁎⁎	1.70⁎⁎⁎	2.49⁎⁎⁎	0.93⁎⁎⁎	2.09⁎⁎⁎	2.53⁎⁎⁎
	(0.33)	(0.63)	(0.34)	(0.32)	(0.55)	(0.35)
Δ Daily Deaths per 100K	−0.87	−2.68	−0.11	−0.35	−1.11	0.08
	(0.53)	(1.73)	(0.56)	(0.32)	(0.96)	(0.27)
Δ OSI	−0.08⁎⁎⁎	−0.10⁎⁎⁎	−0.04⁎⁎	−0.08⁎⁎⁎	−0.10⁎⁎⁎	−0.04⁎⁎⁎
	(0.02)	(0.03)	(0.02)	(0.02)	(0.03)	(0.02)
Lagged Dependent Variable	−0.32⁎⁎⁎	−0.39⁎⁎⁎	−0.22⁎⁎⁎	−0.32⁎⁎⁎	−0.40⁎⁎⁎	−0.23⁎⁎⁎
	(0.03)	(0.04)	(0.07)	(0.03)	(0.04)	(0.07)
R2	0.76	0.80	0.31	0.76	0.80	0.31
Time and country FE?	Y	Y	Y	Y	Y	Y
Num. obs.	559	304	255	559	304	255

Note: This table uses data from CEIC, Ritchie et al. (2020), Dong et al. (2020), Hale et al. (2021), and The Economist (2022). All regressions are run using standard OLS due to the possible issues associated with using reported cases. Time and country fixed effects are used throughout. Robust standard errors (in parentheses) are clustered at the country level.

^⁎⁎p < 0.05;.

^⁎⁎⁎p < 0.01.

*p < 0.10;.

4.4. Addition of an external demand variable

Even an economy with no COVID-19 cases or deaths and no lockdown restrictions could be affected by the pandemic through its effect on global trade, as other countries affected by the pandemic reduce their imports. To gauge the strength of this effect, Table 3 , which reverts to focusing on all countries in our sample, adds the quarterly percent change in global real imports as an explanatory variable. As noted above, for each country, a version of global import growth is used that removes the effect of that country's own imports.13 The coefficients on the other explanatory variables are broadly similar and, not surprisingly, global imports exert a statistically significant positive effect on real GDP growth. Of course, that would be true, even in the absence of the pandemic. To gauge the effect of the pandemic on economies working indirectly through international trade channels, we will need to assess the broad pandemic-induced swing in global trade and how it impacts individual economies, an exercise described in Section 5 below.

Table 3.

Quarter-on-quarter Real GDP Growth – Domestic and External Variables.

	2SEC
	2020 – 2021	2020	2021
	(4)	(5)	(6)
(Intercept)	1.05⁎⁎⁎	0.81⁎⁎⁎	1.76⁎⁎⁎
	(0.03)	(0.03)	(0.15)
Δ Daily Deaths per 100K	−0.75	−5.35⁎⁎⁎	0.28
	(0.84)	(1.98)	(0.72)
Δ OSI	−0.09⁎⁎⁎	−0.15⁎⁎⁎	−0.01
	(0.01)	(0.02)	(0.01)
Lagged Dependent Variable	−0.20⁎⁎⁎	−0.21⁎⁎⁎	−0.24⁎⁎⁎
	(0.03)	(0.04)	(0.05)
% Δ Real World Imports	0.35⁎⁎⁎	0.21⁎⁎⁎	0.02
	(0.04)	(0.06)	(0.10)
R^2	0.69	0.76	0.21
Time and country FE?	Country	Country	Country
Num. obs.	692	358	334

Note: This table uses data from CEIC, Ritchie et al. (2020), Dong et al. (2020), Hale et al. (2021), and IFS (2022a, 2022b). All regressions apply a two-stage process. In a first stage, deaths and OSI are separately regressed on cases. In the second stage, the residuals from these regressions are substituted for deaths and OSI in the regressions for GDP growth. Only country fixed effects are used in the second stage due to the collinearity of time fixed effects with the real world imports variable. Robust standard errors (in parentheses) are clustered at the country level.

*p < 0.10;

^⁎⁎p < 0.05;.

^⁎⁎⁎p < 0.01.

In principle, export growth should have a different effect on GDP growth, depending on the share of exports in the economy. However, we found that when global import growth was interacted with the share of exports in GDP, as shown in Appendix Table 5, the coefficient on this interaction term was not statistically significant and the fit of the equation was little changed. Considering the strong practical and theoretical reasons for believing that global import demand positively affects individual economies’ exports and thus GDP, we retain the equations shown in Table 3 as our baseline model.

4.5. Estimation results for different groups of countries

It is likely that the impact of pandemic variables on economic activity would differ between richer and poorer countries. Table 4 presents separate estimates for both advanced economies (AEs) and emerging market and developing economies (EMDEs), as well as regional sub-groups of EMDEs: Asia, Latin America and the Caribbean (LAC), sub-Saharan Africa, and other (Eastern Europe and Middle East and North Africa).

Table 4.

Quarter-on-quarter Real GDP Growth – Regional Country Groups.

	2SEC, 2020 - 2021
	Global	AEs	EMDEs	EMDE Asia	EMDE LAC	EMDE Africa	EMDE Others
	(1)	(2)	(3)	(4)	(5)	(6)	(7)
(Intercept)	1.05⁎⁎⁎	0.48⁎⁎⁎	1.06⁎⁎⁎	−0.27⁎⁎	0.34⁎⁎⁎	1.22⁎⁎⁎	1.08⁎⁎⁎
	(0.03)	(0.05)	(0.05)	(0.12)	(0.07)	(0.20)	(0.05)
Δ Daily Deaths per 100K	−0.75	−2.40	0.19	5.73	−0.53	3.16	1.51⁎⁎
	(0.84)	(1.45)	(1.34)	(7.87)	(1.03)	(1.70)	(0.68)
Δ OSI	−0.09⁎⁎⁎	−0.07⁎⁎⁎	−0.11⁎⁎⁎	−0.18⁎⁎⁎	−0.11⁎⁎⁎	−0.08	−0.07⁎⁎⁎
	(0.01)	(0.01)	(0.02)	(0.04)	(0.03)	(0.05)	(0.01)
Lagged Dependent Variable	−0.20⁎⁎⁎	−0.15⁎⁎⁎	−0.23⁎⁎⁎	−0.36⁎⁎⁎	−0.15⁎⁎⁎	−0.32⁎⁎⁎	−0.13⁎⁎
	(0.03)	(0.04)	(0.04)	(0.06)	(0.04)	(0.07)	(0.06)
% Δ Real World Imports	0.35⁎⁎⁎	0.42⁎⁎⁎	0.29⁎⁎⁎	0.05	0.62⁎⁎⁎	0.44	0.30⁎⁎⁎
	(0.04)	(0.05)	(0.08)	(0.14)	(0.13)	(0.40)	(0.07)
R^2	0.69	0.80	0.62	0.66	0.77	0.63	0.63
Time and country FE?	Country	Country	Country	Country	Country	Country	Country
Num. obs.	692	292	400	76	88	47	189

Note: This table uses data from CEIC, Ritchie et al. (2020), Dong et al. (2020), Hale et al. (2021), IFS (2022a,b). All regressions apply a two-stage process. In a first stage, deaths and OSI are separately regressed on cases. In the second stage, the residuals from these regressions are substituted for deaths and OSI in the regressions for GDP growth. Appendix Table 1 lists the countries included in each region. Only country fixed effects are used in the second stage due to the collinearity of time fixed effects with the real world imports variable. Robust standard errors (in parentheses) are clustered at the country level.

*p < 0.10;.

^⁎⁎p < 0.05;.

^⁎⁎⁎p < 0.01.

The main difference in the responses of AE and EMDE GDP to the pandemic is that deaths have a much larger effect on economic activity in the AEs, although the difference in these effects is not statistically significant. Conversely, the stringency of lockdowns (OSI) appears to have somewhat smaller effects on GDP in AEs than in EMDEs; this difference is statistically significant at the 10 percent level of confidence.14 These findings make sense – poorer households are less likely to reduce their work unless lockdowns are imposed by the government – and are consistent with findings by Maloney and Taskin (2020). Within the regional groups of EMDEs, Asia exhibits the strongest response to OSI, although it is unclear why.

4.6. The role of structural characteristics

To what extent has the performance of economies during the pandemic been influenced by their structural characteristics such as the shares of their economies devoted to manufacturing, services, exports, and tourism. Table 5 adds these measures to our basic model, which is shown in Column 1, estimated for the slightly smaller set of observations available for these additional explanatory variables. In the remaining columns, each of the structural characteristic variables are interacted with OSI and with deaths.

Table 5.

Quarter-on-quarter Real GDP Growth – Structural Characteristics.

	Baseline	Manufacturing (% of GDP)	Services (% of GDP)	Exports (% of GDP)	Tourism (% of GDP)	Percent of Population with Internet Access	Percent of Jobs Teleworkable	Life Expectancy at Age 10
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
(Intercept)	1.04⁎⁎⁎	1.09⁎⁎⁎	1.04⁎⁎⁎	1.06⁎⁎⁎	1.05⁎⁎⁎	1.04⁎⁎⁎	−0.15*	1.05⁎⁎⁎
	(0.03)	(0.04)	(0.03)	(0.03)	(0.04)	(0.03)	(0.07)	(0.03)
Δ Daily Deaths per 100K	−0.83	−7.04⁎⁎	1.64	−3.46⁎⁎	−0.14	1.86	2.66	26.23
	(0.86)	(3.36)	(7.37)	(1.35)	(1.53)	(6.07)	(2.89)	(16.19)
Δ OSI	−0.10⁎⁎⁎	−0.12⁎⁎⁎	0.13*	−0.12⁎⁎⁎	−0.05⁎⁎⁎	−0.18⁎⁎	−0.13⁎⁎⁎	0.04
	(0.01)	(0.03)	(0.06)	(0.02)	(0.02)	(0.07)	(0.05)	(0.18)
Lagged Dependent Variable	−0.20⁎⁎⁎	−0.21⁎⁎⁎	−0.20⁎⁎⁎	−0.21⁎⁎⁎	−0.20⁎⁎⁎	−0.20⁎⁎⁎	−0.14⁎⁎⁎	−0.20⁎⁎⁎
	(0.03)	(0.03)	(0.03)	(0.03)	(0.03)	(0.03)	(0.03)	(0.03)
% Δ Real World Imports	0.35⁎⁎⁎	0.35⁎⁎⁎	0.34⁎⁎⁎	0.35⁎⁎⁎	0.36⁎⁎⁎	0.36⁎⁎⁎	0.45⁎⁎⁎	0.34⁎⁎⁎
	(0.05)	(0.05)	(0.05)	(0.05)	(0.05)	(0.05)	(0.05)	(0.05)
Char.*ΔDeaths		44.35*	−3.20	5.22*	−9.96	−4.00	−12.00	−0.39
		(22.98)	(12.10)	(2.66)	(13.72)	(8.00)	(9.97)	(0.24)
Char. * ΔOSI		0.16	−0.38⁎⁎⁎	0.04	−0.32⁎⁎⁎	0.00	0.19	−0.00
		(0.24)	(0.11)	(0.03)	(0.10)	(0.00)	(0.14)	(0.00)
R^2	0.69	0.70	0.71	0.70	0.70	0.69	0.72	0.69
Time and country FE?	Country	Country	Country	Country	Country	Country	Country	Country
Num. obs.	668	668	668	668	668	668	400	668

Note: This table uses data from CEIC, Ritchie et al. (2020), Dong et al. (2020), Dingel and Neiman (2020), Hale et al. (2021), IFS (2022a,b), the World Bank (2022), and the World Trade & Tourism Council (2019). All regressions apply a two-stage process. In a first stage, deaths and OSI are separately regressed on cases. In the second stage, the residuals from these regressions are substituted for deaths and OSI in the regressions for GDP growth. Robust standard errors (in parentheses) are clustered at the country level.

^⁎p < 0.10;.

^⁎⁎p < 0.05;.

^⁎⁎⁎p < 0.01.

The results are largely consistent with our intuition and other analyses—both anecdotal and statistical—of the economic effect of the pandemic, although increments to R² are quite low. Column 2 adds the share of GDP in manufacturing—expressed as a fraction, so 65 percent is 0.65—to the model. The coefficient on the interaction term between manufacturing and deaths is positive, indicating that more manufacturing reduces the negative effect of deaths on GDP; this is consistent with widespread evidence that manufacturing weathered the recession relatively well, since it involved less face-to-face contact in its production and consumption. Similarly, a greater concentration of activity in exports, Column 4, also lessens the adverse economic impact of deaths.

Compared to manufacturing, many services require more face-to-face contact. Accordingly, as indicated in Column 3, economies with a greater share of services suffered greater declines in output growth in response to deaths and lockdown restrictions. Similarly, in economies with larger tourism sectors, the adverse effect of deaths and lockdowns is greater.

The final three columns depart from a sectoral focus to address several hypotheses about the economic effect of COVID. Eberly et al. (2021) argue that the potential to work from home should reduce the economic drag from COVID. We address that issue by interacting deaths and OSI with the prevalence of internet access (Column 6) and the share of jobs that can be done remotely (Column 7). Surprisingly, neither of those variables enters significantly into the equation; this bears further research. Finally, it has been suggested that countries with higher overall mortality rates may suffer less economic distress from COVID, as the health risk from COVID looms less large if many other health risks are present. However, as shown in Column 8, an interaction variable between COVID deaths and the general pre-pandemic mortality rate does not help explain GDP growth.

As a robustness check, we re-estimated the equations shown in Table 5, but removed the growth of global imports as an explanatory variable so that we could add back in time fixed effects. The results, not shown, are very similar to those presented in Table 5.

5. Decomposition of global GDP growth during the pandemic

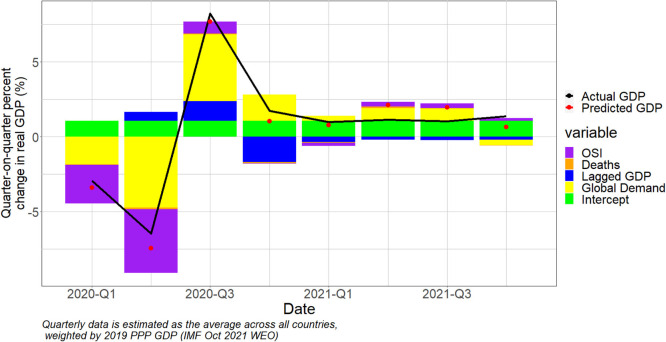
In this section, we use our regression models to estimate the contribution of the different pandemic factors to the evolution of global GDP growth over the course of 2020 and 2021. Fig. 2 displays this decomposition for the entire country sample, based on the model shown in Table 1, Column 4. The solid black line depicts the average quarter-to-quarter growth of real GDP, weighted by each country's 2019 PPP GDP, for the countries in the sample. The red dots represent the corresponding average of growth rates predicted by the model – by and large, they track the actual growth rates fairly well. The colored bars represent the contribution of the different explanatory variables, calculated as the estimated coefficient multiplied by the GDP-weighted average value of the variable in that month. Our methodology identifies only minute contributions of COVID-19 deaths to the evolution of GDP growth in 2020 (an average magnitude of 0.07 percentage points). Instead, the key factors pushing GDP down in 2020 H1 and up in 2020 Q3 appear to have been OSI and global imports. After that, the trajectory of global GDP growth flattens out, as does the contribution of the explanatory variables.

Fig. 2.

GDP Growth Decomposition – All Countries.

Note: This figure presents the decomposition of predicted quarter-over-quarter growth real GDP growth into the contribution of changes in OSI, COVID-19 deaths, global imports, and lagged GDP growth, based on the model shown in Table 4 Column 1, for the global sample of economies. This figure uses data from CEIC, Ritchie et al. (2020), Dong et al. (2020), Hale et al. (2021), IMF (2021), and IFS (2022a, 2022b).

Note that this decomposition is constructed from the standpoint of the individual economies – that is, for a given economy, the effect of the pandemic is estimated as partly reflecting its domestic variables (deaths and OSI) and partly the transmission of the pandemic to that economy through the contraction in global trade. Of course, the contraction in global trade was itself the outcome of pandemic effects on the economy's trade partners, and thus represents the indirect effect, rather than the direct domestic effect, of the pandemic on the economy in question.

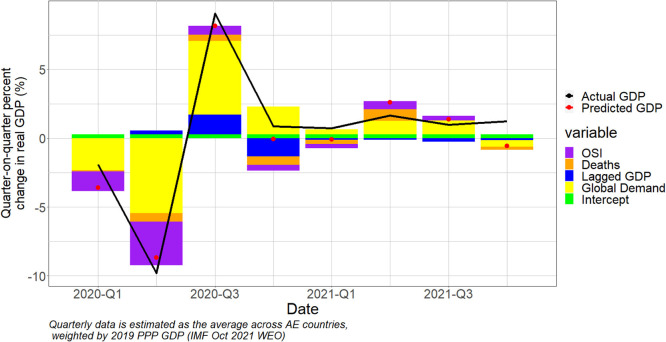
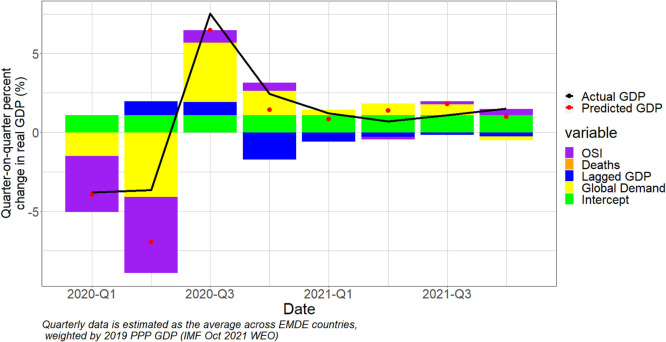
Fig. 3, Fig. 4 repeat the analysis shown in Fig. 2, but applied to the separate country groupings described earlier. The results are broadly consistent with the pattern of estimated coefficients across two groupings. For the advanced economies (AEs), the surge and subsequent decline in pandemic deaths accounts for a discernable, albeit still quite small, part of the collapse and rebound in GDP growth, along with OSI and global trade. Conversely, for the emerging market and developing economies (EMDEs), deaths play no part, with variations in OSI and exports accounting for nearly all the variation. Note that the large miss of the model in 2020 Q2 for EMDEs reflects the high weight of China in the GDP aggregate; the model predicted a substantial decline in Chinese GDP in that quarter, but it actually grew by 11.6 percent. If aggregate GDP growth had been expressed as the median growth of our country sample, the predicted value, −9.94 percent, would have been much closer to the actual value of −9.09 percent.

Fig. 3.

GDP Growth Decomposition – Advanced Economies.

Note: This figure presents the decomposition of predicted quarter-over-quarter growth real GDP growth into the contribution of changes in OSI, COVID-19 deaths, global imports, and lagged GDP growth, based on the model shown in Table 4 Column 2, for the AE sample of countries. This figure uses data from CEIC, Ritchie et al. (2020), Dong et al. (2020), Hale et al. (2021), IMF (2021), and IFS (2022a, 2022b).

Fig. 4.

GDP Growth Decomposition – Emerging and Developing Economies.

Note: This figure presents the decomposition of predicted quarter-over-quarter growth real GDP growth into the contribution of changes in OSI, COVID-19 deaths, global imports, and lagged GDP growth, based on the model shown in Table 4 Column 3 for the sample of EMDEs. This figure uses data from CEIC, Ritchie et al. (2020), Dong et al. (2020), Hale et al. (2021), IMF (2021), and IFS (2022a, 2022b).

6. Conclusion

In this paper, we estimate panel data regressions of the quarterly growth in real GDP on its determinants for 90 countries, as well as subsets of richer and poorer countries, over the period 2020 Q1 through 2021 Q4. We then use our estimated model to decompose the trajectory of GDP growth over the course of the pandemic into the contributions of its various determinants.

We find that readings on the number of COVID-19 deaths had a very small effect on GDP growth in our aggregate sample; it appears to have been a bit more important in the advanced economies, though the difference with EMDEs is not statistically significant. Changes in the stringency of the lockdown measures taken by governments to restrict the spread of the virus, often referred to as lockdown restrictions, are a more important determinant of the growth of GDP than deaths, especially in poorer countries. In addition to these domestic pandemic effects, global trade represented an important channel through which the economic effects of the pandemic spilled across national borders, again especially in poorer countries. Finally, we found that structural characteristics of the economy influenced the extent of the pandemic's drag on the economy. That drag was smaller for economies more focused on manufacturing and exports and larger for economies more dependent on services and especially tourism.

Our work represents some of the first research to gauge the effect of COVID-19 on a direct measure of economic activity – GDP, as contrasted with indirect measures such as Google mobility data – around the world and over the course of the first two years of the pandemic. It is also among the first efforts to distinguish between the role of domestic variables and global trade in transmitting the economic effects of COVID-19. Our findings underscore how globalization makes each country vulnerable not only to the medical contagion of the COVID-19 pandemic, but to the economic contagion as well.

Declaration of Competing Interest

None

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Appendix

Appendix Tables 1–5 .

Appendix Table 1.

Sample Countries.

		Emerging Market and Developing Economies
Advanced Economies		EMDE Africa	EMDE Asia	EMDE LAC	EMDE Other
Australia	Lithuania	Botswana	Brunei	Argentina	Albania	Saudi Arabia
Austria	Luxembourg	Ghana	China	Bolivia	Azerbaijan	Serbia
Belgium	Macau	Kenya	India	Brazil	Bahrain	Palestine
Canada	Malta	Mauritius	Indonesia	Chile	Belarus	Tunisia
Cyprus	Netherlands	Nigeria	Malaysia	Colombia	Bosnia and Herzegovina	Turkey
Czech Republic	New Zealand	South Africa	Mongolia	Ecuador	Bulgaria	Ukraine
Denmark	Norway		Philippines	Mexico	Croatia	United Arab Emirates
Estonia	Portugal		Sri Lanka	Panama	Egypt
Finland	Singapore		Thailand	Paraguay	Georgia
France	Slovak Republic		Vietnam	Peru	Hungary
Germany	Slovenia			Uruguay	Iran
Greece	South Korea				Jordan
Hong Kong SAR	Spain				Kazakhstan
Iceland	Sweden				Kuwait
Ireland	Switzerland				Morocco
Israel	Taiwan				Poland
Italy	United Kingdom				Qatar
Japan	United States				Romania
Latvia					Russia

Note: Classifications are established using the conventions in International Monetary Fund (2021).

Appendix Table 2.

Inverse Hyperbolic Sine of Deaths – Domestic Variables Only.

	OLS			2SEC
	2020–2021	2020	2021	2020–2021	2020	2021
	(1)	(2)	(3)	(4)	(5)	(6)
(Intercept)	0.64⁎⁎	2.05⁎⁎⁎	2.23⁎⁎⁎	−1.16⁎⁎⁎	−0.88⁎⁎	2.31⁎⁎⁎
	(0.30)	(0.54)	(0.27)	(0.33)	(0.40)	(0.28)
Δ ASinH(Quarterly Deaths per 100 K)	−0.24	−0.28	−0.17	−0.35*	−0.49	−0.05
	(0.15)	(0.27)	(0.14)	(0.20)	(0.32)	(0.24)
Δ Quarterly OSI	−0.07⁎⁎⁎	−0.10⁎⁎⁎	−0.02	−0.03⁎⁎⁎	−0.06⁎⁎	−0.02
	(0.02)	(0.03)	(0.01)	(0.01)	(0.02)	(0.01)
Lagged Dependent Variable	−0.35⁎⁎⁎	−0.40⁎⁎⁎	−0.24⁎⁎⁎	−0.37⁎⁎⁎	−0.44⁎⁎⁎	−0.25⁎⁎⁎
	(0.03)	(0.04)	(0.06)	(0.03)	(0.03)	(0.05)
R2	0.72	0.77	0.25	0.71	0.75	0.23
Time and country FE?	Y	Y	Y	Y	Y	Y
Num. obs.	692	358	334	692	358	334

Note: This table uses data from CEIC, Ritchie et al. (2020), Dong et al. (2020), and Hale et al. (2021). We replace the quarterly change in average daily deaths with the change in the inverse hyperbolic sine of quarterly deaths per 100,000 people, as suggested by Goolsbee and Syverson (2021). Time and country fixed effects are used in the second stage. Robust standard errors (in parentheses) are clustered at the country level.

^⁎p < 0.10;.

^⁎⁎p < 0.05;.

^⁎⁎⁎p < 0.01.

Appendix Table 3.

Covariate Lags – Domestic Variables Only.

	OLS			2SEC
	2020–21	2020	2021	2020–2021	2020	2021
	(1)	(2)	(3)	(4)	(5)	(6)
(Intercept)	0.63*	1.94⁎⁎⁎	2.31⁎⁎⁎	0.31	0.41	2.20⁎⁎⁎
	(0.33)	(0.59)	(0.31)	(0.25)	(0.26)	(0.27)
Δ Daily Deaths per 100K	−0.64	−0.84	−0.70	−0.98	−5.37⁎⁎	0.42
	(0.54)	(1.90)	(0.75)	(0.88)	(2.05)	(0.95)
Δ Quarterly OSI	−0.07⁎⁎⁎	−0.11⁎⁎⁎	−0.02	−0.08⁎⁎⁎	−0.11⁎⁎⁎	−0.02
	(0.02)	(0.03)	(0.02)	(0.02)	(0.03)	(0.01)
Lagged Dependent Variable	−0.35⁎⁎⁎	−0.39⁎⁎⁎	−0.25⁎⁎⁎	−0.34⁎⁎⁎	−0.41⁎⁎⁎	−0.24⁎⁎⁎
	(0.03)	(0.05)	(0.05)	(0.04)	(0.05)	(0.05)
Lag of Δ Daily Deaths per 100K	0.64	5.57*	−0.27	1.76*	2.80	0.90
	(0.75)	(3.08)	(0.75)	(1.00)	(3.25)	(0.83)
Lag of Δ Quarterly OSI	−0.01	−0.02	−0.00	−0.00	−0.02	−0.00
	(0.01)	(0.03)	(0.01)	(0.01)	(0.03)	(0.01)
R2	0.72	0.78	0.25	0.72	0.79	0.24
Time and country FE?	Y	Y	Y	Y	Y	Y
Num. obs.	692	358	334	692	358	334

Note: This table uses data from CEIC, Ritchie et al. (2020), Dong et al. (2020), and Hale et al. (2021). Columns 4 through 6 apply a two-stage process. In a first stage, deaths and OSI are separately regressed on cases. In the second stage, the residuals from these regressions are substituted for deaths and OSI in the regressions for GDP growth; the first lag of the residuals are used in Columns 4 through 6. Time and country fixed effects are used throughout. Robust standard errors (in parentheses) are clustered at the country level.

^⁎p < 0.10;.

^⁎⁎p < 0.05;.

^⁎⁎⁎p < 0.01.

Appendix Table 4.

Quarter-on-quarter Real GDP Growth – Domestic 2SLS with Alternative Simultaneity Correction.

	Our 2SEC			2SLS w/ First-Month Changes as Instruments
	2020–2021	2020	2021	2020–2021	2020	2021
	(4)	(5)	(6)	(4)	(5)	(6)
(Intercept)	0.29	0.39	2.30⁎⁎⁎	1.09	2.38	2.21⁎⁎
	(0.25)	(0.26)	(0.27)	(1.23)	(2.05)	(0.88)
Δ Daily Deaths per 100K	−1.57*	−6.09⁎⁎⁎	0.05	−0.97	−3.20*	−0.84⁎⁎
	(0.83)	(2.06)	(0.70)	(0.66)	(1.64)	(0.41)
Δ Quarterly OSI	−0.07⁎⁎⁎	−0.11⁎⁎⁎	−0.02	−0.10⁎⁎⁎	−0.13⁎⁎⁎	−0.01
	(0.02)	(0.03)	(0.01)	(0.01)	(0.02)	(0.01)
Lagged Dependent Variable	−0.35⁎⁎⁎	−0.42⁎⁎⁎	−0.25⁎⁎⁎	−0.34⁎⁎⁎	−0.40⁎⁎⁎	−0.24⁎⁎⁎
	(0.03)	(0.04)	(0.05)	(0.03)	(0.05)	(0.05)
R2	0.72	0.78	0.23	0.72	0.77	0.25
Time and country FE?	Y	Y	Y	Y	Y	Y
First-stage F-statistic	364.95⁎⁎⁎; 30,072.58⁎⁎⁎	167.22⁎⁎⁎; 99,999.00⁎⁎⁎	183.14⁎⁎⁎; 2925.20⁎⁎⁎	321.16⁎⁎⁎	101.67⁎⁎⁎	158.42⁎⁎⁎
Num. obs.	692	358	334	692	358	334

Note: This table uses data from CEIC, Ritchie et al. (2020), Dong et al. (2020), and Hale et al. (2021). Columns 1 through 3 apply our preferred two-stage process as shown in Table 1. In a first stage, deaths and OSI are separately regressed on cases. In the second stage, the residuals from these regressions are substituted for deaths and OSI in the regressions for GDP growth. Time and country fixed effects are used in the second stage. First-stage F-statistics for Columns 1 through 3 show the F-stat for regressions of actual changes in deaths and OSI on residuals from our first-stage process. Since variation in cases only explains 1 percent of variation in OSI, F-statistics for OSI residuals are mechanically large. Columns 4 through 6 employ an alternative simultaneity correction. In the first stage, the quarterly change in OSI and deaths are regressed on the change in OSI and deaths from the last month of the previous quarter to the first month of the current quarter (plus the lagged dependent variable, country FE, and time FE). The predicted values are used in the second stage shown. True first stage F-statistics are reported for Columns 4 through 6. Robust standard errors (in parentheses) are clustered at the country level.

^⁎p < 0.10;.

^⁎⁎p < 0.05;.

^⁎⁎⁎p < 0.01.

Appendix Table 5.

Alternative Specification of Trade Variable.

	2SEC
	2020 – 2021	2020	2021
	(4)	(5)	(6)
(Intercept)	0.19	0.32	2.30⁎⁎⁎
	(0.27)	(0.29)	(0.27)
Δ Daily Deaths per 100K	−1.66⁎⁎	−6.30⁎⁎⁎	0.05
	(0.83)	(2.04)	(0.70)
Δ OSI	−0.07⁎⁎⁎	−0.10⁎⁎⁎	−0.02
	(0.01)	(0.03)	(0.01)
Lagged Dependent Variable	−0.35⁎⁎⁎	−0.41⁎⁎⁎	−0.25⁎⁎⁎
	(0.03)	(0.05)	(0.05)
% Δ Real World Imports * Export Share	−1.09	−0.93	−0.30
	(1.41)	(1.12)	(2.56)
R2	0.72	0.78	0.23
Time and country FE?	Y	Y	Y
Num. obs.	692	358	334

Note: This table uses data from CEIC, Ritchie et al. (2020), Dong et al. (2020), Hale et al. (2021), and IFS (2022a,b). All regressions apply a two-stage process. In a first stage, deaths and OSI are separately regressed on cases. In the second stage, the residuals from these regressions are substituted for deaths and OSI in the regressions for GDP growth. Robust standard errors (in parentheses) are clustered at the country level.

^⁎p < 0.10;.

^⁎⁎p < 0.05;.

^⁎⁎⁎p < 0.01.

Data availability

• Data will be made available on request.